Abstract
Plaque rupture may be triggered by extreme stress/strain conditions. Inflammation is also implicated and can be imaged using novel imaging techniques. The impact of cap inflammation on plaque stress/strain and flow shear stress were investigated. A patient-specific MRI-PET/CT-based modeling approach was used to develop 3D fluid-structure interaction models and investigate the impact of inflammation on plaque stress/strain conditions for better plaque assessment. 18FDG-PET/CT and MRI data were acquired from 4 male patients (average age: 66) to assess plaque characteristics and inflammation. Material stiffness for the fibrous cap was adjusted lower to reflect cap weakening causing by inflammation. Setting stiffness ratio (SR) to be 1.0 (fibrous tissue) for baseline, results for SR=0.5, 0.25, and 0.1 were obtained. Thin cap and hypertension were also considered. Combining results from the 4 patients, mean cap stress from 729 cap nodes was lowered by 25.2% as SR went from 1.0 to 0.1. Mean cap strain value for SR=0.1 was 0.313, 114% higher than that from SR=1.0 model. The thin cap SR=0.1 model had 40% mean cap stress decrease and 81% cap strain increase compared with SR=1.0 model. The hypertension SR=0.1 model had 19.5% cap stress decrease and 98.6% cap strain increase compared with SR=1.0 model. Differences of flow shear stress with 4 different SR values were limited (<10%). Cap inflammation may lead to large cap strain conditions when combined with thin cap and hypertension. Inflammation also led to lower cap stress. This shows the influence of inflammation on stress/strain calculations which are closely related to plaque assessment.
Keywords: Vulnerable plaque, plaque rupture, inflammation, arteriosclerosis, stress
1. Introduction
Extreme mechanical stress and strain conditions have been identified as potential risk factors for plaque rupture, among other risk factors (Bluestein et al., 2008; Friedman et al., 2010; Samady et al., 2011; Tang et al., 2009, 2014; Vengrenyuk et al., 2006). Considerable progress has been made in recent years in medical imaging (Tarkin et al., 2016; Vesey et al., 2016; Underhill et al., 2010; Huibers et al., 2015) and image-based computational modeling (Bluestein et al., 2008; Friedman et al., 2010; Samady et al., 2011; Tang et al., 2004, 2005a, 2005b, 2009, 2014; Stone et al., 2012; Vengrenyuk et al., 2006) for better understanding of plaque progression and rupture. Tang et al. (2014) provided a recent review for plaque biomechanical analysis, covering essential topics including plaque components, tissue, modeling, and limitations and challenges the current technologies are facing. Fleg et al. (2012) gave an authoritative review of findings from several large clinical studies for detection of high-risk atherosclerotic plaques, available techniques, findings from patient follow-up studies, and future recommendations.
While it is believed that inflammation weakens plaque cap and may have considerable impact on cap stress and strain conditions, no single image modality is able to provide vessel geometry, plaque components and inflammation at the same time. Fayad et al. (2011) and others have been developing multi-modality imaging technology using PET/CT (Positron Emission Tomography/ Computed Tomography) and MRI (magnetic resonance imaging) to identify inflammation in arteries (Tarkin et al., 2016; Vesey et al., 2016; Huibers et al., 2015; Fayad et al., 2011; Calcagno et al., 2013). Combining PET/CT with MRI, we are able to obtain plaque morphology with inflammation information on cap surface. This gives us the base for better modeling stress/strain predictions.
The goal of this paper is to investigate the possible impact of cap inflammation on plaque stress/strain and flow shear stress conditions, with plaque and inflammation data provided by PET/CT combined with MRI. A total of 52 models based on data obtained in 4 patients were used to investigate the impact of inflammation combined with thin cap thickness, plaque components and high blood pressure on plaque stress and strain and flow shear stress conditions. It should be noted that this is not a causality study. In particular, it is commonly believed that flow shear stress may be a factor causing inflammation, not vice versa.
2. Method: Data acquisition and Modeling Process
2.1. MRI and PET/CT data acquisition
Data from 4 patients with identified carotid atherosclerotic plaques (m, mean age 66, 2 from Mount Sinai Hospital, 2 from Washington University, St Louis) were acquired with informed consent obtained respectively. The data under consideration were acquired as part of clinical trial imaging patients to assess arterial inflammation within the bilateral carotid arteries and ascending aorta. Patients with coronary heart disease were imaged with MRI and 18F-fluorodeoxyglucose (18F-FDG) PET/CT in separate imaging sessions approximately 12 days apart.
Image Acquisition: For the MRI examination the patients were imaged in a head-first supine position. 2-D multi-contrast (T2-weighted, T1-weighted and proton-density weighted) dark-blood turbo spin-echo images of the bilateral carotids were acquired as part of a longer imaging study. The imaging parameters for all three contrast-weightings were as follows: field of view 140mm × 140mm, in-plane spatial resolution 0.55×0.55mm, 14–16 slices, and slice thickness 3 mm with interslice gap 0.3 mm. Figure 1 provided the MRI slices, segmented contour plots and the 3D re-constructed vessel geometry of Patient 1 showing the locations of a lipid pool and small calcification. Details of the 3D geometry re-constructed procedures can be found in Yang et al. (2009). The PET/CT was performed after the patient had fasted overnight, and 120 min after injection of 15mCi of 18F-FDG. A low-dose, non-contrast-enhanced CT scan was used for attenuation correction and anatomical information for the PET scan. The carotid arteries were imaged with a 15 min PET scan of one bed position in 3D mode.
Figure 1.
MRI, contour plots and re-constructed 3D geometry of a carotid plaque. Ca: calcification.
Image Analysis: The MR images were analyzed by an expert image analyst using the VesselMASS software (Medis Medical Imaging Systems, Leiden University, Netherlands). The outer vessel wall and the lumen wall for each axial slice of the carotid artery were manually traced and the contours saved in the VesselMASS software. The PET/CT images were anatomically matched to the MRI data in OsiriX imaging software (Pixmeo, Geneva, Switzerland). The 18F-FDG uptake in the carotid arteries was measured by placing a circular region-of-interest (ROI) on the co-registered PET/CT axial images so that the ROI included the entire vessel wall. The mean and maximum standard uptake values (SUV), adjusted for body weight and injected 18F-FDG dose, were determined in each ROI. Additional ROIs drawn in the jugular vein were used to correct for background 18F-FDG uptake, and generate the target to background ratio (TBR). Figure 2 shows PET/CT of slices S4–S8 from Patient 1 and enlarged view of S4 with matching MRI slice.
Figure 2.
18F-FDG PET and CT images from S4-S8 with lipid-rich necrotic core and enlarged view of PET on CT for Slice 4 registered with MRI showing Region of Interest (ROI) with 18F-FDG uptake suggestive of inflammation.
2.2 MRI-PET/CT-based modeling with fluid-structure interaction
An MRI-PET/CT-based modeling approach is proposed to develop fluid-structure interaction (FSI) models for human carotid plaque assessment and investigate the effect of inflammation on plaque stress/strain conditions. Blood flow was assumed to be laminar, Newtonian, viscous and incompressible. Inlet and outlet were fixed (after initial pre-stretch) in the longitudinal (axial) direction, but allowed to expand/contract with flow otherwise. Patient-specific arm pressure conditions were used as the imposed pressure conditions (see Fig. 3 (a)). The 3D FSI model was built following established procedures (Tang et al., 2004, 2009). The 3D FSI model is given below:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
where u and p are fluid velocity and pressure, ug is mesh velocity, Γ stands for vessel lumen surface, f•, j stands for derivative with respect to the jth variable, σ and ε are stress and strain tensors, v is solid displacement vector. Material densities for fluid, vessel and plaque components are assumed to be the same for simplicity.
Figure 3.
Imposed pressure condition and material stress-stretch plots. Cap material curves with 4 SR values are shown.
The artery wall was assumed to be hyperelastic, isotropic, incompressible and homogeneous. The nonlinear modified Mooney-Rivlin model was used to describe the material properties of the vessel wall (Tang et al., 2004, 2005b, 2009). The strain energy function was given by,
| (8) |
| (9) |
where I1 and I2 are the first and second strain invariants, C =[Cij] = XTX is the right Cauchy-Green deformation tensor, ci and Di are material parameters chosen to match experimental measurements and the current literature (Humphrey 2002; Holzapfel et al., 2004). Parameter values used in this paper were: vessel/fibrous cap, c1=36.8 kPa, D1=14.4 kPa, D2=2; calcification, c1=368 kPa, D1=144 kPa, D2=2.0; lipid-rich necrotic core, c1=2 kPa, D1=2kPa, D2=1.5; c2 = 0 was set for all materials (Tang et al., 2009).
For the 15-slice MRI/PET/CT data set acquired from the above procedures, inflammation was identified for S4–S10 for Patient 1 (see Figures 1 & 2) and selected slices with lipid-rich pools for other patients. Material stiffness for the fibrous cap was adjusted lower to reflect the cap weakening caused by cap inflammation. Setting stiffness ratio (SR) to be 1.0 for the baseline model, coefficients c1 and D1 in Equation (8) were multiplied by SR=0.5, 0.25, and 0.1 to make the cap softer. D2 was kept unchanged for simplicity. Figure 3 gives the material stress-stretch plots of calcification, lipid core, and the curves for the 4 SR ratios, with SR=1.0 corresponding to normal vessel tissue material properties. Figure 4 shows a plaque sample with inflammation on the lumen surface. It is showing macrophage infiltrations in the fibrous cap. The increased density of macrophages has been shown to reduce the material strength in fibrous cap in aortic atherosclerotic lesions, through release of matrix metalloproteinases (Lendon et al., 1991).
Figure 4.
A plaque sample showing inflammation.
The baseline model was modified to create thin-cap models, calcification models (Ca Model) and a high blood pressure (HP) models. This is a test-of-the-concept approach to observe the impact of inflammation with those complications and seek motivations and justifications for further effort in quantifying inflammation and its link to mechanical factors. The mean cap thickness for S4-S8 of Patient 1 were changed from 0.114, 0.092, 0.083, 0.076 and 0.064 (unit: cm) to 0.073, 0.058, 0.052, 0.046 and 0.064 (cm) by moving the lipid core closer to the lumen in each model, respectively. The average reduction rate for the cap thickness of S4-S7 was 30%. The calcification models were obtained by assigning the calcification material properties to the lipid core geometry so it became calcification in our model. Maximum pressure for the pressure profile was set to 165 mmHg (50% higher than 110 mmHg) to make high blood pressure simulations. The stiffness ratio was set to SR=1.0, 0.5, 0.25 and 0.1 to observe its impact on stress/strain calculations. Results from these models were compared to investigate the combined effects of inflammation with thin cap thickness, plaque components and high blood pressure on plaque mechanical conditions.
2.3 Solution methods
For each patient, we made 4 models with baseline geometry and pressure condition and SR=1.0, 0.5, 0.25, and 0.1, 4 thin cap models with 4 SR values, and 4 hypertension models with 4 SR values. For Patient 1, we also made 4 Ca models with 4 SR values. A total of 52 models were made. The pre-shrink process and component-fitting mesh generation technique were used in our model construction and mesh generation process (Huang et al., 2009; Yang et al., 2009). All the 3D FSI models were solved by a commercial finite element package ADINA (ADINA R & D, Watertown, MA, USA), using unstructured finite element methods for both fluid and solid domains. More details of the computational models and solution methods can be found in Tang et al. (2005, 2009). Plaque cap stress, strain and flow shear stress data from all 4 cap stiffness variations corresponding to peak systolic pressure were recorded for analysis.
3. Results
Results from Patient 1 were used to show the details of stress/strain behaviors slice by slice. Figures 5 & 6 gave stress, strain and flow shear stress plots on the lumen surface of the vessel (with vessel set to be transparent) from the 4 models, showing their local maximum values on the cap nodes for comparison. Figure 7 presented stress and strain cross-section plots on 5 slices with the lipid core showing more details of stress/strain distributions. Tables 1 and 2 summarized local maximum stress/strain values on 7 slices from Patient 1 with caps covering plaque components for easy comparison. Overall mean stress and strain comparisons from the 4 patients were given by Table 3.
Figure 5.
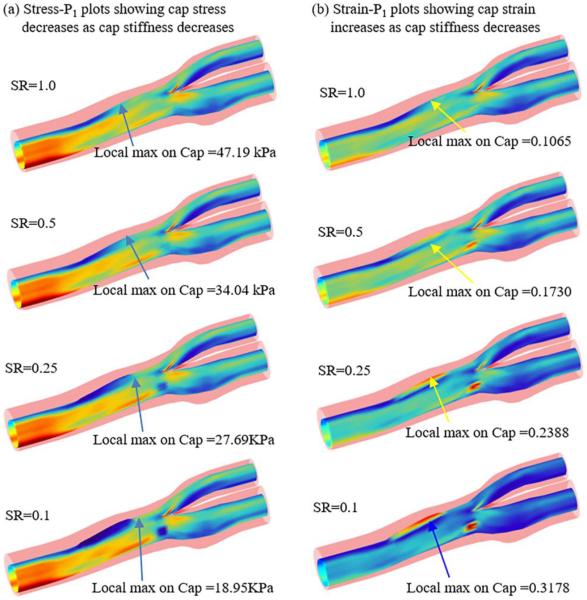
Stress and strain plots from 4 models with baseline geometry and pressure conditions showing weakening cap materials led to decreased cap stress and increased cap strain.
Figure 6.

Flow shear stress plots from 2 models (SR=1.0, SR=0.1) with baseline geometry and pressure conditions showing FSS has small differences in models with different inflammation material stiffness.
Figure 7.
Stress-P1 and Strain-P1 cross-section plots from 2 models showing weakening cap materials led to plaque cap stress decrease and strain increase with slice by slice detailed variations (S5–S8).
Table 1.
Inflammation leads to plaque cap stress decrease and large cap strain increase.
| Max PC-Stress (kPa) | |||||
| Tissue Type | Slice # | SR=1 | SR=0.5 | SR=.25 | SR=.10 |
| lipid | 4 | 50.32 | 51.07 | 52.82 | 55.36 |
| lipid | 5 | 62.99 | 47.07 | 34.89 | 19.55 |
| lipid | 6 | 62.79 | 45.88 | 32.97 | 17.22 |
| lipid | 7 | 55.96 | 44.90 | 33.26 | 18.08 |
| lipid | 8 | 56.35 | 47.65 | 46.39 | 47.04 |
| Ca | 9 | 58.18 | 53.01 | 51.53 | 53.28 |
| Ca | 10 | 48.30 | 48.77 | 51.07 | 54.76 |
| Max PC-Strain | |||||
| lipid | 4 | 0.123 | 0.159 | 0.203 | 0.253 |
| lipid | 5 | 0.144 | 0.223 | 0.307 | 0.409 |
| lipid | 6 | 0.139 | 0.226 | 0.321 | 0.437 |
| lipid | 7 | 0.127 | 0.203 | 0.288 | 0.389 |
| lipid | 8 | 0.132 | 0.147 | 0.173 | 0.218 |
| Ca | 9 | 0.149 | 0.186 | 0.221 | 0.258 |
| Ca | 10 | 0.129 | 0.149 | 0.168 | 0.187 |
| Mean PC-FSS (dyn/cm2) | |||||
| lipid | 4 | 26.11 | 25.95 | 26.02 | 26.34 |
| lipid | 5 | 20.48 | 19.06 | 17.66 | 16.32 |
| lipid | 6 | 17.53 | 16.30 | 15.11 | 13.99 |
| lipid | 7 | 14.97 | 13.90 | 12.90 | 11.94 |
| lipid | 8 | 15.53 | 15.85 | 16.35 | 17.04 |
| Ca | 9 | 19.29 | 19.47 | 19.68 | 19.91 |
| Ca | 10 | 20.76 | 20.81 | 20.96 | 21.07 |
Table 2.
Combined effects of cap inflammation with cap thickness, component and high blood pressure on plaque stress and strain variations.
| Thinner Cap | |||||||||
| Tissue Type | Slice # | Max PC-Stress (kPa) | Max PC-Strain | ||||||
| SR=1 | SR=.5 | SR=.25 | SR=.10 | SR=1 | SR=0.5 | SR=.25 | SR=.10 | ||
| lipid | 4 | 58.57 | 55.79 | 55.41 | 55.79 | 0.134 | 0.170 | 0.204 | 0.241 |
| lipid | 5 | 87.04 | 59.50 | 36.48 | 15.13 | 0.183 | 0.238 | 0.287 | 0.332 |
| lipid | 6 | 85.80 | 57.64 | 31.43 | 15.37 | 0.179 | 0.247 | 0.305 | 0.368 |
| lipid | 7 | 74.36 | 48.22 | 29.12 | 15.98 | 0.149 | 0.208 | 0.268 | 0.340 |
| lipid | 8 | 52.29 | 44.74 | 43.82 | 43.46 | 0.123 | 0.140 | 0.167 | 0.202 |
| Ca | 9 | 58.50 | 53.24 | 51.59 | 53.29 | 0.149 | 0.187 | 0.221 | 0.258 |
| Ca | 10 | 48.37 | 48.82 | 51.10 | 54.79 | 0.129 | 0.149 | 0.168 | 0.187 |
| Lipid Replaced by Calcification | |||||||||
| Tissue Type | Slice # | Max PC-Stress (kPa) | Max PC-Strain | ||||||
| SR=1 | SR=.5 | SR=.25 | SR=.10 | SR=1 | SR=0.5 | SR=.25 | SR=.10 | ||
| lipid | 4 | 38.41 | 36.09 | 34.70 | 35.16 | 0.101 | 0.117 | 0.135 | 0.155 |
| lipid | 5 | 40.23 | 41.46 | 43.84 | 47.97 | 0.098 | 0.112 | 0.136 | 0.166 |
| lipid | 6 | 37.79 | 40.51 | 44.27 | 50.13 | 0.085 | 0.111 | 0.138 | 0.186 |
| lipid | 7 | 35.93 | 38.68 | 42.90 | 49.41 | 0.090 | 0.110 | 0.139 | 0.174 |
| lipid | 8 | 46.72 | 42.22 | 44.66 | 47.95 | 0.112 | 0.112 | 0.118 | 0.128 |
| Ca | 9 | 57.62 | 51.98 | 50.64 | 52.43 | 0.147 | 0.183 | 0.217 | 0.252 |
| Ca | 10 | 48.45 | 48.89 | 51.01 | 54.66 | 0.129 | 0.149 | 0.168 | 0.187 |
| High Blood Pressure | |||||||||
| Tissue Type | Slice # | Max PC-Stress (kPa) | Max PC-Strain | ||||||
| SR=1 | SR=.5 | SR=.25 | SR=.10 | SR=1 | SR=0.5 | SR=.25 | SR=.10 | ||
| lipid | 4 | 78.86 | 79.55 | 81.53 | 84.66 | 0.197 | 0.248 | 0.307 | 0.373 |
| lipid | 5 | 100.08 | 79.47 | 61.20 | 37.95 | 0.228 | 0.344 | 0.460 | 0.599 |
| lipid | 6 | 103.11 | 81.36 | 63.96 | 42.98 | 0.228 | 0.358 | 0.491 | 0.652 |
| lipid | 7 | 93.09 | 77.53 | 64.01 | 44.23 | 0.204 | 0.317 | 0.439 | 0.584 |
| lipid | 8 | 88.36 | 78.28 | 75.76 | 75.69 | 0.207 | 0.235 | 0.276 | 0.335 |
| Ca | 9 | 91.65 | 84.25 | 81.69 | 82.60 | 0.234 | 0.286 | 0.334 | 0.381 |
| Ca | 10 | 75.56 | 76.10 | 82.02 | 87.70 | 0.201 | 0.230 | 0.258 | 0.284 |
Table 3.
Average cap stress and strain from 4 patients: baseline, thinner cap and high blood pressure with stiffness variations.
| Baseline: Data from MRI/CT/PET | |||||||||
| Patient | Cap Nodes # | Mean Cap Stress (kPa) | Mean Cap Strain | ||||||
| SR=1 | SR=.5 | SR=.25 | SR=.10 | SR=1 | SR=0.5 | SR=.25 | SR=.10 | ||
| P1 | 189 | 56.41 | 48.33 | 43.28 | 37.90 | 0.135 | 0.185 | 0.240 | 0.307 |
| P2 | 108 | 65.32 | 56.03 | 51.45 | 46.62 | 0.191 | 0.263 | 0.334 | 0.404 |
| P3 | 324 | 36.60 | 31.39 | 27.69 | 24.55 | 0.105 | 0.132 | 0.177 | 0.273 |
| P4 | 108 | 67.68 | 63.51 | 61.36 | 60.05 | 0.175 | 0.204 | 0.233 | 0.269 |
| All | 729 | 56.50 | 49.81 | 45.94 | 42.28 | 0.151 | 0.196 | 0.246 | 0.313 |
| Thinner Cap | |||||||||
| Patient | Cap Nodes # | Mean Cap Stress (kPa) | Mean Cap Strain | ||||||
| SR=1 | SR=.5 | SR=.25 | SR=.10 | SR=1 | SR=0.5 | SR=.25 | SR=.10 | ||
| P1 | 189 | 66.42 | 52.57 | 42.71 | 36.26 | 0.149 | 0.191 | 0.231 | 0.275 |
| P2 | 108 | 87.05 | 66.57 | 52.98 | 43.07 | 0.222 | 0.288 | 0.344 | 0.395 |
| P3 | 324 | 43.81 | 35.81 | 29.85 | 25.17 | 0.115 | 0.146 | 0.193 | 0.276 |
| P4 | 108 | 74.07 | 67.23 | 63.33 | 59.58 | 0.184 | 0.208 | 0.236 | 0.269 |
| All | 729 | 67.84 | 55.54 | 47.22 | 41.02 | 0.168 | 0.208 | 0.251 | 0.304 |
| High Blood Pressure | |||||||||
| Patient | Cap Nodes # | Mean Cap Stress (kPa) | Mean Cap Strain | ||||||
| SR=1 | SR=.5 | SR=.25 | SR=.10 | SR=1 | SR=0.5 | SR=.25 | SR=.10 | ||
| P1 | 189 | 90.10 | 79.51 | 72.88 | 65.12 | 0.214 | 0.288 | 0.366 | 0.458 |
| P2 | 108 | 107.3 | 93.14 | 86.74 | 82.69 | 0.290 | 0.387 | 0.473 | 0.560 |
| P3 | 324 | 48.47 | 43.47 | 40.34 | 37.00 | 0.140 | 0.187 | 0.261 | 0.399 |
| P4 | 108 | 105.9 | 102.2 | 100.35 | 98.64 | 0.266 | 0.309 | 0.349 | 0.393 |
| All | 729 | 87.96 | 79.56 | 75.08 | 70.86 | 0.228 | 0.293 | 0.362 | 0.453 |
3.1. Cap inflammation leads to lower cap stress values
Since plaque rupture is of local nature and may occur where cap stress has a local maximum (regardless if it was greater or smaller than overall maximum plaque stress), local maximum cap stress values from different models were compared. Figure 5 (a) shows that the local maximum cap stress value without inflammation (SR=1.0) was 47.19 kPa. Corresponding to SR=0.5, 0.25, and 0.1, the local maximum cap stress values were 34.04, 27.69, and 18.95 kPa, respectively. The local maximum cap stress value reduced 60% from SR=1.0 to SR=0.1. Looking at S6 from Fig. 7, the local maximum cap stress value reduced from 62.79 kPa (SR=1.0 case) to 17.22 kPa (SR=0.1), a 72% decrease. On the other hand, local maximum stress values on S4 and S8 were much limited (<20%). Table 1 shows for caps covering the calcification, maximum cap stress variations were even more limited (<10%).
3.2 Cap inflammation leads to higher cap strain values
When the cap becomes softer, cap strain would increase under the same pressure conditions. Compared to the stress decrease observed in 3.1, cap strain variations caused by inflammation were much greater. Figure 5 (b) shows that the local maximum cap strain value without inflammation (SR=1.0) was 0.1065. Corresponding to SR=0.5, 0.25, and 0.1, the local maximum cap strain values were 0.1730, 0.2388 and 0.3178, which was 62.4%, 124%, and 195% higher than that of SR=1.0, respectively. Looking at S6 from Fig. 7, the local maximum cap strain value increased from 0.1392 with SR=1.0 to 0.4372 with SR=0.1, a 214% increase. Strain values on S4 and S8 increased less from SR=1.0 to SR=0.1. But the increases were still around 100%.
3.3 Differences of flow shear stress with different SR values were small
Flow shear stress has been a focus of research for plaque progression. Figure 6 shows that flow shear stress (FSS) on a sagittal cut had an 8% increase from SR=1.0 model to SR=0.1 to model. Table 1 shows FSS mean values on the cap changed from slice to slice, indication of flow pattern changes. All FSS values stayed in a narrow range within their SR=1.0 values.
3.4 Impact of cap thickness combined with inflammation
Cap thickness is a major risk factor and has great impact on cap stress and strain. It is of interest to observe the combined impact of cap thinning and inflammation. Figure 8 (a)–(b) gave stress and strain plots from the thin cap models where cap thicknesses on S4-S7 were reduced by 30%. More stress and strain values were given in Table 2. First of all, local maximum plaque cap stresses and strains from the thin cap model were in general higher than those from the corresponding baseline models. For SR=1.0, thin cap local maximum cap stress and strain were 85.80 kPa and 0.183, about 82% and 72% higher than that from the baseline model. Looking at the thin-cap models, local maximum cap stress from the model with SR=0.1 was 55.79 kPa, a 35% decrease from 85.80 kPa, the value for the SR=1.0 model. Local maximum cap strain from the model with SR=0.1 was 0.305, a 67% increase from 0.183, the value for the SR=1.0 model. So thin cap thickness led to greater absolute cap stress and strain values, but smaller relative stress decrese and strain increase, when combined with inflammation.
Figure 8.
Strain-P1 plots from thin cap, calcification and hypertension models with SR=1.0 and 0.1 showing impact of cap thickness, plaque components and hypertension on cap stress and strain conditions.
3.5 Impact of plaque components combined with inflammation
It is of interest to see the impact if inflammation was observed on cap over a calcification component. The calcification models were made by replacing the lipid core in the baseline model by calcification without changing its shape. Figure 8 (c)–(d) gave stress and strain plots from the calcification (Ca) models. It is easy to see (and understand) that changing cap material properties (this is how we define inflammation) had much less noticeable impact on cap stress and strain values. For SR=1.0, local maximum cap stress and strain from the Ca model were 57.62 kPa and 0.147, about 22% and 13.8% higher than that from the baseline model. Looking at the Ca models with different SR values, local maximum cap stress from the model with SR=0.1 was 52.43 kPa, a mere 9% decrease from the value for the SR=1.0 model. Local maximum cap strain from the model with SR=0.1 was 0.253, a 72% increase from 0.147, the value for the SR=1.0 model. So inflammation on cap covering calcification led to very modest cap stress decrease, but still considerable cap strain relative increase.
3.6 Impact of hypertension combined with inflammation
Hypertension is one of the major risk factor for cardiovascular diseases. The hypertension models were made by adjusting peak systolic blood pressure in the baseline model 50% higher to 165 mmHg. Figure 8 (e)–(f) gave stress and strain plots from the hypertension models. First of all, local maximum plaque cap stresses and strains from the hypertension model were considerably higher than those from the corresponding baseline models. For SR=1.0, local maximum cap stress and strain from the hypertension model were 103.11 kPa and 0.228, about 85% and 86% higher than that from the baseline model, respectively. Looking at the hypertension models with different SR values, local maximum cap stress from the model with SR=0.1 was 87.70 kPa, a mere 15% decrease from the value for the SR=1.0 model. However, local maximum cap strain from the SR=0.1 model was 0.652, a 186% increase from 0.228, the value for the SR=1.0 model. So cap inflammation combined with hypertension led to large cap strain increases.
3.7 Mean cap stress and strain comparisons using all 4 patient cap nodes combined
Comparing local maximum cap stress and strain from one patient leads to high uncertainty. Mean cap stress and strain values from all the cap nodes (729) from the 4 patients were obtained from all the models and compared. For the baseline models, mean cap stress from was lowered by 25.2% as SR went from 1.0 to 0.1. Mean cap strain value for SR=0.1 was 0.313, 114% higher than that from SR=1.0 model. The thin cap SR=0.1 model had 40% mean cap stress decrease and 81% cap strain increase compared with SR=1.0 model. The hypertension SR=0.1 model had 19.5% cap stress decrease and 98.6% cap strain increase compared with SR=1.0 model. Comparisons among baseline, thin cap and high pressure models could also be made to observe their differences.
4. Discussions
4.1. Significance of cap inflammation: huge impact on cap strain, reduced cap stress
Most investigations for atherosclerosis plaque rupture and vulnerability have been focused on flow shear stress and extreme cap stress conditions. Our findings in this paper indicate that inflammation may lead to lower cap stress and higher cap strain. That suggests our future effort should be focused more on cap strain conditions. Indeed, while stress is determined by both material stiffness and strain, strain is more an intrinsic condition of the plaque. Weakened plaque cap becomes softer and its lower stiffness reduces cap stress level. On the other hand, the increased strain may serve as a critical vulnerability indication. Needless to say, mechanical testing of plaque cap materials to find out its material strength would be a task for researchers in this field to provide threshold values to serve as base for model predictions.
4.2. Inflammation combined with thin cap and hypertension may lead to alarming critical cap strain conditions
It is clear from this sample that the impact of inflammation on stress/strain is heavily dependent on cap thickness, hypertension, the location and size of the plaque component, tissue type, and tissue material properties. In particular, results from 3.4 and 3.6 suggested that inflammation combined with thin cap and hypertension may lead to alarming cap strain conditions which may serve as a plaque rupture trigger and should be closely watched. This paper serves as a motivation to demonstrate the impact of inflammation on plaque mechanical conditions and the importance of further investigations.
4.3. Model assumptions, material properties and other limitations
This paper is mainly a conceptual study showing importance of including inflammation in modeling for stress/strain calculations. Patient-specific tissue material properties were not available. Sensitivity analysis of vessel and plaque component material properties (lipid and calcification) were performed in our earlier studies (Tang et al., 2005b). Since material stiffness of plaque cap with inflammation was not available, going from SR=1.0 (no inflammation), we took a bisection approach to reduce SR to 0.5, 0.25, and 0.1. The SR=0.1 case would be an extreme case when the cap is ready to give up. The rupture process involves cap thinning and weakening where inflammation is a major player. We are hoping this work could serve as motivation and justification for further investigations in those directions: imaging, mechanical testing, and modeling.
Acknowledgement
This work was supported in part by NIH grants NIH/NIBIB R01 EB004759, NIH/NHLBI R01 HL071021, and National Sciences Foundation of China grant 11672001, 11171030.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of Interest Statement
This is to state that there is no conflict of interest with any other individuals or government in the paper.
References
- Bluestein D, Alemu Y, Avrahami I, Gharib M, Dumont K, Ricotta JJ, Einav S. Influence of microcalcifications on vulnerable plaque mechanics using FSI modeling. Journal of Biomechanics. 2008;41(5):1111–1118. doi: 10.1016/j.jbiomech.2007.11.029. [DOI] [PubMed] [Google Scholar]
- Calcagno C, Ramachandran S, Izquierdo-Garcia D, Mani V, Millon A, Rosenbaum D, Tawakol A, Woodward M, Bucerius J, Moshier E, Godbold J, Kallend D, Farkouh ME, Fuster V, Rudd JH, Fayad ZA. The complementary roles of dynamic contrast-enhanced MRI and 18F-fluorodeoxyglucose PET/CT for imaging of carotid atherosclerosis. European Journal of Nuclear Medicine and Molecular Imaging. 2013;40(12):1884–93. doi: 10.1007/s00259-013-2518-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fayad ZA, Mani V, Woodward M, Kallend D, Bansilal S, Pozza J, Burgess T, Fuster V, Rudd JH, Tawakol A, Farkouh ME. Rationale and design of dal-PLAQUE: a study assessing efficacy and safety of dalcetrapib on progression or regression of atherosclerosis using magnetic resonance imaging and 18F-fluorodeoxyglucose positron emission tomography/computed tomography. American Heart Journal. 2011;162(2):214–221.e2. doi: 10.1016/j.ahj.2011.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleg JL, Stone GW, Fayad ZA, Granada JF, Hatsukami TS, Kolodgie FD, Ohayon J, Pettigrew R, Sabatine MS, Tearney GJ, Waxman S, Domanski MJ, Srinivas PR, Narula J. Detection of high-risk atherosclerotic plaque: report of the NHLBI working group on current status and future directions. JACC: Cardiovascular Imaging. 2012;5(9):941–55. doi: 10.1016/j.jcmg.2012.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman MH, Krams R, Chandran KB. Flow interactions with cells and tissues: cardiovascular flows and fluid-structure interactions. Annals of Biomedical Engineering. 2010;38(3):1178–1187. doi: 10.1007/s10439-010-9900-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holzapfel GA, Sommer G, Regitnig P. Anisotropic mechanical properties of tissue components in human atherosclerotic plaques. Journal of Biomechanical Engineering. 2004;126(5):657–665. doi: 10.1115/1.1800557. [DOI] [PubMed] [Google Scholar]
- Huang X, Yang C, Yuan C, Liu F, Canton G, Zheng J, Woodard PK, Sicard GA, Tang D. Patient-specific artery shrinkage and 3D zero-stress state in multi-component 3D FSI models for carotid atherosclerotic plaques based on in vivo MRI data. Molecular & cellular biomechanics. 2009;6(2):121–134. [PMC free article] [PubMed] [Google Scholar]
- Huibers A, de Borst GJ, Wan S, Kennedy F, Giannopoulos A, Moll FL, Richards T. Non-invasive Carotid Artery Imaging to Identify the Vulnerable Plaque: Current Status and Future Goals. European Journal of Vascular and Endovascular Surgery. 2015;50(5):563–72. doi: 10.1016/j.ejvs.2015.06.113. [DOI] [PubMed] [Google Scholar]
- Humphrey JD. Cardiovascular Solid Mechanics. Springer-Verlag; New York: 2002. [Google Scholar]
- Lendon CL, Davies MJ, Born GV, Richardson PD. Atherosclerotic plaque caps are locally weakened when macrophages density is increased. Atherosclerosis. 1991;87:87–90. doi: 10.1016/0021-9150(91)90235-u. [DOI] [PubMed] [Google Scholar]
- Samady H, Eshtehardi P, McDaniel MC, Suo J, Dhawan SS, Maynard C, Timmins LH, Quyyumi AA, Giddens DP. Coronary artery wall shear stress is associated with progression and transformation of atherosclerotic plaque and arterial remodeling in patients with coronary artery disease. Circulation. 2011;124(7):779–88. doi: 10.1161/CIRCULATIONAHA.111.021824. [DOI] [PubMed] [Google Scholar]
- Stone PH, Saito S, Takahashi S, Makita Y, Nakamura S, Kawasaki T, Takahashi A, Katsuki T, Nakamura S, Namiki A, Hirohata A, Matsumura T, Yamazaki S, Yokoi H, Tanaka S, Otsuji S, Yoshimachi F, Honye J, Harwood D, Reitman M, Coskun AU, Papafaklis MI, Feldman CL, PREDICTION Investigators Prediction of progression of coronary artery disease and clinical outcomes using vascular profiling of endothelial shear stress and arterial plaque characteristics: the PREDICTION Study. Circulation. 2012;126(2):172–81. doi: 10.1161/CIRCULATIONAHA.112.096438. [DOI] [PubMed] [Google Scholar]
- Tang D, Kamm RD, Yang C, Zheng J, Canton G, Bach R, Huang X, Hatsukami TS, Zhu J, Ma G, Maehara A, Mintz GS, Yuan C. Image-based modeling for better understanding and assessment of atherosclerotic plaque progression and vulnerability: data, modeling, validation, uncertainty and predictions. Journal of Biomechanics. 2014;47(4):834–46. doi: 10.1016/j.jbiomech.2014.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang D, Teng Z, Canton G, Yang C, Ferguson M, Huang X, Zheng J, Woodard PK, Yuan C. Sites of rupture in human atherosclerotic carotid plaques are associated with high structural stresses: an in vivo MRI-based 3D fluid-structure interaction study. Stroke. 2009;40(10):3258–3263. doi: 10.1161/STROKEAHA.109.558676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang D, Yang C, Zheng J, Woodard PK, Saffitz JE, Petruccelli JD, Sicard GA, Yuan C. Local maximal stress hypothesis and computational plaque vulnerability index for atherosclerotic plaque assessment. Annals of Biomedical Engineering. 2005a;33(12):1789–1801. doi: 10.1007/s10439-005-8267-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang D, Yang C, Zheng J, Woodard PK, Sicard GA, Saffitz JE, Yuan C. 3D MRI-based multi-component FSI models for atherosclerotic plaques, a 3-D FSI model. Annals of Biomedical Engineering. 2004;32(7):947–960. doi: 10.1023/b:abme.0000032457.10191.e0. [DOI] [PubMed] [Google Scholar]
- Tang D, Yang C, Zheng J, Woodard PK, Saffitz JE, Sicard GA, Pilgram TK, Yuan C. Quantifying Effects of Plaque Structure and Material Properties on Stress Behaviors in Human Atherosclerotic Plaques Using 3D FSI Models. Journal of Biomechanical Engineering. 2005b;127(7):1185–1194. doi: 10.1115/1.2073668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tarkin JM, Dweck MR, Evans NR, Takx RA, Brown AJ, Tawakol A, Fayad ZA, Rudd JH. Imaging Atherosclerosis. Circulation Research. 2016;118(4):750–69. doi: 10.1161/CIRCRESAHA.115.306247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Underhill HR, Hatsukami TS, Fayad ZA, Fuster V, Yuan C. MRI of carotid atherosclerosis: clinical implications and future directions. Nature Reviews Cardiology. 2010;7(3):165–173. doi: 10.1038/nrcardio.2009.246. [DOI] [PubMed] [Google Scholar]
- Vengrenyuk Y, Carlier S, Xanthos S, Cardoso L, Ganatos P, Virmani R, Einav S, Gilchrist L, Weinbaum S. A hypothesis for vulnerable plaque rupture due to stress-induced debonding around cellular microcalcifications in thin fibrous caps. In Proceedings of National Academy of Sciences of the United States of American. 2006;103(40):14678–14683. doi: 10.1073/pnas.0606310103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vesey AT, Dweck MR, Fayad ZA. Utility of Combining PET and MR Imaging of Carotid Plaque. Neuroimaging Clinics of North America. 2016;26(1):55–68. doi: 10.1016/j.nic.2015.09.005. [DOI] [PubMed] [Google Scholar]
- Yang C, Bach R, Zheng J, El Naqa I, Woodard PK, Teng ZZ, Billiar KL, Tang D. In vivo IVUS-based 3D fluid structure interaction models with cyclic bending and anisotropic vessel properties for human atherosclerotic coronary plaque mechanical analysis. IEEE Transactions on Biomedical Engineering. 2009;56(10):2420–2428. doi: 10.1109/TBME.2009.2025658. [DOI] [PMC free article] [PubMed] [Google Scholar]