A regularized full reference tissue model for PET neuroreceptor mapping

Abstract

The full reference tissue model (FRTM) is a PET analysis framework that includes both free and specifically bound compartments within tissues, together with rate constants defining association and dissociation from the specifically bound compartment. The simplified reference tissue model (SRTM) assumes instantaneous exchange between tissue compartments, and this “1-tissue” approximation reduces the number of parameters and enables more robust mapping of non-displaceable binding potentials. Simulations based upon FRTM have shown that SRTM exhibits biases that are spatially dependent, because biases depend upon binding potentials. In this work, we describe a regularized model (rFRTM) that employs a global estimate of the dissociation rate constant from the specifically bound compartment (k₄). The model provides an internal calibration for optimizing k₄ through the reference-region outflow rate k₂′, a model parameter that should be a global constant but varies regionally in SRTM. Estimates of k₄ by rFRTM are presented for four PET radioligands. We show that SRTM introduces bias in parameter estimates by assuming an infinite value for k₄, and that rFRTM ameliorates bias with an appropriate choice of k₄. Theoretical considerations and simulations demonstrate that rFRTM reduces bias in non-displaceable binding potentials. A two-parameter reduction of the model (rFRTM2) provides robust mapping at a voxel-wise level. With a structure similar to SRTM, the model is easily implemented and can be applied as a PET reference region analysis that reduces parameter bias without substantially altering parameter variance.

Introduction

Reference tissue models (RTMs) have been developed and employed in PET analyses for over two decades. Under the assumption that a reference region in the brain is devoid of specific binding of PET radioligand, RTMs enable calculation of non-displaceable binding potentials (BP_ND) in each brain voxel by comparing the tissue time-activity curve (TAC) to the reference region, which serves as a surrogate of the plasma TAC while also providing an index of non-specific binding (Gunn et al., 2001, Slifstein and Laruelle, 2001). This approach obviates arterial blood sampling by providing a surrogate for plasma radioligand concentrations.

Various RTM approaches have been developed in the literature to address the balance between parameter variance and parameter bias. A full reference tissue model (FRTM) fits four parameters for each TAC (Cunningham et al., 1991, Lammertsma et al., 1996), which may represent a relatively noiseless brain region of interest (ROI) or a much noisier image voxel. The sensitivity of FRTM to noise motivated the simplified reference tissue model (SRTM), which reduces the number of model parameters to three (Lammertsma and Hume, 1996, Gunn et al., 1997). However, even SRTM lacks robustness to noise at the voxel-wise level, and so a two-parameter variant (SRTM2 or MRTM2) often is employed that uses a global value for the washout time constant in the reference region (Wu and Carson, 2002, Ichise et al., 2003). SRTM and SRTM2 have become standard PET analysis strategies and form the foundation of several extended methods that modify basis functions to describe dynamic changes in binding due to within-session functional challenges (Alpert et al., 2003, Zhou et al., 2006, Normandin et al., 2012).

SRTM is predicated upon an assumption of instantaneous equilibration between the free and bound compartments in all tissues. While this assumption is never strictly accurate, the model produces excellent fits to experimental data for many radioligands. Analyses of simulated data that conform to FRTM have found that SRTM generally provides relatively accurate estimation of BP_ND, with errors typically below 10% for selected radioligands when fitting a full 90-minute TAC (Slifstein et al., 2000, Salinas et al., 2015), as commonly done when using a compound labeled by ¹¹C. Three-parameter variants of SRTM overestimate BP_ND in low-binding regions (Salinas et al., 2015) and exhibit a relatively high variance in the presence of noise (Wu and Carson, 2002). The model provides a separate estimate of the washout rate constant (k₂′) in the reference region for each voxel or ROI, which motivated a reduced model that provides regularization by fixing the value of k₂′ as a global parameter. However, many investigators have noted that different regions provide different values for this rate constant, and the method for defining a global value is not standardized; various reports have suggested using the value in a high binding region (Seneca et al., 2006), or the median or average across either the brain (Wu and Carson, 2002) or a series of ROIs (Ichise et al., 2003, Seo et al., 2015). In contrast to the three-parameter SRTM, the two-parameter variant generally underestimates BP_ND in low-binding regions (Schuitemaker et al., 2007), and bias in high-binding regions is smaller and depends upon a subjective choice for k₂′.

Though SRTM biases suggested by previous studies are not large for many radioligands, this level of accuracy is comparable with typical test-retest reproducibility (Cropley et al., 2008, Lee et al., 2013), suggesting that model error cannot be discounted as a source of variance even for studies of basal receptor concentrations. In occupancy studies that measure modulations of available receptors, model bias in BP_ND produces bias in estimates of occupancy. In displacement studies using either a drug or tasks that modulate neurotransmitter levels, a 10% error can be significant, because changes in true occupancy can be subtle when using behavioral tasks or low drug doses. Following administration of large agonist challenges, some PET radioligands exhibit little or no change in apparent occupancy, or even paradoxical increases in binding potential (Laruelle, 2000). Behavioral tasks that attempt to detect changes in dopamine efflux using [¹¹C]raclopride have reported positive or negative changes in BP_ND below 10% (Zald et al., 2004, Hakyemez et al., 2008, Martin-Soelch et al., 2011), a regime where model error can play a major role in drawing scientific inferences.

The goal of this work was to develop a reference tissue model that reduces parameter bias relative to SRTM without substantially altering parameter variance. Our search for an alternative model began with the observation that SRTM2 analyses of occupancies often exhibit a characteristic spatial pattern in the limit of low displacement, with apparent displacement in the highest binding regions and apparent paradoxical increases in BP_ND in surrounding low-binding regions. These patterns are most evident in multi-session averages or spatially smoothed data and suggest a source of bias in these studies that varies monotonically with BP_ND. To devise an alternative model to SRTM, we developed a basis-function approach to FRTM, and we regularize the model by employing a global estimate for the dissociation rate constant from the specifically bound compartment. SRTM is one solution to the model in the limit of infinite k₄, but this solution imparts a bias in the estimate of model parameters relative to FRTM. We describe a method to empirically estimate a global value of k₄ to minimize parameter bias, and we employ simulations to demonstrate that our method reduces bias in the estimation of BP_ND and receptor occupancies.

Methods

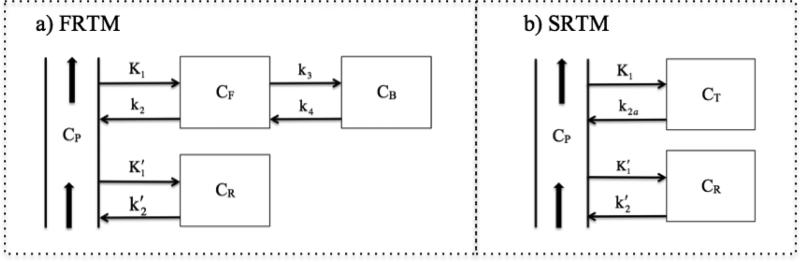
Fig. 1a shows FRTM and the reduction of the model to SRTM. Both models assume that the reference region exhibits one-compartment kinetics representing non-displaceable PET radioligand that is either free or non-specifically bound. FRTM models the target region as a compartmental summation of non-displaceable and specific binding (Gunn et al., 2001), whereas SRTM assumes “1-tissue” kinetics in the limit of fast exchange between free and bound compartments. Eq. A1 presents the differential equations describing FRTM.

Fig. 1.

The full reference tissue model (a) and simplified reference tissue model (b) use a single compartment to describe the concentration of PET radioligand in the reference region (C_R) so that the plasma concentration (C_P) is not needed in analysis. FRTM partitions other tissue concentrations into free (C_F) and specifically bound (C_B) fractions, whereas SRTM assumes fast exchange between these compartments and thus approximates all tissues using a single compartment model.

Regularized FRTM (rFRTM)

Eq. A6 provides an exact expression for FRTM in a form designed to mimic the basis-function approach to SRTM. To derive this formula, we replaced the SRTM approximation of instantaneous equilibrium with an expression (Eq. A3) relating the time dependence of the bound concentration to the total tissue concentration and its derivative. In this way, we model the true bound fraction in the tissue as a function of time. The FRTM model has four parameters, including two rate constants (k₂, k₄), a ratio of rate constants (R₁=k₂/k₂′), and a parameter that depends upon BP_ND (k_2a=k₂/(1+BP_ND). The model incorporates convolution by an exponential equilibration function E(t) = exp(–k₄(1 + BP_ND)t) to account for non-equilibrium conditions that are reflected by a change in the tissue concentration.

$$C_T=R_1{C}_R+k_2\int \left(C_R-{\stackrel{.}{C}}_T\otimes E\right)-k_{2a}\int \left(C_T-{\stackrel{.}{C}}_T\otimes E\right)$$ [1]

The solution to this equation previously has been approached two different ways. The literature approach to FRTM attempts to derive all four parameters for each voxel or ROI, a strategy that is limited by convergence problems, high parameter variance, and long computational times (Lammertsma et al., 1996, Slifstein and Laruelle, 2001). As an alternative to FRTM, SRTM employs the approximation that k₃ and k₄ approach infinity (equivalently, the time constants 1/k₃ and 1/k₄ approach zero) in order to reduce the number of parameters from four to three and produce an equation that is linear in all parameters. In this limit, the convolution terms vanish. This approach reduces parameter variance (Lammertsma and Hume, 1996) but introduces bias in parameter estimates by failing to accurately model the specifically bound fraction of the tissue radioligand concentration. Bias will be more pronounced for slower radioligands (smaller k₄) and for low-binding regions (smaller BP_ND), because the effective rate for equilibration to a steady state in Eq. 1 is k₄ (1+ BP_ND).

We propose a new approach (rFRTM) using a globally constant value of k₄ that is selected in order to minimize regional bias in k₂′. We show below that k₂′, which should take the same value irrespective of the tissue region under analysis, cannot be regionally invariant in SRTM when association and dissociation rates constants are finite. Within the context of FRTM, bias reduction in k₂′ is accompanied by bias reduction in BP_ND, which is the main parameter of interest.

Solution of rFRTM: Overview

Application of the proposed model requires two steps: 1) a method to solve Eq. 1 provided that the best global value for k₄ is known, and 2) a method to determine the best global value for k₄. Although these steps could be combined in principle by simultaneously fitting many voxels or regions of interest, we employed a procedure in which the model first was applied multiple times in a region-of-interest analysis using different values of global k₄ in each analysis, and subsequently the best value of k₄ was identified and used for a final analysis of all regions and voxels. The steps for solving Eq. 1 and identifying the best global k₄ are described in the following two sections.

Solution of rFRTM for individual TACs

Given an a priori estimate of the global value for k₄, Eq. 1 can be solved either by non-linear fitting or by an iterative approach that incorporates repeated application of a linear model; our approach used the latter method. To avoid using the relatively noisy convolution term in basis functions, our implementation rearranged Eq. 1 to add the convolution integral to the dependent variable.

$$C_T+\left(k_2^{(i-1)}-k_{2a}^{(i-1)}\right)\int {\stackrel{.}{C}}_T\otimes E^{(i-1)}=R_1^{\left(i\right)}{C}_R+k_2^{\left(i\right)}\int C_R-k_{2a}^{\left(i\right)}\int C_T$$ [2]

Specifically, we used the following steps to solve Eq. 2.

1. Create three basis functions with “n” time points for C_R, ∫ C_R, and ∫ C_T. These basis functions form a 3-by-n design matrix X. Using an n-by-n diagonal weighting function W to represent the time-changing magnitude of signal variance, compute the 3-by-n matrix M = (X^TW⁻¹X)⁻¹X^TW⁻¹ for use in all iterations. Initialize parameters by SRTM using the weighted least squares estimate β=M C_T, where the vector β = [R₁ k₂ k_2a].

2. Compute BP_ND = k₂ / k_2a – 1 using parameter estimates from the previous iteration. Compute the convolution of the tissue derivative with $E\left(t\right)=\exp (-k_4^{global}(1+B{P}_{ND})t)$ for each time point, where $k_4^{global}$ is a fixed value used for all iterations and all regions. Create a modified tissue vector (C_T′) equal to the left hand side of Eq. 2. Update parameter values as β=M C_T′.

3. Repeat step #2 until a stopping criterion is reached: 1) the change in BP_ND does not exceed some predefined tolerance, 2) the number of iterations exceeds some predefined limit, 3) or BP_ND is negative.

Intuitively, this formulation can be viewed as a model that estimates the tissue concentration profile that would be required to conform to SRTM by adding a correction to the dependent variable to account for overestimation of the bound fraction due to the SRTM approximation of instantaneous equilibrium. Relative to modification of basis functions as suggested by Eq. 1, or alternatively a non-linear fitting approach, this strategy has the additional advantage of simplicity and speed because it proceeds by repeated application of the same linear model for all iterations.

Estimation of global k₄ using post hoc analysis

Implementation of rFRTM requires a global value k₄, and this parameter can be estimated from a post hoc analysis of regional trends in a derived parameter, the reference-region washout rate constant (k₂′ = k₂ / R₁). Although k₂′ is evaluated repeatedly for every voxel or region of interest, it should take the same value irrespective of the region under analysis. However, k₂ cannot in general be the same for both rFRTM and SRTM because it multiplies different basis functions in each model. If rFRTM represents ground truth and the value of k₄ is finite and global, then SRTM biases the k₂ basis function by ignoring the convolution term. Under these conditions, SRTM biases both k₂ and k₂′, particularly at low values of BP_ND where the convolution term becomes larger. More generally, values of k₂′ and BP_ND derived from rFRTM will be biased with dependencies upon the local binding potential through the convolution term unless the value of k₄ assumed in analysis matches the true value. Within the context of rFRTM, reducing bias in k₂′ is equivalent to reducing bias in BP_ND, because an inaccurate estimate of k₄ biases both parameters through the convolution term. This claim is evident from Eq. 1 and also is demonstrated in simulations in this report.

In this work, we estimated $k_4^{global}$ as the value that minimized the dependence of k₂′ upon BP_ND. After defining a series of regions with different values of BP_ND, we performed a series of analyses on these regions with a different value of $k_4^{global}$ used in each analysis. This process generates Q different relationships between $k_2^{\prime \left(qr\right)}$ and $B{P}_{ND}^{\left(qr\right)}$ across the R regions. Rather than perform a purely graphical analysis to determine the value of $k_4^{global}$ that minimizes the dependence k₂′ upon BP_ND, we automated analysis using two different methods that produced very similar results: 1) minimize the mean squared error between k₂′ and the average value of k₂′ using a grid search for $k_4^{global}$, or 2) employ an approximate functional form to simultaneously fit all curves of k₂′ versus BP_ND for a series of stepped values for $k_4^{global}$. For the latter method, we employed an ad hoc functionality designed to satisfy these criteria within the framework of rFRTM:

1. k₂′ should become independent of BP_ND when $k_4^{\left(q\right)}$ matches the optimal value (denoted $k_4^{global}$), because then the model matches the assumed ground truth. The sign of bias in k₂′ should depend upon the relative magnitude of $k_4^{\left(q\right)}$ in relation to $k_4^{global}$, because the sign of bias depends upon the magnitude of the convolution term.

2. Higher values of BP_ND should be associated with less biased values of k₂′, because the convolution term tends toward zero in high-binding regions (i.e., SRTM becomes a more accurate approximation).

According to these principles, we fit the dependencies of k₂′ on BP_ND for all Q values of $k_4^{\left(q\right)}$ as a constant value plus a decreasing exponential function that introduces bias with a sign dependent upon the relative magnitude of $k_4^{global}$ and $k_4^{\left(q\right)}$. For convenience, we employed time constants (1/k₂′ and 1/k₄) rather than rate constants in the fit:

$$1∕k_2^{\prime qr}=1∕k_2^{\prime global}+A\left(1∕k_4^{global}-1∕k_4^q\right)exp\left(-\left(R_0+R_1∕k_4^q\right)\right)B{P}_{ND}^{qr}$$ [3]

The parameters of interest in this fit are the two global rate constants ($k_2^{\prime global}$, $k_4^{global}$). This functionality produces an approximate form across a wide range of values for $k_4^{\left(q\right)}$.

Reduction to rFRTM2

Ultimately, the goal of rFRTM is to enable accurate parameter mapping at a voxel-wise level, and so further regularization is required. Specifically, the goal is to fix two global parameters ($k_4^{global}$, $k_2^{\prime global}$) in order to reduce the model to the same two local parameters used for SRTM2 (k₂, k_2a). Fixing k₂′ in SRTM2 changes the structure of model bias, because k₂′ is not invariant in SRTM. Conversely, rFRTM2 should maintain accuracy while reducing parameter variance, provided that we can accurately identify the value of $k_4^{global}$ that produces invariance in k₂′. The two-parameter reduction of rFRTM2 follows the same strategy used to reduce SRTM2 to two parameters and two basis functions (Ichise et al., 2003).

$$C_T=k_2\left(\frac{C_R}{k_2^{\prime global}}+\int \left(C_R-{\stackrel{.}{C}}_T\otimes E\right)\right)-k_{2a}\int \left(C_T-{\stackrel{.}{C}}_T\otimes E\right).$$ [4]

Note that solution of rFRTM2 follows an approach similar to the one described by Eq. 2 for the 3-parameter implementation of rFRTM. Also, these models need modification to describe a functional challenge, as in a drug occupancy study or a behavioral study using a single synthesis of a radioligand such as raclopride. Such paradigms can be analyzed by applying a temporal dependence to the k_2a parameter (Alpert et al., 2003, Zhou et al., 2006), so that values of k_2a after the functional challenge are associated with a change in BP. To compute changes in occupancy for the simulated data in this report, we use this same strategy such that k_2a → k_2a + Δk_2a f(t), where f(t) in this report is modeled as a rapid change to a new state using a sigmoidal “step function” beginning at time t₀ with f(t′) = t′/sqrt(1 + t′²) and t′ = (t – t₀)/t, where the time constant (τ) was set to a value of 1 min.

Forward-model Simulations

Simulations were used to confirm predictions of theory and to determine bias and variance properties of kinetic models. Simulations within the framework of FRTM tested these hypotheses: 1) An inaccurate estimate of k₄ biases both k₂′ and BP_ND, and reducing bias in k₂′ is equivalent to reducing bias in BP_ND; 2) in the presence of noise, analyses based upon SRTM and rFRTM produce similar variances in estimates of BP_ND, and analyses based upon SRTM2 and rFRTM2 produce similar variances that are lower than the 3-parameter versions of these models; 3) due to bias introduced into BP_ND, estimates of occupancy using within-scan challenges are biased in SRTM and SRTM2, and biases can be mitigated using rFRTM.

Forward-model simulations with and without noise employed the system of differential equations in Eq. A1 to iteratively compute profiles of PET radioligand concentration versus time for selected experimental conditions. Simulations focused on two commonly used radioligands of dopamine receptors that often employ SRTM for analysis. [¹¹C]NNC-112 targets D₁ receptors and can detect extra-striatal binding, which emphasizes the need to accurately model binding parameter across a wide range of binding potentials. [¹¹C]Raclopride is a D₂/D₃ selective ligand that is widely used in applications that characterize changes in basal ganglia dopamine levels in response to behavioral cues or other stimuli. For each of Figures 2-4, input parameters for simulations are shown in Table 1. The temporal shape and magnitude of plasma concentrations were adjusted to roughly match experimentally measured reference-region TACs from the cerebellum of non-human primates (NHP) using the forward model specified by Eq. A1. Occupancy maps in Figure 4 were simulated as instantaneous reductions in k₃ that were localized to the right nucleus accumbens and occurred at 40 minutes into the scan.

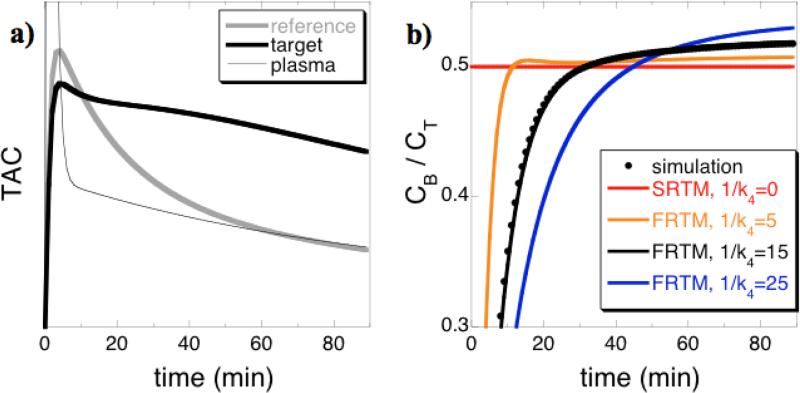
Fig. 2.

a) Simulated time-activities of a reference region (gray) and target region (black) for relatively low-binding regions using (a) BP = 1 and 1/k₄ = 15 min. b) The corresponding ratio of bound to total concentration of PET ligand in the target region versus time (black points) is compared to the model estimate for SRTM (red) and FRTM using values of 1/k₄ from 5 to 25 minutes.

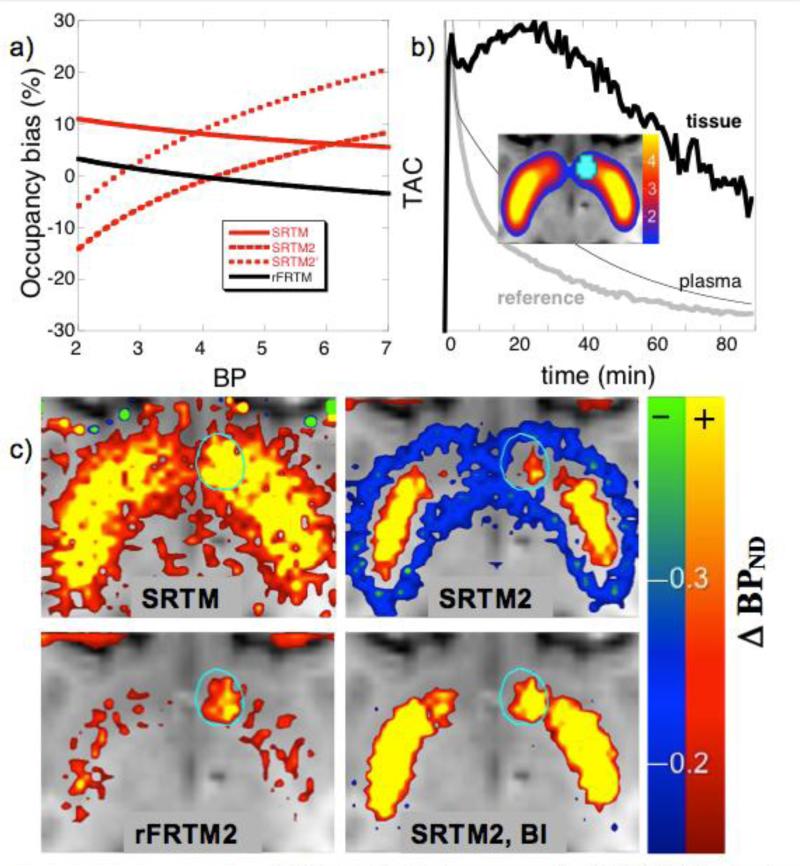
Fig 4.

a) Noiseless simulations of [11C]raclopride bias in occupancy for SRTM, SRTM2 using two different values of k₂′ (see text), and rFRTM2 as calibrated using Eq. 3. b) A typical TAC for simulations of a localized 10% increase in occupancy occurring at 40 minutes in the right nucleus accumbens (cyan); the image shows basal BP_ND values used in simulations. c) Maps of change in BP_ND using different analysis methods; clockwise from top left: SRTM, SRTM2, SRTM2 using a BI infusion, and rFRTM2.

Table 1.

Parameters used in simulations

Fig.	K1’ (ml/ml/min)	1/k2’ (min)	1/k4 (min)	k3/k4 (BP)	R1	Noise Model
2	0.05	16.5	15	1	0.85	None
3a-c	0.05	16.5	15	Variable	0.85	None
3d	0.05	16.5	15	1	0.85	(**)
4	0.15	3.5	10	(*)	(*)	(**)

^(*)Spatial distribution measured across NHP basal ganglia.

^(**)Noise followed a standard model (Logan et al., 2001).

Data presented in Figures 3d and 4 included a standard model of synthetic noise in which signal variance is proportional to signal multiplied by an exponentially increasing decay correction (Logan et al., 2001); for the uniform time bins used in simulations, noise was modeled as $\sigma =\sqrt{S\cdot C\cdot e^{\lambda t}}$, where C is the time-dependent concentration of radioligand, λ is the rate of radioactive decay, and S is a scale factor specifying the level of noise. For Figure 3d, the reference-region curve was assumed to have a relatively low level of noise (S=2 Bq/cc), and the level of noise in tissue regions was increased from zero to a large value (S=200 Bq/cc) that corresponded to a fractional standard deviation in the TAC of about 35% at 90 minutes. For each level of noise, 50,0000 TACs were generated to define standard deviations in estimates of BP_ND.

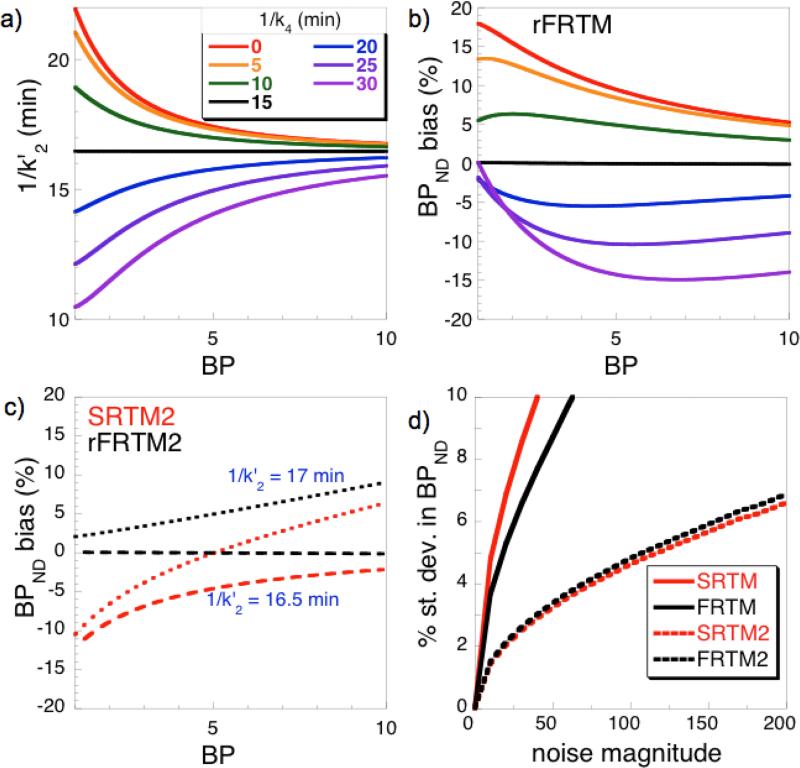
Fig. 3.

Analyses of simulated data. (a) An offset time constant 1/k₄ equal to the true value (15 min) removes the variation of the derived reference-region outflow time constant 1/k₂′ versus BP using rFRTM. A value of 1/k₄ =0 corresponds to SRTM (red). (b) Bias in BP_ND for the same set of k₄ values used in panel (a). (c) Bias in BP_ND for 2-parameter reductions SRTM2 (red) and rFRTM2 (black) using values for 1/k₂′ of 16.5 min (long dashes) or 17 min (short dashes). (d) The percent standard deviation of BP_ND values at varying levels of noise.

Experimental NHP Data

Data were collected in NHP in order to demonstrate that 1) the dependence of k₂′ on BP_ND is consistent with the proposed model, and k₂′ becomes invariant with an appropriate global choice of k₄; 2) the spatial relationship between BP_ND values suggested by SRTM and rFRTM is consistent with simulations; 3) the proposed rFRTM method produces robust voxel-wise maps. All NHP experimental procedures complied with the regulations of the Subcommittee on Research Animal Care at Massachusetts General Hospital. Data were collected from anesthetized NHP using simultaneous PET/fMRI according to methods described previously (Mandeville et al., 2013, Sander et al., 2013, Sander et al., 2015).

Analysis of Simulations and NHP Data

Analyses of simulated and real data employed SRTM, SRTM2, rFRTM, or rFRTM2. Parameters were solved by weighted least squares assuming a noise-free approximation to Poisson weights (Thiele and Buchert, 2008), with convergence for rFRTM and rFRTM2 defined to be a change in BP_ND less than 0.1%. Analyses of simulated occupancy incorporated a sigmoidal regressor to model a change in the parameter k_2a (Alpert et al., 2003, Zhou et al., 2006). To define the value of k₄ to use in rFRTM analyses, analyses of k₂′ versus BP_ND were fit using Eq. 3. When describing simulation results, we denote true binding potentials as BP, defined as the ratio of k₃ to k₄ values that were used as inputs for the forward-model simulations, and BP_ND is a derived quantity from analyses of data. Within simulations, bias in BP_ND was assessed as a percentage relative to the known value of k₃/k₄.

All NHP data were aligned to the INIA19 rhesus macaque brain atlas (Rohlfing et al., 2012) using T1-weighted MRI data, and the known transformation between PET and MRI defined the atlas-based region for the right nucleus accumbens (cyan region, Fig. 4b) in a manner that was spatially consistent with the PET BP_ND map (colored image, Fig. 4b). To define a set of regions that varied systemically versus BP_ND, NHP data were analyzed initially by SRTM2 to generate a map of BP_ND. Brain voxels then were sorted by BP_ND values so that they could be efficiently grouped into less noisy ROIs for further analyses based upon BP_ND similarity. To minimize bias from noise in low-binding regions, ROIs were excluded below a BP_ND threshold, which generally was set to 1 or 2. ROIs were analyzed by rFRTM using five values for k₄, and all data were then fit by Eq. 3 to define the global value of k₄ to use in a final analysis.

Results

Figure 2 provides an intuitive window into assumptions underlying SRTM and rFRTM and how these assumptions bias measurements of BP_ND. Noiseless simulated time-activity curves for a reference region and a target region are shown in Fig. 2a for a relatively low-binding region (BP=1) using a PET radioligand that has an offset time constant from the bound compartment of 1/k₄ = 15 min. Fig. 2b compares the true fraction of the target tissue concentration that is specifically bound (black points) versus values assumed by SRTM (red line) and by rFRTM using different analysis values for 1/k₄. The bound radioligand fraction does not reach the SRTM approximation until about 30 minutes into the scan, and SRTM also does not match the true value at the end of the scan. Because the goal of reference models is to estimate specifically bound tissue fractions in order to define BP_ND, inaccurate estimates of k₄ produce bias in BP_ND. When the analysis value of k₄ matches the true value, the analytical estimate for the bound fraction (Eq. A3) matches the simulated value.

Figures 3a and 3b demonstrate that an inaccurate estimate of k₄ used in analysis introduces bias into both k₂′ and BP_ND, and that this bias is a function of BP. An assumption of instantaneous equilibrium (SRTM, red curves) causes positive bias in both BP_ND and the time constant 1/k₂′. Conversely, both parameters exhibit negative bias when kinetics are assumed be slower than reality (blue and purple curves). The derived parameter k₂′ becomes an invariant quantity only when the value of k₄ used in rFRTM analysis matches the true value used for the forward-model simulation. Note that Fig. 3a provides a graphical motivation for the fitting method of Eq. 3.

When SRTM2 employs a global value for k₂′, bias in BP_ND is similar in magnitude to SRTM, as shown in Fig. 3c. If one defines k₂′ to be the projected asymptotic value in the limit of high BP (long dashes), then SRTM2 (red) underestimates BP_ND at all values of BP. However, literature methods define the value of k₂′ for SRTM2 using analyses of regions with a finite BP_ND (Wu and Carson, 2002, Ichise et al., 2003); in this case, SRTM2 will produce a positive bias in the highest-binding regions and a negative bias in low-binding regions (short dashes). Conversely, rFRTM2 (black) shows very little residual bias (long dashes) when Eq. 3 identifies global values of k₄ and k₂′. Additionally, the figure depicts the effect an incorrect value of k₂′ at the correct value of k₄ (black curve, short dashes). Because rFRTM2 has a model structure similar to SRTM2, it exhibits a similar sensitivity to errors in k₂′.

Parameter bias is not the only criteria for selecting PET kinetic models; parameter variance is another important quantity. Fig. 3d compares percentage standard deviations in estimates of BP_ND at different noise levels. SRTM2 is used as the reference, and so the SRTM2 curve in the figure is the line of identity. As expected, SRTM2 exhibits small variance in BP_ND relative to SRTM. rFRTM2 and SRTM2 have similarly noise sensitivities that are small compared to the three-parameter models.

Inaccuracies in SRTM become problematic in the context of functional studies that attempt to characterize small changes in receptor occupancy; in particular, spatial variations in binding potentials can potentially bias inferences about changes in occupancy. Figure 4a reports analyses of simulated data for a radioligand like [¹¹C]raclopride. SRTM exhibits a positive bias in occupancy (solid red line, Fig. 4a), while SRTM2 (dashed lines) shows a strong monotonic dependence of occupancy on BP with bias dependent upon the global value for 1/k₂′, which was chosen to be 3.8 min from a high-binding region (BP=6) for the long dashed line or 4.4 min from a lower binding region (BP=4). Bias in occupancy for rFRTM was reduced to a few percent using Eq. 3 to estimate the value of k₄ (black line).

Results of Fig. 4a suggest that spatial variations in BP will yield occupancy values with a regional bias, and other panels in Fig. 4 illustrate the potential for reference tissue approaches to exhibit spatial variations in bias that produce false positive results or mask real changes in occupancy. A simulated 10% change in occupancy was localized to the right nucleus accumbens (cyan region, Fig. 4b), with the magnitude of noise in each voxel illustrated by the TACs in Fig. 4b. Analysis of these data by SRTM suggested an increase in occupancy throughout basal ganglia, albeit with high noise in the map due to the inherent instability of three-parameter fits (Fig. 4c). Maps produced by SRTM2 showed a characteristic pattern of apparent positive changes in occupancy in the highest-binding regions surrounded by apparent decreases (Fig. 4c, top right). This pattern was altered either by choosing a different global value of k₂′ or by changing the infusion paradigm; a bolus plus continuous infusion (BI) simulation designed to achieve a stead-state just prior to the challenge showed a different regional pattern of bias (Fig. 4c, bottom right). Conversely, using the fitting method of Eq. 3 to calibrate rFRTM, a change of about the correct magnitude was observed in the correct location with little bias in other areas of basal ganglia (Fig. 4c, bottom left), and this pattern was maintained for either a bolus or a BI injection of radioligand (not shown). Note that the cyan oval curves in these figures demark the lateralized change in simulated occupancy, and other apparent changes in binding potential are artifacts of analysis.

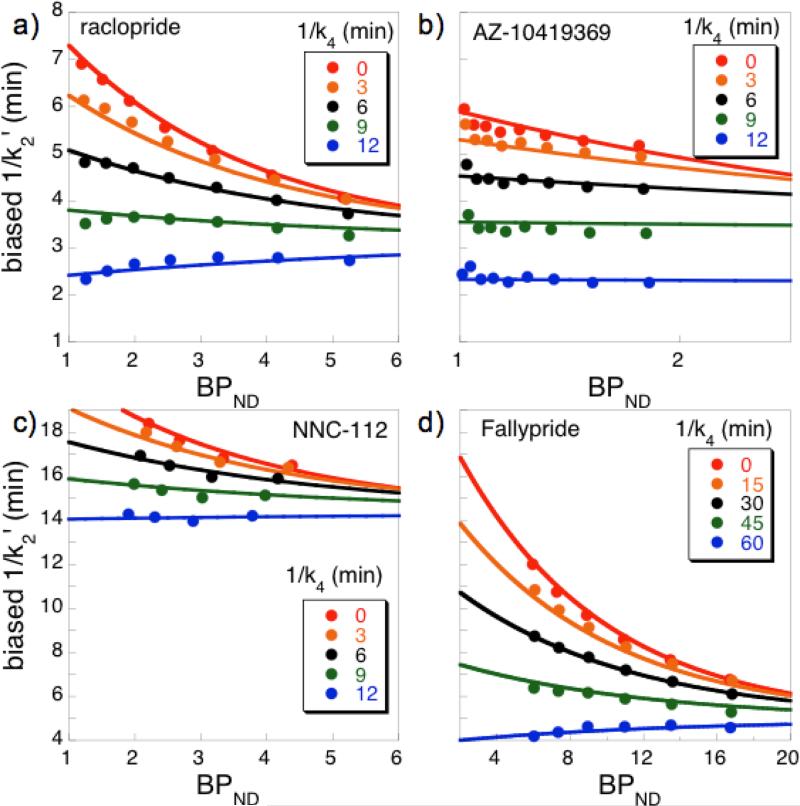
If rFRTM provides a realistic biological model, then application of rFRTM to experimental data should identify and remove correlations between k₂′ and BP_ND that arise in SRTM, in agreement with the simulated data of Fig. 3a. Figure 5 applies rFRTM analyses to representative experimental data collected in anesthetized NHP using four different radioligands. Points in Fig. 5 represent analyses of ROIs created by grouping voxels with similar BP_ND values from a first-pass analysis. Each set of differently colored points in a figure panel represent an analysis using a different global value of k₄. As the analysis time constant 1/k₄ increases from 0 (SRTM, red) to larger values, curves first become flatter until the curvature reverses at low values of BP_ND. The best value of k₄ to use in a final rFRTM analysis is the one that produces invariance of k₂′. Lines in Fig. 5 illustrate application of Eq. 3 to simultaneously fit all the data points for all values of k₄. Optimal values of global 1/k₄ estimated by the fit for these specific experiments were 10.4, 10.6, 11.6, and 56 min for the scans using [¹¹C]raclopride, [¹¹C]AZ-10419369, [¹¹C]NNC-112, and [¹⁸F]fallypride, respectively. In eight repeated measurement in a single NHP using [¹¹C]raclopride, estimates were reproducible with values of 1/k4=9.7 ± 1.0 min (mean ± st. dev.).

Fig. 5.

Data obtained in isoflurane-anesthetized NHP using different PET radioligands. Fitting the BP_ND functionality of the reference region washout time constant (1/k₂′) for different values of the dissociation time constant (1/k₄) facilitated model identification using Eq. 3. Red data points correspond to SRTM analysis (1/k₄=0), and other sets of data points used analysis values of 1/k₄ that were progressively stepped by either 3 min (a-c) or 15 min (d).

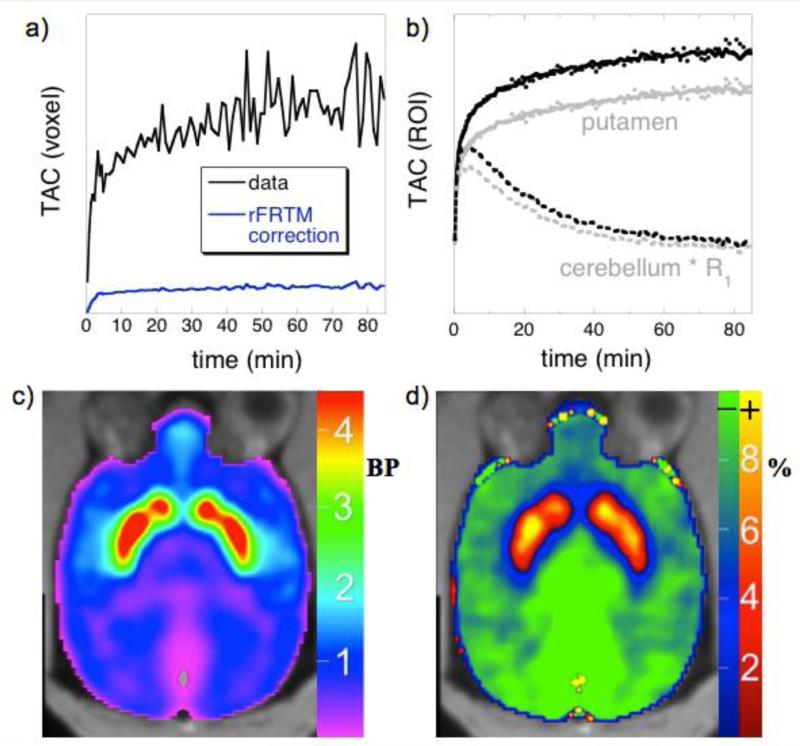
Figure 6 demonstrates ROI and voxel-wise fits of the rFRTM to NHP data using [¹¹C]NNC-112. Fig. 6a compares the two terms on the left-hand side of Eq. 2 in order to demonstrate that the convolution term, which is missing in SRTM, has much less noise than the tissue concentration in a single voxel. Analysis of bilateral putamen by SRTM yields an excellent fit to data (Fig. 3b, gray curve and points), and rFRTM produces a fit of similar quality to the “corrected” data of Eq. 2 (black curve and points). SRTM reports a BP_ND value that is 9% higher than rFRTM in this region. The SRTM value for R₁ is 15% lower than for rFRTM, consistent with the expectation that SRTM underestimates R₁ values (Muzic and Christian, 2006, Thiele and Buchert, 2008).

Fig. 6.

a) A time-activity curve for [¹¹C]NNC-112 from a single voxel in putamen (black) and the rFRTM correction term of Eq. 2 (blue). b) Whole putamen (gray dots) together with an SRTM fit (gray solid line) and the reference-region (cerebellum) scaled by R₁ (gray dashes); the corresponding black points and curves are the rFRTM modified data (Eq. 2), the rFRTM fit, and the R₁ contribution. c) A map of BP_ND produced by rFRTM2 analysis of [¹¹C]NNC-112 in NHP. d) The percent difference of BP_ND values produced by SRTM2 relative to rFRTM2, with blue-green colors indicting smaller SRTM2 values and red-yellow colors indicating larger SRTM2 values.

Simulations suggest the rFRTM should enable robust voxel-wise mapping with parameter variance similar to SRTM, and Fig. 6c shows a map of BP_ND obtained with rFRTM2 in order to illustrate this point. Additionally, relative BP_ND magnitudes obtained by rFRTM2 and SRTM2 are compared as a ratio in Fig. 6d using a percent deviation map, with the blue-green color scale indicating lower BP_ND values for SRTM2 relative to rFRTM2. The map generated by SRTM2 used a global value for k₂′ from putamen following the method that suggests obtaining this value from a high-binding region (Seneca et al., 2006). The selected value (1/k₂′=15.5 min) was higher than the asymptotic value of 14.3 min in Fig. 5c, and so the simulations of Fig. 3c suggest that SRTM2 should underestimate BP_ND in low-binding regions but overestimate BP_ND in the highest-binding regions. The map demonstrates the expected relationship between the two methods and is consistent with simulations.

Voxel-wise analyses using a linear-model formulation of rFRTM2 (Eq. 2) reached convergence in most brain areas after about 5-10 iterations using a 0.1% tolerance on BP_ND, and accordingly the processing time surpassed a linear-model implementation of SRTM2 by a factor of about 5-10. For a typical NHP dataset with 95 frames and 350,000 voxels, processing time increased from 2.5 min using SRTM2 to 15 min using rFRTM2. Relaxing the tolerance will reduce the number of required iterations and the computational time. The iterative linear-model implementation of rFRTM2 converged much faster than non-linear damped least-squares minimization using a Levenberg-Marquardt algorithm, which increased computation time by a factor of about 100 over linear model iteration.

Discussion

SRTM has become a common PET analysis strategy for reversible radioligands that can be appropriately analyzed by reference region methods, and this method has a number of distinct advantages, including deterministic solutions and simple implementation. For many applications that map receptor densities or investigate pharmacological challenges that produce large changes in receptor occupancy, SRTM offers sufficient accuracy while also guarding against instabilities and potentially larger errors that can arise in more complicated models. For ROI analyses, the three-parameter SRTM requires no subjective parameter estimates and generally produces small bias in the highest-binding regions. The two-parameter SRTM2 requires a subjective assignment of one global parameter (k₂′) but increases robustness to noise while offering a level of bias comparable to SRTM. As testament to the popularity of SRTM, two early papers describing the method (Lammertsma and Hume, 1996, Gunn et al., 1997) have garnered about one thousand citations over the past decade (see (Salinas et al., 2015)).

Based upon simulations that assumed a finite rate for k₄ that was consistent with literature estimates (Farde et al., 1989, Pappata et al., 2002), we showed that biases inherent to SRTM can obscure detection of subtle changes in BP_ND, as illustrated by the inability of SRTM-based analyses to accurately identify the simulated BP_ND changes of Fig. 4. Spatially varying patterns of SRTM bias make interpretation difficult even if using a fast radioligand like raclopride. Using SRTM2, estimates of occupancy will vary depending upon a subjective selection of the reference region k₂′ value, which is not globally invariant in that model. Moreover, the degree of apparent occupancy can change dramatically with the size of an ROI, due to spatial variations in bias. In general, both SRTM and SRTM2 exhibit a positive bias in estimates of occupancy in high-binding regions (e.g., Fig. 4), and so analyses based upon these models can produce false positive results.

In order to reduce bias due to model topology using a RTM approach, the SRTM approximation of instantaneous equilibrium must be abandoned, a step that requires inferences about rate constants associated with the specifically bound compartment. Prior versions of FRTM have employed a methodology that attempts to fit four parameters for each voxel or ROI (Lammertsma et al., 1996). PET analyses rarely use this approach, and it is impractical for voxel-wise mapping for several reasons. High-binding regions have little intrinsic sensitivity to the absolute values of k3 or k4, as illustrated by the convergence of curves in Fig. 3a, whereas low-binding regions have limited sensitivity to specific binding parameters in the presence of noise. Fitting a simple TAC becomes unstable with four parameters, as the two local parameters used in SRTM2 generally are sufficient for good fits. Relative to FRTM as used in the literature, SRTM reduces parameter variance at the expense of increased parameter bias.

The model proposed here (rFRTM) offers an alternative to SRTM-based approaches, with the potential to ameliorate parameter bias without substantially altering parameter variance. In fact, SRTM is really just one solution of rFRTM in which the offset time constant is assumed to be zero, as illustrated by Fig. 3. rFRTM2 fits the same two local parameters as SRTM2, but it first requires a step of model identification to select optimal global values for k₂′ and k₄. The former parameter is a property of the reference region that is fit repeatedly for each TAC, a process that conveniently provides a method to calibrate the model by selecting a value of k₄ that produces invariance in k₂′. As shown by simulations within the FRTM model, bias reduction in k₂′ is accompanied by bias reduction in estimates of BP_ND and occupancy.

One of the features of rFRTM is the ability to determine a value for k₄ using a large of portion of data, and our expectation is that estimates provided by this method will exhibit reduced variability relative to existing literature methods that obtain a value from each kinetic analysis. Using rFRTM, our results for k₄ generally compare well to literature results subject to the limitations of large error bars in the literature and relatively few results reported here in anesthetize NHP. For [¹¹C]raclopride, two different kinetic approaches estimated 1/k₄ values in the range 9 to 15 minutes in human subjects (Farde et al., 1989), which are comparable to our result. Our estimate for [¹¹C]AZ-10419369 falls within a reported range of 0 to 16 minutes (Varnas et al., 2011). A human study reported values of 18 to 50 min for [¹¹C]NNC-112. The large 1/k₄ value of nearly one hour for [¹⁸F]fallypride in our NHP study is consistent with the long scan duration required to obtain reliable estimates of BP_ND using this tracer in humans (Vernaleken et al., 2011).

There is scant literature on the magnitude of in vivo biological variations in k₄ across brain regions, subjects, or physiological states. If this rFRTM approach proves to increase precision in estimates of this parameter, even though estimates are global, it might serve an important function by providing in vivo estimates of shifts in the dissociation rate constant, which might differ across subject populations, in response to allosteric modulators (Wootten et al., 2013), or as a consequence of agonist-induced internalization, which has long been suspected as a source of confound in the interpretation of PET occupancies (Chugani et al., 1988, Laruelle, 2000, Ginovart, 2005).

Potential Limitations

Compared to FRTM, which attempts to determine a value for k₄ from each TAC, a potential criticism of rFRTM is that k₄ might not be regionally invariant. However, rFRTM is predicated upon the assumption that the best average value of k₄ can be identified even in the presence of local variations. Experimental data conform to this assumption (Fig. 5) by enabling identification of self-consistent models with invariant values of k₂′ at some selected value for the average offset time constant from the bound compartment. Conversely, using simulations it is easy to show that attempts to estimate k₄ directly from TACs using FRTM can succeed in the absence of noise but will produce severely biased results with even modest amount of noise, and bias becomes particularly pronounced at high values of BP_ND where FRTM becomes insensitive to k₄. The inability of FRTM to accurately determine local values for k₄ limits our ability to address the appropriateness of using a global average value for this parameter.

The proposed method for estimating the global value of k₄ requires a range of BP_ND values and a threshold on BP_ND to reduce noise-induced variations in k₂′ and BP_ND that arise at low BP_ND. Ligands like [¹¹C]NNC-112 and [¹⁸F]fallypride have striatal and extra-striatal binding to generate a wide distribution of BP_ND values using relatively large ROIs, which simplifies the identification of rate constants. Conversely, [¹¹C]AZ-10419369 generally has BP_ND values below 2, which makes identification of k₄ more difficult. This issue could limit applications of the model using very low-binding radioligands. Alternatively, the model could be employed using a fixed value of k₄ for a given radioligand, just as SRTM uses a value of 1/k₄=0, with similar methods employed for choosing k₂′ for voxel-wise mapping.

The specific fitting method we employed in this study for estimating the best global value of k₄ (Eq. 3) was designed to accomplish the more general goal of producing invariance in the parameter k₂′, but other approaches might accomplish the same end with equal or better accuracy. For instance, global k₄ can be selected as the value that minimizes the slope of a simple linear fit of k₂′ versus BP_ND across regions. Alternative approaches, including methods that obviate the need for a threshold on BP_ND, are subjects for continued research.

Achieving a level of accuracy better than 10% in BP_ND or occupancy is challenging, and this study addresses only one source of bias. A recent report discussed other SRTM biases associated with an imperfect reference region, mismatched distribution volumes between reference and target regions, and the failure of reference models to account for blood volume contributions (Salinas et al., 2015). Other sources of bias in BP_ND include time-dependent errors that can arise from image reconstruction, attenuation correction, or radioactive metabolites. Occupancy studies in principle could be affected by modulation of cerebral blood flow and volume, effects that can be addressed experimentally using simultaneous fMRI to measure CBF or CBV during PET (Sander et al., 2014).

Finally, it is important to note that we did not investigate all possible variations of SRTM or other alternative approaches to estimating binding potentials or changes in occupancy. For instance, a study that attempts to measure dopamine release from a within-scan behavioral challenge using a bolus plus continuous infusion of [¹¹C]raclopride might ignore much of the data prior to the challenge to avoid bias from early time points in a weighted-least squares SRTM analysis; this strategy presumably will reduce bias but also sacrifice detection power. While other potential approaches and contributions to parameter bias warrant further study, the SRTM “1-tissue” approximation can be addressed directly with this proposed model.

Conclusions

In conclusion, we described a regularized FRTM approach for analysis of PET binding potentials and changes in occupancy. We demonstrated that the model can be calibrated using invariance in the reference-region outflow rate as an internal standard, and that mapping using the two-parameter rFRTM2 produces robust voxel-wise parameter estimates. Simulations and underlying principles suggest an improved level of accuracy of rFRTM relative to SRTM, without an increase in parameter variance. The main applications of this model are likely to be in functional studies that investigate small changes in occupancy, and potentially also in vivo estimates of the dissociation rate constant.

Appendix

The first-order differential equations that define the FRTM model in Fig. 1a are:

$$\begin{array}{cc}\hfill {\stackrel{.}{C}}_R& =K_1^{\prime }{C}_P-k_2^{\prime }{C}_R\hfill \\ \hfill {\stackrel{.}{C}}_F& =K_1{C}_P-k_2{C}_F-k_3{C}_F+k_4{C}_B\hfill \\ \hfill {\stackrel{.}{C}}_B& =k_3{C}_F-k_4{C}_B\hfill \\ \hfill C_T& =C_F+C_B\hfill \end{array}$$ [A1]

If R₁ is defined as the ratio K₁/K₁′ and the distribution volume of non-specifically bound tracer is equal in all tissues (K₁/K₁′=k₂/k₂′), then the plasma concentration can be eliminated to produce an equation for the target tissue that depends upon the reference region and either the free or bound concentrations:

$${\stackrel{.}{C}}_T=R_1{\stackrel{.}{C}}_R+k_2{C}_R-k_2\left(C_T-C_B\right)$$ [A2]

The bound concentration in this equation is not directly measurable. SRTM (Fig. 1b) addresses this problem by positing fast exchange within the target tissue to produce a “1-tissue model” (Lammertsma and Hume, 1996). As an alternative to the SRTM approximation, one can solve the time dependence of the bound compartment. Eq. A1 provides the differential equation for the bound concentration, and the solution is subject to the initial condition that tissues are devoid of specifically bound PET radioligand at time zero.

$$\begin{array}{cc}\hfill {\stackrel{.}{C}}_B& =-\left(k_3+k_4\right)C_B+k_3{C}_T\hfill \\ \hfill C_B& =k_3{e}^{-(k_3+k_4)t}{\int }_0^t{e}^{(k_3+k_4)t^{\prime }}{C}_T\left(t^{\prime }\right)d{t}^{\prime }\hfill \end{array}$$ [A3]

A more convenient expression can be obtained using integration by parts to write the solution of Eq. A3 in terms of the tissue concentration and derivative, while also defining BP_ND = k₃/k₄ and using notation of a convolution integral ($\otimes$):

$$\begin{array}{cc}\hfill C_B& =k_3{e}^{-(k_3+k_4)t}{\int }_0^t{C}_T{e}^{(k_3+k_4)t^{\prime }}d{t}^{\prime }=k_3{e}^{-(k_3+k_4)t}\left[\frac{e^{(k_3+k_4)t}}{k_3+k_4}{C}_T-{\int }_0^t{\stackrel{.}{C}}_T\frac{e^{(k_3+k_4)t^{\prime }}}{k_3+k_4}d{t}^{\prime }\right]\hfill \\ \hfill & =\frac{B{P}_{ND}}{\left(1+B{P}_{ND}\right)}\left[C_T-{\stackrel{.}{C}}_T\otimes e^{-k_4(1+B{P}_{ND})t}\right]\hfill \end{array}$$ [A4]

Eq. A4 can be substituted into Eq. A2 to write a reference tissue model that no longer depends upon explicitly upon the bound concentration:

$$\begin{array}{cc}\hfill {\stackrel{.}{C}}_T& =R_1{\stackrel{.}{C}}_R+k_2{C}_R-k_2{C}_T+k_2\left(1-\frac{1}{1+B{P}_{ND}}\right)\left[C_T-{\stackrel{.}{C}}_T\otimes e^{-k_4(1+B{P}_{ND})t}\right]\hfill \\ \hfill & =R_1{\stackrel{.}{C}}_R+k_2\left(C_R-{\stackrel{.}{C}}_T\otimes e^{-k_4(1+B{P}_{ND})t}\right)-\frac{k_2}{1+B{P}_{ND}}\left(C_T-{\stackrel{.}{C}}_T\otimes e^{-k_4(1+B{P}_{ND})t}\right)\hfill \end{array}$$ [A5]

We can employ the same definition for k_2a (= k₂ / (1+ BP_ND)) used in SRTM (Lammertsma and Hume, 1996) and integrate both sides of Eq. A5 to produce a form for FRTM that mimics common representations of SRTM.

$$C_T=R_1{C}_R+k_2\int \left(C_R-{\stackrel{.}{C}}_T\otimes e^{-k_4(1+B{P}_{ND})t}\right)-k_{2a}\int \left(C_T-{\stackrel{.}{C}}_T\otimes e^{-k_4(1+B{P}_{ND})t}\right)$$ [A6]

Note that Eq. A6 becomes SRTM in the fast-exchange limit when the rate constants k₃ and k₄ approach infinity, or when the tissue concentration maintains a true steady state, for then the convolution terms disappear. Computation of BP_ND is performed identically for SRTM or rFRTM: BP_ND = k₂ / k_2a – 1.