Neurons as oscillators

Abstract

Regularly spiking neurons can be described as oscillators. In this article we review some of the insights gained from this conceptualization and their relevance for systems neuroscience. First, we explain how a regularly spiking neuron can be viewed as an oscillator and how the phase-response curve (PRC) describes the response of the neuron's spike times to small perturbations. We then discuss the meaning of the PRC for a single neuron's spiking behavior and review the PRCs measured from a variety of neurons in a range of spiking regimes. Next, we show how the PRC can be related to a number of common measures used to quantify neuronal firing, such as the spike-triggered average and the peristimulus histogram. We further show that the response of a neuron to correlated inputs depends on the shape of the PRC. We then explain how the PRC of single neurons can be used to predict neural network behavior. Given the PRC, conduction delays, and the waveform and time course of the synaptic potentials, it is possible to predict neural population behavior such as synchronization. The PRC also allows us to quantify the robustness of the synchronization to heterogeneity and noise. We finally ask how to combine the measured PRCs and the predictions based on PRC to further the understanding of systems neuroscience. As an example, we discuss how the change of the PRC by the neuromodulator acetylcholine could lead to a destabilization of cortical network dynamics. Although all of these studies are grounded in mathematical abstractions that do not strictly hold in biology, they provide good estimates for the emergence of the brain's network activity from the properties of individual neurons. The study of neurons as oscillators can provide testable hypotheses and mechanistic explanations for systems neuroscience.

Spiking Neurons

The firing of spikes (action potentials) is the hallmark of neural function in almost all types of neurons. At the biophysical level, a depolarizing Na⁺ conductance interacts with one or more delayed hyperpolarizing K⁺ conductances. This causes a sharp depolarization, followed by a sharp hyperpolarization of the membrane potential, the action potential (typically lasting <2 ms and having an amplitude >50 mV). Additional ionic currents influence the repetitive firing of action potentials. The biophysical underpinnings of these processes, initially elucidated by Hodgkin and Huxley (1952a, 1952b), are well understood.

In contrast, systems neuroscientists conceptualize spikes as pulses (Rieke et al. 1996). In extracellular recordings, spike waveforms are measured. The spike trains of individual neurons are then frequently reconstructed by spike sorting, with one waveform class being assigned to each neuron. From this point on, each spike train is treated as a series of digital events at the times the spike waveforms were recorded. Systems neuroscientists analyze such spike trains for properties such as rate, spike coincidences, oscillatory activity, or the presence of other temporal pattern. Spike trains are often correlated to sensory inputs by measures such as the spike-triggered average (STA) or the peristimulus time histogram (PSTH).

It is challenging to explain higher level systems neuroscience findings in terms of low-level single-neuron biophysics. In our opinion, viewing neurons as oscillators can partially bridge the divide between these two levels of understanding spikes. In this view, an isolated neuron suitably depolarized is assumed to regularly spike with constant interspike intervals. As for any regularly occurring process, it is then described as an oscillator (Winfree 2001). This simplification significantly reduces the complexity of the description of neural spiking, making it mathematically tractable, while at the same time capturing crucial principles of the spiking process. There is a considerable body of work in mathematical neuroscience investigating neural oscillators, and these studies predict a number of interesting single-neuron and network properties.

Unfortunately, much of this literature contains mathematical jargon and is not easily accessible to the systems neuroscience community. In this review, we aim to present these theoretical insights in an intuitive manner, in plain language, useful to the experimentalist. We first explain how neurons are conceptualized as oscillators, and what assumptions come with this conceptualization. We then introduce the phase-response curve (PRC), an important measure of an oscillator. Next, we review some of the PRCs of cortical neurons that have been measured. We then discuss what predictions the theory of coupled oscillators makes about the dynamics of neurons in networks. We conclude with two examples depicting how this theoretical knowledge can be brought together with the knowledge about PRCs in cortical neurons.

Neurons as Oscillators

Most physical and biological systems that are characterized by regular rhythmicity are generated by underlying oscillators. Whereas it is clear that neurons that produce motor rhythms (for swimming, walking, breathing, and chewing; for detailed examples see Marder et al. 2005; Nishii et al. 1994; Smith et al. 2000) are oscillators, it is somewhat more controversial to view cortical neurons as oscillators given their often seemingly rather irregular activity. However, the assumption that cortical neurons are oscillators still holds in many cases (Smeal et al. 2010; Wilson et al. 2014; Yuste et al. 2005). The main implication of understanding a neuron as an oscillator is not a necessarily a strict regularity but that the complete state of the neuron can be encoded in one single variable called the “phase.”

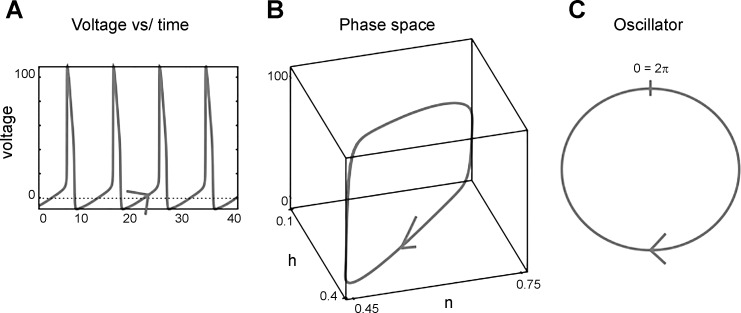
Let us illustrate the concepts of state, limit cycle, phase, and phase space via the classic Hodgkin-Huxley model (1952a, 1952b) of the squid axon. If depolarizing current is applied to the Hodgkin-Huxley model, it will fire repetitive action potentials: it is an oscillator. The Hodgkin-Huxley model consists of four differential equations (equations describing the change of a variable over time) describing four “states”: one for describing the time course of the membrane potential, V, and three for the fractions of the sodium and potassium channels being open at a given time (m, h, n). Figure 1A plots V against time. Instead of plotting the variables against time, we plot three of these four variables (V, m, n, h) against each other: we hence plot them in “phase space” (Fig. 1B). When the model axon is oscillating, it means that each of these four variables also oscillates with the same frequency and returns to the same value once every oscillatory period. One such oscillation of V, m, n, and h corresponds to a spike with its subsequent interspike interval. We can then map the time courses of V, m, n, and h (which form a closed 1-dimensional curve in the 4-dimensional phase space) onto a circle (also a 1-dimensional curve; Fig. 1C). Each rotation along the circle again corresponds to a spike and its subsequent interspike interval. This closed curve in phase space is called a “limit cycle.” We do not concern ourselves with the details of the many ionic conductances of a neuron. These conductances, such as the h-current generating a voltage sag, or a persistent sodium current generating an afterdepolarization, matter for the timing of the next spike, but their dynamics are all summarized in the dynamics of the neuron's phase progression. To understand such an oscillator, we do not necessarily need to know the values of each variable describing it at the detailed biophysical level; it is sufficient to know how far along the circle the oscillator has progressed toward the next spike. The phase of the neural oscillator is the normalized time since the last spike. This normalization to a phase makes each interspike interval range from 0 (previous spike) to 2π (next spike). (In other studies the time is normalized to a phase to lie between 0 and 1.)

Fig. 1.

Abstraction of a regular (oscillatory) spiking process as a phase. A: the voltage of a spiking neuron is plotted against time. B: time is then not explicitly plotted anymore in a phase space plot of the voltage and 2 ion channel activation states (h, n). C: the resulting circular trajectory is mapped onto a simple circle, representing a periodically changing phase variable, ϕ. The circular movement of ϕ is equivalent to the dynamics of the voltage and the ion channel activation states through phase space.

There is nothing about this idea that is restricted to models, since we can equally plot experimentally measured values in phase space. We can eliminate time from the plot in the same manner, by plotting not a variable against time, but two or more variables against each other. Alternatively, we can plot one measured variable against a time-delayed version of itself to arrive at a phase-space plot of the system's limit cycle (Kantz and Schreiber 2004).

In biology, all oscillations exist on stable limit cycles: even if we do not start right on the limit cycle due to noise, all the variables will eventually converge back onto the limit cycle. This implies that we can define the phase of the neuron even when we are not exactly on it. Even if the neuron is somewhat noisy, we can still view it as an oscillator and map its behavior onto the phase of the cycle, since its states will return to the cycle when deviated away from it (Fig. 2C; Schwabedal and Pikovsky 2013; Thomas and Lindner 2014). This is the first of several cases we encounter in our oscillator-based approach to neuroscience where we do not depend on reality to stick precisely to mathematical abstractions.

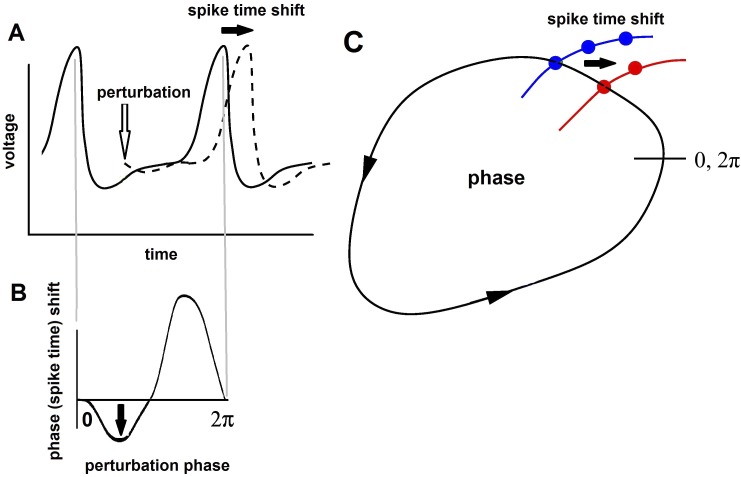
Fig. 2.

Phase-response curves (PRCs). A: spike time shift by a perturbation of the voltage of a neuron. B: the spike time shifts as a function of the phase of the perturbations are shown in the PRC. C: a limit cycle of the states of a neuron, with the spike time shift indicated. The neuron will return to the limit cycle (it is stable) when its states are perturbed away (for instance, along the red and blue curves).

By describing a neuron as an oscillator, we have hit a conceptual sweet spot, both simple and potent in its explanatory power: rather than simulating every voltage dependence of every ionic current of a neuron, we have defined a mathematical description of how these conductances move the state of the neuron from spike to afterhyperpolarization to the next spike (or in our language, from one phase to the next). A correctly chosen description allows us to investigate the dynamics of large numbers of connected neurons without having to simulate a great amount of biological detail (for detailed treatment of phase-based models in neuroscience, see Ashwin et al. 2016; Ermentrout and Terman 2010; Izhikevich 2010; Schultheis et al. 2011). We only need to look at the phase of each neuron and how it moves around!

Assumptions

To regard a neuron as an oscillator, we assume that the neuron fires relatively regularly and that the synaptic connections between them are fairly weak so that they do not cause extra spikes on their own, but only shift the timing of spikes. When we investigate networks of neural oscillators, we often assume that the network is homogenous in terms of its cell types and connections (Schwemmer and Lewis 2011). These assumptions are of course not completely realistic when judged against neurobiological reality. However, in many cases, the predictions of neural behavior derived from work on neural oscillators still hold when these assumptions are partially met. To be considered an oscillator, the neuron or network must be intrinsically rhythmic: its rhythm cannot be imposed by an external rhythmic stimulus. The rhythm must be fairly regular with the interspike intervals fairly similar (CV ∼ <0.2). Smeal et al. (2010) provide a lengthy discussion about the biological relevance of the assumptions and the conditions under which they will hold. They found that in many cases the idea of neurons as oscillators is reasonable.

Despite these caveats, the theory of neurons as oscillators provides us with qualitative predictions, such as the presence of synchronous oscillations or of a bistability. These predictions tend to be robust even in regimes where the mathematical assumptions of perfect oscillators do not formally hold (Smeal et al. 2010). Hence, although the theory of neurons as oscillators is unlikely to provide us with millivolt-precise predictions of measurements from the brain, it is capable of predicting important qualitative features of brain activity such as synchronous activity. These are powerful predictions about a highly complex system (the brain!), nothing systems neuroscientists should ignore.

The Phase-Response Curve

With neurons conceptualized as oscillators, we can utilize the phase-response curve (PRC) to study how neural population behavior can emerge in networks of coupled oscillating neurons. Figure 2A shows the voltage of a spiking neuron and how a small perturbation (such as an excitatory postsynaptic potential) shifts the spike to a later time. We can plot the spike time shift against the time of the perturbation. We also normalize both measures to a phase (0 to 2π) and a phase shift, as mentioned above. The resulting plot is a phase-response curve. Its shape is a fingerprint of a neural oscillator and a powerful predictor of a neuron's behavior in a network (see below and Achuthan et al. 2011).

It is worth noting that we are presenting work principally based on the infinitesimal PRC (iPRC), the response to vanishingly small inputs. This iPRC is a mathematical construct. We derive insights about realistic inputs by convolving the iPRC with those inputs (multiplying them point by point; see appendix and Netoff et al. 2005a).

PRCs tend to have fairly stereotypical shapes in all neurons that spike regularly. First, a neuron is insensitive to any kind of small inputs at the moment of the spike. Hence, PRCs tend to be 0 at the phases of 0 and 2π, the times of the previous and next spike. Next, most PRCs have a single maximum and minimum per cycle. We distinguish between type I and type II PRCs (Brown et al. 2004). Type I PRCs are never negative; spikes can only be advanced. Type II PRCs have a negative lobe, generally right after the previous spike, before becoming positive. In neurons with such PRCs, spikes can be advanced and delayed (Brown et al. 2004; Ermentrout 1996). The type of PRC is crucial for a neuron's behavior in a network, and knowing the PRC types of the neurons in a network alone can allow us to make educated guesses about the dynamics of that network (see below).

We can determine the PRC of both real neurons and neuron models. There are many ways to experimentally estimate the PRC of a neuron (Torben-Nielsen et al. 2010). The direct method consists of recording from a regularly spiking neuron and measuring its interspike interval. We then inject a brief, small perturbation and again measure its interspike interval. We next compare the perturbed and the unperturbed interspike intervals and plot the change against the timing (equivalent to the phase) of the injected perturbation. Plotting this spike time change for a series of perturbations timed between subsequent spikes provides the PRC. The direct method directly measures the PRC as it is defined and described above.

However, this direct method for determining the PRC performs poorly when applied to less than ideally regularly spiking neurons or small data sets. For such cases, a number of more sophisticated methods are available (Netoff et al. 2012; Torben-Nielsen at al. 2010). For example, Ota et al. (2009, 2011) used a Bayesian method to estimate the PRC that is accurate (at least when applied to noisy systems where the real PRC is known) but computationally intensive. Similar methods based on maximum likelihood were used by Nakae et al. (2010). Below, we relate the PRC to some other quantities commonly measured in neurons, and these relationships allow us to also estimate the PRC from noisy data.

Relationship between the PRC and other measures.

Because the PRC measures the effects of perturbations on the spike timing of a neuron, it is not surprising that it is related to other common measures that characterize the response of neurons to external stimuli such as synaptic inputs.

The spike-triggered average (STA) is a popular measure in systems neuroscience. It is calculated by aligning all spikes and then averaging the voltage waveforms before the spikes. The STA tells us what kind of input pattern has, on average, evoked a spike. We previously showed (Ermentrout et al. 2007) that the reversed derivative of the PRC is the STA. In retrospect, this is not surprising, since the STA is the reverse correlation between the spike and the stimulus. The relationship between the STA and the PRC strictly only holds when the input to the neuron is white noise, another assumption that needs to hold at least approximately for the STA-PRC correspondence to hold. For a regularly firing neuron, the STA makes sense for the duration of the average interspike interval.

The peristimulus time histogram (PSTH) measures the probability of a spike occurring at a given time after a stimulus occurs. Gutkin et al. (2005) showed that the PRC is the spike time minus the inverted integral of the PSTH. Hence, there is a direct relationship between the PRC and two measures commonly used in systems neuroscience, the STA and PSTH. For neural oscillators receiving small stimuli, once you know one of these measures, you can extract the other two. This relatedness between measures will come in handy when we will use the PRC to bridge cellular and systems neuroscience. With the PRC we not only have a measure that is well grounded in the mathematical theory of oscillators, but also a measure related to the STA and PSTH, which have been determined for many neurons in a variety of animals, brain regions, and experimental conditions! Again, this shows how useful the PRC can be as a conceptual bridge between cellular and systems neuroscience. In the appendix, we provide exact formulas for the relationships between the STA and the PSTH for the interested reader.

PRCs in Vertebrate Neurons

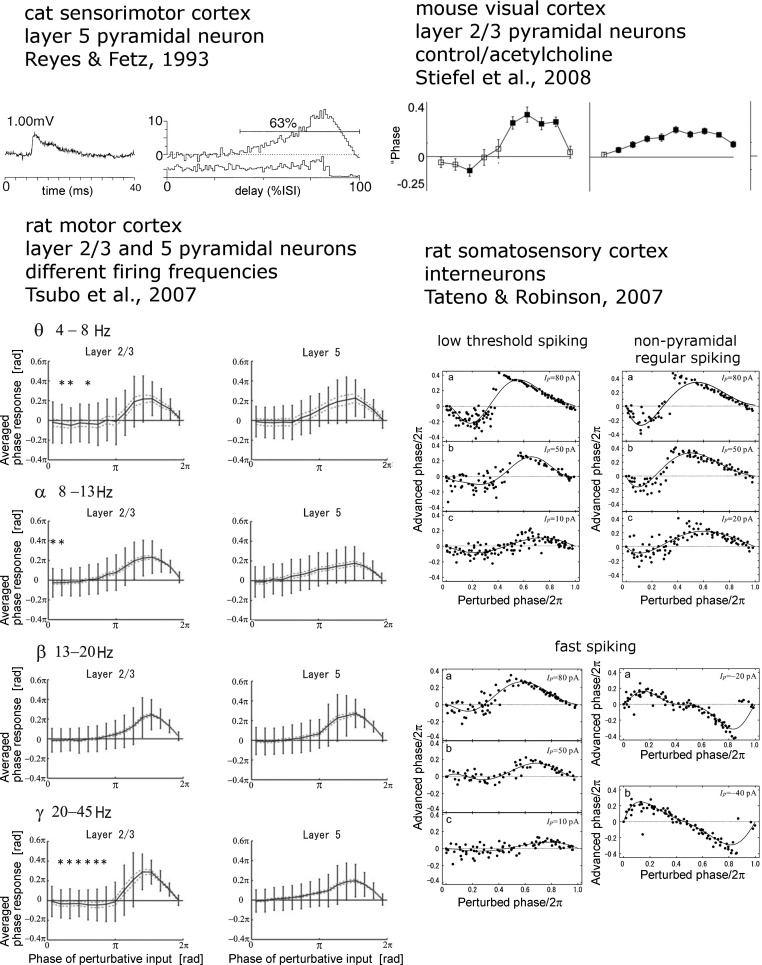
PRCs have been measured in a variety of vertebrate and invertebrate neurons under a variety of conditions. There is some variation in the way the PRCs are determined, how they are plotted, and even what they are called (shortening-delay curves, etc.). However, the basic premise to measure the effect of a timed input on spike timing is similar in all of these studies. A number of studies have investigated PRCs in neurons of the mammalian cortex (see Fig. 3).

Reyes and Fetz (1993) measured the PRC in vitro in pyramidal neurons in the cat sensorimotor cortex. They found a purely positive (spike acceleration only, type I) PRC in these neurons. Tsubo et al. (2007) studied the PRCs of both layer II/III and layer V rat motor cortex pyramidal neurons, at a variety of spiking frequencies. They found that layer II/III neurons, especially when firing at a higher frequency, were more likely to have a biphasic PRC. Tateno and Robinson (2007) measured PRCs of three classes of interneurons in the rat somatosensory cortex: low-threshold spiking, nonpyramidal regular spiking, and fast spiking. They found that these interneurons usually have biphasic PRCs. Stiefel et al. (2008) determined the PRCs of mouse layer II/III cortical pyramidal neurons when subjected to the neuromodulator acetylcholine. In about half of the recorded neurons, acetylcholine caused a shift from a biphasic to a monophasic PRC (type II to I). Burton et al. (2012) measured PRCs in dozens of mitral cells in the mouse olfactory bulb and found a great deal of heterogeneity; nevertheless, they could all be parameterized by a very simple function with just three parameters.

One question that is frequently asked is how does the shape of the PRC depend on the nature of the ionic processes that underlie it (see e.g., Farries and Wilson 2012)? In general, there is no simple mapping from channel type to PRC shape, but there are a few principles that seem to hold. High-threshold potassium channels (such as the calcium-dependent potassium channel) tend to make the PRC flat and nearly zero for a good part of the time after the spike (similar in shape to the β-frequency PRCs in rat motor cortex shown in Fig. 3). Low-threshold potassium currents and the h-current can introduce a negative lobe after the spike such as seen in the control (no acetylcholine) PRCs in mouse visual cortex in Fig. 3. A systematic study of how various channels affect the shape of the PRC for several specific models can be found in Ermentrout et al. (2014). As noted above and discussed elsewhere (Brown et al. 2004; Ermentrout 1996; Goldberg et al. 2007; Hansel et al. 1995; Pfeuty et al. 2005), the shape of the PRC can be related to the way through which the neuron goes from rest to firing. This transition is called a bifurcation (Izhikevich 2010), and there is some relationship between the type of bifurcation and the shape of the PRC (Brown et al. 2004). Because changes in the ionic conductances can change the bifurcation of the neuron, understanding the latter will shed light on how these changes alter the shape of the PRC. The reader might reasonably ask why one would care about the shape of the PRC; the answer to this is provided in Neural Oscillators in Networks, Stochastic synchronization.

Fig. 3.

Experimentally determined PRCs from several types of vertebrate forebrain neurons. Shown are cat somatosensory cortex layer V pyramidal neurons (top left) [Reprinted with permission from Reyes and Fetz (1993).], rat motor cortex layer II/III pyramidal neurons at different firing frequencies (bottom left) [Copyright: 2007 Tsubo et al., Federation of European Neuroscience Societies, and Blackwell Publishing Ltd. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.], rat layer II/III pyramidal neurons with and without cholinergic neuromodulation (top right) [Copyright: 2008 Stiefel et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.], and rat somatosensory cortex interneurons (bottom right) [Reprinted from Biophysical Journal, vol. 102, Tateno T and Robinson HP, Phase resetting curves and oscillatory stability in interneurons of rat somatosensory cortex, p. 683–695, Copyright 2007, with permission from Elsevier.].

A concept related to the PRC is the spike-time response curve (STRC; Acker et al. 2003; Netoff 2014). In creating the STRC, the neuron is stimulated with the biologically appropriate stimulus (such as a synaptic current) and the time shift of the next spike is measured to compute the STRC. The curve can then be used to study synchronization in pairs of neurons (see Netoff et al. 2005b) just as the PRC is, as described below. Given the form of the synaptic input, it is possible to obtain the STRC from the PRC via convolution (see appendix).

Neural Oscillators in Networks

Coupled neurons.

Given that we know the PRCs of a number of cortical neurons, can we deduce from these PRCs anything about cortical network dynamics? Yes, because with knowledge of the neurons' firing frequency and PRC together with knowledge of the type of coupling (inhibitory/excitatory, delay, relative strength), we can derive insights about neural population behavior. All of these values can be experimentally measured, and even though our theoretical predictions are based on a rather abstract model, we can experimentally validate them.

We can implement networks using just the PRC and a simple pulse-like connection between neurons. Every time a neuron fires, it shifts the cycle of the postsynaptic neuron as determined by that neuron's PRC. All the parameters in this model (PRC and synaptic connections) can be experimentally determined and provide us with insights on whether or not the network of neurons under investigation will synchronize.

This approach generalizes to the coupling of neurons with excitatory or inhibitory synapses, and to chains and networks of neurons. The approach is to couple the differential equations describing the PRC of each neuron so that we have one expression describing the “phase difference” between the neurons (see appendix; Netoff et al. 2005b; Schwemmer and Lewis 2011). We can predict the behavior of a pair of mutually coupled rhythmically spiking neurons by taking into account the difference between the intrinsic frequencies of the neurons and the difference between their PRCs. The resulting interaction function describes how the relative phase between the two oscillators changes as a function of the frequency difference, coupling strength, etc. Zeros of the interaction function determine phase relationships between the two neurons, and the slope of the interaction function at such a zero determines the stability. For example, if the two coupled neurons are identical and have the same frequency, there are always at least two zeros to the interaction function: 0 and π, corresponding, respectively, to synchronous oscillations and out-of-phase or anti-phase oscillations.

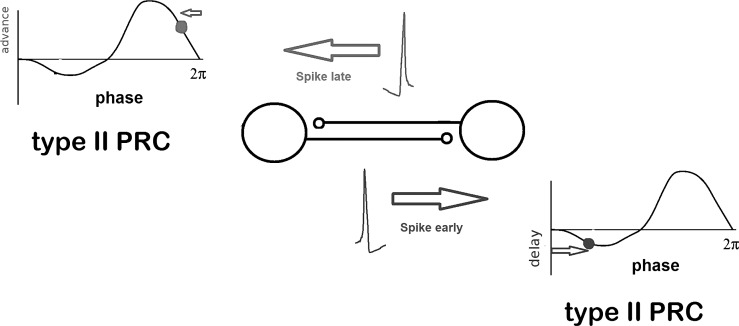
We illustrate the intuition behind this kind of analysis, assuming that there the two neurons are the same and that they have a negative sine-wave PRC. That means that if the stimulus comes in the first half of the cycle (with the spike marking the start of the cycle), then the spike will be delayed, whereas if it comes in the second half of the cycle, it will be advanced. If neuron 1 spikes before neuron 2, then when neuron 1 fires, neuron 2 will be in the latter half of its cycle and will speed up; when neuron 2 fires, neuron 1 will be in the first half of its cycle and will slow down. Thus the neuron that is ahead will be delayed and the neuron that is behind will be advanced, leading to eventual synchrony where the neurons fire with zero spike-time difference (Fig. 4).

Fig. 4.

PRCs and coupled oscillators. A spike occurring too early for synchrony between 2 neurons with a type II PRC will lead to a delay in the next spiking cycle. Inversely, a spike occurring too late will lead to a spike advancement. This mechanism corrects for deviations from synchrony. The critical property of the PRC is the positive slope at the zero-crossing.

During “phase locking,” coupled neural oscillators have fixed timing between spike of each cycle. This is found in central pattern generators (Marder et al. 2005). The swimming central pattern generator in the lamprey produces an oscillation where successive spinal segments have a time lag of roughly 1% of the cycle (Cohen et al. 1992; Nishii et al. 1994). In cortical rhythms, the notion of phase locking is more complex. Multiple cell types in six layers and with highly specific and plastic connections make a simple notion of a stable phase relationship between two cells untenable. However, the rhythmic macroscopic local field potentials measured in the electroencephalogram (EEG) only arise when many neurons fire in close temporal proximity. Hence, we can assume that stable phase relationships exist between neurons in the cortex, and we can study this by treating them as oscillators.

However, more complicated cases than simple phase locking and synchrony can also occur: If the difference between the intrinsic frequencies of the neurons is large enough, then the function describing their phase difference will never be zero, and the two oscillators will drift apart with respect to each other and never lock (see Ermentrout and Rinzel 1984). The effective interaction function between the two neurons is found by convolving the PRC (a point-by-point multiplication) with the synaptic current. Suppose that the PRC was a negative sine and the synaptic current a simple exponential. The effective interaction function will then be a phase-shifted sine; if the synapse is slow enough, the effective PRC could be flipped and thus destroy the possibility of synchrony. Fast synapses lead to an effective interaction function that is the same shape as the PRC. Delays are very common in the transmission of information from one neuron to another and across distances, and the simulation and study of systems with delays is much harder than with nondelayed systems. One of the nice properties of averaging the synaptic current with the PRC is its effects on delay: the effect is just a phase shift of the interaction function that is equal to the product of the delay and the frequency of the neuron (Izhikevich 1998). As with the decay and rise time of synapses, delays can alter the synchronization properties of neurons, changing a stable locked state to an unstable one, and vice versa.

The slope of the effective interaction function near its zero-crossings is a critical determinant in how well a pair of coupled oscillators will synchronize and how tolerant they are of differences in frequency. As explained in the previous paragraph, the shape of this function depends a great deal on the shape of the PRC, and for synapses that are fast enough, the two are equivalent. For this reason, there is much interest in how neural modulators and other manipulations of neurons affect the PRC. Currents such as the h-current, the M-type potassium current, and other low-threshold potassium currents have been shown to exhibit profound effects on the shape of the PRC and thus the synchronization properties of pairs of neurons (Ermentrout et al. 2001, 2014; Fourcaud-Trocmé 2003; Hansel et al. 1995; Oprisan et al. 2004; Schultheis et al. 2010; Stiefel et al. 2008). Active currents in the dendrites have also been shown to have a profound effect on the shape of the PRC (Goldberg et al. 2007). For example, the addition of an M-type potassium current can change a PRC that only advances the phase to one that can both advance and delay the phase (Cui et al. 2009; Stiefel et al. 2008); this change in shape allows an excitatorily coupled pair of oscillators to switch from out-of-phase oscillations to perfect synchrony (Ermentrout et al. 2001).

Experimentalists and theorists have used this type of approach to predict many different aspects of synchrony in two or more neurons (Achuthan and Canavier 2009; Achuthan et al. 2010; Canavier and Achuthan 2010; Maran and Canavier 2008). Mancilla et al. (2007) used the PRCs to determine synchronization in inhibitory neurons connected via gap junctions. Akam et al. (2012) measured the network PRC (that is, the PRC of an intrinsic hippocampal rhythm, via stimulation of dentate axons) and used this to predict the entrainment to optical stimuli.

In the first effort at network analysis, we assumed that the neural oscillators were perfect and that there was no variability at all. In real biological systems, there are many sources for “noise,” such as the stochastic opening and closing of channels or inputs from other sources not included in the model network. We can modify our analysis to take this stochasticity into account: If the noise-free system predicts synchrony, then the presence of independent uncorrelated noise will cause the phase-difference density to be an approximate Gaussian function centered at zero phase difference. The width of the Gaussian is proportional to the slope of the effective interaction function at zero (Pfeuty et al. 2005). These authors also showed that the cross-correlogram of the spikes in such a noisy coupled oscillator model is proportional to the phase-difference density. Details of these relations can be found in the appendix.

In all of these cases, there is a balance between the forces organizing network behavior, such as the neuron's intrinsic currents and their connections, and the noise present in the network. For any noise level, there will be a minimum connection strength necessary for the network behavior to emerge.

Stochastic synchronization.

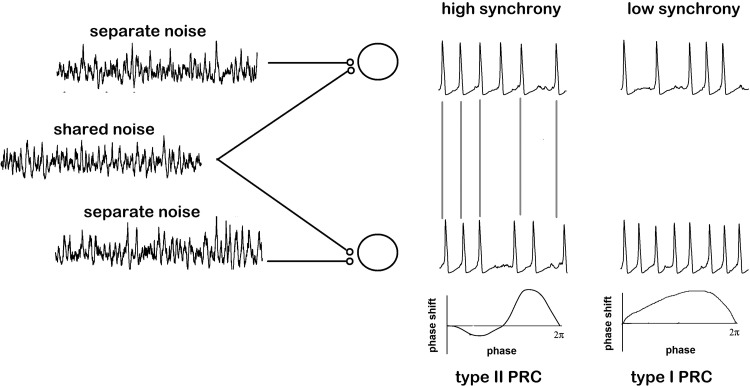
Above, in Coupled neurons, we established how coupling between neural oscillators could lead to synchronization, even in the presence of noise. If neurons receive correlated (common) inputs, their outputs will also be correlated. Let us now look at a concrete case where we can predict the behavior of neural populations from their PRCs and their coupling. Stochastic synchronization is a process by which oscillatory neurons receiving shared noisy inputs can partially synchronize their spike times (Ermentrout et al. 2008; Fig. 5). The measure of correlation can be over time windows of varying length. In the case of long windows, the correlation is measured with respect to the numbers of spikes during the window, and we will call this “spike-count correlation.” Over windows shorter than the mean interspike interval, the timing of individual spikes is what is typically correlated, and we will refer to this as “spike-time correlation” (synchrony). The dependence of the output correlation as a function of the input correlation is the subject of much recent interest (de la Rocha et al. 2007; Litwin-Kumar et al. 2011).

Fig. 5.

Stochastic synchronization. Neurons receiving shared noisy inputs will synchronize more readily if they display type II PRCs.

This is another case where we can apply our phase model of a neuron to elucidate neural population behavior. The phases of the neurons subjected to noise are given by their PRC multiplied by the noise (Teramae and Tanaka 2004; Teramae et al. 2009). Similarly to the coupled noisy oscillator case, we expect that the phase difference or timing difference between the two neural oscillators will be determined by a phase-difference density function. This function will depend on the correlation of the inputs. (See appendix for explicit formulas.) We can indeed figure out how the spike-time correlation of the outputs depends on the input correlation. The result of this work is that neurons with a biphasic (type II) PRC respond more strongly to shared inputs than neurons with monophasic (type I) PRCs (Fig. 5). This fact was first shown by Barreiro et al. (2010) through extensive numerical simulations and was later shown analytically by Abouzeid and Ermentrout (2011). Again, there are simplifying assumptions in these papers, namely, that the PRCs are identical and that the noise is white; however, even extensions to heterogeneous oscillators with “colored” noise can be mathematically analyzed (Zhou et al. 2013).

Interestingly, the sign of the PRC does not matter for the transfer of correlation, and thus for stochastic synchronization, whereas it matters a great deal for synchronization via coupling. Similarly and surprisingly, the magnitude of the PRC does not matter either (also in contrast with coupling). The intuition behind this is that the amplitude will help when the noise signals are the same between the oscillators but will hurt when they are different so that for partial correlations, the effects of amplitude “cancel.” So far, we have talked about spike-time synchronization; synchrony over narrow time windows. For spike-count correlation (long time windows), the opposite conclusion holds and type II PRCs are very bad spike count correlators compared with type I PRCs (Abouzeid and Ermentrout 2011; Barreiro et al. 2010). Intuitively, the reason for this is because type I PRCs are associated with neurons that are integrators rather than resonators (Izhikevich, 2010) and thus are able to “integrate” the common noise and better maintain a correlated spike count.

In summary, the ability of neural oscillators to transfer input correlations to output synchrony depends in a complex way on the shape of the PRC. At low correlations, a PRC with a small average value will improve signal transfer and the ability to synchronize. Looking at the PRCs from various neurons (Fig. 3), those which have a prominent negative lobe after spiking will be better stochastic synchronizers than the ones without such a lobe (since they will have smaller mean value). Similarly, the skew to the right of some of the PRCs will also affect the ability of a PRC to transfer correlation.

The shape of the PRCs is dependent on the neuron's ionic conductances, and these can be altered by various neuromodulators. We can hence imagine scenarios where a network can increase and decrease the transfer of correlation as a function of its functional state (attention, arousal, sleep/wakefulness). Changes in the properties of the membrane can thus have a drastic effect on how information is transferred (Ratté et al. 2013). PRC theory provides a connection between neuronal biophysics and coding capabilities of the neuron.

Insights About Neural Dynamics from the PRC

We think it is a very worthwhile intellectual exercise to contemplate how the experimentally measured PRCs in Fig. 3 relate to the theoretical predictions about network activity based on PRCs in Figs. 4 and 5. Can we combine these neurons' PRCs with the knowledge of how PRCs affect network dynamics and learn something about these neurons' population activity?

An example of such a theoretical–experimental connection is found in the study by Tateno and Robinson (2007). When they found different PRCs for different interneuron types, they wondered what the consequences of these differences could be for the dynamics of the interneurons in vivo. They calculated the Lyapunov exponent, a measure of divergence from the unperturbed state, based on the measured PRCs. The calculations showed them that low-threshold spiking interneurons and nonpyramidal regular-spiking interneurons have greater oscillatory stability in the presence of small noisy inputs than fast-spiking interneurons.

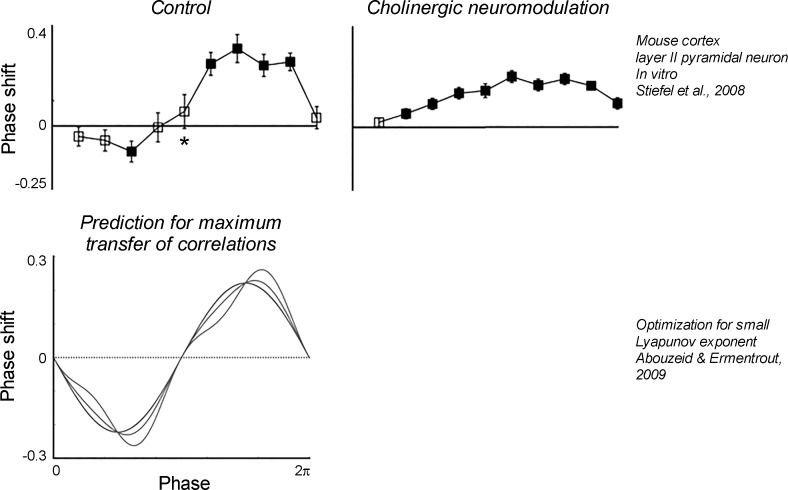
We propose another theoretical–experimental connection, concerning the effect of acetylcholine on the PRCs of cortical neurons. The PRCs measured in layer II/III pyramidal neurons by Stiefel et al. (2008; Fig. 6) and the PRCs optimized for a maximum transfer of correlations (Abouzeid and Ermentrout 2009) are very similar. This similarity indicates that in their base state, about half the pyramidal neurons might be optimized to fire maximally coherently, as is indeed observed in deep (delta wave) sleep. However, the PRCs changed when we experimentally applied the neuromodulator acetylcholine. This neuromodulator is associated with active wakefulness and rapid eye movement (shallow) sleep. It alters a number of K⁺ conductances, and by doing so it changes the originally biphasic PRC of the pyramidal neurons to a purely positive (type I) PRC. The PRCs of the other half of the pyramidal neurons, which were purely positive (type I) to begin with, changed in a quantitatively similar way. Hence, under acetylcholine, the PRCs of pyramidal neurons are less similar to the PRCs predicted to achieve a maximum transfer of correlations. Correlated activity will hence likely decrease with a shift from biphasic to monophasic PRCs. And indeed, cortical coherence is temporally and spatially reduced during gamma oscillations, thought to be evoked by acetylcholine. This line of reasoning connects the biophysical effects of acetylcholine, via the PRC, to the population activity of neurons in a network. It would have been essentially impossible to directly deduce insights about the population activity from the complex biophysical changes triggered by acetylcholine without the intermediate conceptual step of describing neurons as oscillators.

Fig. 6.

Hypothesis: PRCs altered by acetylcholine are near-optimal for the transmission of correlations to neurons with partially shared inputs. Top, PRCs experimentally measured under control conditions (left) and under the influence of a cholinergic agonist (right). [Copyright: 2008 Stiefel et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.] Bottom, PRCs theoretically predicted to optimize the transmission of correlations to neurons with partially shared inputs. These resemble the PRCs experimentally measured under control conditions, indicating that acetylcholine transforms the cortex into a state less likely to transmit correlations. [Reprinted with permission from Abouzeid and Ermentrout (2009).]

We hence believe that the abstraction of neurons as oscillators is at a conceptual sweet spot: although the reduction in model complexity is significant, it retains strong explanatory power, at least under many input conditions. We encourage our colleagues to consider how the insights about neural oscillators combined with measured PRCs can bridge cellular and network neuroscience in their fields of study. Anyone studying neural oscillations at a neural population or EEG level should contemplate what kind of oscillators could be responsible for the observed network oscillations. Phenomena such as phase walk-through (Ermentrout and Rinzel 1984) between oscillators, a lesser or stronger vulnerability of population activity to noise or perturbations, and neural synchrony could all find simple yet powerful explanations in the theory of neural oscillators.

GRANTS

This work was supported by National Science Foundation Grant DMS1219753 (to G. B. Ermentrout).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

K.M.S. and G.B.E. conception and design of research; K.M.S. performed experiments; K.M.S. analyzed data; K.M.S. and G.B.E. prepared figures; K.M.S. and G.B.E. drafted manuscript; K.M.S. and G.B.E. edited and revised manuscript; K.M.S. and G.B.E. approved final version of manuscript.

APPENDIX: MATHEMATICAL DETAILS

Relationship to Other Quantities

Ermentrout et al. (2007) showed that if weak white noise is applied to an oscillator, then the spike-triggered average (STA) of the resulting spike train can be directly related to the phase-response curve (PRC) through a simple relationship:

$$STA(t)=-{\sigma }^{2}PR\mathit{C\prime }(T-t).$$

That is, the STA is proportional to the derivative of the PRC multiplied by the variance of the noise (σ²).

For weak, brief inputs, the peristimulus histogram (PSTH) can also be related to the PRC as follows. Let G(t) = t − PRC(T − t) and let H(t) be its inverse, that is, H[G(t)] = t. Gutkin et al. (2005) showed

$$PSTH(t)=\frac{1}{T}\frac{d}{dt}H(t).$$

Thus, given the PSTH, integrate it to get H(t) and then invert H(t) to get G(t), and finally, note that

$$PRC(t)=t-G(t).$$

As with the STA method, this technique also involves integration, and so a smooth PRC is obtained.

iPRC and PRC and Coupling

In this review we discuss the PRC of neurons, the spike-time shift in response to a perturbation, plotted as a function of the phase of the perturbation. This is a quantity that can be measured experimentally and is easy to grasp intuitively. In the purely theoretical case that the size of the perturbation approaches zero, we get the infinitesimal phase-response curve (iPRC). The iPRC is a mathematical construct that is uniquely determined (up to a phase shift) by the underlying limit cycle oscillator. The advantage of the iPRC is that once you have it, you can obtain the PRC for arbitrary stimuli, as long as they are small enough in amplitude. The small amplitude assumption is necessary because the iPRC is only a linear approximation to the effects of an instantaneous impulse. The PRC and the stimulus used to measure it, S(t), relate to the iPRC convolution:

$$PR{C}_S(\theta )={\displaystyle {\int }_0^{T}S(t)iPRC(\theta -t)}dt.$$

We must emphasize that the PRC for large-amplitude stimuli cannot be obtained from this simple formula because, as we have emphasized, the iPRC is linear in nature.

We can also describe the interaction between two oscillators. When two identical oscillators are mutually coupled, their phases, θ, are determined by their intrinsic frequency, ω, and their PRC at the respective phase, multiplied by the strength of the interaction, a. In this case we assume zero delay in the signaling between the neurons:

$$\frac{d{\theta }_1}{dt}={\omega }_1+a\cdot PRC({\theta }_1-{\theta }_2)$$

$$\frac{d{\theta }_2}{dt}={\omega }_2+a\cdot PRC({\theta }_2-{\theta }_1).$$

The phase difference between the two neurons is ϕ = θ₂ − θ₁, described by

$$\frac{d\varphi }{dt}=v+g(\varphi ):=f(\varphi ),$$

where v = ω₁, ω₂ is the frequency difference, and g(ϕ) = a[PRC(ϕ) − PRC(−ϕ)] is the interaction function. When dϕ/dt = 0, the system is in an equilibrium, phase-locked state. Thus, if we know the PRC of neurons and how they are connected, we can predict the behavior of a pair of mutually coupled rhythmically spiking neurons.

In the presence of white noise, the phase-difference equation is a stochastic differential equation, and because it is a scalar equation, it is possible compute the phase-density function, P(ϕ), that describes the probability of finding the phase difference at a particular phase, ϕ. Pfeuty et al. (2005) showed that when the frequencies of the two neurons are identical (ν = 0), the probability density satisfies

$$P(\varphi )=N{e}^{\frac{-2}{{\sigma }^2}G(\varphi )}$$

where

$$G(\varphi )={\displaystyle {\int }_0^{\varphi }g(s)}ds$$

and N is a constant normalization factor. For example, if g(ϕ) = −a·sin(ϕ), then

$$P(\varphi )=N{e}^{\frac{-2a}{{\sigma }^2}(1-cos\varphi )}.$$

Pfeuty et al. also showed that the spike-time cross-correlation of the two neurons is closely related to Pϕ. Specifically, they showed that

$$C(\tau )=P(-\tau )-1/2\pi .$$

This means that for coupled neural oscillators in the presence of noise, we can relate the spike-time cross-correlation to the integral of the PRC.

Stochastic Synchronization

We provide a number of formulas that are u seful for determining how neural oscillators are able to transfer correlations via stochastic synchronization. Let θ₁, θ₂ be the phases of two identical oscillators that are subjected to Gaussian white noise with correlation c. That is, consider three noisy signals, ξ₁(t), ξ₂(t), ξ₀(t), that are independent with autocorrelation σ²δ(t) (where σ² is the magnitude of the noise). We drive oscillator 1 with noise z₁(t) = $\sqrt{c}$ξ₀(t) + $\sqrt{1-c}$ξ₁(t) and oscillator 2 with z₂(t) = $\sqrt{c}$ξ₀(t) + $\sqrt{1-c}$ξ₂(t). When c = 1, both receive exactly the same noisy signal, whereas when c = 0, there is no correlation. The phases of the neurons satisfy the following (Teramae and Tanaka 2004; Teramae et al. 2009):

$$\frac{d{\theta }_1}{dt}=1+z_1(t)PRC({\theta }_1)$$

$$\frac{d{\theta }_2}{dt}=1+z_2(t)PRC({\theta }_2).$$

As with the noisy phase locking, the main quantity of interest is the phase-difference density function, which we will call R(ϕ). Burton et al. (2012) provide a very simple formula for the phase-difference density. Let

$$h(\varphi )={\displaystyle {\int }_0^{2\pi }PRC(t)PRC(t+\varphi )}dt.$$

where h(ϕ) is the autocorrelation of the PRC. Then

$$R(\varphi )=\frac{N}{1-c\frac{h(\varphi )}{h(0)}},$$

where N is a normalization factor such that R integrates to 1 over the interval from 0 to 2π.

We see that if c = 0, then R(ϕ) = 1/2π as intuitively expected; when there is no input correlation, the phases should be independent and the phase differences are uniformly distributed. For c = 1, there is division by zero when ϕ = 0, and R(ϕ) becomes a delta (impulse) function; the oscillators are perfectly synchronized. The function h(ϕ) is symmetric about ϕ = 0 so that the peak of R(ϕ) is always at synchrony, ϕ = 0, and thus the correlation at zero time lag is the largest and is C(0) = N/(1 − c). For small c (weak input correlations), we get a simple expression for the peak correlation:

$$C(0)=c\frac{1-a}{2\pi },$$

where

$$a=\frac{{\left[{\displaystyle {\int }_0^{2\pi }PRC(s)ds}\right]}^2}{2\pi {\displaystyle {\int }_0^{2\pi }PR{C}^2(s)ds}}.$$