Methyl-CpG/MBD2 Interaction Requires Minimum Separation and Exhibits Minimal Sequence Specificity

Abstract

Determining the pattern of methylation at CpG dinucleotides in a cell remains an essential component of epigenetic profiling. The correlations among methylation, gene expression, and accompanying disease have just begun to be explored. Many experiments for sensing methylation use a relatively inexpensive, high-throughput approach with a methyl-binding domain (MBD) protein that preferentially binds to methylated CpGs. Here, we characterize the cooperativity and sequence specificity of MBD2-DNA binding in a pulldown experiment revealing three potential biases in such experiments. The first is caused by steric clashes between two MBD2 proteins at mCpGs separated by 2 bp or less, which suggests that simultaneous binding at these sites is inhibited. This is confirmed by comparing input versus pulldown high-throughput sequencing data on M.SssI-treated samples, from which we also find that pulldown efficiency sharply increases for DNA fragments with four or more mCpGs. Analysis of these two data sets was again employed to investigate MBD2’s sequence preferences surrounding a methylated CpG (mCpG). In comparing the distributions of bases at positions with respect to an mCpG, statistically significant preferences for certain bases were found, although the corresponding biases in pulldown efficiency were all <5%. While this suggests that mCpG sequence context can mostly be ignored in MBD2 binding, the statistical certainty exhibited by our high-throughput approach bodes well for future applications.

Introduction

The pattern of methylated nucleotides in mammalian genomic DNA (in humans, this is most commonly the methylated cytosines of a CpG) changes with age (1); is affected by the environment (2, 3, 4) and disease (5, 6); and, in an aberrant form, is a hallmark of many forms of cancer (7, 8, 9). An accurate measurement of the methylome—the methylation level of each CpG—is crucial to understanding how the methylome is read out by elements of the cell, influences gene expression, and comprises an important part of the epigenome. In these measurements, the highest possible fidelity should be pursued. Various techniques have been introduced to measure methylation on a genomewide scale. Methods such as whole genome bisulfite sequencing (WGBS) (10)—and the related method of reduced representation bisulfite sequencing (RRBS) (11)—offer single-nucleotide resolution of the methylome. In WGBS and RRBS, the treatment of DNA with sodium bisulfite converts an unmethylated cytosine to a uracil and leaves methylated cytosines untouched. Treated and untreated fragments are sequenced separately, and methylation levels of CpGs are detected by the number of cytosines and thymines observed at each position in the treated sample when compared to the untreated sample. One drawback to WGBS is that it is expensive, and the augmented version of this process, RRBS, works best on areas of high CpG density (12). Neither version can distinguish between methylated cytosine and hydroxy-methylated cytosine (both are unconverted by the bisulfite treatment).

Enrichment-based methods for genomewide DNA methylation determination, on the other hand, rely on a protein or antibody’s high affinity for methylated DNA to pull fragments containing methylated CpGs out of solution. The most reliable of these, so far, uses methyl-binding domain proteins (MBDs) (12, 13). As the name suggests, this family of proteins contains a methyl-binding domain that allows it to preferentially bind to a methylated CpG (mCpG) in DNA. Of the known MBD proteins, MBD2 discriminates most strongly between mCpGs and other genetic sequences (14, 15) and has been incorporated into several commercially available kits for methylation detection (16). A typical MBD pulldown experiment for enrichment of methylated DNA consists of: (1) fragmentation of genomic DNA, (2) introduction of the fragments to the magnetic microbeads coated in biotinylated MBD proteins, (3) an incubation period during which the MBD proteins interact with the DNA fragments and potentially bind, (4) pulldown of the beads (and the protein-bound fragments), (5) elution to free the fragments from the proteins, (6) sequencing of the fragments, and finally (7) an alignment of those fragments to a reference genome. If the proteins have a suitably higher affinity for mCpGs over unmethylated DNA, one can reasonably expect pulldown fragments to contain at least one mCpG, and that fragments with greater numbers of mCpGs are more likely to be pulled down.

There are several advantages and disadvantages to this enrichment method. An MBD pulldown experiment is relatively inexpensive and can supply deep coverage of the entire genome (17). The MBD2 protein is much more sensitive to methylated cytosines than hydroxy-methylated cytosines (18). However, the process of inferring methylation level from pulldown coverage is sensitive to the assumptions we make about the protein binding process and the biases that the protein interaction inevitably introduces to the set of captured, and subsequently mapped, fragments. It is imperative to overcome these challenges to make this method competitive with techniques that readily provide single-nucleotide resolution. To do this, we must understand the biophysical features of MBD2-DNA binding in the pulldown experiment: the sequence specificity of an MBD2 protein binding a single methylated DNA site; the level of binding cooperativity between multiple methylated DNA sites and MBD2 proteins; and the effect of nonspecific binding on the pulldown. Characterizing the biophysical properties of the MBD2-DNA interaction is also important to obtain a better understanding of the physical limitations of these pulldown experiments.

Our contribution to the characterization of MBD2-DNA binding and the biases in MBD pulldown experiments focuses on three effects. The first deals with the structure and size of the MBD2 protein. Certain arrangements of MBD2 proteins on methylated DNA may be prohibited by steric clashes between two proteins if they are too close together, producing a negative cooperativity between the two binding sites. The result is that fragments with differing levels of methylation could have very similar probabilities of being pulled down. We find the motivation for this effect by using the solved structure of an MBD2-mDNA complex to model the geometry of two bound MBD proteins. In addition, we use the statistical power of a large library of pulldown fragments to see the effect that small separations between mCpGs have in a pulldown experiment. We then look at the effect of the number of mCpGs on a fragment, a second source of cooperativity among methylated DNA sites. A greater number of mCpGs not only increases the chance of an MBD protein initially binding, but may also facilitate binding of additional MBDs because the initial binding localizes the DNA fragment to the surface of the bead. Finally, we use this large library of pulldown fragments to investigate the sequence specificity displayed by the MBD2 protein. As suggested by previously published results (19), the sequence around the mCpG may alter how well the protein binds to it.

We find that for two mCpGs separated by two basepairs (bp) or fewer, multiple binding is inhibited, decreasing pulldown for these fragments relative to those with better separated mCpGs. We also find that mCpG number has a nonlinear effect on MBD pulldown, biasing the sample toward fragments with four or more mCpGs. Lastly, we find that the nucleotides neighboring an mCpG have a distinguishable but negligible influence on binding to MBD2, also partially revealing an influence of nonspecific binding. These results can be used in future work to generate more accurate descriptions of a cell’s methylome. At the same time, this article provides an example of the detailed DNA-protein interaction characterizations that are possible with high-throughput sequencing.

Materials and Methods

Structural model of MBD2 binding for small separations

To determine the feasibility of two nearby mCpGs bound by MBD2 domains, we constructed a model of such binding events using structural data of the MBD2-mDNA complex. We defined the separation between two CpGs (MBD2 binding sites) to be the number of nucleotides after the first CpG’s guanine (G) and before the second CpG’s cytosine (C). Molecular graphics and analyses were performed with the UCSF Chimera package (http://www.cgl.ucsf.edu/chimera/). We used a molecular model of an MBD2-mDNA complex (PDB: 2KY8, model 0) from a solution nuclear magnetic resonance (NMR) experiment on chicken MBD2 (cMBD2) methyl binding domain bound to a target methylated DNA sequence (19). A simulated DNA strand composed of (CG)₁₀ was generated by the Make-Na server (http://structure.usc.edu/make-na/server.html). These components were used to construct the model: in the software Chimera, a duplicate was made of the cMBD2-mDNA complex, the original complex was matched onto a simulated DNA strand, and then the duplicated complex was matched onto the same simulated strand, varying the separation of the two complexes and their orientations with respect to each other. Translating the duplicated complex along the experimental DNA segment that is contained in the PDB file of the cMBD2 structure—which is shorter and more irregular—yielded no qualitatively different results.

The matching was done by Chimera’s Match function, which minimizes the root mean square distance between atomic selections. The five atoms of each of the furanose rings of the deoxyriboses—of the mC-G and G-mC basepairs, i.e., the O4′, C4′, C3′, C2′, and C1′ atoms of residues 5CM 115, DG 106, 5CM 105, and DG 116—were selected as match criteria. (Selecting only the furanose rings of one basepair yielded no qualitatively different results.) The resulting root mean square distance was 0.518 Å.

To quantify the feasibility of the binding events modeled, we calculated the number of clashes between the two MBD2 proteins using Chimera’s Findclash function. The function measures overlap between two atoms in the different proteins through the following quantity:

$$\begin{array}{l}overla{p}_{ij}=r_{\text{VDW},i}+r_{\text{VDW,}j}-d_{ij},\\ i\in \text{MBD}{2}_{\text{orig}},\\ j\in \text{MBD}{2}_{\text{duplicated}},\end{array}$$ (1)

where $r_{\text{VDW},i}$ is the van der Waals radius of atom i, and $d_{ij}$ is the distance between atoms i and j. A clash occurs when $overla{p}_{ij}\ge$ cutoff (where we used the default cutoff of 0.6 Å). The final quantity reported is then the total number of atom clashes between the original MBD2 protein and the duplicated protein.

Artificial methylation of DNA and capture-based enrichment

DNA derived from a normal bone marrow donor (collected with signed written consent and approved by the Ohio State University Institutional Review Board) was methylated in vitro by CpG methyltransferase in the presence of S-adenosylmethionine as per manufacturer protocol (M.SssI; NEB, Ipswich, MA) and subjected to fragmentation using a model No. S2 Adaptive Acoustic instrument (Covaris, Woburn, MA). Part of the methylated DNA fragments (150–200 bp) were retained as the “input” sample. The remaining fragments were enriched by MBD2 protein (MethylMiner Methylated DNA Enrichment Kit; Invitrogen, Carlsbad, CA) as described by the manufacturer’s protocol, and denoted the “pulldown” sample. Illumina sequencing libraries were generated from the input and pulldown material as described in Rodriguez et al. (20). Library materials were quantified by fluorometric measurement, and quality of the samples was assessed by Bioanalyzer High Sensitivity DNA analysis (Agilent Technologies, Danbury, CT) before sequencing on the Illumina GAIIx flow cells. Images were captured from the sequencer and analyzed using the Real Time Analysis v. 1.8 software yielding 36-bp single-end sequenced reads. The sequencing files have been deposited to SRA under BioProject ID PRJNA350318 (National Center for Biotechnology Information, https://www.ncbi.nlm.nih.gov/).

Alignment and extension

Sequencing data for pulldown and input samples were aligned to the human reference genome hg18 using Bowtie v. 0.12.7 (21), allowing for up to three mismatches within the first 32 bases. Only uniquely aligned reads were kept, and bowtie -y and –best flags were also set, increasing the Bowtie software’s threshold to search for the best possible and valid alignments for reads.

Sequences of the uniquely mapping reads (29,338,030 reads for the pulldown sample and 149,547,991 reads for the input sample) were then extended to segments of 250 nts (or until the end of the chromosome) for each read, utilizing the aligned location and orientation from bowtie and the genomic sequence from hg18. This length was chosen to ensure that the segments would fully contain even the largest expected fragment length given an average fragment length of ∼100–150 nts. Considering the position, strand, and fragment length (assuming 100 nt) of each aligned read, we find that the pulldown and input samples cover ∼57 and ∼74% of CpGs in hg18, respectively. This ensures broad representation of CpGs in the human genome, even though we note that the genome itself simply provides a repertoire of many different sequence contexts and thus the fact that we include a large number (over a million) of CpGs is more important than the actual coverage of the human genome.

For the following analyses, we extracted only those segments that contained exactly one, two, or any specific number of CpGs (depending on the observable in question) within the range from position 11 to position 89 (where position 1 refers to the 5′-most nucleotide of the sequenced read) with no additional CpGs appearing elsewhere on the segment (hence, the first CpG’s C is allowed to be at position 11, and the last CpG’s G is allowed to be at position 89). These additional steps eliminate CpGs that are encoded in the error-prone first 10 bases and CpGs that are encoded in the genome but may not actually be present in the DNA fragment because the fragment might end before reaching the encoded CpG, i.e., these constraints ensure that the actual DNA fragment present in the pulldown experiment had the specified number of CpGs. When studying the effect of the number of CpGs on pulldown, an additional constraint requiring all consecutive CpGs to be well separated (≥3 bps apart) was imposed as well.

Pulldown efficiency

We define pulldown efficiency (E) to compare the pulldown and input samples as

$$E\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)},$$ (2)

where $p\left(x\right)$ represents a probability distribution as a function of some observable, x, for the pulldown data, and similarly $q\left(x\right)$ is such a probability distribution for the input data. The probability distributions are calculated from the ensemble of all DNA segments that exhibit the observable.

CpG separation

The first observable we considered was the separation between two CpGs. We use the phrase “CpG separation” to refer to the number of bases after the first CpG’s guanine and before the second CpG’s cytosine. Thus, for AACGCGAA, the CpG separation is 0, and for AACGAACGAA, the separation is 2, etc. Under the selection rules described in Alignment and Extension for segments with two CpGs, we were left with 311,103 segments for the pulldown sample and 2,793,304 segments for the input sample. The size discrepancy of our samples is due to both the difference in the number of libraries prepared for each sample (6 for input, 2 for pulldown) and the bias that the pulldown experiment displays for heavily methylated DNA fragments over nonmethylated and even lightly methylated fragments (see Number of CpGs for more details). To generate error bars on our measurement of the pulldown efficiency, we randomly partitioned the data from each sample type into 20 subsets. We classified the sequences in each of the 20 subsets by CpG separation and generated 20 distributions of both $p\left(n\right)$ and $q\left(n\right)$, which give the probability that two CpGs on a segment are separated by n nucleotides in a subset of the pulldown and input samples, respectively. The mean across the 20 subsets for each separation was then reported, as well as the standard deviation from the pulldown distributions. With this and all other measures, we ignored statistical fluctuations due to the input sample as they were found to be much smaller than those from the pulldown data, a consequence of the input data set being much larger than the pulldown data set. We then calculated the ratio of pulldown to input per Eq. 2.

Number of CpGs

For the second observable, we calculated pulldown efficiency as a function of the number of CpGs on the fragment, in a way analogous to how we calculated it as a function of 2-CpG separation (see CpG Separation, above). To also examine the effect of CpG separation on overall pulldown efficiency for any number of CpGs on a strand, we took segments with and without a minimum consecutive CpG separation constraint as described in Alignment and Extension. Without the minimum separation constraint, we had 2,163,738 segments from the pulldown sample and 57,021,714 segments from the input sample, while with the minimum separation constraint, we had 2,041,198 segments from pulldown, and 56,689,705 from input.

The significance of the difference between pulldown efficiencies per CpG count between efficiencies with and without a minimum separation constraint was calculated as follows: The 20 in silico replicates of $p\left(n\right)$ described in CpG Separation, above, were divided by corresponding 20 different $q\left(n\right)$’s directly to generate 20 different pulldown efficiencies per CpG count. These 20 pulldown efficiencies with and without the minimum separation constraint were then compared using a two-sided t-test without assuming equal variance (Welch’s t-test) on CpG counts from 2 to 7 CpGs (CpG counts of eight and larger did not have sufficient coverage to make meaningful comparisons).

Sequence context

The next observable we considered was the sequence context of a single CpG. To probe its effects on pulldown efficiency, we performed a set of statistical tests. We selected segments with exactly one CpG under the additional condition that the 20 bases before the C all appear after the 10th base of the segment, and the 20 bases after the G all appear before the 90th base of the segment, and more specifically, if the segment is shorter than 89 bp (i.e., at the end of a chromosome) the G has to be at least 20 bases removed from the end of the segment to ensure consistent analysis. We also do not include the segment for analysis if there is an unknown base N in this window around the CpG. Finally, because forward and reverse fragments are equally likely to be sequenced, we added the reverse complement of every segment to our data set. In the end, our analysis was performed on n_p = 412,902 pulldown and n_inp = 13,164,090 input segments.

To see whether basepairs were represented preferentially at single positions around the CpG, we calculated the probability distributions $p_i\left(b\right)$ and $q_i\left(b\right)$, which give the probability that base $b\in \left\{\text{A,T,C,G}\right\}$ appears at position i with respect to the CpG, for the pulldown and input distributions, respectively. To illustrate our convention for referencing positions around the CpG: In CACGTC, base T is at position +1, base adenine (A) is at position −1, and base C appears at both −2 and +2. For a set of these positions, we calculated the pulldown efficiency as in the following:

$$E_i\left(b\right)=\frac{p_i\left(b\right)}{q_i\left(b\right)},b\in \left\{\text{A,T,C,G}\right\},\left|i\right|\le 20.$$ (3)

From the underlying forward-reverse symmetry in our data set, we can recover the distribution on the other side of the CpG: $p_{-i}\left(b\right)=p_i\left(b^c\right)$, and similarly for $q_i\left(b\right)$, where $b^c$ is the complementary base of b.

For each $\left(i,b\right)$ pair, we estimated the statistical significance of the deviation of Eq. 3 from unity by assuming Poisson-distributed counting statistics on the number of occurrences of the base b appearing at position i in the pulldown sample. Thus, the relative error on $E_i\left(b\right)$ is $1/\sqrt{p_i\left(b\right)n_p}$. We divided $E_i\left(b\right)-1$ by this relative error to obtain a Z-score, and calculated the corresponding two-tailed integral of the normal distribution to get the p value. Using these p-values, we determined at which positions and for which bases the distribution differed between pulldown and input in a statistically significant way, accounting for multiple testing using the Bonferroni correction.

To separate possible sequence preferences that do not depend on proximity to the CpG (and would reflect non-mCpG-specific binding) from those that do, we also calculated $E_j\left(b\right)/E_{-20}\left(b\right)$ for all $-20\le j\le -1$. We chose the base distributions at position −20 to act as a reference point because it is close enough to the CpG that we could extract a large number of reads from the input and pulldown samples while requiring that a 20 bp-wide window on either side of the CpG remain in the preferred region of each segment, and far enough from the CpG that we can reasonably assume that a base that far removed from an mCpG would not interact with an MBD2 protein bound to the mCpG. For testing the statistical significance of a deviation of $E_j\left(b\right)/E_{-20}\left(b\right)$ from unity, we used the Poisson uncertainty for each $E_i\left(b\right)$ term and added them in quadrature for the relative error on $E_j\left(b\right)/E_{-20}\left(b\right)$. Then we used an analogous procedure to derive a Z-score and p value. For both the pulldown efficiency and the ratio of pulldown efficiencies, the difference between the underlying distributions was considered statistically significant if the p value fell below the Bonferroni-corrected cutoff of 1.25 × 10⁻⁴ for the 80 considered tests.

Results

Structural model of MBD2 binding for small separations

The model we constructed probed the interaction of structural features of two MBD2 proteins. A priori, one might guess that binding is inhibited, and pulldown efficiency significantly diminished, when the two methylated CpGs are too close together, if only due to the steric effects between multiple MBD2 proteins. From an NMR experiment done on a cMBD2 methyl binding domain bound to a target-methylated DNA sequence, we obtained a molecular model of a single MBD2-mDNA complex (PDB: 2KY8). Duplicating this structure and mapping these two complexes onto a simulated strand of DNA, we varied the separation between the two complexes and their orientations with respect to each other. This serves as a model to consider two mCpGs on the same strand bound by MBD2 domains. We presume that in the environment of the methylation capture experiment, a two-MBD2-binding event resulting in an overlap of the two structures in our model is some energetically unfavorable deformation of the rigid structure. Thus, as a proxy for the expected suppression of these binding events, we counted the number of clashes between the atoms of the two MBD2 proteins.

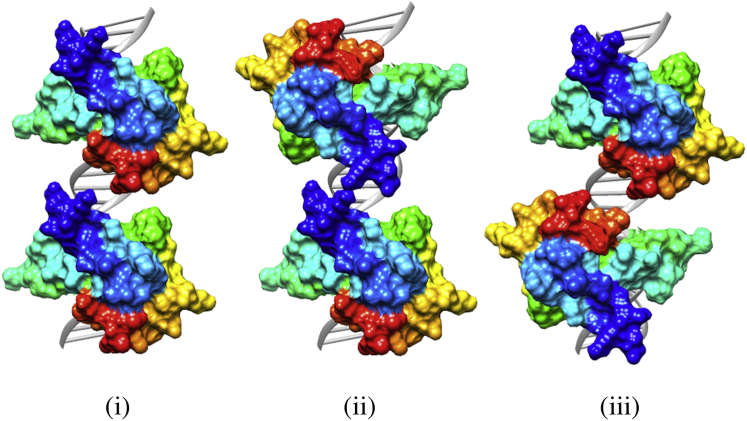
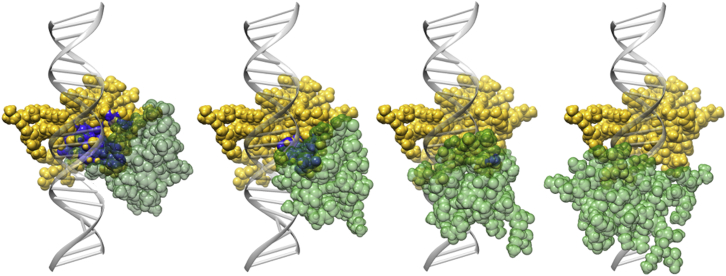
At each separation there are three distinct orientations to consider. When the N-terminus of each protein faces the other along the strand, we call this the “N-facing” orientation; when the C-terminus of each protein faces the other, this is the “C-facing” orientation; and when the C-terminus of one faces the N-terminus of the other, we call this the “in-line” orientation (see Fig. 1). The proteins were matched to CpGs along the DNA strand whose separation was varied from 0 to 3 basepairs (see Fig. 2 for an illustration of this progression in the in-line orientation).

Figure 1.

The three orientations of two MBD2 proteins. The darkest (blue) end of the protein is the N-terminus. (i) In-line; (ii) N-facing; (iii) C-facing. To see this figure in color, go online.

Figure 2.

One MBD2 protein is shown as a second MDB2 protein is translated from a 0 to a 3 bp separation in the in-line orientation. The clashing atoms are highlighted in dark (blue). To see this figure in color, go online.

Table 1 reports the number of clashes as we varied the separation of the CpGs and orientation of the proteins. At a 0 bp separation, all three orientations in our model give rise to several hundred atom clashes. While one should not take the number of clashes given as exact, the scale of the amount of overlap is an indication of the amount of energy that would be required to deform the complex to reduce these clashes and obtain a stable configuration. For hundreds of clashes, that energy is unlikely to be available in the environment of the methylation capture experiment, and the same conclusion is still likely at CpGs separated by 1 bp. At a 2 bp separation, the C-facing orientation is the only orientation in our model in which there are no atom clashes between the proteins. Finally, at a 3 bp (or larger) separation, the proteins are completely separated in all three of the orientations, resulting in zero clashes.

Table 1.

Number of Clashes between Two MBD2 Proteins while Bound to DNA at Different Basepair Separations and Orientations

Separation (bp)	Orientation
	In-line	N-facing	C-facing
0	640	832	1188
1	298	298	108
2	18	77	0
3	0	0	0

Separation between CpGs

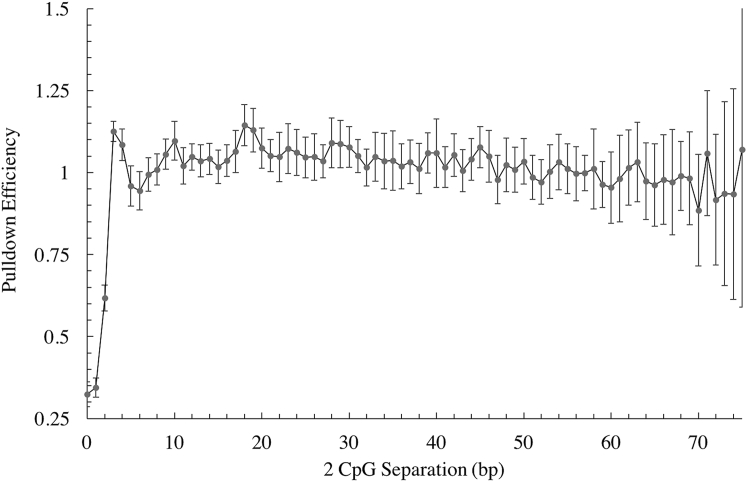
Continuing our investigation of the trends seen in the structural overlap of bound MBD2 proteins, we examined the effect of this separation between the two mCpGs on pulldown efficiency. We generated in vitro methylated DNA fragments from human DNA samples, and performed MBD pulldown on them. Examining pulldown compared to input samples, we found that the separation distance between two CpGs indeed has an effect on pulldown efficiency, as shown in Fig. 3. We see that for a 0–1 bp CpG separation, we have equally low pulldown efficiencies compared to the values of full pulldown (≥3 bp separation). For two basepairs in between the two CpGs, we have an intermediate level of pulldown efficiency, and for separations of three or more basepairs, the pulldown efficiency is essentially independent of the distance between the two CpGs. We note that the actual values of the reduced pulldown levels at small separations are different from the naive expectation of 0.5 due to the nonlinearity of the pulldown process on the number of CpGs, as discussed in the next section.

Figure 3.

Pulldown efficiency at different CpG separations among segments containing exactly two CpGs. We observe that MBD pulldown efficiency for two CpGs recovers as separation between CpGs increases.

Number of CpGs

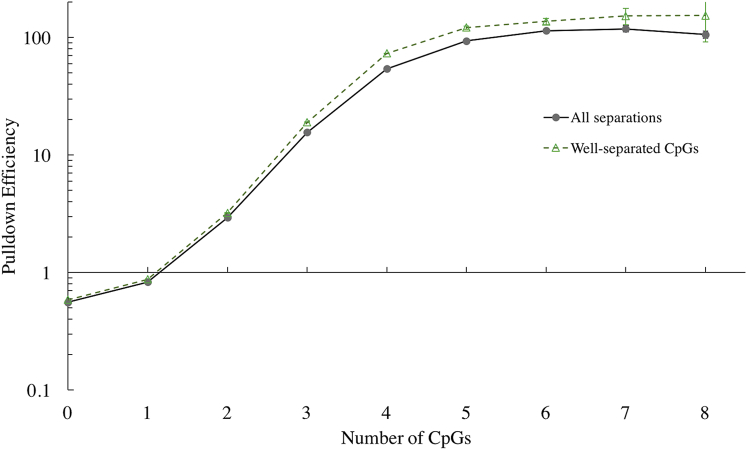
From the same library of input and pulldown samples, we looked more generally at the pulldown efficiency as a function of the number of CpGs on the DNA segment (see Fig. 4). The relationship between CpG number and pulldown efficiency is highly nonlinear. Pulldown efficiency grows by increasing factors until the effect turns over after 3 CpGs and saturates at ∼5 CpGs. Thus, there are relatively small gains in pulldown with 1–2 CpGs compared to the nonspecific binding at 0 CpGs. If only nonspecific binding occurred, pulldown efficiency as a function of mCpG number would be constant and equal to the value for 0 mCpGs, which is $E\left(0\text{mCpG}\right)=0.56$. This represents the background level of nonspecific binding and $E\left(1\text{mCpG}\right)/E\left(0\text{mCpG}\right)=1.49$ sets the scale for the effective binding specificity of MBD2 in a pulldown experiment.

Figure 4.

Pulldown efficiency among segments with a given number of CpGs. The curve marked “All separations” includes all segments that contain the number of CpGs selected for, while the curve marked “Well-separated CpGs” only includes the subset of segments where each CpG is separated by at least 3 bp from any other. For 2≤ CpG number ≤7, a t-test comparison of 20 sub-binned pulldown efficiency calculations shows that the difference between the pulldown efficiencies is statistically significant. We also see that pulldown efficiency increases nonlinearly with CpG number, until the effect saturates at 5 mCpG. To see this figure in color, go online.

We also calculated this pulldown efficiency among segments that only contained well-separated CpGs to see if the decrease in pulldown seen for a pair of close mCpGs can be observed across a range of CpG counts. Based on the results from the previous section, we determined that well-separated CpGs are those that are ≥3 bp away from any other. Comparing the curves in Fig. 4, we find that the pulldown efficiencies among fragments with two or more well-separated CpGs are larger than the pulldown efficiencies calculated among fragments with any spacing allowed between CpGs. This difference is significant for 2–7 CpGs (p value < 0.005, i.e., it remains significant even after correcting for nine tests), beyond which our data are inconclusive due to the low number of fragments with that many CpGs.

From both curves, we see that the pulldown distribution heavily represents DNA fragments with four or more CpGs. A fragment with 1 CpG is ∼1.49 times more likely to be pulled-down and sequenced than a fragment with 0 CpGs, whereas a fragment with four well-separated CpGs is ∼125 times more likely $\left(E\left(4\text{mCpG}\right)/E\left(0\text{mCpG}\right)\right)$.

Sequence context

The interaction between a single MBD2 protein and the basepairs surrounding the mCpG also influences pulldown efficiency. In this section, we discuss how much this additional interaction suppresses or enhances an MBD2 domain binding to an mCpG. Although previous studies have found only weak sequence dependence from smaller-scale experiments, our large sample size allows us to revisit this question with notable precision.

From a subset of isolated CpGs, we compared the frequencies of bases between the pulldown and input sets. The basepairs near an mCpG are most likely to interact with the binding protein, but as the MBD2 protein could display sequence preferences related to nonspecific binding, we selected a wide window around the CpG to consider and calculated the pulldown efficiency $E_i\left(b\right)$ (Eq. 3) for each base at the 20 closest basepairs. Table 2 and Fig. 5 give values of these pulldown efficiencies minus 1.0, so that a positive value corresponds to an enhancement of that base at that position, and a negative value corresponds to a suppression. Correspondingly, we measured the statistical significance of each preference by estimating the probability that a Poisson-distributed counting error in the pulldown distribution could account for the given effect size. Using the Bonferroni correction (22) for 4 × 20 = 80 tests, $E_i\left(b\right)$ was deemed statistically significant if the p value was <0.01/80 = 1.25 × 10⁻⁴. In the end, we find statistically significant differences between input and pulldown distributions for at least one base at all positions considered.

Table 2.

Preference for, or Against, Bases at Positions Before the mCpG

Position	A	T	C	G
−20	0.008991a	0.020060	−0.024163	−0.027140
−19	0.015186	0.015147	−0.032146	−0.021962
−18	0.010261a	0.018965	−0.020827	−0.030077
−17	0.019222	0.016574	−0.029470	−0.032147
−16	0.016058	0.022162	−0.028997	−0.036509
−15	0.016685	0.016373	−0.027418	−0.029210
−14	0.011744	0.016473	−0.023364	−0.24446
−13	0.018341	0.018260	−0.032128	−0.031141
−12	0.010402a	0.023698	−0.023386	−0.036284
−11	0.018130	0.018050	−0.034394	−0.029115
−10	0.012804	0.019100	−0.021739	−0.035455
−9	0.014612	0.021224	−0.024853	−0.038650
−8	0.014696	0.016282	−0.022333	−0.031099
−7	0.020037	0.019475	−0.030435	−0.038883
−6	0.020191	0.023330	−0.030666	−0.041616
−5	0.022456	0.012800	−0.025835	−0.033383
−4	0.007078a	0.024616	−0.026189	−0.026724
−3	0.014643	0.033786	−0.021759	−0.006714a
−2	0.009739a	0.046507	−0.045858	−0.009157a
−1	0.029056	−0.034920	−0.002895a	−0.003161a

Shown is the deviation from unity in the pulldown efficiency for bases at positions labeled with respect to the mCpG. Values are statistically significant with p value < 0.000125 unless otherwise indicated. Fig. 5 visualizes this data with statistically significant values outlined in black.

^aNot statistically significant.

Figure 5.

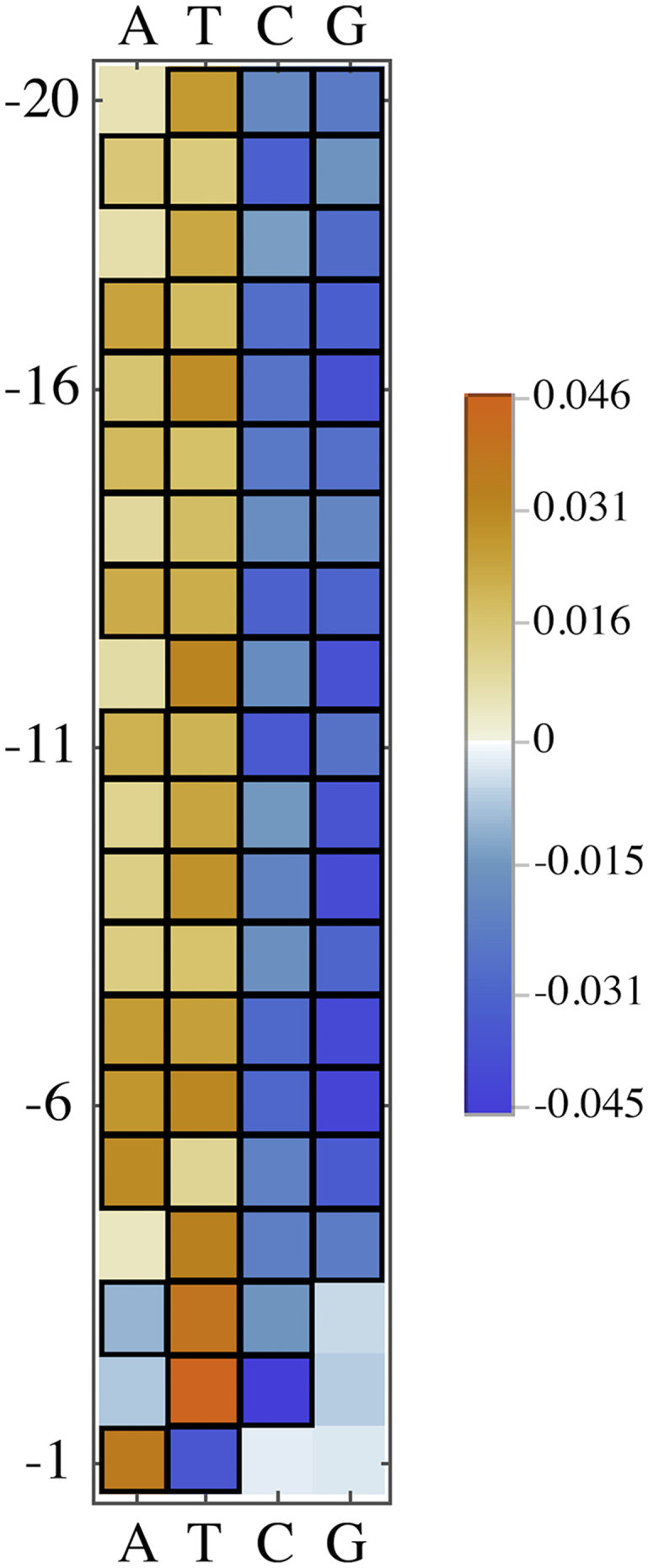
Heatmap visualization of Table 2. Values indicating a statistically significant difference between pulldown and input are outlined in black. To see this figure in color, go online.

To determine if there is a set of sequence preferences related to nonspecific binding that is distinguishable from those sequence preferences that relate to mCpG-specific binding, we compared the pulldown efficiency for each base at each position to the pulldown efficiency for that base at the furthest sampled position from the CpG (here, position ±20). Table 3 and Fig. 6 show the values for $E_i\left(b\right)/E_{-20}\left(b\right)-1$ for each base b and position $-20\le i\le -1$. With the same error model and Bonferroni-corrected p value threshold used previously, we find that only for the three closest basepairs (positions −1, −2, and −3, and equivalently +1, +2, and +3) is at least one base preference statistically different from that far away from the mCpG, indicating that different interactions are being described between our results in the [−20, −4] range and in the [−3, −1] range.

Table 3.

Comparison between Pulldown Efficiencies for Each Base at Positions Before the mCpG and the Corresponding Pulldown Efficiency at Position −20

Position	A	T	C	G
−20	0	0	0	0
−19	0.006140	−0.004816	−0.008181	0.005322
−18	0.001259	−0.001074	0.003418	−0.003020
−17	0.010141	−0.003417	−0.005439	−0.005147
−16	0.007004	0.002060	−0.004954	−0.009631
−15	0.007626	−0.003615	−0.003336	−0.002128
−14	0.002729	−0.003517	0.000819	0.002769
−13	0.009267	−0.001765	−0.008163	−0.004113
−12	0.001399	0.003566	0.000795	−0.009399
−11	0.009058	−0.001970	−0.010484	−0.002031
−10	0.003779	−0.000941	0.002484	−0.008548
−9	0.005571	0.001141	−0.000707	−0.011832
−8	0.005654	−0.003704	0.001875	−0.004070
−7	0.010948	−0.000573	−0.006428	−0.012071
−6	0.011101	0.003206	−0.006664	−0.014880
−5	0.013346	−0.007117	−0.001714	−0.006418
−4	0.001895	0.004467	−0.002076	0.000427
−3	0.023423a	0.013456	0.002463	0.020995a
−2	0.018563a	0.025926a	−0.022233a	0.018484
−1	0.019887a	−0.053899a	0.021795a	0.024648a

Shown is the deviation from unity in the ratio $E_i\left(b\right)/E_{-20}\left(b\right)$ for base b at position i labeled with respect to the mCpG. Values are not considered statistically significant, unless otherwise indicated. Fig. 6 visualizes this data with statistically significant values outlined in black.

^aConsidered statistically significant, with p value < 0.000125.

Figure 6.

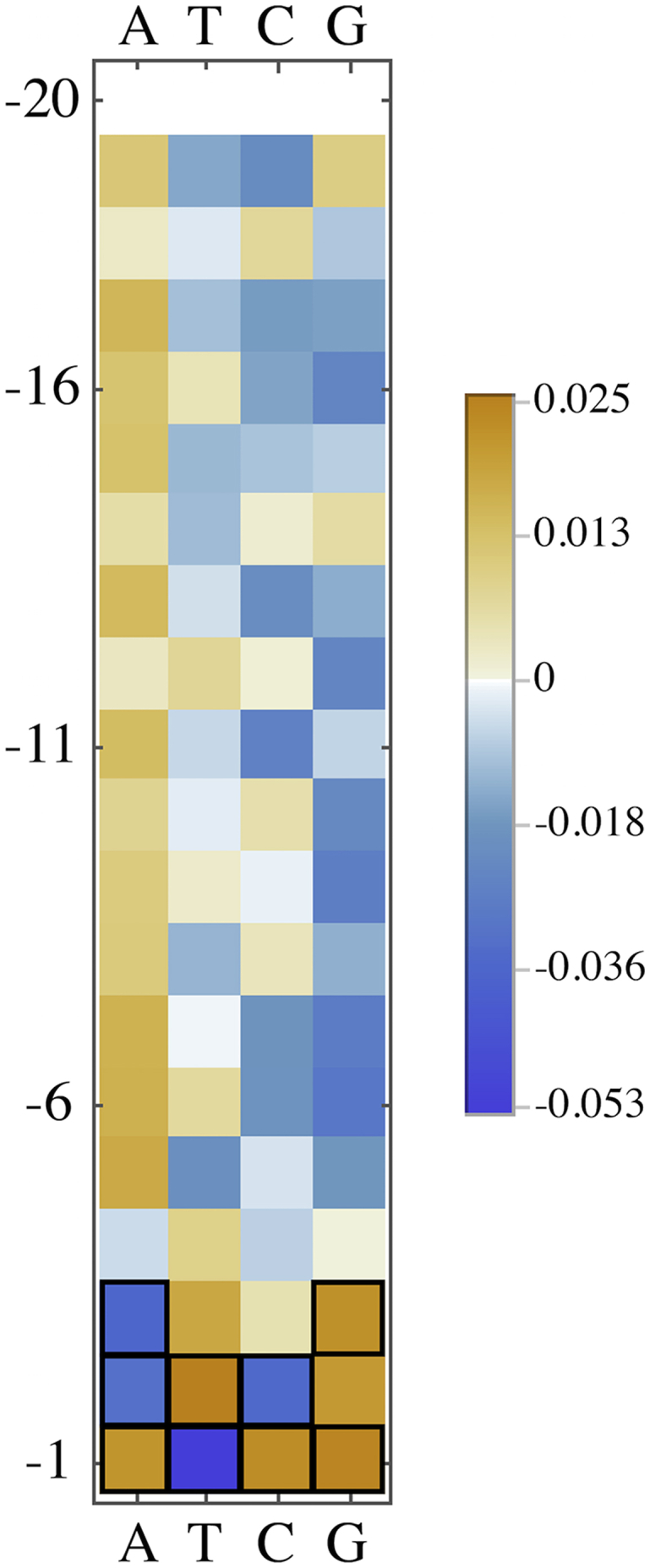
Heatmap visualization of Table 3. Values indicating a statistically significant difference between the pulldown efficiency at that position and at position -20 are outlined in black. To see this figure in color, go online.

While there are statistically significant biases in base composition within this 20 bp-window around the mCpG, the effect this has on interpreting pulldown experiments is likely still small. None of the deviations in Table 2 are larger in magnitude than 0.047. Still, we note that in the [−20, −4] position range, the nucleotide distributions in the pulldown set overrepresent adenines and thymines and underrepresent cystosines and guanines. In the [−3, −1] position range, the distribution of guanines are statistically identical between input and pulldown, while over this range the observed bias in the other three bases reverses direction (bases A, T) or increases and then becomes insignificant (base C).

Discussion

CpG separation

The three distinct states identified in the pulldown efficiency at CpG separations of 0 and 1, 2, and 3 bp support our predictions from our structural model of these two-MBD2-binding events. From the amount of protein overlap in the configurations observed, we expect a large suppression in the pulldown efficiency for separations of 0 or 1, a smaller suppression for a separation of 2 bp (because one orientation admits no clashes), and a stable pulldown efficiency for separations of 3 bp or more.

Because our model used structure data from only cMBD2, one may ask how applicable this should be to methylation capture experiments done with human MBD2 (hMBD2). Sequence alignment by BLAST (23) of the full-length reference hMBD2 (isoform 1, 411 amino acids (aa), NCBI: NP_003918.1) and reference cMBD2 (257 aa, NCBI: NP_001012403.1) showed an 83% identity. More relevant for the effectiveness of our model, however, is the similarity between the domains isolated for methylation capture experiments. We thus restricted the reference hMBD2 sequence to the aa 150–220 subrange that is commercially available and the reference cMBD2 sequence to the aa 2–72 subrange cloned for the NMR experiment (19). Running BLAST alignment on these subranges showed 63/65 identities with no gaps and two substitutions (T200:A57 and S205:C62). The aligned section corresponds to aa 151–215 on hMBD2 and aa 8–72 on cMBD2, and we confirmed that the cysteine substitution in cMBD2 does not form a disulfide bond (which could not be present in hMBD2). While we do not have NMR structure data of hMBD2 for comparison, given their methyl binding domains’ similar functionality, it is reasonable to expect the aligned regions to possess similar geometry. Although terminal sequence differences may affect the amount of clashing observed at separations of 2 and 3 bp, the general behaviors we deduce from our model at separations of 0 and 1 bp are least likely to change.

Number of CpGs

By investigating the pulldown efficiencies of fragments with multiple mCpGs, we have confirmed that MBD2 is indeed a good choice for use in DNA methylation studies: although the added pulldown efficiency for low (1, 2) numbers of mCpGs is relatively minor in comparison with the nonspecific binding of MBD (0 mCpGs), we observe that MBD highly enriches fragments with greater numbers of mCpGs. This result builds on previous work that has reported on read coverage of the MethylMiner kit as a function of local CpG density (24, 25) and CpG number (16), noting low sensitivity to sparsely methylated DNA. Our data uniquely analyzes the explicit property of the DNA fragment (CpG number) with high certainty of methylation level (M.SssI treatment) while accounting for the background frequency of reads with a given CpG count (dividing the fraction of pulldown by the fraction of input) and resolving the bias for less frequent, highly methylated reads.

In our study, the presence of nonspecific binding reduces the apparent effect of any property related to CpG content on pulldown efficiency. In general, low sensitivity and the highly nonlinear effect of the number of CpGs on pulldown efficiency presents additional challenges when attempting to make methylation calls on the single CpG level. Further work is needed to fully utilize this effect in making accurate methylation predictions. Additionally, upon enforcing a constraint that all CpGs must be well separated, we have validated the significance of mCpG separation for MBD accessibility—pulldown efficiencies for fragments with well-separated CpG counts ≥2 are significantly higher, showing that some fragments are less likely to be pulled down compared to fragments with the same number of mCpGs if every mCpG cannot be simultaneously bound.

Sequence context

The shifts in pulldown efficiencies due to sequence context are weak, but we can nevertheless contribute to the discussion on whether MBD2 selects for certain bases around the mCpG due to our much increased strength in statistics. It is important to note, however, that we measure the sequence specificity of the entire experiment, which here includes an artificial methylation step. Therefore, what part of the observed sequence specificity comes from protein preference and what part from possible incomplete methylation during the M.SssI treatment cannot be determined. However, the efficiency of M.SssI to convert every C in a CG dinucleotide context to a 5mC is understood to be nearly complete. Furthermore, experiments using the same kit have observed conversion rates between 98.2% (26) and ∼99.9% (27)—a range with rates high enough to make claims on MBD2’s base-specific interactions being a contributing factor to the observed sequence specificity.

From results in Table 3, we can identify a clear region within 3 bp of the CpG location where the nucleotide distribution biases in the pulldown sample are distinguishable from a background level seen in the [−20, −4] position range. Thus, the [−3, −1] position range is where we presume sequence preferences exhibited by an MBD2 protein bound to the mCpG are exerted. For this position range there is then the question of how the sequence preferences from MBD2 proteins bound at the mCpG can be distinguished from those arising from nonspecific binding events. For a segment where an MBD2 protein is bound to the mCpG, an additional MBD2 protein—following from our results above—is not likely to bind within 2 bp of the mCpG (assuming that the protein’s binding conformation does not dramatically change from specific to nonspecific binding). If every read with 1 mCpG that was pulled down was bound by an MBD2 protein, this would motivate the interpretation that all the values in Table 2 for at least the [−2, −1] position range represent the base preferences co-occurring with specific binding. But because the level of nonspecific binding is nonnegligible—as indicated by $E\left(1\text{mCpG}\right)\sim E\left(0\text{mCpG}\right)$ in number of CpGs—the base preferences we observed most likely still represent a mixture of base preferences arising from both specific and nonspecific binding events.

Previous published experimental results on MBD2 binding affinity either find no evidence of sequence selectivity (28) or find evidence of sequence selectivity based on a particular basepair substitution done on cMBD2 (19).

Scarsdale et al. (19) noted that certain residues in cMBD2 interact with the bases flanking the mCpG. In particular, Y36 and K32 make contact with the T preceding the mCpG, and the G after the mCpG, respectively. When they substituted another T for that G, they saw at least a 10-fold reduction in binding affinity for a range of concentrations of cMBD2. Two main issues prevent a direct comparison to their results: We cannot assign a physical protein concentration for the solution because each paramagnetic bead used for pulldown is coupled to multiple MBD2s, and the sequence/structure differences between cMBD2 and hMBD2 may lead to differences in sequence preferences. Nonetheless, as to their general claim that there is a sequence preference for mCpGG, our data in Table 2 would suggest that averaged over the ensemble of all pulldown reads with 1 CpG, there is no statistically significant under- or overrepresentation of guanines at the +1 position (equivalently, cytosines at the −1 position). However, if we take the average $E_i\left(\text{G}\right)$ for all $3<i\le 20$ to represent the bias from nonspecific binding against G $\left(E^{\text{non-spec}}\left(\text{G}\right)-1\sim -2.7\text{\%}\right)$, then we must have a specific preference for G at position $+1$ $\left(E_{+1}^{\text{spec}}\left(\text{G}\right)>1\right)$ for $E_{+1}\left(\text{G}\right)\sim 1$. Even so, our observed preference in the percent range is very different from the order-of-magnitude preference in binding found in Scarsdale et al. (19), even when taking into account that the relative closeness of the pulldown efficiency of single mCpG and nonspecific binding $\left(E\left(1\text{mCpG}\right)/E\left(0\text{mCpG}\right)\approx 1.49\right)$ strongly dampens the effect of specific binding preferences observed in single mCpG binding events in our experiment.

Klose et al. (28) performed the same Methyl-SELEX experiment on human MeCP2 and MBD2 with all probes methylated at a fixed central CCGG flanked by random DNA (changing the central sequence to GCGC did not affect their results). While MeCP2 showed a preference for A/T-rich sequences, MBD2 exhibited no such preference in their sample. Interestingly, we observe in the region 4 bp or more from the CpG that there is an overrepresentation of adenines and thymines, of ∼$1\text{\%}$. Among the sequences enriched after multiple cycles of binding and amplification with MeCP2, Klose et al. (28) frequently found A/T runs of four or more bases in motifs that occurred 1–3 basepairs and 6–9 basepairs from the methylated CpG. In an analogous experiment with the MBD of MBD2, the overrepresentation of sequences with additional mCpGs was instead the feature that was similarly pronounced. Because the number of selected fragments and unselected fragments were 79 and 86, respectively, it is consistent with our findings that their experiment with MBD2 resolves an overrepresentation of fragments with more than one mCpG (as $E\left(2\text{mCpG}\right)>3.5E\left(1\text{mCpG}\right)$) and not additional sequence preferences. They identify only one significant shift in their electrophoretic mobility shift assay data—although not every electrophoretic mobility shift assay experiment on MeCP2 was carried out on MBD2—and in interpreting the MeCP2 data they find the A/T enrichment to be a requirement for MeCP2 to bind to the mCpG efficiently. Given that we see a consistent enrichment for A/T out to 20 bp away from the CpG, it remains more reasonable to assume that nonspecific binding events are occurring on a wide range of distances with respect to the mCpG than that an MBD2 protein sitting on the mCpG exhibits, itself, both long- and short-range base preferences.

The largest significant differences between the pulldown and input nucleotide distributions in Table 2 are the overrepresentation of T at −2 and underrepresentation of C at −2. Also of note is the largest difference in the specific-binding range from the nonspecific binding range (from Table 3), namely the underrepresentation of T at the −1 position.

Conclusions

Large-scale, genomewide mapping of DNA methylation will be necessary to advance our understanding of what influences, and is influenced by, this epigenetic marker. Enrichment-based pulldown experiments using the MBD2 protein provide a cost-effective and scalable method for obtaining DNA methylation data, but its value will be limited by our understanding of the interaction between the MBD2 protein and fragmented DNA in the context of the experiment. We studied three particular ways this interaction can have an effect on the interpretation of the resulting pulldown data. Through virtual manipulation of a cMBD2-mDNA complex, we found a structural argument for the effect of mCpG separation on pulldown efficiency. From a large library of DNA reads constructed to compare the distribution of mCpGs in the input sample of a pulldown experiment and in the pulldown (output) sample, we found further evidence that pulldown efficiency is significantly decreased if the basepair separation between two mCpGs is 2 or fewer. We conclude that at a separation of 3 bp or greater, the mCpGs can be considered well separated, such that it is possible for both mCpGs to be bound simultaneously. With this library, we also looked at the overall effect of a fragment’s mCpG number on pulldown efficiency. The highly nonlinear relationship saturates at 5 mCpGs and biases the pulldown distribution toward heavily methylated DNA. Finally, we culled a subset of the DNA library with which to investigate possible sequence specificity of the MBD2-mDNA complex. We indeed measured a set of statistically significant biases in pulldown efficiency among bases at single positions, but this amounts to a correction on the order of a percent. This is true in both regimes far from the CpG (>3 bp away) and close to the CpG (≤3 bp away), in which are contained the base preferences concurrent with nonspecific and specific binding, respectively. With these results, we have a refinement on previous considerations of the effect of CpG density, and a clarification on whether the biochemical observation of sequence dependence appears to a similar extent in the context of a pulldown experiment. The results of this study answer rather different questions related to the biophysical characteristics of MBD2-DNA binding with large statistical significance, which points to the power that high-throughput sequencing data can have in examining the downstream effects of complex DNA-protein interactions.

Author Contributions

J.C. and P.Y. prepared the samples and sequencing libraries; B.M. and K.O. analyzed the data and performed the research; R.B., B.M., and K.O. designed the project; and B.M., K.O., P.Y., and R.B. wrote the article.

Editor: David Rueda.