Toward Hydrodynamics with Solvent Free Lipid Models: STRD Martini

Abstract

Solvent hydrodynamics are incorporated into simulations of the solvent-free Dry Martini model. The solvent hydrodynamics are modeled with the stochastic rotation dynamics (SRD) algorithm, a particle-based method for resolving fluid hydrodynamics. SRD does not require calculation of particle-particle distances in the solvent, and so is scalable to arbitrary volumes of solvent with minimal additional computational overhead. The viscosity of the solvent is easily tuned via parameters of the algorithm to span an order of magnitude in viscosity around the viscosity of water at room temperature. The combination “Stochastic Thermostatted Rotation Dynamics (STRD) with Martini” was implemented in Gromacs v.5.01. Simulations of an SRD/palmitoyloleoylphosphatidylcholine membrane demonstrate that the solvent may be included without reparametrizing the lipid model, with minimal perturbation to the thermodynamics. A recent generalization of Saffman-Delbruck theory to periodic geometries by Camley and Brown indicates that lipid dynamics are contaminated by a finite-size effect in typical molecular dynamics (MD) simulations, and that very large systems are required for quantitative simulation of dynamics. Analysis of lipid translational diffusion in this work shows good agreement with the theory, and with explicitly solvated simulations. This indicates that STRD Martini is a viable approach for quantitative simulation of membrane dynamics and does not require massive computational overhead to model the solvent.

Introduction

Experimental methods to observe the spatiotemporal dynamics of membrane proteins and lipids have advanced significantly over the last decade, and especially in the last few years. In live cells, single-particle tracking (1, 2, 3) and fluorescence correlation spectroscopy (FCS) with subdiffraction detection volumes (achieved by stimulated emission depletion microscopy)(4) have revealed the plasma membrane to be heterogeneous on tens of nanometers, with correspondingly heterogeneous dynamics. Taken together, these results suggest a hierarchical membrane organization, with the cytoskeleton influencing transport above 80 nm lengthscales, (5) and lipid-protein interactions operating below this lengthscale (6).

In model systems, mixtures that are comparatively simple are also heterogeneous. Neutron scattering reveals nanoscale liquid-ordered domains in vesicles comprised of a mixture of 3 or 4 components (including cholesterol) (7). In a ternary mixture that supports liquid-ordered/liquid-disordered (L_o/L_d) coexistence nanoscale heterogeneities in composition and dynamics are observed by stimulated emission depletion fluorescence correlation spectroscopy (8), provided the mixture is deposited on a glass support, which pins a fraction of lipids facing the support. In similar mixtures of a uniform L_o phase, heterogeneities are observed on yet smaller lengthscales and timescales by molecular dynamics (MD) simulations (9, 10) and interferometric scattering-based single-particle tracking (11).

Although these experimental results point to essential aspects of spatiotemporal organization—the role of the cytoskeleton in partitioning the membrane, the existence of nanoscale compositional heterogeneity—they are mostly silent on the details of the underlying mechanism. For example, how does actin create a barrier to diffusion? By a simple steric mechanism (3), or by modifying the membrane viscosity in the neighborhood of actin-binding proteins (12), or in some other way? How do nanoscale heterogeneities in composition modify local protein diffusion when observed (i.e., averaged) over the longer length- and timescales relevant to signaling?

Answers to these questions will come from modeling approaches. Based on the above discussion, an appropriate modeling approach must fulfill certain criteria: 1) it must resolve protein-protein and lipid-protein interactions with reasonable chemical specificity; 2) it must span lengthscales from individual lipids to the 100 nm lengthscale of the cortical cytoskeleton mesh; and 3) it must accurately resolve dynamics. To achieve this last point, a modeling approach must account properly for the hydrodynamics of the solvent adjacent to the membrane. This is clear from continuum arguments originally proposed by Saffman and Delbruck (13), and later extended by Hughes, Palinthorpe, and White (14).

As a first step in this direction, we present results for the solvent-free “Dry Martini” (15) model coupled to a computationally fast method for solvent hydrodynamics called “stochastic rotation dynamics” (SRD) (16). Martini is a coarse-grained family of force fields, in which three to four heavy atoms (including water) are grouped into coarse-grained interaction sites (17). Dry Martini is an implicit-solvent version of Martini in which lipid-lipid interactions are reparametrized to account in an effective way for the aqueous solvent. SRD (described in more detail below) has several advantages: 1) it is particle-based, and so naturally interfaces with particle-based MD models; 2) collisions between solvent particles are modeled without direct particle-particle interactions, imparting an inherent computational efficiency relative to discrete particle dynamics-type methods; and 3) properties of the fluid (e.g., viscosity, Reynolds number, and compressibility) are easily controlled via the SRD parameters, in some cases (e.g., viscosity) analytically related. Although the method is applicable to any solvent-free lipid model (18, 19, 20), we chose Dry Martini for the first demonstration, as it 1) is widely used, 2) is under active development, and 3) resolves sufficient chemical detail, including a model for cholesterol, to model coexisting lipid phases. A recent article reported a similar approach using a much more coarse-grained lipid model (21), and other applications of SRD/MPC methods with more coarse-grained membrane models have been published (22, 23). The simulation code has been implemented in an in-house version of Gromacs v5.01. We call our combination of Dry Martini and thermostatted SRD particles “STRD Martini.”

The main contribution of this article is to detail how the parameters of the SRD fluid impact the thermodynamics and the dynamics of a simple lipid bilayer. An important goal is that the addition of the solvent not require reparametrization of the lipid model. However, as discussed in the Results, the introduction of the SRD-lipid interactions adds new contributions to the virial, which if not carefully tuned will have a significant impact on the bilayer thermodynamics. Then the properties of the SRD solvent are discussed, demonstrating tunability of the viscosity and of the low-Reynolds-number, incompressible hydrodynamic regime appropriate to membrane dynamics. Next, the coupling between the SRD solvent and the membrane is discussed, including aspects of the integration protocol and thermostat that need to be considered when the goal is the accurate modeling of dynamics. Finally, lipid diffusion as a function of system size is presented, illustrating that the method obtains Saffman-Delbruck like diffusion.

Materials and Methods

Molecular dynamics

The time evolution of both coarse-grained lipid beads and SRD fluid particles is subject to standard MD. Pairwise forces from lipid-lipid and lipid-solvent interactions are governed by the Dry Martini force field (15). We use standard Dry Martini parameters for nonbonded interactions: van der Waals interactions are modeled with Lennard-Jones potentials shifted to zero from 0.9–1.2 nm. In the “direct coupling” scheme (see below), SRD fluid particles have a purely repulsive interaction with lipid beads, but have no pairwise interactions with one another. All pairwise interactions are calculated with the assistance of a neighbor list using a 1.4 nm cutoff, updated every 100 time steps.

Between collision steps (see below), the system evolves under NVE conditions, integrating the equations of motion with the leapfrog algorithm with an integration timestep, τ_MD, of between 2 and 10 fs. (As discussed below, a smaller timestep is used than in “conventional” Martini simulations which include an explicit water model to control integration artifacts. The extent to which this may be relaxed is revisited in the Discussion.) Constant-temperature schemes that involve gross randomization of velocities must be avoided, as such algorithms do not locally preserve momenta, as required to capture hydrodynamic flows (24). SRD particles are subject to a separate thermostat (25) that conserves mesoscopic hydrodynamic flows, described in more detail below. Simulations are run at constant volume, at an area chosen to enforce zero surface tension. The area corresponding to zero surface tension is determined by equilibrating the system coupled to a Berendsen barostat (26) with τ_B = 6 ps and lateral compressibility of 3 × 10⁻⁵ bar⁻¹. The solvent depth normal to the bilayer surface is fixed at 20 nm by setting the compressibility to zero in that direction. After equilibration, the system is rescaled to match the average equilibrium area at zero surface tension.

SRD dynamics

The SRD algorithm belongs to a class of particle-based Navier-Stokes fluid simulation techniques called multi-particle collision (MPC) dynamics. (More extensive discussions of SRD (25, 27) and MPC (28) can be found elsewhere.) These methods represent the fluid with a number of tracer particles whose dynamics conserve mesoscopic hydrodynamic flows. These particles alternate between “streaming” and “collision” steps. During the streaming step, fluid particles do not interact with one another; their motion is ballistic. At regular intervals, the simulation volume is partitioned into a uniform cubic lattice of “collision cells.” Within each cell, all fluid particles undergo a coarse-grained collision that preserves the mean velocity vector of the cell. The set of all cell velocity vectors is the mesoscopic Navier-Stokes flow field of the fluid, resolved on the lengthscale of the collision cells.

Apart from satisfying conservation rules, MPC methods afford some freedom in how the collision step is implemented. The chosen mechanism should randomly redistribute particle velocities to “average out” the cumulative effect of individual inter-particle collisions, at the same time still respecting the underlying mesoscopic momentum transport. The SRD algorithm implements these collisions through a local rotation of the relative velocity vectors for all particles in a collision cell. More specifically, after the mean velocity vector, $\overrightarrow{\mathbf{u}}$, of the cell is computed, the velocity of each SRD particle relative to $\overrightarrow{\mathbf{u}}$ is rotated by a fixed angle, α, about a randomly chosen axis. Hydrodynamic momentum transport is maintained on the lengthscale of the collision cell, as this operation does not change the cell’s mean momentum. The velocity, ${\stackrel{\rightharpoonup }{v}}_i^{\prime }$, of particle i after a collision is

$${\overrightarrow{v}}_i^{\prime }=\overrightarrow{\mathbf{u}}+{\mathbf{R}}_{\alpha }\left({\overrightarrow{\mathbf{v}}}_i-\overrightarrow{\mathbf{u}}\right),$$ (1)

where ${\mathbf{R}}_{\alpha }$ is the rotation matrix and ${\overrightarrow{\mathbf{v}}}_i$ is the velocity before the collision.

The hydrodynamic properties of the SRD fluid are controlled by five independent parameters: the mass, m, of the SRD particles; the average number, M, of SRD particles per collision cell; the collision cell edge length, a; the collision interval, τ_C; and the collision angle, α. In the application to lipid membrane simulation presented here, the mass is fixed at 72.0 amu, comparable to a Martini interaction site, and the number density of SRD is fixed by requiring that the SRD particles minimally perturb membrane thermodynamics, described in more detail below. Smaller collision cell size is desirable, as it sets a lower limit on the length scale of resolved hydrodynamics. Collision frequency impacts performance in the implementation presented here, as it requires communication of SRD particle velocities. This leaves the collision angle as the most convenient adjustable parameter.

In its original formulation, the SRD algorithm did not respect Galilean invariance (29). As nearby particles repeatedly collide with one another, they build up velocity correlations that couple to the mesoscopic flow field. This oversight is corrected by sampling different groups of SRD particles at each collision step. We implement this with a random shift of the collision cell lattice before each collision, using a uniform random shift of (–a/2, a/2) along each axis.

Lipid-SRD interactions

Solvent free lipid models are obtained by parameterizing the lipid-lipid interactions to include the effect of solvation on bilayer thermodynamics. The lipid-SRD interaction should therefore be chosen to minimally perturb the bilayer thermodynamic properties. In the following, two different methods for implementing lipid-SRD interactions are presented. In the first, which is called the “direct collision” method here, SRD particles interact directly with the membrane via a short-range, purely repulsive (Weeks-Chandler-Andersen type) potential (30). In the second approach, here called “collisional coupling” (CC), lipid phosphate sites participate in the collision updates, but there are otherwise no interactions between lipid and SRD particles.

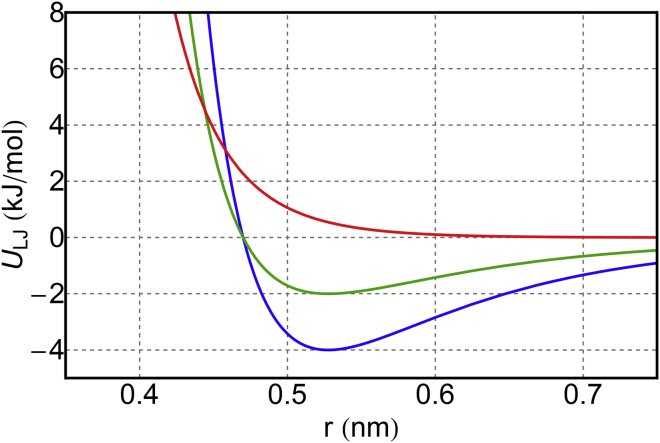
For simplicity of the implementation, in the direct method we mimic the Weeks-Chandler-Andersen potential with a shallow-well Lennard-Jones potential with σ = 0.80 nm and ε = 0.001 kJ/mol. This functional form yields an effective SRD radius comparable to the size of Dry Martini lipid beads (see Fig. 1). If the SRD particles are too small, they penetrate the membrane. If they are too large, the fluid exerts a large, spurious normal pressure on the membrane, as discussed below in Results.

Figure 1.

SRD-lipid interaction for the direct coupling scheme (red) compared with two van der Waals interactions from the Dry Martini force field, level III (blue) and level VIII (green). To see this figure in color, go online.

Thermostatting to preserve hydrodynamics

MD thermostats that randomize velocities disturb hydrodynamic flows by disrupting velocity correlations (24). The algorithm presented here requires a thermostat that conserves the mesoscopic flow field—i.e., the mean collision cell momenta—while maintaining the proper thermodynamic ensemble. For MPC algorithms, these conditions are satisfied by a Monte Carlo-type thermostat similar to that described in (25), which operates on each collision cell independently in the following manner. A scaling factor, S, is chosen, with equal probability, to be either $\left(1+\epsilon \right)$ or ${\left(1+\epsilon \right)}^{-1}$, where ε is an input parameter significantly less than one. Then a uniform random number is chosen, $p\in \left[\mathrm{0,1}\right]$. If this number is less than the acceptance probability, $p_{\text{A}}$ = min(1, A), the relative velocities of SRD particles in the cell are rescaled by S. The parameter A depends on the number of particles in the cell, n, the target temperature, T₀, and the relative kinetic energy of SRD particles in the cell according to

$$A=S^{3\left(n-1\right)}\text{exp}\left(-\frac{m\left(S^2-1\right)}{2k_{\text{B}}{T}_0}\sum _{i=1}^n{\left({\overrightarrow{\mathbf{v}}}_i-\overrightarrow{\mathbf{u}}\right)}^2\right).$$ (2)

This thermostat produces an ensemble of SRD particles with a Maxwellian velocity distribution (25). The thermostat, with $\epsilon$ = 0.1, is applied to the SRD particles immediately after each collision step.

Performance comparison of STRD Martini to conventional Martini

On a single 2.80 GHz Intel i7-4900MQ processor (8 threads), a 20 × 20 × 25 nm conventional Martini simulation (Gromacs v.5.01) obtains a simulation rate of ∼12.5 ns/day. Our STRD Martini simulation achieves a rate of ∼49.9 ns/day, or a factor of 4 speedup, as the STRD Martini simulation eliminates calculation of solvent-solvent distances. Note that these numbers are obtained without any effort whatsoever to optimize the implementation of SRD in Gromacs. Significant performance gains are to be expected after such optimization, especially targeting communication of SRD particle positions. Note that the advantage afforded by the SRD solvent over conventional Martini increases with the amount of solvent included in the simulation. As demonstrated by recent theoretical (31) and simulation (32) data, obtaining accurate diffusion constants from simulation requires a much larger system than is commonly used.

Results

STRD Martini parameters may be tuned to reproduce lipid thermodynamics

Due to the interfacial nature of the lipid bilayer, the direct collision of SRD fluid particles introduces a normal pressure that arises from the virial contribution normal to the interface. Since the SRD-lipid interactions are purely repulsive, this is a positive normal pressure. Furthermore, the balance of normal (z) and tangential (x-y) pressures determines the surface tension via

$${\gamma }_{\text{bilayer}}=L_Z\left(P_{zz}-\frac{P_{xx}+P_{yy}}{2}\right),$$ (3)

where L_z is the dimension of the simulation cell normal to the bilayer and P_αβ is the pressure tensor. The direct collision of SRD particles, which interact through a repulsive interaction with the bilayer, will therefore act to reduce the lateral area of the bilayer when enforcing zero surface tension.

Since this effect arises from the virial, it depends on the range of the SRD-lipid interaction (see Table 1) and the density of the SRD particles, both of which may be controlled to minimize the effect. Reducing the range of the SRD-lipid interaction reduces the spurious normal pressure, but for reasons discussed above, the SRD-Martini range is chosen to be comparable to the interaction range of the Martini force field.

Table 1.

Equilibrium Properties of a 10 × 10 nm STRD Martini Palmitoyloleoylphosphatidylcholine Bilayer

σ (nm)	APL (Å2)	Thickness (nm)
0.40	63.092 ± 0.037	4.232 ± 0.026
0.50	62.434 ± 0.038	4.228 ± 0.025
0.60	59.896 ± 0.039	4.303 ± 0.026
0.70	57.748 ± 0.040	4.399 ± 0.028
0.80	56.458 ± 0.045	4.465 ± 0.031
Dry Martini	63.766 ± 0.039	4.210 ± 0.027

Data are shown for the direct coupling method as the Lennard-Jones parameter σ is increased while ε is held fixed at 0.001 kJ/mol and the SRD particle density is held fixed at N = 10/nm³. Data are also shown for a Dry Martini bilayer without SRD solvent. The thickness is measured from phosphate to phosphate.

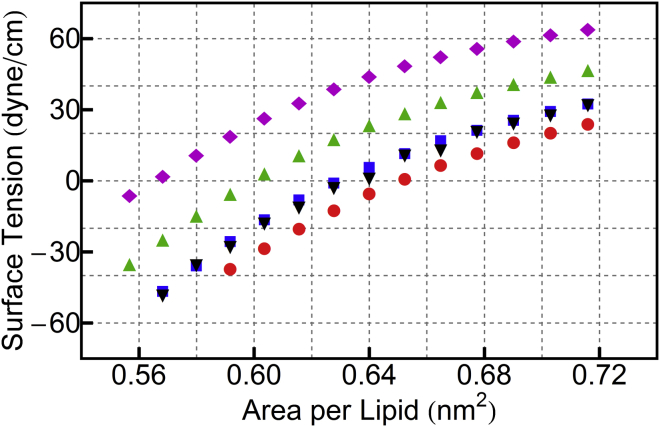
Fig. 2 reports the surface tension (computed via Eq. 3) as a function of membrane lateral area, obtained by simulations under NVT conditions with the radius of the SRD particles fixed at 0.8 nm. Under zero surface tension, the area per lipid (APL) of a conventional Dry Martini simulation is 63.7 Å²—this is the target for the STRD Martini simulations. The direct collision of SRD particles reduces the APL due to the additional normal contribution to the virial. However, at a density of 1 SRD particle/nm³, the APL is reduced from the conventional Dry Martini result to 62.9 Å², a reduction of 1.3%, which leaves the bilayer in the fluid state. Alternatively, one could perform simulations under constant surface tension of ∼10 dyn/cm to enforce the exact Dry Martini APL. In the following, the first approach is used, to report results at zero surface tension. Note also that the area compressibility is linear in all cases in the vicinity of the zero-surface-tension condition in Fig. 2, though the compressibility modulus also depends on N, as reported in Table 2.

Figure 2.

In the direct coupling approach, equilibrium APL and area compressibility depend strongly on the number density, N (in nm⁻³), of SRD fluid particles. Four systems with σ = 0.80 nm and ε = 0.001 kJ/mol are shown: N = 10 (magenta diamonds), N = 5 (green triangles), N = 1 (blue squares), and Dry Martini without SRD (red circles). The SRD parameters are a = 1.0 nm, τ_MD = 2 fs, τ_C = 80 fs, and α = 180°. Data for the CC scheme are also shown (black inverted triangles), with SRD parameters N = 2.5/nm³, a = 2.0 nm, τ_MD = 10 fs, τ_C = 200 fs, and α = 180°. To see this figure in color, go online.

Table 2.

Equilibrium System Size and Area Compressibility for Dry Martini and STRD Martini as a Function of SRD Particle Density

Simulation	APL (Å2)	Area Compressibility (mN/m)
DC, N = 1	63.02 ± 0.10	384 ± 17
DC, N = 5	59.942 ± 0.042	428 ± 13
DC, N = 10	56.459 ± 0.082	378 ± 11
CC, N = 2.5	63.56 ± 0.18	320 ± 33
Dry Martini	65.084 ± 0.054	333 ± 12

Data for both the direct coupling (DC) and collisional coupling (CC) schemes are shown. Area compressibility is calculated from a linear fit of the data in Fig. 2 at zero surface tension.

SRD fluid viscosity and hydrodynamic properties

Both the streaming and collision steps contribute to the viscosity of the fluid, which for SRD can be expressed analytically as a function of the input parameters (28)

$${\eta }_{\text{streaming}}=\frac{k_{\text{B}}TM\tau }{2a^3}\left(\frac{5M}{\left(M-1+e^{-M}\right)\left(2-\text{cos}\left(\alpha \right)-\text{cos}\left(2\alpha \right)\right)}-1\right)$$

$${\eta }_{\text{collision}}=\frac{m}{18a\tau }\left(M-1+e^{-M}\right)\left(1-\text{cos}\left(\alpha \right)\right).$$ (4)

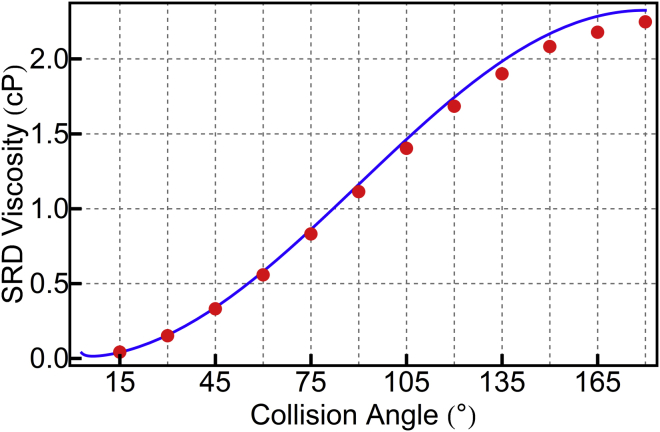
The total viscosity is the sum of these two components. We tested these expressions (Fig. 3) by simulating boxes of pure SRD and calculating the viscosity from the decay of transverse velocity correlations (33), as implemented in the Gromacs “tcaf” tool, which reports a (wavevector) k-dependent viscosity that is expected to converge as k goes to zero. No k dependence was observed for these simulations, so the viscosity was taken as the average from the four lowest k vectors.

Figure 3.

Dynamic viscosity found in simulation (red points) agrees with the theoretical prediction (blue line). SRD parameters are a = 2.0 nm, τ_C = 20 fs, and N = 1/nm³. To see this figure in color, go online.

At the scales relevant to molecular transport in membranes, water is a low-Reynolds-number, nearly incompressible solvent (34, 35). With an appropriate choice of parameters, SRD dynamics capture this hydrodynamic regime (27). Following the approach of Huang et al. (36), analysis of the velocity correlations (Fig. S1 in the Supporting Material) demonstrates that SRD parameters appropriate for lipid simulation achieve the low-Re, incompressible regime.

STRD Martini parameters must be chosen to minimally perturb integration

In a strict sense, the collision step of the SRD algorithm conserves energy—although relative velocity vectors of SRD particles are rotated, their magnitudes are unchanged. From a microcanonical perspective, the SRD collision therefore moves the system from one location to another on a surface of constant energy.

The SRD collisions, however, represent a significant perturbation to the trajectory. Interplay between the coarse-grained site interactions and the rotation of the velocities during the collision step introduces an integration error in the subsequent MD step. Since SRD velocity vectors are no longer determined by integrating the Hamiltonian, we are no longer assured a conserved quantity that we can identify with the system’s energy. The magnitude of the error depends strongly on the collision interval and weakly on the integration timestep (Fig. S2). It is therefore necessary to choose these parameters carefully to ensure a minimally perturbed integration. No heating occurs in simulations of pure SRD particles or membrane-SRD simulations without SRD collisions.

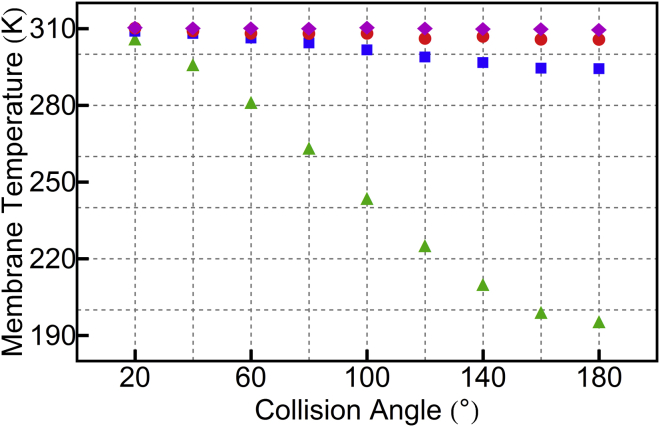
Though a conservative choice for the integration timestep and collision interval minimizes the violation of energy conservation, over the course of a long simulation these violations will eventually lead to significant heating. Small amounts of heating, obtained with conservative choices for τ_MD and τ_c, are controlled via the SRD thermostat. More aggressive choices, however, lead to a significant artifact, as shown in Fig. 4. Since the thermostat is applied only to the SRD particles, a poor choice of collision frequency leads to a temperature difference between the lipids and the solvent. The extent to which the integration is perturbed depends on the collision angle, and so the temperature difference also depends on the collision angle.

Figure 4.

Steady-state membrane temperature depends on the collision angle and timestep. Three data series are shown using direct coupling: τ_MD = 2 fs with collisions every 50 steps (red circles) and every 10 steps (blue squares), and τ_MD = 20 fs with collisions every step (green triangles). SRD parameters for these data are a = 2.0 nm, and N = 1 nm⁻³. In addition, one data series is shown for the CC scheme (magenta diamonds) with τ_MD = 10 fs, a = 2.0 nm, collisions every 20 steps, and N = 2.4 nm⁻³. See Fig. S2 for the membrane temperature as a function of τ_MD and τ_C for the CC scheme. To see this figure in color, go online.

The data in Fig. 4 demonstrate that for the direct coupling scheme with τ_MD = 2 fs and τ_C = 100 fs, the entire range of collision angles is accessible without significantly compromising the quality of the integration. The collisional coupling scheme provides even better integration quality with a larger integration timestep: with τ_MD = 10 fs and τ_C = 200 fs, the temperature difference is negligible. Note that one would need to be extremely cautious when applying a thermostat separately to both lipids and solvent, as this can mask serious artifacts.

Center-of-mass drift

Like applying a thermostat, periodic removal of center-of-mass (CoM) motion can hide integrator artifacts. Such artifacts may be especially pernicious when computing dynamic quantities, like lipid or membrane protein diffusion. For this reason, in the reported simulations the system CoM motion is removed only once, after the initialization of velocities. This is done separately for the solvent and membrane subsystems.

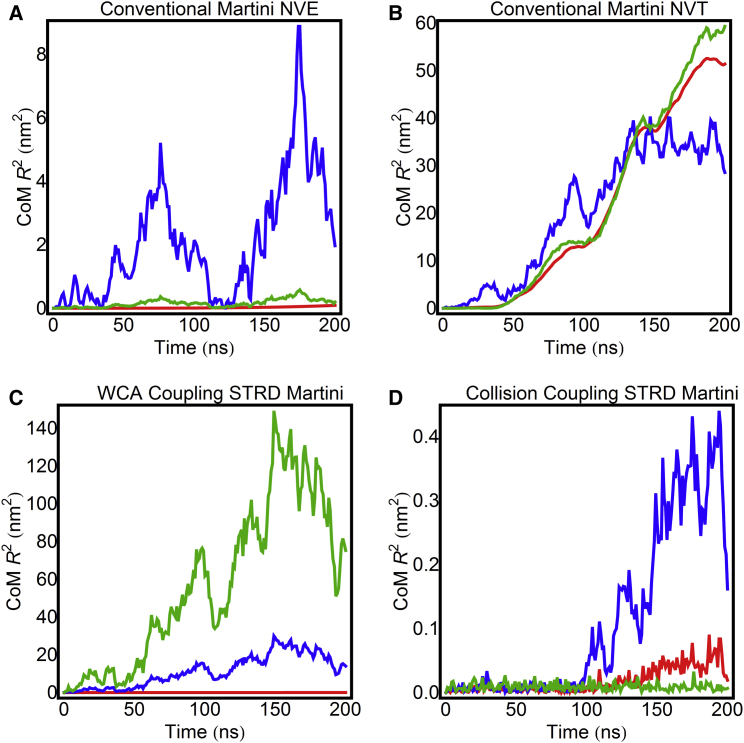
Fig. 5 shows that during a span of 10⁸ integration steps the overall CoM drift (lipids plus solvent) in the lateral direction is negligible in NVE Martini simulations with conventional Martini solvent. Appreciable CoM drift of conventional Martini under NVT conditions is observed using the Bussi-Donadio-Parrinello velocity-rescaling thermostat (37) to control temperature. Both the direct and the collisional coupling schemes for STRD Martini result in negligible overall CoM motion. Note, however, that the solvent and lipid subsystems may move relative to one another, such that the overall CoM drift is negligible, and that this does not indicate a failure of the integration. The extent to which this is possible depends on the lipid-solvent boundary condition—under perfect stick conditions, the momentum of the fluid and of the solvent must be identical at the interface, and relative motion of the lipid and the solvent would not be possible. This is clearly not the case for any of the solvated systems shown in Fig. 5. (Note that in the direction normal to the bilayer, the momenta are constrained to be very nearly equal by virtue of the effective incompressibility of the solvent (see Fig. S3).) The relative motion of the lipid and solvent subsystems therefore provides a qualitative indication of the frictional coupling between solvent and lipid, which is clearly lowest for the STRD Martini simulation. The implications of this point are revisited in the Discussion.

Figure 5.

CoM drift when automatic CoM removal is disabled for the entire system (red line), fluid particles only (green line), and lipids only (blue line). Shown are conventional Martini NVE (A), conventional Martini NVT (B), STRD Martini with direct coupling (C), and STRD Martini with collisional coupling (D). The collision angle for the STRD Martini simulation is 180° to maximize integrator perturbation. Note the difference in vertical scales. The SRD parameters for the direct coupling scheme (C) are a = 2.0 nm, τ_MD = 2 fs, τ_C = 100 fs, and N = 1 nm⁻³, and those for the CC scheme are a = 2.0 nm, τ_MD = 10 fs, τ_C = 200 fs, and N = 2.4 nm⁻³. To see this figure in color, go online.

Lipid diffusion and generalized Saffman-Delbruck mobility

Saffman-Delbruck (SD) theory (13, 14) (referred to in the following as SDHPW to acknowledge the extension by Hughes, Palinthorpe, and White) predicts that the mobility of a membrane-spanning cylinder increases logarithmically with the ratio of the SD length to the radius of the cylinder. The SD length, in turn, is the ratio of the surface viscosity of the membrane to the shear viscosity of the solvent in the bulk. Recently, Camley and Brown recognized that SD lengths typical of lipid simulations yield a significant finite-size artifact when simulating lipid diffusion, and they generalized the SDHPW result to obtain an expression applicable to periodic systems, including a result for the diffusion of cylinders that span a single leaflet.(31) Thus, measurement of lipid diffusion as a function of system size and comparison to the generalized SD theory provides a test of whether the simulation obtains quasi-two-dimensional, SD-like hydrodynamics.

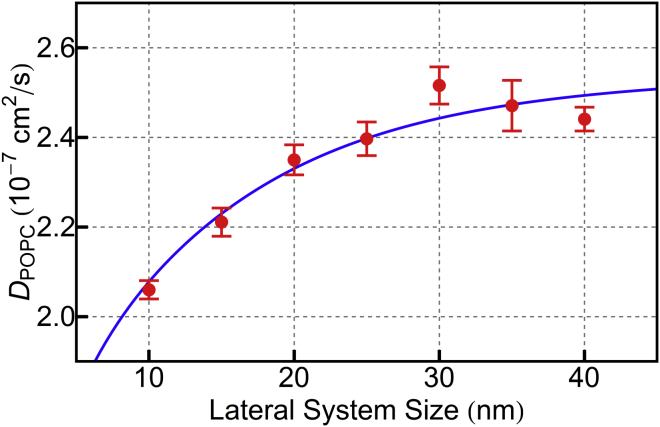
Fig. 6 reports observed lipid diffusion constants as a function of lateral system size, obtained by fits to the mean-square lipid displacements during nonoverlapping 200 ns trajectory segments. (An example set of mean-square lipid displacement plots and fits is shown in Fig. S3.) Seven STRD Martini palmitoyloleoylphosphatidylcholine membranes, ranging in lateral dimension from 10 to 40 nm were simulated with 20 nm between neighboring periodic images in the direction normal to the membrane. The simulation parameters were chosen to minimize perturbations to the thermodynamics and the integration, as shown in Figs. 2 and 4: τ_MD = 10 fs, a = 2.0 nm, collisions occurred every 20 steps, and N = 2.4 nm⁻³.

Figure 6.

STRD Martini lipid diffusion constants obtained by a fit of the time- and ensemble-averaged mean-square lipid displacements as a function of lateral system size. Error bars are the standard error of the slopes of nonoverlapping 200 ns windows, as shown in Fig. S4, and are almost certainly underestimates. The full trajectory is 2000 ns for each point. SRD parameters are a = 2.0 nm, τ_MD = 10 fs, τ_C = 200 fs, and N = 2.4 nm⁻³. The blue curve is a fit to the theoretical prediction of Camley and Brown, as described in the text. To see this figure in color, go online.

Also shown in Fig. 6 is the data fit to the theory of Camley and Brown for half cylinders.(31) The theoretical prediction for the dependence of the diffusion constant on system size depends on the solvent and membrane $\left({\eta }_{\text{m}}\right)$ viscosities and the interleaflet friction, b. The solvent viscosity is fixed by the SRD parameters at 0.6 cP; the membrane surface viscosity and interleaflet friction were left as free parameters, obtaining best fit values of ${\eta }_{\text{m}}$ = 8.69 × 10⁻⁸ P cm and b = 2.87 × 10⁵ P/cm. The interleaflet friction is similar to the value obtained recently for conventional Martini by Pastor and co-workers in unpublished work (R. Pastor, personal communication). The lipid viscosity, however, is a factor of 7 or 8 larger than values reported for conventional Martini, likely because the lipid-lipid interactions in Dry Martini are stronger than their conventional Martini counterparts, to replace the thermodynamic effects of the eliminated water.

Discussion

An approach to incorporate hydrodynamics into particle-based, implicit-solvent simulations of lipid bilayers is presented. The method, called STRD Martini, combines SRD with the Dry Martini model for lipids, but it is applicable to any particle-based, implicit lipid model. In general, the addition of an SRD solvent to an implicit-solvent model will perturb both the thermodynamics and the integration of the lipid trajectories. This perturbation will depend on how the lipid and SRD particles are coupled and on the parameters of the SRD algorithm, especially the frequency of collision steps, the density of SRD particles, and the rotation angle of the collisions.

A direct collision algorithm, in which the SRD particles participate in the MD integration near the membrane surface, adds a new contribution to the normal pressure that depends on the SRD-Martini interaction radius and the density of SRD particles. This in turn changes the surface tension, which will tend to contract the membrane area unless the SRD parameters are carefully tuned to minimize the artifact. Significant improvements are obtained by implementing a solvent-lipid coupling rule in which the lipid phosphate sites participate in the collisions (CC) but there is no direct, Weeks-Chandler-Andersen-like interaction between SRD particles and lipid sites. As there are no direct forces between SRD and lipid particles, there is no additional contribution to the virial, and this approach does not alter the lipid thermodynamics.

The CC scheme also has advantages as regards the lipid-solvent boundary condition. Since the lipid headgoups participate in the collisions, their momenta contribute to the SRD cell’s coarse-grained momenta at the interface. The CC rule therefore enforces continuity of the momenta across the interface, yielding perfect stick boundary conditions. The collision angle, integration timestep, and collision frequency determine the extent to which the integration is preserved, with conservative choices producing minimal perturbation. The results presented here suggest that the CC scheme admits a larger MD timestep than the direct-coupling scheme; future efforts will look for variations that admit even longer integration timesteps. For all these reasons, the CC scheme seems to be the better choice for quantitative simulation of coarse-grained lipid dynamics with STRD Martini.

Implementation of an alternate collision rule—e.g., one that conserves angular momentum (38)—may well have better integration properties than the SRD approach, and may also have the favorable feature that transport properties are analytically related to the fluid parameters (39). Additionally, modest investment in optimization, especially as regards communication protocols for the solvent particles, should yield significant performance gains, especially for large systems. As recently pointed out by Vögele and Hummer (32) on the basis of the theory due to Camley and Brown (31), very large systems, many times the SD length in each dimension, are required to obtain accurate estimates of diffusion constants for lipids. Even with a coarse-grained model like Martini, such simulations would require enormous simulation resources. STRD Martini is designed to address this need.

When using the CC scheme, the system-size dependence of lipid diffusion agrees quantitatively with theoretical predictions based on a generalization of SD theory to periodic geometries (31), recently verified by extensive conventional Martini simulations. (32) This indicates that the STRD Martini approach accurately models the quasi-two-dimensional hydrodynamics of lipid bilayers. The STRD Martini method should therefore find application for modeling more complex problems, such as lipid and protein diffusion in heterogeneous membranes, in non-freestanding geometries, or in membranes coupled to the cytoskeleton, for which there is no theory. The need for modeling approaches that address the complexity of real membranes is critical to the interpretation of modern experimental measurements, which infer membrane structure and organization from direct measurements of lipid and protein mobility (4, 5, 6, 11).

Author Contributions

E.L. and A.Z. designed the research, A.Z. performed the research, and E.L. and A.Z. wrote the manuscript.

Editor: Markus Deserno.