Mechanical Criterion for the Rupture of a Cell Membrane under Compression

Abstract

We investigate the mechanical conditions leading to the rupture of the plasma membrane of an endothelial cell subjected to a local, compressive force. Membrane rupture is induced by tilted microindentation, a technique used to perform mechanical measurements on adherent cells. In this technique, the applied force can be deduced from the measured horizontal displacement of a microindenter’s tip, as imaged with an inverted microscope and without the need for optical sensors to measure the microindenter’s deflection. We show that plasma membrane rupture of endothelial cells occurs at a well-defined value of the applied compressive stress. As a point of reference, we use numerical simulations to estimate the magnitude of the compressive stresses exerted on endothelial cells during the deployment of a stent.

Introduction

It has become increasingly clear over the past two decades that cells feel and respond to physical cues in their environment (1). Endothelial cells in particular have been shown to be highly sensitive to the mechanical forces to which they are subjected (2). Beyond mechanical forces that are naturally present in the body, human intervention may also trigger new and different mechanical forces on the endothelium. For instance, minimally invasive surgical procedures often require the use of catheters, which push strongly against the endothelium. Angioplasty and stenting procedures, which have become routine interventions for about eight million patients each year worldwide (3, 4, 5), also apply great compressive stresses on the endothelium and have been shown to lead to substantial endothelial damage (6). Endothelial damage, in turn, may lead to thrombosis (7), a major cause of stroke and myocardial infarction. It is therefore of great interest to understand the mechanism by which mechanical forces, and in particular compressive forces, can damage endothelial cells.

The goal of this article is to characterize the mechanics of endothelial cell membrane rupture under compressive stress. Endothelial cells line the arterial walls and are continuously subjected to mechanical forces, which often cause membrane wounding. Using mouse models, it has been estimated that under normal physiological conditions and at any given time, between 1% and 18% of aortic endothelial cells exhibit wounded membranes (8). The plasma membrane has the ability to recover from disruption, so that endothelial cells can remain viable in spite of wounding (9). However, under high stresses, such as those arising during the deployment of a stent, endothelial cells can be wounded beyond repair (10). Plasma membrane rupture under compressive stress has previously been studied in red blood cells using atomic force microscopy (AFM) (11, 12) and in mouse myoblasts using a whole-cell compression apparatus (13). However, in those studies, the shape and size of the compressive apparatus was maintained constant, yielding a single critical force value. Here we introduce the technique of tilted microindentation, a versatile tool to study cell mechanics, and we apply this technique to characterize the rupture of endothelial cell membranes under compression applied on contact areas ranging from 1 to ∼100 μm².

AFM is the technique of reference for studying adherent cell mechanics. In AFM, forces are applied onto a cell through a cantilever ending at a sharp tip, with a typical radius at its extremity of ∼10 nm. Such a sharp tip induces high local strains that can exceed the linear regime, thus introducing artifacts in the determination of the cell’s mechanical properties (14, 15). To avoid such artifacts, an alternative technique is often used where a micrometric bead is attached to the tip of the AFM cantilever (16, 17, 18). In AFM, the applied force is deduced from the deformation of the cantilever, whose measurement requires the use of an optical sensor, most commonly a system of photodiodes collecting a laser beam reflected by the cantilever. Although it is precise and versatile, AFM requires expensive equipment; moreover, the AFM head is bulky and restrains access to the sample. In this article, we introduce tilted microindentation, an inexpensive and unobstructive technique to exert controlled compressive nanonewton forces and to characterize cellular mechanics over the μm² scale. Using a micropipette puller and a microforge, we fabricate a glass microindenter consisting of a cantilever beam of adjustable stiffness (0.5–200 nN/μm) and a tip of adjustable shape (spherical or flat) and size (tip diameter of 2–10 μm). The ability to produce indenters of custom size, shape, and stiffness is a significant advantage of the technique proposed here, as it allows discrimination of the effects of force versus stress, as demonstrated in this article. The proposed device is similar to the “cell poker” developed by McConnaughey et al. (19, 20). However, the cell poker requires an optical sensor to deduce the cantilever deflection and the corresponding applied force. In the technique we propose, the microindenter is tilted so that the applied force can be deduced from measuring the horizontal displacement of the microindenter’s tip over the sample. The applied force is hence deduced from the sample image acquired with an inverted microscope, thus eliminating the need for optical sensors and allowing simultaneous fluorescence imaging. The uncertainty of the force measurement is <1 nN when the most flexible microindenter is used.

By using tilted microindenters of different rigidities and tip geometries, and by varying the microindenter’s angle of attack, we show that microindentation-induced membrane rupture occurs at a constant normal stress of 12.4 ± 0.6 kPa. Because our stress criterion is scale-independent over the range of contact areas studied here, we speculate that our criterion is relevant to stent deployment, where the typical strut size is on the order of 100 μm (21). We also present numerical simulations to interpret the mechanics of cell indentation and to estimate the compressive stresses exerted on endothelial cell membranes during stent deployment.

Materials and Methods

Endothelial cells

Bovine aortic endothelial cells (BAECs) were kindly provided by A.-C. Vion and C. Boulanger and used between passages 4 and 12. BAECs were cultured at 37°C and 5% CO₂ in Dulbecco’s modified Eagle’s medium (DMEM; low glucose, Invitrogen, Carlsbad, CA) supplemented with 10% fetal bovine serum (Invitrogen) and 1% penicillin/streptomycin (Invitrogen). One to two days before an experiment, cells were cultured in thin-bottomed Petri dishes (Fluorodish 35 mm, World Precision Instruments, Hitchin, United Kingdom). For experiments in which the cells were exposed to cytochalasin D, we used the same protocol as in Hogan et al. (22): the cells were incubated for 30 min in a solution containing 1 mg/mL cytochalasin D from Zygosporium masonii (Sigma-Aldrich, Taufkirchen, Germany); the Petri dish was then rinsed and experiments were performed in fresh medium.

Microscope and micromanipulator

Experiments were performed on a TE300 inverted microscope (Nikon Instruments, Tokyo, Japan) placed on an air suspension table (CVI Melles Griot, Netherlands). The microscope was equipped with a 100× oil-immersion, 1.3 NA objective (Nikon Instruments) for experiment monitoring and lower magnification objectives (40×, 20×, 10×, 4×, and 2×; Nikon Instruments) for micropipette positioning. Images were acquired using a Flash 4.0 CMOS camera (Hamamatsu Photonics, Hamamatsu City, Japan). The experimental setup was equipped with a motorized micromanipulator (MP285, Sutter Instruments, Novato, CA) carrying a micropipette holder (IM-H1, Narishige, Tokyo, Japan) at a controlled angle, α, and holding a microindenter. The microscope was equipped with a heating stage set to 37°C, guaranteeing a constant temperature slightly lower than 37°C but higher than room temperature. Before each experiment, a Petri dish was taken out of the incubator and medium was exchanged with pre-heated culture medium supplemented with 160 μg/mL propidium iodide (Sigma-Aldrich). The dish was placed on the stage with oil immersion and the 100× objective was focused in the cell-substrate plane under brightfield illumination. The microindenter was positioned in the dish in the center of the field of view and ∼50 μm above the cell level. The microindenter was left at least 10 min in buffer before contacting any cell to let the serum proteins in the medium adsorb onto the tip and avoid its adhesion to cells. The illumination source was an Intensilight lamp (Nikon Instruments), exposure time was set to 80 ms, and a neutral density filter 4 or 8 was used. The fluorescence aperture diaphragm was adjusted to limit exposure in the field of view. A region of interest was defined using Micromanager software (23).

Microindenter fabrication and calibration

Microindenters were prepared as described in Guillou et al. (24). Briefly, borosilicate glass capillaries (15 cm length, 1 mm outer diameter (OD), and 0.78 mm inner diameter; Harvard Apparatus, Holliston, MA) were pulled using a P-97 micropipette puller (Sutter Instruments, Novato, CA). Each microindenter had a constant OD of 1 mm along its length except typically over the last centimeter, where its diameter started decreasing until it reached a size of a few microns at the end. Typically, the OD was 50 μm at 5 mm from the tip. An MF-200 microforge (World Precision Instruments) was used to melt glass at the tip of the micropipette (Movie S6 in the Supporting Material). The microindenter’s bending stiffness was evaluated against standard microindenters that had been previously calibrated. One method to calibrate these standard microindenters was to measure their deflection under the gravitational force exerted on their tip by a piece of ultrathin paper of known mass (25). We confirmed this initial method by using a commercial force probe (model 406A, with a force range of 0–500 nN, Aurora Scientific, Aurora, Ontario, Canada).

Measuring cell membrane rupture

For measurements on the cytoplasm, endothelial cells with flat lamellipodia were chosen. The microindenter was lowered using the finest setting of the micromanipulator. Contact was indicated by the onset of the bead sliding over the surface of the cell, which was defined as the reference position. The illumination was then switched to fluorescence excitation at 580 nm and the indentation process was recorded. The microindenter’s base was lowered by manual control to maintain a mean vertical translation speed of typically 1 μm/s. Our initial protocol involved switching between brightfield and fluorescence illumination to detect the position of the bead at contact. We later identified that under fluorescence illumination, bead contact was detected by the sensitive CMOS camera as a dark spot in the background fluorescence due to the cell’s autofluorescence. The surface of this dark spot was used to measure the contact area (see Supporting Materials and Methods, Fig. S8, and Movies S7 and S8). This approach for measuring contact area was validated by comparing it to an alternative estimate obtained from tracking mitochondria displacement underneath the microindenter (see Supporting Materials and Methods and Fig. S9). As soon as an increase in fluorescence was detected (which was initiated in close vicinity to the microindenter’s tip (Movie S1)), the translation was stopped, and both the horizontal distance from the reference position, Δx, and the vertical displacement of the microindenter’s base, δ (as indicated by the micromanipulator controller), were measured. The microindenter was then retracted by bringing its tip to a resting position at 10 μm above the point of contact with the cell. For experiments with an angle of attack, β, different from 0, the approach angle was set using a virtual axis option available in the micromanipulator controller.

Characterization of the moderate indentation regime

To study the moderate indentation regime and deduce cell mechanical properties, brightfield illumination was used. Once the chosen cell had been centered in the field of view, the microscope was focused on the cell’s basal plane, and a region of interest was selected to limit computer memory usage. Contact with the cell was visually indicated by the deformation of the cell surface. The probe was raised 5 μm above contact before starting the indentation experiment. Indentation induces changes in cell height; thus, if the microscope was focused at the initial bead position, the bead would move out of focus, which would increasingly interfere with the detection of the bead’s edge at increasing indentation. To avoid this bias, we kept a defocused image of the bead by focusing the microscope 3.5 μm below the basal plane of the cell. The acquisition was then started at 100 frames/s and 5 ms exposure time, and a linear translation of the base of the probe was started at 2 μm/s. We used the software ImageJ (26) to measure the position of the edge of the bead as a function of time: we normalized and smoothed the brightfield images and then defined a line coinciding with the straight trajectory of the bead sliding on the surface of the cell. We used this line to obtain a so-called kymogram, i.e., a graph where the intensity level along this line was reported at each frame. The kymogram was then thresholded to select the dark rim of the bead. The image was binarized according to this threshold to obtain coordinates (position and frame number) of the edge of the binary image (see Fig. S2). These coordinates were converted to actual distances and times using the Graphpad Prism software (Graphpad Software, San Diego, CA). In Prism, a least-squares method was applied to fit the curve of bead horizontal displacement over time.

Simulations of cell indentation

In our simulations of cell indentation, the endothelial cell is modeled as a nearly incompressible (14, 27) hyperelastic neo-Hookean (13, 28, 29) material, with a Poisson’s ratio of 0.49 and a Young’s modulus of 1 kPa. The microindenter’s spherical tip is considered infinitely rigid compared to the cell. The deformation of the microindenter’s cantilever is not modeled; rather, the cell indentation, $\Delta z$, is taken as the input. The endothelial cell is fixed on an infinitely rigid substrate to represent the focal adhesions that are observed experimentally on a glass substrate (22). The contact between the microindenter and the cell is implemented using the augmented Lagrangian method with a penalty factor of 10⁵, sufficient to prevent interpenetration. Simulations were performed in FEBio version 1.5.2 (30) with the Pardiso solver (31). The mesh was generated using Gmsh version 2.8.3 (32). The spherical indenter’s tip was meshed using linear four-node tetrahedral elements, with a coarse mesh at the center of the sphere and a fine mesh at the surface that makes contact with the cell. A structured mesh consisting of linear eight-node hexahedral elements was defined throughout the cell. We performed a mesh convergence study and found that the error in the computed forces between the mesh of choice and a very fine mesh having 100 times more elements is 2%. We verified that our numerical results were insensitive to further refinements of the microindenter’s mesh, as well as to an increase in the size of the domain that represents the cell. An example of the indentation simulation results is provided in Movie S4.

Simulations of stent deployment

For the two-dimensional stent implantation simulations, the artery is represented by a 300-μm-thick single layer, modeled as an elastic material with a Poisson’s ratio of 0.45 and a Young’s modulus of 1 MPa (33). The strut of the stent has a 100 μm × 100 μm square cross section, which is modeled as an elastoplastic material with a Young’s modulus of 270 GPa, a Poisson’s ratio of 0.27, a yield strength of 300 MPa, and a tensile strength of 650 MPa, corresponding to 316L stainless steel (34). The stent indentation is an input variable that ranges from 0 to 50% of the stent strut size (35). The external boundary of the arterial wall is subjected to a spring foundation displacement condition, with a spring constant of 300 Pa, chosen to represent the radial elasticity of an artery (36). The contact between the stent strut and the arterial wall is implemented using the augmented Lagrangian method (37). Simulations were performed using the multiphysics finite-element commercial software COMSOL version 5.0 (Comsol AB, Stockholm, Sweden). The mesh was generated with COMSOL mesh generator using linear four-node triangular elements for both the arterial wall and the stent strut, with a refined mesh for both solids in the neighborhood of the contact region. We performed a mesh convergence study and found that the error in the computed pressures between the mesh of choice for the artery and a very fine mesh having 100 times more elements is 2%. A movie illustrating the predicted von Mises stress distributions is available in Movie S5.

Results

Tilted microindentation allows application of a controlled force on adherent cells

A microindenter made of a flexible glass microfiber of bending stiffness k_m with a glass bead of radius R at its tip is held by a micromanipulator placed on an inverted microscope (Fig. 1).

Figure 1.

Description of tilted microindentation. (A) Schematic view of the tilted microindentation setup. The applied normal force, V, can be deduced from the measured horizontal displacement of the microindenter’s tip, $\Delta x$. Membrane rupture occurring at displacement $\Delta x$^∗ is visualized by the fluorescent propidium iodide signal. (B) Application of tilted microindentation to measure the normal force required to induce the rupture of an endothelial cell membrane. Membrane rupture is visualized by the fluorescent propidium iodide signal (see Movie S1). The scale bar represents 10 μm. To see this figure in color, go online.

The microindenter is held at a controlled angle, α, with the horizontal plane of the sample, and its tip is placed on top of an endothelial cell cultured on the bottom of a Petri dish on the microscope’s stage. We impose a displacement to the upper end of the microindenter and record the resulting horizontal displacement of the microindenter’s tip, $\Delta x$ (Fig. 1; Movie S1). From this measurement, and based on an analytical model of the cell response to force, we can deduce the force applied by the microindenter. The analytical model is explained in detail in the Supporting Materials and Methods. Briefly, for moderate indentations, we assume the cell to behave as a nonadhesive homogeneous isotropic linear elastic solid. For strong indentations, the indentation depth reaches a maximum value, $\Delta z=\Delta z_{\text{max}}$, corresponding to the cell becoming infinitely rigid when compared to the microindenter. Indeed, the cell will appear progressively stiffer as the indentation increases relative to the sample thickness (14), saturating at indentations of ∼60% of the cell height, where the cell becomes nearly infinitely rigid (13, 38). Our experimental results indicate that the moderate indentation regime is valid up to $\Delta z_{\text{cutoff}}\approx \Delta {\delta }_{\text{cutoff}}\approx 0.3\mu \text{m}$, corresponding to the initial region of the indentation curve that is well described by Hertz’s contact theory (see Supporting Materials and Methods for details), whereas the maximum indentation is estimated to be on the order of $\Delta z_{\text{max}}\approx 0.6\mu \text{m}$ (see below). Thus, a transitional regime between moderate and strong indentations is experimentally observed but not described by our theoretical model. At moderate indentation, the cell’s reaction to deformation is $V=k_{\text{cell}}{\left(\Delta z\right)}^{3/2}$, where according to Hertz’s model, $k_{\text{cell}}=\left(4/3\right)E^{\ast }\sqrt{R}$ and $E^{\ast }=E/\left(1-{\nu }^2\right)$, with E and ν being the Young’s modulus and Poisson’s ratio, respectively, of the cell (39). Tilted microindentation allows us to analyze moderate indentations to estimate the local apparent Young’s modulus of the cell (see Fig. S3, Movie S2, and Supporting Materials and Methods).

Beyond the maximum indentation $\Delta z=\Delta z_{\text{max}}$, we consider that the cell behaves as a rigid body with Coulomb friction, i.e., we assume $\Delta z=\Delta z_{\text{max}}=\text{constant}$ and a constant dynamic friction coefficient, μ, between the microindenter and the cell membrane. As discussed below, we have shown that in our experiments, μ is negligibly small. As detailed in the Supporting Materials and Methods, the resulting relationship between $\Delta x$ and V at large indentation is

$$V=2k_{\text{m}}\Delta x/\text{sin}\left(2\alpha \right).$$ (1)

To maximize the precision of the measured force, one should maximize the measured value of Δx to minimize its relative uncertainty. This is attained at an optimal tilt angle of $\alpha =45°$, which we have selected for all of our experiments. Thus, from measuring the horizontal displacement at membrane rupture, $\Delta x^{\ast }$, Eq. 1 yields the normal force, $V^{\ast }$, needed to rupture the membrane of an endothelial cell (Movie S1). We use propidium iodide as a reporter of this rupture. Propidium iodide is initially present in the extracellular medium. Upon membrane rupture, this intercalating agent enters the cell cytoplasm and becomes rapidly fluorescent. Other fluorescent probes can also be used, such as the calcium probe Fluo-4 (Movie S1).

The indentation force at membrane rupture is independent of the microindenter’s bending stiffness

Fig. 2 A shows the horizontal displacement of the microindenter’s tip at membrane rupture, $\Delta x^{\ast }$, as a function of the microindenter’s compliance, 1/k_m, for several microindenters with spherically shaped tips of radius 6.1 ± 0.6 μm. The microindenters are tilted at $\alpha =45°$. The figure shows that the applied normal force at rupture, $V^{\ast }=2k_{\text{m}}\Delta x^{\ast }=$ 229 ± 24 nN, is independent of the microindenter’s stiffness. Different stiffnesses yield significantly different tip displacements at rupture, indicating that membrane rupture is induced by the applied force and not by an imposed horizontal stretching associated with the horizontal displacement of the microindenter’s tip.

Figure 2.

Characterization of membrane rupture with tilted microindentation. (A) Horizontal displacement of the microindenter’s tip at cell membrane rupture, Δx^∗, as a function of the microindenter’s compliance, 1/k_m, for microindenters with a spherical tip of radius 6.1 ± 0.6 μm. Microindenters are tilted at $\alpha =45°$. The dashed line is a linear regression through the experimental data. (B) Compressive force at cell membrane rupture, $F^{\ast }$, as a function of the microindenter tip’s radius, R, for a fixed indenter stiffness $k_{\text{m}}=14.9\pm 1.6\text{nN/}\mu \text{m}$ for 10 indenters and 6–13 cells for each indenter. (C) Contact surface area between the microindenter’s spherical tip and the cell, S_contact, as a function of the microindenter’s tip radius, R. The straight line is a linear regression through the experimental data, $S_{\text{contact}}\left(\mu {\text{m}}^2\right)=3.84R\left(\mu \text{m}\right)$. (D) Normalized horizontal displacement of the microindenter’s tip at membrane rupture, Δx^∗, as a function of the microindenter’s compliance, 1/k_m, for different geometries of the microindenter’s tip (inset): spherical tip (solid circles, N = 133 cells), rectangular flat tip (open squares, N = 41 cells), circular flat tip (open circles, N = 134 cells). The encircled crosses correspond to spherical-tip microindentation measurements upon cytochalasin D treatment. Error bars represent the standard error of the mean. For all cases, $\alpha =45°$. The straight line is a fit of Eq. 4. with ${\sigma }^{\ast }=12.4\text{kPa}$. Inset: representation of the range of sizes and geometries used for the microindenter’s tip (from top to bottom: spherical, circular flat, and rectangular flat tips; relative sizes are to scale). The normalized quantities in (D) are chosen such that all data should collapse on a straight line if the rupture criterion is a constant stress. The slope of such line is indicative of the magnitude of the rupture stress. To see this figure in color, go online.

The membrane ruptures at a constant normal microindentation stress

We investigated whether the relevant criterion for indentation-induced membrane rupture should be based on the total force, on an equivalent surface tension (with units of force per unit length), or on the applied stress (force per unit surface area). To distinguish between force and tension/stress, we first varied the tip size. Fig. 2 B shows the rupture force, $F^{\ast }$, obtained for spherical tips of different radii and constant stiffness ($k_{\text{m}}=14.9\pm 1.6\text{nN/}\mu \text{m}$, for 10 indenters and 6–13 cells for each indenter). The rupture force increases linearly with the indenter’s radius, R, up to R ∼ 15 μm. We note here that a critical force increasing linearly with the tip radius is compatible with both a critical tension and a critical stress, as we further discuss below. Beyond R ∼ 15 μm, the measured force no longer systematically increases with R. Indeed, for such large radii, the indenter tip size becomes comparable to the whole cell, so that confining the indented region to the cytoplasm, without also probing thicker regions above the nucleus, is no longer systematically possible. Altogether, measurements in Fig. 2 B show that the rupture force is not constant but depends on tip size.

To distinguish between a rupture criterion based on a critical tension and one based on a critical stress, we next varied the indenter’s shape while at the same time exploring a range of indenter stiffnesses. We fabricated microindenters with tips of different sizes and shapes: spherical tips from 4.6 to 23.2 μm in diameter, flat tips of circular cross section (from 1.8 to 8.6 μm in diameter), and flat tips of rectangular cross section (from 1.4 to 3.0 μm in thickness, 8.9 to 16.8 μm in width, and a relatively constant width/thickness aspect ratio of r = 5.4 ± 0.8). All microindenters are tilted at $\alpha =45°$, so that, according to Eq. 1, the stress exerted by the microindenter tip onto the cell at rupture is $2k_{\text{m}}\Delta x^{\ast }/S_{\text{contact}}$, where $S_{\text{contact}}$ is the contact area between the tip and the cell. For flat tips, S_contact is the tip’s area. For spherical tips, the contact area can be determined experimentally from the shaded region induced by the contact. At low indentation force, the contact area increases with the indentation force, but once the microindenter starts to significantly slide horizontally over the cell, the measured contact area remains constant. Fig. 2 C shows the measured final contact area for spherical-tip microindenters of different radii. The measurements are well fitted by the linear relationship

$$S_{\text{contact}}\left(\mu {\text{m}}^2\right)\approx 3.84R\left(\mu \text{m}\right).$$ (2)

We also investigated the contact area through numerical simulations (Fig. S4). The simulations, which account for large deformations and finite-thickness effects, yield a contact area that is well represented by a modified version of Hertz’s theory,

$$S_{\text{contact}}=\lambda \pi R\Delta z,$$ (3)

where λ = 2 is a correction to Hertz’s theory, taking into account the finite cell thickness. The value λ = 2 corresponds to the membrane perfectly conforming to the spherical shape of the indenter up to the indentation depth Δz, as was also assumed by Hategan et al. (14). The agreement between numerical experiments and Eq. 3 is good in the range $1<R\text{/}h<10$, corresponding to our experimental conditions. By comparing Eqs. 2 and 3, we deduce the maximum depth of indentation of the cell, $\Delta z_{\text{max}}\approx 0.6\mu \text{m}$.

Fig. 2 D shows the normalized horizontal displacement at membrane rupture for various sizes and shapes of the microindenter tip as a function of microindenter stiffness. The measurements are globally well described by a critical rupture stress, ${\sigma }^{\ast }$, i.e.,

$$2\Delta x^{\ast }/S_{\text{contact}}={\sigma }^{\ast }/k_{\text{m}},$$ (4)

which is obtained by dividing Eq. 1 by the contact area. The best fit to the spherical-tip microindenter measurements is obtained with ${\sigma }^{\ast }=12.4\text{kPa}$, which is also a good global fit for all measurements (Fig. S5 A). In contrast, a rupture criterion based on a critical tension, ${\gamma }^{\ast }$, would lead to a rupture force scaling with the perimeter of the contact surface, P_contact. One would thus obtain the relationship $2\Delta x^{\ast }/P_{\mathrm{contact}}={\gamma }^{\ast }/k_{\text{m}}$. Fitting our measurements based on this critical-tension criterion is less convincing, as shown in Fig. S5 B.

We note that, for the same applied average stress, the local maximum stress differs in location and magnitude for different microindenter tip geometries. For a spherical tip, the maximum contact pressure occurs underneath the center of the sphere, and its magnitude is 1.5 times larger than the average applied pressure (39). For a flat punch, the maximum contact pressure occurs at the edge of the punch and it is estimated to be around three times larger than the average applied pressure according to numerical simulations for our punch geometry (Fig. S10). Thus, the pertinent rupture criterion unifying all observations is one based on average stress and not on maximum stress, even if differences in maximum stress location suggest that membrane rupture may start at different locations for different tip geometries. In conclusion, membrane rupture occurs at a critical compressive stress of 12.4 ± 0.6 kPa, regardless of the size, shape, and stiffness of the microindenter.

The stress required to rupture the membrane is insensitive to the integrity of the actin cytoskeleton

Fig. 2 D includes experimental data of cell microindentation performed on endothelial cells treated with cytochalasin D, an inhibitor of actin polymerization. The results in the presence of cytochalasin D (Fig. 2 D, encircled crosses) are indistinguishable from control conditions (Fig. 2 D, solid circles), indicating that the critical stress for microindenter-induced membrane rupture is uncorrelated with the integrity of the cell’s cytoskeleton.

Changing the microindenter’s angle of attack provides quantification of microindenter-membrane friction, which is negligible

To characterize the friction between the microindenter’s tip and the cell membrane, we performed microindentation experiments at fixed angle $\alpha =45°$ and with different values of the microindenter’s angle of attack. In these experiments, the position of the upper end is lowered at a constant speed along a straight trajectory that forms an angle of attack, β, with the vertical direction (note that $\beta =0$ for all cases presented above). For an arbitrary angle of attack, and by assuming that the vertical cell deformation at rupture is small compared to the vertical deformation of the microindenter, an analytical model of cell microindentation (see Supporting Materials and Methods) predicts a horizontal displacement at rupture given by

$$\Delta x^{\ast }={\delta }^{\ast }\left(\tan \alpha -\tan \beta \right)=\frac{V^{\ast }}{k_{\text{m}}}\left(\tan \alpha -\tan \beta \right)\left({\text{cos}}^2\alpha +\text{sign}\left(\beta -\alpha \right)\mu \text{sin}\alpha \text{cos}\alpha \right),$$ (5)

where ${\delta }^{\ast }$ is the vertical displacement of the upper end of the cantilever upon membrane rupture. Fig. 3 A shows the experimentally observed horizontal displacement at rupture, $\Delta x^{\ast }$, as a function of ${\delta }^{\ast }\left(1-\tan \beta \right)$. The measured slope is very close to 1, in agreement with Eq. 5. To estimate the friction coefficient, μ, we plot $k_{\text{m}}\Delta x^{\ast }/\left(S_{\mathrm{contact}}{\sigma }^{\ast }\right)$ versus $\beta$ in Fig. 3 B. We fit the curve with two free parameters, ${\sigma }^{\ast }$ and μ, for each indenter. This leads to ${\sigma }^{\ast }=14\pm 8\text{kPa}$, and μ = 0.12. In the data analysis leading to the estimate of ${\sigma }^{\ast }=12.4\pm 0.6\text{kPa}$, presented above, we had assumed μ = 0. If we reanalyze the previous data (Fig. 2 D) accounting for Coulomb friction with μ = 0.12, we obtain a critical stress of ${\sigma }^{\ast }=16\text{kPa}$, indicating an uncertainty of at most 30% in the reported value of ${\sigma }^{\ast }$ due to a potential friction effect. Since this uncertainty is comparable to other sources of experimental uncertainty, such as cell-to-cell variability, frictional effects can reasonably be neglected when studying membrane rupture. Fig. 3 B shows indeed that Eq. 5, with μ = 0, also provides a very good fit to the experimental results, validating our original assumption that friction force can be neglected with respect to the normal force. This assumption is further supported by our experimental observation that if the vertical motion of the upper end of the microindenter is switched from downward to upward motion, the microindenter’s tip immediately changes gliding direction without detectable stick-slip behavior. It is noted that by changing the angle of attack, we induce membrane rupture for very different values of the horizontal displacement, $\Delta x^{\ast }$, which is even nearly zero for β = 45°. This result supports the conclusion stated above that microindenter-induced membrane rupture occurs at a given value of the normal stress applied onto the cell and is not due to an applied horizontal shear.

Figure 3.

Horizontal displacement of the microindenter’s tip at membrane rupture, Δx^∗, obtained for different microindenter angles of attack, β. Microindenters are tilted at $\alpha =45°$ and their tips are spherical. (A) Δx^∗ equals ${\delta }^{\ast }\left(1-\tan \beta \right)$ (fitted slope of $0.96\pm 0.02$). The symbols are experimental measurements obtained with two different indenters for β varying from 0 to 68° (black, 0°; blue, 22°; green, 45°; orange, 51°; red, 59°; and yellow, 68°). This nondimensional plot can be interpreted as a relationship between the effective horizontal displacement and the vertical indentation, as the additional factor ${\delta }^{\ast }\tan \beta$ simply corrects for the apparent reduction in horizontal displacement when the angle of attack, $\beta$, is not zero. (B) Normalized displacement, $2k_{\text{m}}\Delta x^{\text{∗}}/\left(S_{\text{contact}}{\sigma }^{\text{∗}}\right)$, versus β. The symbols are experimental measurements obtained with three different indenters. The error bars indicate the standard error of the mean. The curves represent the predictions of Eq. 9 after normalization and given that $\alpha =45°$, $2k_{\text{m}}\Delta x^{\text{∗}}/\left(S_{\text{contact}}{\sigma }^{\text{∗}}\right)=\left(1-\tan \beta \right)\left(1+\text{sign}\left(\beta -\alpha \right)\mu \right)$, with μ = 0 (dotted line), μ = 0.12 (solid line), or μ = 0.5 (dashed line). The magnitude of the normalized displacement can be physically interpreted as a ratio between the tangential and vertical forces applied by the microindenter on the cell at rupture. More precisely, the vertical distance between the experimental points and the dotted lines (μ = 0) indicates how much tangential force is resisted by the cell at rupture. To see this figure in color, go online.

The applied compressive force can be measured by measuring the vertical displacement of the upper end of the microindenter, δ, at an arbitrarily chosen angle of attack

The results shown in Fig. 3 A indicate that measuring $\Delta x^{\ast }$ by microscopy is equivalent to measuring the length ${\delta }^{\ast }\left(1-\text{tan}\left(\beta \right)\right)$. From a practical standpoint, the latter method is straightforward if using a motorized micromanipulator that displays the displacement of the upper end of the microindenter, as is the case here. Moreover, this latter method allows studying indentations at α = 45° and β = 45°, for which the horizontal tip displacement, Δx, vanishes (Fig. S6). In this way, tilted microindentation allows applying a controlled compressive force to a fixed location on the cell simply by measuring the displacement, δ, indicated by the micromanipulator controller. This alternative method prevents the tilted microindenter from probing different cell spots, as is the case for an angle of attack β = 0°, and also allows us to compare the rupture force obtained on the thin cytoplasmic regions versus that on top of the cell nucleus (Fig. S7). Interestingly, the obtained displacements, ${\delta }^{\ast }$ (hence, compressive force), are comparable, even if they are slightly larger on top of the nucleus (Fig. S7 A). This indicates that the rupture criterion is essentially the same on the thin and thicker parts of the cell. We note that the reported displacements at rupture ${\delta }^{\ast }$ were independent of the radius of the indenter’s tip (Fig. S7 B). This precludes artifacts due to differences in local curvature on top of the nucleus and on top of the cytoplasm, as well as a finite-thickness effect that would make the indenter essentially probe the rigid substrate. Both such artifacts would yield values of ${\delta }^{\ast }$ that depend on the ratio of the indenter’s tip radius to the cell thickness, which varies from ∼1 μm on top of the cytoplasm to $3.8\pm 0.4\mu \text{m}$ (mean $\pm$ SD of N = 6 cells) on top of the nucleus.

The cell is radially strained in the vicinity of the microindenter

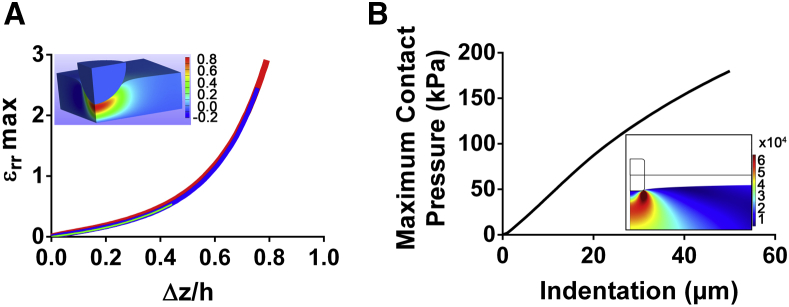
We performed numerical simulations to investigate the mechanism by which a normal stress can induce membrane rupture. Fig. 4 A shows the maximum radial strain induced in a hyperelastic medium by microindenter compression. At large indentation, a small increase of the indentation depth will result in a large increase in the radial strain in the region surrounding the microindenter’s tip. For a typical indentation of $\Delta z_{\text{max}}\approx 0.6\mu \text{m}$ and assuming a typical endothelial cell thickness of $h\approx 1\mu \text{m}$, Fig. 4 A yields a maximum radial deformation of ${\epsilon }_{rr}\approx 1$ μm (or 100%), occurring at the periphery of the microindenter and underneath the cell membrane (see Fig. 4 A, inset).

Figure 4.

Simulations of cell microindentation and strut deployment. (A) Maximum radial cell deformation as a function of the normalized indentation as predicted by numerical simulations. The three curves, which are practically superposed, correspond to $R/h=1$ (thick red line), $R/h=2$ (intermediate blue line), and $R/h=10$ (thin light green line). The inset shows a colormap of the radial deformation under the microindenter for the case $R/h=1$ and $\Delta z/h=0.49$ (Movie S4). (B) Maximum contact pressure evaluated along the contact line between the stent strut and the arterial wall as obtained from two-dimensional numerical simulations of stent deployment. The inset shows a colormap of the von Mises stress in the arterial wall for a value of stent indentation equal to one-half the strut thickness (Movie S5). To see this figure in color, go online.

To confirm the presence of the radial strain predicted by our numerical computations, we have visualized the displacement field in the cell induced by indentation by tracking fluorescently labeled mitochondria using particle image velocimetry software (Movie S3). We observed displacements that are orthogonal to the sliding direction of the microindenter, which are therefore indicative of radial strain. We note that those radial displacements increased with the sliding Δx, which is related by Eq. 1 to the applied compressive stress.

Pressures exerted during the deployment of stents induce rupture of endothelial cell membranes

We compared the critical stress for rupture determined here with typical conditions arising during surgical interventions. To investigate the typical pressures exerted during stent deployment, we have performed two-dimensional numerical simulations of the deployment of a stent onto an arterial wall. In our simulations, the arterial wall is modeled as a uniform elastic material of equivalent elastic modulus of 1 MPa (33). Fig. 4 B shows the pressures exerted on the arterial wall, and thus on the monolayer of endothelial cells, during stent apposition. The inset in Fig. 4 B shows the von Mises stress induced in the arterial wall at maximum indentation. We predict a maximum compressive stress on the order of 180 kPa, which is consistent with values reported for three-dimensional simulations (40).

Discussion

The critical stress established by tilted microindentation is consistent with previous measurements of cell membrane rupture

We showed that, independent of the size, shape, and stiffness of the microindenter, endothelial cell membrane rupture occurs at a normal microindentation stress of 12.4 ± 0.6 kPa. We further showed that this value is approximately constant over different regions of the cell (cytoplasm versus nucleus). The value of the reported critical stress is consistent with typical forces for compression-induced membrane rupture reported in the literature. Using an AFM, Hategan et al. reported an indentation force for rupture of the red blood cell membrane at slow loading of ∼14 nN, and a corresponding indentation depth of 1.23 μm. They estimated the corresponding contact area between their AFM tip and the membrane to be ∼3 μm² (11), which yields a normal stress of ∼11 kPa. Using a flat circular indenter acting over the whole cell surface, which they estimated to be ∼570 μm², Peeters et al. measured a membrane rupture force for mouse myoblasts of 8.7 μN (13), which corresponds to a normal stress of 15 kPa. Using a parallel-plate compression setup, Weiss et al. investigated the conditions leading to loss of membrane integrity of Ehrlich ascites tumor cells. Their results corresponded to a typical compressive stress for membrane rupture on the order of 3–6 kPa, again in reasonable agreement with the order of magnitude of the critical stress reported here (41). Rupturing lipid bilayers by compressing them with an AFM tip, Loi et al. measured forces ranging from 2 to 12 nN for tip radii ranging between 26 and 86 nm (42, 43). As their force curves imply a penetration of the AFM tip of a few nanometers, one can postulate that Eq. 2 is applicable to estimate the contact area, which leads to a compressive stress ranging from 17 to 43 kPa. This also is in reasonable agreement with our results, especially taking into account that incorporating peptides into lipid bilayers (hence getting a model somewhat closer to a cell membrane) makes them easier to break, according to micropipette aspiration (44) and AFM indentation (42) measurements. Kagiwada et al. (45) reported that a typical force of 3 nN is required to insert a nanoneedle of 200 nm in diameter into a cell. Here, the contact area is critical when estimating a compressive force: although using Eq. 2 to estimate S_contact leads to a critical stress of ∼8 kPa, it is probably more accurate to estimate the contact area as that of a spherical cap, S_contact ∼ 2πR², leading to a larger stress of ∼50 kPa. In another study using nanoneedle geometries, Xie et al. (46, 47) investigated the penetration of nanowires fixed to a substrate into cells that adhere to this substrate. They used a cell membrane rupture criterion based on activation energy theory and leading to a critical membrane tension to be reached before rupture (42, 44). In the study of Xie et al., tensile forces of ∼1 nN are applied to the tips of nanowires of radius R = 50 nm. By again considering a contact area equal to half a spherical cap, S_contact ∼ 2πR², one deduces an alternative rupture criterion based on a critical stress of ∼60 kPa, which is again comparable to our results, albeit somewhat larger.

Cell membrane rupture forces have not only been studied in compression. Tan et al. (48) used micropipette aspiration to break the plasma membranes of fibroblasts. They deduced an average transmembrane protein-lipid cleavage strength, ${\gamma }^{\text{∗}}$, of ∼3 mN/m. We convert this value to a typical tensile stress by dividing the force, $F^{\ast }=2\pi {\gamma }^{\ast }R$ (with R ∼ 1 μm being the radius of the micropipette) by the pipette cross-sectional area, $\pi R^2$. This yields a critical rupture stress of $2{\gamma }^{\ast }\text{/}R\sim 6\text{kPa}$, again comparable to our measurements.

To summarize this overview of existing literature, both compressive and pulling stresses deduced from existing measurements are consistent with the critical stress of 12 kPa reported here. We note, however, that the values reported in studies using nanoscale tips are somewhat larger, which may point to differences between the rupture mechanisms induced by nanometric tips and those induced by micrometric tips.

The mechanical rupture criterion based on a critical compressive stress is consistent with a microscopic energetic criterion to nucleate a hole through the membrane

We have concluded that microindentation induces membrane rupture through the normal stress exerted on the cell. The question remains of how this constant compressive stress translates into a mechanism of membrane rupture. Indeed, since publication of the work of Evans et al., who used micropipette aspiration to rupture lipid vesicles, membrane rupture is commonly characterized by a critical tension rather than a critical stress. In the case of micropipette aspiration experiments, this critical tension induces sufficient stretching of the membrane to rupture it (44). However, unlike micropipette experiments, in our work the membrane is confined between the indenter and the substrate. Our setup thus resembles the configuration investigated by Butt et al., who investigated, both experimentally and theoretically, the rupture of a supported lipid bilayer compressed by an AFM tip (42, 43). Following a reasoning similar to that of Butt et al., rupture occurs when release of the elastic energy stored in the indenter suffices to dislodge a sufficiently large number of membrane lipid molecules to nucleate a hole. The elastic energy released by the indenter at membrane rupture is equal to $k_{\text{m}}{\delta }^{\ast }\text{d}z\left(\tan \alpha -\tan \beta \right)$, where dz corresponds to the additional vertical displacement of the indenter allowed by membrane rupture. The energy required to dislodge n lipid molecules is of the order of $n{k}_{\text{B}}T$. If we estimate that n ∼ S_contact/S_lipid, with S_lipid ∼ 1 nm² being the membrane surface area occupied by a lipid molecule, by equating the two energies we obtain a membrane rupture criterion of the form

$${\sigma }^{\ast }=\frac{V^{\ast }}{S_{\text{contact}}}=\frac{k_{\text{B}}T}{\text{d}z{S}_{\text{lipid}}}.$$ (6)

The value of the vertical displacement of the microindenter at rupture, dz, will lie between the thickness of the lipid bilayer (of the order of 10 nm) and the remaining thickness of the compressed cell (of the order of 1 μm), yielding a value of ${\sigma }^{\ast }$ between 10 and 400 kPa. However, we note two reasons why this range is probably overestimated. First, we probably overestimate the number of molecules that must be dislodged to rupture the membrane, which we have taken as the number of lipids in the contact area, since, as pointed out by Butt et al., only a subset of molecules need to be dislodged for the process of rupture to start. Second, as discussed in the Results section, microindentation induces a radial deformation of the cell, thus introducing a membrane stretching energy that will facilitate rupture. Therefore, we presume that a realistic value of ${\sigma }^{\ast }$ afforded by the energetic argument should be toward the lower end of the estimated range above, which is consistent with our measured experimental value.

Membrane rupture may occur during cell-cell interactions

Carman et al. (49, 50) described how T lymphocytes use “invadosome-like protrusions” to probe endothelial cells and to select the location to undergo transcellular diapedesis. This echoes the findings of Shulman et al. (51) that T lymphocytes can be guided during transendothelial migration by intraendothelial chemokine stocks. T lymphocytes reach these stocks by projecting filopodia that invade endothelial cells. Furthermore, Ueda et al. had previously shown that during the formation of the immune synapse, T-cells extend pseudopodia that penetrate deeply into the antigen-presenting cell (52). The pushing forces generated by these filipodia/protrusions were not measured in these studies. However, by using the micropipette force probe that we recently developed (25), we measured that, when brought into contact with activating microbeads, T cells can generate pushing forces in the range of ∼500 pN via a single thin protrusion whose tip can be roughly estimated to have a 50- to 500-nm radius (unpublished data). This leads to a compressive stress of ∼0.5–75 kPa. Together with the results presented here, this suggests that protrusions generated by T cells should be able to rupture the membrane of cells with which they interact.

Rupture of endothelial cell membranes during stent deployment

The experimental and numerical results presented here indicate that given the stress levels during stent deployment, generalized rupture of endothelial cell membranes, and hence massive endothelial damage, cannot be avoided. This conclusion is consistent with medical observations reporting that stent deployment, even if only lasting a few seconds, completely destroys the endothelium along the strut region (6). Consistent with the literature (53), we predict stresses and strains that are highly concentrated at the edge of the stent strut (Fig. 4 B); it is thus in this region that we expect the arterial wall damage to be most acute.

Comparison of the critical compressive stress with variations in blood pressure

The variation of aortic pressure between diastole and systole in a healthy adult is on the order of 50 mmHg, or 6.7 kPa. This is approximately one-half of the critical compressive stress we measured here, above which there is a risk of membrane rupture of endothelial cells. This implies that under normal physiological conditions, pressure variations in the bloodstream are unlikely to cause the membrane damage that is observed in vivo (8). Besides, it is possible that a more spatially uniform pressure, as is found in the bloodstream, causes less damage than the nonuniform compressive stress applied in our experiments. Hence, we speculate that the critical pressure required for membrane rupture in vivo could be even higher than 12 kPa (90 mmHg). We conclude that material resistance properties of endothelial cells are finely tuned to withstand physiological pressure variations, unlike the case of human interventions such as stenting procedures or angioplasties.

Conclusions and perspectives

In summary, we have introduced tilted microindentation, a simple and cost-effective technique to exert controlled compression forces on adherent cells. We have applied this technique to characterize the mechanics of endothelial cells under compression. In our experiments, the friction between the glass microindenter and the cell membrane is negligible; thus, the microindenter applies only a normal force on the cell. At low force (indentation <0.3 μm), cell indentation mechanics can be interpreted using Hertz’s model, from which we deduce an apparent local Young’s modulus of endothelial cells ranging from 5 to 17 kPa (Fig. S3). For a maximum indentation estimated at 0.6 μm, the cell behaves as nearly incompressible, although the compression stress continues to increase with increased indentation. Endothelial cell membrane rupture occurs at a constant compressive stress of 12.4 ± 0.6 kPa, which at the molecular level appears to correspond to the energy required to nucleate a hole through a lipid membrane. This value of critical stress is in agreement with published results for indentation-induced membrane rupture in other cell types measured using other techniques, thus suggesting some degree of generality of this result. Our numerical simulations of stent deployment show that the stresses induced during this surgical procedure are significantly higher than those required to rupture the endothelial cell membrane. Thus, generalized and inevitable damage of endothelial cell membrane occurs during the currently used protocols for stent deployment.

In perspective, tilted microindentation can be used to investigate endothelial cell fate upon membrane damage as well as the mechanisms of membrane repair following rupture. We have previously used micropipettes to rupture the plasma membrane of endothelial cells to study ensuing mitochondrial fission (54). In that study, we did not control the force exerted by the microindenter. The work presented here establishes a technique to predict and control the force necessary to break the membrane. It is important to note that the technique presented here allows us to control the extent of the damage done to the cell membrane. In addition to improving our understanding of endothelial cell responses to membrane rupture, such as mitochondrial fission, tilted microindentation provides a highly versatile tool for studying membrane repair. Indeed, membrane repair processes are expected to differ depending on the size of the wound created in the membrane (55), which can be tuned by applying a controlled force with an indenter of controlled size.

Author Contributions

D.G.-R., E.L., A.I.B., and J.H. designed research; D.G.-R., L.G., F.C., and J.H. performed research; J.L.-J., and A.B. contributed new reagents/analytic tools; D.G.-R., L.G., F.C., and J.H. analyzed data; and D.G.-R., L.G., F.C., A.I.B., and J.H. wrote the article.

Editor: Elsa Yan.

Supporting Material

Movie S1. Tilted Microindentation to Characterize Cell Membrane Rupture

Tilted microindentation of a bovine aortic endothelial cell used to characterize cell membrane rupture. Brightfield illumination is shown in the upper left panel, fluorescence imaging of propidium iodide is shown in the upper right panel, fluorescence imaging of fluo-4 is shown in the lower left panel, and merged channels are shown in the lower right panel. The three channels are obtained using a 100x objective at an acquisition rate of 0.5 frames per second. The movie plays at 10 frames per second, so the movie is accelerated 5 times. Scale bar is 10 μm. Upon membrane rupture, both propidium iodide and extracellular calcium enter the cell cytoplasm, which leads to a rapid increase in the fluorescence levels. It is noted that the two agents exhibit different diffusion rates in the cell cytoplasm.

Movie S2. Tilted Microindentation to Characterize the Moderate Indentation Regime

Tilted microindentation of a bovine aortic endothelial cell used to characterize the moderate indentation regime. We use brightfield illumination, focus the microscope 3.5 μm below the basal plane of the cell’s basal plane, and define a region of interest to limit computer memory usage. The acquisition is performed at 100 frames per second and 5 ms exposure time. Scale bar is 2 μm. The base of the probe is translated at 2 μm/s. We measured the position of the edge of the bead as a function of time as described in Figure S2.3

Movie S3. Particle Image Velocimetry using Mitochondria during Indentation

Tilted microindentation of a bovine aortic endothelial cell with fluorescently labeled mitochondria. On the left side, the fluorescent images are obtained using a 100x objective at an acquisition rate of 10 frames per second. The movie plays at 7 frames per second, so the movie is slowed 1.4 times compared to the experiment. Scale bar is 5 μm. To visualize the mitochondria, BAECs were incubated before the experiment for 30 min in mitotracker M7510, as detailed in Gonzalez-Rodriguez et al. (ref. 40 in main text). On the right side, we used the CRToolbox developed and made freely available online by Julien Diener at https://sites.google.com/site/crtoolbox/home to track the displacements of the mitochondria [Diener et al., 2012, Proceedings of the 7th International Biomechanics Conference, Clermont-Ferrand, p. 179]. From there, we used a custom-made Matlab code to visualize the 2D displacements. Circles indicate a virtual particle that is tracked over time. Lines indicate the displacements of said virtual particles.4

Movie S4. Simulation of Cell Indentation in FEBio

Colormap of the radial deformation under the microindenter for the case R/h=1.The imposed indentation Δz/h, which lies between 0 and 0.79, increases linearly over the movie’s duration. The movie plays at 7 frames per second, corresponding to 7% indentation per second (one frame marks 1% indentation, except for the last three frames in which the indentation steps are slightly smaller).5

Movie S5. Simulation of Stent Deployment

Displacements are represented at scale 1 and the color represents the von Mises stress in the artery wall. The black lines represent the original position of the artery before indentation.6

Movie S6. Fabrication of Microindenters with a Spherical Tip of Different Size

A smartphone was placed on a 3D-printed custom-made adapter to record through the oculus of a microforge while forging a microindenter. On the right of each of both panels, a submillimetric glass bead placed on a heating wire is melted and used to form a microbead at the tip of a micropipette (on the left of both panels) previously cut to the desired diameter. The movie is played in real time and demonstrates how beads of various sizes can be formed at the tip of a microindenter.7

Movie S7. Experimental Determination of the Bead-Cell Contact Surface Area

Tilted microindentation of a bovine aortic endothelial cell with a spherical microindenter. Both brightfield (top) and fluorescence (bottom) illumination are used. Upon indentation, a dark spot appears under the tip of the microindenter. This dark spot is indicative of the bead-cell contact area. The acquisition is performed at 1 frame per second. The scale bar represents 10 μm.8

Movie S8. The Radial Displacement Inside the Cell during Tilted Microindentation Is Tracked Over Time

This is the same tilted microindentation as in movie S3, but instead of reporting the displacement vectors, we show here the radial displacement over time as a heat map. Dark red corresponds to a radial displacement of 4 μm towards the top of the image, while dark blue corresponds to a radial displacement of 4 μm in the opposite direction. We see a rift where the radial displacement switches direction (i.e. where the color map switches from red to blue), which corresponds to the location where the microindenter’s tip has passed.9