Hydrogen Bond Network of Water around Protein Investigated with Terahertz and Infrared Spectroscopy

Abstract

The dynamical and structural properties of water at protein interfaces were characterized on the basis of the broadband complex dielectric constant (0.25 to 400 THz) of albumin aqueous solutions. Our analysis of the dielectric responses between 0.25 and 12 THz first revealed hydration water with retarded reorientational dynamics extending ∼8.5 Å (corresponding to three to four layers) out from the albumin surface. Second, the number of nonhydrogen-bonded water was decreased in the presence of the albumin solute, indicating protein inhibits the fragmentation of the water hydrogen-bond network. Finally, water molecules at the albumin interface were found to form a distorted hydrogen-bond structure due to topological and energetic disorder of the protein surface. In addition, the intramolecular O-H stretching vibration of water (∼100 THz), which is sensitive to hydrogen-bond environment, pointed to a trend that hydration water has a larger population of strongly hydrogen-bonded water molecules compared with that of bulk water. From these experimental results, we concluded that the “strengthened” water hydrogen bonds at the protein interface dynamically slow down the reorientational motion of water and form the less-defective hydrogen-bond network by inhibiting the fragmentation of water-water hydrogen bonds. Nevertheless, such a strengthened water hydrogen-bond network is composed of heterogeneous hydrogen-bond distances and angles, and thus characterized as structurally “distorted.”

Introduction

Water molecules interacting with protein exhibit some anomalous thermodynamical properties, such as freezing temperature (1), adiabatic compressibility (2), and specific heat capacity (3). It is widely believed that these peculiar characteristics of water in the vicinity of proteins provide biological functionalities to the protein molecule (4, 5). For example, inactive dehydrated enzymes are reactivated when they are covered by at least one layer of water (so-called “hydration water”) and a strong coupling between the protein and hydration water triggers the protein dynamical transition (5, 6, 7). Liquid water forms a hydrogen-bond (HB) network with a distorted tetrahedral structure continuously fluctuating at timescales of subpicoseconds to picoseconds (8, 9, 10, 11). When protein “impurities” are introduced, the HB environment in the resulting solution is disturbed. Since macroscopic characteristics, such as thermodynamical properties, originate from the dynamics and structure of the water HB network, the characteristics of the HB network in close vicinity to a protein could provide a deeper and more refined insight into protein functionality.

Molecular dynamics (MD) simulations (12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22) and other experimental approaches (23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37) have revealed the protein is surrounded by dynamically retarded hydration water, with the innermost shell having a density higher than that of bulk water. However, even today, experimentally characterizing the dynamics and the structure of the water HB network in this hydration shell is challenging, because the water-water HB lifetime is very short (typically 1 ps) (38). To observe directly the HB dynamics and structure fluctuating at subpicosecond to picosecond timescales, depolarized light scattering (DLS) (33, 34), optical Kerr effect (OKE) spectroscopy (35), incoherent neutron scattering (INS) spectroscopy (36), and Brillouin spectroscopy (37) were developed, but they all have experimental limitations. DLS and OKE probe weak second-order optical processes, and INS and Brillouin spectroscopy require isotopic substitution, which may alter the native water HB network, if only weakly. Thus, a more sensitive experimental method, free from these limitations, is necessary if water dynamics at the protein interface are to be refined.

Terahertz (THz) spectroscopy may be such a tool, since first-order optical processes at a subpicosecond to picosecond can be directly observed without a need for isotopic substitution. Moreover, the contribution of protein solutes to that of water is negligibly small, compared with that of water in the THz region (39, 40, 41, 42, 43, 44, 45, 46, 47, 48) (see Results and Discussion for details). Thus, the dynamics and structural changes in the water HB network can be “selectively” observed by THz spectroscopy, free from interference from the protein itself. Consequently, by measuring both real (polarization index) and imaginary (absorption index) parts of the complex dielectric constant, the characteristic of water around the solute can be quantitatively discussed in terms of the hydration state and the HB network stability (i.e., HB fragmentation and structural distortion) (45, 46, 47, 48). Therefore, THz spectroscopy is expected to selectively measure characteristics of the water HB network around the protein.

In addition, an O-H stretching vibration around 100 THz (3330 cm⁻¹) has been conventionally used as an index to estimate the HB strength (49, 50, 51, 52, 53, 54, 55, 56, 57, 58). In general, the stronger the HBs that a given water molecule establishes with its neighbors, the more red-shifted is the O-H stretching frequency (49, 57, 58). However, in case of protein aqueous solution, –NH and –OH groups embedded in a protein molecule as well as OH in water contribute to the dielectric response around 100 THz, complicating the analysis of the O-H stretching of water alone. For this reason, despite the capability to look into the water HB network, MIR spectroscopy has been limited in its ability to investigate these water dynamics and their structure in protein aqueous solutions so far. With the aid of THz spectroscopic results, we overcome this problem by developing an analytical method to determine the O-H stretching of water around the protein without excess influence of the protein’s –NH and –OH groups. This analysis thus allow us to discuss the strength of water HBs; an important parameter for both structural and dynamical characteristics of water in the vicinity of protein molecules.

To characterize the water HB network around a protein from multiple points of view, the broadband (0.25–400 THz) dielectric constant of protein aqueous solution is measured and analyzed in this study. From 0.25 to 400 THz, particular attention is paid to the dielectric responses in the THz region (0.25–12 THz) and the O-H stretching frequencies in the MIR region (90–115 THz). The process to precisely determine the broadband complex dielectric constant is described in Materials and Methods. In Results and Discussion, the hydration state, the HB fragmentation state, and the structural distortion of the water HB network are characterized using dielectric responses in the THz region. The HB strength of hydration water relative to bulk is also examined in Results and Discussion on the basis of the O-H stretching band. Then finally, combining the THz and MIR results, the observed dynamical and structural characteristics of water at the protein interface are summarized in Conclusions.

Materials and Methods

Sample preparation

As a model protein to investigate protein-water interactions, human serum albumin was used in this study. Albumin powder was purchased from Wako Pure Chemical (Kyoto, Japan; dialyzed and lyophilized, more than 95% by weight) and used without further purification. The albumin solutions at successive concentration levels (30–150 mg/mL at 15 mg/mL intervals) were prepared by dissolving the albumin powder in pure water (>3.0 MΩ × cm). With the density measurement of albumin aqueous solution, the volume fraction of protein $\left({\varphi }_{\mathit{sol}}\right)$ and water $\left({\varphi }_{\mathit{water}}=1-{\varphi }_{\mathit{sol}}\right)$, and the molar concentration of water $\left(C_{\mathit{water}}\right)$ were derived.

Data acquisition

The complex dielectric constants of pure water and albumin aqueous solutions, between 0.25 and 400 THz, were determined by means of four different experimental setups. First, in the lowest frequency range from 0.25 to 3.0 THz, THz time-domain attenuated total reflection (THz TD-ATR) spectroscopy (59) was employed to directly determine both real and imaginary parts of the complex dielectric constant $\tilde{\epsilon }\left(\omega \right)$. In this measurement, detected time-domain THz pulses with and without a sample were Fourier-transformed into the reflectance $R\left(\omega \right)$ and the phase shift spectrum $\phi \left(\omega \right)$. Subsequently, the complex dielectric constant $\tilde{\epsilon }\left(\omega \right)$ was calculated from $R\left(\omega \right)$ and $\phi \left(\omega \right)$ based on the Fresnel’s equation. All the THz TD-ATR measurements were carried out by a TAS7500 spectrometer (Advantest, Miyagi, Japan): our experimental setup and $\tilde{\epsilon }\left(\omega \right)$ derivation procedure have been detailed elsewhere (45, 46, 47, 48).

Second, far-infrared Fourier-transform attenuated total reflection (FIR FT-ATR) spectroscopy was used for the measurement from 3 to 12 THz. We employed a FARIS-1s spectrometer (Jasco, Tokyo, Japan) equipped with a ceramic light source and a Si bolometer detector (LN-6/C, Infrared Laboratories, Tucson, AZ) for FIR FT-ATR measurements. In this FT-ATR measurement, the reflectance $R\left(\omega \right)$ in the frequency-domain was recorded, and the phase shift spectrum $\phi \left(\omega \right)$ was then mathematically calculated from the following Kramers-Kronig (K-K) relation (60):

$$\phi \left(\omega \right)=-\frac{2}{\pi }\underset{0}{\overset{{\omega }_{\mathit{u}}}{\int }}\frac{{\omega }_{\mathit{a}}\text{ln}\sqrt{R\left({\omega }_{\mathit{a}}\right)}}{{\omega }_{\mathit{a}}^2-{\omega }^2}d{\omega }_a+{\phi }_{\left(\infty \right)},$$ (1)

where ${\omega }_{\mathit{u}}$ is the upper integration limit and ${\phi }_{\left(\infty \right)}$ is the phase shift at $\omega ={\omega }_{\mathit{u}}$. In Eq. 1, the first term was calculated from the experimental result, $R\left(\omega \right)$, and the second term, ${\phi }_{\left(\infty \right)}$, was set as the value that best fits the THz TD-ATR measurement results between 2.8 and 3.2 THz so as to smoothly connect the THz TD-ATR and FIR FT-ATR results at 3.0 THz. Then, on the basis of Fresnel’s equation, the complex dielectric constant $\tilde{\epsilon }\left(\omega \right)$ was derived from $R\left(\omega \right)$ and $\phi \left(\omega \right)$. Details of the K-K transform have been described elsewhere (47, 48).

Third, the frequency range between 18 and 120 THz was measured using a MIR FT-ATR spectrometer, FT/IR-4600 (Jasco). A ceramic heater and deuterated L-alanine triglycine sulfate were employed as the emitter and detector, respectively. Along with FIR FT-ATR, the reflectance $R\left(\omega \right)$ was transformed into the phase shift spectrum $\phi \left(\omega \right)$ by the use of Eq. 1 to determine the complex dielectric constant $\tilde{\epsilon }\left(\omega \right)$. However, unlike in the case of the FIR FT-ATR spectroscopy, where ${\phi }_{\left(\infty \right)}$ best fits to the THz TD-ATR results were substituted into Eq. 1, ${\phi }_{\left(\infty \right)}$ cannot be rigorously determined in this MIR region. Consequently, the complex dielectric constant $\tilde{\epsilon }\left(\omega \right)$ was not precisely determined from the MIR spectroscopy alone. To overcome this problem, we employed near-infrared (NIR) spectroscopy to cover the frequency region from 120 to 400 THz ($\lambda$: 2500–750 nm). In this NIR measurement, 0.1 mm, 1.0 mm, and 10 mm quartz cells were inserted into a V-670 UV-VIS-NIR spectrophotometer (Jasco), and the extinction coefficient $\kappa \left(\omega \right)$ of pure water and albumin aqueous solution samples were determined in a transmission measurement. Then, the refractive index $n\left(\omega \right)$ was theoretically calculated according to another K-K transform as follows:

$$n\left(\omega \right)=\frac{2}{\pi }\underset{0}{\overset{{\omega }_{\text{u}}}{\int }}\frac{{\omega }_{\mathit{a}}\kappa \left({\omega }_{\mathit{a}}\right)}{{\omega }_{\mathit{a}}^2-{\omega }^2}d{\omega }_a+n_{\left(\infty \right)}.$$ (2)

In Eq. 2, instead of ${\omega }_{\mathit{u}}=$ 400 THz, the refractive index at 509 THz ($\lambda =$ 589 nm) was measured by a digital refractometer PAL-RI (Atago, Tokyo, Japan) and substituted into the high-frequency limit of the refractive index $n_{\left(\infty \right)}$. This is valid because the frequency dispersion of the refractive index between 400 and 509 THz is negligibly small (∼0.001 for water) (61). Then, the determined complex refractive index $\tilde{n}\left(\omega \right)=n\left(\omega \right)-i\kappa \left(\omega \right)$ between 120 and 400 THz was converted into the complex dielectric constant $\tilde{\epsilon }\left(\omega \right)$ via the relationship $\tilde{\epsilon }\left(\omega \right)=\tilde{n}{\left(\omega \right)}^2$. Since NIR spectroscopy covers from 120 to 400 THz, ${\phi }_{\left(\infty \right)}$ in the MIR region can be set to a figure that best fits the NIR measurement result at 120 THz. So, the NIR spectroscopy facilitates the K-K transform in the MIR region, thus the complex dielectric constant $\tilde{\epsilon }\left(\omega \right)$ between 18 and 120 THz can be also accurately determined.

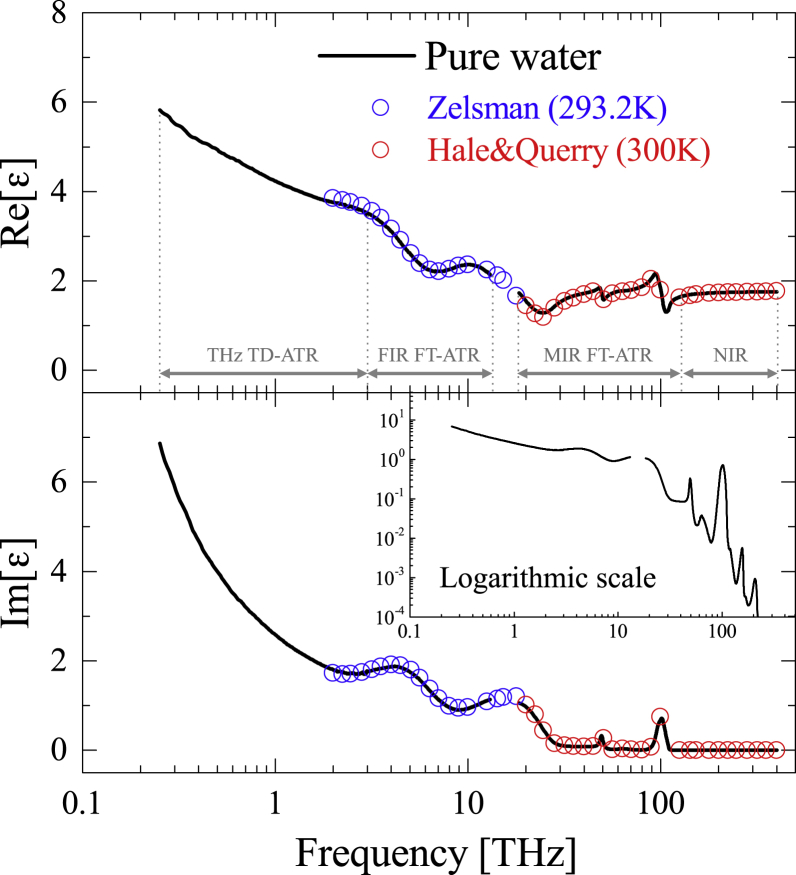
For all four experimental setups, the measurements were carried out at 300 ± 0.1 K, except for the NIR spectroscopy (295 ± 2 K). Five replicate samples at each concentration were measured to confirm the reliability of our systems. The experimental uncertainty (standard error) for the real and imaginary part of the complex dielectric constant were less than 2.5% and 3.0% (THz TD-ATR), 2.0% and 2.5% (FIR FT-ATR), 0.5% and 1.0% (MIR FT-ATR), and 0.7% and 0.7% (NIR spectroscopy), respectively. The resulting complex dielectric constant of pure water, from 0.25 to 400 THz with a gap between 12 and 18 THz, is shown in Fig. 1. The broadband complex dielectric constants obtained were in good agreement with previous infrared spectroscopy results reported by Zelsman (62) and Hale and Querry (63), providing credibility for our spectroscopic measurements and K-K transform. As seen in the inset of Fig. 1, several noticeable resonant peaks are identified in the imaginary part, such as broad intermolecular bands around 5 and 18 THz (62) and relatively sharp intramolecular and overtone/combination bands in the MIR and NIR regions (63). Broader features of intermolecular bands in the THz and FIR regions reflect the heterogeneous structure of liquid water. In the THz region, in addition to the intermolecular vibration modes, two relaxational modes of water also exist (see the section below on data analysis for details).

Figure 1.

The complex dielectric constant of pure water from 0.25 to 400 THz, with a gap between 12 and 18 THz. In addition to the results of our work, the results from infrared spectroscopy by Zelsman (62) and Hale and Querry (63) are shown for comparison. The inset shows a log-log scale of the imaginary part. To see this figure in color, go online.

In addition to the measurements of pure water and albumin aqueous solutions, the complex dielectric constant of albumin itself was also measured from 0.25 and 120 THz. From 0.25 and 12 THz, the polyethylene (PE) pellet mixed with 5 wt% albumin powder was measured by THz time-domain spectroscopy (0.25–3.0 THz) and FIR Fourier-transform spectroscopy (3–12 THz) in a transmission geometry. After these measurements, the PE pellet was ground up and the albumin powder was extracted. The amide-I band spectrum (∼49 THz, 1667 cm⁻¹) of the extracted albumin revealed albumin maintains its native structure, which assures the pellet preparation process did not alter the spherical structure of albumin. For spherical solutes, the complex dielectric constant of the solute itself ${\tilde{\epsilon }}_{\mathit{sol}}\left(\omega \right)$ can be mathematically derived from the Bruggeman’s effective medium theory as follows (64, 65):

$${\varphi }_{\mathit{PE}}\frac{{\tilde{\epsilon }}_{\mathit{PE}}\left(\omega \right)-\tilde{\epsilon }\left(\omega \right)}{{\tilde{\epsilon }}_{\mathit{PE}}\left(\omega \right)+2\tilde{\epsilon }\left(\omega \right)}+{\varphi }_{\mathit{sol}}\frac{{\tilde{\epsilon }}_{\mathit{sol}}\left(\omega \right)-\tilde{\epsilon }\left(\omega \right)}{{\tilde{\epsilon }}_{\mathit{sol}}\left(\omega \right)+2\tilde{\epsilon }\left(\omega \right)}=0,$$ (3)

where $\tilde{\epsilon }\left(\omega \right)$ is the complex dielectric constant of PE pellet with 5 wt% albumin, ${\tilde{\epsilon }}_{\mathit{PE}}\left(\omega \right)$ is the complex dielectric constant of pure PE pellet, and ${\varphi }_{\mathit{PE}}$ and ${\varphi }_{\mathit{sol}}$ are the volume fraction of PE and albumin, respectively. In the range between 18 and 120 THz, the albumin film was directly casted on the ATR prism referring to the solid film method (66) and measured by MIR FT-ATR spectroscopy. From the reflectance spectrum, the complex dielectric constant of albumin itself was determined via the K-K transform (Eq. 1).

Results and Discussion

Contribution of dissolved protein

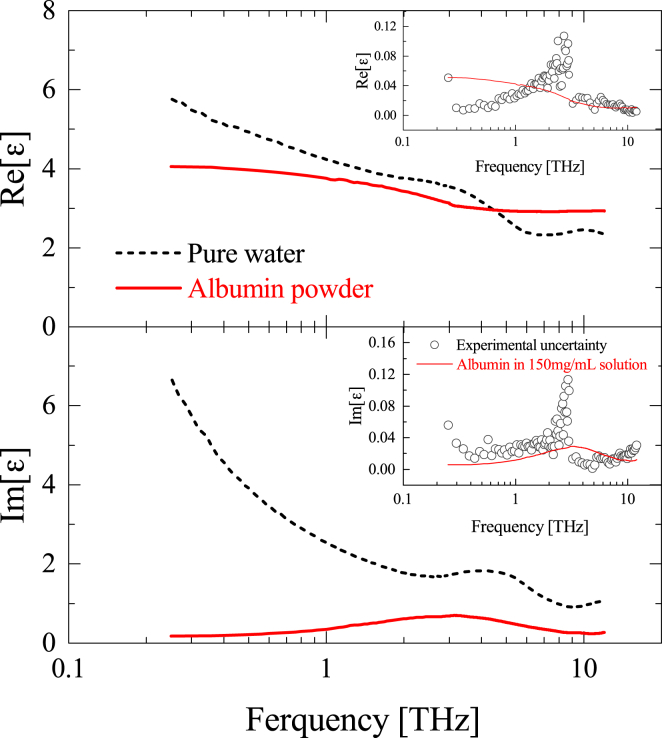
The complex dielectric constant of albumin powder ${\tilde{\epsilon }}_{\mathit{sol}}\left(\omega \right)$ is compared with that of pure water in Fig. 2. We confirmed that other effective medium approximation such as the Maxwell-Garnett theory provides quite similar ${\tilde{\epsilon }}_{\mathit{sol}}\left(\omega \right)$ to that determined from the Bruggeman effective medium theory. One can see that the albumin powder exhibits an absorption peak at ∼3 THz originating from intramolecular collective vibration modes (67, 68), but its frequency dispersion is much smaller than that of pure water. To ascertain the contribution of the dissolved albumin solute to the complex dielectric constant of albumin aqueous solution, ${\tilde{\epsilon }}_{\mathit{sol}}\left(\omega \right)$ weighted by albumin concentration (150 mg/mL, which is highest concentration in this study) was compared with our experimental uncertainty. As Fig. 2 insets show, the contribution of dissolved albumin is equal to or smaller than the experimental uncertainty between 0.25 and 12 THz. This estimate suggests that the vibrational modes of albumin molecules in aqueous solution are negligible in the THz region, if the experimental uncertainty is taken into account in the analysis.

Figure 2.

The complex dielectric constant of pure water and the albumin powder from 0.25 to 12 THz. The insets show comparison of the concentration-weighted albumin powder corresponding to 150 mg/mL aqueous solution and experimental uncertainty (standard error) of pure water. Note that the high frequency limit of albumin in the real part is subtracted in the inset. To see this figure in color, go online.

Data analysis

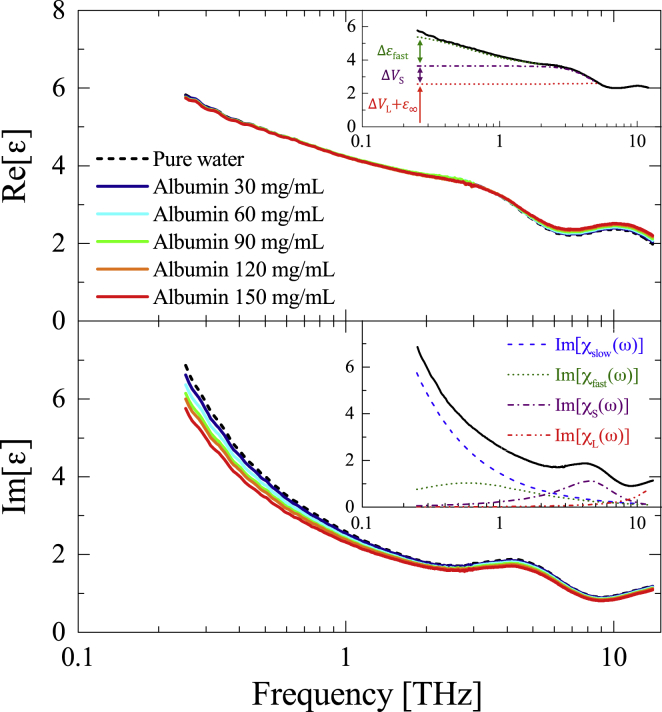
The complex dielectric constants of pure water and albumin aqueous solutions from 0.25 to 12 THz are shown in Fig. 3. Although the imaginary part of the complex dielectric constants exhibits significant concentration dependence over this frequency range, the real part of albumin aqueous solution was almost unchanged from that of pure water. This strong concentration dependence in the imaginary compared with the real part has been confirmed in other biological aqueous solutions (45, 46, 47, 48, 69, 70). In these previous studies, the characteristics of the water HB network around biomolecules were discussed by decomposing the measured complex dielectric constant $\tilde{\epsilon }\left(\omega \right)$ into the constituent complex susceptibilities of the slow relaxation ${\tilde{\chi }}_{slow}\left(\omega \right)$ at ∼0.02 THz, the fast relaxation ${\tilde{\chi }}_{fast}\left(\omega \right)$ at ∼0.6 THz, the intermolecular stretching vibration ${\tilde{\chi }}_S\left(\omega \right)$ at ∼5 THz, and the libration ${\tilde{\chi }}_L\left(\omega \right)$ at ∼18 THz. The slow relaxation mode has been attributed to a collective reorganization of bulk water bound in the HB network (71), whereas the fast relaxation has been assigned to individual rotation of nonhydrogen-bonded (NHB) bulk water molecules that are transiently released from the HB network (72). Thus, the reorientational motion of the hydrogen-bonded water (HB water) can be distinguished from that of the NHB water in the measured frequency range. Therefore, as shown in the insets in Fig. 3, the $\tilde{\epsilon }\left(\omega \right)$ of pure water can be expressed as a superposition of ${\tilde{\chi }}_{slow}\left(\omega \right)$, ${\tilde{\chi }}_{fast}\left(\omega \right)$, ${\tilde{\chi }}_S\left(\omega \right)$, and ${\tilde{\chi }}_L\left(\omega \right)$ (72, 73).

Figure 3.

The complex dielectric constant of pure water and albumin aqueous solutions at 300 K, in the THz and FIR region (0.25∼12 THz). The insets are the decomposed susceptibilities of pure water: slow relaxation ${\tilde{\chi }}_{slow}\left(\omega \right)$, fast relaxation ${\tilde{\chi }}_{fast}\left(\omega \right)$, intermolecular stretching ${\tilde{\chi }}_S\left(\omega \right)$, and libration ${\tilde{\chi }}_L\left(\omega \right)$. To see this figure in color, go online.

Compared with pure water, interpreting $\tilde{\epsilon }\left(\omega \right)$ for the albumin aqueous solution is more challenging, because the dielectric responses of the albumin solute, hydration water, and bulk water overlap. In other words, the relaxation modes of the albumin solute and hydration water, as well as the vibrational modes of albumin need to be taken into consideration. According to a recent study by Cametti et al. (29), however, hydration water has two small relaxation modes at ∼0.1 and 5 GHz, thus the relaxation process of hydration water is negligibly small between 0.25 and 12 THz. Similarly, the relaxation mode of albumin solutes contributes little to the dielectric responses in the THz region, since the relaxation of protein molecules is located in the MHz region (29). In combination with our results in the previous section, both the relaxation and vibration modes of the albumin solute itself are considered negligibly small between 0.25 and 12 THz. As a consequence, the $\tilde{\epsilon }\left(\omega \right)$ of albumin aqueous solution can be also reasonably decomposed into ${\tilde{\chi }}_{slow}\left(\omega \right)$, ${\tilde{\chi }}_{fast}\left(\omega \right)$, ${\tilde{\chi }}_S\left(\omega \right)$, and ${\tilde{\chi }}_L\left(\omega \right)$ in the just the same way as with pure water. Thus the experimental result $\tilde{\epsilon }\left(\omega \right)$ of both pure water and albumin aqueous solutions, from 0.25 to 12 THz, were fitted (46, 47, 48, 72, 73, 74) as follows:

$$\tilde{\epsilon }\left(\omega \right)={\tilde{\chi }}_{\mathit{slow}}\left(\omega \right)+{\tilde{\chi }}_{\mathit{fast}}\left(\omega \right)+{\tilde{\chi }}_{\mathit{S}}\left(\omega \right)+{\tilde{\chi }}_{\mathit{L}}\left(\omega \right)+{\epsilon }_{\infty },$$

$$\tilde{\epsilon }\left(\omega \right)=\frac{\mathit{\Delta }{\epsilon }_{\mathit{slow}}}{1+i\omega {\tau }_{\mathit{slow}}}+\frac{\mathit{\Delta }{\epsilon }_{\mathit{fast}}}{1+i\omega {\tau }_{\mathit{fast}}}+\frac{\mathit{\Delta }{V}_{\mathit{S}}{\omega }_{\mathit{S}}^2}{{\omega }_{\mathit{S}}^2-{\omega }^2+i\omega {\gamma }_{\mathit{S}}}+\frac{\mathit{\Delta }{V}_{\mathit{L}}{\omega }_{\mathit{L}}^2}{{\omega }_{\mathit{L}}^2-{\omega }^2+i\omega {\gamma }_{\mathit{L}}}+{\epsilon }_{\infty },$$ (4)

where $\mathit{\Delta }{\epsilon }_{\mathit{slow}\left(\mathit{fast}\right)}$ is the relaxation strength, ${\tau }_{\mathit{slow}\left(\mathit{fast}\right)}$ is the relaxation time for Debye relaxation functions, $\mathit{\Delta }{V}_{\mathit{S}\left(\mathit{L}\right)}$ is the vibration strength, ${\omega }_{S\left(L\right)}$ is the resonant frequency, ${\gamma }_{S\left(L\right)}$ is the damping constant for Lorentz vibration functions, and ${\epsilon }_{\infty }$ is the high frequency limit of the real part. A nonlinear fitting procedure was carried out employing the Levenberg-Marquardt algorithm until the chi-square becomes smaller than 10⁻¹⁵ by substituting $\tilde{\epsilon }\left(\omega \right)\pm \delta \tilde{\epsilon }\left(\omega \right)$, where $\delta \tilde{\epsilon }\left(\omega \right)$ is the experimental uncertainty, into the left-hand side of Eq. 4. By doing so, the experimental uncertainty as well as the standard deviation in the fitting procedure is reflected in the best-fitted result. Additionally, even in the protein solution, bulk water molecules that are unperturbed by a solute molecule reorient at the same rate with those in pure water (29, 31). Therefore, to obtain reliable fitting results, ${\tau }_{slow}$ was fixed to 7.93 ps for all the samples, which is equal to ${\tau }_{slow}$ of pure water at 300 K (75), and the remaining 10 parameters in Eq. 4 were determined from the nonlinear fitting procedure.

Hydration state

Although there is no contribution from the relaxation mode of hydration water in the THz region, the amount of hydration water can be indirectly estimated if hydration water is defined as water molecules with a distinctively longer relaxation time than ${\tau }_{slow}=$ 7.93 ps (69). Under this condition, the hydration number $N_{\mathit{hyd}}$ (the number of hydration water per albumin molecule) can be quantitatively determined from the decrease in the bulk water relaxation strength $\left(\mathit{\Delta }{\epsilon }_{\mathit{slow}}+\mathit{\Delta }{\epsilon }_{\mathit{fast}}\right)$ (46, 47, 48, 74). It should be noted that all hydration water molecules around the hydrophilic and/or hydrophobic surface, as well as the internally immobilized water molecules, will be counted as “hydration water” in our definition (76).

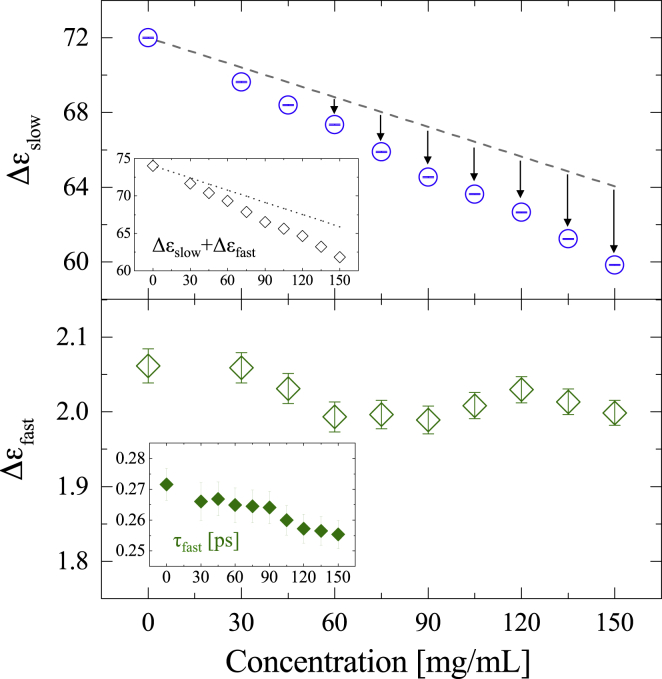
The derived concentration dependence of the slow and fast relaxation strength, $\mathit{\Delta }{\epsilon }_{\mathit{slow}}$ and $\mathit{\Delta }{\epsilon }_{\mathit{fast}}$, respectively, are shown in Fig. 4. Hereafter, the relaxation strength of pure water will be denoted as $\mathit{\Delta }\epsilon \left(0\right)$, whereas that of the albumin solutions at the albumin concentration $\mathit{C}$ will be denoted as $\mathit{\Delta }\epsilon \left(\mathit{C}\right)$. The gray broken lines, which are derived from $\mathit{\Delta }\epsilon \left(0\right)\times {\varphi }_{\mathit{water}}\left(\mathit{C}\right)$, represent virtual values when the volume of water molecules replaced by that of the albumin solutes are taken into account (= water dilution effect). As shown in Fig. 4, the slow relaxation strength $\mathit{\Delta }{\epsilon }_{\mathit{slow}}\left(\mathit{C}\right)$ and the total bulk water relaxation strength $\mathit{\Delta }{\epsilon }_{\mathit{slow}}\left(\mathit{C}\right)+\mathit{\Delta }{\epsilon }_{\mathit{fast}}\left(\mathit{C}\right)$ tend to decrease at a faster rate than the water dilution effect. Taking into account that the relaxation strength is proportional to the number density of dipoles (77), this result indicates that the decrease in the bulk water relaxation strength is not simply explained by the water dilution effect; suggesting a part of bulk water is conversed into hydration water in the presence of albumin solute molecules. On the basis of this framework, the hydration number is calculated as follows.

Figure 4.

Albumin concentration dependence of (top) slow relaxation strength $\mathit{\Delta }{\mathit{\epsilon }}_{\mathit{slow}}$ and (bottom) fast relaxation strength $\mathit{\Delta }{\epsilon }_{\mathit{fast}}$. The gray broken lines represent virtual values assuming the volume of water molecules replaced by that of the albumin solutes are taken into account (which represents water dilution effect). The insets show the total relaxation strength ($\mathit{\Delta }{\mathit{\epsilon }}_{\mathit{slow}}$ + $\mathit{\Delta }{\epsilon }_{\mathit{fast}}$) and the fast relaxation time ${\mathit{\tau }}_{\mathit{fast}}$. To see this figure in color, go online.

Although the relaxation strength is proportional to the number of dipoles, it should be noted that HB bulk water has a larger apparent dipole moment than NHB bulk water due to the enhancement of the dipole correlation via HBs. In other words, if the number of dipoles is the same, the slow relaxation strength $\mathit{\Delta }{\mathit{\epsilon }}_{\mathit{slow}}$ is larger than the fast relaxation strength $\mathit{\Delta }{\epsilon }_{\mathit{fast}}$ by a factor of $g_{HB}/g_{NHB}$, where $g_{HB\left(NHB\right)}$ is Kirkwood’s correlation factor of HB (NHB) bulk water. Then, to estimate quantitatively the amount of bulk water, the fraction of HB water ${\varphi }_{HB}\left(0\right)$ and NHB water ${\varphi }_{NHB}\left(0\right)$ in pure water is defined as

$${\varphi }_{\mathit{HB}}\left(0\right)=\frac{\mathit{\Delta }{\mathit{\epsilon }}_{\mathit{slow}}\left(0\right)/g_{\mathit{HB}}}{\mathit{\Delta }{\mathit{\epsilon }}_{\mathit{slow}}\left(0\right)/g_{\mathit{HB}}+\mathit{\Delta }{\mathit{\epsilon }}_{\mathit{fast}}\left(0\right)/g_{\mathit{NHB}}},{\varphi }_{\mathit{NHB}}\left(0\right)=1-{\varphi }_{\mathit{HB}}\left(0\right).$$ (5)

In the case of pure water, the correlation factor $\left(g_{bulk}\right)$ is assumed to be a superposition of $g_{HB}$ and $g_{NHB}$, and thus described as follows:

$$g_{\mathit{bulk}}={\varphi }_{\mathit{HB}}\left(0\right)\times g_{\mathit{HB}}+{\varphi }_{\mathit{NHB}}\left(0\right)\times g_{\mathit{NHB}}.$$ (6)

Furthermore, according to the Cavell’s equation (77), $g_{bulk}$ is derived by

$$g_{\mathit{bulk}}=\frac{1}{{\mu }_{\mathit{w}}^2}\frac{2{\epsilon }_{\mathit{S}}+1}{{\epsilon }_{\mathit{S}}}\frac{{\epsilon }_0{k}_{\mathit{B}}T}{N_{\mathit{A}}}\frac{{\left(1-f_{\mathit{w}}{\alpha }_{\mathit{w}}\right)}^2}{C_{\mathit{water}}}\left(\mathit{\Delta }{\epsilon }_{\mathit{slow}}\left(0\right)+\mathit{\Delta }{\epsilon }_{\mathit{fast}}\left(0\right)\right),$$ (7)

where ${\mu }_{\mathit{w}}$ is the dipole moment of an individual water molecule, ${\epsilon }_S$ is the static dielectric constant of water, ${\epsilon }_0$ is the permittivity of the vacuum, $k_{B}T$ is the thermal energy, $N_A$ is the Avogadro number, $f_w=2\left({\epsilon }_S-1\right)/\left[4\pi {\epsilon }_0{r}_w^3\left(2{\epsilon }_S+1\right)\right]$ ($r_w=$ 1.93 Å: the radius of a water molecule) is the reaction field factor, and ${\alpha }_w$ is the polarizability of the water molecule (71, 77). In Eqs. 5 and 6, it is reasonable to assume that $g_{NHB}=$ 1.0 because NHB water are isolated water molecules uncorrelated with the water HB network (72). Then, if $\mathit{\Delta }{\epsilon }_{\mathit{slow}}\left(0\right)$ and $\mathit{\Delta }{\epsilon }_{\mathit{fast}}\left(0\right)$ are given, the correlation factor of HB bulk water $g_{HB}$ is uniquely determined by solving simultaneous Eqs. 5–7. In the gas phase, the dipole moment of a water molecule is well known to be ${\mu }_{\mathit{w}}=$ 1.86 D; but in the liquid phase, the large polarization caused by the electric field induced by the surrounding molecules enhances the average value of the dipole moment (${\mu }_{\mathit{w}}\mathrm{\fallingdotseq }$ 3.0 D) (78). Thus, we obtained two different $g_{HB}$ values, originated from ${\mu }_{\mathit{w}}=$ 1.86 D and ${\mu }_{\mathit{w}}=$ 3.0 D. Then, the molar concentration of bulk water $C_{\mathit{bulk}}$ is described as (46, 47, 48, 74)

$$C_{\mathit{bulk}}\left(\mathit{C}\right)=\frac{\mathit{\Delta }{\mathit{\epsilon }}_{\mathit{slow}}\left(\mathit{C}\right)/g_{\mathit{HB}}+\mathit{\Delta }{\mathit{\epsilon }}_{\mathit{fast}}\left(\mathit{C}\right)/g_{\mathit{NHB}}}{\mathit{\Delta }{\mathit{\epsilon }}_{\mathit{slow}}\left(0\right)/g_{\mathit{HB}}+\mathit{\Delta }{\mathit{\epsilon }}_{\mathit{fast}}\left(0\right)/g_{\mathit{NHB}}}\frac{{\rho }_{\mathit{water}}}{M_{\mathit{water}}},$$ (8)

where ${\rho }_{water}$ and $M_{water}$ denote the density and molar weight of water, respectively. Considering all the water molecules are classified as either bulk or hydration water, the molar concentration of hydration water is described as $C_{\mathit{hyd}}\left(\mathit{C}\right)=C_{\mathit{water}}\left(\mathit{C}\right)-C_{\mathit{bulk}}\left(\mathit{C}\right)$. Then, the hydration number $N_{\mathit{hyd}}$ is determined by

$$N_{\mathit{hyd}}\left(\mathit{C}\right)=\frac{C_{\mathit{hyd}}\left(\mathit{C}\right)}{C_{\mathit{sol}}},$$ (9)

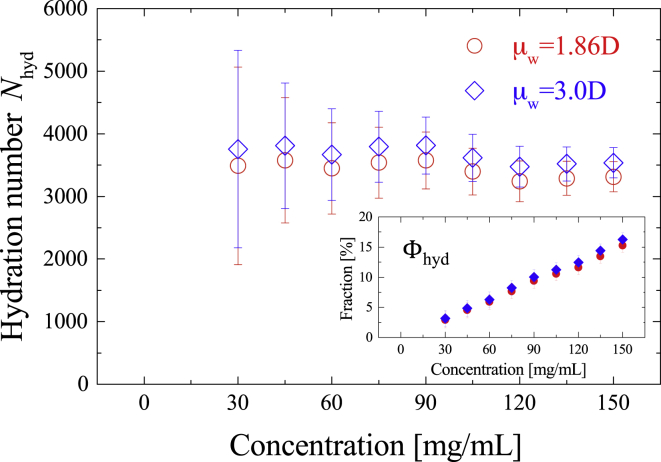
where $C_{\mathit{sol}}$ is the molar concentration of albumin solutes (29). The hydration number of albumin $N_{\mathit{hyd}}$ is summarized in Fig. 5, and the fraction of hydration water ${\varphi }_{\mathit{hyd}}$ $\left(=C_{\mathit{hyd}}/C_{\mathit{water}}\right)$ is inserted. The calculated $N_{\mathit{hyd}}$ does not have a significant concentration-dependence and ${\mu }_{\mathit{w}}$-dependence (∼3430 and 3660 for ${\mu }_{\mathit{w}}=$ 1.86 D and 3.0 D, respectively).

Figure 5.

Hydration number $N_{\mathit{hyd}}$ as a function of albumin concentration with ${\mu }_{\mathit{w}}=$ 1.86 D and ${\mu }_{\mathit{w}}=$ 3.0 D. The error bar was derived from an error-propagation law. The fraction of hydration water to total water $\left({\varphi }_{\mathit{hyd}}=C_{\mathit{hyd}}/C_{\mathit{water}}\right)$ is inserted. To see this figure in color, go online.

Assuming that the hydration water molecules are uniformly distributed around an albumin molecule (47), the thickness of the hydration layer $\left(r_{\mathit{hyd}}\right)$ is calculated to be between 8.3 and 8.8 Å, which corresponds to three to four water layers as estimated from a radial distribution function (79). At the same time, we arithmetically calculated the average surface-to-surface distance $\left(d_{\mathit{s}-\mathit{s}}\right)$ between two neighboring albumin molecules (see (47) for details, the albumin molecular radius was fixed at 27.1 Å as the boundary condition calculated from the partial specific volume and molecular weight (80)), based on the fact that the random close-packing structure of hydration water around an albumin molecule is independent of albumin concentration (81). As a result, we found a $d_{\mathit{s}-\mathit{s}}>2r_{\mathit{hyd}}$ for all concentrations, which suggests that the hydration layers to the nearest albumin molecule do not overlap with each other. Therefore, it is reasonable to postulate that aggregation of the albumin is unsubstantial over the examined concentration range.

As observed in a series of small-angle neutron scattering (SANS) measurements of bovine serum albumin (82, 83), ∼1100 water molecules (corresponding to 0.3–0.4 g H₂O/g albumin) are considered to “bound” around a protein molecule, forming a higher density water layer. Given that a complete hydration monolayer around albumin would contain 1070 water molecules (84), the SANS result represents a single hydration shell around albumin and the existence of further hydration layers was not checked for. In contrast, by defining reorientationally retarded water as hydration water in our study, we found three to four water layers (∼8.5 Å) from the albumin surface exhibit water dynamics that distinguish it from that of bulk water. This “global hydration” view (21, 22, 39, 40, 41, 42, 43, 44) is consistent with recent MD simulations, where the perturbation of water’s orientational structure induced by the protein was found to be long-ranged, propagating out to three to five hydration shells (21, 22).

Fragmentation of water-water HBs

In contrast to the slow relaxation ${\tilde{\chi }}_{slow}\left(\omega \right)$ that is assigned to the cooperative reorientation of the HB bulk water molecules, the individual relaxation of NHB bulk water is characterized by the fast relaxation ${\tilde{\chi }}_{fast}\left(\omega \right)$ (46, 47, 48). This fast relaxation ${\tilde{\chi }}_{fast}\left(\omega \right)$ coupled with changes in the slow relaxation ${\tilde{\chi }}_{slow}\left(\omega \right)$ can be used to define the population of the NHB water molecules, i.e., the fragmentation of HBs in the presence of albumin. It has been pointed out the population of this NHB water is coupled with protein thermal unfolding (85), prompting the need for quantification of NHB water adjacent to the protein molecule but little has been done to date.

To estimate quantitatively the population of NHB water molecules, the molar concentration of the NHB water, $C_{\mathit{NHB}}\left(\mathit{C}\right)$, was first calculated as

$$C_{\mathit{NHB}}\left(\mathit{C}\right)=C_{\mathit{bulk}}\left(\mathit{C}\right)\frac{\mathit{\Delta }{\mathit{\epsilon }}_{\mathit{fast}}\left(\mathit{C}\right)/g_{\mathit{NHB}}}{\mathit{\Delta }{\mathit{\epsilon }}_{\mathit{slow}}\left(\mathit{C}\right)/g_{\mathit{HB}}+\mathit{\Delta }{\mathit{\epsilon }}_{\mathit{fast}}\left(\mathit{C}\right)/g_{\mathit{NHB}}},$$ (10)

where $C_{\mathit{bulk}}\left(\mathit{C}\right)$ is the molar concentration of bulk water determined by Eq. 8. Then, the fraction of the NHB water to total water (including hydration and bulk water), ${\varphi }_{\mathit{NHB}}$, was described as

$${\varphi }_{\mathit{NHB}}\left(\mathit{C}\right)=\frac{C_{\mathit{NHB}}\left(\mathit{C}\right)}{C_{\mathit{hyd}}\left(\mathit{C}\right)+C_{\mathit{bulk}}\left(\mathit{C}\right)}.$$ (11)

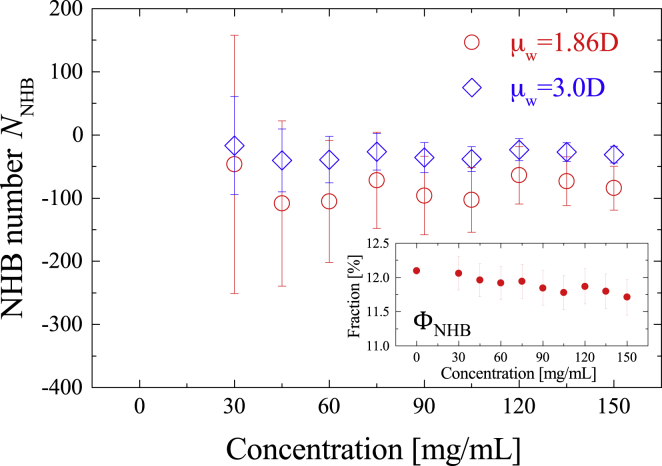
As shown in the inset of Fig. 6, ${\varphi }_{\mathit{NHB}}\left(\mathit{C}\right)$ tends to slightly decrease with albumin concentration increase, which implies albumin inhibits the fragmentation of water-water HBs. However, in ${\varphi }_{\mathit{NHB}}$, the NHB water induced by an albumin solute molecule cannot be distinguished from that inherent in the bulk-phase away from the albumin surface. Then, to isolate the induced NHB water species, we calculated the number of NHB water molecules induced by albumin $\left(N_{\text{NHB}}\right)$ as follows (46, 47, 48, 74):

$$N_{\mathit{NHB}}\left(\mathit{C}\right)=\frac{C_{\mathit{NHB}}\left(\mathit{C}\right)}{C_{\mathit{sol}}}-{\varphi }_{\mathit{NHB}}\left(0\right)\frac{C_{\mathit{water}}\left(\mathit{C}\right)}{C_{\mathit{sol}}},$$ (12)

where ${\varphi }_{NHB}\left(0\right)$ is the fraction of NHB water in pure water and $C_{\mathit{water}}\left(\mathit{C}\right)$ is the molar concentration of water. On the right-hand side of Eq. 12, the first term represents the total number of NHB water per single albumin molecule, and the second term is the number of NHB water expected when the fraction of NHB water is assumed to be equal to that of pure water (12.1% for ${\mu }_{\mathit{w}}=$ 1.86 D). A positive $N_{\mathit{NHB}}$ value would indicate HB fragmentation is being promoted by the solute, whereas a negative $N_{\mathit{NHB}}$ value represents solute inhibits the fragmentation of water-water HBs.

Figure 6.

Number of NHB water induced by albumin $\left(N_{\mathit{NHB}}\right)$ as a function of albumin concentration with ${\mu }_{\mathit{w}}$ = 1.86 D (red) and ${\mu }_{\mathit{w}}$ = 3.0 D. The inset is the fraction of NHB water $\left({\varphi }_{\mathit{NHB}}\right)$ of albumin when the dipole moment of individual water is ${\mu }_{\mathit{w}}$ = 1.86 D. The error bar was derived from an error-propagation law. To see this figure in color, go online.

The calculated $N_{\mathit{NHB}}\left(\mathit{C}\right)$ was negative over the investigated concentration range for both ${\mu }_{\mathit{w}}=$ 1.86 D and 3.0 D (Fig. 6), indicating the fragmentation of the water HB network is inhibited and thus the “less defective” HB structure is formed around the albumin solute. Our previous THz studies of biological aqueous solutions have shown that hydrophilic groups tend to increase the population of NHB water, but $N_{\mathit{NHB}}$ decreases as the ratio of the hydrophobic moiety becomes larger (46, 47, 48, 74). These results suggest hydrophobic groups inhibit the HB fragmentation of water, which is consistent with the recent Monte Carlo simulation study (86). Considering ∼60% of the molar mass at the outmost layer of albumin is occupied by hydrophobic moieties, a small negative $N_{\mathit{NHB}}$ (Fig. 6) reflects the effect of hydrophobic groups slightly exceeding that of hydrophilic ones at the interface of albumin.

Although earlier studies have implied NHB water is correlated with protein unfolding (5, 83), the relationship between protein functionality and NHB water is still obscure due to experimental difficulties in probing NHB water. Further THz experiments are expected to provide deeper insight into the role of NHB water in the biological functionality of proteins, such as enzyme reactions.

Structural distortion of the water hydrogen-bond network

The intermolecular stretching vibration mode ${\tilde{\chi }}_S\left(\omega \right)$ located around 5 THz originates from a translational motion of HB water molecules embedded in the “tetrahedral-like HB network” (87, 88, 89, 90, 91, 92). Thus, this intermolecular stretching is strongly correlated with the neighboring four water molecules (92) and sensitive to the water HB network structure (93). In fact, it is known that temperature increases involve distortion of the tetrahedral HB structure, which induces a slight red-shift and noticeable broadening of this intermolecular stretching vibration mode (62). In this section, the structural distortion of the water HB network in the albumin aqueous solutions will be discussed in terms of the oscillator strength $\left(f_S\right)$, resonant frequency $\left({\omega }_S\right)$, and damping constant $\left({\gamma }_S\right)$.

First, the oscillator strength of the intermolecular stretching vibration, $f_S$, was derived by

$$f_S=\frac{m{c}^2}{\pi e^{2}N}\int {\alpha }_S\left(\text{ω}\right)d\omega \propto \int \text{ωIm}\left[{\tilde{\chi }}_S\left(\omega \right)\right]d\omega ,$$ (13)

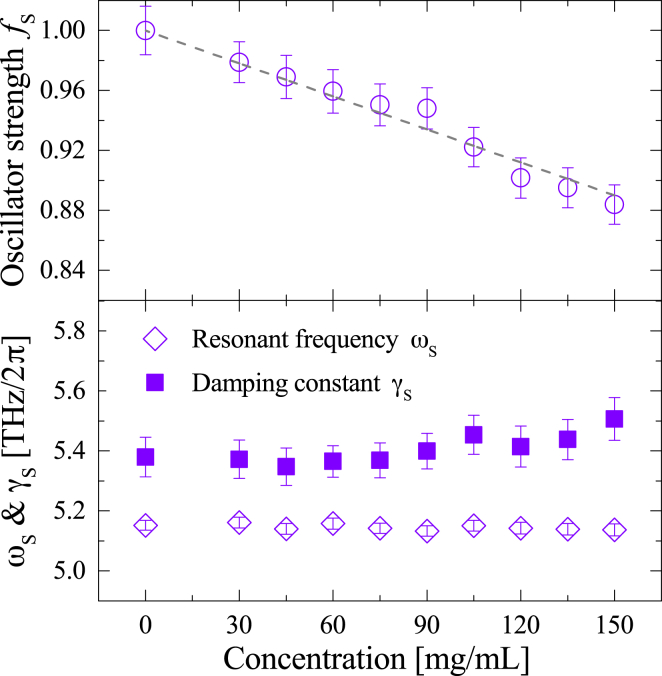
where $m$ is the oscillator mass, $c$ is the speed of light, $e$ is the oscillator charge, $N$ is the number density of dipoles, and ${\alpha }_S\left(\text{ω}\right)$ is the absorption coefficient of the intermolecular stretching vibration mode (94). The derived oscillator strength $f_S$, which is proportional to the square of the transition dipole moment, is shown in Fig. 7. In this figure, the oscillator strength of pure water $f_S\left(0\right)$ is normalized to be 1, and the gray broken line represents the water dilution effect, which is estimated by $f_S\left(0\right)\times {\varphi }_{\mathit{water}}\left(\mathit{C}\right)$. The concentration dependence of $f_S$ is in good agreement with the gray broken line, indicating all the water molecules in the albumin aqueous solution equally contribute to this ${\tilde{\chi }}_S\left(\omega \right)$ mode. This means both bulk and hydration water exhibit a similar transition dipole moment of the intermolecular stretching vibration.

Figure 7.

(Top) Normalized oscillator strength $f_S$ and (bottom) resonant frequency ${\omega }_S$ and damping constant ${\gamma }_S$ of the intermolecular stretching mode, as a function of albumin concentration. The gray broken line (top) represents virtual values assuming the volume of water molecules replaced by that of albumin solutes are taken into account (= water dilution effect). To see this figure in color, go online.

Next, the resonant frequency ${\omega }_S$ and damping constant ${\gamma }_S$ as a function of albumin concentration are shown at the bottom of Fig. 7. Since this ${\tilde{\chi }}_S\left(\omega \right)$ mode reflects all water molecules including bulk and hydration water as revealed above, these changes in ${\omega }_S$ and ${\gamma }_S$ represent “aggregated” values of their structure and dynamics. As shown in Fig. 7, the resonant frequency ${\omega }_S$, which represents the longitudinal modulus of the intermolecular stretch (95), is almost unchanged (±0.5%). On the other hand, in Fig. 7, the damping constant ${\gamma }_S$ tends to increase (+3%) as increasing albumin concentration though this slight increase of ${\gamma }_S$ is within the margin of error. The small volume fraction of hydration water (the volume fraction of bulk water is more than five times larger than that of hydration water even at 150 mg/mL albumin concentration, as seen in the inset of Fig. 5) in albumin aqueous solution masks the variation of the “aggregated” ${\gamma }_S$, but we can assert the damping constant of hydration water is qualitatively larger than that of bulk water. Since the damping constant ${\gamma }_S$ represents the degree of heterogeneity of the HB environment, large ${\gamma }_S$ of hydration water compared with that of bulk claims that hydration water has a heterogeneous HB network structure, which consists of various HB distances and angles, in good accordance with previous experiments (26, 35, 37) and simulations (12, 14, 21, 96, 97). Such heterogeneous HBs are associated with the distortion of the water HB network, since they involve the distortion of the O...O...O angles from the ideal tetrahedral value. The reason for this distorted HB structure around protein is that the protein surface, which is topologically and energetically heterogeneous, is structurally incompatible with the tetrahedral-like HB network of bulk water (16, 17, 18, 19, 20). Considering a distorted tetrahedral structure generally increases water density (98), the small compressibility (2) and the ∼5% to 10% higher density (12, 21, 23) of water in the first hydration shell of protein are closely associated with the structural distortion of the water HB network that stems from topological and energetic disorder of the protein surface. In addition, since such a distorted structure of hydration water is not compatible with freezable water (i.e., regular tetrahedral coordination), the structural distortion imposed by protein is thought to be an origin of nonfreezing characteristics (1) of hydration water.

Derivation of O-H stretching of hydration water

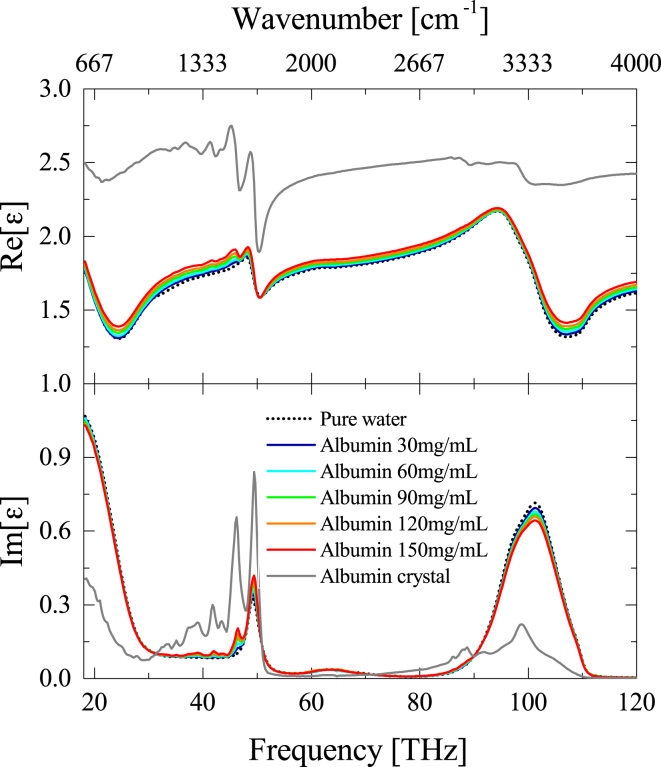
Although the relaxation and the intermolecular vibration modes lie in the THz and FIR frequency range, the complex dielectric constant in the MIR region mainly reflects the intramolecular vibrations. Fig. 8 shows the complex dielectric constants $\tilde{\epsilon }\left(\omega \right)$ of pure water, albumin aqueous solution and albumin crystal (film) in the MIR region. Between 18 and 120 THz (600–4000 cm⁻¹), pure water exhibits two noticeable dispersions assigned to the H-O-H bending (49 THz) and O-H stretching (∼100 THz) (99). Especially, the latter is strongly coupled with intermolecular HB dynamics (49, 50, 51, 52, 55, 56, 57, 58), and in general, the O-H stretching frequency red-shifts as the intermolecular HB becomes stronger (100, 101, 102, 103, 104). On the other hand, the complex dielectric constant of albumin crystal exhibits the several amide bands (66, 105, 106) between 30 and 50 THz, the C-H stretching (87 THz) (107), and N-H stretching (∼100 THz) (66) in the MIR region. Hence, for the complex dielectric constant of albumin aqueous solution, the latter two stretching bands of albumin overlap with the O-H stretching of water, complicating the interpretation of the HB environment of water around protein. To overcome this limitation, the O-H stretching band of hydration water will be mathematically characterized as follows.

Figure 8.

The complex dielectric constant of pure water, albumin aqueous solutions, and albumin crystal between 18 and 120 THz (600 and 4000 cm⁻¹). For pure water, the high frequency tail of the water libration (∼18 THz), the H-O-H bending band (∼49 THz), the combination band (∼65 THz), and the O-H stretching band (∼100 THz) are observed. Additional bands, such as the amide III band (∼37 THz), the COO⁻ band (∼42 THz), the amide II band (∼46 THz), the amide I band (∼50 THz), the C-H stretching band (∼87 THz), and the N-H stretching band (∼100 THz) are noticed in the complex dielectric constants of albumin aqueous solution and albumin crystal. To see this figure in color, go online.

Assuming albumin aqueous solution to be a three-body model with a spherical solute ${\tilde{\epsilon }}_{\mathit{sol}}\left(\omega \right)$ covered by a concentric shell of hydration water ${\tilde{\epsilon }}_{\mathit{hyd}}\left(\omega \right)$, which is uniformly distributed in a continuous bulk water medium ${\tilde{\epsilon }}_{\mathit{bulk}}\left(\omega \right)$, the complex dielectric constant of albumin aqueous solution is replicated by the following Wagner equation (27, 29, 108):

$$\tilde{\epsilon }\left(\omega \right)={\tilde{\epsilon }}_{\mathit{bulk}}\left(\omega \right)\frac{2\left(1-{\varphi }_{\mathit{eq}}\right){\tilde{\epsilon }}_{\mathit{bulk}}\left(\omega \right)+\left(1+2{\varphi }_{\mathit{eq}}\right){\tilde{\epsilon }}_{\mathit{eq}}\left(\omega \right)}{\left(2+{\varphi }_{\mathit{eq}}\right){\tilde{\epsilon }}_{\mathit{bulk}}\left(\omega \right)+\left(1-{\varphi }_{\mathit{eq}}\right){\tilde{\epsilon }}_{\mathit{eq}}\left(\omega \right)},$$ (14)

where ${\varphi }_{\mathit{eq}}={\varphi }_{\mathit{hyd}}+{\varphi }_{\mathit{sol}}$ is the volume fraction of shelled particles (albumin covered with the hydration shell) with the equivalent complex dielectric constant of ${\tilde{\epsilon }}_{\mathit{eq}}\left(\omega \right)$. Then, ${\tilde{\epsilon }}_{\mathit{eq}}\left(\omega \right)$ of the shelled particle is given by

$${\tilde{\epsilon }}_{\mathit{eq}}\left(\omega \right)={\tilde{\epsilon }}_{\mathit{hyd}}\left(\omega \right)\frac{2\left(1-{\varphi }^{\prime }\right){\tilde{\epsilon }}_{\mathit{hyd}}\left(\omega \right)+\left(1+2{\varphi }^{\prime }\right){\tilde{\epsilon }}_{\mathit{sol}}\left(\omega \right)}{\left(2+{\varphi }^{\prime }\right){\tilde{\epsilon }}_{\mathit{hyd}}\left(\omega \right)+\left(1-{\varphi }^{\prime }\right){\tilde{\epsilon }}_{\mathit{sol}}\left(\omega \right)},$$ (15)

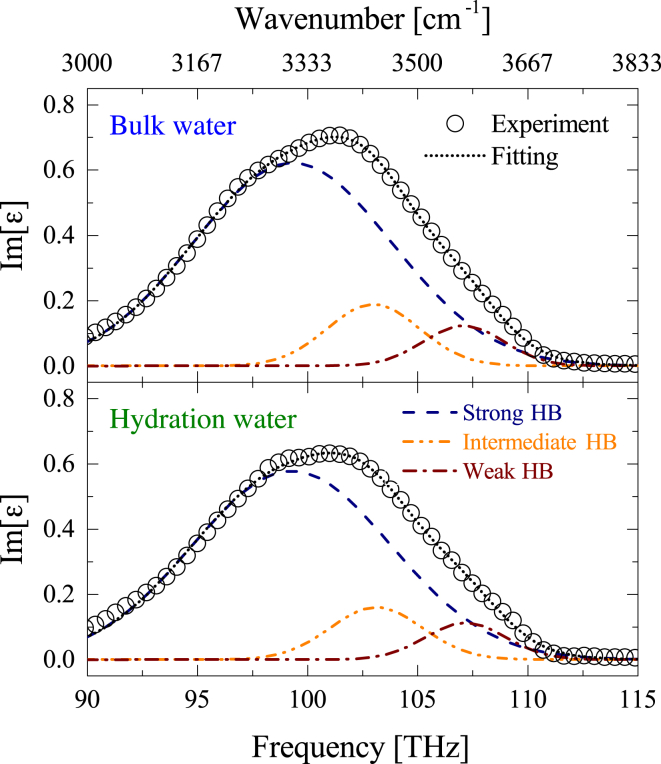
where ${\varphi }^{\prime }={\varphi }_{\mathit{sol}}/{\varphi }_{\mathit{eq}}$ is the volume fraction of the bare albumin with respect to the volume of the shelled albumin (29). The complex dielectric constant of 150 mg/mL albumin aqueous solution was used as $\tilde{\epsilon }\left(\omega \right)$, and our THz spectroscopic result of ${\varphi }_{\mathit{hyd}}$ (corresponding to three to four hydration layers) was used in Eqs. 14 and 15. Furthermore, the complex dielectric constants of pure water and albumin crystal were substituted into ${\tilde{\epsilon }}_{\mathit{bulk}}\left(\omega \right)$ and ${\tilde{\epsilon }}_{\mathit{sol}}\left(\omega \right)$. Thus, solving these equations mathematically derives the only remaining variable, the complex dielectric constant of hydration water ${\tilde{\epsilon }}_{\mathit{hyd}}\left(\omega \right)$. In our case, ${\tilde{\epsilon }}_{\mathit{hyd}}\left(\omega \right)$ represents the “average” dielectric constant in the three to four water layers from the albumin surface, where the reorientation dynamics are more retarded than bulk water. Note that the local heterogeneity in the hydration shell is not considered. As seen in Fig. 9, hydration water ${\tilde{\epsilon }}_{\mathit{hyd}}\left(\omega \right)$ shows a similar O-H stretching band as that of bulk water ${\tilde{\epsilon }}_{\mathit{bulk}}\left(\omega \right)$, but the imaginary part at 102 THz is significantly reduced. We confirmed quite similar ${\tilde{\epsilon }}_{\mathit{hyd}}\left(\omega \right)$ can be obtained from other effective medium approximation, indicating our result is not model-dependent. Because differences in this O-H stretching band reflect the different HB environments of water, a quantitative analysis to characterize the HB network of hydration water will be performed in the next section.

Figure 9.

The imaginary part in the O-H stretching region of bulk water ${\tilde{\epsilon }}_{\mathit{bulk}}\left(\omega \right)$ (top) and hydration water ${\tilde{\epsilon }}_{\mathit{hyd}}\left(\omega \right)$ determined by the Wagner equations (bottom). The experimental result (circle) was successfully reproduced by the sum the three Gaussian subbands. To see this figure in color, go online.

Hydrogen-bond strength

Conventionally, the broad O-H stretching band is satisfactorily described by the superposition of two-Gaussian (51, 53), three-Gaussian (49), or more components (109, 110). In our study, we chose a three-Gaussian subband model to describe the O-H stretching of bulk and hydration water, according to second derivatives of the imaginary part (data not shown). In a nonlinear fitting procedure, the each subband width of hydration water was constrained to the values obtained for bulk water, to avoid uncontrolled and physically meaningless variations. As shown in Fig. 9, the three-Gaussian fitting can provide a good fit to the O-H stretching of bulk water and hydration water. Given that the O-H stretching frequency undergoes red-shift as the intermolecular HB strengthens (49, 100, 101, 102, 103, 104), the three Gaussian subbands were assigned to the three dominant populations of water molecules as follows: “strong HB” (∼99 THz), “intermediate HB” (∼102 THz), and “weak HB” (∼107 THz) water species.

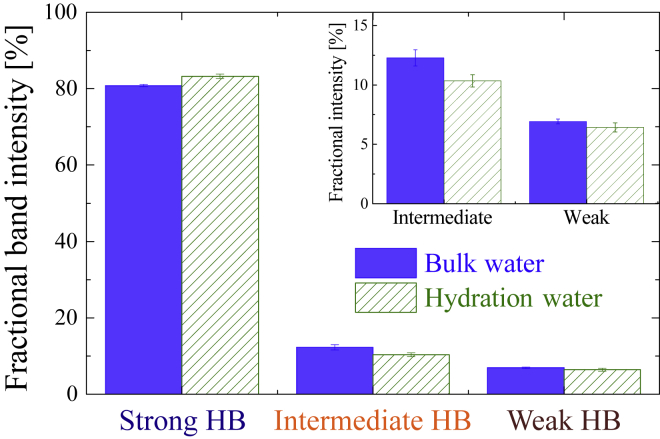
From best-fitted parameters, the fractional band intensity (which equals a relative band area of a subband divided by the total band area) was determined as shown in Fig. 10. Bulk water is dominated by the strong HB water component (>80%), followed by intermediate HB and weak HB species. However, it should be noted this fractional band intensity is not proportional to the population of each component, because the transition dipole moment of weak HB water is smaller than that of strong HB water (non-Condon effect) (111). Thus, this fractional band intensity is a qualitative representation of the HB strength, but not a quantitative one. Compared with bulk water, the strong HB water of hydration water was achieved at the cost of intermediate HB water species. This “intermediate → strong HB transition” trend represents the strengthening of HBs (112, 113), and such a strengthened HB is considered to force water molecules to undergo slower reorientational motion (114, 115). Additionally, we found a slight decrease in the weak HB species for hydration water (though the variation is within the margin of error), which is in line with a reduction of NHB water around albumin.

Figure 10.

Fractional band intensity of bulk water compared with that of hydration water. Note that this fractional band intensity is not proportional to the population of each subband component. The inset shows a close-up of intermediate and weak HB water species. The error bars were derived from an error-propagation law. To see this figure in color, go online.

Conclusions

To characterize the HB network of water around a model protein (albumin), the broadband complex dielectric constraint $\tilde{\epsilon }\left(\omega \right)$ of albumin aqueous solution was determined from 0.25 to 400 THz. From the THz to FIR region (0.25∼12 THz), where we revealed the contribution of dissolved albumin solute is negligibly small, the hydration state and the water HB structure were analyzed. First, by defining hydration water as those water molecules that exhibit dynamically retarded reorientation compared with bulk water, we found $\approx$ 3500 hydration water molecules corresponding to a layer of water molecules extending $\approx$ 8.5 Å (three to four water layers) out from the protein surface, in good agreement with recent MD simulation studies (21, 22). Second, the water HB structure around albumin is discussed in terms of HB fragmentation (the population of NHB water) and the distortion of the HB network. We have proved that the number of NHB water produced per albumin molecule is negative in the investigated concentration range, indicating the albumin solute inhibits the fragmentation of water-water HBs. Such a “less defective” water HB network is mainly due to hydrophobic moieties on the albumin surface. On the other hand, the tetrahedral-like HB structure was revealed to be distorted, consisting of heterogeneous HB distance and angles (12, 14, 21, 96, 97), because of topological and energetic disorder on the protein surface (16, 17, 18, 19, 20). Furthermore, particular attention was paid to the O-H stretching band in the MIR region. Our results pointed to a trend that the fraction of strong HB water species increased at the cost of intermediate HB ones, suggesting hydration water can form more strengthened HBs with respect to bulk water.

To summarize, our experimental results elucidate the characteristics of the water HB network around protein as follows. Because of topological and energetic disorder (16, 17, 18, 19, 20), the protein-water and water-water HBs in the protein hydration shell are structurally incompatible with the native HB network of bulk water. In this scenario, the antifreezing nature below zero degrees centigrade (1), the small compressibility (2), and high local density (12, 13) of hydration water around the protein are associated with the distorted HB structure of hydration water. However, this “distorted” HB network is not fragile: conversely, the HB strength is greater and the population of fragmented NHB water is smaller for hydration water compared with that of bulk water. Such a solid HB network in the vicinity of protein retards the reorientational motion of water up to $\approx$ 8.5 Å from the solute surface.

Author Contributions

K.S. provided acquisition, analysis, and interpretation of data, and drafting and revision of the article; and Y.O. and N.K. provided study conception and design, and drafting and revision of the article.

Editor: Jane Dyson