Structure of the SLC4 transporter Bor1p in an inward‐facing conformation

Abstract

Bor1p is a secondary transporter in yeast that is responsible for boron transport. Bor1p belongs to the SLC4 family which controls bicarbonate exchange and pH regulation in animals as well as borate uptake in plants. The SLC4 family is more distantly related to members of the Amino acid‐Polyamine‐organoCation (APC) superfamily, which includes well studied transporters such as LeuT, Mhp1, AdiC, vSGLT, UraA, SLC26Dg. Their mechanism generally involves relative movements of two domains: a core domain that binds substrate and a gate domain that in many cases mediates dimerization. To shed light on conformational changes governing transport by the SLC4 family, we grew helical membrane crystals of Bor1p from Saccharomyces mikatae and determined a structure at ∼6 Å resolution using cryo‐electron microscopy. To evaluate the conformation of Bor1p in these crystals, a homology model was built based on the related anion exchanger from red blood cells (AE1). This homology model was fitted to the cryo‐EM density map using the Molecular Dynamics (MD) Flexible Fitting method and then relaxed by all‐atom MD simulation in explicit solvent and membrane. Mapping of water accessibility indicates that the resulting structure represents an inward‐facing conformation. Comparisons of the resulting Bor1p model with the X‐ray structure of AE1 in an outward‐facing conformation, together with MD simulations of inward‐facing and outward‐facing Bor1p models, suggest rigid body movements of the core domain relative to the gate domain. These movements are consistent with the rocking‐bundle transport mechanism described for other members of the APC superfamily.

Short abstract

PDB Code(s): 5SV9; EMD-8313

Introduction

The SLC4 family comprises secondary transporters including the anion exchangers (AE) and sodium coupled bicarbonate transporters (NCBT).1, 2 The former exchange ${\text{HCO}}_3^{-}$ and Cl⁻ and are well known for their role in carrying CO₂ across red blood cells membranes, whereas both are widely responsible for maintaining homeostasis of pH throughout the body. Another group of SLC4 family members is responsible for boron transport with representatives in yeast, plants and animals.3 The importance of boron transport in plants is undisputed, where borate serves to crosslink rhamnogalacturonan II in the primary cell wall.4 Indeed, Arabidopsis thaliana has seven different borate transporters (Bor1‐7) with differing expression patterns and roles both in boron uptake and export.1 In yeast, which have neither AEs nor NCBTs, a related boron transporter (Bor1p) is associated with resistance to high levels of boric acid5, 6 and in mammals, the SLC4 family includes Btr1, which is related to the borate transporters in plants and fungi.2 There is evidence that Bor1p mediates electrogenic exchange of H₃BO₃ and protons7 and that Btr1 is a Na⁺‐driven B(OH)₄ ⁻ transporter8 although alternative roles for these transporters have not been ruled out. Despite this uncertainty, there is a clear need for boron homeostasis in mammals. While elevated levels are toxic,3 boron is required for bone strength and maintenance of steroid hormone levels; in addition, boron has been shown to modulate the activity of certain enzymes, including serine proteases and vitamin D‐24‐hydrolase, that affect inflammation, targeting of vitamin D₃, Ca²⁺ absorption and insulin sensitivity.9

Structural studies of SLC4 transporters have so far been limited to AE1, which is prevalent both in red blood cells and in kidney. In red blood cells, AE1 plays dual roles, with the N‐terminal, cytoplasmic domain anchoring the spectrin‐based cytoskeleton to the cytoplasmic membrane and the C‐terminal membrane domain responsible for transport activity.10 In kidney, AE1 is important for urinary acidification.11 X‐ray crystal structures have been solved for the N‐terminal domain12 and, more recently, for the membrane domain.13 The latter revealed a fold with 14 TM helices similar to several other members from the Amino acid‐Polyamine‐organo Cation (APC) superfamily.14 Specifically, structures of UraA15 and UapA,16 both belonging to the nucleobase:cation symporter‐2 (NCS2) family, and a fumarate transporter (SLC26Dg)17 from the SLC26 family revealed a similar arrangement of TM helices, even though the sequence identity is low between the respective families. All of these structures are characterized by two inverted repeats that are intertwined to form two domains, termed the “core” and “gate” domains. The gate domains generally mediate dimerization and the core domains bind ligands in a cleft between helices M3 and M10, which are corresponding elements of the two repeats and which only extend halfway across the membrane. The mechanism of transport has been postulated to involve relative movements between the core and the gate domains.15, 16, 18

The common fold adopted by the SLC4, NCS2, and SLC26 families suggests that transport occurs via similar structural changes. The elevator mechanism and the rocking‐bundle mechanism are two potential models for the conformational change that transforms the molecules between inward‐ and outward‐facing states.19 The elevator mechanism has been demonstrated quite convincingly for NapA,20 apical sodium‐dependent bile acid transporters (ASBT),21 CitS,22 and Glt_Ph transporters.23 According to this mechanism, the core (or transport) domain moves vertically up and down relative to the membrane plane, while the gate (or scaffold) domain anchors the protein in the membrane, often mediating contacts between dimeric or trimeric assemblies. Although none of these elevator‐like transporters belong to the APC superfamily, they all have an analogous core/gate domain architecture, leading Alguel et al.16 to propose that this mechanism also applies to NCS2 family members and, by extension, to the AE family. In contrast, the rocking‐bundle mechanism has been established for other well studied members of the APC superfamily (Mhp1, BetP, AdiC, vSGLT, LeuT), in which the substrate binding site in the core domain serves as a fulcrum for a rigid‐body tilting of the core domain relative to the gate domain.24, 25 However, extension of the rocking‐bundle mechanism to NCS2, SLC26, and AE families is made uncertain by the fact that the APC superfamily comprises two topological types of inverted repeats: 5 + 5 and 7 + 7 (referring to the number of TM elements in each repeat). Although there are distinct similarities in these folds, their evolutionary relationship is uncertain,26 making it difficult to predict whether the rocking‐bundle mechanism employed by the 5 + 5 group of transporters is also employed by NCS2, SLC26, and AE1 families, which have the 7 + 7 topology. A comparison of structures representing different conformations of a given transporter would be very informative in resolving this quandary. Structures of UraA, UapA, and SLC26Dg have all been solved in the inward‐facing state. Although the AE1 structure represents the outward‐facing state, there are substantial differences in the conformation of the gate domain that complicates alignment as well as comparisons of the conformation of these distantly related transporters.

In the current work, we solved the structure of Bor1p from the yeast Saccharomyces mikatae by using cryo‐electron microscopy (cryo‐EM) to image helical crystals of membrane bound protein. On the basis of this experimental structure, we then used molecular dynamics (MD) simulations to produce a model based on the AE1 structure and to study the dynamics of the transporter in a lipid bilayer. The resulting model appears to represent an inward‐facing state, based on the orientation of helical elements and on computational assessment of the water accessibility. Comparisons with the outward‐facing structure of AE1 as well as analysis of domain positions during MD simulations of an outward facing model of Bor1p do not show the vertical movements of the core domain expected for the elevator mechanism, but are more consistent with the rocker‐switch employed by other members of the APC superfamily.

Results

Tubular crystals of Bor1p

Two‐dimensional crystals of Bor1p were produced using a screening strategy that we have developed over the last several years.27, 28, 29, 30 The relatively small size of this transporter (60 kD) and lack of extramembranous domains make it challenging to apply single‐particle cryo‐EM methods. However, by reconstituting the transporter into a lipid bilayer and inducing growth of tubular crystals, we can not only provide a membrane environment but can also facilitate structure determination through the use of helical reconstruction strategies. In particular, helical assemblies increase the mass of particles dramatically, making them easy to identify in micrographs and to align computationally; furthermore, they offer a full range of views that avoid problems with preferred orientations, and provide a high degree of internal symmetry that facilitates the reconstruction process.

Although we have developed screens that systematically sample many relevant parameters governing the crystallization process, we opted in this case to start with conditions that produce 3D crystals of Bor1p. These conditions reflect extensive screening of various forms of Bor1p that ultimately yielded 3D crystals that diffract anisotropically to ∼4.5 Å resolution (results not shown). For 2D crystallization, we performed initial screens using buffers from seven different 3D crystallization conditions, omitting PEG precipitants and focusing instead on testing different lipids and lipid‐to‐protein ratios. After observing membranes with tubular morphology in these initial screens, we performed ∼1800 subsequent screens that sampled different detergents, lipids, buffer compositions, detergent removal techniques, inhibitors and N‐terminal protein truncations. The condition yielding the best‐ordered tubes included the full length Bor1p construct and cardiolipin at a lipid‐to‐protein ratio of 0.44 (by weight) solubilized in heptaethyleneglycol‐n‐dodecylether (C₁₂E₇) detergent in a buffer of 100 mM HEPES, 100 mM NaCl, 2 mM boric acid with a pH between 6.5 and 7.5. Conditions containing other monovalent salts such as NaI, NaBr, (NH₄)₂SO₄ also produced tubular crystals. Inhibitors such as DNDS, DiBac4(5), and DIDS prevented crystal growth, while boric acid analogues (phenyl boronic acid, nitrophenyl boronic acid, 2‐(hydroxymethyl)phenyl boronic acid) did not influence crystal quality.

Fourier–Bessel reconstruction

As is often the case with helical crystals of membrane proteins, the crystallization trials produced a wide range of tube diameters, which generally arise from a common surface lattice but reflect different helical symmetries.31 Small diameters are most amenable to structure determination and we therefore focused on crystallization trials that produced the narrowest tubes. After collecting images from a particularly promising batch of tubular crystals, we identified two prevalent populations of tubes with radii of 164 Å (Type 1) and 157 Å (Type 2) (Fig. 1). These tubes were used to generate 3D reconstructions using both conventional Fourier–Bessel reconstruction and iterative real‐space refinement.

Figure 1.

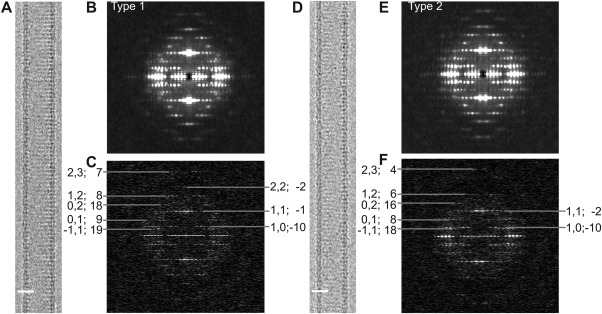
Image data for Bor1p tubular crystals. (A) Image of a Type 1 tubular crystal. (B) Incoherent sum of Fourier transforms from overlapping segments along many Type 1 tubular crystals revealing a characteristic pattern of layer lines. (C) Fourier transform from an individual tubular crystal. Numbers at the periphery (h,k; n) correspond to a Miller index (h,k) and the Bessel order (n) that together reflect the symmetry for this particular helical family. (D) Image of a Type 2 tubular crystal. (E) Incoherent sum of Fourier transforms and (F) Fourier transform from an individual tube with the helical indexing that characterizes Type 2 tubes. Note that the Bessel orders from Type 1 tubes are different from Type 2 tubes. Specifically, the (0,1) layer line has Bessel orders of 9 and 8, respectively.

As a first step in Fourier–Bessel reconstruction, the helical symmetry was characterized using methods that we have previously described in detail.31 This process involved assigning Bessel orders to two principal layer lines that were indexed as (1,0) and (0,1) [Fig. 1(C,F)]. In particular, the corresponding Bessel orders were assigned as 9, −10 for Type 1 tubes and 8, −10, for Type 2 tubes, respectively. Assignments for these principle layer lines then constrained Bessel orders for all of the remaining layer lines. The phase data from these layer lines were consistent with the presence of two‐fold symmetry (D1 point group). After averaging data from the best 41 Type 1 crystals (from a total of 57 with lengths adding up to ∼12 μm) and the best 24 Type 2 crystals (from a total of 34 with lengths adding up to ∼8 μm), we estimated the resolution to be 9‐10 Å, based on comparison of experimental phases to those constrained by two‐fold symmetry (0° and 180°) and on analysis of local resolution by ResMap.32 After masking and aligning these dimeric densities, which correspond to the unit cell of the surface lattice, the Fourier shell coefficients comparing the two maps were consistent with a somewhat higher resolution of 7 Å based on a cutoff of 0.143 (Fig. 2).

Figure 2.

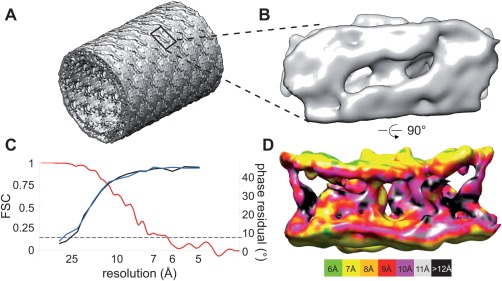
Fourier–Bessel reconstructions from Bor1p tubular crystals. (A) 3D reconstruction from Type 1 tubes showing the tubular morphology. The bilayer is visible as an almost continuous density around the perimeter of the tube. The lack of extramembranous domains in Bor1p means that the surfaces of the tubes are relatively smooth, though a regular lattice is detectable. One unit cell has been outlined. (B) Bor1p dimer extracted from Type 1 tubes and viewed from the outer surface. (C) Resolution of the reconstructions was estimated by phase residuals (black for Type 1 and blue for Type 2) and by FSC between the two independent reconstruction (red trace). Dotted line corresponds to the conventional 0.143 criteria for resolution. (D) Bor1p dimer viewed along the membrane plane. The continuous densities at the top and bottom correspond to the boundary of the membrane, with poorly resolved TM densities running in between. The surface of the map has been colored according to estimates of local resolution as determined by ResMap.32

The two independent maps show the expected tubular morphology with discrete densities arranged within the 50‐Å‐thick wall of the tube, which are consistent with Bor1p dimers embedded in a lipid membrane (Fig. 2). The boundaries of the membrane are evident as high density regions separated by ∼40 Å, and densities crossing this membrane region presumably correspond to the TM elements of Bor1p. Inspection of cross‐sections provides evidence for TM helices (Supporting Information Fig. S1, Movie 3), but these densities are not continuous across the membrane and the overall architecture of Bor1p is not evident from 3D renderings at a single density threshold. This lack of distinct features is consistent with modest 9–10 Å resolution achieved by Fourier–Bessel reconstruction and probably also reflects the entangled, twisting α‐helices that compose this family of transporters.

Real‐space reconstruction

Given that the images had been recorded with a direct detector and appeared to have higher resolution information, we attempted to improve the map by using the real‐space reconstruction strategy implemented in Frealix.33 Unlike the Fourier–Bessel method, which requires long, straight tubes, Frealix uses short (200 Å), overlapping segments and therefore allowed incorporation of more data into the refinement: a total length of ∼21.5 μm from Type 1 tubes ∼15.5 μm from Type 2 tubes were analyzed. Despite the inferior map, Fourier–Bessel analysis played an important role in providing validated helical symmetry parameters and a starting reference for iterative refinement by Frealix. This refinement converged after six cycles and the resulting density map provided greatly improved definition of TM helices (Fig. 3). The resolution estimate based on the FSC (0.143 cutoff) was 6.4 Å and 6.7 Å for the Type 1 and 2 crystals, respectively. The resolution of the maps was further improved by removing noisy segments (amounting to 14% of the dataset) with orientational parameters that were inconsistent with the underlying helical assembly. As a result, the resolution of the map from Type 1 tubes increased to 5.9 Å [Fig. 3(C)]. Furthermore, FSC comparison of the two completely independent reconstructions from Type 1 and Type 2 tubes indicated a high level of consistency, reaching the 0.143 cutoff at ∼6 Å resolution. Although the resolution estimate from ResMap is somewhat lower, this estimate is hampered by the crystalline array, which prevents the program from cleanly distinguishing the structure from the background noise. Both of these Frealix maps revealed discrete sausage‐shaped densities consistent with well‐resolved TM helices [Fig. 3(A–B), Supporting Information Fig. S1, Movie 4]. As is described below, these densities could be readily associated with the 14 expected TM helices of Bor1p.

Figure 3.

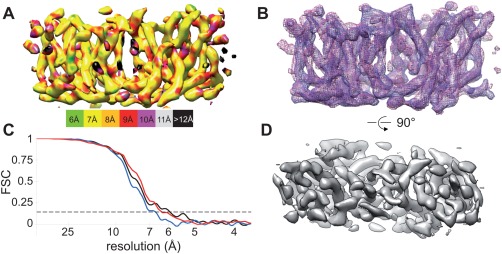
Real‐space reconstruction of Bor1p tubular crystals using Frealix. (A) Bor1p dimer from Type 1 tubes viewed parallel to the membrane plane shows well resolved TM densities. The surface has been colored according to the local resolution as determined by ResMap.32 (B) Overlay of independently determined maps from Type 1 and Type 2 tubes (blue and purple mesh), showing the close correspondence between these structures. (C) Resolution estimates based on the FSC indicate resolutions of 6–7 Å for reconstructions from Type 1 (black trace) and Type 2 (blue trace) tubular crystals (dashed line corresponds to 0.143). Comparison of independent reconstructions Type 1 and Type 2 tubes (red trace) indicate that they are very similar. (D) View of the map from Type 1 tubes perpendicular to the membrane surface.

To understand why the real‐space approach resulted in such a dramatic improvement in resolution, we analyzed the orientations at regular intervals along the individual tubes. Even though the tubes were specifically chosen to be as straight as possible in the images, they can have out‐of‐plane tilt, which is potentially variable along the length of the tube. Thus, it seemed possible that out‐of‐plane curvature accounted for the relatively poor resolution obtained by the Fourier–Bessel approach. Indeed, Supporting Information Figure S2 illustrates out‐of‐plane tilt (θ), which varies by ∼16° along the length of this particular tube. Although the Fourier–Bessel processing devised by Beroukhim and Unwin34 attempts to account for out‐of‐plane curvature by dividing tubes up into non‐overlapping ∼500‐Å long segments, this approach is not capable of following such rapid changes in out‐of‐plane tilt, which in this particular example probably results from the transition from a supported position over the carbon film to an unsupported position over a hole. In contrast, Frealix assigns orientations at 70‐Å intervals along the tube and is thus more effective in compensating for the curvature.

Modeling and simulations

To interpret these maps and to assign the discrete densities to corresponding TM helices, we created a homology model for Bor1p based on the atomic structure of AE1 (PDB 4yzf) and fit it to the density maps. Specifically, after alignment of sequences for Bor1p and AE1 (Supporting Information Fig. S3), MODELLER35 was used to produce a homology model (see Table 1 for summary of models produced for this work). This alignment was based on a 23% sequence identity and produced a P value of 10^−15. 2, indicating that is was overwhelmingly likely that the two proteins have the same fold.36 We then used the Molecular Dynamics Flexible Fitting (MDFF) method37 implemented in NAMD38 to fit this model to our maps. In the case of the Frealix real‐space map, several features were used to establish unambiguously the orientation of the Bor1p model in the membrane. In particular, the distinctive shape of the M13‐M14 hairpin to one side of the molecule was clearly evident, as was density for an N‐terminal helix on the cytoplasmic side of the membrane (H1). Additionally, although the surface helices between M4‐M5 and M11‐M12 are related by pseudo‐symmetry, the surface helix H4 on the cytoplasmic side of the membrane between M12 and M13 is not [Supporting Information Fig. S4(A)] and the corresponding density was clearly present in the map (Supporting Information Movie 4). Thus, two copies of the homology model were docked within this density without any manipulation of individual helices and used as a starting point for MDFF.

Table 1.

Summary of Models Used in This Work

Name	Start model	Map	Method
AE1	PDB 4yzf	N/A	Published X‐ray structure
AE1‐based homology	AE1	N/A	MODELLER using sequence alignment for threading
IF/1	AE1‐based homology (manually manipulated to match map)	Fourier–Bessel	MDFF
IF/2	AE1‐based homology	Frealix, real‐space	MDFF
OF/1	IF/1	Simulated AE1 map	MDFF
OF/2	IF/2	Simulated AE1 map	MDFF

The MDFF simulation converged quickly and produced a highly plausible model in which all 14 TM helices as well as the surface helices were accommodated in corresponding densities (Fig. 4, Supporting Information Movies 1–4). In the case of the Fourier–Bessel map, there was uncertainty about the orientation of the molecule in the membrane, and both orientations were used as starting models for MDFF, after manually reorienting several of the helices to match the density. Inspection of the match between the model and the map suggested that the orientation used for the real‐space map was a better fit, but cross‐correlations did not convincingly distinguish the two possibilities. Furthermore, it is interesting to note that although cross‐correlations clearly showed convergence of the simulation [Fig. 4(C)], they did not reflect the obviously superior structure from real‐space reconstruction, indicating that this parameter was not a reliable way to evaluate the validity of the final MDFF result.

Figure 4.

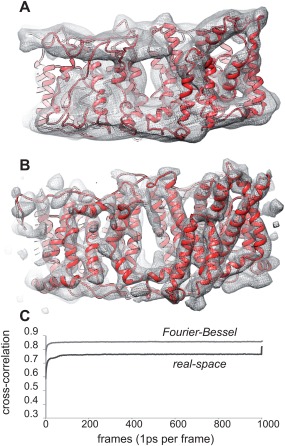
MDFF fitting to Fourier–Bessel and real‐space reconstructions. (A) MDFF model (IF/1) superimposed on the Fourier–Bessel reconstruction from Type 1 tubular crystals (see Supporting Information Movie 1 and 3). (B) MDFF model (IF/2) superimposed on real‐space reconstruction from Type 1 crystals (see Supporting Information Movies 2 and 4). (C) Cross‐correlation coefficients showing the course of the MDFF fitting to both Fourier–Bessel (light grey) and real‐space maps (dark grey). The spike at the end of the latter reflects the final energy minimization step with higher scaling factor (see Materials and Methods).

MDFF entails the use of Langevin molecular dynamics (MD) in vacuo together with additional external forces representing the experimental maps. Although atomic intra‐protein interactions are represented reasonably well by the CHARMM27 force field,39, 40 the dynamical behavior and protein–solvent interactions cannot be evaluated due to the lack of the membrane environment and the presence of artificial biasing forces derived from the map. Therefore, we performed all atom MD equilibrium simulations using explicit solvent and a membrane that incorporated the E. coli lipids used for the tubular crystals.

For the model derived from MDFF using the Fourier–Bessel map (“IF/1”, cf. Table 1), three MD simulations of 1100 ns (simulations IF/1.1–IF/1.3 in Table 2) and a combined sampling time of 3.3 µs showed substantial structural relaxation, with the C _α RMSD exceeding 5 Å (data not shown). Analysis of the per‐residue root mean square fluctuations (RMSF) indicated that primarily the loop regions (M5‐M6, M7‐M8, M8‐M9, M10‐M11, H4‐M13) were responsible for the observed changes in RMSD [Supporting Information Fig. S5(A)]. The geometries of residues in the TM helices, however, retained their α‐helical character reasonably well [Supporting Information Fig. S6(A)]. The C_α RMSD calculated for all secondary structure elements (predominantly the TM helices but also including S1, S2 and H1–H4 while excluding the loop regions, as defined in Supporting Information Fig. S3) ranged between 3 Å and 5 Å and did not appear to reach true equilibrium even after 1 μs [Supporting Information Fig. S7(A)].

Table 2.

Molecular Dynamics Simulations Performed for This Study

Namea	Conformation	Mapb	Atomsc	Lipids	Water	Na/Cl	a (Å)	c (Å)	Repeat number	Timed (ns)
IF/1.1	Inward facing	FBe	127995	445	19117	125/54	140.96	78.4	1	1100
IF/1.2									2	1100
IF/1.3									3	1100
IF/2.1	Inward facing	Frealix	153914	480	26058	154/74	145.25	89.25	1	433.5
IF/2.2									2	451.1
IF/2.3			162339	480	28861	162/82	145.25	94.25	1	433.3
IF/2.4									2	430.1
OF/1.1	Outward facing	FB	138378	450	22231	134/63	140.11	84.61	1	729.7
OF/1.2		MDFF							2	731.1
OF/1.3		AE1	146010	450	24763	140/69	140.11	89.61	1	702.1
OF/1.4									2	687.2
OF/2.1	Outward facing	Frealix	169563	482	31267	167/87	144.6	97.9	1	522.1
OF/2.2		MDFF							2	524.8
OF/2.3		AE1							3	512.1

^aModels are summarized in Table 1.

^bSummary of map and approach that was used to build the model used as starting point for the simulation (see Table I).

^cSystem composition (number of atoms, lipids, and water molecules and ions) as well as the a and c unit cell parameters for the hexagonal simulation cells varied between simulations but were kept identical for repeat simulations.

^dThe total simulated time was 9.5 µs.

Fourier–Bessel

For the model derived from the real‐space reconstruction using Frealix (“IF/2”), four MD simulations of >430 ns each (simulations IF/2.1–IF/2.4 in Table 2) indicated that the TM helices retained the secondary structure that was present in the MDFF model or sometimes gained additional helical turns during the simulation [Supporting Information Fig. S6(B)]. The TM helices themselves as well as the other non‐loop regions relaxed within the membrane environment to a moderate degree as seen in the lower structural drift [C_α RMSD ∼3 Å, Supporting Information Fig. S7(B)]. However, interhelical loops were still not well defined in the MDFF model and displayed large fluctuations, which was reflected in the corresponding per‐residue RMSF values [Fig. 5(A)], Overall, the TM helices appeared well‐resolved in the model and stable in the all‐atom simulations, whereas the conformations of the loops were less reliable. The secondary structure for IF/2 was better maintained than in the IF/1 (Fourier–Bessel‐based model) simulations. In particular, the non‐helical regions S1 and S2 near the putative substrate binding sites retained beta‐strand geometry throughout the simulation [Supporting Information Fig. S6(B)].

Figure 5.

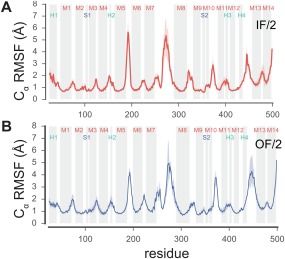
Fluctuation of residues during MD simulations. The root mean square fluctuation (RMSF) for C_α atoms was computed after superposition of all TM helices with RMSD minimization. Transmembrane helices and other secondary structure elements noted in Supporting Information Figures S3 and S4 are indicated as shaded regions. Data represent averages over equivalent simulations and over both chains of the dimer and are representative of all simulations from a given model. Heavy lines correspond to the mean whereas bands indicate an interval containing 95% of the data, as determined by bootstrapping. (A) Data from inward‐facing model based on Frealix reconstruction (simulations IF/2.1 and IF2.2, see Table II). (C) Data from outward‐facing model generated by MDFF (simulations OF/2.1, OF/2.2, and OF/2.3).

For evaluation of solvent accessibility, the MD simulations allowed mapping of the location of water molecules during the simulation. As an alternative, we also used the program HOLE, which searches for cavities within a PDB model.41 Results from the two approaches were consistent. In IF/1 and IF/2 models of Bor1p, which were MDFF fits to the two cryo‐EM maps, analyses of solvent accessibility indicated the presence of a water‐filled cavity between the core and gate domains that opens to the cytoplasmic side of the membrane (Fig. 6, Supporting Information Fig. S8). Although water was also present at lower density on the extracellular side of the protein, no clear, continuous pathway was present and these results indicate that our Bor1p structure represents an inward‐facing conformation.

Figure 6.

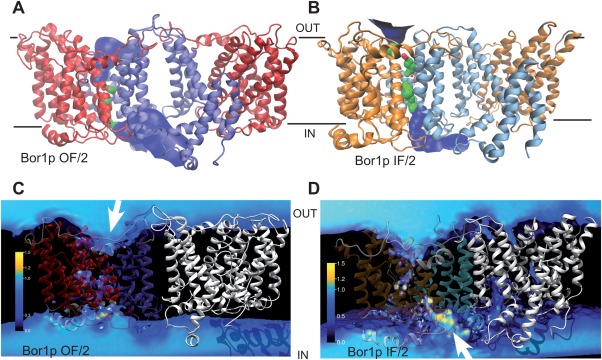
Solvent accessibility of Bor1p models. (A) Solvent accessible surface for outward‐facing model of Bor1p (OF/2) as determined by HOLE,41 which shows a funnel leading to the extracellular side of the membrane. The surface is colored blue (pore radius R > 2.3 Å), green (1.15 Å < R ≤ 2.3 Å) or red (R ≤ 1.15 Å) depending on the width of the channel at each point. The gate domain is colored blue and the core domain red. (B) Solvent accessible surface for inward‐facing model of Bor1p (IF/2) determined by HOLE. In this case, the gate domain is light blue and the core domain is orange. (C) Water density from MD simulations of the outward facing model of Bor1p as determined from the full simulations OF/2.1, OF/2.2, and OF/2.3 from both chains A and B. The density is measured relative to bulk water density at ambient conditions with the color code shown to the left. Transmembrane helices for gate and core domains are colored similar to panel A. (D) Water density from MD simulations of the inward facing model of Bor1p (last ∼100 ns from simulations IF/2.1 and IF2.2). White arrows indicate the entrance to the funnel.

Comparison of Bor1p and AE1 structures

The X‐ray structure of AE1 has been described as an outward‐facing state,13 and HOLE did indeed reveal a water cavity leading to the extracellular surface once the inhibitor molecule DIDS was removed from the structure (Supporting Information Fig. S8). We therefore wanted to compare our Bor1p structure with AE1 to seek evidence for the hypothesis that transport involves movements of the core domain relative to the gate domain. For this comparison, we aligned the gate domains of the AE1‐based homology model, which had backbone geometry virtually identical to AE1, and the Bor1p model fitted to the cryo‐EM map (IF/2). Although the gate domains (M5‐M7 and M12‐M14) aligned well, with an RMSD of 2.4 Å for Cα atoms, the core domain of Bor1p was rotated as a rigid body by ∼10° relative to AE1, with the pivot occurring near the putative substrate binding site at the interface between the half helices M3 and M10 (Fig. 7).

Figure 7.

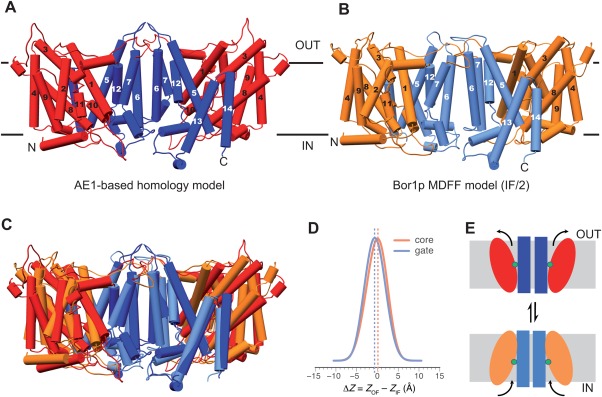
Comparison of outward‐facing and inward‐facing conformations. (A) Homology model of Bor1p obtained from MODELLER using the outward‐facing AE1 structure as a template. Transmembrane helices, which are essentially identical to those seen in the AE1 structure, are numbered according to Supporting Information Figures S3 and S4. Gate domains are colored blue and core domains are red. (B) Bor1p model (IF/2) in an inward‐facing conformation as determined from tubular crystals. Gate and core domains are colored blue and orange. (C) Overlay of outward‐ and inward‐facing conformations. The gate domains are closely aligned, whereas the core domain has a different inclination. There does not appear to be any vertical displacement of the core domain across the membrane. (D) Distribution of differences resulting from the comparison of gate and core domains in outward‐ vs. inward‐facing conformations as determined from MD simulations (see Supporting Information Fig. S9). Both the core (orange) and the gate domain (blue) shift by less than 1 Å relative to the membrane in comparing these two conformations, and even less relative to each other, confirming the lack of vertical displacement that would be expected from an elevator‐type mechanism. (E) Cartoon depicting the inclination of core domain that we propose converts Bor1p from inward‐facing to outward‐facing conformation.

Alignment of the gate domains extended across the dimer interface, meaning that the structural elements mediating the dimer in the Bor1p cryo‐EM structure were very similar to those seen in the AE1 X‐ray structure. The buried surface area for the Bor1p dimer interface (1495 Ų) is somewhat larger than that for AE1 (1036 Ų), but these contacts occur mostly between the surface loops, which are unreliable in our model. However, despite the overall similarity in this interface, there was a slight, ∼6° difference in the angle between dimers about an axis parallel to the membrane plane (Supporting Information Fig. S4), which is consistent with the membrane curvature found in the tubular crystals [Fig. 2(A)] but not in the X‐ray crystals.

Outward facing model of Bor1p

To further these comparisons, we sought to generate an outward‐facing model for Bor1p that retained structural features defined by our cryo‐EM maps, but with the outward‐facing conformation represented by AE1. Although we used MODELLER to build an AE1‐based homology model for Bor1p as a starting point for MDFF [Fig. 7(A)], this threading algorithm relied on sequence alignment and the resulting backbone was essentially identical to that of AE1. To reduce this severe model bias, we used a second round of MDFF to build an outward‐facing model from the cryo‐EM‐based models. For this procedure, we created an artificial density map from the AE1 crystal structure and used it as a template for driving the IF/1 and IF/2 models to a new conformation using MDFF, thus producing OF/1 and OF/2 models, respectively. In this way, the molecular features of the Bor1p model (based on the experimental density map) were combined with the conformation represented by the AE1 structure without having to rely solely on sequence alignment.

MD simulations were then performed on the OF/1 and OF/2 models in a system with explicit membrane and solvent (see Table 2). The overall structural drift over >700 ns, as measured by the RMSD of the non‐loop regions, approached 5 Å for OF/1 [Supporting Information Fig. S7(C)], indicating that this outward‐facing model required substantial relaxation in the membrane environment, similar to the starting IF/1 model. Furthermore, the per‐residue RMSF [Supporting Information Fig. S5(B)] and secondary structure [Supporting Information Fig. S6(C)] were similar in magnitude to the IF/1 model. In contrast, the RMSD for OF/2 remained near 3 Å [Supporting Information Fig. S7(D)] and the per‐residue RMSF and secondary structure were better behaved [Fig. 5(B)], similar to the IF/2 model. This analysis suggests that OF/2 and IF/2 models were of similar structural quality and superior to the OF/1 and IF/1 models. Analysis of the water density showed that the OF/2 model maintained an extracellular funnel through which water was able to reach the putative binding site near the center of the membrane [Fig. 6(C)]. Similar to the IF/2 model, no continuous water pathway was visible, indicating that the IF/2 and OF/2 models represent conformations fully compatible with the alternating access mechanism for secondary transporters. The OF/1 model exhibited a low‐density water pathway across the membrane, which, although probably not wide enough for bulky substrates such as borate ions, is nevertheless an indication of the lower model quality. Water accessibility of the OF/2 model was also assessed with HOLE [Fig. 6(A)], which showed a large extracellular funnel with very similar character to AE1 [Supplemental Information 8(D)].

Domain movements

To assess the movements of the domains that have to occur during the transition from inward to outward‐facing states, we tracked the center‐of‐mass of the core and gate domains during MD simulations of the IF/2 and OF/2 models. The bilayer was used as a frame of reference against which the domain movements were measured. During these MD simulations, the z positions of the domains relative to the membrane plane fluctuated by 4–6 Å around a well‐defined equilibrium position [Supporting Information Figs. S9(A,B)]. As previously seen for the elevator‐type transporter NapA,20 the equilibrium position depended on the conformation of the protein and its interaction with the membrane and may differ between inward‐ and outward‐facing conformations. To evaluate relative movements of core and gate domains, we calculated the difference in the positions for each domain, both in the inward‐ and outward‐facing simulations. By aggregating data from all of the simulations (Table 2), difference distributions were obtained that indicated very small shifts of −0.2 ± 0.0 Å (standard error of the mean) for the core and −0.6 ± 0.0 Å for the gate domain [Fig. 7(D)]. Such small shifts are not consistent with an elevator mechanism, which requires one domain to translocate across the membrane and thus exhibit larger shifts ≥ 6 Å.20

Discussion

In this work, we determined a structure of Bor1p from yeast using cryo‐EM analysis of crystalline arrays within a reconstituted lipid membrane. This structure has a resolution of 6 Å and clearly defines TM helices as well as several surface helices, making it possible to build a model in which these helices are positioned with high fidelity. Based on the alignment score of Bor1p and AE1 (P = 10^−15. 2 and 23% sequence identity) and their membership to the SLC4 family, a high degree of structural homology can be expected.36 This homology is indeed borne out by the arrangement of the 14 TM helices seen in the cryo‐EM map, which allowed us to determine unambiguously the orientation of the molecule with respect to the membrane and to fit the α‐helices of a homology model with high precision. This precision is supported by the similarity of the models obtained from MDFF using two completely independent maps generated from the two different types of tubular crystals: the helices in the two resulting models have virtually identical orientations (Supporting Information Fig. S10), with C_α RMSD of 1.9 Å. Although the surface loops are poorly defined at this resolution, the orientation and extent of the TM and surface helices are distinct and provide a strong basis for evaluating the conformation of the transporter. In MD simulations, the TM helices of the model are stable whereas the loops show considerable flexibility. Thus the structural core of the model is well defined and the observed 10° rocking of the core domain of Bor1p relative to AE1 is highly significant.

Oligomerization is a common theme for transporters and in some cases has been shown to be important for function. For transporters with distinct core and gate domains, the gate domain (variably referred to as hash or scaffold) often mediates the dimer or trimer interface whereas the core domains (also called transport or bundle) are at the periphery of the complex and thus free to move (e.g., AdiC, Glt_Ph, NapA, CitS).20, 22, 23, 42 Nevertheless, the observation of an oligomer in a crystal does not necessarily prove its existence in vivo or imply a functional significance. In both AE1 and UapA structures, the gate domain does indeed mediate a dimer interface. In the case of UapA, a specific functional role for the dimer was suggested by the observation that mutations in one monomer influenced activity of its dimeric partner.16 UraA is in the same family as UapA and, although the structure was not presented as dimeric,15 the gate domain of UraA does mediate an intermolecular contact in the crystal lattice with approximately the same geometry as the UapA dimer. Finally, the fumarate transporter, SLC26Dg, is monomeric in the crystal, but has been reported together with other SLC26 transporters to be dimeric in a lipid membrane.17, 43, 44

Interestingly, the structural elements mediating the UapA and AE1 dimers are different, but in a way that reflects the inverted repeat. In particular, M5–M7 mediate the dimer interface in AE1, whereas the pseudo‐symmetrically related M12–M14 mediate the dimer interface in UapA. Consistent with the inversion of the two pseudo repeats with respect to the membrane, the juxtaposition of helices across the dimer interface are rather similar when the two molecules are viewed from opposite sides of the membrane. However, this difference results in an ∼60° angle between the twofold‐related molecules (Supporting Information Fig. S11) and the UapA dimer is substantially more compact compared to the AE1 dimer, which may facilitate the intermolecular interactions that are reported to govern the function of UapA.16 In the case of AE1 and Bor1p, the innate similarity in the dimer suggests that this interface may have functional relevance, perhaps serving to anchor the gate domain in the membrane in order to counterbalance movement of the core domain during transport. Nevertheless, the slightly different angle of the Bor1p dimer suggests that the dimer is somewhat flexible, perhaps allowing the molecule to adapt to membrane curvature such as that seen in tubular crystals.

Our analysis of water accessibility (Fig. 6) suggests that Bor1p represents an inward‐facing state, in contrast to the outward‐facing conformation of AE1 (Supporting Information Fig. S8).13 Because both structures were solved in the presence of bound ligands, the respective conformations are likely to represent substrate bound states (DIDS in the case of AE1 and borate in the case of Bor1p). Given that substrate binding in other transporters often induces partial closure of the substrate binding site, as the molecule prepares to undergo occlusion and transition to outward‐facing state, the overall extent of the core domain rocking may be larger than the ∼10° seen in our comparison of the two structures.

The SLC4 family is associated with the APC superfamily that also includes well characterized transporters such as LeuT, Mhp1, AdiC, BetP, vSGLT.14 These transporters share related folds, and structures for several have been determined in multiple states, providing insight into the conformational changes responsible for transport.24, 25 Like AE1 and Bor1p, these transporters are distinguished by two domains that move relative to one another and in the case of Mhp1, vSGLT, and AdiC, the conformational change involves rigid‐body rotations of the substrate‐binding, core domain relative to the opposing scaffold or gate domain, though LeuT appears to have more complex movements of individual helices. Based on these observations, the alternating access mechanism for members of the APC superfamily is generally described as a rocking bundle.19, 25

UraA, UapA, and SLC16Dg transporters also belong to the APC superfamily with folds that are more closely related to AE1 and Bor1p (characterized as 7 + 7 inverted repeat topology compared with the 5 + 5 topology for LeuT, Mhp1, etc.).26 Structures of UraA, UapA, and SLC16Dg have all been determined in inward‐facing conformations and thus the conformational changes associated with transport have yet to be determined. Although the AE1 structure represents an outward‐facing conformation, differing organization of helices composing the gate domains makes their alignment imprecise and evaluation of the corresponding conformational changes difficult (Supporting Information Fig. S12). In contrast, gate domains of the more closely related AE1 and Bor1p are readily aligned, revealing rigid body movements that are similar to the rocking bundle movements observed in Mhp1, vSGLT, and AdiC (Fig. 7, Supporting Information S10). Furthermore, the MD simulations of Bor1p models in inward‐ and outward‐facing conformations showed only small (<1 Å) shifts of the domains relative to the membrane [Fig. 7(D)], thus arguing against an elevator‐type mechanism in which one of the domains translates across the membrane. For example, analogous studies of the elevator‐type NapA transporter revealed a shift of ∼6 Å for the translocating core domain and ∼–2 Å for the anchoring dimerization domain.20 Thus, although SLC4 transporters are likely to adopt additional unique conformational states in the absence of ligands, it so far appears that the rocking‐bundle mechanism may be a general property of the APC superfamily.

Materials and Methods

Purification and two‐dimensional crystallization of Bor1p

Bor1p from Saccharomyces mikatae was expressed in Saccharomyces cerevisiae under the control of the ADH2 promoter with a C‐terminal IgG affinity tag and purified as described previously.45, 46 In particular, membranes were prepared from cell lysates and the protein was solubilized in 1% n‐Dodecyl β‐d‐maltoside and bound to an IgG Sepharose affinity column. The detergent was exchanged into C₁₂E₇ while bound to this affinity column and the protein was then eluted by cleaving the tag with rhinovirus C3 protease. The eluant was then further purified by size exclusion chromatography, where it eluted in a fairly broad peak that generally contained a mixture of monomeric and dimeric Bor1p (Supporting Information Fig. S13). Successful crystallization was sensitive to the details of purification, which are described in more detail in Supporting Information.

This preparation of Bor1p was extensively screened for 3D crystallization using a variety of commercial and other screens. Conditions yielding the best X‐ray diffraction were used as starting points for producing two‐dimensional, membrane‐bound crystals suitable for cryo‐EM imaging. Two‐dimensional crystallization was then screened using a high‐throughput toolchain developed in our laboratory.28, 29 The best helical crystals were obtained by mixing purified Bor1p at 0.25 mg mL⁻¹ with Cardiolipin from E.coli (Avanti Polar Lipids) at a 0.44 Lipid‐to‐Protein Ratio (w/w) and 0.2 mg mL⁻¹ C₁₂E₇, followed by dialysis against a buffer composed of 100 mM HEPES pH7, 100 mM NaCl, 2 mM boric acid and 5% NaN₃ for 1 week at 27°C. Crystallization trials were evaluated by negative stain EM prior to being used for cryo‐EM imaging.

Imaging and 3D reconstruction

To prepare samples for cryo‐EM imaging, helical crystals were diluted 10–20× with crystallization buffer, applied to home‐made, holey‐carbon grids, blotted from the side opposite to the carbon film and quick‐frozen in liquid ethane using a manual plunging device. Images were acquired with 1–3 μm defocus on a K2 Summit direct electron detector (Gatan, Inc) in super‐resolution mode using a Tecnai F20 electron microscope (FEI Corp.) operating at 200 kV with a side‐entry, model 626 cryo‐holder (Gatan, Inc). Individual images consisted of 40‐frame movies (250 msec/frame), which were corrected for motion using the MotionCorr program.47 The movie frames were then binned to standard resolution mode, corresponding to 1.82 Å/pixel, and summed to produce 2D images used for computer analysis. Supporting Information Figure S14 shows distributions for defocus, resolution and specimen movement for the dataset.

Images of straight, helical tubes (e.g., Fig. 1, Supporting Information Fig. S2) were analyzed using Fourier–Bessel methods34 as implemented and enhanced in the graphical interface of EMIP.48 These programs facilitated the evaluation of various helical symmetries by assigning Miller indices to individual layer lines, measuring radii of peaks along these layer lines, as well as the radii of tubes in real space. Tubes were segregated into groups based on their real‐space radii and several candidate helical symmetries were established using the methods described in detail by Coudray et al.31 These methods involve analyzing peak positions and phases along the various layer lines that characterize the Fourier transforms in order to assign a self‐consistent set of Bessel orders [c.f., Figs 1(C,F)]. These candidate symmetries, defined by the Bessel orders, were confirmed by calculating phase residuals from the refinement of tube center and out‐of‐plane tilt, which depend on the symmetry assignment, but are not definitive in identifying a single solution. Finally, the correct helical symmetries for each type of tube were established by measuring the dimensions of the surface lattice from collapsed tubes and by comparing the length of the circumferential vectors corresponding to each candidate symmetry to the measured real‐space radius of each type of tubular crystal.31 Density maps were then calculated following standard Fourier–Bessel methods for each of the helical symmetries. The handedness of the structure was established by comparing the densities in the maps with homology models based on atomic structures of AE1 and UraA (see below).

For real space reconstruction, the Fourier–Bessel maps were filtered to 15 Å resolution and used as an initial model for refinement using Frealix.33 Three cycles of refinement were performed in single‐particle mode, using segment lengths of 200 Å and waypoints spaced at 70 Å intervals along the tube. Helical symmetry parameters were derived from the Bessel order assignments established during the Fourier–Bessel analysis (Δ_ϕ,Δ_t = 37.35°, 4.8Å and 38.7°, 9.97Å for Type 1 and Type 2, respectively). Orientational parameters (ϕ, ψ, θ) at each individual segment were compared with those from the entire tube. Because of the helical symmetry, the orientations at successive waypoints are expected to follow a regular pattern. Segments with anomalous orientations were flagged and were removed from the reconstruction if they represented a minority of waypoints along a given tube. Alternatively, if a particular tube had many segments with anomalous orientations, then the entire tube was discarded. After removing poorly aligned segments, an additional three cycles of refinement were performed using a 10 Å resolution cutoff for the reference, thus ensuring that the higher resolution features were not subject to artifacts due to model bias or over refinement.

Several alternative methods were used to assess the resolution of the maps. For Fourier–Bessel maps, we used the two‐fold related phase residuals, which have a maximal value of 45° for random phases. Thus, a cutoff of ∼40° was used to estimate the resolution of Fourier–Bessel reconstructions. Frealix estimates resolution by calculating the Fourier Shell Correlation (FSC) between symmetry‐constrained reconstructions calculated after dividing the data into two equal parts.33 We additionally calculated the FSC comparing Fourier–Bessel and Frealix reconstructions from the two types of tubes after applying a mask with tapered edges to select a dimer. In addition, we used ResMap to estimate the local resolutions directly from the map densities.32

For the final structure, a filter was applied to the map in order to compensate for resolution‐dependent amplitude falloff. To do so, we built a model by arranging UraA in a helical assembly in order to mimic the mass distribution in Bor1p tubes. Fourier transforms from this model and from the experimental maps were then rotationally averaged to produce 1D scattering profiles. The resolution‐dependent amplitude ratio from these profiles was used as a filter that was applied to the experimental amplitudes using SPARX routines.49 Finally, a low‐pass filter was applied with a 5‐Å stop‐band frequency.

Modeling

Four different atomic models were created for Bor1p. To start, a homology model was constructed using human AE1 (UniProtKB p02730) as a template. To build this homology model, a web frontend (http://www.ebi.ac.uk/Tools/msa/clustalo) to CLUSTAL Omega50 was used to align the sequences of Bor1p and AE1, which were then submitted together with the atomic structure for AE1 (PDB 4YZF) to an online implementation of MODELLER (https://toolkit.tuebingen.mpg.de/modeller).35, 51 For the first Bor1p model (IF/1), which was fit to the Fourier–Bessel density map, the helices of this homology model were manually adjusted using Chimera,52 followed by energy minimization using Yet Another Scientific Artificial Reality Application (YASARA) (http://www.yasara.org).53 For the second Bor1p model (IF/2), which was fit to the real‐space Frealix density map, the AE1‐based homology model was used directly. These models were then placed into the experimental density maps using SITUS,54 as a preliminary step to molecular dynamics flexible fitting (MDFF)37 as implemented in VMD55 and NAMD.38 MDFF consists of Langevin molecular dynamics with the CHARMM27 force field39, 40 for all atomic interactions and additional external forces derived from the experimental map. Our protocol closely followed the recommended settings described in the tutorial (http://www.ks.uiuc.edu/Training/Tutorials/science/mdff/tutorial_mdff-html/).37 Specifically, constraints on secondary structure, cis peptides and chirality were applied during the fitting process and the MDFF simulation was performed in vacuo for 10⁶ steps with an integrator timestep of 1 fs and a scaling factor of 0.3 for the forces derived from the map. This simulation was followed by an additional energy minimization step with a scaling factor of 2.

To generate outward facing models of Bor1p, we generated artificial density maps of the AE1 dimer at 6 Å, 7 Å, and 15 Å resolution with the MDFF plugin in VMD. The initial IF/1 model was simulated with MDFF, driven first by the 7‐Å map and then by the 15 Å map to produce the OF/1 model. Reversing the order of the two steps for the IF/1 model produced similar results. Alternatively, the IF/2 model was fitted to the 6‐Å map in a single simulation to produce the OF/2 model using the parameters described above.

Molecular dynamics simulations

Atomistic simulations with explicit solvent were performed with Gromacs 5.1.56 CHARMM‐GUI57 was used to embed an MDFF‐derived model in a model membrane, composed of a mixed 1‐Palmitoyl‐2‐oleoyl‐sn‐glycero‐3‐phosphoethanolamine (POPE): 1‐palmitoyl‐2‐oleoyl‐sn‐glycero‐3‐phosphoglycerol (POPG) bilayer with a 4:1 ratio, which approximates the E. coli lipids present in the tubular crystals. The resulting all‐atom system with explicit solvent was parametrized with the CHARMM36 force field58 and the CHARMM TIP3P water model and contained between 127,995 and 169,563 atoms in a hexagonal unit cell as described in Table 2. The equations of motions were integrated with the leap‐frog integrator with a time step of 2 fs. Production equilibrium simulations were performed in the NPT ensemble (T = 310 K, P = 1 bar), using the stochastic velocity rescaling algorithm59 with coupling time constant 1 ps and the semi‐isotropic Parrinello‐Rahman barostat60 with coupling constant 5 ps. The Verlet neighbor list was computed with a cut‐off of 1.2 nm and updated every 20 steps. Coulomb interactions were computed with the smoothed particle‐mesh Ewald (SPME) method61 with a real‐space cut‐off of 1.2 nm and a FFT grid with 0.12 nm spacing and fourth‐order spline interpolation for the reciprocal contribution. The Lennard–Jones potential was cut off beyond 1.2 nm and the force switched between 1 nm and 1.2 nm. Bonds to hydrogen atoms were constrained with the P‐LINCS algorithm (with a fourth order expansion and two LINCS iterations) or SETTLE for water molecules. Lipids are sensitive to the non‐bonded parameter settings, but we previously showed20 that these settings reproduce the original CHARMM36 values.58

A multi‐step minimization and equilibration process was used to relax the protein‐membrane systems and to achieve stable equilibrium simulations. The procedure is based on the default protocol provided by CHARMM‐GUI for lipid‐bilayer systems.57 Initial restraints and their harmonic force constant values were identical to those provided by CHARMM‐GUI: lipid phosphorus positions (1000 kJ mol⁻¹ nm⁻²), lipid chain double‐bond dihedral angles (1000 kJ mol⁻¹ rad⁻²), protein backbone positions (4000 kJ mol⁻¹ nm⁻²), and side chain carbon positions (2000 kJ mol⁻¹ nm⁻²). An initial energy minimization was carried out with restraints using the steepest‐descent method followed by conjugate‐gradient minimization until the maximum force in the system fell below 500 kJ mol⁻¹ nm⁻¹. Initial equilibration was carried out in five steps using the NVT ensemble (Berendsen thermostat) and small time steps (1 fs) followed by NPT equilibration (Berendsen barostat) using 2 fs time steps. All restraints were gradually reduced to zero over each step, except for the protein backbone positions which were left at 500 kJ mol⁻¹ nm⁻²; a full 5 ns of protein backbone restrained equilibration was performed to allow the bilayer to relax around the protein (using the velocity‐rescaling thermostat and Parrinello‐Rahman barostat). Two final equilibration steps were performed to reduce the backbone restraints to zero. This backbone‐restrained equilibration was necessary to achieve a stable system for the subsequent production simulations. These production equilibrium simulations were initiated from the last frame of the restrained run and varied in length from 433 to 1100 ns for a total simulated time of 9.5 µs (see Table 2).

Analysis of structures and simulations

Analysis of buried surface area was performed with PDBePISA.62 MD simulations were analyzed with code based on MDAnalysis63 including calculation of RMSD and RMSF and water densities. Secondary structure was assigned with DSSP,64 collected with the Gromacs do_dssp tool56 and processed with code that made use of the GromacsWrapper package (https://github.com/Becksteinlab/GromacsWrapper). Solvent accessible cavities in the model were identified based on the penetration of water molecules during the MD simulation and also using the HOLE program.41 Water densities during MD simulation were computed in the reference frame of chain A by using TM helices of chain A to superimpose intermediates in the trajectory to a common reference structure; water oxygen atoms were then histogrammed on a 1‐Å grid from simulation frames sampled every 10 ps. Chain B was also superimposed on chain A in order to double the sampling of the density. In some cases, only the last third to last half of the trajectory was used for the water density analysis to ensure that the systems were well equilibrated.

The distribution of the differences in domain positions relative to the membrane was computed as previously described.20 Briefly, the center‐of‐mass of the TM helices in the gate and core domains (excluding loops to reduce noise due to their dynamic character) were calculated relative to the center‐of‐mass of the membrane at each time step of a trajectory. The time series (Supporting Information Fig. S9) were sub‐sampled at 1‐ns intervals and processed with a Gaussian kernel density estimator as implemented in scipy.stats.gaussian_kde() (https://www.scipy.org/scipylib/) to yield smooth distributions f(Z) of the z coordinate for each domain. The joint distribution representing the difference between inward‐ and outward‐facing states, f(Z _OF – Z _IF), was calculated from a convolution of the individual distributions. The longest correlation time of the domain position data was estimated from a single exponential fit to the autocorrelation function as <199 ps. Data from all IF/2 and OF/2 simulations were used (Table 2) with data from chains A and B being derived independently and later combined. In total, the equivalent of 3.12 µs of OF (N _OF = 2 × 1559 frames at 1‐ns subsampling, with the factor 2 included to account for data from chains A and B) and 3.50 µs of IF (N _IF = 2 × 1748 frames) MD data were used. The 1‐ns sampling interval is five times larger than the correlation time so the samples can be considered independent. We crudely estimated the standard error of the mean of the joint difference distribution as $\sigma \sqrt{{N_{\mathrm{O}\mathrm{F}}}^{-1}+{N_{\mathrm{I}\mathrm{F}}}^{-1}}$ with the standard deviation of the distribution, σ, and the number of independent samples for the OF (N _OF) and IF (N _IF) simulations. For comparison of models, the RMSD was calculated by Chimera;52 both structural alignments and RMSD calculation were restricted to the C_α atoms in helices. Structures were visualized and rendered with Chimera52 or with VMD.55

Note in Added Proof

During review of this article, an X‐ray structure of Bor1 from A. thaliana was reported by Thurtle‐Schmidt and Stroud with a resolution of 4.1 A, showing a very similar backbone and dimer interface.65

Supporting information

Supporting Information Movie 1.

Supporting Information Movie 2.

Supporting Information Movie 3.

Supporting Information Movie 4.

Supporting Information Figure 1.

Supporting Information

Supporting Information