A Philosophical Framework for Integrating Systems Pharmacology Models Into Pharmacometrics

Abstract

The framework for systems pharmacology style models does not naturally sit with the usual scientific dogma of parsimony and falsifiability based on deductive reasoning. This does not invalidate the importance or need for overarching models based on pharmacology to describe and understand complicated biological systems. However, it does require some consideration on how systems pharmacology fits into the overall scientific approach.

Systems pharmacology models have received considerable attention in the past decade. A recent perspective highlighted the need to move away from a reductionist, target‐centric approach of drug development into a new holistic systems approach.1 The change in thinking aligns with consideration of the system as a whole rather than as isolated parts. The study by van der Greef and McBurney1 demonstrated the difficulty in validating a target when considered in isolation of the whole system. Indeed, inference from a model for a target based on a reductionist approach may differ considerably from a model of the same target that considers holistically the system and the myriad of interplay between its individual underpinning components.

Science dictates, however, that we systematically analyze the structure and behavior of a system. The logic most commonly applied to systematic analysis is defined in the process of deduction; a process in which the falsifiability of a proposal (hypothesis) is tested and then empirical inference about the system is gained. Popper2 describes deductive inference as the key to all empirical science, which has been the principle philosophy of biostatistics3 and represents one of the most common approaches used in pharmacometrics. This approach, however, leaves no room for constructing hypotheses and theory based on standard axiomatic principles and observations. It also leaves no room for the action of nonfalsification of a hypothesis. Of note, Fisher4 was a strong protagonist for considering inference from an experiment as aligning with inductive logic because the inference would be used in a setting other than which it was tested. His approach argues that if it were only used in the setting it was tested then it would be of little value.

The purpose of this article is to provide a philosophical framework for considering the place of mechanistically driven systems models in pharmacometrics. Pharmacometrics over the years has been heavily led from a statistical standpoint due to the complexity of nonlinear mixed effects models, which has focused, appropriately, on data analysis. The new kid on the block is systems pharmacology, although complementary to data analysis, it does not naturally fit into the data analysis framework of hypothesis testing, which is the underpinning philosophical basis of many frequentist statistical applications. The complementary nature occurs by virtue of the combination of advanced statistical techniques with advanced mechanistic understanding. The clear benefits of linking wet lab (data generation) with dry lab (hypothesis generation) has been described before by others (see for example the early descriptions by Kitano5, 6). Despite the apparent fit between these two approaches, practitioners are often entrenched in the deductive framework.

Therefore, there is a tension between the reductionist (principally deductive) and holistic (principally inductive) approaches in pharmacometrics.7 The strong historical favor for the deductive approach with testable data‐driven models has led us to believe the aphorism “all models are wrong…,” which is then widely applied to all models.

Why some models may be wrong

We are told, “all models are wrong” – but why are they wrong? George Box wrote “All models are wrong but some are useful” in a Technical Report in 1979.8 In his report, Box referred to the ideal gas law $PV=RT (Pressure\times Volume=R\times Temperature)$ as being a good approximation to the true system. The approximation was based on kinetic assumptions relating to the mass of the gas particles and their collision processes. Since publication, this statement has been quoted extensively (7,020 results in Google Scholar) and particularly in the pharmacokinetic‐pharmacodynamic and pharmacometric literature (and arguably most PhD theses in the discipline).

The question arises as to why all models are wrong, and perhaps this statement has been taken too literally. Here, four reasons are proposed why some models may be wrong:

1. Because the model is linear (and life is not linear).

2. Because the model is built from observed data and conditions and fails to accommodate the unobserved (latent) variables.

3. Because unanticipated recursion is present.

4. Because the model is a simplification based on an approximation.

A further layer to the four listed reasons implies that a model that is developed and “right” for one purpose may not have applicability (i.e., be “wrong”), for another purpose. This will be evident in all of the reasons explored here and relates to how the model is built, that is whether the model is built to describe a particular dataset (data analysis) y or is built to describe a system from which a dataset may arise (systems pharmacology). This difference is the cornerstone of the link between data analysis and systems pharmacology.

Linearity

Linearity and normality are the key to simple inferential regression analyses. These systems solve readily without the need for complicated methods and high‐powered computing. However, we know that life is seldom linear, albeit a linear approach is a common and acceptable approximation to many systems. I quote Box “Equally, the statistician knows, for example, that in nature there never was a normal distribution, there never was a straight line.”9 Any system that has a finite boundary on a response variable or a parameter will show, at the boundaries, evidence of nonlinearity.

In pharmacology, we are reminded by the law of mass action that governs receptor‐binding interactions (an initial exposition by Hill10 was instrumental in our understanding). These reactions follow a rectangular hyperbola with asymptotes at ‐ $K_A$ (the equilibrium dissociation constant for the ligand A) and at the maximum effect (typically occurring at maximal occupancy). Because most receptor‐ligand interactions are governed by these processes, which are evidently nonlinear, then linearity is only ever an approximation to the true state.

A common approach to linear models lies in the disease progression framework. Here, the duration of observation, while long (often years), is much shorter than the life span of the system. Therefore, a linear approximation to the disease process often provides a reasonable approximation. However, these models will fail to predict at limits of the process in which failure of complex biological processes occur and a rapid decline in health is evident.

Latent variables

Any experimental setting will yield a finite array of variables and conditions under which the experiment was studied. This will, therefore, yield a subset of the whole set of the variables (and conditions), which may influence the system. There are likely to be variables that are not observed (and are therefore latent) that may influence the system, either conditionally on an observed variable or independently and directly on the dependent variable (observations). Box11 and later Sheiner12 (who wrote “Analysis of a learning trial proceeds by building a probability model of the relationship between outcome variables on the one hand and exposure and prognostic variables on the other, taking into account the intrasubject correlation of responses due to unmeasured individual prognostic features.”) both recognized the implications of unmeasured variables. Therefore, any regression analysis should, but usually cannot, consider the full model where:

$$\mathit{y}=f\left({\mathit{\theta }}_k,{\mathit{x}}_k, {\mathit{\theta }}_{k^{\prime }}, {\mathit{x}}_{k^{\prime }}\right)+\mathit{\varepsilon }.$$

Here, $\mathit{y}$ is a $n \times 1$ vector of observations, ${\mathit{\theta }}_k$ is a $k\times 1$ vector of parameters that link the observed explanatory variables ${\mathit{x}}_k$ (of dimension $n \times k$) to the response; ${\mathit{\theta }}_{k^{\prime }}$ is a $k^{\prime }\times 1$ vector of parameters that link the nonobserved variables ${\mathit{x}}_{k^{\prime }}$ (an $n \times k^{\prime }$ matrix of latent variables) to the response (see Figure 1) and $\mathit{\varepsilon }$ is a vector of normally distributed random variables with expectation of zero. Because the latent variables either may independently or via dependence structures with other variables influence the response observation, then any model based on $k$ observable variables may lead to wrong conclusions based on extrapolation, although it may be useful for interpolation.

Figure 1.

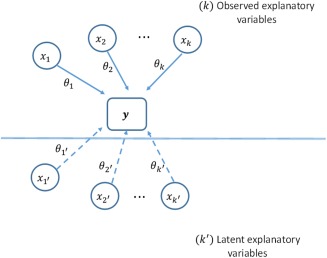
The response variable vector y is observed. There are $k$ explanatory variables (covariates) { ${\mathit{x}}_1$, …, ${\mathit{x}}_k$} that are observed and a model is built that defines the relationship with parameters {θ₁, …, θ_κ}. We see that there are also $k$′ latent variables with associated parameters. The model based on ${\mathit{x}}_k$ may fail to extrapolate beyond the current experiment due to the unforeseen influence of the latent variables.

Recursion

Here, recursion is used to describe a process in which an object is defined in terms of itself. The simplest version of recursion occurs in pharmacological systems in which the object (a state) is subject to a feedback loop that is initiated by the state. Natural loops and feedback are common in biological systems (see, for example, the coagulation system13; see Figure 2 for a conceptual schematic). Approximations to these systems by empirical data analysis approaches are liable to misspecify the system and lead to erroneous interpretation for both interpolated and extrapolated predictions.11 These systems cannot be defined by the observations that are made in isolation of the mechanism of the system.

Figure 2.

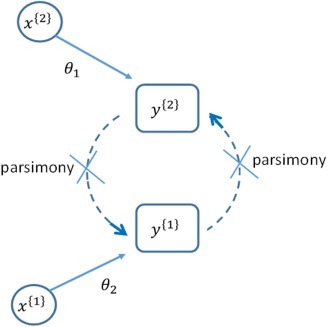
Two response variables are observed y ⁽¹⁾ and y ⁽²⁾. The empirical analysis, driven by parsimony, does not consider that they are linked (recursively) and the subsequent analyses treats them as independent variables with explanatory variables $\mathit{x}$ ⁽¹⁾ and $\mathit{x}$ ⁽²⁾ that drive their respective responses of interest. It will be seen that when the mechanism is ignored that the variables $\mathit{x}$ ⁽²⁾ will be seen to influence y ⁽¹⁾ and vice versa.

If we take a simple example, where there are two response variables for instance insulin and glucose. This example is chosen because the mechanism of action of insulin is not disputed and the mechanistic framework of its actions has been well described. We know that insulin decreases blood glucose concentration and in converse a glucose load increases endogenous plasma insulin concentration. Because, in the diabetic state, the dose of insulin is governed by the physician, then patients with higher fasting blood glucose will receive larger insulin doses. An empirical analysis of these data will find a positive correlation between fasting blood glucose concentration and insulin dose (Figure 3). It might be argued that this finding is trite, as the mechanism is so well known that this is a predictable feature. However, if we imagine another setting in which a recursion was not anticipated, then this finding, in isolation of understanding this simple recursive system, would yield the wrong interpretation that insulin dose (the independent variable) increases blood glucose concentration (the dependent variable). The history of science is littered with examples in which systems were mechanistically misunderstood leading to incorrect inference (e.g., whether the earth orbits the sun or vice versa). The key to interpreting this simple finding lies in anticipating what we think might happen from an experiment. If we see a response that is contradictory to expectation, then we must either review our expectation or be suspicious that an unexpected recursion is present in the system.

Figure 3.

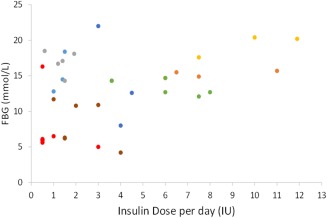
Fasting blood glucose (FBG) is plotted against insulin dose per day. Different colors represent different patients. Because there is a temporal delay in the recursion (FBG was taken prior to the insulin dose being calculated) then the expected trend (that insulin reduces FBG) is reversed and the apparent controllable (independent) variable is dependent on the observation (dependent variable). These data arise from a study on insulin dosing, Ethics (University of Otago Human Ethics Committee [HD16/013]).

Other examples have been clearly determined. A simple but compelling example was described in relation to the link between dose and clearance (CL) for drugs that undergo therapeutic drug monitoring.14 In their work, because the dose is adjusted to achieve a prespecified target concentration, then a natural correlation would seem to be evident between CL and dose, which would then support an erroneous nonlinear model on CL. Further, excellent examples are provided by Lendrem et al.,15 in which they show that intuition‐based designs yield models that fail to deliver appropriate predictions.

Approximations

Data‐driven analysis requires the investigator to assemble a parsimonious model that is identifiable given the available input information and observation data. Parsimony may be driven from (1) the data or from (2) the known mechanism. The former is often (but should not be) confused for the latter. (1) We see the application of the Michaelis‐Menten equation (written in terms of an Emax model) almost ubiquitously for any circumstance in which a drug causes an effect, even if there is an absence of an obvious application of receptor occupancy. In this case, the relationship, while useful, is empirical and serves only to allow for nonlinearity in the response variable over a range of the observable covariates. However, as with all empirical models, all approximations are only good over a (limited) range of the response values and experimental conditions. (2) In other circumstances, the approximations arise via simplification of a known mechanistic model, for instance, application of the Michaelis‐Menten equation for describing target‐mediated drug disposition in circumstances when rapid equilibrium binding is assumed. The approximation can be tested (see for example Ma16) in circumstances when the underlying mechanism is known, but cannot be tested when the approximation is applied in the absence of known mechanism. The key difference between these approaches lies in the deductive approach to testing the model. In approach (1), it is a hypothesis test of fit of the model to the data, whereas in approach (2), it is a test of the applicability of the approximation itself. Although each yields a decision, the decisions are disparate and only the latter yields mechanistic inference.

Why some models may not be wrong

A systems model‐based approach that avoids these issues with empirical models may provide the basis for understanding the system as a whole. In 1967, George Box17 stated, “If we can know mechanistically how a system works and can describe this mathematically then we can use this to predict the behavior under future experimental designs.” It is possible that models that are strongly mechanistically based will avoid the four pitfalls faced above. Certainly, issues around the assumption of linearity, understanding recursive principles that underpin the data structure, and quantification of the limitations with approximations are (in theory) knowable. Issues with latent variables remains unquantified (and perhaps unquantifiable) but may be implicitly handled by considering the system as a whole rather than just a portion of the system that pertains to the observable data.

There are many examples of the mechanism‐driven approach in pharmacometrics. Two examples are described here, which represent different approaches to the problem of identifying mechanism. In the first approach, we see that a mechanism is derived from theory and experimental evidence and is then transformed into a mechanistically driven mathematical model, in this sense, the model was constructed to describe the observations. In the second example, we will see that a fully constructed mathematical model of a system that exists already is used to describe a mechanism that is contained within itself, here the full model contains considerably more structure than is needed to describe the observations at hand.

Example 1

In the first example, the theory of mass action was applied by Mager and Jusko18 to binding of drugs to their target with the prospect that this would provide the basis for understanding their pharmacokinetics, termed target‐mediated drug disposition (a review of this has been described by ref. 19). In the work of Mager and Jusko,18 a theoretical binding model was proposed under the target‐mediated drug disposition framework. This model was developed based on the standard receptor‐binding theory and assessed to understand its implications using simulations. This work demonstrated that a data driven, noncompartmental analysis of the results led to conclusions regarding dose dependence of volume of distribution at steady state and CL that differed depending on the simulation example. This was corroborated in their work with clinical data. The underlying theory of their work is a relaxation of the assumption that the free concentration of ligand ( $C$) greatly exceeds the number of receptors (a function of maximum effect [E_max]) and, hence, binding to the receptor does not normally substantively affect the free concentration (e.g., as per ref. 20). Relaxation of this assumption is a natural kinetic extension of binding and is further described by Cao and Jusko21 to provide the mechanistic basis of target‐mediated drug disposition. Of note, the full kinetic expression of the binding process is identical to the full kinetic model of standard receptor binding. Importantly, these models are based on theoretical constructs of the activity of drugs, which is borne out by experiments. Once the full kinetic framework of binding is established, then it is a matter of choosing an approximation of the system under assumptions of steady state or equilibrium binding (see ref. 16 for discussions on various approximations) that are most well suited to describe the observed data.

Example 2

In the second example (from ref. 22), an existing systems pharmacology model for coagulation was built based on literature evidence13 and later updated.23 This model contains 73 ordinary differential equations and 178 parameters. The research question being asked was related to the recovery of fibrinogen after snakebite by Australian elapid snakes. The input data was binary (bite or no bite) and the observation data consisted of plasma fibrinogen concentrations. The full coagulation model is unidentifiable under this input‐output model structure and, hence, cannot be used for estimation purposes. However, a submodel, relating to snakebite and fibrinogen, is contained within the full model and, therefore, two approaches to modelling the data were possible: (1) develop an empirical/semimechanistic approach based on turnover models and E_max functions, or (2) develop a mechanistic approach by extracting the submodel from the full model. The latter method was chosen and the full model was lumped from 73 to 5 ordinary differential equations using proper lumping (readers are referred to ref. 24 for an overview and application of proper lumping). The submodel was formed and a prediction from the model provided a reasonable prediction of the data. Once the model was extracted, the parameters were estimated based on the data and the model provided a good overall fit.

Both examples require simplification from a fuller model to a submodel (although the scale of simplification is vastly different). However, in both cases, the starting point was a credible mechanism and the final outcome was a model that describes the data accurately and that can be used for inductive inference.

It is important to note that the examples described here do not represent an exhaustive list of potential applications of systems models. Another, and important, use of systems models lies in their ability to direct future research. Currently, when the link between input and output is convoluted, it may be very difficult to set up experiments based on reductionist approaches to assess potentially important mechanisms. Systems models can be used in a pseudo‐deductive manner by eliminating those mechanisms that are not compatible with known data. The recent work of Shivva et al.25 provides an example in which mechanisms relating to submodels were turned on and off to determine the plausible overall mechanistic structure that most closely aligned with their data for absorption of ketones.

The science of pharmacology, and thereby pharmacometrics, should strive to understand, quantify, and capture in mathematical models the underlying mechanisms and biological processes, even if we have little hope (now) of identifying every nuance of the underlying process.

Systems pharmacology models and science

System pharmacology models provide a logical framework for identifying and understanding the mechanisms that underpin drug actions. This process is largely based on inductive inference (i.e., the construction of a framework that provides the scaffold for conjecture and hypotheses that themselves may be subjected to deductive inference). This framework, therefore, does not follow the traditional deductive processes outlined by Popper.2

In contrast to the Popper2 approach, George Box9 proposes that science should be a continual deductive‐inductive cycle in which a hypothesis can be falsified (or not) and modified based on deductive inference. Although not explicitly described in his work, this leaves the opportunity for the hypothesis to remain unchanged if it were not falsified by a “reasonable experiment.” In so doing, strengthening our resolve in our hypothesis. It is therefore expected that the inference gained from failing to falsify is a form of inductive reasoning that scientifically underpins the model and its inferences.

Of importance, here, a “reasonable experiment” is defined as one that has been designed to provide a good test of the hypothesis. Some contention has arisen by the erroneous assumption that any regression analysis based on observational data is sufficient to be deemed a reasonable experiment and, hence, hypotheses are often incorrectly falsified or not falsified based on inadequate scientific reasoning. Anderson and Holford26 raise an interesting case in which they argue that the precision with which the allometric exponent $(=3/4),$ which arises from theory, can be estimated, is generally so poor that a typical pharmacokinetic study may not be able to distinguish three‐quarters from two‐thirds or indeed one. The allometric exponent is used to scale $CL$ to a standard size, typically with the following form:

$$CL=\theta \times {\left(\frac{WT}{W{T}_{ref}}\right)}^{3/4}$$

where $\theta$ is the typical value of $CL$ for an individual of the reference $WT (\mathrm{i}.\mathrm{e}., W{T}_{ref})$, and $WT$ is total body weight. Here, Anderson and Holford26 define “a typical pharmacokinetic study” as a poor experiment for this type of deductive reasoning.

A systems pharmacology model, based on deductive reasoning, is not classified therefore as traditional science. However, if we inductively approach the thoughts of Box9 and Sheiner12 to a logical conclusion, then systems pharmacology provides the overarching mechanistic framework from which individual experiments of interest can be resolved. In this framework, the individual components of a systems pharmacology model are amenable to falsification. However, in contrast with the Popper2 view, a failure to falsify can serve as probabilistic evidence in support of the overarching model. Here, we can say that a failure to falsify satisfies the overall model on the basis that the model itself represents what we believe to be the current state of truth (Figure 4).

Figure 4.

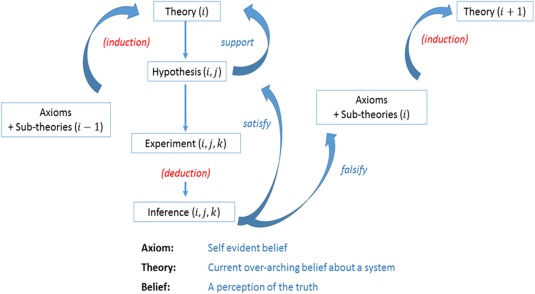
A schematic of the inductive‐deductive reasoning that leads to the development and evaluation of systems pharmacology models. In this schematic, the systems model is described as a theory. The theory is developed iteratively (the i^th iteration is shown) and comprises axioms and many sub‐theories that can serve as hypotheses (the j^th hypothesis is shown). Each of these hypotheses is amenable to falsifiability, which leads to updating the subtheories or support for the existing structure. A failure to falsify is defined as satisfying. Note the axioms remain unperturbed by the cycle.

It is clear that building models based on strong mechanistic axioms and testable subtheories provides a rational basis for constructing a mechanistically relevant mathematical representation of a system. The basis of this model can then be used to provide the underpinning mechanism that avoids the shortfalls of the four issues that face empirical modelers.

A controversy that has faced systems pharmacology models is their (often) extreme size with hundreds of differential equations and hundreds to thousands of parameters. Any such system is defined as a supersaturated system (i.e., one where the number of parameters greatly exceeds the available data) and is typically depicted in pharmacometrics as having excessive degrees of freedom. Such a system can therefore describe almost any observation. Here “almost” is the key distinction, as although, in theory, any observation could be described, the nature of systems pharmacology models means that some sets of conditions, or parameter values, are impossible due to system constraints. For example, parameter values being positive or the more subtle but important issue that only some regions of the parameter space provide settings that are compatible with life. A simple example arising from the insulin‐glucose system. If we consider a system in which the half‐life of endogenous insulin was 1 day and the half‐life of glucose 1 hour, then a glucose meal would result in severe, potentially fatal hypoglycemia.

Nevertheless, despite there being a constrained range of plausible parameter values, the issue remains that systems pharmacology models are grossly underdetermined (from an available data perspective) and, hence, the parameters are unidentifiable. This latter claim is of course based on the eye of the beholder. Let us consider the following simple model:

$$y\left(t\right)={y_{0}e}^{-{(k}_1+k_2).t}.$$

It is straightforward to see that this model is not identifiable as there are an infinite number of values that $k_1$ and (therefore) $k_2$ can take that solve for $y$ (see Figure 5 a). However, if we apply mechanism to this expression and apply the rate constants to the elimination of a drug via two pathways, and we can measure either each pathway separately or one pathway and the sum of both pathways (for instance, if we observe both the central and an output compartment for one of the routes), we can see that the system is now globally identifiable (see Figure 5 b).

Figure 5.

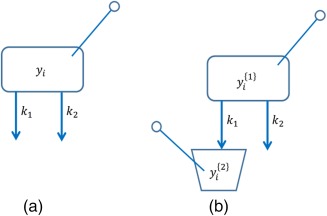
In schematic (a) (left side) there are two first‐order elimination processes from a single compartment which is observed. This model is not identifiable. In schematic (b) (right side) adding an observation compartment for the elimination via $k$ ₁ yields a globally identifiable model.

Large models, therefore, are not obviously identifiable or not identifiable by visualization of a realization of the structure, or based on the number of differential equations or parameters. Rather, it is based on whether a reasonable experiment can be conducted that can render the system to be identifiable. Another approach is to let the data determine identifiability during the modelling process. Although outside the scope of this article, approaches in mathematics for rank reduction during numerical analysis, typically based on Monte Carlo sampling to explore the posterior distribution, can naturally accommodate issues with identifiability.27

CONCLUSION

Models that are constructed to describe a system and its underpinning mechanistic structure holistically are likely to provide a more sound starting position for future interpretation and inference. The shortfalls that occur using reductionist platforms are potentially serious unless they align with knowledge of the bigger system. It is prudent to note, however, that we cannot hope to know mechanism perfectly and therefore all models have the capacity to be both useful and potentially incorrect. The benefit of falsifying and importantly failing to falsify provides the opportunity for future growth and learning.