Evidence and Counterevidence in Motion Perception

Abstract

Sensory neurons gather evidence in favor of the specific stimuli to which they are tuned, but they could improve their sensitivity by also taking counterevidence into account. The Bours–Lankheet model for motion detection uses counterevidence that relies on a specific combination of the ON and OFF channels in the early visual system. Specifically, the model detects pairs of flashes that occur separated in space and time. If the flashes have the same contrast polarity, they are interpreted as evidence in favor of the corresponding motion. But if they have opposite contrasts, they are interpreted as evidence against it. This mechanism provides an explanation for reverse-phi (the perceived reversal of an apparent motion stimulus due to periodic contrast-inversions) that is a conceptual departure from the standard explanations of the effect. Here, we investigate this counterevidence mechanism by measuring directional tuning curves of neurons in the primary visual and middle temporal cortex areas of awake, behaving macaques using constant-contrast and inverting-contrast moving dot stimuli. Our electrophysiological data support the Bours–Lankheet model and suggest that the counterevidence computation occurs at an early stage of neural processing not captured by the standard models.

Introduction

Successful discrimination of sensory inputs requires a stage at which the net sensory evidence is evaluated. Most models of motion discrimination, for example, feature a final stage at which the evidence for leftward motion is subtracted from that for rightward motion (Reichardt 1961; Adelson and Bergen 1985; van Santen and Sperling 1985; Johnston and Clifford 1995). This “opponency” stage for motion discrimination is thought to be situated in the middle temporal (MT) area of the primate brain (Snowden et al. 1991).

Optimally, the sensory evidence that is compared at this stage should reflect not only the evidence in favor of either interpretation, but also the evidence against it. The distinction between these 2 types of evidence is the core difference between 2 otherwise similar models of motion detection, the Mo–Koch and the Bours–Lankheet models (Mo and Koch 2003; Bours et al. 2009). These 2 models are similar in that they measure spatiotemporal correlations between separate, half-wave-rectified detectors of the light and dark parts of the visual stimulus, analogous to the ON and OFF channels in primates (Schiller 1995; Westheimer 2007). Furthermore, both models provide explanations for the reverse-phi illusion, that is, the reversal of perceived direction in apparent motion displays of which the contrast polarity is inverted from one frame to the next (Anstis 1970), but they do so in ways that highlight the distinction between counterevidence and evidence-only models. In the Mo–Koch model, a detector whose output is enhanced by constant-contrast motion in one direction is equally activated by a contrast-inverting stimulus moving in the opposite direction. In other words, contrast-inverting motion provides evidence in favor of the opposite direction. In the Bours–Lankheet model, however, a detector tuned to constant-contrast motion in one direction is suppressed by contrast-inverting motion in the same direction, that is, the contrast-inversion indicates evidence against the occurrence of that particular motion.

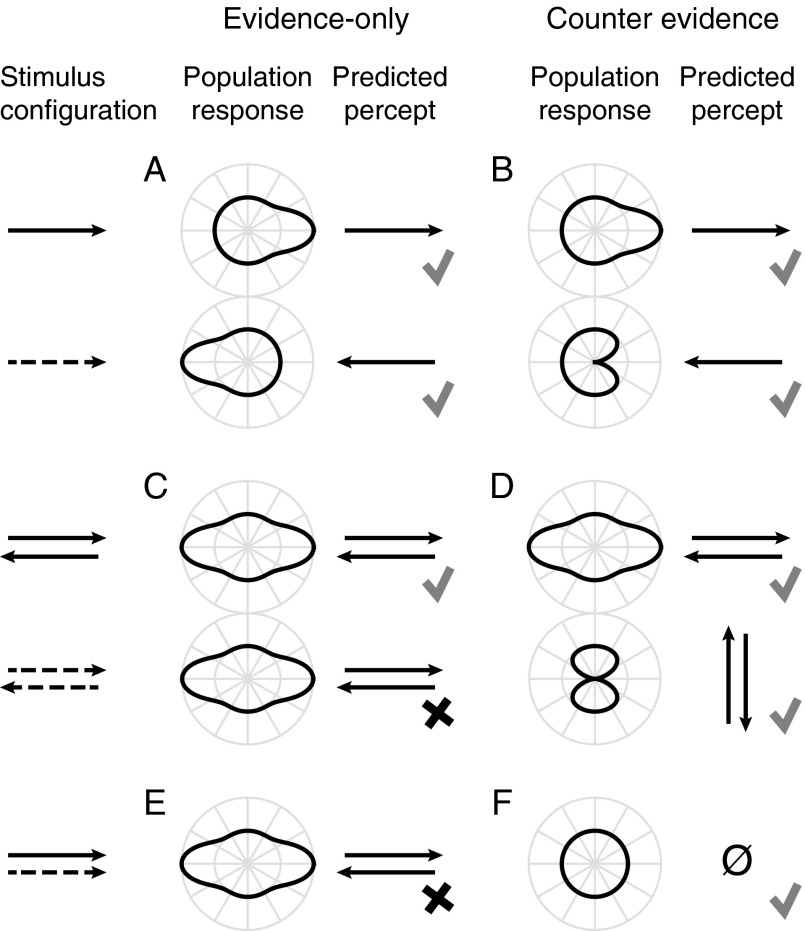
When only 2 directions are considered, the difference between “evidence” and “counterevidence” may not be immediately clear, for, by nature of the subtractive opponency, any evidence in favor of one interpretation is functionally equivalent to evidence against the alternative. However, the difference is easily seen when considering the response of a population of motion detectors tuned to all directions on the circle. The published formulations of the Mo–Koch and Bours–Lankheet models discriminate between left and right only; we extended these one-dimensional models to two dimensions by assuming a regular fall-off of sensitivity from the preferred direction for each detector. Figure 1A shows the hypothetical relation between the population response curves to constant-contrast motion (top) and to inverting-contrast motion (bottom) under the evidence-only assumption of the Mo–Koch model. If, as predicted by Mo–Koch, the phi response to a direction is identical to the reverse-phi response to the opposite direction, the curves should be rotated by 180°, as depicted. Figure 1B shows the tuning curves to constant- (top) and inverting (bottom)-contrast motion under the counterevidence hypothesis of the Bours–Lankheet model. Here, the inhibition by inverting-contrast motion causes a trough in the response at the direction where a peak is observed for constant-contrast motion, resulting in the kidney-shaped population response curve depicted in Figure 1B (bottom). A subsequent step of opponency, for example, by calculating the vector average of the population response curve, would lead to predicted percepts that are consistent with phi and reverse-phi for both models.

Figure 1.

(A) The evidence-only hypothesis predicts that the population response curve to inverting-contrast motion (dashed arrow) is the same but 180° rotated compared with the curve for constant-contrast motion in the same direction (solid arrow). (B) The counterevidence hypothesis predicts that the response to inverting-contrast motion has a trough where the peak is for constant-contrast motion. Through opponency (e.g., by taking the vector average of the population response) both models correctly predict the phi and reverse-phi motion percepts (indicated with check marks). (C‒F) Review 2 psychophysical experiments by Bours et al. (2007). (C) Evidence-only predicts a horizontal transparency percept in displays of overlapping left and right motion of inverting-contrast. (D) However, observers perceived motion that was orthogonal to the 2 components. (E) According to evidence-only, 2 rightward motion components—one of constant contrast, the other inverting—are perceived as horizontal transparent motion. (F) Instead, observers perceived no net motion in such a stimulus. (C‒F) These observations are consistent with the use of counterevidence (check marks) but not with the evidence-only hypothesis (x marks).

Two psychophysical observations provide support for the notion that counterevidence is used in visual motion detection. It is well known that 2 superimposed sets of dots that move in opposite directions lead to a percept of transparent motion where one dot field appears to slide over the other (Qian et al. 1994). Bours et al. (2007) asked what would happen if the dots flipped their contrast polarity from frame to frame. The evidence-only model predicts that the transparency percept should remain unchanged, because of the equivalence of phi motion in one and reverse-phi motion in the opposite direction. This prediction is illustrated in Figure 1C for the left and right motion using a population response curve. For both constant-contrast and inverting-contrast motion, this curve is elongated in the directions of the 2 components, which leads to a percept of transparent motion (Grunewald and Lankheet 1996; Treue et al. 2000). The counterevidence model, however, predicts a different percept for inverting-contrast motion. Because the horizontally moving inverting-contrast components inhibit the detectors tuned to their directions, the population response adopts a figure-eight shape that is taller than it is wide (Fig. 1D). Hence, the counterevidence model predicts that transparency should be seen vertically. The behavioral data by Bours et al. (2007) confirm this hypothesis. In an additional experiment, two stimuli, one of constant and one of inverting-contrast, that both moved physically (not perceptually) in the same direction were superimposed. The Mo–Koch model predicts that transparent motion should be seen in this configuration (Fig. 1E). Instead, Bours and colleagues found that all net motion was abolished, consistent with the counterevidence prediction (Fig. 1F).

In the present work, we compare and contrast the counterevidence and evidence-only models by measuring tuning curves to constant-contrast and inverting-contrast motion of motion-sensitive neurons in the primary visual (V1) and MT cortex areas of the macaque and comparing them with the predictions shown in Figure 1A,B. The mean tuning curves of a sample of single neurons provide an approximation of the mean population response to a single direction (Pouget et al. 2000). We targeted V1 because this is the stage at which the ON and OFF channels are thought to fuse (Schiller 1995; Westheimer 2007). We found the tuning curves in this area to be consistent with the counterevidence hypothesis, that is, the measured tuning curves resembled the predicted population tuning curves in Figure 1B more than those in Figure 1A. We targeted MT because its activity is known to be closely linked to motion perception (Parker and Newsome 1998). Surprisingly, tuning curves in MT corresponded most with the evidence-only prediction (Fig. 1A). We further show how this seeming inconsistency could be resolved with a nonlinear summation of the responses of the V1 neurons. Taken together, our data provide evidence for the view promoted by the Bours–Lankheet model that interesting inferences with striking perceptual consequences occur at the earliest stages of motion processing based on the conceptual distinction between evidence and counterevidence.

Materials and Methods

Subjects and Surgical Preparation

The experiments involved 3 adult Macaca mulatta males: MM, MY, and MN. Experimental and surgical protocols were approved by the Rutgers University Animal Care and Use Committee and complied with guidelines for the humane care and use of laboratory animals of the National Institutes of Health. All surgical procedures were conducted under sterile conditions using ketamine-induced isoflurane anesthesia followed by combined ibuprofen and morphine analgesia. We implanted custom-made titanium head posts and high-density polyethylene recording chambers normally to the skulls, dorsal to the expected location of MT (MM and MN).

We implanted a floating microelectrode array (Microprobes) in the left V1 of MM and 2 such arrays in the left V1 of MY. During this procedure, we created a craniotomy and a durotomy, slowly lowered the arrays into the exposed cortex using a micro-positioner, attached the wires to the edge of the craniotomy using Vetbond tissue adhesive, and covered the entire craniotomy first with a dural growth regeneration matrix (Duragen, Integra), and then with bone cement. Connectors (Omnetics) were placed in a custom-made, tamper-proof, polyethylene chamber affixed to the skull with dental cement.

Electrophysiology

To record from area MT, we penetrated the dura mater with a stainless steel guide tube before each daily recording session to gain access to the cortex. We then used a micro-positioner (NAN Instruments) to lower epoxylite-coated tungsten electrodes (1–2 MΩ at 1 kHz; Fred Haer Co.) through the guide tube into the cortex. We identified area MT on the basis of its estimated anatomical location from structural MRI scans, the high fraction of direction-selective cells as assessed by the response to a circular-path motion stimulus (Schoppmann and Hoffmann 1976; Krekelberg 2008), the small size of the receptive fields (RFs) relative to the neighboring medial superior temporal area, and the contralateral location of the RF centers as mapped with an automated sequence of localized motion pulses (Krekelberg and Albright 2005). The mean RF eccentricity of the MT neurons that were included in this study was 6.2° (SD 4.2) for MM and 2.5° (SD 1.6) for MN.

We recorded from area V1 using permanently implanted floating microelectrode arrays (1.2 × 3.4 mm², 32 electrodes with lengths between 0.6 and 1.5 mm and 0.8–1 MΩ impedance at 1 kHz; Microprobes). MM's V1 RFs were located approximately 2.5° below fixation; those of MY 1.5° below fixation and 2° contralateral.

We digitized (14 bits at 25 kHz) the band-passed (Butterworth, 120 Hz at 12 dB/octave to 6 kHz at 24 dB/octave) electrical signals using an AlphaLab recording system (Alpha Omega Co.). Offline, we detected action potentials by thresholding the voltage trace at 5.0 (MT) or 3.5 (V1) SDs from the mean. We decomposed the waveforms into a wavelet-based feature space (Quiroga et al. 2004) and used KlustaKwik (Kadir et al. 2014) for automated clustering. The resulting clusters were checked and fine-tuned manually using custom-made cluster and waveform visualization software.

Fixation Task

We measured eye-positions using infrared video eye trackers (EyeLink, SR Research). Both eyes of MM and MY were tracked at 500 Hz. The left eye of MN was tracked at 1000 Hz. The monkeys received juice rewards for maintaining their gaze within 1.5° (MM) or 2.0° (MN, MY) from the fixation marker. Whenever fixation was interrupted, the trial was aborted, the data excluded from analysis, and the stimulus-condition repeated at a later time.

Visual Apparatus

We used Neurostim (http://neurostim.sourceforge.net, last accessed September 22, 2015) on a computer with an NVidia 8800 GT graphics card to display stimuli on a 40 × 30 cm CRT monitor (Sony GDM-520) at a vertical refresh rate of 150 Hz and a resolution of 1024 × 768 pixels. The screen was at a distance of 49 cm (MN) or 64 cm (MM and MY) and had a calibrated linear luminance range between 0.5 and 60 cd/m².

Visual Motion Stimuli

Most studies that investigated reverse-phi typically used unlimited lifetime dots or grating stimuli (e.g., Krekelberg and Albright 2005) whose contrast was inverted with each motion step. Such stimuli, however, provide a mixture of inverted-contrast correlations (between one frame and any odd number of frames later) and constant-contrast correlations (between frames separated by any even number of frames). As a consequence, such stimuli cannot fully isolate same and opposite-contrast motion signals and leave open a number of trivial explanations of the reverse-phi illusion (Lu and Sperling 1999).

Here, we used a variant of the single-step dot lifetime (SSDL) stimulus paradigm (Morgan and Ward 1980) that is generalized to the time domain by the use of multiple, uncorrelated SSDL components that are temporally interleaved (Bours et al. 2007, 2009). As in all SSDL stimuli, each dot was displaced with a predefined horizontal and vertical offset, and then randomly refreshed, that is, randomly repositioned within the aperture on the next instance. The advantage of this method over the use of standard SSDL stimuli is that it allows the experimenter to set the delay between the first and second instances of the dots to any multiple of the monitor's frame duration by interleaving any number of stimulus components. To clarify, consider the example of an interleaved-SSDL stimulus with 2 components, A and B. On odd monitor frames, A is shown with one interspersed half of its dots refreshed and the other half stepped relative to the previous presentation of A. In the next presentation of A, 2 monitor frames later, the previously refreshed half is stepped and vice versa. On the intervening even monitor frames, this sequence of operations is performed on B. The result is a motion stimulus with a pure delay of 2 monitor frames between the correlated dot steps. Notice how this is different from manipulating the delay by keeping each dot stationary for 2 consecutive frames before and after the step. That would result in a mixture of delays, that is, the temporal offsets between the first and third, first and fourth, second and third, and second and fourth instances of the stepping dots.

In this study, we chose the parameters of the interleaved-SSDL stimuli to be similar to those that yielded high sensitivity in a study with human observers (Bours et al. 2009). Our stimuli consisted of an equal number of black (1.0 cd/m²) and white (55 cd/m²) dots that were randomly positioned within a circular aperture on a mid-gray background (28 cd/m²). We programmed the stimuli such that the dots either maintained or flipped luminance polarity across their single step to create the so-called constant-contrast and inverting-contrast motion conditions. (We reserve the terms “phi” and “reverse-phi” for the percepts that these stimuli usually elicit.)

The size and position of the aperture was chosen to approximately match the RF of the MT unit or the combined RF of the V1 units being recorded simultaneously (see the “Electrophysiology” section).

The density was 40 or 10 dots/deg² with dots of 1 or 2 pixels diameter, respectively. The change from high-density small dots to medium-density larger dots was motivated by the observation that at the larger eccentricity of some of the MT units, the dots were barely visible. To keep the MT and V1 data comparable, we used both dot densities and sizes also in 12 of the 33 V1 units, the results of which proved similar and have been pooled in this report.

Stimuli lasted 1000 ms in 16/32 MT and 28/33 V1 recordings or 500 ms otherwise. The duration of the blank interval between 2 stimuli normally was 100 ms, or 500 ms when a reward was given to allow some time to drink. This occurred every 3–5 trials, depending on the stimulus duration and the motivation level of the monkey. These interstimulus intervals represent lower-bounds as they were occasionally much longer when the monkey looked away from the fixation marker.

During the presentation interval, the stimulus produced constant speed apparent motion in 1 of 12 evenly spaced directions. In most V1 recordings, we used the speeds 4, 8, and 16°/s, but in some (5/33) the speed 32°/s was added to or substituted the 4°/s conditions. We used a range of speeds for 2 reasons. First, it improved the odds of stimulating each of the simultaneously recorded V1 neurons at near-optimal speed. Second, it has been shown that many V1 neurons exhibit bimodal direction-tuning to high-speed dot stimulus motion, which has been explained in terms of their filter properties in spatiotemporal frequency space (Skottun et al. 1994). Systematic deviations from unimodal tuning could aid in disentangling the counterevidence and evidence-only mechanisms, as will be clarified below (see the “Analysis” section). In the MT recordings, due to the inherent time constraint of the single-electrode technique, only 1 speed or sometimes (6/32) 2 speeds were used from the range 8, 16, 32, and 64°/s. Because only one MT neuron was recorded at a time, we were able to confirm online whether it was sufficiently responsive to the speed chosen or start over with an adjusted speed otherwise. The mean speeds used per unit in this report were on average 17.9°/s (SD 7.5) for V1 and 25.8°/s (SD 14.1) for MT.

We used interleaved-SSDL stimuli with 1, 2, or 3 components in early pilot recordings, after which we settled on using 2 components in the remainder of the recordings. This corresponds to a step-delay of 13.3 ms at the 150-Hz refresh rate of our stimulus display.

To minimize the quantization effect of the monitor's rectangular pixel matrix on the step sizes in different directions, we plotted the dots using OpenGL's anti-aliasing. This method weighs pixel intensity by the fraction of overlap by a virtual dot. Thus, the luminance-weighted center of the cluster of pixels representing a dot maximally coincides with the dot's intended position. We used anti-aliasing in one randomly interleaved half of the trials and regular nearest-neighbor plotting in the other. Separate analyses of these halves of the data yielded similar results (except that twice as many units showed significant direction-tuning when anti-aliasing was used); hence, we present the pooled data in this study.

All conditions were presented in a randomly interleaved fashion and repeated in blocks until the monkey lost the motivation to maintain fixation, or (MT only) the isolation was lost, or sufficient repeats were recorded.

Analysis

We characterized the neural response to each stimulus presentation with the firing rate (action potentials per second) observed between stimulus onset plus an estimate of the neuron's latency (Friedman and Priebe 1998) and the offset of the stimulus. For each unit, we created direction-tuning curves for constant-contrast (TCC) and inverting-contrast motion (TCI) by calculating the mean firing rates per motion direction. A unit was included in our analysis when both its TCC and TCI were significantly non-uniform (Rayleigh test, Zar 1999) at the 5% level.

The critical test in this study was to compare each unit's TCC with non-parametric predictions of that tuning curve based on its TCI. The evidence-only model (see below) predicts that TCC should correspond to TCI rotated by 180°, we use rTCI to refer to this predicted curve. The counterevidence model predicts that TCC should correspond to the TCI curve turned upside down. We call this the inverted TCI (iTCI). Note that rTCI and iTCI only provide different predictions when the TCI deviates sufficiently from a cosine, either by being tuned sharper or broader, or by featuring systematic irregularities such as bimodal direction tuning at high stimulus speeds.

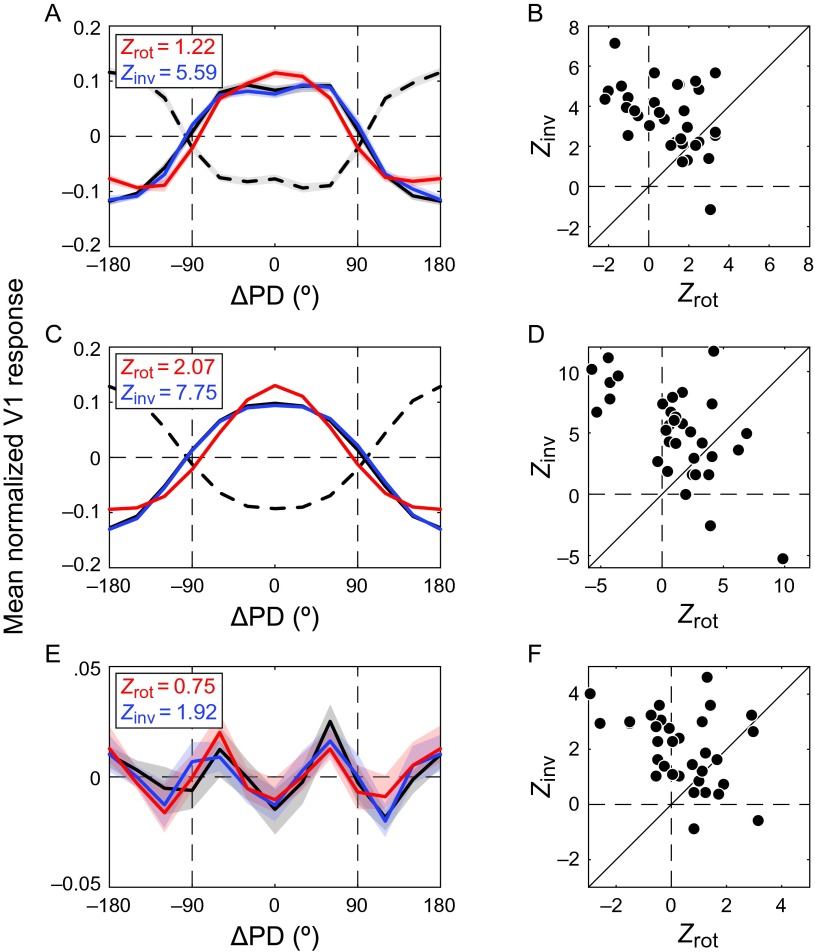
To compare TCC, iTCI, and rTCI, we took the following steps. The tuning curves were normalized by subtracting their respective means and scaling the areas under the curves to unity. rTCI was created by cycling TCI over the motion direction axis by 180°. iTCI was created by flipping the signs of TCI. To create pooled averages of the tuning curves of the V1 (Fig. 3A) and MT (Fig. 4A) units, we defined the preferred direction of constant-contrast motion, that is, the circular average of TCC, as the 0° direction.

Figure 3.

Comparison of the counterevidence and evidence-only predictions in V1 (N = 33). As predicted by the counterevidence hypothesis, TCC (solid black) correlated more strongly with the iTCI (blue) than with the rotated TCI (red). This was true for (A) the mean tuning curve across the population and (B) the population of tuning curves; (C) the fits to the tuning curves in A; and (D) the individual units' fitted tuning curves. Local irregularities of the TCC, that is, the residuals (E) of the fits to the mean population response and the residuals (F) of the individual units' tuning curves, were also best predicted by inversion of the corresponding TCI residuals. ΔPD denotes deviation from the preferred direction. Shaded regions represent SEM.

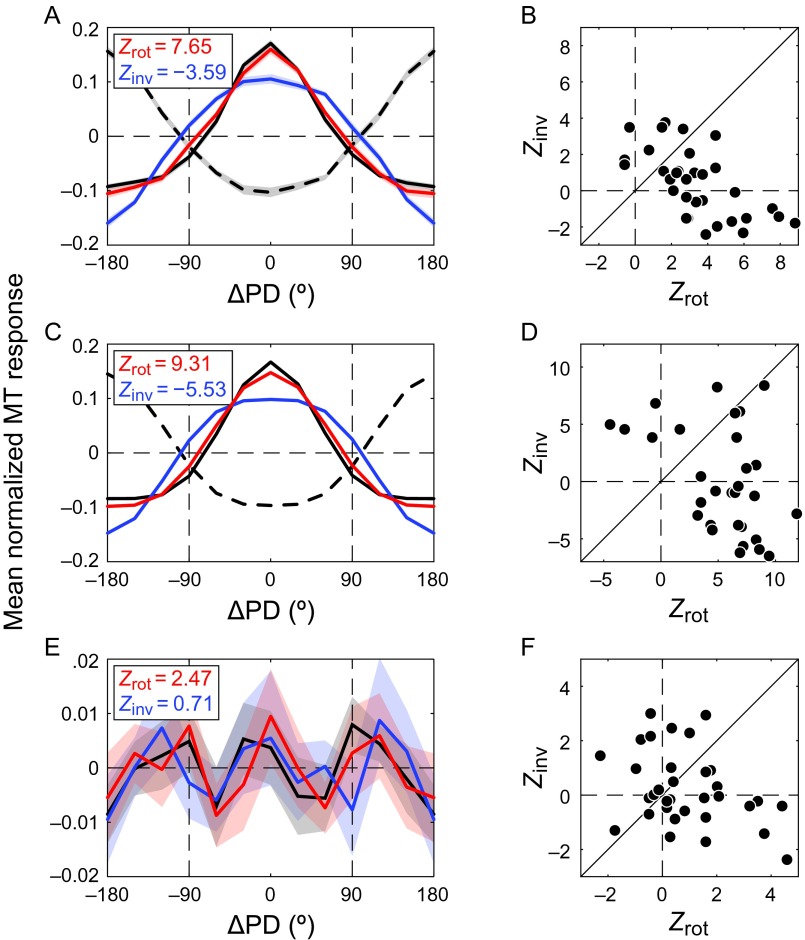
Figure 4.

Comparison of counterevidence and evidence-only predictions in area MT (N = 32). TCC (solid black) correlated strongest with the rotated TCI (red). This was true for (A) the pooled tuning curve and (B) the population of tuning curves; (C) the fits to the pooled population tuning curves in A; and (D) the fits to the individual units' tuning curves. (E) The residual of the fit to the pooled TCC (black) also correlated strongest with the rotated TCI residual (red), but this effect was not significant across the population (F). Same conventions as in Figure 3.

We report the correlations of rTCI and iTCI to TCC in Fisher z-transformed partial correlations (Z_rot and Z_inv). The advantage of this measure over standard R² values is that the variance stabilizing property of this transformation warrants the use of the Wilcoxon's signed rank (WSR) test to compare populations of paired Z_rot to Z_inv values. This test has more statistical power than the sign test. The partial correlation for the rTCI and iTCI predictions was of the form (shown for rTCI)

$$R_{\mathrm{rot}}=\frac{r_{\mathrm{rot}}-r_{\mathrm{inv}}{r}_{\mathrm{rotinv}}}{\sqrt{(1-{r_{\mathrm{inv}}}^2)(1-{r_{\mathrm{rotinv}}}^2)}}$$ (1)

where r_inv is the correlation of iTCI with TCC, r_rot is the correlation of rTCI with TCC, and r_rotinv is the correlation of the 2 predictions. Z-values were calculated as (shown for rTCI):

$$Z_{\mathrm{rot}}=\frac{1}{2}\ln \left(\frac{1+R_{\mathrm{rot}}}{1-R_{\mathrm{rot}}}\right){\nu }^{(-1/2)}$$ (2)

where v is the degrees of freedom, that is, the number of values in the tuning curve (12) minus 3 [adapted from Smith et al. (2005)].

The preceding analysis of tuning curves makes no assumption about the shape of those curves. For completeness, we also performed this analysis on the basis of parametric fits to TCC and TCI, and on the residuals of those fits. The parametric fit was of the form (shown for TCC)

$$\widehat{\text{TCC}}=aW(\theta )+b$$ (3)

where a scales the response amplitude, b provides a direction-independent (untuned) response, and W(θ) is a “warped cosine” function over the domain of motion directions:

$$W(\theta )=\left\{\begin{array}{c}-\frac{{(\cos \theta +1)}^{-c+1}}{2^{-c}}+1,c<0\\ \frac{{(\cos \theta +1)}^{c+1}}{2^c}-1,c\ge 0\end{array}\right.$$ (4)

where c is the warp factor. A positive (negative) value of c results in a cosine-like tuning curve with a narrow (broad) positive lobe; c = 0 results in a perfect cosine. This warped cosine is better suited for tuning curves than the commonly used scaled and offset von Mises function (Mardia and Jupp 2009) because when the concentration parameter (κ) that governs the width of the von Mises is zero, the function is flat and the amplitude parameter has no effect. This degeneracy is problematic because neurons (especially those in V1) often have tuning widths near 180° that require near-zero κ to fit. In contrast, the warped cosine fit (eq. 3) is well behaved in this domain. Half-height tuning widths attainable with this particular warped cosine function are limited between roughly 6° and 354° (−1023 < c <1023) when using 64-bit numerical precision.

Primary Visual to Middle Temporal Cortex Model

To better understand the relationship between V1 neurons and their MT counterparts, we constructed a simple linear–nonlinear model in which the shapes of MT's pooled TCC and TCI (Fig. 4A) are derived from those measured in V1 (Fig. 3A) by means of weighted integration, followed by response normalization, and a stationary nonlinearity:

$$\widehat{[MT]}=[{\mathit{W}}_c\mathbf{\ast }\mathbf{V}1{]}^d.$$ (5)

The operator * represents circular convolution, V1 the response vector of the pooled V1 neurons to the 12 directions, and W a warped cosine weighting profile (eq. 4). Because we were chiefly interested in the relative shapes of the V1 and MT tuning curves, we fit the model to the normalized pooled MT responses $\widehat{[MT]}$. Brackets denote scaling of the enclosed vector between 0 and 1, that is, $[\mathit{x}]=(\mathit{x}-{\mathit{x}}_{min})/({\mathit{x}}_{max}-{\mathit{x}}_{min})$. The model had 2 free parameters. The variable c represents the width of the weighting profile and determines the range of preferred directions over which the MT neurons sample from V1. The variable d specifies the output nonlinearity. The responses of the MT population to constant and inverting-contrast motion (MT_TCC,MT_TCI) were fit to the respective responses of the V1 population to constant and inverting-contrast motion (V1_TCC,V1_TCI) in parallel (i.e., using the same values for c and d). We optimized equation (5) using the quasi-Newton algorithm of Matlab 2014b's fminunc function.

Results

To investigate whether the primate visual system uses counterevidence in motion detection, we measured tuning curves to constant-contrast and inverting-contrast motion in macaque V1 and MT. We recorded 33 V1 units (14 in MM and 19 in MY) and 32 MT units (15 in MM and 17 in MN) that exhibited significant direction-tuning to both motion types (Rayleigh test; P < 0.05). The mean angular offset between the preferred directions of constant and inverting-contrast motion was 183.0° (SD 3.0) in V1 and 180.0° (SD 2.5) in MT. Hence, the reverse-phi effect was reflected in the activity of the V1 and MT units in this study, consistent with previous reports (Ibbotson and Clifford 2001; Livingstone et al. 2001; Livingstone and Conway 2003; Krekelberg and Albright 2005).

Primary Visual Cortex

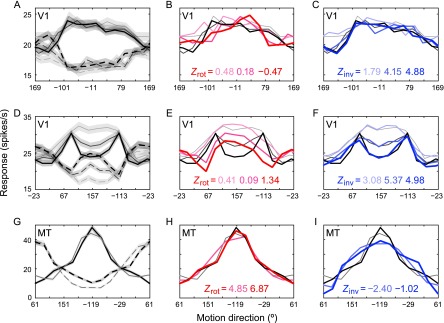
A representative V1 neuron's tuning curves for constant-contrast motion (TCC, solid curves) and inverting-contrast motion (TCI, dashed curves) are shown in Figure 2A for 3 different motion speeds. The TCCs correlated less strongly with the rTCIs (red curves in Fig. 2B) than with the iTCIs (blue curves in Fig. 2C), which suggests that this V1 neuron made use of counterevidence. The example V1 neuron in Figures 2D‒F shows a similar result. The shape of the direction tuning of this neuron depended strongly on the stimulus speed. With increasing speed, the tuning curve became bimodal, with 2 lobes flanking the direction where the single peak was observed at the lowest speed (Skottun et al. 1994). The bimodal shapes are apparent in both the TCIs and the TCCs, and they clearly align much better after inversion than after rotation (Fig. 2E,F).

Figure 2.

(A) The tuning curves of an example V1 neuron to constant-contrast (TCC, solid curves) and inverting-contrast (TCI, dashed curves) motion at speeds of 4, 8, and 16°/s (grayscale, darker indicates faster). Across the range of speeds, the preferred direction to constant- and inverting-contrast motion is roughly 180° apart: a neural correlate of the reverse-phi effect. (B) The TCIs rotated over 180° (red) correlated weakly with the TCCs (low Z_rot values). (C) The iTCIs (blue) correlated strongly with the TCCs (high Z_inv values). This is consistent with the counterevidence hypothesis. (D) Another V1 neuron that also exhibits low Z_rot (E) and high Z_inv (F). Stimulus speed had a profound effect on the shape of this neuron's direction-tuning curves, which became progressively bimodal at higher velocities. (G) The direction-tuning curves of an MT neuron measured at 8 and 16°/s also reflected the reverse-phi effect but rotation of the TCI (H) yielded much stronger correlation with the TCC than inversion (I). Shaded areas represent SEM (shown only once for clarity).

To investigate inversion and rotation across the sample of units, we created one TCC and one TCI per unit, pooling across stimulus speeds. The curves were then centered on zero and scaled to unity area under the curve. The means of these curves, similarly normalized, are shown in Figure 3A. Consistent with the example V1 units in Figure 2, the correlation between rTCI and TCC was much lower (Z_rot= 1.22) than that between iTCI and TCC (Z_inv= 5.59). The scattergraph in Figure 3B shows each individual unit's Z_inv plotted against its corresponding Z_rot. A paired two-sided WSR test on these data showed that Z_inv was indeed superior to Z_rot (WSR_Z = −3.90, P < 0.001).

We performed the same analysis based on parametric fits of the normalized tuning curves (eq. 3). Owing to the normalization, these fits had effectively only a single free parameterc that corresponds to the tuning width. As shown in Figure 3C,D, the TCC-fits correlated more with the iTCI-fits than with the rTCI-fits (Z_inv = 7.75; Z_rot = 2.07; WSR_Z = −3.24, P = 0.001). This means that the superiority of iTCI over rTCI (and therefore counterevidence over evidence-only) was driven at least partially by the overall shape of the tuning curve as captured by the parametric fit.

The parametric fits to the data in Figure 3A, although excellent on average $(R_{\mathrm{TCC}}^2=0.98;R_{\mathrm{TCI}}^2=0.98)$, were unable to capture the bimodality in the tuning curves at high stimulus speeds. We, therefore, also quantified the correlation between the residuals of the TCI fits and the residuals of the TCC fit after inversion or rotation. The mean correlation after inversion (Z_inv = 1.92) was larger than after rotation (Z_rot = 0.75), and this difference was statistically significant at the population level (Fig. 3F; WSR_Z = −3.37, P < 0.001). This analysis shows that the residuals were not uncorrelated noise, but systematic irregularities of the tuning curves that inverted, rather than rotated, when the stimulus was changed from constant-contrast to inverting-contrast motion.

Middle Temporal Cortex

Figure 2G shows the TCCs (solid curves) and TCIs (dashed curves) measured in a single MT neuron using 2 stimulus speeds. The rTCIs (Fig. 2H, red curves) correlated more strongly with their TCC counterparts than the iTCIs did (Fig. 2I, blue curves), which suggests that, in contrast to V1, this MT neuron did not make use of counterevidence. This was consistent across the MT sample (Fig. 4), in which TCC correlated strongest with rTCI. The preference for rotation was statistically significant across the population of normalized MT tuning curves (Fig. 4B, WSR_Z = 3.53, P < 0.001) and their fits (Fig. 4D, WSR_Z = 3.26, P = 0.001), but not for the residuals (Fig. 4F, WSR_Z = 1.44, P = 0.081). The lack of significance for the residuals is likely related to the fact that equation (3) captured the MT tuning curves much better than the V1 tuning curves [i.e., the mean Fisher-transformed goodness-of-fit values $(\text{arctanh}\surd R^2)$ of the MT sample (2.26 SD 0.72) were larger than V1's (1.78 SD 0.54); two-sample t-test, t₁₂₈ = 4.30, P < 0.001]. Hence, systematic irregularities of the MT tuning curves, if they existed, were likely overshadowed by independent noise.

Primary Visual to Middle Temporal Cortex

In summary, the TCCs of V1 neurons correlated most strongly with the iTCIs (consistent with the counterevidence hypothesis), but the TCCs and TCIs of MT matched best through rotation (consistent with the evidence-only hypothesis). Considering that most input to MT stems from V1 (Maunsell and van Essen 1983; Movshon and Newsome 1996), this raises the question how this transition might arise.

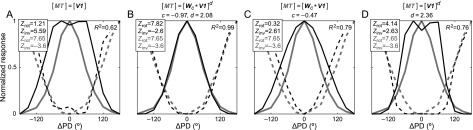
To study this transition in some detail, we created a model in which each MT neuron received a weighted input from the V1 population, followed by a power-law nonlinearity (eq. 5). We found that this two-parameter model captured the transition very well (Fig. 5B). An excellent fit (R² = 0.99) was provided with a 228° wide weighting profile (c = −0.97) and an approximately quadratic nonlinearity (d = 2.08). To examine the contributions of either parameter, we performed additional fits with 2 reduced models.

Figure 5.

V1 to MT signal transformation models. (A) The no-transformation baseline, that is, MT's (gray) normalized TCC (solid) and TCI (dashed) are directly compared with those of V1 (black). (B) The full linear–nonlinear summation model. Convolution of the normalized V1 curves with a 228°-wide filter followed by nearly quadratic nonlinearity provides a close fit to the normalized MT curves. Two reduced models with (C) only weighted integration or (D) only the nonlinearity.

The model with only the weighted integration in place, $\widehat{[MT]}=[{\mathit{W}}_c\ast \mathbf{V}1]$, yielded an R² of 0.79 (Fig. 5C). This represented a significant reduction of fit quality compared with the full model even considering the removal of a free parameter (F_1,22 = 389; P < 10⁻¹⁴). The alternative one-parameter model, $\widehat{[MT]}=[\mathbf{V}1{]}^d$, was about equally impaired (R² = 0.76; F_1,22 = 439; P < 10⁻¹⁵; Fig. 5D). However, unlike the full and the nonlinearity-only models, the weighted integration model failed to capture the Z_rot > Z_inv property of the measured MT curves that is essential to the present results. Visual inspection of the weighted integration model fit (Fig. 5C) shows that its benefit relative to the baseline model, $\widehat{[MT]}=[\mathbf{V}1]$ (R² = 0.62; Fig. 5A), stemmed mainly from smoothing-out the slight bimodality of V1's TCC. The effect of the nonlinearity is that it amplifies higher responses more than lower responses. This provided the tightening of the model TCC in Figure 5D that was also observed experimentally. We conclude that, even though the weighted integration and the expansive nonlinearity are about equally important in terms of minimizing the residuals of the fits, it is the latter property that drives the transition from V1's Z_rot < Z_inv to MT's Z_rot > Z_inv behavior.

TCC and TCI Tuning Parameters

Our analysis focused on comparisons of rotated and inverted tuning curves as direct tests of the model predictions. The parameters of the tuning curve fits (eq. 3), however, provide additional insights into the processing of motion in V1 and MT that were not touched upon in the previous analyses (Fig. 6).

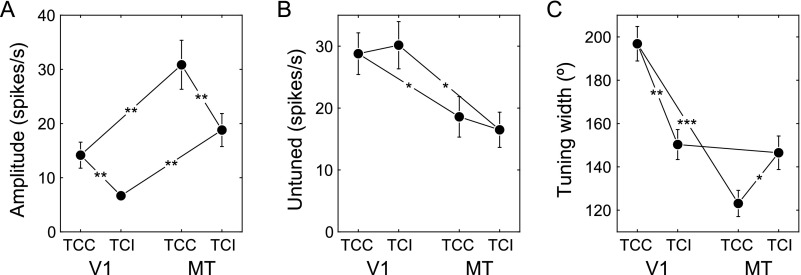
Figure 6.

Quantification of the tuning curve properties in V1 and MT. (A) Amplitude. (B) Untuned response. (C) Half-height tuning width. Connecting lines represent two-sided t-tests (paired within a cortex area, two-sample between areas) with the number of stars indicating significance levels (n+ 1 SD). Error bars represent SEM.

Most notably, TCCs had significantly greater amplitude than TCIs in both areas (Fig. 6A) and while TCC was broader than TCI in V1, the opposite was true in MT (Fig. 6C). In addition, there were differences between the overall responses in areas V1 and MT. For instance, tuning curve amplitudes (Fig. 6A) were higher in MT, whereas the untuned firing rates (Fig. 6B) were higher in V1. This may have resulted from the closer match between the stimulus speeds and the preferred speeds of the MT units, and from the higher signal-to-noise ratio of the MT recordings owing to the use of the single-electrode recording technique in that area.

Discussion

Accidental correlations between parts of a moving scene with opposite contrast occur continually. But, because objects typically do not invert contrast as they move, none of these correlations are consistent with true motion. The visual system could exploit this by taking opposite-contrast spatiotemporal correlations as counterevidence for the motion consistent with those spatiotemporal parameters (Bours et al. 2007). Our data support the view that such a counterevidence strategy is implemented by direction-selective V1 neurons.

A counterevidence strategy was also proposed by Read and Cumming (2007) to solve the correspondence problem in stereopsis. They argued that phase-disparity detectors in V1 provide counterevidence, or in their terms act as “lie-detectors”, to unmask false positives signaled by position-disparity detectors. It would be interesting to find out if these 2 examples of the use of counterevidence in V1 are separate encoding schemes or that they are functionally and mechanistically related.

Reverse-Phi

In terms of the counterevidence hypothesis, inverting-contrast apparent motion is seen as reversed because it selectively activates detectors that pick up evidence against the velocity that is consistent with the spatiotemporal parameters of the apparent motion (Bours et al. 2007). We think this is an interesting idea because it offers a novel interpretation of the reverse-phi effect which has, since its discovery by Anstis in 1970, received relatively little scrutiny compared with illusions of comparable phenomenological strength, such as the motion aftereffect (Mather et al. 1998).

Two reasons for the indifference toward reverse-phi may be that several motion models claim to readily explain the illusion (Reichardt 1961; Adelson and Bergen 1985; van Santen and Sperling 1985; Johnston and Clifford 1995), or that there is nothing to explain (Lu and Sperling 1999). We believe these reasons to be incomplete or incorrect, respectively. To address the latter point first, Lu and Sperling (1999) present the example of a sine-wave grating that steps 90 degrees per frame. Inverting the contrast of such a grating results, of course, in a display that is physically identical to a constant-contrast grating stepping in the opposite direction. Reverse-phi, however, is observed in a wide range of stimuli, not just in 90° stepping sine-wave gratings. Notably, our SSDL stimuli contain none of the motion signals that the model of Lu and Sperling (1999; their Fig. 4) uses to explain reverse-phi.

As to the former point, standard motion models achieve seemingly straightforward explanations of reverse-phi by virtue of using detectors that respond to positive and negative polarity visual inputs with positive and negative neural activity. For instance, stimulating the Reichardt detector with positive (light) and negative (dark) flashes with the appropriate spatiotemporal separation will produce, through multiplication of these signals, a negative outcome that indicates reversal of the detected velocity. In the primate visual system, however, light and dark inputs drive separate ON and OFF channels (Schiller 1995; Westheimer 2007). The Bours–Lankheet and Mo–Koch models are specific elaborations of the Reichardt detector that take this ON–OFF separation into account and generate predictions that are directly testable using electrophysiological data.

The motion-energy model (Adelson and Bergen 1985) also lacks separate ON and OFF channels and would require significant modifications to generate predictions related to counterevidence that could be tested in V1. Conceptually, however, the explanation of reverse-phi in terms of motion energy is that the intermittent contrast-inversions cause a significant amount of motion energy to be displaced in Fourier space, which then activates the opposite detector. As such, reverse-phi arises from evidence in favor of the direction opposite the physical displacement, not from counterevidence. It would be interesting to see what insights into the early visual system could be obtained by elaborating or restructuring the motion-energy models to include ON and OFF channel inputs with counterevidence interactions.

Additional experimental evidence for suppressive interaction between ON and OFF channels can be observed in the data of Livingstone and Conway (2003). They used reverse-correlation to show that the velocities that cause maximal facilitation for same contrast interactions also generate maximal suppression for opposite-contrast interactions (see an example neuron in their Fig. 7). Recent work provides evidence that a similar mechanism exists in fruit flies (Clark et al. 2011).

Our results suggest that V1 neurons enhance their sensitivity to ecologically relevant motion by detecting two-point correlations between as well as within the ON and OFF channels. We interpret this as an example of a neuron's sensitivity to a higher-order statistical regularity. Other examples of such higher-order sensitivity have previously been reported. For instance, neurons in area MT are sensitive to the higher-order correlations created by multiple successive motion steps in the same direction (Mikami et al. 1986), and both fruit flies and humans reliably extract additional motion information from scenes containing three-point diverging and converging spatiotemporal correlations that are invisible to the standard motion models and the Bours–Lankheet model (Hu and Victor 2010; Fitzgerald et al. 2011; Clark et al. 2014). Recent work from our laboratory suggests that networks of recurrently connected neurons are well suited to extract such higher-order statistical regularities dynamically (Richert et al. 2013; Joukes et al. 2014).

Primary Visual Versus Middle Temporal Cortex

We found that in V1 the TCI and TCC related through inversion, whereas in MT they related through rotation. The proposed counterevidence mechanism can only be implemented at a stage where motion detectors have access to separate ON and OFF channels. Even though there is evidence to support the view that MT cells have some polarity sensitivity (Hartmann et al. 2011), this property is much more common in V1 neurons (Schiller 1995; Westheimer 2007). Hence, it should be no surprise that, given that we found it at all, we found support for the counterevidence mechanism in V1.

The difference between the MT and V1 responses, however, is surprising from the perspective that so many of the motion tuning properties in V1 and MT are highly similar (Pack et al. 2006). Our V1 to MT model (eq. 5) demonstrates that simple mathematical operations (convolution, normalization, and exponentiation) that map onto known neurophysiological properties, such as weighted synaptic inputs, divisive response normalization, and rectifying output nonlinearities (Carandini et al. 1997; Rust et al. 2006), can account for this discrepancy. In other words, we do not believe that our finding that MT's TCC and TCI relate through rotation means that MT performs a de novo evidence-only calculation, but that the signature of the counterevidence it inherits from V1, inversion, is masked by a strong nonlinear signal transformation between the 2 areas.

Our V1 to MT model is related to the notion of an opponency stage that is present in most models of motion perception (Adelson and Bergen 1985; van Santen and Sperling 1985; Johnston and Clifford 1995). In its simplest form, this stage combines all negative and positive direction signals into a positive signal in the net direction, which in 2D amounts to calculating the vector average. In V1, there is little opponency (Snowden et al. 1991); hence, the positive and negative signals representing constant and inverting-contrast motion were seen as peaks and troughs in the tuning curves, respectively. In MT, however, opponency produces a positive output in the net direction of motion regardless of whether the input from V1 had a trough in one direction or a peak in the other. Hence, MT is predicted to be oblivious to whether the contrast of the motion it is encoding is constant or inverting, which is consistent with our finding that MT's TCI and TCC had the same (but 180° rotated) shape. This finding also matches well with what can be deduced from the observations that (1) the sensitivities to inverting and constant-contrast motion are similar in humans (Bours et al. 2009) and that (2) there is a close correspondence between perception and neuronal activity in MT (Parker and Newsome 1998).

However, although nearly identical in shape, we found that, in MT, the TCIs had a smaller amplitude than the TCCs (Fig. 6A). According to models of decoding that we (Krekelberg et al. 2006a, 2006b; Krekelberg and van Wezel 2013) and others (Churchland and Lisberger 2001; Priebe and Lisberger 2004) used to relate neural activity to perception, this predicts lower sensitivity to inverting-contrast motion, which seems at odds with the finding that human observers are equally sensitive to both types of motion (Bours et al. 2009). However, we also found a widening of MT's TCIs (Fig. 6C). This widening implies that more neurons respond to inverting-contrast motion than to constant-contrast motion, which could counteract the expected loss of sensitivity (Pouget et al. 1999; Zhang and Sejnowski 1999).

We are at present not certain what causes the reduced amplitude and widening of the tuning of MT neurons to inverting-contrast stimuli. The fact that inhibition cannot reduce firing rates below zero and that inhibition plays a crucial role in the proposed interaction between the ON and OFF channels may contribute. This is supported by the finding that TCIs in V1 already have smaller amplitudes than the corresponding TCCs (Fig. 6A). Another contributing factor could be the specifics of the opponency mechanism operating between V1 and MT, which is more complex than the vector-averaging approximation used in most models (Krekelberg and Albright 2005). For instance, vector averaging could not produce percepts of motion transparency, which are known to be encoded by population responses in MT (Pouget et al. 2000; Treue et al. 2000). Our understanding of the transformation of the motion signal from V1 to MT may be significantly furthered by studying the responses to the transparent motion stimuli used previously in the psychophysics of Bours et al. (2007) (Fig. 1C‒F). Ideally, such a study would use identical visual stimulation in both areas (Patterson et al. 2014), distinguish between the simple and complex subpopulations of V1 (Pack et al. 2006), and include a measure of the connectedness of the neurons under study (Movshon and Newsome 1996).

Funding

This work was supported by National Eye Institute grant R01 EY17605 awarded to B.K.