Abstract
The use of quantitative medical imaging data to initialize and constrain mechanistic mathematical models of tumor growth has demonstrated a compelling strategy for predicting therapeutic response. More specifically, we have demonstrated a data-driven framework for prediction of residual tumor burden following neoadjuvant therapy in breast cancer that uses a biophysical mathematical model combining reaction-diffusion growth/therapy dynamics and biomechanical effects driven by early time point imaging data. Whereas early work had been based on a limited dimensionality reduction (two-dimensional planar modeling analysis) to simplify the numerical implementation, in this work, we extend our framework to a fully volumetric, three-dimensional biophysical mathematical modeling approach in which parameter estimates are generated by an inverse problem based on the adjoint state method for numerical efficiency. In an in silico performance study, we show accurate parameter estimation with error less than 3% as compared to ground truth. We apply the approach to patient data from a patient with pathological complete response and a patient with residual tumor burden and demonstrate technical feasibility and predictive potential with direct comparisons between imaging data observation and model predictions of tumor cellularity and volume. Comparisons to our previous two-dimensional modeling framework reflect enhanced model prediction of residual tumor burden through the inclusion of additional imaging slices of patient-specific data.
Keywords: tumor, mechanics, mathematical, computational, oncology, finite element
1. Introduction
There is considerable interest in the use of computational methods to study and model the growth and behavioral dynamics of cancer [1,2]. With the significant advancement of imaging methodologies [3], efforts have begun to incorporate imaging data into macroscopic models of tumor cell growth in order to include elements of patient specificity into these modeling efforts [4,5]. We [6,7] and others [8,9] have shown the significant potential of using computational methods in a patient-specific and predictive framework to forecast [10] the response of tumors to therapy. This application is particularly compelling as it offers the opportunity for biologically-inspired computational methodologies to direct therapeutic interventions. In particular, predictive modeling strategies are potentially of great clinical significance in the setting of neoadjuvant therapy (NAT; i.e., therapy before surgery) of breast cancer.
In the neoadjuvant setting, breast cancer patients receive therapy to reduce tumor burden to a size more amenable to surgery. Furthermore, patients whose primary breast tumor responds to NAT are more likely to respond systemically, while a lack of response in the primary tumor makes systemic response unlikely. Importantly, patients who have no residual tumor burden (i.e., a pathological complete response, pCR) at the conclusion of NAT have increased survival; conversely, patients who have residual disease at the conclusion of NAT are at increased risk of early recurrence and death [11,12]. If it could be definitively determined—early in the course of NAT—that a particular therapeutic regimen is unlikely to achieve a pCR, the treating physician could discontinue the ineffective (and potentially toxic) treatment and substitute an alternative regimen. With the numerous options for NAT that have become available, development of a method to predict response early in the course of therapy is a highly relevant clinical objective. Unfortunately, conventional, tissue-based biomarkers of response require invasive biopsy with concomitant pain and morbidity as well as sampling errors due to tumor heterogeneity. Standard tumor size-based methods of evaluating response may lag behind biological response and are therefore not well-suited for predicting eventual response [13-15]. Moreover, size-based techniques may underestimate early efficacy for targeted agents exhibiting predominantly cytostatic rather than cytotoxic effects [14-16]. Accurate model prediction strategies would offer the chance to intervene in the case of prediction of failed therapy and potentially allow for a switch to a more effective regimen. To address this problem, we have recently been focused on models of tumor growth and response to therapy that incorporate important biological aspects of the cancer cell niche, such as coupling with the mechanical nature of the extracellular matrix.
Recent evidence has identified an increasingly important role for the supportive extracellular matrix stroma and demonstrated that surrounding tissue mechanics is active in shaping the growth and response of tumors [17-23]. For example, mechanical aspects of the extracellular matrix, such as tissue density and stiffness, have been linked to cancer cell proliferation and motility [24-28], with strong correlations to the aggressiveness of particular tumors. Extracellular matrix stiffness has been shown to act in a mechanoinhibitory role, whereby increased mechanical stiffness limits the expansion (proliferation and migration) in a cancer cell invasiveness-dependent manner [29-31]. These mechanobiology discoveries have motivated efforts to incorporate mechanical coupling into predictive modeling frameworks to enhance biological specificity [6,7,9,32-39]. In previous work [6,7,40], we introduced and tested the hypothesis that interactions between cancer and tissue mechanics at the macroscopic level could be described by a coupled reactive-diffusive mechanics system, where tumor cells grow and diffuse in space depending on their mechanical environment. While there is considerable data on the use of mathematical modeling to describe tumor growth and response to therapy, previous approaches are often not of the form that can be easily applied to clinical data to generate testable predictions in individual patients. Therefore, rather than use our modeling framework to simulate tumor growth de novo, we leverage the rich non-invasive imaging data available to construct and test patient-specific models [5-7]. Thus, we developed a mathematical approach to integrate quantitative in vivo imaging data into biophysical mathematical models of tumor growth in order to predict eventual response based on measurements performed before and early in the course of NAT. More specifically, we modified the reaction-diffusion model of tumor growth to include mechanical coupling to the surrounding tissue stiffness, creating a mechanically-restricted cell diffusion model. The combination of quantitative, medical imaging data to initialize and guide a mechanistic understanding provided by mathematical models has demonstrated a compelling strategy for these complex evaluations. In particular, we have previously shown that model predictions of tumor cellularity are correlated with data observations and predictive of eventual response to therapy [6,7].
In this work, we make an important step forward by extending our work to a full three-dimensional representation of the biophysics. In past work, our strategies had been limited to two-dimensional planar assumptions, i.e. we only assessed the imaging slice at the center of the tumor and assumed a plane strain approximation, implying a thick body where through-plane strain is negated, with similar planar diffusive growth. This dimensionality reduction greatly simplified the computational approach by significantly reducing the degrees of freedom of the forward model as well as allowing for simpler numerical approaches for solution of the inverse parameter estimation problem. However, with full volumetric imaging data readily available, extension to three spatial dimensions is technically feasible and would enhance the amount of patient-specific data included in the model. Thus, in this work we present an important development over our previously described mechanically-coupled, reaction-diffusion modeling framework for predicting the response of breast cancer to NAT using a full three-dimensional volumetric analysis. We present derivations of our forward mathematical model and solution of the inverse parameter estimation problem. We also perform an in silico simulation study to assess the ability of our methodology to accurately estimate key model parameters. Finally, we present preliminary modeling results from two patients (one patient that achieved a pCR at the conclusion of NAT and one patient that did not) in order to demonstrate and assess model predictions on clinical data types.
2. Methods
2.1 Mathematical model for tumor growth and response to therapy
We have previously presented a mechanically-coupled reaction diffusion model to describe the growth and response of tumor cells to NAT [6,7]. The coupled partial differential equations governing this mechanoinhibitory tumor growth behavior are shown in Eqs. (1) - (3):
| (1) |
| (2) |
| (3) |
Eq. (1) describes the change in tumor cell number, N(,t), as a combination of tumor cell diffusion and logistic growth, where D is the apparent cell diffusion coefficient, k is the spatially-dependent growth rate, and θ is the tumor cell carrying capacity. Eq. (1) is coupled to tissue mechanics via Eq. (2), which describes the tumor cell diffusion coefficient as a local modification of the global tumor cell diffusion coefficient, D0, by the von Mises stress, σvm, and an empirically derived coupling constant, γ. As discussed in [7,40], in this model the von Mises stress represents local distortional strain energy and is used to represent a description of the loading conditions due to tumor growth. This behavior replicates the mechanoinhibitory effects widely seen from in vitro and in vivo studies whereby cancer cells exhibit restricted diffusivity when encountering areas of high stress intensity [29-31]. Eq. (3) represents mechanical equilibrium with an expansive force due to tumor cell growth. This tumor cell growth force is determined by changes in cell number and a coupling constant λ. We assume an isotropic Hookean linear elastic constitutive material model:
| (4) |
where u is the displacement vector, and G and v are material properties of shear modulus and Poisson’s ratio, respectively. We use the Galerkin weighted residual method and linear tetrahedrons to perform spatial integration. Therefore, the coupled displacement (u, v, w represent the x, y, z displacements, respectively) and cell number (N) variables are explicitly approximated as:
| (5) |
Thus, using Eq. (5), expansion of Eq. (1) yields:
| (6) |
which can be condensed into:
| (7) |
where,
| (8) |
| (9) |
| (10) |
Using a fully explicit forward Euler solution in the time domain we capture,
| (11) |
which can be condensed as:
| (12) |
Combing the cell number expression, Eq. (12), with the linear elastic mechanical equilibrium expression, Eq. (3) (weighted residual expression not shown), the full weighted residual expression for the system of equations can be written as:
| (13) |
where the coupled solution vector, , is given as,
| (14) |
and the local stiffness matrix, A is:
| (15) |
The right hand side forcing conditions for the previous solution step and boundary conditions, b, are:
| (16) |
This system of equations is solved via a fully explicit finite difference method in the time domain and finite element method (FEM) for the spatial domain. The simulation software is custom built and utilizes PETSc as a sparse matrix solver library [41-43]. To solve, parameter values (D0, k, θ, λ, γ, E, v) are assigned and the stiffness matrix [K] is assembled. As the solution is fully explicit in time, the stiffness matrix can be pre-computed to accelerate the model solution as it does not change during iterative time stepping as all terms with respect to changing cell numbers are applied as a right hand side forcing function. Boundary conditions are applied and the solution is iteratively calculated in a time stepping loop where we assemble b (parameter values, boundary conditions, and data from previous time steps, Nk and σVMk), solve for {Xk+1}, partition the solution into displacements and cell numbers, calculate von Mises stress, and then continue to the next time step.
2.2 Solving the inverse problem (parameter estimation)
The key model parameters, which include a global tumor cell diffusion coefficient (that is locally modified by von Mises stress) and spatially-dependent proliferation coefficients at each node in the FE mesh, are estimated using the model and tumor cell data at two time points. The model is initialized by data obtained at the pre-treatment time point and an initial guess of parameter values, and parameter estimation is performed by iteratively minimizing the objective function using a Polak-Ribiere conjugate gradient algorithm [44,45] using tumor cell data acquired after the first cycle of NAT. The objective function is the sum of squared differences between the model prediction and the data observation at the second time point, and is given by,
| (17) |
where Ndata is the experimentally estimated number of tumor cells and Nmodel is the model predicted number of tumor cells at each node.
The adjoint method is used to evaluate the gradient at each optimization step [9,46-48]. The inverse problem estimates a global tumor cell diffusion coefficient and proliferation coefficients at each node, with approximately 25,000 - 30,000 nodes in a FE mesh for a representative patient. However, due to the size and spatial position of the tumor at the time points used for parameter estimation, approximately 3,000-5,000 proliferation parameters are changed from the initial guess for a representative patient. Use of the adjoint method allows a more efficient calculation of parameter sensitivity over traditional finite-difference based gradient evaluation methods, and is necessary due to the large number of parameters to be estimated. A finite difference based gradient evaluation would require a time-prohibitive amount of forward model evaluations per optimization step (number of parameters + 1) as opposed to the adjoint method which requires only two forward model solves per optimization step [49].
While a brief description of the adjoint state and parameter sensitivity equations follow, for a complete derivation of the adjoint method the interested reader is referred to one of several references [9,46-48]. With Eq. (13) as the primary problem and Eq. (17) as the objective function, the adjoint state equation can be written with respect to the unknown parameter vector, P, as,
| (18) |
where ϕ is the adjoint state variable. The parameter sensitivity of the objective function (i.e., the gradient) can be written as,
| (19) |
Parameters are estimated though an optimization scheme that iteratively minimizes Eq. (17) using Eq. (19) to calculate the parameter sensitivity. The optimization is terminated by satisfying a relative error tolerance condition where the change in error relative to the previous iteration is less than 1 × 10−5.
2.3 Populating the model with patient-specific data
The model is populated and parameterized using patient-specific tumor cell data by processing quantitative magnetic resonance imaging (MRI) data. The MRI data sources used to populate the model are: diffusion weighted MRI (DW-MRI), dynamic contrast enhanced MRI (DCE-MRI), and anatomical THRIVE (T1 high resolution isotropic volume examination). Briefly, DCE-MRI collects images before, during, and after contrast agent infusion [50]. While pharmacokinetic modeling of DCE-MRI data can be used to extract compartmental model parameters describing blood vessel perfusion/permeability and volume fractions, in this work we simply use this data for region-of-interest assignment. We do note, however, that we are actively working to incorporate DCE-MRI data to inform other aspects of tumor growth and response to therapy [51]. DW-MRI collects data that can be used to map the apparent diffusion coefficient (ADC), which describes the rate of thermally induced self-diffusion in tissue [52]. This parameter depends on the amount of microscopic barriers that a diffusing water molecule encounters and thus is used as a correlate to tissue cellularity [52-71]. Finally, THRIVE collects data weighted by the T1 relaxation properties of tissue. It is used in this work to aid segmentation of breast fibroglandular tissue from adipose tissue, as these tissues exhibit contrast in T1 relaxation properties.
Imaging data is acquired at three time points: prior to initiating NAT, after one cycle of NAT (typically one to two weeks after the initial time point), and at the conclusion of NAT (typically eight to twelve weeks after the initial time point) as described previously [6,7]. Briefly, MR images for each patient are longitudinally co-registered across all time points to the initial time point using an adaptive basis algorithm non-rigid registration with a tumor volume preserving constraint [72,73]. Registered DCE-MRI data is used to define a tumor region-of-interest (ROI) by manually segmenting the difference image of pre- and post-contrast images. Areas within the ROI with greater than 80% signal intensity increase between the pre- and post-contrast infusion data are defined as tumor; this value has previously been empirically determined to provide a high degree of correlation to the tumor volume as measured on the excised tissue obtained at the time of surgery [74].
ADC values were obtained by fitting the DW-MRI data on a voxel-by-voxel basis to Eq. (20):
| (20) |
where i is the direction of diffusion-weighting, bi is the amount of diffusion-weighting, S0 is the signal intensity in the absence of diffusion gradients, and Si is the signal intensity in the presence of the diffusion-sensitizing gradient. ADC data for areas defined as tumor were transformed to estimate tumor cell number, N(,t) as described in [57,75],
| (21) |
where θ is the carrying capacity (total number of tumor cells that can be contained within a voxel), ADCw is the ADC of free water at 37° C (set to 3 × 10−3 mm2/s), ADC(,t) is the ADC value at a given position, and ADCmin is the minimum ADC value observed, corresponding to the voxel with the largest number of cells. Further details on this approach have been previously reported [57,76].
The full model parameter set (D0, k, θ, E, v, λ and γ) contains model parameters that are determined by inverse model fitting, assumptions based on literature values, or otherwise empirically determined. Specifically, D0 and k are determined from model fits. The carrying capacity, θ, is calculated by assuming spherical tumor cells with a packing density of 0.7405 [77] and a nominal tumor cell radius of 10 μm. Material properties of Young’s modulus, E, are assumed as 2 and 4 kPa for adipose and fibroglandular tissue, respectively [78]. Anatomical T1-weighted MR images are used to segment the breast into fibroglandular and adipose tissue for assigning tissue-based mechanical properties. Poisson’s ratio, v, is assumed as 0.45, reflecting the nature of soft tissue and avoiding numerical instabilities due to incompressibility within a linear elastic model solution. Coupling constants, λ and γ, are empirically determined as 2.5 × 10−3 and 2 × 10−3 Pa−1, respectively, and were empirically determined to yield physiologically realistic deformation fields and von Mises stress maps in prior work [6,7]. The time step Δt, was selected as 0.25 days and was determined based on an empirical stability analysis. Von Neumann stability analysis [79] of a finite difference forward Euler linear diffusion equation in three dimensions was used to guide the initial selection for the time step based on constraints established on the ratio of the product of the diffusion coefficient and time step to the square of the spatial discretization length (D· dt/h2). For the most restrictive stability conditions, we select a maximal allowable diffusion coefficient of 1 × 10−7 m2/day and find the minimum spatial step size observed in the discretized mesh for all subjects. Following initial selection of step size, forward simulations of the model were analyzed for numerical oscillations and the step size was adjusted as necessary such that the approximate solution remained bounded without amplification of numerical errors. This stability requirement is necessary due to the selection of a conditionally-stable explicit solution algorithm (Section 2.1). While these do constrain the speed of time evolution, they do have significant advantages in algorithmic simplicity. For mesh discretization, an empirical selection of nominal element edge length was used to guide mesh refinement using forward simulations of the model on a mesh with incrementally increasing refinement. Comparison of solutions at prescribed locations within the mesh were assessed for convergence using a tolerance of less than 1% difference in solution from successive simulations at increasing refinement levels (and decreasing nominal element edge length).
2.4 In silico simulation study
We performed an in silico simulation study by assuming an initial tumor seed of 10 percent of the cell carrying capacity and placed centrally within a realistic breast model domain at a single node. A finite element mesh was generated using custom-built mesh generation software [80] and was composed of four-node tetrahedrons with a nominal edge length of 3 mm. Global diffusion, D0, was assigned as 1 × 10−8 m2/day. Spatial growth rate, k, was assigned at each node as 0.1 day−1. Other model parameters were assigned as described in Section 2.3. The model was used to ‘grow’ the tumor to a second time point, 14 days later. Using the initial and ‘grown’ tumor cellularity at each time point as data observations, we estimate diffusion and growth rate parameters as described in Section 2.2 using initial guesses of 8 × 10−9 m2/day and 0.08 day−1 for diffusion and growth rate, respectively. This simulation study represents a controlled system to assess the accuracy of the inverse methodology.
2.5 Experimental study
To demonstrate data-driven model predictions within our full volumetric modeling framework, we performed a limited proof-of-principle experimental study to assess model prediction performance relative to data observations. MRI data from an existing breast NAT patient imaging database [69,81] was retrieved for two patients, one achieving pCR, and one with residual tumor burden at the conclusion of NAT. MRI data sets were collected prior to beginning NAT, after one cycle of NAT (typically 1-2 weeks), and at the conclusion of NAT (typically 8-12 weeks). MRI data acquisition parameters for this study population have been previously reported [69,81]. Briefly, MRI was performed using a Philips 3T Achieva MR scanner (Philips Healthcare, Best, The Netherlands) with a 16-channel double-breast coil. DCE-MRI data was acquired via a 192 × 192 × 20 acquisition matrix over a sagittal square field of view (22 cm2) with slice thickness of 5 mm, one signal acquisition, TR/TE/α = 7.9 ms/1.3 ms/20°, and SENSE factor of 2. Twenty-five time points, with a temporal resolution of 16 seconds, were collected with contrast agent infusion occurring after collection of the third time point. The contrast agent, 0.1 mmol/kg of gadopentetate dimeglumine (Magnevist, Wayne, NJ) was delivered through an antecubital vein catheter at 2 mL/s, followed by a saline flush, via a power injector (Medrad, Warrendale, PA). DW-MRI data was acquired with a single-shot spin echo, echo planar imaging sequence in three orthogonal diffusion-encoding directions with b-values of 0 and 500 or 600 s/mm2, 96 × 96 (reconstructed to 144 × 144) acquisition matrix over a 19.2 cm × 19.2 cm field of view using SENSE parallel imaging (acceleration factor = 2) and spectrally-selective adiabatic inversion recovery fat saturation while subjects were freely breathing. Twelve sagittal slices with slice thickness of 5 mm, TR = 3080 ms, TE = ‘shortest’ 41 or 60 ms), Δ = 19.8 or 29 ms, and δ = 10.7 or 21 ms, and 10 signal averages. THRIVE (T1 high resolution isotropic volume examination) anatomical data was acquired via a 400 × 400 × 129 acquisition matrix over a 20 cm × 20 cm × 12.9 cm transverse field of view, one signal acquisition, TR/TE/α = 6.43 ms/3.4 ms/10°.
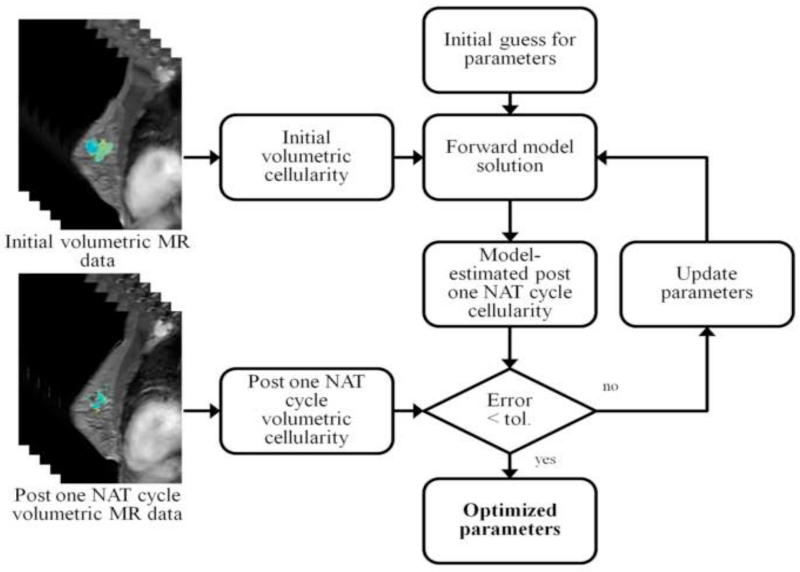
For each patient, a finite element mesh was generated from anatomical imaging data using custom-built, semi-automatic software. Briefly, breast MR image volumes were manually segmented at the chest wall using ITK-SNAP [82]. The boundary surface of the breast was generated through a marching cubes extraction [83] that was followed by radial basis function smoothing (FastRBF toolkit, FarField Technology, Christchurch, New Zealand). A finite element mesh was generated [80] and was composed of four-node tetrahedrons with a nominal edge length of 3 mm. Model parameters were estimated as described in Section 2.2, and the model was run forward in time to generate predictions of tumor burden at the conclusion of NAT. Model predictions were compared to data observations for both total predicted tumor cellularity and tumor volume. A schematic of this procedure is outline in Figure 1.
Figure 1.
Schematic of the inverse parameter estimation procedure. The volumetric MR data from the initial and post one NAT cycle is converted to estimate tumor cellularity at each time point. Given an initial guess of the model parameters, the model is initialized by the tumor cellularity at the initial time point and used to generate an estimate of the tumor cellularity at the post one NAT cycle time point. The model estimate is compared to the data observation for the post one NAT cycle cellularity and parameters are iteratively refined until convergence below a preset tolerance to yield an initial estimate of the parameters.
For comparison of the full-volumetric extension to our prior work, we also performed a two-dimensional model prediction for one patient with residual tumor burden at the conclusion of NAT, using a two-dimensional planar assumption that assessed the imaging slice at the center of the tumor, as described previously [6,7].
2.6 Biomechanical constitutive model simulation study
To demonstrate the effects of biomechanical constitutive model selection, we performed a limited study to investigate simulations of tumor growth and response to therapy with respect to changing the assumed biomechanical constitutive model used for mechanical coupling to our mechano-inhibitive, reaction-diffusion model of tumor growth. We compared the results of coupling to a linear elastic biomechanical model, as described in Section 2.1, and a hyperelastic neo-Hookean nonlinear biomechanical model [84] given by the strain energy function:
| (22) |
where I1 is the first invariant of the right Cauchy-Green deformation tensor, J is the Jacobian of the deformation tensor, and μ and λ are Lamé parameters defined as:
| (23) |
| (24) |
The open-source biomechanical nonlinear finite element solver FEBio [85] with a custom-designed pre-processing interface based on GIBBON [86] was used for neo-Hookean biomechanical model coupling. Estimated model parameters were taken from the experimental study (Section 2.5). For the neo-Hookean model, assumed Poisson’s ratio was varied between 0.45, as used in the linear elastic biomechanical model, to a value of 0.499. The forward model, with either linear elastic or neo-Hookean biomechanical model coupling, was used to simulate tumor growth and response to therapy from the initial time point to the post one NAT cycle time point and predicted tumor cellularity and volume were compared for the two models.
3. Results
3.1 In silico simulation study
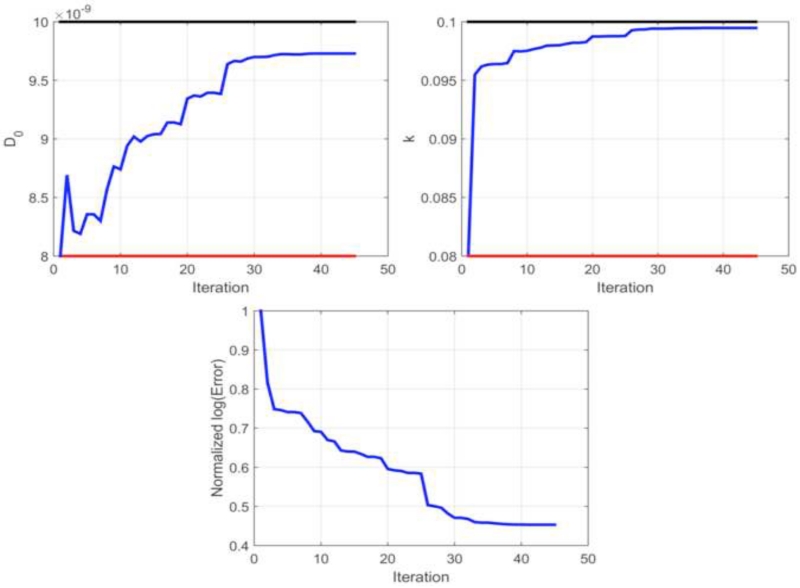
We assessed the accuracy of our parameter estimation approach, by performing an in silico simulation study. Using the initial and ‘grown’ tumor cellularity at each time point as data observations, we evaluated the accuracy of our parameter estimation approach. In this controlled study, we found an estimation error less than 3% for diffusion and growth rate. As shown in Table 1, the error in estimating global tumor cell diffusion, D0, was 2.59% and the error in estimating the growth rate was 0.5%. Parameter estimation performance is shown in Figure 2, reflecting the behavior in diffusion, growth rate, and objective function error over approximately 50 iterations prior to termination of iterative estimation due to relative error convergence criteria.
Table 1.
Performance results for in silico parameter estimation of global diffusion and local proliferation reflect the initial guess, ground truth, parameter estimate, and percent error of the parameter estimate as compared to ground truth.
| Initial Guess | Ground truth | Estimated | Error | |
|---|---|---|---|---|
| D0 | 8.00×10−9 | 1.00×10−8 | 9.74×10−9 | 2.59% |
| k | 0.0800 | 0.1000 | 0.0995 | 0.5% |
Figure 2.
Parameter estimation performance for the in silico study. Top: Tumor cell diffusion, D0, and local proliferation, k, are initialized at the first iteration with a guess, given by the value at the red line, and the iterative parameter estimation continues until convergence, given by the blue line. The parameter estimation procedure is shown to exhibit accurate performance in generating parameters estimates as compared to ground truth, given by the value at the black line). Bottom: Log transformed objective function error is normalized to the value at the initial iteration and shows iterative minimization throughout the parameter estimation procedure.
3.2 Experimental study
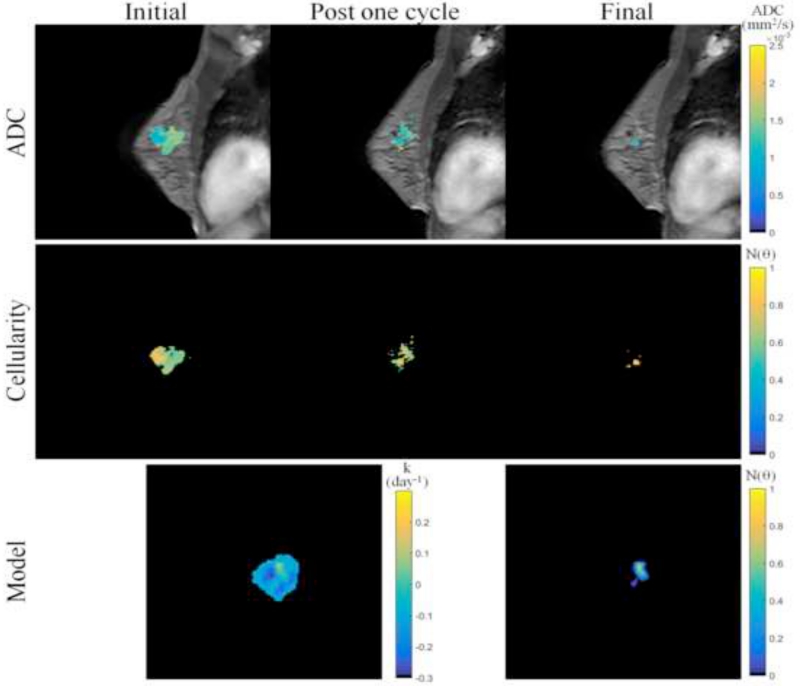
Figures 3 and 4 show data from parameter reconstruction and model prediction for a patient achieving pathological complete response at the conclusion of NAT. While we performed a full volumetric analysis, for visualization purposes, Figure 3 shows data and results at the central slice of the tumor. After converting MRI data (Figure 3, top row) to tumor cellularity data (Figure 3, middle row), we used the model to estimate global diffusion and local growth rate parameters (Figure 3, bottom row, left). Following parameterization, we used the model to estimate the residual tumor burden at the end of NAT (Figure 3, bottom row, right). While this patient was evaluated pathologically as achieving complete response (i.e., no residual tumor burden), the imaging data at the final time point reflected a slight focal residual tumor burden. Figure 4 shows three-dimensional volumetric representations of the tumor volume at each data observation time point (Figure 4, top row) as well as the model prediction (Figure 4, bottom row). The model is seen to accurately predict a small residual tumor burden, with similar total cellularity (see Table 2). However, the model is shown to overestimate the volume as well as incorrectly identify the location of the residual tumor burden, placing the predicted residual tumor slightly inferior to the observed location (approximately 1.3 cm).
Figure 3.
MR imaging data and mathematical model prediction results for a patient achieving a pathological complete response at the completion of NAT. ADC data at the initial, post one NAT cycle, and final time points (top row) is converted to estimates of tumor cellularity (middle row) using Eq. (21). Global diffusion and spatial proliferation (bottom row, left) model parameters are estimated and the model is used to predict tumor cellularity at the final time point (bottom row, right) and compared to data observations. Though the patient was evaluated at surgery as having achieved a pathological complete response, the imaging data and model predictions at the final time point reflect a very small focal residual tumor. (Note that although we performed a volumetric analysis, for visualization purposes, this figure displays data and results at the central slice of the tumor; see Figures 4 and 7 for volumetric renderings.)
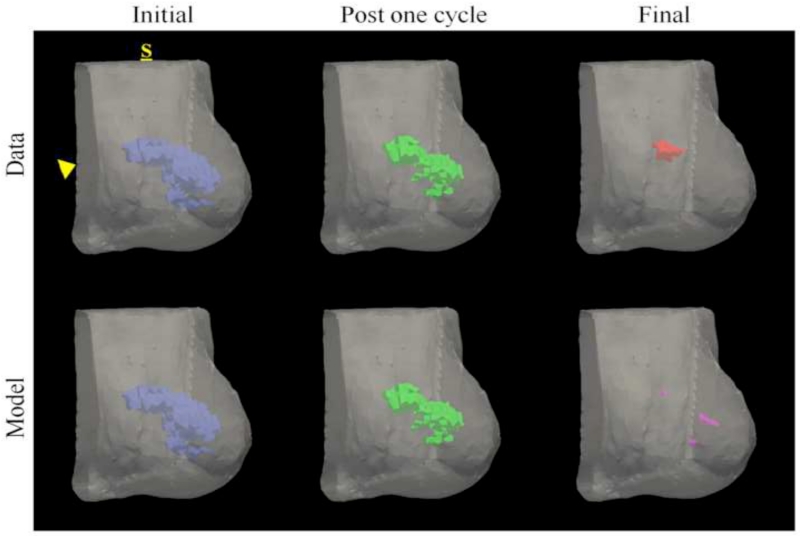
Figure 4.
Volumetric rendering of the tumor cell volumes taken from imaging data and model prediction are displayed within the breast volume, segmented at the chest wall (arrowhead), for a patient achieving a pathological complete response. Data is collected at the initial (blue), post one NAT cycle (green), and final (red) time points. The model is informed with data at the initial time point and parameters are estimated to minimize model/data error the post one NAT cycle time point. The model is then used to predict the residual tumor burden at the final time point (purple). The label, S, designates the superior position of the breast. This patient was evaluated at surgery as having achieved pCR, but imaging data and model prediction at the final time point reflect a very small focal residual tumor. Similar to imaging observation, the model predicts a small residual tumor burden; however, the model incorrectly predicts the location of the residual tumor burden as slightly inferior to the observed location.
Table 2.
Tumor cellularity and volumetric results reflect the imaging-based estimation of tumor burden at the initial, post one NAT cycle, and final time points in addition to the model prediction results at the final time point. Cellularity numbers are normalized by 1 × 109 tumor cells and volumes are expressed as cm3.
| Initial | Post one NAT cycle |
Final | Prediction | |
|---|---|---|---|---|
| Responsive Cellularity |
1.435 | 0.406 | 0.056 | 0.097 |
| Non-responsive Cellularity |
3.751 | 1.425 | 0.165 | 0.179 |
| Responsive Volume |
9.338 | 2.532 | 0.302 | 1.155 |
| Non-responsive Volume |
23.99 | 9.355 | 1.084 | 2.417 |
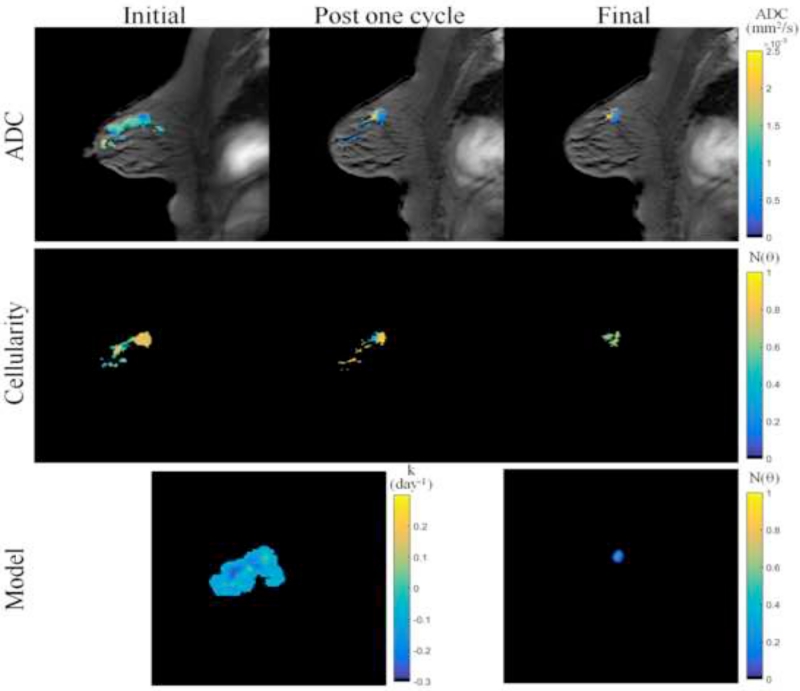
Similarly, Figures 5 and 6 show data for a patient identified pathologically with residual tumor burden at the end of NAT. MR data (Figure 5, top row) is converted to estimate tumor cellularity (Figure 5, middle row), and the model is used to estimate parameters and predict the residual tumor burden at the final time point (Figure 5, bottom row). Again, while we performed a full volumetric analysis, the central slice plane of imaging data is shown for visualization purposes. The model is shown to accurately predict total tumor cellularity (Table 2), but is seen to overestimate the volume and misidentify the spatial location of the residual tumor (Figure 6). While a portion of the predicted residual tumor is located within the area of the observed tumor burden, the model predicts additional focal lesions outside that of the area observed in the data observation.
Figure 5.
MR imaging data and mathematical model prediction results for a patient with residual tumor burden at the completion of NAT. ADC data at the initial, post one NAT cycle, and final time points (top row) is converted to estimates of tumor cellularity (middle row) using Eq. (21). Global diffusion and spatial proliferation (bottom row, left) model parameters are estimated and the model is used to predict tumor cellularity at the final time point (bottom row, right) and compared to data observations. (Note that although we performed a volumetric analysis, for visualization purposes, this figure displays data and results at the central slice of the tumor; see Figures 6 and 7 for volumetric renderings.)
Figure 6.
Volumetric rendering of the tumor cell volumes taken from imaging data and model prediction are displayed within the breast volume, segmented at the chest wall (arrowhead), for a patient with residual tumor burden. Data is collected at the initial (blue), post one NAT cycle (green), and final (red) time points. The model is informed with data at the initial time point and parameters are estimated to minimize model/data error the post one NAT cycle time point. The model is then used to predict the residual tumor burden at the final time point (purple). The label, S, designates the superior position of the breast. While there is significant response to NAT, residual focal tumor burden is observed. A portion of the predicted residual tumor is located within the area of the observed tumor burden, however the model predicts additional focal lesions outside that of the area observed in the imaging data.
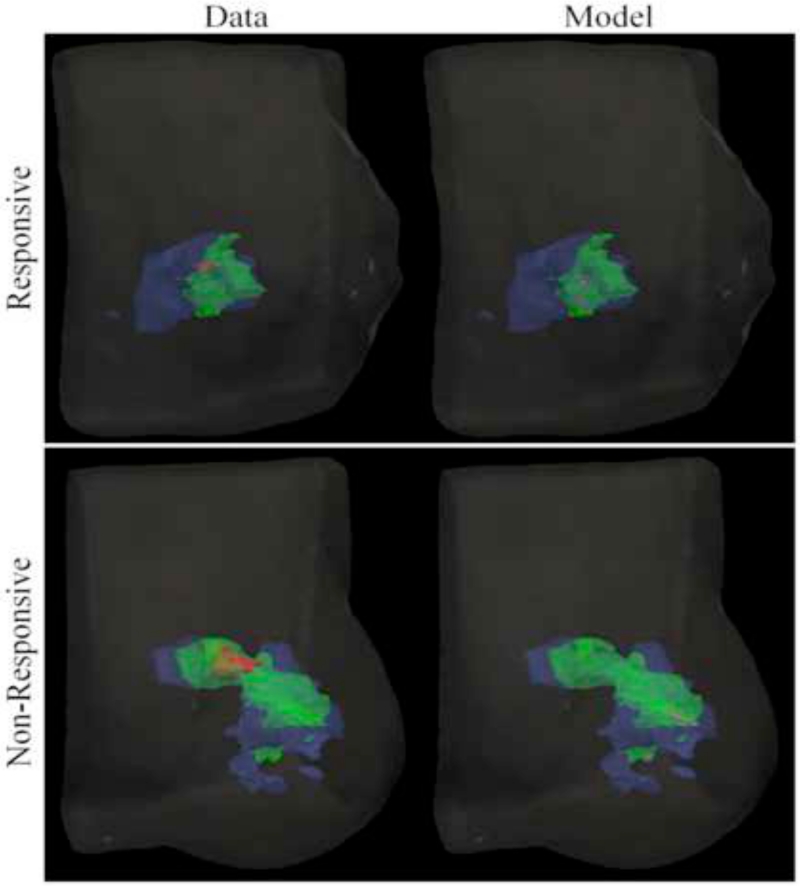
Figure 7 shows merged and smoothed volumetric renderings reflecting the time course of tumor volumetric changes in both imaging data observation and model prediction during the course of NAT for patients with both pCR and non-pCR tumors. Model estimated parameter results shown in Table 3 reflect slight differences in proliferation and tumor cell diffusion parameters between tumor types. The patient with a pCR tumor is seen to have a slightly lower mean and maximum proliferation and tumor cell diffusion than the patient with a non-pCR tumor.
Figure 7.
Merged volumetric renderings of the tumor cell volumes taken from imaging data and model predictions are smoothed and displayed within the breast volume for patients with pCR and non-pCR tumors. Data is collected at the initial (blue), post one NAT cycle (green), and final (red) time points. The model is calibrated using data at the initial and post one NAT cycle time points and used to predict the residual tumor burden at the final time point (purple).
Table 3.
Model estimated parameter results reflect the mean, maximum, and minimum spatial proliferation rates and tumor cell diffusion coefficients for the responsive and non-responsive patients.
| Mean proliferation |
Max proliferation |
Min proliferation |
Tumor cell diffusion |
|
|---|---|---|---|---|
| Responsive | −0.1179 | 0.1398 | −0.2860 | 5.06×10−9 |
| Non-responsive | −0.1158 | 0.1671 | −0.3186 | 7.91×10−8 |
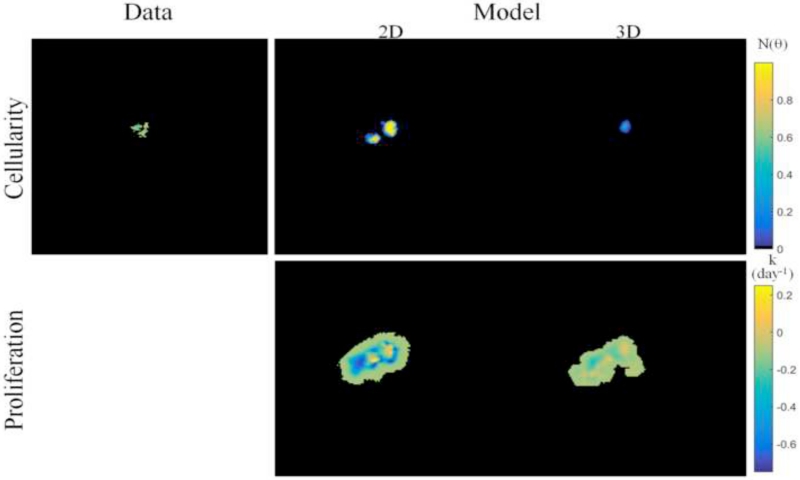
Comparison of model prediction results from the reduced spatial dimensionality model, presented in prior work, to the full volumetric model presented within this study are shown in Figure 8 for a patient with residual tumor burden at the conclusion of NAT. Tumor cellularity (Figure 8, top row) predicted from the two-dimensional model reflects a significant overestimation of cellularity and volume as compared to the imaging data observation, whereas the model prediction from the three-dimensional model more closely matches imaging data. Comparison of the estimated proliferation maps (Figure 8, bottom row and Table 4) reflect large differences in spatial pattern and magnitude between the two models.
Figure 8.
Comparison of two-dimensional (from prior work) to three-dimensional image-based mathematical model prediction results for a patient with residual tumor burden at the completion of NAT. For two-dimensional model prediction, ADC-based estimates of tumor cellularity at the central imaging slice, as shown in Figure 5, are used to calibrate the model and predict residual tumor burden. Tumor cellularity at the final time point (top row) are shown for imaging data, two-dimensional model prediction, and three-dimensional model prediction (at the central imaging slice) and reflect that three-dimensional model prediction is seen to more closely match imaging data observations than the two-dimensional model. Spatial proliferation maps (bottom row) reflect differences in estimated model parameters for each model. (Note that although we performed a full volumetric analysis for the three-dimensional model, for comparisons to the two-dimensional case, this figure displays results at the central slice of the tumor.)
Table 4.
Model estimated parameter results reflect the mean, maximum, and minimum spatial proliferation rates for the non-responsive patient assessed with the two-dimensional and three-dimensional (assessed at the same central imaging slice) modeling frameworks.
| Mean Proliferation |
Max Proliferation |
Min Proliferation |
|
|---|---|---|---|
| 2D | −0.2012 | 0.3229 | −0.8762 |
| 3D (central slice) |
−0.1094 | 0.0398 | −0.2707 |
3.3 Biomechanical constitutive model simulation study
We assessed the effects of constitutive biomechanical model selection within our tumor growth model in a limited simulation study. Total tumor cellularity and volume results are compared in Table 5 with a tumor growth model based on coupling to a biomechanical model with a linear elastic or a neo-Hookean nonlinear hyperelastic assumption. Three different values of Poisson’s ratio are used for the neo-Hookean model, representing a gradually more incompressible behavior in hyperelasticty. When varying the biomechanical model from linear elastic to nonlinear hyperelastic, both predicted total tumor cellularity and volume reflect a maximum difference of less than 10% in this simulation scenario.
Table 5.
Tumor cellularity and volumetric results for constitutive model simulation study comparing linear elastic and neo-Hookean hyperelastic biomechanical coupling. Cellularity numbers are normalized by 1 × 109 tumor cells and volumes are expressed as cm3. Percent difference is expressed relative to the linear elastic model.
| Tumor Cellularity |
% Difference | Tumor Volume |
% Difference | |
|---|---|---|---|---|
| Linear Elastic | 0.3674 | n/a | 3.572 | n/a |
| Neo-Hookean (v = 0.45) |
0.3657 | 0.469% | 3.563 | 0.249% |
| Neo-Hookean (v = 0.49) |
0.3385 | 7.87% | 3.287 | 7.96% |
| Neo-Hookean (v = 0.499) |
0.3317 | 9.70% | 3.225 | 9.70% |
4. Conclusions
We have presented an extension of our image-based mechanically-coupled mathematical model of tumor response to NAT into three spatial dimensions. Using an in silico study, we used the model to simulate the growth of a tumor, given an initial tumor ‘seed’ location. The predictive modeling framework demonstrates accuracy in estimation of the model parameters of diffusion and growth rate with less than 3% error when compared to the ground truth parameters used to simulate tumor growth. In a preliminary experimental study to demonstrate predictive performance, we used our modeling approach to predict the response to NAT for two patients, one that achieved pathological complete response and one that did not. The model accurately predicts the residual tumor cellularity as compared to observed quantitative imaging data estimates of tumor cellularity. In our preliminary data, however, the model is challenged with accurate spatial placement of the predicted location of residual tumor burden, with one patient showing slight misalignment and one patient with more pronounced misalignment demonstrating additional focal tumor lesions that were found to have completely resolved in follow-up imaging. However, it is important to note that the prediction framework is based on a very challenging, but clinically significant, timeframe of imaging data acquisition in which imaging data is collected before and after only a single cycle of NAT and is used to predict eventual tumor burden. Patients continue to receive additional cycles of NAT, approximately 8-12 total, prior to data observations at the final time point. Therefore it is important to recognize the value of predictive modeling for guidance of suspicion for residual tumor burden within the context of clinical goals for interventional therapy (i.e. discriminating between pCR and non-pCR), rather than exact prediction of tumor spatial placement. While a predictive framework that could accurate resolve exact tumor location would be ideal, there are additional nonlinear effects currently unaccounted for in the model that occur between the final time point of data used to inform predictive models and the time point at which model prediction is compared to data observation. We return to this limitation below.
We also present a comparison of our results from the full volumetric model predictions of this study to that of the reduced spatial dimensionality modeling framework presented in prior work. We show that incorporating additional patient-specific imaging data results in large changes to the parameter estimates extracted from the model. This additional data is then shown to enhance the accuracy of the model predicted cellularity, more closely matching imaging data observations. In previous investigations that used our simplified reduced spatial dimensionality model, we have demonstrated qualitative and quantitative comparisons demonstrating the improved performance of our model-to-data match using our mechanoinhibitive model of tumor growth [6,7]. In future work we will more fully explore the increased fidelity that can be achieved using the fully three dimensional realization presented herein.
While in this work we have eliminated the assumption of reduced spatial dimensionality, several limitations still remain in our current approach. One such limitation of this study is that we assume an isotropic Hookean linear elastic constitutive mechanical model. However, the true constitutive nature of soft tissue is well-known to exhibit particularly complex non-linear and multi-physics behavior. Therefore, selection of an appropriate constitutive model for use in computational analysis of biological tissue is often controversial and presents unique challenges. Soft tissue, unlike conventional materials, exhibits many highly complex intrinsic properties in addition to the computational challenges encountered in implementing, solving, and determining accurate material properties for more sophisticated constitutive models. Investigators have employed anisotropic [87], hyperelastic [88], viscoelastic [89], and poroelastic [90] material models to represent soft tissue in mechanical modeling efforts, among others. In a limited simulation study, we show that the first-order linear elastic simplification we employ in this effort introduces a small degree of numerical model error, but is less than the uncertainty of the underlying ADC-based measurement of observed cellularity [91-93]. This study, while preliminary, suggests that the uncertainty due to biomechanical constitutive model selection is contained within the experimental error of a data-driven tumor growth modeling framework. However, it is important (in future efforts) to more fully understand the true nature of material model assumptions, both simplified and complex, with robust validation studies to further explore the consequences of model selection and reducing first order assumptions from the perspective of clinical and interventional goals for prediction of NAT response. Additional technical model limitations include the limited degrees of freedom associated with the use of linear tetrahedral elements rather than quadratic tetrahedral or hexahedral elements.
Another limitation is the use of ADC from DW-MRI data as a linear correlate to tumor cellularity. ADC can also be shown to depend on several factors other than cellularity, such as extracellular matrix density, edema, and inflammatory infiltrates, among others. While we agree that exact ADC-to-cellularity relationships are likely influenced by other mitigating factors, previous studies confirm its use as a first order approximate relationship. ADC has been shown to correlate inversely with cellularity, and has also demonstrated strong potential as an independent measure for assessing treatment response for anti-cancer therapy in both preclinical and clinical studies [52-71]. Additionally, preclinical validation studies have shown strong significant correlation of ADC to histologically confirmed extracellular space fraction [71].
Lastly, it is important to recognize that predictions are synthesized by a calibration/fitting process that uses only two imaging time points, before and after a single cycle of NAT. The consequences of this limitation are that it implicitly assumes a fixed spatial proliferation rate map in time for subsequent cycles of NAT. Subsequent cycles of NAT will undoubtedly change the spatial proliferation and migration characteristics, however we have no additional imaging data to guide the spatiotemporal evolution of proliferation or migration terms. Additionally, many patients receive multi-agent therapy with temporal delays in the administration of therapeutic agents which may occur after the acquisition of imaging data. Future studies that include additional imaging time points (currently ongoing), or predictive models that can simulate additional specific therapeutic agent effects de novo, will be important for further development of a model that can compensate for this effect.
5. Summary
The modeling methodology presented in this contribution represents a data-driven framework for prediction of residual tumor burden in breast cancer patients following neoadjuvant therapy. Previously, we have taken a commonly used reaction-diffusion tumor growth model and extended it by incorporating known mechanoinhibitory effects that have been previously demonstrated in biological perturbation studies [27-31]. We previously demonstrated that a reduced spatial dimensionality predictive model exhibits significant potential for use as a predictor of response to therapy and indicates the promise of image-driven predictive modeling for therapeutic intervention [6]. In this study, we addressed a fundamentally limiting assumption of two-dimensional central slice analysis by extending our modeling framework to full volumetric analysis. We demonstrated technical feasibility and performed initial studies showing enhanced predictive capacity. Our modeling framework represents a general approach whereby models of tumor growth and response can be extended by gradually incorporating additional model complexity and then validating model predictions by directly comparing against data observations. Other extensions to our model, such as biologically-inspired perturbations, may be similarly incorporated and validated. Using our data-driven approach, model perturbations in the setting of response of breast cancer to NAT can be incorporated to more fully realize the goal of model-assisted therapeutic intervention.
Highlights.
Medical imaging data can be used to inform mathematical models of tumor growth
Models may assist therapeutic intervention for breast cancer therapeutic response
We present a volumetric extension of our data driven mathematical model predictions
Inclusion of additional volumetric patient-specific data enhances model predictions
Acknowledgements
We thank the National Institutes of Health for funding through NCI K25CA204599, NCI R01CA186193, NCI U01CA174706, NCI U01CA142565, NIBIB R21EB022380, and CPRIT RR00016. T.E.Y. is a CPRIT Scholar in Cancer Research.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Byrne HM. Dissecting cancer through mathematics: from the cell to the animal model. Nat Rev Cancer. 2010;10(3):221–30. doi: 10.1038/nrc2808. [DOI] [PubMed] [Google Scholar]
- [2].Anderson AR, Quaranta V. Integrative mathematical oncology. Nat Rev Cancer. 2008;8(3):227–34. doi: 10.1038/nrc2329. [DOI] [PubMed] [Google Scholar]
- [3].Yankeelov TE, Mankoff DA, Schwartz LH, Lieberman FS, Buatti JM, Mountz JM, Erickson BJ, Fennessy FM, Huang W, Kalpathy-Cramer J, Wahl RL, Linden HM, Kinahan PE, Zhao B, Hylton NM, Gillies RJ, Clarke L, Nordstrom R, Rubin DL. Quantitative Imaging in Cancer Clinical Trials. Clin Cancer Res. 2016;22(2):284–90. doi: 10.1158/1078-0432.CCR-14-3336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Yankeelov TE. Integrating Imaging Data into Predictive Biomathematical and Biophysical Models of Cancer. ISRN Biomath. 2012;2012:287394. doi: 10.5402/2012/287394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Yankeelov TE, Atuegwu N, Hormuth D, Weis JA, Barnes SL, Miga MI, Rericha EC, Quaranta V. Clinically relevant modeling of tumor growth and treatment response. Sci Transl Med. 2013;5(187):187ps9. doi: 10.1126/scitranslmed.3005686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Weis JA, Miga MI, Arlinghaus LR, Li X, Abramson V, Chakravarthy AB, Pendyala P, Yankeelov TE. Predicting the Response of Breast Cancer to Neoadjuvant Therapy Using a Mechanically Coupled Reaction-Diffusion Model. Cancer Res. 2015;75(22):4697–707. doi: 10.1158/0008-5472.CAN-14-2945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Weis JA, Miga MI, Arlinghaus LR, Li X, Chakravarthy AB, Abramson V, Farley J, Yankeelov TE. A mechanically coupled reaction-diffusion model for predicting the response of breast tumors to neoadjuvant chemotherapy. Phys Med Biol. 2013;58(17):5851–66. doi: 10.1088/0031-9155/58/17/5851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Rockne RC, Trister AD, Jacobs J, Hawkins-Daarud AJ, Neal ML, Hendrickson K, Mrugala MM, Rockhill JK, Kinahan P, Krohn KA, Swanson KR. A patient-specific computational model of hypoxia-modulated radiation resistance in glioblastoma using 18F-FMISO-PET. J R Soc Interface. 2015;12(103) doi: 10.1098/rsif.2014.1174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Hogea C, Davatzikos C, Biros G. An image-driven parameter estimation problem for a reaction-diffusion glioma growth model with mass effects. Journal of Mathematical Biology. 2008;56(6):793–825. doi: 10.1007/s00285-007-0139-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Yankeelov TE, Quaranta V, Evans KJ, Rericha EC. Toward a science of tumor forecasting for clinical oncology. Cancer Res. 2015;75(6):918–23. doi: 10.1158/0008-5472.CAN-14-2233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Carey LA, Dees EC, Sawyer L, Gatti L, Moore DT, Collichio F, Ollila DW, Sartor CI, Graham ML, Perou CM. The triple negative paradox: primary tumor chemosensitivity of breast cancer subtypes. Clin Cancer Res. 2007;13(8):2329–34. doi: 10.1158/1078-0432.CCR-06-1109. [DOI] [PubMed] [Google Scholar]
- [12].Liedtke C, Mazouni C, Hess KR, Andre F, Tordai A, Mejia JA, Symmans WF, Gonzalez-Angulo AM, Hennessy B, Green M, Cristofanilli M, Hortobagyi GN, Pusztai L. Response to neoadjuvant therapy and long-term survival in patients with triple-negative breast cancer. J Clin Oncol. 2008;26(8):1275–81. doi: 10.1200/JCO.2007.14.4147. [DOI] [PubMed] [Google Scholar]
- [13].Kamel IR, Liapi E, Reyes DK, Zahurak M, Bluemke DA, Geschwind JF. Unresectable hepatocellular carcinoma: serial early vascular and cellular changes after transarterial chemoembolization as detected with MR imaging. Radiology. 2009;250(2):466–73. doi: 10.1148/radiol.2502072222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Tuma RS. Sometimes size doesn’t matter: reevaluating RECIST and tumor response rate endpoints. J Natl Cancer Inst. 2006;98(18):1272–4. doi: 10.1093/jnci/djj403. [DOI] [PubMed] [Google Scholar]
- [15].Ratain MJ, Eckhardt SG. Phase II studies of modern drugs directed against new targets: if you are fazed, too, then resist RECIST. J Clin Oncol. 2004;22(22):4442–5. doi: 10.1200/JCO.2004.07.960. [DOI] [PubMed] [Google Scholar]
- [16].Wolchok JD, Hoos A, O’Day S, Weber JS, Hamid O, Lebbe C, Maio M, Binder M, Bohnsack O, Nichol G, Humphrey R, Hodi FS. Guidelines for the evaluation of immune therapy activity in solid tumors: immune-related response criteria. Clin Cancer Res. 2009;15(23):7412–20. doi: 10.1158/1078-0432.CCR-09-1624. [DOI] [PubMed] [Google Scholar]
- [17].Marsh T, Pietras K, McAllister SS. Fibroblasts as architects of cancer pathogenesis. Biochimica Et Biophysica Acta-Molecular Basis of Disease. 2013;1832(7):1070–1078. doi: 10.1016/j.bbadis.2012.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Pietras K, Ostman A. Hallmarks of cancer: Interactions with the tumor stroma. Experimental Cell Research. 2010;316(8):1324–1331. doi: 10.1016/j.yexcr.2010.02.045. [DOI] [PubMed] [Google Scholar]
- [19].Johansson A, Jones J, Pietras K, Kilter S, Skytt A, Rudolfsson SH, Bergh A. A stroma targeted therapy enhances castration effects in a transplantable rat prostate cancer model. Prostate. 2007;67(15):1664–1676. doi: 10.1002/pros.20657. [DOI] [PubMed] [Google Scholar]
- [20].Lu PF, Weaver VM, Werb Z. The extracellular matrix: A dynamic niche in cancer progression. Journal of Cell Biology. 2012;196(4):395–406. doi: 10.1083/jcb.201102147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Pickup MW, Mouw JK, Weaver VM. The extracellular matrix modulates the hallmarks of cancer. Embo Reports. 2014;15(12):1243–1253. doi: 10.15252/embr.201439246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Oudin MJ, Jonas O, Kosciuk T, Broye LC, Guido BC, Wyckoff J, Riquelme D, Lamar JM, Asokan SB, Whittaker C, Ma D, Langer R, Cima MJ, Wisinski KB, Hynes RO, Lauffenburger DA, Keely PJ, Bear JE, Gertler FB. Tumor Cell-Driven Extracellular Matrix Remodeling Drives Haptotaxis during Metastatic Progression. Cancer Discov. 2016;6(5):516–31. doi: 10.1158/2159-8290.CD-15-1183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Jain RK, Martin JD, Stylianopoulos T. The role of mechanical forces in tumor growth and therapy. Annu Rev Biomed Eng. 2014;16:321–46. doi: 10.1146/annurev-bioeng-071813-105259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Engler AJ, Berry M, Sweeney HL, Discher DE. Substrate compliance alters human mesenchymal stem cell morphology. Molecular Biology of the Cell. 2004;15:298a–298a. [Google Scholar]
- [25].Engler AJ, Feng H, Sweeney HL, Discher DE. Cells on gels: Skeletal muscle cell differentiation and adhesion on flexible substrates. Molecular Biology of the Cell. 2002;13:63a–63a. [Google Scholar]
- [26].Engler AJ, Berry M, Sweeney HL, Discher DE. Substrate elasticity directs adult mesenchymal stem cell differentiation. Biorheology. 2005;42(1-2):33–33. [Google Scholar]
- [27].Lo CM, Wang HB, Dembo M, Wang YL. Cell movement is guided by the rigidity of the substrate. Biophysical Journal. 2000;79(1):144–152. doi: 10.1016/S0006-3495(00)76279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Yeung T, Georges PC, Flanagan LA, Marg B, Ortiz M, Funaki M, Zahir N, Ming WY, Weaver V, Janmey PA. Effects of substrate stiffness on cell morphology, cytoskeletal structure, and adhesion. Cell Motility and the Cytoskeleton. 2005;60(1):24–34. doi: 10.1002/cm.20041. [DOI] [PubMed] [Google Scholar]
- [29].Helmlinger G, Netti PA, Lichtenbeld HC, Melder RJ, Jain RK. Solid stress inhibits the growth of multicellular tumor spheroids. Nature Biotechnology. 1997;15(8):778–783. doi: 10.1038/nbt0897-778. [DOI] [PubMed] [Google Scholar]
- [30].Stein AM, Demuth T, Mobley D, Berens M, Sander LM. A mathematical model of glioblastoma tumor spheroid invasion in a three-dimensional in vitro experiment. Biophysical Journal. 2007;92(1):356–365. doi: 10.1529/biophysj.106.093468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Cheng G, Tse J, Jain RK, Munn LL. Micro-environmental mechanical stress controls tumor spheroid size and morphology by suppressing proliferation and inducing apoptosis in cancer cells. PLoS One. 2009;4(2):e4632. doi: 10.1371/journal.pone.0004632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Voutouri C, Mpekris F, Papageorgis P, Odysseos AD, Stylianopoulos T. Role of Constitutive Behavior and Tumor-Host Mechanical Interactions in the State of Stress and Growth of Solid Tumors. Plos One. 2014;9(8):e104717. doi: 10.1371/journal.pone.0104717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Katira P, Bonnecaze RT, Zaman MH. Modeling the mechanics of cancer: effect of changes in cellular and extra-cellular mechanical properties. Front Oncol. 2013;3:145. doi: 10.3389/fonc.2013.00145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Angeli S, Stylianopoulos T. Biphasic modeling of brain tumor biomechanics and response to radiation treatment. J Biomech. 2016;49(9):1524–31. doi: 10.1016/j.jbiomech.2016.03.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Kim M, Gillies RJ, Rejniak KA. Current advances in mathematical modeling of anti-cancer drug penetration into tumor tissues. Front Oncol. 2013;3:278. doi: 10.3389/fonc.2013.00278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Kim Y, Stolarska MA, Othmer HG. The role of the microenvironment in tumor growth and invasion. Prog Biophys Mol Biol. 2011;106(2):353–79. doi: 10.1016/j.pbiomolbio.2011.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Ambrosi D, Mollica F. On the mechanics of a growing tumor. International journal of engineering science. 2002;40(12):1297–1316. [Google Scholar]
- [38].Liu Y, Sadowski SM, Weisbrod AB, Kebebew E, Summers RM, Yao J. Patient specific tumor growth prediction using multimodal images. Med Image Anal. 2014;18(3):555–66. doi: 10.1016/j.media.2014.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Chen X, Summers RM, Yao J. Kidney tumor growth prediction by coupling reaction-diffusion and biomechanical model. IEEE Trans Biomed Eng. 2013;60(1):169–73. doi: 10.1109/TBME.2012.2222027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Garg I, Miga MI. Preliminary investigation of the inhibitory effects of mechanical stress in tumor growth; SPIE Medical Imaging 2008: Visualization, Image-Guided Procedures, and Modeling Conference; 2008. [Google Scholar]
- [41].Balay S, Abhyankar S, Adams MF, Brown J, Brune P, Buschelman K, Dalcin L, Eijkhout V, Gropp WD, Kaushik D, Knepley MG, McInnes LC, Rupp K, Smith BF, Zampini S, Zhang H, Zhang H. PETSc Users Manual. Argonne National Laboratory; 2016. [Google Scholar]
- [42].Balay S, Abhyankar S, Adams MF, J Brown, Brune P, Buschelman K, Dalcin L, Eijkhout V, Gropp WD, Kaushik D, Knepley MG, McInnes LC, Rupp K, Smith BF, Zampini S, Zhang H, Zhang H. PETSc Web page. 2016 Available from: http://www.mcs.anl.gov/petsc.
- [43].Balay S, Gropp WD, McInnes LC, Smith BF. Efficient Management of Parallelism in Object Oriented Numerical Software Libraries, in Modern Software Tools in Scientific Computing. Birkhäuser Press; 1997. pp. 163–202. [Google Scholar]
- [44].Polak E, Ribiere G. Note surla convergence des méthodes de directions conjuguées. Rev. Fr. Imform. Rech. Oper. 1969;16:35–43. [Google Scholar]
- [45].Fletcher R, Reeves CM. Function minimization by conjugate gradients. The computer journal. 1964;7(2):149–154. [Google Scholar]
- [46].Chavent G. Identification of functional parameters in partial differential equations; Joint Automatic Control Conference; 1974. [Google Scholar]
- [47].Knopoff DA, Fernandez DR, Torres GA, Turner CV. Adjoint method for a tumor growth PDE-constrained optimization problem. Computers & Mathematics with Applications. 2013;66(6):1104–1119. [Google Scholar]
- [48].Natterer F. Adjoint Methods as Applied to Inverse Problems. Encyclopedia of Applied and Computational Mathematics. 2015:33–36. [Google Scholar]
- [49].Oberai AA, Gokhale NH, Doyley MM, Bamber JC. Evaluation of the adjoint equation based algorithm for elasticity imaging. Physics in Medicine and Biology. 2004;49(13):2955–2974. doi: 10.1088/0031-9155/49/13/013. [DOI] [PubMed] [Google Scholar]
- [50].Yankeelov TE, Gore JC. Dynamic Contrast Enhanced Magnetic Resonance Imaging in Oncology: Theory, Data Acquisition, Analysis, and Examples. Curr Med Imaging Rev. 2009;3(2):91–107. doi: 10.2174/157340507780619179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Barnes SL, McKenna MT, Hormuth DA, II, Weis JA, Arlinghaus LR, Li X, Rericha EC, Tyson D, Miga MI, Quaranta V, Yankeelov TE. Incorporating Patient-Specific Imaging Data and Treatment Regimes to Predict Treatment Response in a Multi-Scale Model of Breast Cancer; ISMRM Workshop on MRI in the Management of Breast Disease: Past, Present & Future; 2015. [Google Scholar]
- [52].Padhani AR, Liu G, Koh DM, Chenevert TL, Thoeny HC, Takahara T, Dzik-Jurasz A, Ross BD, Van Cauteren M, Collins D, Hammoud DA, Rustin GJ, Taouli B, Choyke PL. Diffusion-weighted magnetic resonance imaging as a cancer biomarker: consensus and recommendations. Neoplasia. 2009;11(2):102–25. doi: 10.1593/neo.81328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Stejskal EO, Tanner JE. Spin Diffusion Measurements: Spin Echoes in the Presence of a Time-Dependent Field Gradient. Journal of Chemical Physics. 1965;42(1):288–+. [Google Scholar]
- [54].Le Bihan D, Breton E, Lallemand D, Aubin ML, Vignaud J, Laval-Jeantet M. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology. 1988;168(2):497–505. doi: 10.1148/radiology.168.2.3393671. [DOI] [PubMed] [Google Scholar]
- [55].Chenevert TL, Brunberg JA, Pipe JG. Anisotropic diffusion in human white matter: demonstration with MR techniques in vivo. Radiology. 1990;177(2):401–5. doi: 10.1148/radiology.177.2.2217776. [DOI] [PubMed] [Google Scholar]
- [56].Sugahara T, Korogi Y, Kochi M, Ikushima I, Shigematu Y, Hirai T, Okuda T, Liang L, Ge Y, Komohara Y, Ushio Y, Takahashi M. Usefulness of diffusion-weighted MRI with echo-planar technique in the evaluation of cellularity in gliomas. J Magn Reson Imaging. 1999;9(1):53–60. doi: 10.1002/(sici)1522-2586(199901)9:1<53::aid-jmri7>3.0.co;2-2. [DOI] [PubMed] [Google Scholar]
- [57].Anderson AW, Xie J, Pizzonia J, Bronen RA, Spencer DD, Gore JC. Effects of cell volume fraction changes on apparent diffusion in human cells. Magn Reson Imaging. 2000;18(6):689–95. doi: 10.1016/s0730-725x(00)00147-8. [DOI] [PubMed] [Google Scholar]
- [58].Guo Y, Cai YQ, Cai ZL, Gao YG, An NY, Ma L, Mahankali S, Gao JH. Differentiation of clinically benign and malignant breast lesions using diffusion-weighted imaging. Journal of Magnetic Resonance Imaging. 2002;16(2):172–178. doi: 10.1002/jmri.10140. [DOI] [PubMed] [Google Scholar]
- [59].Sinha S, Lucas-Quesada FA, Sinha U, DeBruhl N, Bassett LW. In vivo diffusion-weighted MRI of the breast: Potential for lesion characterization. Journal of Magnetic Resonance Imaging. 2002;15(6):693–704. doi: 10.1002/jmri.10116. [DOI] [PubMed] [Google Scholar]
- [60].Pickles MD, Lowry M, Manton DJ, Gibbs P, Turnbull LW. Role of dynamic contrast enhanced MRI in monitoring early response of locally advanced breast cancer to neoadjuvant chemotherapy. Breast Cancer Research and Treatment. 2005;91(1):1–10. doi: 10.1007/s10549-004-5819-2. [DOI] [PubMed] [Google Scholar]
- [61].Humphries PD, Sebire NJ, Siegel MJ, Olsen OE. Tumors in pediatric patients at diffusion-weighted MR imaging: apparent diffusion coefficient and tumor cellularity. Radiology. 2007;245(3):848–54. doi: 10.1148/radiol.2452061535. [DOI] [PubMed] [Google Scholar]
- [62].Patterson DM, Padhani AR, Collins DJ. Technology Insight: water diffusion MRI - a potential new biomarker of response to cancer therapy. Nature Clinical Practice Oncology. 2008;5(4):220–233. doi: 10.1038/ncponc1073. [DOI] [PubMed] [Google Scholar]
- [63].Roe K, Kakar M, Seierstad T, Ree AH, Olsen DR. Early prediction of response to radiotherapy and androgen-deprivation therapy in prostate cancer by repeated functional MRI: a preclinical study. Radiation Oncology. 2011;6:1. doi: 10.1186/1748-717X-6-65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Gaustad JV, Pozdniakova V, Hompland T, Simonsen TG, Rofstad EK. Magnetic resonance imaging identifies early effects of sunitinib treatment in human melanoma xenografts. Journal of Experimental & Clinical Cancer Research. 2013;32:1. doi: 10.1186/1756-9966-32-93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Moestue SA, Huuse EM, Lindholm EM, Bofin A, Engebraaten O, Maelandsmo GM, Akslen LA, Gribbestad IS. Low-Molecular Contrast Agent Dynamic Contrast-Enhanced (DCE)-MRI and Diffusion-Weighted (DW)-MRI in Early Assessment of Bevacizumab Treatment in Breast Cancer Xenografts. Journal of Magnetic Resonance Imaging. 2013;38(5):1043–1053. doi: 10.1002/jmri.24079. [DOI] [PubMed] [Google Scholar]
- [66].Sahani DV, Jiang T, Hayano K, Duda DG, Catalano OA, Ancukiewicz M, Jain RK, Zhu AX. Magnetic resonance imaging biomarkers in hepatocellular carcinoma: association with response and circulating biomarkers after sunitinib therapy. Journal of Hematology & Oncology. 2013;6:1. doi: 10.1186/1756-8722-6-51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Graham TJ, Box G, Tunariu N, Crespo M, Spinks TJ, Miranda S, Attard G, de Bono J, Eccles SA, Davies FE, Robinson SP. Preclinical Evaluation of Imaging Biomarkers for Prostate Cancer Bone Metastasis and Response to Cabozantinib. Journal of the National Cancer Institute. 2014;106(4) doi: 10.1093/jnci/dju033. [DOI] [PubMed] [Google Scholar]
- [68].Aryal MP, Nagaraja TN, Keenan KA, Bagher-Ebadian H, Panda S, Brown SL, Cabral G, Fenstermacher JD, Ewing JR. Dynamic Contrast Enhanced MRI Parameters and Tumor Cellularity in a Rat Model of Cerebral Glioma at 7 T. Magnetic Resonance in Medicine. 2014;71(6):2206–2214. doi: 10.1002/mrm.24873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Li X, Kang H, Arlinghaus LR, Abramson RG, Chakravarthy AB, Abramson VG, Farley J, Sanders M, Yankeelov TE. Analyzing Spatial Heterogeneity in DCE- and DW-MRI Parametric Maps to Optimize Prediction of Pathologic Response to Neoadjuvant Chemotherapy in Breast Cancer. Transl Oncol. 2014;7(1):14–22. doi: 10.1593/tlo.13748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70].Reischauer C, Froehlich JM, Pless M, Binkert CA, Koh DM, Gutzeit A. Early Treatment Response in Non-Small Cell Lung Cancer Patients Using Diffusion-Weighted Imaging and Functional Diffusion Maps - A Feasibility Study. Plos One. 2014;9(10):e108052. doi: 10.1371/journal.pone.0108052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Barnes SL, Sorace AG, Loveless ME, Whisenant JG, Yankeelov TE. Correlation of tumor characteristics derived from DCE-MRI and DW-MRI with histology in murine models of breast cancer. NMR Biomed. 2015;28(10):1345–56. doi: 10.1002/nbm.3377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72].Li X, Dawant BM, Welch EB, Chakravarthy AB, Freehardt D, Mayer I, Kelley M, Meszoely I, Gore JC, Yankeelov TE. A nonrigid registration algorithm for longitudinal breast MR images and the analysis of breast tumor response. Magn Reson Imaging. 2009;27(9):1258–70. doi: 10.1016/j.mri.2009.05.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Li X, Dawant BM, Welch EB, Chakravarthy AB, Xu L, Mayer I, Kelley M, Meszoely I, Means-Powell J, Gore JC, Yankeelov TE. Validation of an algorithm for the nonrigid registration of longitudinal breast MR images using realistic phantoms. Med Phys. 2010;37(6):2541–52. doi: 10.1118/1.3414035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [74].Li X, Arlinghaus LR, Ayers GD, Chakravarthy AB, Abramson RG, Abramson VG, Atuegwu N, Farley J, Mayer IA, Kelley MC, Meszoely IM, Means-Powell J, Grau AM, Sanders M, Bhave SR, Yankeelov TE. DCE-MRI analysis methods for predicting the response of breast cancer to neoadjuvant chemotherapy: pilot study findings. Magn Reson Med. 2014;71(4):1592–602. doi: 10.1002/mrm.24782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [75].Atuegwu NC, Colvin DC, Loveless ME, Xu L, Gore JC, Yankeelov TE. Incorporation of diffusion-weighted magnetic resonance imaging data into a simple mathematical model of tumor growth. Phys Med Biol. 2012;57(1):225–40. doi: 10.1088/0031-9155/57/1/225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [76].Atuegwu NC, Arlinghaus LR, Li X, Welch EB, Chakravarthy BA, Gore JC, Yankeelov TE. Integration of diffusion-weighted MRI data and a simple mathematical model to predict breast tumor cellularity during neoadjuvant chemotherapy. Magn Reson Med. 2011;66(6):1689–96. doi: 10.1002/mrm.23203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [77].Martin I, Dozin B, Quarto R, Cancedda R, Beltrame F. Computer-based technique for cell aggregation analysis and cell aggregation in in vitro chondrogenesis. Cytometry. 1997;28(2):141–6. doi: 10.1002/(sici)1097-0320(19970601)28:2<141::aid-cyto7>3.0.co;2-i. [DOI] [PubMed] [Google Scholar]
- [78].McKnight AL, Kugel JL, Rossman PJ, Manduca A, Hartmann LC, Ehman RL. MR elastography of breast cancer: Preliminary results. American Journal of Roentgenology. 2002;178(6):1411–17. doi: 10.2214/ajr.178.6.1781411. [DOI] [PubMed] [Google Scholar]
- [79].Lynch DR. Numerical partial differential equations for environmental scientists and engineers: a first practical course. Springer Science & Business Media; 2004. [Google Scholar]
- [80].Sullivan JM, Jr, Charron G, Paulsen KD. A three-dimensional mesh generator for arbitrary multiple material domains. Finite Elements in Analysis and Design. 1997;25(3):219–241. [Google Scholar]
- [81].Li X, Abramson RG, Arlinghaus LR, Kang H, Chakravarthy AB, Abramson VG, Farley J, Mayer IA, Kelley MC, Meszoely IM, Means-Powell J, Grau AM, Sanders M, Yankeelov TE. Multiparametric magnetic resonance imaging for predicting pathological response after the first cycle of neoadjuvant chemotherapy in breast cancer. Invest Radiol. 2015;50(4):195–204. doi: 10.1097/RLI.0000000000000100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [82].Yushkevich PA, Piven J, Hazlett HC, Smith RG, Ho S, Gee JC, Gerig G. User-guided 3D active contour segmentation of anatomical structures: significantly improved efficiency and reliability. Neuroimage. 2006;31(3):1116–28. doi: 10.1016/j.neuroimage.2006.01.015. [DOI] [PubMed] [Google Scholar]
- [83].Lorensen WE, Cline HE. ACM Siggraph Computer Graphics. ACM; 1987. Marching cubes: A high resolution 3D surface construction algorithm. [Google Scholar]
- [84].Bonet J, Wood RD. Nonlinear continuum mechanics for finite element analysis. Cambridge university press; 1997. [Google Scholar]
- [85].Maas SA, Ellis BJ, Ateshian GA, Weiss JA. FEBio: finite elements for biomechanics. J Biomech Eng. 2012;134(1):011005. doi: 10.1115/1.4005694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [86].Moerman KM. GIBBON (Hylobates Lar) 2016. doi:10.5281/zenodo.44404. [Google Scholar]
- [87].Clatz O, Sermesant M, Bondiau PY, Delingette H, Warfield SK, Malandain G, Ayache N. Realistic simulation of the 3-D growth of brain tumors in MR images coupling diffusion with biomechanical deformation. IEEE Trans Med Imaging. 2005;24(10):1334–46. doi: 10.1109/TMI.2005.857217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [88].Mohamed A, Davatzikos C. Finite element modeling of brain tumor mass-effect from 3D medical images. Med Image Comput Comput Assist Interv. 2005;8(Pt 1):400–8. doi: 10.1007/11566465_50. [DOI] [PubMed] [Google Scholar]
- [89].Holmes MJ, Sleeman BD. A mathematical model of tumour angiogenesis incorporating cellular traction and viscoelastic effects. J Theor Biol. 2000;202(2):95–112. doi: 10.1006/jtbi.1999.1038. [DOI] [PubMed] [Google Scholar]
- [90].Sarntinoranont M, Rooney F, Ferrari M. Interstitial stress and fluid pressure within a growing tumor. Ann Biomed Eng. 2003;31(3):327–35. doi: 10.1114/1.1554923. [DOI] [PubMed] [Google Scholar]
- [91].Whisenant JG, Ayers GD, Loveless ME, Barnes SL, Colvin DC, Yankeelov TE. Assessing reproducibility of diffusion-weighted magnetic resonance imaging studies in a murine model of HER2+ breast cancer. Magn Reson Imaging. 2014;32(3):245–9. doi: 10.1016/j.mri.2013.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [92].O’Flynn EAM, Morgan VA, Giles SL, deSouza NM. Diffusion weighted imaging of the normal breast: reproducibility of apparent diffusion coefficient measurements and variation with menstrual cycle and menopausal status. European Radiology. 2012;22(7):1512–1518. doi: 10.1007/s00330-012-2399-0. [DOI] [PubMed] [Google Scholar]
- [93].Koh DM, Blackledge M, Collins DJ, Padhani AR, Wallace T, Wilton B, Taylor NJ, Stirling JJ, Sinha R, Walicke P, Leach MO, Judson I, Nathan P. Reproducibility and changes in the apparent diffusion coefficients of solid tumours treated with combretastatin A4 phosphate and bevacizumab in a two-centre phase I clinical trial. Eur Radiol. 2009;19(11):2728–38. doi: 10.1007/s00330-009-1469-4. [DOI] [PubMed] [Google Scholar]