A Note on the Minimax Solution for the Two-Stage Group Testing Problem

Abstract

Group testing is an active area of current research and has important applications in medicine, biotechnology, genetics, and product testing. There have been recent advances in design and estimation, but the simple Dorfman procedure introduced by R. Dorfman in 1943 is widely used in practice. In many practical situations, the exact value of the probability p of being affected is unknown. We present both minimax and Bayesian solutions for the group size problem when p is unknown. For unbounded p, we show that the minimax solution for group size is 8, while using a Bayesian strategy with Jeffreys’ prior results in a group size of 13. We also present solutions when p is bounded from above. For the practitioner, we propose strong justification for using a group size of between 8 and 13 when a constraint on p is not incorporated and provide useable code for computing the minimax group size under a constrained p.

1. INTRODUCTION

The purpose of this article is to propose a practical and simple group testing procedure that performs well in a wide range of situations. Group testing procedures save cost and time and have wide spread applications, including blood screening (Dorfman 1943; Finucan 1964; Gastwirth and Johnson 1994; Litvak, Tu, and Pagano 1994; Delaigle and Hall 2012; McMahan, Tebbs, and Bilder 2012; Tebbs, McMahan, and Bilder 2013), quality control in product testing (Sobel and Groll 1959, 1966), computation biology (De Bonis, Gasieniec, and Vaccaro 2005), DNA screening (Du and Hwang 2006; Golan, Erlich, and Rosset 2012), and photon detection (van den Berg et al. 2013). According to Hughes-Oliver (2006), group testing began as early as 1915, when it was used in dilution studies for estimating the density of organisms in a biological medium.

In his 1950 book, William Feller nicely described the group testing problem as (Feller 1950):

A large number, N, of people are subject to a blood test. This can be administered in two ways. (i) Each person tested separately. In this case N tests are required. (ii) The blood samples of k people can be pooled and analyzed together. If the test is negative, this one test suffices for the k people. If the test is positive, each of the k persons must be tested separately, and in all k + 1 tests are required for the k people. Assume the probability p that the test is positive is the same for all and that people are stochastically independent.

Procedure (ii) is commonly referred to as the Dorfman two-stage group testing procedure (DTSP; Dorfman 1943; Samuels 1978). Interesting historical comments related to this problem can be found in the introduction of the book by Du and Hwang (1999).

Let E(k, p) be the expected number of tests per person using DTSP with a group size k and probability of infection p. Then E(1, p) = 1 and E(k, p) = 1 − (1 − p)^k + k⁻¹ for k ≥ 2. An important issue for the DTSP is to find an optimal value of k, k^* = k^*(p), that minimizes the expected number of tests for a given p.

Samuels (1978) solved this optimization problem as follows. Let [x] and {x} = x − [x] denote the integer and fractional parts of x, respectively. k^* is a nonincreasing function of p, which is 1 for p > 1 − 1/3^1/3 ≈ 0.31, and otherwise is either 1 + [p^−1/2] or 2 + [p^−1/2]. If {p^−1/2} < [p^−1/2]/(2[p^−1/2] + {p^−1/2}), then k^* = 1 + [p^−1/2]. If {p^−1/2} > [p^−1/2]/(2[p^−1/2] + {p^−1/2}), then to find out which of the values k′ = 1 + [p^−1/2] or k″ = 2 + [p^−1/2] is optimal, one plugs them into E(k, p).

The DTSP is not an optimal procedure and can be improved by introducing more than two stages (e.g., Sobel and Groll 1959 for known p). However, the optimal testing algorithm (unknown p) is unknown, and it is a difficult optimization problem (Du and Hwang 1999). Ungar (1960) proved that if p > (3 − 5^1/2)/2 ≈ 0.38, then there does not exist an algorithm that is better than individual one-by-one testing. Sobel and Groll (1966) presented a Bayesian model for the multistage group testing problem based on a prior distribution of p. Schneider and Tang (1990) derived adaptive procedures for the two-stage group testing problem based on a beta prior distribution. Although the DTSP is not optimal, it is often used in practice due to its simplicity (Tamashiro et al. 1993; Moore et al. 2000; Westreich et al. 2008).

In many practical situations, the exact value p of the probability of being affected (e.g., disease prevalence) is unknown, and therefore the optimal group size cannot be calculated. In this note, we derive both the minimax group size as well as the Bayesian solution under reasonable prior distributions for the DTSP. A comparison of the solutions under these different alternatives will aid the practitioner in the design of future applications of group testing. We first present the loss function needed for the minimax solution.

2. LOSS FUNCTION

If we know the value of p, then by using the result from Samuels (1978) we achieve the minimum value for E(k, p) in DTSP by

$$E(k^{\ast }(p),p)=\{\begin{array}{cc}1-{(1-p)}^{k^{\ast }(p)}+\frac{1}{k^{\ast }(p)}& \text{for}0<p\le 1-{(1/3)}^{1/3}\\ 1& \text{otherwise.}\end{array}$$ (1)

where we can write the expected number of tests per person in a group of size k as

$$E(k,p)=\{\begin{array}{ccc}1-{(1-p)}^k+\frac{1}{k}& \text{for}& k>1\\ 1& \text{for}& k=1.\end{array}$$ (2)

It is important to note that according to Samuels (1978), k^*(p) is a nonincreasing function of p, and k^*(p) → ∞ as p ↓ 0. Combining this fact with (1) and using the particular form of k^*(p), it is possible to show (see Appendix B) that E(k^*(p), p) → 0, as p ↓ 0. Also, from Comment A.2 (Appendix A) it follows that E(k^*(p), p) is a nondecreasing function of p.

We define the loss in DTSP as a difference between the expected number of tests and the expected number of tests under an optimal DTSP. Specifically,

$$L(k,p)=E(k,p)-E(k^{\ast }(p),p).$$ (3)

It is important to note that this type of loss function was considered by Robbins (1952) for the two-armed bandit problem. Although Robbins (1952) discussed a different problem from ours, there is a similarity between the two problems in that both try to quantify the loss “due to ignorance of the true state of affairs” and to seek a minimax solution.

Another loss function is

$$L_2(k,p)=\frac{E(k,p)}{E(k^{\ast }(p),p)}-1,$$ (4)

which reflects a relative rather than absolute change. However, it cannot be used since lim_p↓0 E(k^*(p), p) = 0 and the measure becomes undefined when p is near 0. Also, it is important to note that the expected number of tests per person, E(k, p), itself is not an appropriate loss function for obtaining the minimax solution since E(k, p) is a nondecreasing function of p for any k (i.e., E(k, p) is maximized at the upper bound of p for all k).

3. MINIMAX SOLUTION FOR UNBOUNDED P

We define the minimax group size as a group size that minimizes the largest loss L(k, p),

$$k^{\ast \ast }=arg\underset{k\in {\mathbb{N}}^{+}}{min}\underset{p\in (0,1-{(1/3)}^{1/3}]}{sup}L(k,p).$$ (5)

From Equation (1) it follows that the DTSP has utility only when p is in the range (0, 1 − (1/3)^1/3], while individual testing is optimal outside this range. Also it is important to note that

$$\underset{p\in (0,1-{(1/3)}^{1/3}]}{sup}L(k,p)=\underset{p\in (0,1)}{sup}L(k,p)$$ (6)

(see Appendix B, Result B.1). In Appendix C, Lemma C.1, we are able to obtain a closed-form expression for k^** in (5). The proof uses the following two steps to show that k^** = 8.

• Step 1: Fix k, k ∈ {1, 2, 3,...,}. Find p^*(k) = arg sup_{p∈(0,1−(1/3)^1/3]} L(k, p).

• Step 2: Find k^**, where

  $$k^{\ast \ast }=arg\underset{k\in \{1,2,3,\dots \}}{min}L(k,p^{\ast }(k)).$$ (7)

In addition to the proof (see Appendix) we present a heuristic argument for finding the minimax solution, which we present as follows (we also use the same argument when additional information on an upper bound of p is incorporated: see Section 5).

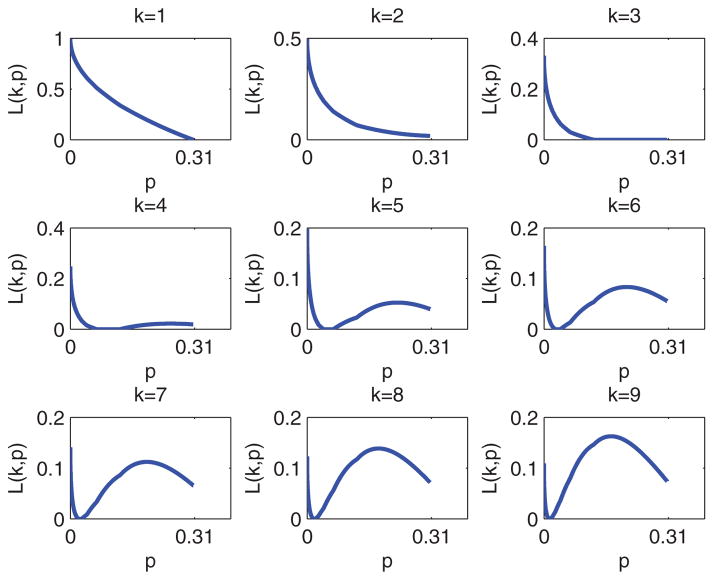
In Step 1, we performed a grid search with incremental steps of 10⁻⁶. We present the graphs of L(k, p) as a function of p ∈ (0, 1 − (1/3)^1/3] for k = 1,..., 9 (Figure 1). We noticed that p^*(1) = p^*(2) = ··· = p^*(7) = 0 and therefore L(k, p^*(k)) = 1/k for k = 1, 2,..., 7. It is clear that there is a jump at k = 8 for p^*(k), reflecting the worst case for p (largest loss) in Step 1.

Figure 1.

L(k, p) as a function of p ∈ (0, 1 − (1/3)^1/3].

Note that the loss function (3) is not a smooth function of p. In Result C.1 (Appendix C), we prove that L(k, p^*(k)) is a unimodal function of k for k ≥ 1. We also obtain a close-form expression for p^*(k) (see Remark C.1, Appendix C).

Table 1 presents the results of the maximization of the loss function (Step 1) as a function of p for a given k. The minimax solution is then obtained by minimizing the loss function as a function of k (Step 2) (we present Matlab code for the two-step procedure in Appendix D).

Table 1.

Two-step (heuristic) solution

k	1	2	3	···	7	8	9	10
p*(k)	0	0	0	···	0	0.178	0.167	0.158
L(k, p*(k))	1	1/2	1/3	···	1/7	0.138	0.162	0.184
k	25	50	100	1000		10,000
p*(k)	0.083	0.049	0.029	0.004		0.0005
L(k, p*(k))	0.382	0.516	0.628	0.858		0.949

As shown in Table 1, the minimax solution is k^** = 8. To evaluate the performance of the minimax solution, we compare it with the optimal solution assuming p is known. Specifically, we compare the optimal expected number of tests per individual E(k^*(p), p) with the minimax expected number of tests E(k^**, p). Table 2 presents the ratio of these two quantities defined as RE(p) = E(k^**, p)/E(k^*(p), p) for different values of p.

Table 2.

Relative efficiency of minimax design

p	0.0001	0.0005	0.001 0.005	0.01	0.05	0.10	0.25	0.30
RE(p)	6.305	2.900	2.118 1.181	1.034	1.082	1.169	1.124	1.078
REJ1 (p)	3.921	1.875	1.432 1.007	1.020	1.322	1.385	1.156	1.078

Table 2 suggests that as long as p is not very small (p < 0.005), the minimax solution is close to optimal. In the situation where we believe that p is very small and we know the upper bound for p, we can obtain the minimax solution in the restricted parameter space. This is discussed in Section 5. In Table 2, we also present the relative performance of the Bayesian solution under a Jeffreys’ prior to the optimal solution as the ratio ${\text{RE}}_{J_1}(p)=E(k_{J_1}^{\ast },p)/E(k^{\ast }(p),p)$, where $k_{J_1}^{\ast }$ is the optimum group size under a Jeffreys’ prior. This will be discussed in Section 4.

In practice, it is useful to identify the range of the values of p for which minimax design k^** = 8 is optimal. More specifically, for any group size l we can compute the range [ $p_l^{\ast },p_l^{\ast \ast }$] of the values of p for which the group size l is optimal. The derivation of $p_l^{\ast }$ and $p_l^{\ast \ast }$ is presented in Appendix A as Proposition A.1. As a consequence of Proposition 1, we find that the minimax design is optimal over a range of p of $p_8^{\ast }=0.0157$ to $p_8^{\ast \ast }=0.0206$.

In the next section, we propose a Bayesian alternative to the minimax solution.

4. BAYESIAN SOLUTION

For the Bayesian design, we are required to specify a prior distribution π(p) for the probability p of being affected. The basic assumption of our model is that the affected status X_i, i = 1, 2,... are iid Bernoulli random variables with parameter p (i.e., X_i | p ~ Ber(p)). Under the Bayesian consideration with the specified prior distribution p, the analog to the loss function (3) is

$$L_{\pi }(k)=\int L(k,p)\pi (p)dp=E_{\pi }(k)-E_{\pi }^{\ast },$$ (8)

where E_π (k) = ∫ E(k, p) π (p) dp, $E_{\pi }^{\ast }=\int E(k^{\ast }(p),p)\pi (p)dp$. After choosing a prior, the loss function $L_{\pi }(k)=E_{\pi }(k)-E_{\pi }^{\ast }$ is a function of k only, and the optimal value of k is simply,

$$k_{\pi }^{\ast }=\underset{k}{min}L(k,\pi )=\underset{k}{min}{E}_{\pi }(k).$$ (9)

It is clear that the optimal group size $k_{\pi }^{\ast }$ in (7) is a function of the prior distribution π.

4.1 Uniform Prior

If we do not have any prior information about the disease prevalence p, that is, all values of p are equally likely, then the uniform prior is reasonable. Denote the uniform prior by π = I_U, where U is an upper bound of the distribution support, and E_π (k) can be written as

$$E_{I_U}(k)=1+\left\{\frac{1}{k}+\frac{1}{k+1}({(1-U)}^{k+1}-1)\right\}{1}_{\{k>1\}}.$$ (10)

For unbounded p, U = 1, $E_{I_1}(k)=1+\frac{1}{k}{1}_{\{k>1\}}$, and therefore $k_{I_1}^{\ast }=1$. As we will discuss in Section 5 (see Tables 3, 4, and E.1), the Bayesian solution is not 1 for bounded p (i.e., U < 1).

Table 3.

Minimax and Bayesian solution (group size) when upper bound U of p is specified

U	0.0001	0.0005	0.001	0.005	0.01	0.05	0.10	0.15	0.30
$k_U^{\ast \ast }$	201	91	64	30	21	11	8	8	8
$k_{I_U}^{\ast }$	142	64	45	21	15	7	5	5	4
$k_{J_U}^{\ast }$	181	79	56	25	18	9	7	6	5

Table 4.

Relative efficiencies of restricted minimax and Bayesian designs

	U = 0.0005			U = 0.005			U = 0.05
p	0.0001	0.0003	0.0005	0.001	0.003	0.005	0.005	0.01	0.05
REU(p)	1.0048	1.0994	1.2474	1.0028	1.1055	1.2433	1.0392	1	1.2249
REIU(p)	1.1030	1.0044	1.0596	1.0901	1.0060	1.0606	1.2749	1.0778	1.0429
REJU(p)	1.0289	1.0461	1.1556	1.0310	1.0392	1.1343	1.1159	1.0103	1.1282
k*(p)	101	58	45	32	19	15	15	11	5
$k_U^{\ast \ast }$	91	91	91	30	30	30	11	11	11
$k_{I_U}^{\ast }$	64	64	64	21	21	21	7	7	7
$k_{J_U}^{\ast }$	79	79	79	25	25	25	9	9	9

4.2 Jeffreys’ Prior

Another possibility is to find a prior distribution π(p) that has a small effect on the posterior π(p|x) distribution. Thus, we want to find a prior distribution π(p) that produces the maximum value of the Kullback–Leibler information, K(π(p | x), π (p)), for discrimination between two densities, π(p) and π(p | x), where the latter is the posterior that reflects the sampling density. The Kullback–Leibler information for discrimination between two densities, f and g is defined as

$$K(f,g)=E_f\left(log\frac{f}{g}\right).$$ (11)

A prior that maximizes the Kullback–Leibler information is by default a reference prior (for the general discussion of choosing a reference prior, we refer to Jeffreys (1946), Berger, Bernardo, and Sun (2009), and Shemyakin (2014)). The above approach to the construction of the reference prior is due to Bernardo (1979) (an excellent summary is given in Lehmann and Casella 1998 and the recent developments in Berger, Bernardo, and Sun 2009, 2012). We cannot directly use K(π (p | x), π (p)) because it is a function of x. Therefore, we consider the expected value of K(π (p | x), π (p)) with respect to the marginal distribution of X, which is the Shannon information

$$S(\pi )=\int K(\pi (p\mid x),\pi (p))m_{\pi }(x)dx,$$ (12)

where m_π (x) = ∫ f (x|p) π (p)dp is the marginal distribution of X.

The following lemma is due to Clarke and Barron (1990) and is taken from Lehmann and Casella (1998):

Lemma 1

Let X₁,..., X_n be an iid sample from f (x|p), and let S_n(π) denote the Shannon information of the sample. Then, as n → ∞,

$$S_n(\pi )=\frac{1}{2}log\frac{n}{2\pi e}+\int \pi (p)log\frac{{\mid I_n(p)\mid }^{1/2}}{\pi (p)}dp+o(1),$$ (13)

where I_n(p) is the Fisher information contained in the sample X₁,..., X_n, and o(1) is a notation of the function h(n) = o(1) such that h(n) → 0 as n → ∞.

The Fisher information contained in the sample of size n is defined as

$$I_n(p)=-E\left\{\frac{{\partial }^2}{\partial p^2}logf(X_1,\dots ,X_n\mid p)\right\}=\frac{n}{p(1-p)}.$$ (14)

The last equality in (14) is because X_i given p follows a Bernoulli distribution.

From Jensen’s inequality, it follows that the right-hand side of Equation (13) is maximized when the prior distribution is proportional to the square root of the Fisher information, that is,

$${\pi }_J(p)=arg\underset{\pi }{sup}{S}_n(\pi )\propto {\mid I_n(p)\mid }^{1/2}\propto \frac{1}{{(p(1-p))}^{1/2}}.$$ (15)

The last expression $\frac{1}{{(p(1-p))}^{1/2}}$ in (15) is known as Jeffreys’ prior (see, e.g., Lehmann and Casella 1998), where the normalizing constant for Jeffreys’ prior is

$$c_U={\int }_0^U\frac{1}{{(p(1-p))}^{1/2}}dp=2arcsin\sqrt{U}.$$ (16)

Under this approach if 0 < p ≤ U ≤ 1, then

$${\pi }_J(p)=\frac{1}{c_U}\frac{1}{{(p(1-p))}^{1/2}}.$$

Under this prior, the expected number of tests per person with a group size k is

$$E_{J_U}(k)=\frac{1}{c_U}{\int }_0^{U}E(k,p)\frac{1}{{(p(1-p))}^{1/2}}dp.$$ (17)

Numerically evaluating (17) (Appendix D), the optimum group size under a Jeffreys’ prior is

$$k_{J_1}^{\ast }=arg\underset{k}{min}{E}_{J_1}(k)=13.$$

First, from a Bayesian perspective, the minimax design performs well relative to the optimal Bayesian design under a Jeffreys’ prior (i.e., E_J1(13)/E_J1 (8) = 0.9219/0.9286 = 0.993). From a frequentist point of view, the Bayesian design performs well for small p but not as well as the minimax design for p > 0.01 (see the third row of Table 2, where ${\text{RE}}_{J_1}(p)=E(k_{J_1}^{\ast },p)/E(k^{\ast }(p),p))$.

It is important to note that theoretically we can define the min-imax group size under the Bayesian setup (see, e.g., Ferguson 1967, p. 57) in the following way:

$$k_B^{\ast }=\underset{k}{min}\underset{\pi }{sup}{L}_{\pi }(k).$$

Unfortunately, maximization with respect to all possible prior distributions π(p) is intractable. Even if we consider a beta prior, the problem remains intractable unless we limit the range of the parameters.

5. MINIMAX AND BAYESIAN SOLUTIONS FOR BOUNDED p

Define the minimax solution in the restricted parameter space (when we know an upper bound U of p) as

$$k_U^{\ast \ast }=arg\underset{k\in {\mathbb{N}}^{+}}{min}\underset{p\in (0,U]}{sup}L(k,p).$$ (18)

The minimax solution subject to an upper bound on p denoted as $k_U^{\ast \ast }$ can be evaluated with a two-step procedure similar as to that presented in Section 3. The difference is that the support of p is changed to (0, U] and the grid step is changed accordingly. Table 4 demonstrates both minimax and Bayesian solutions in the restricted parameter space of p (only the upper bound is specified).

Define ${\text{RE}}_U(p)=E(k_U^{\ast \ast },p)/E(k^{\ast }(p),p)$ as an index of the efficiency of the minimax test (in the restricted parameter space) relative to that of the optimal DTSP test. In Table 4, we present RE_U(p) for different values of U and p.

A comparison between Tables 2 and 4 demonstrates the clear advantage of a minimax estimator in the restricted parameter space in comparison to the minimax estimator in the unrestricted parameter space. For example, when p = 0.001, bounding the parameter space by U = 0.005 increases the relative efficiency by 2.11(= 2.118/1.0028). Table 4 shows that the minimax solution in the restricted parameter space performs the worst relative to an optimal design when p = U.

In Table 4, we also present the performance of the optimal Bayesian (under Uniform and Jeffreys’ priors) design in the restricted parameter space. In the restricted parameter space, the optimal group size under Jeffreys’ prior is $k_{J_U}^{\ast }=arg{min}_k{E}_{J_U}(k)$, where E_JU(k) can be evaluated using (16) and (17) for a particular upper bound U. The ninth row in Table 4 presents $k_{J_U}^{\ast }$, and the fifth row presents the relative efficiency ${\text{RE}}_{J_U}(p)=E(k_{J_U}^{\ast },p)/E(k^{\ast }(p),p)$. The optimal Bayesian group size for bounded p is similar to the minimax group size, with the relative efficiencies of both designs being near optimum.

6. SUMMARY

This note presents both unconstrained and constrained minimax group size solutions for group testing within the DTSP framework. We found that a group size of eight is the unconstrained minimax solution. We also present novel methodology to evaluate the range of the values of p for which the minimax design is optimal. When we have prior information that establishes an upper bound on p, we show that the constrained performs substantially better than the unconstrained minimax. An advantage of the minimax solution is their simplicity within the two-stage group testing framework. In addition, we developed a Bayesian design under both constrained and unconstrained settings, which in most cases performed similarly to the minimax design in terms of the relative efficiency. This article has important design implications in practice. For example, Pilcher et al. (2004) used a DTSP with a group size of 10 to detect acute HIV infection. This is consistent with our design result that suggested a group size of between 8 and 13 given that no information on the primary infection rate (p) was known a priori. Further, with known constraint on support of p, we provide computer code (Appendix D) that easily can be applied by the practitioner. Research in more general algorithms (e.g., more than two-stage) is needed, but any such algorithm will be complex and difficult for the practitioner to implement.

APPENDIX A. INVERSE OF THE SAMUELS RESULT

Proposition A.1

Let q = 1 − p. Define $q_2^{\ast }=1/3^{1/3}$ and $q_l^{\ast }$, l ≥ 3 be the larger real root of equation $q^l(1-q)=\frac{1}{l(l+1)}$. If q ≤ 1/3^1/3, then k^*(q) = 1. If q > 1/3^1/3 and $q_{l-1}^{\ast }<q<q_l^{\ast }$, l ≥ 3, then k^*(q) = l.

For example, for the minimax group size k^** = 8, $q_8^{\ast }\approx 1-0.0157$ is the larger real root of equation $q^8(1-q)-\frac{1}{8(8+1)}=0$, and $q_7^{\ast }\approx 1-0.0206$ is the larger real root of equation $q^7(1-q)-\frac{1}{7(7+1)}=0$. Therefore, the minimax group size k^** = 8 is optimal for any q in the range (1 − 0.0206, 1 − 0.0157) or, alternatively, for any p in the range (0.0157, 0.0206).

Comment A.1

The Corollary in Samuels (1978) (Equation (2)) provides the lower and upper bounds for E(k^*(p), p). The upper bound is not sharp, and in fact is invalid since it is greater than one when p is larger than 0.1485 (since 0.1485 is the real zero of 4x³ + 2x − 1, x = p^1/2). A simple upper bound for E(k^*(p), p) follows directly from Proposition A.1: if p ≤ 1 − 1/3^1/3, then E(k^*(p), p) < E(3, p) = 1 − q³ + 1/3.

Proof of Proposition A.1

We obtain the proof from the analyzing Samuels (1978) method. Assume that p ≤ 1 − 1/3^1/3. First, from the Samuels (1978) theorem (Section 1), it follows that k^*(p) ≥ 2. Second, Proposition 1 in Samuels (1978) says that k^*(p) is never 2. Therefore, k^*(p) should be at least 3. Third, following Samuels (1978) notation, define r₁(k) and r₂(k) as the smaller and larger roots of the equation

$$\begin{array}{l}{\mathrm{\Delta }}_k(q)=E_{k+1}(q)-E_k(q)\\ =q^k(1-q)-\frac{1}{k(k+1)}=0,k\ge 3.\end{array}$$ (A.1)

Samuels (1978) showed that $\frac{k}{k+1}={max}_q{\mathrm{\Delta }}_k(q),{\mathrm{\Delta }}_k(\frac{k}{k+1})>0$, Δ_k (0) = Δ_k (1) < 0 and that both r₁(k) and r₂(k) are increasing functions of k. Combining points one to three, we can conclude that if q < r₂(3) then E₃ < E₄, if q < r₂(4) then E₄ < E₅, and so on. The inequality r₂(3) < r₂(4) < ⋯ completes the proof.

Comment A.2

It follows from the proof of Proposition A.1 that E(k^*(p), p) is a nondecreasing function of p, p ∈ (0, 1).

APPENDIX B. SUPPORT OF THE LOSS FUNCTION WITH RESPECT TO p

Result B.1

sup_{p∈(0,1−(1/3)^1/3]}L(k, p) = sup_p∈(0,1) L(k, p).

Proof

First we show that lim_p↓0 E(k^*(p), p) = 0. Recall, that according to Samuels (1978), if 0 < p ≤ 1 − (1/3)^1/3 then k^* is 1 + [p^−1/2] or 2 + [p^−1/2] and in this case from (1) we have $E(k^{\ast }(p),p)=1-{(1-p)}^{k^{\ast }(p)}+\frac{1}{k^{\ast }(p)}$. Specifically, for any p satisfies 0 < p ≤ 1 − (1/3)^1/3, we have 1 > (1 − p)^k*(p) ≥ (1 − p)^2+p−1/2. From the facts that lim_p↓0(1 − p)² = 1 and ${lim}_{p\downarrow 0}\frac{1}{p^{1/2}}log(1-p)=0$, it follow that lim_p↓0(1 − p)^k*(p) = 1. Combining this with Samuels (1978) result that k^*(p) → ∞ as p ↓ 0, we prove that lim_p↓0 E(k^*(p), p) = 0.

For k = 1. We have L(1, p) = 1 − E(k^*(p), p). Hence, sup_p∈(0,1) L(1, p) = 1 − inf_p∈(0,1) E(k^*(p), p) = 1 − lim_p↓0 E(k^*(p), p), where the last equation follows from Comment A.2. Therefore,

$$\underset{p\in (0,1-{(1/3)}^{1/3}]}{sup}L(1,p)=\underset{p\in (0,1)}{sup}L(1,p).$$ (B.1)

For k ≥ 2. Define p₀ = 1 − (1/3)^1/3. For any p ∈ (p₀, 1), from (1) and (3) it follows that L(k, p) = E(k, p) − 1 = 1/k − (1 − p)^k is an increasing function of p, and therefore from (1) and (2) it follows that

$$\underset{p\in (p_0,1)}{sup}L(k,p)=E(k,1)-1=1/k.$$ (B.2)

Again, from Comment A.2 and (2), it follows that lim_p↓0 L(k, p) = 1/k. Therefore,

$$\underset{p\in (0,p_0]}{sup}L(k,p)\ge 1/k.$$ (B.3)

Combining, (B.2) and (B.3), we get

$$\underset{p\in (0,p_0]}{sup}L(k,p)\ge \underset{p\in (p_0,1)}{sup}L(k,p).$$ (B.4)

Equations (B.1) and (B.4) complete the proof.

APPENDIX C. BEHAVIOR OF p^*(k) AND UNIMODALITY OF L(k, p^*(k))

Result C.1

p^*(k) = 0, for k = 1, 2, . . ., 7, $p^{\ast }(8)=1-{(\frac{3}{8})}^{1/(8-3)}\approx 0.178$. Moreover, L(k, p^*(k)) is a unimodal function of k for k ≥ 1.

Proof

Define q₀ = 1 − p₀. Recall that it was shown in (B.3) that sup_p∈(0,p0] L(k, p) ≥ 1/k. Also we have lim_p↓0 L(k, p) = 1/k. Therefore, if sup_p∈(0,p0] L(k, p) = 1/k, then p^*(k) = 0, and if sup_p∈(0,p0] L(k, p) > 1/k then p^*(k) > 0. Now L(k, p) > 1/k if and only if

$$q^{k^{\ast }}-q^k>\frac{1}{k^{\ast }}.$$ (C.1)

It is clear, that the necessary condition for the inequality (C.1) is

$$k^{\ast }<k.$$ (C.2)

We know (Samuels 1978 and Proposition A.1 above) that for q > q₀, k^* is a piecewise nonincreasing (nondecreasing) function of p(q) and k^* is at least 3. From this and (C.2), it follows that p^*(k) = 0, for k = 1, 2, 3. Using Proposition A.1, we can verify that for k = 7, there does not exist a q (q ∈ [q₀, 1)) such that (C.1) holds. From direct logic it follows that if there exists q such that Equation (C.1) holds for k′, then (C.1) holds for any k > k′. It is the same to say that if for any q (in the appropriate range) the Equation (C.1) does not hold for k″, then it does not hold for any q and for any k < k″. Therefore, p^*(k) = 0 and L(k, p^*(k)) = 1/k, for k = 1, 2, . . ., 7.

Again using Proposition A.1, we can verify that for k = 8, Equation (C.1) holds only for some values of q that corresponds to k^* = 3. Therefore, finding sup_p∈(0,p0] L(8, p) is equivalent to finding ${sup}_{q_2^{\ast }<q<q_3^{\ast }}\{q^3-q^8\}$, where $q_2^{\ast }$ and $q^{\ast }(8)=q_3^{\ast }$ are defined in Proposition A.1. A simple calculation then shows that q^*(8) = (3/8)^1/5 (correspondingly p^*(8) = 1− (3/8)^1/5 ≈ 0.1781) and L(8, p^*(8)) = 437/3152 ≈ 0.1386.

From above, it follows that for k ≥ 8, there exists a q such that $q_2^{\ast }<q<q_3^{\ast }$ and Equation (C.1) holds. Now, for such a q, it follows from the last inequality from the last paragraph in the proof of Proposition A.1 that L(9, p) − L(8, p) = E(9, p) − E(8, p) > 0, p = 1 − q. Therefore,

$$\begin{array}{l}L(8,p^{\ast }(8))=\underset{p\in (0,p_0]}{sup}L(8,p)<\underset{p\in (0,p_0]}{sup}L(9,p)\\ =L(9,p^{\ast }(9)).\end{array}$$ (C.3)

Proceeding by induction on k = 10, 11, . . . we complete the proof of unimodality of L(k, p^*(k)) for k ≥ 1.

Remark C.1

The function p^*(k) is a decreasing function of k for k ≥ 8 and p^*(k) has a form 1 − (k^*/k)^1/(k−k*) for k ≥ 8 and for k^* that satisfied Equation (C.1) and the condition $q_{k^{\ast }-1}^{\ast }<q<q_{k^{\ast }}^{\ast }$ of Proposition A.1. But we have not proved it rigorously.

Lemma C.1

k^** = 8.

Proof

Follows immediately from Result C.1 and the proof that L(k, p^*(k)) is the unimodal function of k with the minimum at k = 8.

APPENDIX D: MATLAB CODE

1. Matlab function “MinMaxValue,” which has input K and uses all three functions (ii), (iii), (iv) given below.

   function minmax=MinMaxValue(K,U)

   R=[];

   step=1/1000000;

   for k=1:1:K

   output=zeros(1000001,3);

   counter=0;

   for p=0:step:U

   counter=counter+1;

   prophet=ProphetNumberTestPerPerson(p);

   player=PlayerNumberTestPerPerson(p,k);

   l=player-prophet; output(counter,:)=[k p l];

   end

   m=max(output(:,3)); pl=find(output(:,3)==m); R=[R;output (pl,:)];

   end

   mm=min(R(:,3)); mmm=find(R(:,3)==mm); minmax=R(mmm, 1);

2. Matlab function “OptimalGroupSize,” which has input p ∈ (0, 1) and the output is the optimum group size k^*(p) (based on Samuels 1978):

   function kOpt=OptimalGroupSize(p)

   if p <= 1 − (1/3)^1/3;

   q = 1 − p; w = p^(−1/2);

   int=floor(w); frl=w-int;

   I nd = (f rl < int/(2 * int + f rl));

   k1 = int + 1; k2=int+2;

   f 1 = 1/k1 + 1 − q^k1; f 2 = 1/k2 + 1 − q^k2;

   f = min(f 1, f 2); I nd1 = (f == f 1);

   kOpt = ((1 + int)^{I nd}) * (((k1)^{I nd1}) * ((k2)^{1−I nd1}))^{1−I nd};

   else

   kOpt = 1;

   end

3. Matlab function “PlayerNumberTestPerPerson” calculates the expected number of tests per person in a group of size k with probability of infection p.

   function player=PlayerNumberTestPerPerson(p,k)

   q=1−p;

   player= 1 − q^k + 1/k;

4. Matlab function “ProphetNumberTestPerPerson” calculates the expected number of tests per person in a group of the optimal size k^*(p) with probability of infection p.

   function prophet=ProphetNumberTestPerPerson(p)

   kOpt=OptimalGroupSize(p); q=1−p; prophet = 1 − q^{k Opt} + 1/kOpt;

5. Matlab function “JeffreyOptGroupsize” calculates the optimal group size under Jeffreys’ prior with upper bound for support of p equal to U.

   function kj=JeffreyOptGroupsize(U)

   S=[];

   for k=1:1:400

   s=PlayerNumTestPerBetta1(k,U,1/2,1/2); S=[S;k s];

   end

   m=min(S(:,2)); l=find(S(:,2)==m);kj=S(l,1);

6. Matlab function “PlayerNumTestPerBetta1” calculates the expected number of tests under Beta prior with upper bound for support of p equal to U.

   function player=PlayerNumTestPerBetta1(k,U,a,b)

   c = @(p)p^(a−1) * (1 − p)^(b−1);

   f = @(p)(1 − ((1 − p)^k) + 1./k) * p^(a−1) * (1 − p)^(b−1);

   player = (quad(c, 0, U))⁽⁻¹⁾ * quad(f, 0, U);

APPENDIX E. RELATIVE EFFICIENCY

Table E.1.

Relative efficiencies of restricted minimax and Bayesian designs

	U = 0.10			U = 0.20			U = 0.30
p	0.01	0.05	0.10	0.10	0.15	0.20	0.20	0.25	0.30
REU(p)	1.0342	1.0830	1.1694	1.1694	1.1853	1.1655	1.1655	1.1244	1.0778
REIU(p)	1.2732	1	1.0263	1	1.0122	1.0232	1.0232	1.0243	1.0198
REJU(p)	1.0778	1.0429	1.1190	1.0263	1.0516	1.0621	1.0621	1.0562	1.0420
k*(p)	11	5	4	4	3	3	3	3	3
$k_U^{\ast \ast }$	8	8	8	8	8	8	8	8	8
$k_{I_U}^{\ast }$	5	5	5	4	4	4	4	4	4
$k_{J_U}^{\ast }$	7	7	7	5	5	5	5	5	5