Confirmatory factor analysis and invariance testing between Blacks and Whites of the Multidimensional Health Locus of Control scale

Abstract

The factor structure of the Multidimensional Health Locus of Control scale remains in question. Additionally, research on health belief differences between Black and White respondents suggests that the Multidimensional Health Locus of Control scale may not be invariant. We reviewed the literature regarding the latent variable structure of the Multidimensional Health Locus of Control scale, used confirmatory factor analysis to confirm the three-factor structure of the Multidimensional Health Locus of Control, and analyzed between-group differences in the Multidimensional Health Locus of Control structure and means across Black and White respondents. Our results indicate differences in means and structure, indicating more research is needed to inform decisions regarding whether and how to deploy the Multidimensional Health Locus of Control appropriately.

Introduction

The current “crisis in healthcare” has produced an increased focus on identifying variables which are related to health behavior, health status, and healthcare utilization which may be amenable to intervention. For example, the new variable, “patient activation,” and the somewhat older variable of “self-efficacy” have both been explored recently in relation to hospital and emergency department (ED) utilization patterns (Begum et al., 2011; Greene and Hibbard, 2011). Health locus of control (LOC), defined as an individual’s belief system about control over health outcomes (Wallston et al., 1976), is one variable which has been examined in this context (Bazargan et al., 1998; Chambers et al., 2013). While the evidence for a relationship between health LOC and health outcomes or utilization is mixed, there have been many studies examining the construct of health LOC in general and the Multidimensional Health Locus of Control (MHLC) scale (Wallston, 2005) in particular. Health LOC has been measured using the MHLC scale for the past 40 years (Wallston et al., 1976, 1978). Despite this long history of use, some questions regarding the underlying structure of the MHLC tool remain, and there is a need for testing structure across racial, ethnic, and/or cultural groups. Since application of a valid measurement device is imperative for studies identifying predictor variables in relation to health, further investigation of the proper application and interpretation of the MHLC is needed.

In this article, we review the published literature on exploratory factor analysis (EFA) and confirmatory factor analysis (CFA) of the MHLC scale and then present a CFA of the scale performed on data collected in a large urban sample. We also provide evidence bearing on the factor structure and mean differences between Black and White respondents in our sample.

The MHLC scale focuses on the individual difference variable LOC specifically as it pertains to health conditions and/or health-related behaviors (Wallston et al., 1976). It comprises three subscales: the Internal subscale represents the degree to which a person believes he or she is in control of his or her own health. The Powerful Others subscale (External) indicates the extent to which a person perceives that others (e.g. doctors and important others) control his or her health, while the Chance subscale represents the degree to which one views fate and luck as controlling one’s health outcomes. While not without debate, the construct validity of the MHLC appears to hold for some health behaviors, under certain conditions. For example, those who have a high Chance health LOC orientation are likely to be less engaged in positive health behaviors, whereas those high on the Internal dimension are more likely to have a health-oriented approach (Ludenia and Donham, 1983; Norman and Bennett, 1996). Researchers have demonstrated a relationship between health LOC and patients’ healthcare utilization in specific contexts (Bazargan et al., 1998; Chambers et al., 2013; Goldsteen et al., 1994). Patients who scored higher on the Powerful Others and/or Chance dimensions were likely to have higher utilization rates, while those who scored higher on the Internal construct were likely to have fewer visits to the ED, fewer hospital admissions, and fewer ambulatory physician visits (Bazargan et al., 1998; Chambers et al., 2013). Similarly, Goldsteen et al. (1994) also reported that patients with more of a Powerful Others locus of control (PLOC) and/or Chance locus of control (CLOC) were likely to have a higher incidence of hospitalizations and physician visits. Additionally, patients’ PLOC has been shown to positively correlate with trust in physicians (Brincks et al., 2010).

The MHLC scale

We conducted a thorough review of the literature, including unpublished studies, of EFA and CFA of the MHLC scale; however, this should not be construed as a systematic review.

The MHLC scale has two equivalent versions—Form A has typically been used with samples of generally healthy individuals, while Form B has historically been used with participants faced with chronic illness(es) (Chaplin et al., 2001). Wallston (2005) claimed that Forms A and B are nearly equivalent based on strong correlations between the subscales across forms (Wallston et al., 1978) and across studies; thus, the research reviewed below concerning the factor structure of the scale will be limited to only those studies in which Form A and/or Form B was administered. We omit discussion here of the more recent Form C, designed to be used with patients who have an existing medical condition and assesses health LOC specific to one’s illness or disease (Wallston et al., 1994). We also omit discussion here of the final member of the family of MHLC instruments, the God Locus of Health Control (Wallston et al., 1999).

Factor structure

The current three-subscale structure implies that there are three underlying dimensions being measured with the 18 items, and many studies have supported this structure. However, there is also support for a two-factor structure, which generally suggests that items comprising the Powerful Others external and Chance external LOC subscales arise from the same underlying latent variable. Our literature review did not unequivocally support either a two- or a three-factor model structure. We found 15 EFA studies, 8 CFA studies, and 2 studies that presented both EFA and CFA of the scale. These studies are reviewed below and summarized in Table 1. Of note in this review is that of the eight CFA studies we found, six used sample sizes of less than 250.

Table 1.

Summary of CFA and EFA studies of the MHLC.

Reference	Analysis type (EFA/CFA/both)	MHLC form	Sample	Result	Notes
EFA
Astrom and Blay (2002)	Principal component analysis	Unspecified	504 Ghanaian adolescents	2 factors (1: Powerful Others and Chance; 2: Internal). 41% PVE	Included only 4 of the 6 PHLC items
Casey et al. (1993)	Principal component analysis, varimax rotation	A	678 participants	3 factors. 41.5% PVE
Coelho (1985)	Principal component analysis	A	146 chronic cigarette smokers (53 men)	2 factors (1: Internal; 2: Powerful Others). 74% PVE
Cooper and Fraboni (1990)	Principal component analysis, varimax rotation	A and B	82 staff members at a psychiatric hospital	2-factor solution (1: Internal; 2: Chance and Powerful Others). PVE not reported
Buckelew et al. (1990)	Least squares with oblimin rotation	Unspecified	160 patients in a pain clinic	3 factors, PVE not reported	Separation between Chance and Powerful Others factors appeared adequate (r = .03)
Hartke and Kunce (1982)	EFA unspecified extraction	A	86 medical patients	3 factors. PVE not reported	16 of the 18 items had their highest loading on the factor that corresponded to their appropriate subscale
Hisama and Kinoshita (1997)	Extraction with varimax rotation	Unspecified	339 Japanese college students	4 factors with eigenvalues >1.5. PVE not reported	5/6 Internal and External items but 3/6 Chance items, loaded to the subscale factors
Russell and Ludenia (1983)	Principal axis factoring with varimax rotation	A and B	100 inpatients on the Alcohol dependency Treatment Unit at a Veterans Administration Medical Center	3-factor solution. PVE not reported	Combined items from Forms A and B and created 12-item subscales as opposed to 6-item subscales
Stanton et al. (1995)	Principal component analysis	Unspecified. Adapted items were from Form A	Adolescents from New Zealand, Time 1 (age: 13 years): N = 721; Time 2 (age: 15 years): N = 837	2 factors: Time 1 at age 13 years (1: Internal and Powerful Others; 2: Chance along with 2 PHLC items). Time 2 at age 15 years (1: Internal and Chance; 2: Powerful Others).	Longitudinal study. Item 4 did not load highly on any factor at either age
Marshall et al. (1990)	Principal component analysis with varimax rotation	A	181 Veterans Administration medical outpatients	3 factors. 41% PVE	17 of the 18 items had significant loadings only with their a priori subscale. Item 7 did not load on PLOC subscale
Moshki et al.(2007)	Principal component analysis	A	496 Iranian college students	3 factors 59% PVE	3 factors corresponded closely to Wallston et al.’s (1978) model; Item 14 did not load on PLOC
O’Looney and Barrett (1983)	EFA performed separately for males and females—principal component analysis with direct oblimin rotation	A and B	70 male and 77 female British college students	Female: 3 factors 44% PVE on Form A and 48% on Form B Male: 2 factors (1: Internal and Chance; and 2: Powerful Others). 38% PVE on Form A and 41.3% on Form B	Overall, the items loaded on their a priori subscales
Paine et al. (1994)	Principal axis factoring with oblimin rotation	18 items adapted from Forms A and B	280 middle-class Brazilians (208 women)	3 factors 25% PVE	5 items loaded on PHLC; Item 7 did not load. 5 items loaded on CHLC. 6 items loaded on IHLC; 1 item (Item 15) identified a priori as loading on CHLC loaded on IHLC
Umlauf and Frank (1986)	Principal axis analysis with orthogonal rotation	A	107 inpatients staying at a rehabilitation unit	2 factors (1: Internal and 2: Powerful Others and Chance). Results did not confirm independence of subscales. Factor 1 comprises 3 CHLC items and 2 PHLC items. Factor 2 was the same as Wallston et al.’s (1978) Internal factor. Factor 3 included 3 CHLC items and 2 PHLC items
Wall et al. (1989)	Principal axis analysis with orthogonal rotation and CFA	A and B	60 psychiatric patients	EFA results: 3 factors CFA results: support for a reasonable fit of the 3-factor model solution	Originally, combined items from Forms A and B and created 12-item subscales as opposed to 6-item subscales. Due to multicollinearity, parallel items from both forms were averaged together
Winefield (1982), Study 1	Principal components with varimax rotation	A	152 first-year medical and dental students	2 factors (1: Internal and 2: Powerful Others). Less coherence found for the Chance subscale. Items 14, 15, and 16 did not load on any factor
CFA
Malcarne et al. (2005)	CFA, then EFA	A	College students: 1122 Caucasian Americans, 281 Filipino Americans, and 462 Latino Americans	Did not demonstrate a good fit to 3-factor model using CFA. Using EFA, found evidence of 3 factors; 3 items loaded on each factor
Hubley and Wagner (2004)	CFA	A and B	245 non-clinical participants	Form A: 3 factor produced marginal fit; Form B did not provide adequate fit
Hewson and Charlton (2005)	CFA on 2-factor and 3-factor models	A	Internet data (N = 167). Paper data (N = 200)	3-factor model provided better fit than 2-factor model for both samples, although the fit as still fair at best	Internet data were nearly equivalent to paper data at reproducing factor structure of MHLC
Robinson-Whelen and Storandt (1992)	CFA	B	197 non-diabetic and 171 diabetic adults	CFA using 14 items yielded fairly good fit of the model for both diabetic and non-diabetic samples	4 items (1, 7, 14, and 15) were removed because they loaded on more than one factor
Talbot et al. (1996)	CFA on 2-factor and 3-factor models	A	224 non-clinical group of college students; 132 diabetics	Neither a 2-factor nor a 3-factor model provided a good fit, although 3-factor model was better. Invariance testing revealed differences across the non-clinical and clinical groups in terms of the structure of the MHLC (specifically items 3 and 13)	Model-fitting for a 3-factor model was continued using modifications that included 9 correlated error covariances. This final model provided satisfactory fit
Kelly et al. (2006)	CFA		1206 from 3 osteoarthritis studies	3-factor model was a good fit when 2 items were removed. Invariance testing detected no differences between men and women
Gehlert and Chang (1998)	CFA		143 epileptic patients	Supported 3-factor model
Gala et al.(1995)	CFA		524 non-clinical sample	Supported 3-factor model

CFA: confirmatory factor analysis; EFA: exploratory factor analysis; MHLC: Multidimensional Health Locus of Control; PVE: proportion of variance explained; PLOC: Powerful Others locus of control; External: Powerful Others External.

Factor solution refers to the a priori 3 factor structure.

Two-factor model structure: EFA

Cooper and Fraboni (1990) collected data from 82 staff members at a psychiatric hospital and reported high item-factor loadings for the Internal subscale (for both Forms A and B), but a less clear distinction between the item-factor loadings for the Chance and Powerful Others latent variables. Coelho (1985) and Umlauf and Frank (1986) also investigated the factor structure of the MHLC (Form A only), among 146 chronic cigarette smokers (53 men) and 107 inpatients staying at a rehabilitation unit. Based on their results, Coelho concluded that there was a lack of support for the MHLC as a three-dimensional construct; rather, a two-dimensional construct consisted of an Internal factor and a Powerful Others factor provided a better fit. Umlauf and Frank conducted a principal axis factor analysis with orthogonal rotation, which also supported a two-factor model with Internal and Powerful Others/Chance factors.

O’Looney and Barrett (1983) investigated the factor structure of Forms A and B using principal component factor analysis with British college students. Importantly, the investigators conducted separate analyses for each gender. They found that while the EFA in the female sample produced three factors, the EFA in the male sample resulted in only two factors. The factors for the males included a combined Internal/Chance factor, with a separate Powerful Others factor. The factor structure in the female participants produced all three factors.

Astrom and Blay (2002) investigated the MHLC among 504 Ghanaian adolescents. A principal component analysis originally extracted three factors with eigenvalues above 1, although the third factor explained only 6.9 percent of the variance; in addition, the Powerful Others and Chance subscales were highly correlated, and the factor structure suggested a great deal of overlap between these dimensions. Thus, the authors forced a two-factor solution that explained 41 percent of the total variance: Powerful Others and Chance loaded on Factor 1 and Internal loaded on Factor 2. They concluded support for a two-factor model where Powerful Others and Chance represented an external health LOC.

An EFA performed on data collected from 152 first-year medical and dental students who had completed Form A also produced a two-factor structure with evidence for an Internal factor and a Powerful Others factor; a Chance factor was less evident (Winefield, 1982). As a second study, Winefield (1982) compared the responses on Form A of the MHLC from 53 patients who had recently suffered myocardial infarction (MI) to 52 participants serving as controls. Although a factor model was not analyzed, Winefield’s findings were still informative as he found that MI patients, who were both older and of lower average social status, scored higher on the Powerful Others domain, but not the Internal or Chance domains, compared to the control participants. Furthermore, when Winefield followed up with 28 of the MI patients 7 months after their discharge from the hospital, test–retest scores indicated that the Internal and Powerful Others dimensions remained stable over time, whereas the Chance dimension did not.

Finally, in a longitudinal study (Stanton et al., 1995) conducted with adolescents from New Zealand, a principal component factor analysis provided support for a two-factor model solution when participants were both aged 13 and 15 years. However, the composition of the two-factor model solutions at the two different time points varied. At age 13, the majority of Internal and Powerful Others items loaded on Factor 1, and Chance items along with two Powerful Others items loaded on Factor 2. At the age of 15 years, Internal and Chance items loaded on Factor 1, and Powerful Others items loaded on Factor 2. Based on their results, the authors contended that there was some support for a three-factor solution with a model structure similar to the MHLC scale (Wallston et al., 1978). We did not find any CFAs that supported a two-factor model structure. Therefore, despite the findings of the studies reviewed above, a clear rationale for either rejecting or confirming a two-factor model structure was not demonstrated.

Three-factor model structure: EFA

Other researchers have continued to find support for the more generally accepted three-factor model solution. An EFA principal component analysis conducted (with Form A) using 496 Iranian college students (Moshki et al., 2007) found three factors which corresponded to the three-factor structure proposed by Wallston et al. (1978). Similarly, Marshall et al. (1990) examined the factor structure of Form A of the MHLC using 181 Veterans Administration medical outpatients. Results from the principal component analysis with orthogonal rotation largely supported a three-factor structure. Five factors with eigenvalues greater than 1.0 were identified, although a scree plot indicated that three factors should be extracted, consistent with Wallston et al.’s (1978) proposed structure. In another study, Buckelew et al. (1990) found support for a three-factor model structure of the MHLC using EFA with oblique rotation performed on data from 160 participants referred to a pain management center.

An EFA was also performed by Casey et al. (1993) using principal component analysis with varimax rotation on 678 participants who completed Form A. Three factors were extracted which provided support for Wallston et al.’s (1978) proposed three-factor model. Similarly, Hartke and Kunce (1982) studied 86 medical patients and found support for a three-factor structure using a principal axis factor analysis with oblimin rotation. Gala et al.(1995) reported support for the three-factor model structure with a non-clinical sample of 524 participants who completed both Forms A and B, approximately 4–6 days apart. Their EFA with varimax rotation was able to account for 42 percent of the total variance. Paine et al. (1994) also conducted a principal axis factor analysis with oblimin rotation which produced a three-factor structure similar to the one proposed by Wallston et al. (1978). These results were produced in a sample of 280 middle-class Brazilians who completed an adapted version of Forms A and B combined. Russell and Ludenia (1983) reported similar results with 100 inpatients. They administered both Forms A and B and then combined the scales for a total of 36 items in order to have higher reliabilities for each subscale. Using the principal axis method, three factors were extracted that corresponded with Internal, Powerful Others, and Chance.

Three-factor model structure: CFA

Hewson and Charlton (2005) conducted a CFA for both an Internet administration (N = 167) and a paper administration (N = 200) separately. Given previous findings that a two-factor structure may be a better fit for the MHLC (Chaplin et al., 2001), both a two-factor and a three-factor CFAs were specified for the Internet sample and paper sample separately. Results illustrated that the three-factor structure model provided the best fit for both the Internet and paper data, although neither CFA produced good model fit, and both analyses had a significant chi-square, despite the relatively small sample sizes.

Robinson-Whelen and Storandt (1992) performed a CFA using 197 non-diabetic and 171 diabetic adults who had completed Form B. The CFA on the non-diabetic sample provided adequate support for a three-factor model, although they suggested that four items be eliminated to provide a better fit. Items 1, 7, 14, and 15 were removed from analyses, and the models were refit to the remaining 14 of the original 18 items from the MHLC; a fairly good fit to the three-factor model was found for both the diabetic and the non-diabetic samples. Similar to Robinson-Whelen and Storandt, Kelly et al. (2006) reported reasonable support for the three-factor model structure among individuals with osteoarthritis, after Items 7 and 8 were removed from the analyses. Moreover, they detected no differences in model structure between men and women. Also, Fasol et al. (1998) reported more support for Wallston et al.’s (1978) three-factor model once Items 7 and 15 were omitted from the model structure. Gehlert and Chang (1998) conducted a CFA with 143 epileptic patients who completed Form A and found an acceptable fit for the model in which all items on the scale loaded onto their a priori subscale.

More recently, Hubley and Wagner (2004) conducted a CFA with 245 non-clinical participants using both Forms A and B. The CFA using a three-factor model for Form A produced a marginal fit; however, the CFA for Form B did not show adequate fit.

None of the reviewed CFA studies support an unambiguous model structure for the MHLC. Additionally, no substantive studies of measurement invariance with the MHLC have been published, with the exception of the study described below, and the study conducted by Malcarne et al. (2005), described in the next section. Neither of these definitively supports a three-factor model.

Talbot et al. (1996) conducted two CFAs in order to compare the three-factor structure to a two-factor structure which has been supported by research (Coelho, 1985; Cooper and Fraboni, 1990; O’Looney and Barrett, 1983; Winefield, 1982). These investigators used a non-clinical group of college students (N = 224) as well as a clinical group of diabetics (N = 132), and all participants completed Form A. Results from the CFAs demonstrated that neither the two-factor model nor the three-factor model provided a good fit to the data, although the fit of the three-factor model was better. Moreover, with invariance testing, Talbot et al. concluded that there were differences in the structure of the MHLC between the two samples.

Three-factor model structure: multiple analyses

Wall et al. (1989) performed both an EFA and a CFA on Forms A and B averaged together using 60 psychiatric patients. The EFA component of the analysis suggested three factors—Internal, Chance, and Powerful Others, with all items loaded on their a priori subscales. The CFA found “reasonable support” for a three-factor structure of the MHLC.

Malcarne et al. (2005) also conducted a CFA and an EFA. Importantly, despite the growing size of the non-White population in the United States, Malcarne et al. were the first—and we believe to date the only—investigators to conduct a CFA separately for individuals (college students) from different racial and ethnic groups (1122 Caucasian Americans, 281 Filipino Americans, and 462 Latino Americans) who completed Form A of the MHLC. In this study, fit indicators did not demonstrate a good fit to the three-factor model in any of the three ethnic groups. Next, Malcarne et al. conducted EFAs using varimax rotation and found evidence for the three dimensions of the MHLC scale across all three ethnic groups. However, each dimension was represented with only three items, rather than the most commonly used six-item format.

Purpose of this research

As reviewed above, CFA studies of the MHLC have not been consistent in their support of a specific factor structure. Also, with the exception of Malcarne et al. (2005) and the Kelly et al. (2006), sample sizes for the CFA studies have tended to be small and within specialized samples (e.g. college students only or inpatients). Importantly, we note a dearth of studies investigating factorial invariance of the MHLC across ethnic/racial groups, with the exceptions noted above, despite a recent call for more cultural sensitivity in the MHLC scale (Luszczynska and Schwarzer, 2005) and despite the existence of an extensive and growing body of literature documenting racial and ethnic differences in health beliefs (Ayalon and Young, 2005; Barroso et al., 2000; Bourjolly et al., 1999; Copeland, 2005; Lewis and Green, 2000; Spalding, 1995; Sproles, 1977; Wallston and Wallston, 1981; Weitzel et al., 1994). One exception to this is the O’Hea et al. (2009) study which, although it is a CFA, we excluded from our review as it was based on the MHLC Form C.

The literature further demonstrates that differences in health beliefs are associated with differences in health behaviors. For example, racial differences in cancer screening behavior relative to mammography have been documented (Harmon et al., 2014), as have differences in colon cancer and prostate screening (Harmon et al., 2014), mental health screening and treatment preferences (Jimenez et al., 2013), and diabetes self-care (Johnson et al., 2014) between Blacks and Whites, differences which have implicated health beliefs explicitly.

Given the lack of definitive findings in the literature, we sought to confirm a three-item latent variable structure for the MHLC in a large sample. Our analysis sought to investigate between-group differences in the MHLC scale structure within a larger and more general population of Black and White participants—adult visitors to two urban EDs. As part of examining differences in the scale across Black and White respondents, we tested for differences in the means between groups, as well. This research is the first of its kind to explore variations in the MHLC factor structure and scores specifically as a function of Black and White race.

Method

Participants

We collected data from 863 adults in two urban EDs over a period of 5 months. “All-comers” who presented in the ED were approached during their visit and asked to take part in a short paper-and-pencil survey. The refusal rate was 40.6 percent. Participants were predominantly White (45.5%) and Black (42.6%). A total of 10 percent reported “other ethnicity.” Additionally, 8.2 percent self-identified as Hispanic (not mutually exclusive with race). A total of 55 percent of respondents were females. They ranged from 19 to 94 years, with a mean age of 48.8 years (standard deviation (SD) = 17.2 years). For the purposes of this study, we removed cases where respondents identified a race or ethnicity other than “White” or “Black” (n = 99). The survey was conducted anonymously, and therefore comparisons could not be made between demographics of those who elected to participate and those who refused.

Patients were approached in ED examination rooms by research assistants trained to collect data for ED studies. Written consent was obtained, and no compensation was offered. Inclusion criteria were adult (aged >17 years) and English speaking. We excluded patients with high acuity as determined by the Emergency Severity Index. This study received approval from the Thomas Jefferson University Institutional Review Board.

Measures

Age and race were collected from all participants in the study. The MHLC scale–Form B was administered. In this sample, the scale showed moderate internal consistency: Cronbach’s alpha for the total scale was .70; Cronbach’s alpha for the individual subscales was .64 (Internal), .57 (Chance), and .67 (Powerful Others).

Design and analysis

Descriptive analyses and data cleaning were performed in IBM SPSS, version 22. We compared our samples’ subscale means to published normative MHLC data and compared the Black and White samples to each other, using independent-samples t-tests. CFA and invariance testing were performed in the IBM SPSS AMOS software, version 22 (IBM Corp. Released, 2013).

Data screening

A total of 23 cases were removed for missing data. We examined the distributions of each item individually through visual inspection of box-and-whisker plots for outliers, and through calculation of each item’s skew/standard error and kurtosis/standard error ratios; 28 cases with ratios >2 were removed this way. We also examined the subscale distributions for normality for the evaluation of the assumptions of the t-test; all subscales met this assumption.

Items within each subscale of the three-factor model were examined for multicollinearity through a series of regressions, using a single item as the criterion variable, and all the other items from that subscale as predictors. The R² for these models was used for evidence of multicollinearity, with a cut-off value of >.80. No models exceeded this threshold (no model had an R² value >.30). We also calculated Mardia’s coefficient for multivariate normality and used a rule of thumb of −3 to +3 for skew and −7 to +7 for kurtosis. We removed an additional 52 cases to correct for significant skew or kurtosis. The final analyzed N was 691.

CFA

We used structural equation modeling (SEM) to perform the CFA of the MHLC, beginning by specifying an a priori model. We specified the three-factor model of the instrument corresponding to the latent variables Internal locus of control (ILOC), PLOC, and CLOC, with the six model-based items (specified in each subscale) forced to load on each of these latent variables. We allowed all item variances, and latent variable covariances, to be freely estimated from the data. Although the original conception of the MHLC was that the Internal and Powerful Others subscales were orthogonal (Wallston et al., 1976), we made the decision to allow the latent variables to be correlated based on the reviewed literature (Paine et al., 1994; Russell and Ludenia, 1983) and the theoretical rationale that these three types of loci of control are unlikely to demonstrate complete orthogonality (Luszczynska and Schwarzer, 2005).

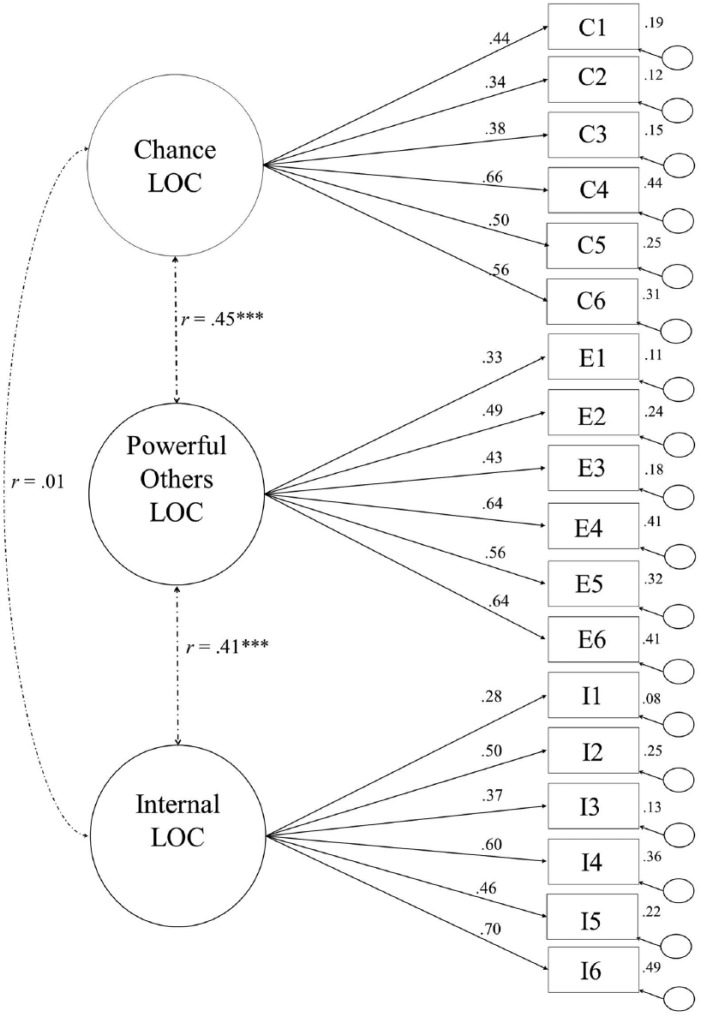
This produced the a priori model shown in Figure 1 and presented as Model 1 in Table 2. The fit of this model was evaluated (as described below), and it was also compared to an “independence model,” which specifies all item indicators to load on one latent variable (Model 0 in Table 2). Because any a priori model must fit better than a single-factor model, the independence model was compared to the a priori structural model as a first test in order to provide a basis for testing more complex models.

Figure 1.

Results of the combined sample CFA.

Table 2.

Results of invariance testing.

Model	Invariance testing strategy	Parameters estimated			df	χ2	χ2/df ratio	AGFI	TLI	RMSEA
0. 1-factor independence model	Combined groups: 1 set of parameters estimated across the groups	18 total, across groups (15 betas, 3 latent variances)			153	2143.73, p < .001	14.01	.62	.00	.14
1. 3-factor constrained model	Combined groups: 1 set of parameters estimated across the groups	39 total, across groups (15 betas, 18-item variances, 3 latent variances, 3 latent covariances)			132	596.18, p <.001	4.52	.877	.730	.071
2. 3-factor unconstrained model	Test of configural invariance separate groups: 2 sets of parameters estimated separately within each group	78 total: all within groups	Group 1 (39): 15 betas, 18-item variances, 3 latent variances, 3 latent covariances	Group 2 (39): 15 betas, 18-item variances, 3 latent variances, 3 latent covariances	264	730.12, p < .001	2.77	.896	.729	.051
3. Measurement weights model	Test of metric invariance separate groups: constrains the betas to be equal across groups, estimates other parameters freely within groups	63 total: 15 betas across groups	Group 1 (24): 18-item variances, 3 latent variances, 3 covariances	Group 2 (24): 18-item variances, 3 latent variances, 3 covariances	279	753.75, p < .001	2.70	.861	.739	.050
χ2 difference test, compared to unconstrained model							χ2 (15) = 23.6, p = .07	.04	.10	−.001
4. Structural covariance model	Test of construct variance/covariance invariance constrain the latent variable covariances only	75 total, 3 latent covariances across groups	Group 1: 18-item variances, 15 betas 3 latent variances	Group 2: 18-item variances, 15 betas 3 latent variances	267	747.69	2.80	.856	.723	.051
χ2 difference test, compared to unconstrained model							χ2(3) = 17.57, p < .001	.00	−.000	.001

betas: regression coefficients; AGFI: adjusted goodness of fit index; RMSEA: root mean square error of approximation; TLI: Tucker–Lewis index.

Model fit for the CFA

We used several commonly accepted measures to evaluate model fit. First, the χ² test for the model was reviewed, where desired values are non-significant. However, since χ² is sensitive to large sample size, it is possible to obtain a large and significant value even when the fit of the model to the data is acceptable. To address this, a widely used “rule of thumb” was also evaluated, the ratio of the χ² to its degrees of freedom, which is suggested to reflect “good fit” at values <4.0 (Joreskog, 1993) and “excellent fit” at values <2.0 (Hair et al., 2009).

We also evaluated the adjusted “goodness of fit” index (AGFI), which provides a fit index by comparing the proportion of the observed covariance matrix that is explained by the model-implied covariance matrix (Kline, 2011). The Tucker–Lewis index (TLI), which penalizes complexity, was also used. Hu and Bentler (1999) recommend values >.95. The root mean square error of approximation (RMSEA) for each model was also evaluated. Hu and Bentler (1999) showed that a cut-off of .06 for RMSEA indicates good model fit.

Logic of invariance testing

In this research, our goal for invariance testing was to examine potential structural and measurement differences in the MHLC scale across two groups of participants—Black and White respondents. In order to accomplish this, we used a multigroup CFA (MGCFA) approach and followed guidance from Vandenburg and Lance (2000) and Kline (2011). We took a “model trimming” approach to invariance testing, where the baseline model for invariance testing was specified as a fully unconstrained model (Model 2 in Table 2), with all parameters allowed to vary freely within the two groups separately, thereby estimating two complete sets of parameter estimates from two sets of sample moments. This model reflects the extent to which the a priori model structure fits the data when the groups are allowed to have their own parameter estimates. This model provides a test of configural invariance because when there are differences between groups in any parameter estimates, this model should fit significantly better than a model where all parameters are forced to equality in the combined groups.

Adequate fit was found for Model 2, indicating that the form of the structural model (item to latent variable relationships) was invariant between Blacks and Whites. Therefore, increasingly restrictive nested models were fitted to the data in steps, and change in fit was evaluated. This nested model approach compares competing models against each other, where the nested model is obtained by fixing (to a specific value) or eliminating parameters from the original model, thereby resulting in a simpler model with more degrees of freedom (Joreskog, 1993). The specific hierarchical nested model comparisons we evaluated are shown in Table 2.

We examined sets of parameter estimates separately to investigate which parameter estimates, if any, differed between the groups. We began by constraining all of the regression path coefficients from each item to its latent variable to be equal across the groups, but freely estimating the other parameters (the “Measurement Weights” model—Model 3 in Table 2). A finding that this model does not change the fit compared to the first model, or improves it, suggests that the regression path coefficient estimates are the same between the groups.

Next, we constrained the latent variable covariances to be equal between the groups but allowed for beta coefficients and item variances to be freely estimated within the groups. If this model (Model 4 in Table 2) is a worse fit to the data, the inference would be made that the groups likely differ in these coefficients.

At each step, a null hypothesis is tested that the more constrained model (a “smaller” model with fewer estimated parameters) is a better fit to the data (Bollen, 1989). The chi-square difference test, ${\chi }_{\mathrm{D}}^2$, was used at each step to evaluate changes in fit where

$$\begin{array}{c}{\chi }_{\mathrm{D}}^2={\chi }^2\left(\mathrm{more\; restrictive\; model}\right)-{\chi }^2\left(\mathrm{less\; restrictive\; model}\right),\mathrm{with}\\ df\left(\mathrm{more\; restrictive\; model}\right)-df\left(\mathrm{less\; restrictive\; model}\right)\end{array}$$

Results

Comparisons to normative data

Our combined sample had mean loci of control as follows: M_Internal = 26.06 (SD = 5.38), M_Poloc = 23.62 (SD = 6.03), and M_Chance = 18.39 (SD = 6.67). We compared these mean values to published normative data, specifically to Wallston and Wallston’s (1981) original validation results and also to the combined sample of 1206 osteoarthritis patients in the Kelly et al. (2006) study, which we feel most closely resembles our sample. The results of the six independent groups’ t-tests we performed are presented in Table 3 and indicated that our sample scored significantly higher on both the Chance and Powerful Others subscales than both comparison samples (p < .001). Additionally, within our own sample, Black respondents scored significantly higher than White respondents on the CLOC subscale.

Table 3.

Means and mean differences.

Sample	ILOC		PLOC		CLOC
	M (SD)	t(df), p	M (SD)	t(df), p	M (SD)	t(df), p
Current: total (N = 691)	26.06 (5.38)		23.62 (6.03)		18.39 (6.67)
Current: Black (N = 336)	26.54 (5.34)		24.01 (6.32)		19.46 (7.31)
Current: White (N = 355)	25.61 (5.29)		23.96 (5.72)		17.37 (5.83)
Compare Black to White		t(691) = 2.30, p = .022		t(689) = .11, p = .91		t(689) = 4.14, p < .0001
Compare total to Kelly PA, Kallen MA and Suárez-Almazor ME (2006)	26.44 (5.61)	t(1895) = 1.44, p = .26	20.22 (6.64)	t(1895) = 11.09, p < .0001	16.96 (6.05)	t(1895) = 4.65, p < .001
Compare total to Wallston and Wallston (1981) Form B (N = 115)	25.30 (4.63)	t(804) = 1.43, p = .15	15.46 (5.18)	t(804) = 14.35, p < .0001	20.96 (5.48)	t(804) = 3.92, p < .0001

SD: standard deviation; ILOC: Internal locus of control; PLOC: Powerful Others locus of control; CLOC: Chance locus of control.

Statistical tests show the current total sample versus the normative study in that row comparison. A Bonferroni-adjusted α = .0042 was used to establish statistical significance for each pairwise comparison.

CFA

In this sample, the CFA failed to confirm a three-factor structure. Model fit was poor to marginal, with RMSEA = .071, AGFI = .877, and TLI = .730 (Model 1, the “Constrained Model,” Table 2). In addition to the fit, of note in this model is the finding that the squared multiple correlation coefficients (R²s) describing the variance explained in each item indicator by the presumed latent variable to which it is specified to load ranged from a low of .08 (Item I1) to a high of .45 (Item C4), indicating that the underlying latent variables are generally inadequate at capturing item variance (Figure 1). All unstandardized path coefficients were significant and in the predicted directions, and the model converged using full maximum likelihood estimation.

Invariance testing

Because the CFA of Model 1 suggested marginal fit, we used this information as a starting point in invariance testing. One-way poor fit may result in misspecification of the structural model as identical in the two groups, so we next estimated a model which allowed for all parameter estimates to be estimated freely within the groups separately in a MGCFA (Model 2). The fit of this model was evaluated and found to be reasonable, RMSEA = .051, TLI = .729, and AGFI = .896. Finding that this model is adequate fit to the data suggests configural invariance, that is, the patterns of latent variables, covariances, and item loadings are the same across groups. Additionally, finding that this model is a better fit than one which constrains all model coefficients to be equal across groups suggests that some estimates are likely not the same between the groups and provides the rationale for further invariance testing.

Next, we investigated a model in which all unstandardized regression weights (indicator to latent paths) were constrained to be equal between the groups, while the other model parameters were estimated individually, commonly called a “measurement weights” model (Model 3) and compared it to Model 2 as a test of metric invariance. This comparison was not significant, χ²(15) = 23.6, p = .07, supporting equality of regression coefficients between the groups.

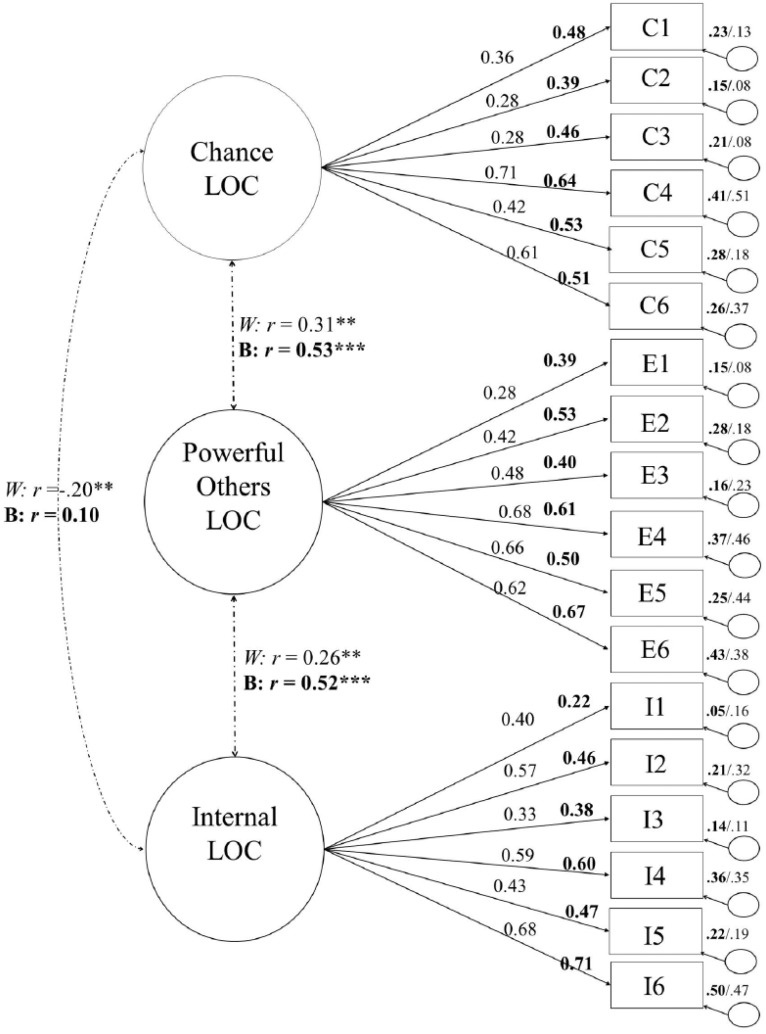
Next, we evaluated a model that constrained the latent variable covariances to be equal but allowed the other parameter estimates to differ between the groups. Model 4 was compared to Model 2, and that comparison was significant, χ²(3) = 17.57, p < .001, indicating that the latent variable covariances differ between the groups. In these data, all the covariances were significantly different across the groups; for relationships between the CLOC and PLOC latent variables, Z = 3.92, p < .01; between the CLOC and ILOC latent variables, Z = 3.48, p < .01; and between the ILOC and PLOC, Z = 2.09, p < .05. Among Black respondents, the correlations between the latent variables were CLOC–ILOC = −.20, CLOC–PLOC = .31, and ILOC–PLOC = .27. In White participants, the correlations were CLOC–ILOC = .10, CLOC–PLOC = .53, and ILOC–PLOC = .52. See Figure 2 for all coefficients in both groups separately.

Figure 2.

Results of the multigroup CFA analysis showing all coefficients estimated within the groups separately. Bolded coefficients were estimated within the sample of Black respondents.

Because of the evidence for invariance in latent variable covariances, we did not proceed to a test of variance/covariance invariance because it is a more restrictive model.

Discussion

In this study, we (1) reviewed the published literature on the factor structure of the MHLC scale, (2) analyzed MHLC data collected from “all comers” in two urban EDs to compare means across studies and between Black and White respondents in our sample, (3) conducted a CFA for a three-factor model structure, and (4) performed invariance testing of the instrument across Black and White respondents.

Our analyses found significant mean differences between Black and White respondents in the CLOC subscale, consistent with other published research. It is a relatively common finding in the literature that Black respondents hold higher “chance” control beliefs about their health. For example, racial differences in cancer screening behavior relative to mammography are well documented (Harmon et al., 2014), which are associated with African-American women’s higher CLOC about breast cancer (Barroso et al., 2000). A large study focused on health beliefs among African-American participants specifically showed that 30 percent of respondents indicated that their health was primarily based on fate or destiny (Lewis and Green, 2000). There are also documented differences in colon cancer and prostate screening (Harmon et al., 2014), mental health screening and treatment preferences (Jimenez et al., 2013), and diabetes self-care (Johnson et al., 2014) between African-Americans and Caucasians, differences which have implicated health beliefs particularly. Also of note in the comparison of our sample to two normative samples are the significantly higher Chance externality and Powerful Others externality loci of control in our sample. We reason that this reflects the fact that our data were collected in ED settings, which may bias the sample toward those individuals with a greater likelihood of holding these control beliefs.

On the basis of the literature review and our analyses, we conclude that the latent variable structure of the MHLC scale remains in question. One possibility for this may be small sample sizes in many of both the EFA and the CFA studies (see Table 1). A low item-to-person ratio is undesirable in factor analysis and can produce sample specific and ungeneralizable results. Another potential reason for differing findings across the studies with respect to model fit for latent variable structure may be differences in latent variable structure or item functioning across groups, a possibility which can be addressed with invariance testing. We confirmed in our data that models which permitted differences in factor loadings based on respondent race (Models 2–4 in Table 2) were a better fit than a more constrained model (Model 1 in Table 2), indicating differences in model coefficients between groups.

Our CFA results failed to confirm a three-factor model. The three-factor model yielded only marginal-to-poor fit of the data to the model. Because we were moving forward with invariance testing, we did not attempt to re-specify this model to improve fit, although examination of the modification indices suggested that the residual terms for the items are highly correlated with each other, and with the latent variables, consistent with our finding that the total proportions of variance accounted for in the items by their latent variables is low overall.

The results of invariance testing demonstrated that allowing parameter estimates to vary between Black and White participants produces a better fitting model than constraining them to be equal across the groups, providing evidence for differences in model coefficients between groups. To follow up, we first established that a model constraining the regression coefficients to be equal between groups does not worsen model fit relative to the model where all parameters are freely estimated, although this difference in model fit was marginally significant (p = .072). We interpreted this as evidence of metric invariance despite the marginally significant χ² difference test for two reasons: first, the individual pairwise comparisons of beta coefficient parameter estimates were themselves all non-significant, and the χ² difference test between Models 2 and 3 was non-significant. This result allows for the inference that the items are interpreted the same between the racial groups investigated in our study.

Next, we constrained the latent variable covariances to be equal across groups but allowed all other parameters to be freely estimated. This model was a significantly worse fit to the data than the model allowing all parameters to be freely estimated. Pairwise comparisons of estimates revealed that all the covariances were significantly different between groups, and in fact, for the CLOC–ILOC latent variable relationship, these coefficients were in the opposite directions. Indeed, our data indicate that for White respondents, these constructs are significantly inversely related, while for Black respondents, they are positively related. This is a striking finding, indicating that the relationships among these constructs should be investigated further and in particular investigated with potential between-group differences made explicit. This finding partially explains the apparent orthogonality of the latent variables when race is not accounted for, as in Figure 1 which shows a near zero correlation and which is a common assumption in the literature. Furthermore, this finding is consistent with some of the published literature which finds a chance external orientation associated with an internal orientation, such as O’Looney and Barrett (1983) which found a Chance–Internal factor in males only. Also, O’Hea et al. (2009) reported that a Powerful Others–doctors factor and an internal factor are not only positively related in their all low-socioeconomic status (SES) African-American patients but in fact form the same factor (with the caveat that their factor solution included the “god” LOC subscale and so was different from the typical three-factor solution). They interpret this to mean that in their sample, internal control beliefs are confounded with control beliefs about the healthcare system, an interesting suggestion worthy of future research.

Differences in item functioning (i.e. metric invariance) are potentially difficult to address when using the scale in practice, as they imply different meanings of the underlying dimensions between groups—a threat to construct validity. In our study, this hypothesis could not be ruled out definitively and so we recommend that Black/White comparisons of mean scores on the MHLC be interpreted with caution and when possible be accompanied with item mean comparisons as well. Studies using MHLC mean scores should also consider race as an analytic covariate and should consider adding interaction terms into statistical models. Of note, although we do not present the data here, these data were derived from a larger study of the associations between MHLC subscales and ED visits and hospital admissions (Mautner et al., 2015). In that study, we did use race as a covariate for analyses because of the finding that the race was significantly associated with both ILOC and CLOC and with both outcome variables. Finding that the subscales are differentially related to outcomes between groups provides additional evidence of potential problems with construct validity with the MHLC. Further invariance testing should include a test of the hypothesis of strong scalar invariance which we did not test here. This test would speak more directly to analyses which attempt to directly compare Black/White mean scores on MHLC subscales.

The issue of the non-equivalency of latent variable covariances is less of a problem for the use of the scale in practice, but does imply that more work is needed on the theory of health LOC and health LOC differences between Black and White populations, empirical work which appears to be underway, as we review above. Factor analytic studies should begin with a non-orthogonal rotation of the factors. Additionally, the God LOC subscale could be considered in studies with Black participants to potentially attribute correctly the overlap between the Chance/Powerful Others orientation and the Internal orientation. Finally, although we only undertook confirmatory analyses here, EFA studies should be undertaken to confirm the dimensional invariance of the MHLC between Black and White respondents.

The results of this study are limited in generalizability to urban settings. Furthermore, there is a suggestion in these data that our sample overrepresented those with a high CLOC and high PLOC, not surprising given that these data was collected in an ED. Therefore, caution should be used interpreting these results beyond this setting.