Single-gene negative binomial regression models for RNA-Seq data with higher-order asymptotic inference

Abstract

We consider negative binomial (NB) regression models for RNA-Seq read counts and investigate an approach where such NB regression models are fitted to individual genes separately and, in particular, the NB dispersion parameter is estimated from each gene separately without assuming commonalities between genes. This single-gene approach contrasts with the more widely-used dispersion-modeling approach where the NB dispersion is modeled as a simple function of the mean or other measures of read abundance, and then estimated from a large number of genes combined. We show that through the use of higher-order asymptotic techniques, inferences with correct type I errors can be made about the regression coefficients in a single-gene NB regression model even when the dispersion is unknown and the sample size is small. The motivations for studying single-gene models include: 1) they provide a basis of reference for understanding and quantifying the power-robustness trade-offs of the dispersion-modeling approach; 2) they can also be potentially useful in practice if moderate sample sizes become available and diagnostic tools indicate potential problems with simple models of dispersion.

1. INTRODUCTION

During the past few years, RNA sequencing (RNA-Seq) has been widely adopted as the technology of choice for quantifying gene expression profiles and dynamics under different environmental or experimental conditions due to its unprecedented throughput, comprehensiveness, resolution and sensitivity [12, 13, 26]. In a typical RNA-Seq experiment, mRNA is isolated from cells of interest, converted to complementary DNA (cDNA) either before of after being randomly fragmented, ligated with library adapters, and enriched by a limited number of polymerase chain reaction (PCR) cycles. The resulting cDNA library is covalently attached to a flow cell, amplified and sequenced in a massively parallel fashion to produce hundreds of millions of short RNA-Seq reads. To infer gene expression, the RNA-Seq reads are aligned to sequence features in a reference database. The relative frequency of RNA-Seq reads that match sequence features of a gene serves as a measure of that gene’s expression.

The negative binomial (NB) distribution is a useful model for RNA-Seq read counts and serves as the basis of several statistical packages for assessing differential expression from RNA-Seq data, including edgeR [17], DESeq [1], NBPSeq [6], and the recent version of Cuffdiff (http://cufflinks.cbcb.umd.edu/manual.html) in Cufflinks [22]. The technical variability in RNA-Seq read counts has been demonstrated to be near Poisson [9], but RNA-Seq reads from independent biological samples commonly show extra-Poisson variation (i.e., overdispersion) and practically useful models must also incorporate this biological variability. The NB distribution, which may be derived as a gamma mixture of Poisson distributions, is a flexible and convenient choice. The NB distribution uses a dispersion parameter to capture the extra-Poisson variation. These statistical packages differ in how they handle the modeling and estimation of the NB dispersion parameter.

Regression models are essential for exploring gene expression as a function of explanatory variables and for comparing gene expression between groups while accounting for other factors. The R package MASS [23] and recent versions of edgeR, DESeq and NBPSeq all include implementations of NB regression models. Gene expression analysis from RNA-Seq data often involves fitting separate regression models to thousands of genes and testing the regression coefficients in each fitted model, but current RNA-Seq studies tend to be based on small sample sizes (for example, three biological replicates for each of two treatment groups, for a total sample size of six). The large number of genes combined with the small sample size causes more attention than usual on the power of the statistical tests. One power-saving strategy explored by edgeR, DESeq, and NBPSeq is to model the NB dispersion as a simple parametric or smooth function of the estimated expression level and thus pool information from all genes to jointly estimate the NB dispersion. If the assumption that the dispersion is similar for genes with similar expression levels is valid, the dispersion-modeling approach can effectively save one degree of freedom from each regression model. This can translate into considerable power improvement, especially in small-sample situations. However, the power benefit of the dispersion-modeling approach relies on the estimated dispersion models being adequate. It is not well understood how robust the approach is if the fitted dispersion models are inadequate. We believe at least two further developments are needed to accurately quantify the power benefit and address the robustness concerns of the dispersion-modeling approach. First, a goodness-of-fit test is needed to assess the adequacy of the NB dispersion models. Mi et al. [11] provides one recent such attempt. Second, single-gene models not reliant on a dispersion model and accurate inference tools for such models are needed to serve as a basis of reference. This second point is the focus of the current paper.

In this paper, we investigate a more basic approach that does not rely on a dispersion model. We consider NB regression models fitted to each gene separately where, in particular, the NB dispersion is estimated from each gene separately without assuming commonalities between genes. One motivation for studying such single-gene models is that they provide a basis of reference for understanding and quantifying the power-robustness trade-offs of the dispersion-modeling approach. We will use simulation studies to illustrate the utility of single-gene models in power-robustness investigations. Single-gene models can also be potentially useful in practice if moderate sample sizes are available and diagnostic tools [see, e.g., 11] indicate potential problems with simple models of dispersion.

One particular statistical challenge we address is that there is no exact test for testing the regression coefficients in an NB regression model. Asymptotic tests—most notably the Wald test and the likelihood ratio test—are available, but are mathematically justified only for large sample sizes. We consider likelihood ratio tests with a higher-order asymptotic (HOA) adjustment [20]. In an earlier study [5], we have demonstrated that the HOA-adjusted likelihood test is very accurate when the dispersion parameter can be treated as known—it provides type I error that matches the nominal specification even when the sample size is as small as six. In this paper, we will demonstrate that the accuracy of HOA inference extends to situations where the dispersion is unknown and needs to be estimated from a small sample size.

This rest of the paper is organized as follows. Section 2 clarifies the NB regression model. Section 3 reviews HOA inference. In Section 4, we use simulations to demonstrate the accuracy of HOA inference and illustrate its utility in assessing the power and robustness of the dispersion-modeling approach. Section 5 includes a discussion and conclusion. The Appendix provides additional technical details.

2. NB REGRESSION MODEL

We restrict attention to read counts mapped to a single gene. Let Y_j represent the number of RNA-Seq reads from biological sample j attributed to a gene and let X_jk be the value of the k-th explanatory variable associated with biological sample j, for j = 1,..., n and k = 1,..., p. The explanatory variables are numerical representations of factors such as treatment type, genotype, time after treatment, and so on. Let N_j be the total number of unambiguously aligned sequencing reads associated with biological sample j, which we refer to as the (observed) library size of sample j. Our NB regression model for describing the mean expression as a function of explanatory variables includes the following two components:

1. An NB probability distribution for the frequency of reads:

   $$Y_j~NB({\mu }_j,\varphi )$$ (1)

   where μ_j is the mean and ϕ is the NB dispersion parameter such that $\text{Var}(Y_j)={\mu }_j+\varphi {\mu }_j^2$. We assume that frequencies Y_j are independent of one another.

2. A log-linear regression model for the mean as a function of explanatory variables

   $$log({\mu }_j)=log(N_j)+log(R_j)+\sum _{k=1}^p{\beta }_k{X}_{jk},$$ (2)

   where ${\beta }_k^{\prime }$s are unknown regression coefficients and R_j’s are optional normalization factors, explained below.

The structure of the model resembles a generalized linear model [10], but it is important to note that the dispersion parameter, ϕ, is unknown. This aspect of the model also contrasts with the NB regression models implemented in edgeR [17], DESeq [1], and NBPSeq [6, 5]. In those packages, the dispersion parameters are modeled as a simple parametric (NBPSeq) or smooth function (DESeq and edgeR) of the mean or some other measure of read abundance. The dispersion model is estimated from all genes combined and, in current implementations of these software packages, the estimated values of the dispersion are then treated as the truth in tests of differential expression. If the dispersion can be adequately modeled by a simple parametric function as in the NBPSeq approach, likelihood inferences can be made with the weaker assumption that the parameters in the dispersion model (rather than the fitted values of the dispersion) are known [see 5, for more dicussion on this point]. EdgeR also provides options for estimating the dispersion as a weighted average of genewise estimates and fitted values from a constant or smooth function under an empirical Bayes framework. With this option, genewise estimation is possible by choosing appropriate prior weights, but, again, the dispersion estimates are treated as the truth in tests for regression coefficients.

In model (2), the observed library sizes N_j differ due to chance variation in the preparation and sequencing of the samples. The NB regression model directly accounts for variable library sizes. The normalization factors R_j have to do with the apparent reduction or increase in relative read frequencies of non-differentially expressing genes simply to accommodate the increased or decreased relative read frequencies of truly differentially expressing genes. Anders and Huber [1], Robinson and Oshlack [18], and Li et al. [7] discussed the need to include R_j’s and methods for estimating them. The quantity N_jR_j is often referred to as “effective library size”, “normalized library size” or “sequencing depth” in other papers.

3. WALD TEST, LIKELIHOOD RATIO TEST AND HIGHER ORDER ASYMPTOTIC ADJUSTMENT

In a regression setting, testing differential gene expression can usually be reduced to testing that one or more of the regression coefficients equals zero. In general, there does not exist an exact test for this purpose. We consider two well-known classical asymptotic tests, the Wald test and the likelihood ratio test, and a more recent development, the likelihood ratio test with higher-order asymptotic adjustment (HOA). We refer to the latter as the HOA test. Although there are ongoing works on creating general-purpose routines for computing HOA tests that require only a function for computing the likelihood and a function for simulating observations under the model considered (personal communication with Professor Don Pierce), in current practices, the HOA test usually requires specific implementations for different likelihood functions. In an earlier study [5], we have implemented and demonstrated the excellent performance of the HOA test in NB regression models where the NB dispersion parameter can be treated as known. The present situation, with the dispersion parameter unknown, is more challenging. The new technical contribution of this paper is the implementation of the HOA test in the NB regression model when dispersion is unknown.

In the following paragraphs of this section, we briefly review the three asymptotic tests and put them in the NB regression context. In particular, we summarize the key ideas behind the HOA adjustment. This background information will help readers better understand the results in the following sections.

In the NB regression model in Section 2, the unknown parameters are the vector of regression coefficients, β = (β₁,..., β_p), and the dispersion parameter ϕ. For computational purposes, it is easier to use the size parameter κ = 1/ϕ instead of ϕ. We wish to test hypotheses about components of β. Without loss of generality, suppose that θ = (ψ, ν), where ψ = (β₁,..., β_q) and ν = (β_q+1,..., β_p, κ), and the null hypothesis is ψ = ψ₀. In regard to this hypothesis, the q-dimensional parameter ψ is the parameter of interest and ν is a nuisance parameter. We let θ̂ = θ̂(y) = (ψ̂, ν̂) be the maximum likelihood estimator of the full parameter vector and θ̃ = θ̃(y) = (ψ₀, ν̃) be the maximum likelihood estimator under the null hypothesis.

Under the usual regularity conditions, the likelihood ratio statistic,

$$\lambda =2(l(\widehat{\theta })-l(\stackrel{\sim }{\theta })),$$

converges in distribution to a chi-square distribution with degrees of freedom q under the null hypothesis [27]. When ψ is one-dimensional (q = 1), the signed square root of the likelihood ratio statistic λ, also called the directed deviance,

$$r=\text{sign}(\widehat{\psi }-{\psi }_0)\sqrt{\lambda },$$ (3)

converges to a standard normal distribution. The Wald test [24, 25] is based on the Wald statistic,

$$w=\frac{(\widehat{\psi }-{\psi }_0)}{\sqrt{{[j^{-1}(\widehat{\theta })]}_{\psi \psi }}},$$ (4)

where j(θ̂) is the observed information computed at θ̂ and [...]_ψψ refers to the square submatrix corresponding to the ψ component. We use the observed information here since the Fisher (expected) information does not have closed-form expression when the dispersion is unknown in the NB regression model. Under the null hypothesis, the Wald statistic also converges to a standard normal distribution.

For testing a one-dimensional parameter (q = 1), Barndorff-Nielsen [2, 3] has derived a modified directed deviance

$$r^{\ast }=r-\frac{1}{r}log(z),$$ (5)

where z is an adjustment term to be discussed below. Under the null hypothesis ψ = ψ₀, r^* is, in wide generality, asymptotically standard normally distributed to a higher order of accuracy than the directed deviance r itself. Tests based on higher-order asymptotic (HOA) adjustment to the likelihood ratio statistic, such as r^* or its approximation (explained below), are referred to as HOA tests. They generally have better accuracy than corresponding unadjusted likelihood ratio tests, especially in situations where the sample size is small and/or when the number of nuisance parameters is large. It was insightfully pointed out in Pierce and Peters [15] and Pierce and Bellio [14] that there are two aspects of the HOA adjustment: one reducing the effects of nuisance parameter estimation and the other improving the normal approximation to r when the information for the parameter of interest is small. Reducing the effect of nuisance parameter estimation is particularly relevant when the dispersion is unknown in the NB regression model.

In practice, however, the definition and computation of the adjustment term z in Barndorff-Nielsen’s original formulation are generally difficult [notable exceptions include full-rank exponential families, see, e.g., 15]. In a major step forward, Skovgaard [19] developed accurate approximations to Barndorff-Nielsen’s original formulation that involve only calculations similar to those involved in computing the expected information. With Skovgaard’s approximations, the HOA test becomes practical for general use. Skovgaard [20] gave a comprehensive review of the development of the theory and practice of higher order asymptotics. That paper also presented a generalization of Barndorff-Nielsen’s r^* statistic to tests for multidimensional parameters (q > 1), but the computation is more complicated. In this paper, we will focus on testing one-dimensional parameters only. In Appendix A, we provide implementation details of the HOA test with Skovgaard’s approximations in the context of the NB regression model.

4. SIMULATION RESULTS

In Sections 4.1 and 4.2, we present Monte Carlo simulation results comparing type I errors and power of the three large-sample tests: Wald, likelihood ratio, and HOA tests. In Section 4.3, we discuss the cost—in terms of statistical power or sample size requirement—of estimating the unknown dispersion parameter as compared to treating it as known in single-gene models. Finally, in Section 4.4, we present results from a simple power-robustness investigation of the dispersion-modeling approach, the major point being that single-gene models serve as an important reference in such investigations.

4.1 Type I error simulations

We use simulations to compare the accuracy—in terms of producing Type I error rates that match the nominal levels—of three asymptotic tests: the HOA test based on the r^* statistic in (5), the unadjusted likelihood ratio (LR) test based on the r statistic in (3), and the Wald test based on the w statistic in (4). For a one-dimensional parameter of interest, all three of these tests (HOA, LR, and Wald) have the same asymptotic null distribution—a standard normal distribution.

We start with a series of two-group comparison examples. The regression model (2) includes the two-group comparison model as a special case. To model RNA-Seq read counts in two groups (say groups 1 and 2), two covariates X₁, X₂ are needed (p = 2). One can define the intercept term X_j1 = 1 for all samples j = 1,..., n, and define

$$X_{j2}=\{\begin{array}{ll}0\hfill & \text{if}\text{sample}j\text{is}\text{from}\text{group}1,\hfill \\ 1\hfill & \text{if}\text{sample}j\text{is}\text{from}\text{group}2.\hfill \end{array}$$

Then β₁ will represent the log relative mean of group 1 and β₂ the log fold change in relative means between the two groups. Testing differential gene expression between the two groups amounts to testing β₂ = 0. In the following examples, we fixed N_j = 10⁶ for all j in equation (2) and set group means by specifying β values. For example, when β₁ = −9.21, β₂ = 0, the mean counts will be 100 for both groups. We will avoid the issue of count normalization and let R_j = 1 for all samples and treat them as known when fitting the NB regression model.

Tables 1 and 2 show Monte Carlo type I error rates for the three large-sample tests from simulated NB two-group comparisons, indicating the superiority of the HOA test—in producing accurate type I error rates—over the Wald and the unadjusted LR tests. Results in each subtable were based on 10,000 simulated two-group data sets. Each data set contains 6 NB counts, divided into two groups: one of size 2 and one of size 4. We used the three large-sample tests to test the two possible one-sided alternatives. When the group sizes are not balanced, it can happen that the asymptotic test p-values are more accurate in one tail of the test statistic distribution than in the other. Using one-sided tests and unbalanced group sizes enabled us to investigate the behaviors of the asymptotic p-values in both tails of the test statistic distribution. In Table 1, we fixed the dispersion at ϕ = 0.1 and varied the mean values from 10 to 1,000. In Table 2, we fixed the mean value at μ = 100 and varied the dispersion from 0.3 to 0.02. In all cases, the type I error rates for the LR and Wald tests are substantially inflated. The maximum standard error of simulation is approximately 0.005 in this set of simulations, so there is a hint of evidence that the type I error rates for the HOA test are also slightly inflated in some simulated data sets, but the accuracy of the HOA test should be adequate for practical applications.

Table 1.

Monte Carlo Type I error rates of one-sided HOA, LR and Wald tests for two-group comparisons at nominal levels (alpha) 1%, 5%, 10%, and 20%. Results are based on 10,000 simulated two-group data sets. Each data set contains 6 NB counts, divided into two groups: one of size 2 and one of size 4. The alternative hypothesis is that the group with size 4 has a smaller (tables (a), (c) and (e)) or greater (tables (b), (d) and (f)) mean. The simulations were performed under the null hypothesis: both groups were simulated to have the same means (10, 100, or 1,000). The dispersion parameters were simulated to be 0.1

(a) μ = 10, ϕ = 0.1
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.007	0.019	0.034
0.05	0.049	0.075	0.089
0.10	0.095	0.128	0.139
0.20	0.195	0.227	0.230

(b) μ = 10, ϕ = 0.1
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.008	0.018	0.023
0.05	0.049	0.081	0.086
0.10	0.101	0.140	0.144
0.20	0.204	0.248	0.250

(c) μ = 100, ϕ = 0.1
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.012	0.035	0.065
0.05	0.057	0.100	0.120
0.10	0.109	0.163	0.174
0.20	0.210	0.253	0.257

(d) μ = 100, ϕ = 0.1
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.011	0.037	0.068
0.05	0.056	0.106	0.132
0.10	0.108	0.167	0.187
0.20	0.210	0.267	0.275

(e) μ = 1000, ϕ = 0.1
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.014	0.037	0.064
0.05	0.059	0.103	0.122
0.10	0.111	0.160	0.172
0.20	0.211	0.255	0.259

(f) μ = 1000, ϕ = 0.1
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.012	0.039	0.072
0.05	0.056	0.107	0.135
0.10	0.108	0.173	0.189
0.20	0.210	0.272	0.281

Table 2.

Monte Carlo Type I error rates of one-sided HOA, LR and Wald tests for two-group comparisons at nominal levels (alpha) 1%, 5%, 10%, and 20%. Results are based on 10,000 simulated two-group data sets. Each data set contains 6 NB counts, divided into two groups: one of size 2 and one of size 4. The alternative hypothesis is that the group with size 4 has a smaller (tables (a), (c) and (e)) or greater (tables (b), (d) and (f)) mean. The simulations were performed under the null hypothesis: both groups were simulated to have the same mean 100. The dispersion parameters were simulated to be 0.3, 0.1, 0.05, or 0.02

(a) μ = 100, ϕ = 0.3
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.012	0.034	0.056
0.05	0.054	0.096	0.114
0.10	0.107	0.156	0.167
0.20	0.210	0.248	0.250

(b) μ = 100, ϕ = 0.3
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.011	0.037	0.074
0.05	0.054	0.111	0.140
0.10	0.109	0.176	0.195
0.20	0.208	0.273	0.282

(c) μ = 100, ϕ = 0.1
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.012	0.035	0.065
0.05	0.057	0.100	0.120
0.10	0.109	0.163	0.174
0.20	0.210	0.253	0.257

(d) μ = 100, ϕ = 0.1
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.011	0.037	0.068
0.05	0.056	0.106	0.132
0.10	0.108	0.167	0.187
0.20	0.210	0.267	0.275

(e) μ = 100, ϕ = 0.05
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.013	0.037	0.062
0.05	0.057	0.098	0.116
0.10	0.105	0.157	0.168
0.20	0.205	0.247	0.251

(f) μ = 100, ϕ = 0.05
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.013	0.035	0.062
0.05	0.058	0.104	0.127
0.10	0.110	0.167	0.183
0.20	0.211	0.266	0.273

(g) μ = 100, ϕ = 0.02
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.009	0.027	0.047
0.05	0.053	0.093	0.110
0.10	0.108	0.152	0.163
0.20	0.208	0.248	0.252

(h) μ = 100, ϕ = 0.02
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.010	0.025	0.045
0.05	0.054	0.089	0.105
0.10	0.105	0.147	0.159
0.20	0.201	0.248	0.254

Table 3 shows further simulation results for a simple regression setting. Table 4 shows simulation results for testing the interaction term in an experiment with a 2 × 2 treatment structure and with 3 replicates per treatment group. These results show similar conclusions—the HOA test produces type I error rates consistently and substantially closer to the nominal error rates than the Wald and unadjusted LR tests.

Table 3.

Monte Carlo Type I error rates of one-sided HOA, LR and Wald tests for the coefficient of X in an NB log-linear regression model, log(μ) = log(N) + β₀ + β₁X, at nominal levels (alpha) 1%, 5%, 10%, and 20%. Results are based on 10,000 simulated NB samples of size 6, with the predictor X = 1, 2, 4, 8, 16, and 32. These simulations were performed under the true null hypothesis where β₁ = 0, β₀ = −9.21 and N=10⁶, so the mean frequencies were μ = 100 for all counts. The dispersion parameter was simulated to be 0.1. The alternative hypotheses are β₁ < 0 (left side of table) and β₁ > 0 (right side of table)

(a)
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.011	0.037	0.072
0.05	0.058	0.110	0.135
0.10	0.110	0.170	0.189
0.20	0.211	0.270	0.278

(b)
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.011	0.034	0.056
0.05	0.054	0.095	0.111
0.10	0.102	0.148	0.160
0.20	0.203	0.242	0.245

Table 4.

Monte Carlo Type I error rates of one-sided tests for negative (left side of table) or positive (right side of table) interaction in a 2 × 2 design at nominal levels (alpha) 1%, 5%, 10%, and 20%. The corresponding regression model is log(μ) = log(N) + β₀ + β₁X₁ + β₂X₂ + β₃X₁X₂, where X₁ and X₂ are indicator variables for two two-level factors. Results are based on 10,000 simulated NB samples of size 12 (3 replicates per treatment group). These simulations were performed under the true null hypothesis, so there was no interaction effect in the simulations (β₃ = 0). Other parameters were specified as N = 10⁶, β₀ = −9.21, β₁ = 0.41, β₂ = 0.69, and the mean frequencies ranged from 100 to 300. The dispersion parameter was simulated to be 0.1

(a)
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.013	0.034	0.049
0.05	0.056	0.098	0.111
0.10	0.108	0.159	0.167
0.20	0.211	0.261	0.264

(b)
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.012	0.032	0.045
0.05	0.052	0.094	0.107
0.10	0.104	0.154	0.162
0.20	0.205	0.252	0.255

We note that the LR and Wald tests are much less accurate when the dispersion is unknown than when the dispersion can be treated as known. As a comparison, in Table 5, we show one set of Monte Carlo type I error rates for HOA, LR and Wald tests when the dispersion ϕ was treated as known. These results are to be compared with those in Table 1. More numerical results in the dispersion-known cases can be found in Di et al. [5]. These results, combined with results from Table 2, suggest that the increased inaccuracy of HOA and LR tests in the dispersion-unknown case has more to do with the fact that we have to estimate the unknown dispersion parameter rather than the amount of dispersion in the data. We explained in Section 3 that one aspect of the HOA adjustment is to reduce the effects of estimating nuisance parameters. The simulations here confirm the effectiveness of this aspect of HOA adjustment.

Table 5.

Monte Carlo Type I error rates of one-sided HOA, LR, and Wald tests for two-group comparisons at nominal levels (alpha) 1%, 5%, 10%, and 20%, when the dispersion ϕ was treated as known. The simulation models, simulated data sets and test hypotheses are all the same as in Table 1. The p-values of the LR and Wald tests are much closer to the nominal levels here

(a) μ = 10, ϕ = 0.1
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.009	0.008	0.007
0.05	0.049	0.047	0.045
0.10	0.096	0.092	0.092
0.20	0.197	0.189	0.189

(b) μ = 10, ϕ = 0.1
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.009	0.011	0.008
0.05	0.050	0.053	0.051
0.10	0.103	0.107	0.107
0.20	0.200	0.211	0.211

(c) μ = 100, ϕ = 0.1
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.011	0.011	0.009
0.05	0.051	0.049	0.045
0.10	0.105	0.100	0.097
0.20	0.207	0.199	0.196

(d) μ = 100, ϕ = 0.1
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.010	0.011	0.013
0.05	0.050	0.056	0.061
0.10	0.107	0.113	0.117
0.20	0.204	0.214	0.217

(e) μ = 1000, ϕ = 0.1
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.008	0.008	0.007
0.05	0.052	0.049	0.046
0.10	0.104	0.099	0.094
0.20	0.205	0.199	0.196

(f) μ = 1000, ϕ = 0.1
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.012	0.013	0.016
0.05	0.053	0.057	0.061
0.10	0.105	0.111	0.116
0.20	0.205	0.215	0.218

Finally, we remark that the performance of all three asymptotic tests will improve as the sample size increases, which is to be expected. Table 6 shows Monte Carlo type I errors for the HOA, LR and Wald tests from simulated NB two-group comparisons where the sample sizes have been increased to 30.

Table 6.

Monte Carlo Type I error rates of one-sided HOA, LR and Wald tests for two-group comparisons at nominal levels (alpha) 1%, 5%, 10%, and 20%. Results are based on 10,000 simulated two-group data sets. Each data set contains 30 NB counts, divided into two groups: one of size 10 and one of size 20. The alternative hypothesis is that the group with size 20 has a smaller (left side of table) or greater (right side of table) mean. The simulations were performed under the null hypothesis: both groups were simulated to have the same mean (10, 100 or 1,000). The dispersion parameters were simulated to be 0.1

(a) μ = 10, ϕ = 0.1
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.011	0.014	0.018
0.05	0.048	0.054	0.059
0.10	0.099	0.107	0.109
0.20	0.199	0.207	0.208

(b) μ = 10, ϕ = 0.1
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.010	0.013	0.015
0.05	0.048	0.056	0.058
0.10	0.094	0.106	0.109
0.20	0.198	0.211	0.212

(c) μ = 100, ϕ = 0.1
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.008	0.010	0.013
0.05	0.049	0.055	0.058
0.10	0.100	0.107	0.109
0.20	0.204	0.209	0.209

(d) μ = 100, ϕ = 0.1
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.012	0.015	0.019
0.05	0.051	0.059	0.065
0.10	0.099	0.111	0.116
0.20	0.203	0.216	0.219

(e) μ = 1000, ϕ = 0.1
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.012	0.015	0.017
0.05	0.051	0.057	0.060
0.10	0.097	0.105	0.107
0.20	0.196	0.202	0.202

(f) μ = 1000, ϕ = 0.1
alpha	Estimated Type I Error Rates
	HOA	LR	Wald
0.01	0.011	0.015	0.019
0.05	0.050	0.058	0.064
0.10	0.102	0.117	0.121
0.20	0.205	0.220	0.222

4.2 Power simulations

We also compared the power of the three large-sample tests under two-group comparison settings using Monte Carlo simulation. We considered two different alternative scenarios since the relative performance of the tests depends upon whether the larger or smaller group has the larger mean. In each case, we simulated 100,000 two-group data sets. Each data set contains 6 NB counts, divided into two groups: one of size 2 and one of size 4. The dispersion was simulated to be 0.1 for both groups, but was treated as unknown when performing the test. The mean of the group with size 2 was simulated to be 100 and the mean of the group with size 4 was either 50 or 200. Since the actual type I errors from the likelihood ratio and the Wald tests do not match the nominal level, we report size-corrected power. We determine the critical value of a test (Wald, LR or HOA) also through Monte Carlo simulation—performing the test on 100,000 data sets simulated under the null and taking the α-th quantile of the resulting p-values.

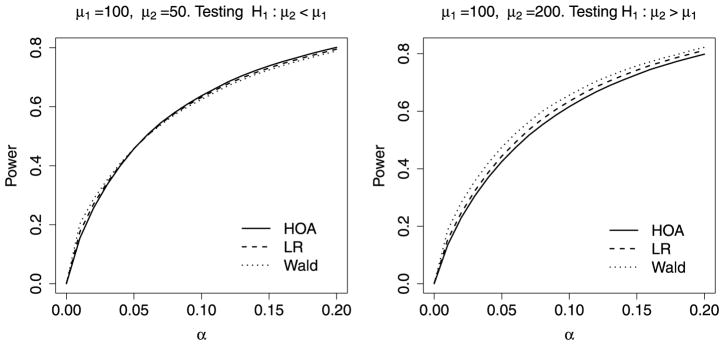
Figure 1 summarizes the size-corrected power for the HOA, LR and Wald tests at different alpha levels under the two two-group comparison settings described above. We noticed that when the larger group (group with size 4) has a larger mean, the Wald test has better power than the LR test, and the LR test has better power than the HOA test. When the larger group has a smaller mean, there is less difference between the power of the three tests and none of the tests will dominate at all alpha levels. These behaviors differ somewhat from what we observed in Di et al. [5] where the dispersion was treated as known. In that study, we did not see notable difference in power between the three tests when testing the two possible one-sided alternatives in two-group settings. This suggests that the power difference revealed in the current simulation is closely related to the additional uncertainty introduced by the unknown dispersion parameter.

Figure 1.

Monte Carlo power of one-sided HOA tests for two-group comparisons. Each power estimate was based on 100,000 simulated two-group data sets. Each data set contains 6 NB counts, divided into two groups: one of size 2 and the other of size 4. The group mean was simulated to be μ₁ = 100 for the group with size 2 and the mean was a) μ₂ = 50 (left panel) or b) μ₂ = 200 (right panel) for the group with size 4. The dispersion was simulated to be ϕ = 0.1, but was treated as unknown when performing the tests. The curves summarize the size-corrected power of the one-sided HOA, LR, and Wald tests. At each α level, the power was determined by comparing test p-value to a critical value determined by Monte Carlo simulation under the null.

4.3 The cost of estimating the dispersion parameter

With the HOA technique, inferences with correct type I errors can be made about the regression coefficients in an NB regression model even when the dispersion parameter is unknown and the sample size is small. The single-gene NB regression models, together with the HOA inference, can serve as a basis of comparison in power and sample size analyses. We illustrate this point using further simulations in two-group comparison settings.

The single-gene NB regression models we considered in this paper do not rely on a dispersion model, but there is necessary cost in statistical power associated with having to estimate the NB dispersion parameter. Figure 2 compares the power of the HOA test when the dispersion is unknown to the power of the HOA test when the dispersion is known. Under such a small sample situation (the sample size is only six), the power benefit of knowing the dispersion is substantial, especially at a small nominal significance level. For example, for detecting a fold change of 2 in mean at a significance level 0.01, the power of the HOA test is almost doubled (32.3% versus 59.8%) when the dispersion can be treated as known than when the dispersion is unknown.

Figure 2.

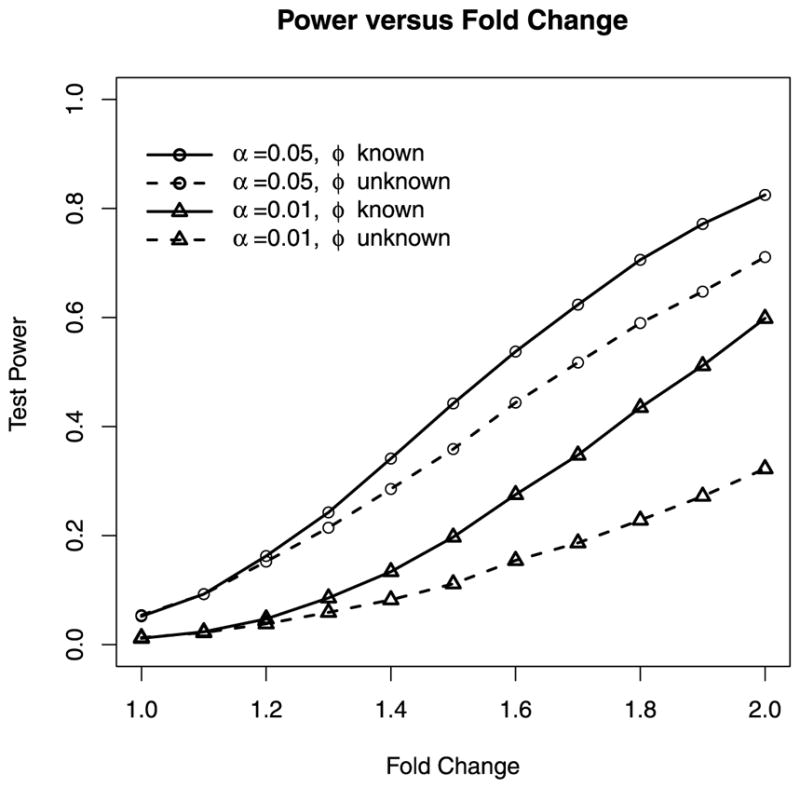
Monte Carlo power of one-sided HOA tests for two-group comparisons at nominal levels 0.05 and 0.01 as the fold change in group means increases from 1 (no change) to 2. Each power estimate is based on 10,000 simulated two-group data sets. Each data set contains 6 NB counts, divided into two groups of size 3 each. The group mean is 100 for the first group and ranges from 100 to 200 for the second group. The one-sided alternative is that the second group has a greater mean. The solid curves are power of the HOA test when the dispersion (ϕ = 0.1) is treated as known. The dashed curves are the power of the HOA test when the dispersion is unknown. The top two curves are power at the significance level α = 0.05. The bottom two curves are the power at the significance level α = 0.01.

Another way to quantify the cost of estimating the dispersion parameter is to examine the power and sample-size relationship. In Figure 3, we show the power of the HOA tests for two-group comparisons at three nominal significance levels, 0.05, 0.01, and 0.0001, as the sample sizes increase from 6 to 60. Under this simulation setting, at the nominal significance level α = 0.05, about 2 additional observations are needed for the HOA test with unknown dispersion to match the power of the HOA test with known dispersion before the power curves eventually level off. As the nominal significance level is lowered to 0.01 and 0.0001, the number of additional observations needed to match power increases to 4 and 8 respectively. For example, the sample sizes needed to achieve 60% power at levels 0.05, 0.01 and 0.0001 are 10, 18, and 42 respectively when the dispersion is known, and are 12, 22, and 50 when the dispersion is unknown. In other words, the cost of estimating the unknown dispersion is higher when a lower significance level needs to be used, for example, when we need to adjust for multiple testing.

Figure 3.

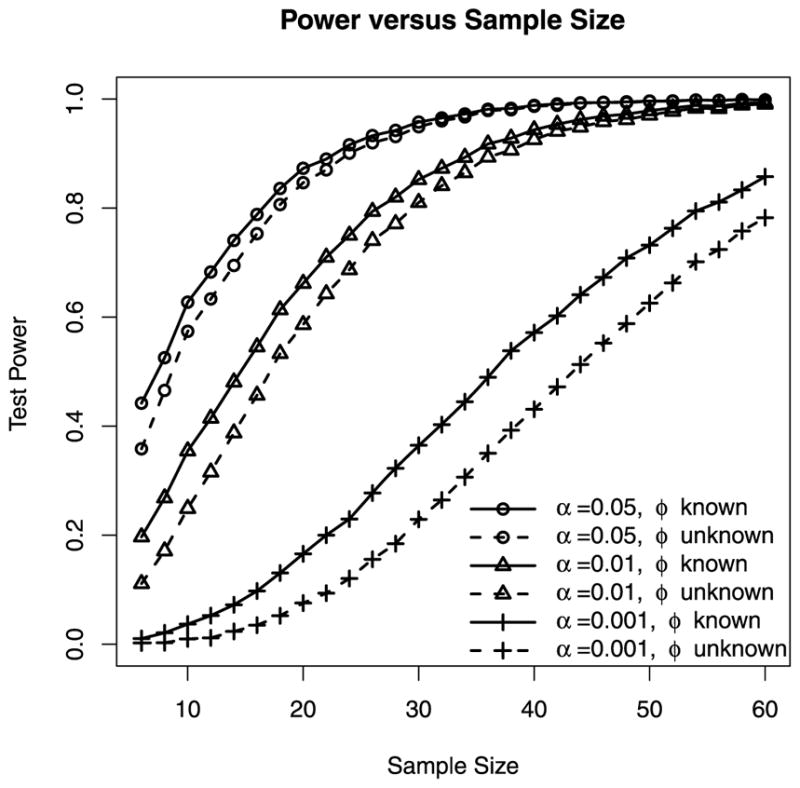
Monte Carlo power of one-sided HOA tests for two-group comparisons at nominal levels 0.05, 0.01 and 0.0001 as the sample sizes increases from 6 to 60. Each power estimate is based on 10,000 simulated two-group data sets. Each data set contains two groups of NB counts of equal sizes. The group mean is 100 for the first group and 150 for the second group. The one-sided alternative is that the second group has a greater mean. The solid curves are power of the HOA test when the dispersion (ϕ = 0.1) is treated as known. The dashed curves are the power of the HOA test when the dispersion is unknown. The top two curves are power at the significance level α = 0.05. The middle two curves are the power at the significance level α = 0.01. The bottom two curves are the power at the significance level α = 0.0001.

We emphasize that the power in the dispersion-known cases represents ideal scenarios: in practice, the dispersion is unknown. The results here indicate the potential power benefits of the dispersion-modeling approach where the dispersion is modeled as a simple function and estimated from a large number of genes. Whether and to what degree those benefits can be realized in practice, however, depend on many factors: the adequacy of the dispersion model, the uncertainties associated with model fitting, and so on.

4.4 Comparison to the dispersion-modeling approach

In Sections 1 and 2, we mentioned methods that model the NB dispersion as a parametric or smooth function of the estimated mean or other measures of abundance of the expression level and then treat the estimated dispersion values as the truth in subsequent tests for differential expression. Intuitively, methods using such a dispersion-modeling approach should perform well if and only if the dispersion model adequately captures the dispersion-mean dependence. Furthering understanding of the power-robustness trade-offs in the dispersion-modeling approach is one key motivation of the present study. In this section, we present simulation results in a scenario where the fitted dispersion model becomes increasingly inadequate in capturing the true dispersion-mean dependence. We investigate how the performance of the dispersion-modeling approach deteriorates under such a scenario. The single-gene models we developed will serve as a useful baseline for comparison in this investigation.

To keep the discussion and presentation simple, we will consider only one of the methods that use the dispersion-modeling approach, the NBQ method, which models the log dispersion as a quadratic function of the log mean relative frequencies. The NBQ model extends the NBP model discussed in Di et al. [6] to allow slight curvature in the dispersion-mean dependence. Several dispersion-modeling methods have been proposed in recent years, but our experience indicates that the difference between the different modeling methods—in terms of size-corrected statistical power—is much less significant than the difference between whether or not to use the modeling approach. [In 11, we provided more comprehensive review and comparisons between different dispersion-modeling methods.]

In this study, we simulated several two-group comparison data sets using the Arabidopsis data studied in Di et al. [6] as a template. In each data set, we simulated NB RNA-Seq read counts for 10,000 genes from 6 samples, divided in two groups of size 3 each. The library sizes N_j were set to 10⁶. We specified the mean relative frequencies of each gene in group 1 by sampling 10,000 estimated mean relative frequencies for the Arabidopsis data. For group 2, 500 genes were simulated to be over-expressed (with a common fold change FC), another 500 genes were simulated to be under-expressed (with a common fold change 1/FC), and the remaining 9,000 genes were not differentially expressed and had the same mean relative frequencies as in group 1. In order to specify the dispersion values, we first specified an NBQ model

$$log({\varphi }_{ij}^{\mathit{NBQ}})={\alpha }_0+{\alpha }_{1}log({\pi }_{ij})+{\alpha }_2{(log({\pi }_{ij}))}^2,$$ (6)

where i = 1, 2,..., 10,000 indexes genes, j = 1, 2,..., 6 indexes samples, and π_ij ’s are the mean relative frequencies (i.e., π_ij = μ_ij /N_j). The parameters (α₀, α₁, α₂) = (−1.396, −0.596, 0.117) were estimated from the Arabidopsis data. We then added normal noises to the dispersion values,

$$log({\varphi }_{ij})=log({\varphi }_{ij}^{\mathit{NBQ}})+{\epsilon }_i,$$ (7)

where ε_i’s were identically and independently distributed according to N(0, σ²).

In different simulated data sets, we varied the levels of DE (F C = 1.5 or 2.0) among the 1,000 DE genes (500 over-expressed and 500 under-expressed) and the amount of noise (σ = 0, 0.5, 1.0 or 2.0) added to the true dispersion model. (F C and σ were constant within each data set.) For each simulated data set, we performed the DE tests using 1) the single-gene NB regression models fitted to each gene separately assuming the dispersion as unknown, and 2) the NBQ approach where we first estimated the dispersion by fitting an NBQ dispersion model (6) to all genes and then treated the estimated dispersion values as the truth when performing the DE tests.

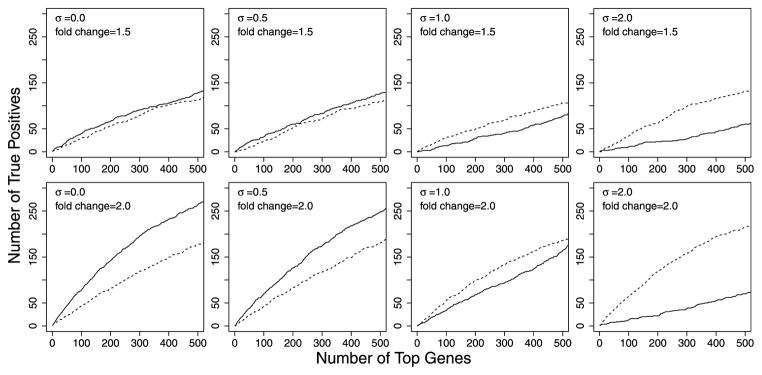
In Figure 4, we compared performances of the two approaches. We compared the numbers of truly DE genes among a specified number of top genes obtaining the smallest p-values from each method. When the fitted NBQ model does not fully capture the mean-dispersion variation, the p-values from the NBQ approach in general do not match their nominal levels. This issue is common to all methods using the dispersion-modeling approach [see, e.g., 8]. The comparison presented in Figure 4 is equivalent to comparing the size-corrected power. In practical application of the dispersion-modeling approach, though, one still needs to think about how to adjust the dispersion-modeling approach to provide the correct p-values even when the fitted model shows lack of fit. This is indeed a challenging issue and is one of our future research topics.

Figure 4.

Comparison between the single-gene approach and the NBQ approach. Each plot shows the number of truly DE genes (y-axis) among a specified number of top genes obtaining the smallest p-values (x-axis) from each method: solid curves correspond to the NBQ approach, dashed curves correspond to the single-gene approach. Each plot is based on 10,000 simulated genes from 6 samples, divided in two groups of size 3 each. Mean relative frequencies in group 1 were sampled from the estimated values for an Arabidopsis data set. In group 2, 500 genes were simulated to be over-expressed, 500 genes were simulated to be under-expressed, and the remaining 9,000 genes were simulated to be not DE. For the top row, the fold change was simulated to be 1.5 for all DE genes. For the bottom row, the fold change was 2.0. From left to right, the noise levels in the dispersion simulation model were σ = 0.0, 0.5, 1.0 and 2.0 (see equation (7)).

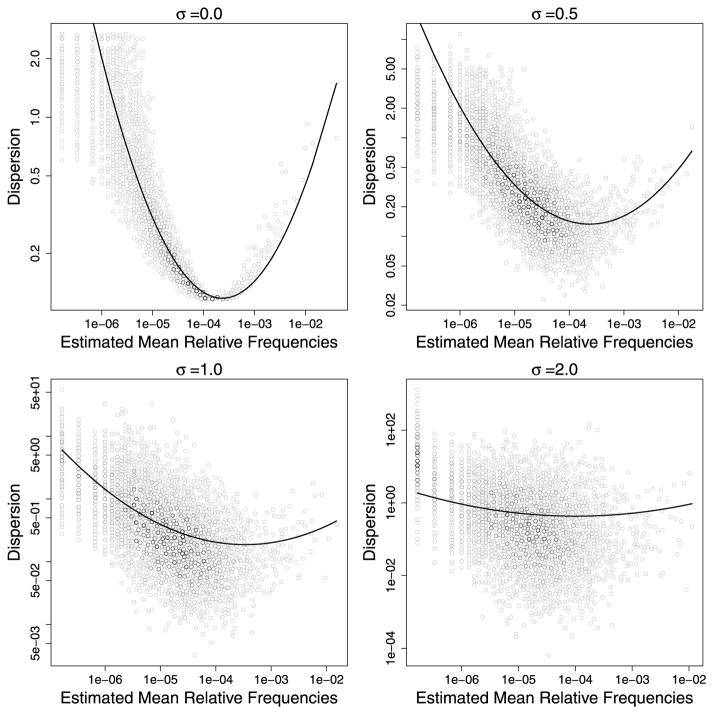
The results in Figure 4 generally agree with our intuition. When the level of noise, σ, is low in the dispersion simulation model (see equation (7)), we see that the dispersion-modeling approach has better power to identify DE genes. In other words, the dispersion-modeling approach can be robust to moderate deviation from the fitted dispersion model. As the noise level increases, however, the dispersion-mean relationship becomes less and less likely to be adequately summarized by a simple parametric function (see Figure 5), the dispersion-modeling approach starts to fail.

Figure 5.

As the noise level σ increases in the simulation model, the fitted dispersion model shows increasing lack of fit. In each plot above, the x-axis is the estimated mean relative frequencies, the solid curve corresponds to the fitted NBQ dispersion model, and black dots are the true dispersion values from the simulation model (see equations (6) and (7)). Note that when fitting the NBQ model (6), the true values of π_ij were unknown and needed to be replaced by the estimated values. The estimation errors in π_ij contributed to the estimation errors in the fitted dispersion model even when σ = 0.

5. DISCUSSION AND CONCLUSION

We have demonstrated that, with the HOA technique, accurate inferences can be made for regression coefficients in a single-gene NB regression model even when the dispersion parameter is unknown and the sample size is small. The effect of estimating the unknown dispersion parameter from a small sample is improved by the HOA adjustment (see Section 4.1). The single-gene models do not rely on a dispersion model and thus require fewer assumptions about the dependence of the dispersion on the mean or other predicting variables.

The power simulations in Section 4.3 reveal that the cost of estimating the unknown dispersion parameter—in terms of statistical power—can be high in small-sample situations especially when a stringent significance level is used. These results give some justification for the dispersion-modeling approach currently used in edgeR, DESeq and NBPSeq (see Sections 1 and 2 for more details) where the dispersion is modeled as a simple function of the mean and estimated from all genes combined. However, to fully understand the power-robustness trade-offs of the dispersion-modeling approach requires additional considerations: the adequacy of the dispersion model, the effect of treating the estimated dispersions as known, and so on. To this end, Lund et al. [8] discussed the issue of uncertainty in dispersion estimates and [11] proposed a goodness-of-fit test for the adequacy of the dispersion models. Our simulation study in Section 4.4 reveals that the dispersion-modeling approach is robust to moderate deviation from the fitted dispersion model. The single-gene NB regression models and HOA inference examined in this paper served as a basis for comparison in this power-robustness investigation. We believe more work is needed on the general topic of power-robustness as NB regression methods for RNA-Seq data continue to evolve. In particular, our simulation study indicates that it is crucial to accurately quantify the amount of variation that cannot be explained by the fitted dispersion model. We are currently developing methods for this purpose.

Our simulations in Section 4.3 also show that the cost of estimating the dispersion parameter is relatively lower if a moderate sample size becomes available and when a less stringent significance level is used (see Figure 3). This indicates that the single-gene models can be practically useful in targeted investigations of a few selected genes. In such situations, the burden of multiple testing is lower. In studies where false discovery rate [21] is used to determine p-value cutoffs, the critical values needed to call a gene significant depend on the total number of genes as well as the number of truly differentially expressing genes. A larger proportion of truly differentially expressing genes usually leads to a less stringent p-value cutoff.

The R [16] programs for performing the simulations are available from the author.

APPENDIX A. IMPLEMENTATION DETAILS OF THE HOA TEST

We first give the general formula for the adjustment term z in Barndorff-Nielsen’s r^* statistic with Skovgaard’s approximations, and then provide details on quantities needed for computing z and r^* for the NB regression models.

Let θ = (ψ, ν) where ψ is a one-dimensional parameter of interest and ν is a nuisance parameter and we wish to test the null hypothesis ψ = ψ₀. Let θ̂ = (ψ̂, ν̂) denote the maximum likelihood estimate of the full parameter vector θ and θ̃ = (ψ₀, ν̃) denote the maximum likelihood estimate of ν under the null hypothesis. Let l(θ) = l(θ; y) denote the log-likelihood, D₁(θ; y) denote the score vector

$$D_1(\theta ;y)=\frac{\partial }{\partial \theta }l(\theta ;y),$$

and j(θ) and i(θ) denote the observed and the Fisher information matrices respectively:

$$\begin{array}{c}j(\theta )=j(\theta ;y)=-\frac{{\partial }^2}{\partial {\theta }^2}l(\theta ;y).\\ i(\theta )={\text{Var}}_{\theta }{D}_1(\theta ;y)={\mathrm{E}}_{\theta }(j(\theta ;y)).\end{array}$$

With Skovgaard’s approximations plugged in, the general expression for the adjustment term z in Barndorff-Nielsen’s r^* statistic $r^{\ast }=r-\frac{1}{r}log(z)$ is

$$z\approx {\mid j(\widehat{\theta })\mid }^{-1/2}\mid i(\widehat{\theta })\mid {\mid \widehat{S}\mid }^{-1}{\mid j{(\stackrel{\sim }{\theta })}_{\nu \nu }\mid }^{1/2}\frac{r}{{[{\widehat{S}}^{-1}\widehat{q}]}_{\psi }},$$ (8)

where j(θ̃)_νν refers to the submatrix corresponding to ν and the [Ŝ⁻¹q̂]_ψ refers to the component corresponding to ψ. The two unfamiliar quantities in (8),

$$\widehat{S}={\text{Cov}}_{\widehat{\theta }}(D_1(\widehat{\theta };y),D_1(\stackrel{\sim }{\theta };y))$$ (9)

and

$$\widehat{q}={\text{Cov}}_{\widehat{\theta }}(D_1(\widehat{\theta };y),l(\widehat{\theta };y)-l(\stackrel{\sim }{\theta };y)),$$ (10)

are approximations to the so-called sample space derivatives. Note that the quantities involved in computing z are similar to those involved in computing the observed and Fisher information matrices. Specifically, the quantities needed for computing r^* are: θ̂, θ̃, l(θ̂, y), l(θ̃, y), j(θ̂), i(θ̂), Ŝ and q̂. For computing the last three, we need score vectors at θ̂ and θ̃ : D₁(θ̂ ; y) and D₁(θ̃ ; y).

The probability mass function of a single NB random variable Y with mean μ and size (shape) parameter κ (the reciprocal of the dispersion) is

$$Pr(Y=y;\mu ,\kappa )=\frac{\mathrm{\Gamma }(\kappa +y)}{\mathrm{\Gamma }(\kappa )\mathrm{\Gamma }(1+y)}{\left(\frac{\mu }{\mu +\kappa }\right)}^y{\left(\frac{\kappa }{\mu +\kappa }\right)}^{\kappa }.$$

Under the NB log-linear regression model introduced in Section 2,

$$\begin{array}{c}{Y}_j~\text{NB}({\mu }_j,\varphi ),\\ log({\mu }_j)=log(N_j{R}_j)+X_j^T\beta ,\end{array}$$

where X_j = (X_j1,..., X_jp)^T, β = (β₁,..., β_p)^T. The likelihood of θ = (β, κ), with κ = 1/ϕ, from a single observation

$$l_j(\theta ;y_j)=log(\mathrm{\Gamma }(\kappa +y_j))-log(\mathrm{\Gamma }(\kappa ))+ylog({\mu }_j)+\kappa log(\kappa )-(y_j+\kappa )log({\mu }_j+\kappa ),$$ (11)

where ${\mu }_j={\mu }_j(\beta )=N_j{R}_{j}exp(x_j^T\beta )$. For a set of independent NB counts, y = (y₁,..., y_n), from the NB regression model,

$$l(\theta ;y)=\sum _{j=1}^n{l}_j(\theta ;y_j).$$ (12)

For testing one of regression coefficients, say, β₁, in the NB regression model, ψ = β₁ is the parameter of interest and ν = (β₂,..., β_p, κ) is a nuisance parameter. The score vector is $D_1(\theta ;y)=(\frac{\partial l}{\partial \beta },\frac{\partial l}{\partial \kappa })$ with components

$$\begin{array}{c}\frac{\partial l}{\partial \beta }=\sum _j\frac{\partial l_j}{\partial {\mu }_j}\frac{\partial {\mu }_j}{\partial \beta }=\sum _j\frac{y_j-{\mu }_j}{{\sigma }_j^2}{\mu }_j{x}_j,\\ \frac{\partial l}{\partial \kappa }=\sum _j\left[\mathrm{\Psi }(\kappa +y_j)-\mathrm{\Psi }(\kappa )+ln(\kappa )+1-ln({\mu }_j+\kappa )-\frac{\kappa +y_j}{{\mu }_j+\kappa }\right],\end{array}$$

where ${\sigma }_j^2={\mu }_j+{\mu }_j^2/\kappa$ and Ψ is the digamma function. The components in the observed information j(θ) are

$$\begin{array}{ll}\hfill -\frac{{\partial }^{2}l}{\partial {\beta }^2}=& -\sum _{j=1}^n\left[\frac{{\partial }^{2}l}{\partial {{\mu }_j}^2}\frac{\partial {\mu }_j}{\partial \beta }{\frac{\partial {\mu }_j}{\partial \beta }}^T+\frac{\partial l}{\partial {\mu }_j}\frac{{\partial }^2{\mu }_j}{\partial \beta \partial {\beta }^T}\right]\hfill \\ \hfill =& -\sum _{j=1}^n\left[\left(-\frac{y_j}{{\mu }_j^2}+\frac{y_j+{\kappa }_j}{{({\mu }_j-{\kappa }_j)}^2}\right){\mu }_j^2+\frac{(y_j-{\mu }_j){\mu }_j}{{\sigma }_j^2}\right]x_j{x}_j^T,\hfill \\ \hfill -\frac{{\partial }^{2}l}{\partial {\kappa }^2}=& -\sum \left[{\mathrm{\Psi }}_1(\kappa +y_j)-{\mathrm{\Psi }}_1(\kappa )+{\kappa }^{-1}-2{({\mu }_j+\kappa )}^{-1}+\frac{\kappa +y_j}{{({\mu }_j+\kappa )}^2}\right],\hfill \end{array}$$

and

$$-\frac{{\partial }^{2}l}{\partial \beta \partial \kappa }=-\sum _j\left[-{({\mu }_j+\kappa )}^{-1}+\frac{\kappa +y_j}{{({\mu }_j+\kappa )}^2}\right]{\mu }_j{x}_j,$$

where Ψ₁ is the trigamma function.

For computing z in equation (8), we also need the Fisher information

$$i(\widehat{\beta })={\text{Var}}_{\widehat{\beta }}(D_1(\widehat{\beta };Y)),$$

Ŝ in equation (9), and q̂ in equation (10). These quantities do not have closed-form expressions, but can be approximated using Monte Carlo simulations. For that purpose, we simply need to simulate NB counts from the NB regression model under the full model (i.e., θ = θ̂).

For finding the maximum likelihood estimate of θ under the null and the alternative models, we use the R function optimize [16, 4] to maximize the profile likelihood

$$l_p(\kappa )=\underset{\beta }{max}l(\beta ,\kappa ),$$

where max_β l(β, κ) means maximizing the likelihood over β for fixed κ, which can be done using the standard Fisher scoring algorithm for generalized linear models [see, e.g., 10].