Abstract
The increasing use of biomarkers in cancer have led to the concept of personalized medicine for patients. Personalized medicine provides better diagnosis and treatment options available to clinicians. Radiological imaging techniques provide an opportunity to deliver unique data on different types of tissue. However, obtaining useful information from all radiological data is challenging in the era of “big data”. Recent advances in computational power and the use of genomics have generated a new area of research termed Radiomics. Radiomics is defined as the high throughput extraction of quantitative imaging features or texture (radiomics) from imaging to decode tissue pathology and creating a high dimensional data set for feature extraction. Radiomic features provide information about the gray-scale patterns, inter-pixel relationships. In addition, shape and spectral properties can be extracted within the same regions of interest on radiological images. Moreover, these features can be further used to develop computational models using advanced machine learning algorithms that may serve as a tool for personalized diagnosis and treatment guidance.
Keywords: Radiomics, informatics, texture, machine learning, Breast, Magnetic Resonance Imaging, treatment response, proton, diffusion-weighted imaging, DWI, ADC map, cancer, Genetics
Introduction
Radiological imaging techniques are powerful noninvasive tools used for the detection, differentiation, and diagnosis of different tissue characteristics in patients. These imaging methods include X-Ray, Computed Tomography(CT), Magnetic Resonance Imaging (MRI), Nuclear Medicine (NM) Positron Emission Tomography(PET) and Ultrasound(US). Each of these modalities creates different tissue contrast based on whether the tissue is normal or abnormal. These different tissue contrast mechanisms are exploited by the radiologist to identify patterns to reach a diagnosis. However, each of the radiological images contains more information content not visible to the clinician’s eye and this “hidden” information creates a “radiological texture” which can provide much more information about the tissue of interest than previously thought. Thus, Radiomics was introduced as a “new” method to discover and translate the metrics obtained by using texture and other analysis techniques on radiological images. However, Radiomics is a new application using established techniques, specifically, Texture, Entropy, Haralick and other features1–4. The novel aspect of Radiomics is the comparison of these measures to surrogate endpoints and the advent of increased computational power available today. The main idea behind Radiomics is that information is “hidden” within the radiological images can be extracted using advanced texture and shape analysis. From this extraction of data, a high dimensional space is created. Intuitively, texture is used by everyone to define objects either visually or by touch. The terms commonly used to describe texture are roughness, smoothness, coarseness, etc., but for digital data, analytical methods were needed to better “describe” the information content within digital objects. Therefore, texture analysis was born, in part, is based on information theory developed in 1948 by Claude Shannon and extended by Haralick, Galloway, and others that incorporated different statistical measures to include gray level matrix operations on the input data1–4.
Historically, one of the first applications of texture analysis was in analyzing aerial photographs6 then later applied to medical and other images2,7. Currently, texture feature analysis is used in many different areas of research, especially, with increased computational power and digital storage capacity8–11. Moreover, given a region of interest, shape based features can also be extracted along with texture analysis5.
Recently with the availability of increased computer technology to reduce the computational complexity into investigations of using texture and shape analysis led to the development of a new area of research termed Radiomics. By definition, Radiomics is the high throughput extraction of quantitative features from radiological images creating a high dimensional data set followed by data mining for potentially improved decision support12–14, however, Radiomics is based on texture, shape and gray level statistics within images to discern different relationships compared to clinicopathologic data. But, the correlation to true biological meaning is needed. But, through the use of Radiomic features in medical imaging, it may be possible to decode tissue pathology that is not normally visible to the naked eye. How is this possible? Tumors are spatially and temporally heterogeneous and maybe undersampled during medical procedures, for example, during biopsy. Therefore, the whole tumor is not completely characterized and this could be detrimental in determining treatment options. This challenge can be potentially overcome by using a Radiomics approach which is capable of extracting quantitative features over the whole tumor and the results can be compared to the tumors pathological results or other information, such as, survival14.
This article reviews and outlines historical, mathematical, and more recent applications of radiomics techniques in detecting tumor characteristics and demonstrates that radiomics methods are promising in the near future for clinical applications. Moreover, this review will give a summary of the state of the art knowledge of radiomics and texture analysis in different cancers, and conclude with an outlook on potential future of radiomics in the era of “personalized medicine” cancer therapies.
Radiomics Algorithm
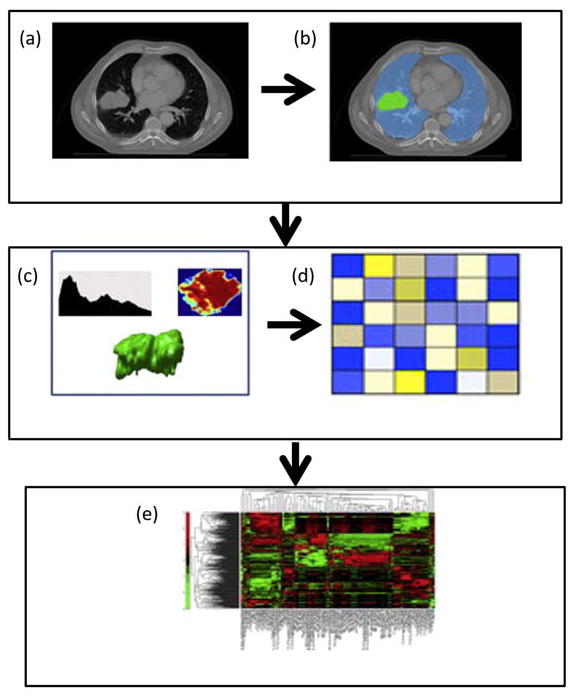
The framework for radiomics use in clinical settings is shown in Figure 1. The first step involves radiological image acquisition of MRI, CT, PET, etc., depending on the imaging modality used for diagnostic and/or treatment planning. Then, the second step involves identifying region of interest in the acquired images. This region of interest can be either lesion tissue or a normal tissue depending on the application. The identification and segmentation of the tissue of interest is accomplished manually by radiological experts or automated segmentation software. The third step involves extraction of radiomic features from the region of interest based on the texture and shape properties. This step produces a large number of radiomic features based on the statistical, filtering and morphological analysis and creates a high dimensional feature space14. Then, the “highly” informative features are selected based on the user defined criteria. The final step involves classification of the features to defined by the user, for example, distinguishing malignant tumor from benign tumors or survival.
Figure 1.
Illustration of the radiomics algorithm. (a) Initial Computed Tomography (CT) scan. (b) Segmentation is performed on the lesion using a region of interest(ROI). (c) Radiomic features are extracted from the ROI based on the gray level patterns, inter-voxel relationships, and shape. (d) A subset of the extracted radiomic features is selected for classification (e) The selected features are used as inputs into a classification model to produce a diagnosis or correlation to a prognostic marker. Data from5,12.
Radiomic feature extraction
Radiomic feature extraction methods are based into primarily three categories consisting of statistical, filtering and morphological features. In this paper, we discuss the fundamental feature extraction methods from all the three categories, however, there are some other feature extraction methods such as gray level size zone matrix based features, Minkowski functionals, and others used in radiomics applications that will not been discussed here15,16.
Statistical texture features
Statistical texture features characterize the stochastic or random properties of the spatial distribution of gray levels within an image using statistical measures, such as, marginal-probabilities (defined below). Currently, there are two levels of statistical methods used for Radiomics, first and higher order methods as shown in figure 2. These statistical methods have been applied to different imaging modalities used in several different diseases and are outlined below.
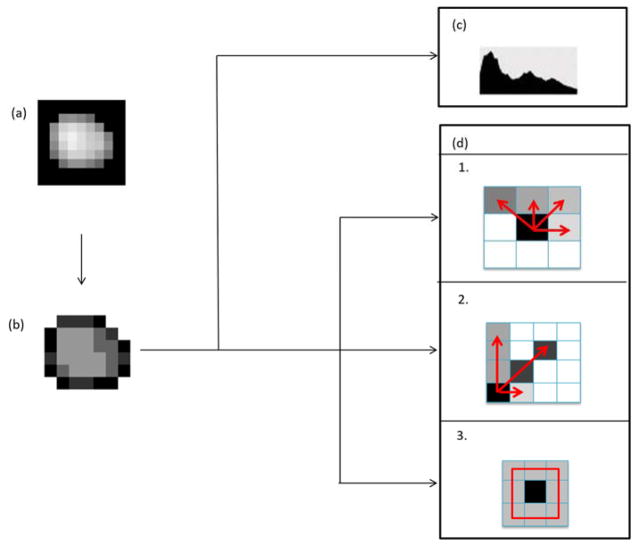
Figure 2.
Illustration of statistical texture feature extraction. (a) Segmented tumor image (b) Segmented tumor image quantized to four intensity levels (c) First order statistical features corresponding to first order histogram (d) Higher order statistical features corresponding to 1. GLCM (gray level co-occurrence matrix), 2. GLRLM (gray level run length matrix) and 3. NGTDM (neighborhood gray tone difference matrix). Data from16.
First order texture statistics
First order texture statistics are based on the first order histogram that describes distribution of voxel intensities in an image. For example, a normalized first order histogram (H) is computed by dividing the voxel intensities (I) in an image into B equally spaced bins and computing the proportion of voxels in each bin as defined by the equation.
| (1) |
Entropy and uniformity are the two commonly used features computed using the histogram. Let H be the first order histogram with B bins, then the entropy1 and the uniformity are given by the following equations:
| (2) |
where K is a positive constant and is determined by the units of the application.
However, since we are dealing with bits of information, K =1 and the equation used in most digital applications is given as
| (3) |
and
| (4) |
Entropy measures the inherent randomness in the gray level intensities of an image. The maximum value of entropy (Log2(B)) occurs when all the gray level intensities in an image occur with equal probability1. On the other hand, uniformity, measures the uniformity of gray level intensities within an image or ROI. For example, the maximum uniformity of one occurs when all the pixels in an image or ROI have the same gray level intensity.
Both the first and second order statistics can give different values based on the number of bins and the number of bins is a critical parameter defined by the user. If the number of bins is selected either too small or very large, then the histogram may not be able to correctly represent the underlying distribution with the image or ROI. Several methods exist for determining the optimal number of bins without making any assumptions regarding the underlying data distribution17,18. However, if different sized ROIs in a study have a different number of bins in the first order histograms, then becomes difficult to directly compare the results between studies. To potentially overcome this difficulty, another approach would be to use the same number of bins for all ROIs. Unfortunately, this leads to an issue of dependence of first order statistic features on the size of ROI. For example, if we consider two ROIs of sizes 128 and 1024 voxels and bin the gray level intensities within these two ROIs into 1024 bins per R0I (as we are using the same number of bins), then the entropy values of data distributions with maximum randomness (each voxel has a different intensity) would be equal to 7 for 128 voxel-sized and 10 for 1024 voxel-sized ROIs respectively. Optimal binning is a major issue for all statistical approaches, since they depend on the preprocessing step of image quantization. Thus, some form of feature normalization is required with respect to size in cases when the same number of bins is used for all the ROIs and with respect to the of number of bins when different numbers of bins are used for different ROIs. Typically, these binning issues are not addressed in many publications.
A number of first order statistical texture features have been applied to applications across different medical imaging modalities for characterization of several biological tissues of interest5,7,16,19–63,64. Table 1 summarizes the quantitative values of first order entropy for different organs and pathologies as reported in the literature. Depending on the organ being imaged and the imaging modality, the first order histograms may or may not have been the same across all the applications. However, as shown in Table 1, entropy values are higher in malignant than in corresponding benign tissue.
Table 1.
Quantitative values of first order statistical entropy as reported in the literature
| Reference | Tissue | Image/Object type | Pathology | |||
|---|---|---|---|---|---|---|
| Benign | Malignant | |||||
| Sinha et al76 | Breast | Normalized radial length of tumor | 1.46 | 1.6 | ||
| Ertas et al35 | Breast | nMITR projection | 5.4 | 6.77 | ||
| Suo et al57 | Urinary bladder | DWI, b=700 | 4.08 | 4.06 | ||
| Urinary bladder | DWI, b=1500 | 3.97 | 3.78 | |||
| Kierans et al51 | Adnexal lesion | ADC | 4.54 | 4.94 | ||
| Low grade | High grade | |||||
| Ryu et al56 | Glioma | ADC | 6.26 | 6.86 | ||
| Volunteers | Healthy | |||||
| Brinkmann et al22 | Liver | MRS | 7.6 | 4.7 | ||
| Healthy adult | Elderly | CSM patients | ||||
| Cui et al187 | Spinal cord | FA map | 6.07 | 6.01 | 5.32 | |
| Young | Middle aged | Non demented elderly | Elderly (AD) | |||
| Chen et al48 | Brain | cortical surface structure | 1.2 | 1.24 | 1.28 | 1.33 |
Higher order texture statistics
The features generated from first order statistics provide information about the distribution of voxel intensities in an image but they do not provide any information about the inter-voxel relationships within the image. The inter-voxel relationships in an image can be quantified using several different techniques, the gray level co-occurrence matrix, gray level run length matrix and neighborhood gray tone difference matrix method and they are outlined below1–4.
Gray level co-occurrence matrix
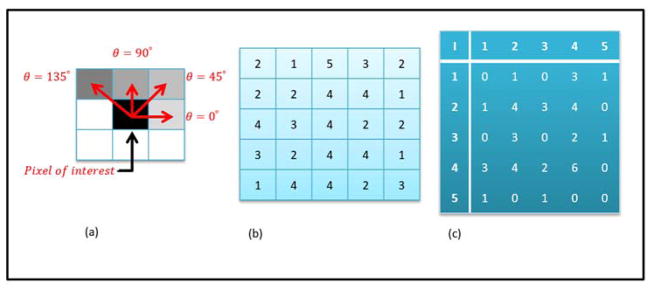
The spatial distribution of gray level intensities within an image can be extracted by using the gray level co-occurrence matrix (GLCM)2. The GLCM is constructed by considering the relationship between voxel pairs and the frequency of each intensity pairs within an image or a region of interest 2. The relationship between voxel pairs is characterized by two user defined parameters, the distance (d) and angle (θ) and illustrated in Figure 3a using the parameter, θ. If the number of gray levels in the image is Ng, the number of possible voxel pairs would be Ng × Ng. The frequency of each voxel pair in the image or a region of interest is computed and stored in the NgxNg GLCM matrix. The GLCM constructed can be either symmetric 2 or asymmetric depending on the ordering of values in voxel pairs. Mathematically, the GLCM of an image of size NxxNy with Ng gray levels is given by the following equation2:
| (5) |
where (r, s), (t, v) ∈ Nx × Ny; ; I represents the image as a function I Nx × Ny → {1,2, …, Ng}; and |·| denotes the cardinality of a set
Figure 3.
(a) Illustration of the inter-pixel relationships characterized by the user defined parameter, θ (b) An example 5 × 5 matrix with gray values ranging from 1 to 5. (c) The resultant symmetric gray level co-occurrence matrix (GLCM) obtained by multiplying the asymmetric GLCM with its transpose.
The GLCM obtained from equation (5) is an asymmetric GLCM and can be converted to a symmetric GLCM by multiplying by the transpose (Gsym = G × GT).
The range of input parameters is θ ∈{0°, 45°, 90°, 135°}, d ∈ {1, 2, 3,…, n} for a two dimensional image and by extending to a three dimensional image, the range for theta increases to a total of 13 angles. Figure 3 demonstrates an example 5×5 matrix with the corresponding symmetric GLCM for θ = 0° and d = 1.. Therefore, based on different values of theta and d, a large number of GLCMs can be produced and for each GLCM, fourteen textural features were developed by Haralick, et al2 and current research into texture analysis has led to construction of more features, with most recent applications using up to twenty-two GLCM based features5.
Studies have found no significant differences in changing the number of gray levels (eg, 64, 128, etc) in the image to define the GLCM based features to determine benign form malignant lesions or treatment response65–66. From the twenty-two GLCM texture features. The most commonly used features are given below:
| (6) |
| (7) |
| (8) |
| (9) |
The notation used in the above equations is explained in table 2.
Table 2.
Notation used in the equations for computing texture features using gray level co-occurrence matrix
| Gnorm | Normalized gray level co-occurrence matrix |
| Gx | Marginal probability matrix obtained by summing the rows of Gnorm |
| Gy | Marginal probability matrix obtained by summing the columns of Gnorm |
| μx | Mean of Gx |
| μy | Mean of Gy |
| σx | Standard deviation of Gx |
| σy | Standard deviation of Gy |
The angular second moment (ASM) feature is the measure of uniformity in an image. A uniform image will have a few gray level transitions with the maximum uniformity of one representing only a single type of gray level transition through the image. In contrast, the entropy feature, increases as different types of gray level transitions are present in an image. Visually an image with higher entropy will appear heterogeneous. Similarly, an image with a higher contrast feature value will have a higher frequency of large intensity differences between each neighbor. A simple example of a high contrast image is a checkerboard. Finally, the correlation feature measures the linear dependence between any two neighboring voxels throughout the image i.e. an image with higher contrast will generally have lower correlation. In addition, texture features obtained from the GLCM are not rotationally invariant. Rotationally invariant features can be obtained by taking mean and range of texture values obtained in all directions (four for 2D images and thirteen for 3D volumes). Computation of rotationally invariant features for 3D is not straightforward because voxel spacing along the third dimension may not be same as voxel spacing in the other two dimensions. Thus, using the same value of d (GLCM input parameter) as voxel spacing in all three dimensions is very important to achieve rotationally invariant texture features.
For many applications, GLCM based features are the most commonly used textural features applied to different medical imaging modalities for characterization of biological tissue of interest5,16,19–21,26,28,30,31,34,37,39–41,47,49,50,54,56,58–63,65–101. These applications used symmetric GLCMs for texture analysis as defined by Haralick et al 2; however recent applications of GLCM based features have also used asymmetric GLCMs with some success5. Chen et al. compared the GLCMs generated from 2D slices vs. 3D volume on breast DCE-MRI and showed that 3D GLCM texture features performed significantly better than 2D GLCM texture features in classifying malignant from benign breast lesions65.
Gray level run length matrix
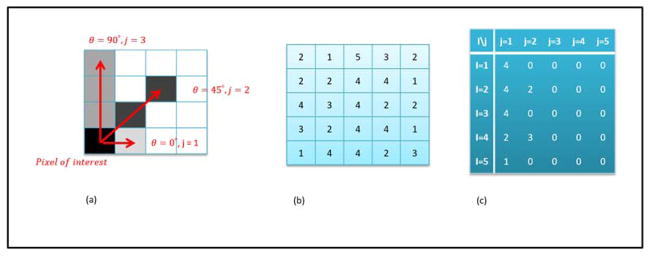
The gray level run length matrix (GLRL) is defined as the number of contiguous voxels that have the same gray level value and it characterizes the gray level run lengths of different gray level intensities in any direction3. Elements (i,j) in the matrix represents the number of times, j, a gray level value, i, appears in the image. Based on the direction angle, θ (4 for two dimensions and 13 for three dimensions), different GLRL matrices can be constructed. The inter-pixel relationship based on the user defined parameters of angle, θ and run length, j is illustrated in figure 4a. Mathematically GLRL of an image of size Nx×Ny with Ng gray levels is given by the following equation:
| (10) |
where (m, n) ∈ Nx × Ny; ; I represents the image as a function: Nx × Ny → {1,2, …, Ng}; and |·| denotes the cardinality of a set
Figure 4.
(a) Illustration of the inter-pixel relationships characterized by the user defined parameters, angle θ and run length j. (b) Example 5 × 5 matrix with values ranging from 1 to 5. (c) Resultant gray level run length matrix (GLRL) for run lengths of 1 to 5 and θ = 0°.
Galloway et al developed five features from the GLRL matrix viz. short runs emphasis (SRE), long runs emphasis (LRE), gray level nonuniformity (GLN), run length nonuniformity (RLN) and run percentage (RP) given by the following equations:
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
where Nr is the number of different run lengths measured to compute GLRL matrix and P is the total number of voxels in the image. A total of eleven features based on gray level run length matrices have been proposed in the literature 3,102,103. Current applications in texture analysis use the complete set of eleven features derived from GLRL matrix5.
An example 5×5 input matrix and the corresponding GLRL matrix for horizontal direction are shown in figure 4b and 4c respectively. The GLRL matrices are generally normalized (by the total number of entries in the matrix) in order to facilitate consistency between different scans of different patients as well as different scans for same patient considered across a time interval. GLRL matrix based features have also been applied to a number of applications across different medical imaging modalities for characterization of biological tissue of interest 5,16,19,21,28,30,31,34,37,39,41,42,50,54,58,60–63,69,79.
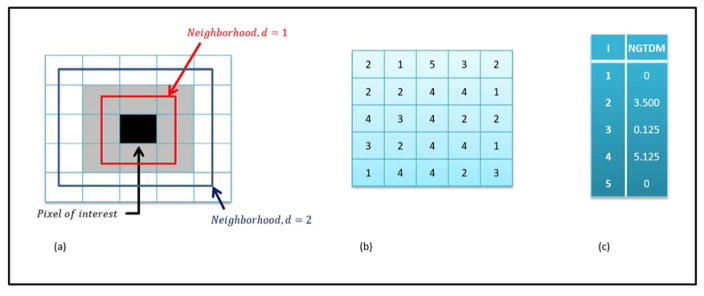
Neighborhood gray tone difference matrix
The neighborhood gray tone difference matrix (NGTDM) is a texture analysis method based on the visual properties of an image 4. Neighborhood gray tone difference matrix (NGTDM) is a one dimensional matrix computed such that the each gray level entry, defined as gt, in the NGTDM is the summation of the differences between all the pixels with gray level value, gt and the average gray level value of its neighborhood. The size of the neighborhood is defined by the user. Mathematically, NGTDM of an image (Nx × Ny) with Ng gray levels is given using the following set of equations:
| (16) |
| (17) |
Here, ANGT is the average neighborhood gray tone in the neighborhood of the pixel at position (i,j), W=(2d+1)2 and d = size of the neighborhood (e.g. 1 in case of 3 × 3 neighborhood). There are five features derived from the NGTDM and are given by the following equations:
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
where Pi is the probability of occurrence of a gray level value I, n is the number of entries in the NGTDM and Nt is the total number of gray levels present in the image.. For example, figure 5 demonstrates the application to a 5×5 gray level input matrix.
Figure 5.
(a) Illustration of the neighborhood around the pixel of interest based on the user defined neighborhood parameter, d (b) Example 5×5 input matrix with values ranging from 1 to 5. (c) Neighborhood gray tone difference matrix for d=1.
The NGTDM features have been developed to correlate the quantitative values of texture features as closely as possible to the visual interpretation of texture by humans. For example, coarseness provides a quantitative measure of local uniformity while contrast provides quantitative information about the difference in the intensity levels of neighboring regions. Similarly, busyness tells us how “busy” (rapid intensity changes) are the neighborhoods in a given image or a region of interest. Furthermore, complexity, as the name suggests, quantifies the complexity of the spatial information present in an image. Finally, texture strength can be defined as characterizing the visual aesthetics of an image. Images with higher texture strength are generally more attractive to look at than images with low texture strength. The NGTDM features have been applied to some medical image applications 16,49,104.
Morphological features
Morphological features are used in many settings to define the shape of an object. For example, the shape of the tumor can be quantified using fractal dimension105,106. Fractal dimension is a measurement of irregularity in the shape of the tumor. Different methods proposed in the literature for computing the fractal dimension of a pattern are discussed in107. Other methods based on volume and surface area of the tumor have been summarized in5. However different fractal sets having different textures may have the same fractal dimension values. Consequently, Mandelbrot introduced the concept of lacunarity for characterization of texture in an image 106. Lacunarity quantifies how fractals fill space, i.e., larger the gaps, higher the lacunarity. Different methods proposed in the literature for computing the fractal dimension of a pattern are discussed in107. Li et al 108 evaluated four methods for computing fractal dimension of parenchymal patterns obtained from mammography in assessment of breast cancer risk. The four methods evaluated included conventional box counting method, modified box counting method using linear discriminant analysis (LDA), global Minkowski method and modified Minkowski method using LDA. The authors observed that the advanced methods using LDA resulted in better classification between low and high risk patterns (AUC=0.9 for modified box counting method and AUC=0.93 for modified Minkowski method). Likewise, Guo et al109 compared five different methods for computing the fractal dimension as well as lacunarity analysis of breast regions obtained from mammography to classify breast masses from normal parenchyma. The fractal dimension methods tested in this study were Reticular cell counting method110, differential box counting method111, blanket method112, Fourier power spectrum method113 and fractional Brownian motion model(FBM) 114. The highest AUC of 0.84 was achieved for the FBM method. Moreover, when FBM method was combined with lacunarity, the AUC increased to 0.90. Morphological features based on Renyl fractal dimension, shape analysis, volume and surface area of the tumor have also been implemented in the literature5,115,116.
Filtering approaches
The basic idea of filtering approaches is that the original textured image is subjected to some form of linear or nonlinear transform, followed by statistical analysis of the transformed image to obtain texture information. A comparative study of different filtering approaches can be found in117. In this paper, we discuss the filtering techniques commonly used for texture analysis of medical images.
Spatial filtering techniques
Spatial filtering techniques are based on neighborhood operations on the original textured input images. These neighborhood operations are based on filters or kernels of size n × n, where n determines the size of the neighborhood considered by the kernel. Some examples of commonly used filters for texture analysis include statistical filters like average filter, range filter and entropy filter or edge filters like Prewitt filter, Sobel filter, Laplacian filter and Laplacian of Gaussian (LoG) filter. The input image is convolved with the desired kernel to produce filtered images highlighting specific texture information in the original texture image. The resultant filtered images are analyzed using first order statistics (mean, median, standard deviation, etc.). Statistical and edge filtering techniques have been applied to medical images for texture analysis in a number of applications7,59,118–126.
Apart from statistical and edge kernels, special kernels have also been designed for identifying different types of textures. For example, Laws designed three sets of one dimensional convolution masks of different sizes corresponding to different types of textures such as level, edge, spot, wave, ripple, undulation and oscillation127,128. All the convolution masks were center weighted, symmetric or asymmetric and zero-sum except the level convolution masks. Using a vector product between the masks of the same sizes, different spatial domain filters or kernels of size 3×3, 5×5 and 7×7 were generated by Laws. Laws texture energy measures have been used in filtering input medical images for texture analysis in many applications39,129–140. Another example of a specially designed kernel is the fractal dimension kernel designed by Al Kadi et al141. Examples of different techniques for filtering in the spatial domain have been illustrated in figure 6. The value of n (size of the kernel neighborhood) is determined by the spatial resolution of the image being filtered. Higher the spatial resolution of the image being filtered, higher the value of neighborhood, n, used for filtering. However, further research is required to standardize the size of the neighborhood for different resolution images acquired using different imaging modalities.
Figure 6.
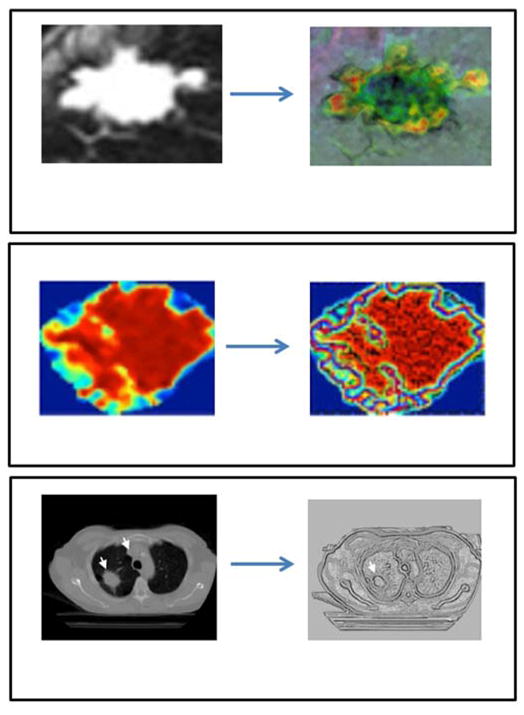
Illustration of different techniques used for spatial domain filtering (a) statistical kernel (e.g. median filter) (b) Edge kernel (e.g. Laplacian of Gaussian filter) (c) Special kernel (e.g. Fractal dimension filter). Data from59,141,170
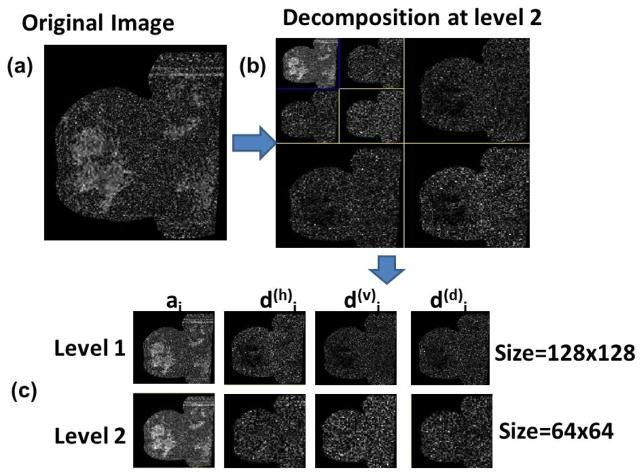
Multi-resolution image scaling
The frequency of variations in the gray level values in a region of interest is dependent on the scale of the region of interest. The frequency content within an image can be analyzed at different scales using wavelets142–145. Image texture can be analyzed at different scales by representing the image in a pyramid structure. Using discrete wavelet transform, four low resolution images can be obtained from the original image viz. ILL, ILH, IHL and IHH. By repeatedly applying discrete wavelet transform on ILL at each level, hierarchical pyramid structure for different resolutions can be created.
Texture analysis can be done by computing statistical texture features at each level or averaging the results across multiple resolutions. Wavelets have been extensively used in multiresolution texture analysis of medical images 5,38,50,58–63,70,73,77,88,140,146. The use of multiresolution can decompose the data into different frequency components, thereby facilitating the study of each component with a resolution matched to its scale. Figure 7 illustrates multiresolution scaling on an example breast MRI diffusion weighted image147.
Figure 7.
Multiresolution methods applied to a diffusion-weighted image (b=500): a) the original size 256×256; b) compressed image (64×64) at different levels. c) For compression 2D biorthogonal spline wavelets were used. d(h)j, d(v)j and d(d)j respectively are detail components corresponding to vertical, horizontal, and diagonal. aj, is the approximation (coarse) component at decomposition level. Data from 147
Feature selection
The next step is to select a subset of features that can characterize the tissue of interest. The challenge here is that even using one d value and thirteen theta values, a large number of GLCM features are extracted. Reduction of these features needs to be done in order to avoid the potential problem of overfitting. In the event of overfitting, the statistical model will better reflect noise in the image than the original data. There are a number of strategies available for countering the problem of overfitting. Tpyically, If a particular set of features have been shown to be most relevant in the particular application of interest, then those features can be manually selected for subsequent analysis. In addition, by using regression analysis, correlations between different features can be analyzed and redundant features maybe be removed. Thus, the feature selection procedure can be either supervised or unsupervised. In supervised feature selection, most informative features are selected based on some ground truth knowledge about the task at hand. As the biological meaning of different radiomic features has not yet been established, the ground truth used for feature selection is generally the final class label (e.g. benign or malignant). The supervised feature selection can be accomplished using a filtering or a wrapper method. Filtering methods evaluate one feature at a time for its importance or predictive ability. Some examples of filtering methods include Fisher’s criterion, Wilcoxon rank sum test, Student t-test, etc148. Parmar et al62 compared the performance of fourteen such feature selection methods in predicting overall survival in lung cancer patients using CT scans. They found that the Wilcoxon test based method had the best performance and maximum stability. One major disadvantage of filtering methods is that they do not consider the dependencies between different features that may lead to better prediction. Wrapper methods, on the other hand, evaluate subsets of features for their combined predictive power. As a result, wrapper methods are capable of examining the dependencies between different features. However, due to very high dimensionality of radiomics feature space, evaluation of complete feature subset space is computationally NP-hard149. Some examples of computationally efficient wrapper methods include greedy forward selection and greedy backward elimination as they do not evaluate all possible feature subsets. Finally, supervised feature selection methods are prone to overfitting and may not scale well across applications.
The unsupervised feature selection approach is based on dimensionality reduction algorithms. Dimensionality reduction algorithms transform the high dimensional feature space into a meaningful representation of its intrinsic dimensionality. Dimensionality reduction algorithms can be linear or nonlinear. Linear dimensionality reduction algorithms assume the high dimensional features to lie on or near a linear subspace of some high dimensional topological space while nonlinear dimensionality reduction algorithms do not rely on the linearity assumption. Some examples of linear dimensionality reduction algorithms include principal component analysis (PCA) and multidimensional scaling (MDS) 150,151. Examples of nonlinear dimensionality reduction algorithms are Isometric mapping (Isomap), locally linear embedding (LLE) and diffusion map152–154. A review on different dimensionality reduction algorithms can be found in155. The dimensionality reduction algorithms are not prone to overfitting; however, but, they may not always give optimal low dimensional representations. In medical imaging, Kassner et alused PCA to transform four GLCM textural features obtained from texture analysis of T1-weighted post contrast brain images for prediction of hemorrhagic transformation in acute ischemic stroke in a set of patients, however, there was no longitudinal data91. Texture was found to be potentially useful in discriminating hemorrhagic transformation from non-hemorrhagic transformation when compared to visual examination. Both supervised and unsupervised feature selection methods have their advantages and disadvantages. Further research is required to determine an optimal hybrid approach that combines the advantages of both feature selection methods.
Classification
The final step in the radiomics framework is the classification of the features for quantifying the tissue of interest and prediction. This is done using either a supervised or unsupervised classifier. Supervised classifiers require the user to provide input for the patients for which the underlying pathology is already known. Using the data provided by the user, supervised classifiers learn a classification model to categorize any new patient with unknown pathology. Some examples of supervised classifiers include support vector machine (SVM), random forest (RF), k-nearest neighbors (kNN), etc156–159.
In contrast to supervised classifiers, unsupervised classifiers do not need any training data. Unsupervised classifiers group the patients based on some form of distance metric, such as, Euclidean distance, angular distance, etc. Unsupervised classifiers are very useful when the goal of classification step is to identify a patient or a group of patients in the database that are most similar to the new patient with unknown pathology. The diagnosis and treatment details for the known patients may be then used to efficiently diagnose or determine outcomes for the patient. Some examples of unsupervised classifiers include k-means clustering, hierarchical clustering, consensus clustering, etc 160–162. A recent study compared the performance of twelve different supervised classifiers in predicting overall survival in lung cancer patients using CT scans and found the random forest classifier to have relatively the best performance with low AUC=0.662. However, since Radiomics is a new and ever expanding area of research and with the development of better classification algorithms, the optimal method is not clearly defined and will depend on the application.
Radiomics applications
In early applications to medical imaging, the majority of methods used Texture analysis, which, then evolved into the current application of Radiomics. An extensive review on the applications of both texture and radiomics analysis in neurologic pathologies can be found in163. In this paper, we reviewing the application of these methods to mostly body and cancer applications.
Lung
a) X-Ray
Texture analysis was first used in 1972 for automatic classification of pulmonary disease by Sutton and Hall7. They employed texture measures of symmetry, directional gradient and Fourier domain energy on a dataset of 24 patients to classify between lung tissue using linear discriminant analysis. The authors observed that the texture features based on directional gradient gave the best classification accuracy. The training classification accuracy was achieved at 92% while the testing classification accuracy was achieved at 84%. This study was directed towards demonstrating the usefulness of texture in automatic screening of chest radiographs.
b) Computed Tomography
Al-Kadi and Watson implemented the differential box counting based fractal analysis method as well as lacunarity analysis on contrast enhanced (CE) CT images for differentiation of aggressive malignant lung tumors from the nonaggressive ones on a cohort of 15 patients141. The authors achieved an accuracy of 83.3% for distinguishing between these two groups using average fractal dimension. The authors also observed high correlation between the average fractal dimension and tumor uptake of 18FDG obtained using PET.
Ganeshan et al developed texture features using multiscale (fine to coarse) application of spatial domain filtering algorithm LoG (Laplacian of Gaussian) followed by extraction of statistical features of mean gray intensity (MGI) along with entropy (E) and uniformity (U) on unenhanced CT scans of 18 non-smal cell lung cancer patients to correlate with tumor glucose metabolism and stage121. The authors found significant associations between coarse texture features and tumor standard uptake value (SUV) and fine texture features and tumor stage. In another study, Ganeshan et al used the texture feature of uniformity to associate with patient survival in a study of 54 patients124. The authors observed that patients with coarse texture uniformity of less than 0.62 did not survive more than two and a half years. The same research group further extended their research to correlate texture features with histopathological markers of angiogenesis and hypoxia on a dataset of 14 patients with unenhanced as well as CE CT images 125. The same texture analysis method was employed with different statistical features (standard deviation (SD) along with mean (MPP) and uniformity (UPP) of positive pixel distribution). The results indicated significant associations between texture features and average intensity of tumor staining with pimonidazole, tumor Glut-1 expression and tumor CD34 expression. The relationships between image features and the histograms generated at different scales using spatial domain filtering algorithm, LoG have also been analyzed by the same group to provide clinical understanding of results164.
Aerts et al used texture features based on first order statistics, GLCMs, GLRL matrices at multiple scales using wavelets on CT images of 1019 patients with non-small cell lung cancer or head-and-neck(H&N) cancer to associate radiomic features with primary tumor stage as well as patient survival5. The radiomic features of first order statistics energy, shape compactness and gray level nonuniformity (GLRL feature) obtained from unscaled data as well as wavelet HLH scaled data were found to be most significant. Good to moderate prediction concordance indices (CIs) of 0.65, 0.69 and 0.69 were achieved on one lung cancer validation dataset of 225 patients and two H&N datasets of 136 and 95 patients. The authors found significant associations between radiomic features and gene expression patterns indicating the utility of radiomic features in characterizing underlying biological mechanisms. Strong correlations were observed between the radiomic features (GLRL gray level non uniformity obtained from unscaled data as well as wavelet HLH scaled data) and cell cycling pathways, demonstrating higher proliferation for more heterogeneous tumors.
Recent studies by the same group achieved low AUCs of 0.66 (lung cancer) using random forest and CIs of 0.6 (lung cancer) and 0.68 (H&N cancer) using consensus clustering on the same set of radiomic features for predicting patient survival, which needs further investigation62,63. Moreover, using consensus clustering, the authors also found either no or some association between consensus clusters and lung stage (AUC =0.61), lung histology (AUC=0.56), H&N stage (AUC=0.77) and H&N histology (AUC=0.58) based on the poor AUC. However, these are essentially low AUCs and more research is needed.
The same group used additional texture features based on first order statistics obtained after the application of LoG filter in addition to the other radiomic features used previously on a cohort of 182 patients to predict probability of distant metastasis in lung adenocarcinoma in addition to patient survival59. The authors found thirty five radiomic features to be somewhat prognostic for distant metastasis (CI>0.6) and twelve features for patient survival (CI=0.55). The authors reported four features based on the LoG filter to be trending for potentially prognostic for distant metastasis and patient survival. A recent study by the same group tested two new features of entropy ratio and convexity for association with patient survival in lung adenocarcinoma using two independent patient cohorts of 61 and 47 patients64. The authors found significant association between the two features and patient survival for only the first cohort.
In summary, statistical features obtained from LoG based spatial domain filtering of tumors at coarse level were found to be more predictive in different applications than statistical features obtained at fine level. A LoG filter highlights the edges within an ROI, suggesting that edges found by the filter using a wider Gaussian were more informative than edges produced using a narrow Gaussian. This may be because edges found using a narrow Gaussian are more susceptible to noise in the input image, Furthermore, LoG based features were also found to be more informative than statistical features based on first order statistics, GLCM and GLRL59.
c) PET
Cook et al investigated the texture features obtained from NGTDM extracted from FDG PET images of 53 non-small cell lung cancer patients for association with chemoradiotherapy response and survival104. The texture features were compared to the three survival groups (overall survival (OS), progression free survival (PFS) and local PFS (LPFS) obtained using RECIST (Response Evaluation Criteria in Solid Tumors) criteria. The authors found the texture features of coarseness, busyness and contrast to significantly predict survival in the patient cohort as summarized in Table 3. The authors observed that responders had lower coarseness but higher contrast and busyness than non-responders. This suggests that the texture obtained for tumors corresponding to responders is less uniform with high frequency of intensity changes i.e. they are more heterogeneous than tumors corresponding to nonresponders.
Table 3.
Summary of coarseness, contrast, busyness and complexity values corresponding to responders and non-responders of NSCLC obtained using Lung PET as reported in the literature104.
| Pathology | Coarseness | Contrast | Busyness | Complexity |
|---|---|---|---|---|
| Responders | 0.01 | 0.11 | 0.76 | 1938 |
| Non-responders | 0.03 | 0.04 | 0.37 | 1926 |
d) PET-CT
Vaidya M et al used FDG-PET/CT dataset of 27 patients for characterization of radiotherapy tumor response in non-small cell lung cancer47. Texture features of first order statistics and gray level co-occurrence matrix features were combined with the SUV/HU (Halsted units) measurements in this study. The model was built using logistic regression and resampling methods of cross validation and bootstrapping. The authors observed that the first order statistics features obtained from intensity volume histogram correlated more strongly with loco-regional control in contrast with the GLCM based features which correlated more strongly with local control.
Breast
a) Mammogram
Texture analysis was first used on mammograms in 1986 by Magnin et al to evaluate the risk for developing breast cancer 67. GLCM based texture features were used in this study. However this study did not yield very good results with reproducibility barely reaching 80%. Wei et al successfully implemented GLCM based texture analysis at multiple scales using wavelets on 672 ROIs to classify between biopsy proven masses and normal parenchyma using linear discriminant analysis70. They achieved an AUC of 0.89 on the training set and an AUC of 0.86 on the test set. A study by Chan et al investigated the use of texture analysis on mammograms for associating the presence of clustered microcalcifications with malignant pathology75. The authors implemented the GLCM texture features on a set of 86 mammograms followed by a backpropagation artificial neural network classifier to achieve an AUC of 0.88. Multiple studies have since investigated the use of texture analysis on mammograms for detection of masses39,77,79,81,88,109,115,131,134,165–168 with an average AUC of 0.87 and a maximum AUC of 0.96 39 achieved with texture features obtained using first order statistics based features, GLCM based features, GLRL matrix based features and Law’s texture energy measures. The quantitative values of the fractal dimension obtained from breast mammograms corresponding to normal, mass and architectural distortion as reported in the literature are summarized in table 4.
Table 4.
Summary of fractal dimension values corresponding to different breast tissue classes obtained using mammogram as reported in the literature109,167.
| Tissue class | Fractal dimension |
|---|---|
| Normal | 2.64 |
| Mass | 2.39 |
| Architectural distortion | 2.52 |
b) Ultrasound
Garra et al performed texture analysis (first order statistics, GLCM and fractal dimension) on breast ultrasound in a cohort of 80 patients20. The authors were able to identify malignant lesions with a sensitivity of 100% and specificity of 80% (78% for fibroadenoma, 73% for cysts and 91% for fibrocystic nodules). The best features identified in this study were GLCM based contrast with θ = 45° and GLCM based correlation with θ = 0°. Numerous studies have since used texture analysis to differentiate between benign and malignant breast lesions using ultrasound 83,140,146,169.
c) MRI
The first application of texure analysis in breast MRI was in 1997 by Sinha et al 76. This study included 43 breast cases (23 benign and 20 malignant) and used eight texture features in combination with patient age and the DCE-MRI parameter of maximum enhancement to obtain sensitivity and specificity of 93% and 95% respectively. In reality, it was Radiomics, since they compared the results to an outcome or clinical variable. Moreover, Gibbs et al implemented GLCM based texture features to differentiate between benign and malignant breast tumors on post contrast MRI images from 79 patients85. Texture features of variance, entropy and sum entropy were found to be most significant using logistic regression analysis and the ROC analysis resulted in an excellent AUC of 0.92. Similarity, Ertas et al extracted first order statistics from normalized maximum intensity-time ratio (nMITR) projection generated using DCE-MRI to classify between benign and malignant breast tumors in 46 patients35. The texture features of entropy, mean, standard deviation and maximum were observed to be the most significant (p<0.001) with excellent AUCs between 0.86 and 0.97.
Nie et al used GLCM based features along with morphological features to distinguish between benign and malignant tumors using post contrast MRI images of 71 patients89. The authors found the texture features of compactness, normalized radial length entropy, volume and GLCM based features of entropy, sum average and homogeneity to most significantly differentiate benign and malignant tumors and obtained an AUC of 0.82. The same group compared the two feature selection and classification methods of logistic regression and artificial neural network for the task of classifying malignant breast tumors from benign breast tumors92. The authors found there was no significant difference in the results obtained from the two methods.
Instead of using post contrast MRI images, Karahaliou et al used parametric maps derived from DCE-MRI (e.g. signal enhancement ratio map) to extract GLCM based features94. The authors found the GLCM ASM, GLCM entropy and GLCM sum entropy obtained from signal enhancement ratio (SER) map as the most discriminative features producing an AUC of 0.92. Agner et al used kernels based on GLCM features along with other filters on the DCE MRI images in a dataset containing 41 patients for differentiating malignant from benign breast tumors170. The authors created textural kinetic curves by computing the mean of the filtered image within the region of interest across the DCE sequence of images. The textural kinetic curves were classified using a probabilistic boosting tree and achieved sensitivity and specificity of 99% and 76% respectively. In a recent study, Wang et al used morphological and GLCM texture features in combination with pharmacokinetic parameters obtained from DCE-MRI to classify between benign and malignant breast tumors101. The authors found the texture feature of GLCM entropy, GLCM energy and compactness along with pharmacokinetic parameters of rate constant (kep) and volume of plasma (vp) to be the most discriminative with sensitivity and specificity of 91% and 92% respectively. Cai et al used GLCM based texture features from DCE-MRI in combination with ADC, kinetic curve features and morphological features to distinguish between benign and malignant breast tumors on a cohort of 234 patients99. The authors achieved sensitivity and specificity of 85% and 89% respectively. They also tested the same set of features on a validation dataset consisting of 93 patients and achieved sensitivity and specificity of 69% and 91% respectively98.
Holi et al applied texture analysis (first order statistics, GLCM, GLRL) on T1-weighted pre contrast, post contrast and subtraction breast MRI datasets from twenty patients in order to associate texture features with histological types of invasive breast cancer (lobular vs. ductal) 42. The authors identified the entropy based GLCM features to be the most effective features and were able to achieve a maximum accuracy of 100% using linear discriminant analysis (LDA) and nonlinear discriminant analysis (NDA) on the first subtraction and contrast images.
A recent study by Ahmed et al performed GLCM based features on breast MRI to predict chemotherapy response in 100 breast cancer patients66. The authors found the texture features of contrast, variance, difference in variance, sum variance, sum entropy, sum average, cluster shade and cluster prominence showed significant difference between responders and partial responders of chemotherapy when implemented on post contrast images. Parikh et al used multiscale LoG (Laplacian of Gaussian) filter followed by extraction of first order statistical features from T2-weighted MRI of 36 patients to predict chemotherapy response171. The authors found the texture features of entropy and uniformity showed significant different between responders and non-responders with an AUC of 0.84.
In summary, post contrast enhanced MRI was the most frequently used image for texture analysis of breast tumors. This is consistent with the clinical environment where radiologists also use post contrast enhanced MRI to discern textural features corresponding to breast tumors.
The quantitative values of the texture features obtained using post contrast enhanced breast MRI images for benign and malignant lesions reported in the literature are summarized in table 5. The quantitative texture values of entropy, energy, etc obtained from various studies maybe difficult to compared due to several reasons. For example, the use of different magnet strengths (1.5 or 3T), differnent preprocessing steps, binning methods, and gray level normalization. However, a trend in the quantitative values can still be observed, for example, entropy, energy (uniformity), and contrast values tend to be increased compared to benign and/or normal tissue. These metrics may provide an insight into the heterogeneity of the tumor tissue. Based on the current literature, It may be inferred that malignant tumor tissue is more heterogeneous (high entropy, low uniformity and high contrast) than benign tumor tissue and seen in pathological samples172. This correlation is the impetus for further Radiomics research in developing noninvasive tools for clinical decision.
Table 5.
Summary of quantitative values of four GLCM based features obtained using post contrast enhanced breast MRI images for benign and malignant lesions as reported in the literature 65,66,76,85,94.
| Image Metrics | Benign lesion | Malignant lesion | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Reference | Acquisition | Pre-processing | gray levels | Dimension | ASM | Entropy | Contrast | Correlation | ASM | Entropy | Contrast | Correlation |
| Sinha et al76 | Post contrast DCE-MRI | None | 16 | 2D | 0.02 | 1.96 | 34.3 | - | 0.01 | 2.27 | 535.8 | - |
| Ahmed et al66 | Post contrast DCE-MRI | H.Eq | 16 | 2D | - | - | - | - | 0.01 | 7.13 | 8.5 | 0.8 |
| Gibbs et al65,85 | Post contrast DCE-MRI | H,Eq | 32 | 2D | 0.004 | 5.85 | 25.5 | 0.84 | 0.004 | 5.94 | 23.2 | 0.86 |
| Chen et al63 | Post contrast DCE-MRI | H.Eq | 32 | 2D | 0.01 | 5.41 | 52.1 | 0.6 | 0.01 | 5.44 | 75.8 | 0.6 |
| Chen et al65 | Post contrast DCE-MRI | H.Eq | 32 | 3D | 0.01 | 5.12 | 67.5 | 0.5 | 0.01 | 5.26 | 69.2 | 0.55 |
| Karahiliou et al94 | SER map | None | 64 | 2D | 0.025 | 1.71 | 12.8 | 0.37 | 0.01 | 2.12 | 23.8 | 0.51 |
H.Eq =histogram equalization, SER= signal enhancement ratio and ASM = angular second moment.
Liver
a) Computed Tomography
Mir et al implemented texture analysis based on GLCMs and GLRL on the liver CT images of 60 patients to classify the CT images as normal liver, clearly visible malignancy and invisible malignancy69. The authors found the texture features of entropy (normal: 1.65±0.12, visible malignancy: 2.13±0.17, invisible malignancy: 1.64±0.08), local homogeneity (normal: 2.30±0.25, visible malignancy: 1.48±0.21, invisible malignancy: 2.23±0.15) and gray level distribution (normal: 5.54±0.31, visible malignancy: 2.09±0.61, invisible malignancy: 4.72±0.54) to be the most significant. Chen et al used fractal analysis along with GLCM based features to classify the liver tumors as hemangioma or hepatoma in a dataset of 30 patients80. Using modified probabilistic neural network classifier, the authors were able to achieve classification accuracy of 83%. In a study by Gletsos et al, GLCM based features were used to classify the CT focal liver lesions of 147 patients into four classes (normal, hepatic cysts, hemangioma and hepatocellular carcinomas) 86. The authors used three sequentially placed feed forward neural networks and achieved excellent accuracies of 97%, 100% and 82% in classifying the normal from abnormal, hepatic cysts from others and hemangioma from hepatocellular carcinomas respectively. Huang et al173 used autocovariance function on a dataset of 164 liver CT images to classify malignant (hepatocellular carcinomas and colorectal metastases) lesions from benign lesions and achieved moderate sensitivity and specificity of 75% and 88% respectively.
b) MRI
Jirak et al extracted first order statistical and GLCM based texture features using T2-weighted MRI images obtained from 43 patients to classify between healthy and cirrhotic liver26. The authors achieved classification error around 8%. Along with T2-weighted MRI images, Mayerhoefer et al also extracted texture features (first order statistics, GLCM, GLRL matrix) from T1-weighted images to classify focal liver lesions achieving error rates of 12–18% on T2-weighted images and 16–18% to T1-weighted images41. Fujimoto et al used entropy of ADC to classify normal from abnormal fibrosis stage (AUC =0.94, p<0.001, entropy cutoff = 1.30) 46. ADC maps were created using diffusion weighted MRI (b =0 and 1000 s/mm2). O’ Connor et al quantified tumor heterogeneity using first order statistics on voxel-wise Ktrans, ve and vp and fractal dimension analysis on DCE-MRI data obtained from 10 patients with 26 colorectal cancer liver metastases to predict shrinkage in tumor volume in response to bevacizumab and cytotoxic chemotherapy45. The authors found the median ve, tumor enhancing fraction (Ef) and microvascular uniformity obtained using fractal dimension to be the most significant features and the median classification error was achieved at 12%.
c) Ultrasound
Texture analysis was first implemented on liver ultrasound images in 1985 by Raeth et al to classify liver into normal, diffuse parenchymal and malignant disease on a dataset of 71 patients with an accuracy of 96%19. Wu et al used multiresolution fractal analysis to classify between normal liver, hepatoma and cirrhosis on a dataset of 40 patients and achieved an accuracy of 90%68. The authors observed that multiresolution fractal analysis features outperformed the GLCM based texture features as well as Laws texture energy measures. Sujana et al extracted first order statistical features along with GLCM and GLRL matrix based features to classify liver ultrasound images from 113 patients into normal, hemangioma and malignant categories21. Using artificial neural network, the authors were able to achieve classification accuracy of 100%. Horng et al developed a new texture analysis method called texture feature coding to classify liver ultrasound images into normal, hepatitis and cirrhosis on 120 patients (30 training and 90 test images) 84. The authors achieved an accuracy of 86.7% as compared to 75.7% obtained by the same group using GLCM, texture spectrum and fractal dimension based features71. Yoshida et al used multiresolution analysis on a dataset of 44 patients and obtained an AUC of 0.92 in classifying malignant from benign lesions29.
Numerous studies have since used texture analysis to classify focal hepatic lesions using ultrasound132,136,174–180. A comparative study of different texture analysis approaches implemented in the literature can be found in 181. A recent implementation by Mitrea et al extracted GLCM based texture features from the Laws texture energy images obtained from filtering liver ultrasound images and achieved an accuracy of 90% in liver cancer detection139.
Colorectal cancer
a) Computed Tomography
A study by Ganeshan et al investigated the use of texture analysis of liver on 28 patients with colorectal cancer119. The authors used multiscale (fine to coarse) application of the spatial domain filtering algorithm LoG (Laplacian of Gaussian) followed by extraction of first order statistical features. The authors observed that the relative scale texture parameter correlated inversely with the corresponding PET SUV metric (r=−0.59, p=0.007) and hepatic phosphorylation index(HPFI) (r=−0.59, p=0.006). There was apositive correlation with the total hepatic perfusion (THP) (r=0.51, p=0.02-) and hepatic portal perfusion (HPP) (r=0.45,0.05) for patients without liver metastases. The same research group used the same set of texture features obtained from liver CT to predict survival in patients with colorectal cancer120. The texture feature of uniformity was obtained for the scale ratios of 1.5 (fine) to 2.5 (course) and 2 (medium) to 2.5(coarse) were observed to be significant (p<0.005) prognostic factors for surival. Goh et al extracted fractal dimension based features from colorectal perfusion CT images of 20 patients to differentiate between colon cancer and normal bowel182. The authors found the fractal dimension and fractal abundance were significantly (p≤0.001) higher for colon cancer (1.71±0.07 and 7.82±0.62) than normal bowel (1.61±0.07 and 6.89±0.47). Cui et al used fractal dimension analysis on CT images obtained from 228 patients to classify the status of lymph nodes in rectal cancer as benign or malignant183. The authors were able to classify the malignant nodes from benign nodes with an accuracy of 88%.
Ganeshan et al used their previously developed multiscale texture analysis algorithm on dynamic contrast enhanced CT of the liver obtained from 27 patients to classify between node negative and not positive non metastatic colororectal cancer122. The authors observed significant difference in entropy and uniformity of the node negative and node positive patients. Using fine texture entropy of the images obtained between 26 and 30 seconds after contrast injection, the authors were able to achieve sensitivity and specificity of 100% and 71% respectively in identifying node positive patients (entropy cutoff ≤ 0.0807). The same group used texture analysis of the colorectal tumor obtained from contrast enhanced CT of 57 patients to define biomarkers for 5-year survival126. The authors used the texture features of fine scale entropy, uniformity, kurtosis, skewness and standard deviation to define the five year survival rate with the corresponding cutoffs at less than 7.89 for entropy, greater than 0.01 for uniformity, less than 2.48 for kurtosis, greater than 20.38 for skewness and less than 61.83 for standard deviation.
Head and Neck
a) Computed Tomography
Leijenaar et al 60 chose four radiomic features (Energy, compactness, GLRL non uniformity and wavelet GLRL non uniformity obtained by Aerts et aldescribed previously5 to investigate their prognostic ability on 542 oropharyngeal squamous cell carcinoma (OPSCC) patientsthat underwent CT.. The features were weighted in a Cox model to develop and test a prognostic index for validation of the radiomic signatures. The authors observed that the Kaplan-Meiyer survival curves were significantly different (p<0.05) between low and high radiomic signature predictions using a log-rank test, however, the C-index was 0.628 which is lower than reported in previous reports (C index=0.686 and 0.685)5
b) PET
El Naqa et al explored the GLCM texture and features on a cohort of nine Head & Neck patients and 14 cervical cancer patients undergoing chemoradiotherapy and imaged with PET90. The most discriminative features from the GLCM included energy, contrast, local homogeneity and entropy. The authors were able to achieve moderate to high AUCs of 0.76 (cervical cancer) and 1.0 (H&N) and 0.76 (cervical cancer) on the very small datasets indicating a potential usefulness of texture in PET imaging. For cervical cancer, the GLCM entropy of the CTV (clinical tumor volume) was much lower (3.6) than that of the tumor (5.3). Similar trend was observed for H&N cancer as well where entropy of the CTV was 3.8 and that of the tumor was 4.7.
Esophageal cancer
a) PET
Tixier et al used first order texture features from the GLCM, GLRL matrix and NGTDM on a PET dataset to classify between response in 41 esophageal cancer patients treated with chemoradiation16. The authors found the texture features of GLCM entropy (sensitivity=79%, specificity=91%) and GLCM angular second moment (sensitivity=88%, specificity=73%) along with size (sensitivity=76%, specificity=91%) and intensity variabilities (sensitivity=76%, specificity=91%) of uniform zones were the most discriminative between responders and non-responders compared to the SUVmax (sensitivity=46%, specificity=91%).
Adnexal lesion
a) MRI
Kierans et al extracted first order statistical features of entropy from ADC maps to classify between benign and malignant adnexal lesions in 37 patients51. The average entropy ADC was significantly higher for malignant (4.94±0.4) than benign (4.54±0.44) lesions. However, the sensitivity (66.7%) and specificity (82.4%) of the entropy ADC was low in diagnostic performance.
Prostate lesions
a) MRI
Wibmer et al performed GLCM texture analysis on T2-weighted and diffusion weighted MRI of prostate obtained from 147 patients and compare with the Gleason score as well as cancer detection184. The authors used five GLCM features of inertia, entropy, energy, correlation and homogeneity for analysis. According to the authors, the texture features of cluster shade and cluster prominence “over-emphasize” the other GLCM features such as energy, entropy, homogeneity and contrast and hence were not used. There were a total of 186 cancerous lesions in the 147 patients with 143 lesions in posterior zone (PZ) and 43 lesions in transition zone (TZ). The authors observed similar trend in the GLCM texture features obtained from PZ tissue in both ADC map and T2WI as well as from TZ tissue in ADC map. For all these cases, the GLCM texture features of entropy and inertia were significantly higher for cancer while the remaining three features were significantly lower for cancer than non-cancerous tissue (p<0.008). Furthermore, the authors observed that only the GLCM texture features inertia (p=0.001) and correlation (p=0.04) obtained from T2-weighted were significantly different between TZ cancerous and non-cancerous tissue. Moreover, when compared to Gleason score, GLCM energy was lower while GLCM entropy was higher for increased Gleason scores (p<0.05 for all inter-score GLCM feature values).
Discussion
Radiomics and texture analysis have been widely used for diagnosis and prognosis in many different applications. In fact, some of the initial applications of texture analysis date back to 1970s. The most commonly implemented features across all the applications are based on GLCMs. The reason behind the popularity of GLCMs as the texture analysis method of choice is because the GLCM features analyze the inter-voxel relationships in both voxels that are in immediate neighborhood as well as voxels that are far apart. Moreover, GLCMs are easy to implement and the features are more intuitive to interpret. In spite of being the most popular method, the features identified as the most predictive GLCM features are not consistent across different applications. In fact, the most predictive GLCM features are not even consistent within the same organ, same modality and the same diagnostic application. For example, in breast MRI, the texture features identified as the most important for diagnosis were not consistent across different implementations in the literature. Sinha et al76 observed the GLCM features of difference entropy, contrast, sum entropy and inverse difference of moments to be the most predictive, Gibbs et al85 observed the GLCM features of variance, entropy and sum entropy as the most predictive and Nie et al89 observed the GLCM features of entropy, sum average and homogeneity as the most predictive in classifying benign from malignant breast lesions. Moreover, all the studies demonstrated excellent results. The variations in the radiomics results may arise from the image preprocessing steps such as segmentation, image quantization (for statistical features), neighborhood size (for statistical and filtering features) or the modeling steps of feature selection and classification.
The development of a texture feature set that is consistent across different modalities, organs and pathologies may not be possible or practical. This is because different modalities highlight separate characteristics of the tissue of interest. Furthermore, different organs may have distinct inherent texture. However, it is very important to develop a consistent feature subspace for each application even though different applications may have different feature subspaces. Furthermore, consistency in feature subspaces is also required to understand and correlate the texture features with tissue biology. For example, if the entropy values of benign and malignant tumors are significantly different for one region and not for another, it is not possible to establish any correlation between tumor biology and texture values. Thus, extensive research on large patient datasets is required to standardize the radiomics workflow.
Five year view
Radiomics is a relatively new field of research even though it uses established methods for feature extraction. As discussed earlier, extensive research is required to evaluate the preprocessing steps such as quantization for the statistical methods. In the next five years, a consensus will be achieved on the optimal method for data binning as well as feature normalization for the statistical methods. On the other hand, a standard for optimal neighborhood sizes for different image resolutions corresponding to different imaging modalities will be established for filtering techniques. Establishing the standards for these parameters will require extensive theoretical research along with practical validations. Once the standards for feature extraction are established, the next step would include standardization of feature selection and classification methods.
The majority of texture analysis studies have focused on extracting features from a single slice or 3D volume using a specific imaging modality. However, extracting texture features from a combined dataset of multiple images obtained from multiparametric imaging methods (e.g. MRI) or obtained from different modalities (e.g. PET-CT) might be able to better correlate with tissue biology. Representation learning of multispectral datasets has already been achieved in the computer vision community using advanced machine learning methods such as deep learning185,186. In the next five years, we will also see radiomic feature representations emerge based on these advanced machine learning techniques. In conclusion, as the field of radiomics matures, radiological reports will also evolve into mineable patient data spaces built using imaging biomarkers, finally realizing the goal of precision medicine for providing an improved decision support system.
Key Issues.
Radiomics is a new field of research and targeted for precision medicine.
The mathematical basis for radiomics is well grounded in texture, shape, and information theory.
Development and identification of radio-clinicopathologic features to radiomics features are critical for wide spread use of radiomics in precision medicine.
Further research is needed to determine the optimal processing steps needed for reproducible application of radiomics to different imaging applications, for example, imaging modality, histogram binning, voxel spacing, size of the image or ROI, and size of the spatial filtering kernel, to name a few.
Standardization of “relevant” radiomic features for clinical application is needed for improved diagnostic ability; most studies to date have low to moderate AUCs. Thus, every step of the radiomics framework needs extensive analysis, validation and standardization for radiomics to achieve its true potential as a decision support system.
Advanced data algorithms will be needed to identify the significant features in the high dimensional feature space created by the radiomics method.
Prospective trials and follow up studies are needed to fully define the impact of radiomics for diagnosis and precision medicine.
Footnotes
Financial & competing interests disclosure
The authors were supported by the following grants: NIH - P50CA103175, 5P30CA06973 (IRAT), 1R01CA190299, U01CA140204 The authors have no other relevant affiliations or financial involvement with any organization or entity with a financial interest in or financial conflict with the subject matter or materials discussed in the manuscript apart from those disclosed.
References
- 1.Shannon CE. A mathematical theory of communication. The Bell System Technical Journal. 1948 Jul;27(3):379–423. [Google Scholar]
- 2.Haralick RM, Shanmugam K, Dinstein IH. Textural features for image classification. IEEE Transactions on Systems, Man and Cybernetics. 1973;(6):610–621. [Google Scholar]
- 3.Galloway MM. Texture analysis using gray level run lengths. Computer graphics and image processing. 1975;4(2):172–179. [Google Scholar]
- 4.Amadasun M, King R. Textural features corresponding to textural properties. IEEE Transactions on Systems, Man and Cybernetics. 1989;19(5):1264–1274. [Google Scholar]
- 5.Aerts HJ, Velazquez ER, Leijenaar RT, et al. Decoding tumour phenotype by noninvasive imaging using a quantitative radiomics approach. Nature communications. 2014;5:4006. doi: 10.1038/ncomms5006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kaizer H. Tech Note. Boston University Research Lab; Boston, Massachusetts: 1955. A quantification of textures on aerial photographs; p. 121. [Google Scholar]
- 7.Sutton RN, Hall EL. Texture measures for automatic classification of pulmonary disease. IEEE Transactions on Computers. 1972;(7):667–676. [Google Scholar]
- 8.Bardeen JM, Carter B, Hawking SW. The Four laws of black hole mechanics. Commun Math Phys. 1973;31(2):161–170. [Google Scholar]
- 9.Bekenstein JD. Black Holes and Entropy. Physical Review D. 1973 Apr 15;7(8):2333–2346. [Google Scholar]
- 10.Sonntag R, Borgnakke C, Van Wylen G. Fundamentals of thermodynamics. the University of Michigan: Wiley; 1998. [Google Scholar]
- 11.Eisert J, Cramer M, Plenio MB. Area laws for the entanglement entropy. Reviews of Modern Physics. 2010 Feb 04;82(1):277–306. [Google Scholar]
- 12.Lambin P, Rios-Velazquez E, Leijenaar R, et al. Radiomics: extracting more information from medical images using advanced feature analysis. European Journal of Cancer. 2012;48(4):441–446. doi: 10.1016/j.ejca.2011.11.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kumar V, Gu Y, Basu S, et al. Radiomics: the process and the challenges. Magn Reson Imaging. 2012 Nov;30(9):1234–1248. doi: 10.1016/j.mri.2012.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gillies RJ, Kinahan PE, Hricak H. Radiomics: Images Are More than Pictures, They Are Data. Radiology. 2015:151169. doi: 10.1148/radiol.2015151169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Larkin TJ, Canuto HC, Kettunen MI, et al. Analysis of image heterogeneity using 2D Minkowski functionals detects tumor responses to treatment. Magnetic Resonance in Medicine. 2014;71(1):402–410. doi: 10.1002/mrm.24644. [DOI] [PubMed] [Google Scholar]
- 16.Tixier F, Le Rest CC, Hatt M, et al. Intratumor heterogeneity characterized by textural features on baseline 18F-FDG PET images predicts response to concomitant radiochemotherapy in esophageal cancer. Journal of Nuclear Medicine. 2011;52(3):369–378. doi: 10.2967/jnumed.110.082404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Knuth KH. Optimal data-based binning for histograms. 2006 arXiv preprint physics/0605197. [Google Scholar]
- 18.Shimazaki H, Shinomoto S. A method for selecting the bin size of a time histogram. Neural computation. 2007;19(6):1503–1527. doi: 10.1162/neco.2007.19.6.1503. [DOI] [PubMed] [Google Scholar]
- 19.Raeth U, Schlaps D, Limberg B, et al. Diagnostic accuracy of computerized B-scan texture analysis and conventional ultrasonography in diffuse parenchymal and malignant liver disease. Journal of Clinical Ultrasound. 1985 Feb;13(2):87–99. doi: 10.1002/jcu.1870130203. [DOI] [PubMed] [Google Scholar]
- 20.Garra BS, Krasner BH, Horii SC, Ascher S, Mun SK, Zeman RK. Improving the distinction between benign and malignant breast lesions: the value of sonographic texture analysis. Ultrasonic Imaging. 1993;15(4):267–285. doi: 10.1177/016173469301500401. [DOI] [PubMed] [Google Scholar]
- 21.Sujana H, Swarnamani S, Suresh S. Application of artificial neural networks for the classification of liver lesions by image texture parameters. Ultrasound in medicine & biology. 1996;22(9):1177–1181. doi: 10.1016/s0301-5629(96)00144-5. [DOI] [PubMed] [Google Scholar]
- 22.Brinkmann G, Melchert UH, Lalk G, et al. The total entropy for evaluating 31P-magnetic resonance spectra of the liver in healthy volunteers and patients with metastases. Invest Radiol. 1997 Feb;32(2):100–104. doi: 10.1097/00004424-199702000-00005. [DOI] [PubMed] [Google Scholar]
- 23.Mayr NA, Yuh WT, Arnholt JC, et al. Pixel analysis of MR perfusion imaging in predicting radiation therapy outcome in cervical cancer. Journal of Magnetic Resonance Imaging. 2000;12(6):1027–1033. doi: 10.1002/1522-2586(200012)12:6<1027::aid-jmri31>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
- 24.Bernasconi A, Antel SB, Collins DL, et al. Texture analysis and morphological processing of magnetic resonance imaging assist detection of focal cortical dysplasia in extra-temporal partial epilepsy. Annals of neurology. 2001;49(6):770–775. [PubMed] [Google Scholar]
- 25.Hayes C, Padhani AR, Leach MO. Assessing changes in tumour vascular function using dynamic contrast-enhanced magnetic resonance imaging. Nmr in Biomedicine. 2002 Apr;15(2):154–163. doi: 10.1002/nbm.756. [DOI] [PubMed] [Google Scholar]
- 26.Jirak D, Dezortová M, Taimr P, Hájek M. Texture analysis of human liver. Journal of Magnetic Resonance Imaging. 2002;15(1):68–74. doi: 10.1002/jmri.10042. [DOI] [PubMed] [Google Scholar]
- 27.Bernasconi A. Advanced MRI analysis methods for detection of focal cortical dysplasia. Epileptic disorders: international epilepsy journal with videotape. 2003 Sep;5(Suppl 2):S81–84. [PubMed] [Google Scholar]
- 28.Bonilha L, Kobayashi E, Castellano G, et al. Texture analysis of hippocampal sclerosis. Epilepsia. 2003;44(12):1546–1550. doi: 10.1111/j.0013-9580.2003.27103.x. [DOI] [PubMed] [Google Scholar]
- 29.Yoshida H, Casalino DD, Keserci B, Coskun A, Ozturk O, Savranlar A. Wavelet-packet-based texture analysis for differentiation between benign and malignant liver tumours in ultrasound images. Physics in Medicine and Biology. 2003 Nov 21;48(22):3735–3753. doi: 10.1088/0031-9155/48/22/008. [DOI] [PubMed] [Google Scholar]
- 30.Chabat F, Yang G-Z, Hansell DM. Obstructive Lung Diseases: Texture Classification for Differentiation at CT 1. Radiology. 2003;228(3):871–877. doi: 10.1148/radiol.2283020505. [DOI] [PubMed] [Google Scholar]
- 31.Herlidou-Meme S, Constans J, Carsin B, et al. MRI texture analysis on texture test objects, normal brain and intracranial tumors. Magnetic resonance imaging. 2003;21(9):989–993. doi: 10.1016/s0730-725x(03)00212-1. [DOI] [PubMed] [Google Scholar]
- 32.Chang YC, Huang CS, Liu YJ, Chen JH, Lu YS, Tseng WY. Angiogenic response of locally advanced breast cancer to neoadjuvant chemotherapy evaluated with parametric histogram from dynamic contrast-enhanced MRI. Phys Med Biol. 2004 Aug 21;49(16):3593–3602. doi: 10.1088/0031-9155/49/16/007. [DOI] [PubMed] [Google Scholar]
- 33.de Lussanet QG, Backes WH, Griffioen AW, et al. Dynamic contrast-enhanced magnetic resonance imaging of radiation therapy-induced microcirculation changes in rectal cancer. International journal of radiation oncology, biology, physics. 2005 Dec 1;63(5):1309–1315. doi: 10.1016/j.ijrobp.2005.04.052. [DOI] [PubMed] [Google Scholar]
- 34.Xu Y, Sonka M, McLennan G, Guo J, Hoffman E. MDCT-based 3-D texture classification of emphysema and early smoking related lung pathologies. IEEE Transactions on Medical Imaging. 2006;25(4):464–475. doi: 10.1109/TMI.2006.870889. [DOI] [PubMed] [Google Scholar]
- 35.Ertas G, Gulcur HO, Tunaci M. Improved lesion detection in MR mammography: three-dimensional segmentation, moving voxel sampling, and normalized maximum intensity-time ratio entropy. Acad Radiol. 2007 Feb;14(2):151–161. doi: 10.1016/j.acra.2006.11.003. [DOI] [PubMed] [Google Scholar]
- 36.Jackson A, O’Connor JP, Parker GJ, Jayson GC. Imaging tumor vascular heterogeneity and angiogenesis using dynamic contrast-enhanced magnetic resonance imaging. Clinical Cancer Research. 2007;13(12):3449–3459. doi: 10.1158/1078-0432.CCR-07-0238. [DOI] [PubMed] [Google Scholar]
- 37.Caban JJ, Yao J, Avila NA, Fontana JR, Manganiello VC. Texture-based computer-aided diagnosis system for lung fibrosis. Proc SPIE 6514, Medical Imaging: Computer-Aided Diagnosis. 2007:651439. [Google Scholar]
- 38.Depeursinge A, Sage D, Hidki A, et al. Lung tissue classification using wavelet frames. 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society; 2007. pp. 6259–6262. [DOI] [PubMed] [Google Scholar]
- 39.Karahaliou A, Skiadopoulos S, Boniatis I, et al. Texture analysis of tissue surrounding microcalcifications on mammograms for breast cancer diagnosis. Br J Radiol. 2007 Aug;80(956):648–656. doi: 10.1259/bjr/30415751. [DOI] [PubMed] [Google Scholar]
- 40.Kontos D, Bakic PR, Carton A-K, Troxel AB, Conant EF, Maidment AD. Parenchymal texture analysis in digital breast tomosynthesis for breast cancer risk estimation: a preliminary study. Academic radiology. 2009;16(3):283–298. doi: 10.1016/j.acra.2008.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Mayerhoefer ME, Schima W, Trattnig S, Pinker K, Berger-Kulemann V, Ba-Ssalamah A. Texture-based classification of focal liver lesions on MRI at 3.0 Tesla: A feasibility study in cysts and hemangiomas. Journal of Magnetic Resonance Imaging. 2010;32(2):352–359. doi: 10.1002/jmri.22268. [DOI] [PubMed] [Google Scholar]
- 42.Holli K, Lääperi A-L, Harrison L, et al. Characterization of breast cancer types by texture analysis of magnetic resonance images. Academic radiology. 2010;17(2):135–141. doi: 10.1016/j.acra.2009.08.012. [DOI] [PubMed] [Google Scholar]
- 43.Chuah TK, Poh CL, Sheah K. Quantitative texture analysis of MRI images for detection of cartilage-related bone marrow edema. Conference proceedings: … Annual International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE Engineering in Medicine and Biology Society. Annual Conference; 2011; 2011. pp. 5112–5115. [DOI] [PubMed] [Google Scholar]
- 44.Cui J-L, Wen C-Y, Hu Y, Li T-H, Luk KD-K. Entropy-based analysis for diffusion anisotropy mapping of healthy and myelopathic spinal cord. Neuroimage. 2011;54(3):2125–2131. doi: 10.1016/j.neuroimage.2010.10.018. [DOI] [PubMed] [Google Scholar]
- 45.O’Connor J, Rose C, Jackson A, et al. DCE-MRI biomarkers of tumour heterogeneity predict CRC liver metastasis shrinkage following bevacizumab and FOLFOX-6. British journal of cancer. 2011;105(1):139–145. doi: 10.1038/bjc.2011.191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Fujimoto K, Tonan T, Azuma S, et al. Evaluation of the mean and entropy of apparent diffusion coefficient values in chronic hepatitis C: correlation with pathologic fibrosis stage and inflammatory activity grade. Radiology. 2011;258(3):739–748. doi: 10.1148/radiol.10100853. [DOI] [PubMed] [Google Scholar]
- 47.Vaidya M, Creach KM, Frye J, Dehdashti F, Bradley JD, El Naqa I. Combined PET/CT image characteristics for radiotherapy tumor response in lung cancer. Radiotherapy and Oncology. 2012;102(2):239–245. doi: 10.1016/j.radonc.2011.10.014. [DOI] [PubMed] [Google Scholar]
- 48.Chen Y, Pham TD. Sample entropy and regularity dimension in complexity analysis of cortical surface structure in early Alzheimer’s disease and aging. Journal of neuroscience methods. 2013 May 15;215(2):210–217. doi: 10.1016/j.jneumeth.2013.03.018. [DOI] [PubMed] [Google Scholar]
- 49.Chicklore S, Goh V, Siddique M, Roy A, Marsden PK, Cook GJ. Quantifying tumour heterogeneity in 18F-FDG PET/CT imaging by texture analysis. European journal of nuclear medicine and molecular imaging. 2013;40(1):133–140. doi: 10.1007/s00259-012-2247-0. [DOI] [PubMed] [Google Scholar]
- 50.Leijenaar RT, Carvalho S, Velazquez ER, et al. Stability of FDG-PET Radiomics features: An integrated analysis of test-retest and inter-observer variability. Acta Oncologica. 2013;52(7):1391–1397. doi: 10.3109/0284186X.2013.812798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kierans AS, Bennett GL, Mussi TC, et al. Characterization of malignancy of adnexal lesions using ADC entropy: comparison with mean ADC and qualitative DWI assessment. Journal of Magnetic Resonance Imaging. 2013;37(1):164–171. doi: 10.1002/jmri.23794. [DOI] [PubMed] [Google Scholar]
- 52.Foroutan P, Kreahling JM, Morse DL, et al. Diffusion MRI and novel texture analysis in osteosarcoma xenotransplants predicts response to anti-checkpoint therapy. PLoS One. 2013;8(12):e82875. doi: 10.1371/journal.pone.0082875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Sato JR, Takahashi DY, Hoexter MQ, Massirer KB, Fujita A. Measuring network’s entropy in ADHD: a new approach to investigate neuropsychiatric disorders. Neuroimage. 2013 Aug 15;77:44–51. doi: 10.1016/j.neuroimage.2013.03.035. [DOI] [PubMed] [Google Scholar]
- 54.Suoranta S, Holli-Helenius K, Koskenkorva P, et al. 3D texture analysis reveals imperceptible MRI textural alterations in the thalamus and putamen in progressive myoclonic epilepsy type 1, EPM1. PLoS One. 2013;8(7):e69905. doi: 10.1371/journal.pone.0069905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Cao MQ, Suo ST, Zhang XB, et al. Entropy of T2-weighted imaging combined with apparent diffusion coefficient in prediction of uterine leiomyoma volume response after uterine artery embolization. Acad Radiol. 2014 Apr;21(4):437–444. doi: 10.1016/j.acra.2013.12.007. [DOI] [PubMed] [Google Scholar]
- 56.Ryu YJ, Choi SH, Park SJ, Yun TJ, Kim JH, Sohn CH. Glioma: application of whole-tumor texture analysis of diffusion-weighted imaging for the evaluation of tumor heterogeneity. PLoS One. 2014;9(9):e108335. doi: 10.1371/journal.pone.0108335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Suo ST, Chen XX, Fan Y, et al. Histogram analysis of apparent diffusion coefficient at 3.0 T in urinary bladder lesions: correlation with pathologic findings. Acad Radiol. 2014 Aug;21(8):1027–1034. doi: 10.1016/j.acra.2014.03.004. [DOI] [PubMed] [Google Scholar]
- 58.Parmar C, Velazquez ER, Leijenaar R, et al. Robust radiomics feature quantification using semiautomatic volumetric segmentation. PloS one. 2014;9:e102107. doi: 10.1371/journal.pone.0102107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Coroller TP, Grossmann P, Hou Y, et al. CT-based radiomic signature predicts distant metastasis in lung adenocarcinoma. Radiotherapy and Oncology. 2015;114(3):345–350. doi: 10.1016/j.radonc.2015.02.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Leijenaar RT, Carvalho S, Hoebers FJ, et al. External validation of a prognostic CT-based radiomic signature in oropharyngeal squamous cell carcinoma. Acta Oncologica. 2015:1–7. doi: 10.3109/0284186X.2015.1061214. [DOI] [PubMed] [Google Scholar]
- 61.Panth KM, Leijenaar RT, Carvalho S, et al. Is there a causal relationship between genetic changes and radiomics-based image features? An in vivo preclinical experiment with doxycycline inducible GADD34 tumor cells. Radiotherapy and Oncology. 2015;116:462–466. doi: 10.1016/j.radonc.2015.06.013. [DOI] [PubMed] [Google Scholar]
- 62.Parmar C, Grossmann P, Bussink J, Lambin P, Aerts HJ. Machine Learning methods for Quantitative Radiomic Biomarkers. Scientific reports. 2015;5:13087. doi: 10.1038/srep13087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Parmar C, Leijenaar RT, Grossmann P, et al. Radiomic feature clusters and Prognostic Signatures specific for Lung and Head & Neck cancer. Scientific reports. 2015;5:11044. doi: 10.1038/srep11044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Grove O, Berglund AE, Schabath MB, et al. Quantitative Computed Tomographic Descriptors Associate Tumor Shape Complexity and Intratumor Heterogeneity with Prognosis in Lung Adenocarcinoma. PloS one. 2015;10(3):e0118261. doi: 10.1371/journal.pone.0118261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Chen W, Giger ML, Li H, Bick U, Newstead GM. Volumetric texture analysis of breast lesions on contrast-enhanced magnetic resonance images. Magnetic Resonance in Medicine. 2007;58(3):562–571. doi: 10.1002/mrm.21347. [DOI] [PubMed] [Google Scholar]
- 66.Ahmed A, Gibbs P, Pickles M, Turnbull L. Texture analysis in assessment and prediction of chemotherapy response in breast cancer. Journal of Magnetic Resonance Imaging. 2013;38(1):89–101. doi: 10.1002/jmri.23971. [DOI] [PubMed] [Google Scholar]
- 67.Magnin IE, Cluzeau F, Odet CL, Bremond A. Mammographic texture analysis: an evaluation of risk for developing breast cancer. Optical Engineering. 1986;25(6):156780–156780. [Google Scholar]
- 68.Wu C-M, Chen Y-C, Hsieh K-S. Texture features for classification of ultrasonic liver images. IEEE Transactions on Medical Imaging. 1992;11(2):141–152. doi: 10.1109/42.141636. [DOI] [PubMed] [Google Scholar]
- 69.Mir A, Hanmandlu M, Tandon S. Texture analysis of CT images. IEEE Engineering in Medicine and Biology Magazine. 1995;14(6):781–786. [Google Scholar]
- 70.Wei D, Chan HP, Helvie MA, et al. Classification of mass and normal breast tissue on digital mammograms: multiresolution texture analysis. Medical Physics. 1995;22(9):1501–1513. doi: 10.1118/1.597418. [DOI] [PubMed] [Google Scholar]
- 71.Sun Y, Horng M-H, Lin X, Wang J-Y. Ultrasonic image analysis for liver diagnosis. IEEE Engineering in Medicine and Biology Magazine. 1996 Nov-Dec;15(6):93–101. [Google Scholar]
- 72.Lucht R, Brix G, Lorenz W. Texture analysis of differently reconstructed PET images. Physics in medicine and biology. 1996;41(10):2207–2219. doi: 10.1088/0031-9155/41/10/025. [DOI] [PubMed] [Google Scholar]
- 73.Petrick N, Chan HP, Wei D, Sahiner B, Helvie MA, Adler DD. Automated detection of breast masses on mammograms using adaptive contrast enhancement and texture classification. Medical Physics. 1996;23(10):1685–1696. doi: 10.1118/1.597756. [DOI] [PubMed] [Google Scholar]
- 74.Sahiner B, Chan H-P, Petrick N, et al. Classification of mass and normal breast tissue: a convolution neural network classifier with spatial domain and texture images. IEEE Transactions on Medical Imaging. 1996;15(5):598–610. doi: 10.1109/42.538937. [DOI] [PubMed] [Google Scholar]
- 75.Chan H-P, Sahiner B, Petrick N, et al. Computerized classification of malignant and benign microcalcifications on mammograms: texture analysis using an artificial neural network. Physics in Medicine and Biology. 1997;42(3):549–567. doi: 10.1088/0031-9155/42/3/008. [DOI] [PubMed] [Google Scholar]
- 76.Sinha S, Lucas-Quesada FA, Debruhl ND, et al. Multifeature analysis of Gd-enhanced MR images of breast lesions. Journal of Magnetic Resonance Imaging. 1997;7(6):1016–1026. doi: 10.1002/jmri.1880070613. [DOI] [PubMed] [Google Scholar]
- 77.Wei D, Chan H-P, Petrick N, et al. False-positive reduction technique for detection of masses on digital mammograms: Global and local multiresolution texture analysis. Medical Physics. 1997;24(6):903–914. doi: 10.1118/1.598011. [DOI] [PubMed] [Google Scholar]
- 78.Freeborough P, Fox NC. MR image texture analysis applied to the diagnosis and tracking of Alzheimer’s disease. IEEE Transactions on Medical Imaging. 1998;17(3):475–478. doi: 10.1109/42.712137. [DOI] [PubMed] [Google Scholar]
- 79.Sahiner B, Chan H-P, Petrick N, Helvie MA, Goodsitt MM. Computerized characterization of masses on mammograms: The rubber band straightening transform and texture analysis. Medical Physics. 1998;25(4):516–526. doi: 10.1118/1.598228. [DOI] [PubMed] [Google Scholar]
- 80.Chen E, Chung P-C, Chen C-L, Tsai H-M, Chang C-I. An automatic diagnostic system for CT liver image classification. Biomedical Engineering, IEEE Transactions on. 1998;45(6):783–794. doi: 10.1109/10.678613. [DOI] [PubMed] [Google Scholar]
- 81.Mudigonda NR, Rangayyan RM, Desautels JL. Gradient and texture analysis for the classification of mammographic masses. IEEE Transactions on Medical Imaging. 2000;19(10):1032–1043. doi: 10.1109/42.887618. [DOI] [PubMed] [Google Scholar]
- 82.Kovalev V, Kruggel F, Gertz H-J, Von Cramon DY. Three-dimensional texture analysis of MRI brain datasets. IEEE Transactions on Medical Imaging. 2001;20(5):424–433. doi: 10.1109/42.925295. [DOI] [PubMed] [Google Scholar]
- 83.Sivaramakrishna R, Powell KA, Lieber ML, Chilcote WA, Shekhar R. Texture analysis of lesions in breast ultrasound images. Computerized medical imaging and graphics. 2002;26(5):303–307. doi: 10.1016/s0895-6111(02)00027-7. [DOI] [PubMed] [Google Scholar]
- 84.Horng MH, Sun YN, Lin XZ. Texture feature coding method for classification of liver sonography. Computerized medical imaging and graphics: the official journal of the Computerized Medical Imaging Society. 2002 Jan-Feb;26(1):33–42. doi: 10.1016/s0895-6111(01)00029-5. [DOI] [PubMed] [Google Scholar]
- 85.Gibbs P, Turnbull LW. Textural analysis of contrast-enhanced MR images of the breast. Magnetic Resonance in Medicine. 2003;50(1):92–98. doi: 10.1002/mrm.10496. [DOI] [PubMed] [Google Scholar]
- 86.Gletsos M, Mougiakakou SG, Matsopoulos GK, Nikita KS, Nikita AS, Kelekis D. A computer-aided diagnostic system to characterize CT focal liver lesions: design and optimization of a neural network classifier. Information Technology in Biomedicine, IEEE Transactions on. 2003;7(3):153–162. doi: 10.1109/titb.2003.813793. [DOI] [PubMed] [Google Scholar]
- 87.Mahmoud-Ghoneim D, Toussaint G, Constans J-M, Jacques D. Three dimensional texture analysis in MRI: a preliminary evaluation in gliomas. Magnetic resonance imaging. 2003;21(9):983–987. doi: 10.1016/s0730-725x(03)00201-7. [DOI] [PubMed] [Google Scholar]
- 88.Pereira RR, Jr, Marques PMA, Honda MO, et al. Usefulness of texture analysis for computerized classification of breast lesions on mammograms. Journal of digital imaging. 2007;20(3):248–255. doi: 10.1007/s10278-006-9945-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Nie K, Chen J-H, Hon JY, Chu Y, Nalcioglu O, Su M-Y. Quantitative analysis of lesion morphology and texture features for diagnostic prediction in breast MRI. Academic radiology. 2008;15(12):1513–1525. doi: 10.1016/j.acra.2008.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.El Naqa I, Grigsby P, Apte A, et al. Exploring feature-based approaches in PET images for predicting cancer treatment outcomes. Pattern recognition. 2009;42(6):1162–1171. doi: 10.1016/j.patcog.2008.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Kassner A, Liu F, Thornhill RE, Tomlinson G, Mikulis DJ. Prediction of hemorrhagic transformation in acute ischemic stroke using texture analysis of postcontrast T1-weighted MR images. Journal of Magnetic Resonance Imaging. 2009;30(5):933–941. doi: 10.1002/jmri.21940. [DOI] [PubMed] [Google Scholar]
- 92.McLaren CE, Chen WP, Nie K, Su MY. Prediction of malignant breast lesions from MRI features: a comparison of artificial neural network and logistic regression techniques. Acad Radiol. 2009 Jul;16(7):842–851. doi: 10.1016/j.acra.2009.01.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Mayerhoefer ME, Welsch GH, Riegler G, et al. Feasibility of texture analysis for the assessment of biochemical changes in meniscal tissue on T1 maps calculated from delayed gadolinium-enhanced magnetic resonance imaging of cartilage data: comparison with conventional relaxation time measurements. Invest Radiol. 2010 Sep;45(9):543–547. doi: 10.1097/RLI.0b013e3181ea363b. [DOI] [PubMed] [Google Scholar]
- 94.Karahaliou A, Vassiou K, Arikidis NS, Skiadopoulos S, Kanavou T, Costaridou L. Assessing heterogeneity of lesion enhancement kinetics in dynamic contrast-enhanced MRI for breast cancer diagnosis. The British Journal of Radiology. 2010;83(988):296–309. doi: 10.1259/bjr/50743919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Korfiatis PD, Karahaliou AN, Kazantzi AD, Kalogeropoulou C, Costaridou L. Texture-based identification and characterization of interstitial pneumonia patterns in lung multidetector CT. IEEE Transactions on Information Technology in Biomedicine. 2010;14(3):675–680. doi: 10.1109/TITB.2009.2036166. [DOI] [PubMed] [Google Scholar]
- 96.Mayerhoefer ME, Stelzeneder D, Bachbauer W, et al. Quantitative analysis of lumbar intervertebral disc abnormalities at 3.0 Tesla: value of T(2) texture features and geometric parameters. NMR Biomed. 2012 Jun;25(6):866–872. doi: 10.1002/nbm.1803. [DOI] [PubMed] [Google Scholar]
- 97.Gatenby RA, Grove O, Gillies RJ. Quantitative imaging in cancer evolution and ecology. Radiology. 2013;269(1):8–14. doi: 10.1148/radiol.13122697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Cai H, Liu L, Peng Y, Wu Y, Li L. Diagnostic assessment by dynamic contrast-enhanced and diffusion-weighted magnetic resonance in differentiation of breast lesions under different imaging protocols. BMC Cancer. 2014;14:366. doi: 10.1186/1471-2407-14-366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Cai H, Peng Y, Ou C, Chen M, Li L. Diagnosis of breast masses from dynamic contrast-enhanced and diffusion-weighted MR: a machine learning approach. PLoS One. 2014;9(1):e87387. doi: 10.1371/journal.pone.0087387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Stember JN, Deng FM, Taneja SS, Rosenkrantz AB. Pilot study of a novel tool for input-free automated identification of transition zone prostate tumors using T2- and diffusion-weighted signal and textural features. Journal of magnetic resonance imaging: JMRI. 2014 Aug;40(2):301–305. doi: 10.1002/jmri.24375. [DOI] [PubMed] [Google Scholar]
- 101.Wang TC, Huang YH, Huang CS, et al. Computer-aided diagnosis of breast DCE-MRI using pharmacokinetic model and 3-D morphology analysis. Magn Reson Imaging. 2014 Apr;32(3):197–205. doi: 10.1016/j.mri.2013.12.002. [DOI] [PubMed] [Google Scholar]
- 102.Chu A, Sehgal CM, Greenleaf JF. Use of gray value distribution of run lengths for texture analysis. Pattern Recognition Letters. 1990;11(6):415–419. [Google Scholar]
- 103.Dasarathy BV, Holder EB. Image characterizations based on joint gray level—run length distributions. Pattern Recognition Letters. 1991;12(8):497–502. [Google Scholar]
- 104.Cook GJ, Yip C, Siddique M, et al. Are Pretreatment 18F-FDG PET Tumor Textural Features in Non–Small Cell Lung Cancer Associated with Response and Survival After Chemoradiotherapy? Journal of Nuclear Medicine. 2013;54(1):19–26. doi: 10.2967/jnumed.112.107375. [DOI] [PubMed] [Google Scholar]
- 105.Mandelbrot BB. How long is the coast of Britain. Science. 1967;156(3775):636–638. doi: 10.1126/science.156.3775.636. [DOI] [PubMed] [Google Scholar]
- 106.Mandelbrot BB. The fractal geometry of nature. Vol. 173. Macmillan; 1983. [Google Scholar]
- 107.Lopes R, Betrouni N. Fractal and multifractal analysis: a review. Medical image analysis. 2009;13(4):634–649. doi: 10.1016/j.media.2009.05.003. [DOI] [PubMed] [Google Scholar]
- 108.Li H, Giger ML, Olopade OI, Lan L. Fractal analysis of mammographic parenchymal patterns in breast cancer risk assessment. Academic radiology. 2007;14(5):513–521. doi: 10.1016/j.acra.2007.02.003. [DOI] [PubMed] [Google Scholar]
- 109.Guo Q, Shao J, Ruiz VF. Characterization and classification of tumor lesions using computerized fractal-based texture analysis and support vector machines in digital mammograms. International journal of computer assisted radiology and surgery. 2009;4(1):11–25. doi: 10.1007/s11548-008-0276-8. [DOI] [PubMed] [Google Scholar]
- 110.Gagnepain J, Roques-Carmes C. Fractal approach to two-dimensional and three-dimensional surface roughness. Wear. 1986;109(1):119–126. [Google Scholar]
- 111.Sarkar N, Chaudhuri B. An efficient differential box-counting approach to compute fractal dimension of image. IEEE Transactions on Systems, Man and Cybernetics. 1994;24(1):115–120. [Google Scholar]
- 112.Peleg S, Naor J, Hartley R, Avnir D. Multiple resolution texture analysis and classification. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1984;(4):518–523. doi: 10.1109/tpami.1984.4767557. [DOI] [PubMed] [Google Scholar]
- 113.Pentland AP. Fractal-based description of natural scenes. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1984;(6):661–674. doi: 10.1109/tpami.1984.4767591. [DOI] [PubMed] [Google Scholar]
- 114.Mandelbrot BB, Van Ness JW. Fractional Brownian motions, fractional noises and applications. SIAM review. 1968;10(4):422–437. [Google Scholar]
- 115.Rangayyan RM, Mudigonda NR, Desautels JL. Boundary modelling and shape analysis methods for classification of mammographic masses. Medical and Biological Engineering and Computing. 2000;38(5):487–496. doi: 10.1007/BF02345742. [DOI] [PubMed] [Google Scholar]
- 116.Rose CJ, Mills SJ, O’Connor JP, et al. Quantifying spatial heterogeneity in dynamic contrast-enhanced MRI parameter maps. Magnetic Resonance in Medicine. 2009;62(2):488–499. doi: 10.1002/mrm.22003. [DOI] [PubMed] [Google Scholar]
- 117.Randen T, Husoy JH. Filtering for texture classification: A comparative study. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1999;21(4):291–310. [Google Scholar]
- 118.Ganeshan B, Miles KA, Young R, Chatwin C. Hepatic entropy and uniformity: additional parameters that can potentially increase the effectiveness of contrast enhancement during abdominal CT. Clinical radiology. 2007;62(8):761–768. doi: 10.1016/j.crad.2007.03.004. [DOI] [PubMed] [Google Scholar]
- 119.Ganeshan B, Miles KA, Young RC, Chatwin CR. In search of biologic correlates for liver texture on portal-phase CT. Academic radiology. 2007;14(9):1058–1068. doi: 10.1016/j.acra.2007.05.023. [DOI] [PubMed] [Google Scholar]
- 120.Miles KA, Ganeshan B, Griffiths MR, Young RC, Chatwin CR. Colorectal Cancer: Texture Analysis of Portal Phase Hepatic CT Images as a Potential Marker of Survival 1. Radiology. 2009;250(2):444–452. doi: 10.1148/radiol.2502071879. [DOI] [PubMed] [Google Scholar]
- 121.Ganeshan B, Abaleke S, Young RC, Chatwin CR, Miles KA. Texture analysis of non-small cell lung cancer on unenhanced computed tomography: initial evidence for a relationship with tumour glucose metabolism and stage. Cancer Imaging. 2010;10(1):137–143. doi: 10.1102/1470-7330.2010.0021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Ganeshan B, Burnand K, Young R, Chatwin C, Miles K. Dynamic contrast-enhanced texture analysis of the liver: initial assessment in colorectal cancer. Investigative radiology. 2011;46(3):160–168. doi: 10.1097/RLI.0b013e3181f8e8a2. [DOI] [PubMed] [Google Scholar]
- 123.Wachinger C, Navab N. Entropy and Laplacian images: Structural representations for multi-modal registration. Medical Image Analysis. 2012;16(1):1–17. doi: 10.1016/j.media.2011.03.001. [DOI] [PubMed] [Google Scholar]
- 124.Ganeshan B, Panayiotou E, Burnand K, Dizdarevic S, Miles K. Tumour heterogeneity in non-small cell lung carcinoma assessed by CT texture analysis: a potential marker of survival. European radiology. 2012;22(4):796–802. doi: 10.1007/s00330-011-2319-8. [DOI] [PubMed] [Google Scholar]
- 125.Ganeshan B, Goh V, Mandeville HC, Ng QS, Hoskin PJ, Miles KA. Non–small cell lung cancer: histopathologic correlates for texture parameters at CT. Radiology. 2013;266(1):326–336. doi: 10.1148/radiol.12112428. [DOI] [PubMed] [Google Scholar]
- 126.Ng F, Ganeshan B, Kozarski R, Miles KA, Goh V. Assessment of primary colorectal cancer heterogeneity by using whole-tumor texture analysis: contrast-enhanced CT texture as a biomarker of 5-year survival. Radiology. 2013;266(1):177–184. doi: 10.1148/radiol.12120254. [DOI] [PubMed] [Google Scholar]
- 127.Laws KI. Rapid texture identification. Proc SPIE 0238, Image Processing for Missile Guidance. 1980:376–381. [Google Scholar]
- 128.Laws KI. PhD Dissertation. Los Angeles, California: Image Processing Institute, University of Southern California; 1980. Textured image segmentation. [Google Scholar]
- 129.Cox G, Hoare F, de Jager G. Experiments in lung cancer nodule detection using texture analysis and neural network classifiers. Third South African Workshop on Pattern Recognition. 1992;31:136–142. [Google Scholar]
- 130.Miller P, Astley S. Classification of breast tissue by texture analysis. Image and Vision Computing. 1992;10(5):277–282. [Google Scholar]
- 131.Chu Y, Li L, Goldgof DB, Qui Y, Clark RA. Classification of masses on mammograms using support vector machine. Proc SPIE 5032, Medical Imaging: Image Processing. 2003:940–948. [Google Scholar]
- 132.Poonguzhali S, Ravindran G. Automatic classification of focal lesions in ultrasound liver images using combined texture features. Information Technology Journal. 2008;7(1):205–209. [Google Scholar]
- 133.Awad J, Krasinski A, Parraga G, Fenster A. Texture analysis of carotid artery atherosclerosis from three-dimensional ultrasound images. Medical Physics. 2010;37(4):1382–1391. doi: 10.1118/1.3301592. [DOI] [PubMed] [Google Scholar]
- 134.Dheeba J, Tamil Selvi S. Classification of malignant and benign microcalcification using SVM classifier. International Conference on Emerging Trends in Electrical and Computer Technology (ICETECT) 2011:686–690. [Google Scholar]
- 135.Barata C, Marques JS, Mendonça T. Bag-of-features classification model for the diagnose of melanoma in dermoscopy images using color and texture descriptors. Image Analysis and Recognition. 2013:547–555. [Google Scholar]
- 136.Virmani J, Kumar V, Kalra N, Khandelwa N. Pca-SVm based caD System for Focal liver lesions using B-mode ultrasound Images. Defence Science Journal. 2013;63(5):478–486. [Google Scholar]
- 137.Pereyra LC, Rangayyan RM, Ponciano-Silva M, Azevedo-Marques PM. Fractal analysis for computer-aided diagnosis of diffuse pulmonary diseases in HRCT images. IEEE International Symposium on Medical Measurements and Applications (MeMeA) 2014:1–6. [Google Scholar]
- 138.Dilger S, Judisch A, Uthoff J, Hammond E, Newell J, Sieren J. Improved pulmonary nodule classification utilizing lung parenchyma texture features. Proc SPIE 9414, Medical Imaging: Computer-Aided Diagnosis. 2015:94142T. doi: 10.1117/1.JMI.2.4.041004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Mitrea D, Nedevschi S, Abrudean M. Classification of the liver tumors Using Co-Occurrence Matrices of textural Microstructures. Journal of Communication and Computer. 2015;12:6–12. [Google Scholar]
- 140.Singh BK, Verma K, Thoke A. Adaptive Gradient Descent Backpropagation for Classification of Breast Tumors in Ultrasound Imaging. Procedia Computer Science. 2015;46:1601–1609. [Google Scholar]
- 141.Al-Kadi OS, Watson D. Texture analysis of aggressive and nonaggressive lung tumor CE CT images. IEEE Transactions on Biomedical Engineering. 2008;55(7):1822–1830. doi: 10.1109/TBME.2008.919735. [DOI] [PubMed] [Google Scholar]
- 142.Haar A. Zur theorie der orthogonalen funktionensysteme. Mathematische Annalen. 1910;69(3):331–371. [Google Scholar]
- 143.Daubechies I. Orthonormal bases of compactly supported wavelets. Communications on pure and applied mathematics. 1988;41(7):909–996. [Google Scholar]
- 144.Daubechies I. Ten lectures on wavelets. Vol. 61. Society for Industrial and Applied Mathematics; 1992. [Google Scholar]
- 145.Mallat SG. A theory for multiresolution signal decomposition: the wavelet representation. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1989;11(7):674–693. [Google Scholar]
- 146.Chen D-R, Chang R-F, Kuo W-J, Chen M-C, Huang Y-L. Diagnosis of breast tumors with sonographic texture analysis using wavelet transform and neural networks. Ultrasound in medicine & biology. 2002;28(10):1301–1310. doi: 10.1016/s0301-5629(02)00620-8. [DOI] [PubMed] [Google Scholar]
- 147.Akhbardeh A, Jacobs MA. Comparative analysis of nonlinear dimensionality reduction techniques for breast MRI segmentation. Medical physics. 2012;39(4):2275–2289. doi: 10.1118/1.3682173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 148.Duda RO, Hart PE. Pattern classification and scene analysis. Vol. 3. Wiley; New York: 1973. [Google Scholar]
- 149.Amaldi E, Kann V. On the approximability of minimizing nonzero variables or unsatisfied relations in linear systems. Theoretical Computer Science. 1998;209(1):237–260. [Google Scholar]
- 150.Pearson KL., III On lines and planes of closest fit to systems of points in space. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 1901;2(11):559–572. [Google Scholar]
- 151.Torgerson WS. Multidimensional scaling: I. Theory and method. Psychometrika. 1952;17(4):401–419. doi: 10.1007/BF02289530. [DOI] [PubMed] [Google Scholar]
- 152.Coifman RR, Lafon S, Lee AB, et al. Geometric diffusions as a tool for harmonic analysis and structure definition of data: Diffusion maps. Proceedings of the National Academy of Sciences of the United States of America. 2005;102(21):7426–7431. doi: 10.1073/pnas.0500334102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Tenenbaum JB, De Silva V, Langford JC. A global geometric framework for nonlinear dimensionality reduction. Science. 2000;290(5500):2319–2323. doi: 10.1126/science.290.5500.2319. [DOI] [PubMed] [Google Scholar]
- 154.Roweis ST, Saul LK. Nonlinear dimensionality reduction by locally linear embedding. Science. 2000;290(5500):2323–2326. doi: 10.1126/science.290.5500.2323. [DOI] [PubMed] [Google Scholar]
- 155.Van Der Maaten L, Postma E, Van den Herik J. Dimensionality reduction: a comparative. J Mach Learn Res. 2009;10:66–71. [Google Scholar]
- 156.Keller JM, Gray MR, Givens JA. A fuzzy k-nearest neighbor algorithm. IEEE Transactions on Systems, Man and Cybernetics. 1985;(4):580–585. [Google Scholar]
- 157.Cover T, Hart P. Nearest neighbor pattern classification. IEEE Transactions on Information Theory. 1967;13(1):21–27. [Google Scholar]
- 158.Breiman L. Bagging predictors. Machine learning. 1996;24(2):123–140. [Google Scholar]
- 159.Cortes C, Vapnik V. Support-vector networks. Machine learning. 1995;20(3):273–297. [Google Scholar]
- 160.MacQueen J. Some methods for classification and analysis of multivariate observations. Proceedings of the fifth Berkeley symposium on mathematical statistics and probability. 1967;1(14):281–297. [Google Scholar]
- 161.Fred AL, Jain AK. Data clustering using evidence accumulation. 16th International Conference on Pattern Recognition; 2002; 2002. pp. 276–280. [Google Scholar]
- 162.McQuitty LL. Hierarchical linkage analysis for the isolation of types. Educational and Psychological Measurement. 1960;20(1):55–67. [Google Scholar]
- 163.Kassner A, Thornhill R. Texture analysis: a review of neurologic MR imaging applications. American Journal of Neuroradiology. 2010;31(5):809–816. doi: 10.3174/ajnr.A2061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 164.Miles KA, Ganeshan B, Hayball MP. CT texture analysis using the filtration-histogram method: what do the measurements mean? Cancer Imaging. 2013;13(3):400–406. doi: 10.1102/1470-7330.2013.9045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 165.de Melo RH, Vieira EdA, Conci A. Characterizing the lacunarity of objects and image sets and its use as a technique for the analysis of textural patterns. Advanced concepts for intelligent vision systems. 2006:208–219. [Google Scholar]
- 166.Nandi R, Nandi AK, Rangayyan RM, Scutt D. Classification of breast masses in mammograms using genetic programming and feature selection. Medical and Biological Engineering and Computing. 2006;44(8):683–694. doi: 10.1007/s11517-006-0077-6. [DOI] [PubMed] [Google Scholar]
- 167.Tourassi GD, Delong DM, Floyd CE., Jr A study on the computerized fractal analysis of architectural distortion in screening mammograms. Physics in medicine and biology. 2006;51(5):1299–1312. doi: 10.1088/0031-9155/51/5/018. [DOI] [PubMed] [Google Scholar]
- 168.Rangayyan RM, Nguyen TM. Fractal analysis of contours of breast masses in mammograms. Journal of Digital Imaging. 2007;20(3):223–237. doi: 10.1007/s10278-006-0860-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 169.Chen D-R, Chang R-F, Huang Y-L, Chou Y-H, Tiu C-M, Tsai P-P. Texture analysis of breast tumors on sonograms. Seminars in Ultrasound, CT and MRI. 2000;21(4):308–316. doi: 10.1016/s0887-2171(00)90025-8. [DOI] [PubMed] [Google Scholar]
- 170.Agner SC, Soman S, Libfeld E, et al. Textural kinetics: a novel dynamic contrast-enhanced (DCE)-MRI feature for breast lesion classification. Journal of Digital Imaging. 2011;24(3):446–463. doi: 10.1007/s10278-010-9298-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 171.Parikh J, Selmi M, Charles-Edwards G, et al. Changes in primary breast cancer heterogeneity may augment midtreatment MR imaging assessment of response to neoadjuvant chemotherapy. Radiology. 2014 Jul;272(1):100–112. doi: 10.1148/radiol.14130569. [DOI] [PubMed] [Google Scholar]
- 172.Gerlinger M, Rowan AJ, Horswell S, et al. Intratumor Heterogeneity and Branched Evolution Revealed by Multiregion Sequencing. New England Journal of Medicine. 2012;366(10):883–892. doi: 10.1056/NEJMoa1113205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 173.Huang Y-L, Chen J-H, Shen W-C. Diagnosis of hepatic tumors with texture analysis in nonenhanced computed tomography images. Academic radiology. 2006;13(6):713–720. doi: 10.1016/j.acra.2005.07.014. [DOI] [PubMed] [Google Scholar]
- 174.Poonguzhali S, Ravindran G. Performance evaluation of feature extraction methods for classifying abnormalities in ultrasound liver images using neural network. IEEE 28th Annual International Conference of the Engineering in Medicine and Biology Society; 2006; 2006. pp. 4791–4794. [DOI] [PubMed] [Google Scholar]
- 175.Mittal D, Kumar V, Saxena SC, Khandelwal N, Kalra N. Neural network based focal liver lesion diagnosis using ultrasound images. Computerized Medical Imaging and Graphics. 2011;35(4):315–323. doi: 10.1016/j.compmedimag.2011.01.007. [DOI] [PubMed] [Google Scholar]
- 176.Virmani J, Kumar V, Kalra N, Khadelwal N. A rapid approach for prediction of liver cirrhosis based on first order statistics. 2011 International Conference on Multimedia, Signal Processing and Communication Technologies (IMPACT); 2011. pp. 212–215. [Google Scholar]
- 177.Jeon JH, Choi JY, Lee S, Ro YM. Multiple ROI selection based focal liver lesion classification in ultrasound images. Expert Systems with Applications. 2013;40(2):450–457. [Google Scholar]
- 178.Virmani J, Kumar V, Kalra N, Khandelwal N. SVM-based characterisation of liver cirrhosis by singular value decomposition of GLCM matrix. International Journal of Artificial Intelligence and Soft Computing. 2013;3(3):276–296. [Google Scholar]
- 179.Virmani J, Kumar V, Kalra N, Khandelwal N. Prediction of liver cirrhosis based on multiresolution texture descriptors from B-mode ultrasound. International Journal of Convergence Computing. 2013;1(1):19–37. [Google Scholar]
- 180.Xian G-m. An identification method of malignant and benign liver tumors from ultrasonography based on GLCM texture features and fuzzy SVM. Expert Systems with Applications. 2010;37(10):6737–6741. [Google Scholar]
- 181.Virmani J, Kumar V, Kalra N, Khandelwal N. A comparative study of computer-aided classification systems for focal hepatic lesions from B-mode ultrasound. Journal of medical engineering & technology. 2013;37(4):292–306. doi: 10.3109/03091902.2013.794869. [DOI] [PubMed] [Google Scholar]
- 182.Goh V, Sanghera B, Wellsted DM, Sundin J, Halligan S. Assessment of the spatial pattern of colorectal tumour perfusion estimated at perfusion CT using two-dimensional fractal analysis. European radiology. 2009;19(6):1358–1365. doi: 10.1007/s00330-009-1304-y. [DOI] [PubMed] [Google Scholar]
- 183.Cui C, Cai H, Liu L, Li L, Tian H, Li L. Quantitative analysis and prediction of regional lymph node status in rectal cancer based on computed tomography imaging. European radiology. 2011;21(11):2318–2325. doi: 10.1007/s00330-011-2182-7. [DOI] [PubMed] [Google Scholar]
- 184.Wibmer A, Hricak H, Gondo T, et al. Haralick texture analysis of prostate MRI: utility for differentiating non-cancerous prostate from prostate cancer and differentiating prostate cancers with different Gleason scores. European radiology. 2015;25(10):2840–2850. doi: 10.1007/s00330-015-3701-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 185.Bengio Y, Courville A, Vincent P. Representation learning: A review and new perspectives. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2013;35(8):1798–1828. doi: 10.1109/TPAMI.2013.50. [DOI] [PubMed] [Google Scholar]
- 186.LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015;521(7553):436–444. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- 187.Cui JL, Wen CY, Hu Y, Li TH, Luk KD. Entropy-based analysis for diffusion anisotropy mapping of healthy and myelopathic spinal cord. Neuroimage. 2011 Feb 1;54(3):2125–2131. doi: 10.1016/j.neuroimage.2010.10.018. [DOI] [PubMed] [Google Scholar]