Evaluation and Minimization of Uncertainty in ITC Binding Measurements

Abstract

Background

Isothermal titration calorimetry (ITC) is uniquely useful for characterizing binding thermodynamics, because it straightforwardly provides both the binding enthalpy and free energy. However, the precision of the results depends on the experimental setup and how thermodynamic results are obtained from the raw data.

Methods

Experiments and Monte Carlo analysis are used to study how uncertainties in injection heat and concentration propagate to binding enthalpies in various scenarios. We identify regimes in which it is preferable to fix the stoichiometry parameter, N, and evaluate the reliability of uncertainties provided by the least squares method.

Results

The noise in the injection heat is mainly proportional in character, with ~1% and ~3% uncertainty at 27C and 65C, respectively; concentration errors are ~1%. Simulations of experiments based on these uncertainties delineate how experimental design and curve fitting methods influence the uncertainty in the final results.

Conclusions

In most cases, experimental uncertainty is minimized by using more injections and by fixing N at its known value. With appropriate technique, the uncertainty in measured binding enthalpies can be kept below ~2% under many conditions, including low C values.

General Significance

We quantify uncertainties in ITC data due to heat and concentration error, and identify practices to minimize these uncertainties. The resulting guidelines are important when ITC data are used quantitatively, such as to test computer simulations of binding. Reproducibility and further study are supported by free distribution of the new software developed here.

1. Introduction

The thermodynamic characterization of noncovalent binding interactions is important in both basic and applied fields, including molecular biophysics and drug design. While binding free energies, ΔG, can be measured by a range of methods, such as spectrometry, surface plasmon resonance¹, and enzyme inhibition², the method of isothermal titration calorimetry (ITC)^3–8 is unique in providing not only the binding free energy but also the binding enthalpy, ΔH, from measurements taken at a single temperature. Binding enthalpies are of interest because they offer further information regarding the physics of noncovalent interactions, such as the phenomenon of entropy-enthalpy compensation^9–13, and can bear on mechanisms of protein folding and drug action. For example, modes of drug-receptor binding can sometimes be assigned based on knowledge of both ΔG and ΔH^14,15. Moreover, the determination of ΔH, in addition to ΔG, expands the dataset available to test and improve the accuracy of molecular simulations: much as heats of vaporization and sublimation played a central role in defining the force field parameters used for liquid-state simulations^16–19, so binding enthalpy data, particularly for experimentally and computationally tractable host-guest systems, should be useful to test and improve the force fields used for simulations of noncovalent binding^20,21. For all of these applications, it is desirable to use procedures that minimize the uncertainty in the thermodynamic results and to have a quantitative understanding of these uncertainties.

Sources of uncertainty in ITC data may include^3,22–28 errors in the quantification of released heat by the instrument; errors in the concentrations of the solutions; baseline error, due to instrument problems or environmental perturbations; nonideality of the solutions; and procedural problems, such as the presence of air bubbles in the cell or use of non-optimal stirring speeds. Each of these sources of error can produce its own pattern in the data, and can propagate in its own way to the fitted binding free energy and enthalpy. For example, procedural and baseline errors can yield abnormal-looking enthalpograms, whereas noise in the measured heat released from successive injections can produce a jagged or noisy-looking Wiseman plot. Concentration error, in contrast, does not yield obviously pathological graphs, but can nonetheless propagate to the fitted thermodynamic results. Finally, as already widely recognized^7,29,30, when molecules release or take up protons on binding, the consequent uptake or release of protons by the buffer can lead to added enthalpic changes which obscure the heat signature of the binding event itself. The magnitude of this effect depends on the buffer; for example, it is particularly large for Tris³¹, and small for phosphate³¹. Arguably, buffer ionization heats do not lead to experimental errors, but rather to errors of interpretation.

The literature affords divergent views of the level of uncertainty in ITC data. On one hand, it is not uncommon to see published ITC data with reported experimental uncertainties in the hundredths of kcal/mol. On the other hand, the ABRF-MIRG’02 study³², in which 17 laboratories independently measured the binding thermodynamics of the same protein and small molecule, suggested that experimental uncertainties might be as high as 20%. Much of the error in this study appears to be procedural, as omitting the four results for which the representative enthalpograms and/or Wiseman plots are obviously abnormal or noisy (graphs 2, 7, 8 and 14 in Figure 4 of reference 32 leads to a less problematic standard deviation of 11% in ΔH. Further analysis led to the suggestion that that errors in the concentration of the syringe reactant represented a major source of the variation in the reported binding enthalpies²⁵; and the potential sensitivity of binding enthalpy results to errors in the syringe concentration has been emphasized elsewhere as well^26,27. Importantly, the errors observed in the ABRF-MIRG’02 study are not necessarily representative of typical published ITC data, as the participants were not required to be experts, and novices were explicitly welcomed and included (Michael Doyle, personal communication).

The uncertainties in binding free energies and enthalpies obtained from ITC experiments can be mitigated by appropriate experimental design, execution, and analysis^{7,22–24,26,33,34}. Thus, as early noted³, it is helpful to design experiments with a C value -- the binding constant times the cell concentration and stoichiometry -- within an appropriate range, though it has also been argued that experimental data with low C values can still yield useful thermodynamic data³⁴. Additionally, good laboratory practices can minimize uncertainties stemming from environmental noise; one should be cautious in applying ITC when the heat of reaction is small in magnitude, as the small magnitudes of the injection heats being measured in such cases can lead to a low signal-to-noise ratio; and pathological enthalpograms should be discarded. Note, too, that sophisticated methods of baseline determination have been developed to minimize error that may stem from drift or inconsistencies across experiments²⁴.

The method used to fit theoretical curves to the experimental data also can affect uncertainties in ITC results. For example, fixing the binding stoichiometry, N, in the data analysis process, rather than allowing it to be optimized as an additional fitting parameter, may reduce experimental error for experiments at low C values³⁴. On the other hand, allowing N to float, instead of fixing it, is widely regarded as a useful means of reducing the sensitivity of the results to errors in the concentration of the cell solution²⁵; accordingly, the software distributed with many ITC instruments defaults to this option. (Another approach is to use global fitting over multiple Wiseman plots, obtained under different experimental conditions, keeping N fixed at a known integral value and treating concentration error explicitly^35,36.) The problem of determining whether to treat N as fixed or let it float is complicated by the fact that the commonly used least squares (LS) error analysis method does not propagate concentration error to the reported thermodynamic results, as recently highlighted²⁶, so it might provide misleading guidance as to which curve-fitting procedure is best. It is therefore of interest to use more robust error propagation methods, such as Monte Carlo simulations^22,33,37 to study how syringe and cell concentration error affect errors in the binding free energy and enthalpy, and how this propagation is influenced by the treatment of N in the curve fitting process.

Another source of error in ITC measurements is heat error, the noise in the heat measured for each injection. This can result from random variations in the injection volumes, relative to what was intended; or from noise in the measurement of the heat released from each injection. Like concentration error, heat error propagates through to the thermodynamic results, and it has been argued that using fewer ITC injections can mitigate the resulting errors²². The analysis was predicated on a specific model of heat error, with a fixed 0.28 μcal/injection measurement error and an additional contribution due to error in the injection volume, but the literature contains additional models for heat error. For example, prior studies have assumed fixed errors of 0.6 μcal/injection³³, 0.25 μcal/injection⁷ and 0.1 μcal/injection³⁷; another assumed a mixed error model, in which injections with smaller heat release were associated with a fixed error of 0.5 μcal/injection, but injections with heat release more than 100 μcal were associated with a proportional error of 0.5%³⁴. Another study included a proportional term in the overall estimate of error, but it was insignificant for heat releases smaller than 300 μcal³⁸. Wiseman and coworkers early examined the variance in measured heat for a series of small electrical pulses of fixed magnitude³, but did not report how the variance changed as a function of the amount of heat released. Additionally, the heat error reported for a series of water-into-water injection was found to be about 0.06 μcal, considerably less than predicted by some of the assumed fixed errors listed above³⁹. Thus, it is not clear that the literature contains empirical data that would direct one toward any particular model for the noise in the heat measured per injection.

The present study addresses a number of these issues regarding the design and analysis of ITC experiments, focusing on a model case of 1:1 binding. In particular, we empirically evaluate uncertainties in injection heats and solution concentrations, and use Monte Carlo data modeling to examine how these uncertainties propagate to uncertainties in the derived binding enthalpies, for experiments at low and optimal C values, and with the value of N fixed or allowed to float. We focus primarily on binding enthalpies as opposed to binding free energies, because (as shown below) free energies are comparatively insensitive to experimental error, while errors in binding enthalpies are generally larger and present more of a challenge to fit with high precision^26,40. However, we also provide results showing uncertainty in binding free energies given realistic experimental errors, as part of a global examination of errors encountered in what might be a typical ITC experiment. The present results have implications for how uncertainties in binding thermodynamics are assigned, and for how to design and analyze ITC experiments in a manner that reduces these uncertainties.

2. Materials and Methods

2.1 Materials

β-cyclodextrin (catalog no. C-4767, purity > 97%) was obtained from Sigma-Aldrich Company (St. Louis, MO). Initial batches of β-cyclodextrin that we had stored for over a year showed some evidence of aggregation⁴¹ in newly made concentrated solutions that had stood for on the order of an hour or more, based on slight clouding and confirmatory spectrophotometry, so a new batch was purchased and used for the present experiments. Solutions made from the new lot showed no evidence of aggregation. Thermogravimetric analysis of the initial batch of β-cyclodextrin confirmed Sigma-Aldrich’s specification of 8 mole of water per mole of β-cyclodextrin, and the amounts weighed to achieve a target concentration were adjusted to compensate for the water content. NMR spectroscopy was used to confirm the structure and purity of the new lot of β-cyclodextrin. Succinic acid and NaOH were both obtained from Fisher Scientific through the chemistry stockroom at University of California, San Diego.

2.2 Isothermal Titration Calorimetry Experiments

ITC experiments were performed using a MicroCal model VP-ITC (MicroCal, Northampton, CT, Serial Number 01-08-930). It has been emphasized that even seemingly minor deflections in the power baseline during an ITC experiment can lead to nontrivial errors whose remediation, when feasible, requires detailed analysis²⁴. We therefore sought to minimize environmental sources of baseline noise. We found that small, deliberate vibrations of the laboratory bench on which the calorimeter was set caused significant deflections in baseline. To prevent this, the calorimeter was placed in an isolated room on a 2″ thick block of urethane foam. This setup eliminated deflections during deliberate vibration of the bench and provided a more stable baseline. A purpose-built, clear acrylic shield was furthermore used to reduce possible temperature shifts due to drafts. The instrument’s built-in Y-axis calibrations were performed, at 27 C°, to verify that the instrument was responding to known power inputs within the 1% error tolerance prescribed by the manufacturer.

Following a previously published procedure⁴², we determined the uncertainty of the heat release per injection by repeatedly injecting fixed amounts of succinic acid solution into an excess of NaOH and determining the variance of the integrated heats across the series of injections. In principle, all injections should yield essentially the same heat, due to the excess of NaOH. The succinic acid and NaOH solutions were prepared at 2 mM and 20 mM respectively. Masses of dry succinic acid were measured with a Sartorius CPA225D Micro Balance, while the NaOH solution was prepared by dilution of 1M stocks as purchased. Solutions were prepared in 25 mL volumetric flasks. Measurements were taken with injection volumes of 10, 5, and 2.5 μL injections, with twenty injections per experiment. The reference power was set at 25 μcal /sec for all experiments. In order to determine whether the observed drop in variance with diminishing injection volume in these initial experiments should be attributed to variations in injection volume versus variations in the measurement of released heat, additional experiments were done in which the injection volumes were held at 10 uL, and the concentration of succinic acid was instead reduced to generate solutions ranging from 20 mM to 0.5 mM, leading to reduced heat release per injection. We additionally performed water-into-water experiments, which generate very small injection heats, to look at the minimal variance in injection heat, at temperatures of 27 °C and 65 °C. Origin 7.0 was used to integrate the heat released from the injection heats. For 2.5 μL injections, the first two injections were discarded; for 5 and 10 μL injections, the first injection was discarded. This is due to the typically smaller first injection in ITC experiments, possibly due to diffusion of syringe material into the cell during equilibration.

2.3 Measurement of Concentration Uncertainty

The solutions of β-cyclodextrin for concentration error analyses were prepared in 250 mL volumetric flasks, with 2.00 g β-cyclodextrin per 250 mL batch of solution; and in 25 mL volumetric flasks, with 0.200 g of β-cyclodextrin per 25 mL batch. Masses were measured with a Sartorius CPA225D Micro Balance. Each solution of β-cyclodextrin was prepared from the same stock of 0.5% (v/v) acetonitrile in water (prepared prior to dissolution of weighed β-cyclodextrin at 1 L), to provide a consistent standard peak for NMR measurements. Proton NMR measurements were carried out on a Varian NPA600, using 10% deuterium oxide in the 0.5% acetonitrile solution used to make up each sample of beta-cylodextrin, in order to lock to ²H. To evaluate the uncertainty in the concentrations of the cyclodextrin solutions, we prepared four independent solutions at each volume (250 mL, 25 mL) as described above, obtained the proton NMR spectrum of each solution, and integrated the five peaks corresponding to glucose protons, using Bruker TopSpin software, as well as the acetonitrile peak. The ratio of the peak integrals from the β-cyclodextrin to the peak integral of acetonitrile was measured, and compared amongst solutions to determine the overall standard deviation of the concentration of solutions. This does not provide systematic error in concentrations, but rather the variation of concentrations amongst four solutions prepared using identical methods. Note that spectrophotometry could not be used for this purpose, because β-cyclodextrin does not absorb significantly in the UV-Vis range.

2.4 Generation and Analysis of Artificial ITC Data

We generated and analyzed artificial Wiseman plots based on thermodynamic parameters for the reversible association of a model system previously studied by both our laboratory and others⁴³: the adamantyl-based drug rimantadine with the cyclic oligosaccharide β-cyclodextrin, with thermodynamic binding parameters ΔH = −6500 cal/mol and K = 36000 M⁻¹, N=1. The data were modeled for our own (unpublished) experimental setups with rimantadine in the cell and cyclodextrin in the syringe, with a favorable C value of 50 (C_syringe=13mM, C_cell=1.4 mM) and an unfavorable C value lowered to 0.50 by lowering concentrations (C_syringe=3.5 mM, C_cell=0.014 mM). Except as otherwise noted, the simulated experiments used 25 injections of 10 μL each, leading to maximum saturation of 99% for both the low and high C cases. In selected cases, we also modeled low C experiments run to only 55% saturation (C_syringe = 0.32 mM, C_cell = 0.014 mM), where the amount of injectant was diminished by reducing the concentration in the syringe. No heat of dilution was incorporated into the simulated Wiseman plots, so the nominal injection heats provided by the model derive only from the binding reaction.

The equations for a single set of identical sites^3,44 were implemented in Python scripts, which produced ideal Wiseman plots based on the desired K, ΔH, concentration values, injection volumes and numbers of injections. The volume of the ITC cell was set to that of our VP-ITC instrument, 1.4614 mL, and the expressions used accounted for dilution of the sample cell during the experiment, as typically done by Origin 7.0. We verified that fitting artificial plots based on these parameters, with both Origin 7.0 and our Python code, returned the thermodynamic parameters used to generate them. The resulting Wiseman plots were analyzed by additional Python scripts that automated the subsequent curve-fitting procedures, using an implementation of the Marquardt-Levenberg nonlinear optimization method available in the SciPy library. This procedure yields best-fit values of K and ΔH for a given Wiseman plot, along with LS uncertainties like those provided by the Origin software.

2.5 Error Analysis by Monte Carlo Sampling

Experimental uncertainties in ITC results are commonly estimated from the residuals and partial derivatives of the LS fit. For example, it is the LS uncertainties that are reported by the widely used Origin software⁴⁴. However, as detailed in Results, this method is itself subject to error, tending to yield uncertainties that are unrealistically low. Here, therefore, we follow others^7,22,33 in using a more rigorous Monte Carlo sampling method to determine how uncertainties in concentration and measured heat release propagate to the reported thermodynamics quantities. These reference results are then compared with the more commonly reported LS uncertainties to assess the limitations of the latter. The Monte Carlo method was implemented as follows. The uncertainty in the injection heats was modeled by associating the heat release for each injection with a Gaussian distribution of heat release with the ideal mean value, μ_Q, and a user-defined standard deviation σ_Q following Eq (1) (below). Two thousand different plots of raw heats were generated by randomly resampling the raw heat value at each point from its respective Gaussian. We confirmed for several test cases that increasing the number of plots from 2,000 to 10,000 led only to ~0.1% changes in reported binding enthalpy uncertainties, for even the most error prone conditions. Concentration error was modeled by using syringe and cell concentrations drawn from Gaussian distributions, with their means set to their nominal concentrations, μ_C, and their standard deviations set to a user-defined value, σ;_C. In each case, the resampled raw heats were normalized based on the erroneous syringe concentration to generate a new Wiseman plot. Values of K and ΔH were then fitted to each resulting Wiseman plot, using the Python script described above, to yield a statistical distribution of these fitted quantities, from which we computed the mean and standard deviation of ΔH (μ_H and σ_H, respectively) and ΔG (μ_G and σ_G), where the spreads are determined by the uncertainties in heat release and solution concentration, as manifest in the resampled Wiseman plots. The LS fitting routine rarely generated pathological results, with very high reported LS errors, apparently due to occasional failure of the solver. To avoid incorporating these pathological cases into the statistics, results for which the reported LS error was in the top first percentile were discarded.

3. Results

This section first reports on the experimental characterization of heat error, and how this error, in the absence of concentration error, propagates to measured binding thermodynamics, for both normal (C value = 50) and low (C value = 0.5) C value experiments. It then reports, analogously, on measurements of concentration error and on how concentration error without heat error propagates to the binding enthalpy. Finally, it reports on global analyses in which both heat and concentration error are present, in order to gain insight into how to assess and minimize uncertainty in measurements of binding thermodynamics. Although we focus primarily on how errors propagate to binding enthalpies, as these are more susceptible to error than free energies, selected analyses are also done for the free energy, and Section 3.4 assesses errors in both enthalpy and free energy for a range of realistic experimental conditions.

3.1 Heat noise in enthalpograms: character and propagation

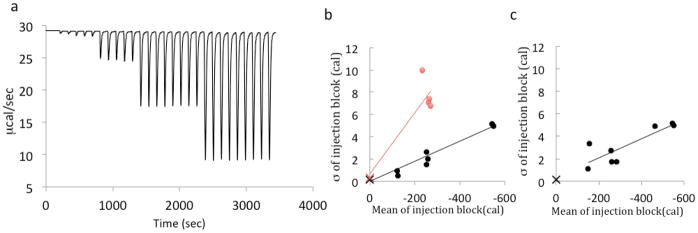
Random noise in the integrated peaks of the VP-ITC enthalpogram was measured in terms of the peak-to-peak variation across a series of nominally uniform peaks, which were generated by injection of 2 mM aqueous succinic acid into 20 mM sodium hydroxide solution. Due to the excess of hydroxide in the cell, each injection of succinic acid should be equally exothermic, with only slight loss of heat over the course of a single experiment due to dilution of the hydroxide, as evident in sample data (Figure 1a); see SI for details (Supplementary Table 1). We find that the standard deviation of the injection heats, σ_Q, across a series of nominally identical injections, at 27 °C, is approximately proportional to the mean heat released during the injection, Q, across injections of various volumes (Figure 1b, black circles). The slope of a linear fit to these data is a temperature dependent coefficient of proportional error, with the form ζ (27°) = 0.01, which corresponds to 1% uncertainty in the heat measurements. Note that the range of heats in the succinic acid/NaOH experiment (Figure 1b) is in the middle of that occurring in the ITC experiments at optimal C modeled in this study. Because we have observed noisier enthalpograms at higher temperatures, we also examined the standard deviation of the peaks at 65 °C. As shown in Figure 1b (red circles), the error, about 3% of the measured heat, is significantly greater than at 27 °C; we estimate ζ (65°) ≈ 0.03, based on the locations of the red “x” and the red circles in Figure 1b.

Figure 1.

Injection of succinic acid into NaOH. (A) A raw enthalpogram of varying injection sizes of 2 mM succinic acid into 20 mM NaOH. Peaks shown (from smallest to largest) are 0.5 μL, 2.0 μL, 5 μL, and 10 μL. The slight increase in peak size on the 0.5 and 2.0 μL peaks stems from the well-known diffusion of syringe reactant prior to the start of the experiment. As noted in the Methods section, for experimental data the first one or two injections were discarded. (B) Plots of means of heat vs. standard deviations with varying volume. Black points show data at 27 °C, red points at 65 °C. The black and red Xs are water-water experiments at 27 C and 65 C, respectively. (C) Plots of means of heats vs. standard deviation for constant volume succinic acid injections. The red X is a water-water experiment at 27C.

Additionally, water-into-water experiments were performed to assess any underlying error, since water-into-water injections generate extremely small amounts of heat (Figure 1b, c, red x’s). This minimum level of noise presumably is associated with fluctuations in the calorimeter’s baseline signal, perhaps coupled to variations in measured Joule heating. As this irreducible heat variance potentially results from processes different from those that generate the proportional noise observed in the present succinic acid/NaOH study, we assume that both processes operate simultaneously and independently. As a consequence, the total variance of the heat per injection should be estimated as the sum of the variances of the two processes, so that their standard deviations add in quadrature:

$${\sigma }_Q(T)\approx {\left\{{\left[\zeta (T)Q\right]}^2+{\sigma }_{\mathit{irr}}{(T)}^2\right\}}^{\frac{1}{2}}$$ (1)

Here, σ_Q is the standard deviation of the measured injection heat; ζ (T) is the temperature dependent coefficient of the proportional error component; and σ_irr(T) is the standard deviation of the temperature-dependent irreducible heat noise. Adding the two variances affords an error model which is conservative, relative to prior models that assign the irreducible noise minimum as the floor of a proportional model^34,37 rather than as an additive noise component. Our water-into-water studies yield σ_irr (27) of 0.13 μcal, and σ_irr (65) of 0.39 μcal, with a mean heat release of 0.36 and 0.70 μcal, respectively. These may be compared with a prior report of 0.06 μcal³⁹ for σ_irr (27).

Because the differences in mean heat reported in the prior paragraph and illustrated in Figure 1b were generated by changing the injection volume while using a single syringe solution, it was possible that the increase in noise with increased heat release resulted not from the increase in heat release as such, but instead from the increase in the volume of fluid injected, due to some property of the syringe mechanism. We therefore checked whether the uncertainty in the enthalpogram would remain proportional to peak size if we kept the injection volume constant (10 μL) and instead adjusted the heat per injection by using solutions of different concentrations. We found that, across injections of constant volume, the standard deviation of the heat per injection, σ_Q, still is approximately proportional to the mean heat release, μ_Q, with a constant of proportionality ζ(T) = 0.008–0.009 (Figure 1c), depending on whether or not the linear fit was forced through the origin. Because these values are close to the prior value of 0.01 (above), we conclude that the increase in noise with increasing heat release per injection is attributable to noise in the heat measurement rather than to changes in the injection volume. This result appears to disagree with a prior model in which a non-fixed component of the heat error was considered to result from variance in the injection volumes²².

It is of interest to determine whether the heat measurements from successive injections were mutually correlated, because such correlation could affect the estimated error of the fitted thermodynamic quantities²². For three independent series of 10 μL injections, the R² values between successive (i, i+1) injection heats were 0.05, 0.33, and 0.07, and, for three independent series of 5 μl injections, the analogous R² values were 0.50, 0.27, and 0.39. Substantially smaller values of R² were observed for the ith and (i+2)th heats. The fitted slopes of linear regressions between the ith and (i+1)th heats were positive, with values on the order of 0.5. Thus, there appears to be a weak correlation between successive injection heats, but the correlation coefficients are variable from one study to the next, the correlation does not persist across multiple peaks, and the degree of correlation appears to be greater for smaller peaks. Given the modest and inconsistent strengths of the correlations, we treated successive peaks as uncorrelated when modeling experimental error in the present study. Sample correlation plots are shown in the SI (Supplementary Figure 1).

We next used Monte Carlo sampling to study how the heat errors reported above propagate to uncertainties in the derived values of ΔH. As detailed in Methods, multiple artificial Wiseman plots were generated, each with its own set of random, uncorrelated Gaussian errors added to the injection heats, using the proportional error model of Equation 1, for values of ζ ranging from 0 to 0.03, and for values of C equal to 50 and 0.50. As mentioned above, an irreducible error was added in quadrature to the proportional component. Based on the previously mentioned water-water experiments, the baseline error was set as σ_irr =13 ζ μcal. Samples of these artificial Wiseman plots (with ζ = 0.01) are provided in the SI (Supplementary Figure 2). A separate least squares (LS) fitting for each Wiseman plot, with N either fixed or allowed to float, yielded a value of ΔH and a report of uncertainty from the LS fit. The mean, μ_H, and standard deviation, σ_H, of the resulting values of ΔH, were computed, and we also computed the mean of the uncertainties reported by the LS method across each set of MC samples. With the present model for heat error (Eq. 1), we observed a small exothermic bias in μ_H relative to its nominal value, rising to a maximum of about 5% at ζ =0.03, in cases where N is allowed to float and C = 0.5 (Supplementary Figure 4). However, the scatter of the fitted enthalpies, σ_H, in this case is so large that it effectively drowns out the bias (Supplementary Figure 4). This bias disappears at higher C values and when N is fixed.

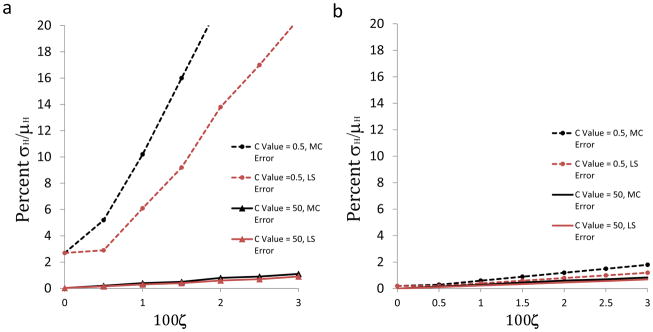
As shown in Figure 2, the uncertainty in the enthalpy, σ_H, depends strongly on the values of ζ and C, and on whether N is treated as fixed or floating. Thus, when C has the favorable value of 50 and N is allowed to float, as is commonly done, both the Monte Carlo and the LS estimates of σ_H remain below 2%, even when the proportional part of the heat error rises to 3% (ζ= 0.03), the value observed at 65 °C; see solid black and red lines, respectively, in Figure 2a. However, when C has the unfavorable value of 0.5, and N is allowed to float, both the Monte Carlo and LS estimates of σ_H are much higher. Indeed, the Monte Carlo result goes above 20% when the heat error is 1.5% (dashed black line, Figure 2a). Notably, the LS uncertainties somewhat underestimate the reference Monte Carlo results, as they reach only about half the respective Monte Carlo error estimate. Fixing the value of N at its nominal value of 1 somewhat reduces the already low errors when C=50 (black and red solid lines, Figure 2b), and markedly reduces the uncertainty in the enthalpy when C=0.5 (black and red dashed lines, Figure 2b). The observation that fixing N at its nominal value can reduce the propagation of heat error is consistent with prior observations³⁴. The results for C=0.5 in Figure 2 were obtained in modeled experiments where the cell reactant was 99% saturated with the syringe reactant at the end of the titration. Results for experiments reaching only 55% saturation are furthermore provided in Table 2 and Table 3.

Figure 2.

Relative uncertainty in ΔH as a function of heat error coefficient, ζ, with σ_irr = 13ζμcal added in quadrature. Black lines are uncertainties from Monte Carlo resampling; red lines are mean uncertainties provided by LS fitting only. Solid lines: C=50; dashed lines: C=0.5. a) results for floating N; b) results for N fixed at one. No concentration error is included in this analysis.

Table 2.

Uncertainties of fitted binding enthalpies for various experimental conditions and assumptions regarding heat and concentration error, where syringe and concentration uncertainties are assumed to be the same. For ζ = 0.01, σ_irr = 0.13 μcal; for ζ = 0.03, σ_irr = 0.39 μcal. See text for details.

		Concentration Error				MC Statistics
		Heat Err, ζ	Syr	Cell	N Float/Fixed	ΔH MC Error %	Mean LS ΔH Error %	%SD of N
		Optimal C=50
High Sat. (99%)	Low Conc. Error	1%	0.6%	0.6%	Fixed	0.5	0.3
		1%	0.6%	0.6%	Float	0.7	0.3	0.8
		3%	0.6%	0.6%	Fixed	1.0	0.8
		3%	0.6%	0.6%	Float	1.3	0.9	1
	High Conc. Error	1%	1.1%	1.1%	Fixed	0.8	0.4
		1%	1.1%	1.1%	Float	1.1	0.3	1.5
		3%	1.1%	1.1%	Fixed	1.2	0.9
		3%	1.1%	1.1%	Float	1.6	0.9	1.6
		Low C=0.5
High Sat. (99%)	Low Conc. Error	1%	0.6%	0.6%	Fixed	0.9	0.4
		1%	0.6%	0.6%	Float	10.5	6.3	9.6
		3%	0.6%	0.6%	Fixed	1.9	0.5
		3%	0.6%	0.6%	Float	36.2	23.8	26.1
	High Conc. Error	1%	1.1%	1.1%	Fixed	1.3	0.4
		1%	1.1%	1.1%	Float	10.5	6.3	9.6
		3%	1.1%	1.1%	Fixed	2.1	1.2
		3%	1.1%	1.1%	Float	36.2	24	26.2
Low Sat. (55%)	Low Conc. Error	1%	0.6%	0.6%	Fixed	2.2	2.1
		1%	0.6%	0.6%	Float	26.1	27.2	18.2
		3%	0.6%	0.6%	Fixed	6.0	5.9
		3%	0.6%	0.6%	Float	44.5	54.4	34.1
	High Conc. Error	1%	1.1%	1.1%	Fixed	2.5	2.0
		1%	1.1%	1.1%	Float	26.2	27.3	18.3
		3%	1.1%	1.1%	Fixed	6.4	6.3
		3%	1.1%	1.1%	Float	44.5	54.2	34.1

Table 3.

Same as prior table, but with mixed combinations of syringe and cell concentration uncertainties.

	Concentration Error				MC Statistics
	Heat err, ζ	Syr	Cell	N Float/Fixed	ΔH MC Error %	Mean LS ΔH Error %	%SD of N
	Optimal C=50
High Sat. (99%)	1%	0.6%	1.1%	Fixed	0.8	0.4
	1%	0.6%	1.1%	Float	0.7	0.3	1.3
	3%	0.6%	1.1%	Fixed	1.2	0.8
	3%	0.6%	1.1%	Float	1.3	0.9	1.4
	1%	1.1%	0.6%	Fixed	0.6	0.4
	1%	1.1%	0.6%	Float	1.2	0.3	1.4
	3%	1.1%	0.6%	Fixed	1.0	0.8
	3%	1.1%	0.6%	Float	1.6	0.9	1.4
	Low C=0.5
High Sat. (99%)	1%	0.6%	1.1%	Fixed	1.3	0.4
	1%	0.6%	1.1%	Float	10.5	6.2	9.6
	3%	0.6%	1.1%	Fixed	2.3	1.2
	3%	0.6%	1.1%	Float	36.2	24.0	26.2
	1%	1.1%	0.6%	Fixed	0.9	0.4
	1%	1.1%	0.6%	Float	10.6	6.2	10.0
	3%	1.1%	0.6%	Fixed	1.9	1.2
	3%	1.1%	0.6%	Float	36.1	23.6	26.1
Low Sat. (55%)	1%	0.6%	1.1%	Fixed	2.4	2.1
	1%	0.6%	1.1%	Float	26.1	27.1	18.0
	3%	0.6%	1.1%	Fixed	6.4	6.3
	3%	0.6%	1.1%	Float	44.5	54.2	34.5
	1%	1.1%	0.6%	Fixed	2.2	2.1
	1%	1.1%	0.6%	Float	26.4	27.1	17.8
	3%	1.1%	0.6%	Fixed	6.2	6.2
	3%	1.1%	0.6%	Float	44.4	54.3	34.3

3.2 Concentration error: characterization and propagation

We empirically evaluated the uncertainty in the concentrations of stock solutions of β-cyclodextrin made up in 250mL and 25mL volumetric flasks. In each case, we made four solutions of β-cyclodextrin and took NMR spectra, integrated peaks corresponding to glucose protons and the reference acetonitrile peak, and computed the standard deviations of the ratio of the glucose peaks to the reference peak, as described in Methods. This procedure yielded a relative uncertainty, σ_C/Conc, of 0.6% in the concentration, when solutions are prepared in 250 mL volumetric flasks, and 1.1% when solutions are prepared in 25 mL volumetrics. We then used model calculations to examine how concentration errors propagate to the reported enthalpy, in the absence of heat error, as detailed below.

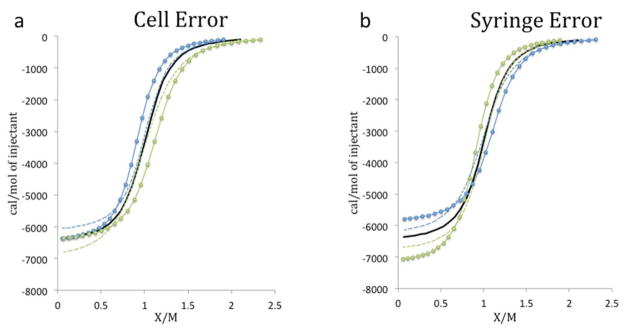
Whereas heat noise leads to rough-looking Wiseman plots (Supplementary Figure 2), concentration error yields Wiseman plots that are distorted, but smooth, as illustrated in Figure 3, which uses syringe and cell concentration errors of ±10% to help with visualization. The curves are smooth because errors in the solution concentrations affect the entire Wiseman plot in a consistent manner. Because the x-axis of the Wiseman plot is the molar ratio of syringe to cell concentration, error in the cell concentration rescales the plot along the x-axis (Figure 3a). Error in the syringe concentration also rescales the graph along the x-axis, though in the opposite sense from error in the cell concentration, and it additionally rescales the y-axis, due to renormalization of the heat released per mole of injectant (Figure 3b). The effects of these ±10% concentration rescalings on the fitted values of the binding enthalpy, ΔH_fit, are summarized in Table 1, which includes results for not only syringe-only and cell-only concentration errors, but also their combinations. (The combination Wiseman plots are provided in Supplementary Figure 5.) The errors are given as ΔH_fit − ΔH_nominal, where ΔH_nominal is the nominal binding enthalpy of −6.5 kcal/mol. A number of interesting observations emerge.

Figure 3.

Influence of concentration error on Wiseman plots (C value = 50). Black line: nominal result. Points represent Wiseman plots with 10% concentration error either added (blue) or subtracted (green) from the nominal syringe or cell concentration. Lines of the respective colors are the corresponding LS fits. Solid: N floating; dashed: N fixed at 1.

Table 1.

Analysis of unsigned errors in fitted binding enthalpy (ΔH Error) due to error in syringe and cell concentration for both N floating and N fixed. Results shown are from a C value of 50, with 99% saturation. The unsigned uncertainty reported from the least squares fit (LS Err) is also shown, along with the reported value of N, when it is allowed to float. The nominal ΔH is −6.5 kcal/mol for all conditions.

Percent Conc Error		N floating				N = 1
Syringe	Cell	ΔHfit	ΔH Error	LS Err	N	ΔHfit	ΔH Error	LS Err
0	0	−6.5	0.0	0.0	1.0	−6.5	0.0	0.0
−10	0	−7.2	0.7	0.0	1.1	−6.8	0.3	0.17
+10	0	−5.9	0.6	0.0	0.9	−6.4	0.1	0.14
0	−10	−6.5	0.0	0.0	0.9	−6.2	0.3	0.14
0	+10	−6.5	0.0	0.0	1.1	−7.1	0.6	0.17
+10	−10	−5.9	0.6	0.0	1.0	−5.9	0.6	0.0
+10	+10	−5.9	0.6	0.0	1.2	−7.2	0.7	0.35
−10	−10	−7.2	0.7	0.0	0.8	−6.6	0.1	0.32
−10	+10	−7.2	0.7	0.0	1.0	−7.2	0.7	0.0

First, allowing N to float prevents propagation of cell concentration error to the binding enthalpy, but allows syringe error to propagate nearly linearly, in the sense that 10% concentration error generates about 10% enthalpy error. (The modest degree of nonlinearity presumably results from the rescaling of the Wiseman plot along not only the y-axis, but also the x-axis; see above.) Nonetheless, the LS error is always zero when N is allowed to float, whether or not the enthalpy is correct, because including N as a fitting parameter allows the smooth Wiseman plots that result from pure concentration error to be perfectly fit by theoretical curves. This is illustrated in Figure 3, which shows how Wiseman plots shift with various concentration errors. For example, increasing the concentration in the cell to 10% above its nominal value pushes the curve to the left, because the x coordinate, X/M, becomes smaller due to the larger cell concentration. Furthermore, in cases where the syringe and cell concentration errors are equivalent (e.g., both +10%), the fitted value of N reverts to its nominal value of 1, but the actual errors in the binding enthalpy are among the largest listed in the table. The appearance of LS errors of zero for cases where the actual error is nontrivial highlights an important limitation of this statistic.

When N is fixed at its nominal value of 1, both cell and syringe error can propagate to the enthalpy (Table 1), and the LS error is nonzero in most cases, because theoretical curves with N=1 are unable to exactly fit experimental curves with concentration error (Figure 3). The exception occurs when the cell and syringe errors happen to be the same; i.e., +10% or −10%. In these cases, a theoretical curve can perfectly fit the Wiseman plot, but the fitted enthalpy is wrong by about 10%. Interestingly, although fixing N=1 yields larger LS errors than allowing N to float, the MC analysis shows that fixing N yields enthalpies that are, on average, more accurate. Thus, for the present examples, the mean unsigned errors for all of the concentration error cases in Table 1 are 0.41 for N floating and 0.38 for N =1. In summary, for these model calculations, allowing N to float tends to increase actual error but decreases the error reported by the LS method. Additionally, even when N=1, the LS error does not correlate with the actual error in the enthalpy, as shown in Figure 4.

Figure 4.

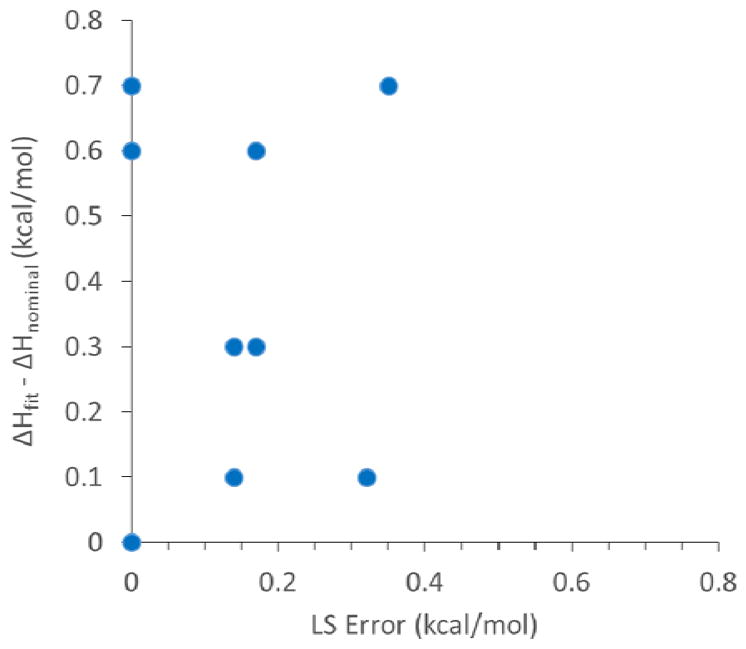
Plot of actual unsigned error, abs (ΔH_fit − ΔH_nominal) vs. reported LS error with fixed N; data are from Table 1.

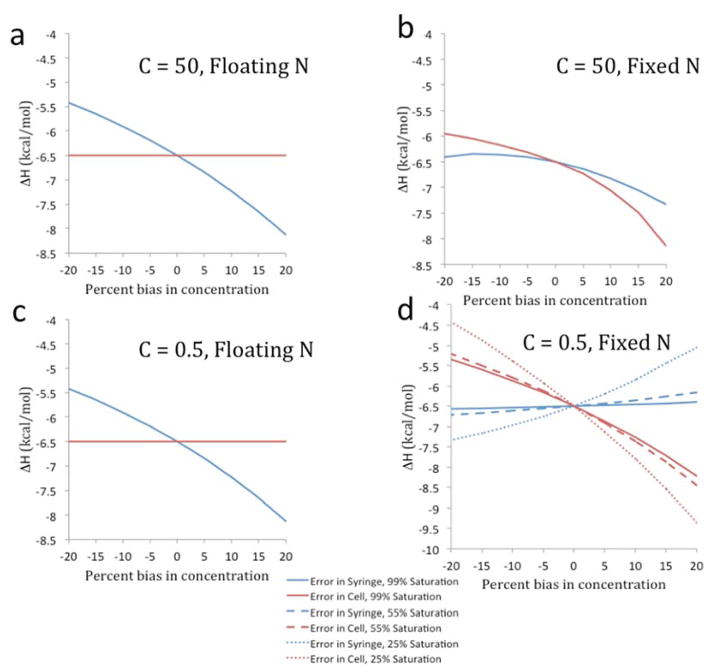
Finally, Figure 5 examines how errors in the syringe and cell concentrations map to errors in the enthalpy, under conditions of optimal and low C; with N fixed or floating; and, for the low C case, experiments run to 99%, 55% and 25% saturation of the cell reactant. Several interesting points emerge from this analysis. First, as well recognized, when N is allowed to float (Figure 5a,c), the enthalpy remains independent of cell concentration error and varies nearly in proportion to syringe concentration error, for both optimal and low C values. For experiments at optimal C values, fixing N (Figure 5b) increases the sensitivity of the enthalpy to the cell concentration error, while reducing its sensitivity to the syringe concentration. In addition, both dependencies have more curvature. Finally, for low C value experiments with fixed N (Figure 5d), the sensitivity of the enthalpy to both the syringe and cell concentration errors depends on saturation, with decreasing saturation leading to increased sensitivity. In particular, whereas it was previously shown that the enthalpy can be virtually insensitive to syringe concentration at low C values and with N fixed³⁴, the present extended analysis shows that this holds only at high saturation, and that the sensitivity of the enthalpy to both the syringe and the cell concentration becomes more problematic for experiments run to lower saturation: the sensitivity increases slightly for a maximum saturation of 55% and increases markedly at 25% saturation.

Figure 5.

Plots of fitted enthalpy with either cell or syringe concentration error applied to either Wiseman plots with C value of 50 (with N floating in a, or N fixed in b) or 0.5 (with N floating in c, or N fixed in d). For C values of 50, 99% saturation was used only. For C values of 0.5, multiple saturations (25% dotted line, 55% dashed line, 99% solid line) were used. These are only evident in panel d; all saturations gave identical results in panel c (floating N).

3.3 Propagation of Combined Heat Error and Concentration Error

The prior sections examine the character and propagation of heat noise and concentration error separately. Here we use Monte Carlo sampling of heat and concentration error simultaneously to examine when or whether it is advantageous to use fewer versus more injections, and when or whether N should be allowed to float versus being treated as fixed.

3.3.1 Number of injections

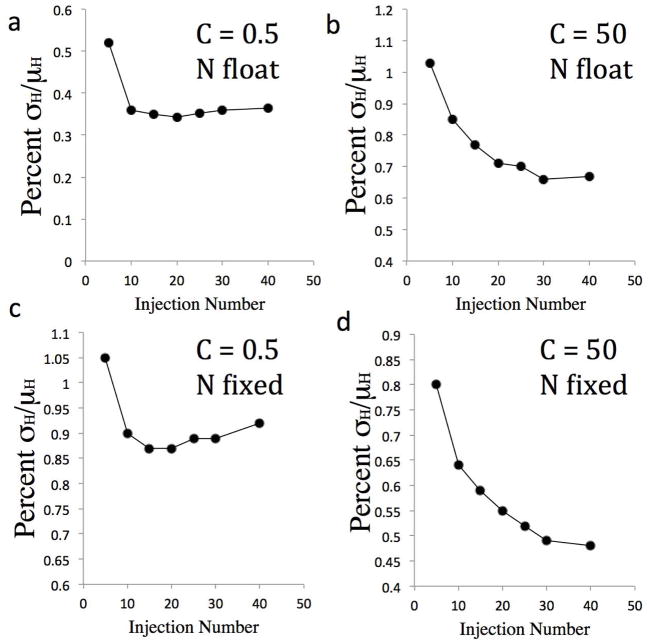
It has been suggested that using fewer injections reduces the propagation of heat error to the thermodynamic data^23,26. However, the prior study was based on a different model of heat error and used an artificially large fixed component of the heat error. We therefore investigated how the number of injections affects the uncertainty σ_H when the present empirical heat error model is applied, by realistically modeling experiments that spread the same amount of injected cyclodextrin across from 5 to 40 injections, with other experimental parameters held constant. Monte Carlo sampling was used to generate artificial Wiseman plots with 1% proportional heat error (ζ= 0.01 ), 0.13 μcal baseline error (σ_irr), and 0.6% concentration error, and LS curve-fitting was used to obtain the corresponding values of the binding enthalpy. Results were obtained with both optimal (C=50) and low (C=0.5) values of the C parameter, and the results were analyzed with N allowed to float and N fixed at its nominal value of 1. For all data points, the total heat release was kept constant.

Under all conditions examined, the uncertainty in ΔH is found to decrease when more injections are used (Figure 6). The trend is strong in the case of low C when N is allowed to float (Figure 6a), as the percent error in the binding enthalpy falls from 35% to 10% as the number of injections is increased from 5 to 40. The same trend is present but weaker for the other cases, with uncertainties improving by several tenths percent on going from 5 to 40 injections. A corresponding analysis for ΔG (Supplementary Figure 3) reveals trends similar to those for ΔH when C is optimal (C = 50), but shows that, when N is fixed at low C values, the error in ΔG is insensitive to injection number. Overall, the combination of these two analyses indicates that increasing the number of injections is likely to improve uncertainty in both ΔG and ΔH.

Figure 6.

Uncertainty of fitted enthalpy as a function of number of injections in model experiments. The ordinates report standard deviations of ΔH relative to the magnitude of the nominal enthalpy across LS fits to 2,000 Monte Carlo sampled Wiseman plots for nominal ΔH = −6.5 kcal/mol, K=36,000, N=1. Note that total heat released in each modeled experiment was kept constant, by running all model experiments to 99% saturation of the cell reactant. Left panels: C=0.5; right panels: C=50. Top panels: LS fits done with N allowed to float; bottom panels: LS fits done with N fixed at 1. In all cases, the heat error from Eq 1 was modeled with ζ=0.01, σ_irr=0.13 μcal, and 0.6% concentration error in both syringe and cell.

3.3.2 Floating versus fixing the stoichiometry, N

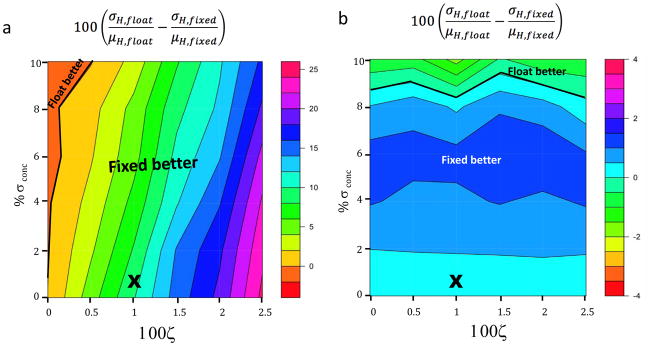
The analyses above show that fixing N can reduce the propagation of heat error and syringe concentration error to the binding enthalpy, relative to letting N float, but can, on the other hand, increase the propagation of cell concentration error. As a consequence, it is not immediately clear whether or when it is best to let N float, as is commonly done, or instead to treat N as fixed, and it would be useful to understand how fixing N affects the uncertainties in fitted parameters that arise due to both heat error and concentration error. Thus, we studied this choice by using Monte Carlo sampling to evaluate the uncertainty in the enthalpy when N is allowed to float, σ_H,float, and when N is fixed at 1, σ_{H, fixed}, for multiple combinations of heat and concentration error, where both the syringe and cell reactants were assumed to have the same concentration error. The percentage change in uncertainty, $100\left(\frac{{\sigma }_{H,\mathit{float}}}{{\mu }_{H,\mathit{float}}}-\frac{{\sigma }_{H,\mathit{fixed}}}{{\mu }_{H,\mathit{fixed}}}\right)$, is negative under conditions where floating N yields a more precise value of ΔH than fixing N, and vice versa. This quantity is mapped as a function of ζ(T) and percent concentration error, for low and optimal C values (Figure 7a,b). The contour at which σ_{H, float} − σ_{H, fixed} = 0 divides two regions of the map: one where it is better to let N float, the other where it is better to fix N=1.

Figure 7.

Contour plots depicting the difference between the percent uncertainties in the fitted enthalpy when N is allowed to float versus being held fixed at 1; i.e., $100\left(\frac{{\sigma }_{H,\mathit{float}}}{{\mu }_{H,\mathit{float}}}-\frac{{\sigma }_{H,\mathit{fixed}}}{{\mu }_{H,\mathit{fixed}}}\right)$. Percent heat uncertainty (ζ(T)) is shown along the x-axis, concentration uncertainty is shown along the y-axis. In all cases, the modeled experiments were run to 99% saturation of the cell reactant. a) C value = 0.5; b) C value = 50. Heavy black lines indicate the boundary between the region where fixing N is preferred and that where floating N is preferred. “X” indicates typical experimental conditions, based on the present study. For both experiments, we assumed σ_irr = 13ζ μcal.

The contour maps show that it is preferable, under most of the conditions plotted here, to fix N at its nominal value of 1 rather than to let it float. At low C (Figure 7a), floating N reduces the uncertainty in the enthalpy only under conditions of unrealistically low heat error; while at high C (Figure 7b), floating N is advantageous only when the concentration errors are greater than ~9%, no matter what the heat error is. Fixing N is clearly advantageous under the typical error conditions found empirically in this study (1% proportional heat error and 0.6% concentration error), which are marked by “x”s in the graphs. For completeness, analogous results for low C experiments run to 55% saturation, rather than 99%, are provided in Supplementary Figure 6. The region in which floating N is preferred becomes larger in this case, but fixing N is still, in general, preferred.

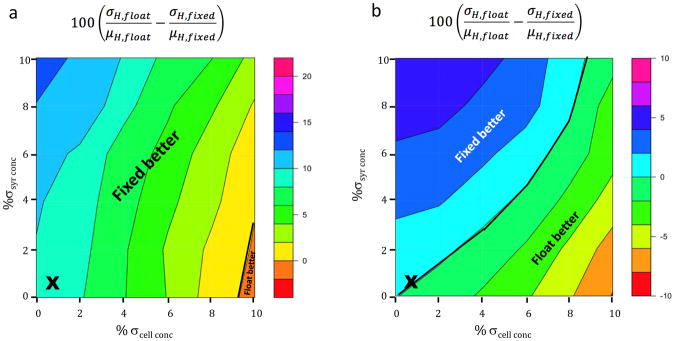
Because allowing N to float reduces the propagation of cell concentration error while amplifying the propagation of syringe concentration error, it is also of interest to examine the differential effects of these two errors in the context of typical heat noise. Figure 8 therefore plots $100\left(\frac{{\sigma }_{H,\mathit{float}}}{{\mu }_{H,\mathit{float}}}-\frac{{\sigma }_{H,\mathit{fixed}}}{{\mu }_{H,\mathit{fixed}}}\right)$ as a function of syringe and cell concentration errors, with ζ=0.01 and σ_irr = 0.13 μcal in all cases. At low C (Figure 8a, note larger scale), fixing N yields lower errors in the enthalpy, except where syringe error is less than ~4% and cell error is greater than ~9%. At optimal C (Figure 8b), the region where fixing N yields lower error is only slightly larger than that where floating N is preferred; here, to a good approximation, floating N is preferred when the cell error is clearly larger than syringe error, and fixing N is preferred otherwise. Increasing the heat noise to ζ=0.03 and σ_irr = 0.39 μcal, to model measurements at 65 C°, produces a modest shift of the contours to favor the use of fixed N (Supplementary Figure 7) in optimal C value plots, while making fixing N favorable everywhere in low C value plots, consistent with the observation (above) that fixing N reduces the propagation of heat noise to the enthalpy. Again, for completeness, the analogous plot for C=0.5 and 55% saturation (Supplementary Figure 8) is similar, except that floating N yields lower error in a larger region, where error in syringe concentration is less than 9% and error in cell concentration is greater than 7%. However, again, under normal operating conditions, indicated by the “x”s, treating N as fixed consistently yields lower errors than allowing it to float.

Figure 8.

Same as prior figure except that ζ=0.01 and σ_irr=0.13 μcal everywhere and the syringe and cell concentration uncertainties are varied independently.

3.4 Uncertainty Estimates for Realistic Experimental Scenarios

This section applies the MC sampling method, with realistic heat and concentration errors, to compute uncertainties in both binding enthalpy and binding free energy for experimental scenarios spanning optimal and low C values, high and low final saturation of the cell reactant, low and high heat noise, low and high concentration uncertainties, and treatment of N as fixed or floating. In all cases, the experiments modeled use 25 injections. Table 2 provides uncertainties in the enthalpy for modeled experiments in which the uncertainties of the syringe and cell reactants are the same, while Table 3 provides enthalpy results in which these uncertainties are mixed, and Tables 4 and 5 present corresponding uncertainties in the binding free energy. The MC statistics reported are the uncertainty in the fitted value of ΔH or ΔG, the average LS error assigned to ΔH or ΔG across the MC samples, and the standard deviation of N across the MC samples, for cases where it was allowed to float. In all cases, the mean values of ΔH and ΔG deviated minimally from their nominal values (−6.5 kcal/mol and −6.2 kcal/mol, respectively), and the mean value of N, when allowed to float, remained essentially equal to 1, so these quantities are not listed. The key figure of merit in both tables is the error in ΔH (Tables 2,3) and ΔG (Tables 4,5) from MC, as this is the expected uncertainty in the experimental result; the lower this value, the greater the precision of the experiment.

Table 4.

Uncertainties of fitted binding free energies for various experimental conditions and assumptions regarding heat and concentration error, where syringe and concentration uncertainties are assumed to be the same. For ζ = 0.01, σ_irr = 0.13 μcal; for ζ = 0.03, σ_irr = 0.39 μcal. See text for details.

		Concentration Error				MC Statistics
		Heat Err, ζ	Syr	Cell	N Float/Fixed	ΔG MC Error %	Mean LS ΔG Error %	%SD of N
		Optimal C=50
High Sat. (99%)	Low Conc. Error	1%	0.6%	0.6%	Fixed	0.2	0.3
		1%	0.6%	0.6%	Float	0.2	0.2	0.8
		3%	0.6%	0.6%	Fixed	0.6	0.7
		3%	0.6%	0.6%	Float	0.6	0.6	1
	High Conc. Error	1%	1.1%	1.1%	Fixed	0.4	0.4
		1%	1.1%	1.1%	Float	0.3	0.3	1.5
		3%	1.1%	1.1%	Fixed	0.7	0.8
		3%	1.1%	1.1%	Float	0.7	0.7	1.6
		Low C=0.5
High Sat. (99%)	Low Conc. Error	1%	0.6%	0.6%	Fixed	0.2	0.08
		1%	0.6%	0.6%	Float	0.3	0.1	9.6
		3%	0.6%	0.6%	Fixed	0.5	0.1
		3%	0.6%	0.6%	Float	1.0	0.6	26.1
	High Conc. Error	1%	1.1%	1.1%	Fixed	0.2	0.08
		1%	1.1%	1.1%	Float	0.3	0.1	9.6
		3%	1.1%	1.1%	Fixed	0.5	0.1
		3%	1.1%	1.1%	Float	1.0	0.6	26.2
Low Sat. (55%)	Low Conc. Error	1%	0.6%	0.6%	Fixed	0.3	0.3
		1%	0.6%	0.6%	Float	1.3	1.1	18.2
		3%	0.6%	0.6%	Fixed	1.0	1.0
		3%	0.6%	0.6%	Float	4.3	4.3	34.1
	High Conc. Error	1%	1.1%	1.1%	Fixed	0.3	0.3
		1%	1.1%	1.1%	Float	1.4	1.1	18.3
		3%	1.1%	1.1%	Fixed	1.0	1.0
		3%	1.1%	1.1%	Float	4.3	4.3	34.1

Table 5.

Same as prior table, but with mixed combinations of syringe and cell concentration uncertainties.

	Concentration Error				MC Statistics
	Heat err, ζ	Syr	Cell	N Float/Fixed	ΔG MC Error %	Mean LS ΔG Error %	%SD of N
	Optimal C=50
High Sat. (99%)	1%	0.6%	1.1%	Fixed	0.3	0.4
	1%	0.6%	1.1%	Float	0.2	0.2	1.3
	3%	0.6%	1.1%	Fixed	0.6	0.8
	3%	0.6%	1.1%	Float	0.6	0.6	1.4
	1%	1.1%	0.6%	Fixed	0.3	0.4
	1%	1.1%	0.6%	Float	0.2	0.3	1.4
	3%	1.1%	0.6%	Fixed	0.6	0.6
	3%	1.1%	0.6%	Float	0.7	0.6	1.4
	Low C=0.5
High Sat. (99%)	1%	0.6%	1.1%	Fixed	0.2	0.08
	1%	0.6%	1.1%	Float	0.3	0.2	9.6
	3%	0.6%	1.1%	Fixed	0.5	0.2
	3%	0.6%	1.1%	Float	1.0	0.7	26.2
	1%	1.1%	0.6%	Fixed	0.2	0.07
	1%	1.1%	0.6%	Float	0.3	0.2	10.0
	3%	1.1%	0.6%	Fixed	0.5	0.2
	3%	1.1%	0.6%	Float	1.0	0.7	28.8
Low Sat. (55%)	1%	0.6%	1.1%	Fixed	0.4	0.4
	1%	0.6%	1.1%	Float	1.3	1.3	18.0
	3%	0.6%	1.1%	Fixed	1.2	1.2
	3%	0.6%	1.1%	Float	4.4	4.3	34.5
	1%	1.1%	0.6%	Fixed	0.4	0.4
	1%	1.1%	0.6%	Float	1.4	1.3	17.8
	3%	1.1%	0.6%	Fixed	1.2	1.1
	3%	1.1%	0.6%	Float	4.3	4.2	34.3

A central result is that experimental error in ΔH is consistently less when N is fixed than when N is allowed to float. The sole exception is the case of high saturation with higher uncertainty in the cell concentration than in the syringe concentration (first two rows of Table 3), and even here floating N improves the uncertainty only from 0.8% to 0.7%. By contrast, there are cases where fixing N improves the uncertainty more than tenfold, relative to floating N. Using Tables 2 and 3, the average ratio of uncertainties from fixing N to uncertainties from floating N is 0.30, indicating the overall improvement of ΔH offered by fixing N. The benefit of fixing N is greatest for the low C experiments. In fact, with N fixed, even a low C experiment with the high 3% heat error associated with measurements at 65 °C (above), can provide results with uncertainties of only ~2%. A notable observation is that the sub-optimal 55% saturation low C value plots are more sensitive to heat error than 99% saturation low C value plots (Tables 2, 3). This may be due to the smaller raw heats in the 55% saturation plots than the 99% saturation plots. However, even here, fixing N can yield reasonable uncertainties, even in 3% heat error scenarios. This observation extends the prior observation³⁴ that useful precision can be obtained from experiments with low C values. Indeed, it appears that the successes reported there derived less from running the experiments to high saturation, as suggested, and more from the additional step taken in the prior study of fixing N. It is worth mentioning that some experimental uncertainties are below 1%, chiefly in cases where C is optimal. Finally, it is of interest that, when heat and concentration error are combined, as done here, floating N tends to increase the LS error, whereas it was found to reduce the LS error in all cases, when only concentration error was considered (Table 1). More generally, the LS error tends to underestimate uncertainty in ΔH, relative to the more reliable MC error: from Tables 2 and 3, the average ratio of MC error to LS error is 1.7, with minimum of 0.8 and maximum of 3.9.

We also report uncertainties in ΔG for the same combinations of error (Tables 4 and 5). Comparison of Tables 4 and 5 with Tables 2 and 3 shows that the errors in the free energy are smaller than those in the enthalpy, as anticipated. Thus, the ratio of the MC error for ΔH to that for ΔG has a minimum of 1.6, maximum of 36, and mean of 11. We also observe that fixing N is usually advantageous for ΔG, as in the case of ΔH, though not by as much. Thus, for ΔH, the mean ratio of MC error for N fixed versus N float averages 0.30, with minimum and maximum of 0.05 and 1.1, respectively, while for ΔG, the corresponding ratios are 0.7, 0.2 and 1.5. Note that, for both quantities, there are a few instances where fixing N increases uncertainty somewhat, but this weak effect is outweighed by other cases where fixing N is strongly advantageous. The LS error produces similar underestimates of uncertainty for ΔG as for ΔH: the average ratio of MC error to LS error is 1.7, with minimum 0.6 and maximum 1.6. This seems to be dependent on the degree of saturation and the C value used.

4. Discussion

The present study empirically characterizes two key sources of variance in ITC measurements of binding thermodynamics -- the variance in the heat release of each injection, and the variance in the concentration of the syringe solution -- and uses Monte Carlo analysis to determine how these uncertainties propagate to the final binding enthalpies under varying different experimental conditions and with different treatments of the stoichiometry during curve-fitting. One general observation is that the manner in which errors in injection heat and concentration propagate to the uncertainty of the binding enthalpy depends on multiple aspects of how the experiments are run, such as the C value and the maximal saturation of the cell reactant. We have tried to explore conditions fairly broadly, and a number of useful and general observations have emerged, as discussed below. Nonetheless, there may be experimentally relevant conditions that were not examined here. So that readers may explore these on their own, and also so they may replicate the present results, we have made the software used here available at (https://github.com/GilsonLabUCSD/Isothermal-Titration-Calorimetry). It is also worth remarking that the present study addresses the precision of the results, not their accuracy; that is, it does not address systematic error. For example, if the calorimeter consistently overestimated heat release by 5%, then all measured enthalpies would be systematically too favorable, but this would not be apparent in the present analysis of variance. We did not probe here for the possibility of such problems with the calibrations of the balance, the volumetric flasks, or the calorimeter. The following subsections summarize the chief results of this study and discuss their significance.

4.1 Advantage of fixing the stoichiometry, N

In many ITC studies, N is allowed to float during the curve fitting process, in order to “absorb” cell concentration error. Indeed, with N floating, cell concentration error does not propagate to ΔH or K, only to N. However, we find that fixing N at its nominal value reduces the uncertainty in ΔH under almost all realistic conditions studied, and this improvement can be dramatic for studies at low C value. Fixing N also tends to reduce the uncertainty in ΔG, but to a lesser extent. It is worth noting that prior studies using global ITC fitting (fitting multiple Wiseman plots) also fix N at an integral number^35,36. One of the ways that fixing N improves uncertainty in ΔH is by reducing the sensitivity of the fitted Wiseman plot to heat error, σ_Q(T). For low C value experiments, where heat error is more problematic, fixing N leads to greatly improved uncertainties. In optimal C value plots, heat error does not propagate to ΔH as severely, but fixing N still leads to small improvements in the uncertainty. The only setting in which allowing N to float may be advantageous is when one knows that the uncertainty in the cell concentration is considerably greater than that of the syringe concentration. For example, if one reactant is a protein that is unstable or of uncertain purity, it may be advantageous to place this in the cell and allow N to float, or to use a global fitting method in which N is fixed and the concentration uncertainty is explicit. However, in the case of 1:1 binding, where both compounds are robust and well characterized, the uncertainties in their concentrations are normally similar and low. In this setting, fixing N=1 provides better precision than allowing N to float, and this would be our recommended standard procedure.

It has previously been reported that experiments at low C values can yield useful results if they are run to sufficient saturation of the cell reactant³⁴. Our results are largely consistent with those. However, we find that the key is not only running to full saturation, but also fixing N. In fact, with C=0.5, even if the experiments are run to a sub-optimal 55% saturation, fixing N affords uncertainties in the binding enthalpy of only a few percent, whereas the uncertainties are much higher when N is allowed to float. It is also worth noting that, although it is often written that error in the syringe concentration propagates proportionally to error in the enthalpy, this is only true when N is allowed to float: fixing N reduces the sensitivity of the enthalpy to the syringe concentration, for experiments at both low and optimal C values. On the other hand, although it has been suggested that fixing N can essentially eliminate the propagation of syringe concentration error to enthalpy error³⁴, we find that this holds only for experiments run to high saturation at low C values. At low saturation and low C, syringe concentration error does lead to enthalpy error, although less so with N fixed than when N is allowed to float; while, for high C value plots, syringe and cell error both propagate when N is fixed.

Intuitively, it is reasonable that error in the thermodynamic results should be minimized by locking the value of N to its true value (N fixed), rather than allowing it to take on a nonphysical value (N floating). Mathematically, the fact that fixing N typically reduces the uncertainty in ΔH traces to the fact that it reduces the propagation of both syringe concentration error and heat error, and these advantages typically outweigh the increased propagation of cell concentration error. The changes in sensitivity to concentration error upon fixing N trace to the fact that allowing N to float essentially allows the x-axis to be rescaled in a manner that optimizes the fit of the theoretical to the experimental curve, and this can compensate for the effective rescaling along the x-axis that results from any concentration error. Cell concentration error leads to pure x-axis rescaling, and can be completely compensated by allowing N to float, while fixing N removes this compensation mechanism and leaves the fit susceptible to cell concentration error. Errors in the syringe concentration similarly rescale the x-axis, since this is the ratio of the syringe and cell concentrations, but syringe errors also lead to rescaling along the y-axis, as they generate error in the renormalization of the raw heats to molar heats. When N is fixed the effects of these two rescalings on the fitted enthalpy tend to cancel each other, leading to reduced error in the final result. In contrast, when is allowed to float, the x-axes rescaling is corrected by N, leaving the effect of the syringe error on the y-axis uncompensated.

As noted above, the uncertainties in ΔG tend in general to be smaller than the uncertainties in ΔH, but fixing N can still lead to some improvement. The patterns of error appear to be somewhat different from what is observed in ΔH, however, and may warrant additional investigation. For example, there may be cases where fixing N gives the most accurate ΔH, but floating N gives the most accurate ΔG.

4.2 Choosing the number of injections

We find that increasing the number of ITC injections tends to reduce the uncertainty in the binding enthalpy and, to a lesser extent, in the binding free energy. The improvement is marked when C is low and N is allowed to float, and modest when C is normal and/or N is treated as fixed. These results differ from prior results showing lower uncertainties in the case of fewer injections²². The difference presumably stems from differences in the experiments modeled and in the assumed magnitude of the heat noise. In particular, the prior study used parameters based on an early-model microcalorimeter³; in addition, the author noted that an “artificially large” error was assumed. In contrast, we used the succinic acid/NaOH measurements to develop an empirical error model for the MicroCal VP-ITC, and then used it to model error in typical experiments on the same instrument. From a theoretical standpoint, it has been argued^22,45 that the relative error (noise-to-signal ratio) of each injection will rise when more injections are used, as each injection becomes smaller. However, this holds only when the fixed component of the heat noise is dominant; for the experiments modeled here, most of the heat error is proportional in character (Eq 1), so the relative error of each injection does not rise much as the number of injections is increased. Under these conditions, there is no significant penalty for dividing the experiment across more injections, and doing so may improve precision by providing a more detailed delineation of the binding isotherm. Of course, if the heat is divided so much that the proportional part of the error falls below the irreducible part of the error, then every peak will have a similar fixed error, likely leading to the same conclusions observed previously.

Thus, it would appear optimal to maximize the number of injections, subject to the constraint that the smaller injections still yield heats for which the proportional error is greater than or equal to the irreducible error. That said, experiments with good C values and/or low C values and fixed N can yield excellent results with only a few (e.g., 10–15) injections. In such cases, the modest increase in uncertainty from reducing the number of injections may well be acceptable. Finally, it should be noted that, for a different calorimeter, the fixed heat error might dominate over the proportional error, in which case, fewer injections might indeed be preferable.

4.3 Variance in injection heat

Using the succinic acid experiment described in the Results, we found that the heat error may be described as a combination of a term proportional to the amount of heat released per injection, and a small irreducible error (Eq 1), and that there is low correlation across injections during an experiment. The constant of proportionality, ζ(T), is about 0.01 at room temperature and rises to 0.03 at 65 °C; and the irreducible error σ_irr, similarly rises threefold over this temperature range, from 0.13 to 0.39 μcal/injection. We are not aware of any prior report that the heat uncertainty depends upon the temperature. It should be emphasized that these results are specific to the VP-ITC instrument we studied, and different results could be obtained for different calorimeters. Indeed, a prior study of this type for the iTC200 instrument does not show a clear pattern of proportional error⁴², although the scatter in the data points makes this difficult to pin down. Fortunately, the succinic acid experiment is straightforward and the materials are inexpensive, so it may easily be used to characterize the heat error for whatever instrument one is using.

Our observation that the uncertainty in the injection heat is mainly proportional to the heat evolved, and is not dependent on injection volume, runs counter to models that the heat error is independent of the injection heat^33,37; or that, that, for the VP-ITC, the heat error comprises a large, constant heat-measurement error plus a constant volume-delivery error²². Although the latter model is based on uncertainties reported by Wiseman and coworkers³, Wiseman and coworkers did not describe how the heat uncertainty depended on the heat of injection or the volume, so it is not clear whether their uncertainties conformed to this particular model. In addition, their study was apparently carried out on a pioneering early calorimeter, rather than the commercial VP-ITC unit, and it is probable that the two instruments have quite different patterns of error.

Importantly, we observe much larger values of the heat noise, for typical injections, than the value of 0.1 μcal previously suggested as a simple constant model. For example, a 1% error on a 200 μcal heat of injection will result in a roughly 2 μcal error. It is also worth mentioning that, although a prior error model for the heat error also include both a proportional part and an irreducible part³⁴, instead of adding the variances in order to model two independent noise processes, they set the irreducible standard deviation as a floor to a proportional component with a temperature-independent coefficient:

$${\sigma }_Q\approx max\left(\zeta Q,{\sigma }_{\mathit{irr}}\right)$$ (2)

Estimating overall error by adding the variances³⁸, as done here (Eq (1), would seem to be on a more solid statistical footing and also gives a somewhat more conservative (i.e., larger) estimate of the uncertainty. However, the small magnitude of the irreducible error makes this distinction relatively unimportant. Finally, the data in Figure 2c would argue against a prior model in which the non-fixed component of the heat error was assumed to result from variance in the injection volumes¹¹, as reducing concentration while keeping injection volumes constant shows the same proportional trend.

A minor note of interest is the possible correlation between successive injection heats seen in our results. Although the R² is small and variable across datasets, there still seems to be some positive correlation. This could arise from baseline drift, where the baseline steadily moves in a particular direction, so that adjacent peaks have similar biases. This might be correctable by using software that more rigorously analyzes baselines^24,46. Regardless, the effect seems small and unlikely to significantly influence the uncertainty in the thermodynamic results.

4.4 Concentration errors

It has been suggested that the high variance in binding enthalpies in the ABRF-MIRG’02 study result largely from variance in the concentration of the syringe reactant, 4-carboxybenzenesulfonamide (CBS)³². This attribution is based on the fact that the participants’ data measured apparent extinction coefficients of CBS ranging over at least 1100–1400 L/mol/cm, a range of about 25%. The participants had been provided with powdered CBS, and thus made up their own solutions. Nonetheless, we would not have expected that this procedure would yield such large errors, so we ran a simple empirical test, using β-CD as the solute, and found concentration uncertainties on the order of 1%, which is more consistent with the nominal precision of a typical balance and flask. Given that CBS was shown to be stable³², it is not clear how 20-fold larger concentration errors could have arisen in the prior study, even if some participants were new to ITC, and we would be cautious about assuming that such high concentration errors are typical, particularly as there was no direct verification of their existence.

4.5 Experimental uncertainties in binding thermodynamics measured by ITC

It has been noted previously that the LS method of estimating uncertainties does not account for concentration error²⁶. However, we find that, with N fixed, the LS uncertainty can to some degree capture the consequences of concentration error. Similarly, LS uncertainty can mostly capture uncertainty due to heat error, often modestly underestimating the actual uncertainty. Indeed, comparison with the more rigorous error estimates provided by the MC method indicates that the LS uncertainty provided by commonly used software packages can underestimate the actual uncertainty in both the binding enthalpy and the binding free energy in certain circumstances. Thus, the decision to trust LS derived uncertainties may depend in part on the situation; i.e., whether N is allowed to float, or what the C value of the Wiseman plots in question is.

An additional observation is that low C value Wiseman plots run to a sub-optimal 55% saturation are much more sensitive to heat error than plots run to 99% saturation, as evidenced in Tables 2 and 3. This may be the result of these Wiseman plots being more dominated by irreducible error (due to the raw injection heats being smaller). Notably, fixing N is sufficient to bring even the highly error prone 3% heat error cases down to more reasonable uncertainties of about 6%, suggesting that, even under high heat error scenarios, low saturation plots can give fairly good estimates of binding enthalpy when N is fixed. These plots show much less severe uncertainties in fitted ΔG, as evidenced in Tables 4 and 5, even at 3% heat error when N is allowed to float.

Under some realistic experimental conditions and error assumptions, we observe small systematic errors in the reported values of the binding enthalpy, for reasons that are unclear. However, this bias arises only when N is allowed to float; and, when observed, the bias only exceeds 5% at around 3% heat error, and, in this regime, the uncertainty in the binding enthalpy is several times larger than the bias and for most purposes effectively drowns it out.

The present study suggests that, with a MicroCal VP in good working condition, for optimal C value experiments at room temperature, where solutions are made up in larger volumetric flasks, it is reasonable to expect uncertainties of 0.5% in the binding enthalpy and 0.2% in the binding free energy. If one is forced to work with smaller volumetrics, due, for example, to limited compound availability, the uncertainties in enthalpy and free energy may rise to on the order of 1–2% and 0.4–0.7%, respectively. At lower C values, which may be difficult to avoid in the case of weak binding and/or low solubility, one may still anticipate keeping uncertainties in enthalpy below about 2%, rising to about 4% for measurements at 65 °C. The corresponding values for free energies are 0.2% and 0.5% Note that these values depend on keeping N fixed; floating N allows the uncertainties for the same experiments to approach 50% in the most challenging cases considered here. Thus, so long as N is held fixed during curve-fitting, it should be possible to obtain quite precise thermodynamic data on a wide range of binding systems at various temperatures.

5. Conclusions

In summary, the present study yields several broad conclusions regarding the design and interpretation of isothermal titration microcalorimetry experiments.

• For the instrument studied here, the standard deviation of the heat of injection is approximately proportional to the integrated heat of the injection, with proportionality coefficients of 1% at room temperature and 3% at 65 °C. The proportional error is accompanied by a small irreducible uncertainty of about 0.13μ cal at room temperature and 0.39μ cal at 65 °C.

• Experimental evaluation of concentrations of solutions made in our laboratory indicate a 0.6–1.1% uncertainty, depending on the volume of solution made up.

• Fixing N alleviates the propagation of heat error to the binding enthalpy, especially for low C value Wiseman plots.

• Concentration errors propagate depending on how N is treated: floating N allows a near-linear propagation of syringe error to fitted enthalpies of binding; fixing N introduces sensitivity to cell error while simultaneously decreasing sensitivity to syringe error. When one fixes N in fitting low C value experiments, the sensitivity of the enthalpy to the syringe concentration error depends strongly on the degree of saturation to which the experiment is run.

• Under a wide range of experimental conditions and designs, fixing N at its nominal value yields less uncertainty in the binding enthalpy and free energy than does allowing N to float. This is particularly true for low C value experiments. Of the conditions examined here, floating N is preferable only when the concentration uncertainty of the cell reactant is high, and particularly when the experiment is done at a high C value.

• Experimental uncertainties are typically considerably lower for binding free energies than for binding enthalpies.

• Error estimates from least squares fitting tend to somewhat underestimate the more realistic error estimates obtained by Monte Carlo analysis, particularly in the case of high saturation binding enthalpies. In the case of binding free energies, least squares fitting tends to underestimate errors in low C value, high saturation cases, but not in high C value and low C value, low saturation cases.

• Given stable and well-characterized reagents, and with N treated as fixed, it is realistic to expect uncertainties in binding enthalpies within about 2% for ITC measurements under a wide range of experimental conditions, with lower uncertainties for the corresponding binding free energies

• The present study does not address all conditions that may arise in practice, and the software used in the present study may be utilized to explore other experimental setups of interest.

Highlights.

• The uncertainty in injection heat for a VP-ITC microcalorimeter is roughly proportional to heat release

• Over a wide range of experimental conditions, fixing the stoichiometry, N, reduces uncertainty in calorimetry results, relative to letting N float

• Reducing the number of titration steps tends to degrade the precision of ITC results

• Binding thermodynamics can often be precisely fit from low C value plots, given that N is held fixed

Abbreviations

ITC

isothermal titration calorimetry

LS

least squares

MC

Monte Carlo