Aspects of Weak Interactions between Folate and Glycine Betaine

Abstract

Folate, or vitamin B₉, is an important compound in one-carbon metabolism. Previous studies have found weaker binding of dihydrofolate to dihydrofolate reductase in the presence of osmolytes. In other words, osmolytes are more difficult to remove from the dihydrofolate solvation shell than water; this shifts the equilibrium toward the free ligand and protein species. This study uses vapor-pressure osmometry to explore the interaction of folate with the model osmolyte, glycine betaine. This method yields a preferential interaction potential (μ₂₃/RT value). This value is concentration-dependent as folate dimerizes. The μ₂₃/RT value also tracks the deprotonation of folate’s N3–O4 keto–enol group, yielding a pK_a of 8.1. To determine which folate atoms interact most strongly with betaine, the interaction of heterocyclic aromatic compounds (as well as other small molecules) with betaine was monitored. Using an accessible surface area approach coupled with osmometry measurements, deconvolution of the μ₂₃/RT values into α values for atom types was achieved. This allows prediction of μ₂₃/RT values for larger molecules such as folate. Molecular dynamics simulations of folate show a variety of structures from extended to L-shaped. These conformers possess μ₂₃/RT values from −0.18 to 0.09 m^–1, where a negative value indicates a preference for solvation by betaine and a positive value indicates a preference for water. This range of values is consistent with values observed in osmometry and solubility experiments. As the average predicted folate μ₂₃/RT value is near zero, this indicates folate interacts almost equally well with betaine and water. Specifically, the glutamate tail prefers to interact with water, while the aromatic rings prefer betaine. In general, the more protonated species in our small molecule survey interact better with betaine as they provide a source of hydrogens (betaine is not a hydrogen bond donor). Upon deprotonation of the small molecule, the preference swings toward water interaction because of its hydrogen bond donating capacities.

How do two molecules come together and form a complex? Two steps are typically involved, desolvation and association. While forces that drive association are reasonably well understood, the role water plays is difficult to predict. For example, water can fill voids in structures and also provide a bridge between surfaces.¹⁻⁵ While high concentrations of water are present in test tube studies, the situation becomes more complicated in the cell because of the presence of many other molecules. If other solutes, for example, osmolytes, interact with ligands and/or proteins, they need to be removed to form the protein–ligand complex. While these solute–ligand interactions are weak, the relative strength of the ligand–osmolyte interaction versus that of the ligand–water interaction can affect binding to the protein partner. Binding will be either facilitated or made more difficult, resulting in altered K_d values between macromolecules and their ligands.

In most cases, the binding constant becomes tighter in the presence of osmolytes as the desolvation penalty is minimized.⁶⁻¹² An example of this is binding of the cofactor NADPH to R67 dihydrofolate reductase (DHFR).¹³ Similar results of tighter cofactor binding were also seen with Escherichia coli chromosomal DHFR.¹⁴ However, if osmolytes prefer to interact with the ligand or protein, and if removing them is more difficult than shedding water, then the binding constant is weakened. This case is exemplified by binding of dihydrofolate to various DHFRs.¹³⁻¹⁶ In this model, shown in Figure 1, the osmolytes shift the binding equilibrium toward the free species (substrate and DHFR) compared to the protein–ligand complex. One osmolyte that weakens binding of DHF to R67 DHFR by 3.6-fold is glycine betaine [20% (w/v)]. Note that DHFR catalyzes reduction of dihydrofolate (DHF) to tetrahydrofolate (THF) using NADPH as a cofactor. There are two types of DHFRs. Type I is encoded by the chromosome, and type II is carried by a resistance plasmid; an example is R67 DHFR. Neither the structures nor mechanisms are homologous in these DHFRs.¹⁷ Additionally, as DHFR is an important drug target, understanding how folate-mimic compounds interact with osmolytes, such as betaine, may be informative in drug design efforts. Here we use vapor-pressure osmometry to improve our understanding of our binding results.

Figure 1.

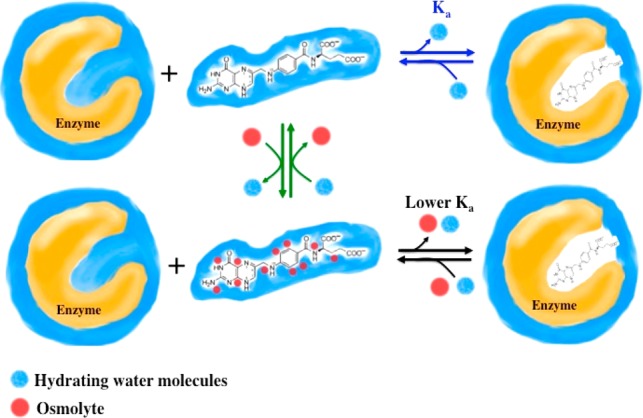
Cartoon depicting preferential interaction of osmolytes with free DHF. In the absence of osmolytes, DHF binds tightly to its target enzyme and water (blue) is released. Added osmolytes (red spheres) interact weakly with DHF. For DHF to bind to the enzyme, both osmolytes and water must be released. Osmolytes that interact more strongly than water would have larger effects on the DHF K_a, while the more weakly bound osmolytes would have smaller effects. (Note that this model does not exclude the possible binding of osmolytes to the enzyme.) We have used high hydrostatic pressure as an orthogonal technique to examine the top row of the model (blue equilibrium arrows).⁷⁶ We have also used nuclear magnetic resonance to observe interactions between folate and osmolytes (middle column, green equilibrium arrows).¹⁵ Both sets of results are consistent with this model.

Glycine betaine or N,N,N-trimethyl glycine is proposed to be one of the most effective osmoprotectants in E. coli cells as it is efficient in maintaining growth under osmotic stress.¹⁸ Betaine is unable to act as a hydrogen bond donor; thus, it is strongly excluded from the surface of proteins, facilitating macromolecular functions.

How does betaine interact with folate? Homonuclear (¹H) nuclear Overhauser effect spectroscopy (NOESY) experiments found NOEs between the protons on the C7 atom of folate and protons on the C9 and C3′/C5′ atoms, and between the C9 proton and the C3′/C5′ protons (see Figure S1 for the structure and atom numbering of folate).¹⁵ However, a change in sign for the NOE between the C9 and C3′/C5′ protons from positive (without betaine) to negative (with betaine) was observed. The change in the sign for the NOE suggested a slower rotational rate for the p-amino-benzoyl ring protons, indicative of an interaction between betaine and this ring.¹⁵ As folate has limited protons on its pterin ring, it is difficult to discern from our nuclear magnetic resonance (NMR) results if osmolytes interact with this moiety. Thus, we turned to alternate techniques.

Our previous osmometry studies support interactions between betaine and the folate fragments, p-aminobenzoyl-glutamate (p-ABA-Glu) and pterin-6 carboxylate.¹⁵ To extend this study, we use vapor-pressure osmometry (VPO) to measure μ₂₃/RT values, which are closely related to preferential interaction coefficients. The μ₂₃/RT value measures the change in chemical potential of a small test compound with the change in molality of the osmolyte in solution. For our study, the μ₂₃/RT value measures the preference of small molecules to interact with betaine compared to water. The Record lab has pioneered this VPO approach along with a water-accessible surface area (ASA) analysis to quantify and analyze the thermodynamics of interaction of osmolytes (betaine, proline, PEG, and urea) with model compounds displaying biomolecular functional groups.¹⁹⁻²² The VPO method measures the preference of a small molecule interacting with an osmolyte as compared to water in a three-component system [(1) water, (2) test compound, and (3) osmolyte]. Capp et al. studied the interaction of betaine with a set of model compounds containing carboxylate, phosphate, amide, hydroxyl, ammonium, guanidinium, and aliphatic and aromatic hydrocarbon moieties.¹⁹ Positive μ₂₃/RT values for phosphate (0.85 ± 0.04 m^–1) and citrate (1.2 ± 0.1 m^–1) indicate a strong preference for water over betaine, whereas negative μ₂₃/RT values for benzoate (−0.091 ± 0.007 m^–1) and urea (−0.093 ± 0.005 m^–1) indicate a preference for betaine over water.

The preferential interaction potentials, or μ₂₃/RT values, obtained for those compounds were dissected into additive contributions from chemically distinct functional groups. The calculated set of atomistic preferential interaction potentials per unit of water-accessible surface area (ASA) of each surface type, also called α values, can be coupled with the ASA information to predict the μ₂₃/RT of any compound.

Because of the instability of 7,8-dihydrofolate, we use folate in the VPO studies presented here. Folate binds to the same site as DHF on chromosomal DHFR, and likewise, folate and DHF share the same binding site on R67 DHFR. Additionally, folate can be reduced by DHFR enzymes, albeit with a much reduced catalytic rate compared to that of DHF.²³⁻²⁵ We take this approach to understand how folate interacts with betaine as well as effects of betaine on the binding of folate to DHFR.

Methods

Some details are provided in the Supporting Information.

Vapor-Pressure Osmometry (VPO)

In VPO experiments, the change in osmolality of bulk water is measured in a multicomponent system containing components 1–3, which denote water, the test compound, and betaine (osmolyte), respectively. This technique monitors the change in osmolality (ΔOsm) of a solution, which is a quantitative measure of the favorable or unfavorable interaction of the two solutes (test compound and osmolyte) relative to their interactions with water.¹⁹⁻²² As the solution osmolality increases due to increasing betaine concentrations, any change in measured osmolality arises because of the interaction of betaine with the test compound. If betaine is excluded from the surface of the test compound, the betaine concentration in the bulk medium (relative to the betaine only control) is increased. This in turn decreases the bulk water concentration and increases the osmolality of the solution. If there is no preference for betaine or water to interact with the test compound, the osmolalities of betaine and the small molecule are additive. If betaine prefers to interact with the test compound, the betaine concentration in the bulk medium is decreased, which increases the bulk water concentration and decreases the solution osmolality. The difference in osmolality between the solutions with and without the test compound and the solution of the test compounds without the osmolyte, ΔOsm, when plotted versus the product of betaine and the test compound molality, m₂m₃, yields a linear plot, the slope of which is the μ₂₃/RT value

1

where m₂ and m₃ are molal concentrations of the test compound and betaine, respectively, and μ₂₃/RT is the relative chemical potential of the test compound in betaine. If μ₂₃ is independent of m₂ and m₃, it approximates the preferential interaction potential.

Experiments were performed on a Wescor Vapro 5520 osmometer. The instrument was calibrated using standard solutions of 0.100, 0.290, and 1.000 osmol. An additional linear calibration curve was made by measuring 1.000, 1.500, and 2.000 osmol standards to correct for osmolality readings above 1.000 osmol. A betaine stock solution (2 m) was prepared daily using a gravimetric method. Betaine (2 g) was weighed and dissolved to make a 10 mL stock solution in a preweighed tube. The weight of water was determined by subtracting the weight of betaine from the weight of the solution, which was then used to calculate the molal concentration of the stock. Typically, 30–500 mg of the test compound (for example, folate) was added to a preweighed microfuge tube, and stock solutions were prepared fresh daily in water. The molality of the stock solutions was determined using the weight of the solution. A series of betaine solutions were prepared, and the osmolality of each was measured in triplicate. Then, solutions containing a desired concentration of the test compound with betaine concentrations equivalent to that of the betaine only line were prepared and incubated at room temperature for 10 min. The osmolalities of the solutions were then measured in triplicate. The concentration of the test compound was constant in each experiment. Solutions were prepared such that the osmolality ranged between 0.1 and 2 Osm, which typically spanned the range of betaine concentrations from 0.1 to 1.25 m, and test compound concentrations from 0.04 to 0.5 m. The data were fit to eq 1.

We used this method to determine μ₂₃/RT values for folate at pH 7 and 10. Capp et al. suggested not adjusting the pH of the stock solutions to avoid additional components in the system.¹⁹ However, as folic acid has a low solubility, we adjusted the pH using sodium hydroxide (1 N) to form folate. To ensure that we could compensate for the addition of NaOH, we precipitated the sodium folate salt at pH 10 in acetone and isopropanol, lyophilized it, and again performed the VPO experiments. The μ₂₃/RT values were the same. Additionally, thermogravimetric analysis of folic acid indicates that ∼8% of the mass can be removed by heating to 100 °C.^26,27 This 8% mass difference has been attributed to two molecules of water. Accounting for this water mass changes our μ₂₃/RT values by 10%, which was within experimental error.

As folate dimerizes at high (nonphysiological) concentrations,²⁸ we additionally monitored the μ₂₃/RT value as a function of folate concentration. The data were fit to a dimerization function (eq 2) adapted from Duff et al.¹⁵

2

where μ₂₃/RT_obs is the observed μ₂₃/RT, μ₂₃/RT_(M) and μ₂₃/RT_(D) are the μ₂₃/RT values for the monomer and dimer, respectively, K_d is the dimerization constant, and [F]_tot is the total folate concentration.

Folate also undergoes a keto–enol tautomerization at the N3–O4 atoms and can deprotonate at the O4 position at high pH.²⁸ Thus, we studied the effect of pH on the folate μ₂₃/RT value. The data were fit to a pK_a titration (eq 3) adapted from Duff et al.¹⁵

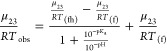3

where μ₂₃/RT_obs is the observed value while μ₂₃/RT_(fh) and μ₂₃/RT_(f) are the μ₂₃/RT values of protonated and deprotonated folate, respectively.

Interaction of Betaine with Heterocyclic Test Compounds

To examine how other small molecules containing aromatic carbons and/or nitrogens interact with betaine, we performed additional VPO studies, mostly at pH 7.0. The test compounds and their structures are listed in Table S1.

α Value Calculation by Analysis of μ₂₃/RT Values

The μ₂₃/RT values of test compounds are proposed to be additive contributions from the interaction of betaine with individual functional surface types on the test compounds. Specifically, the contribution of each type of surface to the molecule’s μ₂₃/RT value is the product of a chemical interaction potential (μ₂₃/RTASA)_i and the accessible surface area (ASA) of that surface type i. Capp et al. deconvoluted molecular μ₂₃/RT values into surface type μ₂₃/RT values (also called α values) using eq 4.¹⁹

4

where the μ₂₃/RTASA value is the α value, which is the measure of interaction of betaine with 1 Ų of surface type i on any compound, (ASA)_i is the water-accessible surface area in square angstroms of surface type i, and ν_j(μ₂₃/RT)_j is the product of the number of salt ions per salt test compound and the assigned contribution (μ₂₃/RT)_j or the β value, of that type of ion to μ₂₃/RT. The Record lab has calculated α values for many atom types using a β value for the sodium ion of zero.¹⁹

The structure files of the test compounds were obtained from either the Biological Magnetic Resonance Bank (http://www.bmrb.wisc.edu/) or the Protein Data Bank (PDB, http://www.rcsb.org) or were built in MOE (versions 2012.10 and 2015.1001, Chemical Computing Group, Montreal, QC). Table S1 lists the structures and sources of each test compound. Some of the small molecule structures were obtained from the ligand-bound protein complex structures in the PDB after deleting the protein and minimizing the ligand in MOE. The water-accessible surface area (ASA) for each atom in the molecule was then calculated using SurfaceRacer.²⁹ The van der Waals radii from Richards³⁰ were used as well as a 1.4 Å probe radius for water. Conformational sampling of nucleotides was performed using MOE to account for areas from all conformers. There was no significant difference in the average areas for all the conformations when compared to the areas from the minimized structures of each nucleotide. In a multilinear fit, all experimental μ₂₃/RT values along with the (ASA)_i information were fit to eq 4, and the α values (μ₂₃/RTASA)_i were calculated for each surface type. MATLAB (version R2016A) was used for fitting (a sample Excel sheet along with the MATLAB code is provided in the Supporting Information). Errors were calculated using eq S17 from the supplement of Knowles et al.²²

Solubility Assays

The solubilities of folate in water or in 1 M betaine were determined at pH 7 and 10 using the method of Liu and Bolen.³¹ Folate was weighed in increasing amounts in 10 preweighed plastic vials. The range of concentrations was selected so that approximately half of the solutions were unsaturated while the remaining suspensions were saturated. The concentrations ranged from 20 to 500 mM. Solutions were adjusted to the desired pH using 1 N NaOH, and the vials were weighed again. After the pH was adjusted, ≤1% of the weight of the sample was lost on the electrode. This loss of solution mass accounted for ≤1% error in the final analysis of the solubility. The vials were then capped and incubated in the dark in a shaker at 25 °C. After 24 h, the vials were centrifuged at 4000 rpm for 5 min, and the supernatant was collected. The density of each supernatant was measured using an Anton Paar DMA 35 density meter and plotted against the molality of folate. Solubilities of folate were determined from the plots of density versus molality as described by Auton and Bolen.³² The apparent free energy of transfer of folate from water to betaine was determined using eq 5.³²

5

where ΔG° is the apparent transfer free energy for folate measured on a molal scale, n_i,w and n_i,bet are the number of moles of folate that are soluble in 1000 g of water and in 1000 g of a 1 M betaine solution, respectively, and wt_w and wt_bet are the total masses of water and of a 1 M betaine solution, respectively.

An acidic pH was also used; however, folate is sparingly soluble at pH 5. Thus, only 2–100 μM folate (in water) and 2–150 μM folate (in 1 M betaine) were used in a similar fashion as described above. After incubation, centrifugation, and filtration, the concentration of folate in the supernatant was measured by the absorbance at 282 nm. The absorbance was measured upon dilution of the samples in MTA buffer (pH 7.0) (ε of folate at 282 nm and pH 7.0 of 27000 M^–1 cm^–1).³³ This concentration was plotted against the composition (weight/100 g) of folate for each sample. The solubility of folate and its apparent free energy of transfer were determined as described above.

Simulation of Folate in Water

Computer simulations of folate in water were performed using the AMBER simulation package.³⁴ For system preparation, a single folate molecule was placed in the center of a periodic box surrounded by water (SPC/E water model)³⁵ such that the boundary of the box was at least 10 Å from the edges of the folate molecule. AMBER’s parm 14SB force field was used, and the folate molecule was parameterized using the procedure outlined in the AMBER manual. The charges for folate atoms were calculated using electronic structure calculations at the restricted Hartree–Fock 6-31G** level of theory. The prepared system was slowly equilibrated as previously described.³⁶ A 200 ns production run was performed at 300 K in an NVE ensemble using 2 fs time steps. A total of 200 conformations (every 1 ns) were used for analysis. A similar procedure was used for simulating folate in water with betaine (see the Supporting Information for details).

Results

VPO Measurements of Folate at pH 7

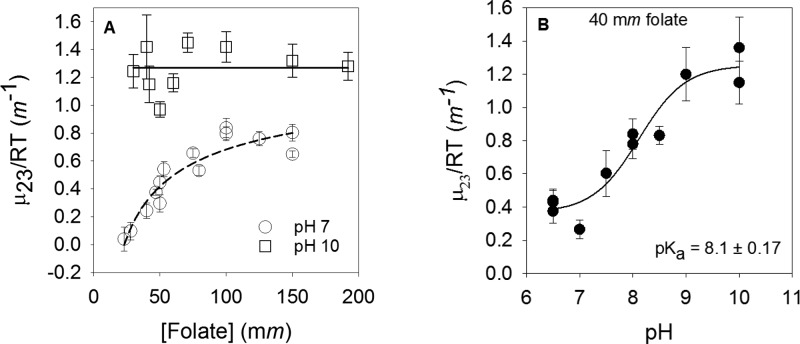
Figure 2A shows the concentration dependence of folate interaction potentials (μ₂₃/RT) with betaine measured by VPO experiments at pH 7. A value near zero indicates similar interaction preferences of folate for water and betaine. A positive value predicts an interaction preference for water, while a negative value indicates a preference for betaine. We observed an increase in the folate μ₂₃/RT values from 0.04 ± 0.09 m^–1 (at 23 mm) to 0.80 ± 0.06 m^–1 (at 150 mm). These observed μ₂₃/RT values indicate that at low concentrations, folate interacts with both water and betaine while at higher concentrations, folate favors water.

Figure 2.

Preferential interactions between folate and betaine show effects of folate concentration and pH. (A) Folate concentration dependence of μ₂₃/RT at pH 7 (○) and pH 10 (□). A fit to eq 2 describing folate dimerization (R² = 0.88) gave large errors for data at pH 7, and no concentration dependence was noted at pH 10; thus, the lines provided are to aid the eye. (B) pH dependence of μ₂₃/RT values for 40 mm folate (●). The data were fit to eq 3 with an R² of 0.93 to yield a pK_a describing deprotonation of the N3–O4 enol tautomer.

The concentration dependence in Figure 2A is consistent with previous observations of folate dimerization, which occurs in a head-to-tail fashion such that each pterin ring stacks with the p-ABA ring of the other monomer and the glutamate tails are free to rotate.²⁸ Previously, Capp et al. have found betaine interacts with aromatic carbons, amide nitrogens, and cationic nitrogens and is excluded from aliphatic carbons, hydroxyl oxygens, amide oxygens, carboxylate oxygens, and phosphate oxygens.¹⁹ Thus, the observed increase in μ₂₃/RT values at high folate concentrations is consistent with decreased accessible surface area for the aromatic ring surfaces due to ring stacking.

Unfortunately, we obtained a poor fit when the concentration-dependent data were fit to eq 2 describing dimerization. While the fit had a decent R² (0.88), it yielded an unrealistic negative value with a large error (1500%) for the lower limit. The poor fit may be due to not having a good lower limit for the μ₂₃/RT of monomeric folate (due to poor signal-to-noise levels at low folate concentration) as well as the variable effects of different folate and betaine concentrations associated with each point on the plot. As the addition of betaine alters the K_d describing folate dimerization,¹⁵ there may be additional effects contributing to the titration observed in Figure 2A. Another contributor may be the possible formation of higher oligomerization states.³⁷

VPO Measurements of Folate at pH 10

Using an NMR approach, Poe found folate dimerization is pH-dependent.²⁸ The N3–O4 atoms in the pterin ring undergo a keto–enol tautomerization as shown in Figure S1B. Deprotonation of the enol (pK_a ∼ 8) results in a negatively charged O4 atom. The dimerization constant for neutral folate is 20 mM, while the value for basic folate is 340 mM.²⁸ To potentially determine a μ₂₃/RT value for monomeric folate, we repeated the VPO study at pH 10. We measured the μ₂₃/RT values of folate at concentrations ranging from 30 to 190 mm. The average μ₂₃/RT at this pH was 1.27 ± 0.36 m^–1, which indicates strong exclusion of betaine from the anionic folate surface. No concentration dependence of μ₂₃/RT values was observed (see Figure 2A), consistent with folate being monomeric at pH 10. This observation is also consistent with our one-dimensional ¹H NMR experiments performed at pH 10 (see Figure S2 and Table S2 for details). A high μ₂₃/RT value for anionic, monomeric folate is surprising as the addition of one negatively charged oxygen might be expected to increase the μ₂₃/RT value slightly, while a higher proportion of monomeric folate, with a greater fraction of aromatic surface areas compared to that of the dimer, should decrease the μ₂₃/RT value, relative to that at pH 7. However, quantum mechanical calculations by Soniat et al. on anionic pterin report delocalization of the negative charge on the ring.³⁸ This view supports the studies of Felitsky et al.,³⁹ who found betaine was strongly excluded from anionic surfaces.

Because of the large difference in μ₂₃/RT values for neutral and anionic folate, we monitored preferential interaction coefficients for 40 mm folate from pH 6.5 to 10. While dimers are likely present at neutral pH at this concentration, the data display higher signal-to-noise levels and possess smaller errors. Figure 2B shows a plot of μ₂₃/RT values versus pH. The data were fit to eq 3, yielding a pK_a of 8.1 ± 0.17. This value is similar to values of 7.94 and 8.38 obtained by NMR^15,40 and 7.98 obtained by capillary electrophoresis studies.⁴¹ The fit also yields μ₂₃/RT values of 0.36 ± 0.06 and 1.25 ± 0.07 m^–1 for the neutral (protonated) and basic (deprotonated) forms, respectively. Our data indicate that VPO experiments can be used to monitor pK_a values if the protonated and deprotonated species possess different μ₂₃/RT values.

VPO Measurements of Nonheterocyclic Aromatic Compounds

To extend the list of aromatic compounds used to predict α values for aromatic carbons, the μ₂₃/RT values for p-amino-benzoate, m-amino-benzoate, o-amino-benzoate, p-amino-benzoyl-glutamate (p-ABA-Glu), p-toluic acid, quinolinic acid, phenylalanine hydrochloride, and N-acetyl-tyrosine were measured. The experimental μ₂₃/RT values for the amino-benzoates and phenylalanine are listed in Table 1. These values for the rest of the aromatic compounds are listed in Table S3. All amino-benzoates and phenylalanine slopes are negative (Figure 3A), consistent with aromatic carbon atoms preferring to interact with betaine compared to water. For the o-, m-, and p-amino-benzoate series, the μ₂₃/RT values were within error of each other, suggesting the relative ring position of the substituents does not have a large effect.

Table 1. List of All Test Compounds with Their Experimental and Predicted μ₂₃/RT Values^a.

compound	experimental μ23/RT (m–1)	predicted μ23/RT (m–1)	pH
Nonheterocyclic Aromatic
p-amino-benzoate	–0.44 ± 0.03	–0.46 ± 0.02	7
m-amino-benzoate	–0.50 ± 0.03	–0.46 ± 0.02	7
o-amino-benzoate	–0.51 ± 0.03	–0.46 ± 0.02	7
phenylalanine hydrochloride	–0.21 ± 0.03	–0.24 ± 0.02	5
Heterocyclic Aromatic
nicotinamide	–0.38 ± 0.03	–0.27 ± 0.02	unadjusted (6.3)
pyrimidone	0.13 ± 0.01	0.08 ± 0.03	unadjusted (5)
indole acetate monosodium	–0.39 ± 0.02	–0.20 ± 0.02	7
pyrrole 2-carboxylate	–0.18 ± 0.04	–0.12 ± 0.02	7
5′AMP disodium	0.33 ± 0.03	0.18 ± 0.04	7
5′GMP disodium	0.41 ± 0.04	0.46 ± 0.04	8.1
3′UMP disodium	1.07 ± 0.03	0.9 ± 0.04	7.6
5′dTMP disodium	0.81 ± 0.03	1.00 ± 0.04	8
2′CMP disodium	0.32 ± 0.04	0.34 ± 0.04	7
pH-Dependent Heterocyclic Aromatic
pyridoxine hydrochloride	0.02 ± 0.02	0.02 ± 0.02b	2
pyridoxine hydrochloride	0.01 ± 0.02	–	unadjusted (2.6)
pyridoxine	0.25 ± 0.02	0.06 ± 0.02	10
		0.26 ± 0.02b
nicotinic acid	–0.27 ± 0.03	–	unadjusted (3.5)
nicotinic acid	–0.04 ± 0.02	–0.04 ± 0.02	7

^aThe predicted μ₂₃/RT values were obtained using α values listed in Table 2 and eq 4. The pH at which each compound was tested is also listed.

^bValues obtained from the fit limits of the pH titration data for pyridoxine hydrochloride using eq 3.

Figure 3.

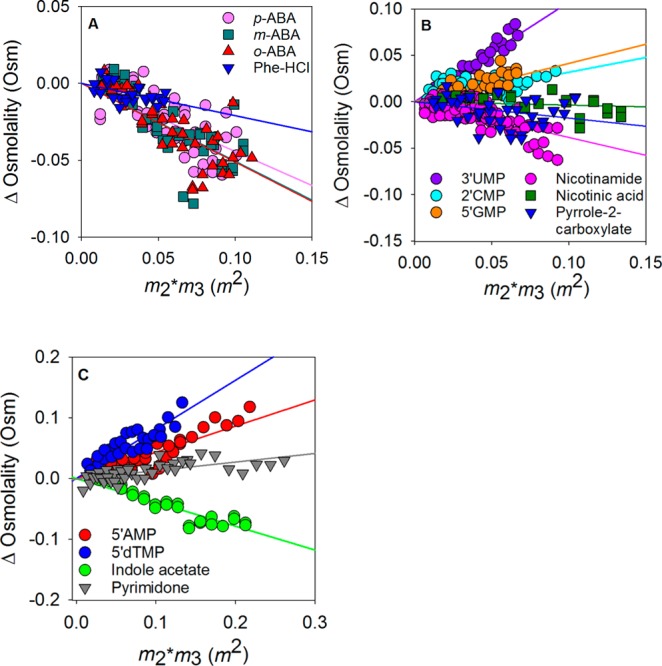
Quantification of preferential interactions of betaine with test compounds. The panels show the raw data plots of ΔOsm vs the product of the molal concentration of the test compound and betaine obtained from VPO experiments. (A) Data for the nonheterocyclic aromatic compounds. (B and C) Data for heterocyclic (nitrogen-containing) aromatic compounds. Data in panel B include those of nicotinamide, nicotinic acid (pH 7), pyrrole 2-carboxylate, guanosine 5′-phosphate (5′GMP), cytosine 2′-phosphate (2′CMP), and uridine 3′-phosphate (3′UMP). These are compounds with lower solubilities and therefore span shorter concentration ranges. Panel C shows plots for adenosine 5′-phosphate (5′AMP), deoxythymidine 5′-phosphate (5′dTMP), pyrimidone, and indole acetate, which have higher solubilities.

VPO Measurements of Compounds Containing Aromatic Nitrogen Atoms

As folate contains aromatic nitrogen atoms and its μ₂₃/RT value showed pH effects, we were interested in studying interactions of betaine with compounds containing titratable aromatic nitrogens. Compounds for this study were chosen on the basis of their solubility, lack of dimerization, and pK_a values. Table S1 gives the structures of the compounds, while panels B and C of Figure 3 show the experimental VPO data. The measured μ₂₃/RT values are listed in Tables 1 and Table S3. Pyridoxine and nicotinic acid were chosen because they contain aromatic nitrogens with near neutral pK_as and were highly soluble. The sections that follow provide more details about the pH effects observed in a few of our studies. A section on imidazole is provided in the text of the Supporting Information and Figure S3.

Pyridoxine Hydrochloride

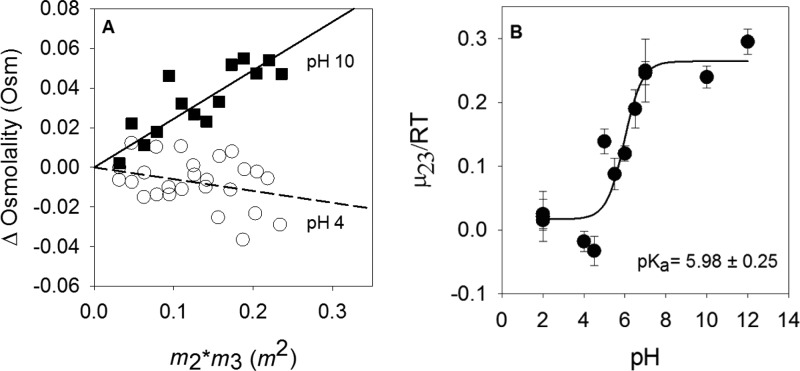
As pyridoxine possesses titrations in the physiological pH range,⁴² we measured μ₂₃/RT values for pyridoxine from pH 2 to 12. Figure 4A shows the slopes (μ₂₃/RT) for protonated and deprotonated pyridoxine. The μ₂₃/RT values at lower pHs are slightly negative, while at higher pH values, the values are positive. The pH dependence of the μ₂₃/RT values is shown in Figure 4B. The data were fit to eq 3, and a pK_a of 5.98 ± 0.25 was obtained, which is higher than the range of pK_as reported previously, from 4.7 to 5.^43,44 The lower and upper limits for the μ₂₃/RT values were 0.017 ± 0.018 and 0.26 ± 0.02 m^–1, respectively. These results indicate that the protonated form of pyridoxine interacts more strongly with betaine than the deprotonated form does.

Figure 4.

Vapor-pressure osmometry studies of pyridoxine showing pH effects. (A) Data for pyridoxine at pH 4 (○) and 10 (■). The dashed and solid lines represent the slopes of the plots for pH 4 and 10 data, respectively. (B) pH titration of μ₂₃/RT for pyridoxine. Data were fit to eq 3, and best fit values are 0.017 ± 0.018 m^–1 for the protonated form and 0.26 ± 0.02 m^–1 for the deprotonated form.

Nicotinic Acid (vitamin B₃)

Nicotinic acid is an aromatic heterocyclic compound with nitrogen in a six-membered ring. VPO experiments found this compound possessed a slightly negative preferential interaction potential at pH 7 as seen in Figure 3B. The μ₂₃/RT value for nicotinic acid was observed to change with pH, consistent with titration of the aromatic nitrogen, which has previously been observed to have a pK_a of 4.9.⁴⁵ The acidic form of nicotinic acid at pH 3 yielded a more negative μ₂₃/RT value, indicating a stronger preference for interaction with betaine than with the deprotonated form at pH 7.

Analysis of μ₂₃/RT Values and Calculation of α Values

To deconvolute which atoms of folate are involved in the interactions with betaine, we use the α value analysis developed by the Record lab.¹⁹⁻²² This approach uses multiple linear regressions (based on the number of compounds used), which describe all the surface types present in the molecules. We added our 15 compounds to the list of 27 molecules published by Capp et al.¹⁹ As our model compounds were mostly nitrogen-containing aromatic heterocycles, we aimed to calculate α values for aromatic N surface types in addition to the surface types analyzed by the Record lab.¹⁹⁻²² Because several atom types that appeared in our molecules were not included in the Record lab study, we added an amine N off aromatic rings to our atom types.

Aromatic ring systems are complicated. In our fittings, we considered other atom types in the AMBER (ff14SB) force field that describe different aromatic carbons and nitrogens.⁴⁶ Some considerations about whether to include atom types were whether its ASA was significant and whether the amplitudes for the related atom type in our fits overlapped and/or whether the error was small. Some of the other atom types we tried included protonated aromatic nitrogens, differentiating between aromatic nitrogens in five- and six-membered rings, carbonyls that are part of aromatic systems (as is the case with the nucleotides and O4 of folate), and aromatic carbons in five- or six-membered ring systems. The α values were not significantly different, and within error, for nitrogens and carbons of the five- and six-membered rings. Carbonyls that are part of aromatic systems also were very similar to amide oxygens. Therefore, we did not pursue these atom types further. While we tried many combinations, ultimately, we just added an aromatic nitrogen and an amine nitrogen off an aromatic ring to the list of atom types as too many variables can affect error analysis.

All compounds were included in our fit except p-ABA-Glu, N-acetyl-tyrosine, imidazole, quinolinic acid, and the acidic forms of pyridoxine and nicotinic acid. We did not include imidazole as it dimerizes at the concentrations needed to obtain a VPO signal. As only two compounds with protonated aromatic nitrogens were available (acidic pyridoxine and acidic nicotinic acid), we were concerned with the ability of only two atoms to provide good statistics for this atom type. Addition of p-ABA-Glu, N-acetyl-tyrosine, p-toluic acid, and quinolinic acid significantly caused the R² of our fit to drop, from 0.93 to 0.8 (with all compounds added). For N-acetyl-tyrosine and quinolinic acid, this is likely due to their low solubilities that necessitated the use of low concentrations, a potential source of error. It is not clear why p-ABA-Glu and p-toluic acid were outliers in our fit. Perhaps mixed effects from the different electron-donating and -withdrawing groups off the aromatic rings play a role.

Our α values are listed in Table 2 along with those from the Record lab. While the amplitudes of our α values are different from those of the values from the Record lab, the overall trend is the same. Both this study and ref (20) obtain positive α values for oxygens in hydroxyl, amide, carboxylate, and phosphate groups. We add the information that aromatic nitrogens display positive α values. The Record group and the study presented here find that amide nitrogens show a negative α value. We add that amine nitrogens off aromatic rings do, as well. Finally, while the Record group had a positive α value for aliphatic carbon [(3 ± 3) × 10^–4m^–1 Å^–2], the addition of our compounds tips the balance toward a small negative value. On the other hand, we obtain a positive β value for Cl^– [(8 ± 1) × 10^–2m^–1], which is outside the range [(−4 ± 4) × 10^–2m^–1] of Guinn et al.²⁰

Table 2. Comparison of α and β Values from This Study vs Those from ref (20)^a.

α values from this study		α values from ref (20)
surface type, i	αi (×104 m–1 Å–2)	surface type, i	αi (×104 m–1 Å–2)
aliphatic C	–3 ± 1	aliphatic C	3 ± 3
hydroxyl O	7 ± 1	hydroxyl O	1 ± 2
amide O	49 ± 3	amide O	28 ± 10
amide N	–33 ± 2	amide N	–20 ± 7
carboxylate O	28 ± 1	carboxylate O	29 ± 2
cationic N	–14 ± 1	cationic N	–12 ± 4
aromatic C	–31 ± 1	aromatic C	–23 ± 4
phosphate O	48 ± 2	phosphate O	49 ± 4
amine N off aromatic rings	–53 ± 3	amine N off aromatic rings	–
aromatic N	27 ± 3	aromatic N	–

inorganic ion	βion (×102 m–1)	inorganic ion	βion (×102 m–1)
K+	8 ± 2	K+	5 ± 2
Cl–	7 ± 1	Cl–	–4 ± 4

^aCalculations used eq 4. Data for 15 compounds from this study were used in addition to data for 27 compounds from ref (19). α values for an amine N off an aromatic ring and an aromatic N atom types were calculated in addition to the atom types in ref (20).

Finally, we note Diehl et al.²¹ compared their proline VPO results with those from solubility or group transfer free energy (GTFE) assays. While the preferences of many amino acids to interact with betaine instead of water were similar for the two techniques, they also found significant differences. For example, solubility assays noted a weak preference of valine and leucine for betaine compared to water while the VPO results indicated a weak preference of valine for water. In another difference, GTFE experiments found sodium salts of glutamate and aspartate strongly prefer to interact with betaine while VPO results indicate a strong preference for water. These differences suggest that while our α values are somewhat different from those of refs (19) and (20), this variability is not surprising, given that the compounds used in the analysis are different and that GTFE assays can show somewhat different patterns. On the other side of the coin, the α values reflect the compounds used in the calculations. Accordingly, our fits likely converge to somewhat different values because of the extra information provided by the additional compounds used in our experiments.

Solubility Assays

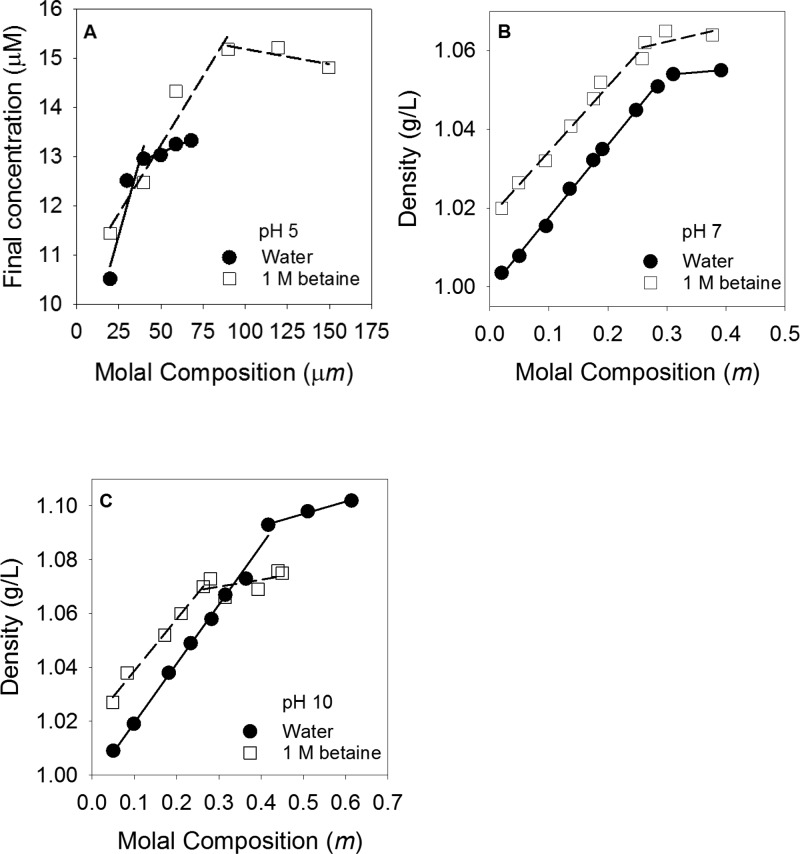
A second approach to investigating how betaine interacts with folate uses a solubility assay. Thus, we measured the solubility of folate in water versus 1 M betaine at various pH values. Figure 5 shows the data that were analyzed as described by the Bolen lab.^31,32 The composition versus density plots for pH 7 and 10 were each fit to two lines as shown. The intersection of the lines provided the concentration at which the solution was saturated with folate in either water or 1 M betaine. At pH 5, the solubility of folate in 1 M betaine was higher than in water (Figure 5A). The transfer free energy of folate was calculated to be −297 ± 22 cal/mol where a negative free energy indicates a preference for the betaine solution over water. At pH 7, folate is almost equally soluble in water and 1 M betaine (Figure 5B). The transfer free energy from water to betaine was found to be 89 ± 30 cal/mol. The data at pH 10 (Figure 5C) indicate that folate is more soluble in water than in betaine with a transfer free energy of 500 ± 150 cal/mol. These solubility assays indicate folate prefers to interact with betaine compared to water in the lower pH range. In contrast, folate prefers to interact with water over betaine as the pH increases and the deprotonated enol tautomer of folate predominates. The general trend observed in the solubility and VPO experiments is the same.

Figure 5.

pH dependence of folate solubility in 1 M betaine (□) and water (●). (A) Folate concentration measured by absorbance vs folate composition at pH 5. (B and C) Solution density vs the molal composition at pH 7 and 10, respectively. The data were fit to two solid lines for water and two dashed lines for betaine. The intersection of the lines for each solution condition gave the saturation concentration of folate. The transfer free energies at pH 5, 7, and 10 are −297 ± 22, 89 ± 30, and 500 ± 150 cal/mol, respectively.

According to Auton and Bolen,³² the activity coefficients of compounds in water and 1 M betaine will contribute to the apparent transfer free energy when the solubility of the compound is sufficiently high. For folate, the solubility at pH 5 is low enough that the effects of the activity coefficients of folate in water and 1 M betaine can be ignored. However, at pH 7 and 10, folate is readily soluble, and the activity coefficients will now contribute to the apparent transfer free energy. Therefore, some of the discrepancy between comparing the results of VPO and solubility assays may arise from the contributions of the activity coefficients. We also note that depending on the pH, the dimer K_d, and the folate concentration, monomer and/or dimer species may be present.

Prediction of Folate μ₂₃/RT Values from Simulation Data

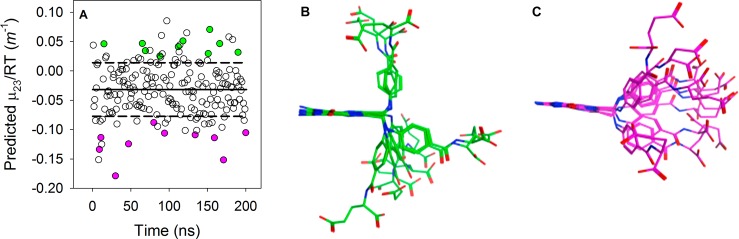
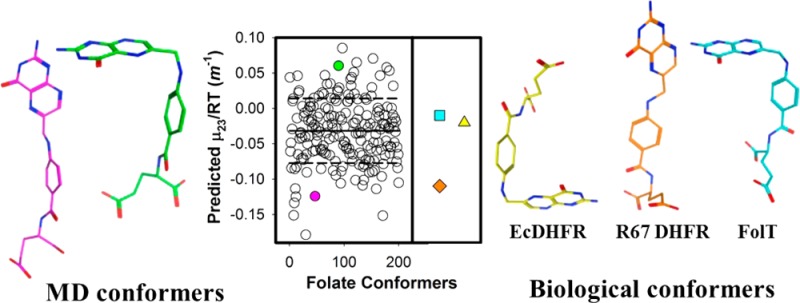
In the molecular dynamics (MD) simulation of folate in water, folate adopted a range of conformations. For each of these conformations, a μ₂₃/RT was calculated from α values. Similar calculations were also performed for the simulations of folate in water and 1.35 M betaine. A relatively large variation in the predicted μ₂₃/RT values for folate was noted over the course of both simulations (see Figure 6A and Figure S4). The average μ₂₃/RT value for folate in water was −0.03 ± 0.05 m^–1, while the value for folate in 1.35 M betaine was −0.05 ± 0.05 m^–1. Slightly more than 30% of the structures fall above, or below, one standard deviation of the average. This suggests that folate can adopt a range of conformations that can have significantly different interactions with betaine. The average μ₂₃/RT values for folate in water and 1 M betaine are within error, suggesting that betaine has no effect on folate conformation.

Figure 6.

(A) Predicted μ₂₃/RT values for folate associated with its MD simulation in water (○). The average of the μ₂₃/RT values is shown as a solid line. The dashed lines show one standard deviation from the average value. Ten representative folate conformers are superimposed on their pterin rings and are shown in panel B for more (green) and panel C for less (magenta) than one standard deviation corresponding to the filled circles in panel A. Oxygen and nitrogen atoms are colored red and blue, respectively.

Discussion

Folate Is an Interesting Molecule

There are many differences between folate and the small molecule compounds and proteins previously studied by the osmometry approach. First, it contains aromatic nitrogen atoms. Our deconvolution of μ₂₃/RT values down to α values indicates aromatic nitrogens prefer to interact with water rather than betaine. This is consistent with betaine not being a H bond donor, leaving water to interact with the aromatic nitrogens. Second, folate dimerizes, allowing the pterin and p-ABA rings to stack. This results in a concentration-dependent μ₂₃/RT value. Using our α values, we can predict μ₂₃/RT values. For the dimeric folate model proposed by Poe,²⁸ this value is 0.81 ± 0.03 m^–1. We note the predicted values are based on specific structures of folate while the experimental value describes the solution conformation(s). Differences between the predicted and experimental values can describe variances in the solution conformation(s) versus our minimized structures. We find that our predicted μ₂₃/RT value is sensitive to the monomeric folate conformation. For example, an extended folate structure from R67 DHFR⁴⁷ yields a μ₂₃/RT of −0.11 m^–1, while L-shaped folates from EcDHFR (PDB entry 1RX7) and FolT, a folate transporter (PDB entry 4Z7F), provide μ₂₃/RT values of −0.02 and −0.01 m^–1, respectively. The bound conformations of folate are not the only ones that are present in solution. To assess the possible folate conformations present in solution, we performed a population analysis. We analyzed 200 folate conformations from a MD trajectory of folate in water, calculated their ASAs with SurfaceRacer, and used MATLAB to calculate μ₂₃/RT values. Figure 6A plots the range of μ₂₃/RT values predicted, which is −0.18 to 0.09 m^–1. This range of μ₂₃/RT values easily corresponds to the lower limit of the titration seen in Figure 2A. As shown in panels B and C of Figure 6, the folates with negative μ₂₃/RT values show extended structures while folates with positive values show more bent structures. Analysis of the ASA contributions to the change in μ₂₃/RT value indicates alterations in the N10 and aromatic ring areas are most important. We note the biological relevance of the p-ABA-Glu tail flexibility was explored previously by covalent tethering of folate to R67 DHFR, which results in lower enzyme activity.⁴⁸ In addition, MD simulations found that flexibility in the p-ABA-Glu tail orients the pterin ring for the hydride transfer event in the active sites of both R67 DHFR⁴⁷ and EcDHFR.⁴⁹

A third interesting characteristic associated with folate is deprotonation of the N3–O4 enol tautomer, which affects folate’s μ₂₃/RT value. The pK_a measured by VPO (8.1 ± 0.17) is similar to those previously monitored by NMR (7.94, 8.38)^15,40 and capillary electrophoresis (7.98).⁴¹ As O4 titrates from an enol to an enolate and N3 concomitantly loses its proton, a high μ₂₃/RT value results (1.25 ± 0.07 m^–1). As the N3 can no longer serve as a H bond donor, this part of the folate molecule prefers to interact with water. Another consideration arises from quantum mechanical calculations by Soniat et al. on anionic pterin, which report delocalization of the negative charge on the ring.³⁸ Exclusion of betaine from a delocalized negative charge on the pterin ring is consistent with the work of Felitsky et al.,³⁹ who found betaine was strongly excluded from anionic surfaces.

Other compounds with aromatic nitrogens such as pyridoxine and nicotinic acid also showed pH effects on their μ₂₃/RT values. Our measured pyridoxine pK_a was 5.98 ± 0.25. This compares to pK_a values of 5.1 ± 0.02 and 9.0 ± 0.03 for the aromatic nitrogen and phenol hydroxyl, respectively, measured by potentiometry.⁵⁰ However, other studies indicate pyridoxine in aqueous solution at neutral pH exists as a mixture of neutral and zwitterionic species.⁵¹⁻⁵³ While the identity of the titrating species is not clear, the pH dependence of μ₂₃/RT is evident. The general trend is for protonated species to be more interactive with betaine than with the deprotonated species. This is true for folate (pK_a ∼ 8), pyridoxine (pK_a = 5–6), and nicotinic acid (pK_a ∼ 5). Again, this is consistent with neither betaine nor the small molecule (at the position of interest) being a good H bond donor. In contrast, water competes well under these conditions.

Deconvolution of μ₂₃/RT into α Values

Our α values are listed in Table 2. As mentioned above, our α values mostly show the same sign as those from the Record group; however, the amplitudes are different. This may be due to different ASAs calculated for the small molecules. Other differences may be due to whether dimerization occurs as we add aromatic compounds to the list of small molecules. Dimerization was observed in our folate studies as well as imidazole.⁵⁴ Another possible difference is the influence of ionization state on μ₂₃/RT values. We (mostly) maintained pH 7 conditions and also considered relevant pK_a values. The Record lab also considered ionization states in their study of PEG interactions as they included two different oxygen atom types, -COOH and -COO^–. The α values for interaction of these atom types with glycerol are 0.0446 and 0.467 m^–1, respectively.²² An additional issue is whether uracil is aromatic. While a recent publication suggested it is not, we treated the ring atoms as aromatic.⁵⁵ Even with all these caveats, the R² for our MATLAB fit of 42 compounds was 0.93. We found that removing each of the 15 compounds and refitting to eq 4 yielded similar R² values. Also, the α values did not change significantly in these various fits.

To test our α value calculations, we predicted μ₂₃/RT values for our test compounds using eq 4 and compared them to the experimental values. A plot of predicted versus experimental μ₂₃/RT values is linear as can be seen in Figure 7. The good correlation between predicted and experimental values supports this type of analysis for interactions of betaine with small molecules.

Figure 7.

Comparison of predicted μ₂₃/RT values vs experimental μ₂₃/RT values. The red squares are from ref (19), and the black circles are from our additional compounds. Many of our compounds have negative μ₂₃/RT values. The black line shows a slope of 1 for a fit through 0,0. The blue line shows the best linear fit of the data with an R² of 0.93. The 90% confidence intervals for the fit are shown as green lines.

K_p values represent the microscopic local bulk partition coefficients that can be calculated from the α values (see the Supporting Information for the method), and Table S4 lists K_p values obtained for each surface type. A value of <1 indicates water accumulates around the atom more than betaine. K_p values of >1 indicate the opposite, where betaine accrues more readily around the atom surface. Carbon and nitrogen atoms, except for aromatic nitrogens, have K_p values of >1. On the other hand, all types of oxygens, as well as aromatic nitrogens, have K_p values of <1. Therefore, these atom types prefer to be hydrated by water over betaine. A representation of K_p values for the atom types in folate is shown in Figure S5.

Solubility versus VPO Assays

We studied the interaction of folate with betaine using solubility assays and VPO experiments. Both approaches yielded similar results. At pH 7, solubility assays find that folate interacts with both water and betaine with a transfer free energy of 89 ± 30 cal/mol. In our VPO studies depicted in Figure 2A, the μ₂₃/RT value approaches zero at low folate concentrations. Within error, the solubility and VPO techniques converge to similar conclusions. They also qualitatively agree with the prediction of μ₂₃/RT values from our α values for the various folate conformers as shown in Figure 6.

At pH 10, the solubility assays indicate folate prefers interaction with water over that with betaine with a transfer free energy of 500 ± 150 cal/mol. Our VPO studies agree, yielding a μ₂₃/RT of 1.27 ± 0.36 m^–1.

In conclusion, at neutral pH, betaine interacts strongly with aromatic carbon surfaces of folate. This interaction is likely due to formation of cation−π pairs.⁵⁶⁻⁵⁸ Betaine also strongly interacts with the folate amine groups, indicating betaine is a better H bond partner for this group than water. In contrast, betaine is excluded from aromatic nitrogens, carboxylates, and amide oxygens. This scenario occurs as water can provide H bonds to these groups while betaine cannot.

Do these results provide any insights into our previous studies

in which betaine weakens binding of folate to R67 DHFR and EcDHFR? A means of checking the adequacy of predicting μ₂₃/RT values is to look at the effects of betaine on folate, or DHF, binding to enzymes. We have examined the effects of betaine on binding of polyglutamylated folates to R67 DHFR (see the Supporting Information for details, and Figure S6 and Table S5). Previous ITC studies have looked at the effects of betaine on binding of DHF to E. coli chromosomal DHFR (EcDHFR) and R67 DHFR.^13,14 To determine how accurately the current α values predict betaine’s effects, Δμ₂₃/RT values for binding of DHF and folate to EcDHFR and the R67 DHFR·NADP⁺ (or NADPH) complex were calculated using available protein structures (Table 3). Similar calculations were performed using the α values from ref (20). The signs of the predicted and experimental Δμ₂₃/RT values match, although the amplitudes vary. Also, sometimes the α values of ref (20) provide a better match to experiment, and sometimes the values from Table 2 provide a better match. Variations between predicted and experimental values may be due to the Met20 loop, which is disordered in the apoenzyme and occluded in the NADP⁺ binary, folate binary, and DHF binary complexes.⁵⁹ Another factor concerning apo EcDHFR is that it exists in two conformations (E1 and E2) prior to binding ligand.⁶⁰ Thus, conformational heterogeneity could play a role in the ability of computational predictions to match experimental values.

Table 3. Predictions of the Δμ₂₃/RT Values for the Effects of Betaine on the Binding of Ligands to Two Different Dihydrofolate Reductases^a.

		Δμ23/RT (m–1)
protein–ligand complex formed	ligand	using an α value from ref (20)l	using an α value from Table 2	using eq S1 with ITC data
EcDHFR·NADP+b,c	NADP+	–0.51	–0.88	–0.23m
EcDHFR·NADPHc,d	NADPH	–0.43	–0.77	–0.28m
EcDHFR·DHFc,e	DHF	0.52	0.59	0.57m
EcDHFR·folatec,f	folate	0.57	0.37	0.90n
EcDHFR·NADP+·DHFg	DHF	0.30	0.54	0.68m
R67 DHFR·NADP+h,i	NADP+	–0.77	–0.52	–0.84o
R67 DHFR·NADP+·DHFj	DHF	0.23	0.46	0.61o
R67 DHFR·NADPH·folatek	folate	0.19	0.34	0.86n

^aThe Δμ₂₃/RT values were calculated by subtracting the sum of the μ₂₃/RT values of the ligand and the apoenzyme (or binary complex) from the μ₂₃/RT values for the binary complex (or the ternary complex). The predicted values for complex formation were compared with the Δμ₂₃/RT values calculated from ITC data.

^bPDB entry 1RX9 was used in the calculations.⁷²

^cThe apoenzyme in PDB entry 5DFR(74) was also used in the calculations.

^dPDB entry 1RX1.⁷²

^ePDB entry 1RF7(72) was used with the missing carboxylate group of the glutamate tail added to the bound DHF.

^fPDB entry 1RX7.⁷²

^gPDB entry 4PDJ.⁶⁷

^hPDB entry 2RK2.⁶¹

ⁱThe first two residues of the apoprotein (PDB entry 1VIE)⁷⁵ were removed to be consistent with the other structures.

^jThe DHF structure has the p-ABA-Glu tail added.⁴⁷

^kThe structure from Kamath et al. with the pterin ring converted to folate was used.⁴⁷

^lα values from Table 1 of ref (20).

^mData from ref (14).

ⁿData from Table S5.

^oData from ref (13).

Comparison of the predicted and experimental effects of betaine on binding of ligands to R67 DHFR is quite different than for binding to EcDHFR. Again, the sign of the prediction matches that of the experiment, with variations in the amplitude. A possible issue affecting the ability of the calculation to match experiment is the disordered p-ABA-Glu tail of the bound substrate.^47,48,61 Different poses can yield different protein surfaces involved in binding and different substrate conformers, which would both affect the calculated μ₂₃/RT value. Finally, water bridges between R67 DHFR and DHF occur, and SurfaceRacer does not take these bridging atoms into account.

A general issue that may affect both experimental data sets is uptake or loss of protons upon binding. Our ITC results have previously found uptake of a proton by R67 DHFR upon binding folate.⁶² Additionally, resonance Raman studies find protonation of DHF by the active site of EcDHFR in the ternary complex.^63,64 This event is not necessarily identified by ITC, which measures only the net number of protons taken up or released.⁶⁵ However, binding of NADPH and NADP⁺, as measured by ITC, does involve release of a proton.¹⁴ At least in the cases of binding of folate to R67 DHFR and binding of DHF to EcDHFR, the protonation states of either the ligand or protein may change upon binding.^{14,62−64,66,67} Discrepancies between our experimental and predicted Δμ₂₃/RT values may arise due to these protonation effects not being included in our predictions of Δμ₂₃/RT values. Another potential issue in our prediction of μ₂₃/RT values using eq 4 may arise due to deviations from the principle of additivity for macromolecules.^68,69 While the chemical additivity of small molecules is common, additivity does not always occur in large biochemical molecules. The predicted μ₂₃/RT values of the DHFRs may be overestimated if the interaction potentials of individual groups with betaine are nonadditive.

We conclude that this approach to analyzing binding has its limitations. As with folate (Figure 6), proteins are likely to have conformational changes associated with their structures. Indeed, loop movement and other dynamics have long been associated with binding of ligand to EcDHFR.⁷⁰⁻⁷² This suggests that it will likely be difficult to predict μ₂₃/RT values for proteins that release and/or take up protons upon binding, undergo dynamic motion, or use “wet interfaces” for binding, for intrinsically disordered sequences and for protein folding, although the Record lab has had some success with the latter case.^21,73

Conclusion

While betaine is an excellent osmolyte for protein stability and folding, it is less helpful for folate to function as a substrate and/or cofactor as the aromatic pterin and p-ABA rings prefer to interact with betaine compared to water. This preferential interaction results in weaker binding affinities of folate(s) for DHFRs. As the aromatic pterin ring is lost in dihydrofolate (DHF) and tetrahydrofolate (THF), the predicted μ₂₃/RT values for these more reduced states increase to −0.06 ± 0.03 (for the DHF conformation in the EcDHFR·NADP⁺·DHF complex). As DHF and THF contain the same atom types, the predicted μ₂₃/RT values do not change. These values predict the effects of osmotic stress on other folate pathway enzymes. These effects could be mitigated if the enzymes involved prefer polyglutamylated substrates.

Glossary

Abbreviations

ASA

accessible surface area

DHF

dihydrofolate

DHFR

dihydrofolate reductase

GTFE

group transfer free energy

ITC

isothermal titration calorimetry

K_d

dissociation constant

MD

molecular dynamics

MTX

methotrexate

MTA buffer

100 mM MES, 50 mM Tris, and 50 mM acetic acid

NADP⁺ and NADPH

oxidized and reduced nicotinamide adenine dinucleotide phosphate, respectively

NMR

nuclear magnetic resonance

NTA

nitrilotriacetic acid

p-ABA-Glu

p-amino benzoyl glutamic acid

PDB

Protein Data Bank

PEG

polyethylene glycol

THF

tetrahydrofolate

VPO

vapor-pressure osmometry.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.biochem.6b00873.

• MATLAB program used in our fit (TXT)

• Excel sheet for use in fitting with MATLAB (XLSX)

• Materials, an NMR method for studying folate dimerization, protein purification details for R67 DHFR and EcDHFR, ITC experiments for folate and pteroyl-tetra-γ-l-glutamate binding to R67 DHFR and EcDHFR, details of a MD simulation of folate in betaine and water, and calculation of Δμ₂₃/RT values for ligand binding with ITC data. A figure showing the folate structure and atom numbers, dimer model, and betaine structure is given. This figure also describes the keto–enol tautomerization of folate and the pK_a of the enol species. In addition, a table showing structures and sources of the compounds used in the VPO studies is provided. Another table listing the μ₂₃/RT values for several compounds not used in the α value fit is given. The results section includes a figure showing the proton chemical shifts and fits of NMR data along with a table describing K_ds for folate dimerization. The discussion of results with imidazole and a figure showing the results at low and high pH are provided. The discussion of results for folate simulation in betaine and water and a figure showing the comparison of folate simulations with and without betaine are also provided. A table showing K_p values for each surface type and a representative figure showing the K_p values for each atom in the folate molecule are also given. A figure of ln(K_a) versus betaine osmolality for folate and pteroyl-tetra-γ-l-glutamate binding to R67 DHFR and EcDHFR as well as a table with all the thermodynamic fit parameters obtained for the effects of betaine on folate and pteroyl-tetra-γ-l-glutamate binding to R67 DHFR and EcDHFR is included. (PDF)

This work was supported by National Institutes of Health Grants GM 110669 (to E.E.H.) and GM105978 (to P.K.A.).

The authors declare no competing financial interest.