Summarizing Simulation Results using Causally-relevant States

Abstract

As increasingly large-scale multiagent simulations are being implemented, new methods are becoming necessary to make sense of the results of these simulations. Even concisely summarizing the results of a given simulation run is a challenge. Here we pose this as the problem of simulation summarization: how to extract the causally-relevant descriptions of the trajectories of the agents in the simulation. We present a simple algorithm to compress agent trajectories through state space by identifying the state transitions which are relevant to determining the distribution of outcomes at the end of the simulation. We present a toy-example to illustrate the working of the algorithm, and then apply it to a complex simulation of a major disaster in an urban area.

1 Introduction

Large-scale multiagent simulations are becoming increasingly common in many domains of scientific interest, including epidemiology [9], disaster response [23], and urban planning [22]. These simulations have complex models of agents, environments, infrastructures, and interactions. Often the goal is to study a hypothetical situation or a counter-factual scenario in a detailed and realistic virtual setting, with the intention of making policy recommendations.

In practice, this is done through a statistical experiment design, where a parameter space is explored through multiple simulation runs and the outcomes are compared for statistically significant differences.

As simulations get larger and more complex, however, we encounter two kinds of situations where it is difficult to apply this methodology. First, if a simulation is too computationally intensive to run enough number of times, we don’t obtain the statistical power necessary to find significant differences between the cells in a statistical experiment design. Second, if the interventions are not actually known ahead of time, we don’t even know how to create a statistical experiment. This can be the case, e.g., when the goal of doing the simulation is actually to find reasonable interventions for a hypothetical disaster scenario.

New methodologies and new techniques are needed for the analysis of such complex simulations. Part of the problem is that large-scale multiagent simulations can generate much more data in each simulation run than goes into the simulation, i.e., we end up with more data than we started with. Sense-making in this regime is a challenge.

As a first step towards addressing these kinds of problems, we introduce the problem of simulation summarization. The goal of this problem is to come up with a summary description of a single large multiagent simulation run. The method we introduce is based on a deep theory of causal states in stochastic processes (see Section 3). It is simple to implement, which is essential when applying to very large simulations, and is actually more meaningful the larger the simulation, since larger numbers of agents give more statistical power.

The rest of this paper is organized as follows. First we describe the simulation summarization problem and discuss some related work. Then we review the idea of causal states for extracting patterns from time series data. After that we describe how we adapt this idea to the analysis of the results of large-scale simulations. Then we present a toy example to illustrate the effectiveness of our method, before applying it to a large and complex simulation of an improvised nuclear detonation in an urban area. We show how our method finds a number of meaningful causal patterns in the simulation results, while also greatly compressing the results. We end with a discussion of applications and extensions of our method.

2 Problem description

What constitutes a good summary? This is a question that has been studied in domains such as natural language processing where the goal is to summarize a document or a corpus [16, 17], but, as far as we know, is entirely novel for multiagent simulations.

Our perspective on summarizing a multiagent simulation is that the summary representation should capture the causally-relevant states of the simulation. We use the phrase “causally-relevant” instead of causal to side-step the well-known problems with finding causality. There are many efforts aimed at establishing (various forms of) causality in data [21, 11, 13, 12, e.g.]. Our goal here is not to establish causality, but to compress the simulation results while retaining meaningful states. The intuition is that finding causally-relevant states of the simulation is the most meaningful way to compress it.

In line with this intuition, we adapt the approach of “causal states” that has been developed over the last several years, as reviewed in the next section. By “causally-relevant”, in this context, we mean agent states that are maximally informative about outcomes of interest.

Even in simulation scenarios where the set of interventions or cases to study is not known a priori, i.e., simulations which are intended to be exploratory in nature, there is a set of outcomes we care about. For instance, in a disaster simulation we explore in sections 6 and 7, the outcome of interest is the health of the agents. Causally-relevant states in this simulation are all the states which have a measurable impact on agent health, even if the impact is delayed. For example in this simulation, being exposed to radiation has an impact on health state only after several hours have passed. The summary should be able to reveal that it is the exposure to radiation that is the causally-relevant state, not the actual change in the agent’s health state (since that follows deterministically once exposure has happened).

Next we describe the formalism of causal states which is more broadly applicable to stochastic processes before turning to our approach for simulation summarization.

3 Causal states

Crutchfield and others have developed the theory of minimal causal representations of stochastic processes, termed computational mechanics [7, 18]. We briefly review the concepts here before describing how we have adapted them for the summarization problem.

Consider a stochastic process as a sequence of random variables X_t, drawn from a discrete alphabet, 𝒜. We will write X← to denote the past of the sequence, i.e., the sequence X_−∞ … X_t−2X_t−1X_t, and X⃗ to denote the future of the sequence, i.e., the sequence X_t+1X_t+2 … X_∞, following [6, 8].

The mutual information between the past and the future of the sequence is termed its excess entropy:

$$\mathbf{E}=I[\overleftarrow{X};\overrightarrow{X}].$$ (1)

This quantifies the amount of information from the past of the process that determines its future. For example, E = 0 would mean that the future of the process is independent of the past.

Crutchfield and Young [7] suggested a simple method for modeling a stochastic process that captures the information being communicated from X← to X⃗: group all the histories that predict the same future. This gives rise to a state machine which they call an ε-machine, defined in [8]:

$$\epsilon (\overleftarrow{x})=\{{\overleftarrow{x}}^{\prime }\mid Pr(\overrightarrow{X}\mid \overleftarrow{x})=Pr(\overrightarrow{X}\mid {\overleftarrow{x}}^{\prime })\}.$$ (2)

In other words, the states of an ε-machine correspond to sets of histories that are equivalent in terms of the probability distributions they assign to the future of the process. ε-machines have a number of interesting and useful properties. For instance, causal states are Markovian because X← is statistically independent of X⃗ given the current causal state of the process. They are also optimally predictive because they capture all of the information in X← that is predictive of X⃗.

Shalizi and Shalizi have presented an algorithm for learning ε-machines from time series data, known as Causal State Splitting Reconstruction (CSSR) [19]. CSSR learns a function, η, that is next-step sufficient and that can be calculated recursively. A next-step sufficient function is a function that can predict the next step of the time series optimally. If it is also recursively calculable, then it can be used to predict the entire future of the time series optimally.

CSSR learns an ε-machine as a Hidden Markov Model (HMM) in an incremental fashion. The HMM is initialized with just one state and, as the algorithm processes the time series, more states are added when a statistical test shows that the current set of states is insufficient for capturing all the information in the past of the time series.

Informally, the CSSR algorithm works as follows. It tests the distribution over the next symbol given increasingly longer past sequences. Let L be the length of the past sequences considered so far, and let Σ be the set of causal states estimated so far.

In the next step, CSSR looks at sequences of length L + 1. If a sequence of the form ax^L, where x^L is a sequence of length L and a ∈ 𝒜 is a symbol, belongs to the same causal state as x^L, then we would have [19],

$$Pr(X_t\mid a{x}^L)=Pr(X_t\mid \widehat{S}=\widehat{\epsilon }(x^L)),$$ (3)

where Ŝ is the current estimate of the causal state to which x^L belongs. This hypothesis can be tested using a statistical test such as the Kolmogorov-Smirnov (KS) test. If the test shows that the LHS and RHS of equation 3 are statistically significantly different distributions, then CSSR tries to match the sequence ax^L with all the other causal states estimated so far. If Pr(X_t|ax^L) turns out to be significantly different in all cases, a new causal state is created and ax^L is assigned to it. This process is carried out up to some length L_max.

After this, transient states are removed and the state machine is made deterministic by splitting states as necessary. Details of this step can be found in [19] but are not relevant for the present work.

4 Our approach

Our approach adapts the causal state formalism by treating the trajectory of each agent in the simulation as an instance of the same stochastic process.

In our approach, a multiagent simulation consists of a set of agents, each of which is defined by a k-dimensional state vector x(t) = [x₁(t), x₂(t), … x_k(t)]^⊤, which evolves over time. Let d_i be the number of possible values x_i can take. The simulation proceeds in discrete time steps from t = 0 to t = T. Let the number of agents be denoted by N.

We use the term state in a broad sense. It can include, e.g., the action taken by the agent at each time step. It can also include historical aggregations of variables, e.g., it might include a variable that tracks if an agent has ever done a particular action, or the cumulative value of some variable so far.

Our goal is not to learn an ε-machine for a simulation, for two reasons. First, the set of states discovered (through CSSR, e.g.), can be hard to interpret. Second, in general, we don’t need to predict every step of the simulation. We only care about particular outcomes and the state transitions that are causally-relevant to those outcomes.

Thus, our goal is to compress the trajectory of each agent through state space to a small number of important states that have a significant impact on the outcomes we care about. Let the outcome variable for agent i be denoted by y_i. We assume that y_i is an instance of a random variable Y. Our algorithm for summarization proceeds as follows.

We divide the agent population into a set of clusters, C(t) = {C₁(t)∪C₂(t) ∪ … C_m(t)} at each time step. Initially, all the agents are grouped into just one cluster, i.e., m = 1 at t = 0. At each subsequent time step, the state of each agent changes because at least one of x₁, … x_k changes. The number of ways in which x can change is d = d₁ × d₂ × … × d_k.

Consider an arbitrary cluster of agents, C_i(t). At time step t+1, it can split into up to d groups, based on how each agent’s state changes. However, not all of these changes may have a significant impact on the outcome. We treat each group derived from C_i(t) as a candidate cluster, denoted by CC_i,j(t + 1), where j ∈ 1 … d. At each step, we compare Pr(Y |C_i(t)) with Pr(Y |CC_i,j(t+1) using the Kolmogorov-Smirnov (KS) test. Here Pr(Y |C_i(t)) is the probability distribution over the final outcomes for all agents that belong to cluster C_i(t) at time step t. If Y is a discrete variable, Pr(Y = y|C_i(t)) can be computed as a naive maximum likelihood estimate, i.e., ratio of the number of agents who belong to cluster C_i(t) at time step t and have final outcome Y = y to the number of agents who belong to cluster C_i(t) at time step t. Similarly, Pr(Y |CC_i,j(t+1)) is the probability distribution over the final outcome for all agents who belong to candidate cluster CC_i,j(t+1) at time step t + 1 which is a subset of agents who belong to cluster C_i(t) at time step t and can be computed in a similar fashion. Our null hypothesis (analogous to equation 3) is,

$$Pr(Y\mid C{C}_{i,j}(t+1))=Pr(Y\mid C_i(t)).$$ (4)

We also introduce a parameter δ, which is a threshold on the “effect size”, which we measure as the KullbackLeibler divergence (KL-divergence) between Pr(Y |C_i(t)) and Pr(Y |CC_i,j(t+1)). If the null hypothesis is rejected at a level α (say 0.001) and D_KL(Pr(Y |C_i(t))||Pr(Y |CC_i,j(t + 1))) > δ, then candidate cluster CC_i,j(t + 1) is accepted as a new cluster at time step t + 1. The need for the effect size threshold is explained further below. If none of the candidate clusters at time step t+1 are accepted, then C_i(t) is added to the set of clusters for time step t + 1.

Thus, the entire simulation is decomposed into a tree structure of agent clusters. Furthermore, each cluster splits only when the corresponding state change is informative about the final outcome of concern.

The trajectory of each agent traces a path through this tree structure. We compress the trajectory by retaining only those time steps at which the cluster to which the agent belongs splits off from its parent cluster. The parameter δ allows us to control how many new clusters are formed at each step, and consequently, how much compression of trajectories we achieve. Setting δ to a high value will retain only the clusters which have a large difference in outcomes from their parent clusters. The summarization algorithm is presented using pseudo-code in algorithm 1.

Algorithm 1.

Simulation Summarization.

The set of compressed agent trajectories ultimately constitutes our summary representation of the simulation. It can be queried for various quantities of interest, as will be illustrated in the experiments below. We next present a toy example to illustrate the working of the algorithm, before turning to a large-scale complex disaster scenario simulation.

5 Experiments with a toy domain

Here, we present results from a toy example where a set of agents do a random walk on a 5-by-5 grid. There are 100K agents and all of them start at the same location (2, 2) on the grid. At each time step, they move to a neighboring cell (including staying at the same cell) at random. An agent gets a reward when it reaches cell (5, 5). For simplicity, once an agent gets a reward, it does not move.

The condition under which agents obtain reward is unknown to them. Please note that we are not actually learning a policy to maximize the reward. It is just a simple process to illustrate the functioning of our algorithm and to see if it can identify the states that provide information about their chances of getting a reward.

We run this simulation for 30 iterations and about 26500 agents got rewards at the end of the simulation. We tried two different values of KL-divergence threshold, δ: 0.3 and 0.5.

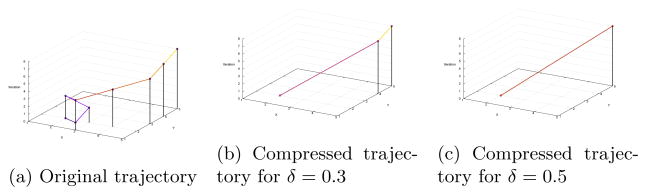
Figures 1a, 1b, and 1c show a sample trajectory and corresponding compressed trajectories for δ values 0.3 and 0.5, respectively. The high value of δ (0.5) can only identify states that cause sudden changes in probability distribution over final outcomes and hence identifies cell (5, 5) as the causal state. While the lower δ (0.3) can detect gradual changes and hence identifies neighbors of cell (5, 5) also as once an agent reaches cell (5, 4), it is easy to reach cell (5, 5).

Fig. 1.

A sample trajectory at various levels of compression.

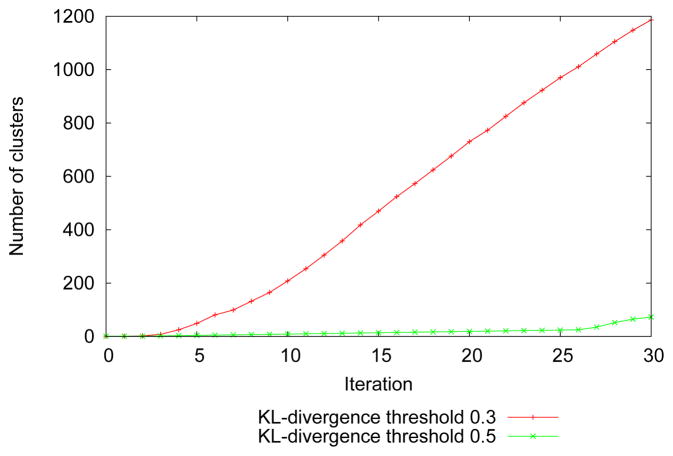
Figure 2 shows the number of clusters vs. iteration for different threshold values. As small values of δ mean identifying gradual changes, the number of clusters are more. As δ increases the number of clusters decreases. Please note that the minimum size of a cluster is constrained to be 30 (so that the number of samples in a cluster are enough for performing a statistical test) and this poses a limit on splitting and hence identifying states that do not appear enough number of times.

Fig. 2.

Number of clusters vs. iteration

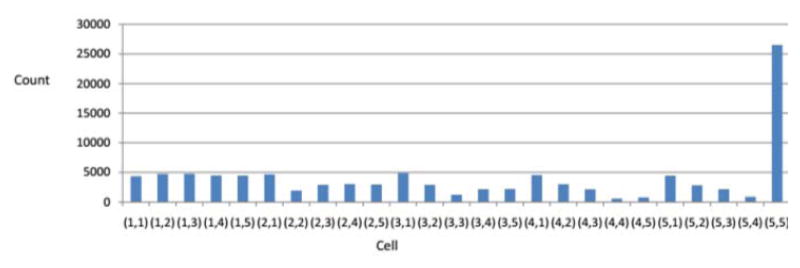
Overall compression defined as ratio of average length of compressed trajectory to length of uncompressed trajectory is 0.051 and 0.0333 for δ=0.3 and δ=0.5, respectively. As expected, higher value of δ leads to higher compression. It also captures the most relevant state (5, 5) (Figure 3). Figure 3 shows the number of times a given cell appears in a compressed trajectory for δ=0.5. Other cells appear in compressed trajectories only in later iterations. These are the cells from which an agent can not reach cell (5, 5) by iteration 30. So the values of state variables (cell here) along with the reward probability give information about state-reward structure.

Fig. 3.

Frequency distribution for cells in compressed trajectories.

6 Large-scale disaster simulation

Now, we turn to a very complex multiagent simulation of a human-initiated disaster scenario. Our simulation consists of a large, detailed “synthetic population” [3] of agents, and also includes detailed infrastructure models. We briefly summarize this simulation below before describing our experiments with summarizing the simulation results and the causally-relevant states our algorithm discovers.

6.1 Scenario

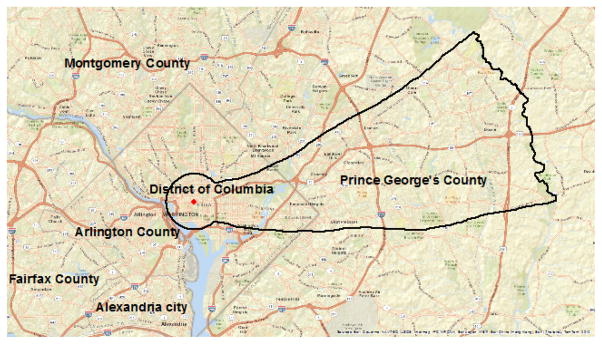
The scenario is detonation of 10kT hypothetical improvised nuclear device in Washington DC. The fallout cloud spreads mainly eastward and east-by-northeastward. The area that is studied is called the detailed study area (DSA; Figure 4) which is the area under the largest thermal effects polygon (circle) and the area under the widest boundary of the fallout contours within DC region county boundaries (which consists of DC plus surrounding counties from Virginia and Maryland).

Fig. 4.

The detailed study area (DSA).

The blast causes significant damage to roads, buildings, power system, and cell phone communication system. The full simulation uses detailed data about each of these infrastructures to create models of phone call and text message capacity [5], altered movement patterns due to road damage [1], injuries due to rubble and debris, and levels of radiation protection in damaged buildings.

6.2 Agent Design and Behavior

The scenario affects all people present in DSA at the time of detonation which includes area residents, transients (tourists and business travelers), and dorm students. Health and behavior of an individual depends upon its demographics as well as its location in the immediate aftermath of the event. This information is obtained from synthetic population [2]. Synthetic population is an agent-based representation of a population of a region along with their demographic (e.g, age, income, family structure) and activity related information (e.g. type of activity, location, start time). Detailed description about creating residents, transients, and dorm students can be found in [2, 15, 14]. There are 730,833 people present in DSA at the time of detonation which is same as the number of agents in the simulation.

Apart from demographics and location (as obtained from synthetic population), agents are defined by a number of other variables like health (modeled on a 0 to 7 range where 0 is dead and 7 corresponds to full health), behavior (described in the next paragraph), whether the agent is out of the affected area, whether the agent is the group leader, whether the agent has received emergency broadcast (EBR), the agent’s exposure to radiation, etc.

Each agent keeps track of knowledge about family members’ health states which could be unknown, known to be healthy, or known to be injured. This knowledge is updated whenever it makes a successful call to a family member or meets them in person.

Follow-the-leader behavior is also modeled, i.e., once family members encounter each other, they move together from there on. One of them becomes the group leader and others follow him. This kind of behavior is well-documented in emergency situations. Similarly when a person is rescued by someone he travels with him until he reaches a hospital or meets his family members.

Agent behavior is conceptually based on the formalism of decentralized semi-Markov decision process (Dec-SMDP) with communication [10] using the framework of options [20]. Here, high level behaviors are modeled as options, which are policies with initiation and termination conditions. Agents can choose among six options: household reconstitution (HRO), evacuation, shelter-seeking (Shelter), healthcare-seeking (HC-seeking), panic, and aid & assist. High level behavior options correspond to low level action plans which model their dependency with infrastructural systems. These actions are: call, text or move. Whom to call or text and where to move depends upon the current behavior option, e.g., in household reconstitution option, a person tries to move towards a family member and/or call family members while in healthcare-seeking option, a person tries call 911 or move towards a hospital. Details of the behavior model can be found in [14].

7 Experiments

Our goal here is to generate a summary for the disaster simulation. Agents and locations that they visit are represented by about 40 variables which could take binary, categorical or continuous values, leading to a very large state space. Hence, here we focus on subsets of these variables for generating summary.

We use data for the first 30 iterations and use the probability distribution over the final health state (in iteration 100, 48 hours after the blast) to identify causal states that affect the final health state.

7.1 Effect of behavior and emergency broadcast

In first experiment, we only use two variables to split clusters: if received emergency broadcast (EBR, 1 if received and 0 otherwise) and behavior. Here, apart from the six behavior options mentioned in the previous section, behavior variable also includes two categories indicating if an agent is in healthcare location (in HC loc) and if it is out of area.

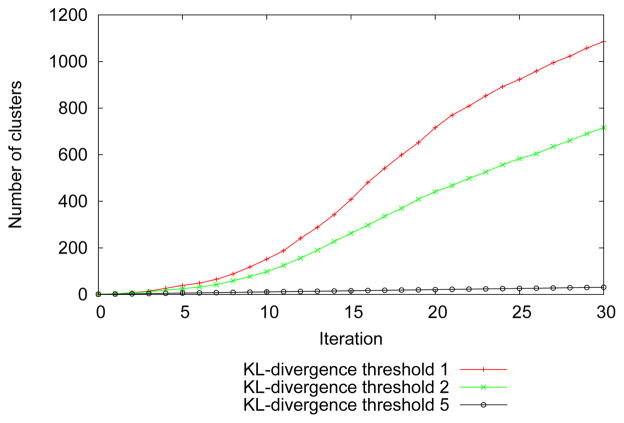
We try three different values of δ: 1, 2, and 5. Figure 5 shows number of clusters for different values of threshold. As higher values of δ can only identify sudden changes in the outcomes, δ=5 only identifies changes when agents die. We compare the causal states identified by other two threshold values next.

Fig. 5.

Number of clusters when considering EBR and behavior only.

We save the compressed trajectories in a database table along with the expected value of final health state. This table can be used to query any subpopulation for the outcome of interest. For example, Identify transitions by iteration 6 (within first hour) where the expected final health state is improved, order by expected improvement in descending order. Top results for δ=2 and δ=1 are as shown in Tables 1 and 2, respectively.

Table 1.

Effect of EBR and behavior, δ =2

Rank	Iteration	EBR	Behavior
1	2	0	out of area
2	3	0	out of area
3	5	0	in HC loc
4	6	0	in HC loc

Table 2.

Effect of EBR and behavior, δ =1

Rank	Iteration	EBR	Behavior
1	2	0	out of area
2	3	0	out of area
3	6	0	in HC loc
4	4	1	out of area
5	4	1	in HC loc
6	3	0	evacuation
7	4	0	out of area
8	2	0	evacuation
9	5	0	in HC loc

Here, δ=2 shows that being at healthcare location and out of area are important for improving health outcomes. As expected, δ=1 shows more gradual transitions and shows that evacuation is also important from health perspective. It is evacuation behavior that leads to out of area.

7.2 Effects of other variables

Here, apart from EBR and behavior, we also include current health state, radiation exposure level (with four levels: low, medium, high, and very high), if received treatment, and distance from ground zero (with three levels (based on damage zones as described in [4]): less than 0.6 miles, between 0.6 and 1 mile, and greater than 1 mile). We set δ=5 and evaluate four queries as below:

Query 1

Identify top 10 transitions by iteration 10 where current health state remains same (so improvement is not due to current health state) but the expected fianl health state is improved, order by expected improvement in descending order. Top results are as shown in Table 3.

Table 3.

Top results for query 1.

Rank	Iteration	Health state	EBR	Behavior	Radiation exposure	Treatment	Distance from ground zero
1	8	5	0	in HC loc	high	0	>0.6 mile, <1 mile
2	8	7	1	panic	medium	0	>1 mile
3	10	5	0	out of area	medium	0	>1 mile
4	9	6	0	out of area	medium	0	>1 mile
5	4	4	0	in HC loc	high	0	>0.6 mile, <1 mile
6	7	7	0	out of area	medium	0	>1 mile
7	3	4	0	in HC loc	high	0	>0.6 mile, <1 mile
8	8	7	0	out of area	medium	0	>1 mile
9	8	6	0	out of area	medium	0	>1 mile
10	9	7	0	out of area	medium	0	>1 mile

Results show that for agents who are within 1 mile of ground zero, are in health state 4 or 5, reaching healthcare location by iteration 10 helps improving health, even if the exposure level is high. Here, the value of treatment variable is zero which means that these agents have reached healthcare location but have not yet received treatment. This suggests that atleast initially (within first 3 hours) there are not long queues at these healthcare locations and so once an agent reaches healthcare location, it is quite likely that it will receive treatment which leads to an improved health. For agents in healthstate 5 to 7, who are far from ground zero though with medium exposure, getting out of area helps. Also, for agents in health state 7, who are far from ground zero, with medium exposure, and panicing, receiving EBR helps (as it provides information about the event and recommends sheltering).

Please note that the algorithm only finds states that affect the final outcomes significantly. Interpretation of the results requires some domain knowledge. For example, it is our knowledge that suggest that reaching healthcare location helps even if the exposure to radiation is high, not receiving high radiation exposure at healthcare location.

Next we identify states that reduce the expected health state by iteration 10.

Query 2

Identify top 10 transitions by iteration 10 where current health state remains same (so reduction is not due to current health state) but the expected final health state is reduced, order by expected reduction in descending order. Top results are as shown in Table 4.

Table 4.

Top results for query 2.

Rank	Iteration	Health	EBR	Behavior	Radiation	Treatment	Distance from state exposure ground zero
1	10	3	0	HC-seeking	low	0	>1 mile
2	9	3	0	HC-seeking	low	0	>1 mile
3	7	7	0	HRO	high	0	<0.6 mile
4	5	3	0	panic	low	0	>1 mile
5	5	3	0	HC-seeking	low	0	>1 mile
6	4	3	0	HC-seeking	low	0	>1 mile
7	9	7	0	HRO	high	0	<0.6 mile
8	8	7	0	HRO	high	0	<0.6 mile
9	4	3	0	panic	high	0	>1 mile
10	7	3	0	panic	high	0	>1 mile

For agents who are currently in a full health, close to ground zero, and have high exposure level, doing household reconstitution (HRO) reduces their expected outcome. Even if the current health state is good, this accounts for the delayed effect of radiation. For people who are already in low health (health state 3), panicing or seeking healthcare (which makes them travel to healthcare location and exposed to more radiation) deteriorates expected health state, even if far from ground zero.

For people who are close to ground zero (within 0.6 mile from ground zero which is a severe damage zone [4]), the likelihood of survival is very low while for people who are further than 1 mile (in light damage zone [4]), though they may have minor injuries, they can survive by themselves. However, survival is more complicated between 0.6 to 1 mile (defined as moderate damage zone) and hence next we run queries to see what people who started between 0.6 to 1 mile did that improved or reduced their expected final health.

Query 3

For people who started between 0.6 and 1 mile, identify top 10 transitions where current health state remains same and current distance is less than 1 mile (so improvement is not due to current health state or current distance) but the expected final health state is improved, order by expected improvement in descending order. Top results are as shown in Table 5.

Table 5.

Top results for query 3.

Rank	Iteration	Health	EBR	Behavior	Radiation	Treatment	Distance from state exposure ground zero
1	29	5	0	Shelter	medium	0	>0.6 mile, <1 mile
2	24	5	0	Shelter	medium	0	>0.6 mile, <1 mile
3	25	5	0	Shelter	medium	0	>0.6 mile, <1 mile
4	4	4	0	in HC loc	high	0	>0.6 mile, <1 mile
5	21	6	0	Shelter	low	1	>0.6 mile, <1 mile
6	3	4	0	in HC loc	high	0	>0.6 mile, <1 mile
7	14	5	0	Shelter	medium	0	>0.6 mile, <1 mile
8	23	5	0	Shelter	medium	0	>0.6 mile, <1 mile
9	4	5	0	in HC loc	low	0	>0.6 mile, <1 mile
10	3	5	0	in HC loc	medium	0	>0.6 mile, <1 mile

Results show that for people who started between 0.6 and 1 mile, reaching healthcare location early on (within first hour) helps improving expected final health, even if moderately injured (health state 4) and have high radiation exposure. For people with minor injury (health state 5) and with medium exposure to radiation, sheltering later on helps. Please not that eventhough our algorithm suggests so, it is not just sheltering in these particular iterations (14, 23, 24, 25 or 29) that helps but it is sheltering for a long period prior to and upto these iterations which improves expected health. This is because currently our algorithm does not detect effects of a sequence of particular actions (e.g., sheltering for a long period of time) and we would like to adapt it in future for detecting effects of sequential actions.

Query 4

For people who started between 0.6 and 1 mile, identify top 10 transitions where current health state remains same (so reduction is not due to current health state) but the expected final health state is reduced, order by expected reduction in descending order. Top results are as shown in Table 6.

Table 6.

Top results for query 4.

Rank	Iteration	Health state	EBR	Behavior exposure	Radiation	Treatment	Distance from ground zero
1	9	3	0	HC-seeking	low	0	>1 mile
2	7	7	0	HRO	high	0	<0.6 mile
3	17	7	0	Aid & assist	high	0	<0.6 mile
4	12	3	0	HC-seeking	low	0	>1 mile
5	4	3	0	HC-seeking	low	0	>1 mile
6	9	7	0	HRO	high	0	<0.6 mile
7	8	7	0	HRO	high	0	<0.6 mile
8	4	3	0	Panic	low	0	>1 mile
9	5	7	0	HRO	high	0	>0.6 mile, <1 mile
10	3	3	0	HC-seeking	low	0	>1 mile

For people who started between 0.6 and 1 mile, who are currently in full health (health state 7) and with medium radiation exposure, household reconstitution and aid & assist reduces their expected final health. While for people who are already in low health (health state 3), though with low radiation exposure, panicing or seeking healthcare reduces health. This is because these behaviors make them go outside looking for information, family members, other injured people, or nearest healthcare locations, exposing them to further radiation.

We see, in the above queries, that a number of meaningful states have been discovered by the summary.

8 Conclusion

As large-scale and complex simulations are becoming common, there is a need for methods to effectively summarize results from a simulation run. Here, we present a simulation summarization problem as a problem of extracting causal states (including actions) from agents’ trajectories. We present an algorithm that identifies states that change the probability distributions over final outcomes. Such causal states compress agent trajectories in such a way that only states that change the distribution of final outcomes significantly are extracted.

These extracted trajectories can be stored in a database and queried. A threshold on effect size is used to specify what change is considered significant. Higher value of this threshold identify states that cause sudden changes in final outcomes while smaller values can identify gradual changes.

We present a toy example to show the effectiveness of our algorithm and then apply it to a large-scale simulation of the aftermath of a disaster in a major urban area. It identifies being in a healthcare location, sheltering, evacuation, and being out of the area as states that improve health outcomes while panic, household reconstitution, and healthcare-seeking as states (behaviors) that worsen health.

There are several directions for future work. Summary representations can be used to compare simulations with different parameter settings to identify if parameter changes result in changes in causal mechanisms. Summary representations can potentially also be used for anomaly detection.