Abstract
Objective
Transcranial direct current stimulation (tDCS) aims to alter brain function noninvasively via electrodes placed on the scalp. Conventional tDCS uses two relatively large patch electrodes to deliver electrical currents to the brain region of interest (ROI). Recent studies have shown that using dense arrays containing up to 512 smaller electrodes may increase the precision of targeting ROIs. However, this creates a need for methods to determine effective and safe stimulus patterns as the degrees of freedom is much higher with such arrays. Several approaches to this problem have appeared in the literature. In this paper, we describe a new method for calculating optimal electrode stimulus pattern for targeted and directional modulation in dense array tDCS which differs in some important aspects with methods reported to date.
Approach
We optimize stimulus pattern of dense arrays with fixed electrode placement to maximize the current density in a particular direction in the ROI. We impose a flexible set of safety constraints on the current power in the brain, individual electrode currents, and total injected current, to protect subject safety. The proposed optimization problem is convex and thus efficiently solved using existing optimization software to find unique and globally optimal electrode stimulus patterns.
Main results
Solutions for four anatomical ROIs based on a realistic head model are shown as exemplary results. To illustrate the differences between our approach and previously introduced methods, we compare our method with two of the other leading methods in the literature. We also report on extensive simulations that show the effect of the values chosen for each proposed safety constraint bound on the optimized stimulus patterns.
Significance
The proposed optimization approach employs volume based ROIs, easily adapts to different sets of safety constraints, and takes negligible time to compute. In-depth comparison study gives insight into the relationship between different objective criteria and optimized stimulus patterns. In addition, the analysis of the interaction between optimized stimulus patterns and safety constraint bounds suggests that more precise current localization in the ROI, with supposably improved safety criterion, may be achieved by careful selection of the constraint bounds.
1 Introduction
tDCS modulates brain activity noninvasively [1–5]. tDCS is of great current interest to support treatment of various brain disorders (stroke [6], epilepsy [7], Parkinson's Disease [8,9], depression [10,11], etc.). In other applications, tDCS has been successfully employed on healthy subjects e.g. to increase cognitive brain function [12–14].
Because tDCS uses electrodes placed on the scalp to inject current, it is difficult to precisely control the current flow in the head and brain in order to elicit the desired current density field in a remote target ROI. In particular, current delivery to the ROI is limited due to the shunting effect of the scalp and cerebrospinal fluid (CSF) [15, 16]. Moreover, simply controlling the magnitude of the current density in the ROI may not be sufficient to achieve a desired modulation outcome; current direction is also critical [1,17,18]. This introduces additional difficulties in achieving the desired level of control over the injected current. Finally, subject comfort and safety considerations require careful attention to prevent unintended consequences of current application on the scalp (e.g. skin burns, itching sensations) and in the brain (e.g. fatigue, headache, phosphenes) [4,19]. Thus, investigators and clinicians have been particularly interested in improving the precision of targeting in tDCS to efficiently utilize the current delivered to the brain and incur minimal adverse effects.
Conventional tDCS uses two relatively large (25-35 cm2 contact area) patch electrodes to deliver electrical currents to the brain ROI. One approach to improve targeting in conventional tDCS is to optimize the placement of these two patch electrodes. Optimal placement may change depending on whether maximum focality or directionality at the target ROI is desired [20]. When the goal is to maximize electric field strength at the target site, for example, ‘standard’ two patch electrode montages recommended for modulating cortical ROIs such as primary motor cortex (anode over the primary motor cortex - cathode above the supraorbital area [1,12]) and dorsolateral prefrontal cortex (anode at F3 - cathode above the supraorbital area [21]) are not necessarily optimal [20,22].
Another approach to increase the focality of the modulation over conventional tDCS is to use dense electrode arrays, consisting of a large number of smaller (1-2 cm2 contact area) electrodes instead of the conventional patch electrodes [23–27]. However, the availability of a large number of electrodes, with the ability to control individualized current to each, provides a dramatic increase in the number of degrees of freedom, and therefore it is important to devise systematic approaches to determine optimal current injection patterns with these dense arrays. In this work, we introduce, solve, and test an optimization problem whose solution finds optimal current injection patterns for dense array tDCS. To the best of our knowledge, the only other systematic approaches on this subject are reported in [28–32]. Optimization problems introduced in these reports differ in various ways: optimization objective, safety constraints considered, and the methods used to find the stimulus pattern. In this paper we will describe our approach in detail, contrast it with two of the existing approaches, and present some detailed comparisons of current patterns optimized by each of the three methods. In addition, as we will describe, our own implementations of all three methods will be made freely available to enable further comparison by the tDCS community.
To summarize previous reports, Im and colleagues proposed a method to optimize two patch electrode positions, followed by an algorithm to determine the currents on a 4×4 electrode array that replaced the anode patch for higher focality at the target [22, 28, 29]. Their approach does not necessarily provide a unique and global solution. Sadleir and colleagues [30] adopted the idea of maximizing the average current density in the ROI by shaping the currents applied through an array of 19 large patch electrodes (22 cm2 contact area). The authors applied safety constraints on the current in the non-ROI regions and included the capability of having extra-cranial electrodes; however, their approach also fails to find a unique and global solution, which limits its generalizability.
A variety of problem formulations that do provide unique and global stimulus patterns have been studied by Dmochowski and colleagues [31]. The authors found optimal electrode stimulus patterns that increase either focality or intensity of the modulation in focal ROIs. The work by Ruffini and colleagues [32] added the flexibility of choosing a subset from a set of predetermined electrode locations and defining spatially extended cortical ROIs. They first determined electrode number and locations using a genetic algorithm and then optimized electrode currents using least squares. Their method used 27 potential electrode locations, however, the extension to arrays containing higher number of electrodes is not trivial due to the genetic algorithm step.
In this study, we present an alternative approach for optimization of current injection pattern employing multi-electrode configurations. We formulate an optimization problem that provides a unique1 and global current injection pattern as a solution. The proposed approach employs volume based ROIs, can be easily adapted to incorporate different sets of safety constraints, takes negligible time to compute, and relies on open source software (SCIRun [33], BrainStimulator [34], CVX [35]).
In what follows, we report exemplary results for four anatomical ROIs: the medial orbitofrontal cortex (MFC), anterior cingulate cortex (ACC), parahippocampal gyrus (PHCG), and precuneus (PC). These regions were chosen for evaluation because they are deep within the cerebral hemisphere, and are important to both cognitive and neurophysiological function. We then show the effect of a very large number of choices for the safety constraint bounds on the achievable targeting. We also compare our results to results from the two most similar studies in the literature: [31] by Dmochowski and colleagues (2011), and [32] by Ruffini and colleagues (2014).
Our results show that the proposed optimization approach is a good alternative to existing methods and may extend the capabilities and specificity of tDCS. It can readily be extended to allow directional targeting of multiple ROIs distributed across the entire brain at small computational cost and with the flexibility to add a variety of constraints to ensure safety and comfort for the subject.
2 Methods
In this section, we present in detail the construction and solution of the proposed optimization problem. We start by giving a high level description of the model used in the simulations. A finite element method (FEM) section describes how the current density in the head was estimated numerically. We then describe our optimization formulation in detail and briefly compare it with the two most similar existing methods, followed by a detailed description of a reformulation of the optimization problem which leads to a computationally fast solution. We conclude this section with a description of the simulation studies we report on in the sequel.
2.1 Realistic head model
Previously acquired multi-modal imaging data (magnetic resonance imaging (MRI), computed tomography (CT), and diffusion tensor imaging (DTI)) was used to generate a high-resolution, realistic head model. We used the software package Cleaver [36] to generate a tetrahedral mesh consisting of 8 million nodes and 47 million tetrahedral volume elements (Figure 1), with 8 modeled tissue layers (scalp, skull, CSF, grey matter (GM), white matter (WM), eye, internal air, and electrode sponge). Table 1 lists conductivity specifications for different layers in the volume conduction model.
Figure 1.
The tetrahedral head mesh used in the simulations. An array of 126 cylindrically shaped electrodes (transparent gray), each with 1 cm diameter and 0.5 cm thickness, were placed on the scalp. A realistically shaped ROI (precuneus) is shown in red.
Table 1.
The conductivity specifications for 8 tissue types in the head model.
| Tissue type | Conductivity (S/m) | Notes |
|---|---|---|
| Scalp | 0.33 | [32, 37] |
| Skull | min = 0.0064 (hard bone) max = 0.0259 (soft bone) |
Based on CT [38]. Linear scaling of HU units between min and max [27, 39]. |
| CSF | 1.79 | [32, 37] |
| GM | 3×3 tensors. | Based on DTI [40–42]. |
| WM | 3×3 tensors. | Based on DTI [40–42]. |
| Eye | 0.40 | [43] |
| Internal air | 1e-15 | [31] |
| Electrode sponge | 1.4 | [44] |
2.2 Finite element analysis
Assuming there are no interior current sources in the head, the potential field can be mathematically described with Laplace's equation: ∇·σ∇ϕ = 0, σ and ϕ being tissue conductivity tensor (value) and electrical potential, respectively. Solving Laplace's equation analytically in a realistic head is intractable and thus, as has generally been done in this field, we approximated the electrical potential numerically using the FEM. We used the complete electrode model to allow the current density to vary on the electrode surface and to incorporate the contact impedance of 5kΩ.m2 at the electrode-scalp interface [45].
In what follows, our notation distinguishes two closely related vector variables for the array of electrode currents. Ĩ denotes the full electrode current array, with one entry for each electrode, while I denotes the array with a chosen reference electrode excluded2:
where L is the total number of electrodes and .
Once the domain is discretized into volume elements and boundary conditions are specified, the unknowns are node potentials (u) and electrode potentials (U), for which a set of linear equations are derived from FEM (for details see [46,47]):
| (1) |
M is the so called global matrix and 0 is the zero vector. For computational reasons we explicitly computed the transfer matrix T that links the electrode current array I to node potentials u from (1) using an efficient lead field approach [31]:
| (2) |
T then is integrated into the optimization formulation to reduce the computational time significantly, noting that T is fixed as long as the head model remains unchanged.
2.3 Electrode current pattern optimization
We first introduce our objective and safety constraints and then describe an equivalent and computationally much more efficient form of the resulting constrained optimization problem.
2.3.1 Objective function
We assume that the ROI boundary and the desired directional field3 for the current density in the ROI are known. Given that, we maximize the projection of the induced current density J on this directional field inside the ROI:
| (3) |
where J(r) is the current density and d(r) is a dimensionless vector field of unit magnitude representing the desired direction for the current density at location r. The operator ‘□’ represents the vector dot product and ΩROI denotes the brain target region, which can be of any size and could be the union of disjoint volumes.
The objective function in (3) can be seen as a generalization of the objective function used by Dmochowski and colleagues in [31] to maximize the current intensity from point-like targets to volumetric ROIs. This choice of objective function is different from the least squares approaches [31, 32] used in the comparison study below, and we want to point out here the difference and some of the expected consequences. Specifically, in contrast to the least squares approaches in [31,32], we specify only the desired orientation field for the current density in the ROI; the magnitude along that directional field is left as a free variable to be maximized. The comparison methods specify an explicit desired electric field in the ROI and in the brain, and minimize a measure of the difference (weighted least squares) between that desired field and the optimized result. One consequence of different objective function definitions is that in our approach we are not required to specify the desired magnitude, only the ROI and the desired directional field. Another is that the reported implementations of the comparison methods choose a uniform magnitude desired field in the ROI, implicitly penalizing for variability, while our approach allows the optimum field in the ROI to vary as long as the integral of the total projected current is maximized. Another is that our objective does not take into account the component of the optimized field normal to the desired directional field. On the other hand, the comparison methods implicitly penalize the electric field component normal to the desired field. Finally, our objective integrates over the ROI using the FEM basis functions, while the comparison methods use point-wise computation on the mesh nodes; thus we take into account differences in the volumes of the finite elements themselves.
2.3.2 Safety constraints
We impose three safety constraints. In order to prevent excessive current delivery to the brain, the current power in the brain outside the ROI is constrained:
| (4a) |
where Ωbrain represents the entire brain. Another safety constraint limits the total current entering the head:
| (4b) |
where ‘∥∥p’ represents the p-norm. Since constraint C2 (4b) may not be sufficient to prevent high current densities locally, especially with small electrodes, we also impose constraints on each individual electrode current:
| (4c) |
where ‘⪯’ stands for ‘element-wise less than or equal’.
2.3.3 Computationally efficient optimization formulation
With the assumption that the desired directional field is treated as constant within each individual volume element, the integrals in (3) and (4a) become weighted sums. We evaluated these integrals (see Appendix A) and reduced them to linear and quadratic functions of the electrode current array; after doing so, the overall optimization problem becomes:
| (5) |
| (6a) |
| (6b) |
| (6c) |
We can think of w as the array of weights representing the relative importance of each electrode current on the directional current density in the ROI. The matrix Q links these electrode currents to the current power in the brain outside the ROI. The sizes of w and Q are L-1 × 1 and L-1 × L-1, respectively, since, as described above, the number of independently controlled electrodes is one less than the total number of electrodes L.
The optimization problem with the objective (5) and constraints (6a-c) is convex, and thus has a unique, global solution. In addition, the problem size is L – 1, which is many orders of magnitude smaller than the number of nodes in the mesh. By pre-calculating w and Q, we avoid the need to find the current density at each iteration to evaluate the objective criterion and constraints. Thus the problem size is small enough that we are able to simply employ CVX, a disciplined convex optimization solver package for Matlab [35], to compute the solution. Despite using such a general convex optimization solver, the execution time of an optimization for a given set of objectives and constraints, on a typical modern desktop computer, is on the order of seconds.
2.4 Simulations
We chose four anatomical ROIs, shown in Figure 2, to display exemplary results of the proposed method. All four ROIs were deep rather than superficial, and thus challenging as targets, with the PHCG ROI being significantly deeper than the other three. The desired directional field for all four ROIs was based on the local cortical surface normal. Since the size of the tetrahedral elements was significantly smaller than the thickness of the cortex, to determine the cortical surface normal field through the full ROI, we first computed the surface normal on the cortical surface and on the white matter boundary and then interpolated into the interior of the cortex.
Figure 2.
Four anatomical ROIs used in the simulations: (red) medial orbitofrontal cortex (MFC), (blue) anterior cingulate cortex (ACC), (green) parahippocampal gyrus (PHCG), and (yellow) precuneus (PC).
In these simulations the total current entering the head was limited to 2 mA (ımax = 2 mA). Each individual electrode current was limited to 0.30 mA (−Imin = Imax = 0.30 mA). We chose these values so that maximum scalp current density was comparable to that of conventional tDCS4. The current power in the brain outside the ROI was limited to 10−6 A2/m, which was based on the literature [18].
With this set of constraints in place, we report on our investigation of the interaction between these constraints and optimal stimulus patterns. We carried out a study on one of the ROIs (MFC) in which we calculated the optimal current patterns for a wide range of constraint bounds. We analyzed the changes in modulation strength and maximum current density in the brain due to changes in the constraint bounds, leveraging the low computational cost of our formulation of the optimization problem.
In order to validate our methodology, we compared our results to the results from two other studies [31,32] that use convex formulations for optimizing dense electrode array stimulus patterns. We implemented two least squares methods from these studies and computed optimal patterns for M1 motor cortex area as the target ROI to facilitate comparisons with the results reported in the cited papers. In contrast to the anisotropic model used in the first set of simulations, we used an isotropic head model for these simulations5 because both comparison methods optimize and constrain the electric field while ours uses the current density. Isotropic conductivities ensure current density field and electric field are proportional to each other by a scalar conductivity value in each tissue layer and thus again facilitate comparison.
Because each of these three methods imposes different sets of safety constraints, as seen in Table 2, we adapted the following procedure to optimize the current stimulus patterns. We first optimized the stimulus pattern using our implementation of one of Dmochowski et al.'s least squares problems [31], setting the constraint bound for individual electrode currents to 1 mA. The total injected current resulting from that solution was used to set the constraint bound for total injected current to 3.62 mA for the other two methods. We then solved Ruffini et al.'s least squares problem with these constraint bounds. To imitate the constraint C1 (4a) in our formulation, we set the bound on the electric power in the brain outside the ROI to 44.04 V2m, which was the minimum of the electric power delivered to the brain outside the ROI with the comparison method solutions.
Table 2.
Objective and constraints for all three methods used in the comparison study.
| Dmochowski et al. [31] | Ruffini et al. [32] | Guler et al. | |
|---|---|---|---|
| Objective: | Minimize least squares error between desired and achievable electric field in the brain | Minimize least squares error between desired and achievable electric field component normal to the cortex | Maximize integral of current density component normal to the cortex over the ROI |
| Constraints: | Individual electrode currents | Individual electrode currents and total injected current | Individual electrode currents, total injected current and current power in the brain outside ROI |
We note that there are multiple optimization formulations to maximize either focality or intensity at the target ROI by Dmochowski and colleagues in [31]; we have implemented only one of the least squares approaches to compare our method with. The other least squares method in [31] uses only a total injected current constraint, without any constraint on individual electrode currents. This approach can be expected to lead to very sparse solutions with higher current intensities on only a few electrodes, so we concluded it is not an appropriate comparison method. The other two methods in [31] use point-wise rather than volumetric objectives; one of them, like ours, maximizes current along a desired direction but only at a point. Thus direct comparison with our approach would be difficult, and indeed our objective can be seen as an integration over an ROI volume of the objective in [31]. We also note that we only implemented the least squares step by Ruffini and colleagues in [32], assuming that the number and locations of the electrodes were known. The number and locations of the electrodes are determined in their work by their genetic algorithm step. Since implementations of the genetic algorithm can be highly variable, we felt implementing our own version and then using it in the optimization would just introduce confusion into the comparison.
3 Results
As described above, we first report on our optimization results for the four aforementioned anatomical ROIs. We then report on a comprehensive study of the effect of safety constraint choices on the optimal solution. Finally, we compare our method with two existing approaches, listed in Table 2.
3.1 Exemplary results on four ROIs
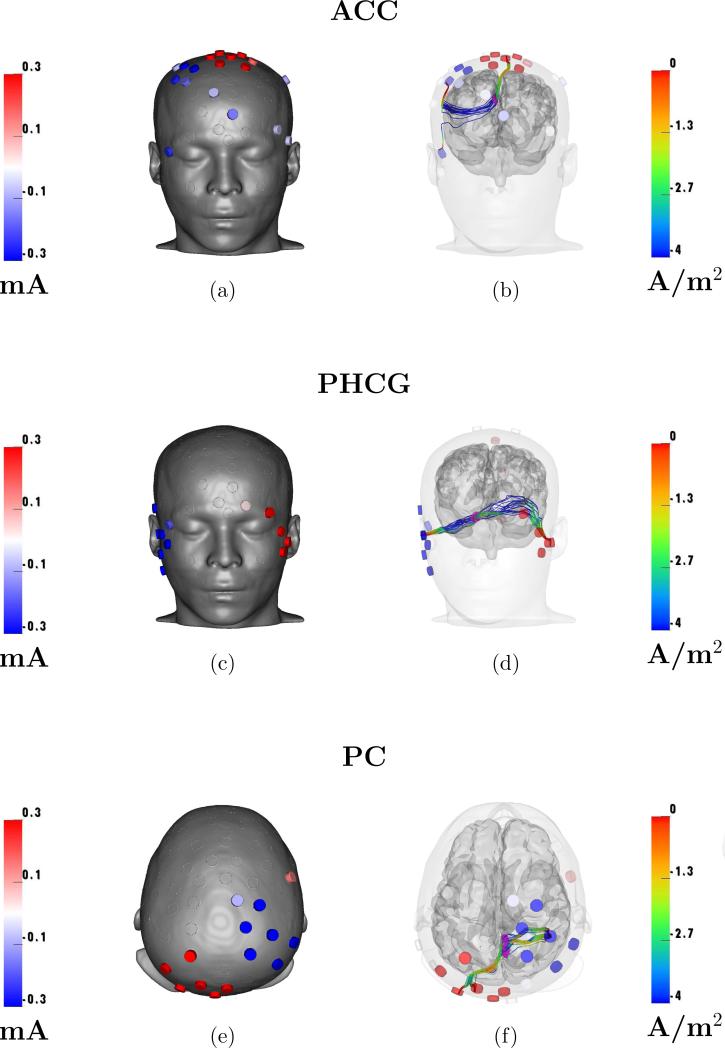
We summarize our findings for the four anatomical ROIs in Figures 3 and 4. In Figure 3, we show six views of the optimized results for one of the ROIs, the MFC. Panel (a) shows the optimized electrode current stimulus pattern, panel (b) the corresponding electrical potential on the scalp. Panels (c) and (d) show two visualizations of current density streamlines through the ROI. Panel (c) illustrates how the streamlines connect to the electrodes, while panel (d) shows the relationship, in the ROI, between the optimized current and the desired directional field, shown in pink. Since the streamlines in panel (c) do not show any current outside the ROI, panel (e) shows the current density on an axial slice through the ROI. Panel (f) visualizes the current density magnitude on the cortex. We observe from panels (e) and (f) that the cortical regions surrounding the ROI are exposed to much higher currents than the ROI, which may be pointing to the physical limitation of applying currents via scalp electrodes. In Figure 4, we show optimized stimulus patterns (left column) and streamlines through the ROI (right column) for the other three ROIs (ACC, PHCG, PC). We want to point out again that the streamline visualizations on panels (b), (d), and (f) show only the current that goes through the ROI and thus the current distribution across the entire head is not shown.
Figure 3.
Optimization results for targeting MFC. (a) optimal electrode current stimulus pattern, (b) electrical potential field on the scalp, (c) current density streamlines through ROI, (d) current streamlines (rainbow colored lines) and desired directional field (pink lines) in the ROI, (e) current density on an axial slice through ROI, and (f) current density magnitude on the cortex. The colorbars in (c) and (e) are log-scaled.
Figure 4.
Optimization results for targeting ACC, PHCG, and PC. (left) optimal electrode stimulus patterns, and (right) current streamlines through ROI. The colorbars for the current streamlines are log-scaled.
To provide more quantitative results, we tabulated median and peak values for current density magnitudes, of ROI and six tissue types for all four ROIs in Table 3. Although median of current density magnitude for the ROI is lower in the PHCG ROI compared to the other three, it is higher in the grey matter. This may be an indicator of the expected difficulty of targeting deeper brain structures with scalp electrodes. To more fully describe how the current density is distributed in the head for each ROI, we show current density magnitude histograms of different tissue layers in Figure 5. In more detail, each curve on a given plot shows the distribution of current density magnitude in the corresponding tissue type. Since each of the ROIs is much smaller in volume than, say, the grey matter, we normalized all the curves to have unit volume6 for each layer for better visualization. These plots show the degree to which we are able to focus current in the ROI in comparison to the surrounding tissues. Although there are regions in grey matter that receive higher currents than the ROI, the average current in the ROI is much higher than in the remaining grey matter as a whole. In particular we see that most of the current density in the ROI has higher magnitude than most of the grey matter in the MFC, ACC and PC ROIs. In contrast, the ROI and grey matter histograms in the PHCG are much closer together. These findings again are consistent with the expectation that modulation of deeper regions will be less focal than of shallower ROIs.
Table 3.
Median (Med) and maximum (Max) current densities of different tissue types for all four ROIs (Units: A/m2).
| MFC | ACC | PHCG | PC | |||||
|---|---|---|---|---|---|---|---|---|
| Tissue type | Med | Max | Med | Max | Med | Max | Med | Max |
| ROI | 0.069 | 0.214 | 0.050 | 0.086 | 0.034 | 0.103 | 0.050 | 0.203 |
| GM | 0.015 | 0.412 | 0.013 | 0.304 | 0.021 | 0.221 | 0.016 | 0.346 |
| WM | 0.011 | 0.300 | 0.011 | 0.245 | 0.016 | 0.200 | 0.013 | 0.348 |
| Scalp | 0.034 | 10.86 | 0.013 | 10.64 | 0.085 | 8.663 | 0.007 | 9.983 |
| Skull | 0.004 | 0.560 | 0.004 | 0.674 | 0.009 | 0.301 | 0.001 | 0.453 |
| CSF | 0.081 | 7.308 | 0.083 | 1.623 | 0.114 | 3.680 | 0.099 | 0.930 |
| Eye | 0.198 | 0.572 | 0.045 | 0.177 | 0.201 | 0.589 | 0.004 | 0.006 |
Figure 5.
Current density magnitude histograms of scalp, skull, CSF, GM and ROI for all four ROIs. (a) MFC, (b) ACC, (c) PHCG, and (d) PC modulation, all in cortical surface normal direction.
3.2 Effect of constraints
We chose the safety constraint bounds, as described above, to be consistent with approaches in the literature. However, these values are necessarily rough choices, so we leveraged the computational efficiency of our formulation to carry out a systematic sensitivity study of the effect of each constraint by solving the optimization problem repeatedly with a wide range of values for the bounds. We visualize the results in Figure 6 for the MFC ROI. Specifically, the figure shows objective function isolines as a function of individual electrode current bound and current power in the brain outside the ROI bound, where the total injected current bound was set to a constant (1 mA). The background color in the figure represents the maximum current density at any location in the brain, thus enabling us to detect any local “hot spots”. To aid the reader in interpreting this figure, we make some observations here about the results. First, we note that for significant portions of the constraint space, objective function isolines are almost parallel to one or the other of the axes. This indicates that relaxing the constraint bounds in those regions will have little effect; increasing the individual electrode current bound above the knee of a given contour, for example, will not improve the objective function but will cause higher peak values for the current in the brain. Second, both the objective function value and the maximum current density in the brain are sensitive to both bounds, but not in exactly the same way, suggesting that setting the bounds to achieve a desired value of the objective function can be done without necessarily causing a significant increase in the maximum current density. Third, the important region on the plot is an arc-shaped region going from the bottom-left corner up and to the right; in this region, increasing either of the constraint bounds improves the objective function. Finally, the sparsity of the optimal stimulus pattern and bounds for the safety constraints are closely related; relaxing the constraint bounds is likely to yield sparser optimal patterns. Thus, these results suggest that there is a region in constraint space in which we should choose the combination of bounds, taking into account both safety and the ability to increase potential modulation effect.
Figure 6.
Objective function isolines as a function of constraint bounds on the individual electrode currents and on the current power in the brain outside the ROI. The numbers on the isolines represent achievable directional current density in the ROI for a given set of constraint bounds. Note that the vertical axis is shown as the negative log of the current power bound in A2/m so that the bound gets larger as we move up the axis. The background color represents the maximum current density in the brain, whose colorbar is shown on the right and is log-scaled.
3.3 Comparison with other existing methods
We compared our method with two methods reported by Dmochowski and colleagues [31], and by Ruffini and colleagues [32]. Figure 7 shows the three optimized electrode current patterns on the scalp, along with the ROI. Figure 8 shows some comparisons of these three optimized patterns. The highest individual electrode current in magnitude differed in the optimal solutions (0.61, 0.75, and 0.91 mA). In addition, the total current was more uniformly distributed across the electrodes in Dmochowski et al.'s solution than in Ruffini et al.'s solution and than in Guler et al.'s solution.
Figure 7.
Optimized electrode stimulus patterns for targeting (a) M1 ROI in cortical surface normal direction, using (b) Dmochowski et al.'s, (c) Ruffini et al.'s, and (d) Guler et al.'s optimization formulation.
Figure 8.
Comparison of three optimal patterns. Top panel shows optimized currents for the electrodes with current magnitude higher than 0.1 mA in either of the three optimal patterns. Bottom panel shows the highest 20 electrode current magnitudes in each solution. Note that these sets of 20 ‘significant’ electrodes might differ across solutions. The residuals, i.e. sum of the injected current magnitudes for the remaining least significant 106 electrodes, were 1.79, 1.50, and 1.51 mA in Dmochowski et al.'s, Ruffini et al.'s, and Guler et al.'s solution, respectively.
Table 4 summarizes the statistics of the optimized electric field as well as the constraint bounds used in each optimization. We observe that our method produced a solution that yielded higher average electric field in the ROI (+%17) and lower in the brain (−%60) compared to Dmochowski et al.'s solution. In contrast, the average electric field with our solution is slightly lower both in the ROI (−%14) and in the brain (−%12) compared to Ruffini et al.'s solution, which presumably is due to relatively low constraint bound on the electric power in the brain outside the ROI.
Table 4.
Comparison of the statistics of electric fields optimized by our method and by the comparison methods. Mean value for the electric field in a particular region was calculated by integrating the electric field magnitude over the region, divided by the region volume. All units are V/m except where noted. The numbers with asterisk (*) are used as the constraint bounds for the corresponding method.
| Dmochowski et al. | Ruffini et al. | Guler et al. | |
|---|---|---|---|
| Brain | |||
| Max | 0.12 | 0.17 | 0.13 |
| Median | 3.4E-4 | 1.3E-3 | 2.5E-4 |
| Mean | 3.8E-3 | 1.7E-3 | 1.5E-3 |
| Electric power (ROI excluded) (V2m) | 44.04 | 116.46 | 44.04* |
| ROI | |||
| Mean | 0.05 | 0.07 | 0.06 |
| Head | |||
| Max | 70.08 | 70.93 | 74.38 |
| Highest electrode current in magnitude (mA) | 0.61 | 0.75 | 0.91 |
| Individual electrode bound (mA) | 1* | 1* | 1* |
| Total injected current (mA) | 3.62 | 3.62* | 3.62* |
4 Discussion
In this simulation study, we formulated and solved a multi-constraint optimization problem on the electrode current stimulus pattern to achieve, in our computational model, precise targeting and polarity in dense array tDCS. Computer-based simulations on a realistic head model showed ROI characteristics (e.g. depth) may have a significant effect on the optimal patterns and the current flow in the head. We recognize that these simulations must be tested by experimental results that provide validation that the intended current is actually delivered effectively. The sensitivity study on the effect of safety constraint bounds on the optimal patterns showed that relaxing the constraint bounds do not necessarily improve the objective function. Finally, we compared our method with the other two similar methods in the literature and found similar optimized stimulus patterns, with slight differences due to presumably different problem formulations.
In our simulations, we used dense arrays consisting of electrodes much smaller than the patch electrodes, which may result in high current densities at the electrode edges due to small contact area between the electrode and the scalp [16]. To this end, we imposed constraints on the individual electrode currents and also used the complete electrode model to more accurately estimate the non-uniform current density distribution at the electrode-scalp interface. Another approach to prevent high current densities locally would be to impose additional constraints on the elements closest to the electrode edges, where highest currents occur due to edge effect [48]. This, however, could mean imposing many more constraints and higher computational burden. A simpler yet more effective solution may be to design electrodes that distribute the current across electrode-scalp interface more uniformly by, for example, varying the sponge depth through the electrode [49].
Because the current flow in the head is very complex due to factors such as anatomical structures, tissue characteristics, electrode positions and shape [4, 50], there may be need, in particular settings, for additional current power constraints to prevent excessive current delivery to the critical regions in the brain. Although here we only constrained the current power in the brain outside the ROI, the optimization problem is readily capable of incorporating multiple critical regions, each assigned with its own safety bound, to allow the flexibility of defining subject-specific critical regions. As an illustration, in Figure 9, we added an additional constraint on the current power in the eye to simulate the desire to prevent phosphenes. We observe from the two solutions that the current patterns differ significantly when this additional constraint is imposed on the solution. The objective value reached with the additional eye constraint was 33% lower than the value reached without the eye constraint.
Figure 9.
Optimized electrode stimulus patterns (a) without and (b) with additional constraint on the current power in the eye.
Having an optimization problem with multiple safety constraints, it is important to understand the influence of each on the optimal stimulus pattern. Thus, we investigated the effect of each constraint bound on the objective function as well as on the maximum current density in the brain. Because our optimization was so computationally efficient, we were able to solve for the best stimulus pattern repeatedly, with varying constraint bounds. Results showed that loose constraint bounds don't necessarily yield higher desired current in the ROIs but they may allow higher peak currents in the brain. Carefully chosen safety bounds in the presence of multiple safety constraints are important in extending the range of tDCS applications.
Comparing our method with two other methods in the literature, we observe the solutions differ somewhat due to the difference in problem formulation. Because Dmochowki and colleagues’ method is a least squares fitting problem, high electric field magnitudes in the ROI are also penalized. Thus, we observe the highest electrode current magnitude in the optimal pattern is 0.61 mA although individual electrode current bound was set to 1 mA. In Ruffini and colleagues’ method, only the electric field component along the cortical surface normal is considered in the least squares fitting and thus there is more flexibility due to the unconstrained component tangential to the cortical surface. This, we speculate, is why this solution has a higher maximum electrode current magnitude (0.75 mA) than Dmochowski and colleagues’ solution. In our method, in addition to not constraining the component of the current tangential to the cortical surface, we also let the magnitude of the component normal to the cortical surface vary, which might produce solutions with higher currents for a subset of the electrodes. The only consideration in our formulation is to have the direction of the current density match the desired directional field.
In the case where it is useful to target several regions believed to be functionally or anatomically connected, perhaps even with differing relative importance, the ROI may be defined according to a weighted mapping scheme. For example, functional connectivity maps can be used to weight the ROI when the target entails the whole cortical surface [32]. We can easily adjust our objective function to achieve this goal by weighting the desired directional field such that each location in the joint ROI has its own weight (ω) associated with it, as in (7). Adding such weights does not affect the complexity of the problem and enables us to assign relative importance to different parts of the ROI:
| (7) |
All our results consider only the directed magnitude of stimulus current in the ROI. Of course the real goal of tDCS is effective modulation of neural activity, not just optimizing control over current density localization. The relationship between local density of injected current and modulatory effect is complex and, to-date, not well understood. This suggests that our method, and our comparison to competing methods, should be tested experimentally to better understand the efficacy of the results. Such testing is not trivial because of both the difficulty of defining adequate metrics of success and the need to exercise proper care in experimenting with the brains of human subjects, but some studies are being carried out, for example by using changes in TMS stimulus strength needed to obtain motor response, for motor cortex stimulation, under tDCS, as a surrogate for tDCS efficacy [51].
Another practical consideration is that dense array tDCS optimization schemes generally assume there are as many current sources available as the number of electrodes, which may be practically inconvenient, especially when the number of electrodes is as high as 100 or even larger. Thus it may be useful to develop optimization methods to find good stimulus patterns that use fewer current sources than electrodes. However the corresponding optimization problem is combinatorial and the number of configurations to check increases exponentially in both the number of current sources and the number of electrodes. Further research on how such solutions could be found using combinatorial optimization approaches is needed.
5 Conclusion
This study presents a novel method for calculating electrode current stimulus pattern in dense array tDCS that maximizes the current density along a desired directional field in the ROI. The proposed method provides a unique and global stimulus pattern for a given ROI and a desired directional field for the current density in the ROI. Simulation results on four anatomical ROIs suggests the difficulty of targeting deeper brain regions. Moreover, it was shown that increasing the constraint bounds may not improve the objective function but may cause higher peak values for the current density in the brain. The solutions found by our method and the two comparison methods appeared similar, with minor differences due to different objective and safety constraint choices.
Acknowledgment
This study was supported in part by the NIH/NIGMS Center for Integrative Biomedical Computing, P41 GM103545-17. The use of bone images (skull CT) for computing the conductivity effects in relation to electrical analysis and stimulation of head tissues is protected by US Pat. No. 6,529,759.
A Evaluating the integrals on a discretized domain
In this section, equivalent forms of integrals in (3) and (4a), after domain discretization, are derived. In linear FEM, potential field is assumed to be linear within each finite volume element and thus the potential at any point inside mth volume element can be written as:
| (8) |
where (x, y, z) is the position and am, bm, cm, dm are the linear coefficients. This linearity condition is satisfied at the nodes of the same element:
| (9) |
where denotes the potential at the jth node of the mth element and is the position of the jth node of the mth element, for j = 1, 2, 3, 4 and m = 1, 2 · · · M, M being the total number of volume elements in the mesh. Rewriting the set of equations in (9) in matrix form, we get:
| (10) |
where we defined um as the vector of potentials at the nodes of mth element and Pm as the position matrix of the nodes of the same element. The linear coefficients can then be found as:
| (11) |
Let Am represent the last three rows of matrix . Then . Note that um is a subset of the potentials at all nodes of the mesh and thus um = Smu, where Sm is a selection matrix of size 4×N. The current density at any point r in the mth element is found as:
| (12) |
All the terms on the right hand side of (12) are independent of the position. We can drop the position argument of the current density and use only Jm to denote current density at any point inside the mth element. The fact that current density is constant within each finite volume element is used to find equivalent forms for the integrals in the objective function (3) and power constraint (4a). The objective function (3) becomes a linear function of electrode currents:
| (13) |
where Ωm and vm denote the domain and volume of the mth finite volume element, respectively, and we assumed that the desired directional field is fixed through each finite element. Similarly, we can find an equivalent form for the power constraint (4a):
| (14) |
w and Q remain fixed through the optimization if the mesh, the desired directional field, and the ROI boundary remain unchanged. The size of w is #(electrodes)-1 × 1, and the size of Q is #(electrodes)-1 × #(electrodes)-1. Precalculation of w and Q before the optimization thus reduces the computation time significantly.
Footnotes
Conflict of interest
Sergei Turovets, Phan Luu, and Don Tucker are employees of EGI, manufacturer of dense array EEG and electrical neuromodulation systems.
Theoretically, there may be multiple solutions depending on the exact choice of constraint bounds, although this is highly unlikely to occur.
Note that since the algebraic sum of all currents entering the head must be equal to 0, the number of free electrode current variables in the optimization is 1 less than the number of electrodes; here we enforce that by choosing one electrode to be the reference and excluding it from the optimization.
Note that the desired directions can vary freely through the ROI; for example, a likely choice would be the cortical surface normal through the ROI, which, given the convoluted nature of the human cortex, would lead to a highly variable directional field through the region.
The total circumference of 7 dense array electrodes with a typical diameter of 1 cm is close to the circumference of a 5 cm × 5 cm patch electrode and the current is mostly concentrated at the electrode edges [16].
Instead of varying conductivity specifications for skull, GM and WM volume elements in the head model, we assigned constant conductivity values (skull = 0.01, GM = 0.33, and WM = 0.142 S/m) to each of these tissue layers.
Sum of the stair heights in each histogram is equal to 1.
References
- 1.Nitsche MA, Paulus W. Excitability changes induced in the human motor cortex by weak transcranial direct current stimulation. J Physiol. 2000 Sep;527(Pt 3):633–639. doi: 10.1111/j.1469-7793.2000.t01-1-00633.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Miranda PC, Lomarev M, Hallett M. Modeling the current distribution during transcranial direct current stimulation. Clin Neurophysiol. 2006 Jul;117(7):1623–1629. doi: 10.1016/j.clinph.2006.04.009. [DOI] [PubMed] [Google Scholar]
- 3.Holdefer RN, Sadleir R, Russell MJ. Predicted current densities in the brain during transcranial electrical stimulation. Clin Neurophysiol. 2006 Jun;117(6):1388–1397. doi: 10.1016/j.clinph.2006.02.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Nitsche MA, Cohen LG, Wassermann EM, Priori A, Lang N, Antal A, Paulus W, Hummel F, Boggio PS, Fregni F, Pascual-Leone A. Transcranial direct current stimulation: State of the art 2008. Brain Stimul. 2008 Jul;1(3):206–223. doi: 10.1016/j.brs.2008.06.004. [DOI] [PubMed] [Google Scholar]
- 5.Priori A. Brain polarization in humans: a reappraisal of an old tool for prolonged non-invasive modulation of brain excitability. Clin Neurophysiol. 2003 Apr;114(4):589–595. doi: 10.1016/s1388-2457(02)00437-6. [DOI] [PubMed] [Google Scholar]
- 6.Fregni F, Boggio PS, Nitsche M, Pascual-Leone A. Transcranial direct current stimulation. Br J Psychiatry. 2005 May;186:446–447. doi: 10.1192/bjp.186.5.446. [DOI] [PubMed] [Google Scholar]
- 7.Fregni F, Thome-Souza S, Nitsche MA, Freedman SD, Valente KD, Pascual-Leone A. A controlled clinical trial of cathodal dc polarization in patients with refractory epilepsy. Epilepsia. 2006 Feb;47(2):335–342. doi: 10.1111/j.1528-1167.2006.00426.x. [DOI] [PubMed] [Google Scholar]
- 8.Boggio PS, Ferrucci R, Rigonatti SP, Covre P, Nitsche M, Pascual-Leone A, Fregni F. Effects of transcranial direct current stimulation on working memory in patients with parkinson's disease. J Neurol Sci. 2006 Nov;249(1):31–38. doi: 10.1016/j.jns.2006.05.062. [DOI] [PubMed] [Google Scholar]
- 9.Fregni F, Simon DK, Wu A, Pascual-Leone A. Non-invasive brain stimulation for parkinson's disease: a systematic review and meta-analysis of the literature. J Neurol Neurosurg Psychiatry. 2005 Dec;76(12):1614–1623. doi: 10.1136/jnnp.2005.069849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Boggio PS, Bermpohl F, Vergara AO, Muniz AL, Nahas FH, Leme PB, Rigonatti SP, Fregni F. Go-no-go task performance improvement after anodal transcranial dc stimulation of the left dorsolateral prefrontal cortex in major depression. J Affect Disord. 2007 Aug;101(1-3):91–98. doi: 10.1016/j.jad.2006.10.026. [DOI] [PubMed] [Google Scholar]
- 11.Fregni F, Boggio PS, Nitsche MA, Marcolin MA, Rigonatti SP, Pascual-Leone A. Treatment of major depression with transcranial direct current stimulation. Bipolar Disord. 2006 Apr;8(2):203–204. doi: 10.1111/j.1399-5618.2006.00291.x. [DOI] [PubMed] [Google Scholar]
- 12.Nitsche MA, Schauenburg A, Lang N, Liebetanz D, Exner C, Paulus W, Tergau F. Facilitation of implicit motor learning by weak transcranial direct current stimulation of the primary motor cortex in the human. J Cogn Neurosci. 2003 May;15(4):619–626. doi: 10.1162/089892903321662994. [DOI] [PubMed] [Google Scholar]
- 13.Kincses TZ, Antal A, Nitsche MA, Bartfai O, Paulus W. Facilitation of probabilistic classification learning by transcranial direct current stimulation of the prefrontal cortex in the human. Neuropsychologia. 2004;42(1):113–117. doi: 10.1016/s0028-3932(03)00124-6. [DOI] [PubMed] [Google Scholar]
- 14.Fregni F, Boggio PS, Nitsche M, Bermpohl F, Antal A, Feredoes E, Marcolin MA, Rigonatti SP, Silva MT, Paulus W, Pascual-Leone A. Anodal transcranial direct current stimulation of prefrontal cortex enhances working memory. Exp Brain Res. 2005 Sep;166(1):23–30. doi: 10.1007/s00221-005-2334-6. [DOI] [PubMed] [Google Scholar]
- 15.Dymond AM, Coger RW, Serafetinides EA. Intracerebral current levels in man during electrosleep therapy. Biological Psychiatry. 1975;10(1):101. [PubMed] [Google Scholar]
- 16.Eichelbaum S, Dannhauer M, Hlawitschka M, Brooks D, Knösche TR, Scheuermann G. Visualizing simulated electrical fields from electroencephalography and transcranial electric brain stimulation: A comparative evaluation. NeuroImage. 2014;101:513–30. doi: 10.1016/j.neuroimage.2014.04.085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sparing R, Mottaghy FM. Noninvasive brain stimulation with transcranial magnetic or direct current stimulation (tms/tdcs)-from insights into human memory to therapy of its dysfunction. Methods. 2008 Apr;44(4):329–337. doi: 10.1016/j.ymeth.2007.02.001. [DOI] [PubMed] [Google Scholar]
- 18.Wagner T, Valero-Cabre A, Pascual-Leone A. Noninvasive human brain stimulation. Annu Rev Biomed Eng. 2007;9:527–565. doi: 10.1146/annurev.bioeng.9.061206.133100. [DOI] [PubMed] [Google Scholar]
- 19.Poreisz Csaba, Boros Klára, Antal Andrea, Paulus Walter. Safety aspects of transcranial direct current stimulation concerning healthy subjects and patients. Brain research bulletin. 2007;72(4):208–214. doi: 10.1016/j.brainresbull.2007.01.004. [DOI] [PubMed] [Google Scholar]
- 20.Rampersad S, Stegeman D, Oostendorp T. Op 11. optimized tdcs electrode configurations for five targets determined via an inverse fe modeling approach. Clinical Neurophysiology. 2013;124(10):e61–e62. [Google Scholar]
- 21.Boggio PS, Rigonatti SP, Ribeiro RB, Myczkowski ML, Nitsche MA, Pascual-Leone A, Fregni F. A randomized, double-blind clinical trial on the efficacy of cortical direct current stimulation for the treatment of major depression. Int J Neuropsychopharmacol. 2008 Mar;11(2):249–254. doi: 10.1017/S1461145707007833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Im CH, Jung HH, Choi JD, Lee SY, Jung KY. Determination of optimal electrode positions for transcranial direct current stimulation (tdcs). Phys Med Biol. 2008 Jun;53(11):N219–N225. doi: 10.1088/0031-9155/53/11/N03. [DOI] [PubMed] [Google Scholar]
- 23.Datta A, Bansal V, Diaz J, Patel J, Reato D, Bikson M. Gyri-precise head model of transcranial direct current stimulation: improved spatial focality using a ring electrode versus conventional rectangular pad. Brain Stimul. 2009 Oct;2(4):201–7. 207, e1. doi: 10.1016/j.brs.2009.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kwon YH, Ko MH, Ahn SH, Kim YH, Song JC, Lee CH, Chang MC, Jang SH. Primary motor cortex activation by transcranial direct current stimulation in the human brain. Neurosci Lett. 2008 Apr;435(1):56–59. doi: 10.1016/j.neulet.2008.02.012. [DOI] [PubMed] [Google Scholar]
- 25.Borckardt JJ, Linder KJ, Ricci R, Li X, Anderson B, Arana A, Nahas Z, Amas-sian V, Long J, George MS, Sackeim HA. Focal electrically administered therapy: device parameter effects on stimulus perception in humans. J ECT. 2009 Jun;25(2):91–98. doi: 10.1097/YCT.0b013e318183c6a4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Faria P, Leal A, Miranda PC. Comparing different electrode configurations using the 10-10 international system in tdcs: a finite element model analysis. Conf Proc IEEE Eng Med Biol Soc. 2009;2009:1596–1599. doi: 10.1109/IEMBS.2009.5334121. [DOI] [PubMed] [Google Scholar]
- 27.Dannhauer M, Lanfer B, Wolters CH, Knösche TR. Modeling of the human skull in EEG source analysis. Human Brain Mapping. 2011;32(9):1383–99. doi: 10.1002/hbm.21114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Park Ji-Hye, Bong Hong Seung, Kim Do-Won, Suh Minah, Chang-Hwan Im. A novel array-type transcranial direct current stimulation (tdcs) system for accurate focusing on targeted brain areas. Magnetics, IEEE Transactions on. 2011;47(5):882–885. [Google Scholar]
- 29.Jung Young-Jin, Kim Jung-Hoon, Kim Daejeong, Chang-Hwan Im. An image-guided transcranial direct current stimulation system: a pilot phantom study. Physiological measurement. 2013;34(8):937. doi: 10.1088/0967-3334/34/8/937. [DOI] [PubMed] [Google Scholar]
- 30.Sadleir RJ, Vannorsdall TD, Schretlen DJ, Gordon B. Target optimization in transcranial direct current stimulation. Front Psychiatry. 2012;3:90. doi: 10.3389/fpsyt.2012.00090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Dmochowski JP, Datta A, Bikson M, Su Y, Parra LC. Optimized multi-electrode stimulation increases focality and intensity at target. J Neural Eng. 2011 Aug;8(4):046011. doi: 10.1088/1741-2560/8/4/046011. [DOI] [PubMed] [Google Scholar]
- 32.Ruffini Giulio, Fox Michael D, Ripolles Oscar, Cavaleiro Miranda Pedro, Pascual-Leone Alvaro. Optimization of multifocal transcranial current stimulation for weighted cortical pattern targeting from realistic modeling of electric fields. Neuroimage. 2014;89:216–225. doi: 10.1016/j.neuroimage.2013.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.SCIRun development group . SCIRun: A Scientific Computing Problem Solving Environment. Scientific Computing and Imaging Institute (SCI); http://www.scirun.org. [Google Scholar]
- 34.Dannhauer M. BrainSimulator: A toolkit for simulations of noninvasive brain stimulation. Scientific Computing and Imaging Institute (SCI); https://www.sci.utah.edu/cibc-software/scirun/brainstimulator.html. [Google Scholar]
- 35.Grant Michael, Boyd Stephen, Ye Yinyu. Cvx: Matlab software for disciplined convex programming. 2008 [Google Scholar]
- 36.CIBC . Cleaver: A MultiMaterial Tetrahedral Meshing Library and Application. Scientific Computing and Imaging Institute (SCI); 2015. Download from: http://www.sci.utah.edu/cibc/software.html. [Google Scholar]
- 37.Cavaleiro Miranda Pedro, Mekonnen Abeye, Salvador Ricardo, Ruffini Giulio. The electric field in the cortex during transcranial current stimulation. NeuroImage. 2013;70:48–58. doi: 10.1016/j.neuroimage.2012.12.034. [DOI] [PubMed] [Google Scholar]
- 38.Tucker D, Tucker SE. Method for mapping internal body tissue. 2003 Mar 4; US Patent 6,529,759.
- 39.Akhtar M, Bryant HC, Marnelak AN, Flynn ER, Heller L, Shih JJ, Mandelkern M, Matlachov A, Ranken DM, Best ED, DiMauro MA, Lee RR, Sutherling WW. Conductivities of three-layer live human skull. Brain Topography. 2002;14:151–167. doi: 10.1023/a:1014590923185. [DOI] [PubMed] [Google Scholar]
- 40.Tuch DS, Wedeen VJ, Dale AM, George JS, Belliveau JW. Conductivity mapping of biological tissue using diffusion mri. Ann N Y Acad Sci. 2001;888:314–316. doi: 10.1111/j.1749-6632.1999.tb07965.x. [DOI] [PubMed] [Google Scholar]
- 41.Tuch DS, Wedeen VJ, Dale AM, George JS, Belliveau JW. Conductivity tensor mapping of the human brain using diffusion tensor mri. PNAS. 2001;98(20):11697–11701. doi: 10.1073/pnas.171473898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Rullmann M, Anwander A, Dannhauer M, Warfield SK, Duy FH, Wolters CH. EEG source analysis of epileptiform activity using a 1 mm anisotropic hexahedra finite element head model. Neuroimage. 2009 Jan;44(2):399–410. doi: 10.1016/j.neuroimage.2008.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Datta A, Baker JM, Bikson M, Fridriksson J. Individualized model predicts brain current flow during transcranial direct-current stimulation treatment in responsive stroke patient. 2011;4:169–74. doi: 10.1016/j.brs.2010.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Minhas P, Datta A, Bikson M. Cutaneous perception during tdcs: Role of electrode shape and sponge salinity. Clinical Neurophysiology. 2011;122(4):637–638. doi: 10.1016/j.clinph.2010.09.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Cheng KS, Isaacson D, Newell JC, Gisser DG. Electrode models for electric current computed tomography. IEEE Trans Biomed Eng. 1989 Sep;36(9):918–924. doi: 10.1109/10.35300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Dannhauer Moritz, Brooks Dana, Tucker Don, MacLeod Rob. A pipeline for the simulation of transcranial direct current stimulation for realistic human head models using scirun/biomesh3d. In Conference proceedings:... Annual International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE Engineering in Medicine and Biology Society. Conference. 2012 doi: 10.1109/EMBC.2012.6347236. NIH Public Access, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Jin Jian-Ming. The finite element method in electromagnetics. John Wiley & Sons; 2014. [Google Scholar]
- 48.Wagner Tim, Fregni Felipe, Fecteau Shirley, Grodzinsky Alan, Zahn Markus, Pascual-Leone Alvaro. Transcranial direct current stimulation: a computer-based human model study. Neuroimage. 2007;35(3):1113–1124. doi: 10.1016/j.neuroimage.2007.01.027. [DOI] [PubMed] [Google Scholar]
- 49.Song Y, Lee E, Woo EJ, Seo JK. Optimal geometry toward uniform current density electrodes. Inverse Problems. 2011;27(7):1–17. [Google Scholar]
- 50.Fiederer LDJ, Vorwerk J, Lucka F, Dannhauer M, Yang S, Dümpelmann M, Schulze-Bonhage A, Aertsen A, Speck O, Wolters CH, et al. The role of blood vessels in high-resolution volume conductor head modeling of eeg. NeuroImage. 2016;128:193–208. doi: 10.1016/j.neuroimage.2015.12.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Lang Nicolas, Siebner Hartwig R, Ernst Diana, Nitsche Michael A, Paulus Walter, Lemon Roger N, Rothwell John C. Preconditioning with transcranial direct current stimulation sensitizes the motor cortex to rapid-rate transcranial magnetic stimulation and controls the direction of after-effects. Biological psychiatry. 2004;56(9):634–639. doi: 10.1016/j.biopsych.2004.07.017. [DOI] [PubMed] [Google Scholar]