Margin based ontology sparse vector learning algorithm and applied in biology science

Abstract

In biology field, the ontology application relates to a large amount of genetic information and chemical information of molecular structure, which makes knowledge of ontology concepts convey much information. Therefore, in mathematical notation, the dimension of vector which corresponds to the ontology concept is often very large, and thus improves the higher requirements of ontology algorithm. Under this background, we consider the designing of ontology sparse vector algorithm and application in biology. In this paper, using knowledge of marginal likelihood and marginal distribution, the optimized strategy of marginal based ontology sparse vector learning algorithm is presented. Finally, the new algorithm is applied to gene ontology and plant ontology to verify its efficiency.

1. Introduction

The term “Ontology” refers to a knowledge representation and conceptual shared model. It is widely used in gene computing, knowledge management and information retrieval, which also witnesses its effectiveness in the various applications. Besides, the concept semantic model was welcomed and borrowed by scholars in social science, medical science, biology science, pharmacology science and geography science (for instance, see Gregor et al., 2016, Kaminski et al., 2016, Forsati and Shamsfard, 2016, Pesaranghader et al., 2016, Huntley et al., 2016, Brown et al., 2016, Palmer et al., 2016, Terblanche and Wongthongtham, 2016, Farid et al., 2016, Carmen Suarez-Figuero et al., 2016).

Traditionally, we take ontology model as a graph $G=(V\text{,}E)$, where each vertex v in the ontology graph G represents a concept and each edge $e=v_i{v}_j$ of it represents a relationship between concepts $v_i$ and $v_j$. A few years ago, ontology similarity-based technologies were quite popular among researchers due to its wide range of applications. For instance, GO-WAR algorithm was raised by Agapito et al. (2016) to explore cross-ontology association rules in which GO terms present in its sub-ontologies of GO. What’s more, after mining publicly available GO annotated datasets which show how GO-WAR outperforms current state of the art approaches, a deep performance evaluation of GO-WAR was discovered. Chicco and Masseroli (2016) put forward a computational pipeline which can predict novel ontology-based gene functional annotations by means of various semantic and machine learning methods. Then, in order to categorize the predicted annotations by their likelihood of being correct, a new semantic prioritization rule was achieved in their papers. The definition of GO ontological terms, molecular function, biological process and cellular components were given in detail by Umadevi et al. (2016), and he also found the relations to that of the disease genes with p-value < 0.05. Bajenaru et al. (2016) raised the constituent parts and architecture of the proposed ontology-based e-learning system and a framework for its application in reality. However, based on the OWL2 rules and the reasoning process of the OntoDiabetic system, Sherimon and Krishnan (2016) shifted his attention to the modeling and implementation of clinical guidelines. In terms of fuzzy logic, Bobillo and Straccia (2016) extended it to classical ontologies. With the help of pre-existing information about ontologies, such as terminology and ontology structure, Trokanas and Cecelja (2016) worked out a framework for evaluation of ontology for reuse to calculate a compatibility metric of ontology suitability for reuse and hence integration. To illustrate, the framework was explained in a Chemical and Process Engineering perspective. With the aim to allow users to quickly compute, manipulate and explore Gene Ontology (GO) semantic similarity measures, Mazandu et al. (2016) proposed A-DaGO-Fun. Auffeves and Grangier (2016) raised a new quantum ontology to make usual quantum mechanics fully compatible with physical realism. Hence, the physical properties in the ontology are attributed jointly to the system. In addition, Hoyle and Brass (2016) defined a statistical mechanical theory which expresses the process of annotating an object with terms selected from an ontology.

With the consideration of ontology similarity measure and ontology mapping, some effective learning tricks turn out to work well. With the harmonic analysis and diffusion regularization on hypergraph, Gao et al. (2013) proposed a new ontology mapping algorithm. Gao and Shi (2013) raised a novel ontology similarity computation technology considering operational cost in the real applications. Using ADAL trick, an ontology sparse vector learning algorithm was worked out by Gao et al. (2015) to make contributions to the ontology similarity measuring and ontology mapping. Then, Gao et al. (2016) proposed an ontology optimization tactics using distance calculating and learning. Several theoretical analysis of ontology algorithm mentioned but not defined in detail in this paper can refer to Gao et al., 2012, Gao and Xu, 2013, and Gao and Zhu (2014).

The marginal based ontology algorithm for ontology similarity computation and ontology mapping are given in the paper. By means of the sparse vector, the ontology graph is mapped into a real line and vertices into real numbers. Then, based on the difference between their corresponding real numbers, the similarity between vertices is measured. The rest of the paper is structured like this: the notations and setting are presented in Section 2; the ontology sparse vector optimization algorithm is raised in Section 3, in addition, the technologies to tackle the details in algorithm are also included here; and, the experiments on gene science and plant science are taken to show the efficiency of the algorithm in the last section.

2. Setting

Let V represent an instance space. Concerning each vertex in ontology graph, a p dimension vector represents the information: its name, instance, attribute and structure, and semantic information of the concept. All the information is related to the vertex and that is contained in name and attributes components of its vector. Let v = {v₁, … , v_p} be a vector that corresponds to a vertex v. To make the representation, clearer and further, we take a try to confuse the notations. So we consider using v to denote both the ontology vertex and its corresponding vector. The ontology learning algorithms are set to obtain an optimal ontology (score) function f: $V\to \mathbb{R}$, and the similarity between two vertices is determined by the difference between two corresponding real numbers. The core of this algorithm is dimensionality reduction, i.e., choosing one dimension vector to express p dimension vector. Specifically, an ontology function f is a dimensionality reduction function f: ${\mathbb{R}}^p\to \mathbb{R}$.

In the real application, one sparse ontology function is expressed by

$$f_{\beta }(v)={\displaystyle \sum _{i=1}^p}{v}_i{\beta }_i+\delta \text{.}$$ (1)

Here $\mathit{\beta }=({\beta }_1\text{,}\dots \text{,}{\beta }_p)$ is a sparse vector and $\delta$ is a noise term. The sparse vector $\mathit{\beta }$ is used to decrease the components that is not necessary to zero. Then, we learn the sparse vector $\mathit{\beta }$, so that we can determine the ontology function f.

The general versions for learning $\mathit{\beta }$ is learned in the paper. Let ${\{v_i\text{,}{y}_i\}}_{i=1}^n$ be a sample set with n vertex, $V\in {\mathbb{R}}^{n\times p}$ be the matrix of n samples such that each sample vertex lies in a p dimension space, and $\mathit{y}=({\mathit{y}}_1\text{,}\dots \text{,}{\mathit{y}}_{\mathit{n}})\in {\mathbb{R}}^{\mathbb{n}}$ be the vector of outputs of the these n sample vertex. Hence, the regression function Eq. (1) can be expressed as the linear model:

$$\mathit{y}=\mathit{V}\mathit{\beta }+\delta \text{,}$$ (2)

where $\delta$ is the n dimension vector for noise which are normally distributed, $N_p(\mathbf{0}\text{,}{\sigma }^2{\mathit{I}}_p)$ with variance ${\sigma }^2$.

An estimate of the sparse vector is obtained from the general regression obtains after solving the optimization problem below:

$${\displaystyle \underset{\mathit{\beta }\in {\mathbb{R}}^p}{\min }}l(\mathit{\beta })+\lambda \Vert \mathit{\beta }{\Vert }_1\text{,}$$ (3)

where $l(\mathit{\beta })=\frac{1}{2}\Vert \mathit{y}-\mathit{V}\mathit{\beta }{\Vert }_2^2$ is the loss term, $\Vert \mathit{\beta }{\Vert }_1={\sum }_{i=1}^p|{\beta }_i|$ is the $l_1$-norm balance term that measures the sparseness of vector $\mathit{\beta }$, and $\lambda >0$ is the balance parameter which controls the sparsity level. On the selection of the balance parameter $\lambda$, readers can refer to Mancinelli et al., 2013, Mukhopadhyay and Bhattacharya, 2013, Ishibuchi and Nojima, 2013, and Varmuza et al. (2014) for more details about the method of cross-validation.

3. Ontology algorithm describing

In our paper, we consider the special case of Eq. (3), and it can be stated as

$${\displaystyle \underset{\mathit{\beta }\in {\mathbb{R}}^p}{\min }}{(\mathit{y}-\mathit{V}\mathit{\beta })}^{\text{T}}(\mathit{y}-\mathit{V}\mathit{\beta })+\lambda {\displaystyle \sum _{j=1}^p}|{\beta }_j{|}^{\gamma }\text{,}$$ (4)

where $\gamma \in \{0\text{,}1\text{,}2\}$.

We suppose the normal likelihood $\mathit{y}|\mathit{\beta }\text{,}{\sigma }^2\sim N(\mathit{V}\mathit{\beta }\text{,}{\sigma }^2\mathit{I})$ have independent priors about the ontology coefficients of the expression $p({\beta }_j|\lambda )\propto \exp \{-\lambda |{\beta }_j{|}^{\gamma }\}$, $\lambda >0$, $0<\gamma <1$ and a representative conjugate prior have the error precision ${\sigma }^{-2}\sim \Xi (c_0\text{,}{d}_0)$. It’s clear to those who fully grasp the criterion Bayesian patterns in which the exponential power class prior can’t be a conjugate prior with the normal likelihood for $\gamma \ne 2$.

Let $N(\alpha \text{,}\varsigma )$ be a normal probability distribution function with mean $\alpha$ and variance $\varsigma$, $g({\tau }_j)\propto {\tau }^{-\frac{1}{2}}q({\tau }_j)$ where $q({\tau }_j)$ is denoted as the density of stable distribution of index $\frac{\gamma }{2}$. Then, the above mentioned class of distributions can be formulated as

$$p({\beta }_j|\lambda \text{,}\gamma )={\int }_0^{\infty }N(0\text{,}{\tau }_j^{-1}{\lambda }^{-\frac{2}{\gamma }})g({\tau }_j)d{\tau }_j$$ (5)

Let $\Gamma (·)$ be the standard Gamma function. In terms of placing the independent normal priors on the ontology coefficients $p({\beta }_j|{\tau }_j\text{,}\lambda \text{,}\gamma )=\sqrt{\frac{{\tau }_j\pi }{2}}{\lambda }^{\frac{1}{\gamma }}{e}^{\frac{-{\tau }_j{\lambda }^{\frac{2}{\gamma }}{\beta }_j^2}{2}}$ and considering $g({\tau }_j)$ as the hyperprior on ${\tau }_j$, we infer

$$\frac{{\lambda }^{\frac{1}{\gamma }}}{2\Gamma \left(1+\frac{1}{\gamma }\right)}{e}^{-\lambda |{\beta }_j{|}^{\gamma }}={\int }_0^{\infty }p({\beta }_j|{\tau }_j\text{,}\lambda \text{,}\gamma )g({\tau }_j)d{\tau }_j\text{.}$$ (6)

Our ontology framework will be presented as follows and then approximate marginal distributions for ontology parameters can be obtained, too. The marginal likelihood of the given ontology data in Eq. (4) or in many other non-trivial patterns can’t be yielded analytically. But the integral can easily be approximated in which the marginal likelihood conditional on $\lambda$ and $\gamma$ can be decomposed. Set $\theta =(\beta \text{,}{\sigma }^2\text{,}\tau )$. For fixed $\lambda$ and $\gamma$, we deduce

$$\log p(\mathit{y}|\lambda \text{,}\gamma )=L_{\lambda \text{,}\gamma }-\mathit{KL}(q||p)\text{,}$$ (7)

where $L_{\lambda \text{,}\gamma }={\int }_{\Theta }q(\mathit{\theta }|\lambda \text{,}\gamma )\log \frac{p(\mathit{\theta }\text{,}\mathit{y}|\lambda \text{,}\gamma )}{q(\mathit{\theta }|\lambda \text{,}\gamma )}d\mathit{\theta }$ denote the lower bound on the marginal likelihood and $\mathit{KL}(q||p)={\int }_{\Theta }q(\mathit{\theta }|\lambda \text{,}\gamma )\log \frac{p(\mathit{\theta }|\mathit{y}\text{,}\lambda \text{,}\gamma )}{q(\mathit{\theta }|\lambda \text{,}\gamma )}d\mathit{\theta }$ is the Kullback–Leibler divergence between two distributions. Since $\mathit{KL}(q||p)$ is a strict non-negative function which equals to zero if and only if $p(\mathit{\theta }|\mathit{y}\text{,}\lambda \text{,}\gamma )=q(\mathit{\theta }|\lambda \text{,}\gamma )$, the first term $L_{\lambda \text{,}\gamma }$ in Eq. (7) forms the lower bond of $\log p(\mathit{y}|\lambda \text{,}\gamma )$. Assume $q(\mathit{\theta }|\lambda \text{,}\gamma )$ be the approximation of the posterior density $p(\mathit{\theta }|\mathit{y}\text{,}\lambda \text{,}\gamma )$. We have $\max L_{\lambda \text{,}\gamma }=\min \mathit{KL}(q||p)$.

Let ${\mathit{\theta }}_i$ be the subvector of $\mathit{\theta }$ and $E_{i\ne j}(·)$ be the expectation with respect to distributions $q_j({\mathit{\theta }}_j)$ with $i\ne j$. We consider the factorized expression

$$q(\mathit{\theta }|\lambda \text{,}\gamma )={\displaystyle \prod _i}{q}_i({\mathit{\theta }}_i|\lambda \text{,}\gamma )\text{.}$$ (8)

In terms of maximizing the lower bound with respect to $q_i({\mathit{\theta }}_i|\lambda \text{,}\gamma )$, we infer

$$q_i({\mathit{\theta }}_i|\lambda \text{,}\gamma )=\frac{e^{E_{i\ne j}(\log p(\mathit{y}\text{,}\mathit{\theta }|\lambda \text{,}\gamma ))}}{{\int }_{{\Theta }_i}{e}^{E_{i\ne j}(\log p(\mathit{y}\text{,}\mathit{\theta }|\lambda \text{,}\gamma ))}d{\mathit{\theta }}_i}$$ (9)

By virtue of the above mentioned normal mixture expression of the exponential power distribution and the solution obtained from Eq. (9), the error variance and the approximate marginal posterior distributions of ontology coefficients can be determined. However, since the mixing distribution $g({\tau }_j)$ is unknown, the explicit expression for $q({\tau }_j)$ can’t be calculated. Fortunately, using the value of $q(\mathit{\beta }|\lambda \text{,}\gamma )$, the expression of $E({\tau }_j)$ can be deduced.

Let

$$\widehat{\mathit{\beta }}=E({\sigma }^{-2}){\mathrm{\Sigma }}_{\mathit{\beta }}{\mathit{V}}^{\text{T}}\mathit{y}\text{,}$$

$${\mathrm{\Sigma }}_{\mathit{\beta }}={({\mathit{V}}^{\text{T}}\mathit{V}E({\sigma }^{-2})+\mathit{T})}^{-1}\text{,}$$

$$\mathit{T}={\lambda }^{\frac{2}{\gamma }}\text{Diag}(E({\tau }_j))\text{,}$$

$$\widehat{c}=\frac{n}{2}+c_0\text{,}$$

and

$$\widehat{d}=\frac{1}{2}{\mathit{y}}^{\text{T}}\mathit{y}-{\mathit{y}}^{\text{T}}\mathit{V}E(\mathit{\beta })+\frac{1}{2}{\displaystyle \sum _{i=1}^n}{v}_{i}E(\mathit{\beta }{\mathit{\beta }}^{\text{T}})v_i^{\text{T}}+d\text{.}$$

The approximate marginal posterior distributions of the ontology coefficients and the error precision can be stated as follows:

$$q(\mathit{\beta }|\lambda \text{,}\gamma )\stackrel{d}{=}N(\widehat{\mathit{\beta }}\text{,}{\mathrm{\Sigma }}_{\mathit{\beta }})\text{,}$$ (10)

$$q({\sigma }^{-2}|\lambda \text{,}\gamma )\stackrel{d}{=}\Xi (\widehat{c}\text{,}\widehat{d})\text{.}$$ (11)

According to the fact that we don’t get an available explicit form for its approximate distribution, these above presented moments are clear except for $E({\tau }_j)$. We infer $E(\mathit{\beta })=\widehat{\mathit{\beta }}$, $E(\mathit{\beta }{\mathit{\beta }}^{\text{T}})={\mathrm{\Sigma }}_{\beta }+E(\mathit{\beta })E({\mathit{\beta }}^{\text{T}})$, and $E({\sigma }^{-2})=\frac{\widehat{c}}{\widehat{d}}$. In view of (9), we can express the approximate marginal distribution of ${\tau }_j$ as

$$q({\tau }_i|\lambda \text{,}\gamma )\frac{e^{E(\log p({\beta }_j|{\tau }_j\text{,}\lambda \text{,}\gamma ))+E(\log g({\tau }_j))}}{{\int }_0^{\infty }{e}^{E(\log p({\beta }_j|{\tau }_j\text{,}\lambda \text{,}\gamma ))+E(\log g({\tau }_j))}d{\tau }_j}$$ (12)

In terms of Eq. (6), $q({\tau }_i|\lambda \text{,}\gamma )$ evaluated at ${\beta }_j^2=E({\beta }_j^2)$ is the normalizing constant for this term. Moreover, we deduce the following fact by derivation of both sides of Eq. (6) with respect to ${\beta }_j^2$ and evaluate it again at ${\beta }_j^2=E({\beta }_j^2)$,

$$\frac{{\lambda }^{1-\frac{1}{\gamma }}\gamma E{({\beta }_j^2)}^{\frac{\gamma }{2}}}{2\Gamma \left(1+\frac{1}{\gamma }\right)}{e}^{-\lambda E{({\beta }_j^2)}^{\frac{\gamma }{2}}}={\int }_0^{\infty }{\tau }_j\frac{{\lambda }^{\frac{1}{\gamma }}{\tau }_j}{\sqrt{2\pi }}{e}^{-\frac{1}{2}{\tau }_j{\lambda }^{\frac{2}{\gamma }}E({\beta }_j^2)}g({\tau }_j)d{\tau }_j\text{.}$$ (13)

Then, by normalization operation, we have

$$E({\tau }_j)={\lambda }^{1-\frac{2}{\gamma }}\gamma E{({\beta }_j^2)}^{\frac{\gamma }{2}-1}\text{.}$$ (14)

From what we discussed above, we conclude the following facts:

$$L_{\lambda \text{,}\gamma }=E(\log p(\mathit{y}|\mathit{\beta }\text{,}{\sigma }^2))+E(\log p(\mathit{\beta }|\tau \text{,}\lambda \text{,}\gamma ))+E(\log p({\sigma }^{-2}))+E(\log g(\tau ))-E(\log q(\mathit{\beta }|\lambda \text{,}\gamma ))-E(\log q({\sigma }^{-2}|\lambda \text{,}\gamma ))-E(\log q(\tau |\lambda \text{,}\gamma ))\text{,}$$

$$E(\log p(\mathit{y}|\mathit{\beta }\text{,}{\sigma }^2))=-\frac{1}{2}{\displaystyle \sum _{i=1}^n}{n}_i(\log 2\pi -E(\log {\sigma }^{-2}))-E({\sigma }^{-2})(\widehat{d}-d_0)\text{,}$$

$$E(\log p(\mathit{\beta }|\tau \text{,}\lambda \text{,}\gamma ))=-\frac{p}{2}\log 2\pi +\frac{1}{2}{\displaystyle \sum _{j=1}^p}E(\log {\tau }_j)+{\gamma }^{-1}\log \lambda -{\lambda }^{\frac{2}{\gamma }}{\displaystyle \sum _{j=1}^p}E({\tau }_j)E\left({\beta }_j^2\right)\text{,}$$

$$E(\log p({\sigma }^{-2}))=c_0\log d_0+(c_0-1)E(\log {\sigma }^{-2})-d_{0}E({\sigma }^{-2})-\log \Gamma (c_0)\text{,}$$

$$E(\log g(\tau ))={\displaystyle \sum _{j=1}^p}E(\log g({\tau }_j))\text{,}$$

$$E(\log q(\mathit{\beta }|\lambda \text{,}\gamma ))=-\frac{p}{2}(\log 2\pi +1)-\frac{1}{2}\log |{\mathrm{\Sigma }}_{\beta }|\text{,}$$

$$E(\log q({\sigma }^{-2}|\lambda \text{,}\gamma ))=\widehat{c}\log \widehat{d}+(\widehat{c}-1)E(\log {\sigma }^{-2})-\widehat{d}E({\sigma }^{-2})-\log \Gamma (\widehat{c})\text{,}$$

$$E(\log q(\tau |\lambda \text{,}\gamma ))={\displaystyle \sum _{j=1}^p}E(\log p({\beta }_j|{\tau }_j\text{,}\lambda \text{,}\gamma ))+p\log 2+{\displaystyle \sum _{j=1}^p}E(\log g({\tau }_j))-p{\gamma }^{-1}\log \lambda +p\log \Gamma \left(1+\frac{1}{\gamma }\right)+\lambda {\displaystyle \sum _{j=1}^p}E{\left({\beta }_j^2\right)}^{\frac{\gamma }{2}}\text{.}$$

Based on simplifications, we have

$$L_{\lambda \text{,}\gamma }=-\frac{n}{2}\log (2\pi )+\frac{p}{2}+\frac{1}{2}\log |{\mathrm{\Sigma }}_{\beta }|+c_0\log d_0-\widehat{c}\log \widehat{d}-\log \Gamma (c_0)+\log \Gamma (\widehat{c})+p{\gamma }^{-1}\log \lambda -p\log 2-p\log \Gamma \left(1+\frac{1}{\gamma }\right)-\lambda {\displaystyle \sum _{j=1}^p}E{\left({\beta }_j^2\right)}^{\frac{\gamma }{2}}\text{.}$$ (15)

Finally, the iterative produce for ontology coefficients can be stated as

$$E_{k+1}(\mathit{\beta })={\displaystyle \underset{\mathit{\beta }}{\text{arg min}}}{(\mathit{y}-\mathit{V}\mathit{\beta })}^{\text{T}}(\mathit{y}-\mathit{V}\mathit{\beta })+\lambda \gamma E_k{({\sigma }^{-2})}^{-1}{\displaystyle \sum _{j=1}^p}{\beta }_j^2{E}_k{\left({\beta }_j^2\right)}^{\frac{\gamma }{2}-1}\text{,}$$ (16)

where $E_k(·)$ denotes the expectation determined at the k-th iteration.

4. Simulation studies

In this section, two simulation experiments related to ontology similarity measure are presented. In order to be close to the setting of ontology algorithm, we choose a vector with p dimension to express each vertex’s information. All the information of name, instance, attribute and structure of vertex is contained in the vector. Here the instance of vertex means the set of its reachable vertex in the directed (or, undirected) ontology graph.

In order to make comparisons more accurate, the main algorithm runs in C++, in view of available LAPACK and BLAS libraries for linear algebra computations. All experiments are taken on a double-core CPU with memory of 8 GB.

4.1. Experiment on biology data

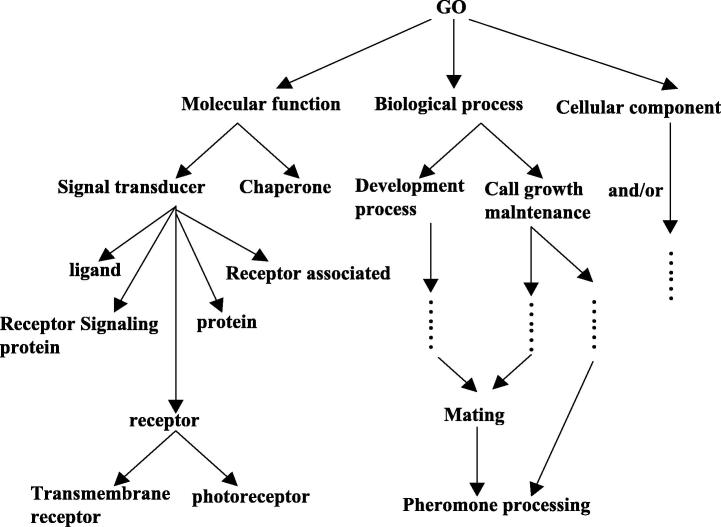
In the first experiment, we choose “Go” ontology O₁ whose basic structure can be shown in http://www.geneontology.org (Fig. 1 shows the basic structure of O₁). P@N (Precision Ratio, see Craswell and Hawking (2003) for more detail) is traditionally used to judge the equality of the experiment, and we also choose it for its efficiency. At first, the experts give the closest N concepts for every vertex on the ontology graph. Then using the algorithm, we compute the precision ratio, so that we can get the first N concepts for every vertex on ontology graph. Ontology algorithms in Gao et al., 2013, Gao et al., 2016, Gao and Shi, 2013 are also applied into “Go” ontology. At last, the precision ratio obtained from the four methods is gotten and given in Table 1.

Figure 1.

“Go” ontology.

Table 1.

Experiment data for ontology similarity measure.

	P@3 average precision ratio	P@5 average precision ratio	P@10 average precision ratio	P@20 average precision ratio
Our Algorithm	56.49%	68.27%	81.24%	93.71%
Algorithm in Gao et al. (2013)	56.46%	67.72%	78.38%	79.39%
Algorithm in Gao and Shi (2013)	56.44%	65.73%	78.39%	89.72%
Algorithm in Gao et al. (2016)	49.87%	63.64%	76.02%	85.46%

From the data in Table 1, we can find that when N = 3, 5, 10 or 20, the precision ratio obtained from our algorithm is higher than that obtained by algorithms proposed in Gao et al., 2013, Gao et al., 2016, Gao and Shi, 2013. Particularly, such precision ratios are increasing apparently with N increasing. Thus, our algorithm is better than the method presented by Gao et al., 2013, Gao et al., 2016, Gao and Shi, 2013.

4.2. Experiment on plant data

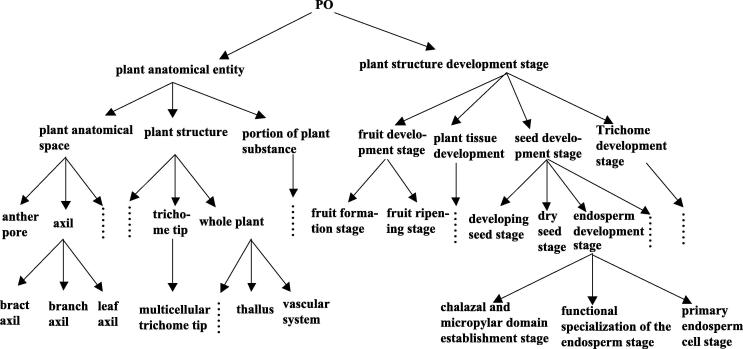
In this subsection, we use “PO” ontology O_2, whose structure is presented in http://www.plantontology.org. (Fig. 2 shows the basic structure of O₂), to check the efficiency of our new algorithm in ontology similarity measuring. Similarly, we use the P@N again for this experiment. Moreover, the ontology methods in Gao et al., 2013, Gao et al., 2016, Gao and Shi, 2013 are applied to the “PO” ontology. We calculate the data using the three algorithms, and then we compare the results with that gotten from the new algorithm. Part of the data can be referred to Table 2.

Figure 2.

“PO” ontology O_2.

Table 2.

Experiment data for ontology similarity measure.

	P@3 average precision ratio	P@5 average precision ratio	P@10 average precision ratio	P@20 average precision ratio
Our Algorithm	53.60%	66.64%	90.04%	96.73%
Algorithm in Gao et al. (2013)	36.63%	44.60%	58.45%	70.06%
Algorithm in Gao and Shi (2013)	36.96%	45.08%	60.17%	73.99%
Algorithm in Gao et al. (2016)	53.58%	65.17%	88.21%	93.85%

From the data in Table 2, we can find that when N = 3, 5, 10 or 20, the precision ratio gotten from our algorithm is higher than that from algorithms proposed in Gao et al., 2013, Gao et al., 2016, Gao and Shi, 2013. Particularly, such precision ratios are increasing apparently with N increasing. Thus, our algorithm is better and more effective than the method presented by Gao et al., 2013, Gao et al., 2016, Gao and Shi, 2013.

5. Conclusions

Borrowed the marginal technology for ontology sparse vector computation in this paper, we proposed a new computation algorithm on the basis of the marginal distribution and the analysis of the convergence criterion problem. The simulation data obtained from the experiments shows the high efficiency of our newly proposed algorithm in biology and plant science. Hence, the ontology sparse algorithm sees the promising application prospects for biology science.