Abstract
We have quantified the photomovement behavior of a suspension of Euglena gracilis representing a behavioral response to a light gradient. Despite recent measurements of phototaxis and photophobicity, the details of macroscopic behavior of cell photomovements under conditions of light intensity gradients, which are critical to understand recent experiments on spatially localized bioconvection patterns, have not been fully understood. In this paper, the flux of cell number density under a light intensity gradient was measured by the following two experiments. In the first experiment, a capillary containing the cell suspension was illuminated with different light intensities in two regions. In the steady state, the differences of the cell numbers in the two regions normalized by the total number were proportional to the light difference, where the light intensity difference ranged from 0.5–2.0 μmol m−2 s−1. The proportional coefficient was positive (i.e., the bright region contained many microorganisms) when the mean light intensity was weak (1.25 μmol m−2 s−1), whereas it was negative when the mean intensity was strong (13.75 μmol m−2 s−1). In the second experiment, a shallow rectangular container of the suspension was illuminated with stepwise light intensities. The cell number density distribution exhibited a single peak at the position where the light intensity was about Ic ≃ 3.8 μmol m−2 s−1. These results suggest that the suspension of E. gracilis responded to the light gradient and that the favorable light intensity was Ic.
1 Introduction
Euglena gracilis is a unicellular flagellated photosynthetic alga; the body is approximately 10 μm wide and 50–100 μm long. E.gracilis carries a stigma (eyespot) in the anterior part, which is red owing to carotenoid pigments contained in the body termed pigment granules. Individuals of E. gracilis respond to light via the shading of the stigma onto the paraflagellar body (PFB) at the base of the flagellum. The photo-response behavior of E. gracilis can be categorized into phototaxis, photokinesis, and photophobic response [1].
Through phototaxis, E.gracilis swims toward a light source if the intensity is less than a critical value (positive phototaxis) and swims away if the intensity is above the critical value (negative phototaxis) [2]. In this paper, we define the phototaxis of the cell flux as photoresponse motion in which the mean swimming velocity is parallel to the light vector according to Vincent and Hill [3]. Häder et al. [4] measured the phototaxis of E. gralicis for several illuminances of white light and found that the phototaxis behavior is almost marginal around 250 lx, which is equivalent to 1.05 Wm−2 according to the conversion relationship. Giometto et al. [5] measured the phototaxis exhibited under the light distribution generated by a point light source. E. gracilis also exhibits a taxis for polarized light [6, 7].
Photokinesis refers to the phenomenon that the linear swimming velocity depends on the light intensity. Noda investigated the swimming velocity of E. gracilis under light intensities ranging from 200–2500 lx (S. Noda, Master thesis in Hiroshima University, 2012). It was found that the swimming speed was approximately 60 μm s−1 if the light intensity was less than 1000 lx but that it increased as the light intensity increased, with a maximum speed of approximately 90 μm s−1 at 2500 lx.
Photophobic response is a light-induced shock response that occurs when the illumination intensity around the microorganism is suddenly changed. Matsunaga et al. [8] measured the statistics of the swimming direction change under sudden temporal change of the light intensity. They measured both the “step-up” change; i.e., the increase of light intensity from the no light condition, and the “step-down” intensity; i.e., the decrease the light intensity to the no light condition. They also defined a photophobic index and measured the index for light with different wavelengths (260nm-520nm) and intensities (0.3–100 μmol m−2 s−1) and found that the index increased for light intensities in the range 0.1–10 μmol m−2 s−1, although the detailed behavior depended on the wavelength. In addition, Iseki et al. [9] identified the flavoprotein responsible for the “step-up” responses.
Photomovements of E. gracilis cause an interesting macroscopic pattern: bioconvection [3, 10–14]. If a suspension of E. gracilis is illuminated from the bottom with strong light, the pattern is spatially localized [15, 16]. Such localized structures can be classified into two groups: one is a single region of high cell density sandwiched with two counter-rotating convection rolls (bioconvection unit), and the other is a traveling wave in a confined region (localized traveling wave). These elementary structures can be obtained in an annular container [15].
Strong illumination from below is a necessary condition for generating these localized bioconvection patterns. Conversely, if the light intensity is weak, the localization pattern is not observed [17]. Whereas a photo response behavior is likely responsible for the localization mechanism, the above-mentioned photomovements appear to be insufficient to describe the observed localization patterns. In particular, movement of the microorganisms owing to phototaxis is parallel to the light vector. In a vertical light vector setup, this is important for the microorganisms to accumulate near the surface and to cause Rayleigh-Taylor instability [18]; however, macroscopic horizontal flux of the cell density to cause the observed spatial localization is not included in this effect.
Vincent and Hill [3] analyzed a hydrodynamic bioconvection model generated by positive phototaxis, where the suspension was illuminated from above. In their model, the phototaxis term induced the cell density flux in the vertical direction alone. The scattering of light has been considered in bioconvection illuminated from above by Ghorai and his coworkers [19, 20]; however, the averaged cell density flux owing to the phototaxis was directed vertically as in the Vincent and Hill model. It therefore appears that localized convection patterns require another photomovement that might be lateral to enhance spatial disturbance.
In this study we assume that the lateral movement is due to photomovement determined by the light gradient, by which an effective accumulation of individuals is possible because when the suspension is illuminated from below, the region near the surface that is Euglena-rich is darker compared with other regions. Comparatively, Williams and Bees [21] included an effct of the photomovement owing to the light gradient on the torque applied in the microorganism cell, assuming that the individual cell was able to detect the light gradient. In addition, studies of conditions such as the spatial light trap [7] or photophobic response [8] have suggested some responses of E. gracilis to a light gradient.
Giometto et al. [5] obtained an equation of the cell density that includes a spatial potential to cause a population velocity in the direction of the light gradient. However, their measurements are performed under the illumination of point light source. So the light vector is not vertical except the onset of the light source, thus, their equation can not be applied directly to the configuration of the spatially homogeneous illumination (flat light source) which is related to many problems including bioconvection problems. An equation to describe the flux of cells under the light gradient generated by flat light sources will be useful, however, there no direct measurements of the cell density flux of E. gracilis under a light gradient have been reported. Here, we focus on the macroscopic behavior of the flux of cell number density (referred to as ‘cell density’ hereafter) and present evidence that the light gradient actually causes a bias of the cell density within heterogeneous illumination. In particular, in this study we measured the photomovement of E. gracilis owing to a light gradient. After summarizing the experimental setups below (section 2), we show that the flux of the cell density comprises the sum of diffusion and of another flux that is proportional to the light gradient and the mean cell density (section 3). We estimate the coefficients of the flux as a function of the mean light intensity (section 4) and discuss the observed photomovement behavior in the context of other phenomena such as chemotaxis (section 5).
2 Experimental Setups
E. gracilis was pre-cultured using Koren-Hutner medium for 2–4 weeks with continuous light illumination at room temperature. Then, the cells were inoculated into 1 g/L HYPONeX solution with periodic light illumination (14 h bright light/10 h dark). After 4–21 days culture in the HYPONeX aqueous solution, the suspension was used for each experiment during the circadian time (CT) 10–14 h.
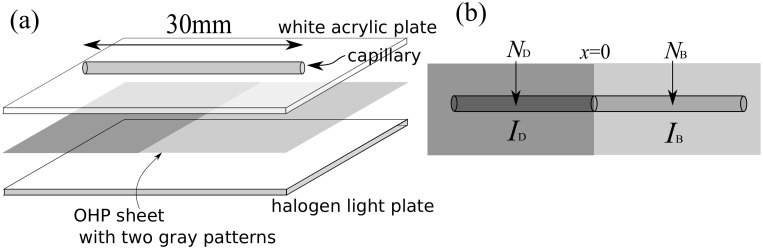
The flux of the cell density was measured under a light field with two different intensity regions (section 3). The HYPONeX culture was diluted to 2.50 × 105 cells mL−1 in cell density and was put into a capillary glass (volume V = 1μL, length = 30 mm, inner radius = 0.10 mm). The capillary glass with the cell culture was illuminated for 60 min from below with a halogen flat light source (YAHATA, Megalight 100) through a white acrylic plate (1 mm in thickness) to diffuse the light (Fig 1(a)). Two regions with different light intensities were prepared using photo-mask of an OHP sheet on which a grayscale mask was printed using a laser printer (Canon MF8350). The photo flux density (PFD) at the observation point, I, was measured with the illumination photometer (Deltaohm, HD2302.0) on the white acrylic plate. The difference in PFD between the darker region (ID) and the brighter region (IB) was varied from 0.5 to 2.0 μmol m−2 s−1 while keeping the average intensity (ID + IB)/2 constant (Fig 1(b)). In the region near x = 0, the boundary of the light intensities, the light intensity exhibited the gradient. The maximum light gradient was -0.314 μmol m−2 s−1 ⋅ μm−1. To count the cell numbers contained in the darker (ND) and brighter (NB) parts, the capillary glass was cut at the center and the culture was removed onto a glass plate before rinsing the inside of the capillary glass once with distilled water. Then, the number of cells was counted in the photograph taken from the top of the glass plate with a micro lens (Raynox Universal Adapter UAC 3500) attached to the digital camera (GC-PX1, JVC, Japan). For each set of IB − ID and IB + ID, ten experiments were performed. Although a normalized difference in two regions was used in later analysis, the distribution for ND and NB were characterized by 60.30 ± 19.41 and 151.80 ± 22.75 (mean ± standard deviation) for the case (ID + IB)/2 = 1.25 μmol m−2 s−1 and IB − ID = 1.5 μmol m−2 s−1, for example.
Fig 1.
(a) Experimental setup. (b) Symbols for the numbers of cells and for the photo flux densities in the left and right part of the setup.
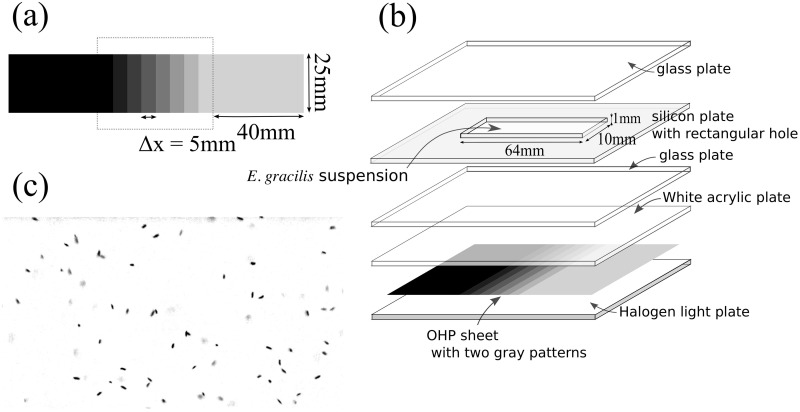
Steady-state cell density was estimated under illumination with a gradient of light intensity (section 4). Stepwise light intensities were generated by a photomask with an OHP sheet. Two kinds of discrete patterns were prepared as follows: The first pattern had eight steps and the light intensity increased from 1.47 μmol m−2 s−1 to 25.76 μmol m−2 s−1 with 3.47 μmol m−2 s−1 in step with the rectangular regions (5 mm in width, 25 mm in height) (Sheet A; Fig 2(a), inside the dotted rectangle). The second pattern had seven steps and the light intensity increased from 1.47 μmol m−2 s−1 to 8.41 μmol m−2 s−1 with 1.16 μmol m−2 s−1 in step (Sheet B). The patterns were sandwiched with two wider rectangular regions (40 mm in width, 25 mm in height) and the grayscale of each wide rectangular pattern was the same as that of the adjacent rectangular to eliminate boundary effects.
Fig 2.
(a) Grayscale pattern on the OHP sheet. (b) Experimental setup. (c) An example of photograph (I = 23.25 μmol m−2 s−1. 84 individuals are shown).
A silicon plate with 1 mm thickness with a rectangular hole was prepared and was sandwiched with glass plates to generate a Hele-Shaw cell (64 mm in width, 10 mm in height, and 1 mm in thickness). The HYPONeX culture was diluted to 0.50 × 105 in cell density and was sealed into the Hele-Shaw cell. The Hele-Shaw cell was illuminated from below with the halogen flat light through the photo-mask and white acrylic plate (Fig 2(b)). After 2 h illumination, the cells in each rectangular region were photographed using the same optics as in the previous experiment. The optics was mounted on an apparatus that allows horizontal motion mechanically so that the height of focus was the same for all the regions during one scanning sequence. Also, the height of focus was carefully chosen to avoid near-boundary regions. The photographed region comprised a rectangle (2.9 mm × 2.2 mm) in the central part of each rectangular region and then the number of the cells was counted. We prepared two photographs taken with the interval of one second, converted them to grayscale images (Fig 2(c)), and counted the dark spots that moved between two images. For each density region, ten measurements were performed. We note that the width of the rectangular region was chosen so that it is larger than both the thickness of the Hele-Shaw cell and the width of the photograph region.
3 Cell density flux owing to the light gradient
In the first experiment (Fig 1), if NB and ND depend on the difference in the light intensity, IB − ID, the cell density flux has another factor depending on the light environment. Here we modeled the population motion rather than individual motion. According to the result by Giometto et al. [5] that the cell density distribution satisfies a diffusion equation, we assumed that the cell density flux J was the sum of the diffusion effect and an extra term, Jp, which was unknown at that moment, as follows.
| (1) |
Our purpose in this experiment was to clarify whether Jp depends on the light intensity difference, ΔI = IB − ID, and to quantify the dependence on ΔI. For this purpose, the following formula was used. In the steady state, J = 0. We integrated Eq (1) over an interval [−ε, ε] (where 2ε is the characteristic width of the transition layer of the light intensity on the both sides) to obtain
| (2) |
Regarding n(ε), n(−ε) as the mean cell density in the bright region and that in the dark region, NB/(V/2), ND/(V/2), respectively, we obtained
| (3) |
Thus the averaged flux in the interval [−ε, ε], , is represented as
| (4) |
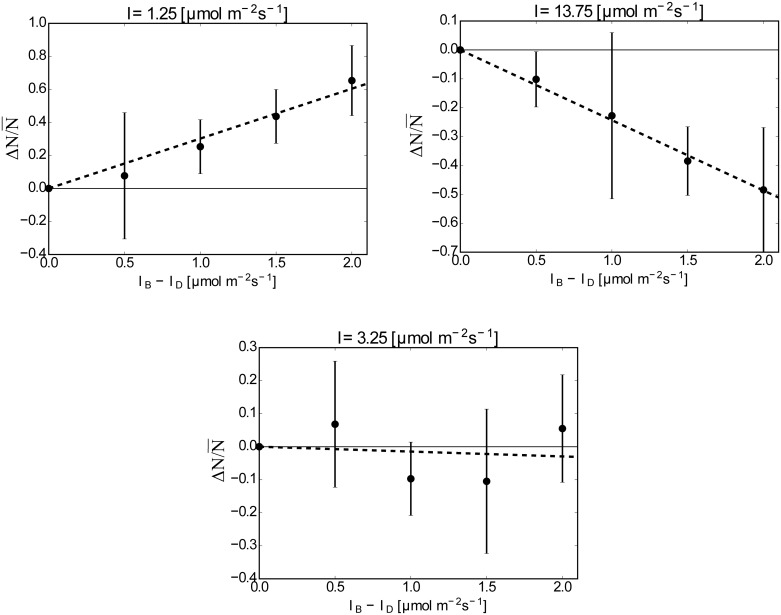
This formula gives the relationship between and ΔN, and ΔN was measured experimentally. We measured ΔN for different ΔI while keeping the mean light intensity Imean = (ID + IB)/2. The results are summarized in Fig 3, where is plotted for ΔI for Imean = 1.25, 3.25 and 13.75 μmol m−2 s−1. The cell number in the capillary, (ND + NB), ranged from 135 to 319, whereas the number was estimated as 250 cells from the mean cell density of the culture. When Imean = 1.25 μmol m−2 s−1, the mean values of NB for each value of ΔI were always larger than those of ND; that is, the individuals tended to accumulate in the brighter region on average. On the other hand, when Imean = 13.75 μmol m−2 s−1, the mean values of NB were always smaller than those of ND and the individuals tended to accumulate in the darker region on average. These two cases show that the horizontal light gradient causes a bias of the cell density and that the direction of the cell density flux depends on Imean. An almost neutral case, Imean = 3.25 μmol m−2 s−1, is also shown, where the average values of ND and NB were almost the same even though the light gradient was present.
Fig 3. vs. ΔI for Imean = 1.25, 3.25, 13.75 μmol m−2 s−1.
The averaged values and the standard deviations are shown by points and bars. Fitted lines are drawn by broken lines. The slopes are: 0.302 ± 0.0252 for Imean = 1.25 μmol m−2 s−1, −0.0147 ± 0.0226 for Imean = 3.25 μmol m−2 s−1 and −0.243 ± 0.0217 for Imean = 13.75 μmol m−2 s−1.
Furthermore, Fig 3 suggests that is proportional to ΔI:
| (5) |
where k is a constant determined by the mean light intensity and . Then, we could determine the flux as
| (6) |
where is the averaged light intensity gradient.
Taking the limit ε → 0, we obtained the following form of Jp:
| (7) |
where the coefficient 2k was replaced with a function of the light intensity, f(I).
4 Function of the photomovement owing to the light gradient
Next, we estimated f(I) experimentally. We used the following formula. By Eq (1) and the form of Jp (Eq (7)), we assumed the following form of the cell density flux in one-dimensional case as
| (8) |
In the steady state, J = 0. Then,
| (9) |
Thus, we could estimate f(I) by measuring the cell density distribution in the steady state, n(x), under the prescribed light intensity distribution I(x). For this purpose, the experiment in Fig 2 was performed.
The total field of the light intensity can be regarded as stepwise, whereas the average linear light gradient dI/dx = γ in the sheet A was γ = γA = 0.694 μmol m−2 s−1 ⋅ mm−1 and that in the sheet B was γ = γB = 0.231 μmol m−2 s−1 ⋅ mm−1. In the following, we assumed that dI/dx = γ.
Because the cell density was dilute and the suspension depth was shallow, we could exclude the effect of self-shading of E. gracilis; in particular, no bioconvection occurred. In addition, the depth of focus of the camera, a, was small compared with the depth of the Hele-Show cell, d. Thus, the counted number in each region, N, was estimated by the cell density multiplied with a and the observation region A: N = nAa. In the actual measurements, we used the averaged frequency distribution of N, n′, which is also proportional to n. From these measured values, we could obtain f(I) as
| (10) |
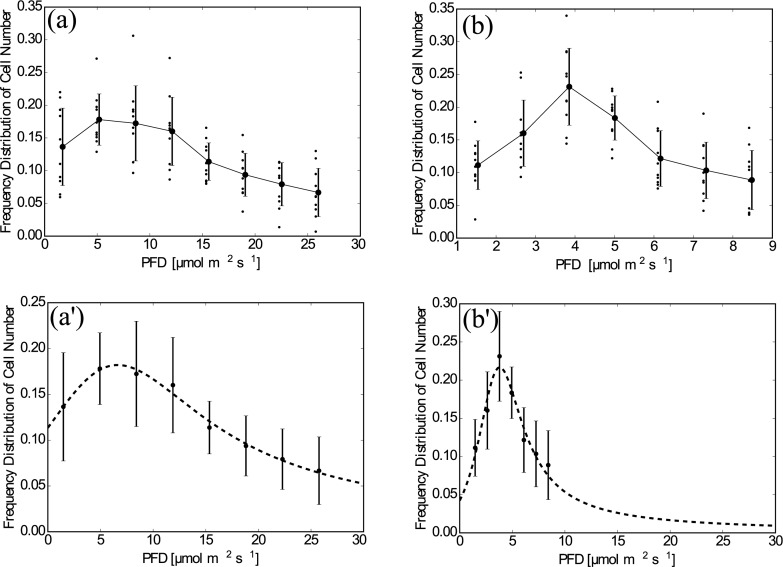
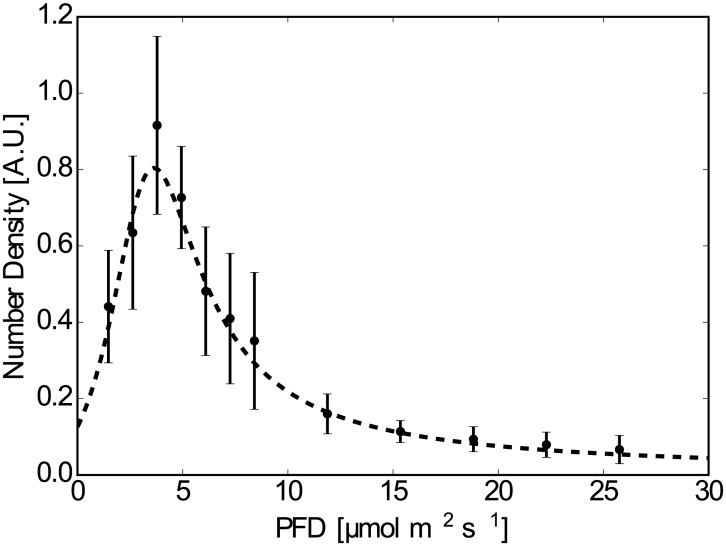
Fig 4 shows the frequency distribution of the counted numbers of cells, n′. Through all the experiments, no global flow or self-shading of individuals was observed. The results for sheet A show a slow decay (I−1) of n′ when I > 15 μmol m−2 s−1. There are single peaks in both graphs; in particular, I = 3.80 μmol m−2 s−1 for sheet B. These results show that the E. gracilis prefers a certain intensity of light and moves according to the light gradient. The distribution using sheet B suggests that n(x) has a large variation in the region I < 10 μmol m−2 s−1; the data for Sheet A is smoothed out in this region.
Fig 4. Plotted data of n′(x).
(a) Sheet A, raw data. The averaged values and the standard deviations are shown by points and bars, which are slightly shifted to the right to avoid overlapping with the raw data. (b) As in (a) but for Sheet B. (a)’ Sheet A, The curve fitted by Eq (11). The averaged values and the standard deviations are shown by points and bars. (b)’ As in (a)’ but for Sheet B and the horizontal range was set the same as for (a)’.
The obtained distributions qualitatively agree with the result obtained when considering cell density flux, where E. gracilis moved to the brighter region when I = 1.25 μmol m−2 s−1 whereas it preferred the darker region when I = 13.75 μmol m−2 s−1.We assumed that the measured value of the frequency distribution of the cell number, , which is proportional to the cell density distribution, was represented by a fractional function of the following form:
| (11) |
where the independent variable was replaced with I using the relationship I(x) = γx. This form was selected so that when I was large, as reflected from the result of Sheet A (Fig 4(a)).
Fitted values of a, b, c and d obtained by the Levenberg-Marquardt method as well as the light intensity giving the peak of the fitted curve, I*, are listed in Table 1 for both cases of Sheet A and Sheet B. The fitted function takes the maximum at I = Ic = 3.8 μmol m−2 s−1 for Sheet B.
Table 1. Tables of fitted parameters.
‘Merged model’ stands for the merged model for Sheet A and Sheet B.
| Sheet A | Sheet B | merged model | |
|---|---|---|---|
| a | 1.327448 × 101 | 7.596000 × 10−1 | 1.980453 × 100 |
| b | 8.988007 × 10−1 | 1.974052 × 10−1 | 1.018627 × 100 |
| c | 1.169945 × 102 | 1.797669 × 101 | 1.565095 × 101 |
| d | −8.334796 × 100 | −6.699378 × 100 | −6.001808 × 100 |
| Ic | 6.636932 | 3.804651 | 3.632495 |
| α* | - | - | 3.96 |
These two experiments give the cell density distribution in different light regions; the decay law in the bright region was obtained by the experiment using Sheet A and the detailed distribution near the maximum of n′ was examined by the experiment using Sheet B. Here we remark that the cell density n(I) was expected to be proportional to ; however, their proportional coefficients are not the same at a particular value of I (or x) because of the following two reasons: (1) (and the depicted data) do not represent the cell density itself but a normalized value by using the total count of the number of cells. (2) The cell number distribution depends on both the mean cell density and the light distribution. Therefore, we cannot merge the results for Sheet A and Sheet B directly.
To obtain the function f(I) using these data, we did not need the absolute value of the cell density because the proportionality does not change f(I): f(I) is invariant under the transformation n′ → αn′(α is a constant). By utilizing this fact, we estimated the number distribution function covering the whole experimental region as follows. Let us define the data set of the light intensity and the cell density in the experiments using Sheet A and Sheet B as SA and SB, respectively. Here, SA and SB are , where M is the number of data. We define a critical light intensity separating the decaying region and the detailed region by I = Ib = 10μmol m−2 s−1. We merge SA and SB with consideration that each set has an uncertain factor of the cell density, which results from the different light gradient region. Without loss of generality, we can assign the uncertain factor to the data set SA alone. Now, the merged data set S(α) is defined as
| (12) |
| (13) |
Fitting the function to the data set S(k) is performed as follows. We define the error of fitting as a function of α as:
| (14) |
| (15) |
where is a function proportional to the cell density distribution. Here we adopted the difference between the logarithm of the data and the functions to weight the data in the decaying region, so that the tail part of the distribution would also contribute to the error estimation. To find the set of α and (a, b, c, d) to minimize E(α; a, b, c, d), we found the parameters (a, b, c, d) to minimize E(α; a, b, c, d) for a given value of α. The value of the minimized error was defined as . Then, we find the minimizer α = α* such that to determine the best parameters of α and (a, b, c, d). In practical application, we calculate in the interval 1 ≤ α ≤ 5 with increments of 0.01 and find α* so that is minimum. The results are listed in Table 1(Right), where α* = 3.96 and I* = 3.63 were obtained. The fitted function for the dataset S(k) is shown in Fig 5.
Fig 5. Fitted function to the data set S(α*).
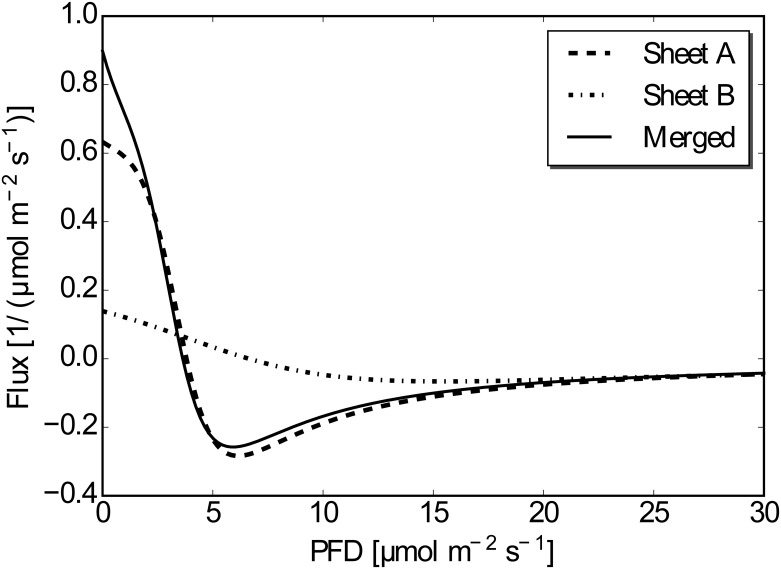
Substituting functions and to n′ in Eq (10), we calculate the function f(I). Here we remark again that the constant uncertainty does not affect the calculation of f(I), so both and can be used to calculate f(I). The calculated functions of f(I) are shown in Fig 6. The overall shape of the function for Sheet A is similar to that for the merged one except for smaller values of the light intensity. The shape of the function for Sheet B is similar to the merged one for larger values of the light intensity, whereas it deviates from the shape for the merged one owing to coarse data. The value of f(I) should be identical to the value of 2k obtained when considering cell density flux; k = 0.302, −0.0147, −0.243 for Imean = 1.25, 3.25 and 13.75μmol m−2 s−1, respectively. The value k = 0.302 (Imean = 1.25 μmol m−2 s−1) deviates from the result, because it is outside the region of the measured value and the fitted function thus cannot well represent the data. The other two values show reasonable agreement with the estimated value of f(I).
Fig 6. The function f(I) for the data set SA, SB, S(α*).
The sign of f(I) changes at I = Ic by Eq (10). Thus, if the light intensity is less than Ic, E. gracilis tend to move toward a brighter region. If the light intensity is larger than Ic, E. gracilis tend to move toward a darker region. However, the function f(I) takes a value of almost zero where I is large (e.g., 15 μmol m−2 s−1), so E. gracilis is almost neutral with respect to the light gradient if the mean light intensity is large enough.
5 Concluding Remarks
In this study, we performed two experiments to examine the distribution of cell density of a suspension of E. gracilis under a light intensity gradient. In the first experiment, the flux of the cell density was measured and the result suggested that the flux was proportional to the light intensity gradient and the cell density. The proportional coefficients could be both positive and negative, depending on the mean light intensity. In the second experiment, the coefficient was estimated as a function of the light intensity. The obtained results showed that E. gracilis tended to accumulate toward the region with a particular light intensity (approximately 3.8 μmol m−2 s−1) when the suspension was illuminated from below in such a manner that a linear gradient of light intensity was generated, although the critical value for individuals might have a diversity. In these experiments, the major phototaxis effect was vertical because of vertical illumination, which is a different setup from that used by Giometto et al., in which point light source was used and the mean light vector was tilted [5].
According to the experiment of localized bioconvection using E. gracilis [15, 16], we took the typical cell density as ρ = 106 cells/mL and the depth of the suspension as d = 5mm. The absorption coefficient of the suspension of E. gracilis, ka, is 2.84 × 10−10 m2/cells (S. Noda, Master thesis in Hiroshima University, 2012). Using the Lambert-Beer law, we can estimate the light intensity at the top of the suspension illuminated below with the light intensity I0, I, as
If we take I0 = 30 μmol m−2 s−1, corresponding to about 1200 lx, we obtain I = 7.2 μmol m−2 s−1, which is above the threshold Ic. Therefore, if there is perturbation in the corresponding uniform cell density distribution in the whole region, the perturbation grows owing to the light gradient. This instability does not depend on the wavelength of the perturbation and is independent of the Rayleigh-Taylor instability that causes many kinds of (non-localized) bioconvection. In this sense, the photomovement owing to the light gradient might represent the major reason of the localization.
The mechanism of the accumulation is still an open question. Because E. gracilis has a single paraflagellar body, which acts as a sensory organ, an individual of E. gracilis cannot detect an instantaneous light gradient. However, the present results suggest that E. gracilis behave as if they can sense the light gradient. A theoretical model of the biochemical kinetic processes of photoreceptors has been proposed to reveal the mechanism of photophobic reactions [7]. However, the present characteristics of f(I) cannot be completely explained through this model alone. Several alternate candidates for the mechanism are listed below.
The first candidate is a phototaxis-based mechanism. In effect, E. gracilis might integrate the information of the scattering light in a light gradient environment. In the current setup, we used an acrylic plate to diffuse the light so that an individual cell in the light gradient environment would detect scattering light vectors not only from directly below but also from obliquely below. Light vectors from obliquely below are tilted and their intensities are not uniform. Thus, an integration of the phototactic response of different magnitudes might lead to the observed response to the light gradient. This scenario would be confirmed if the phototaxis response changes at the same value of light intensity as that at which the function f(I), the response function to the light gradient, takes zero, i.e. 3.8 μmol m−2 s−1, under the same light condition. The critical value of the change of the phototaxis behavior determined by Häder et al. was around 250 lx (= 1.05 Wm−2) [4]. The exact conversion of the irradiance to the photo flux density requires the spectrum of the source light, which is not available. An estimation under the assumption that the light had a single peak at 470 nm gives that 1.05 Wm−2 = 4.1 μmol m−2 s−1. We stress that this value gives only an order of the photo flux density; however, it is notable that it has the same order as our critical value.
The second possibility is a photophobic-based mechanism. When an individual cell of E. gracilis swims under the light gradient environment, the light intensity changes according to the swimming path, which might cause a change of swimming direction. According to the experiment by Matsunaga et al. [8], an increase or decrease of light intensity by a few μmol m−2 s−1 change might increase the occasion of velocity change in a statistical sense. The value of light intensity is also the same order as the critical value of our experiments, although their experiments examined the behavioral change between light and the no light conditions.
To understand how the kinematical mechanism might achieve a gradient-sensing, the chemotaxis mechanism in Escherichia coli and some other bacteria is suggestive. E. coli and some other bacteria show similar phenomena to the step-down (step-up) photophobic reaction of E. gracilis [22–27]. Here, E. coli exhibits a temporal increase of its tumbling rate for changing its swimming direction, termed adaptation, consequent to sudden decreases (increases) in the concentrations of a chemoattractant (chemorepellent). The chemotaxis of E. coli has also been extensively investigated experimentally and theoretically [22–32]. Recently, a theoretical study using a model of chemoreceptor biochemical kinetics derived the experimentally observed form of a function, which depends on the background chemical concentration relationship to the chemotaxis sensitivity; this function corresponds to f(I) in the present study. [32].
Our experiments suggest that the flux of a suspension of E. gracilis depends on the light gradient. The measurements give other aspects of collective motion of E. gracilis, which might be useful to understand the collective behavior of a suspension of E. gracilis, especially the spatially localized bioconvection patterns.
Data Availability
All relevant data are within the paper.
Funding Statement
This work was supported by JSPS KAKENHI 26400396 MI https://www.jsps.go.jp/english/e-grants/, and CREST PJ74100011 MI http://www.jst.go.jp/kisoken/crest/en/index.html. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Diehn B. Phototaxis and sensory transduction in Euglena. Science. 1973;181:1009–1015. 10.1126/science.181.4104.1009 [DOI] [PubMed] [Google Scholar]
- 2. Lebert M. Phototaxis of Euglena gracilis—flavins and pterins In Comprehensive Series in Photosciences 1: Photomovement(Chapter 11), ed. Häder D.-P. and Jori G., 2001. [Google Scholar]
- 3. Vincent RV, Hill NA. Bioconvection in a suspension of phototactic algae. Journal of Fluid Mechanics. 1996;327:343–371. 10.1017/S0022112096008579 [DOI] [Google Scholar]
- 4. Häder D-P, Colombetti G, Lenci F, Quaglia M. Phototaxis in the flagellates, Euglena gracilis and Ochromonas danica. Archives of Microbiology. 1981;130:78–82. 10.1007/BF00527076 [DOI] [Google Scholar]
- 5. Giometto A, Altermatt F, Maritan A, Stocker R, Rinaldo A. Generalized receptor law governs phototaxis in the phytoplankton Euglena gracilis. Proceedings of the National Academy of Sciences of the United States. 2015;112:7045–7050. 10.1073/pnas.1422922112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Häder D-P. Polarotaxis, gravitaxis and vertical phototaxis in the green flagellate, Euglena gracilis. Archives of Microbiology. 1987;147:179–183. 10.1007/BF00415281 [DOI] [PubMed] [Google Scholar]
- 7. Creutz C, Diehn B. Motor Responses to Polarized Light and Gravity Sensing in Euglena gracilis. The Journal of Protozoology. 1976;23:552–556. 10.1111/j.1550-7408.1976.tb03838.x [DOI] [Google Scholar]
- 8. Matsunaga S, Hori T, Takahashi T, Kubota M, Watanabe M, Okamoto K, Masuda K and Sugai M. Discovery of signaling effect of UV-B/C light in the extended UV-A/blue-type action spectra for step-down and step-up photophobic responses in the unicellular flagellate alga Euglena gracilis. Protoplasma. 1998;201:45–52. 10.1007/BF01280710 [DOI] [Google Scholar]
- 9. Iseki M, Matsunaga S, Murakami A, Ohno K, Shiga K, Yoshida K, et al. A blue-light-activated adenylyl cyclase mediates photoavoidance in Euglena gracilis. Nature. 2002;415:1047–1051. 10.1038/4151047a [DOI] [PubMed] [Google Scholar]
- 10. Wager H. On the Effect of Gravity upon the Movements and Aggregation of Euglena viridis, Ehrb., and other Micro-Organisms. Philosophical Transactions of the Royal Society B: Biological Sciences. 1911;201:333–390. 10.1098/rstb.1911.0007 [DOI] [Google Scholar]
- 11. Platt JR. “Bioconvection Patterns” in Cultures of Free-Swimming Organisms. Science. 1961;133:1766–1767. 10.1126/science.133.3466.1766 [DOI] [PubMed] [Google Scholar]
- 12. Childress S. Mechanics of swimming and flying. Cambridge University Press; 1981. [Google Scholar]
- 13. Pedley TJ, Kessler JO. Hydrodynamic phenomena in suspensions of swimming microorganisms. Annual Review of Fluid Mechanics. 1992;24:313–358. 10.1146/annurev.fl.24.010192.001525 [DOI] [Google Scholar]
- 14. Hill NA, Pedley TJ. Bioconvection. Fluid Dynamics Research. 2005;37:1–20. 10.1016/j.fluiddyn.2005.03.002 [DOI] [Google Scholar]
- 15. Shoji E, Nishimori H, Awazu A, Izumi S, Iima M. Localized Bioconvection Patterns and Their Initial State Dependency in Euglena gracilis Suspensions in an Annular Container. Journal of the Physical Society of Japan. 2014;83:043001 10.7566/JPSJ.83.043001 [DOI] [Google Scholar]
- 16. Suematsu NJ, Awazu A, Izumi S, Noda S, Nakata S, Nishimori H. Localized Bioconvection of Euglena Caused by Phototaxis in the Lateral Direction. Journal of the Physical Society of Japan. 2011;80:064003 10.1143/JPSJ.80.064003 [DOI] [Google Scholar]
- 17. Suematsu NJ, Biseibutsu no soukousei ni tomonau kyokuzai tairyu pata-n no hikari outou. RIMS Kokyuroku. 2014;1900:85–90. [Google Scholar]
- 18. Chandrasekhar S. Hydrodynamic and Hydromagnetic Stability. Dover Publications; 1981. [Google Scholar]
- 19. Ghorai S, Panda MK, Hill NA. Bioconvection in a suspension of isotropically scattering phototactic algae. Physics of Fluids. 2010;22:071901 10.1063/1.3457163 [DOI] [Google Scholar]
- 20. Ghorai S, Panda MK. Bioconvection in an anisotropic scattering suspension of phototactic algae. European Journal of Mechanics—B/Fluids. 2013;41:81–93. 10.1016/j.euromechflu.2012.07.001 [DOI] [Google Scholar]
- 21. Williams CR, Bees MA. Photo-gyrotactic bioconvection. Journal of Fluid Mechanics. 2011;678:41–86. 10.1017/jfm.2011.100 [DOI] [Google Scholar]
- 22. Berg HC, Brown DA. Chemotaxis in Escherichia coli analysed by three-dimensional tracking. Nature. 1972;239:500–504. 10.1038/239500a0 [DOI] [PubMed] [Google Scholar]
- 23. Macnab RM, Koshland DE. The Gradient-Sensing Mechanism in Bacterial Chemotaxis. Proceedings of the National Academy of Sciences of the United States. 1972;69:2509–2512. 10.1073/pnas.69.9.2509 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Block SM, Segall JE, Berg HC. Impulse responses in bacterial chemotaxis. Cell. 1982;31:215–226. 10.1016/0092-8674(82)90421-4 [DOI] [PubMed] [Google Scholar]
- 25. Mesibov R, Ordal GW, Adler J. The Range of Attractant Concentrations for Bacterial Chemotaxis and the Threshold and Size of Response over This Range: Weber law and related phenomena. The Journal of General Physiology. 1973;62:203–223. 10.1085/jgp.62.2.203 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Brown DA, Berg HC. Temporal stimulation of chemotaxis in Escherichia coli. Proceedings of the National Academy of Sciences of the United States of America. 1974;71:1388–1392. 10.1073/pnas.71.4.1388 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Segall JE, Block SM, Berg HC. Temporal comparisons in bacterial chemotaxis. Proceedings of the National Academy of Sciences of the United States of America. 1986;83:8987–8991. 10.1073/pnas.83.23.8987 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Barkai N, Leibler S. Robustness in simple biochemical networks. Nature. 1997;387:913–917. 10.1038/43199 [DOI] [PubMed] [Google Scholar]
- 29. Bray D, Levin MD, Morton-Firth CJ. Receptor clustering as a cellular mechanism to control sensitivity. Nature. 1998;393:85–88. 10.1038/30018 [DOI] [PubMed] [Google Scholar]
- 30. Mello BA, Tu Y. Effects of adaptation in maintaining high sensitivity over a wide range of backgrounds for Escherichia coli chemotaxis. Biophysical journal. 2007;92:2329–2337. 10.1529/biophysj.106.097808 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Tu Y, Shimizu TS, Berg HC. Modeling the chemotactic response of Escherichia coli to time-varying stimuli. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:14855–14860. 10.1073/pnas.0807569105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Namba T, Nishikawa M, Shibata T. Biophysical Journal. The Relation of Signal Transduction to the Sensitivity and Dynamic Range of Bacterial Chemotaxis. Biophysical journal. 2012;103:1390–1399. 10.1016/j.bpj.2012.08.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All relevant data are within the paper.