Intensity‐dependent timing and precision of startle response latency in larval zebrafish

Abstract

Key points

• Using high‐speed videos time‐locked with whole‐animal electrical recordings, simultaneous measurement of behavioural kinematics and field potential parameters of C‐start startle responses allowed for discrimination between short‐latency and long‐latency C‐starts (SLCs vs. LLCs) in larval zebrafish.

• Apart from their latencies, SLC kinematics and SLC field potential parameters were intensity independent.

• Increasing stimulus intensity increased the probability of evoking an SLC and decreased mean SLC latencies while increasing their precision; subtraction of field potential latencies from SLC latencies revealed a fixed time delay between the two measurements that was intensity independent.

• The latency and the precision in the latency of the SLC field potentials were linearly correlated to the latencies and precision of the first evoked action potentials (spikes) in hair‐cell afferent neurons of the lateral line.

• Together, these findings indicate that first spike latency (FSL) is a fast encoding mechanism that can serve to precisely initiate startle responses when speed is critical for survival.

Abstract

Vertebrates rely on fast sensory encoding for rapid and precise initiation of startle responses. In afferent sensory neurons, trains of action potentials (spikes) encode stimulus intensity within the onset time of the first evoked spike (first spike latency; FSL) and the number of evoked spikes. For speed of initiation of startle responses, FSL would be the more advantageous mechanism to encode the intensity of a threat. However, the intensity dependence of FSL and spike number and whether either determines the precision of startle response initiation is not known. Here, we examined short‐latency startle responses (SLCs) in larval zebrafish and tested the hypothesis that first spike latencies and their precision (jitter) determine the onset time and precision of SLCs. We evoked startle responses via activation of Channelrhodopsin (ChR2) expressed in ear and lateral line hair cells and acquired high‐speed videos of head‐fixed larvae while simultaneously recording underlying field potentials. This method allowed for discrimination between primary SLCs and less frequent, long‐latency startle responses (LLCs). Quantification of SLC kinematics and field potential parameters revealed that, apart from their latencies, they were intensity independent. We found that increasing stimulus intensity decreased SLC latencies while increasing their precision, which was significantly correlated with corresponding changes in field potential latencies and their precision. Single afferent neuron recordings from the lateral line revealed a similar intensity‐dependent decrease in first spike latencies and their jitter, which could account for the intensity‐dependent changes in timing and precision of startle response latencies.

Key points

• Using high‐speed videos time‐locked with whole‐animal electrical recordings, simultaneous measurement of behavioural kinematics and field potential parameters of C‐start startle responses allowed for discrimination between short‐latency and long‐latency C‐starts (SLCs vs. LLCs) in larval zebrafish.

• Apart from their latencies, SLC kinematics and SLC field potential parameters were intensity independent.

• Increasing stimulus intensity increased the probability of evoking an SLC and decreased mean SLC latencies while increasing their precision; subtraction of field potential latencies from SLC latencies revealed a fixed time delay between the two measurements that was intensity independent.

• The latency and the precision in the latency of the SLC field potentials were linearly correlated to the latencies and precision of the first evoked action potentials (spikes) in hair‐cell afferent neurons of the lateral line.

• Together, these findings indicate that first spike latency (FSL) is a fast encoding mechanism that can serve to precisely initiate startle responses when speed is critical for survival.

Abbreviations

ChR2

Channelrhodopsin‐2

FP

field potential

FP max amplitude

maximum peak‐to‐peak amplitude of the first biphasic peak observed

FSL

first spike latency

LLC

long‐latency C‐start

M‐cell

Mauthner cell

NM

posterior lateral line neuromast

PLLg

posterior lateral line ganglion

SLC

short‐latency C‐start

Introduction

The rapid and precise encoding of sensory information is essential for the initiation of reflexes that are critical for survival. For startle responses, the magnitude and proximity of a threat is likely to determine the probability, onset time (latency) and precision of a response (Eaton, 1984; Koch, 1999). Thus, the precise initiation of an acoustic startle response depends on the accurate transduction of stimulus intensity by sensory hair cells and encoding of trains of action potentials (spikes) in afferent neurons. The intensity dependence of startle response latency and its precision may therefore rely on the timing of spikes that arrive at the command neuron(s) that initiate the reflex circuit (Eaton et al. 1977; Zottoli, 1977; Weiss et al. 2009; Gómez‐Nieto et al. 2014). One possible mechanism for this dependence comes from the timing and precision (jitter) of first evoked spikes. By decreasing first spike latency (FSL) and its jitter with increasing stimulus intensity, startle responses can be triggered more quickly and precisely, which would ensure escape from larger and more immediate threats. Here, we combined optogenetics with behavioural and physiological recordings from larval zebrafish to test the hypothesis that FSL serves as a mechanism for determining the latency and precision of evoked startle responses.

The larval zebrafish provides an ideal platform to examine the pathway of the C‐start startle response, from its encoded stimulus input to its evoked behavioural output (Kimmel et al. 1974; Eaton & Farley, 1975; Fero et al. 2011; Del Bene & Wyart, 2012; Haehnel‐Taguchi et al. 2014). Following stimulation of hair‐cell sensory receptors, depolarization of the receptor potential leads to synaptic vesicle fusion and neurotransmitter release at ribbon synapses, which ultimately leads to spike generation in afferent neurons. Propagating spikes then arrive at command neurons that form electrical and chemical synapses with the afferent neuron (Furshpan, 1964; Szabo et al. 2006; Curti & Pereda, 2010; Yao et al. 2014). Based on the type of command neuron, startle responses take the form of either short‐latency (Mauthner) or long‐latency (non‐Mauthner) C‐starts (Eaton et al. 1984; Kohashi & Oda, 2008). The primary, short‐latency C‐start (SLC) is predominantly initiated by excitation of Mauthner cells (M‐cells), two large fast‐conducting reticulospinal command neurons located in rhombomere 4 of the hindbrain (Burgess & Granato, 2007; Kohashi & Oda, 2008; Issa et al. 2011). In contrast, non‐Mauthner responses, also termed long‐latency C‐starts (LLCs), are initiated by M‐cell homologs Mid2cm and Mid3cm, located in rhombomeres 5 and 6 (Liu & Fetcho, 1999; Weiss et al. 2006; Kohashi & Oda, 2008). Following M‐cell activation, a single spike is propagated down a large, contralaterally projecting axon, collectively activating motoneurons and muscle cells along the entire contralateral trunk. The concerted muscle contraction results in a C‐shaped body bend that characterizes the C‐start startle response.

Prior studies have noted differences in the latencies of SLC and LLC escape behaviours and have confirmed with Ca²⁺ imaging and laser ablation that SLC responses, unlike LLCs, are initiated by the M‐cell (Burgess & Granato, 2007; Issa et al. 2011; Lacoste et al. 2015; Marsden & Granato, 2015). In addition, this and other compelling research often uses kinematic analysis of high‐speed videos to calculate average SLC and LLC latencies from populations of larval responses using a cutoff latency value to categorize the two response types. These studies also describe how lower magnitude stimuli decrease the probability of evoking an SLC while increasing the probability of observing either LLC responses or failures. Given that SLCs are the primary form of fast startle response in zebrafish (Fero et al. 2011), here we sought to establish an accurate and repeatable method to discriminate between SLC and LLC responses that would also allow us to investigate the underlying mechanisms for the intensity dependence of both the latency and precision of the SLC startle response.

Although hair cells in the zebrafish inner ear have been shown to primarily initiate the startle reflex (Kohashi & Oda, 2008; Kohashi et al. 2012; Lacoste et al. 2015), direct recordings from their afferent neurons have not been achieved. Therefore, we chose the lateral line as a platform to examine hair cell intensity encoding. Importantly, lateral line hair cells are remarkably similar to auditory hair cells in their structure and physiological function, as well as in their afferent innervation (Sheets et al. 2011; Ricci et al. 2013; Olt et al. 2014). Moreover, hair‐cell afferent neurons in the lateral line make contact with the M‐cell (Liao & Haehnel, 2012; Pujol‐Martí & López‐Schier, 2013). While the lateral line alone is not likely to evoke startle responses, it does play a role in the directionality and latency of the startle reflex (Mirjany et al. 2011 a), and in the discrimination of harmful versus harmless stimuli (Pujol‐Martí & López‐Schier, 2013).

Here, we examined the components of the C‐start startle response at multiple levels of the reflex circuit. First, we took advantage of a transgenic line of zebrafish with the light‐activated protein, channelrhodopsin‐2 (ChR2), expressed in hair cells of the ear and lateral line sensory systems. We then head‐fixed larvae and acquired high‐speed videos of C‐starts together with simultaneous field potential recordings following optical excitation of hair cells. With these techniques, we were able to identify and discriminate between SLC and LLC responses. We then examined the intensity dependence of SLC behavioural kinematics and SLC field potential parameters. The simultaneous collection of both measurements allowed us to determine how C‐start latencies and their precision might correlate with field potential latencies and their precision for each acquired SLC response. Finally, we took advantage of an established in vivo preparation (Obholzer et al. 2008; Trapani & Nicolson, 2010; Olt et al. 2014; Haehnel‐Taguchi et al. 2014; Levi et al. 2014) to examine the latencies and jitter of evoked spikes from single hair‐cell afferent neurons in the transgenic zebrafish's lateral line. Together, these techniques allowed us to investigate the intensity‐dependent relationship among the encoded spike trains of afferent neurons, the parameters of whole‐animal field potentials, and the kinematics of evoked startle responses.

Methods

Ethical approval

Animal protocols were approved by the Institutional Animal Care and Use Committee (IACUC) at Amherst College under assurance number 3925‐1 with the Office of Laboratory Animal Welfare.

Animals

Zebrafish (Danio rerio) were maintained on a 14 h light–dark cycle at 28.5°C. All experiments used 5–7 day‐old Ekkwill zebrafish (Ekkwill Waterlife Resources, Ruskin, FL, USA) of either sex. Wild‐type and transgenic Tg(myo6b:ChR2‐EYFP) larvae were obtained from outcrosses to wild‐type animals. All experiments were performed at room temperature following a 10 min acclimation period.

Field potential and behavioural recordings

Startle responses were evoked in ChR2‐positive transgenic larvae across a range of optical stimuli, while wild‐type larvae did not respond to optical stimuli (n = 5 larvae). For simultaneous behavioural and field potential experiments, larvae were head‐embedded, ventral side down, in 1% low‐melting‐point agarose, pinned to a silicone‐lined (Sylgard 184, Dow Corning, Midland, MI, USA) dish and covered in deionized water. A larva was precisely aligned between two field‐potential recording electrodes (stainless steel insect pins) placed exactly 1 cm from the body along the rostro‐caudal axis. The location of the electrodes with respect to the larva was kept constant because field potential waveform size and polarity varies with electrode position (Monesson‐Olson et al. 2014 b). Field potentials were measured using a differential amplifier (Model 3000, A‐M Systems Inc., Carlsborg, WA, USA) with a 300 Hz high‐pass filter, 3 kHz low‐pass filter, ×5000 gain, and acquired at 10 kHz sample rate using a PowerLab 26T DAQ device and LabChart software (AD Instruments, Colorado Springs, CO, USA). The recording chamber was mounted on a custom made aluminum platform with a light box mounted below the stage for sample illumination, a dissection microscope with a high‐speed camera, and a stimulating LED. The LED was fixed in place at a ∼45 deg angle, ∼1.3 cm horizontal distance and ∼5 cm vertical distance from the agarose‐embedded larva. The entire preparation was enclosed in a copper Faraday cage to shield interfering electrical noise.

Behavioural responses were recorded for 2 s, at 1000 frames s⁻¹, using an IL3 camera (Fastec Imaging, San Diego, CA, USA) mounted on the dissection microscope (SZ40, Olympus, Saucon, PA, USA). As mentioned above, the machined platform fixed the position of the microscope, recording chamber, and stimulus LED. Stimulus light was filtered by an amber filter before entering the microscope to keep the video from saturating during light flashes. Videos (800 × 600 pixels) were trimmed to 5 frames before and 400 frames after stimulus delivery using FasMotion software (Fastec Imaging, San Diego, CA, USA). In each trial, 100 ms light flashes were delivered from a blue LED bulb (460–490 nm, LEDSupply.com, Randolph, VT, USA) using an optic lens (Carclo, Latrobe, PA, USA), connected to a 1000 mA driver. Light power was determined by the output voltage from the PowerLab using LabChart. Output intensities (see Calibrating stimulus intensity section) were measured by a digital light power meter at 470 nm (PM100D sensor area = 70.8 mm²; ThorLabs, Austin, TX, USA) placed directly on the aluminum platform. Stimulus delivery, field potential recordings, and acquisition of videos were time‐locked using a custom circuit box that allowed linear control of voltage in an arrangement that triggered all devices simultaneously within 1 μs.

Field potential and behavioural data analysis

Data were obtained from ChR2‐positive larvae at 10 light intensities with 5 trials per intensity and 100 s between trials (startle recovery time was determined to be 10 s). Field potentials were analysed using LabChart to quantify three features of the field potential traces: FP latency (defined as the time between stimulus onset and the first local minimum), FP max amplitude (maximum peak‐to‐peak amplitude of the first biphasic peak observed), and FP maximum slope (defined as the most negative derivative of the initial biphasic peak of the field potential waveform). For each larva, all FP max amplitudes acquired for every tested stimulus intensity were normalized to the smallest FP max amplitude within the population of responses. The precision of FP latencies was determined as the standard deviation of the FP latencies at each stimulus intensity.

Videos (1 kHz frame rate; 994 μs exposure time) of the behaviour were cropped using ImageJ (National Institutes of Health, Bethesda, MD, USA) and frame numbers for C‐start initiation and the end of the first C‐bend were determined by manual inspection of individual frames. These two frames defined the image sequence that was sent to an automated program written in MATLAB (MathWorks, Natick, MA, USA) that extracted the tail angle from each frame. In the program, first a pixel intensity threshold is selected to separate the darker larval body from the lighter background. Next, the program creates a contour line (∼70 points mm⁻¹) on each side of the body and identifies the points on the contour line at the midline of the head and the tip of the tail. The point at the midline of the head does not change due to the larval head being embedded in agar, and the peak in the derivative of the contour line identifies the tip of the tail. Using these two points as a reference, the program calculates the midline of the larval body by determining the average distance between opposing contour line points. From this midline, four analysis markers are tracked for all imported frames: top of head (defined as the most rostral point on the midline), bottom of head (located 60 points on the midline from top of head), bottom of tail (located 10 points before the most caudal point on the fish), and top of tail (located 60 points from the most caudal point on the fish). Manual inspection of the markers in each frame identified incorrect points about 5% of the time, which were then manually adjusted. A list of tail angles for every frame analysed was generated by calculating the angle formed by the intersection of the line through the two head markers (top and bottom of head) and the two tail markers (top and bottom of tail), and then subtracting from 180 deg (Fig. 1 A). Kinematic data were analysed with Igor Pro (Wavemetrics, Portland, OR, USA) to quantify the change in tail angle over time, which was then differentiated to obtain the change in maximum angular velocity over time. The maxima in these plots were recorded as the maximum tail angle and maximum angular velocity, respectively. The precision of the SLC response latencies was determined as the standard deviation of the mean SLC latencies at each stimulus intensity. The measured error in tail angle was estimated as 4 deg, and the error in angular velocity was estimated as 0.4 deg s⁻¹ as obtained by measuring the standard deviation of these values over 20 frames just prior to a startle response.

Figure 1. Combined field potential recordings and high‐speed videos of C‐starts allow for discrimination between SLCs and LLCs.

A, diagram of recording apparatus depicting a transgenic larval zebrafish head‐mounted in agarose (grey square inside light blue Petri dish). C‐starts were evoked by activating ChR2 with a blue LED. Field potentials and videos were recorded simultaneously and were time‐locked to stimulus onset. B, representative field potentials from an SLC (top) and LLC (bottom) response. Blue arrow indicates stimulus onset. Inset: large, initial biphasic peak of the SLC field potential waveform. C, selected frames (1 ms per frame) from videos of C‐starts that occurred with the field potentials in B. First frame is at stimulus onset (Stim on; t = 0 ms). Subsequent frames show initiation of tail movement (C‐start onset), time of maximum angular velocity (Max ang vel), and time of the maximum tail angle (Max tail angle). D and E, change in tail angle (D) and angular velocity (E) over time (1 circle per 1 ms frame) for the SLC (top) and LLC (bottom) responses shown in C with coloured symbols corresponding to coloured times in C. Asterisks in C–E indicate the subtle contraction seen at onset of all LLCs. [Colour figure can be viewed at wileyonlinelibrary.com]

Afferent neuron recordings

Afferent neuron recordings were performed using 5‐dpf transgenic ChR2‐positive larvae as described previously (Olt et al. 2016). Larvae were anaesthetized in 0.016% tricaine (MS‐222, Sigma‐Aldrich, St Louis, MO, USA) and mounted onto a silicone‐lined (Sylgard 184, Dow Corning, Midland, MI, USA) recording chamber (PC‐R, Siskiyou, Grants Pass, OR, USA) by inserting tungsten pins behind the eye and through the tail. The heart of the fish was then injected with 125 μm α‐Bungarotoxin (Abcam, Cambridge, MA, USA) to block all muscle movement. The larva was then rinsed to remove the anaesthetic and left in extracellular solution (130 mm NaCl, 10 mm Hepes, 2 mm KCl, 2 mm CaCl₂, 1 mm MgCl₂, pH 7.8). The recording chamber was placed under a ×40 water‐immersion objective (BX51WI, Olympus, Saucon, PA, USA), and the recording electrode and fluid jet were positioned using micromanipulators (MPC‐200, Sutter Instrument Company, Novato, CA, USA). The recording electrode was fabricated using a Flaming‐Brown pipette puller (P‐1000, Sutter Instrument Company) and filled with extracellular solution (pipette resistance = 6–10 MΩ). The electrode was then positioned against an individual soma of an afferent neuron in the posterior lateral line ganglion (PLLg). A loose‐patch configuration recording was established (seal resistances ∼25–60 MΩ) and was characterized by observing measurable spontaneous spiking. Data were collected using an EPC9 patch‐clamp amplifier and Patchmaster software (HEKA Elektronik, Bellmore, NY, USA). Data were sampled at 20 kHz and filtered at 2.9 kHz. Recordings were made from afferent neurons that displayed phase‐locked spiking from fluid jet stimulation of the most anterior primary neuromast (L1).

Microphonic potentials

Extracellular recordings of microphonic potentials were performed using 5‐dpf ChR2‐positive zebrafish larvae as described previously (Olt et al. 2016). Microphonic potentials represent the depolarization of the hair‐cell receptor potential in response to transepithelial currents, including those through MET channels. Measurements were performed with an Axon Instruments 200B (Molecular Devices, Sunnyvale, CA, USA) amplifier in current‐clamp mode (20 kHz sample rate; ×500 gain; 1 kHz filter). Potentials were further amplified (×100) and low‐pass filtered (100 Hz) using a Model 440 amplifier (Brownlee Precision, Palo Alto, CA, USA) and data were acquired with an ITC‐16 DAQ device using Patchmaster software (HEKA Elektronik, Bellmore, NY, USA). In order to remove background noise from the microphonic potential recordings, 200 consecutive measurements (repetitions) were averaged to produce a single microphonic trace. The total magnitude of each microphonic potential (‘total microphonic potential’) in microvolts (μV) was then calculated from the integral of the evoked portion of the microphonic trace divided by the duration of the stimulus interval (i.e., μV s (0.05 s)⁻¹). In order to generate dose–response plots from multiple recordings, the values of total microphonic potential acquired at each tested stimulus intensity were normalized to the largest value measured for that neuromast recording.

Electrophysiology stimulation

Hair cells from L1 neuromasts were stimulated both mechanically and optically for 50 ms, which represents a duration that is >90% of all SLC C‐start latencies (Fig. 2 B). The inter‐repetition interval was 1.5 s, where full recovery from adaptation between repetitions occurred at maximum intensity, and 10 repetitions were acquired at each intensity with 10 s between subsequent intensity trials. For mechanical stimulation, a fluid jet with an ∼40 μm diameter tip opening was filled with extracellular solution and aligned with the anteroposterior axis of the L1 neuromast. A high‐speed pressure clamp (HSPC‐1, ALA Scientific Instruments, Farmingdale, NY, USA) was used to control and deliver pressure (10 mV = 2.5 mmHg; see Calibrating stimulus intensity section). Mechanical deflection of stereocilia with high‐speed videos during fluid jet stimulation at multiple intensities revealed that the latency of the mechanical deflection was not dependent on intensity (mean latency = 4.9 ± 0.1 ms; n = 50). For optical stimulation, cyan light (460–482 nm excitation filter within light source) was triggered from a multi‐channel SpectraX light driver (Lumencor Inc., Beaverton, OR, USA) with percentage‐intensity levels controlled by custom procedures written in Igor Pro (Wavemetrics). Output light passed through a 50% neutral density filter and was focused onto an individual neuromast via the ×40 water‐immersion objective. Focused light intensity at the recording chamber (area = ∼9 mm²) was quantified (3.4 ± 0.02 W m⁻² (% intensity)⁻¹) and determined to be linear (F = 43707, P < 0.0001; linear fit R ² = 0.998) across delivered intensities using a PM100D digital optical power meter set at 470 nm wavelength.

Figure 2. SLCs and LLCs have overlapping latencies with response probabilities that depend on stimulus intensity.

A, relative frequency histogram of C‐start startle responses for SLCs (black bars), LLCs (grey bars), and failures (white bars) at each delivered intensity. Failures were defined as responses where the larva did not perform a C‐bend upon optical stimulation. Light intensities are binned at 50 W m⁻² per bin. B, relative frequency histogram of C‐start latencies for the population of 205 SLCs (black bars) and 29 LLCs (grey bars). Startle latencies are binned at 20 ms per bin.

All data were analysed using custom programs written in Igor Pro. First spike latency (FSL) was calculated as the time difference from stimulus onset to the first evoked spike, and FSL jitter was determined from the standard deviation (SD) of FSL values across 10 consecutive repetitions. Spike number was determined from the duration of the stimulus plus 10 ms to capture any events that occurred at stimulus offset, and mean spike number plus SD was calculated from 10 consecutive repetitions. Spike number within the maximal, moderate, and minimal field potential latencies was determined in a similar manner with the detection interval set to the mean FP_intensity latency for each intensity value (see next section).

Calibrating stimulus intensity

Differences in the methods used to record and deliver light stimuli during the whole‐animal and afferent neuron recordings contributed to the different ranges in light intensity required for the two preparations. For behavioural recordings, minimal optical intensity was the lowest intensity that evoked >50% SLC responses (see Fig. 2 A). For each afferent recording with optical and mechanical stimuli, minimal intensity (arbitrarily set at 1%) was the lowest intensity that evoked spikes above background. For all forms of stimulation (behavioural and afferent neuron), maximal intensity was determined from the plateau component of a single‐phase exponential decay equation (see Statistics and curve fitting section) that was fitted to the group data for FP latency, optical and mechanical FSL, and optical and mechanical spike number. The moderate intensity values were defined as 20% of the calculated maximal intensity value for each experiment.

Statistics and curve fitting

Wild‐type and ChR2‐positive larvae were randomly selected from the offspring of three to five mating pairs of adult fish. For the high‐speed video and field potential experiments, more than six larvae were chosen and only data from those that survived the experiment and recovered normally afterwards were kept. Single neuron recordings were performed on four or more larvae, depending on condition. Data were analysed and plotted using Prism 6 (GraphPad, La Jolla, CA, USA) and Adobe Illustrator (Adobe Systems Incorporated, San Jose, CA, USA) software. Curve fitting and statistical analysis was performed using Prism 6 and significance was determined with α = 0.05. Linear regression (Y = Y _intercept + Slope × X), single‐phase exponential decay (Y = (Y ₀ − Plateau) × exp(−K × X) + Plateau), and Hill (Y = Plateau_Bottom + (Plateau_Top − Plateau_Bottom)/(1 + 10^((LogEC₅₀ − X) × HillSlope)) equations were used without constraints on any parameters unless specifically stated. For each curve fitting, selection of the preferred equation was determined by comparison between the above equations using an extra sum of squares F test with the simpler model selected when the P value was less than α. Linear regressions were analysed with an F test to determine whether the slope of the fitted line was significantly non‐zero. C‐start kinematic and field potential parameter values in the text are reported as means ± SEM. The latency and precision values are reported as means ± SD. For comparison between two means, data were analysed with a non‐parametric Mann‐Whitney U test. To test for correlation between variables, a non‐parametric Spearman correlation rank test was performed. The test‐statistic, n value, and two‐tailed P value are reported for each test.

Results

We quantitatively examined C‐starts in larval zebrafish by acquiring high‐speed videos synchronized with electrophysiological recordings of C‐start generated field potentials. To ensure accurate and repeatable quantification of both behavioural kinematics and field potential waveforms, we developed a specialized recording apparatus that held an individual, head‐mounted larva in a fixed position relative to the stimulus source, recording electrodes, and video camera (Fig. 1 A; n = 6 larvae). In order to maintain precise control of stimulus onset, duration and intensity, we examined optically evoked C‐starts using transgenic larvae (Tg(myo6b:ChR2‐EYFP)) with stable expression of the light‐gated ion channel Channelrhodopsin‐2 (ChR2) in hair cells of both the auditory and lateral line systems (Monesson‐Olson et al. 2014 a). By using optical stimulation, we could deliver similar stimulation protocols and intensities across our whole‐animal and single afferent neuron experiments.

SLC and LLC C‐starts correspond to two different field potential waveforms and behavioral kinematics

Delivery of 100 ms light flashes at 10 different intensities evoked C‐starts in 78% of trials (n = 300 total trials), which provided us with a population of C‐starts (n = 234) where each was captured simultaneously with both a video and a field potential recording. Failure trials always lacked both a measurable field potential response and a behavioural response. Each evoked C‐start was characterized by a C‐shaped body bend and resulted in one of two different field potential waveforms that were previously shown to correspond to either an SLC or LLC behavioural response (Issa et al. 2011). The population of SLC field potentials each had initial, large‐amplitude, biphasic peaks and relatively short mean latencies from stimulus onset (22.0 ± 0.9 ms; n = 205; Fig. 1 B). In contrast, the LLC‐generated field potentials lacked the initial large‐amplitude peak, had longer average latencies, and occurred with less frequency (52.0 ± 5.0 ms; n = 29; Fig. 1 B). The initial, large‐amplitude peak represented a distinct difference between the two types of responses across all 234 C‐start responses.

Because our entire population of C‐starts was obtained using fixed‐position larvae and captured with both a video and field potential recording, we were able to sort all responses as either SLCs or LLCs – regardless of their individual latency – based on the presence or absence of the initial large‐amplitude peak of their field potentials. Given the distinct neural circuits that generate the two reflexes (Burgess & Granato, 2007; Kohashi & Oda, 2008; Issa et al. 2011), we started with the assumption that sorting based on this field potential parameter provided two true populations of responses that would allow us to closely determine kinematic differences between the two C‐start populations.

After sorting all responses, we analysed the video of each C‐start for three kinematic features: C‐start latency (onset time of the C‐start), maximum tail angle, and maximum angular velocity. These parameters were quantified by calculating the change in tail angle per video frame over the length of each recording (Fig. 1 C–E). Consistent with our field potential data, SLCs had relatively short C‐start latencies (26.1 ± 0.9 ms; n = 205), while LLCs, which predominantly occurred at low stimulus intensities (see Fig. 2 A), had longer average C‐start latencies (57.5 ± 4.7 ms; n = 29). Other significant differences between the two responses were the maximum tail angle (SLC 82.6 ± 1.3 vs. LLC 75.6 ± 2.1 deg; Mann‐Whitney U = 2300, P < 0.05) and the maximum angular velocity (SLC 13.6 ± 0.2 vs. LLC 12.5 ± 1.0 deg (ms)⁻¹; Mann‐Whitney U = 2044, P < 0.01).

Further analysis of the kinematic properties of the two populations of behavioural responses revealed an additional difference between SLCs and LLCs. All LLC responses displayed a visible lag in contraction of the most distal tail segment just after initiation of the C‐start (n = 29; Fig. 1 C, asterisk). This kinematic feature was unique to all LLC responses and appeared as a local maximum in plots of LLC tail angle over time (see Fig. 1 D, asterisk) and plots of LLC tail‐angular‐velocity over time (see Fig. 1 E, asterisk). This counter‐bend of the distal tail segment was not observed in any SLC (n = 205) and represents a distinct kinematic difference between the two C‐start types, which further justified our use of the field potential waveform to sort SLCs from LLCs.

We next investigated the intensity dependence of C‐start initiation across our population of C‐starts. Increasing stimulus intensity decreased the number of failures and increased the probability of evoking an SLC, while decreasing the likelihood of evoking an LLC (Fig. 2 A). However, by sorting responses based on their field potential waveform, we observed LLC responses with latencies that fell within the range of SLC latencies (Fig. 2 B). This result strengthens our argument that by head fixing larvae and obtaining a field potential with every video‐captured C‐start, we were able to classify the entire population of responses at every intensity tested, despite overlapping latencies for the two response types. The increasing proportion of SLC responses relative to LLC responses at greater stimulus intensities indicates that as stimulus intensity was increased, the probability of initiating the faster SLC response increased accordingly.

Intensity‐dependent C‐start latencies and their precision are correlated with SLC field potential latencies and their precision

We next set out to examine the effect of stimulus intensity on SLC startle responses and their underlying field potentials. Given that each SLC generated its own unique field potential, we were able to examine the intensity dependence of both the field potential parameters and C‐start kinematics for each SLC response. We quantified three parameters of the SLC field potential (FP latency, FP maximum slope, and FP maximum amplitude) together with the three kinematic parameters of the SLC (C‐start latency, maximum tail angle, and maximum angular velocity; Fig. 3 A). We then determined whether each of these six parameters significantly covaried with light intensity and found that FP maximum amplitude and maximum slope, as well as C‐start maximum tail angle and maximum angular velocity, were not correlated with stimulus intensity (Fig. 3 C). This result suggests that once initiated, the startle response proceeds in an all‐or‐none fashion that is independent of stimulus intensity.

Figure 3. Timing and precision of SLC field potentials and C‐starts are correlated with light intensity.

A, left panel: diagram of the features of the field potential (FP): FP latency, FP max amplitude, and FP slope. A, right panel: diagram of three features of the C‐start: C‐start latency, tail angle, and angular velocity. B, representative SLC field potentials (left) and tail angle vs. time plots (right) from a single larva evoked at increasing stimulus intensities. C, box plots of parameters from SLC field potentials and C‐starts (n = 6 animals). Coloured symbol represents mean, box represents 25th to 75th percentiles, and whiskers represent minimum to maximum values. FP max amplitude was normalized for each animal. Numbers in top panel correspond to total trial number (n) from all animals for each intensity bin (50 W m⁻²) across all panels in C–E. D, dose–response plots of mean FP latency (left top) and mean C‐start latency (left bottom) versus stimulus intensity are fitted by single‐phase exponential decay equations. Data are represented as means ± SD (shaded area). The SD at each intensity bin for FP latencies (right top) and C‐start latencies (right bottom) are also fitted by single‐phase exponential decay equations. E, plots of the difference between the mean FP latency and the C‐start latency (left) and between the FP latency SD and the C‐start latency SD (right) at each intensity. The results were fitted by linear equations with zero slope. F, the latencies of C‐starts and underlying field potentials are linearly correlated (dashed line) with a slope of approximately 1. The Y‐intercept (4.9 ± 0.3 ms) of the linear fit corresponds to the mean time delay between field potential onset and initiation of the C‐start. G, the mean delay is also determined by subtraction of FP latency from C‐start latency for every recorded SLC response (n = 205). The resulting values are normally distributed with a histogram fitted by a Gaussian distribution. [Colour figure can be viewed at wileyonlinelibrary.com]

In contrast to the above results, we observed a significant decrease in both FP latency (Spearman ρ = −0.93; P = 0.0003; n = 10 pairs) and C‐start latency (Spearman ρ = −0.90; P = 0.0008; n = 10 pairs) with increasing stimulus intensity (Fig. 3 B and D, left panels). In addition, increasing stimulus intensity led to a significant increase in the precision of latencies for both the field potentials (Spearman ρ = −0.87; P = 0.002; n = 10 pairs) and C‐starts (Spearman ρ = −0.87; P = 0.0022; n = 10 pairs). In order to directly observe the intensity dependence of latency precision, we plotted the standard deviation of the FP latencies and C‐start latencies as a function of stimulus intensity (Fig. 3 D, right panels). Both plots were fitted by single‐phase exponential decay equations, which suggests that there is a plateau in the precision of the latency (FP_Plateau = 2.64 ± 0.53 ms; C‐start_Plateau = 2.61 ± 0.54 ms). Perhaps animals increase their probability of survival by responding to larger stimuli with faster and more precisely evoked startle responses.

The difference in time between the field potential onset and C‐start onset may represent the circuit delay from initiation of a spike in the M‐cell to initiation of contraction in the muscle cells following their excitation. To determine whether this delay time is dependent on stimulus intensity, we subtracted the mean FP latency from the mean C‐start latency (Fig. 3 E, left panel) and also calculated the difference in the precision of the latencies (Fig. 3 E, right panel) at each intensity. The slope of the linear fit in both plots was not significantly greater than zero (∆latency P = 0.16; ∆SD P = 0.90), which suggests that the delay from onset of the startle circuit to initiation of the C‐start contraction is fixed and does not change with stimulus intensity. To further investigate this finding, we plotted field potential latency versus C‐start latency for each SLC response and found a strong linear correlation (F = 5905; P < 0.001; linear fit R ² = 0.97; Fig. 3 F) with a slope of approximately 1, which supports the intensity independence of the time delay. The linear fit also provides an estimate of the fixed time interval between the two latencies as approximated by the Y‐intercept (4.9 ± 0.3 ms). Alternatively, the delay time can be calculated directly by subtracting the FP latency from the C‐start latency of every SLC response (4.1 ± 0.2 ms, n = 205). A histogram of these calculated delta values was fitted by a Gaussian equation, providing further evidence that the time delay is intensity independent (R ² = 0.996; Mean= 4.2 ± 0.1 ms; SD = 0.6 ± 0.1 ms; n = 21 bins; Fig. 3 G). Together, these results correlating each and every field potential latency with its corresponding C‐start latency support the argument that the field potential represents activity from the population of excitable cells that generate the startle response. The data also suggest that there is a ∼4 ms delay between onset of this electrical activity and onset of the behavioural response. An earlier electrophysiological study on adult goldfish estimated a similar of delay of ∼8 ms (Weiss et al. 2006). Given the differences in overall length and muscle mass between an adult goldfish and larval zebrafish, the difference in timing between the two estimates may be appropriate. These findings are also in agreement with the intensity‐independent field potential and kinematic parameters shown in Fig. 3 C. Taken together, our results thus far support the hypothesis that the intensity dependence of startle response latencies and their precision occurs upstream of the M‐cell.

Afferent spike number and FSL are dependent on stimulus intensity

The prediction that the intensity‐dependent mechanism is upstream from or at the level of the M‐cell implies that the temporal features of spike trains evoked in hair‐cell afferent neurons may determine the intensity‐dependent precision of startle response latencies. To test this hypothesis, we performed loose‐patch recordings of evoked spikes from single afferent neurons during hair‐cell stimulation of the innervated lateral‐line neuromast (Fig. 4 A). In response to 50 ms optical stimulation of neuromast hair cells, spike number increased and first spike latency decreased with increasing stimulus intensity (Fig. 4 B–D). Across five larvae, we observed a significant increase in the number of spikes (Spearman ρ = 0.79; P < 0.0001; n = 14 pairs; Fig. 4 E) with no change in the precision of spike number (Spearman ρ = 0.13; P = 0.65; n = 14 pairs; Fig. 4 E, right panel) with increasing stimulus intensity.

Figure 4. Intensity‐dependent changes in evoked spike trains in afferent neurons during optical hair‐cell stimulation.

A, cartoon diagram of recording setup for optical stimulation of ChR2‐expressing hair cells within a single neuromast. PLLg = posterior lateral line ganglion of afferent neurons. NM = posterior lateral line neuromast. B, representative responses from a single afferent neuron to 50 ms optical stimuli of different intensity. C, mean spike number (n = 10 repetitions) per stimulus interval from the recording in B for a range of stimulus intensities. D, mean FSL (n = 10 repetitions) from the recording in B as a function of stimulus intensity. E, left panel: mean spike number (n = 5 neurons) within the 50 ms stimulus interval (open circles) and within the FP Latency interval for minimal, moderate and maximal light intensities (see Methods section; filled squares). E, right panel: SD of spike number plotted as a function of stimulus intensity. F, left panel: mean FSL (n = 5 neurons) for each stimulus intensity (filled circles). F, right panel: intensity‐dependent changes in jitter. G, comparison of mean FP Latency (n > 20 repetitions; n = 6 larvae) versus mean FSL at minimal, moderate and maximal light intensities. Data are represented as means ± SD (bars in C, D and G and shaded area in E and F). Data in C were fitted by a Hill equation (dashed line) and data in D–G were fitted by either a single‐phase exponential decay or linear regression equation (dashed lines). [Colour figure can be viewed at wileyonlinelibrary.com]

If spike number were encoding intensity for the startle reflex, then increasing intensity should increase the number of evoked spikes that occur within the onset time of the SLC field potential. That is, we should see intensity‐dependent changes in the number of spikes during an interval defined by the field potential latency. Using the mean FP latency at defined minimal, moderate, and maximal intensities (see Methods) from our behavioural experiments (FP Latency_minimal = 48.7 ± 3.7 ms, FP Latency_moderate = 27.2 ± 1.4 ms, FP Latency_maximal = 13.0 ± 0.5 ms; n = 205 trials), we determined the mean number of evoked spikes within each interval at corresponding minimal, moderate, and maximal neuromast stimulation intensities (Spikes_minimal = 0.2 ± 0.1, Spikes_moderate = 1.0 ± 0.2, Spikes_maximal = 1.1 ± 0.2; n = 5 recordings; Fig. 4 E, left panel). This analysis suggests that it is unlikely that more than one spike arrives from an afferent neuron prior to onset of the reflex. Furthermore, the intensity‐independent precision of spike number does not agree with the increase in precision of field potential and C‐start latencies seen with increasing stimulus intensity.

In contrast to spike number, we found that first spike latencies (FSL; Spearman ρ = −0.96; P < 0.0001; n = 5) and their jitter (Spearman ρ = −0.87; P = 0.00001; n = 5) both decreased with increasing stimulus intensity (Fig. 4 F). In addition, subtraction of the mean FSL at the highest intensity from the mean FSL at lowest intensity provides an estimate of the overall intensity dependence of latency (∼25 ms). When combined with FSL jitter and the delay time between the field potential onset and C‐start onset, this range in timing can account for the breadth of behavioural latencies observed in our experiments (see Fig. 3 D).

FSL and FSL jitter are correlated to startle response field potentials

The intensity dependence of both FSL and FSL jitter in our afferent neuron recordings strongly resembled the intensity dependence of field potential latencies and their precision seen in Fig. 3 D. Therefore, we examined this relationship by comparing field potential latencies and their precision with FSL and FSL jitter at corresponding minimal, moderate, and maximal intensities (FSL_minimal = 38.9 ± 8.3 ms, FSL_moderate = 24.0 ± 4.4 ms; FSL_maximal = 9.7 ± 1.1 ms; n = 5 recordings) and found a linear correlation between the latencies (F = 139, P = 0.05; linear fit R ² = 0.99; Fig. 4 G). The slope of the linear fit is approximately 1, which indicates that there are no intensity‐dependent effects. The linear fit of the data also has a negative Y‐intercept, which suggests that the time delay between the spike arrival and onset of the field potential is quite small. Together, the above results support the hypothesis that increasing stimulus intensity decreases the latency of the first spikes arriving from afferent neurons at fast chemical and electrical synapses with the M‐cell (Szabo et al. 2006).

Given that our series of experiments were performed through direct optical depolarization of the hair cell receptor potential, we sought to confirm the physiological relevance of our results by observing intensity‐dependent changes in the mechanotransduction currents that depolarize the receptor potential of hair cells and in spike trains of afferent neurons during mechanical stimulation of hair cells with a fluid jet. In the inner ear and lateral line, the mechanotransduction process begins with mechanical stimuli deflecting the stereocilia that project in a stair‐cased fashion from the apical end of hair cells (Vollrath et al. 2007). Displacement of this ‘hair bundle’ leads to mechanical gating of mechanoelectrical transduction (MET) channels located at the tips of stereocilia and connected by tip links to the taller, adjacent stereocilium (Beurg et al. 2009). MET channel opening then generates inward cation currents that depolarize the receptor potential and ultimately result in neurotransmitter release and spiking in afferent neurons.

To estimate the intensity‐dependent change in the hair cell receptor potential with fluid jet stimulation, we measured microphonic potentials that are generated in part by mechanotransduction currents through MET channels (Nicolson et al. 1998). Consistent with an increase in mechanotransduction currents with larger deflection of the hair bundle, we observed a dose‐dependent increase in microphonics (Fig. 5 A) that saturated at maximal intensities and was fitted by a sigmoidal Hill equation (Fig. 5 B and C). In addition, we determined that the onset time of microphonic potentials was not dependent on intensity (mean latency = 8.7 ± 0.2 ms, n = 5 neuromasts from n = 4 larvae; see Fig. 5 A, red line). Together, the intensity‐dependent increase in microphonic potentials and their non‐variable onset time suggest that any changes we observed in FSL during afferent neuron recordings were not due to a mechanical artifact or differences in the onset time of depolarization of the receptor potential.

Figure 5. Intensity‐dependent changes in amplitude of microphonic potentials generated by stimulation of neuromast hair cells with a fluid jet mechanical stimulus.

A, average traces (n = 200 repetitions) of microphonic potentials displayed for multiple pressure intensities in response to a 50 ms square‐wave stimulation (bottom trace) delivered to a single neuromast. The dashed red line indicates the onset time of the microphonic potential (∼8 ms) after stimulus onset. B, plot of the total microphonic potential (quantified as the area under the evoked portion of the microphonic waveform divided by the duration of stimulus, 50 ms) at each recorded stimulus intensity from the recordings of a single neuromast in A. C, plot of normalized data from multiple neuromast recordings (n = 5 neuromasts; n = 4 larvae). Data in B and C were fitted by Hill equations (dashed line). [Colour figure can be viewed at wileyonlinelibrary.com]

Given its similarities with the auditory system, we set out to test the hypothesis that mechanically evoked spikes in the lateral line would display intensity‐dependent changes in latency and number. We recorded evoked spikes from single lateral‐line afferent neurons during fluid jet stimulation of innervated hair cells (Fig. 6 A). Consistent with the mechanotransduction process in hair cells, increasing stimulus intensity increased the number of evoked spikes and decreased first spike latency (Fig. 6 B–D). The intensity‐dependent changes in mechanical pressure significantly increased the number of evoked spikes (Spearman ρ = 0.90; P < 0.001; n = 12 pairs; Fig. 6 Ea) but did not change their precision (Spearman ρ = −0.17; P = 0.59; n = 12 pairs; Fig. 6 Eb). We also found a significant decrease in both first spike latencies (Spearman ρ = −0.99; P < 0.0001; n = 12 pairs; Fig. 6 Fa) and their jitter (Spearman ρ = −0.62; P = 0.037; n = 12 pairs; Fig. 6 Fb) with increasing mechanical stimulus intensity. Both spike number and first spike latency values were similar to our optical stimulation experiments (compare with Fig. 4 E and F), which supports our use of ChR2 for depolarizing the hair‐cell receptor potential. Our results were also similar to intensity‐dependent changes in spiking measured in an in vitro study on the lateral line of Xenopus laevis (Harris & Milne, 1966). Altogether, intensity‐dependent spike encoding in afferent neurons in the lateral line was consistent with well‐described mechanisms for intensity‐dependent changes in afferent spiking observed in vertebrate auditory neurons, including those of mammals (Fay, 1978; Feng, 1982; Saunders et al. 2002; Heil, 2004; Fuchs, 2005).

Figure 6. Intensity‐dependent changes in evoked spike trains in afferent neurons during mechanical stimulation of hair cells.

A, cartoon diagram of recording setup for mechanical stimulation of PLL hair cells using a fluid jet. PLLg = posterior lateral line ganglion of afferent neurons. NM = posterior lateral line neuromast. B, representative responses from a single PLL afferent neuron to 50 ms mechanical stimuli at different pressure intensities (same neuron from Fig. 4 B–D). C, mean spike number (n = 10 repetitions) per stimulus interval from the recording shown in B for a range of stimulus intensities. D, mean FSL (n = 10 repetitions) from the recording in B as a function of stimulus intensity. Ea, mean spike number (n = 5 neurons) within the 50 ms mechanical stimulus interval. Eb, intensity‐dependent changes in SD of spike number. Fa, mean FSL (n = 5 neurons) for each stimulus intensity. Fb, intensity‐dependent changes in jitter. Data are represented as means ± SD (bars in C and D and shaded area in E and F). Data in C–F were fitted by either a single‐phase exponential decay or linear regression equation (dashed lines). [Colour figure can be viewed at wileyonlinelibrary.com]

Discussion

Previous work on rats (Pilz et al. 1987) and humans (Blumenthal, 1996) has shown that startle latency is dependent on stimulus intensity. In addition, recent work examining cortical activity shows that neuronal latency is predictive of behavioural latency (Lee et al. 2016). Here, our experiments show intensity‐dependent changes in SLC latencies and their precision in zebrafish. We examined the mechanism for this dependence at multiple levels of the reflex, from stimulus input to behavioural output by taking advantage of a transgenic line of zebrafish with hair‐cell expression of ChR2. We found that SLC response latency and precision co‐varied with the latency and precision of generated field potentials with a fixed time between onset of the two responses. This result indicated that the intensity‐dependent mechanism occurs upstream of the command neurons that initiate the reflex. Recordings from hair‐cell afferent neurons in the lateral line showed that the number of evoked spikes increases with stimulus intensity, but not within a time period that can account for the latency shift in startle responses. Furthermore, the precision of spike number does not increase with increasing stimulus intensity, indicating that it is not the source of intensity‐dependent precision of field potential latency. In contrast, we observed an intensity‐dependent decrease in first spike latency and jitter that was correlated with the intensity‐dependent decreases in field potential latencies with increasing precision. Together, our data show that the latency and jitter of first spikes arriving at the command neuron can account for the intensity‐dependent changes in the timing and precision of SLC startle response latency.

SLCs and LLCs are kinematically different and generated by distinct neural pathways

By distinguishing between SLCs and LLCs based on the different waveforms of their field potentials, we observed a previously unidentified difference in the kinematics of the tail contraction between the two C‐start types. Specifically, there is a counter‐bend of the distal portion of the tail during an LLC response that is absent in SLCs, where tail contraction proceeds as a smooth pivot from near the apical start of the tail. This difference in contraction suggests that the faster SLC response is a more continuous, simultaneous mechanism of contraction, perhaps from a more synchronized activation of motoneurons and muscle cells. In contrast, LLCs lack the large amplitude, initial peak of the SLC field potential and also have a longer average latency. Combined, these results point toward a less synchronized musculature contraction that would also explain the smaller magnitude of the LLC kinematic parameters that we observed. Thus, the presence of the large‐amplitude peak of the SLC field potential together with the mean shorter latency of SLC responses and smooth tail contraction support the notion that the waveform of the SLC field potential is generated following activation of the large M‐cell and the subsequent, nearly synchronous activation of motoneurons and axial muscle cells (Prugh et al. 1982; Featherstone et al. 1991; Issa et al. 2011). Altogether, our observed differences between the field potential and behavioural responses of the SLC and LLC startle responses agree with their known initiation through different command neuron pathways and support our novel use of optogenetics for examining hair‐cell evoked startle responses.

An accurate method for identifying SLC and LLC startle responses

By sorting responses based on their unique field potential waveforms, we obtained a complete population of SLC responses and field potentials that allowed us to examine their dependence on stimulus intensity. Interestingly, we did not observe a significant change in any of the kinematic properties of the C‐start behaviour or features of the field potential waveform other than their latencies. This result confirms previous work showing that after initiation of the startle response, the subsequent properties of the reflex are not changed (Eaton & Emberley, 1991; Burgess & Granato, 2007). In other words, once a stimulus of sufficient intensity brings the command neuron to threshold, the reflex proceeds as an all‐or‐none response.

We also observed that increasing intensity decreased the likelihood of initiating LLCs while concomitantly increasing the probability of evoking SLCs with shorter latencies. Despite this effect, we still observed LLCs with latencies that were shorter than some SLC latencies. Perhaps these LLCs would have been miscategorized as SLCs if a traditional temporal cutoff method for categorization were used. Evidence for a physiological role for LLC versus SLC responses may come from differences in their initiation. The number of evoked spikes in afferent neurons is known to play an important role in rate encoding for perception of sensory stimuli. Given the longer latencies of LLC startle responses, this method of encoding may be used in generation of LLCs because, unlike SLCs, their longer latency would allow for the arrival of more than one spike per afferent neuron at the command neurons. Further studies may help to elucidate the role of spike number in LLC initiation and auditory perception in zebrafish (Bhandiwad et al. 2013).

Factors influencing startle responses and lateral line activity

Although wild‐type (non‐GFP‐positive) larvae did not display any light‐evoked behaviour that we could capture with our high‐speed camera, we cannot rule out a modulatory effect of the blue‐light flash on the evoked startle reflex of ChR2‐positive larvae. In particular, visual inputs have been shown to modulate the M‐cell response, enhancing sound detection and perhaps improving sound discrimination (Mu et al. 2012). Furthermore, a recent study showed that excitatory interneurons in the hindbrain, known as spiral fibre neurons, wrap the axon hillock of the M‐cell and are required for the generation of short‐latency startle responses (Lacoste et al. 2015). Future work is needed to further examine the potential contribution of these pathways to the intensity dependence of C‐start latency and precision.

Our afferent neuron recordings from the lateral line displayed similar intensity dependence as startle responses evoked by whole‐animal stimulation. Given that afferent neuron spiking was generated by stimulation of a single neuromast with on average four to eight hair cells contacting the single afferent neuron (Faucherre et al. 2009), this similarity argues that auditory hair‐cell stimulation that results in the startle response evokes a similar pattern of spiking in afferent neurons that we measured in the lateral line. Furthermore, acoustic stimuli used to generate startle responses by activation of saccular hair cells in fish are typically presented to the entire animal (Zottoli, 1977; Weiss et al. 2009; Mirjany et al. 2011 b) and would presumably simultaneously excite a similar number of hair cells as our whole‐animal optical method. In addition, mechanical stimulation of neuromast hair cells with a fluid jet produced similar results as our optical experiments, further supporting the use of ChR2 as a means to depolarize the hair cell receptor potential.

When field potential latencies were compared with first spike latencies recorded in the lateral line, the correlation resulted in a linear fit with a negative intercept of ∼2ms (see Fig. 4 G). Given that the primary inputs to the M‐cell are from saccular hair‐cell afferents and our FSL values are recorded from lateral line hair‐cell afferents, differences in cable properties and axon length may contribute to this timing offset. While lateral line spikes may arrive later than those from the ear, because the lateral line plays a role in the directionality of the startle reflex (Mirjany et al. 2011 a), they are predicted to still arrive before or at the onset of M‐cell activation in order to modulate the reflex.

FSL and FSL jitter are correlated with startle response latencies and their precision

Our recordings from afferent neurons indicate that on average, one spike from each innervating neuron would arrive at the M‐cell prior to onset of the startle‐evoked field potential. For somatosensory neurons, single spikes from single neurons are shown to be sufficient to generate an M‐cell response (Douglass et al. 2008). However, for hair‐cell inputs it is likely that single first spikes from multiple afferent neurons are required to collectively excite the Mauthner cell through their coincident arrival (Faber et al. 1991; Korn & Faber, 2005; Yao et al. 2014). Indeed both lateral line afferent neurons (Obholzer et al. 2008; Liao, 2010; Trapani & Nicolson, 2011), and auditory afferent neurons from other vertebrates and mammals (Pfeiffer & Kiang, 1965; Geisler, 1998; Smotherman & Narins, 2000; Heil et al. 2007; Heil & Peterson, 2015) show spontaneous spiking in the absence of stimulation that is likely to generate subthreshold postsynaptic potentials at the M‐cell (Yao et al. 2014). Thus, as opposed to single, stochastic arrival of spontaneous spikes from innervating neurons, a startling stimulus – that decreases the latency and jitter of evoked spikes across multiple afferent neurons – results in coincident spike arrival, temporal summation of the postsynaptic potential, and initiation of an M‐cell spike. With increased stimulus intensity, jitter of first spike latencies would decrease further, resulting in earlier and more precise initiation of the startle reflex. This notion is supported by the correlation of FSL latencies and their jitter with field potential latencies and their precision, which are correlated to the timing and precision of C‐start latencies. The C‐start is primarily to direct rapid escape away from a threatening source (Korn & Faber, 2005), and fast encoding precision is important for determining the directionality of this escape (Weiss et al. 2009). Being alerted to or escaping from more intense threats with earlier and more precise responses is therefore an ideal physiological result of this encoding mechanism.

Pre‐ and postsynaptic mechanisms for intensity dependence of first spike latency

The location of the intensity‐dependent mechanism may exist at the level of hair‐cell synaptic transmission, postsynaptic excitation, or afferent neuron spike generation or all three. One postsynaptic source of intensity‐dependent time delay may come from summation of excitatory postsynaptic potentials (EPSPs) at the spike generator of the afferent neuron. A recent study from rat spiral ganglion neurons showed that spike latency varied by ∼2 ms with increasing size of EPSPs (Rutherford et al. 2012). Because this latency was measured from a one‐to‐one synapse of a mammalian auditory neuron, the multiple active zones of a zebrafish lateral line neuron may increase this latency effect as a result of the multiple EPSPs that presumably summate in order to reach threshold at the spike generator. A recent study of hair‐cell afferent fibres showed that summation of multiple excitatory postsynaptic currents (EPSCs) is more efficient at generating a spike (Schnee et al. 2013), which could then serve as the mechanism for increased precision for neurons receiving input from more than one active zone.

At the level of the hair cell, a specialized mechanism that could account for both the decrease in FSL and concomitant decrease in FSL jitter is provided by the ribbon synapse (Nouvian et al. 2006; Moser et al. 2006; Safieddine et al. 2012; Li et al. 2014). Modelling of the readily releasable pool of vesicles that lie beneath the ribbon shows that multiple vesicles must be released in order to precisely encode spikes in afferent neurons, and that increasing the hair cell receptor potential decreases the mean and jitter of the latency to first exocytosis (Wittig & Parsons, 2008). Furthermore, mutation of the synaptic protein, bassoon, results in detached ribbons and a marked disruption of both FSL and FSL jitter (Khimich et al. 2005; Buran et al. 2010). Whether disruption of the readily releasable pool or the summation of EPSPs has effects on startle response latencies and their precision remains to be determined.

Altogether, our findings support a model in which increasing stimulus intensity leads to initiation of action potentials with shorter latencies and less jitter in sensory afferent neurons. This encoding mechanism results in the coincidental arrival of spikes at the M‐cell command neuron, where, with increasing stimulus intensity, they summate to trigger a more immediate and precise startle response (Fig. 7 A). While FSL is known to be an important mechanism in perceptual encoding (Johansson & Birznieks, 2004; Heil, 2004; Chase & Young, 2007) and sound localization (Furukawa & Middlebrooks, 2001), here we provide in vivo evidence that supports the role (Fig. 7 B) of first spike latency in determining the rapid and precise onset of a reflex.

Figure 7. Cartoon model of the mechanism underlying intensity‐dependent changes in the timing and precision of SLC startle response latencies in larval zebrafish.

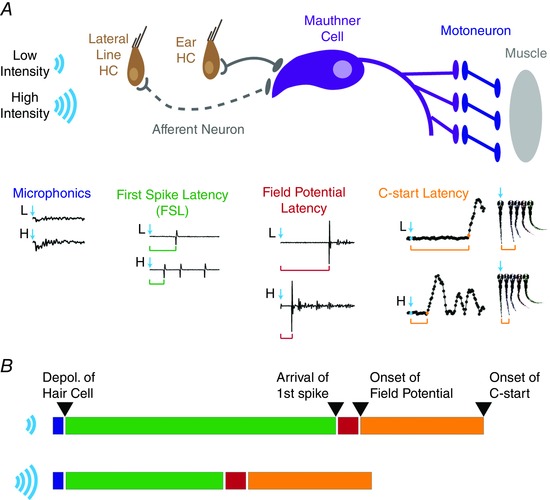
A, stimuli of increasing intensity generate a greater depolarization of the receptor potential of hair cells (microphonic traces beneath brown hair cells), which leads to faster and larger release of neurotransmitter and more rapid and precise initiation of action potentials in afferent neurons (green traces below grey afferent neurons). The afferent neuron from the lateral line is represented by a dashed line as lateral line inputs have not been shown to evoke startle responses independently from ear afferent neurons. Earlier arrival of first spikes with less jitter at the Mauthner cell (purple) leads to more rapid spiking of the M‐cell with greater precision. Propagation of the M‐cell spike generates excitation of motoneurons (blue) and muscle cells (grey) that together produce the whole‐animal field potential (red traces beneath the M‐cell) and initiate the rapid, C‐shaped contraction of the larval zebrafish (orange traces and images beneath the muscle cells). B, data presented here are consistent with the intensity‐dependent changes in latency of startle responses occurring downstream of hair cell depolarization (blue bars; fixed length) and upstream of spike arrival at the M‐cell (green bars; variable length), which would include presynaptic vesicle fusion, neurotransmitter release, postsynaptic depolarization, and spike initiation. Following a short delay before onset of the field potential (red bar; fixed length), there is a time delay of approximately 4 ms (from Fig. 3 F and G) from onset of the startle circuit until onset of the C‐start contraction (orange bar; fixed length), which probably arises from signal propagation through the M‐cell, motoneurons, and muscle cells that generate the startle response. [Colour figure can be viewed at wileyonlinelibrary.com]

Additional information

Competing interests

The authors declare no competing financial interests.

Author contributions

E.L.T., A.J.O., T.F.S., R.A.B., A.R.C. and J.G.T. conceived and designed the research; E.L.T., A.J.O., T.F.S., and R.A.B. performed the research; E.L.T., A.J.O., T.F.S., R.A.B., A.R.C. and J.G.T. analysed and interpreted the data; and E.L.T., A.R.C. and J.G.T. wrote the paper with significant intellectual contributions from all authors. All authors have approved the final version of the manuscript and agree to be accountable for all aspects of the work. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Funding

This work was supported in part by funding to J.G.T. from the National Science Foundation (NSF IOS‐#1456866) and from an Amherst College Faculty Research Award from the H. Axel Schupf ’57 Fund for Intellectual Life.