Role of Cl⁻–HCO₃ ⁻ exchanger AE3 in intracellular pH homeostasis in cultured murine hippocampal neurons, and in crosstalk to adjacent astrocytes

Abstract

Key points

• A polymorphism of human AE3 is associated with idiopathic generalized epilepsy. Knockout of AE3 in mice lowers the threshold for triggering epileptic seizures. The explanations for these effects are elusive.

• Comparisons of cells from wild‐type vs. AE3^–/– mice show that AE3 (present in hippocampal neurons, not astrocytes; mediates HCO₃ ^– efflux) enhances intracellular pH (pH_i) recovery (decrease) from alkali loads in neurons and, surprisingly, adjacent astrocytes.

• During metabolic acidosis (MAc), AE3 speeds initial acidification, but limits the extent of pH_i decrease in neurons and astrocytes.

• AE3 speeds re‐alkalization after removal of MAc in neurons and astrocytes, and speeds neuronal pH_i recovery from an ammonium prepulse‐induced acid load.

• We propose that neuronal AE3 indirectly increases acid extrusion in (a) neurons via Cl^– loading, and (b) astrocytes by somehow enhancing NBCe1 (major acid extruder). The latter would enhance depolarization‐induced alkalinization of astrocytes, and extracellular acidification, and thereby reduce susceptibility to epileptic seizures.

Abstract

The anion exchanger AE3, expressed in hippocampal (HC) neurons but not astrocytes, contributes to intracellular pH (pH_i) regulation by facilitating the exchange of extracellular Cl^– for intracellular HCO₃ ^–. The human AE3 polymorphism A867D is associated with idiopathic generalized epilepsy. Moreover, AE3 knockout (AE3^–/–) mice are more susceptible to epileptic seizure. The mechanism of these effects has been unclear because the starting pH_i in AE3^–/– and wild‐type neurons is indistinguishable. The purpose of the present study was to use AE3^–/– mice to investigate the role of AE3 in pH_i homeostasis in HC neurons, co‐cultured with astrocytes. We find that the presence of AE3 increases the acidification rate constant during pH_i recovery from intracellular alkaline loads imposed by reducing [CO₂]. The presence of AE3 also speeds intracellular acidification during the early phase of metabolic acidosis (MAc), not just in neurons but, surprisingly, in adjacent astrocytes. Additionally, AE3 contributes to braking the decrease in pH_i later during MAc in both neurons and astrocytes. Paradoxically, AE3 enhances intracellular re‐alkalization after MAc removal in neurons and astrocytes, and pH_i recovery from an ammonium prepulse‐induced acid load in neurons. The effects of AE3 knockout on astrocytic pH_i homeostasis in MAc‐related assays require the presence of neurons, and are consistent with the hypothesis that the AE3 knockout reduces functional expression of astrocytic NBCe1. These findings suggest a new type of neuron–astrocyte communication, based on the expression of AE3 in neurons, which could explain how AE3 reduces seizure susceptibility.

Key points

• A polymorphism of human AE3 is associated with idiopathic generalized epilepsy. Knockout of AE3 in mice lowers the threshold for triggering epileptic seizures. The explanations for these effects are elusive.

• Comparisons of cells from wild‐type vs. AE3^–/– mice show that AE3 (present in hippocampal neurons, not astrocytes; mediates HCO₃ ^– efflux) enhances intracellular pH (pH_i) recovery (decrease) from alkali loads in neurons and, surprisingly, adjacent astrocytes.

• During metabolic acidosis (MAc), AE3 speeds initial acidification, but limits the extent of pH_i decrease in neurons and astrocytes.

• AE3 speeds re‐alkalization after removal of MAc in neurons and astrocytes, and speeds neuronal pH_i recovery from an ammonium prepulse‐induced acid load.

• We propose that neuronal AE3 indirectly increases acid extrusion in (a) neurons via Cl^– loading, and (b) astrocytes by somehow enhancing NBCe1 (major acid extruder). The latter would enhance depolarization‐induced alkalinization of astrocytes, and extracellular acidification, and thereby reduce susceptibility to epileptic seizures.

Abbreviations

AE3

Cl⁻–HCO₃ ⁻ exchanger 3

AE3^–/–

AE3 knockout

AE3_A^–/–

AE3^–/– astrocyte

AE3_AOC^−/−

AE3^−/− astrocytes from astrocyte‐only cultures

AE3_N^–/–

AE3^–/– neuron

AOC

astrocyte‐only culture

AOI

area of interest

BCECF‐AM

(2',7'‐bis‐2‐carboxyethyl)‐5(and‐6) carboxyfluorescein acetoxymethyl ester

DIA

depolarization‐induced alkalization

(dpH_i/dt)_early

initial acidification rate during metabolic acidosis exposure

(dpH_i/dt)_late

acidification rate late in metabolic acidosis

HBS

Hepes‐buffered saline

HC

hippocampus

J_E

acid extrusion

J_L

acid loading

k_down

rate constant when pH_i is descending

k_up

rate constant when pH_i is ascending

MAc

metabolic acidosis

NBCe1

electrogenic Na⁺/HCO₃ ⁻ cotransporter

NBCn1

electroneutral Na⁺/HCO₃ ⁻ cotransporter

NDCBE

Na⁺‐driven Cl⁻–HCO₃ ⁻ exchanger

NHE

Na⁺–H⁺ exchanger

pH_i

intracellular pH

pH_o

extracellular pH

WT

wild‐type

WT_A

WT astrocyte

WT_N

WT neuron

WT_AOC

WT astrocytes from astrocyte‐only cultures

Introduction

Changes in extracellular pH (pH_o) or intracellular pH (pH_i) have important effects on a wide range of cell functions (Busa & Nuccitelli, 1984; Busa, 1986; Chesler, 2003; Putnam et al. 2004). Metabolic acidosis (MAc), which is a decrease in pH_o caused by a decrease in extracellular [HCO₃ ^–]_o at a fixed extracellular [CO₂]_o, is a common pH_o disturbance that can affect the extracellular microenvironment in the central nervous system. When challenged by MAc, neurons (Ritucci et al. 1998; Wang et al. 2002; Bouyer et al. 2004; Salameh et al. 2014) and astrocytes (Salameh et al. 2014) generally exhibit a fall in pH_i.

In the steady state, pH_i is stable because the overall rate of acid extrusion (J _E, determined by H⁺ efflux, HCO₃ ^– influx, etc.) equals the overall rate of acid loading (J _L, determined by H⁺ influx, HCO₃ ^– efflux, metabolic production of acid, etc.). The pH_i response of a cell to MAc depends on how MAc affects pH_i dependence of J _E and J _L (Roos & Boron, 1981; Boron, 2004; Bevensee & Boron, 2013). In the hippocampus (HC), the major acid extruders are: Na⁺‐coupled bicarbonate transporters in the SLC4 family (Schwiening & Boron, 1994; Bevensee et al. 2000; Giffard et al. 2000; Romero et al. 2013), Na⁺–H⁺ exchangers in the SLC9 family (Ma & Haddad, 1997; Donowitz et al. 2013), vacuolar H⁺ pumps (Murata et al. 2002), monocarboxylate cotransporters in the SLC16 family that can mediate the efflux of lactate acid (Pierre et al. 2000; Halestrap, 2013), and the voltage‐gated proton channel Hv1 (Wu et al. 2012; DeCoursey, 2013). Conversely, major acid loaders in the HC include Na⁺‐independent Cl⁻–HCO₃ ⁻ exchangers (AE3) in the SLC4 family (Alper, 2009; Romero et al. 2013). Recent work shows that the electrogenic Na⁺/HCO₃ ⁻ cotransporter NBCe1 (SLC4A4) readily reverses during intracellular alkali loads, when it can behave as an acid loader (Theparambil et al. 2015). Cl⁻–HCO₃ ⁻ exchangers in the SLC26 family are also present in the brain (Alper & Sharma, 2013) and potentially contribute to HCO₃ ^– efflux in the HC. Neurons and astrocytes have different complements of the previously mentioned acid–base transporters, which underlie fundamental differences in pH_i homeostasis between these important cell types.

A major difference in acid–base physiology between HC neurons and astrocytes – and one that could be important in the response to MAc – is that neurons but not the astrocytes express AE3 (Kopito et al. 1989; Hentschke et al. 2006; Svichar et al. 2009). AE3 contributes to acid loading by facilitating the exchange of intracellular HCO₃ ^– for extracellular Cl⁻. A role for AE3 in neuronal electrical activity was first implied by a human chromosomal‐mapping study that identified the region 2q36, which includes the SLC4A3 gene, as a region of interest associated with common idiopathic generalized epilepsy (Sander et al. 2000). Two years later, a follow‐up study linked the SLC4A3 polymorphism A867D to idiopathic generalized epilepsy (Sander et al. 2002). Later work on HEK293 cells showed that this polymorphism decreases AE3 activity without changing the protein expression levels or its trafficking to the plasma membrane (Vilas et al. 2009). Based on these data, one might hypothesize that decreased AE3 activity leads to a higher neuronal pH_i and, because high pH is generally associated with increased excitability, to an increased susceptibility to epilepsy. To further investigate the role of AE3 in epilepsy, Hentschke et al. developed an AE3 knockout (AE3^−/−) mouse and showed that, indeed, AE3 loss increases susceptibility to seizures (Hentschke et al. 2006). However, because these authors found that the steady‐state pH_i is no higher in HC neurons from AE3^−/− mice than from wild‐type (WT) mice, the mechanism by which AE3 dysfunction promotes epilepsy was not immediately clear. Nevertheless, AE3 does indeed function as an acid loader in HC neurons because the rapid rise in pH_i caused by the influx of NH₃ is substantially higher in hippocampal neurons from AE3^−/− than from WT mice (Svichar et al. 2009).

In the present study, we examine the effect of knocking out AE3 on the ability of HC mouse neurons and co‐cultured astrocytes to recover from intracellular alkali loads, and the ability of these cells to resist the pH_i effects of MAc. We find that, in hippocampal neurons, AE3 is a major contributor to the pH_i recovery (i.e. acidification) from acute alkali loads, and also to the rapid, initial descent of pH_i during MAc. However, paradoxically, AE3 is important for limiting the overall fall in neuronal pH_i during MAc and, after an acid load imposed by an NH₃/NH₄ ⁺ prepulse, promoting acid extrusion. Another set of paradoxes emerge from the analyses of data from the adjacent astrocytes (which lack AE3). Compared to hippocampal astrocytes from WT mice, those from AE3^−/− mice recover more slowly from acute alkali loads, have a lower steady‐state pH_i under control acid–base conditions, exhibit a slower initial pH_i decrease during MAc, and a slower initial pH_i increase while recovering from MAc. The lower steady‐state pH_i and the MAc‐related phenotype disappear when we culture astrocytes in the absence of neurons.

Methods

Ethical approval

Protocols for housing and handling of mice were approved by the Institutional Animal Care and Use Committee at Case Western Reserve University.

Cell culture

Hippocampal neurons and astrocytes in mixed cultures

In this study, we used WT and AE3^−/− animals. The knockout animals were generated by Hentschke et al. (2006), and provided by Professor Hübner on a C57BL6 background. We then backcrossed these mice for 7–10 generations onto our standard laboratory WT strain of C57BL6 mice, which we derived from mice originally provided by Professor Alan Verkman as heterozygotes for the aquaporin 1 knockout (AQP1^+/–). We obtained primary co‐cultures (never passaged) of hippocampal CA1 neurons and astrocytes from WT and AE3^−/− mice, as described previously (Bouyer et al. 2004; Salameh et al. 2014). Briefly, we decapitated unanaesthetized postnatal day (P) 0 to P2 pups of both sexes and isolated the HC CA1 region. We then digested the tissue in a pH 7.40 Hepes‐buffered saline solution (37°C) that contained 1% papain (cat. no. LS003162, Worthington Biochemical Corp., Lakewood, NJ, USA), 5.5 mm l‐cysteine, and 1.1 mm EDTA. After 10 min of digestion, we triturated the tissue at 37°C in a 9.5% minimum essential medium (MEM, cat. no. 61100–103; GIBCO, BRL, Life Technologies Inc., Gaithersburg, MD, USA) to which we added 22 mm HCO₃ ^–, 1.5% bovine serum albumin (cat. no. A7906, Sigma‐Aldrich, St Louis, MO, USA) and 1.5% trypsin inhibitor (cat. no. T9253, Sigma‐Aldrich). This trituration medium was equilibrated with 5% CO₂ in a 37°C incubator, and had a pH of 7.40. Finally, we diluted the triturated suspension to a concentration of ∼1 × 10⁵ cells ml⁻¹ and plated the cells on 12 mm gridded coverslips coated with 0.1% poly‐l‐ornithine and 2% laminin. The culture was incubated at 37°C and 5% CO₂/balance air, in 1 ml of a culture media (70% complete media + 30% neurobasal media, cat. no. 21103, GIBCO), supplemented with 0.02% B27 (cat. no. 17504‐044, GIBCO), 10 ng ml⁻¹ FGF‐5 (cat. no. F4537, Sigma‐Aldrich), and 1 ng ml⁻¹ bFGF (cat. no. F0291, Sigma‐Aldrich). We made the complete (i.e. preconditioned) media in advance by incubating 200 μl of freshly dissociated cells (obtained as above after trituration) in MEM solution supplemented with 10% fetal bovine serum (FBS; cat. no. 26140‐079, GIBCO) and 0.02% penicillin/streptomycin (cat. no. 15140‐122, GIBCO) for 1 week, followed by filtration. We used the cells for physiological studies between days 14 and 30 in culture.

Astrocyte‐only cultures

To obtain primary astrocyte‐only cultures, we followed the protocol described by Du et al. (2010). Briefly, we obtained the HC tissue following the surgical procedure discussed above. To enrich astrocytes in the culture, we used a growth medium that consisted of Dulbecco's modified Eagle's medium (DMEM) containing, 2 mm glutamine, 10% FBS and 1% penicillin/streptomycin. We plated the cells on poly‐l‐ornithine‐coated glass coverslips at 37°C in a 5% CO₂ incubator for at least 14 days. We changed the media every 3 days.

Solutions

Table 1 summarizes the compositions of the physiological solutions used in this study. For the solutions that contained CO₂ and HCO₃ ^–, we used NaOH to titrate the non‐CO₂/HCO₃ ^– components to the desired pH at 37°C, then added the HCO₃ ^–, and finally equilibrated with CO₂ for 30−40 min using a computerized gas‐mixing system (Series 4000; Environics, Tolland, CT, USA). We measured solution osmolalities using a vapour‐pressure osmometer (5520; Wescor Inc., Logan, UT, USA), and adjusted the osmolality to 300 ± 5 mosmol kg⁻¹. We delivered the solutions to the experimental chamber via Tygon tubing (because of its low CO₂ permeability) at 4 ml min⁻¹ using syringe pumps (model 33; Harvard Apparatus, Holliston, MA, USA). We selected among solutions using a computerized valve system, and maintained solution temperature at 37°C by means of a water‐jacket system placed between the valves and the chamber.

Table 1.

Summary of physiological solutions

	1	2	3	4	5	6	7
Components	Hepes‐ buffered saline (HBS)	10% CO2 pre‐load solution	Control CO2/HCO3 − solution (Ctrl)	Metabolic acidosis solution (MAc)	MAc with 20 mm NH4 +	Control with 20 mm NH4 +	Metabolic acidosis 0 mm Cl− (MAc0Cl)
NaCl	124	80	102	110	90	82	0
KCl	3	3	3	3	3	3	0
CaCl2	2	2	2	2	2	2	0
MgCl2	2	2	2	2	2	2	0
NaHCO3	0	44	22	14	22	22	14
NaH2PO4	1.3	1.3	1.3	1.3	1.3	1.3	1.3
Glucose	10.5	10.5	10.5	10.5	10.5	10.5	10.5
Sodium gluconate	0	0	0	0	0	0	110
Potassium gluconate	0	0	0	0	0	0	3
Magnesiumgluconate	0	0	0	0	0	0	4
Calcium gluconate	0	0	0	0	0	0	6
NH4Cl	0	0	0	0	20	20	0
CO2 (%)	0	10	5	5	5	5	5
Hepes	32.5	32.5	32.5	32.5	32.5	32.5	32.5
pH	7.4	7.4	7.4	7.2	7.2	7.4	7.2

The concentrations are in mm except for CO₂ (given in %). In Cl⁻‐free solutions, we increase [Ca²⁺] and [Mg²⁺] as described previously (Schwiening & Boron, 1994) because gluconate is a Ca²⁺ chelator.

Fluorescence recordings

For pH_i recording, we used the same equipment as described previously (Bouyer et al. 2004; Salameh et al. 2014). Briefly, a gridded coverslip with cells attached was removed from the incubator and fixed to our perfusion chamber, forming its floor. To the assembled chamber, we added a few drops of a variant of Hepes‐buffered saline (HBS) (Table 1, solution 1 at room temperature) that contained 10 μm of the pH‐sensitive dye (2′,7′‐bis‐2‐carboxyethyl)‐5(and‐6) carboxyfluorescein acetoxymethyl ester (BCECF‐AM). We then mounted the chamber on the automated stage of an Olympus IX‐81 microscope equipped with epi‐fluorescence imaging. After ∼15 min, we commenced flow of HBS at 37°C, alternately exciting the BCECF at 440 nm and 490 nm, while recording at emission wavelengths >530 nm, to record changes in pH_i. The exposure time for each of the two excitation wavelengths was 100 ms, separated by ∼20 ms. We acquired a 440 nm and a 490 nm data pair every 5 s. Slidebook 5.0 software (Intelligent Imaging Innovation, Denver, CO, USA) provided data acquisition. We calculated the rate constant for the disappearance of dye (−k ₄₄₀) for neurons and astrocytes continuously throughout our experiments. We show two examples of −k ₄₄₀ time courses in Fig. 5. We regarded the cells as healthy if the absolute value of −k ₄₄₀ is less than 5% min^–1 (Bevensee et al. 1995), and only included healthy cells in the analysis.

Figure 5. Responses of pH_i to Cl^– removal during NH₃/NH₄ ⁺ washout in WT hippocampal neurons and astrocytes in mixed culture.

A, example of a pH_i record from a HC neuron (representative of 11 neurons from 2 cultures on 4 coverslips). B, example of a pH_i record from a HC astrocyte (representative of 9 astrocytes from the same 2 cultures and the same 4 coverslips as in the neuron experiments). In both cases, we switched from extracellular solution 4 to solution 5, and then to solution 7. The pH_i records in A and B come from the same experiment (i.e. cells on the same coverslip). The lower portions of each panel show the time course of –k ₄₄₀, computed as described in Methods; –k ₄₄₀ values <4% min^–1 correlate with good cell health.

In separate experiments, we obtained five calibration points, at pH values of 5.8, 6.4, 7.0, 7.6 and 8.5, for the WT and the AE3^−/− cells, using the high‐K⁺ nigericin technique (Thomas et al. 1979). We used the calibration points to generate four unique calibration curves for (1) WT HC neurons, (2) WT HC astrocytes, (3) AE3^−/− HC neurons, and (4) AE3^−/− HC astrocytes following the approach of Boyarsky et al. (1988). To calibrate the dye in our physiological experiments, we obtained a single‐point calibration at pH 7.00 at the end of each experiment, and then calculated pH_i values from the above calibration curves.

Thermodynamic analysis of acid–base transporters

Here we provide our approach for calculating the [HCO₃ ^–]_i and the pH_i at which each of several transporters – as relevant for the Discussion – would reverse, given particular extracellular and intracellular concentrations.

Na⁺‐driven Cl⁻–HCO₃ ⁻ exchanger (NDCBE)

We define the electrochemical potential energy difference for NDCBE (see Parker & Boron, 2013), operating as an acid extruder (i.e. apparent HCO₃ ^– influx), as

where R is the universal gas constant and T the temperature in kelvins. The intracellular HCO₃ ^– concentration at which NDCBE would reverse in HC neurons:

Finally, assuming CO₂ is equilibrated across the cell membrane (i.e. [CO₂]_i = [CO₂]_o) and that the pK values are the same inside and outside the cell, we compute (see Bevensee & Boron, 2013) the pH_i at which the transporter (i.e. NDCBE or any of the others below) would reverse as

If the actual pH_i exceeds (pH_i)_rev, the transporter (e.g. NDCBE) must cease to behave as an acid extruder; if it operates at all, it will function as an acid loader.

The electrogenic Na⁺/HCO₃ ⁻ cotransporter

NBCe1 is expressed both in hippocampal neurons (Svichar et al. 2011) and astrocytes (Bevensee et al. 1997 a). We define the electrochemical potential energy difference for NBCe1, operating as an acid extruder (i.e. apparent HCO₃ ^– influx), as

where F is the Faraday constant and V _m is the membrane potential. The intracellular HCO₃ ^– concentration at which NBCe1 would reverse is

For neurons, we assume a V _m of −60 mV (Magistretti & Ransom, 2002; Khirug et al. 2005). For astrocytes we assume a V _m of −85 mV (McKhann et al. 1997; Magistretti & Ransom, 2002).

The electroneutral Na⁺/HCO₃ ⁻ cotransporter (NBCn1) and the Na⁺–H⁺ exchanger (NHE)

We define the electrochemical potential energy differences for NBCn1 and NHE, operating as acid extruders (i.e. apparent HCO₃ ^– influx or H⁺ efflux), as

$$\mathrm{\Delta }\tilde{\mu }=\underset{\mathrm{NBCn}1}{\underbrace{RT\ln \frac{{[\mathrm{N}{\mathrm{a}}^{+}]}_{\mathrm{i}}{[\mathrm{HC}{{\mathrm{O}}_3}^{-}]}_{\mathrm{i}}}{{[\mathrm{N}{\mathrm{a}}^{+}]}_{\mathrm{o}}{[\mathrm{HC}{{\mathrm{O}}_3}^{-}]}_{\mathrm{o}}}}}=\underset{\mathrm{NHE}}{\underbrace{RT\ln \frac{{[\mathrm{N}{\mathrm{a}}^{+}]}_{\mathrm{i}}{\left[{\mathrm{H}}^{+}\right]}_{\mathrm{o}}}{{[\mathrm{N}{\mathrm{a}}^{+}]}_{\mathrm{o}}{\left[{\mathrm{H}}^{+}\right]}_{\mathrm{i}}}}}.$$

We compute ([HCO₃ ^–]_i)_rev as

The anion exchanger AE3

We define the electrochemical potential energy difference for AE3, operating as an acid extruder (i.e. apparent HCO₃ ^– influx), as

$$\mathrm{\Delta }\tilde{\mu }=RT\ln \frac{{[\mathrm{HC}{{\mathrm{O}}_3}^{-}]}_{\mathrm{i}}{[\mathrm{C}{\mathrm{l}}^{-}]}_{\mathrm{o}}}{{[\mathrm{HC}{{\mathrm{O}}_3}^{-}]}_{\mathrm{o}}{[\mathrm{C}{\mathrm{l}}^{-}]}_{\mathrm{i}}},$$

and calculate ([HCO₃ ^–]_i)_rev as

After calculating (HCO₃ ^–)_rev for NBCe1, NBCn1, NHE, or AE3, we compute (pH_i)_rev as outlined for NDCBE.

Data analysis and statistics

Selection of areas of interest

For each cell analysed, we selected an area of interest (AOI) by using the outline tool in Slidebook to encompass the cell body. We avoided soma that obviously overlapped, although thin astrocytic processes were likely beneath many neurons. For astrocytes, we choose AOIs that contained no obvious neuronal processes, although tiny neuronal processes may have overlain some astrocyte AOIs.

Calculation of pH_i

Within each AOI, Slidebook: (1) calculates the mean pixel intensity with a 490 nm excitation; (2) from this mean, subtracts the background (obtained in a region with no cells) to obtain the background‐subtracted 490 nm signal (I ₄₉₀); and (3) divides this last value by the background‐subtracted 440 nm signal (I ₄₄₀). We then convert the fluorescence excitation ratios (I ₄₉₀/I ₄₄₀) to pH_i values using the high‐K⁺/nigericin technique (Thomas et al. 1979), using a single‐point calibration (Boyarsky et al. 1988).

Final pH_i in an experimental period

We compute the final pH_i of a particular period as described by Salameh et al. (2014). Briefly, we used a least‐squares method to fit a straight line to the pH_i data corresponding to the last minute of the period in question, just before a solution change. Into the equation of best fit, we insert the time corresponding to the last point before the solution change. The resulting pH_i value represents the best‐fit final pH_i.

Exponential rate constant of pH_i recovery

To obtain an exponential rate constant (k) for a pH_i recovery from an alkali load, a MAc exposure, or an acid load, we fitted the time course of pH_i – starting from the first data point during which pH_i begins its most rapid ascent/descent – to the single‐exponential decay function pH_i = ae^{− kt} + (pH_i)_∞. We abandoned attempts to fit the data to a double‐exponential decay function because, for any given fitting attempt, at least one coefficient had a value within one standard deviation of zero.

Linear rate of pH_i change

To obtain the early rate of pH_i decrease with respect to time, we used the least‐squares regression method to fit a straight line to the pH_i data. To compute (dpH_i/dt)_early in MAc experiments, we started from the first data point at which pH_i begins its most rapid descent, and extended the fit forwards in time until the slope inexorably became less negative. This fit typically encompassed ∼70 s. The best‐fit slope represents (dpH_i/dt)_early.

To obtain the rate of pH_i decrease near the end of a MAc period, that is, (dpH_i/dt)_late, we similarly fitted a line to the pH_i data starting at 420 s into the MAc period (i.e. the end of the MAc), and extended the fit backwards in time until just before the slope inexorably rises (reflecting contamination for rapid, early pH_i descent). This fit typically encompassed ∼3 min.

To obtain the maximal rate of pH_i increase as we transitioned from MAc to control (Ctrl) – that is, (dpH_i/dt)_final – we followed an approach analogous to that for (dpH_i/dt)_early, except that we extended the fit forwards in time until the slope inexorably became less positive (i.e. ∼70 s).

To obtain a change in pH_i, during Cl^– removal – that is, (dpH_i/dt)_Cl removal – we fitted a line to the pH_i data starting from the first data point during which pH_i begins its most rapid ascent, then extended the fit forwards in time until the slope inexorably declines (reflecting stabilization of pH_i). This fit typically encompassed ∼2 min.

Statistical analysis

To assess statistical significance between data from WT and AE3^−/− cells in the scatter plots in the main panels in the figures, we applied the multivariate ANOVA test, considering P < 0.05 as statistically significant. To examine statistical significance between data from WT and AE3^−/− cells summarized in bar graphs, we compared means using an unpaired two‐tailed Student's t test, considering P < 0.05 as statistically significant. To compare the means for multiple data sets, we used a one‐way ANOVA with Tukey's pairwise comparison, considering P < 0.05 as statistically significant. We report the data as mean ± SEM.

Analytical software

For exponential and linear curve fitting, we used Origin 2015. For the statistical tests, we used Minitab 17 statistical software.

Results

The presence of neuronal AE3 increases net acid‐loading rate not only in hippocampal CA1 neurons but also in astrocytes

Acute intracellular alkali load via CO₂ efflux for WT and AE3^−/− cells

Our first goal was to determine the contribution of AE3 to intracellular acid loading in neurons, which we did by acutely alkali loading the cells and monitoring the subsequent pH_i recovery (i.e. decrease). Figure 1 A shows two pairs of images, each pair representing a different experiment (presented below), and comprising a differential interference contrast (DIC) image and a fluorescence image of the same field. The pair on the left comes from a WT mixed culture, whereas that on the right comes from an AE3^−/− mixed culture. The traces around the bodies of neurons and astrocytes show the areas of interest used in the pH_i analyses. Although not shown in the experimental records, we began experiments by recording pH_i while flowing HBS (Table 1, solution 1, 37°C) over a mixed culture of HC neurons and astrocytes, obtained from either WT or AE3^−/− mice. After 5 min, we switched to 10% CO₂/44 mm HCO₃ ^– (solution 2). This manoeuvre caused a rapid decrease in pH_i, due to the CO₂ influx, followed by a slower pH_i recovery (i.e. increase), due to acid extrusion. Finally, after 10 min of this pretreatment, we switched to 5% CO₂/22 mm HCO₃ ^– (Ctrl, solution 3), as schematized in a model of a neuron in Fig. 1 B (step 1). This sudden decrease in [CO₂]_o leads to a rapid efflux of CO₂ (step 2), which decreases [CO₂]_i, and shifts the intracellular CO₂/HCO₃ ^– equilibrium to consume H⁺ (step 3). The result is a robust pH_i increase in both a WT and an AE3^−/− neuron (segment ab in Fig. 1 C) and in both a WT and an AE3^−/− astrocyte (segment ab in Fig. 1 D). The middle portions of Fig. 1 C and D show that – not just for neurons but also for astrocytes – the ΔpH_i during segment ab is significantly greater for cells from AE3^−/− than for WT mice. For this and the following figures, we present the details on the numbers of cells, cultures and coverslips in the figure legend.

Figure 1. Recovery of pH_i from an acute alkali load in hippocampal neurons and astrocytes in mixed culture.

A, two representative image pairs for WT (left pair) and AE3^−/− (right pair) mixed cultures. Each white outline surrounds a portion of the soma of a neuron or an astrocyte and encompasses an area of interest that led to the data in C and D. B, schematic model describing the anticipated acid–base‐related events in a neuron in response to switching the extracellular solution from 10% CO₂/44 mm HCO₃ ⁻/pH 7.40 (solution 2 in Table 1) to 5% CO₂/22 mm HCO₃ ⁻/pH 7.40 (solution 3). The resulting CO₂ efflux produces an alkali load, followed by a slower pH_i recovery. The white numerals on black squares describe the postulated sequence of events. C, examples of pH_i responses in two HC neurons, WT (black) and AE3^−/− (red). The black record comes from the identified neuron in the left portion of A, whereas the red record comes from the identified neuron in the right portion of A. In the upper portion of panel C, the squares on the black trace and the circles on the red trace represent some of the points at which we calculated dpH_i/dt from exponential curve fits. The middle portion summarizes ∆pH_i between the steady‐state pH_i just before switching from 10% to 5% CO₂ (point a) and the peak pH_i (point b) just before the recovery of pH_i from alkalosis for 39 individual WT neurons (black squares; from 5 cultures on 11 coverslips) and 37 individual AE3^−/− neurons (red circles; from 3 cultures on 7 coverslips). The lower portion shows plots of dpH_i/dt and pH_i for the WT and AE3^−/− neurons in the main portion of the panel. The slopes of the lines (not shown) through each set of points represent the exponential rate constant k _down – computed as described in Methods – whereas the x‐intercepts represent the hypothetical pH_i at infinite time, (pH_i)_∞. Supplementary Fig. S1 in the online supporting material includes plots of dpH_i/dt and pH_i for all neurons in this part of the study. D, examples of pH_i responses in two HC astrocytes, WT (grey) and AE3^−/− (pink). The grey record comes from the identified astrocyte in the left portion of panel A, whereas the pink record comes from the identified astrocyte in the right portion of panel A. The middle and lower portions are comparable to those in C, but for 29 individual WT astrocytes (grey diamonds; from 5 cultures on 11 coverslips) and 20 individual AE3^−/− astrocytes (pink triangles; from 3 cultures on 7 coverslips). Supplementary Fig. S2 includes plots of dpH_i/dt and pH_i for all astrocytes in this part of the study. E, relationship between k _down and (pH_i)_∞ for 39 individual WT neurons (black squares) and 37 individual AE3^−/− neurons (red circles). The two arrows identify the neurons in the upper portion of D. The inset shows mean k _down values, computed over all (pH_i)_∞ values. The vertical dashed lines represent the calculated reversal pH_i values for the transporters NDCBE and NBCe1, as described in Table 3. F, relationship between k _down and (pH_i)_∞ for 29 individual WT astrocytes (grey diamonds) and 20 individual AE3^−/− astrocytes (pink triangles). The two arrows identify the astrocytes in the upper portion of panel D. The inset is comparable to that in E. For the two upper insets in C and D, and for the insets in E and F (i.e. bar graphs), we performed two‐tailed unpaired t tests between WT and AE3^−/− cells. For the main portions of E and F (i.e. scatter plots), we performed multivariate ANOVA between WT and AE3^−/− cells. WT_N, neuron(s) cultured from a wild‐type mouse; AE3_N ^−/−, neuron(s) cultured from an AE3^–/– mouse; WT_A, astrocyte(s) cultured from a wild‐type mouse; AE3_A ^−/−, astrocyte(s) cultured from an AE3^–/– mouse; NS, no significant difference.

We expect the segment ab rise in pH_i to inhibit the acid extruders (decreasing J _E; step 4a) and to stimulate the acid loaders (increasing J _L; step 4b). In neurons, the acid loaders would include AE3, whereas in astrocytes, they presumably would include the reversed electrogenic Na⁺/HCO₃ ⁻ cotransporter NBCe1 (Boron & Boulpaep, 1983; Romero et al. 1997; Theparambil et al. 2015). These changes in transport rates shift the J _E–J _L balance in favour of acid loading, and lead to a gradual decrease in pH_i (Fig. 1 B, step 5ab), as shown by segments bc in Fig. 1 C and D. For each cell, we fitted the single‐exponential decay function pH_i = ae^{− kt} + (pH_i)_∞ to the time course of pH_i recovery from alkalosis, thereby obtaining the rate constant (k _down) and (pH_i)_∞, the latter of which is an estimate of the asymptote for pH_i. For the neuron data in Fig. 1 C, the squares overlying the black trace (WT) and the circles on the red trace (AE3^−/−) represent some of the points at which we calculated dpH_i/dt from exponential curve fits. The lower portion of Fig. 1 C shows the linear pH_i dependence of the dpH_i/dt values that we computed at each identified point for the WT neuron (shades of black) and the AE3^−/− neuron (shades of red). The slopes of the lines represent the best‐fit k _down values. Compared to that for the WT neuron, the plot of dpH_i/dt and pH_i for the AE3^−/− neuron is shifted toward higher pH_i values and has a smaller slope. If the intracellular buffering powers are the same in the two neurons, these data indicate that, as we might have anticipated, AE3 makes a substantial contribution to the recovery of pH_i from an alkaline load. Acid‐loading mechanisms other than AE3 must be responsible for the residual segment‐bc pH_i recovery in the red record of Fig. 1 C. As we will see in the Discussion, reversal of acid extruders such as NDCBE and NBCe1 could in principle contribute to this residual pH_i recovery.

The lower portion of Fig. 1 D shows the comparable plots of the computed dpH_i/dt and pH_i for the WT astrocyte (shades of grey) and the AE3^−/− astrocyte (shades of pink). If the intracellular buffering powers are the same in the two astrocytes, these data indicate that – quite unexpectedly, inasmuch as AE3 is not present in astrocytes – the presence of AE3 in neurons somehow contributes to the recovery of pH_i from an alkaline load in astrocytes.

Comparison of rate constants for pH_i recovery from alkali loads (k _down) for WT and AE3^−/− cells

In analysing the best‐fit parameters for these data, we plot the relationship between (pH_i)_∞ and k _down for a total of 39 WT and 37 AE3^−/− neurons in Fig. 1 E. Compared to those for the WT neurons, the ((pH_i)_∞, k _down) ordered pairs for the AE3^−/− neurons tend to be shifted toward higher (pH_i)_∞ values and have lower k _down values, consistent with a decreased ability of the AE3‐deficient neurons to recover from an acute alkaline load. Multivariate ANOVA reveals that the relation between (pH_i)_∞ and k _down is significantly different (P < 0.001) for WT and AE3^−/− neurons. The inset shows that the difference between the mean k _down values computed over all (pH_i)_∞ values for WT vs. AE3^−/− is borderline significant (P = 0.06). In summary, the right shift and overall lower k _down values of AE3^–/– neurons point to an inhibition of acid loading.

Figure 1 F summarizes the relationship between (pH_i)_∞ and k _down for 29 WT and 20 AE3^−/− astrocytes. Compared to those for the WT astrocytes, the ((pH_i)_∞, k _down) ordered pairs for the AE3^−/− astrocytes tend to be shifted toward higher (pH_i)_∞ values, consistent with a decreased ability of the AE3‐deficient astrocytes to recover from an acute alkaline load. Multivariate ANOVA reveals that the relationship between (pH_i)_∞ and k _down is significantly different (P = 0.007) for WT vs. AE3^−/− astrocytes. As shown in the inset, an unpaired two‐tailed t test reveals a significant difference between the mean k _down values of WT vs. AE3^−/−.

The presence of neuronal AE3 speeds the initial MAc‐induced acidification in both neurons and astrocytes

pH_i trajectories in WT neurons and astrocytes during MAc

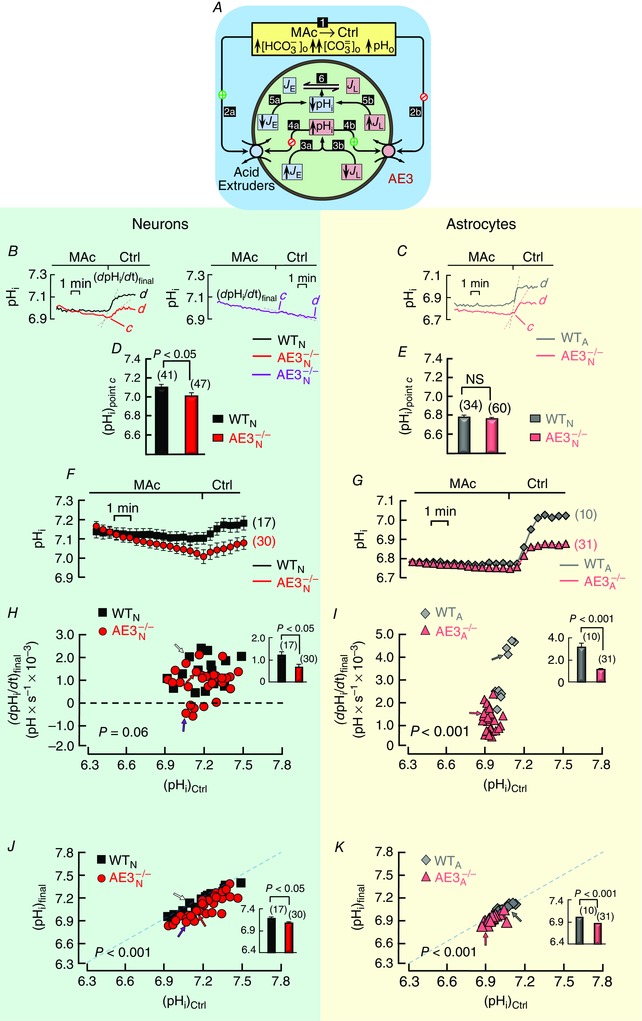
Our second goal was to investigate the role of AE3 in the pH_i response of neurons and astrocytes to MAc. We compared mixed cultures from WT and AE3^−/− mice, beginning our experiments – as in the preceding section of the paper – by flowing HBS (solution 1) for 5 min. However, for the experiments in Fig. 2 and the remaining protocols, we switched directly to 5% CO₂/22 mm HCO₃ ^– (solution 3) for 10 min and allowed pH_i to stabilize. Finally, we challenged our cells with MAc (solution 4) for 7 min (Fig. 2 A; step 1). We expected that the imposition of MAc – with the simultaneous decreases in [HCO₃ ^–]_o, [CO₃ ²⁻]_o, and pH_o – would inhibit the acid extruders (step 2a) but stimulate the acid loaders (step 2b). These alterations ought to shift the acid–base dynamics so that J _E < J _L, and pH_i falls (steps 3ab). We did indeed observe a near‐immediate pH_i descent for both WT neurons (segment ab, black record in left panel of Fig. 2 B) and WT astrocytes (grey record in Fig. 2 C). For both the WT neuron and the WT astrocyte, pH_i soon reached a near‐stable value. This presumably occurs because the gradual decrease in pH_i during segments ab secondarily stimulates the acid extruders (step 4a) but inhibits the acid loaders (step 4b), actions that counteract both the initial decrease in J _E (step 5a) and the initial increase in J _L (step 5b), and thereby bring J _E and J _L into balance (step 6), albeit at a pH_i lower than the control value.

Figure 2. Responses of pH_i to MAc exposure in hippocampal neurons and astrocytes in mixed culture.

A, schematic model describing the anticipated acid–base‐related events in a neuron in response to switching the extracellular solution from 5% CO₂/22 mm HCO₃ ⁻/pH 7.40 (solution 3) to 5% CO₂/14 mm HCO₃ ⁻/pH 7.20 (solution 4). The white numerals in black squares described the postulated sequence of events. B, examples of pH_i responses in HC neurons. The left panel shows records from a WT neuron (black) and one extreme of pH_i trajectories for AE3^−/− neurons (red). The steeper pair of dashed lines represent the maximal initial rates of pH_i decline ((dpH_i/dt)_early) and the shallower pair of dashed lines represent the rates of pH_i decline late during MAc ((dpH_i/dt)_late) when pH_i was declining linearly. In Methods, we describe the linear‐fitting procedure. The right panel shows the other extreme of pH_i trajectories for AE3^−/− neurons. C, examples of pH_i responses in HC astrocytes. These records from a WT (grey) and AE3^−/− (pink) astrocyte are comparable to those in B. D, mean control (i.e. starting) pH_i values ((pH_i)_Ctrl) for 41 WT neurons (black bar; from 6 cultures, 11 coverslips) and 47 AE3^−/− neurons (red bar; from 8 cultures, 11 coverslips), just before MAc exposure, computed as described in Methods. E, mean control pH_i values for 34 WT astrocytes (grey bars; from 4 cultures, 7 coverslips) and 60 AE3^−/− astrocytes (pink bars; from 5 cultures, 7 coverslips), just before MAc exposure. F, summary of pH_i responses to MAc in HC neurons. The panel shows mean responses of 41 WT neurons (black squares) and 47 AE3^−/− neurons (red circles) to extracellular MAc. G, summary of pH_i responses to MAc in HC astrocytes. The panel shows mean responses of 34 WT astrocytes (grey diamonds) and 60 AE3^−/− astrocytes (pink triangles) to extracellular MAc. H, relationship between (dpH_i/dt)_early and (pH_i)_Ctrl for 41 individual WT neurons (black squares) and 47 individual AE3^−/− neurons (red circles). The arrows identify the neurons in panel B. The inset shows mean (dpH_i/dt)_early values, computed over all (pH_i)_Ctrl values. I, relationship between (dpH_i/dt)_early and (pH_i)_Ctrl for 34 individual WT astrocytes (grey diamonds) and 60 individual AE3^−/− astrocytes (pink triangles). The arrows identify the astrocytes in panel C. The inset is comparable to that in panel H. Supplementary Fig. S3 includes an alternative analysis, plots of the exponential rate constant k _down vs. (pH_i)_Ctrl for WT neurons, WT astrocytes and AE3^−/− astrocytes in this part of the study. J, relationship between (dpH_i/dt)_late and (pH_i)_Ctrl for 41 individual WT neurons (black squares) and 47 individual AE3^−/− neurons (red circles). The inset is comparable to that in panel H, but for (dpH_i/dt)_late. K, relationship between (dpH_i/dt)_late and (pH_i)_Ctrl for 34 individual WT astrocytes (grey diamond) and 60 individual AE3^−/− astrocytes (pink triangles). The inset is comparable to that in J. For the bar graphs in panels D and E and in the insets to F, H, G and I, we performed two‐tailed unpaired t tests between WT and AE3^−/− cells. For the main portions of F, H, G and I (i.e. scatter plots), we performed multivariate ANOVA between WT and AE3^−/− cells.

pH_i trajectories in AE3^−/− neurons and astrocytes during MAc

In the AE3^−/− neurons, the pH_i trajectories during MAc can have one of two extreme patterns, or a blend of these patterns. One extreme is exemplified by the red record (left panel of Fig. 2 B), which is similar to the black record for the WT neuron, except that the initial pH_i descent for the red AE3^−/− record is slower and pH_i continues to fall even late during the 7 min MAc period. An example of the other extreme is the purple record (right panel of Fig. 2 B). Here, during the early phase of MAc, pH_i descends considerably more slowly than for either the black or red records, but continues to descend with a trajectory that is more linear. A hallmark of AE3^−/− neurons – whether they follow the red or purple trajectory, or something intermediate – is a tendency for pH_i to drift downward during segment bc at a considerably greater rate than for WT neurons.

In AE3^−/− astrocytes, the pH_i trajectories – an example of which is in Fig. 2 C – are more similar to those of their WT counterparts than is the case for the WT and AE3^−/− neurons. However, as is the case for AE3^−/− neurons, in AE3^−/− astrocytes, pH_i continues to drift downward at a relatively high rate during segment bc.

Mean values of control pH_i

While in the Ctrl solution, the WT and AE3^−/− neurons have initial pH_i values, (pH_i)_Ctrl, that are indistinguishable (Fig. 2 D). These neuron data agree with the earlier work of Hentschke et al. on WT and AE3^−/− neurons (Hentschke et al. 2006). Unexpectedly, we find that the initial pH_i values in WT astrocytes are significantly higher than in AE3^−/− astrocytes (Fig. 2 E).

Summary of pH_i responses in neurons and astrocytes to MAc exposure

Figure 2 F summarizes the pH_i trajectories in response to MAc for 41 WT (black) and 47 AE3^−/− (red) neurons, three of which are shown in Fig. 2 B. Similarly, Fig. 2 G summarizes the pH_i trajectories in response to MAc for 34 WT (grey) and 60 AE3^−/− (pink) astrocytes, two of which are shown in Fig. 2 C.

Comparison of rates of pH_i descent early in MAc for WT and AE3^−/− neurons

To obtain the initial rate of pH_i descent, we fitted a line to the steepest portion of the pH_i time course during MAc. The slope of the line is (dpH_i/dt)_early. In Fig. 2 H we plot the relationship between (dpH_i/dt)_early and the pH_i prevailing under Ctrl conditions (i.e. (pH_i)_Ctrl) – just before we switched to the MAc solution – for 41 individual WT (Fig. 2 H black) and 47 AE3^−/− (Fig. 2 H red) neurons. Our motivation for plotting (dpH_i/dt)_early vs. (pH_i)_Ctrl rather than vs. (pH_i)_∞ was threefold. First, (pH_i)_Ctrl is more akin to (pH_i)_∞ in Fig. 1 E and F, where that asymptotic pH_i refers to control conditions. Second, in their work on freshly dissociated rat HC neurons, Bevensee et al. plotted the rate constant of the pH_i recovery from an acid load (k _up; discussed later in the present paper) and the initial pH_i, as can be seen in their Fig. 2 C (Bevensee et al. 1996). And third, it was this Bevensee paper that first reported the surprising observation that k _up rises steeply as (pH_i)_Ctrl rises in neurons.

Compared to those for the WT neurons, the ordered pairs ((pH_i)_Ctrl, (dpH_i/dt)_early) for the AE3^−/− neurons tend to have the same (pH_i)_Ctrl range but less negative (dpH_i/dt)_early values (Fig. 2 H), consistent with a decreased ability of the AE3‐deficient neurons to acidify during MAc exposure. Multivariate ANOVA reveals that the relation between (pH_i)_Ctrl and (dpH_i/dt)_early is significantly different (P < 0.001) for WT and AE3^−/− neurons.

The inset in Fig. 2 H shows that, early in the MAc exposure, the mean (dpH_i/dt)_early of AE3^−/− neurons (e.g. Fig. 2 B, dashed red and purple lines) is significantly less negative than that of WT neurons (e.g. Fig. 2 B, dashed black line). Thus, AE3 is essential for the robust intracellular acidification of neurons during the early phase of MAc.

Comparison of rates of pH_i descent early in MAc, for WT and AE3^−/− astrocytes

Figure 2 I shows that the ordered pairs ((pH_i)_Ctrl, (dpH_i/dt)_early) for the AE3^−/− astrocytes, compared to those of WT astrocytes, tend to have a somewhat lower (pH_i)_Ctrl range and decidedly less negative (dpH_i/dt)_early values, consistent with a decreased ability of the AE3^−/− astrocytes to acidify during MAc exposure. Multivariate ANOVA reveals that the relation between (dpH_i/dt)_early and (pH_i)_Ctrl is significantly different (P < 0.001) for WT vs. AE3^−/− astrocytes. The inset in Fig. 2 I shows that (dpH_i/dt)_early, computed over all (pH_i)_Ctrl values, is less negative in AE3^−/− (i.e. Fig. 2 C, dashed pink line) than in WT astrocytes (i.e. Fig. 2 C, dashed grey line). Thus, unexpectedly, neuronal AE3 is also essential for the robust intracellular acidification of astrocytes during the early phase of MAc.

Comparison of rates of pH_i descent late in MAc, for WT and AE3^−/− neurons

For this analysis, we obtain a linear fit of the pH_i time course late in segment bc, the slope of the line of best fit being (dpH_i/dt)_late. In Fig. 2 J we plot the relationship between (dpH_i/dt)_late and (pH_i)_Ctrl for WT and AE3^−/− neurons. The figure reveals a substantial downward shift for AE3^−/− neurons, which indicates a faster late pH_i descent. The multivariate ANOVA indicates a significant difference (P < 0.001) between WT and AE3^−/−, and the inset shows that the mean (dpH_i/dt)_late of AE3^−/− neurons, computed over all (pH_i)_Ctrl values, is substantially more negative than that of WT neurons.

Comparison of rates of pH_i descent late in MAc, for WT and AE3^−/− astrocytes

In Fig. 2 K we plot (dpH_i/dt)_late vs. (pH_i)_Ctrl for WT and AE3^−/− astrocytes. As was the case for AE3^−/− neurons in Fig. 2 J, Fig. 2 K reveals a significant downward shift for AE3^−/− astrocytes, and thus a more negative (dpH_i/dt)_late. The multivariate ANOVA reveals that the (dpH_i/dt)_late–(pH_i)_Ctrl relationship is significantly different (P < 0.001) between WT and AE3^−/− astrocytes, and the inset shows that (dpH_i/dt)_late, computed over all (pH_i)_Ctrl values, is much more negative in AE3^−/− than in WT astrocytes.

Figure 2 J and K show that, neither in AE3^−/− neurons nor AE3^−/− astrocytes, does the combination of the expected rise in J _E (Fig. 2 A; step 4a) or the expected fall in J _L (step 4b) proceed sufficiently to bring J _E and J _L into balance during the 7 min period of MAc.

Taken together, the results summarized in Fig. 2 suggest that, during MAc, AE3 has two effects in neurons: during the first ∼1 min, AE3 accentuates J _L over J _E (making pH_i fall more rapidly), whereas during the last few minutes, AE3 accentuates J _E over J _L (braking the fall in pH_i). Figure 2 also shows that AE3 produces similar net effects in astrocytes, even though astrocytes do not express AE3.

The presence of AE3 paradoxically increases the rate of pH_i recovery during the switch from MAc to Ctrl in both neurons and astrocytes

pH_i trajectories in WT neurons and astrocytes during MAc removal

Our next goal was to investigate the role of AE3 in the recovery of pH_i during the transition from MAc back to Ctrl. Here, we expect that the removal of MAc (Fig. 3 A; step 1) – with the simultaneous increase in [HCO₃ ^–]_o, [CO₃ ²⁻]_o and pH_o – will stimulate acid extruders (step 2a) but inhibit the acid loaders (step 2b). These alterations ought to shift the acid–base dynamics so that J _E > J _L (steps 3ab), and cause pH_i to rise, as we indeed observe in WT neurons and (segments cd, black record in left panel of Fig. 3 B) as well as in WT astrocytes (pink record in Fig. 3 C). However, for both WT neurons and WT astrocytes, pH_i eventually stabilizes. This presumably occurs because the gradual increase in pH_i during segment cd secondarily inhibits acid extrusion (step 4a) but stimulates acid loading (step 4b), actions that raise J _L (step 5a) but lower J _E (step 5b), and thereby bring J _E and J _L into balance (step 6), and cause pH_i to stabilize, albeit at a higher pH_i at point d than at point c. Note that the black record in Fig. 3 B is from the same neuron as in Fig. 2 B, and that the grey record in Fig. 3 C is from the same astrocyte as in Fig. 2 C.

Figure 3. Recovery of pH_i from MAc exposure in hippocampal neurons and astrocytes in mixed culture.

A, schematic model describing the anticipated acid–base‐related events in a neuron in response to switching the extracellular solution from MAc (solution 4) back to 5% CO₂/22 mm HCO₃ ⁻/pH 7.40 (solution 3). The white numerals in black squares describe the postulated sequence of events. B, examples of pH_i responses in HC neurons. The left panel shows records from a WT neuron (black) and one extreme of pH_i trajectories for AE3^−/− neurons (red). The dashed lines represent the maximal initial rates of pH_i ascent ((dpH_i/dt)_final). In Methods, we describe the linear‐fitting procedure. The right panel shows the other extreme of pH_i trajectories for AE3^−/− neurons. The three neurons here are the same as the three in Fig. 2 B. C, examples of pH_i responses in HC astrocytes. These records from a WT (grey) and AE3^−/− (pink) astrocyte are comparable to those in panel B. The two astrocytes here are the same as the two in Fig. 2 C. D, mean pH_i values for 41 WT neurons (black bar) and 47 AE3^−/− neurons (red bar), just before MAc removal (point c in B), computed as described in Methods. The 41 and 47 neurons here are the same as those in Fig. 2 D. E, mean pH_i values for 34 WT astrocytes (grey bar) and 60 AE3^−/− astrocytes (pink bar), just before MAc removal (point c in C). The 34 and 60 astrocytes here are the same as those in Fig. 2 E. F, summary of pH_i responses to MAc removal in HC neurons. The panel shows the mean responses of 17 WT neurons (black squares; from 6 cultures, 11 coverslips) and 30 AE3^−/− neurons (red circles; from 8 cultures, 11 coverslips) to MAc removal. These 17 WT and 30 AE3^–/– neurons represent a subset of the 41 WT and 47 AE3^–/– neurons described in Fig. 2 F (we used other neurons in other protocols). G, summary of pH_i responses to MAc removal in HC astrocytes. The panel shows the mean responses of 10 WT astrocytes (grey squares; from 1 culture; 3 coverslips) and 31 AE3^−/− astrocytes (pink circles; from 3 cultures; 3 coverslips) to MAc removal. These 10 WT and 31 AE3^–/– astrocytes represent a subset of the 34 WT and 60 AE3^–/– astrocytes described in Fig. 2 G. H, relationship between (dpH_i/dt)_final – computed as described in Methods – and (pH_i)_Ctrl for 17 WT individual neurons (black squares) and 30 individual AE3^−/− neurons (red circles). The arrows identify the neurons in B. The inset shows mean (dpH_i/dt)_final values, computed over all (pH_i)_Ctrl values. I, relationship between (dpH_i/dt)_final and (pH_i)_Ctrl for 10 individual WT astrocytes (grey diamonds) and 31 individual AE3^−/− astrocytes (pink triangles). The arrows identify the astrocytes in C. The inset is comparable to that in H. Supplementary Fig. S4 includes an alternative analysis, plots of the exponential rate constant k _up vs. (pH_i)_Ctrl for WT neurons, WT astrocytes and AE3^−/− astrocytes in this part of the study. J, relationship between the final pH_i ((pH_i)_final) after the recovery from MAc (point d in B) and (pH_i)_Ctrl for 17 individual WT neurons (black squares) and 30 individual AE3^−/− neurons (red circles). The inset shows mean (pH_i)_final values, computed over all (pH_i)_Ctrl values. K, relationship between the final pH_i after the recovery from MAc (point d in panel C) and (pH_i)_Ctrl for 10 individual WT astrocytes (grey diamond) and 31 individual AE3^−/− astrocytes (pink triangles). The inset is comparable to that in panel J. For the bar graphs in D and E and in the insets to H, I, J and K (i.e. bar graphs), we performed two‐tailed unpaired t tests between WT and AE3^−/− cells. For the main portions of H, I, J, and K (i.e. scatter plots), we performed multivariate ANOVA between WT and AE3^−/− cells.

pH_i trajectories in AE3^−/− neurons and astrocytes during MAc removal

In the AE3^−/− neurons, the pH_i trajectories during MAc removal can have one of two extreme patterns, or a blend. At one extreme is the red record in the left panel of Fig. 3 B. This trajectory is similar to the black record for the WT neuron, except that the segment‐cd pH_i increase for the red AE3^−/− record is slower. An example of the other extreme is the purple record in the right panel of Fig. 3 B. Here, during MAc removal, pH_i continues to descend with a quasi‐linear trajectory that indicates that J _E remains lower than J _L.

In AE3^−/− astrocytes, the pH_i trajectories – an example of which is in Fig. 3 C – are more similar to those of their WT counterparts than is the case for the WT and AE3^−/− neurons. Note that the red and purple records in Fig. 3 B are from the same neurons as in Fig. 2 B, and that the pink record in Fig. 3 C is from the same astrocyte as in Fig. 2 C.

Summary of pH_i responses in neurons and astrocytes to MAc removal

Figure 3 F summarizes the pH_i trajectories in response to MAc removal for 17 WT (black) and all 30 AE3^−/− (red) neurons. Figure 3 G summarizes the pH_i trajectories in response to MAc removal for 10 WT (grey) and 31 AE3^−/− (pink) astrocytes.

Comparison of rates of pH_i ascent after MAc removal for WT and AE3^−/− cells

We obtain rates of pH_i increase during MAc removal (( dpH_i/dt)_final) by fitting a line to the time course of pH_i. Figure 3 H reveals that the differences between ((pH_i)_Ctrl, (dpH_i/dt)_final) ordered pairs for WT vs. AE3^−/− neurons are borderline significant. Moreover, the inset in Fig. 3 H, which summarizes the mean (dpH_i/dt)_final, computed over all (pH_i)_Ctrl values, reveals a significant difference between WT and AE3^−/− neurons. On balance, we conclude that (dpH_i/dt)_final is larger for WT than for AE3^−/− neurons, a pattern that is paradoxical because AE3 is an acid loader. Figure 3 I summarizes comparable but even more striking data for astrocytes. Our conclusion that the knockout of AE3 reduces acid extrusion is doubly surprising because AE3 is not only an acid loader, but absent from WT astrocytes.

Comparison of starting pH_i and final pH_i for WT and AE3^−/− cells

In order to investigate the role of AE3 in re‐establishing pH_i values after a cycle of MAc exposure and removal, we now plot the relationship between (pH_i)_Ctrl and (pH_i)_final. Figure 3 J reveals that the points defining the relationship between the initial (i.e. Ctrl) and final pH_i values for WT neurons (black squares) lie along the line of identity; that is, WT neurons tend to return to their initial pH_i. For AE3^−/− neurons (red circles), the relationship remains linear but is shifted downward; that is, AE3^−/− neurons tend to return to a pH_i value less than the initial one. Multivariate ANOVA reveals a significant difference between WT and AE3^−/−.

According to the fundamental law of pH_i regulation (Roos & Boron, 1981), pH_i is in a steady state when J _E = J _L. For WT neurons, the pH_i at which J _E and J _L come into balance is about the same before and after MAc. The simplest explanation for this behaviour, although by no means the only one, is that the profiles of J _E vs. pH_i and J _L vs. pH_i under control conditions are not altered by an intervening period of MAc. However, for AE3^−/− neurons, the intervening period of MAc must shift at least one of these profiles, such that J _E reaches a balance with J _L at a lower pH_i value. The inset in Fig. 3 J shows a significant difference between WT and AE3^−/− neurons in mean (pH_i)_final, computed over all (pH_i)_Ctrl values.

Figure 3 K is like Fig. 3 J, but for WT and AE3^−/− astrocytes. Again, the WT cells tend to fall along the line of identity, whereas the AE3^−/− cells fall below it. Multivariate ANOVA reveals a significant difference between WT and AE3^−/− astrocytes (P < 0.001), and the inset shows significant differences between WT and AE3^−/− in mean (pH_i)_final, computed over all (pH_i)_Ctrl values.

The presence of AE3 increases the net acid‐extrusion rate in neurons but not astrocytes under MAc conditions

NH₄ ⁺ prepulse protocol under MAc conditions

Because AE3^−/− neurons and, to a lesser extent, astrocytes tend to acidify during the plateau phase of MAc (segments bc in Fig. 2 B and C), we next ask whether the absence of AE3 hinders net acid extrusion during MAc. To achieve this goal, we compare mixed cultures from WT and AE3^−/− mice, beginning our experiments as in Fig. 2 by superfusing the cells with HBS (solution 1; not shown) for 5 min, followed by Ctrl (solution 3; not shown) for 10 min, and then a transition to MAc (solution 4) for ∼2 min, the last portion of which we show in Fig. 4 A and B. We then acid load the cells under MAc conditions, utilizing the ammonium pre‐pulse technique (Boron & De Weer, 1976). The 2.5 min exposure to 20 mm NH₃/NH₄ ⁺ (solution 5) causes a rapid increase in pH_i (segment ab) due to the rapid influx of NH₃, followed by a slower decrease (segment bc) generated by the influx of NH₄ ⁺ and other acid‐loading processes. The subsequent removal of the NH₃/NH₄ ⁺ (i.e. return to MAc; solution 4) produces a sharp decrease in pH_i (segment cd) due to the efflux of NH₃ as opposed by acid‐extruding processes, followed by a gradual increase (segment de) mediated by acid‐extruding processes as opposed somewhat by acid‐loading processes. For each cell, we fitted the single‐exponential decay function to the segment‐de pH_i recovery from acidosis (i.e. cells under MAc conditions).

Figure 4. Recovery of pH_i from an acute acid load in hippocampal neurons and astrocytes in mixed culture.

A, examples of pH_i responses in two HC neurons; WT (blue) and AE3^−/− (brown) under conditions of MAc. At the indicated times, we switched the extracellular solution from 5% CO₂/14 mm HCO₃ ⁻/pH 7.20 (solution 4 in Table 1) to 5% CO₂/14 mm HCO₃ ⁻/20 mm NH₃/NH₄ ⁺/pH 7.20 (solution 5), and then back again (solution 4). The NH₃/NH₄ ⁺ washout produces an acid load, followed by a slower pH_i recovery. The squares on the blue trace and the circles on the brown trace represent some of the points at which we calculated dpH_i/dt from exponential curve fits. The inset shows plots of dpH_i/dt vs. pH_i for the WT and AE3^−/− neurons in the main panel. Supplementary Fig. S5 includes plots of dpH_i/dt and pH_i for all neurons in this part of the study. The slopes of the lines (not shown) through each set of points represent the exponential rate constant k _up, computed as described in Methods. B, examples of pH_i responses in two HC astrocytes; WT (light blue) and AE3^−/− (orange), to an acute acid load imposed via a NH₃/NH₄ ⁺ prepulse under MAc conditions. The right inset is comparable to that in panel A. Supplementary Fig. S6 includes plots of dpH_i/dt and pH_i for all astrocytes in this part of the study. C, relationship between k _up and (pH_i)_Ctrl for 26 individual WT neurons (blue squares; from 3 cultures, 6 coverslips) and 25 individual AE3^−/− neurons (brown circles; from 3 cultures, 5 coverslips) under MAc conditions. The arrows identify the neurons in panel A. The inset shows mean k _up values, computed over all (pH_i)_Ctrl values. D, relationship between k _up and (pH_i)_Ctrl for 10 individual WT astrocytes (light blue diamonds, from 3 cultures, 6 coverslips) and 9 individual AE3^−/− astrocytes (orange triangles, from 3 cultures, 5 coverslips) under MAc conditions. The arrows identify the astrocytes in panel B. The inset is comparable to that in panel C. E, relationship between k _up and (pH_i)_Ctrl for 17 individual WT neurons (black squares; from 2 cultures, 4 coverslips) and 14 individual AE3^−/− neurons (red circles; from 2 cultures, 4 coverslips) under Ctrl conditions. Our protocol (not shown) was similar to that in panel A, except that we switched from extracellular solution 3 to solution 6, and then back to solution 3. The inset is comparable to that in panel C. Supplementary 7 includes plots of dpH_i/dt and pH_i for all neurons in this part of the study. F, relationship between k _up and (pH_i)_Ctrl for 21 individual WT astrocytes (grey diamonds; from 2 cultures, 4 coverslips) and 17 individual AE3^−/− astrocytes (pink triangles; from 2 cultures, 4 coverslips) under Ctrl conditions. The inset is comparable to that in panel C. Supplementary Fig. S8 includes plots of dpH_i/dt and pH_i for all astrocytes in this part of the study. For the insets in panels C, D, E and F (i.e. bar graphs), we performed two tailed unpaired t tests between WT and AE3^−/− cells. For the main portions of panels C, D, E and F (i.e. scatter plots), we performed multivariate ANOVA between WT and AE3^−/− cells.

The points overlaid onto segments de for both neurons (Fig. 4 A) and astrocytes (Fig. 4 B) represent some of the time points for which we derived the dpH_i/dt values from the aforementioned exponential curve fits. The inset to Fig. 4 A shows the linear pH_i dependence of the dpH_i/dt values that we computed at each identified point for the WT neuron (shades of blue) and the AE3^−/− neuron (shades of brown). The inset to Fig. 4 B shows the comparable plots for the WT astrocyte (shades of light blue) and the AE3^−/− astrocyte (shades of orange).

Comparison, under MAc conditions, of rate constants for pH_i recovery from acid loads (k _up) for WT and AE3^−/− cells

In analysing the best‐fit parameters for these data obtained under MAc conditions, we plot the relationship between k _up and (pH_i)_Ctrl for WT neurons (Fig. 4 C, blue), AE3^−/− neurons (Fig. 4 C, brown), WT astrocytes (Fig. 4 D, light blue), and AE3^−/− astrocytes (Fig. 4 D, orange).

Figure 4 C shows ((pH_i)_Ctrl, k _up) ordered pairs for 26 WT and 25 AE3^−/− neurons. Compared to those for the WT neurons, the points for the AE3^−/− neurons tend to be shifted toward higher (pH_i)_Ctrl values and have lower k _up values, consistent with a decreased ability of the AE3‐deficient neurons to recover from an acute acid load. Multivariate ANOVA reveals that the relation between (pH_i)_Ctrl and k _up is significantly different (P < 0.001) for WT vs. AE3^−/− neurons, and the inset reveals that mean k _up values, computed over all (pH_i)_Ctrl values, also are significantly different between WT and AE3^−/− neurons.

Figure 4 D summarizes comparable data for 10 WT and 9 AE3^−/− astrocytes. The reason that we have fewer astrocytes is that these cells tended not to withstand the rigors of an ammonium prepulse under conditions of MAc. In contrast to the multivariate ANOVA for the neuron data, that for the astrocyte data reveals only a borderline significant difference between WT and AE3^−/− astrocytes (P value = 0.078), perhaps reflecting low statistical power. The bar graph shows that the difference between groups for mean k _up values, computed over all (pH_i)_Ctrl values, does not reach statistical significance at the 0.05 level (P value = 0.092).

Comparison, under Ctrl conditions, of k _up for WT and AE3^−/− cells

To determine whether acid–base status impacts the role of AE3 in supporting acid extrusion, we extended our ammonium pre‐pulse protocol – thus far studied only under MAc conditions – to neurons and astrocytes under Ctrl conditions (experiments not shown). Here we began our experiments as usual by superfusing the cells with HBS (solution 1) for 5 min, followed by Ctrl (solution 3) for 10 min. We then exposed the cells to 20 mm NH₃/NH₄ ⁺ under Ctrl conditions (solution 6) for 2.5 min before returning to Ctrl.

As we did in Fig. 4 C and D for cells studied under MAc conditions, we now plot ((pH_i)_Ctrl, k _up) ordered pairs for cells studied under Ctrl conditions, namely, WT neurons (Fig. 4 E, black), AE3^−/− neurons (Fig. 4 E, red), WT astrocytes (Fig. 4 F, grey), and AE3^−/− astrocytes (Fig. 4 F, pink). The inset of Fig. 4 E reveals no significant difference for 17 WT and 14 AE3^−/− neurons regarding k _up values, computed over all (pH_i)_Ctrl values. However, the scatter plot of ((pH_i)_Ctrl, k _up) ordered pairs shows that, compared to those for WT neurons, the points for AE3^−/− neurons tend to be shifted toward higher (pH_i)_Ctrl values. This pattern is consistent with a decreased ability of AE3‐deficient neurons to recover from acute acid loads, even under Ctrl conditions. Multivariate ANOVA reveals that the relation between (pH_i)_Ctrl and k _up is significantly different (P = 0.033) for WT and AE3^−/− neurons.

Figure 4 F summarizes ((pH_i)_Ctrl, k _up) ordered pairs for 21 WT and 17 AE3^−/− astrocytes. Unlike the situation in Fig. 4 D, where the knockout of AE3 produces only a borderline‐significant effect by multivariant ANOVA on k _up for astrocytes studied under MAc conditions, here in Fig. 4 F – under Ctrl conditions – the knockout produces a statistically significant effect (P = 0.007) for WT vs. AE3^−/− astrocytes. The blue box in the main portion of Fig. 4 F encompasses nearly all of the AE3^−/− data. The bar graph in the left inset of Fig. 4 F summarizes the mean k _up values for WT and AE3^–/–, computed over all (pH_i)_Ctrl values within the narrow (pH_i)_Ctrl range of 7.05–7.17. An analysis of the WT and AE3^–/– data within this blue box shows that the knockout produces a significant increase in k _up ((25 ± 2) × 10^–3 s−¹ vs. (15 ± 2) × 10^–3 s−¹; P = 0.027). The right inset reveals that mean k _up values, computed over all (pH_i)_Ctrl values, are also significantly different between WT and AE3^−/− astrocytes.

In the following two paragraphs, we re‐analyse the data from Fig. 4 C–F in two different ways.

Four comparisons of k _up for MAc vs. Ctrl conditions

For all four cell types in Fig. 4 C–F, one might have expected acid extrusion to be slower under MAc than Ctrl conditions. For data on WT neurons (Fig. 4 C and E) – analysed by unpaired, two‐tailed t tests within a (pH_i)_Ctrl range where the k _up data overlap – k _up values are paradoxically greater (P = 0.006) under MAc conditions (squares in Fig. 4 C: k _up = (14 ± 2) × 10^–3 s−¹) than Ctrl conditions (squares in Fig. 4 E: k _up = (8 ± 1) × 10^–3 s−¹). However, for AE3^−/− neurons, k _up values were not significantly different (P = 0.283) between MAc (circles in Fig. 4 C: k _up = (6 ± 1) × 10^–3 s−¹) and Ctrl (circles in Fig. 4 E: k _up = (8 ± 1) × 10^–3 s−¹). Multivariate ANOVA of all of the WT data plotted in Fig. 4 C and E confirms a difference between MAc and Ctrl (P = 0.033), whereas a comparable multivariate ANOVA of all AE3^−/− neuron data in Fig. 4 C and E confirms no significant difference for these cells (P = 0.514).

The pattern for astrocytes is opposite that for neurons. For astrocytes, k _up values tend to be greater under MAc conditions (Fig. 4 D) than Ctrl conditions (Fig. 4 F) for AE3^−/− astrocytes (triangles; k _up = (40 ± 2) × 10^–3 s−¹ vs. (25 ± 2) × 10^–3 s−¹; unpaired, two‐tailed t test, P = 0.039) but not for WT astrocytes (diamonds; k _up = (25 ± 2) × 10^–3 s−¹ vs. (21 ± 4) × 10^–3 s−¹, P = 0.167). Multivariate ANOVA confirm these conclusions (P = 0.001 for AE3^−/− astrocytes, and P = 0.273 for WT astrocytes).

In summary, in none of the four cases did the data bear out our expectation that k _up would be greater under Ctrl than under MAc conditions.

Four comparisons of k _up for neurons and astrocytes

One last set of observations from Fig. 4 is that astrocytes – whether WT or AE3^−/−, and whether studied under Ctrl or MAc conditions – tend to have greater k _up values than their adjacent neurons (compare Fig. 4 D vs. C, and compare Fig. 4 F vs. E). Note that the y‐axis scales in Fig. 4 D and F are twice as large as those in Fig. 4 C and E. These differences are consistent with our observation in Fig. 1 that astrocytes tend to recover more rapidly than do neurons from alkaline loads.

Neurons but not astrocytes require Cl⁻ for the recovery of pH_i from an acid load

One potential explanation for why acid extrusion is more robust in WT than in AE3^−/− neurons (Fig. 4 C and E) is that [Cl^–]_i is sufficiently high that, in WT neurons, AE3 reverses (i.e. mediates HCO₃ ^– uptake and Cl^– efflux) at the low pH_i and [HCO₃ ^–]_i values prevailing near the pH_i nadir (point d in Fig. 4 A and B) after removal of NH₃/NH₄ ⁺. However, as noted in the Discussion, pH_i would have to fall to ∼6.34 under Ctrl conditions or to ∼6.16 under MAc conditions – circumstances that are not met in our experiments – before AE3 would reverse and contribute to net acid extrusion.

A second potential explanation for why acid extrusion is more robust in WT than in AE3^−/− neurons is that AE3 – when operating in its normal or forward direction (i.e. exchanging intracellular HCO₃ ^– for extracellular Cl^–) – promotes Cl^– uptake, especially during MAc. Thus, AE3 would replenish Cl^– removed from neurons by NDCBE, which is a powerful acid extruder in neurons (Schwiening & Boron, 1994; Schmitt et al. 2000; Coley et al. 2013). In some systems, a relatively high [Cl^–]_i also somehow promotes Na⁺–H⁺ exchange (Davis et al. 1994; Rajendran et al. 1995, 1999; Hogan et al. 1997; Bevensee et al. 1999). Thus, AE3‐mediated Cl^– uptake could enhance acid extrusion by promoting both NDCBE and NHE activity.

Although the most direct approach to test this second hypothesis would be to monitor [Cl^–]_i under Ctrl and MAc conditions, our attempts to do so were not technically satisfactory. Therefore, we decided to determine, in a way that is independent of AE3, whether cytosolic Cl⁻ promotes acid extrusion from neurons. Our approach was to impose MAc and then, in the continued presence of MAc, impose an intracellular acid load using the NH₄ ⁺ pre‐pulse technique with co‐cultured WT neurons and astrocytes, as in Fig. 4 A and B. However, here, we remove extracellular Cl⁻ (solution 7) as we wash out NH₃/NH₄ ⁺. Figure 5 A shows a representative response of a WT neuron to this manoeuvre. In sharp contrast to what we observe when Cl^– is present, that is, a rapid pH_i fall (segment cd in Fig. 4 A) followed by a robust pH_i recovery (segment de in Fig. 4 A) during NH₃/NH₄ ⁺ washout, here in Fig. 5 A we observe a triphasic pH_i trajectory with the simultaneous removal of Cl^– and NH₃/NH₄ ⁺: (1) pH_i at first falls rapidly (segment cc′ in Fig. 5 A), which reflects the dominant early effects of NH₃ efflux; (2) pH_i then temporarily rises slowly (segment c′c′′), presumably because, as the NH₃ efflux wains, two processes triggered by Cl⁻ removal (i.e. reversal of AE3 and stimulation of acid extrusion via NDCBE) now become temporarily dominant; finally, (3) pH_i descends slowly (segment c′′c′′′), presumably because the alkalinizing events in phase 2 deplete the neuron of intracellular Cl^–, so that the alkalinization is self‐limited and the pH_i dynamics of the neuron now reflect the dominance of an AE‐independent acid‐loading process (e.g. the one remaining in the AE3^−/− neuron in Fig. 1). The lower panel of Fig. 5 A shows that the rate of BCECF disappearance (–k ₄₄₀) from the neuron is extremely low, consistent with a tight neuronal membrane (Bevensee et al. 1995). Even if processes other than those we postulate contribute to the unusual pH_i trajectory in segment c′c′′c′′′ of Fig. 5 A, it seems clear that the recovery of pH_i during segment de of Fig. 4 A requires Cl^–, presumably intracellular Cl^–.

Figure 5 B shows representative data from an astrocyte on the same coverslip as the neuron in Fig. 5 A. We see that simultaneous removal of NH₃/NH₄ ⁺ and Cl^– in Fig. 5 B produces the expected rapid decrease in pH_i (segment cd), followed by a recovery (segment de), similar to the pattern in Fig. 4 B for an astrocyte in which we removed NH₃/NH₄ ⁺ in the continuous presence of Cl^–. Thus, the segment‐de pH_i recovery in our astrocytes does not have a major dependence on Cl^–. This conclusion is consistent with that of an earlier study on cultured rat HC astrocytes (Bevensee et al. 1996). After the recovery is complete in Fig. 5 B, pH_i slowly declines by a small amount (segment ee′). We observed a similar ee′ pattern in 5 of 9 astrocytes recorded on four coverslips.

In astrocyte‐only cultures, the knockout of AE3 has no effect on the astrocytic pH_i phenotype

MAc protocol

The data summarized in Figs 1, 2, 3, 4 are consistent with the hypothesis that AE3‐dependent crosstalk between neurons and astrocytes affects the pH_i physiology of astrocytes. To examine further the role of AE3 in this neuron–astrocyte pH_i communication, we generated astrocyte‐only cultures (AOCs) from WT and AE3^−/− mice and subjected the cells to our MAc protocol. Figure 6 A shows representative traces for a WT (dark green) and an AE3^−/− (light green) astrocyte from AOCs. Figure 6 B summarizes the pH_i trajectories in response to MAc for 23 WT and 20 AE3^−/− astrocytes.

Figure 6. Responses of pH_i to MAc exposure in hippocampal astrocytes in astrocytes‐only cultures (AOCs).

A, examples of pH_i responses in two HC astrocytes; WT_AOC (dark green) and AE3_AOC ^−/− (light green) to MAc. B, summary of pH_i responses to MAc in AOC astrocytes. The panel shows the mean responses of 23 WT_AOC astrocytes (dark green squares; from 2 cultures, 3 coverslips) and 20 AE3_AOC ^−/− astrocytes (light green circles; from 2 cultures, 4 coverslips) to MAc. C, mean control pH_i (point a in panel A) for 23 WT_AOC astrocytes (dark green bar) and 20 AE3_AOC ^−/− astrocytes (light green bar) before MAc exposure. D, relationship between (dpH_i/dt)_early and (pH_i)_Ctrl for 23 individual WT_AOC astrocytes (green diamonds) and 20 individual AE3_AOC ^−/− astrocytes (light green triangles) to MAc. The arrows identify the astrocytes in panel A. Supplementary Fig. S9 includes plots of k _down vs. (pH_i)_Ctrl for all astrocytes in this part of the study. E, relationship between (dpH_i/dt)_late (segment bc in panel A) and (pH_i)_Ctrl for 23 individual WT_AOC astrocytes and 20 individual AE3_AOC ^−/− astrocytes. F, mean pH_i (point c in panel A) for 23 WT_AOC astrocytes (dark green) and 20 AE3_AOC ^−/− astrocytes (light green) before MAc removal. G, relationship between (dpH_i/dt)_final and (pH_i)_Ctrl for 23 individual WT_AOC astrocytes (green diamond) and 20 individual AE3_AOC ^−/− astrocytes (light green triangles). Supplementary Fig. S10 includes plots of dpH_i/dt vs. pH_i for all astrocytes in this part of the study. H, relationship between (pH_i)_final and (pH_i)_Ctrl for 23 individual WT_AOC astrocytes and 20 individual AE3_AOC ^−/− astrocytes. The bar graphs in panels C and F, and the insets in panels D, E, G and H show comparisons of the means among astrocytes in mixed culture (Figs 2 and 3) and AOC, computed over all (pH_i)_Ctrl values. For the bar graphs in the main portions of panels C and F we performed two‐tailed unpaired t tests between WT and AE3^−/− cells. For the six insets, we used ANOVA with Tukey's pairwise comparison. P _overall is the P value from the ANOVA. For the main portions of panels D, E, G and H (i.e. scatter plots), we performed multivariate ANOVA between WT and AE3^−/− cells. NS, not significant; ^*0.05 ≥ P; ^**0.001 ≥ P.

Comparison of (pH_i)_Ctrl values

Figure 6 C shows that, in astrocyte‐only cultures, the initial pH_i values in the Ctrl solution for AE3^−/− astrocytes (AE3_AOC ^−/−, light green) is slightly but significantly higher than those for WT astrocytes (WT_AOC, dark green). This (pH_i)_Ctrl relationship between AE3^−/− and WT astrocytes in AOCs is just the opposite of what we observed in mixed neuron–astrocyte cultures (Fig. 2 E). The basis for this inversion is not the behaviour of the AE3^−/− astrocytes – their mean initial pH_i values are not significantly different in AOCs (light green bar in Fig. 6 C) vs. mixed cultures (pink in Fig. 2 E). Rather, the difference is the behaviour of WT astrocytes, which have a much lower initial pH_i in AOCs (dark green bar in Fig. 6 C) than in mixed cultures (grey bar in Fig. 2). Thus, we conclude that the presence of neurons – that is, the presence of neurons per se or the differences in methodology used to achieve mixed and astrocyte‐only cultures – in mixed neuron–astrocyte cultures somehow causes astrocytes to have a relatively high initial pH_i in CO₂/HCO₃ ^– (i.e. Ctrl), but only if the neurons contain AE3.

Comparison of (dpH_i/dt)_early data

In Fig. 6 D, we plot the relationship between (dpH_i/dt)_early – segment ab in Fig. 6 A – and (pH_i)_Ctrl for both AE3_AOC ^−/− and WT_AOC. Note that in AOCs, multivariate analysis shows no significant difference (NS) in (dpH_i/dt)_early between AE3^−/− (light green triangles) and WT (dark green diamonds). The inset in Fig. 6 D shows that (dpH_i/dt)_early for WT astrocytes in mixed culture is significantly greater than (dpH_i/dt)_early for WT astrocytes in AOCs as well as for AE3^−/− astrocytes, regardless of whether they are in mixed cultures or AOCs. For AE3^−/− astrocytes, (dpH_i/dt)_early is not significantly different between AOCs (light green bar) and mixed cultures (pink bar).

Comparison of (dpH_i/dt)_late data

Figure 6 E summarizes the relationship between (dpH_i/dt)_late and (pH_i)_Ctrl. Multivariate analysis shows no significant difference between WT_AOC and AE3_AOC ^−/−. The inset in Fig. 6 E shows that for WT and AE3^−/− astrocytes, (dpH_i/dt)_late is greater in AOCs than mixed culture (dark green vs. grey bar, light green vs. pink bar). In other words, the presence of neurons markedly decreases the magnitude of (dpH_i/dt)_late. On a percentage basis, this decrease is greater if the neurons contain AE3.

Comparison of pH_i values at point c

Figure 6 F shows that the mean pH_i values achieved at point c are not significantly different between any two of the four groups.

Comparison of (dpH_i/dt)_final data

Figure 6 G summarizes the relationship between (dpH_i/dt)_final – segment cd in Fig. 6 A – and (pH_i)_Ctrl. Multivariate analysis reveals no significant differences between AE3_AOC ^−/− and WT_AOC. The inset in Fig. 6 G shows that, for WT astrocytes, (dpH_i/dt)_final is substantially less in AOCs (dark green bar) than mixed cultures (grey bar). However, for AE3^−/− astrocytes, (dpH_i/dt)_final is not significantly different between AOCs (light green bar) vs. mixed cultures (pink bar). Thus, the presence of neurons increases (dpH_i/dt)_final, but only if the neurons contain AE3.

Comparison of (pH_i)_final data

Our last observation, summarized in Fig. 6 H, is that the ordered pairs ((pH_i)_Ctrl, (pH_i)_final) are not significantly different for WT vs. AE3^−/− astrocytes in AOCs. The inset in Fig. 6 H shows that, for AE3^−/− astrocytes, the (pH_i)_final values in AOCs (light green bar) and mixed cultures (pink bar) are indistinguishable. However, for WT astrocytes, (pH_i)_final is significantly less in AOCs (dark green bar) than in mixed cultures (grey bar). In other words, the presence of neurons somehow causes astrocytes to have a relatively high (pH_i)_final, but only if the neurons contain AE3. This is the same pattern as for (pH_i)_Ctrl (Fig. 6 C).

Extracellular Cl⁻ removal reverses MAc effects on pH_i in neurons, but not astrocytes

Cl^–‐removal protocol for WT cells

Published data indicate that neurons but not astrocytes express AE3 (Kopito et al. 1989; Hentschke et al. 2006). In order to verify that astrocytes in our studies lack functional Cl⁻–HCO₃ ⁻ exchange, particularly under conditions of MAc, we performed the experiments summarized in Fig. 7. The experiments began with our usual transition to MAc (solution 4). However, after the 7 min MAc exposure, we removed extracellular Cl⁻ (solution 7) in the continued presence of MAc. Figure 7 A shows pH_i records for a WT neuron (black record) and a WT astrocyte (grey record) on the same coverslip. Before the neuron reaches point c, AE3 is exchanging intracellular HCO₃ ^– for extracellular Cl⁻. At point c, we remove extracellular Cl⁻, forcing neuronal AE3 to reverse and exchange intracellular Cl⁻ for extracellular HCO₃ ^–. This manoeuvre causes pH_i to rise in the neuron (segment cx) but to fall slightly in the astrocyte.

Figure 7. Responses of pH_i to Cl^– removal during MAc in hippocampal neurons and astrocytes in mixed culture.

A, examples of pH_i time courses in a WT neuron and astrocyte on the same coverslip. At the indicated times, we switched from extracellular solution 3 to solution 4, and then to solution 7. B, examples of pH_i time courses in an AE3^–/– neuron and astrocyte on the same coverslip. C, mean responses of 16 WT (black squares; from 3 cultures, 4 coverslips) and 9 AE3^−/− (red circles; from 3 cultures, 3 coverslips) neurons to Cl^– removal during MAc. These 16 WT and 9 AE3^–/– neurons represent a subset of the 41 WT and 47 AE3^–/– neurons described in Fig. 2 F. D, mean responses of 20 WT (grey squares; from 2 cultures, 4 coverslips) and 23 AE3^−/− (pink circles; from 3 cultures, 3 coverslips) astrocytes to Cl^– removal during MAc. These 20 WT and 23 AE3^–/– astrocytes represent a subset of the 34 WT and 60 AE3^–/– neurons described in Fig. 2 F. The inset between panels C and D summarizes comparable data from 17 WT neurons and 12 WT astrocytes, but obtained under Ctrl (as opposed to MAc) conditions. E, mean pH_i for WT (black bar) and AE3^−/− neurons (red bar), just before Cl^– removal (point c in panel A), computed as described in Methods. E is analogous to Fig. 3 D. F, mean pH_i for WT (grey bar) and AE3^−/− astrocytes (pink bar), just before Cl^– removal (point c in panel A). F is analogous to Fig. 3 E. G, relationship between the most rapid rate of pH_i change after Cl^– removal ((dpH_i/dt)_Cl removal) – computed as described in Methods – and (pH_i)_Ctrl for 16 individual WT neurons (black squares) and 9 individual AE3^−/− neurons (red circles) under MAc conditions. The arrows identify the neurons in panel A. The inset shows mean (dpH_i/dt)_Cl removal values, computed over all (pH_i)_Ctrl values. H, relationship between (dpH_i/dt)_Cl removal and (pH_i)_Ctrl for 20 individual WT astrocytes (grey diamonds) and 23 individual AE3^−/− astrocytes (pink triangles) under MAc conditions. The arrows identify the astrocytes in panel A. The inset is comparable to that in panel G. I, relationship between the change in pH_i caused by Cl^– removal ((∆pH_i)_Cl removal) and (pH_i)_Ctrl for 16 individual WT neurons (black squares) and 9 individual AE3^−/− neurons (red circles) under MAc conditions. We define (∆pH_i)_Cl removal as the difference between pH_i values at points y and c in panel A – these pH_i values were computed as described in Methods. The left inset is comparable to that in panel G, but for (∆pH_i)_Cl removal. The right inset shows pH_i records from two neurons that have the same (dpH_i/dt)_Cl removal but different (∆pH_i)_Cl removal. J, relationship between (∆pH_i)_Cl removal and (pH_i)_Ctrl for 20 individual WT astrocytes (grey diamonds) and 23 individual AE3^−/− astrocytes (pink triangles) under MAc conditions. The inset is comparable to the left inset in panel I. For the bar graphs in panels E and F and in the insets to panels G, H, I, and J (i.e. bar graphs), we performed two‐tailed unpaired t tests between WT and AE3^−/− cells. For the main portions of panels G, H, I and J (i.e. scatter plots), we performed multivariate ANOVA between WT and AE3^−/− cells.

Cl^–‐removal protocol for AE3^−/− cells

Figure 7 B shows records for an AE3^−/− neuron (red record) and an AE3^−/− astrocyte (pink record), again on the same coverslip. Here, pH_i continuously decreases during MAc, confirming the pattern we observed in Fig. 2 B for an AE3^−/− neuron and Fig. 2 C for an AE3^−/− astrocyte. When we remove extracellular Cl⁻, the pH_i of the AE3^−/− neuron stops falling and rises somewhat before continuing on a downward trend, whereas the pH_i of the AE3^−/− astrocyte initially falls at an accelerated rate. In the case of the AE3^−/− neuron, the transient rise in pH_i may be due to reversed Na⁺‐driven Cl⁻–HCO₃ ⁻ exchange activity, caused by Cl^– removal (Parker et al. 2008).

Summary of pH_i responses to Cl^– removal

For experiments like those in Fig. 7 A and B, Fig. 7 C summarizes the mean pH_i time courses for the neurons, and Fig. 7 D does the same for astrocytes. The inset below Fig. 7 C and D is a summary of the pH_i time courses of WT and AE3^−/− neurons when we remove Cl^– under Ctrl (rather than MAc) conditions.

Comparison of pH_i values at point c

Figure 7 E summarizes the mean pH_i values for neurons during a MAc pulse, just before Cl⁻ removal (point c in Fig. 7 A). Figure 7 F does the same for astrocytes.

Comparison of (dpH_i/dt)_Cl removal data for neurons

In Fig. 7 G, we plot, as a function of (pH_i)_Ctrl, the initial slope of the pH_i trajectory during Cl⁻ removal ((dpH_i/dt)_Cl removal) for WT and AE3^−/− neurons. Multivariate ANOVA indicates a significant difference between the two groups. These results are consistent with substantially greater Cl⁻–HCO₃ ⁻ exchange activity in WT than AE3^−/− neurons. The inset in Fig. 7 G shows that the mean (dpH_i/dt)_Cl removal, computed over all (pH_i)_Ctrl values, is significantly different between the groups.

Comparison of (dpH_i/dt)_Cl removal data for astrocytes

In Fig. 7 H we plot (dpH_i/dt)_Cl removal vs. (pH_i)_Ctrl for WT and AE3^−/− astrocytes. Multivariate ANOVA shows a significant difference between the WT and AE3^−/− data. These data indicate that neither WT nor AE3^−/− astrocytes have detectable Cl⁻–HCO₃ ⁻ exchanger activity. The inset in Fig. 7 H shows that the mean (dpH_i/dt)_Cl removal values, computed over all (pH_i)_Ctrl values, of WT and AE3^−/− astrocytes are significantly different, with the AE3^−/− astrocytes having a paradoxically negative slope.

Comparison of ΔpH_i data during Cl^– removal, for neurons

In Fig. 7 I we plot (∆pH_i)_Cl removal – the pH_i difference between point y and point c (7 min Cl^– removal in Fig. 7 A) – vs. (pH_i)_Ctrl for WT and AE3^−/− neurons. The plot has a somewhat different pattern from that in Fig. 7 G because of differences in pH_i trajectory after the initial trajectory summarized in Fig. 7 G. In the upper‐right inset in Fig. 7 I, we show an example of such a difference between the pH_i records of two WT neurons on the same coverslip. Multivariate ANOVA of the data in the main panel of Fig. 7 I reveals a significant difference between WT and AE3^−/− neurons. The upper‐left inset in Fig. 7 I shows borderline significance in the overall (∆pH_i)_Cl removal between the groups.

Comparison of ΔpH_i data during Cl^– removal, for astrocytes

In Fig. 7 J we plot (∆pH_i)_Cl removal vs. (pH_i)_Ctrl for WT and AE3^−/− astrocytes. Multivariate ANOVA shows a significant difference between the two groups. The inset in Fig. 7 J shows a statistically significant difference between mean ΔpH_i values, computed over all (pH_i)_Ctrl values, with ΔpH_i being around zero for WT astrocytes, but negative for AE3^−/− astrocytes.

From the results in Fig. 7, we conclude that, in neurons but not astrocytes, the presence of AE3 enhances the increase in pH_i elicited by the removal of extracellular Cl⁻. WT astrocytes do not exhibit a statistically significant (dpH_i/dt)_Cl removal or ΔpH_i during Cl^– removal under MAc conditions, but AE3^−/− astrocytes exhibit a paradoxical acidification.

Discussion

When neurons and astrocytes are subjected to MAc, they usually exhibit a decrease in pH_i (Salameh et al. 2014). However, before the present study, the mechanism of the decrease was unclear. We find that, in neurons, it is AE3 that largely mediates the rapid fall in pH_i, early during MAc. In addition, we show that AE3 paradoxically is important in braking a further decrease of pH_i later during MAc. Even more unexpectedly, we find that the presence of AE3 in neurons leads to complex changes in the kinetics of acid–base transport in astrocytes. The net effect is an elevation of astrocytic pH_i under Ctrl conditions, and an increased uptake of acid during MAc that, in the intact brain, would tend to protect the neurons from acidosis. These effects of neuronal AE3 on astrocyte acid–base physiology could account for why the knockout of AE3 promotes epilepsy even though the knockout has no effect on resting neuronal pH_i.

Limitation of our study

Neurons and astrocytes in mixed culture often grow on top of one other. Thus, a neuronal soma that was part of our analysis may have been above a thin bed of astrocytic processes, and an astrocytic soma may have been underneath tiny neuronal processes. Such overlaps unavoidably lead to some degree of cross‐contamination between the BCECF signals of neurons and astrocytes. Nevertheless, we believe that the cross‐contamination had at most a minor effect in our analyses because large BCECF signals from the relatively thick soma would have overwhelmed small signals from thin astrocytic layers or tiny neuronal processes. Support for this intuition comes from our data. The pH_i trajectories from AOIs identified as neurons vs. astrocytes, as well as the values derived from these pH_i data, are quite different, as evidenced in all figures (except Fig. 6) that contain both cell types. In fact, we find no examples in which any ‘neuron panel’ of any figure could be confused with its corresponding ‘astrocyte panel.’ To the extent that cross‐contamination did occur, it would have caused us to underestimate the true degree of difference between neurons and astrocytes.

Role of AE3 in neurons

Acid loading

The role of AE3 as an acid loader in neurons was first implied based on its structural homology with the anion exchanger AE1 (Kopito et al. 1989). Although functional studies involving different cell models verified this hypothesis (Kopito et al. 1989; Hentschke et al. 2006; Vilas et al. 2009), none investigated the role of AE3 in acid loading the cytosol in neurons per se. In the present work, we show that HC neurons lacking AE3 have (1) a greater pH_i increase during CO₂ efflux (upper portion of Fig. 1 C), (2) a smaller (i.e. slower) k _down during the recovery from intracellular alkalosis (Fig. 1 E), (3) a relatively high (pH_i)_∞ following the recovery from alkalosis (Fig. 1 E), and (4) a smaller magnitude of (dpH_i/dt)_early when subjected to extracellular MAc (Fig. 2 H). All these observations are consistent with the hypothesis that AE3 is the major acid loader in HC neurons.

As noted in the Results, neurons lacking AE3 exhibit a slow residual recovery from an intracellular alkaline load (segment bc in Fig. 1 C and red circles in Fig. 1 E). Therefore, HC neurons either express an unknown acid loader or have an acid extruder that reverses direction at high pH_i and temporarily acts as an acid loader. To assess the latter possibility, we calculated the reversal pH_i, (pH_i)_rev, for each major acid extruder expressed in HC neurons, based on the extracellular and intracellular ion concentrations summarized in Table 2. We define (pH_i)_rev as the pH_i value at which the thermodynamic driving force for a specific transporter, as summarized in Table 3, equals zero. Hence, a transporter will operate as an acid extruder when pH_i < (pH_i)_rev, but may operate as an acid loader (i.e. backwards) when pH_i > (pH_i)_rev. For HC neurons, we conclude, based on the approach outlined in Methods under ‘Thermodynamic analysis of acid–base transporters’, that NBCn1 and NHE each have (pH_i)_rev values of 8.32, and thus could not have reversed during our experiments. However, NDCBE has a (pH_i)_rev of 7.33. From Fig. 1 E we see that ∼21% of AE3^−/− neurons have a (pH_i)_∞ ≥ 7.33 (indicated by left vertical line in Fig. 1 E). Thus, if NDCBE reversed, it would have contributed to the full extent of the pH_i recovery from alkaline loads in these neurons. For NBCe1, as noted in the ‘Thermodynamic analysis of acid–base transporters’, the neuronal membrane potential is ∼ −60 mV, hence, (pH_i)_rev is ∼7.37 (indicated by right vertical line in Fig. 1 E). About 16% of AE3^–/– neurons have a (pH_i)_∞ ≥ 7.37 and, in these, NBCe1 could have contributed to the full extent of the pH_i recovery. Even for many neurons in which (pH_i)_∞ for NDCBE or NBCe1 was below the relevant (pH_i)_rev, NDCBE or NBCe1 could have contributed to the pH_i recovery over part of the extent of the decrease. Nevertheless, for at least some of the neurons in Fig. 1 E, even the peak pH_i (point b in Fig. 1 C) was less than 7.33. For these, NDCBE or NBCe1 could not have contributed, and the residual k _down must represent an acid‐loading process other than AE3 (e.g. another transporter or metabolism).

Table 2.

Summary of intracellular and extracellular ion concentrations

Ion	Extracellular concentration (mm)	Intracellular neuronal concentration (mm)	Intracellular astrocytic concentration (mm)	References
Na+	140	16.2	18.3	(Friedman & Haddad, 1994; Rose & Ransom, 1996, 1997; Theparambil et al. 2015)
HCO3 –	22 (Ctrl) 14 (MAc)	Calculated	Calculated
Cl–	113 (Ctrl) 121 (MAc)	10.1	—	(Hara et al. 1993; Khirug et al. 2008; Markova et al. 2008)

All concentrations in mm. Extracellular values come from Table 1. The cited references provide the sources for the intracellular concentrations. The value 16.2 mm is the mean of three values (25, 14.6, 8.9 mm) from the cited references. The value 10.1 mm is the mean of three values (11.4, 7.9, 11 mm) from the cited references.

Table 3.

Summary of reversal [HCO₃ ⁻] and pH_i

Transporter	([HCO3 −]i)rev (mm)	(pHi)rev	Potentially reverse in present study?
NDCBE	18.9	7.33	Yes*
NBCe1 in neurons	20.6	7.37	Yes*
NBCe1 in astrocytes	11.8	7.13	Yes*
NBCn1 and NHE1	182 (for NBCn1)	8.32	No
AE3 during Ctrl conditions	1.97	6.35	No†
AE3 during MAc conditions	1.17	6.12	No

^*During moderate alkaline loads. ^†Given a [Cl^–]_i of ∼10 mm (Table 2), AE3 could reverse only rarely, during extreme acid loads.

As an acid loader (mediating Cl^– influx/HCO₃ ^– efflux), AE3 does not operate in a vacuum. In addition to depending on pH_i per se, AE3 depends to at least some extent on [HCO₃ ^–] and [Cl^–] on both sides of the plasma membrane. [HCO₃ ^–] near the plasma membrane depends on HCO₃ ^– transporters per se, as well as on [CO₂] and pH and the carbonic anhydrase enzymes that catalyse the overall reaction CO₂ + H₂O ↔ HCO₃ ^– + H⁺. [Cl^–]_i depends on Cl^– transporters and channels. The Na⁺/K⁺/Cl^– cotransporter (NKCC; Arroyo et al. 2013; Kaila et al. 2014) and GABA‐ or glycine‐activated Cl^– channels (Hubner & Holthoff, 2013) usually mediate Cl^– influx, and thus raise [Cl^–]_i, which may in turn reduce acid loading via AE3. On the other hand, K⁺/Cl^– cotransporters (KCCs; Gagnon & Delpire, 2013) usually mediate Cl^– efflux and may have opposite effects on AE3. Thus, the acid loader AE3 – as well as the acid extruders NDCBE and NHEs, which depend on [Cl^–]_i – may be under multiple dynamic and interacting influences from HCO₃ ^– and other acid–base transporters, as well as Cl^– transporters and channels.

In addition to their roles discussed above, NKCC1 and KCCs may play additional roles by carrying NH₄ ⁺ in place of K⁺ (Heitzmann et al. 2000; Bergeron et al. 2003; Liu et al. 2003; Williams & Payne, 2004) during the application, presence and removal of NH₃/NH₄ ⁺ in experiments like those in Fig. 4 A and B.

Acid extrusion

Because AE3 is an acid loader, one might have speculated that its absence would enhance the net rate of pH_i recovery from an acid load (particularly at the higher end of the pH_i range where AE3 is most likely to be active) and increase steady‐state pH_i. One would not anticipate that the absence of AE3 would affect the activity of acid extruders per se. In the present study, we find that neurons lacking AE3 have (1) a steady‐state pH_i that is not different from that of WT neurons under Ctrl conditions, confirming the work of others (Hentschke et al. 2006); (2) a reduced ability to stabilize (i.e. prevent a decrease in) pH_i during the late phase of MAc (segment bc in Fig. 2 B), (3) a reduced (slower) k _up after the transition from MAc to Ctrl (segment cd in Fig. 3 B), (4) a lower steady‐state pH_i after recovery from MAc (Fig. 3 D), and (5) a reduced (slower) k _up during the pH_i recovery from acute acid load imposed by an NH₄ ⁺ prepulse (Fig. 4 C and E). These observations contradict the previously mentioned speculations and suggest that the presence of AE3 is important for acid extrusion.

A trivial explanation for why AE3 increases J _E is that pH_i falls sufficiently to cause AE3 to reverse direction and temporarily function as an acid extruder. Based on the approach outlined in Methods (see ‘Thermodynamic analysis of acid–base transporters’) and the concentrations listed in Table 2, we estimate that pH_i would have to fall to <6.35 under Ctrl conditions, or to <6.12 under MAc conditions, in order for AE3 to reverse its activity and exchange intracellular Cl⁻ for extracellular HCO₃ ^–. In the present study, pH_i transiently fell <6.35 under Ctrl conditions only in 2 of 26 cells, one that fell as low as 6.22 and another that fell as low as 6.16. The pH_i never fell <6.12 under MAc conditions. Thus, we can rule out the hypothesis that reversal of AE3 makes a substantial contribution to the AE3‐dependent augmentation of acid extrusion in the present study, where [Cl^–]_i is ∼10 mm. On the other hand, in vivo, sustained high levels of GABA‐ or glycine‐induced Cl^– channel activity or NKCC activity could raise [Cl^–]_i above ∼10 mm, and thereby raise (pH_i)_rev correspondingly above our estimated value of ∼6.35. Even so, AE3 molecules probably spend only a miniscule fraction of their lifetime in the plasma membrane operating in the reverse direction (i.e. Cl^– outward/HCO₃ ^– inward).

Another explanation is that AE3 provides neurons with the Cl^– that supports neuronal acid‐extrusion mechanisms. NDCBE requires Cl^– directly (Russell & Boron, 1976; Boron & Russell, 1983) and in several systems NHEs require Cl^– indirectly (Parker, 1983; Davis et al. 1994; Rajendran et al. 1995, 1999; Hogan et al. 1997; Bevensee et al. 1999). For instance, in barnacle muscle fibres, shrinkage‐induced activation of NHE requires intracellular, but not extracellular, Cl^– (Davis et al. 1994). The intracellular Cl^– dependence of NHE1 reflects the intrinsic activity of individual NHE1 molecules, and specifically requires the carboxy‐terminal portion of NHE1, which may interact with Cl^– directly or via an intermediary protein (Aharonovitz et al. 2001). In the present study, support for the hypothesis that Cl^– supports neuronal acid extrusion comes from Fig. 5 A, which shows that Cl^– depletion prevents the usual recovery of pH_i from an acid load imposed via an NH₃/NH₄ ⁺ prepulse. This Cl^– dependence of acid extrusion in neurons could explain the well‐known but paradoxical observation that the knockout of AE3 does not cause the expected increase of steady‐state neuronal pH_i (Hentschke et al. 2006). Note that the knockout of an acid loader like AE3 can raise steady‐state pH_i only if the expected reduction in J _L overwhelms any unexpected reduction in J _E. We hypothesize that the elimination of AE3 not only lowers J _L directly but also, by reducing [Cl^–]_i, lowers J _E indirectly, so that steady‐state pH_i is unchanged.

The hypothesis that AE3 contributes to acid extrusion by tending to elevate [Cl^–]_i is especially germane for MAc experiments, where (1) the stimulation of AE3 not only plays a major role in lowering pH_i but also should tend to raise [Cl^–]_i, and (2) NDCBE, although initially inhibited by the low pH_o, should tend to accelerate as pH_i falls, and thus tend to deplete the neuron of Cl^–. AE3 would thus play a dual role during MAc: promoting the initial acidification by mediating HCO₃ ^– efflux, but putting a brake on the pH_i decline by mediating Cl^– uptake and thereby supporting acid extrusion.

Role of neuronal AE3 in astrocytes

Absence of AE3 from astrocytes

Previous authors, using in situ hybridization in mouse brain (Kopito et al. 1989) and Western blotting of lysates from astrocyte‐only cultures (Hentschke et al. 2006), report that astrocytes do not express AE3. In the present study, our physiological data show that Cl^––HCO₃ ^– exchange activity is negligible in astrocytes, both under Ctrl conditions (inset beneath Fig. 7 C and D) and MAc conditions (Fig. 7 B, D and H). Thus, our data extend those of previous studies, so that we can conclude that astrocytes have no demonstrable AE3 mRNA, AE3 protein, or AE3 activity.

pH_i regulation in astrocytes

Previous work shows that NBCe1‐C (Bevensee et al. 2000) is highly expressed in HC astrocytes (Majumdar et al. 2008). Moreover, in the presence of CO₂/HCO₃ ^–, NBCe1‐C mediates virtually all acid extrusion in the pH_i range 6.8–7.0 (Bevensee & Boron, 2008), that is, modestly below resting pH_i. At lower pH_i values, the contribution of NHE1 (Sardet et al. 1989) – with a small contribution from V‐type H⁺ ATPase (Pappas & Ransom, 1993) – begins to increase in an exponential‐like manner (Bevensee et al. 1997 b; Bevensee & Boron, 2008), and appears to become dominant at very low pH_i values (6.2–6.3). This exponential‐like J _NHE vs. pH_i profile is similar to that reported in cardiac myocytes (Vaughan‐Jones et al. 2009). Thus, for acid extrusion in astrocytes, NBCe1 is virtually the only acid extruder near the resting pH_i, but NHE1 becomes increasingly dominant at lower values.

Regarding acid loading, Theparambil et al. (2015) recently showed that during the recovery from intracellular alkalosis, NBCe1 can reverse direction and function as the dominant acid loader in cortical astrocytes. Based on the approach outlined in Methods to calculate NBCe1 (pH_i)_rev, our calculations support this conclusion, and indicate that NBCe1 should reverse and become an acid loader at an average pH_i > 7.16, which is just slightly above the resting pH_i of WT and AE3^–/– astrocytes.

Evidence for AE3‐dependent neuron–astrocyte communication

Knowing that astrocytes lack AE3, we expected that knocking out AE3 would have no effect on astrocyte pH_i physiology. However, as outlined in Table 4, we find that AE3^−/− astrocytes have a pH_i phenotype that differs from that of their WT counterparts. First, knocking out AE3 decreases astrocyte J _L at high pH_i values. Because NBCe1 – operating in reverse – is the dominant acid loader in astrocytes (Theparambil et al. 2015), the most straightforward hypothesis is that the knockout of AE3 reduces the activity of NBCe1 operating in reverse. Second, knocking out AE3 decreases astrocyte J _E, in the pH_i range near the steady‐state pH_i that prevails under Ctrl and MAc conditions. Because NBCe1 – operating in the forward direction – is the only acid extruder active in this pH_i range, we hypothesize that the knockout of AE3 reduces the activity of NBCe1 operating in the forward (i.e. acid‐extruding) direction. Finally, knocking out AE3 modestly increases astrocyte J _E under Ctrl conditions at the lower pH_i values that prevail during recovery from an NH₃/NH₄ ⁺ prepulse (the effect is not statistically significant under MAc conditions). It is at these low pH_i values where NHE becomes a more dominant acid extruder in astrocytes (Bevensee & Boron, 2008). Even so, we expected that a reduction in NBCe1 activity in AE3^–/– cells would have reduced J _E to some extent, even at low pH_i. That the knockout increases J _E at low pH_i implies that the knockout of neuronal AE3 enhances astrocytic NHE1 activity. Based on the above observations, we hypothesize that the presence of AE3 in neurons somehow communicates to astrocytes a message that results in alterations in pH_i regulation, most likely a stimulation of NBCe1 activity and an inhibition of NHE1 activity.

Table 4.

Summary of effects on astrocytes of knocking out neuronal AE3

Figure number	Parameter	Effect of AE3 KO on parameter	Predicted effect of AE3 KO on (J E − J L)	Hypothesis
Fig. 1 C and E	k down (rate constant of pHi recovery [decrease] after 10% → 5% CO2 transition)	↓	↑	At pHi > 7.13, NBCe1 could reverse and become an acid loader (see ‘Thermodynamic analysis of acid–base transporters’: NBCe1), and contribute to k down. Above supports conclusions of Theparambil et al. (2015). ↓ k down is consistent with ↓ J L, due to ↓ NBCe1 activity.
Fig. 2 C and E	(pHi)Ctrl	↓	↓	↑ J L, unlikely because of Fig. 1 conclusion no. 3, or ↓ J E, consistent with ↓ NBCe1 activity (see Fig. 1 conclusions).
Fig. 2 C, G and I	(dpHi/dt)early (rate of pHi decrease during transition Ctrl → MAc)	↓ magnitude	↑	Either ↓ J L, consistent with Fig. 1 conclusions, or ↓ baseline J E, consistent with ↓ NBCe1 activity → ↓ (pHi)Ctrl (see Fig. 2 C and E conclusion no. 2) → altered kinetics → ↓ (dpHi/dt)early (i.e. ↓ (pHi)Ctrl per se lowers (dpHi/dt)early), or ↓ baseline J E, consistent with ↓ NBCe1 activity → MAc produces smaller absolute inhibition of J E (i.e. less J E for MAc to inhibit; see model in Fig. 2 A).
Fig. 2 C and K	(dpHi/dt)late (rate of pHi downward drift during last several mins of MAc)	↑ magnitude	↓	↑ J L, unlikely (conflicts with Fig. 1 conclusions). ↓ J E, consistent with ↓ NBCe1 activity (see Fig. 2 C and E conclusion no. 2).
Fig. 3 C and G	(dpHi/dt)final (rate of pHi increase during transition MAc → Ctrl)	↓	↓	↑ J L, unlikely (conflicts with Fig. 1 conclusions). ↓ J E, consistent with ↓ NBCe1 activity (see Fig. 2 C and E conclusion no. 2).
Fig. 3 C and K	(pHi)final (steady‐state pHi after MAc removal)	↓	↓	↑ J L, unlikely (conflicts with Fig. 1 conclusions). ↓ J E, consistent with ↓ NBCe1 activity (see Fig. 2 C and E conclusion no. 2).
Fig. 4 B and D	k up (rate constant of pHi recovery [increase] in MAc after NH4 + prepulse)	None	None	At low pHi values, KO of AE3 does not have a statistically significant effect on J E during MAc. Hypothesis: ↑ NHE1 activity (increasingly active at low pHi) compensates for ↓ NBCe1 activity in MAc (see Fig. 2 C and E conclusion no. 2).
Fig. 4 F	k up (rate constant of pHi recovery [increase] in Ctrl after NH4 + prepulse)	↑	↑	↑ J E (i.e. at low pHi values, KO of AE3 enhances J E under Ctrl conditions). Hypothesis: ↑ NHE1 (see Fig. 4 B and D conclusion) slightly overcompensates for ↓ NBCe1 activity in Ctrl (see Fig. 2 C and E conclusion no. 2).
Fig. 6 A and C (astrocyte‐only cultures)	(pHi)Ctrl	None	None	Presence of neurons is required for KO of AE3 to modify acid–base status in astrocytes (compare with Fig. 2 C and E conclusions).
Fig. 6 A and D (astrocyte‐only cultures)	(dpHi/dt)early (rate of pHi decrease during transition Ctrl → MAc)	None	None	Presence of neurons is required (compare with Fig. 2 C, G and I conclusions).
Fig. 6 A and E (astrocyte‐only cultures)	(dpHi/dt)late (rate of pHi downward drift during last several mins of MAc)	None	None	Presence of neurons is required (compare with Fig. 2 C and K conclusions).
Fig. 6 A and G (astrocyte‐only cultures)	(dpHi/dt)final (rate of pHi increase during transition MAc → Ctrl)	None	None	Presence of neurons is required (compare with Fig. 3 C and G conclusions).
Fig. 6 A and H (astrocyte‐only cultures)	(pHi)final (steady‐state pHi after MAc removal)	None	None	Presence of neurons is required (compare with Fig. 3 C and K conclusions).
Fig. 7 B and J	(∆pHi)Cl removal (pHi drift elicited by Cl– removal under MAc conditions)	↓	↓	↓ J E. Hypothesis: ↓ [Cl–]o → ↓ [Cl–]i → ↓ NHE activity, known to be Cl– dependent in other cells.

KO, knockout.

Communication between neurons and astrocytes

Neuron‐to‐astrocyte and astrocyte‐to‐neuron communications are important for synaptic plasticity and metabolic coupling between the two cell types (Volterra & Meldolesi, 2005). These interactions occur in several forms that differ in the type of the stimulus that the origin cell generates, and the type of the response that the target cell produces.

A well‐studied example of neuron–astrocyte communication is the neuronal release of a transmitter that leads to the astrocytic release of a transmitter. When a neuron releases the neurotransmitter glutamate during synaptic transmission, [Ca²⁺]_i in adjacent astrocytes increases (Porter & McCarthy, 1996) and triggers astrocytes to release gliotransmitters (Paixão & Klein, 2010), such as glutamate itself (Parpura et al. 1994; Bezzi et al. 1998; Parpura & Haydon, 2000; Malarkey & Parpura, 2008), ATP (Guthrie et al. 1999; Lee et al. 2015), or d‐serine (Wolosker et al. 1999; Wolosker, 2006; Horn et al. 2013). Consequently, the presence of these gliotransmitters in the tripartite synapse modulates neuronal synaptic strength.

Another form of communication occurs when neuronal action potentials produce an increase in [K⁺]_o, which in turn leads to the release of a transmitter or a change in metabolic state. An example of transmitter discharge is non‐vesicular GABA release. Here, the rise in [K⁺]_o depolarizes neurons and astrocytes, so that GABA transporters reverse in both cell types and release GABA to the extracellular space, followed by neuronal inhibition (Wu et al. 2001; Song et al. 2013). An example of a K⁺‐induced altered metabolic state, discussed in more detail in the last section of this paper, is neuronal firing, which raises [K⁺]_o, which in turn leads to a depolarization‐induced alkalization or DIA (Siebens & Boron, 1987 a,b, 1989 a,b) in astrocytes and a parallel acidification of the extracellular fluid, which reduces neuronal excitability (Chesler & Kraig, 1987; Grichtchenko & Chesler, 1994; Pappas & Ransom, 1994; Ransom, 2000; Svichar et al. 2011). In addition, the rise in astrocytic pH_i during DIA leads to an increase in [HCO₃ ^–]_i that binds to and activates soluble adenylyl cyclase (sAC), to enhance glycogen breakdown, glycolysis and lactate production (Choi et al. 2012). This lactate then shuttles to active neurons to serve as an energy source (Pellerin & Magistretti, 1994).

An additional form of communication between neurons and astrocytes, especially during development, is the direct interaction between membrane proteins. For example, neurons and astrocytes use the Eph–ephrin system, in which an ephrin protein expressed on an astrocyte interacts with an Eph receptor expressed on a neuron, to induce synaptic plasticity (Filosa et al. 2009) and morphological changes (Murai et al. 2003). Another example is the interaction of contactin protein 1 expressed on neurons with the carbonic anhydrase–like domain (CALD) of the receptor protein tyrosine phosphatase ζ (RPTPζ), which is expressed on the surface of astrocytes. Contactins 3−6, also expressed on neurons, interact with the CALD RPTPγ, which is also expressed in neurons (Bouyain & Watkins, 2010), an example of a neuron–neuron interaction. Recent reports suggest that RPTPγ is a CO₂/HCO₃ ^– sensor (Boedtkjer et al. 2016; Zhou et al. 2016).

In the present study, we describe a novel variant of neuron–astrocyte communication, in which neuronal AE3 modulates astrocytic pH_i regulation (Table 4), perhaps by stimulating NBCe1 and inhibiting NHE1. This interaction requires both AE3 and the presence of neurons. A remaining question is how does this communication occur? One might speculate that neuronal AE3 interacts directly with an astrocytic membrane protein that in turn regulates NBCe1 and NHE1 in astrocytes. Another possibility is that the presence or activity of AE3 in neurons indirectly leads to the expression or modification of a surface protein, or to the release of a soluble substance (e.g. an ion, small molecule, secreted protein, membrane‐protein fragment) or an exosome (Koumangoye & Delpire, 2016) that initiates, in astrocytes, downstream signalling pathways that ultimately modulate NBCe1, NHE1, and possibly other acid–base transporters. If the AE3‐dependent signal is a soluble substance, the response in astrocytes must be sufficiently long‐lived that we can observe it even after the transfer of the coverslip from a Petri dish with stationary media to a chamber with continuous flow (a process requiring ∼15 min).

Physiological relevance of AE3 in the function of CA1 neurons and astrocytes

The initial hint that AE3 has a role in the electrical activity of hippocampal neurons was the association of the human polymorphism AE3‐A867D SLC4A3 with idiopathic generalized epilepsy (Sander et al. 2000, 2002). Subsequent studies showed that this polymorphism causes a decrease in the transport activity of human AE3 as expressed in HEK293 cells (Vilas et al. 2009), and the absence of AE3 causes an increase in susceptibility to epilepsy in mice (Hentschke et al. 2006). A plausible explanation could have been that, because AE3 is an acid loader, its knockout would lead to an increase in neuronal pH_i, which in turn would increase susceptibility to epilepsy. However, steady‐state pH_i in the HC neurons from AE3^–/– mice is paradoxically indistinguishable from neurons in WT mice (Hentschke et al. 2006), as confirmed in the present study. An alternative explanation for the pro‐epileptic phenotype associated with diminished AE3 activity might focus on Cl^–. For example, is AE3, like the K⁺/Cl^– cotransporter 2 (KCC2), anti‐epileptic because it helps maintain a low [Cl^–]_i and thereby promotes hyperpolarizing currents through GABA‐ and glycine‐activated Cl^– channels? Except during brief periods when pH_i is very low (i.e. lowering [HCO₃ ^–]_i) or the aforementioned Cl^– currents are very high (raising [Cl^–]_i), AE3 would operate in the direction of Cl^– influx. Thus, from the perspective of its Cl^– transport, AE3 is usually pro‐epileptic, and the reduction of AE3 function caused by the polymorphism A867D or the knockout of AE3 would be anti‐epileptic. Thus, the mechanism by which AE3 dysfunction promotes epilepsy has remained elusive. The data from the present study lead to explanations for both (1) why pH_i does not rise in HC neurons from AE3^–/– mice and (2) the pro‐epileptogenic phenotype of the AE3^–/– mice.

As far as the unexpectedly low pH_i is concerned, we hypothesize that the direct tendency of AE3 to lower pH_i because AE3 mediates HCO₃ ^– efflux (neuron in Fig. 8) is approximately balanced by the indirect tendency of AE3 to raise pH_i because AE3 mediates Cl^– influx, which supports such Cl^–‐dependent acid‐extruders as NDCBE and NHE1. Thus, it is not unreasonable to find that the knockout of AE3 fails to cause a significant increase in pH_i.

Figure 8. Model of neuron–astrocyte crosstalk, based on acid–base‐related events.

Schematic model of a hypothesis describing the role of AE3 in crosstalk between a neuron (left) and an astrocyte (right). The white numerals on black squares describe the postulated sequence of events.

Regarding the pro‐epileptic phenotype in the intact brain and in slices, we suggest a model based on two levels of crosstalk between neurons and astrocytes. When a neuron fires action potentials (Fig. 8, step 1), the release of K⁺ from the neuron (step 2) causes an increase in [K⁺]_o that depolarizes adjacent astrocytes (step 3). This depolarization increases the driving force for the electrogenic NBCe1 (step 4) and thus results in the increased uptake of HCO₃ ^–, that is, a DIA (step 5a). Accompanying this intracellular alkalization is an extracellular acidification (i.e. MAc; step 5b), which in turn inhibits neuronal ion channels (step 6a), such as voltage‐gated Na⁺ channels (Tombaugh & Somjen, 1996), NMDA receptors (Tang et al. 1990) and glutamate receptors (Traynelis et al. 2010), and puts a brake on neuronal activity. Steps 1–6a have been proposed by others (Chesler & Kraig, 1987; Grichtchenko & Chesler, 1994; Ransom, 2000; Svichar et al. 2011). We extend this model by proposing that MAc also stimulates AE3 (step 6b), which lowers [HCO₃ ^–]_i and thus pH_i in the neuron (step 7a) and also stimulates acid extruders (step 7b). We also propose that the presence of AE3 in neurons somehow increases the functional activity of NBCe1 in astrocytes (step 8), the net effect of which will be to accentuate the action‐potential–induced DIA and MAc, and thereby enhance the brake put on neuronal firing. Thus, the knockout of AE3 would reduce the stimulation of NBCe1 in astrocytes, reduce the negative feedback on neuronal firing, and thus reduce the threshold for triggering an epileptic seizure.

Additional information

Competing interests

None declared.

Author contributions

A.I.S. contributed to the conception and design of the research; performed the experiments, analysed the data, prepared the figures, and wrote the first draft of the manuscript; and contributed to the interpretation of the results, and to the revision of the manuscript. C.A.H. contributed to the interpretation of the data, and to the critical revision of the manuscript. W.F.B. contributed to the conception and design of the research, the interpreted results, and to the revision of the manuscript. All authors approved the final version of the manuscript and agree to be accountable for all aspects of the work. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed. Experiments were carried out at Case Western Reserve University, Cleveland OH, USA.

Funding

This work was supported by NIH grants NS18400 (W.F.B.), P01‐613 HD032573 (PI: Gabriel G. Haddad, Project 2: W.F.B.) and NIH grant T32 HL 007913 (PI: Kingman Strohl, supports: A.I.S.).

Supporting information

Disclaimer: Supporting information has been peer‐reviewed but not copyedited.

Supplementary Figs S1–10. Alternative approaches for analysing pH_i trajectories for all cells in a particular data set. These analyses include: (1) plots of dpH_i/dt vs. pH_i, and (2) plots of exponential rate constants vs. (pH_i)_Ctrl.