Abstract
Key points
Purkinje cells are the sole output of the cerebellar cortex and fire two distinct types of action potential: simple spikes and complex spikes.
Previous studies have mainly considered complex spikes as unitary events, even though the waveform is composed of varying numbers of spikelets.
The extent to which differences in spikelet number affect simple spike activity (and vice versa) remains unclear.
We found that complex spikes with greater numbers of spikelets are preceded by higher simple spike firing rates but, following the complex spike, simple spikes are reduced in a manner that is graded with spikelet number.
This dynamic interaction has important implications for cerebellar information processing, and suggests that complex spike spikelet number may maintain Purkinje cells within their operational range.
Abstract
Purkinje cells are central to cerebellar function because they form the sole output of the cerebellar cortex. They exhibit two distinct types of action potential: simple spikes and complex spikes. It is widely accepted that interaction between these two types of impulse is central to cerebellar cortical information processing. Previous investigations of the interactions between simple spikes and complex spikes have mainly considered complex spikes as unitary events. However, complex spikes are composed of an initial large spike followed by a number of secondary components, termed spikelets. The number of spikelets within individual complex spikes is highly variable and the extent to which differences in complex spike spikelet number affects simple spike activity (and vice versa) remains poorly understood. In anaesthetized adult rats, we have found that Purkinje cells recorded from the posterior lobe vermis and hemisphere have high simple spike firing frequencies that precede complex spikes with greater numbers of spikelets. This finding was also evident in a small sample of Purkinje cells recorded from the posterior lobe hemisphere in awake cats. In addition, complex spikes with a greater number of spikelets were associated with a subsequent reduction in simple spike firing rate. We therefore suggest that one important function of spikelets is the modulation of Purkinje cell simple spike firing frequency, which has implications for controlling cerebellar cortical output and motor learning.
Key points
Purkinje cells are the sole output of the cerebellar cortex and fire two distinct types of action potential: simple spikes and complex spikes.
Previous studies have mainly considered complex spikes as unitary events, even though the waveform is composed of varying numbers of spikelets.
The extent to which differences in spikelet number affect simple spike activity (and vice versa) remains unclear.
We found that complex spikes with greater numbers of spikelets are preceded by higher simple spike firing rates but, following the complex spike, simple spikes are reduced in a manner that is graded with spikelet number.
This dynamic interaction has important implications for cerebellar information processing, and suggests that complex spike spikelet number may maintain Purkinje cells within their operational range.
Abbreviations
- CS
complex spike
- CV2
coefficient of variation
- ISI
interspike interval
- PETH
peri‐event time histogram
- RMS
root mean squared
- SNR
signal‐to‐noise ratio
- SS
simple spike
Introduction
Central to all major theories of cerebellar function is the interaction between the two distinct types of discharge by Purkinje cells: the complex spikes and simple spikes. Simple spikes are generated intrinsically (Eccles, 1967; Gähwiler, 1975; Häusser & Clark, 1997; Raman et al. 1997; Raman & Bean, 1999) and also by activity in the mossy fibre‐granule cell‐parallel fibre pathway and occur at highly variable rates (∼20–200 Hz) (Armstrong & Rawson, 1979; Jirenhed et al. 2013; Chen et al. 2016). By contrast, complex spikes are generated by activity in the climbing fibre pathway and only occur at ∼1 Hz. The best characterized interaction between complex spikes and simple spikes is the transient cessation in simple spike activity that immediately follows a complex spike (Granit & Phillips, 1956; Thach, 1967; Bell & Grimm, 1969). However, longer modulatory effects (over hundreds of milliseconds) have also been described (Ebner & Bloedel, 1981; McDevitt et al. 1982; Sato et al. 1992; Wise et al. 2010).
Although most studies consider both simple spikes and complex spikes as unitary events, this is only the case in reality for simple spikes. Complex spikes are composed of an initial spike followed by a variable number of secondary components termed spikelets. These spikelets can produce an intense burst of activity (∼500 Hz) and are therefore capable of signalling events that are distinct from those signalled by simple spikes (Campbell & Hesslow, 1986; Yang & Lisberger, 2014). Whether or not a relationship exists between the number of spikelets in a complex spike and the simple spike activity of the same Purkinje cell is unclear (Mano, 1970; Gilbert, 1976). Gilbert (1976) reported a positive relationship between background simple spike firing rate and spikelet number, whereas Mano (1970) and Warnaar et al. (2015) found no relationship between complex spike waveform and the preceding simple spike firing rates. With regard to behaviour, a recent study in monkeys has shown that learning‐related reductions in simple spike activity correlate with the duration of complex spikes during motor learning (Yang & Lisberger, 2014). A complex spike waveform may therefore drive experience‐dependent changes in simple spike activity. However, the opposite is equally possible in that simple spike activity could modulate the complex spike waveform, such that complex spikes provide information regarding the recent history of the Purkinje cell (Servais et al. 2004).
Another not mutually exclusive possibility is that complex spikes have a homeostatic function and regulate the intrinsic simple spike activity of Purkinje cells (Colin et al. 1980; Montarolo et al. 1982; Cerminara & Rawson, 2004). Furthermore, evidence exists suggesting that simple spike activity predicts the timing of a complex spike (Miall et al. 1998; Chaumont et al. 2013; Witter et al. 2013). However, in none of these studies was the complex spike spikelet number considered. Thus, considerable uncertainty remains regarding the relationship between simple spike activity and the number of spikelets elicited during a complex spike. The present in vivo study aimed to help clarify this important issue and determine the dynamic interplay between simple spike activity and the number of spikelets within a complex spike. We provide evidence consistent with the possibility that the number of spikelets regulates simple spike firing frequency, keeping Purkinje cells within their operational range.
Methods
Recordings of Purkinje cells were obtained from two different research laboratories (one in Bristol, UK; the other in New York, NY, USA). The data obtained from both laboratories have been used previously but for different analysis (Wise et al. 2010; Xiao et al. 2014). The Bristol experiments were performed in accordance with the UK Animals (Scientific Procedures) Act 1986 and were approved by the University of Bristol Animal Welfare and Ethical Review Body. Experimental protocols in New York were approved by the Institutional Animal Care and Use Committees of New York University School of Medicine. In brief, adult male Wistar rats (Bristol, n = 10, ∼300 g) and female Sprague–Dawley rats (NYU, n = 10, ∼250 g) were anaesthetized with ketamine (100 mg kg‐1) and xylazine (5 mg kg‐1 or 8 mg kg‐1) i.p., and supplementary doses of anaesthetic were administered as required. The depth of anaesthesia was regularly assessed by a paw pinch to monitor reflex muscle tone. Rectal temperature was maintained at 37°C. To gain access to the cerebellum, animals were placed in a stereotaxic frame, and a craniotomy was performed to expose the posterior lobe of the cerebellum.
Purkinje cell recordings and peripheral stimulation
Bristol experiments
Extracellular single unit Purkinje cell recordings were made with glass insulated tungsten microelectrodes (impedance 2 MΩ; Alpha‐Omega, Nazareth, Israel) from copula pyramidis, the paramedian lobule and crus IIa of the posterior cerebellum. The spontaneous and evoked activity of complex spikes and simple spikes of individual Purkinje cells were obtained in the same recording session. Recordings were bandpass filtered between 0.3 and 5.0 kHz and digitized on‐line (sampling rate, 21 kHz) using a Cambridge Electronic Design (CED, Cambridge, UK) 1401 analogue‐to‐digital converter and Spike2 software (CED).
As well as spontaneous Purkinje cell activity, recordings were obtained in response to peripheral electrical stimulation. Bipolar percutaneous stimulating electrodes were inserted into the contralateral whisker pad and the ipsilateral forelimb, and stimuli were given (single pulse; 0.1 ms duration, 1 Hz) at an intensity sufficient to evoke a small but visible muscle twitch from the stimulated body part.
To determine whether the findings found in the anaesthetized rat were also present in awake animals, a small sample of Purkinje cells (n = 4) with a sufficiently high signal to noise ratio to reliably discriminate individual complex spikes, their associated spikelets and simple spikes were obtained in the lateral part of crus I in a chronically implanted cat (for surgical and recording details, see Miles et al. 2006; Cerminara et al. 2009). Sample recordings were obtained when the animal was sitting quietly at rest (length of each recording ∼4 mins, involving typically 150–200 complex spikes). Further details of analysis and spike sorting are provided below.
New York experiments
Extracellular single unit Purkinje cell recordings were made in crus II and vermis lobule VIII using glass microelectrodes filled with 2.0 m NaCl solution and mounted on a motorized 3D manipulator (MCL‐3; Lang GmbH & Co. KG, Hüttenberg, Germany). Neural activity was recorded using a multichannel recording system (MultiChannel Systems, Reutlingen, Germany) with a 25 kHz/channel sampling rate, gain of 1000× and band pass filters set at 0.2–8.0 kHz.
Purkinje cell complex spike and simple spike sorting
Bristol experiments
In the case of Purkinje cell recordings in anaesthetized rats, simple spike and complex spike activity were discriminated independently off‐line via a template‐matching algorithm (principal component analysis, PCA, Spike2, CED). To detect the spikelets within the complex spike, a positive or negative threshold crossing was manually adjusted and the template duration altered to ensure the capture of the entire complex spike. PCA was then used to cluster the spikelets.
Only Purkinje cell recordings with sufficient signal‐to‐noise ratios (SNRs) to reliably discriminate between secondary spikelets of complex spikes and simple spikes were used in the present analysis (Fig. 1 A). SNR was calculated for each individual recording as the mean complex spike amplitude/RMS noise (where RMS = root mean square of the baseline activity when no spiking is present). Only Purkinje cell recordings with a SNR that exceeded 40 were included in the analysis (range 43.2 to 123.4, mean = 78). This SNR is sufficient to distinguish all spikelets from baseline noise. Recordings were also only selected if the peak amplitude of both the simple spikes and complex spikes remained stable throughout the entire recording period (∼60 min, range 17–143 min). The characteristic cessation in simple spike activity following each complex spike (the climbing fibre pause) was used to confirm that recordings were single units and that both types of activity were derived from the same cell (Eccles et al. 1966 b; Thach, 1967; Sato et al. 1992).
Figure 1. Purkinje cell and spikelet number.
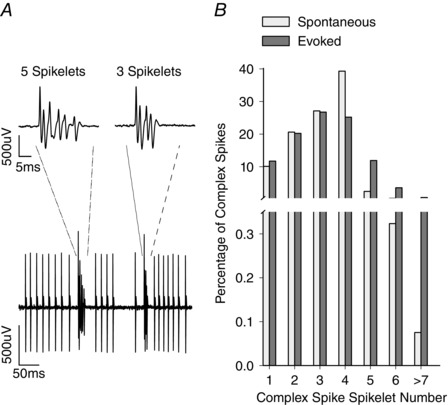
A, example recording from a Purkinje cell showing complex spikes and simple spikes. Two complex spikes are shown with different spikelet numbers occurring close in time. The two complex spikes, representing complex spikes with five and three spikelets, are shown at an expanded time base in the insets. B, distribution of spikelet number for spontaneous (white bars) and evoked (grey bars) complex spikes from n = 61 and n = 27 Purkinje cells, respectively.
For the awake data, the complex spike spikelet number was determined using a Python script (Python Software Foundation. Python Language Reference, version 2.7.7; http://www.python.org) based on a peak detection algorithm that detected the individual time points of the spikelets within the complex spike duration. Simple spikes were discriminated as above.
New York experiments
To count spikelet numbers, all complex spikes were high‐pass filtered at 300–400 Hz and automatically processed using a custom‐written procedure (Igor Pro; WaveMetrics Inc., Portland, OR, USA), which detected all deflections with a peak‐to‐peak level exceeding a pre‐defined threshold level.
The resultant spikelet counts for both the Bristol and New York data were manually verified independently by at least two investigators and, on the rare occasion where discrepancies were observed, necessary deletions and/or additions were made.
Data analysis
Extracted spike and spikelet times were analysed using Python. The initial spike of the complex spike was not included in the spikelet number count because this did not vary across complex spikes. Complex spikes with more than 7 spikelets, although consistent with the general trends found for other spikelet numbers, were excluded from statistical analysis because they accounted for <0.5% of the total complex spike population and were present in only three Purkinje cells and therefore not amenable to statistical analyses.
Complex spikes that occurred within 500 ms of another complex spike were also excluded from our analyses (except in the case of pause duration and interspike intervals; ISI, see below). This was to ensure that any interactions between spikelet number and simple spikes could not be explained by paired pulse depression (which may cause a decrease in the number of spikelets in a subsequent complex spike; Hashimoto & Kano, 1998) or by the modulation of simple spike activity following another complex spike within the time windows tested. Complex spikes that occurred within 0–50 ms after the peripheral stimulation were included in the analysis of evoked responses.
For display purposes, peri‐event time histograms (PETHs; bin width 20 ms) of simple spike firing were constructed around the occurrence of spontaneous or evoked complex spikes with different numbers of spikelets. To aid comparison across all Purkinje cells, histograms were normalized to the number of complex spikes that occurred for each spikelet number and the mean simple spike rate within each Purkinje cell. In all cases, time zero was taken as the onset of the initial spike of the complex spike. Subsequent analysis was performed on raster data rather than on these discretized histograms.
To examine the relationship between spikelet number and simple spike activity, specific interactions (Fig. 2) were investigated; first, for each individual Purkinje cell and then for the pooled dataset (Maruta et al. 2007).
Simple spike rate preceding a complex spike (Pre‐CS): the simple spike rate before the complex spike was calculated as the number of simple spikes in three time epochs: –50 to 0 ms, –150 to 0 ms and –400 to 0 ms before the occurrence of the complex spike at time zero, divided by the duration of the time window (Fig. 2 A).
Pause duration (P, ISICS‐SS): defined as the time interval between the initial spike of the complex spike and the time of the first simple spike following the complex spike (ISICS‐SS). In 5–10% of cases, another complex spike occurred before simple spike activity resumed and these were excluded from the analysis. To account for the possible influence of simple spike rate on pause duration, pause duration was normalized to mean ISISS/2. In brief, any effect that baseline simple spike firing rate would have on pause duration is excluded by normalizing to the expected pause duration if both simple and complex spike activity were independent. This is equal to half the average ISISS because, under the independence assumption, a complex spike could fall anywhere between two successive simple spikes with equal probability (Fig. 2 B) (Xiao et al. 2014).
Rebound duration (R): defined as the time from the first simple spike after the complex spike to the simple spike occurring before the ISISS equal to or greater than the mean ISISS. Purkinje cells that showed either no rebound effect or a heightened simple spike rate that failed to decrease within a 500 ms cut‐off time were excluded from the analysis of rebound duration. Rebound duration is reported in absolute values because no relationship was found with simple spike rate (Fig. 2 B).
Rebound frequency: calculated as the total number of simple spikes during the rebound divided by rebound duration. Rebound frequencies were normalized to the mean spontaneous simple spike rate observed throughout the spontaneous recording of each Purkinje cell.
Post simple spike rate (post‐CS): to quantify the simple spike rate following a complex spike, the number of simple spikes 100 ms after the occurrence of the complex spike within three time epochs (100–150 ms, 100–250 ms and 100–500 ms) was divided by the duration of the time window. The analysis was performed 100 ms after the onset of the complex spike to exclude the average effects of both the pause and rebound (Fig. 2 A).
The time interval between a complex spike and the preceding simple spike (ISISS‐CS): determined and normalized to the mean ISISS/2, as above for the pause duration (Fig. 2 B).
Interval between complex spikes (ISICS‐CS): calculated and normalized to the mean ISICS for each Purkinje cell. Only spontaneous complex spikes were analysed because peripheral stimulation evokes complex spikes with well‐defined latency (Fig. 2 C).
The change in simple spike rate before and after each individual complex spike: for each complex spike, the simple rate during the –150 to 0 ms time window before the complex spike was subtracted from the simple spike rate during the 100–250 ms time window after the complex spike (which excludes the post‐complex spike pause and rebound). This gave an indication of whether the simple spike rates after individual complex spikes with different numbers of spikelets were lower (negative value), higher (positive value) or the same (0) as before the complex spike.
The mean coefficient of variation (CV2) for adjacent ISIs: the regularity of simple spike firing was quantified by determining CV2. This was calculated as CV2 = 2|ISIn + 1 − ISIn|/(ISIn + 1 + ISIn).
Figure 2. Features of Purkinje cell activity analysed in relation to spikelet number.
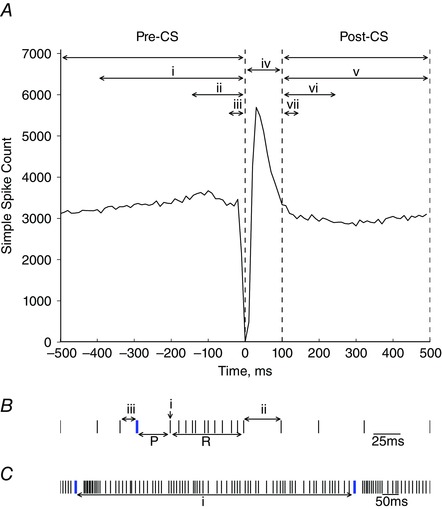
A, PETH of simple spike activity around the time of the complex spikes (time = 0 ms). Spikelet number was compared with the simple spike rate before the complex spike in three epochs: (i) –400 to 0 ms; (ii) –150 to 0 ms; and (iii) –50 to 0 ms. (iv) The time interval 0–100 ms after the complex spike that represents the average post‐complex spike pause and rebound in simple spike activity. Spikelet number was also compared with the simple spike rate after the complex spike in three epochs: (v) 100 to 500 ms; (vi) 100 to 250 ms; and (vii) 100 to 150 ms. B, schematic raster plot showing simple spikes (black) and complex spikes (blue). Pause duration (P) is calculated as the time from the initial spike in the complex spike to the subsequent simple spike. Rebound duration (R) is defined as the time from the first simple spike after the complex spike (i) to the next simple spike where ISISS is equal to, or greater than the mean ISISS (ii). The interspike interval between the simple spike and complex spike (ISISS‐CS) is represented by (iii). C, the interspike interval between complex spikes (ISICS‐CS) is illustrated by (i).
Statistical analysis
All values given in the Results are expressed as the mean ± SD (or the mean ± SEM where indicated), except for pause duration, which was strongly affected by outliers and so the median is given. A two‐tailed unpaired Student's t test was used to test for statistical differences between two groups when comparing averages between spontaneous and evoked data. Linear regression analysis was used to assess the relationship between spikelet number and the various parameters tested for individual cells and on pooled data, with the exception of spikelet number vs. rebound frequency and time from the preceding simple spike in the evoked conditions, because these relationships were non‐linear and therefore Spearman's rank correlation was used.
Results
General characteristics
In the anaesthetized experiments, a total of 27 Purkinje cells from the Bristol dataset and a total of 34 Purkinje cells from the New York dataset met the criteria to be included in our analysis (see Methods). When analysed separately, the two datasets produced similar results; therefore, the data are considered together (n = 61). The exception was the analysis of evoked activity, which was obtained solely for the Bristol dataset (see below). For all Purkinje cells (average ∼28 min recording duration), none displayed activity related to an injured cell, which typically consists of a progressive reduction over time in simple spike and complex spike amplitudes and abnormally high rates of firing that can be oscillatory in pattern (Eccles et al. 1966; Armstrong & Rawson, 1979; Hensbroek et al. 2014).
In agreement with previous experiments in awake and anaesthetized preparations (Armstrong & Rawson, 1979; Cerminara & Rawson, 2004; Shin et al. 2007; Bosman et al. 2010; Rasmussen et al. 2014), spontaneous simple spike activity occurred with an average firing frequency of 31.9 ± 17.3 Hz (mean ± SD; range 1.7–70.7 Hz; n = 61), whereas average complex spike firing rates were 0.89 ± 0.49 Hz (mean ± SD; range 0.15–2.19 Hz; n = 61). Rhythmic patterns of complex spike activity were only observed in five Purkinje cells (8%) and were not investigated further.
For individual Purkinje cells, the number of secondary spikelets within a given complex spike was highly variable. Overall, the number of spikelets ranged from 0–9, although complex spikes with three or four spikelets were most common (Fig. 1). From the range of spikelets (0–9), there was no statistically significant difference in spikelet number, regardless of whether generated spontaneously or evoked by peripheral stimulation (P = 0.36, paired Student's t test, n = 27 Purkinje cells, Bristol dataset). Mean spikelet number was also similar for spontaneous (mean ± SD: 3.24 ± 1.36) and evoked (mean ± SD: 3.18 ± 1.40) complex spikes (paired Student's t test, P = 0.06, n = 27 Purkinje cells, Bristol dataset).There was a significant negative correlation between complex spike firing rate and the number of spikelets generated, with low complex spike rates generating complex spikes with more spikelets (r = –0.541, P < 0.001, linear regression, n = 61 Purkinje cells). However, it should be noted that, although Purkinje cells with higher complex spike rates tend to have a lower than average spikelet number, Purkinje cells with a high complex spike rate show the full range of spikelet number and could also elicit a high number of spikelets.
We were unable to find any relationship between complex spikes with different spikelet numbers and the time when they occurred during the recording (i.e. spikelet number was unrelated to whether the complex spike occurred at the beginning, middle or end of the recording period). Taken together with the highly stable and ultra‐low noise recording conditions, we therefore consider it safe to conclude that any systematic differences in spikelet number are most probably not a result of variations in the quality of the recording.
Relationship between previous simple spike activity and complex spike spikelet number
As a first step in investigating the relationship between complex spike spikelet number and simple spike activity, we analysed spikelet number in relation to the preceding simple spike firing frequency. The different periods of analysis around the complex spikes are shown in Fig. 2 A. Example PETHs for two Purkinje cells constructed from spike trains during periods of spontaneous activity and when evoked by peripheral stimulation are shown in Fig. 3 A and B, respectively. In these two examples, the Purkinje cells discharged complex spikes that varied from one to six spikelets. In both cases, when the spontaneous simple spike firing frequency preceding a complex spike (pre‐CS, Fig. 2 A) was greater than the mean firing rate, subsequent complex spikes displayed a greater number of spikelets (linear regression, P < 0.001 in both examples).
Figure 3. Complex spike spikelet number correlates with simple spike activity.
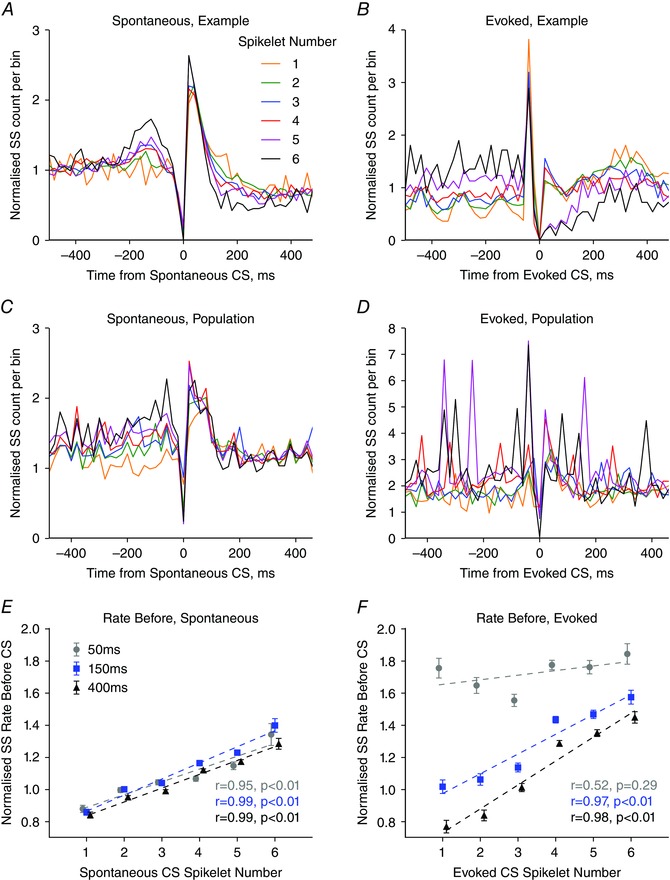
A and B, example simple spike PETH from single Purkinje cell recordings showing simple spike activity around spontaneous (A) and evoked (B) complex spikes with each number of spikelets. A bin height of 1 represents mean simple spike rate. Bin width = 20 ms. C and D, as in (A) and (B) but population average normalized simple spike PETHs for (C) spontaneous (n = 61 Purkinje cells) and (D) evoked (n = 27 Purkinje cells) complex spikes for each spikelet number. E, relationship between simple spike rate before the spontaneous complex spikes and spikelet number were positively correlated for the three epochs tested (–50 to 0 ms, grey filled circles; r = 0.955, P = 0.003; –150 to 0 ms blue filled squares; r = 0.988, P < 0.001; –400 to 0 ms, black filled triangles; r = 0.993, P < 0.001, n = 61 Purkinje cells). F, relationship between simple spike rate before the evoked complex spike were positively correlated with spikelet number for two of the three time epochs tested (–50 to 0 ms, grey filled circles; r = 0.517, P = 0.293, –150 to 0 ms blue filled squares; r = 0.967, P = 0.002; –400 to 0 ms, black filled triangles; r = 0.981, P = 0.001, n = 27 Purkinje cells. Linear regression performed on complex spikes with one to six spikelets. Each data point represents the mean across all complex spikes with that spikelet number. Error bars indicate the SEM.
The largest number of Purkinje cells (34/61; 56% of our sample) showing a significant positive relationship between spikelet number and preceding simple spike frequency was found when the 150 ms epoch was analysed. A possible reason for a subpopulation of Purkinje cells not displaying the effect is provided in the Discussion. Importantly, the relationship between spikelet number and preceding simple spike frequency was also evident when the complex spike data from all Purkinje cells were pooled (n = 61, Fig. 3 C; n = 27, Fig. 3 D). For this reason, the subsequent results relate to population analyses.
There was a strong positive correlation between simple spike activity prior to a spontaneous complex spike and the number of spikelets within the complex spike for all time epochs tested (–50 to 0 ms, grey filled circles; r = 0.955, P = 0.003; –150 to 0 ms blue filled squares; r = 0.988, P < 0.001; –400 to 0 ms, black filled triangles; r = 0.993, P < 0.001; linear regression, complex spikes with one to six spikelets; Fig. 3 E). By contrast, no relationship was found between the variance in simple spike activity before, as measured using the mean CV2 value, and spikelet number. Spontaneous complex spikes with only one spikelet were preceded by simple spike rates that were on average 86 ± 2% (n = 61 Purkinje cells) of the mean simple spike firing frequency. Conversely, complex spikes composed of six spikelets were preceded by simple spike rates that exceeded the mean simple spike firing rate by 135 ± 5% (n = 61 Purkinje cells). Thus, the number of spikelets in a complex spike correlates positively with preceding simple spike activity.
Similar to the findings for the spontaneous data, a strong positive correlation was also evident between average simple spike rate before an evoked complex spike and spikelet number for two of the three epochs tested (–150 to 0 ms blue filled squares; r = 0.967, P = 0.002; –400 to 0 ms, black filled triangles; r = 0.981, P = 0.001; linear regression, based on complex spikes with one to six spikelets; Fig. 3 F). The exception was for the 50 ms time epoch immediately prior to the complex spike (–50 to 0 ms, grey filled circles; r = 0.517, P = 0.293, linear regression, complex spikes with one to six spikelets; Fig. 3 F).
Complex spike and simple spike timing affects spikelet number
The finding that simple spike rate preceding a complex spike is correlated to spikelet number could partly be a result of the timing of the last simple spike prior to the complex spike. This is because there is a greater likelihood that the last simple spike will occur closer in time to the complex spike when firing frequency is high. Consistent with this possibility, spontaneous complex spikes that were preceded by simple spikes closer in time were found to be composed of a greater number of spikelets, which persisted even after normalizing to the mean simple spike rate (r = –0.965, P = 0.002, linear regression, complex spikes with one to six spikelets; Fig. 4 A). A negative, non‐linear, correlation was also observed for evoked complex spikes (r s = –0.829, P = 0.042, Spearman's rank correlation, complex spikes with one to six spikelets; Fig. 4 B).
Figure 4. Relationship between number of spikelets in the complex spike and interspike interval of simple and complex spikes.
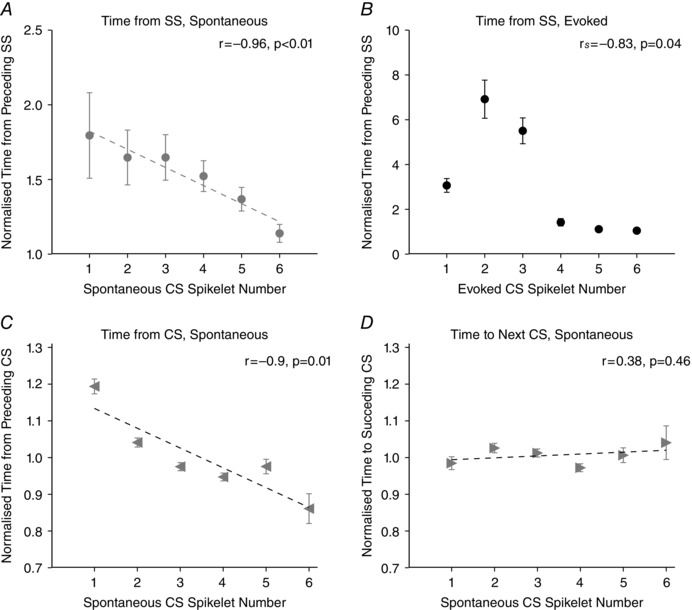
A, spikelet number of spontaneous complex spikes is inversely related to latency from the preceding simple spike (r = –0.965, P = 0.002, n = 61 Purkinje cells). B, as in (A) but for evoked complex spikes (r s = –0.829, P = 0.042, n = 27 Purkinje cells, Spearman's rank correlation). C, spikelet number for spontaneous complex spikes is inversely related to the latency from the preceding complex spike (r = –0.903, P = 0.014, n = 61 Purkinje cells), although no correlation exists between spikelet number and latency to the subsequent spontaneous complex spike (D, r = 0.381, P = 0.457, n = 61 Purkinje cells). Linear regression analysis and Spearman's rank correlation performed on complex spikes with one to six spikelets for (A) and (B), respectively. Data are expressed as the mean ± SEM.
To establish whether the preceding simple spike rate is correlated with spikelet number rather than the precise timing of the last simple spike, we analysed the simple spike rate preceding complex spikes with each spikelet number for time epochs that did not overlap (–450 to –150 ms, –150 to –50 ms and –50 to 0 ms. We found that a strong positive correlation still exists between simple spike rate prior to the complex spike and spikelet number for each epoch for spontaneous complex spikes (–50 to 0 ms, grey filled circles; r = 0.963, P = 0.002; –150 to –50 ms, blue filled squares; r = 0.976, P = 0.001; –400 to –150 ms, black filled triangles; r = 0.989, P < 0.001; Fig. 5 A) and two out of the three epochs for evoked complex spikes (–50 to 0 ms, grey filled circles; r = 0.517, P = 0.293; –150 to –50 ms, blue filled squares; r = 0.985, P < 0.001; –400 to –150 ms, black filled triangles; r = 0.990, P < 0.001; linear regression, complex spikes with one to six spikelets; Fig. 5 B). This suggests that the simple spike rate preceding the complex spike is influential to spikelet number.
Figure 5. Relationship between simple spike rate before the spontaneous complex spikes and spikelet number for non‐overlapping time windows.
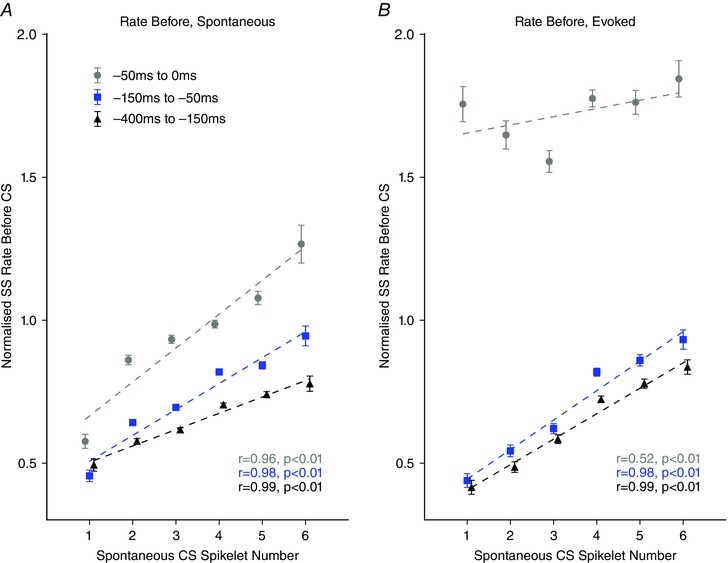
A, relationship between simple spike rate before the spontaneous complex spikes and spikelet number positively correlates for the three epochs tested (–50 to 0 ms, grey filled circles; r = 0.963, P = 0.002; –150 to –50 ms blue filled squares; r = 0.976, P = 0.001; –400 to –150 ms, black filled triangles; r = 0.989, P < 0.001; n = 27 Purkinje cells). B, as in (A) but for evoked complex spikes (–50 to 0 ms, grey filled circles; r = 0.517, P = 0.293; –150 to –50 ms blue filled squares; r = 0.985, P < 0.001; –400 to –150 ms, black filled triangles; r = 0.990, P < 0.001; n = 27 Purkinje cells. Linear regression analysis performed on complex spikes with one to six spikelets. Error bars indicate the SEM.
It is also possible that spikelet number relates to the timing of the preceding complex spike. In this case, there was a negative correlation between the number of spikelets elicited in the complex spike and the latency from the preceding complex spike (r = –0.903, P = 0.014, linear regression, based on complex spikes with one to six spikelets; Fig. 4 C). Complex spikes with six spikelets were on average preceded by an ISICS that was 86% of the mean ISICS, whereas complex spikes with one spikelet tended to be preceded by an ISICS that was 119% of the mean ISICS. By contrast, the number of spikelets in a given complex spike was not correlated with the timing of the subsequent complex spike (r = 0.381, P = 0.457, linear regression, complex spikes with one to six spikelets; Fig. 4 D).
In summary, a number of pre‐complex spike events are correlated with spikelet number, including simple spike frequency and the timing of the preceding simple spike and complex spikes. The previous activity of a Purkinje cell appears therefore to be important in shaping the spikelet number of somatic complex spikes.
Short‐term interactions between spikelet number and subsequent simple spike activity
Additional analysis examined the relationship between spikelet number and subsequent short‐term changes in simple spike activity. Short‐term interactions were defined as those occurring within 100 ms immediately after a complex spike. This time period includes the post‐complex spike cessation in simple spike activity (pause) and any subsequent transient increase in simple spike activity (rebound). The median pause duration was found to be 68.6 ms (n = 61 Purkinje cells) following spontaneous complex spikes and 48.4 ms (n = 27 Purkinje cells) after evoked complex spikes.
No statistically significant correlation was found between the number of spikelets in a complex spike and the duration of the subsequent pause during spontaneous Purkinje cell activity (r = 0.746, P = 0.089, linear regression, complex spikes with one to six spikelets), nor when Purkinje cell activity was evoked by electrical stimulation of the leg or face (r = –0.411, P = 0.419, linear regression, complex spikes with one to six spikelets; data not shown). Thus, even though complex spikes cause the well‐documented pause in simple spike firing, pause duration appears to be independent of the number of spikelets within the complex spike.
A subsequent rebound in simple spike activity (see Methods for definition) was observed in the majority of our sample of Purkinje cells (51/61; 83.6%). Rebound duration varied considerably across Purkinje cells, but on average lasted 77.1 ± 55.4 ms (mean ± SD; range 5.5–362.4 ms; n = 61 Purkinje cells). The average simple spike rate during the rebound was 82.8 ± 30.1 Hz (mean ± SD; range 30.1–374.27 Hz; n = 61 Purkinje cells) following spontaneous complex spikes and 70.5 ± 19.9 Hz (mean ± SD; range 27.2–105.8 Hz; n = 27 Purkinje cells) for evoked complex spikes. No significant correlation was observed between spikelet number and average rebound duration for spontaneous complex spikes (r = –0.726, P = 0.102, linear regression, complex spikes with one to six spikelets; data not shown), nor for evoked complex spikes (r = 0.395, P = 0.439, linear regression, based on complex spikes with one to six spikelets; data not shown).
However, a statistically significant positive correlation was found between the firing rate of simple spikes during the rebound and spikelet number during spontaneous Purkinje cell activity (r = 0.944, P = 0.005, linear regression, complex spikes with one to six spikelets; Fig. 6 A) but not when complex spikes were evoked by peripheral stimulation (r s = –0.771 P = 0.072, Spearman's rank correlation, complex spikes with one to six spikelets; Fig. 6 B). This suggests that complex spikes may affect the rate of simple spike firing during the subsequent rebound activity in a manner dependent on the number of spikelets.
Figure 6. Relationship between spikelet number and frequency of simple spikes during the rebound.
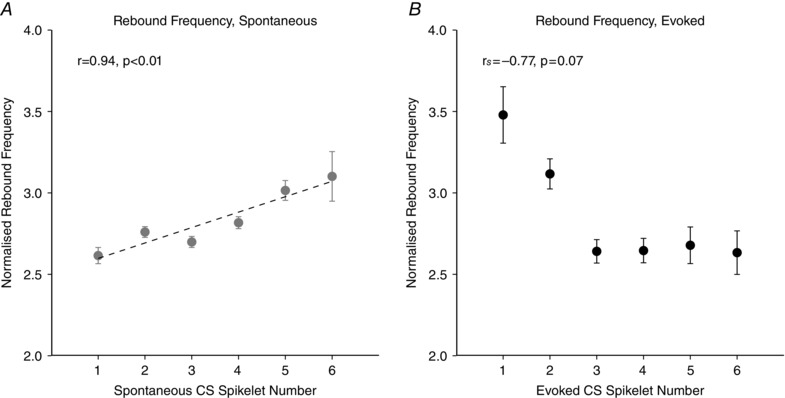
There is was a significant, positive correlation between spikelet number and the rate of simple spikes in the rebound for spontaneous (A, r = 0.944, P = 0.005, n = 61 Purkinje cells, linear regression) but not evoked complex spikes (B, r s = –0.771 P = 0.072, n = 27 Purkinje cells, Spearman's rank correlation). Analysis performed on complex spikes with one to six spikelets. Data normalized to mean simple spike rate. Error bars indicate the SEM.
Longer‐term interactions between spikelet number and subsequent simple spike activity
We also examined the time period after the post‐complex spike pause and any rebound effects (post‐CS, defined as the time window 100–500 ms after a complex spike, see Methods, Fig. 2). Overall, a significant decrease in average simple spike firing rate was observed following complex spikes (simple spike rate before = 30.1 ± 19.2 Hz, mean ± SD, simple spike rate after = 24.4 ± 16.4 Hz, mean ± SD, P < 0.001, two‐tailed unpaired Student's t test, n = 20507 complex spikes). A negative correlation was found between spikelet number and simple spike rate following spontaneous complex spike events for time windows >100 ms. This relationship, however, was observed in only 26% of our sample of individual Purkinje cells (16/61) but was evident even when data from all cells were pooled (spontaneous complex spikes; 100–150 ms grey filled circles: r = –0.800, P = 0.056, 100–250 ms blue filled squares: r = –0.884, P = 0.019, 100–500 ms, black filled triangles: r = –0.843, P = 0.035, linear regression, complex spikes with one to six spikelets; Fig. 7 A). However, the difference in the simple spike rate following complex spikes with one spikelet compared to six spikelets was modest (∼12%). By comparison, for evoked complex spikes, no correlation was found between spikelet number and simple spike rate after the complex spike for all three time epochs tested (evoked complex spikes; 100–150 ms grey filled circles: r = 0.654, P = 0.159, 100–250 ms blue filled squares: r = 0.164, P = 0.756, 100–500 ms black filled triangles: r = –0.812, P = 0.050, linear regression, based on complex spikes with one to six spikelets; Fig. 7 B). Therefore, following evoked complex spikes (and their associated pause and rebound activity) the simple spike rate was not only indistinguishable across complex spikes with different numbers of spikelets, but also from mean simple spike rates. This is in stark contrast to the preceding simple spike rate, which differed systematically with spikelet number for both spontaneous and evoked complex spikes (Fig. 3 E and F).
Figure 7. Interactions between spikelet number and simple spike rate after the complex spike.
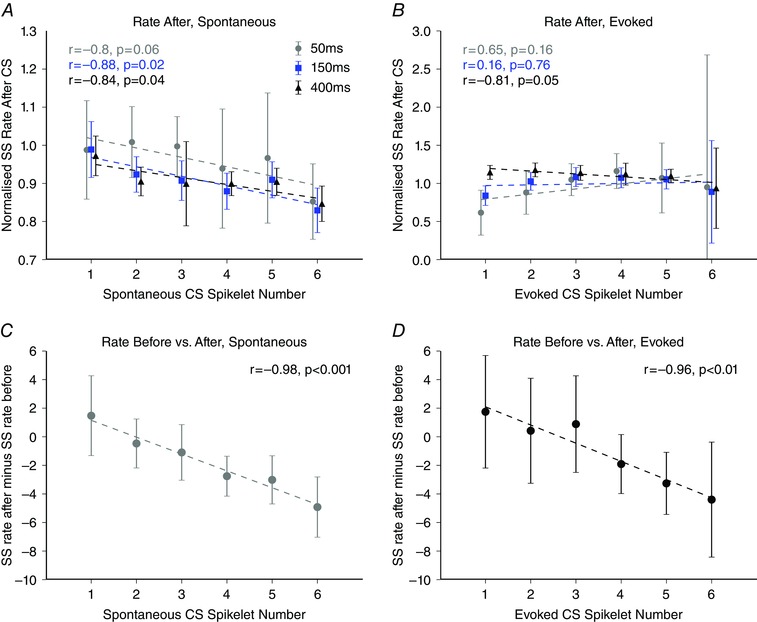
A, relationship between spikelet number and simple spike rate after spontaneous complex spike events. A negative correlation exists between spontaneous spikelet number and simple spike rate after the complex spike event for two of the three epochs tested (100 to 150 ms, grey filled circles: r = –0.800, P = 0.056; 100 to 250 ms blue filled squares: r = –0.881, P = 0.019; 100 to 500 ms, black filled triangles: r = –0.843, P = 0.035). B, as in (A) but for evoked complex spikes. No correlation was observed for evoked complex spikes (100 to 150 ms, grey filled circles: r = 0.654, P = 0.159; 100 to 250 ms, blue filled squares: r = 0.164, P = 0.756; 100 to 500 ms, black filled triangles: r = –0.812, P = 0.050). C and D, magnitude of simple spike depression following a complex spike event was graded with spikelet number for both spontaneous (r = –0.984, P < 0.001, n = 61 Purkinje cells) and evoked Purkinje cell activity (r = –0.964, P = 0.002, n = 27 Purkinje cells), respectively. Linear regression analysis performed on complex spikes with one to six spikelets. Error bars indicate the SEM.
The magnitude of simple spike depression following a complex spike event, in comparison with before, appeared to be graded with spikelet number. To test the hypothesis that high simple spike rates prior to a complex spike event are converted to lower rates after the complex spike, in a graded manner depending on spikelet number, we compared the simple spike rate before and after each individual complex spike and related this to spikelet number (see Methods, Fig. 7 C). For each individual complex spike, a comparison was made between the rate during the 0 to –150 ms time window before the complex spike and the simple spike rate during the 100–250 ms time window after the complex spike (which excludes the post‐complex spike pause and rebound). This gives an indication of how the simple spike rates vary around complex spike events at the level of individual complex spikes. Spontaneous complex spikes with a greater number of spikelets were associated with subsequent reductions in simple spike firing rate (r = –0.984, P < 0.001, linear regression, complex spikes with one to six spikelets; Fig. 7 C). Similarly, when we compared the simple spike rate before and after evoked complex spikes as a function of spikelet number, there was also a decrease in simple spike activity, that increased progressively with increasing numbers of spikelets in the complex spike (r = –0.964, P = 0.002, linear regression, complex spikes with one to six spikelets).
Data obtained in the awake animal
From a much larger pool of recordings of Purkinje cells obtained from crus I in the awake cat, we determined that the spike trains of four cells had a sufficiently high signal to noise ratio to reliably determine whether any of the interactions found in the anaesthetized preparation were also present in the awake animal. When sitting quietly at rest, simple spike firing rates were on average 40.1 ± 35.9 Hz (mean ± SD; range 5.9–89.3 Hz, n = 4), whereas complex spike rates were on average 0.77 ± 0.17 Hz (mean ± SD; range 0.57–0.95 Hz, n = 4). Similar to the much more extensive data obtained in the anaesthetized rat, the number of spikelets in each complex spike in the awake animal ranged from one to eight, with three spikelets being the most common. Also consistent with the data in the anaesthetized rat, a statistically significant positive relationship between pre‐CS simple spike activity and spikelet number was found in two of the Purkinje cells (50%, cell 1, r = 0.201, P = 0.012 n = 139 complex spikes; cell 2, r = 0.160, P = 0.019, n = 158 complex spikes; linear regression; for comparison, 56% of Purkinje cells showed such an effect in the anaesthetized preparation). A negative correlation between spikelet number and the simple spike rate after the complex spike was found in one Purkinje cell (25%, r = –0.288, P = 0.001, n = 189 complex spikes, linear regression; for comparison, 26% of Purkinje cells showed such an effect in the anaesthetized preparation). Despite the small sample, the proportion of cells showing an effect in the awake cat is therefore in remarkably good agreement with the proportions showing the same effect in the anaesthetized rat.
Discussion
The major findings arising from the present study (Table 1) are that: (i) a strong positive correlation exists between simple spike rate prior to a complex spike and the number of spikelets comprising the complex spike; (ii) spikelet number is related to the timing between the complex spike and the prior occurrence of a simple spike; (iii) spikelet number is positively correlated to the subsequent post‐pause rebound in simple spike rate; and (iv) complex spikes with greater spikelet numbers are followed by simple spike rates that are depressed compared to the rate observed prior to the complex spike event. Thus, the results raise the possibility that spikelet number may be regulating Purkinje cell activity.
Table 1.
Summary of main findings
| Spontaneous CSs | Evoked CSs | |
|---|---|---|
| Preceding SS rate | Positive correlation | Positive correlation |
| Preceding ISISS | Negative correlation | Negative correlation |
| Pause duration | None | None |
| Rebound duration | None | None |
| Rebound frequency | Positive correlation | None |
| Following SS rate | Negative correlation | None |
| Preceding ISICS | Negative correlation | NA |
| Succeeding ISICS | None | NA |
NA, not applicable.
Our findings are in agreement with Gilbert (1976) who found a positive correlation between spikelet number and background simple spike rates in a small population of Purkinje cells located in the anterior lobe of awake monkeys. By contrast, Mano (1970) found no correlation between simple spike rate and spikelet number in Purkinje cells recorded from the oculomotor vermis in awake primates (see also Warnaar et al. 2015). This difference is probably not related to species or the effects of anaesthesia because similar findings were found in our small sample of cells from the awake cat.
One possible reason for the discrepancy with the findings of Mano (1970) and Warnaar et al. (2015) may be differences in the recording site location, particularly given the emerging evidence that Purkinje cells in zebrin‐positive and zebrin‐negative bands show different firing properties (Paukert et al. 2010; Lang et al. 2014; Xiao et al. 2014; Zhou et al. 2014; Cerminara et al. 2015). The proportion of cells showing a relationship between simple spikes and spikelet number in the present study may also be related to whether Purkinje cells are located in zebrin‐positive or zebrin‐negative bands.
Regarding whether the number of spikelets can be modulated by previous complex spike activity, Servais et al. (2004) found no such relationship, whereas other studies have found that complex spikes preceded by a complex spike occurring closer in time have both greater spikelet numbers (Campbell & Hesslow, 1986) and duration (Warnaar et al. 2015). However, the opposite relationship has also been reported (Hashimoto & Kano, 1998; Maruta et al. 2007); the difference may be a result of the in vitro techniques and analysis methods, respectively. Our findings add to the observation suggesting that, when two complex spikes occur close in time, the second complex spike has a greater number of spikelets.
Although a relationship between spikelet number and preceding simple spike rate was found for spontaneous complex spike activity for all three time epochs investigated, when the complex spikes were evoked by peripheral stimulation, no such relationship was found for simple spikes in the 50 ms time window preceding the complex spikes, nor for simple spike rate in the subsequent rebound. It might be that simple spike activity generated extrinsically, which signals events from the periphery, may require more time to drive changes in cortico‐nucleo‐olivary loops (see below).
Ionic control of spikelet modulation
Complex spikes are generated as a result of interactions between Na+, Ca2+ and K+ currents (Schmolesky et al. 2002; Hurlock et al. 2008) with the initiation of the complex spike and its spikelets occurring at the Purkinje cell axosomatic membrane (Zagha et al. 2008; Veys et al. 2013). Resurgent Na+ currents and Kv3.3 currents are critical determinants of the complex spike waveform by underpinning repetitive spikelet generation (Raman et al. 1997; Raman & Bean, 1999; Zagha et al. 2008; Veys et al. 2013). The I h current is also important in determining the relationship between complex spike events and simple spike firing patterns (Loewenstein et al. 2005). It is possible therefore that the interactions between I h, Kv3.3 and resurgent sodium currents establish the relationship observed in the present study between complex spike spikelet number and simple spike rates.
Despite the varying simple spike firing frequencies observed prior to complex spikes with varying numbers of spikelets, our findings suggest that the simple spike rate appears to equalize to some extent after complex spikes, especially in the evoked condition where simple spike rates return to mean firing frequencies after complex spikes with each spikelet number despite the variations observed before. Simple spike activity is dependent on a balance between Na+ and K+ conductances (Llinas & Sugimori, 1980; Raman & Bean, 1997, 1999). Previous studies have shown that climbing fibres can control simple spike firing rate via the activation of Ca2+‐dependent K+ currents, as triggered by the rise in intracellular Ca2+ that occurs with climbing fibre activation (Tank et al. 1988; Eilers et al. 1995; Womack & Khodakhah, 2004; McKay et al. 2007; Rinaldo & Hansel, 2010). Variations in spikelet number could cause fluctuations in the level of intracellular Ca2+ and accompanying Ca2+‐dependent K+ currents, which in turn would govern the rate of Purkinje cell discharge.
Cerebellar circuit control of spikelet number and Purkinje cell activity
The evidence available to date suggests that the pause in simple spike firing that follows a complex spike, is driven by extrinsic events such as local interneurone activity (Granit and Phillips, 1956; Sato et al. 1992; Jörntell and Ekerot, 2003). And evidence indicates that this is driven by climbing fibre connections with molecular layer interneurones (Marshall and Lang, 2009; Mathews et al. 2012). In the present study, the number of spikelets was not found to correlate with pause duration; therefore, it follows that the regulation of spikelet number is probably a result of direct olivary network effects on the target Purkinje cells.
One alternative mechanism that could regulate spikelet number is the number of spikes in olivary bursts (Mathy et al. 2009; Bazzigaluppi et al. 2012), in addition to factors that alter the amplitude and/or phase of olivary subthreshold oscillations (Mathy et al. 2009; Bazzigaluppi et al. 2012; De Gruijl et al. 2012) and the synchronization of complex spikes (Lang et al. 2014). The cerebellar nuclei possess a population of inhibitory GABAergic neurones that project to the inferior olive (Andersson et al. 1988; Nelson & Mugnaini, 1989); thus, the olivo‐cortico‐nuclear projections form a closed loop, suggesting that simple spike activity, via its action on nucleo‐olivary neurones, could help determine spikelet numbers by altering the state of the inferior olive. Evidence that the simple spike activity of each cortical region does indeed help control its own complex spike activity was first provided as a result of the pharmacological manipulation of simple spike levels, which induced correlated changes in local complex spike firing rates and synchrony levels (Marshall and Lang 2009). Consistent with these findings, optogenetic stimulation of the nucleo‐olivary projection has been shown to cause a dampening or cessation of subthreshold oscillations and a reduction in the coupling of olivary cells (Lefler et al. 2014). Moreover, optogenetic activation of Purkinje cells was found to disinhibit the inferior olive, resulting in the subsequent activation of complex spikes with a latency of ∼100 ms (Chaumont et al. 2013; Witter et al. 2013). Thus, to some extent, Purkinje cell output can control afferent climbing fibre activity and thereby control complex spike spikelet number via the ionic mechanisms outlined above. Consistent with this, we observed a small peak in simple spike activity ∼100 ms prior to spontaneous complex spike events (Fig. 3 A). The combination of the current and previous results therefore suggests that cortico‐nucleo‐olivary loops are important in controlling complex spike activity. Moreover, changes in complex spike waveform (and spikelet content specifically) have been correlated with complex spike synchrony levels (Lang et al. 2014). Thus, Purkinje cells, via their influence on nucleo‐olivary neurones, may be capable of controlling spikelet number.
Miall et al. (1998) proposed that the ongoing activity of parallel fibres would, if left unchecked, lead to an ever increasing level of Purkinje cell simple spike firing. They suggested that complex spike activity in the absence of movement may have an ‘autocorrective’ effect, in that the increasing simple spike activity will increase climbing fibre activity via the cortico‐nuclear‐olivary loop. In support of this, high frequency stimulation of climbing fibres causes a reduction in simple spike firing rates and conversely, olive lesioning and the inhibition of complex spikes results in high rates of simple spike discharge (Colin et al. 1980; Rawson & Tilokskulchai, 1982; Cerminara and Rawson, 2004; Bengtsson and Hesslow, 2013). Moreover, variations in simple spike activity (both pharmacological and spontaneous) are correlated with changes in complex spike firing rates (Marshall and Lang, 2009). The present study supports this suggestion, and develops the concept by proposing that spikelet number may be an important determinant of the level of autocorrection. Complex spikes with higher numbers of spikelets were found to depress simple spike rates to a greater degree than those with fewer spikelets.
Function of spikelets
A variety of different functions have been proposed for the climbing fibre system, including the regulation of simple spike rates, a role in motor timing and a role in motor learning (Simpson et al. 1996). With respect to motor learning, complex spikes are assumed to represent an error or teaching signal (Ito, 2001) and recent studies have shown that the type of plasticity induced by complex spikes is dependent on the number of spikelets: a single climbing fibre impulse paired with parallel fibre stimulation results in long‐term potentiation, whereas bursts of climbing fibre impulses in conjunction with parallel fibre stimulation result in long‐term depression (Mathy et al. 2009). Graded climbing‐fibre induced calcium signals have also been observed in Purkinje cell dendrites in response to eye‐blink conditioning (Najafi et al. 2014), which may have implications for short‐ and long‐term plasticity. Indeed, behavioural studies have also shown that, during learning of smooth pursuit eye movements, simple spike activity undergoes trial‐by‐trial depression that is related to the duration of complex spikes (Yang & Lisberger, 2014). Furthermore, bursts of climbing fibre stimulation have been shown to result in the acquisition of Purkinje cell conditioned responses during eye blink conditioning, whereas single climbing fibre impulses cause extinction of the previously acquired response (Rasmussen et al. 2013). Taken together, these previous findings therefore suggest that spikelet number appears to be closely linked to learning processes in the cerebellum.
However, as outlined above, another possible function of complex spikes may be to regulate cerebellar cortical activity. Previous investigations have found that simple spikes evoked by peripheral sensory stimulation after the occurrence of a complex spike exhibit a short lasting (∼200 ms) enhancement in their responsiveness (Ebner et al. 1983; Ebner & Bloedel, 1984). Furthermore, Rawson and Tiloskulchai (1982) found that the intrinsic simple spike activity of Purkinje cells is suppressed by repetitive stimulation of climbing fibres, whereas simple spike responses evoked by parallel fibre stimulation were not. Taken together, these studies suggest that complex spikes produce a ‘gain change’ in simple spike activity to incoming signals (the gain change hypothesis; Ebner and Bloedel, 1981). The present study adds the possibility that spikelet number plays a role in determining simple spike activity levels. We found that simple spike rate during the rebound positively correlates with spikelet number; thus, complex spikes with greater numbers of spikelets result in higher transient increases in gain. This is followed by a subsequent return or a modest undershoot to baseline levels of simple spike activity. Spikelets could also lead to a reduction in intrinsic simple spike discharge such that extrinsic activity is accentuated. This is in line with recent studies indicating that complex spikes may have the capacity to multiplex (Ohmae & Medina, 2015); the number of spikelets in a complex spike may maintain Purkinje cells within their operational range at the same time as signalling extrinsic events related to cerebellar learning.
Additional information
Competing interests
The authors declare that they have no competing interests.
Funding
This work was supported by the MRC (RA, NLC), Wellcome Trust (AB, AKW, CH, RA) and the National Science Foundation (JX, TT, CH, EJL).
Author contributions
Experiments were performed at The University of Bristol and New York University. EJL, RA and NLC were responsible for the study design. AKW, JX, TT, EJL and NLC carried out the experiments. AB, JX, TT, CH, TT, CYS, EJL, RA and NLC analysed and interpreted the data. AB, RA and NLC drafted the paper. All authors revised the article critically for important intellectual content. All authors have approved the final version of the manuscript and agree to be accountable for all aspects of the work. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.
Contributor Information
Richard Apps, Email: r.apps@bristol.ac.uk.
Nadia L. Cerminara, Email: n.cerminara@bristol.ac.uk
References
- Andersson G, Garwicz M & Hesslow G (1988). Evidence for a GABA‐mediated cerebellar inhibition of the inferior olive in the cat. Exp Brain Res 72, 450–456. [DOI] [PubMed] [Google Scholar]
- Armstrong DM & Rawson JA (1979). Activity patterns of cerebellar cortical‐neurons and climbing fibre afferents in the awake cat. J Physiol 289, 425–448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bazzigaluppi P, Ruigrok T, Saisan P, De Zeeuw CI & de Jeu M (2012). Properties of the nucleo‐olivary pathway: an in vivo whole‐cell patch clamp study. PloS ONE 7, e46360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bell CC & Grimm RJ (1969). Discharge properties of purkinje cells recorded on single and double microelectrodes. J Neurophysiol 32, 1044‐&. [DOI] [PubMed] [Google Scholar]
- Bengtsson F & Hesslow G (2013). Feedback control in the olivo‐cerebellar loop In The Handbook of the Cerebellum and Cerebellar Disorders, eds. Manto MU, Gruol D, Schmahmann JD, Koibuchi N. & Rossi F, pp. 1079–1099. Springer, Dordrecht. [Google Scholar]
- Bosman LWJ, Koekkoek SKE, Shapiro J, Rijken BFM, Zandstra F, van der Ende B, Owens CB, Potters J‐W, de Gruijl JR, Ruigrok TJH & De Zeeuw CI (2010). Encoding of whisker input by cerebellar Purkinje cells. J Physiol 588, 3757–3783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell NC & Hesslow G (1986). The secondary spikes of climbing fibre responses recorded from Purkinje‐cell somata in cat cerebellum. J Physiol 377, 207–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cerminara NL, Apps R & Marple‐Horvat DE (2009). An internal model of a moving visual target in the lateral cerebellum. J Physiol 587, 429–442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cerminara NL, Lang EJ, Sillitoe RV & Apps R (2015). Redefining the cerebellar cortex as an assembly of non‐uniform Purkinje cell microcircuits. Nat Rev Neurosci 16, 79–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cerminara NL & Rawson JA (2004). Evidence that climbing fibres control an intrinsic spike generator in cerebellar Purkinje cells. J Neurosci 24, 4510–4517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaumont J, Guyon N, Valera AM, Dugue GP, Popa D, Marcaggi P, Gautheron V, Reibel‐Foisset S, Dieudonne S, Stephan A, Barrot M, Cassel J‐C, Dupont J‐L, Doussau F, Poulain B, Selimi F, Lena C & Isope P (2013). Clusters of cerebellar Purkinje cells control their afferent climbing fibre discharge. ProcNatl Acad Sci USA 110, 16223–16228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen S, Augustine GJ & Chadderton P (2016). The cerebellum linearly encodes whisker position during voluntary movement. Elife 5, e10509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colin F, Manil J & Desclin JC (1980). Olivocerebellar system .1. Delayed and slow inhibitory effects ‐ overlooked salient feature of cerebellar climbing fibres. Brain Res 187, 3–27. [DOI] [PubMed] [Google Scholar]
- De Gruijl JR, Bazzigaluppi P, de Jeu MTG & De Zeeuw CI (2012). Climbing fibre burst size and olivary sub‐threshold oscillations in a network setting. PloS Comput Biol 8, e1002814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ebner TJ & Bloedel JR (1981). Temporal patterning in simple spike discharge of Purkinje‐cells and its relationship to climbing fibre activity. J Neurophysiol 45, 933–947. [DOI] [PubMed] [Google Scholar]
- Ebner TJ & Bloedel JR (1984). Climbing fibre action on the responsiveness of Purkinje‐cells to parallel fibre inputs. Brain Res 309, 182–186. [DOI] [PubMed] [Google Scholar]
- Ebner TJ, Yu QX & Bloedel JR (1983). Increase in Purkinje‐cell gain associated with naturally activated climbing fibre input. J Neurophysiol 50, 205–219. [DOI] [PubMed] [Google Scholar]
- Eccles J (1967). The Cerebellum as a Neuronal Machine. Springer, New York, NY. [Google Scholar]
- Eccles JC, Llinas R & Sasaki K (1966. a). Excitatory synaptic action of climbing fibres on Purkinje cells of cerebellum. J Physiol 182, 268–296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eccles JC, Llinas R, Sasaki K & Voorhoev, PE (1966. b). Interaction experiments on responses evoked in Purkinje cells by climbing fibres. J Physiol 182, 297–315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eilers J, Augustine GJ & Konnerth A (1995). Subthreshold synaptic Ca2+ signalling in fine dendrites and spines of cerebellar Purkinje neurons. Nature 373, 155–158. [DOI] [PubMed] [Google Scholar]
- Gähwiler BH (1975). Effects of GABA, picrotoxin and bicuculline on spontaneous bioelectric activity of cultured cerebellar Purkinje‐cells. Brain Res 99, 85–95. [DOI] [PubMed] [Google Scholar]
- Gilbert PFC (1976). Simple spike frequency and number of secondary spikes in complex spike of cerebellar Purkinje‐cell. Brain Res 114, 334–338. [DOI] [PubMed] [Google Scholar]
- Granit R & Phillips CG (1956). Excitatory and inhibitory processes acting upon individual Purkinje cells of the cerebellum in cats. J Physiol 133, 520–547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hashimoto K & Kano M (1998). Presynaptic origin of paired‐pulse depression at climbing fibre Purkinje cell synapses in the rat cerebellum. J Physiol 506, 391–405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Häusser M & Clark BA (1997). Tonic synaptic inhibition modulates neuronal output pattern and spatiotemporal synaptic integration. Neuron 19, 665–678. [DOI] [PubMed] [Google Scholar]
- Hensbroek RA, Belton T, van Beugen BJ, Maruta J, Ruigrok TJH & Simpson JI (2014). Identifying Purkinje cells using only their spontaneous simple spike activity. J Neurosci Methods 232, 173–180. [DOI] [PubMed] [Google Scholar]
- Hurlock EC, McMahon A & Joho RH (2008). Purkinje‐cell‐restricted restoration of Kv3.3 function restores complex spikes and rescues motor coordination in Kcnc3 mutants. J Neurosci 28, 4640–4648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ito M (2001). Cerebellar long‐term depression: characterization, signal transduction, and functional roles. Physiol Rev 81, 1143–1195. [DOI] [PubMed] [Google Scholar]
- Jirenhed DA, Bengtsson F & Jörntell H (2013). Parallel fibre and climbing fibre responses in rat cerebellar cortical neurons in vivo. Front Syst Neurosci 7, 16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jörntell H & Ekerot CF (2003). Receptive field plasticity profoundly alters the cutaneous parallel fibre synaptic input to cerebellar interneurons in vivo. J Neurosci 23, 9620–9631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lang EJ, Tang T, Suh CY, Xiao J, Kotsurovskyy Y, Blenkinsop TA, Marshall SP & Sugihara I (2014). Modulation of Purkinje cell complex spike waveform by synchrony levels in the olivocerebellar system. Front Syst Neurosci 8, 210–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lefler Y, Yarom Y & Uusisaari MY (2014). Cerebellar inhibitory input to the inferior olive decreases electrical coupling and blocks subthreshold oscillations. Neuron 81, 1389–1400. [DOI] [PubMed] [Google Scholar]
- Llinas R & Sugimori M (1980). Electro‐physiological properties of in vitro Purkinje‐cell dendrites in mammalian cerebellar slices. J Physiol 305, 197–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loewenstein Y, Mahon S, Chadderton P, Kitamura K, Sompolinsky H, Yarom Y & Häusser MH (2005). Bistability of cerebellar Purkinje cells modulated by sensory stimulation. Nat Neurosci 8, 202–211. [DOI] [PubMed] [Google Scholar]
- Mano NI (1970). Changes of simple and complex spike activity of cerebellar Purkinje cells with sleep and waking. Science 170, 1325–1327. [DOI] [PubMed] [Google Scholar]
- Marshall SP, Lang EJ (2009). Local changes in the excitability of the cerebellar cortex produce spatially restricted changes in complex spike synchrony. J Neurosci 29, 14352–14362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maruta J, Hensbroek RA & Simpson JI (2007). Intraburst and interburst signalling by climbing fibres. J Neurosci 27, 11263–11270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathews PJ, Lee KH, Peng Z, Houser CR & Otis TS (2012). Effects of climbing fibre driven inhibition on Purkinje neuron spiking. J Neurosci 32, 17988–17997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathy A, Ho SSN, Davie JT, Duguid IC, Clark BA & Haeusser M (2009). Encoding of oscillations by axonal bursts in inferior olive neurons. Neuron 62, 388–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDevitt CJ, Ebner TJ & Bloedel JR (1982). The changes in Purkinje‐cell simple spike activity following spontaneous climbing fibre inputs. Brain Res 237, 484–491. [DOI] [PubMed] [Google Scholar]
- McKay BE, Engbers JDT, Mehaffey WH, Gordon GRJ, Molineux ML, Bains JS & Turner RW (2007). Climbing fibre discharge regulates cerebellar functions by controlling the intrinsic characteristics of Purkinje cell output. J Neurophysiol 97, 2590–2604. [DOI] [PubMed] [Google Scholar]
- Miall RC, Keating JG, Malkmus M & Thach WT (1998). Simple spike activity predicts occurrence of complex spikes in cerebellar Purkinje cells. Nat Neurosci 1, 13–15. [DOI] [PubMed] [Google Scholar]
- Miles OB, Cerminara NL & Marple‐Horvat DE (2006). Purkinje cells in the lateral cerebellum of the cat encode visual events and target motion during visually guided reaching. J Physiol 571, 619–637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montarolo PG, Palestini M & Strata P (1982). The Inhibitory effect of the olivocerebellar input on the cerebellar Purkinje‐cells in the rat. J Physiol 332, 187–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Najafi F, Giovannucci A, Wang SS & Medina JF (2014). Coding of stimulus strength via analog calcium signals in Purkinje cell dendrites of awake mice. Elife 3, e03663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson B & Mugnaini E (1989). Origins of GABA‐ergic inputs to the inferior olive In The Olivocerebellar System in Motor Control, ed. Strata P, pp. 86–107. Springer, Berlin. [Google Scholar]
- Ohmae S & Medina JF (2015). Climbing fibres encode a temporal‐difference prediction error during cerebellar learning in mice. Nat Neurosci 18, 1798–1803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paukert M, Huang YH, Tanaka K, Rothstein JD & Bergles DE (2010). Zones of enhanced glutamate release from climbing fibres in the mammalian cerebellum. J Neurosci 30, 7290–7299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raman IM & Bean BP (1997). Resurgent sodium current and action potential formation in dissociated cerebellar Purkinje neurons. J Neurosci 17, 4517–4526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raman IM & Bean BP (1999). Ionic currents underlying spontaneous action potentials in isolated cerebellar Purkinje neurons. J Neurosci 19, 1663–1674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raman IM, Sprunger LK, Meisler MH & Bean BP (1997). Altered subthreshold sodium currents and disrupted firing patterns in Purkinje neurons of Scn8a mutant mice. Neuron 19, 881–891. [DOI] [PubMed] [Google Scholar]
- Rasmussen A, Jirenhed D‐A, Wetmore DZ & Hesslow G (2014). Changes in complex spike activity during classical conditioning. Front Neural Circuits 8, 90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasmussen A, Jirenhed D‐A, Zucca R, Johansson F, Svensson P & Hesslow G (2013). Number of spikes in climbing fibres determines the direction of cerebellar learning. J Neurosci 33, 13436–13440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rawson JA & Tilokskulchai K (1982). Climbing fibre modification of cerebellar Purkinje‐cell responses to parallel fibre inputs. Brain Res 237, 492–497. [DOI] [PubMed] [Google Scholar]
- Rinaldo L & Hansel C (2010). Ataxias and cerebellar dysfunction: involvement of synaptic plasticity deficits? Funct Neurol 25, 135–139. [PMC free article] [PubMed] [Google Scholar]
- Sato Y, Miura A, Fushiki H & Kawasaki T (1992). Short‐term modulation of cerebellar Purkinje‐cell activity after spontaneous climbing fibre input. J Neurophysiol 68, 2051–2062. [DOI] [PubMed] [Google Scholar]
- Schmolesky MT, Weber JT, De Zeeuw CI & Hansel C (2002). The making of a complex spike: ionic composition and plasticity. Ann NY Acad Sci 978, 359–390. [DOI] [PubMed] [Google Scholar]
- Servais L, Bearzatto B, Hourez R, Dan B, Schiffmann SN & Cheron G (2004). Effect of simple spike firing mode on complex spike firing rate and waveform in cerebellar Purkinje cells in non‐anaesthetized mice. Neurosci Lett 367, 171–176. [DOI] [PubMed] [Google Scholar]
- Shin S‐L, Rotter S, Aertsen A & De Schutter E (2007). Stochastic description of complex and simple spike firing in cerebellar Purkinje cells. Eur J Neurosci 25, 785–794. [DOI] [PubMed] [Google Scholar]
- Simpson JI, Wylie DR & DeZeeuw CI (1996). On climbing fibre signals and their consequence(s). Behav Brain Sci 19, 384–398. [Google Scholar]
- Tank DW, Sugimori M, Connor JA & Llinas RR (1988). Spatially resolved calcium dynamics of mammalian Purkinje‐cells in cerebellar slice. Science 242, 773–777. [DOI] [PubMed] [Google Scholar]
- Thach WT (1967). Somatosensory receptive fields of single units in cat cerebellar cortex. J Neurophysiol 30, 675–696. [DOI] [PubMed] [Google Scholar]
- Veys K, Snyders D & De Schutter E (2013). Kv3.3b expression defines the shape of the complex spike in the Purkinje cell. Front Cell Neurosci 7, 205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warnaar P, Couto J, Negrello M, Junker M, Smilgin A, Ignashchenkova A, Giugliano M, Thier P & De Schutter E (2015). Duration of Purkinje cell complex spikes increases with their firing frequency. Front Cell Neurosci 9, 122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wise AK, Cerminara NL, Marple‐Horvat DE & Apps R (2010). Mechanisms of synchronous activity in cerebellar Purkinje cells. J Physiol 588, 2373–2390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witter L, Canto CB, Hoogland TM, de Gruijl JR & De Zeeuw CI (2013). Strength and timing of motor responses mediated by rebound firing in the cerebellar nuclei after Purkinje cell activation. Front Neural Circuits 7, 133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Womack MD & Khodakhah K (2004). Dendritic control of spontaneous bursting in cerebellar Purkinje cells. J Neurosci 24, 3511–3521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao J, Cerminara NL, Kotsurovskyy Y, Aoki H, Burroughs A, Wise AK, Luo Y, Marshall SP, Sugihara I, Apps R & Lang EJ (2014). Systematic regional variations in Purkinje cell spiking patterns. PloS ONE 9, e105633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y & Lisberger SG (2014). Purkinje‐cell plasticity and cerebellar motor learning are graded by complex‐spike duration. Nature 510, 529–532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zagha E, Lang EJ & Rudy B (2008). Kv3.3 channels at the Purkinje cell soma are necessary for generation of the classical complex spike waveform. J Neurosci 28, 1291–1300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou H, Lin Z, Voges K, Ju C, Gao Z, Bosman LWJ, Ruigrok TJ, Hoebeek FE, De Zeeuw CI & Schonewille M (2014). Cerebellar modules operate at different frequencies. Elife 3, e02536. [DOI] [PMC free article] [PubMed] [Google Scholar]


