Abstract
Heterogeneity is well recognized as a common property of cellular systems that impacts biomedical research and the development of therapeutics and diagnostics. Several studies have shown that analysis of heterogeneity: gives insight into mechanisms of action of perturbagens; can be used to predict optimal combination therapies; and to quantify heterogeneity in tumors where heterogeneity is believed to be associated with adaptation and resistance. Cytometry methods including high content screening (HCS), high throughput microscopy, flow cytometry, mass spec imaging and digital pathology capture cell level data for populations of cells. However it is often assumed that the population response is normally distributed and therefore that the average adequately describes the results. A deeper understanding of the results of the measurements and more effective comparison of perturbagen effects requires analysis that takes into account the distribution of the measurements, i.e. the heterogeneity. However, the reproducibility of heterogeneous data collected on different days, and in different plates/slides has not previously been evaluated. Here we show that conventional assay quality metrics alone are not adequate for quality control of the heterogeneity in the data. To address this need, we demonstrate the use of the Kolmogorov-Smirnov statistic as a metric for monitoring the reproducibility of heterogeneity in an SAR screen, describe a workflow for quality control in heterogeneity analysis. One major challenge in high throughput biology is the evaluation and interpretation of heterogeneity in thousands of samples, such as compounds in a cell-based screen. In this study we also demonstrate that three heterogeneity indices previously reported, capture the shapes of the distributions and provide a means to filter and browse big data sets of cellular distributions in order to compare and identify distributions of interest. These metrics and methods are presented as a workflow for analysis of heterogeneity in large scale biology projects.
Keywords: Heterogeneity, phenotypic profiling, high content screening, systems biology, drug discovery
1 Introduction
Heterogeneity is a property of cellular systems that implies the presence of cell-to-cell variability with respect to one or more measurable traits (phenotypes) at the molecular-cellular level. Because heterogeneity is a property of the population of cells, it can be complex and therefore difficult to characterize as a single parameter. Large scale biology projects typically span many days or even months, and non-biological variation in heterogeneity over the course of a study could mask the true biological heterogeneity, suggesting the need for quality control. The details of the distributions of a trait can be visualized as a histogram of the cell population, but visualization of the large numbers of histograms generated in high throughput phenotypic screens is not practical without appropriate informatics tools, and qualitative comparisons are not sufficient for quality control. In this chapter we present a simple metric for quality control of heterogeneity, and an approach to evaluating heterogeneity in large-scale biology and drug discovery programs consisting of measurements on thousands to millions of samples, which can be applied to High Content Screening, High Throughput Microscopy, flow cytometry, digital pathology or any method that generates large datasets of cells [1-6].
1.1 Implications of cellular heterogeneity in biomedical research, drug discovery and diagnostics
It is now well established that cellular heterogeneity is an intrinsic feature observed in cell systems, even when composed of isogenic populations of cells. Cell-to-cell variability is not simply the result of intrinsic noise in molecular networks; rather it is often the result of deterministic regulatory molecular mechanisms that remain largely uncharacterized [7-9]. There is growing evidence that some heterogeneity is related to physiological and evolutionary adaptations to new challenges [10, 11]. A recent study suggests that heterogeneity can be decomposed into different groups of biomarkers that are consistent with known signaling pathways, implying a mechanistic basis for the cell-to-cell variation [12]. It has also been shown that patterns of signaling heterogeneity can distinguish cellular populations with different drug sensitivities [13, 14]. It has been proposed that combination therapies can be devised through computational analysis of heterogeneity [15]. Furthermore, the association between cellular heterogeneity and adaptation [10] suggests that ignoring the heterogeneity in the cellular response may lead to the selection of compounds to which cells will rapidly adapt, leading to a loss of efficacy in drug development programs. Thus, it is important to incorporate heterogeneity analysis in large scale screens in drug discovery, and phenotypic profiles in basic biomedical research, where the goal is to relate a cellular phenotype with some condition, such as a disease state, compound effect, protein knockdown, or other sample state or treatment.
Pluripotent stem cells are a platform with tremendous potential for development of patient specific disease models, for modeling biological development, and for regenerative medicine. However, stem cells exhibit heterogeneity on several levels: in the functional capacity to differentiate; in mRNA expression profiles; and in epigenetic and genetic state [16]. Studies of differentiating cells have found that heterogeneity reflects the presence of an evolving mixture of phenotypically distinct subpopulations, consistent with a hypothesis that differentiating cells transit through multiple robust and discrete phenotypic states [17-19]. Improved understanding and manipulation of the differentiation of stem cells will require tools to reliably characterize and monitor the evolution of the distributions of these subpopulations and their associated phenotypes.
In typical cell-based phenotypic assays, compound activity is characterized by the well average value of a feature or a combination of features, but the cell level data is usually ignored in order to achieve higher throughput. Metrics have been developed to address assay variability for large scale screens/profiles including signal-to-background and Z’-factor for inter-plate and inter-day variability [20-22]. However, these metrics do not address the biological heterogeneity present in individual cell populations. Therefore, new tools and criteria are required for analyzing and comparing biological heterogeneity in large scale screens/profiles, and for sorting and identifying perturbagens with potentially interesting or novel effects on the distribution of cell response among a large number of patterns of cellular activity. Measuring heterogeneity is particularly important when applying quantitative systems pharmacology (QSP) to drug discovery programs. A key tenet of our implementation of QSP is the need to have the phenotypic assays that reflect the heterogeneity in patients as determined by a range of “omics” profiles.
1.2 Challenges in the Analysis and Interpretation of Heterogeneity in High Content Phenotypic Screens/Profiles
There are several challenges to large scale analysis of heterogeneity and the comparison of heterogeneity between samples, assay runs, and laboratories. These challenges include: 1) large size and complexity of the cell level data in high content screens/profiles; 2) lack of a standard approach to quality control in measuring heterogeneity; 3) lack of standards for the characterization of the assay and detection system contributions to the measured heterogeneity; and 4) lack of adequate tools to quickly quantify, compare, review and interpret heterogeneous responses.
In large scale analysis of biological activity taking the average of a population is a quick way to reduce the data to a size that can be more easily managed, filtered and interpreted, but neglects the information contained in the distribution of cellular responses. The complexity of the cell distributions and the lack of a standard analytical approach for interpreting heterogeneity remains a barrier to incorporating such analyses into a project, despite evidence that investigation of heterogeneity leads to new insights into the underlying cellular functions [23, 24]. Analyzing all the cellular data in a compound screen, RNAi screen, genome-wide mutagenesis [25] or other large biology project is a “big data” problem that has not been adequately addressed. For a screen of 100,000 compounds and 1,000 cells/well there will be 100 million data points for each feature (potentially 4-20 or many more) measured in the screen. Similarly, an SAR of ~240 compounds with 10 concentrations, triplicate wells, duplicate runs and ≥ 1,000 cells/well, such as the data set evaluated in this chapter, can easily amount to well over 10 million cells. Data that is well organized in a database may be easily extracted by query, but efficiently analyzing 30-500 million or more data points acquired over several months for patterns in population distributions at least requires some thought and planning, and tools for manipulating and comparing distributions. In this chapter we present an approach to that process.
A second challenge in the heterogeneity analysis is quality control. The standardization of quality control in high throughput screening through the use of the Z’-factor [22, 26], or the strictly standardized mean difference [27], has enabled comparison of assay performance over a wide range of assay types, routine monitoring of assay performance during a screen, and a statistical basis for understanding the impact of assay variability on the selection of hits from a screen. For dose-response assays, the V-factor, a generalization of the Z-factor, provides a robust QC measure that takes into account the complete dose-response, rather than just the maximum and minimum response [21, 28]. To be able to compare cellular heterogeneity in order to interpret the biological meaning, standards and quality control are needed to ensure reproducibility. Present assay development guidelines for high content phenotypic screens address metrics for assay variability [20, 21], but do not address the reproducibility of the distributions within the wells. The normalization of well average data to on plate controls adequately corrects for plate-to-plate variability at the well level but is not typically applied to the cell level data. It is important to emphasize that in typical use, good Z’-factors do not necessarily indicate that the cellular distributions (i.e. heterogeneity) within the wells are consistent from plate-to-plate, as we demonstrate here.
A third challenge in heterogeneity analysis is the lack of reference standards for calibration or characterization of most high content methods and in particular phenotypic methods. For example, in HCS spatial or temporal variation of illumination intensity or detection sensitivity can contribute “detection system variation” to the measured values. While approaches to detection system calibration and characterization have been published [14, 29-31], so far standards such as those routinely used in flow cytometry [32] have not been widely adopted in imaging. Typically in screening, each plate will be normalized to the control wells [20, 21]. This approach compensates for the average signal level on each plate; however, to compare distributions from plate-to-plate also requires normalization of the cell level data between plates. Optimally, attention to protocols during assay development, validation and screening/profiling can minimize the variation from plate-to-plate. Here we demonstrate that normalization can be an effective means to compensate for plate-to-plate variation in the range of intensities, but not necessarily the variation in the shape of the distributions. Although there are many published reports of heterogeneity in cellular systems, the measurements have been made using different methods and each laboratory has taken a different approach to characterizing the heterogeneity [3, 14, 33-35]. As a result, there are no established metrics for heterogeneity. The methods developed and presented here are based on analysis of the distributions of the cellular features and should therefore, be generally applicable to any measurement which captures the cell-to-cell variation in a parameter(s). In this chapter we suggest a workflow for quality control of the heterogeneity in phenotypic assays and metrics for monitoring heterogeneity from plate-to-plate.
A final challenge is to quickly quantify, compare, review and interpret large numbers samples which exhibit varying heterogeneity in cellular responses. One approach has been to segment the population into discrete subpopulations using Gaussian mixture models or k-means clustering which effectively reduce the scale of the data [12, 36]. This approach can be effective when discrete subpopulations can be identified, but may not be effective in large scale projects where the changes in heterogeneity may be more subtle, or the heterogeneity may be more complex. An alternative approach is to characterize the heterogeneity using shape parameters [14, 34]. This approach makes no assumptions about the shape of the distribution, or the number of subpopulations, but does not provide the detailed segmentation of the cell population. Here we demonstrate the use of a general set of heterogeneity indices, in combination with an informatics tool in a workflow that organizes large numbers of distributions to compare and identify subsets of interest. This approach enables analysis of heterogeneity on a large scale, and could also be used to identify distributions that would benefit from more detailed segmentation analysis.
2 Material and methods
2.1 Sample preparation
Reagents and Cells
Formaldehyde (37%), Triton X-100, and Tween 20 were purchased from Sigma-Aldrich (St. Louis, MO). Recombinant human interleukin-6 (IL-6) was purchased from R & D Systems, Inc. (Minneapolis, MN). Mouse monoclonal anti-pSTAT3-Y705 (Cat# 612357) primary antibodies were purchased from Becton Dickenson Biosciences (San Diego, CA). The secondary goat anti mouse-IgG conjugated with Alexa Fluor 488 (Cat# A11001) was purchased from Life Technologies (Grand Island, NY). Hoechst 33342 was purchased from Invitrogen (Eugene, OR). Black, clear bottom, 384 well HCS Assay Plates (Cat# 781091) were purchased from Greiner Bio-One (Monroe, NC). Cal33 human head and neck squamous cell carcinoma (HNSCC) cells [37, 38] were kindly provided by Dr. Gerard Milano (University of Nice, Nice, France). The cell line was maintained in Dulbecco’s modified Eagle’s medium (DMEM, Life Technologies) supplemented with 10% fetal bovine serum (Gemini Bio-Products, West Sacramento, CA), 100 U/ml penicillin and 100 mg/ml streptomycin (HyClone, Logan, UT). Cells were maintained in humidified incubators at 37°C with 5% CO2.
Compound Dilutions
Compounds were tested as 10-point, 3-fold serial dilutions over a range from 50 μM-2.5nM (except as noted), in triplicate on the plate, and in duplicate runs. Master compound dilutions were prepared from 10 mM stock concentrations (except as noted for specific compounds) in DMSO in 384 well plates by serial dilution into 100% DMSO on the Bravo liquid handling platform (Velocity11, Menlo Park, CA). Replicate daughter plates containing 2 μL of the serially diluted compounds were prepared using a 384-well transfer on the Bravo. Aluminum adhesive plate seals were applied and plates were stored at −20°C. Each assay plate included 32 negative (+IL-6) and 32 positive (−IL-6) control wells which were used to calculate the Z’-factor and for normalization.
Assay Plate Processing
Cal33 cells were seeded in 384-well plates using a MultiDrop (Thermo Scientific) to dispense 2000 cells in 40 μL/well to reach 50% confluence on the day of fixation. The cells were incubated at 37°C for 24 hours, then the medium was replaced with serum free medium and the cells were incubated for another 24 hours. To establish the optimal IL-6 concentration, STAT3 phosphorylation was induced by IL-6 in a 2-fold serial dilution for 10 final concentrations descending from 100 ng/mL. For inhibition of STAT3 phosphorylation, compound daughter plates were withdrawn from storage, thawed in a 37°C dry oven, centrifuged for 1–2 min at 50 × g, and the plate seals were removed. Intermediate dilution plates were generated using a Matrix pipette to transfer 38 mL of serum free medium (SFM) into the wells of the daughter plates. The diluted compounds were mixed by repeated aspirate-dispense cycles on the Bravo, and then 5 μL of diluted compound was transferred into the assay plates. After 3 hours of compound incubation at 37°C, 5 μL of a 10x stock solution of IL-6 was added using the Bravo for a final concentration of 50 ng/mL, and the plates were spun at 50 × g for 1 minute then incubated for 14 minutes. The plates were fixed by the addition of 50 μL of 7.4% paraformaldehyde (37°C) containing 4 μg/mL Hoechst 33342 in PBS using the Elx405 plate washer dispenser (BioTek, Winooski, VT). After 30 min at room temperature (RT), the fixed cells were washed twice with 80 μL PBS. PBS was aspirated, and the fixed cells were permeabilized by the addition of 50 μL of 95% ice-cold methanol. After 30 min on ice, the 95%methanol was removed from the assay plates and the cell monolayers were washed twice with Tween 20 blocking buffer, and then incubated for 30 min at RT in blocking buffer. 24.5 μL of a 1:100 dilution of mouse anti-pSTAT3-Y705 primary antibody was added using a Matrix pipette and incubated for 1 h at RT in the dark. After washing twice with blocking buffer on the plate washer, the plates were incubated 15 min. at RT, the buffer was aspirated and 24.5 μL of a 1:1000 dilution of the secondary antibody added with a Matrix pipette and incubated for 1 h at RT in the dark. The plates were then washed twice with 80 μL PBS, sealed with foil and stored at 4°C.
2.2 High Content Screening
Images were collected on the ImageXpress Ultra (IXU) (Molecular Devices LLC, Sunnyvale, CA) a point-scanning confocal HCS platform. The IXU was used to sequentially acquire two fluorescence channels, Hoechst (Ch1) and Alexa 488 (Ch2), for 2 fields per well using a 20x (0.45-NA) ELWD objective. The Hoechst channel was excited using the 405nm laser at 10% power with emission at 447±60nm, and the Alexa488 channel used the 488nm laser at 10% power with emission at 514±17nm. Pixels were binned by 2 with 2000 scan lines collected over an area 800x800um. Image analysis was carried out using the Translocation Enhanced (TE) application in the MetaExpress software (Molecular Devices LLC, Sunnyvale, CA) as follows. The nuclear compartment was identified in Ch1 with a threshold intensity of 1500 above background and an area of 20-1000μm2 with auto separation of touching compartments (the nuclear mask). Analysis of the distributions of nuclear intensities on all of the plates in this data set showed that although there was some variation in the range of intensities from plate-to-plate the vast majority of nuclei on all the plates had average intensities that were well above the threshold used to segment the images, resulting in consistent nuclear regions. The nuclear mask was eroded 1μm to avoid edge effects and to create the Inner region mask in Ch2. The activation of STAT3 in each cell was measured as the Mean Inner IntensityCh2 (MII) of the Alexa 488 label within the Inner region mask in Ch2. For each well the average STAT3 activity was calculated as the average of the MII for all the cells in the well. All the calculated cell and well features were automatically stored in the MDCStore (Molecular Devices, Sunnyvale, CA) SQL-Server (Microsoft, Redmond, WA) database. For the analyses presented here, the data were extracted directly into Spotfire (TIBCO, Boston, MA) using SQL queries.
2.3 Quality Control
2.3.1 Assay Quality Control
On each plate, columns 1,2,23 and 24 were used for a total of 32 negative and 32 positive control wells, split equally in each column. The assay parameter for the negative and positive control wells, MII, was used to calculate the Z’-factor [22] and the signal-to-background (S/B = Mean[Well Average MII(negative control)]/Mean[Well Average MII(positive control)]) for each plate. During the screen plates with a Z’<0.3, or S/B<5 were rejected. There were 117 plates (384 well) that passed the QC for the screen, with a Z’≥ 0.3, and a S/B≥5.
2.3.2 Heterogeneity Quality Control
Normalization
We normalized the cell level data in each well to a common median to minimize the variation in the cellular distributions across the 117 plates in this data set that is related to sample preparation, image acquisition and/or algorithm performance. We maintained a nominal assay scale by normalizing to a reference distribution. We selected 8 plates to use as a virtual ‘validation’ plate set and pooled the cell level data from the negative control wells to establish the reference distribution and the normalization value. The median of the reference distribution was used for normalization of the plates. Since the positive control in this assay was no stimulation with IL-6, resulting in essentially no pSTAT3 signal above background, single point normalization to the median in the reference distribution from the validation plates was used as follows:
| (1) |
where MII () is the measured value of cell i on plate p, Median(MII (ref)) is the median MII of the reference distribution, and Median() is the median value of the pooled cells in the negative control wells on plate p.
Quality Control Metric
To measure the plate-to-plate reproducibility of the heterogeneity in the cellular responses, we compared the cellular distributions in the negative control wells on all plates to reference distributions from the selected ‘validation’ plates using the Matlab function ‘kstest2()’ to calculate the Kolmogorov-Smirnov (KS) statistic as a quality control metric (QC-KS):
| (2) |
where is the cumulative distribution function of the distribution of the MII in a negative control well w on plate p and CDFref is the cumulative distribution function for the reference distribution. The use of the KS statistic as a very general assay parameter is well known in HCS [39-44], but here we use it for quality control. To establish a QC-KS threshold we used the median(QC-KS) + 3*K*MAD for the pooled control wells on all the plates in this data set, where MAD is the median absolute deviation of the QC-KS value for the plates and K = σ/MAD for a normal distribution (1.4286). To gain insight into the variation in the distributions we evaluated 5 additional metrics for potential correlation with the pass/fail scoring of the plates, Cell Count, %Active, and three previously published heterogeneity indices (HIs), the quadratic entropy (QE), non-normality (nNRM) and percent outliers (%OL) [14]. Cell count was provided by the imaging algorithm as a nuclear count in Ch1, and %Active was calculated as the percent of cells with MII > 3 standard deviations above the MII of the positive control in Ch2 on the same plate.
2.4 Indices of Heterogeneity
2.4.1 Selection of the Heterogeneity Indices
A primary goal in the quantitation of heterogeneity was to select indices that reflect properties of the distribution that could be related to the underlying biology. The selected indices reflect: 1) the overall diversity in the cell population, QE; 2) the presence of subpopulations, nNRM; and 3) the number of outlier cells, %OL. We selected the quadratic entropy (QE) as a measure of cellular diversity that incorporates information not only on the number of different phenotypes, but also the magnitude of the differences between phenotypes [46, 47]. The QE has been shown to be useful in quantitation of the cellular diversity in cancer tissue sections for diagnostic applications [34].
To identify the presence of subpopulations (macro-heterogeneity as defined by Huang [7]) we adopted a measure of Normality. The nNRM index uses the KS statistic as a measure of the difference between the test distribution and a Normal distribution with the same mean and standard deviation. As a result, the nNRM value is 0 for a Normal distribution and increases with increasing deviation from a Normal distribution, as would be expected for subpopulations with distinct phenotypes. Examples of macro-heterogeneity include the distinct states of progenitor vs. differentiated cells, the phases of the cell cycle and the time dependent changes in the intracellular distribution of proteins such as transcription factors.
The %OL indicates the presence of outlier cells that respond distinctly from the majority, which is expected to be important in the development of therapeutics, where a small number of resistant sub-clones may exist prior to treatment, and potentially result in high rates of relapse [49]. The %OL index is based on the standard statistical definition of outliers used in box plots.
2.4.2 Calculation of Heterogeneity Indices
The three HIs were defined previously, as were the methods used for calculation [14]. The three HIs are defined by the following equations:
| (3) |
| (4) |
| (5) |
In equation (3) dij is a distance matrix that linearly weights the product of the subpopulation probabilities, pi and pj, by the magnitude of the intensity difference. In equation (4) CDFwell is the cumulative distribution in a test well, and CDFnorm is the cumulative distribution function for a normal distribution with the same mean and variance as the cells in the test well. In equation (5) Count(LIF:UIF) is the count of cells in the range from the lower inner fence to the upper inner fence, as defined for a standard box plot, and N is the total number of cells in the distribution. The HIs were calculated using a Matlab script.
2.5 Measuring the performance of the HIs
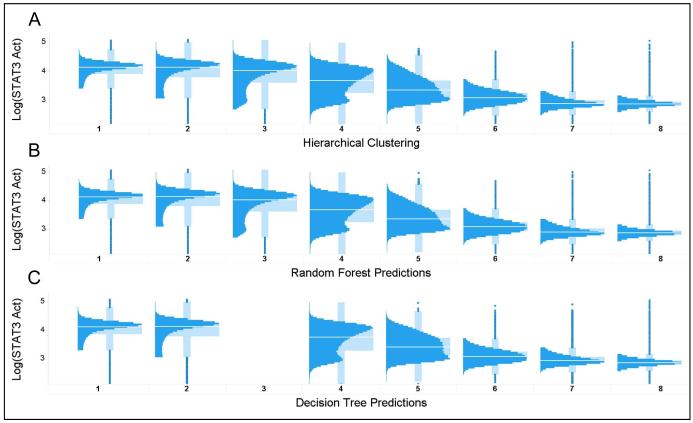
To evaluate the performance of the HIs in distinguishing distributions, two classifiers were developed to predict 8 target distributions using only the HIs as inputs. The 8 target distributions were constructed by hierarchical clustering of the distributions from 19 plates with standard compounds. The distributions were binned into 30 equal intensity ranges and then clustered using the Matlab function clusterdata. The minimum similarity threshold was adjusted to give the 8 distributions with the highest similarity. The Random Forest (RF) and Binary Decision Tree (BTree) models were constructed using the R[50] package rattle [51]. The input data had 585 observations and the parameters for the Random Forest model were Number of Trees=500, Number of Variables (at each split)=1 and for the BTree model were Min Split=20, Min Bucket=7, Max Depth=30 and Complexity=0.01, which resulted in a tree with 8 nodes and a depth of 5.
2.6 Visualization of distributions
The cellular distributions in Figures 1, 2, 4 and 5 are presented as histo-box plots as previously discussed [14]. The histo-box plots were generated in Spotfire (TIBCO, Boston, MA) by overlaying the histogram of intensity (vertical axis) on a conventional box plot, a standard feature in the boxplot graphic in Spotfire.
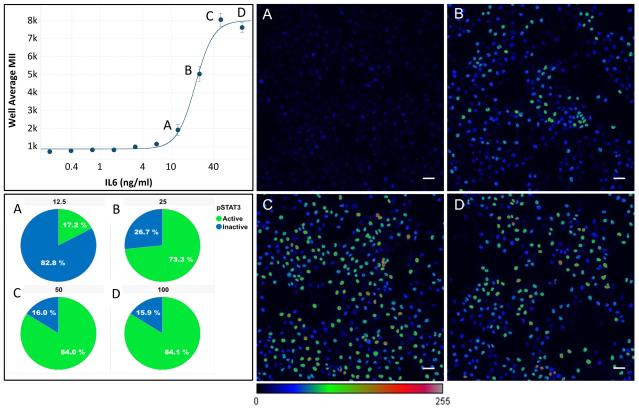
Figure 1.
Dose response characterization of the activation of STAT3 by IL-6. The graph shows the activation of STAT3 by two-fold serial dilutions of IL-6 starting at 100 ng/mL. A-D) Images of STAT3 labeling illustrate the high level of variation in STAT3 activation at concentrations from (A) 12.5 ng/mL to (D).100 ng/mL. Original images were all scaled to a dynamic range of 100-40,000, then converted to 8-bit and pseudo-colored using the color lookup table shown. Cells with a labeling intensity ≥ Mean(positive control) + 3 Stdev(positive control) are considered Activated, and the % Activated cells is shown in the pie charts.
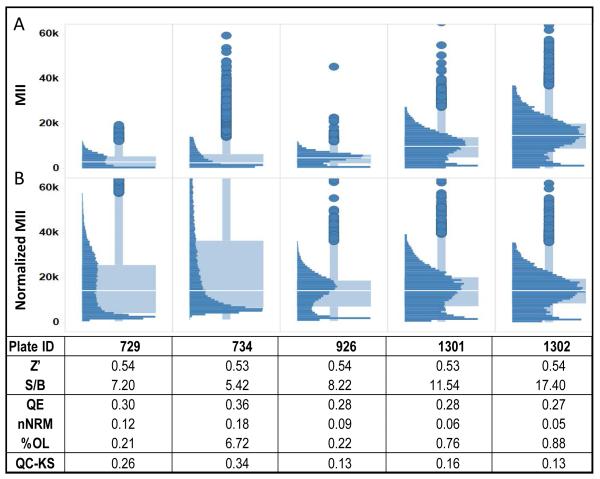
Figure 2.
Standard assay quality measures are not sufficient for assessing the reproducibility of heterogeneity. Similar Z’-factors indicate consistent well-to-well assay reproducibility across plates but provide no indication of the variability of cellular response distributions. Even after plate-to-plate normalization there remains variation in the shapes of the distributions. Comparison of the cellular distributions of STAT3 activity in the IL-6+ control wells on five plates with essentially the same Z’-factor shows that the distributions can be very different from plate-to-plate. The S/B of the assay does give some indication of variation in the range of the data. As a result, the heterogeneity indices, QE, nNRM and %OL vary from plate-to-plate, with Plate 734 having the largest deviations. The QC-KS value provides a quantitative measure of the deviation of the distribution from the reference distributions established during assay validation. In this case, Plates 926 and 1302 have the lowest deviation (0.13) from the validation distributions.
Figure 4.
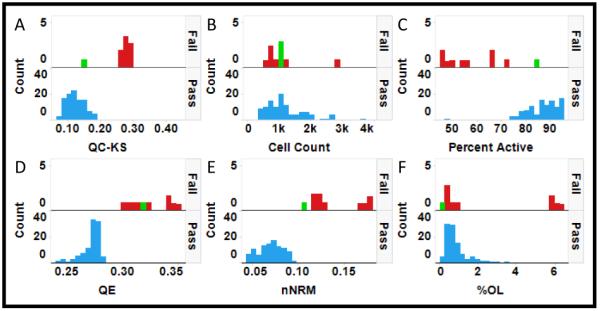
Selection of a QC metric of reproducibility in heterogeneity analysis. Each pair of histograms (A-F) indicates the distribution of plates labeled as Fail (red) or Pass (blue). A single Failed plate (888) with a clipped distribution is highlighted in green for reference. A) The KS statistic, QC-KS, provides a clear interpretation and good discrimination between Pass and Fail, except for plate 888. B) Although cell count might contribute to the distribution of cellular response on a plate, in this case there is no significant difference in cell count between Passed and Failed plates. C) Differences in the percent activated cells also might result in variation in the distributions, and that does appear to be the case in this assay. D) The Failed plates have a much broader distribution as indicated by the increase in QE. E) The Failed plates have a less normal distribution as indicated by the increased nNRM. F) Some of the Failed plates have an increased number of outliers indicated by the increased %OL.
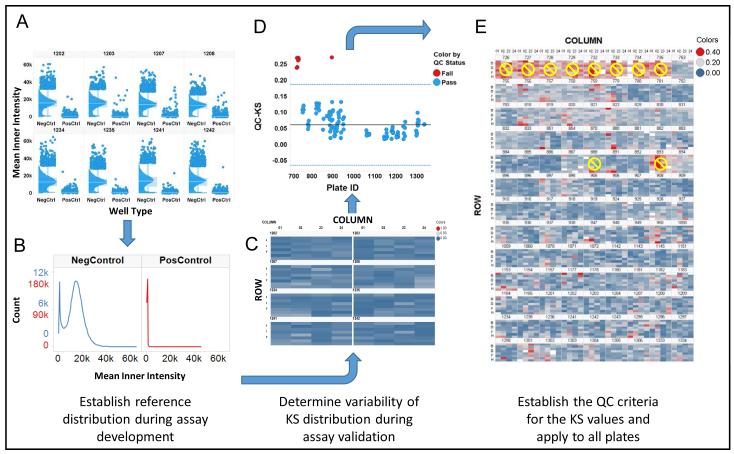
Figure 5.
Quality Control workflow for heterogeneity analysis. A. To establish and quality control heterogeneity in high throughput imaging projects, the distributions in the control wells are evaluated during validation to assess the reproducibility of the heterogeneity. B. The distributions from the control wells on the validation plates are pooled to establish reference distributions. C. Each control well on the validation plates is compared with the reference distribution using the KS statistic (QC-KS), results are shown here as a heatmap, to quantitatively assess reproducibility. D. The QC-KS statistic is used to monitor the distributions during a screening campaign. The solid horizontal line is the median(QC-KS), and the dashed lines represent the median ± 3*MAD*K, the selected QC limit. E. The heatmap of the control wells on all the plates shows the variation in the QC-KS values from well-to-well and plate-to-plate, and the 10 plates that were Failed. In a new project, the Failed plates would be flagged for review.
2.7 Informatics tool for reviewing and comparing heterogeneity in large scale screens/profiles
The browser shown in Figure 8 was developed as a dashboard in Spotfire that combines visualizations of the cell level data along with the well level data. The views are linked so that the data selected in one view is also selected in all other views. The browser is available for non-commercial use from the authors as a Spotfire file with example data.
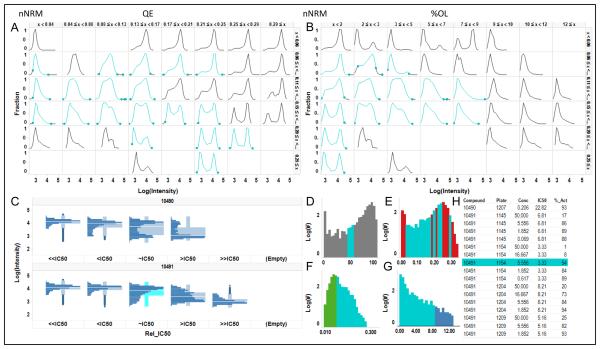
Figure 8.
Heterogeneity Browser for High Throughput Cytometry. The filtering concept in Figure 7 was expanded into an interactive Heterogeneity Browser in which the cellular heterogeneity in the wells can be identified and reviewed in a variety of ways. All data in the browser is linked, so that selection of data in one graph highlights the data in all other graphs. Here, the distributions with %Activation=45-55% have been selected in D, and are highlighted in cyan in all the views. A. 2D matrix of distributions with increasing QE index on the horizontal axis and increasing normality (decreasing nNRM) on the vertical axis. B. 2D matrix with increasing % OL on the horizontal axis and again decreasing nNRM on the vertical axis. C. The dose-response of distributions for a two compounds. The interface allows scrolling through all the compounds in the selection. D-G. Histograms of the percent activated cells and the 3 HIs for the pooled replicate wells over the whole data set. D. % activated cells. E. QE index. F. nNRM index. G. %OL index. H. List of all compounds highlighting one in the current selection.
3 Results and Discussion
3.1 The need for quality control for heterogeneity analysis in screens/profiles
It is important in heterogeneity analysis to clearly distinguish between detection system or assay variability and biological heterogeneity. In imaging based systems, such as HCS, spatial variation of illumination intensity or detection sensitivity (or both), often seen as reduced intensity in the corners, can contribute to apparent variation in the cell-to-cell measurements. Methods for correcting non-uniform illumination or detection sensitivity are available [52, 53], but often are not used because variation across the field, especially when it is stable from field-to-field, has little impact on the population average values that are most often used as assay readouts. However, for heterogeneity analysis it is important to understand the impact of the detection system on cell-to-cell variation. Comparative studies between imaging and flow cytometry that established the reproducibility limit for this assay on a wide field HCS system were previously reported (see for example Figure S3 in [14]). Because this was a retrospective study we were not able to correct images from the IXU prior to data extraction. However, because point scanning laser confocal systems like the IXU scan a stabilized laser light source to each pixel, in general illumination uniformity is less of an issue than in wide field systems. Comparison of the cell distributions from the control wells collected on the IXU with previously published distributions collected on intensity corrected images from a wide field HCS system showed that they were essentially the same, suggesting comparable performance for the two detection systems.
The standard metrics used for assay quality control in screening are designed to measure the well-to-well, plate-to-plate and day-to-day repeatability of the well level assay features (e.g. average or total intensity, area, etc.), but do not indicate anything about the distribution of cellular responses within the well. To evaluate reproducibility for the heterogeneity in the individual cellular responses, we used data from a high content, cell-based, phenotypic SAR screen of compounds that inhibit STAT3 activation by IL-6. The data set consisted of 117 microplates (384 wells) with triplicate, 10 point, 3-fold dilutions of 261 compounds, some of which were run multiple times. In this screen plates with a Z’ < 0.3 or a S/B < 5 were failed and repeated. The concentration of IL-6 used for this screen, 50 ng/mL, was selected to produce a maximal activation of STAT3 without an excess of IL-6. Figure 1 shows the dose-response of STAT3 to IL-6. The selected concentration (1C) results in significant variation in the activation of STAT3 that can be seen in image C, with 84% activation (1, Pie Chart C). The higher concentration of 100 ng/mL (1D) produced similar heterogeneity in the image (1D) and %Activation (1, Pie Chart D), indicating that 50 ng/mL IL-6 was sufficiently near the maximum value.
Evaluation of population distributions in the +IL-6 control wells on these plates indicated there was significant variability, independent of the Z’-factor (Figure 2). Figure 2A shows the raw MII of the IL-6 induced cells in the negative control wells. The distributions clearly vary in the range of intensities. After normalization of the intensity range to the median of the reference distribution (Figure 2B), the median MII is the same for all five plates but there are clearly some differences in the shapes of the distributions. For example, plate 734 lacks the peak of STAT3 activity around 20K that is obvious on plates 928, 1301 and 1302. Plate 729 has a smaller peak at an intensity of just over 20K. There are some differences in the S/B measured during the course of the screen that are perhaps indicative of the differences in the distributions, but because the S/B>5 on all the plates, no distinction was made between them during the screen. We calculated the three HIs for these five plates to evaluate the potential impact of this variability on measurements of heterogeneity. On plate 734 the QE, NRM, and %OL are all much higher, indicating a broader distribution that is less normal and has more outliers than the other plates. Plate 729 also has a somewhat different distribution when compared with plates 928, 1301 and 1302; however the differences in the HIs on this plate are lower, as might be expected, with only the nNRM indicating a substantial difference in normality. The variation in these distributions and measured HIs suggested a need for a QC metric to quantitate the reproducibility of the cellular distributions on the plates. Because the KS statistic is designed for comparing distributions, we adopted it as a new metric, the quality control-KS (QC-KS) that, as described below and can be easily used to monitor the population distributions over time in large scale biology projects.
3.2 Workflow for quality control of heterogeneity in phenotypic screens/profiles
It is clear from Figure 2, that a similar Z’-factor does not imply consistency in cell level distributions from plate-to-plate. It is important though to note that the high reproducibility of this assay, as indicated by a robust Z’-factor, suggested that good reproducibility in the distributions could be achieved, as was the case here. Optimally, the data acquisition would be controlled to minimize variation in the assay data range and allow comparison of biological heterogeneity across plates, and especially over long times, however, here it was essential to normalize the data prior to applying the quality control.
To correct for the plate-to-plate variation in the intensity range, the data from each well was normalized to the reference distribution using equation 1. The resulting normalized distributions for the +IL-6 controls on all 117 plates are shown in Figure 3. After normalization the median of the distributions were consistent, although there were still small differences in the shapes of some of the distributions. A component of those differences is in the relative height of the activated cells (upper peak) vs non-activated cells (lower peak). As previously reported, a fraction of the cells in this assay, ranging from about 7-12% of the cells in a well are not activated by IL-6, even though essentially all the cells were shown to be capable of STAT3 activation when stimulated by Oncostatin-M [14]. The variation in distributions remaining after normalization was evaluated quantitatively using the QC-KS.
Figure 3.
Normalization of the distributions for all 117 plates. The plates were normalized to the median of the pooled reference validation plate controls. A. Histograms of the distributions in the pooled IL-6+ control wells indicate that the normalization is effective in establishing a consistent signal range across all plates.
The QC-KS statistic was selected as a quantitative QC measure of the difference between the distributions in the control wells on each plate and a reference distribution. To evaluate performance of the QC-KS metric the distributions in the negative controls on all 117 plates (Figure 3) were reviewed and 9 plates were identified that appeared to have “abnormal” distributions (Figure 3): plates 726-735 in the first row and plate 893 in the fourth row. In addition, a tenth plate, 888 in the fourth row, appears to have a “clipped” distribution, with no intensities above about 25K, but otherwise the distribution is reasonably consistent with the other plates. Based on this qualitative comparison, these 10 plates were labeled as failed and used to evaluate the QC-KS statistic. Figure 4 compares the distributions in passed (blue) and failed (red) plates for several metrics. For the QC-KS metric (Figure 4A) passed plates have a QC-KS<0.2, while failed plates generally have a QC-KS>0.25. Only plate 888 (green), which was failed for a clipped distribution, has a QC-KS<0.2. Because cell density might have contributed to the difference between passed and failed plates we compared the distributions of cell density (Figure 4B). The distributions in cell count on passed and failed plates were essentially the same, suggesting that the abnormal distributions were not associated with a variation in cell density. Another factor that might have contributed to the differences in the distributions is the degree of activation by IL-6. Figure 4C shows that the percent active cells was consistently lower in failed plates, except for plate 888, and one passed plate, number 759. Further evaluation of plate 759 found that it had a 2 fold higher background in the positive control, leading to a lower determination of percent active, even though the negative control distribution looks normal. This lower level of activation of the cells on the failed plates suggested that it was a contributing factor in the difference.
An important question though, was whether the differences in distribution on the failed plates would significantly impact the measurement of the HIs. Figures 4D, 4E and 4F show the histograms of the QE, nNRM and %OL for passed and failed plates. Both QE and nNRM show clear differences between passed and failed plates, while only some of the failed plates show a level of %OL that is consistent with the passed plates. These results suggest that comparisons of HI measurements between passed and failed plates would not be meaningful. Furthermore, the results suggest that the QC-KS is a useful metric to QC plates for heterogeneity analysis. To select a threshold QC-KS value by which to flag plates we used the median QC-KS value + 3*K*MAD (see materials and methods) of the QC-KS values for all 117 plates, which gave a threshold value of 0.19. Applying that threshold in Figure 2, for example, the QC-KS values for the plates show that plates 729 and 734 would be flagged by this criterion. In Figure 4A, all 9 plates that were failed for abnormal distributions would be flagged, while plate 888 which was failed for an artifact would not be flagged.
Figure 5 illustrates the workflow that was adopted for quality control of biological heterogeneity. Since this was a retrospective analysis, we did not have true validation plates generated during assay development, so we pooled the negative control wells from 8 plates prepared on 4 different days to establish the reference distributions of the negative controls. In new projects we use a set of validation plates to establish the reference distributions, along with the signal-to-background, Z’-factor and other assay variability metrics. Figure 5A illustrates the consistency of the distributions on those 8 plates after normalization. We specifically selected plates prepared on 4 different days so the variability would be similar to a set of validation plates prepared on different days in a de novo screening project. The positive and negative controls are pooled to construct the reference distributions (Figure 5B) and then the QC-KS values are calculated for all the individual control wells on the validation plates and visualized as a heat map (Figure 5C). The predominant blue color in the heat map indicates consistent QC-KS values, which are generally below 0.2, and therefore distributions that are similar to the reference distributions, as expected. There are several (0-5) wells on each plate where the QC-KS value is between 0.2-0.3 (blue-gray), but the average in each case is well below 0.2. Using the distribution of QC-KS values on the validation plates a pass/fail threshold of 0.2 was selected and used to score the average QC-KS on the 117 plates in the project (Figure 5D). Nine plates were flagged by this criterion, and examination of the distributions on those plates (Figure 3) and the heat map of the wells on those plates (Figure 5E) confirmed that the distributions were not consistent with the other plates, so they were not used in the remaining analysis. In general, the distributions on the failed plates appear to show a lower level of induction of STAT3. One other plate, number 888, was failed due to an apparent data processing error that clipped the distribution, leaving a total of 107 plates for heterogeneity analysis.
3.3 Use of the heterogeneity quality control work flow in HCS, high throughput microscopy and other high throughput cytometry methods
The KS statistic is a standard metric for comparing distributions and has been used in different ways in high throughput microscopy, flow cytometry and high content assays and screens. The KS statistic measured between the distribution in a sample and the distribution of the plate controls has been used in cytometry as a very general assay metric that avoids any assumption about the nature of the distribution of cellular responses [39, 44, 54]. The KS statistic has also been used as a normality test by comparing a sample distribution to a normal distribution with the same mean and standard deviation [14, 44, 48] and is used in the non-Normality (nNRM) heterogeneity index [14]. Here we present another application of the KS statistic as a QC metric (QC-KS) for measuring the plate-to-plate or day-to-day reproducibility of cellular distributions in HCS, high throughput microscopy and high throughput flow cytometry. The integration of this measure and workflow into a screening or profiling project would be greatly facilitated by the incorporation of KS analysis in the software for HCS and other cellular analysis platforms, which would allow the QC-KS value to be produced as a standard feature, along with Z’-factor, V-factor, S/B and other assay metrics. The QC-KS statistic can also be easily be calculated in most statistics and numerical analysis packages. While it would be useful to establish general QC limits for the QC-KS metric, the extent of variation in the cellular distributions and the tolerance for variability in the project should be established during assay development and validation, along with the QC-KS threshold. In this study we found that a threshold of 0.2 worked well to reject plates with clearly different distributions.
3.4 Application of Heterogeneity Indices to Large Scale Analysis of Heterogeneity
One of the challenges in large scale analysis of heterogeneity is sorting through large numbers of distributions to identify a subset of interest. On the 107 plates in this SAR project there are more than 20,000 compound test wells and therefore more than 20,000 distributions to evaluate. Although the heterogeneity indices were previously shown to be useful in characterizing cellular distributions as heterogeneous or not, micro vs macro heterogeneity, and with or without outliers [14], we wanted to test whether these three indices captured sufficient information about the distributions to enable their use as filters to identify common, or unusual patterns of responses. To construct a classifier that used only the three heterogeneity indices to predict the shapes of the cellular distributions, we selected a subset of plates that contained control compounds with known STAT3 activity, to ensure that there were a significant fraction of active wells. Hierarchical clustering of the 837 distributions on the standard plates was used to create 8 target distribution classes (Figure 6A). Although the compounds on the standard plates were all active, because the plates were from a concentration series there were also many inactive wells. Table 1 shows the number of distributions that contribute to each target class, clearly indicating that 2/3 of the distributions were of class 1 or 2 (activated STAT3) (Figure 6A). The data were divided into training (535 observations) and test (302 observations) sets and used to construct 2 classifiers, a Random Forest (RF) and a Binary Decision Tree (BTree).
Figure 6.
Evaluating the performance of the Heterogeneity Indices in predicting the shape of the cellular distributions. A. Hierarchical clustering was used to group distributions from all the wells on 19 plates into 8 distinct classes. B. The distributions were then split into a training set and test set to construct a Random Forest classifier to predict the cluster number using only the 3 heterogeneity indices. C. A simpler decision tree model was also constructed to predict the distribution class. Although the performance was pretty good, Cluster 3 was not successfully separated from clusters 1, 2 and 4.
Table 1.
Distribution of target clusters for classifier development
| Class from Clustering | ||||||||
|---|---|---|---|---|---|---|---|---|
| Observations | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Number | 335 | 218 | 75 | 75 | 25 | 17 | 59 | 33 |
| Fraction of total | 0.40 | 0.26 | 0.09 | 0.09 | 0.03 | 0.02 | 0.07 | 0.04 |
Figure 6B illustrates the results of the classification of the distribution in each well on the standard plate using the RF classifier using only the three heterogeneity indices as inputs. As can be seen by comparison of the distributions in Figures 5A & 5B, and the confusion matrix for the RF classifier (Table 2), the RF model does an excellent job of classifying the distributions. The classifier performs best on classes 4-7, having the least confusion where the distributions indicate various degrees of inhibition. The performance on these classes of intermediate inhibition, which are near the IC50s, are of significant interest, as it is these patterns of inhibition that are hypothesized to be associated with specific mechanisms of action [13, 55]. The other classes, where the distributions are more like the negative or positive controls, have about a 10% error rate. The relative importance of the three HIs in the RF classifier is shown in Table 3 and indicates that all three HIs contribute significantly to the majority of the classes.
Table 2.
Random Forest Confusion Matrix
| Predicted | ||||||||
|---|---|---|---|---|---|---|---|---|
| Actual | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 319 | 17 | 3 | 0 | 0 | 0 | 0 | 0 |
| 2 | 24 | 199 | 3 | 0 | 0 | 0 | 0 | 0 |
| 3 | 8 | 2 | 60 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 70 | 1 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 23 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 17 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 50 | 3 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 37 |
Table 3.
Variable Importance in Random Forest Classifier
| Class from Clustering | ||||||||
|---|---|---|---|---|---|---|---|---|
| HI | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| QE | 57.11 | 31.86 | 7.93 | 40.33 | 22.79 | 13.81 | 73.29 | 38.39 |
| nNRM | 37.12 | 19.21 | 12.07 | 58.12 | 26.17 | −0.97 | 8.03 | 43.85 |
| %OL | 31.79 | 49.31 | 6.58 | 5.32 | 20.67 | 13.32 | 41.87 | 17.26 |
Figure 6C illustrates the results of classifying the distributions using the BTree classifier. The BTree uses a series of binary nodes to split the distributions into classes based on a threshold at each node. Comparison of the distributions in Figures 5A & 5C, and the confusion matrix in Table 4, indicates that although the performance of the BTree is not as good at the RF, it still provides good classification of the distributions. The BTree also provides a simple set of rules for using the HI values to identify a specific class of distribution, for example, most of the Class 6 distributions (64%) can be found with QE=0.016-0.032 and nNRM≥0.055. As with the RF classifier the BTree performs best on classes 4-7, missing class 3 completely. It is clear from the confusion matrix in Table 4 that most Class 3 distributions were assigned equally to classes 1 & 2, with about 15% assigned to class 4. So although the BTree is not as efficient at distinguishing classes 1-3, it works reasonably well for the most interesting classes, 4-7.
Table 4.
Binary Decision Tree Confusion Matrix
| Predicted | ||||||||
|---|---|---|---|---|---|---|---|---|
| Actual | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 297 | 42 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 76 | 146 | 0 | 4 | 0 | 0 | 0 | 0 |
| 3 | 31 | 29 | 0 | 10 | 0 | 0 | 0 | 0 |
| 4 | 0 | 1 | 0 | 60 | 11 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 23 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 2 | 13 | 2 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 7 | 42 | 4 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 37 |
The results of the classification indicate that the three HIs used in this study effectively distinguish distributions in the range where there is partial inhibition of STAT3. The performance of the HIs in predicting population distributions suggests that they can be used effectively to filter population distributions and identify distribution classes of interest in HCS, high throughput imaging and other cytometry projects.
3.5 Comparisons of compound heterogeneity in large data sets
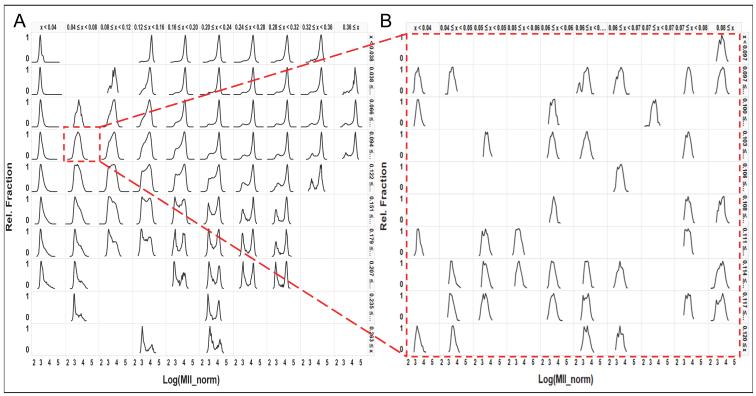
A goal of this project was to develop a method to evaluate heterogeneity in large data sets. The data set in this study consisted of over 20,000 distributions comprised of over 30 million cells. Clearly some means of organizing or filtering the data is needed. Figure 7A illustrates one approach that we have found to be useful. The data is arranged and binned using the HIs in order to provide an overview of the range of distributions in the data set. In this graphical view, generated in Spotfire (TIBCO), the QE and nNRM indices are divided into 10 equal size bins over the full range of the HIs in this data set, and the histograms of the distributions are displayed as a 10×10 matrix with QE increasing in the horizontal direction (left to right) and the nNRM increasing in the vertical direction (top to bottom). Each histogram in this view is comprised of all the cells in all the wells in that HI bin, and the arrangement exposes the range of distributions in the dataset. For example, in the lower right, high QE, high nNRM, there is a series of bimodal distributions, which is a clear indication of differential compound sensitivity among subpopulations of cells. In column 2 row 4, the distribution highlighted in red is clearly more unimodal, although the width of the distribution suggests micro-heterogeneity in that population. We expect that the individual distributions that comprise the highlighted distribution all have a similar shape because they are in the same row and column in this table so they all have a similar QE and nNRM, and this is supported by examination of the individual distributions. Zooming in to the underlying distributions (Figure 7B) confirms that they are consistent in median value, width and shape and therefore exhibit a similar degree of micro-heterogeneity.
Figure 7.
Filtering and drilling into 22,000 distributions using the Heterogeneity Indices. A. The QE and KS-norm indices were binned into 10 uniformly sized bins, and then used to sort the cell distributions in the horizontal and vertical directions, respectively. This provides an overview of the general distribution shapes. Each distribution in this view is composed of all the cells from all the wells for which the QE and KS-norm indices fell within that bin. B. Selecting a single bin to zoom in to the distributions that comprise that bin, but are now displayed with finer resolution on the binning for more detailed review of the distributions within that subset of wells.
The use of the HIs to arrange distributions for comparison is expected to be a valuable approach to the analyzing the evolution of population distributions in the differentiation of stem cells. Evolution of the distribution of phenotypes may not always lead to discrete subpopulations, therefore direct comparisons of the distribution shape using the method described here, coupled with a quantitative measure of the magnitude of the difference using the KS statistic, should be a useful approach..
3.6 Browsing for patterns of heterogeneity in compound screens
Although using the HIs to create multiscale views of heterogeneity provides a quick means to select and review distributions by shape, we wanted an interface that would also enable the selection of distributions of interest by other characteristics, such as compound ID, compound series, inhibition state, or the HIs, and then to view the patterns of response in individual concentration –response series. Figure 8 shows a view of the Heterogeneity Browser tool that was developed for interactive analysis and review of cellular distributions. All the views (Figure 8A-H) are linked so that selection of data in one view selects the same data in all the other views. Figure 8A is essentially the same view of the data as shown in Figure 7A reduced from a 10×10 matrix of distributions to 6×8. This view shows the range of distributions in the data set and selection of one or more distributions in this view will highlight the selection in all views and allow the user to zoom into the component distributions as shown in Figure 7B. Figure 8B is similar to Figure 8A except the distributions are organized by increasing %OL on the horizontal axis and increasing normality on the vertical axis. The view in Figure 8C enables the comparison of the distributions of activity over the dose-response around the IC50 value. In this view, the dose-responses are aligned by ‘relative IC50’, with the dose closest to the IC50 (~IC50) in the center, the dose below (<IC50) or above (>IC50) that dose on the left or right respectively, and the combined distributions for doses ≥2 dilutions below (<<IC50) or above (>>IC50) the IC50 on the far left and right respectively. This view enables the comparison of heterogeneity independent of compound potency. The views in Figure 8D-G show histograms of the distributions of percent activity (8D), QE (8E), nNRM (8F) and %OL (8G) for the combined replicate wells across all the plates in the data set. These histograms show the range of the metrics for the data currently displayed in the browser, in this case the full data set, and allows selection of a range of interest. The last view in the browser is the list of compounds (8H). This view allows the selection of specific compound(s) for evaluation or comparison, as well as displaying the list of compounds selected in other views.
As an example of the use of the browser, in Figure 8D all distributions with a %Active Cells in the range from 45-55% were selected (highlighted in cyan). In all other views the same distributions and the compound names are also highlighted in cyan. Figures 7A & 7B indicate the wide range of distributions, from unimodal to bimodal that can be seen around the 50% activation. The nNRM histogram in Figure 8F shows that in the selected activation range the distributions are mostly non-normal. Figure 8H shows one of the compounds and the concentration which inhibited about 50% of the cells, compound 10491, and Figure 8C shows the distribution of activity for that compound around its IC50 value. The browser illustrated in Figure 8 enables the user to:
Select compounds to view the distributions as a function of concentration
Select distribution shapes to view the compounds and concentrations with that shape,
Select a range of activity within a well to identify the distributions in that activity range,
Select a range of heterogeneity using the heterogeneity indices to identify distributions with macro-heterogeneity (high QE), non-normal distributions (high nNRM) or unusually high number of outliers (high %OL).
3.7 A workflow for heterogeneity analysis
Figure 9 summarizes the workflow established for heterogeneity analysis that includes QC to ensure consistent distributions of activity over the course of a screen. Optimally, heterogeneity analysis starts early in a project, during assay development (Step 1). Knowledge of the phenotype distributions induced by the control compounds will inform the selection of the best control compound, as well as establish reference distributions for assay validation. To maintain reproducibility in the distributions throughout a project, the range of assay values in the controls must be consistent from plate-to-plate (Step 2). In HCS this can be accomplished by setting the acquisition parameters based on the signal and background in the control wells. Depending on the platform this may require controlling the intensity of the light source, the gain of the detector, the integration time and any averaging over time or pixels. Normally, assay validation will include the production of replicate all positive and all negative plates. The data from these plates should be used to create reference set of distributions by combing the replicate control wells as illustrated in Figure 5 (Step3). These reference distributions should be used to evaluate the reproducibility of the distributions from well-to-well and plate-to-plate, and relative to the reference development distributions, using the QC-KS statistic. The variability in the distributions on the validation plates should be used to establish a threshold for the QC-KS metric to be used to flag plates where the control distributions are outside the acceptable range. We used a threshold of the median + 3*K*MAD (see details in Methods). Once the reference distributions and QC thresholds are established they can be routinely applied during the project (Step 4) to enable the reliable calculation and comparison of heterogeneity from plate-to-plate and day-to-day for the duration of a large scale biology project (Steps 5-6).
Figure 9.
The recommended workflow for heterogeneity analysis in screens or large scale biology projects. For new projects, heterogeneity analysis should be incorporated early in the development of the assay. For retrospective projects, step 1 should be to evaluate the range of the distributions of the positive and negative controls in the whole data set, and step 2 would be to normalize the data if necessary to establish consistent distributions from plate-to-plate. Steps 3-6 would remain the same.
4 Conclusions
4.1 Quality control for heterogeneity analysis in HCS, high throughput microscopy, flow cytometry and other high throughput cytometry methods
When performing heterogeneity analysis on large data sets in drug discovery and development or biomedical research using a range of cytometric analysis platforms, it is important to evaluate and to control the consistency of the biological distributions from plate-to-plate and over the duration of the project. We demonstrated that good Z’-factors are not sufficient for ensuring the distributions are reproducible, especially plate-to-plate. We adapted and applied the Kolmogorov-Smirnov statistic to measure the reproducibility of the cellular heterogeneity (QC-KS). Reference distributions should be established early in the project to track the performance of the assay in terms of the reproducibility of the distributions. Normalization of the median on each plate to the median of the reference distribution appeared to work well for correcting variations in the intensity range of the distributions. There are many possible sources for this variation in range including variation in reagents, assay timing, acquisition factors, instrument factors, or image analysis algorithms. As with other large data methods, such a DNA or protein microarrays, normalization is an effective approach to correcting for many of these assay variables [56]. Here we show that the KS statistic is an effective QC metric for quality control where the distribution of the data is important, as well as the population average.
4.2 Performance of the heterogeneity indices in classifying heterogeneity
The three heterogeneity indices were previously shown to be useful in categorizing heterogeneity [14] but here they were shown to be effective in classifying heterogeneity into discrete distributions defined by hierarchical clustering of the cellular distributions, based on histogram shape. The performance of the heterogeneity indices in predicting the shape of the distributions indicates that they successfully capture the important features of the distributions and that they can effectively be used to filter or arrange distributions for analysis.
4.3 Discovering patterns of heterogeneity in large data sets
The heterogeneity indices were used to create and demonstrate a hierarchical approach to drilling down into the distributions in a large data set. A summary of over 20,000 distributions in a 2D matrix (Figure 7), ordered by the QE and nNRM indices, displays the range of distribution shapes in the data set. Drilling down into the summary data provides a more detailed view of the distributions with that general shape. This hierarchical approach to browsing the distributions allows access to a very large number of histograms, in this case each level represents on the order of 100 fold reduction in the number of distributions, giving access to nearly all the 20,000 distributions in this data set in 2 levels. Browsing 1 million distributions would require just 3-4 levels. This visualization was incorporated into an interactive browser (Figure 8) to simplify selecting and filtering distributions. Using this browser, with a couple of clicks the user could see: the evolution of the heterogeneity for a compound series in an SAR; the variation in the distribution of phenotypes in a stem cell differentiation media series; the rank order compounds by similarity of the cell inhibition distribution; and many other analyses that relate phenotype distributions to cell treatments.
4.4 Impact of heterogeneity analysis in HCS, high throughput imaging and other methods for high throughput cytometry
It is well established that heterogeneity is common in cellular systems, yet the majority of cell based assays assume a normal distribution and report an average value, or compensate for “outliers” by reporting the median [44]. By ignoring the cell level data and depending on the well level average, most studies miss the opportunity to understand the effects of candidate therapeutics or other perturbagens on essential subpopulations. There is a growing body of evidence that analysis of heterogeneity reveals novel insights into cellular functions and response to perturbation, of critical importance in drug discovery, research and development of diagnostics and stem cell differentiation and maturation [2, 9, 11, 17, 57, 58]. Studies have shown that analysis of heterogeneity provides insights into network topology [59, 60] and can reveal interactions between independent networks [61]. Heterogeneity is also a key component of biological adaptation [10], which can lead to reduced or even loss of efficacy. In cancer for example, one study found that in the majority of cases of relapse in acute myeloid leukemia, the dominant clone at relapse was a minor clone found at diagnosis that was resistant to treatment and underwent further expansion to form the dominant clone [24].
Heterogeneity can be inherent to a population of cells [62], induced by the microenvironment [63], or induced by compound or reagent treatment [14, 61, 64, 65]. The differential sensitivity to drugs by subpopulations of cells, or cells of different types, can provide an indication of compound mechanism of action [2, 7-9, 12, 13, 66]1. In one study it was shown that cells treated with drugs of similar mechanism of action induce similar heterogeneity [64], while in another study, the analysis of the heterogeneity induced by a drug led to the development of a hypothesis of interacting networks [61]. One major advantage of phenotypic screens is the ability to screen many targets and pathways in situ, in one screen, however, in the end, little is known about the targets of the compounds. Analysis of heterogeneity in those assays, especially in comparison with compounds of known mechanism, may provide a useful starting point for identifying the targets of hits in a screen, or for evaluating whether activity in an SAR driven by a phenotypic assay remains on target. Heterogeneity can also directly indicate other compound properties that may be useful for prioritization. For example, the first population of cells that respond to a compound may be a robust indication of critical compound properties, such as the ability of the compound to penetrate cells and hit the target [44].
Analysis of heterogeneity early in drug development would allow drug design that addresses complex cellular interactions and differential drug sensitivity [10, 13] or that adopts an approach that uses combination therapy [14, 15]. The tools described here will facilitate the identification and analysis of heterogeneity in large-scale biology projects and therefore help drive the application of heterogeneity analysis in basic biomedical research and drug discovery.
Acknowledgements
This work was funded by a Pennsylvania Department of Health CURE research grant (SAP# 4100054875) and used the University of Pittsburgh Cancer Institute (UPCI) Chemical Biology Facility that is supported in part by award P30CA047904, an NIH-National Cancer Institute, Cancer Center Support Grant to the UPCI. The data analyzed in this project was generated under the NExT-CBC Agreement Number 29XS131-TO6 funded by the National Cancer Institute to D. L. Taylor. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Abbreviations
- QC-KS
a heterogeneity quality control metric that uses the KS statistic
- HI
heterogeneity index
- QE
quadratic entropy, an HI
- nNRM
non-normality, an HI
- %OL
percent outliers, an HI
Footnotes
Manuscript in preparation
6 References
- 1.Giuliano KA, Haskins JR, Taylor DL. Advances in high content screening for drug discovery. Assay Drug Dev Technol. 2003;1(4):565–77. doi: 10.1089/154065803322302826. [DOI] [PubMed] [Google Scholar]
- 2.Gough A, et al. High-Content Analysis with Cellular and Tissue Systems Biology: a Bridge between Cancer Cell Biology and Tissue-Based Diagnostics. In: Mendelsohn J, et al., editors. The molecular basis of cancer. Saunders/Elsevier; Philadelphia, PA: 2015. pp. 369–392. [Google Scholar]
- 3.Balluff B, et al. De novo discovery of phenotypic intratumour heterogeneity using imaging mass spectrometry. J Pathol. 2015;235(1):3–13. doi: 10.1002/path.4436. [DOI] [PubMed] [Google Scholar]
- 4.Black CB, et al. Cell-based screening using high-throughput flow cytometry. Assay Drug Dev Technol. 2011;9(1):13–20. doi: 10.1089/adt.2010.0308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Spiller DG, et al. Measurement of single-cell dynamics. Nature. 2010;465(7299):736–45. doi: 10.1038/nature09232. [DOI] [PubMed] [Google Scholar]
- 6.Liberali P, Snijder B, Pelkmans L. Single-cell and multivariate approaches in genetic perturbation screens. Nat Rev Genet. 2015;16(1):18–32. doi: 10.1038/nrg3768. [DOI] [PubMed] [Google Scholar]
- 7.Huang S. Non-genetic heterogeneity of cells in development: more than just noise. Development. 2009;136(23):3853–62. doi: 10.1242/dev.035139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Snijder B, Pelkmans L. Origins of regulated cell-to-cell variability. Nat Rev Mol Cell Biol. 2011;12(2):119–25. doi: 10.1038/nrm3044. [DOI] [PubMed] [Google Scholar]
- 9.Altschuler SJ, Wu LF. Cellular heterogeneity: when do differences make a difference? Cell. 2010;141(4):559–63. doi: 10.1016/j.cell.2010.04.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tawfik DS. Messy biology and the origins of evolutionary innovations. Nat Chem Biol. 2010;6(10):692–6. doi: 10.1038/nchembio.441. [DOI] [PubMed] [Google Scholar]
- 11.Meacham CE, Morrison SJ. Tumour heterogeneity and cancer cell plasticity. Nature. 2013;501(7467):328–37. doi: 10.1038/nature12624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Steininger RJ, et al. On comparing heterogeneity across biomarkers. Cytometry Part A. 2015;87(6):558–567. doi: 10.1002/cyto.a.22599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Singh DK, et al. Patterns of basal signaling heterogeneity can distinguish cellular populations with different drug sensitivities. Mol Syst Biol. 2010;6:369. doi: 10.1038/msb.2010.22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gough AH, et al. Identifying and Quantifying Heterogeneity in High Content Analysis: Application of Heterogeneity Indices to Drug Discovery. PLoS One. 2014;9(7):e102678. doi: 10.1371/journal.pone.0102678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhao B, et al. Addressing Genetic Tumor Heterogeneity through Computationally Predictive Combination Therapy. Cancer Discovery. 2014;4(2):166–74. doi: 10.1158/2159-8290.CD-13-0465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cahan P, Daley GQ. Origins and implications of pluripotent stem cell variability and heterogeneity. Nat Rev Mol Cell Biol. 2013;14(6):357–68. doi: 10.1038/nrm3584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chang HH, et al. Transcriptome-wide noise controls lineage choice in mammalian progenitor cells. Nature. 2008;453(7194):544–7. doi: 10.1038/nature06965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Loo LH, et al. Heterogeneity in the physiological states and pharmacological responses of differentiating 3T3-L1 preadipocytes. J Cell Biol. 2009;187(3):375–84. doi: 10.1083/jcb.200904140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Huang S, Ingber DE. A non-genetic basis for cancer progression and metastasis: self-organizing attractors in cell regulatory networks. Breast Dis. 2006;26:27–54. doi: 10.3233/bd-2007-26104. [DOI] [PubMed] [Google Scholar]
- 20.Buchser W, et al. Assay Development Guidelines for Image-Based High Content Screening, High Content Analysis and High Content Imaging. In: Sittampalam GS, et al., editors. Assay Guidance Manual [Internet] Eli Lilly & Company and the National Center for Advancing Translational Sciences; Bethesda (MD): [Updated 2014 Sep 22]. Oct 1, 2012. Available from: http://www.ncbi.nlm.nih.gov/books/NBK100913/ [Google Scholar]
- 21.Bray M, Carpenter A. Advanced Assay Development Guidelines for Image-Based High Content Screening and Analysis. In: Sittampalam GS, et al., editors. Assay Guidance Manual [Internet] Eli Lilly & Company and the National Center for Advancing Translational Sciences; Bethesda (MD): [Updated 2013 May 1]. Nov 16, 2012. Available from: http://www.ncbi.nlm.nih.gov/books/NBK126174/ [Google Scholar]
- 22.Zhang J-H, Chung TDY, Oldenburg KR. A Simple Statistical Parameter for Use in Evaluation and Validation of High Throughput Screening Assays. Journal of Biomolecular Screening. 1999;4(2):67–73. doi: 10.1177/108705719900400206. [DOI] [PubMed] [Google Scholar]
- 23.Polyak K. Tumor Heterogeneity Confounds and Illuminates: A case for Darwinian tumor evolution. Nat Med. 2014;20(4):344–6. doi: 10.1038/nm.3518. [DOI] [PubMed] [Google Scholar]
- 24.Kleppe M, Levine RL. Tumor Heterogeneity Confounds and Illuminates: Assessing the implications. Nat Med. 2014;20(4):342–4. doi: 10.1038/nm.3522. [DOI] [PubMed] [Google Scholar]
- 25.Koike-Yusa H, et al. Genome-wide recessive genetic screening in mammalian cells with a lentiviral CRISPR-guide RNA library. Nat Biotechnol. 2014;32(3):267–73. doi: 10.1038/nbt.2800. [DOI] [PubMed] [Google Scholar]
- 26.Sittampalam GS, et al. Assay Guidance Manual [Internet] Eli Lilly & Company and the National Center for Advancing Translational Sciences; Bethesda (MD): 2004. Available from: http://www.ncbi.nlm.nih.gov/books/NBK53196/ [PubMed] [Google Scholar]
- 27.Zhang XD. A pair of new statistical parameters for quality control in RNA interference high-throughput screening assays. Genomics. 2007;89(4):552–61. doi: 10.1016/j.ygeno.2006.12.014. [DOI] [PubMed] [Google Scholar]
- 28.Ravkin I, et al. Multiplexed high-throughput image cytometry using encoded carriers. Proceedings of the SPIE. 2004;5322:52–63. [Google Scholar]
- 29.Bray M-A, et al. Workflow and Metrics for Image Quality Control in Large-Scale High-Content Screens. Journal of Biomolecular Screening. 2012;17(2):266–274. doi: 10.1177/1087057111420292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Stack RF, et al. Quality assurance testing for modern optical imaging systems. Microsc Microanal. 2011;17(4):598–606. doi: 10.1017/S1431927611000237. [DOI] [PubMed] [Google Scholar]
- 31.Grunwald D, et al. Calibrating excitation light fluxes for quantitative light microscopy in cell biology. Nat Protoc. 2008;3(11):1809–14. doi: 10.1038/nprot.2008.180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hoffman RA. Standardization, calibration, and control in flow cytometry. Curr Protoc Cytom. 2005 doi: 10.1002/0471142956.cy0103s32. Chapter 1: p. Unit 1 3. [DOI] [PubMed] [Google Scholar]
- 33.Loo LH, et al. An approach for extensibly profiling the molecular states of cellular subpopulations. Nat Methods. 2009;6(10):759–65. doi: 10.1038/nmeth.1375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Potts SJ, et al. Evaluating tumor heterogeneity in immunohistochemistry-stained breast cancer tissue. Lab Invest. 2012;92(9):1342–57. doi: 10.1038/labinvest.2012.91. [DOI] [PubMed] [Google Scholar]
- 35.Schwarz RF, et al. Phylogenetic quantification of intra-tumour heterogeneity. PLoS Comput Biol. 2014;10(4):e1003535. doi: 10.1371/journal.pcbi.1003535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Heindl A, Nawaz S, Yuan Y. Mapping spatial heterogeneity in the tumor microenvironment: a new era for digital pathology. Lab Invest. 2015;95(4):377–84. doi: 10.1038/labinvest.2014.155. [DOI] [PubMed] [Google Scholar]
- 37.Gioanni J, et al. Two new human tumor cell lines derived from squamous cell carcinomas of the tongue: establishment, characterization and response to cytotoxic treatment. Eur J Cancer Clin Oncol. 1988;24(9):1445–55. doi: 10.1016/0277-5379(88)90335-5. [DOI] [PubMed] [Google Scholar]
- 38.Bauer VL, et al. Establishment and Molecular Cytogenetic Characterization of a Cell Culture Model of Head and Neck Squamous Cell Carcinoma (HNSCC) Genes (Basel) 2010;1(3):388–412. doi: 10.3390/genes1030388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Young IT. Proof without prejudice: use of the Kolmogorov-Smirnov test for the analysis of histograms from flow systems and other sources. J Histochem Cytochem. 1977;25(7):935–41. doi: 10.1177/25.7.894009. [DOI] [PubMed] [Google Scholar]
- 40.Giuliano KA, Chen Y-T, Taylor DL. High-Content Screening with siRNA Optimizes a Cell Biological Approach to Drug Discovery: Defining the Role of P53 Activation in the Cellular Response to Anticancer Drugs. J Biomol Screen. 2004;9(7):557–568. doi: 10.1177/1087057104265387. [DOI] [PubMed] [Google Scholar]
- 41.Perlman ZE, et al. Multidimensional drug profiling by automated microscopy. Science. 2004;306(5699):1194–8. doi: 10.1126/science.1100709. [DOI] [PubMed] [Google Scholar]
- 42.Huang S. Statistical issues in subpopulation analysis of high content imaging data. J Comput Biol. 2010;17(7):879–94. doi: 10.1089/cmb.2009.0071. [DOI] [PubMed] [Google Scholar]
- 43.Ng AY, et al. A cell profiling framework for modeling drug responses from HCS imaging. J Biomol Screen. 2010;15(7):858–68. doi: 10.1177/1087057110372256. [DOI] [PubMed] [Google Scholar]
- 44.Haney SA. Rapid Assessment and Visualization of Normality in High-Content and Other Cell-Level Data and Its Impact on the Interpretation of Experimental Results. J Biomol Screen. 2014 doi: 10.1177/1087057114526432. [DOI] [PubMed] [Google Scholar]
- 45.Shannon CE. A Mathematical Theory of Communication. Bell System Technical Journal. 1948;27(3):379–423. [Google Scholar]
- 46.Rao CR. Diversity and Dissimilarity Coefficients - a Unified Approach. Theoretical Population Biology. 1982;21(1):24–43. [Google Scholar]
- 47.Schleuter D, et al. A User's Guide to Functional Diversity Indices. Ecological Monographs. 2010;80(3):15. [Google Scholar]
- 48.Lilliefors HW. On the Kolmogorov-Smirnov Test for Normality with Mean and Variance Unknown. Journal of the American Statistical Association. 1967;62(318):399–402. [Google Scholar]
- 49.Garraway LA, Janne PA. Circumventing cancer drug resistance in the era of personalized medicine. Cancer Discov. 2012;2(3):214–26. doi: 10.1158/2159-8290.CD-12-0012. [DOI] [PubMed] [Google Scholar]
- 50.R Core Team . R: A language and environment for statistical computing. R Foundation for Statistical Computing; Vienna, Austria: 2015. http://www.R-project.org/ [Google Scholar]
- 51.Williams GJ, SpringerLink (Online service) Use R! Springer; New York: 2011. Data mining with Rattle and R the art of excavating data for knowledge discovery; p. xx.p. 374. p. 1 online resource. [Google Scholar]
- 52.Singh S, et al. Pipeline for illumination correction of images for high-throughput microscopy. J Microsc. 2014;256(3):231–6. doi: 10.1111/jmi.12178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Zwier JM, et al. Quantitative image correction and calibration for confocal fluorescence microscopy using thin reference layers and SIPchart-based calibration procedures. J Microsc. 2008;231(Pt 1):59–69. doi: 10.1111/j.1365-2818.2008.02017.x. [DOI] [PubMed] [Google Scholar]
- 54.Giuliano KA, et al. Systems Cell Biology Knowledge Created from High Content Screening. ASSAY and Drug Development Technologies. 2005;3(5):501–514. doi: 10.1089/adt.2005.3.501. [DOI] [PubMed] [Google Scholar]
- 55.Rice SD, et al. Analysis of chemotherapeutic response heterogeneity and drug clustering based on mechanism of action using an in vitro assay. Anticancer Res. 2010;30(7):2805–11. [PubMed] [Google Scholar]
- 56.Irizarry RA, et al. Exploration, normalization, and summaries of high density oligonucleotide array probe level data. Biostatistics. 2003;4(2):249–64. doi: 10.1093/biostatistics/4.2.249. [DOI] [PubMed] [Google Scholar]
- 57.Marusyk A, Almendro V, Polyak K. Intra-tumour heterogeneity: a looking glass for cancer? Nat Rev Cancer. 2012;12(5):323–34. doi: 10.1038/nrc3261. [DOI] [PubMed] [Google Scholar]
- 58.Pelkmans L. Cell Biology. Using cell-to-cell variability--a new era in molecular biology. Science. 2012;336(6080):425–6. doi: 10.1126/science.1222161. [DOI] [PubMed] [Google Scholar]
- 59.Farkash-Amar S, et al. Noise genetics: inferring protein function by correlating phenotype with protein levels and localization in individual human cells. PLoS Genet. 2014;10(3):e1004176. doi: 10.1371/journal.pgen.1004176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Wang Y, et al. Identifying network motifs that buffer front-to-back signaling in polarized neutrophils. Cell Rep. 2013;3(5):1607–16. doi: 10.1016/j.celrep.2013.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Gascoigne KE, Taylor SS. Cancer cells display profound intra- and interline variation following prolonged exposure to antimitotic drugs. Cancer Cell. 2008;14(2):111–22. doi: 10.1016/j.ccr.2008.07.002. [DOI] [PubMed] [Google Scholar]
- 62.Sisan DR, et al. Predicting rates of cell state change caused by stochastic fluctuations using a data-driven landscape model. Proc Natl Acad Sci U S A. 2012;109(47):19262–7. doi: 10.1073/pnas.1207544109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Chen F, et al. New horizons in tumor microenvironment biology: challenges and opportunities. BMC Med. 2015;13:45. doi: 10.1186/s12916-015-0278-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Slack MD, et al. Characterizing heterogeneous cellular responses to perturbations. Proc Natl Acad Sci U S A. 2008;105(49):19306–11. doi: 10.1073/pnas.0807038105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Toriello NM, et al. Integrated microfluidic bioprocessor for single-cell gene expression analysis. Proc Natl Acad Sci U S A. 2008;105(51):20173–8. doi: 10.1073/pnas.0806355106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Gerdes MJ, et al. Emerging understanding of multiscale tumor heterogeneity. Front Oncol. 2014;4:366. doi: 10.3389/fonc.2014.00366. [DOI] [PMC free article] [PubMed] [Google Scholar]