On the link between the speckle free nature of optoacoustics and visibility of structures in limited-view tomography

Abstract

Similar to pulse-echo ultrasound, optoacoustic imaging encodes the location of optical absorbers by the time-of-flight of ultrasound waves. Yet, signal generation mechanisms are fundamentally different for the two modalities, leading to significant distinction between the optimum image formation strategies. While interference of back-scattered ultrasound waves with random phases causes speckle noise in ultrasound images, speckle formation is hindered by the strong correlation between the optoacoustic responses corresponding to individual sources. However, visibility of structures is severely hampered when attempting to acquire optoacoustic images under limited-view tomographic geometries. In this tutorial article, we systematically describe the basic principles of optoacoustic signal generation and image formation for objects ranging from individual sub-resolution absorbers to a continuous absorption distribution. The results are of relevance for the proper interpretation of optoacoustic images acquired under limited-view scenarios and may also serve as a basis for optimal design of tomographic acquisition geometries and image formation strategies.

1. Introduction

Optoacoustic (photoacoustic) pressure signals are generated via thermal expansion resulting from transient absorption of light. In biological tissues, visible and near-infrared light is mainly absorbed by endogenous chromophores, such as hemoglobin or melanin [1], [2], [3], [4]. Normally, an order of 10²–10³ molecules are necessary for generating detectable optoacoustic responses from biological tissues [5], thus individual endogenous optoacoustic sources (absorbing molecules) cannot be imaged. Even when more efficient exogenous contrast agents, such as plasmonic nanoparticles, are employed for contrast enhancement [6], [7], [8], their typical absorption cross-sections are not sufficient for resolving them individually. Thereby, the optoacoustic signal excitation mechanism is usually modelled by assuming a continuous optical absorption distribution [9], [10], [11], [12], [13]. Yet, a more accurate understanding of optoacoustic signal generation and image rendering may be achieved if the light absorption in individual optoacoustic sources is considered.

Likewise, the presence of a speckle pattern in pulse-echo ultrasound images can be explained by analyzing back-scattered signals from individual acoustic sources (scatterers) [14]. Ultrasound speckles are generated via interference between a number of back-scattered waves with random phases originated at sub-resolution sources. Added contribution of time-resolved A-mode signals with random oscillations leads to a granular pattern in ultrasound B-scans, deteriorating spatial resolution and contrast of the images and adversely affecting their diagnostic value. Conversely, it is well-known that the superposition of optoacoustic waves excited by sub-resolution absorbers does not result in speckle noise in the reconstructed images [15]. This is due to the high correlation between bipolar optoacoustic signals generated by individual sources, which cancel out for equivalent neighboring absorbers. Instead, constructive interference is produced at the interfaces between absorbers. Thereby, while pulse-echo ultrasound images are usually characterized by relatively uniform random speckle patterns, optoacoustic images exhibit prominent peaks at the boundaries of large absorbing structures. As a result, utilization of conventional linear array configurations and ultrasound beamforming methods for optoacoustic image acquisition would commonly result in severe limited-view artifacts and poor visibility of structures [16], [17], [18]. By considering a continuous absorption distribution, it was previously established both theoretically and experimentally that accurate optoacoustic imaging implies that the object is fully enclosed ( >π angular coverage) by the measurement locations [19], [20], [21], [22]. Several methods have been suggested for enhancing the visibility under limited-view scenarios [23], [24], [25] and specifically designed concave array geometries have shown to significantly enhance the optoacoustic imaging performance [26], [27], [28], [29]. However, the link between the speckle-free nature of optoacoustics and visibility under limited-view tomographic conditions has not been discussed in detail.

In this tutorial, we systematically describe the signal generation and image formation mechanisms for samples ranging from sparse individual optoacoustic sources, to densely-packed absorbers, all the way to a continuous absorption distribution. In a first step, we describe how partial waves generated by individual absorbers superimpose to form time-resolved optoacoustic signals. Subsequently, we analyze how the acquired sinograms relate to the images rendered with beamforming approaches for different absorber densities. It is further compared how the image quality is affected by selection of the angular tomographic coverage. Finally, we compare images obtained by considering a large number of individual optical absorbers and a continuous absorption distribution. The results are of value for better interpretation and quantification of optoacoustic images as well as for optimal design of optoacoustic imaging systems and image reconstruction approaches.

2. Optoacoustic signals generated by a finite number of absorbers

In this section, we develop mathematical expressions for pressure waves generated by individual absorbing sources and analyze how partial waves excited by multiple absorbers contribute to a complete time-resolved optoacoustic waveform captured by the detector.

For typically used laser pulse durations below the acoustic and thermal confinement times, the light excitation source can be approximated by an impulse-type time profile. The wave equation characterizing the optoacoustic pressure wave generated by a point source located at r’ can then be expressed as [9]

$$\frac{{\partial }^{2}p\left(r,t\right)}{\partial t^2}-c^2{\nabla }^{2}p\left(r,t\right)=\Gamma \delta \left(r-r^{\prime }\right)\frac{\partial \delta \left(t\right)}{\partial t}\text{.}$$ (1)

The solution of Eq. (1) is given by

$$p\left(r,t\right)=\frac{\Gamma }{4\pi c^2\left|r-r\text{'}\right|}\frac{\partial }{\partial t}\left[\delta \left(t-\frac{\left|r-r\text{'}\right|}{c^2}\right)\right]\text{,}$$ (2)

which represents a time-confined pressure wave of infinite bandwidth. In practice, the bandwidth of the waves is limited by the duration of the light source while the collected signals are further affected by the detection bandwidth of the ultrasound sensor. More importantly, the shape and dimensions of finite-size absorbers further condition the frequency spectrum of the waves, where larger absorbers generally generate lower frequency components. Following Green’s function approach, the time-profile of the pressure wave p_Δ(r,t) generated by a finite-size absorber results from the superposition (interference) of elementary waves generated by point absorbers with absorption density H(r’), i.e.,

$$p_{\Delta }\left(r,t\right)=\frac{\Gamma }{4\pi c^2}\frac{\partial }{\partial t}{{\displaystyle \int }}^{\hspace{0.17em}}\frac{H\left(r^{\prime }\right)}{\left|r-r\text{'}\right|}\delta \left(t-\frac{\left|r-r\text{'}\right|}{c^2}\right)dr\text{'.}$$ (3)

The solution of Eq. (3) can be analytically calculated for specific absorber shapes. For example, a spherical absorber with diameter ϕ located at r′ = 0 and having unit amplitude generates characteristic N-shape pressure waves p_ϕ(r,t) given by

$$p_{\varphi }\left(r,t\right)=\{\begin{array}{c}\hfill \frac{\Gamma }{2r}\left(r-ct\right)\mathrm{i}\mathrm{f}\left|t-\frac{r}{c}\right|\le \frac{\varphi }{2c}\hfill \\ \hfill 0\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\hfill \end{array}$$ (4)

The pressure wave p_N(r,t) generated by a finite number of absorbers (optoacoustic sources) can be expressed via superposition (interference) of partial waves corresponding to each source, i.e.

$$p_N\left(r,t\right)=\sum _i^{}{p}_{{\Delta }_i}\left(r,t\right),$$ (5)

which converges to Eq. (3) for an infinite number of infinitely small absorbers.

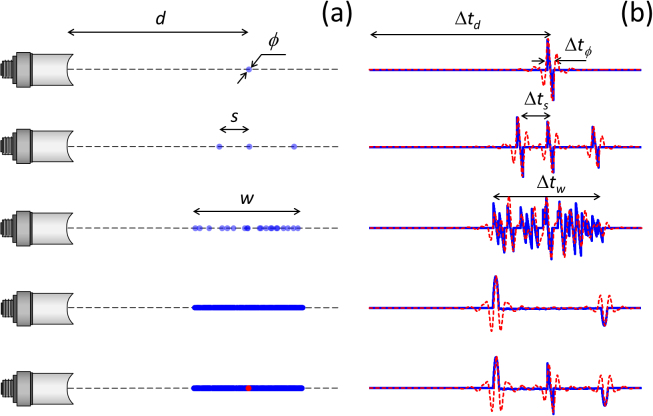
An illustrative example of how partial waves from individual sources contribute to the eventually detected optoacoustic waveform is depicted in Fig. 1. Without loss of generality, we considered spherical absorbers with diameter ϕ = 1 mm aligned with the point where the pressure signal is acquired (Fig. 1a). In this case, time-resolved optoacoustic signals (blue curves) represent depth profiles along this line (Fig. 1b). These signals were calculated for 3000 instants for a sampling frequency of 100 megasamples per second (MSPS). The first row of Fig. 1 represents the optoacoustic signal generated by a spherical absorber. The distance (depth) of the source from the transducer d = cΔt_d as well as the diameter of the absorber ϕ = cΔt_ϕ can be both estimated from the signal if the speed of sound in the medium is constant and known, e.g. c = 1500 m/s in water. The signal generated by sufficiently separated absorbers (s > > ϕ) is shown in the second row of Fig. 1. Much like in the case of an isolated absorber, N-shape profiles corresponding to individual absorbers can be distinguished and equivalent information is contained in the time-resolved signals. However, as shown in the third row of Fig. 1, interference between partial waves is produced for a larger number of absorbers (20 spheres) and individual sources can no longer be resolved. As a result, complex oscillations similar to speckle noise in ultrasound echoes are produced in the optoacoustic signals for a time interval Δt_w = w/c, being w = 20 mm the length of the region containing the absorbers. Thereby, optoacoustic signals corresponding to a relatively sparse distribution of sources can still be used for accurate estimation of the dimensions of bulk absorbers. One may expect that a better accuracy in dimension characterization is achieved for a larger number of individual absorbers. However, partial waves from neighboring absorbers tend to cancel out and constructive interference is only produced for sources located at the edges of bulk absorbing structures. The fourth row of Fig. 1 shows the resulting time-resolved optoacoustic signal for a dense distribution of optoacoustic sources (1,000,000 individual sources). The dimensions of the absorbing region are not obvious in this signal as it may be erroneously interpreted that the absorption only occurs at two locations that actually correspond to the edges of an extended structure. The small equally absorbing sources located inside the structure do not appear to be visible in the signals. Yet, more prominent absorbers can still be distinguished. The fifth row of Fig. 1 shows the time resolved signal corresponding to the same distribution as in the fourth row, where a 100-fold more intense absorber was included (red dot). In this case, the partial wave generated by the new source is not cancelled out by weaker neighboring absorbers and is still distinguished in the optoacoustic signal. The dashed red lines in Fig. 1b correspond to the time-resolved signals after application of a narrowband band-pass filter with cut-off frequencies between 0.1 and 2 MHz. The same conclusions regarding source visibility can be extracted from these signals, except that the minimal distance between sources in order for them to be individually resolved is larger due to signal broadening.

Fig. 1.

Time-resolved optoacoustic signals (b) generated by different distributions of spherical absorbers (a) with unit amplitude (blue dots) and with 100-fold higher amplitude (red dot). The blue lines correspond to the theoretical time-resolved signals and the dashed red lines represent the same signals after application of a narrowband band-pass filter.

3. Optoacoustic images for a finite number of absorbers

In this section, we describe how the results presented in the previous section relate to the sinograms and the reconstructed images for different acquisition geometries (transducer array configurations) and different absorber densities. The analysis is performed for two-dimensional acquisition geometries, where all optoacoustic sources are assumed to be confined in a plane, yet the conclusions can be directly extrapolated to arbitrary three-dimensional configurations.

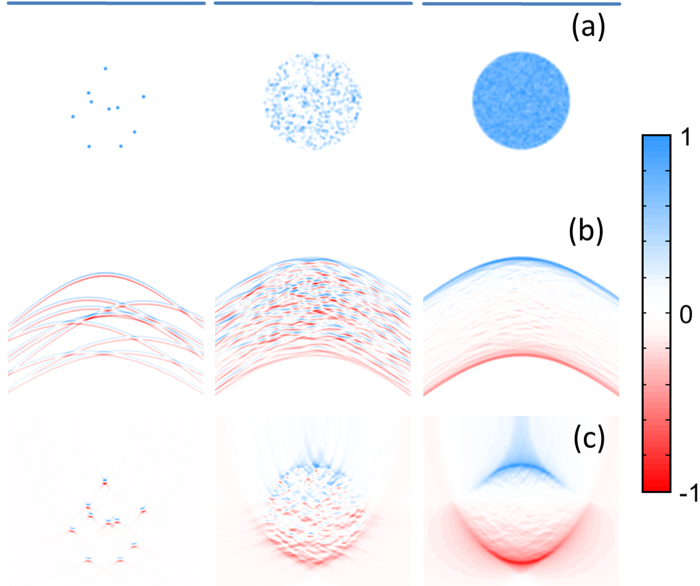
Here the individual sources were assumed to have a truncated parabolic optical absorption profile, for which the optoacoustic signals can be calculated analytically [11]. All simulations performed for a finite number of absorbers are based on a superposition of individual signals calculated with this analytical formulation. The absorbers were confined within a circular 20 mm diameter region. Three distributions of 10, 10³ and 10⁵ absorbers with 1 mm diameter were considered (Fig. 2a). In a first step, a linear array with 1000 elements and 40 mm length located 20 mm above the center of the absorbing region was considered (blue line in Fig. 2a). The array was assumed to have infinitely small elements with infinite detection bandwidth. The optoacoustic waveforms detected by all the array elements were calculated for 1000 time instants (at sampling rate of 37.5 Msps) and stacked together to form the sinograms displayed in Fig. 2b. Much like in the signals shown in the previous section, individual absorbers can be distinguished in the sinograms if they are sufficiently separated, a random pattern is produced for a sparse distribution of absorbers while prominent boundaries are observed for densely-packed optoacoustic sources.

Fig. 2.

Optoacoustic simulations for three distributions of 10 (left), 10³ (middle) and 10⁵ (right) absorbers being imaged with a linear transducer array (blue horizontal line). (a) Actual distribution of individual absorbers. (b) Optoacoustic sinograms. (c) Optoacoustic images reconstructed using a simple delay-and-sum algorithm. All images were normalized.

Optoacoustic images can be rendered by just combining the individual signals with standard beamforming approaches used in ultrasonography. In this way, each pixel of the image is obtained by delaying and summing up signals according to the distance of the pixel to each element of the array. The images obtained by using this approach are displayed in Fig. 2c. Positive and negative values are rendered for each separated absorber, which are attributed to the bipolar nature of optoacoustic signals. On the other hand, since delay-and sum is a linear reconstruction method, the optoacoustic image for a given number of absorbers corresponds to the superposition of the images of each individual source. Images of individual absorbers are then expected to superimpose (interfere) in a similar manner as the associated partial waves. Indeed, a granular pattern is observed for an image reconstructed from the object containing 10³ individual absorbers, whereas only the boundaries of the absorbing region are visible when imaging an object with 10⁵ absorbers due to cancelation of the positive and negative values for neighboring absorbers.

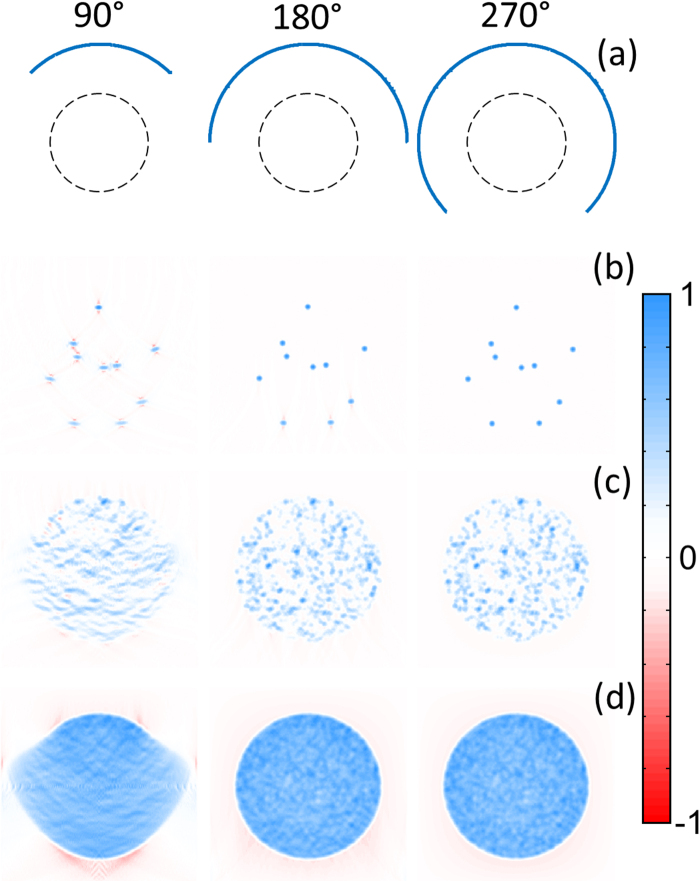
As mentioned, a linear array geometry is not optimal for optoacoustic image acquisition while more accurate tomographic reconstruction algorithms have been developed that outperform the simple delay-and-sum approach. We simulated the time-resolved optoacoustic signals generated by the same distribution of absorbers shown in Fig. 2 for curved (tomographic) array geometries and further performed optoacoustic tomographic reconstructions with an accurate model-based algorithm [30]. Note that, since the latter reconstruction approach relies on the exact optoacoustic wave generation model, it is generally expected to provide more accurate reconstructions as compared with the delay-and-sum approach used in Fig. 2. However, limited-view effects would still affect the reconstructed images. Three different curved arrays with 1000 elements, 90°, 180° and 270° angular coverage (Fig. 3a) and 20 mm radius located above the region enclosing the absorbers (dashed circle in Fig. 3a) were considered and the detected signals were again calculated for 1000 instants at 37.5 MSPS. The model-based inversion algorithm is based on a discretization of the same optoacoustic forward model used to calculate the signals for the truncated parabolic absorbers [11], [30]. It can be seen that negative shadows are present in the reconstructed individual absorbers for the 90° array (Fig. 3b), although not so prominent as in Fig. 2c. Negative shadows are only present in the lower part of the image for the 180° array and completely disappear for the 270° array. Note that it has been previously shown that accurate optoacoustic reconstructions are only possible for >π angular coverage [19]. Reconstructed individual absorbers for the 90° array are also elongated along the lateral direction due to the very limited angular coverage. When analyzing reconstructions from the objects with different absorber densities, negative absorption values are still present in the images reconstructed from a denser distribution of absorbers for the 90° array (Fig. 3c and d). The shape of the absorbing region is also laterally elongated in the tomographic reconstructions obtained with the 90° array (Fig. 3d). Furthermore, the boundaries of the absorbing region for a dense distribution of absorbers are enhanced for densely-packed absorbers reconstructed with the 90° array (Fig. 3d), although not as prominently as in Fig. 2c. On the other hand, accurate reconstructions are obtained in all cases for the 270° tomographic coverage and no significant artefacts appear for the 180° array, even in the lower part of the image where the angular coverage is incomplete.

Fig. 3.

Tomographic model-based reconstructions for three arc arrays with 90°, 180° and 270° angular coverage (a). The same distributions of 10 (b), 10³ (c) and 10⁵ (d) absorbers shown in Fig. 2a were simulated.

4. Continuous absorption distribution

In this section, we compare the optoacoustic images obtained from a relatively sparse distribution of absorbers, a very dense distribution of absorbers versus images acquired considering a continuous light absorption distribution. For a finite number of absorbers, the pressure signals are given by Eq. (5) whereas pressure signals for a continuous distribution of absorption are given by Eq. (3). Note that Eq. (3) becomes equivalent to Eq. (5) for an infinite number of infinitely small absorbers. For a very large number of finite-size absorbers, the optoacoustic sources tend to behave like a continuous absorption distribution, particularly when they are smaller than the resolution cell of the imaging modality. Eq. (3) can alternatively be expressed as [31]

$$p\left(r,t\right)=\frac{\Gamma }{4\pi c}\frac{\partial }{\partial t}{\int }_{\mathrm{S}\text{'}\left(t\right)}^{}\frac{H(r^{\prime })}{\left|r-r\text{'}\right|}d\mathrm{S}\text{'}\left(t\right),$$ (6)

where $S^{\prime }\left(t\right)$ is a time-dependent spherical surface for which $|r-r^{\prime }|=ct$. If the optoacoustic sources are confined in a plane, Eq. (6) can be simplified in arbitrary units as [11], [30]

$$p\left(r,t\right)=\frac{\partial }{\partial t}{\int }_{\mathrm{L}\text{'}\left(t\right)}^{}\frac{H\left(r^{\prime }\right)}{\left|r-r\text{'}\right|}dL\text{'}\left(t\right),$$ (7)

where $L^{\prime }(t)$ is an arc for which $|r-r^{\prime }|=ct$. Eq. (7) represents the spherical Radon transform. Thus, optoacoustic signals become mathematically equivalent to e.g. X-ray CT projections, so that optoacoustic imaging of a continuous absorption distribution is inherently representing a tomographic imaging approach. Much like in other tomographic imaging modalities, the k-space representation of the imaged region is encoded in the acquired signals from multiple orientations while limited-view artefacts are necessarily produced if the tomographic coverage is insufficient [32]. Specifically, it has been theoretically established and experimentally verified that optoacoustic images are affected by limited-view effects if the measuring locations enclose an angle lower than π, as was also demonstrated in Fig. 3.

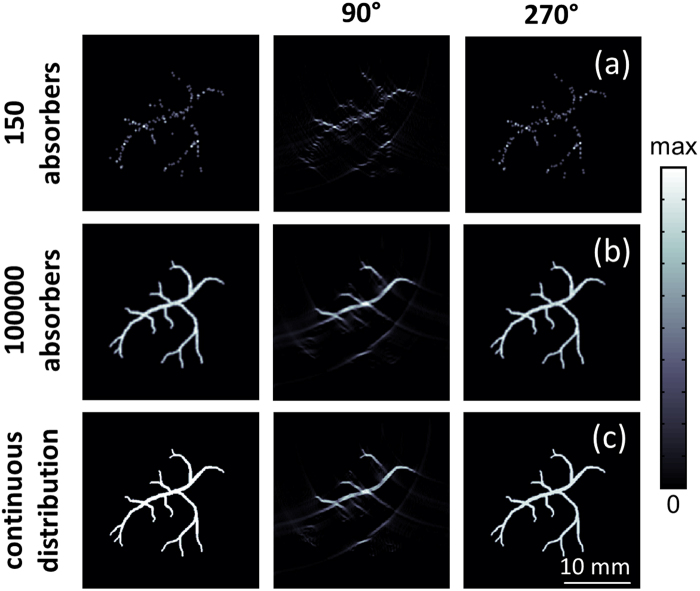
A theoretical image mimicking vascular structures was approximated by considering 150 (Fig. 4a, left) or 10⁵ truncated parabolic absorbers (Fig. 4b, left) and the corresponding optoacoustic signals were calculated. In addition, the optoacoustic signals for a continuous 27 × 27 mm² absorption distribution corresponding to the same theoretical image (Fig. 4c, left) were simulated by considering the theoretical model given by Eq. (7). The theoretical model is described in more detail in [11]. In both cases, the theoretical signals were calculated for 1000 instants at 37.5 MSPS and subsequently band-pass filtered between 25 kHz and 5 MHz prior to applying the model-based reconstruction. In this case, a non-negative constraint was also incorporated in the inversion procedure [33]. The resulting images obtained with the same 90° and 270° arrays shown in Fig. 3a are depicted in the second and third columns of Fig. 4, respectively. The detection arrays are located on top of the imaged region. For a sparse distribution of absorbers, the visibility of structures is very similar for both arrays. However, limited-view effects clearly affect the visibility of vertical structures in images obtained with the 90° array for a dense distribution of absorbers, while accurate images are reconstructed with 270° angular coverage. As expected, very similar results are obtained by considering a continuous absorption distribution or very densely-packed absorbers, which showcases the equivalence of both approaches.

Fig. 4.

Comparison of the optoacoustic non-negative model-based tomographic reconstructions for a distribution of 150 absorbers (a), 10⁵ absorbers (b) and for a continuous absorption distribution (c). The theoretical images are depicted in the left panels whereas the middle and right panels show the images obtained with the 90° and 270° transducer arrays in Fig. 3a, respectively.

5. Discussion and conclusions

In this tutorial, it was shown that optoacoustics and pulse-echo ultrasound signals and images are generated in a fundamentally different manner. Even though information is carried by high frequency pressure waves in both modalities, optoacoustic image formation is conceptually different and its specific characteristics must be taken into account for proper interpretation of the images and efficient design of the tomographic image acquisition strategy. The main distinction stems from the fact that in optoacoustics an initial pressure increase is always produced upon laser excitation of optical absorbers distributed in the sample. Thereby, interferences between the individual pressure waves generated by a sufficiently dense distribution of optoacoustic sources do not result in random signal fluctuations responsible for the speckle pattern in ultrasound images. Instead, partial pressure waves generated by sub-resolution absorbers cancel out except for boundaries corresponding to changes in the macroscopic optical absorption density. This is consistent with the conclusions rendered when considering a continuous model of the optical absorption distribution, which generally holds true in reality since most chromophores cannot be detected or resolved individually.

The presence of speckle in ultrasound images is generally undesirable as it deteriorates image quality and hampers human interpretation and diagnosis. For example, a granular pattern within parenchymal tissue can erroneously be interpreted as an actual structure. We have shown that speckle-free optoacoustic images are rendered from objects containing a large number of individual absorbers as well as from objects representing a continuous optical absorption distribution. The lack of speckle comes however to the detriment of structure visibility when employing limited-view geometries, such as standard ultrasound linear array configurations, for optoacoustic image acquisition. We have also shown that the visibility of vascular structures can be enhanced with a sparse distribution of absorbers, which anticipates that efficient optoacoustic contrast agents may also play an important role in image quality enhancement in limited-view scenarios. It was further shown that accurate reconstruction of the optical absorption distribution is possible for array configurations providing a sufficient ( >π) angular coverage of the object, so that optoacoustic imaging becomes inherently tomographic. For typical small animal imaging scenarios, the imaged object (e.g. a mouse) can be efficiently surrounded by multiple ultrasound detectors, which results in accurate speckle-free images of internal structures with ultrasound resolution [26], [34], [35], [36], [37]. However, it is often not feasible to enclose the imaged area with detectors, for instance in the case of hand-held human imaging where the tissue is only accessible from one side. Although the effective angular coverage can be maximized with specifically-designed concave arrays [38], [39], limited-view effects are inherently present when employing the hand-held scanning approach.

Here we have shown that lower concentration of small individual absorbers may contribute to a better visibility under limited-view optoacoustic tomography conditions. In particular, it was shown that for a relatively low density of absorbing sources enclosed within a bulk structure, a granular pattern appears in the image similar to the speckle grains in ultrasound. Although the granular pattern is undesirable, it allows estimating the actual shape and dimensions of the structure, which is not possible when the absorber density is increased so that only the boundaries are visible in the reconstructed image. On the other hand, it was also showcased that individual absorbers with a higher optical absorption than the background are clearly distinguishable. The above effects can be exploited to improve visibility of structures under limited-view optoacoustic tomography conditions. For example, it was previously shown that breaking the spatial continuity with speckle illumination leads to granular images with significantly better visibility [40]. Indeed, light speckle grains represent sparsely distributed individual optoacoustic sources while, by further combining multiple images with random light speckle patterns, a continuous image can be formed. It is important to notice that images must be combined in a non-linear manner as superposition of images obtained with a linear reconstruction method is equivalent to the reconstruction of the superimposed sources, which would again result in the same type of limited-view artifacts. On the other hand, such non-linear combination may result in images that are not proportional to the optical absorption distribution, which may hamper quantification purposes. Another approach consists in artificially creating individual optoacoustic sources within a tissue by heating a specific point with high-intensity ultrasound and exploiting the temperature dependence of the optoacoustic signals. By raster-scanning the ultrasound focus and non-linearly combining the images, a limited-view-free image is obtained [24]. Limited-view effects can also be avoided by dynamic visualization of flowing particles using a real-time optoacoustic imaging system [41]. A relatively dense distribution of particles leads to a speckled image similar to ultrasound B-scans. By non-linearly combining a sequence of images, good visibility under limited-view conditions is achieved. Naturally, applicabilty of this method for bio-imaging greatly depends on availability of biocompatible absorbers that can be detected and resolved individually. The size of individual absorbers must remain well below the optoacoustic resolution cell in order to maintain diffraction limited spatial resolution [42].

The numerical simulations performed in this work are based on sources excited with an infinitely short pulsed laser and captured with an infinite bandwidth transducer. Yet, similar visibility was obtained when the individual time-resolved signals were filtered to render them bandwidth limited. The limited bandwidth of the detected optoacoustic signals is generally associated with the final duration of the excitation light pulse or otherwise has to do with the detection bandwidth of the ultrasound sensor [43]. An additional aspect is frequency dependent acoustic attenuation, which may further limit the effectively detected signal bandwidth [44]. In general, limited detection bandwidth may lead to blurring of structures and loss of resolution, thus resulting in smearing of the boundaries. This may hamper visibility of strong absorbers located within the homogenous part of the object. The number of absorbers that can be individually resolved is also reduced for narrowband signals, in a way that a granular pattern appears for a sparser distribution of optoacoustic sources.

In conclusion, efficient design of optoacoustic imaging systems and accurate image interpretation imply deep understanding and careful consideration of the basic optoacoustic signal generation and image formation principles. Those are unique for the optoacoustic modality and cannot be adopted from other techniques such as pulse-echo ultrasound. Of particular importance are limited-view scenarios, which are inevitable in cases where the sample cannot be tomographically covered, e.g. for clinical hand-held imaging.

Biographies

Daniel Razansky earned his B.Sc. and M.Sc.degrees in electrical engineering and his Ph.D. degree in biomedical engineering, all from the Technion-Israel Institute of Technology, and completed a postdoctoral training at the Harvard Medical School. Since 2007, he has been the Director of the Lab for Optoacoustics and Molecular Imaging Engineering at the Institute for Biological and Medical Imaging (IBMI), Helmholtz Center Munich and is also a Professor of Molecular Imaging Engineering at the Technical University of Munich. He has published more than 80 peer-reviewed journal articles and holds 10 patents and patent applications in bio-imaging and bio-sensing disciplines. He has also delivered more than 50 invited and plenary lectures worldwide and serves on a number of editorial boards of international journals and research council review boards. Professor Razansky is the recipient of a number of prizes and awards, among them the BioVaria spin-off Award and the ERC starting grant, and has been selected to appear in the “Young elite: Top 40 scientists under 40” list by the Capital magazine in 2011 and 2012.

Xosé Luís Deán-Ben received the diploma in automatics and electronics engineering from the Universidade de Vigo in 2004. He received the PhD degree from the same university in 2009. Since 2010, he serves as a postdoctoral fellow at the Lab for Optoacoustics and Molecular Imaging Engineering at the Institute for Biological and Medical Imaging (IBMI), Helmholtz Center Munich. His major research interests are the development of new optoacoustic systems for preclinical and clinical applications and the elaboration of mathematical algorithms for fast and accurate imaging performance.