A unified perspective on ankle push-off in human walking

ABSTRACT

Muscle–tendon units about the ankle joint generate a burst of positive power during the step-to-step transition in human walking, termed ankle push-off, but there is no scientific consensus on its functional role. A central question embodied in the biomechanics literature is: does ankle push-off primarily contribute to leg swing, or to center of mass (COM) acceleration? This question has been debated in various forms for decades. However, it actually presents a false dichotomy, as these two possibilities are not mutually exclusive. If we ask either question independently, the answer is the same: yes! (1) Does ankle push-off primarily contribute to leg swing acceleration? Yes. (2) Does ankle push-off primarily contribute to COM acceleration? Yes. Here, we summarize the historical debate, then synthesize the seemingly polarized perspectives and demonstrate that both descriptions are valid. The principal means by which ankle push-off affects COM mechanics is by a localized action that increases the speed and kinetic energy of the trailing push-off limb. Because the limb is included in body COM computations, this localized segmental acceleration also accelerates the COM, and most of the segmental energy change also appears as COM energy change. Interpretation of ankle mechanics should abandon an either/or contrast of leg swing versus COM acceleration. Instead, ankle push-off should be interpreted in light of both mutually consistent effects. This unified perspective informs our fundamental understanding of the role of ankle push-off, and has important implications for the design of clinical interventions (e.g. prostheses, orthoses) intended to restore locomotor function to individuals with disabilities.

Summary: Despite historical controversy, ankle push-off primarily contributes to both leg swing and center of mass acceleration during walking. Interpretation of ankle mechanics should abandon an either/or contrast of these mutually consistent effects.

Introduction

The functional role of the ankle–foot musculature during human walking has been pondered for centuries. Aristotle (384–322 BCE) is often credited with the earliest written descriptions of the actions of muscles and joints during locomotion (Medved, 2000), and his writings allude to push-off by the trailing limb during walking: ‘For they are moved, not by the foot which they put in front, but by that which they step off’ (Peck and Forster, 1968). Likewise, text from Leonardo da Vinci's (1452–1519) sketchbook indicates that he too was keenly interested in the contributions of the ankle–foot to whole-body movement: ‘…quickly lifting the heel of the lower foot. With this push he lifts himself upward’ (Da Vinci, 2013; Klette and Tee, 2008). However, it was not until the 1800s and early 1900s that technology was developed and applied to record human motion and force during dynamic movement (Braune and Fischer, 1895; Braune and Fischer, 1987; Marey, 1873, 1894; Medved, 2000; Muybridge, 1887; Weber and Weber, 1836). Throughout the 20th century there were marked advances in movement analysis technology (Baker, 2007; Klette and Tee, 2008; Sutherland, 2001, 2002, 2005). Over the last several decades, the integration of various sensing modalities, improvements in measurement accuracy and the development of automatic tracking capabilities have enabled more widespread and comprehensive biomechanical testing (Baker, 2007; Sutherland and Hagy, 1972). This has provided the empirical basis for understanding the role of ankle push-off mechanics (see Glossary) during gait, which has implications for the design of clinical interventions (e.g. prostheses, orthoses) for individuals with locomotor impairments or disabilities.

Although the empirical data collected during gait analysis studies are often similar (e.g. kinematics, electromyography, force), the use of different computational analyses has led to a chasm in interpretation and thus in our understanding of gait, specifically related to ankle push-off function. Some research studies support the hypothesis that the primary role of ankle push-off during walking is to help initiate leg swing (e.g. Meinders et al., 1998; Winter and Robertson, 1978), while other studies emphasize that its main function is to redirect the body's center of mass (COM; see Glossary) during the step-to-step transition (e.g. Kuo et al., 2005).

The ankle has been the focus of much scientific attention because the plantarflexor muscles and tendons (see Glossary) acting about this joint are observed to be the primary generators of positive power during the step-to-step transition in human walking (Cappozzo et al., 1976; Elftman, 1939; Hof et al., 1983; Winter, 1983). Hip muscles (iliopsoas and others) contribute a lesser amount of positive power to this step-to-step transition, whereas the knee and foot are estimated to perform net negative work during this phase of the gait cycle (Zelik et al., 2015a). Various measurements and analyses provide evidence that a burst of positive power is performed about the ankle at the end of stance phase in walking, often termed ‘push-off’ (Fig. 1). This ankle power (work rate; see Glossary) is produced by the triceps surae (soleus, medial and lateral gastrocnemius) and other extrinsic foot muscle–tendon units. Peak ankle push-off power is due partly to elastic recoil of the Achilles tendon (Fukunaga et al., 2002; Ishikawa et al., 2005; Lichtwark and Wilson, 2007, 2008; Sawicki et al., 2009) – which returns energy stored by tendon stretch resisting ankle dorsiflexion (tibial progression) – and partly to concentric muscle contraction. This brings us to the questions: (1) to what aspects of motion does this ankle push-off contribute directly; and (2) why and/or how does it facilitate walking overall? The aim of this article is to discuss the first question, in an effort to garner consensus and in anticipation of addressing the more challenging second question.

Fig. 1.

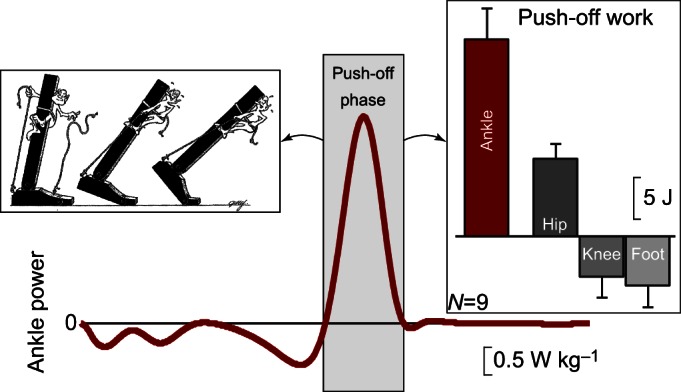
Ankle power and work. Ankle power for one leg plotted across a full stride cycle from foot contact to subsequent ipsilateral foot contact. Left inset: cartoon adapted from Inman et al. (1981) depicts ankle push-off behavior. Right inset: ankle push-off work versus the push-off work performed by other ipsilateral lower-limb joints and segments (hip, knee, foot). Work values were obtained by computing the time integral of power during push-off phase. Inter-subject power and work means, and work standard deviations are depicted for walking at 1.4 m s⁻¹, based on 6-degree-of-freedom joint mechanics analysis (N=9; Zelik et al., 2015a).

Perspectives on ankle push-off

In the mid-20th century, Verne Inman noted that ankle push-off contributes to both initiating leg swing and propelling the body over the leading stance limb: ‘it produces a thrust upward through the leg. Part of this force is transmitted to the body and assists it to “climb the hill” over the extended opposite leg; the remainder initiates hip and knee flexion on the same side and starts the leg swinging’ (Inman, 1966). However, more recent studies on gait mechanics have often sought to identify a single, primary role of ankle push-off. These publications have typically been more polarized, emphasizing ankle push-off contributions to either (1) accelerating the trailing limb into its aerial swing phase or (2) accelerating or redirecting the body's COM. Here we summarize these perspectives, explain their differing consequences and propose a unifying perspective that we hope will make future interpretation more complete.

List of symbols and abbreviations.

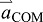
acceleration of the body's COM

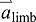
acceleration of the push-off limb

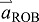
acceleration of the ROB

COM

center of mass

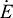
time rate of energy change

HAT

head–arms–trunk

M

body mass

m_limb

mass of the push-off limb

m_ROB

mass of the ROB

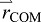
position of the body's COM

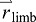
position of the push-off limb

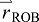
position of the ROB

ROB

remainder of body (leading limb plus HAT)

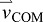
velocity of the body's COM

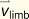
velocity of the push-off limb

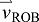
velocity of the ROB

Leg swing acceleration

The ‘leg swing’ school of thought was advanced by the works of David Winter and others in the 1970s. After performing a segmental energy flow analysis on human walking data (Quanbury et al., 1975; Winter and Robertson, 1978), Winter and colleagues concluded that ‘the vast majority of this power is being generated by the ankle plantarflexors,’ but that only ‘a small part of this power continues across the hip joint into HAT [head–arms–trunk]’ and that most of the ‘increased energy is stored in the swinging leg’ (Winter and Robertson, 1978). Their results indicated that the burst of positive ankle push-off work (approximately +22 J, which we estimated post hoc based on the reported peak ankle power; Winter and Robertson, 1978) occurs simultaneously with an increase in the energy of the ipsilateral limb segments (approximately +14 J). Nearly all of this swing limb energy change was due to increasing speed (i.e. acceleration) of the thigh and shank, which increased the translational kinetic energy of these limb segments (Winter et al., 1976). Meanwhile, changes in potential energy and rotational kinetic energy of the swing limb were observed to be negligible during ankle push-off. Thus, their results suggested that ankle push-off primarily contributes to powering leg swing by accelerating the segments of the push-off limb (see Glossary). More recently, Meinders et al. (1998) estimated +31.9 J of ankle push-off work during walking and, simultaneously, a +28.7 J increase in energy of the ipsilateral limb. Because knee work during push-off was negative, hip work was only 9.2 J and only 2.1 J were transferred through the hip joint (from trunk to limb), these authors concluded that the acceleration of the leg into swing was primarily due to ankle push-off. Ultimately, they concluded that only +4.2 J of the ankle plantarflexion push-off work was transferred to the trunk, and thus the majority of ankle push-off work contributed to increasing leg energy. Additional studies have also reported corroborating findings. Hof et al. (1992) performed a study using an electromyography-to-force analysis to approximate ankle muscle contributions in conjunction with segmental energy estimates, and found that the ankle plantarflexor work corresponded in timing and slope to the energy change of the ipsilateral limb during push-off. Lipfert et al. (2014) applied a different form of power transfer analysis to human walking data, and concluded that little of the power generated at the ankle reaches the pelvis/trunk, and that most of the push-off contributes to acceleration of the ipsilateral limb (specifically the shank and thigh) to initiate leg swing. The authors noted that this acceleration of limb mass indirectly affects the COM mechanics, and they proposed that push-off should be further subdivided into an alleviation phase during which body weight support is discontinued, and a launching phase when ankle push-off (largely owing to the release of stored elastic energy) accelerates the limb into swing.

Glossary.

Ankle plantarflexors

Muscle–tendon units that contribute to extending (plantarflexing) the ankle joint, most notably the triceps surae (soleus and gastrocnemius).

Ankle power

Net mechanical power generated by biological tissues (muscles, tendons, etc.) about the ankle joint.

Ankle push-off

Positive power/work generated about the ankle joint at the end of stance phase in human walking.

Center of mass (COM)

The average position of the mass of the body.

Peripheral (capitalized)

Relative to COM.

Push-off (capitalized)

The period of positive push-off limb COM power near terminal stance and immediately prior to foot-lift.

Push-off limb

The trailing limb during the step-to-step transition in walking.

Remainder of body (ROB)

All body segments except the push-off limb.

Total (capitalized)

COM plus Peripheral.

COM acceleration

The COM-focused perspective has advanced in conjunction with the study and development of dynamic walkers. Dynamic walkers are mechanical systems (or models), often devoid of actuators or controllers, which move dynamically in a stable cyclic motion that resembles human gait (McGeer, 1990). Dynamic walking simulations indicate that push-off by the trailing limb can preemptively accelerate the body's COM upward and forward during the step-to-step transition (Adamczyk and Kuo, 2009; Bregman et al., 2011; Kuo, 2002; Zelik et al., 2014). By redirecting the COM velocity, this push-off can reduce the collisional energy losses associated with landing on the contralateral limb. Reduced energy loss is posited to be beneficial for economy of locomotion, because energy dissipated during collision (the period of energy absorption immediately following foot contact) must be compensated for by active work from muscles or actuators in order to maintain steady gait speed (Adamczyk et al., 2006; Bertram and Hasaneini, 2013; Donelan et al., 2002a; Kuo, 2007; Kuo and Donelan, 2010; Kuo et al., 2005; Ruina et al., 2005).

Empirical evidence indicates that substantial work is indeed performed by the trailing limb on the COM during the step-to-step transition in walking (Donelan et al., 2002b), which increases the speed and thus kinetic energy of the body's COM (Winter, 1979). This push-off work is derived mostly from ankle plantarflexor muscles and tendons (Fig. 1). COM work exhibits similar timing and magnitude to trailing limb ankle push-off work (Fig. 2A) (Kuo et al., 2005; Zelik and Kuo, 2010). The summed work contributions from other body joints (e.g. ipsilateral hip and knee, contralateral hip, knee and ankle, trunk and arm joints) and segments (e.g. feet) are far too small to explain this observed magnitude of COM push-off work (Zelik et al., 2015a). The ankle and COM push-off magnitudes are observed to scale together with increasing speed (e.g. 16.2 versus 14.9 J at 0.9 m s⁻¹, 23.6 versus 20.3 J at 1.4 m s⁻¹ and 30.0 versus 28.9 J at 1.8 m s⁻¹; Zelik and Kuo, 2010). In clinical populations with decreased ankle push-off capabilities (e.g. individuals with lower-limb amputation wearing conventional passive prosthetic feet), COM push-off has also been observed to decrease (Adamczyk and Kuo, 2015; Caputo and Collins, 2014; Collins and Kuo, 2010; Herr and Grabowski, 2012; Houdijk et al., 2009; Zelik et al., 2011), further supporting the contention that the burst of ankle push-off work contributes to energy changes of the COM. When ankle push-off was increased in a prosthesis (e.g. with a bionic foot), then COM push-off also increased, in rough proportion (Herr and Grabowski, 2012; Zelik et al., 2011). For example, on average, a 7.8 J increase in prosthetic ankle push-off work resulted in an 8.0 J increase in COM push-off work for amputees wearing an energy-recycling versus conventional prosthetic foot (Zelik et al., 2011). Likewise, when ankle push-off work was reduced using a restrictive ankle–foot orthosis, COM push-off work decreased in proportion (linear regression slope±confidence interval of 0.75±0.3, R²=0.59; Huang et al., 2015). Finally, COM push-off work increased with ankle push-off work even in the absence of leg swing, as observed in cyclical rocking tasks designed to isolate the step-to-step transition phase of walking (Soo and Donelan, 2010). These authors reported 11 J of positive ankle work versus 12 J of positive COM work during push-off at the shortest step length tested (60% of leg length), and 33 versus 27 J at the longest step length (100% of leg length). Meanwhile, the knee and hip were estimated to contribute only 10% and 2% of the positive COM push-off work, respectively.

Fig. 2.

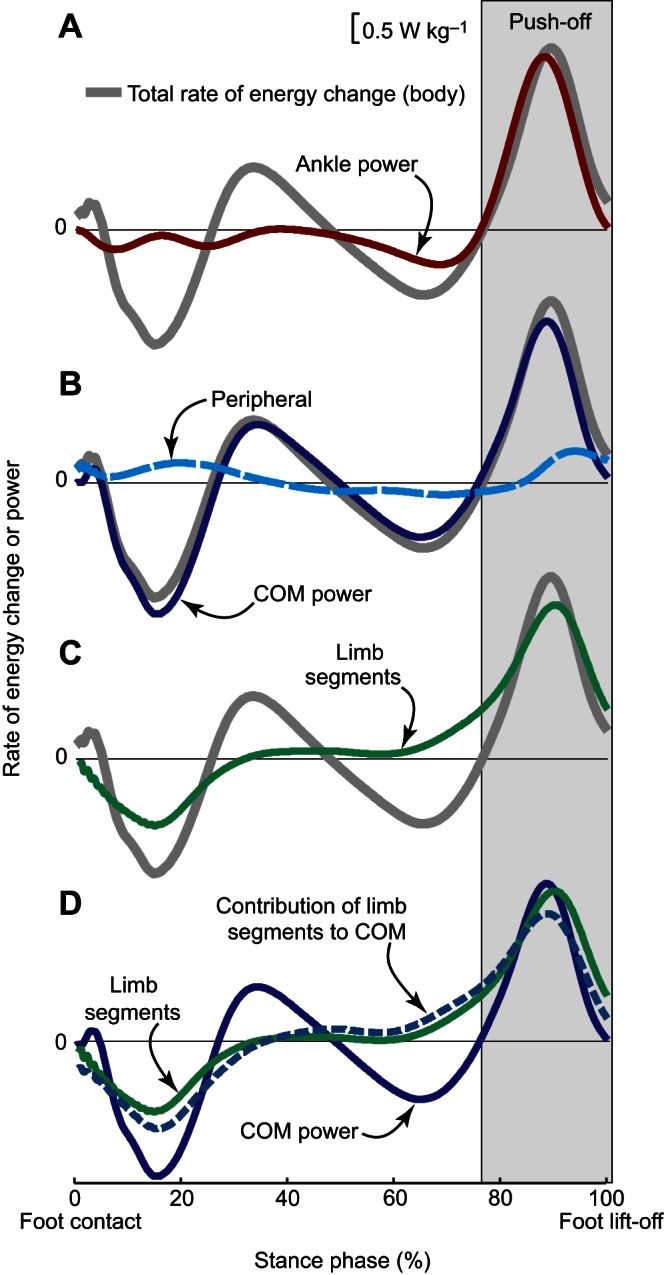
Rate of energy change (Ė) and power (work rate) estimates for an individual limb during human walking. The integrated area under each curve during Push-off (light gray box) represents the magnitude of Push-off work or energy change. (A) Ankle power (red line) overlaid on Total Ė [gray line, due to motion of and about the body's center of mass (COM)]. (B) The majority of Total Ė during Push-off is attributable to COM Ė (blue line, defined here as the rate of energy change due to push-off limb power production), and smaller contributions are from Peripheral Ė (due to segmental motion relative to the COM; dashed cyan line). (C) The majority of Total Ė during Push-off is also attributable to segmental Ė from the push-off limb (green line). (D) The contribution of limb segmental Ė (green line) to overall COM Ė (solid blue line) is shown here as a dashed blue line. During Push-off, the majority of the limb Ė goes into this contribution, which in turn accounts for the majority of COM Ė. Data depicted are inter-subject means at 1.4 m s⁻¹ (N=9; Zelik et al., 2015a).

Controversy: how does ankle push-off contribute to human walking?

In summary, two plausible descriptions have been offered to explain ankle push-off contributions during walking. There is reasonable empirical evidence to support each perspective, yet these descriptions appear to be in contradiction. Caputo and Collins’ (2014) recent study using a custom-built universal device emulator to systematically vary the magnitude of ankle push-off encapsulates the dilemma nicely: on the one hand, they observed that increased ankle push-off work led to proportional increases in COM push-off work; on the other hand, they found that increased ankle push-off reduced the concurrent ipsilateral hip work that acts to pull the limb into swing, suggesting that ankle push-off contributes to leg swing acceleration.

Resolving these perspectives on the role of ankle push-off

The objective of this article is to unify these two descriptions of ankle push-off function by showing that they are not actually at odds, and that in fact both descriptions are crucial to a comprehensive understanding of gait. Below, we present several empirical biomechanical estimates of energy change and work during level-ground walking, and discuss their implications for our understanding of ankle push-off. Based on the biomechanical evidence, we conclude that the principal means by which ankle push-off affects COM mechanics is by a localized action that increases the speed and thus kinetic energy of the trailing limb – hereafter referred to as the push-off limb.

Consider the total change in mechanical energy (kinetic plus potential) of the human body over a finite period of time. Theoretically, one way to partition whole-body mechanical energy change is into (1) energy changes that are due to the motion of the body's COM, plus (2) energy changes that are due to motion relative to the body's COM (Greenwood, 1988). We refer to these as COM and (capitalized) ‘Peripheral’ energy changes, respectively. Empirically, these quantities can be estimated from the time integrals of COM and Peripheral rates of energy change. We can also sum COM and Peripheral rates of energy change together before integrating, and we refer to the resultant time integral as (capitalized) ‘Total’ energy change (Zelik et al., 2015a). Standard gait analysis measures can be analyzed to provide reasonable estimates of COM (Cavagna et al., 1963; Donelan et al., 2002b), Peripheral (Cavagna et al., 1964, 1977; Willems et al., 1995) and Total mechanical energy changes (Zelik and Kuo, 2012; Zelik et al., 2015a) during various locomotor activities. When studying walking, it is preferable to parse out contributions from the leading and push-off limbs, which oppose each other during double support (Donelan et al., 2002b). However, to discuss individual limb contributions it is necessary to momentarily shift our language to COM work (or its derivative, COM power), as this can be estimated empirically for each limb, from the limb's ground reaction force (Donelan et al., 2002b; Zelik et al., 2015a). Individual limb COM work reflects the mechanical work that would be performed by the ground reaction force under one foot if it were applied directly to the COM as it moves; it is used as an estimate of work contributions from the entire limb. During the ‘Push-off’ phase of walking, there is a large burst of COM work from the push-off limb, whereas Peripheral energy change of the push-off limb is relatively small (Fig. 2B). Here, we use the capitalized term ‘Push-off’ to unambiguously signify the period of positive push-off limb COM power near terminal stance and immediately prior to foot-lift (Fig. 2) (Kuo et al., 2005; Zelik and Kuo, 2010). Thus, when partitioning energy into COM versus Peripheral terms, we conclude that push-off limb COM work (i.e. the contribution of push-off limb forces to COM energy change) is dominant during Push-off (Fig. 2B).

An alternative way to partition Total mechanical energy change is into contributions from individual body segments. For simplicity of discussion, it is convenient to group segments into subsets: (1) push-off limb (thigh, shank, foot of the push-off limb), (2) leading limb and (3) head–arms–trunk (HAT). If one records three-dimensional whole-body kinematics and treats the body as a system of rigid linkages, then it is straightforward to estimate changes in kinetic (translational and rotational) and potential (gravitational) energy of each body segment during the Push-off phase of walking. This accounting neglects any elastic potential energy (e.g. stored in tendons and ligaments acting about the joints), because it cannot be captured using this segmental approach. Nonetheless, results from this segmental energy analysis indicate that the vast majority of positive energy change during Push-off is due to increasing energy of the push-off limb (Fig. 2C), specifically to increasing speed and kinetic energy of the limb segments (not gravitational potential energy), consistent with prior observations (Hof et al., 1992; Meinders et al., 1998; Winter and Robertson, 1978). Energy changes due to the remainder of the body (leading limb plus HAT) are comparatively small during Push-off (Winter, 1979). Thus, when partitioning energy according to different groups of segments, we conclude that push-off limb energy change is dominant during Push-off (Fig. 2C).

Next, we can ask the crucial question to resolve these apparently discrepant results: how much of this limb segmental energy change during Push-off also appears as COM energy change? To answer this question, we need an estimate of the push-off limb's contribution to COM energy change. To obtain this estimate, we begin with the push-off limb's absolute change in energy (Fig. 2C) during Push-off, and then subtract out its Peripheral energy change (i.e. change in push-off limb energy relative to the body's COM; Fig. 2B). Under normal walking conditions (1.4 m s⁻¹), the vast majority (>85%, Fig. 2D) of push-off limb energy change contributes directly to COM energy change during Push-off. This observation is consistent across gait speed: at 0.9 m s⁻¹, >80% of segmental energy change contributes to COM energy change, and at 2 m s⁻¹ this contribution is >90% (based on re-analysis of data from Zelik et al., 2015a).

Unified understanding of ankle push-off

Based on the work and energy analyses above, we posit that the principal means by which ankle push-off affects COM mechanics is by a localized action accelerating (increasing the speed of) the push-off limb. The key to this unified understanding is that even though the mass of the limb is a small part of the mass of the body, it contributes significantly to the body's dynamics owing to its substantial velocity changes. Thus, limb motion has substantial influence on COM energy changes. To illustrate this, consider if the body's whole mass were concentrated in a single rigid limb, and the HAT were massless. In this case, leg swing (motion of a rigid pendulum) would correspond directly with the COM motion. This is similar to a playground swing: as a child swings back and forth, the COM of the system follows the swing motion. An external power input (i.e. a push) could be said to primarily contribute to the swinging action and also primarily contribute to the motion of the system's COM. This characterization remains accurate even if the mass of the swing set's frame is included: the system's COM location and velocity are dominated by the heavier frame, but changes in these states (and thus in kinetic and potential energy) are still controlled by the mass of the lighter swinging child. In a similar way, acceleration of swing limb mass (the child in the analogy), though it is only a small portion (∼20%; Dumas et al., 2007) of the total body mass (frame plus child), is a dominant contributor to changes in COM energy and momentum.

The relationship between limb motion and COM motion can be formalized by considering the whole body as a system of segments, divided into two subgroups called the push-off ‘limb’ (mass m_limb) and ‘remainder of body’ (ROB, mass m_ROB of leading limb plus HAT). The whole-body COM (mass M=m_limb+m_ROB, position 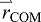) is defined by the COM positions of the two segment groups, 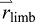and :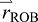

(1)

Successive time derivatives of COM position yield COM velocity and acceleration:

(2)

(3)

The first term on the right of Eqn 3 shows that limb acceleration contributes to COM acceleration according to the limb's fraction of body mass: 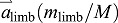. Furthermore, Eqn 3 shows that even though m_limb is relatively small, 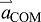can be dominated by 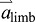if 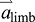is large compared with 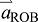(i.e. limb acceleration is large compared with acceleration of the ROB). This is precisely the situation in human walking during push-off: limb acceleration 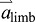is large, forward and upward, while 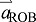is small, downward and rearward (Lipfert et al., 2014). Analogous derivations can also be performed to show that the same analytical relationships exist for kinetic and potential energy of the COM. Smaller masses can contribute significantly to whole-body energy change when they undergo sufficiently large velocity or positional changes. Note that this derivation considers only linear motion of the COM. Because COM energy changes are observed to be dominant during Push-off (Fig. 2B, compared with Peripheral), we conclude that this simplified derivation (Eqns 1–3) captures the main effects of interest.

Implications

This unified view provides an analytical link between the whole-body and segmented (limb versus ROB) perspectives. Future studies should clearly specify the intended perspective whenever an interpretation is made. Furthermore, it is important to maintain the unified viewpoint at all stages, lest a limited perspective lead to incorrect conclusions. For example, consider the hypothesis that push-off reduces collisional energy loss associated with landing on the contralateral leading limb. This hypothesis appears prima facie incompatible with the finding that energy from ankle push-off does not propagate through the hip joint to the ROB (Hof et al., 1992; Lipfert et al., 2014; Meinders et al., 1998; Winter and Robertson, 1978). However, such a conclusion erroneously attributes the subsequent landing dynamics only to the ROB. In fact, the push-off limb is still part of the body, and therefore still affects leading-limb dynamics (load, deflection and energy absorption). If the push-off limb were not launched up and forward by push-off, it would have to be yanked up and forward by a hip joint reaction force just to stay attached to the body. This joint force would increase the force transmitted to ground through the leading limb, and thereby potentially increase limb deflection and energy absorption. Thus, push-off can act locally on one limb, and yet still have effects on remote segments of the body, as suggested by COM mechanics analyses (Adamczyk et al., 2006; Bertram and Hasaneini, 2013; Donelan et al., 2002a; Kuo, 2007; Kuo and Donelan, 2010; Kuo et al., 2005; Ruina et al., 2005). However, it is important to note that the magnitude of this effect (e.g. collision reduction) may be less than predicted from simple models with concentrated pelvic mass and rigid collisions. Overall, this example illustrates the need for continual vigilance when comparing and contrasting results obtained with different methods and interpreted from different perspectives.

The means by which ankle push-off affects COM mechanics also has important implications for understanding simultaneous hip power contributions during Push-off. Because ankle push-off provides a localized action increasing the energy of the push-off limb, increased ankle push-off may serve to reduce hip-powering demands. Likewise, increased hip powering (pulling the limb into swing) may reduce ankle push-off demands. There is empirical evidence in support of both of these contentions: increased ankle push-off reducing hip work (Caputo and Collins, 2014; Koller et al., 2015; Lewis and Ferris, 2008) and increased hip powering reducing ankle push-off (Lenzi et al., 2013).

A key contributor to the historical confusion and disagreement over the role of ankle push-off may be that multiple, disparate definitions of ‘leg swing’ are found in the biomechanics literature. Studies that have emphasized leg swing acceleration as the primary role of ankle push-off have generally used the term ‘leg swing’ to refer to the absolute motion (or energy change) of the push-off limb relative to the ground (e.g. Meinders et al., 1998; Winter and Robertson, 1978). In contrast, studies emphasizing COM mechanics typically define leg swing as relative motion (or energy change) of the push-off limb, with respect to the hip or COM (e.g. Doke et al., 2005; Kuo, 2007). The problem is, if the former definition is applied, then one observes substantial leg swing energy change during Push-off (limb segment energy change; Fig. 2C), whereas with the latter definition, one finds very little leg swing energy change (Peripheral energy change; Fig. 2B). Both definitions are reasonable, but they apply to different effects and questions. Furthermore, these are not the only two conceivable definitions of leg swing (e.g. one could define leg swing solely as motion orthogonal to the limb itself). To avoid further confusion, future publications should be careful to explicitly define leg swing and to properly contextualize findings and interpretations.

Limitations of this perspective

One limitation to the empirical biomechanical analyses presented in Fig. 2 is that they are unable to capture multiarticular muscle kinetics, which can have complex and often non-intuitive effects on inter-segmental dynamics (Cleather et al., 2015; Siegel et al., 2004; Zajac et al., 2002). Thus, none of these experimental methods provides a definitive answer on how work performed by muscle–tendon units about the ankle transfers to non­adjacent segments, or how (mechanistically) ankle push-off facilitates economical gait. Given that both the foot (distal to the ankle) and the knee are estimated to perform substantial negative work during Push-off (Siegel et al., 1996; Takahashi and Stanhope, 2013; Zelik et al., 2015a), some of the ankle push-off work may not directly accelerate the swing limb, nor the COM. Rather, a portion of ankle push-off might instead serve to offset simultaneous energy absorption or dissipation elsewhere in the body (e.g. because of soft tissue deformations or negative muscle work). The use of computational modeling approaches in conjunction with empirical measurements of muscle mechanics may offer promise in unveiling multiarticular muscle dynamics (e.g. Honert and Zelik, 2016), which could help advance our mechanistic understanding of ankle push-off dynamics. Another limitation is that the energy analyses presented are used to understand speed (scalar) changes of the body segments, but not velocity (vector) changes. This energy approach was useful to explore the role of ankle push-off work (also a scalar quantity), but alternative analyses such as impulse-momentum calculations (Lipfert et al., 2014) may be more appropriate to explore and understand the individual vector components of acceleration. Generally, where we have discussed acceleration in this Commentary we are referring specifically to the time rate of change of speed (a scalar quantity), and not to acceleration orthogonal to the velocity vector, as this alters the orientation but not magnitude of the velocity. Finally, we note that although the energy analysis presented here was useful for understanding the dominant burst of ankle push-off work in walking, this type of analysis alone may be less effective at elucidating situations in which there are multiple sources of work on a similar scale. For instance, if two muscles (or joints) each performed substantial positive work while two other muscles performed comparable negative work, then it may be unclear how these muscle contributions should be interpreted (e.g. whether one muscle could be identified as the primary source of any net change in energy) without additional information or auxiliary analysis.

Alternative perspectives on ankle push-off

Other perspectives on the role of ankle push-off during gait have also been presented in the literature. For example, one perspective contends that the primary function of the ankle plantarflexors is to preserve the forefoot rocker (the progression of the limb over the metatarsal joints after heel rise; Perry, 1992), a description framed principally in terms of the kinematic behavior of the foot. This idea is partially in line with the idea that the ankle plantarflexors facilitate leg swing (at least over the second half of push-off), but not entirely in agreement regarding the primary function of ankle push-off (Perry, 1992). Likewise, Saunders et al. (1953) described the role of the ankle plantarflexors kinematically, as a means to smooth the COM trajectory during the step-to-step transition. Sutherland et al. (1980) focused on the role of the plantarflexors in stabilizing the ankle and knee, restraining forward rotation of the tibia and minimizing vertical oscillation of the COM. These interpretations are essentially kinematic, and they represent early efforts to describe the complex interplay between foot geometry and limb dynamics. Ankle–foot interplay is not yet fully understood (Zelik et al., 2015b), but is the subject of active research in theoretical biomechanics (Adamczyk and Kuo, 2013; Adamczyk et al., 2006; Hansen and Wang, 2010; Hansen et al., 2004; Ruina et al., 2005; Srinivasan et al., 2009), as well as in applied domains such as prosthetics (Barocio et al., 2014; Boone et al., 2013; Curtze et al., 2011; Hansen and Childress, 2010; Hansen et al., 2006) and orthotics (Fatone and Hansen, 2007; Fatone et al., 2009; Vanderpool et al., 2008). Because the aforementioned kinematic perspectives do not directly address the question of what happens to the large burst of ankle push-off power, they are not amenable to the energy/work analysis and interpretation provided here. We have therefore limited our discussion to the controversy related to the two main kinetic interpretations, leaving further convergence with kinematic aspects for future work.

Conclusions

 The debate whether push-off from ankles

 powers leg swing or COM rankles.

  But a unified view

  indicates both are true:

 two effects inextricably tangled.

The purpose of this article was to coalesce the descriptions of ankle push-off during normal, healthy human gait. Our intention was not to generalize these interpretations to every gait pattern (e.g. it is known that walking is also possible without an ankle joint), nor was our goal to answer the more challenging question of why the ankle musculature performs push-off. It is worth noting that some such explanations have been proposed, but none have been conclusively demonstrated. For instance, the push-off-collision hypothesis (Adamczyk and Kuo, 2009; Kuo, 2002; Kuo et al., 2005; Ruina et al., 2005) has led to a variety of empirical observations, some in apparent support of this hypothesis (e.g. Adamczyk and Kuo, 2015; Houdijk et al., 2009; Huang et al., 2015; Jackson and Collins, 2015; Segal et al., 2012; Soo and Donelan, 2012; van Engelen et al., 2010) and some in apparent contradiction (e.g. Caputo and Collins, 2014; Malcolm et al., 2015; Vanderpool et al., 2008).

In summary, ankle push-off primarily contributes to both leg swing and to COM acceleration during human walking. Work provided by ankle push-off manifests principally as increased speed of the push-off limb. The push-off limb increases in segmental kinetic energy with little energy transferred to the torso through the hip. But because the limb is included in body COM computations, this localized segmental acceleration also accelerates the COM, and most of the segmental energy change also appears as COM energy change. It is, in fact, the same energy change in both the limb and the COM, with only a small part of limb energy being purely Peripheral (non-COM). Thus, interpretation of ankle mechanics should abandon an either/or contrast of leg swing versus COM acceleration. Instead, ankle function should be interpreted in light of both mutually consistent effects.