Learning temporal rules to forecast instability in continuously monitored patients

Abstract

Inductive machine learning, and in particular extraction of association rules from data, has been successfully used in multiple application domains, such as market basket analysis, disease prognosis, fraud detection, and protein sequencing. The appeal of rule extraction techniques stems from their ability to handle intricate problems yet produce models based on rules that can be comprehended by humans, and are therefore more transparent. Human comprehension is a factor that may improve adoption and use of data-driven decision support systems clinically via face validity. In this work, we explore whether we can reliably and informatively forecast cardiorespiratory instability (CRI) in step-down unit (SDU) patients utilizing data from continuous monitoring of physiologic vital sign (VS) measurements. We use a temporal association rule extraction technique in conjunction with a rule fusion protocol to learn how to forecast CRI in continuously monitored patients. We detail our approach and present and discuss encouraging empirical results obtained using continuous multivariate VS data from the bedside monitors of 297 SDU patients spanning 29 346 hours (3.35 patient-years) of observation. We present example rules that have been learned from data to illustrate potential benefits of comprehensibility of the extracted models, and we analyze the empirical utility of each VS as a potential leading indicator of an impending CRI event.

Introduction

Step-down units (SDUs) are hospital wards that admit patients with disease severity requiring increased monitoring and care beyond what is routinely provided in standard hospital wards, yet not requiring active organ support, as is the case in intensive care units. Patients admitted to SDUs are presumed to have a significant potential for complications manifested by physiologic instability. Accordingly, cardiorespiratory instability (CRI) is frequent in SDU patients and routinely requires acute interventions and, at times, transfers to higher levels of care. Enhanced ability to identify patients with impending CRI prior to its overt manifestation could benefit SDU patients by allowing earlier interventions with less intensive treatment and fewer potential complications. Situationally aware clinicians could potentially prevent such sentinel CRI events from improving these patients’ processes of care and outcomes. Several early warning scoring and integrated monitoring systems have been recently developed.^1–5 For example, we previously reported the ability of such a system to detect CRI an average of 9 minutes before a sentinel event.⁵ However, such systems suffer from 3 major weaknesses: (1) the integrated indices convey a measure of the present risk without considering the likely future trajectory of risk, (2) the scores represent mortality risk and not instability in advance of mortality, and (3) the derivation of the present status is quantified in terms of a single numeric score with limited or no information about the specific factors contributing to that score. Such “black-box” approaches are unappealing to clinicians. Indeed, a system that could provide both a reliable forecast of future instability and some comprehension of the reasons on which the forecast is based might lead to better system acceptance due to increased transparency. We present a rule-based, data-driven approach to develop a reliable CRI forecasting system that constructs models comprehensible to clinicians, providing an interpretable explanation through the rules on which the early warnings of potential future CRI events are generated.

Materials and Methods

Clinical dataset

Our dataset includes 297 SDU admissions, registered over 8 weeks, totaling 29 346 hours of multivariate physiologic monitoring data. Patients had undergone continuous noninvasive measurement of common vital signs (VSs): heart rate (HR), respiratory rate (RR), and blood capillary oxygen saturation (SpO₂), and intermittent noninvasive measurements of blood pressure (BP). These VSs are sampled every 20 seconds, except for BP, which is sampled at a minimum every 2 hours. CRI events are first identified based on clinically accepted thresholds defining instability,⁶ forming the ground-truth set for the events to forecast, and then annotated by a committee of expert physicians through a previously described and validated protocol,⁷ detailed below:

1. Identify all periods in patient data where at least 1 of the following CRI threshold limit criteria is exceeded for >80% of the last 3 minutes:

2. HR <40 or >140 beats per minute

3. RR <8 or >36 breaths per minute

4. SpO₂ <85%

5. Systolic BP <80 or >200 mmHg

6. Diastolic BP >110 mmHg

7. Each identified event is then separately adjudicated by 2 expert physicians who annotate it as real or artifact based on their prior clinical expertise in clinically viewing real event and artifactual monitoring signatures. Additionally, the physicians quantify the confidence of their determination (using an integer score between 0 and 3). Physicians are blinded to their paired physician’s scores.

8. If the 2 physicians agree and indicate a sufficient confidence (≥2), the analyzed event is labeled accordingly.

9. If the 2 physicians disagree, or indicate lack of confidence (<2), the case is escalated to a third independent reviewer. If there is still disagreement or low confidence, the event is reviewed and discussed at a 4-member committee meeting.

10. If the committee cannot agree on the event, it is considered too uncertain for model training and set apart.

11. All artifacts are excluded from training data.

12. All non-excluded events are considered as real CRI episodes.

Of the 297 patients, 43% exhibited at least 1 real CRI event during their SDU stay. Once patients exhibit CRI, they have a substantially increased propensity for CRI reoccurrence.⁸ Our analysis focused on forecasting the initial CRI, because we presumed reactive treatment to the initial CRI event could obfuscate prediction rules for subsequent CRI events. The cumulative time span of the resulting censored dataset decreased to 1.43 patient-years and included 130 initial CRI events.

Data preparation

Raw VS data records contained 5 channels of measurement: HR, RR, SpO₂, systolic BP (SysBP), diastolic BP (DiaBP), and mean BP (MeanBP) reported at 1/20 Hz. We processed each resulting time series to convert them into features that would be suitable for use with our temporal rule-learning algorithm.

We first extracted scalar features. These included multiple statistical characteristics of VS time series observed at various time scales, plus various measures of signal quality. An example of a scalar feature is a “moving average of the HR over the last 5 minutes” (eg, its value at 11:37 a.m. for a particular patient on a specific day of an SDU stay reflects the mean value of the patient’s HR observed between 11:32 a.m. and 11:37 a.m.). Next, each scalar feature was discretized to be represented using event features. Event features typically reflect change points in time series. An example of an event feature is a discrete entry generated whenever “5-minute average of HR becomes ≥80 bpm.” This specific event informs about a particular exceedance of a specific HR statistic. We extracted a wide variety of such event features using different base statistics (eg, 5-minute moving average) and various thresholds (eg, HR ≥80 bpm). Note that the number of thresholds used at this stage of data processing was much larger than thresholds used to define CRI. Their number and granularity was a design decision (eg, for HR we used every integer threshold value between 30 and 150 bpm; for RR, all integer values between 2 and 50; and for SpO2, all integer values between 80 and 95). Additionally, calendar and time-of-day information was added in scalar (eg, current clock time) or event feature form (eg, “today is Monday”).

A total of 8299 distinct features were extracted from VS data, including 225 scalar and 8074 event features, not including the target events to be forecasted. Event features varied in sparsity, but the total number of their unique instances exceeded 100 million (8730 different events on average per monitoring hour, or 1 event of each type occurring on average every 55 minutes). Similar to our previous work,⁹ VS feature extraction aimed to be comprehensive by design, as we could not be certain a priori which of the large number of extracted features, or their combinations, would be informative of the impending CRI. We allowed our inductive learning algorithm to identify these informative features automatically, and our rule fusion algorithm helped to create conservative sets of induced rules to remedy overfitting.

Extraction of temporal association rules

We considered association rules with conjunctive statements serving as preconditions, and consequents in the form of distributions of probability of occurrence of a specific type of an event, spanning specific time intervals, so-called Temporal Interval Tree Association (TITA) rules. A TITA rule can be applied to data available at a certain point in time in an attempt to forecast a particular event of interest for which it was trained, if the current data matches its precondition. The precondition, also referred to as the rule's body, is a set of symbols connected with temporal constraints. TITA rules are able to simultaneously express both sequences of discrete events and numerical threshold equations. Figure 1 shows 3 simple examples of TITA rules.

Figure 1.

Three examples of TITA rules: e1, e2, and e3 are generic events; s1 is a scalar and is assigned to a numerical value at each point in time. Histograms represent the probability distributions of the time difference between activation of the rule body and activation of the rule head. When the body of a rule is matched, the histogram is used to infer the probability distribution of the predicted event’s time of occurrence. Intervals between 2 events in the rule’s body define constraints on the time difference between the occurrences of these 2 events. Note that in this work, we focused on forecasting CRI events, therefore the head of the rules (ie, e1 events) will always be CRI.

To extract TITA rules from data, we used a TITA Rule Learning (TITARL) algorithm previously described,¹⁰ and later extended to forecasting applications.¹¹ In brief, the TITARL rule extraction procedure was as follows:

1. Extract all unit rules with a single component in its precondition statement (eg, “IF HR crosses-up 88 bpm, THEN CRI will occur within the next hour”).

2. For each newly available rule, identify and evaluate the information gain of each of the available additional components in its precondition statement (eg, “IF HR crosses-up a threshold of 88 bpm AND if the RR is <8 breaths/minute, THEN CRI will occur within the next hour”). Various optimizations were developed to efficiently handle the large amount of possible additional components.¹⁰

3. Select a (non-uniform) random subset of additional components generated in step 2.

4. Build and store the (single) rule created from the most informative additional components selected in step 3.

5. Repeat step 2 until the user-selectable maximum number of rules has been extracted.

In the process, rules exhibiting low confidence (probability of observing an event of interest when a rule's precondition statement is true) and/or low support (fraction of predicted events of interest) and/or low usage (number of instances when the rule’s precondition statement is true) are discarded by the algorithm using various constraints and heuristics (eg, a priori support pruning¹¹). In the application scenario presented here, we extracted rules that expressed correlations between CRI events (target events) and the VS data observed during periods of time preceding the events.

Assembly of a forecasting model

TITARL, like any inductive rule-learning algorithm, may and often does extract very large sets of presumably useful rules. Applying all such rules individually to forecast events of interest may work for relatively small uncomplicated datasets, but this approach often fails in most real-world applications due to overtraining, dataset complexities, and intra-rule redundancies. As an example, finding 2 distinct rules that match data in close temporal proximity to each other may or may not be indicative of an elevated probability of CRI to occur, when compared to the probability stemming from each of these rules individually. This can happen if the rules are not fully independent. In datasets without apparent highly predictive rules, resolving such interdependencies is essential to obtain reliable forecasting models.

Instead of using a direct prediction, we aggregated the complete set of extracted TITA rules into a single forecasting model using a rule fusion algorithm introduced previously.¹¹ The resulting model $P_h^w\left(t\right)$ is the fused probability at time t, across a set of rules, that CRI will happen between h and h + w in the future, while only considering data available both at and before time t. Here, $\text{h}$ denotes the forecast horizon and $\text{w}$ denotes the width of the time window of predicted occurrence of a future CRI event.

The rule fusion algorithm works by considering each rule as an individual characteristic or feature of a dataset. The value of each rule's feature in this dataset is the predicted probability of observing the target event according to this rule. The mapping function from the rule-based features to the resulting forecast model $P_h^w\left(t\right)$ can be learned using a classifier, such as a Random Forest model. The following summarizes the procedure:

Function $P_h^w\left(t\right)$ is as follows:

1. For each rule $r_i$, we define the score metric $f_i(t)$ as the probability of observing a target CRI event in the time window $\left[t+h,t+h+w\right]$ according to the rule $r_i$ while only considering data available at and before time t, which is referenced to the subsequent CRI event.

2. We populate a classification dataset $M$ where each row represents a unique time such that at least 1 TITARL rule is activated, and each column represents 1 of the scores $f_i(t)$. $M_{j,i}$ is equal to the value of $f_i(t_j)$ with $t_j$ being the time associated with row j.

3. The output of each row j is defined as the presence or absence of the target CRI event in the time window$\left[t_j+h,t_j+h+w\right]$.

4. Finally, we train a Random Forest classifier on $M$. This classifier represents $P_h^w\left(t\right)$.

Although alternative classification models capable of handling highly dimensional numeric data could also be used, we chose Random Forest based on favorable previous experience when applied to similar tasks.

Metrics of performance

Our primary aim was to quantify the operational utility of the obtained CRI forecasting models. We also studied the importance of the individual rules, specific VSs, and the individual features extracted from VS data in making event forecast decisions.

We characterized the utility of forecasting models using the Activity Monitoring Operating Characteristic (AMOC) approach, which is a useful method for evaluating event detection and event forecasting systems.¹² It depicts the tradeoff between forecast horizon and specificity of predictions made by the evaluated system. An AMOC curve is obtained by changing a sensitivity setting of the evaluated system and tracking the resulting changes in the attainable prediction look-ahead time and the correlated changes in the rate of false predictions made by the system. Typically, longer forecast horizons imply higher rates of false alerts, and vice versa.

We also used a temporal version of a Receiver Operating Characteristic (ROC). ROC summarizes the predictive abilities of binary classifiers by plotting their performance with regard to true positive rates (also called recall or sensitivity) and false positive rates (1 − specificity). Standard ROCs do not reflect temporal aspects of performance, which can be resolved by producing a number of separate ROCs, 1 for each of the selected settings of the forecast horizon. Alternatively, we used a Temporal ROC (T-ROC) to depict the tradeoff between the true positive rate and the forecast horizon.

In our quantitative performance analyses, we used a 10-fold cross-validation protocol. To ensure minimum bias of the results, each patient’s VS data prior to the CRI event was used exclusively in either training or testing subsets of data in each iteration of the cross-validation procedure.

We compared the empirical performance of our temporal rule learning models to a standard Random Forest classifier¹³ operating on the same input feature set. Random Forest often outperforms other approaches on complex datasets or on datasets with large numbers of input dimensions.^13–17 For completeness, we also reported performance that can be attained by directly using the individual VS to forecast instability (increase and decrease in HR and RR, and decrease in SpO₂). By convention, we assigned the name of an index based on a single VS as composed of the name of the VS followed by an up or down arrow indicating the direction of exceedance (eg, HR↑ stands for increasing heart rate over a given threshold). We reported the empirical performance of these models using the AMOC and T-ROC frameworks.

In order to characterize the importance of individual rules used by our system, we also evaluated their individual impact on making effective forecast predictions.

Results

Forecasting performance

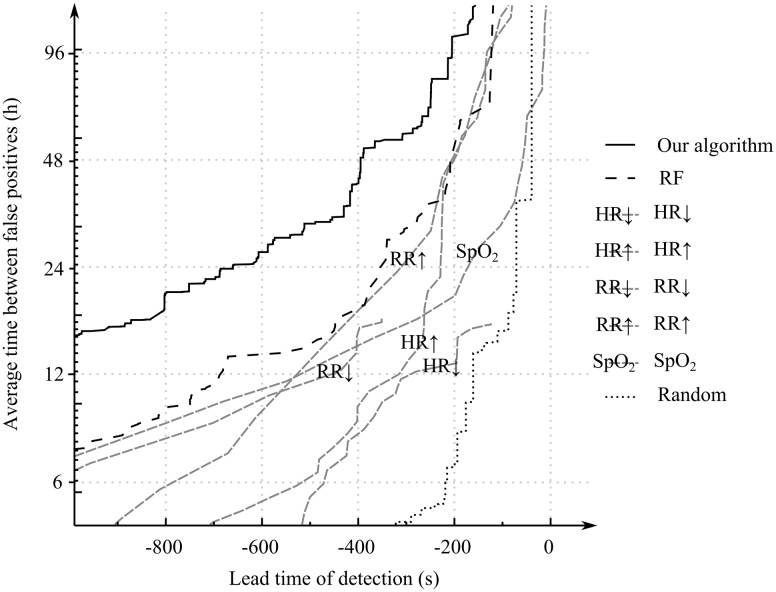
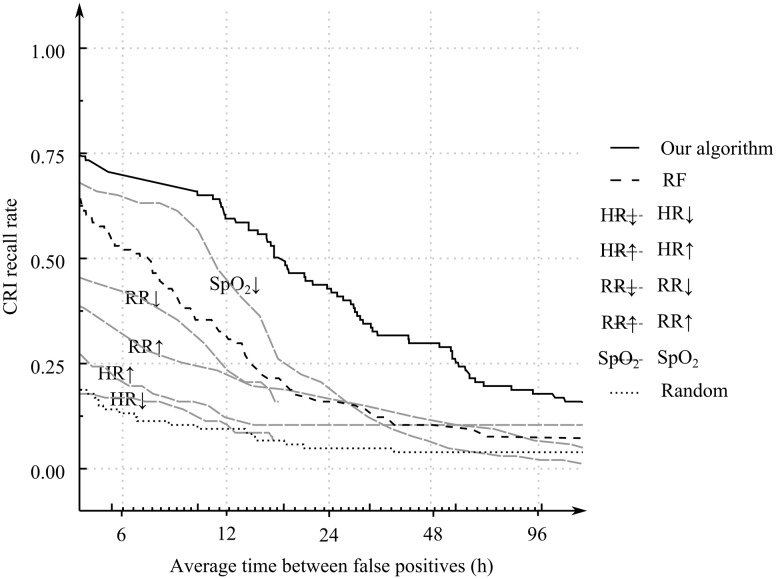
Figure 2 shows the results of the 10-fold cross-validation–based AMOCs of our temporal rule learning system, the Random Forest model applied to the featurized VS data directly without using TITARL, and those obtained via direct use of VSs as predictors of future CRI events. Table 1 presents selected performance scores that can be read from the AMOC plots shown in Figure 2. Figure 3 shows results of the T-ROC of our TITARL + Fusion algorithm, Random Forest, and direct use of VSs as predictors of future CRI events. The sensitivity of the TITARL + Fusion algorithm is consistently better than all competing models.

Figure 2.

Activity Monitoring Operating Characteristics of TITARL + Fusion algorithm, Random Forest, individual vital sign–based forecast models (using, respectively, HR, RR, SpO₂), and the random predictor

Table 1.

Average forecast horizon for fixed average intervals between consecutive false positive alerts and average interval between consecutive false positive alerts for fixed forecast horizons

Reported value	Avg. forecast horizon		Avg. false positive interval
Fixed parameter	Avg. false positive interval		Avg. forecast horizon
Fixed parameter value	12 h	24 h	2 min	10 min
TITARL + Fusion	17 min 52 s	10 min 58 s	171 h	28 h
Random Forest	11 min 25 s	5 min 52 s	75 h	14 h
SpO2 ↓	8 min 38 s	2 min 50 s	29 h	11 h
HR ↑	5 min 14 s	3 min 46 s	102 h	5.2 h
HR ↓	4 min 50 s	–	–	3.7 h
RR ↑	8 min 45 s	5 min 10 s	98 h	9.3 h
RR ↓	7 min 35 s	–	–	10 h
Random	2 min 39 s	1 min 9 s	14 h	–

Figure 3.

Temporal Receiver Operating Characteristics of TITARL + Fusion algorithm, Random Forest, individual vital sign–based forecast models (using, respectively, HR, RR, SpO₂), and the random predictor

The 2 criteria applied directly to VS data that provided the best performance in this class of very simple models included detection of low SpO₂ values (SpO₂↓) and high respiratory rate values (RR↑). Random Forest enables condensing of the information provided in all VSs simultaneously, and it is not surprising that it performed better than any model based on an individual VS, while TITARL + Fusion provided the best result overall and was found consistently better than the competing models. Our algorithm was able to issue CRI forecast alerts on average 17 minutes and 51 seconds before onset of the CRI events if false alerts are tolerated at an average frequency of once every 12 hours. If the tolerance of false alerts is reduced twofold (to once every 24 hours), the average effective forecast horizon reduces to 10 minutes and 58 seconds, whereas the Random Forest classifier yielded effective forecast horizons of, respectively, 11 minutes and 24 seconds and 5 minutes and 51 seconds for the same settings of false alert tolerance (12 and 24 hours). Fixing the average forecast horizon to 2 and 10 minutes yielded 171 hours and 28 hours of average interval between false alerts when using TITARL + Fusion. Corresponding results for the Random Forest were 75 hours and 14 hours. The performance of other tested alternatives was markedly worse. These results illustrate the importance of extracting specialized temporal and sequential patterns such as temporal rules when forecasting discrete events using noisy, sparse, and complex multidimensional data.

Specific rules learned from data

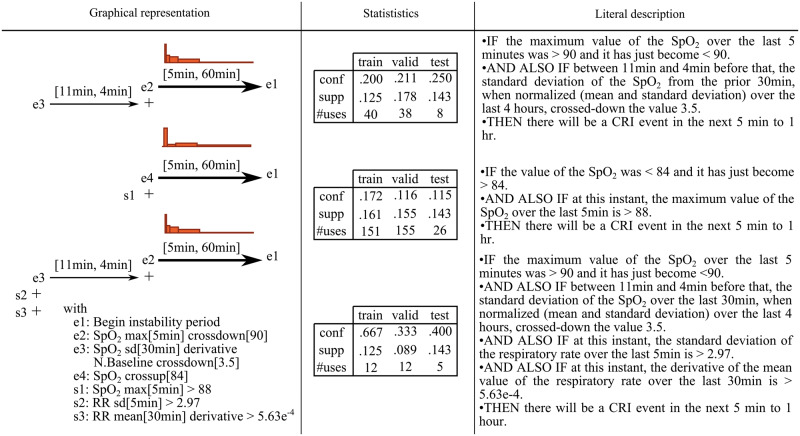
TITARL forecasts are generated from the association rules it has extracted, but not all rules are equally important. Removing one rule might significantly impact the performance of the model, while removing another rule might have only marginal impact. Due to the overwhelming number of attainable rules, it is generally unfeasible for a user to study each rule individually. Therefore, the ability to automatically order the rules by their importance and then present the top rules to clinicians for interpretability is a potentially powerful approach to both validate the existing domain knowledge and discover new clues. To address this, we used a Random Forest measure of feature importance to characterize the usefulness of each rule. Typically, rules with small confidence, overtrained rules, or rules subsumed by some other more powerful predictive rules bring a low relative gain of information to the joint model and therefore have low importance. Figure 4 shows the 3 rules with the highest importance measure values (the first rule being the most important). Looking at these rules, we first observe that SpO₂ level is strongly correlated with upcoming CRI events. However, the SpO₂ value is not used directly, but derived features are used instead. We note that 2 of the top 3 rules rely on comparing SpO₂-derived features to a long-term baseline. Operationally, any single rule may carry a rather low predictive value, but when the rules are combined into a joint forecasting model using our fusion algorithm, predictive reliability typically increases substantially.

Figure 4.

The 3 most important temporal association rules extracted to forecast CRI identified by TITARL. For each rule, we show its graphical representation and report basic statistics (confidence, support, and number of uses) observed on the training, validation, and testing data, respectively. We also provide a literal, plain English description of each rule. Since the experiment was run with a 10-fold cross-validation, the test dataset is 9 times smaller than the train and validation dataset in each iteration. This explains lower usage frequencies of the rules observed on the testing data when compared to the same figures for the training and validation sets.

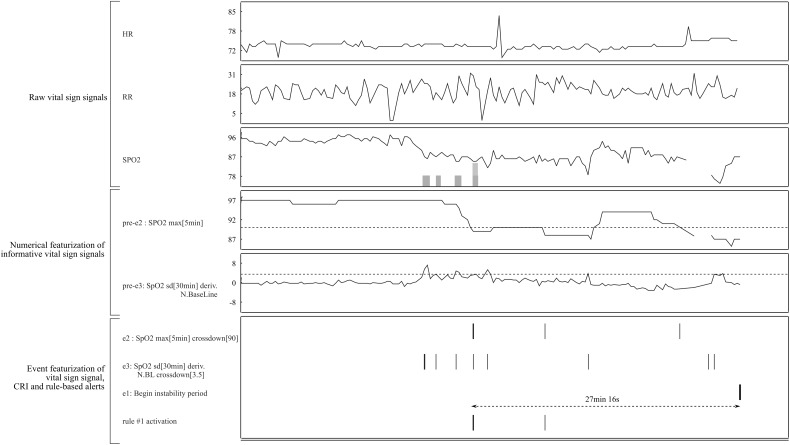
In practice, multiple rules can be active at any given time. When the system raises an alert, displaying the most important active rules can provide insight as to the reason for this alert to trained users. For other users, augmenting the display of the VS according to the structure of the active rules (without explicitly displaying the rules) could increase both confidence in and acceptance of the system without requiring users to view and interpret perhaps complex rules. Figure 5 shows an example of a display enhanced for a particular CRI alert preceded by activation of the first rule in Figure 4. In practice, all features derived from the same VSs could be displayed on the same plot with specific background/foreground coloring.

Figure 5.

Example of an enhanced bedside monitor display for a particular CRI alert (the right part of the plot). Top rule #1 (Figure 4) becomes active 27 minutes before the onset of the CRI. This rule relies on 2 events (e2 and e3), which in turn rely on the featured signal (pre-e2 and pre-e3). When the rule activates, displaying the current and past values of e2, e3, pre-e2, pre-3 amd the thresholds used to compute e2 and e3 can provide an indication of the reason for issuing the alert. To further simplify display of the justification, we can show just the raw time series of the VSs observed during periods of time that led to rule activation (in this case, periods of suspicious behavior of SpO₂ marked by the shaded areas overlaid in the plot of its time series).

Discussion

CRI events are common in SDU patients. Our method and evaluation framework provide grounds to enhance the power of CRI forecasting systems while optimizing and reducing false alerts. We introduced a new specialized temporal machine learning algorithm and evaluated its capabilities to forecast future CRI events in SDU patients. We evaluated our method using a rigorous 10-fold cross-validation protocol and compared it to a state-of-the-art machine learning algorithm, as well as to the predictions that can be obtained by using individual VS observations directly. Our findings demonstrate that a specialized temporal machine learning algorithm can significantly improve the sensitivity of CRI forecasting at an extremely low false alert rate. This result has the potential to serve as an underlying platform for an alerting system that could permit preventative CRI treatment and reduce alarm fatigue, a problem induced by the large number of false alerts generated by current physiologic monitors. Knowing the operational capacity of an SDU, one can use AMOC to identify the clinically optimal forecast horizon corresponding to a preset limit of false alert frequency. If the relative benefit of the marginal extension of the forecast horizon versus the marginal cost of increased false alert probability is known, one can identify the operationally optimal setting of the system.

This work corroborates the intuition that careful evaluation of VS departure from patients’ individual baselines and their evolution toward abnormality can be accomplished in practice, and has the potential to be clinically informative as well. This is an important consideration, since each individual may have a distinct physiological level of normalcy, in reference to which a risk of possible CRI evolution can be evaluated and quantified with greater accuracy than when using a population-based reference.¹⁸ Thus, the proposed approach can add precision to personalized medicine.

As in any machine learning exercise, data preparation and extraction of features is a crucial step and can impact performance significantly. While featurization is usually accomplished by extracting standard statistical measures or implementing current domain literature, using too many features can impair the performance of some algorithms. We demonstrate that both stages of the TITARL + Fusion methods (a priori rule mining and learning a classification model to enable fusion) provide a plausible solution to this problem.

Importantly, reported performance of any machine learning results is heavily dependent on the nontrivial problem of manually annotating medical records to provide ground truth for the algorithm. We believe that the improvements in the annotation process we previously described,¹⁹ and briefly summarized here, may also lend improvements to the performance of the presented method.

It is unlikely that all good forecasting rules map to a biologic mechanism that would make immediate physiological sense to clinicians. Yet the ability to map a few important rules to clinical mechanisms is desirable to maintain face validity of the forecast. In addition, highlighting the intervals of those VS time series that activate the rules, which in turn impacts forecast of CRI, should support clinical intuition related to the particular patient being monitored. These are relatively new utility and usability concerns, but they underscore the importance of a common forecasting rule set that must be readily interpretable from a clinical perspective to be acceptable to clinicians.

Our study has several limitations. First, patients experiencing CRI are likely to have subsequent CRI, and some patients will undergo a number of such events. We focused on predicting the first CRI of each patient (if any) to make the prediction focus uniform across patients and the prediction problem independent of prior CRIs and their potential treatments. Clearly, unstable patients may present repetitive CRI events, each defined by different physiologic processes, and it is not clear how well our approach and extracted rules would forecast the subsequent CRI events. This is a topic for further research. Second, some of the extracted rules suggest complex physiologic interactions and adaptations that may not be easily quantifiable by bedside clinicians. Thus, these rules should be used in parallel with standard VS monitoring protocols. Third, it may be helpful to test the rules extracted from our current dataset on a larger and more diverse SDU patient dataset to assess generalizability. Finally, it is unclear whether the proposed approach is amenable to application in other settings with different patient care time courses, such as the operating room, intensive care unit, general hospital ward, or outpatient setting. This will require further testing. It is reasonable, however, to expect that these same machine learning methods and protocols could be applied in other care domains where both a long forecast horizon and a low number of false alerts are required. Given the increase in the amount and types of numerical data being captured by hospital information systems, we believe that our approach has the potential to serve as an integral part of future smart alerting systems integrated with bedside monitoring and electronic health records.

Contributors

M.G.B., A.D., M.H., D.W., G.C., and M.R.P. conceived and designed the evaluation protocol and the annotation software. M.H., G.C., and M.R.P. coordinated the data acquisition and analysis and annotated the records. D.W. developed the annotation software. M.G.B. and A.D. designed and developed the proposed machine learning algorithm and ran the analysis. M.H., G.C., and M.R.P. validated the medical significance of the analysis. M.G.B. wrote the first draft of the manuscript. All authors contributed to subsequent and final drafts.

Funding

This work was partially supported by National Science Foundation grant number 1320347 and National Institutes of Health grant number NR013912.

Competing Interests

The authors have no conflicts of interest to report.