Predicting mortality over different time horizons: which data elements are needed?

Abstract

Objective: Electronic health records (EHRs) are a resource for “big data” analytics, containing a variety of data elements. We investigate how different categories of information contribute to prediction of mortality over different time horizons among patients undergoing hemodialysis treatment.

Material and Methods: We derived prediction models for mortality over 7 time horizons using EHR data on older patients from a national chain of dialysis clinics linked with administrative data using LASSO (least absolute shrinkage and selection operator) regression. We assessed how different categories of information relate to risk assessment and compared discrete models to time-to-event models.

Results: The best predictors used all the available data (c-statistic ranged from 0.72–0.76), with stronger models in the near term. While different variable groups showed different utility, exclusion of any particular group did not lead to a meaningfully different risk assessment. Discrete time models performed better than time-to-event models.

Conclusions: Different variable groups were predictive over different time horizons, with vital signs most predictive for near-term mortality and demographic and comorbidities more important in long-term mortality.

Objective

The increasing availability of electronic health records (EHRs) offers vast and unique opportunities for biomedical research, at the core of which are predictive modeling and analytics. The presence of diverse data elements allows for the construction of prediction models using a wealth of predictors that may not all be available in more standard settings. Depending on the EHR and other linkable sources, it is generally possible to ascertain information on patients’ demographics, health service utilization, diagnosed comorbidities, prescribed medications, results from laboratory tests, and vital signs. In total, these represent a source of “big data” analytics in clinical research. Owing to these variable data elements, EHRs present the opportunity to develop risk models over a range of time horizons. Studies have predicted events from within the next 12 hours¹ to up to 8 years.² Examples include predicting the risk of adverse outcomes, including administrative events such as hospital readmission,³ and discrete clinical events such acute kidney injury.⁴ As such, each study has abstracted different pieces of information from its respective EHR.With this in mind, we sought to explore the role EHR data elements play in predicting mortality over different time horizons. This could inform future model development efforts by prioritizing limited resources toward collecting the predictors that provide the most useful information for the selected prediction timeline. We addressed this question among patients with end-stage renal disease (ESRD) undergoing hemodialysis (HD). ESRD patients are at high risk of mortality, with a 46% 3-year mortality rate after HD initiation.⁵ Moreover, traditional models to predict mortality have performed poorly, particularly in older populations.⁶ Using EHR and administrative data from a national sample, we hypothesized that more dynamic clinical characteristics (ie, vitals and laboratory measures) would result in stronger predictions in the near term, whereas more stable metrics (ie, demographics and comorbidities) would result in stronger predictions over a longer time horizon.

Materials and methods

Data sources

We used 2 data sources for this analysis: the United States Renal Data System (USRDS) and the EHR from DaVita Inc. The USRDS⁷ is a national registry that includes almost all persons with ESRD. It contains all medical claims submitted by health care providers to Medicare (Parts A and B) for eligible patients, including claims for prescription medications, which are covered by the Part D benefit component of Medicare. DaVita Inc. is the second largest chain of outpatient dialysis centers in the country. We used an anonymous crosswalk generated by the USRDS Coordinating Center to link the 2 datasets, resulting in >97% linkage.

Sample

The study sample consisted of all patients 66 and older who initiated HD at a DaVita Inc. facility within 30 days of their diagnosis of ESRD, and who were alive at day 30, between July 1, 2006, and December 31, 2008. Follow-up data were available through December 31, 2011. Since our objective was to illustrate the roles of different data elements, we used the large amount of data to create a “clean” analytic cohort. While the full description is available in the supplemental material, in brief, in order to allow for adjudication of comorbidities and medication usage, we required all individuals to have a minimum amount of coverage of Medicare Parts A, B, and D, which cover outpatient, inpatient, and medication-related claims.

Outcome

The primary outcome of interest was mortality from any cause over a series of 7 time horizons: 7 days, 30 days, 90 days, 180 days, 1 year, 2 years, and 3 years, with the index date being the the 30th day of dialysis. By having follow-up through 2011, we ensured that all individuals had the potential for at least 3 years of follow-up regardless of when they started dialysis service, ie, no censoring. Furthermore, by focusing on mortality, we ensured that competing risks would not be an issue.

Predictor variables

We identified 120 baseline predictor variables and grouped them into 6 mutually exclusive categories (see Supplemental Table 1). These consisted of demographics (n = 5), health service utilization (n = 4), comorbidities (n = 48), prescription medications (n = 30), laboratory measures (n = 21), and vital signs (n = 12). See Supplemental Methods for variable definitions.

Predictive modeling

To fit the predictive model, we used a version of logistic regression that is appropriate when the expectation is that many predictors will not be related to the outcome of interest, referred to as LASSO (least absolute shrinkage and selection operator⁸; see supplemental material for model description). To obtain final predictions, we performed 10-fold cross-validation across the full dataset. Within each cross-validation fold we imputed any missing data using mean imputation.For each of the 7 time horizons for prediction of mortality, we fit a LASSO logistic regression model using all available covariates (7 models). Additionally, we fit separate models using just the variables in each individual covariate group (42 models), as well as models with all variables except those in the covariate group (42 models). This resulted in a total of 91 models. We estimated the discriminatory ability of each model via the c-statistic and calculated a 95% CI⁹ and the calibration of each model using the calibration slope.¹⁰ As a secondary analysis, instead of fitting a logistic model to a specific time point, we fit a time-to-event model. We used the LASSO analog of the Cox proportional hazards model,¹¹ using all available variables. We then calculated the c-statistic at each of the 7 time points.¹² Finally, as a sensitivity analysis, we redid the analyses without any cohort exclusions. All analyses were conducted in R 3.1.2.¹³ This work was deemed exempt by the Institutional Review Board at Duke University Medical School.

Results

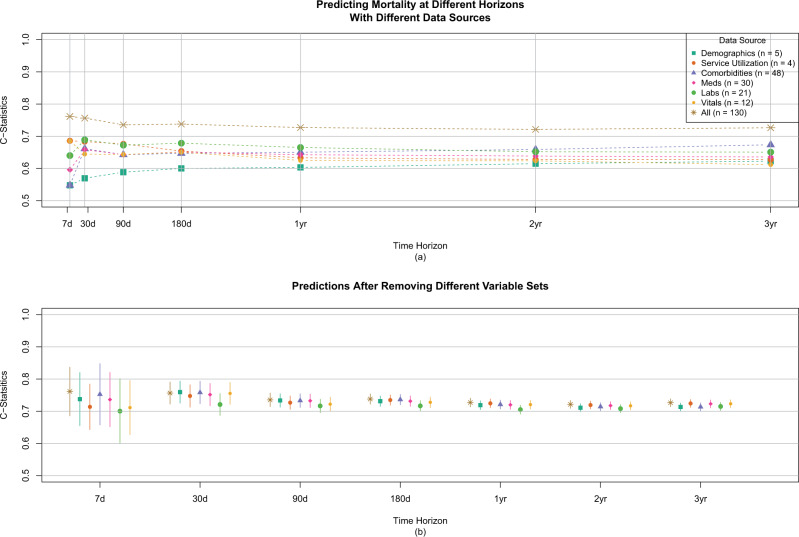
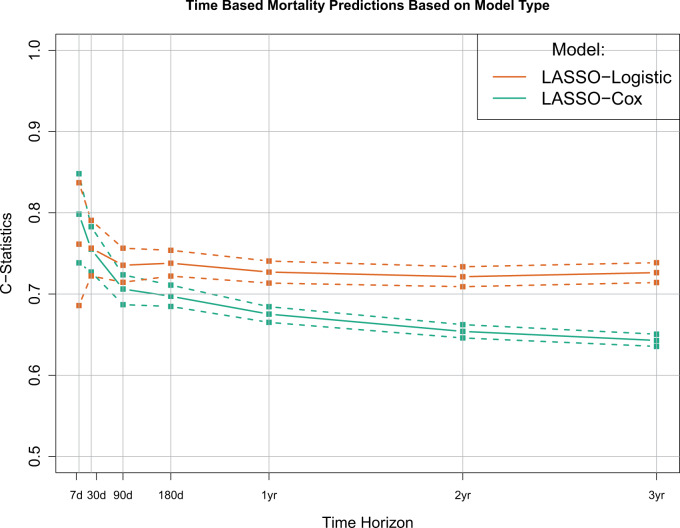
Between July 1, 2006, and December 31, 2008, 28 740 patients 66 years of age or older initiated hemodialysis treatment in a DaVita Inc. center and were alive at day 30. After applying the stated inclusion criteria, the final analytical cohort consisted of 6561 individuals (Figure 1). Patient characteristics on a subset of the variables are shown in Table 1, with all variables shown in Supplemental Table 2. By 3 years, 3846 (59%) patients died; median survival was 2.2 years. Overall patient survival is shown in Supplemental Figure 1.C-statistics for the 49 prediction models based on the individual variable sets are shown in Figure 2a, and with 95% confidence intervals in Table 2. The models using all available information had similar predictive performance for all time horizons, with c-statistics ranging from 0.72 (95% CI, 0.71-0.73) to 0.76 (95% CI, 0.67-0.84), with the 30-day model performing the best. Conversely, calibration of the various models differed over the time horizons, with the longer-term models having the best calibration. Individual regression coefficients for all models are presented in Supplemental Figure 2.When focusing on individual categories of variables, some noticeable patterns emerge. Generally, the number of attributes in the variable set did not relate to the overall c-statistic, and using all variables performed better than any subset. Vital signs and services utilization formed the best predictors in the near term, each having a c-statistic of 0.69 for 7 days out and then decreasing over time. Conversely, comorbidities formed the best predictor in the longer term, increasing over time to a maximum c-statistic of 0.67 for a 3-year prediction. Laboratory values were a consistently strong predictor, while demographics were consistently weak. When we considered the impact of removing individual predictor sets (Figure 2b), we found that no single variable group had a meaningful impact on the prediction assessment. When we explored fitting a single time-to-event model versus individual logistic models, the individual logistic models performed best, as expected (Figure 3). Finally, after redoing the analysis with all available data, results were very similar (Supplementary Table S4 and Figure S3). The exception was the medication results, which showed no predictive ability, likely owing to the higher percentage of people without Medicare Part D and therefore missing this information.

Figure 1.

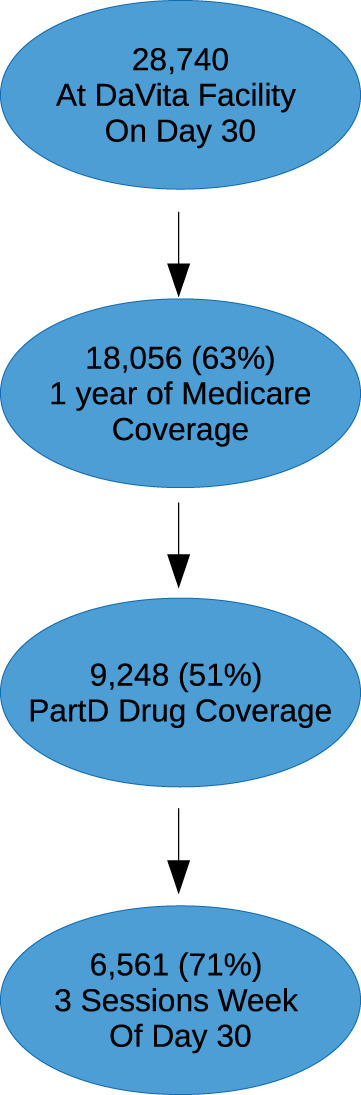
Cohort selection. All DaVita patients who were alive at day 30 of dialysis were eligible. Patients had to have 1 year of Medicare coverage and 6 months of Part D coverage prior to index date.

Table 1.

Reduced Demographics

Descriptor	All People	Never Die	Die in 3 Years	Die in 2 Years	Die in 1 Year	Die in 180 Days	Die in 90 Days	Die in 30 Days	Die in 7 Days
Number of people	6561	2715	3846	2976	1889	1145	647	201	31
Agea	75 (70, 81)	74 (69, 79)	77 (71, 82)	77 (72, 83)	77 (72, 83)	78 (72, 83)	78 (72, 83)	78 (73, 83)	79 (72.5, 84)
Sex (male)b	3606 (0.55)	1521 (0.56)	2085 (0.54)	1618 (0.54)	1017 (0.54)	626 (0.55)	366 (0.57)	111 (0.55)	12 (0.39)
Raceb
White	3837 (0.58)	1398 (0.51)	2439 (0.63)	1931 (0.65)	1240 (0.66)	759 (0.66)	437 (0.68)	135 (0.67)	21 (0.68)
Black	1514 (0.23)	702 (0.26)	812 (0.21)	611 (0.21)	384 (0.2)	236 (0.21)	129 (0.2)	35 (0.17)	6 (0.19)
Hispanic	750 (0.11)	389 (0.14)	361 (0.09)	263 (0.09)	158 (0.08)	84 (0.07)	49 (0.08)	22 (0.11)	1 (0.03)
Other	460 (0.07)	226 (0.08)	234 (0.06)	171 (0.06)	107 (0.06)	66 (0.06)	32 (0.05)	9 (0.04)	3 (0.1)
Number of hospital daysa	15 (7, 27)	12 (5, 23)	18 (9, 30)	19 (10, 31)	20 (11, 33)	22 (12, 35)	22 (13, 36)	22 (14, 36)	21 (12, 41)
Nephrology visitsa	4 (1, 7)	4 (1, 8)	3 (1, 7)	3 (1, 7)	3 (1, 6)	2 (1, 6)	2 (1, 5)	2 (1, 5)	2 (0, 5.5)
Number of comorbiditiesa	7 (5, 10)	7 (4, 9)	8 (6, 11)	8 (6, 11)	8 (6, 11)	9 (6, 11)	9 (6, 11)	9 (7, 12)	9 (6, 10.5)
Number of medicationsa	9 (7, 12)	9 (7, 11)	9 (7, 12)	10 (7, 12)	9 (7, 12)	9 (7, 11)	9 (7, 11)	9 (7, 11)	9 (6.5, 11)

^aMedian and interquartile range.

^bCount and percentage.

Full demographics available in appendix.

Figure 2.

(a) C-statistics for different variable sets over different time horizons. The model with all variables performs the best. The most dynamic variables (eg, vitals) are most predictive in the near term, and the more stable variables (eg, comorbidities) are most predictive in the short term. (b) C-statistics after excluding different variable sets. Removal of any 1 variable set does not lead to meaningful differences in model performance.

Table 2.

C-statistics across prediction models and variable sets

Variable Group	7 days	30 days	90 days	180 days	1 year	2 years	3 years
All	0.761 (0.686-0.837)	0.756 (0.722-0.791)	0.735 (0.714-0.756)	0.738 (0.722-0.754)	0.727 (0.713-0.741)	0.721 (0.709-0.734)	0.726 (0.714-0.739)
Demographics	0.548 (0.437--0.658)	0.569 (0.529-0.61)	0.588 (0.565-0.611)	0.600 (0.582-0.618)	0.603 (0.588-0.618)	0.615 (0.601-0.628)	0.623 (0.609-0.636)
Service Utilization	0.686 (0.603-0.769)	0.684 (0.647-0.72)	0.676 (0.655-0.698)	0.654 (0.636-0.671)	0.633 (0.618-0.648)	0.628 (0.614-0.641)	0.627 (0.614-0.641)
Comorbidities	0.548 (0.454-0.642)	0.661 (0.625-0.697)	0.643 (0.621-0.665)	0.647 (0.629-0.664)	0.650 (0.636-0.665)	0.659 (0.646-0.672)	0.673 (0.660-0.687)
Medications	0.596 (0.501-0.691)	0.658 (0.62-0.696)	0.643 (0.621-0.665)	0.651 (0.634-0.669)	0.643 (0.628-0.657)	0.639 (0.625-0.652)	0.636 (0.622-0.649)
Labs	0.640 (0.551-0.729)	0.689 (0.649-0.729)	0.672 (0.649-0.695)	0.679 (0.661-0.696)	0.665 (0.650-0.680)	0.652 (0.639-0.665)	0.651 (0.637-0.664)
Vitals	0.685 (0.590-0.781)	0.645 (0.602-0.687)	0.643 (0.621-0.666)	0.650 (0.632-0.668)	0.625 (0.610-0.640)	0.624 (0.610-0.637)	0.612 (0.598-0.625)

Bolded represents predictor group.

Figure 3.

Comparison of models based on discrete time and time-to-event analyses. The discrete time models perform best.

Discussion

This analysis highlights the roles different EHR data elements play in predicting mortality in patients on dialysis over different time periods. Overall, we found that a “kitchen-sink” approach that utilizes all available data performs better than focusing on any particular set of information. While the full model performed best, as we explored the role of different variable groups, we observed that vital signs, which can be highly variable, were the most predictive for a 7-day risk, but the least predictive for a 3-year prediction. Conversely, demographic characteristics, which tend to be very stable, showed a steady increase in importance over time. These results correspond with previous studies using EHR data to develop risk models, illustrating that EHR-based models perform better with nearer-term events.^14–21 Moreover, when comparing the “important” variables over different time horizons, previous work has similarly suggested that more “dynamic” metrics are important for nearer-term outcomes and more “stable” metrics are important for longer-term events.¹⁷This finding stresses the importance of machine-learning methods capable of handling large numbers of disparate predictor variables. With a large number of variables, particularly correlated ones, regularized methods such as LASSO are highly effective, since they stabilize regression coefficients via shrinkage. Therefore, in the age of EHRs where many predictors are available, preselection of variables may not be necessary. Unfortunately, this counters the tendency in the field to use limited variable sets to develop predictive models with EHR data.²²As expected, we found that a time-to-event model performed worse than the corresponding time-specific model. While logistic regression approximates the Cox model²³ and some previous work suggests that survival-based predictions perform better than time-specific ones,²⁴ the likely reason the Cox model performed worse was that the hazards for various predictors are not proportional over time. This nonproportionality is directly suggested by the variable associations by the different predictor sets. While overall time-to-event models provide more flexibility—a single model can be applied to multiple time horizons—in this scenario they result in less precise predictions.²³ Therefore, if the goal is to focus on specific time horizons (eg, 30-day readmission), a time-specific model (either logistic or Cox-based) might be preferential.As more researchers and clinicians turn to EHRs to inform risk assessment and clinical decision-making, this work highlights the types of variables that should be captured and used in these analyses. Currently, the motivation behind most EHR systems is to improve billing and operations in the hospital. For this reason, diagnosis codes, which are tied to billing, tend to be well captured.²⁵ Conversely, more acute clinical metrics tend to be not as well captured and easily retrieved.²⁶ However, as our results indicate and previous work has suggested, models to predict mortality based solely on administrative data⁶ perform worse than models based on clinical data.²⁷ An open clinical question is how to assess near-term risk of disease.²⁸ This work shows how this is possible: through the use of dynamic data. Since EHRs most readily capture vital signs and laboratory tests, they may be ideally suited for such short-term prediction. However, one challenge in implementing such models will be discerning their clinical utility. Since the rate of near-term events is so low (0.5%), the positive predictive value will be correspondingly low. Such issues require further consideration.Overall, this study had several strengths and limitations. We used a large source of data to create a well-defined cohort of individuals starting HD treatment for ESRD. While we selected a small proportion of the overall population, we were able to ensure full capture of a range of data elements with minimal missing data. Even when we used the full, more limited cohort, the results were similar. However, it should be noted that this study utilized only 1 EHR in 1 disease area, for 1 outcome. We focused on predicting mortality to avoid the complication of competing risks, but it is likely that different outcomes would show different patterns. Also not all EHR systems will have the benefit of linkage with alternative data sources (eg, Medicare claims) for adjudication of information.

Conclusions

This study illustrates how different data elements, regularly captured by an EHR, relate to prediction of mortality over different time periods. We show that models that contain all available predictors outperform those that do not, and that time-specific models perform better than time-general ones.

Disclosures

This work was supported by National Institute of Diabetes and Digestive and Kidney Diseases (NIDDK) career development award K25 DK097279 (B.A.G.), and NIDDK R01DK090181 and R01DK095024 (W.C.W.). W.C.W. enjoys salary and research support through the endowed Gordon A. Cain Chair in Nephrology at the Baylor College of Medicine.

• -The authors have no competing interests to declare.

• -All authors contributed to the preparation of the manuscript. B.A.G. conceived of the study, performed the data analysis, and wrote the manuscript. M.J.P. conceived of the analysis and edited the manuscript. M.M.R. helped with data analysis and edited the manuscript. W.C.W. provided data and edited the manuscript.

SUPPLEMENTARY MATERIAL

Supplementary material is available online at http://jamia.oxfordjournals.org/.