The Evolution of Haploid Chromosome Numbers in the Sunflower Family

Abstract

Chromosome number changes during the evolution of angiosperms are likely to have played a major role in speciation. Their study is of utmost importance, especially now, as a probabilistic model is available to study chromosome evolution within a phylogenetic framework. In the present study, likelihood models of chromosome number evolution were fitted to the largest family of flowering plants, the Asteraceae. Specifically, a phylogenetic supertree of this family was used to reconstruct the ancestral chromosome number and infer genomic events. Our approach inferred that the ancestral chromosome number of the family is n = 9. Also, according to the model that best explained our data, the evolution of haploid chromosome numbers in Asteraceae was a very dynamic process, with genome duplications and descending dysploidy being the most frequent genomic events in the evolution of this family. This model inferred more than one hundred whole genome duplication events; however, it did not find evidence for a paleopolyploidization at the base of this family, which has previously been hypothesized on the basis of sequence data from a limited number of species. The obtained results and potential causes of these discrepancies are discussed.

Introduction

The remarkable diversity of land plants is associated with striking variation in genome sizes and chromosome numbers (Lysák and Schubert 2013). Whereas genome size of land plants varies more than 2,300-fold, from 64 Mb (Genlisea aurea; Greilhuber et al. 2006) to approximately 150,000 Mb (Paris japonica; Pellicer et al. 2010), chromosome numbers vary from n = 2 in six angiosperm species (Vanzela et al. 1996; Cremonini 2005) to n > 320 in Sedum suaveolens (Uhl 1978). This large variation in chromosome numbers has been driven by two major mechanisms operating in opposite directions: increases through polyploidy (whole genome duplications [WGD]) and decreases or increases through structural chromosomal rearrangements (chromosome fusion, i.e., descending dysploidy; and chromosome fission, i.e., ascending dysploidy) (Lysák and Schubert 2013). Indeed, polyploidy is considered one of the main mechanisms responsible for the evolutionary success of many species, in particular by enabling the adaptation of newly arisen polyploids to different habitats. For example, the recurrent presence of polyploids in habitats different from those of their diploid progenitors constitutes strong evidence of the ability of polyploids to colonize new environmental niches (Hegarty and Hiscock 2008). Still, the evolutionary success of polyploids has been a controversial topic, with some authors considering that, in general, fairly recent polyploids have reduced diversification rates when compared with their diploid relatives and fail to persist (Mayrose et al. 2011, 2014). Other authors state that polyploidy is a fundamental process in the evolution of flowering plants (Soltis and Soltis 2000; Hegarty and Hiscock 2008; Lim et al. 2008; Soltis et al. 2014). Regardless of the effect of polyploidy in diversification patterns (Van de Peer et al. 2009; Wood et al. 2009; Fawcett and Van de Peer 2010; Vanneste et al. 2014; Tank et al. 2015), phylogenomic analyses of sequenced plant genomes have shown WGD in ancestral lineages before the diversification of extant seed plants, angiosperms, and eudicots (Jaillon et al. 2007; Jiao et al. 2011; Jiao et al. 2012; Amborella Genome Project 2013). In contrast, dysploidy has been thought to arise accidentally, and no adaptive reason has been found that could explain its predominant occurrence in particular clades (Chacón et al. 2014; Escudero et al. 2014). Nevertheless, in plants, changes in chromosome number have long been recognized as important evolutionary forces, their study being of utmost importance.

The development of new molecular and bioinformatic techniques has facilitated the inference of ancient WGDs. Until recently, the study of ancient WGDs implied the use of threshold techniques to infer the occurrence and location of polyploidy events (from Stebbins 1938 to Wood et al. 2009). However, in most cases, these studies did not consider the phylogenetic relationships among taxa and the possible occurrence of aneuploidy or dysploidy events during genome evolution (Glick and Mayrose 2014). Alternative methods such as comparative genetic mapping, analysis of specific gene families, identification of duplicated genes in expressed sequence tag (EST) collections, and fingerprinting techniques (e.g., AFLP) have also been used (Ainouche et al. 2003; Bowers et al. 2003; Schranz and Mitchell-Olds 2006; Mondragón-Palomino et al. 2009; Jiao et al. 2011); still, their application in large clades and using broad sampling is hardly feasible. Recently, a probabilistic model of chromosome evolution within a phylogenetic framework, chromEvol, was made available (Mayrose et al. 2010), and is already in its second iteration (Glick and Mayrose 2014). This model uses the haploid chromosome number, defined as the number of apparently original unique chromosomes in a haploid set (Cusimano et al. 2012; Glick and Mayrose 2014), to describe the evolution of chromosome numbers in a given lineage, working under a robust probabilistic inference framework that considers both dysploidy and polyploidy. Therefore, it is now possible to evaluate the importance of genomic events, such as WGDs, dysploidy, and demipolyploidy, in the evolution of a group. This constitutes a great opportunity to explore the occurrence of ancient WGDs and their evolutionary implications (Glick and Mayrose 2014).

Since its launch, the chromEvol approach (Mayrose et al. 2010) has been applied to the study of chromosome number evolution in about a dozen cases, either using simulated or empirical data sets (Mayrose et al. 2011: 63 clades of vascular plants; Ness et al. 2011: Pontederiaceae; Cusimano et al. 2012: Araceae; Ocampo and Columbus 2012: Portulaca, Portulaceae; Cristiano et al. 2013: Atta and Acromyrmex, leafcutter ants of tribe Attini; Harpke et al. 2012: Crocus, Iridaceae; Metzgar et al. 2013: Cryptogramma, Pteridaceae; Soza et al. 2013: Thalictrum, Ranunculaceae; Chacón et al. 2014: Colchicaceae; Pellicer et al. 2014: Melanthiaceae; Sousa et al. 2014: Araceae). In addition, Escudero et al. (2014) modeled the tempo and mode of chromosome number evolution and its possible correlation with cladogenesis in 15 angiosperm clades. In these studies, no particular bias toward any of the chromosomal events that the model considers was observed.

In this study, we used this probabilistic method to infer chromosomal change events (dysploidy and polyploidy) in the evolution of the sunflower family (Asteraceae). This family comprises the largest number of described species of flowering plants with 24,000–30,000 species distributed in 1,600–1,700 genera (Funk et al. 2009). Its members occur in all continents except Antarctica and occupy a great variety of habitats (Funk et al. 2005). Considering this very large number of species and the comparatively young age of the family (Barreda et al. 2012), it is not surprising that Asteraceae possess one of the highest rates of diversification among flowering plants, being also indicative of the high ecological and evolutionary success of its members (Funk et al. 2009). Due to its size and importance, Asteraceae taxa have long been characterized cytogenetically and are likely the family of flowering plants with the highest number of chromosome counts (128,855 records as compiled in the Index to Chromosome numbers in Asteraceae [last assessed July 17, 2014]). So far, a very large range of chromosome numbers has been described in Asteraceae: n = 2 to n = ca. 216 chromosomes, with n = 9 the most frequently observed haploid number (Semple and Watanabe 2009). Many authors suggested x = 9 as the base number of this family (Stebbins 1950; Solbrig 1977; Cronquist 1981; Bremer 1994; Semple and Watanabe 2009; Bala and Gupta 2013), but x = 8 has also been proposed (Vallès et al. 2005). In a previous study, Barker et al. (2008) examined gene duplication and retention in Asteraceae and found that at least three ancient WGDs have occurred in this family. One WGD was placed near the origin of the family just prior to the rapid radiation of its tribes, whereas the other two were located near the base of the tribes Mutisieae and Heliantheae (Barker et al. 2008).

In this study, we reconstructed the ancestral chromosome number of Asteraceae and the occurrence of chromosomal change events by applying the probabilistic model of Glick and Mayrose (2014) to the largest phylogenetic framework of the Asteraceae (Funk et al. 2009). This approach allowed us to incorporate a very high number of taxa (588 taxa), in an attempt to improve precision in the detection and localization of chromosomal change events in the evolution of Asteraceae. Overall, 655 chromosomal change events were inferred, which could facilitate the identification of target groups for more in-depth studies on gene duplication and chromosomal evolution.

Materials and Methods

Phylogenetic Hypothesis

We used the phylogenetic supertree of the Asteraceae provided by Funk et al. (2009) with 757 taxa. This supertree mainly represents phylogenetic relationships among genera; still, some problematic species were also considered. The supertree covers approximately 46% of the ca. 1,650 genera of the Asteraceae family. In order to obtain a phylogenetic supertree with branch length information, a time-calibrated supertree was obtained following the procedure of Torices (2010). The supertree (Funk et al. 2009) was first translated into a Newick tree file format. Then, using the BLADJ function of Phylocom v.4.0.1b software (Webb et al. 2008), nodes with known age, including the root of the tree, were fixed according to the information on clade age estimates available in the literature (supplementary table S2, Supplementary Material online). Most of the age estimates were selected based on molecular dating through fossil calibration although other dating methods were also considered in particular cases (e.g., geological dating; see supplementary table S2, Supplementary Material online). As clade age estimates are usually given as time intervals, and as the BLADJ function only accepts one age per node, the average value of the minimum and the maximum time estimates was calculated and used as calibration age (supplementary table S2, Supplementary Material online). In some cases, the age clade data were not consistent among sources. In these situations, the age estimate more consistent with previous estimations was selected.

Chromosome Number Collection

The number of chromosomes of the genera and species that belong to Asteraceae and of the outgroup families Calyceraceae and Goodeniaceae were collected from the Index to Chromosome numbers in Asteraceae (http://www.lib.kobe-u.ac.jp/infolib/meta_pub/G0000003asteraceae_e; last assessed 17 July 2014) and from the Chromosome Counts Database (CCDB; http://ccdb.tau.ac.il/; last assessed 22 February 2016; Rice et al. 2015). We first searched the databases for taxa included in the supertree, including the outgroup families. Considering the information available in the databases, we collected chromosome numbers for 588 taxa, resulting in a final total coverage of chromosome number data for 77.7% of the taxa included in the supertree.

Chromosome numbers were coded using the following approach: first, all reported chromosome numbers of each genus were annotated; B chromosome data, odd numbers, and cases where chromosome counts were given as intervals of numbers were not considered and were excluded from the analysis. Second, the available chromosome information at the diploid level was converted into haploid chromosome numbers. After this conversion, 319 monomorphic (54.25%) and 269 polymorphic (45.75%) genera were obtained.

The evolution of haploid chromosome numbers was analyzed using two approaches, either considering chromosome number polymorphism (hereafter polymorphic data) or not (hereafter single data). In the latter case, one chromosome number had to be selected from the polymorphic data set. For that, the most frequent chromosome number was chosen. The frequency of each chromosome number was calculated considering all the species within a genus. Each species was counted only one time, for each chromosome number. Thus, all species of each genus had the same weight, and the frequency reveals the number of different species with each chromosome number and not the number of available counts. When more than one chromosome number had the same frequency, the smallest chromosome number was selected. This latter strategy was considered because, according to Mayrose et al. (2010), the smallest haploid chromosome numbers are typically assumed to represent the non-duplicated state, i.e., the basic chromosome number.

Evolutionary Models of Haploid Chromosome Number Change

The evolution of haploid chromosome numbers of Asteraceae was inferred using chromEvol software v.2.0 (Glick and Mayrose 2014; http://www.tau.ac.il/∼itaymay/cp/chromEvol/index.html). This software is based on a probabilistic model of chromosome number evolution that assumes that changes in chromosome number over time result from a combination of polyploidy (demiduplication and duplication events) and dysploidy (ascending or descending, by chromosome fission or fusion events, respectively) along branches of a phylogeny (Mayrose et al. 2010). By comparing the fit of the different models to biological data, it is possible to test the probability of those events, enabling us to understand the pathways of chromosome number evolution (Mayrose et al. 2010) and to estimate the ancestral chromosome numbers at the internal nodes of the tree (Glick and Mayrose 2014). The software offers 10 models based on different combinations of nine parameters: chromosome loss rate (δ) that considers that the number of chromosomes might decrease by one, with rate δ; chromosome gain rate (λ) that assumes that the number of chromosomes might increase by one, with rate λ; chromosome duplication rate (ρ) that considers that the number of chromosomes might double, with rate ρ; chromosome demiduplication rate (μ) that assumes the union of reduced and unreduced gametes leading to, for example, triplication events, with rate μ; linear chromosome loss rate (δ₁) that considers that the chromosome loss rate depends on the current number of chromosomes; linear chromosome gain rate (λ₁) that considers that the chromosome gain rate depends on the current number of chromosomes; base chromosome number (β) that is the monoploid chromosome number; base chromosome number rate for transitions (ν); and the possibility to define whether the base-number is optimized by the program or not. According to Glick and Mayrose (2014), in complex data sets such as the one used in this study, it is recommended to keep the base chromosome number fixed to the value given by β. Therefore, for those models that included a base chromosome number rate, considering the information available in the literature (Stebbins 1950; Solbrig 1977; Cronquist 1981; Bremer 1994; Semple and Watanabe 2009; Bala and Gupta 2013), the hypothetical base number of Asteraceae was fixed to x = 9. Four of these models consider only constant rates (Mc1, Mc2, Mc3, and Mc0), whereas the other four include two linear rate parameters (Ml1, Ml2, Ml3, and Ml0; supplementary table S1, Supplementary Material online). Both sets have a null model (Mc0 and Ml0) that assumes no polyploidization events. Finally, two models (Mb1 and Mb2) consider that the evolution of chromosome number can also be influenced by the base number and by its transition rates (supplementary table S1, Supplementary Material online).

To estimate the model and respective parameters of chromosome evolution in Asteraceae, two approaches were followed: first, all models were fitted to the data without performing simulations to infer the best-fitted model (i.e., the one with the lowest Akaike Information Criteria (AIC) value; Burnham and Anderson 2004); second, averaged parameters were estimated by weighing each rate parameter by the AIC weights of each model (Bolker 2007); then, each parameter’s value was compared with those obtained with the best model. All models were fitted twice considering either single or polymorphic data, and the null hypothesis (no polyploidy) was tested using an AIC test.

In the software, the minimum chromosome number was set to 2, whereas the maximum number was set to 5 units higher than the highest chromosome number found in the empirical data. The branch lengths were scaled according with the software author’s instructions. To compute the expected number of changes along each branch, as well as the ancestral haploid chromosome numbers at internal nodes, the best-fitted model for both data sets was rerun using 5,000 simulations.

Ancestral Chromosome Number of Asteraceae

To test which haploid chromosome number is most likely to be present at the root of Asteraceae, the chromosome numbers inferred by the best-fitted model (see above) were fixed at the root and the likelihood of the resulting models was compared. The following haploid chromosome numbers were tested: 2 as the ancestral chromosome number obtained under maximum likelihood (ML), and 9 and 10, as the chromosome numbers with the highest PP under the Bayesian analysis. Only the polymorphic coding scheme was used as it includes all chromosome numbers, being the most complete data set under analysis and the one with the highest amount of genetic variation observed at this level. To summarize, we reran the best model using the polymorphic data and fixed the root with each one of the hypothetical chromosome numbers. The model with the lowest AIC was then considered the most likely ancestral state.

Polyploidization Events

The duplication and demiduplication events inferred in the best-fitted model were mapped onto the phylogenetic tree. Each type of genomic event was mapped according to these expectation categories: ≥ 0.5 and < 0.8,  ≥ 0.8 and < 0.95, and ≥ 0.95. As chromEvol only enables identification of those branches in which a polyploidization event occurred, but not the exact period of time along the branch, polyploidization events were simply depicted in the middle of the respective branches.

Results

Models of Chromosome Evolution in Asteraceae

Regardless of the coding scheme, the best model was always Mc2 (table 1). This model considers three parameters (supplementary table S1, Supplementary Material online), i.e., chromosome gain rate, chromosome loss rate, and chromosome duplication rate, assuming that duplication and demiduplication rates are equal. This result supports the conclusion that genome duplications (including whole- and demiduplications), and dysploidy (including both ascending and descending) were very important events in the evolution of Asteraceae. In addition, the Mc0 model that considers no polyploidization events on the evolution of haploid chromosome number was always the model with the worst score (table 1); this result further supports the importance of genome duplications in the evolution of Asteraceae.

Table 1.

Goodness of Fit of the 10 Different Models of Chromosome Number Evolution Applied to Both Polymorphic and Single Coding Schemes

Coding scheme		Polymorphic data		Single data
		AICa	wi	AIC	wi
Modelsb	Mc0	4365.36 (10)	0.00	4521,52 (10)	0.00
	Mc1	3212.72 (7)	0.00	3344.48 (7)	0.00
	Mc2	3010.22 (1)	0.70	3175.18 (1)	0.67
	Mc3	3012.02 (2)	0.28	3176.98 (2)	0.27
	Ml0	3886.44 (9)	0.00	3925.98 (9)	0.00
	Ml1	3180.42 (6)	0.00	3294.32 (5)	0.00
	Ml2	3018.10 (3)	0.01	3180.84 (3)	0.04
	Ml3	3019.84 (4)	0.01	3183.28 (4)	0.01
	Mb1	3488.58 (8)	0.00	3496.40 (8)	0.00
	Mb2	3169.84 (5)	0.00	3300.90 (6)	0.00

Note.—w_i = AIC relative weights.

^aIn bold, the lowest AIC value for each data set indicates the best model.

^bIn brackets, the numbers indicate the descending order of the best model

In each coding scheme, the rates of chromosome loss (δ), gain (λ), and duplication (ρ) were equal when the best model or all models were averaged (using the weighting procedure). Slightly larger differences were observed between coding schemes, especially for the rates of chromosome loss. For the demiduplications rate, the obtained value was always lower for the averaging models than for the best model, independent of the coding scheme (table 2). The linear rate parameters (i.e., linear chromosome loss, δ_1, and linear chromosome gain, λ_1, rates) and the base chromosome number rate for transitions (ν) always presented very low values (table 2).

Table 2.

Rate Parameter Values and Frequency of the Four Possible Event Types with the Expectation ≥ 0.5 in the Best Model and by Averaging All Models, for Each Data Coding Scheme

				Rate parametersa							Events inferred with expectation ≥ 0.5
Coding scheme	Best model	ML	AIC	δ	λ	ρ	μ	δ1	λ1	ν	Losses	Gains	Dupl.	Demi-dupl.
Polym.	Mc2	-1502.11	3010.2	0.038	0.020	0.017	0.017	-	-	-	273.47	141.97	121.69	117.38
	Averaging			0.038	0.020	0.017	0.005	8.651e−6	1.553e−5	2.193e−39
Single	Mc2	-1584.59	3175.2	0.054	0.027	0.021	0.021	-	-	-	366.71	188.19	145.32	141.87
	Averaging			0.054	0.027	0.021	5.965e−3	7.126e−6	5.722e−5	1.392−31

Note.—The maximum likelihood (ML) and AIC value of the best model in each case is also given.

^aAccording to the branch length modifications made (this work) and following chromEvol author’s suggestion, the values of rate parameters were multiplied by 0.0053 and 0.0047 for single and polymorphic data, respectively.

The Expected Number of Changes along Each Branch

Regardless of the coding scheme, the most commonly inferred events (with an expectation > 0.5) were chromosome losses, followed by chromosome gains (table 2). The number of events was always higher for the single data than for the polymorphic data, independent of the type of chromosomal change event (table 2).

More than two hundred chromosome duplications (including demiduplications) were inferred by the best model (table 2). The number of chromosome duplications was higher than the number of chromosome demiduplications independently of the coding scheme (table 2). In all cases, the observed differences were very small (table 2).

The Ancestral Haploid Chromosome Number in Asteraceae

The two methods used to infer the ancestral chromosome number of Asteraceae provided very different results. For both single and polymorphic data sets, the ML method inferred n = 2 as the most probable ancestral chromosome number for Asteraceae. In the case of Bayesian analysis of the single data, n = 9 was inferred as the ancestral chromosome number with the highest posterior probability (PP) (table 3, fig. 1 and supplementary fig. S1, Supplementary Material online) and n = 10 as the second best haploid ancestral chromosome number (table 3). For Bayesian analysis of the polymorphic data, n = 9 was the only inferred number (table 3). Finally, when the most recent common ancestor of Asteraceae was fixed with each one of these haploid numbers (n = 2, 9, or 10), the lowest AIC and likelihood values were always obtained when the root was fixed with n = 9 (table 4).

Table 3.

Chromosome Number of the Most Recent Common Ancestor of the Asteraceae Family and of the Main Tribes, under the Best Model of Chromosome Evolution for Each Coding Scheme (Polymorphic and Single Data) and Considering Both Methods of chromEvol for Inferring Ancestral States (Bayesian Phylogenetic Inference, Bayes)

Family/Tribe	Bayes best n (PP); Bayes 2nd best n (PP); ML		Hypothesized base numbers
	Polymorphic data	Single data
Asteraceae	9 (1.00); 2	9 (0.99); 10 (0.004); 2	9a, 8b
Barnadesieae	9 (0.91); 8 (0.08); 9	9 (0.74); 8 (0.24); 8	8, 9, 12, 27c,***
Stifftieae	18 (0.37); 27 (0.24); 27	18 (0.36); 27 (0.18); 27	9*
Onoserideae	9 (0.47); 18 (0.23); 18	9 (0.78); 10 (0.11); 9	No data
Mutisieae	13 (0.38); 12 (0.37); 12	12 (0.33); 11 (0.24); 12	9d,*
Nassauvieae	9 (0.44); 13 (0.26); 12	9 (0.45); 10 (0.29); 9	No data
Hyalideae	27 (0.77); 18 (0.11); 27	27 (0.66); 18 (0.13); 27	-
Wunderlichieae	27 (0.35); 18 (0.20); 18	27 (0.28); 18 (0.19); 18	No data
Gochnatieae	9 (0.49); 14 (0.16); 12	9 (0.43); 14 (0.14); 12	4; 9; 23e,***
Hecastocleideae	9 (1.00); 2	9 (1.00); 2	8f,***
Dicomeae	9 (0.93); 10 (0.06); 10	9 (0.95); 10 (0.03); 6	10; 11*
Oldenburgieae	18 (0.57); 9 (0.37); 18	9 (0.87); 10 (0.07); 9	9*
Tarchonantheae	18 (0.77); 9 (0.20); 18	9 (0.93); 8 (0.03); 9	9*
Cardueae	9 (0.85); 10 (0.10); 10	9 (0.88); 8 (0.08); 6	10*; 7–16g1 ***, 17g2
Pertyeae	13 (0.39); 9 (0.27); 6	13 (0.36); 9 (0.26); 12	13h,***
Gymnarrheneae	9 (1.00); 2	9 (1.00); 2	10*
Cichorieae	9 (0.95); 8 (0.05); 6	9 (0.85); 8 (0.12); 6	9i,*/***
Heterolepis	9 (0.99); 8 (0.01); 6	9 (0.98); 8 (0.02); 6	6j,***
Eremothamneae	9 (0.32); 8 (0.16); 6	9 (0.24); 8 (0.16); 6	-
Arctotideae_Arct	9 (0.94); 10 (0.03); 6	9 (0.88); 10 (0.06); 6	9*
Arctotideae_Gort	8 (0.52); 9 (0.40); 5	8 (0.47); 9 (0.43); 5	9*
Plathycarpheae	9 (0.75); 10 (0.22); 5	9 (0.67); 10 (0.27); 5	-
Liabeae	9 (1.00); 9	9 (0.99); 10 (0.01); 9	7; 9*; 12; 14; 16; 18k,***
Distephanus	10 (0.62); 9 (0.38); 10	10 (0.70); 9 (0.29); 10	No data
Moquinieae	10 (0.36); 9 (0.29); 10	10 (0.33); 9 (0.25); 10	-
Vernonieae	10 (0.96); 9 (0.04); 10	10 (0.96); 9 (0.04); 10	10*
Corymbieae	9 (0.70); 10 (0.29); 15	9 (0.62); 10 (0.36); 15	8l,***
Senecioneae	10 (0.91); 9 (0.09); 10	10 (0.91); 9 (0.09); 10	5; 10m,*
Calenduleae	9 (0.77); 10 (0.21); 16	9 (0.71); 10 (0.26); 17	8; 9; 10*
Gnaphalieae	8 (0.48); 9 (0.25); 8	8 (0.52); 9 (0.42); 8	6; 7; 10*; 11; 12; 13; 14n,*/***
Anthemideae	9 (0.97); 10 (0.03); 9	9 (0.93); 10 (0.06); 10	9°; 10*/***
Astereae	9 (0.99); 10 (0.01); 9	9 (0.97); 10 (0.03); 9	9p,*/***
Inuleae	9 (0.70); 10 (0.29); 10	9 (0.61); 10 (0.37); 10	5, 8, 9, 10q1,*, 7–11q2/***
Athroismeae	10 (0.80); 9 (0.16); 11	10 (0.73); 9 (0.17); 11	7; 10r,*/***
Feddeeae	9 (0.90); 10 (0.10); 13	9 (0.79); 10 (0.20); 12	No data
Helenieae	9 (0.93); 10 (0.04); 13	9 (0.80); 10 (0.14); 11	18**
Coreopsideae	9 (0.79); 10 (0.08); 12	9 (0.72); 10 (0.26); 10	12; 16*
Neurolaeneae	9 (0.80); 10 (0.13); 11	9 (0.79); 10 (0.17); 10	11*
Tageteae	9 (0.81); 12 (0.10); 12	9 (0.93); 10 (0.05); 9	18**
Chaenactideae	9 (0.45); 8 (0.43); 9	7 (0.39); 8 (0.38); 8	9*
Bahieae	10 (0.68); 11 (0.12); 11	10 (0.49); 11 (0.17); 10	17**
Polymnieae	9 (0.92); 10 (0.07); 10	9 (0.85); 10 (0.14); 10	15s
Heliantheae	18 (0.74); 9 (0.14); 18	18 (0.65); 9 (0.17); 18	8, 9, 17–19, 18t
Millerieae	9 (0.55); 8 (0.35); 9	9 (0.46); 8 (0.42); 9	9; 10; 11; 12; 14u
Perityleae	18 (0.83); 9 (0.16); 18	18 (0.78); 9 (0.19); 18	18v,**
Eupatorieae	9 (0.80); 10 (0.19); 9	9 (0.71); 10 (0.24); 9	10; 17; 18w
Madieae	9 (0.97); 8 (0.02); 9	9 (0.88); 8 (0.07); 9	19**

Note.—The base numbers already reported in the literature for Asteraceae and its main tribes are also given. The dash (-) present on the base number of some tribes indicates the absence of data, according to Funk et al. (2009).

^aThe two most probable ancestral chromosome numbers obtained through the Bayesian phylogenetic inference (Bayes), with the probability (PP) of occurrence given in parentheses, as well as, the result of the maximum likelihood (ML) are provided. Arct. = Arctotidinae subtribe; Gort. = Gorteriinae subtribe.

^aSolbrig (1977), Cronquist (1981), Bremer (1994), and Bala and Gupta (2013).

^bVallès et al. (2005).

^cStuessy et al. (2009), chapter 13; x = 27 (Watanabe et al. 2007).

^dx = 9 seems to be available for all or nearly all the base numbers listed.

^ex = 4, x = 9, x = 23 (reviewed by Sancho and Freire (2009), chapter15.

^fBased on a single count of 2n = 16 (Funk and Hind 2009), chapter 16.

^g1Susanna and Garcia-Jacas (2009), chapter 20.

^g2Watanabe et al. (2007).

^hFreire (2009), chapter 21.

ⁱRaven et al. (1960); Funk and Chan (2009), chapter 23.

^jFunk and Karis (2009), chapter 31.

^kDillon et al. (2009), chapter 27.

^lBased on a single count of 2n = 16 in Corymbium congestum (Nordenstam and Funk 2009), chapter 32.

^mRaven et al. (1960) and Vallès et al. (2005).

ⁿVallès et al. (2005), Watanabe (2009) cited in Watanabe et al. (2007), and Ward et al. (2009), chapter 36.

^oVallès et al. (2005), Watanabe et al. (2007), and Oberprieler et al. (2009), chapter 38.

^pRaven et al. (1960); Watanabe et al. (2007); Brouillet et al. (2009), chapter 37.

^q1Raven et al. (1960) and Vallès et al. (2005).

^q2Watanabe et al. (2007), Robinson et al. (1997) presented x = 10, and Anderberg (2009a, 2009b) presented the base numbers of x = 9 or x = 10, chapter 39.

^rAnderberg (2009a), chapter 40.

^sEstes and Beck (2011).

^tx = 9 or its multiples (Raven et al. 1960) or also x = 18 (Watanabe et al. 2007); x = 17–19 (Smith 1975) and x = 8 (Stuessy 1977) cited in Robinson (1981).

^uBlöch et al. (2009).

^vRobinson (1981) and Baldwin et al. (2002).

^wx = 10 (Robinson et al. 1997), x = 17 (Watanabe et al. 1995), x = 18 (Watanabe et al. 1999) cited in Watanabe et al. (2007).

*Estimated by Funk et al. (2009).

**Estimated by Baldwin et al. (2002).

***Funk et al. (2009).

Fig. 1.—

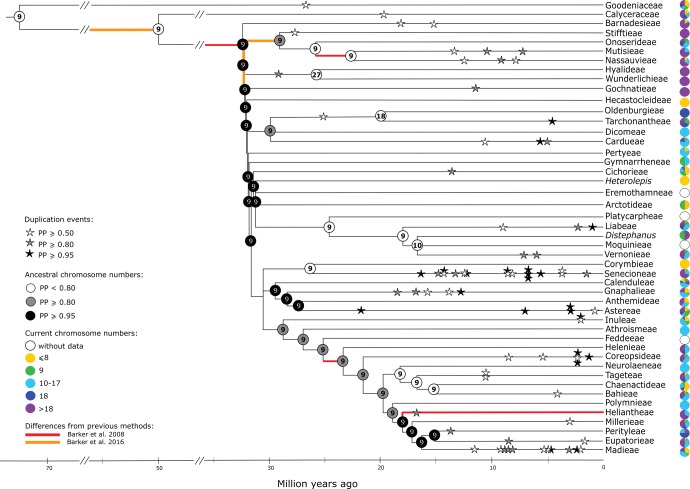
Chromosome number evolution of the Asteraceae, using the polymorphic data and according to the best-fitted model obtained. The main tribes were collapsed. Stars represent the expected chromosome number duplication events, while the circles at the tips of each branch represent the percentage (%) of the current chromosome numbers known for each tribe. Inside each circle (at interior nodes) the ancestral chromosome number with the highest probability is given. The differences observed between our study and previous ones (Barker et al. 2008, 2016) are highlighted as red and orange branches, respectively. Overall, our approach did not infer any paleoploidization events near the base of the family, nor any paleoploidization shared with the sister family, Calyceraceae. Also, no paleoploidization event was detected near the base of the tribe Mutisieae. Colors and shading are explained in the inset. For further and more precise information about the percentage of the current chromosome numbers for each tribe, please see the supplementary table S3, Supplementary Material online.

Table 4.

AIC and ML Values Obtained with and without Fixing the Asteraceae Root with a Certain Haploid Chromosome Number

	AIC	ML
Root not fixed	3010.22	-1502.11
Root fixed at 2	3036.40	-1515.20
Root fixed at 9	2990.68	-1492.34
Root fixed at 10	3000.14	-1497.07

Note.—For the root fixed analyses, the ancestral number given by ML method and the two best ancestral numbers as inferred by the Bayesian analyses were considered. All analyses were performed with the polymorphic data only, using the best model (Mc2). The lowest AIC and ML values are shown in bold.

For most of the main lineages of Asteraceae, the estimated ancestral haploid numbers were mainly n = 9 and n = 10 with some exceptions, ranging from n = 7 to n = 27 (table 3, fig. 1, and Supplementary Data Figure S1). A detailed analysis of the results obtained for each tribe reveals that in 71.74% of the cases the use of polymorphic data resulted in higher posterior probabilities than single data in 27.27% of the tribes with a PP higher than 0.90. Also, in 39.13% of the tribes, the Bayesian inference and the ML method reconstructed the same ancestral number (table 3).

Polyploidy and the Evolution of the Family

Based on the best-fitted model, we found a significant number (n = 22, or 28.95% of the total) of polyploidy events with an expectation ≥ 0.95 (fig. 1). We found 22 (28.95%) and 32 (42.10%) additional polyploidy events when considering the lower expectations of ≥ 0.80 and ≥ 0.50, respectively. Also, these events were not randomly distributed across the tree: some lineages, including the Senecioneae (17), Madieae (11), and Coreopsideae (6) presented a higher frequency of duplication events than others (fig. 1 and supplementary fig. S2, Supplementary Material online).

Polyploidization events were inferred mainly toward the tips of the tree (fig. 1). Only two genome duplication events were inferred deeper in the phylogeny: one in the base of the Hyalideae and Wunderlichieae tribes (expectation of 0.81) and another in the base of the Oldenburgieae and Tarchonantheae tribes (expectation of 0.58). This is in accordance with the chromosome number transition observed between the ancestor (n = 9) and the common ancestor of these tribes (n = 27 and n = 18, respectively) (fig. 1 and supplementary fig. S2, Supplementary Material online).

The best-fitted model did not support any duplication event at the origin of the family or at the diversification of the main lineages of Asteraceae (fig. 1). The absence of polyploidization events at the base of the tree is in agreement with the maintenance of the ancestral chromosome number of n = 9 inferred for the main tribes (fig. 1 and supplementary fig. S1, Supplementary Material online).

Discussion

According to the model that best explained our data (Mc2 model), the evolution of haploid chromosome numbers in Asteraceae was a very dynamic process. This model inferred that the most probable ancestral chromosome number of Asteraceae is n = 9. Also, more than one hundred WGD events and a large number of descending dysploidy events were inferred. Interestingly, the proposed paleopolyploidization events at the origin of the family or at the time of divergence of the main lineages of this family were not detected. These events were hypothesized by Barker et al. (2008, 2016) on the basis of single species Ks plots of gene duplications and Multi-tAxon Paleopolyploidy Search (MAPS), respectively. Below, we discuss our results and potential causes of discordance with previous studies.

Models of Chromosome Evolution in Asteraceae

Our analyses of chromosome number evolution in Asteraceae revealed that the haploid chromosome number shifted frequently during the evolution of the family. The best-fitted evolutionary model (Mc2 model) showed that dysploidy and polyploidy were very frequent events (table 1). More precisely, descending dysploidies, most likely through chromosome fusion, were the most common genetic mechanism of chromosome number change during the evolution of Asteraceae (table 2). These results are similar to those obtained for the Araceae (Cusimano et al. 2012), Melanthiaceae (Pellicer et al. 2014), and Colchicaceae (Chacón et al. 2014), where descending dysploidy was also the most frequently inferred event. In the particular case of some tribes of Asteraceae, previous studies that utilized different approaches have also shown that dysploidies (more precisely, descending dysploidy) and genome duplications were two frequent and important processes of chromosome number change (Ito et al. 2000; Funk and Chan 2009; Semple and Watanabe 2009; Susanna and Garcia-Jacas 2009; Ward et al. 2009; Anderberg 2009b). In other tribes of the family, such as Barnadesieae and Cichorieae, polyploidy alone seems to have played the most important role (Robinson 1981; Vallès et al. 2005; Baldwin 2009; Kilian et al. 2009; Oberprieler et al. 2009; Sancho and Freire 2009; Stuessy et al. 2009). A recent study exploring karyotypic changes in 15 clades of angiosperms also highlighted the co-occurrence of dysploidy and polyploidy (Escudero et al. 2014). Thus, our results, and those of previous studies, emphasize the importance of these phenomena in the evolution of chromosome numbers of flowering plants.

The reduction of chromosome number polymorphisms within a taxon to a single count could impact the number of reconstructed events of chromosomal change. In our case, the use of different chromosome number coding schemes affected the number of events that occurred along the branches of the tree, but did not affect the selection of the best model of chromosome evolution. Both coding schemes supported the same model, with similar parameter values being obtained (table 2), but the use of single data inferred almost 30% more chromosomal change events than polymorphic data. The impact of different coding schemes needs further scrutiny in the future, for example, by using simulations that may allow testing for differences between the inferences and the real data. Nevertheless, the use of data that includes several counts and accounts for the frequency of these counts seems preferable in order to reduce the assumptions associated with summarizing several counts to one single representative count.

Ancestral Chromosome Numbers

Our model of chromosome number evolution allowed inference of the ancestral haploid numbers for the sunflower family using an evolutionary model and a robust and statistically well-understood approach (Cusimano et al. 2012; Cusimano and Renner 2014) (fig. 1; for further and more precise information on all the ancestral numbers inferred, see Supplementary Data Figure S1). Overall, our results are in agreement with previous hypotheses of ancestral chromosome numbers for the Asteraceae and for many of its tribes (table 3); i.e., n = 9 (under Bayesian inference) is the most probable ancestral haploid chromosome number (Solbrig 1977; Cronquist 1981; Bremer 1994; Semple and Watanabe 2009; Bala and Gupta 2013). Unexpectedly, the ancestral number for Asteraceae obtained under the ML approach was n = 2, a very low and seemingly unrealistic number (table 3). Considering the fact that across the tree other ancestral ML estimations were very consistent with those obtained using the Bayesian approach, it is difficult to envisage the causes for this large discrepancy in the ancestral number of the family.

Still, several discrepancy between inferences (for ancestral and base chromosome number) obtained in this study and those of previous works were observed (e.g., in Mutisieae, Hecastocleideae, and Corymbieae; table 3). Two main factors might have contributed to these discrepancies: 1) the use of different approaches, in particular the use of the haploid chromosome number (used in this study) instead of the base chromosome number (in other studies) and 2) incomplete taxon sampling. Previous estimations were frequently based on algebraic inferences, or the authors only considered the lowest available haploid count as the ancestral condition instead of using explicit models of chromosome evolution (Powell et al. 1974; Weitz 1989). Despite the fact that our analysis makes use of the largest phylogenetic tree of the family to date, it should be noted that it still represents an incomplete data set. Therefore, future studies should be performed using more complete phylogenetic trees (when made available) that will enable better inferences of ancestral states and to clarification of whether the discrepancies are related to the lack of complete sampling or are due to other reasons.

Polyploidy and the Evolution of the Family

The present study also revealed the occurrence of several WGDs along the evolution of several lineages of Asteraceae. Our best model inferred some of the WGDs suggested in previous analyses of ESTs (Barker et al. 2008), but not all of them. For instance, in the present study, a WGD event with a high expectation (≥ 0.8) was observed near the base of the Heliantheae tribe (fig. 1; for further and more precise information of all the duplication and demiduplication events inferred, see supplementary fig. S2, Supplementary Material online). This result partially supports previous evidences from genomic and cytological analyses that revealed independent genome duplications near the base of this lineage (Baldwin et al. 2002; Barker et al. 2008, 2016). Nevertheless, according to our results, a paleopolyploidization event seems to have occurred at the base of the Heliantheae tribe sensu stricto (s.s.), instead of having occurred at the base of the Heliantheae alliance, that is, Heliantheae sensu lato (s.l.), which includes several tribes, from Helenieae to Madieae, as has been suggested.

Other paleopolyploidization events inferred by phylogenomic analyses (Barker et al. 2008, 2016) were not observed in our study (fig. 1 and supplementary fig. S2, Supplementary Material online). In particular, a paleopolyploidization event near the origin of the family, just prior to the rapid radiation of its tribes, as recently suggested (Barker et al. 2008, 2016) to be shared with Calyceraceae (the sister family of Asteraceae) was not observed in our case. Also, a paleohexaploidization event in the ancestry of the core of Asteraceae (except Barnadesia) (Barker et al. 2016) and an independent WGD near the base of the tribe Mutisieae (Barker et al. 2008) were not inferred by the evolutionary models of chromosomal number change.

The discrepancy between our study and previous work (Barker et al. 2008) observed at the origin of Asteraceae might be due to the use of different approaches. Barker et al. (2008) performed a comparative study of thousands of ESTs from 18 Asteraceae species and two outgroups (Solanum lycopersicon and Arabidopsis thaliana). Although their study provides a valuable perspective, the number of species used can be considered a small sampling of this large plant family. Also, considering the outgroups used, the WGD attributed to the origin of Asteraceae might have occurred before the origin of this family, as the most common recent ancestor of both outgroups is much deeper (dated at 93–100 Mya for S. lycopersicon, and at 117–121 Mya for A. thaliana), than the most common recent ancestor of the three families we used (Asteraceae, Calyceraceae, and Goodeniaceae). The duplication event reported by Barker et al. (2008) may have occurred somewhere after the divergence of Asteraceae and Solanaceae, namely in the split between Campanulids and Lamiids (Soltis et al. 2011), a considerable phylogenetic distance from the origin of Asteraceae.

More recent analyses performed by Barker et al. (2016) using a new algorithm, MAPS, evidenced the occurrence of a shared paleotetraploidization event at the base of Calyceraceae, and that most Asteraceae (except Barnadesia) are descendants of a paleohexaploid. In our case, no WGD events were observed at the base of Calyceraceae or at the base of the Barnadesieae tribe. Instead, we inferred a WGD and a demiduplication event along the evolution of Calyceraceae, and two WGD events within Barnadesieae (fig. 1 and supplementary fig. S2, Supplementary Material online). Thus, the evolutionary model of chromosome number change used here inferred independent WGD events in different lineages, whereas phylogenomic analyses (Barker et al. 2008, 2016) seem to interpret these duplication events as the result of a shared duplication event occurring in the common ancestor of the analyzed taxa. In the near future, with the increasing number of available transcriptomes, it should be possible to have a clearer picture of these paleopolyploidization events.

Finally, Barker et al. (2008) suggested the occurrence of another WGD at the base of the tribe Mutisieae. In our study, which includes 11 species/genera of the tribe, three WGD events were observed: two events along the evolution of Brachyclados and Chaptalia and another before the diversification of Adenocaulon, together with two demiduplication events along the evolution of Trichocline and Leibnitzia. Still, none of these events are related to the origin of the tribe or with the origin of the sister tribe Nassauvieae (fig. 1 and supplementary fig. S2, Supplementary Material online), as suggested by Barker et al. (2008). Nevertheless, Mutisieae s.l. is considered a very complex group that still lacks full resolution of its phylogenetic relationships (Funk et al. 2009). Further, chromosome count information is absent for many of the genera in tribe Mutisieae s.l. Therefore, all these results should be considered with caution and deserve further detailed analyses once the present limitations are overcome.

The majority of the WGDs reconstructed were observed toward the tips of the tree (fig. 1 and supplementary fig. S2, Supplementary Material online). The same pattern was observed in Araceae (Cusimano et al. 2012) and Melanthiaceae (Pellicer et al. 2014). This result, as well as the lack of congruence with the results of Barker et al. (2008, 2016), may be related to the fact that deep polyploidization events may be harder to detect than recent ones using the chromEvol algorithm due to genomic changes and rearrangement following polyploidization. For example, in Arabidopsis and in some close relatives, species are regarded as genetically diploid based on chromosome number, but based on genomic data, it has been shown that multiple paleopolyploid duplications were likely followed by evolutionarily younger WGD events, but are masked due to massive genome repatterning and descending dysploidy (Barker et al. 2009; Mandáková et al. 2010). Alternatively, most ancient events may have led to lineages that did not survive until present times. As genomic changes and rearrangements after duplication can only be detected via genomic approaches, further studies combining evolutionary models of chromosome number change and phylogenomic approaches are fundamental to a full assessment of the reliability of these results and to give further insights into genome evolution in Asteraceae. We believe that the use of chromEvol gives valuable estimates of chromosomal evolution, providing exciting hypotheses that can be examined in the future. However, using chromosomal data alone can lead to incorrect inference of genome duplication events, and thus it should regarded as a first approximation that needs to be further confirmed with genomic approaches. The combination of both approaches could provide an effective tool in phylogenetic placement of genomic events (see Crowl et al. 2016), as well as the study of potential diploidization events after WGD.

In conclusion, this study supports the hypothesis that the evolution of Asteraceae was marked by a considerable number of chromosomal change events, including polyploidy. However, genome duplications seem to have occurred after the main diversification of the tribes. In addition, those lineages that have experienced WGDs before their diversification, such as Hyalideae, Wunderlichieae, Oldenburgieae, or Tarchonantheae, are much less species rich than other lineages where WGDs were not observed, such as in Senecioneae, Astereae, Anthemideae, and Cichorieae. Therefore, further studies are needed to fully understand the importance of these genomic mechanisms in the evolution of Asteraceae and of the angiosperms.

Supplementary Material

Supplementary tables S1–S3 and figures S1 and S2 are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).