Machine learning in genetics and genomics

Abstract

The field of machine learning promises to enable computers to assist humans in making sense of large, complex data sets. In this review, we outline some of the main applications of machine learning to genetic and genomic data. In the process, we identify some recurrent challenges associated with this type of analysis and provide general guidelines to assist in the practical application of machine learning to real genetic and genomic data.

1 Introduction

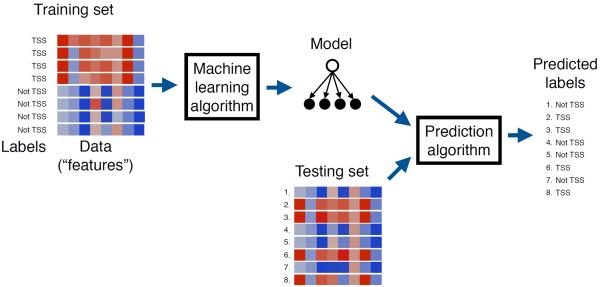
The field of machine learning is concerned with the development and application of computer algorithms that improve with experience [1]. Thus, for example, in genomics machine learning can be used to “learn” how to recognize the locations of transcription start sites (TSSs) in a genome sequence [2]. The process typically proceeds in three stages (Figure 1). First, a machine learning researcher develops an algorithm that they believe will lead to successful learning. Second, the algorithm is provided with a large collection of TSS sequences as well as, optionally, a list of sequences that are known not to be TSSs. The annotation indicating whether a sequence is a TSS or not is known as the label. The algorithm processes these labeled sequences and stores a model. Third, novel, unlabeled sequences are given to the algorithm, and it uses the model to predict labels (“TSS” or “not TSS”) for each sequence. If the learning was successful, then all or most of the predicted labels will be correct. If the labels associated with test set examples are known—i.e., if these examples were held out of the training set on purpose for use in testing the performance of the learning system—then the performance of the machine learning algorithm can be assessed immediately. Otherwise, in a prospective validation setting, the TSS predictions produced by the machine learning system must be tested independently in the lab. Note that this is an example of a subtype of machine learning called “supervised learning,” which is described in more detail below(Section 2).

Figure 1. Machine learning.

A canonical example of a machine learning application. A training set of DNA sequences is provided as input to a learning procedure, along with binary labels indicating whether each sequence is centered on a TSS or not. The learning algorithm produces a model which can then be subsequently used, in conjunction with a prediction algorithm, to assign predicted labels to unlabeled test sequences.

This process of algorithm design, learning, and testing is simultaneously analogous to the scientific method on two different levels. First, the design-learn-test provides a principled way to test a hypothesis about machine learning: “I hypothesize that algorithm X can successfully learn to recognize TSSs.” Second, the algorithm itself can be used as a hypothesis generator: “I hypothesize that sequence Y is a TSS.” In this second setting, the resulting scientific theory is instantiated in the model produced by the learning algorithm. In this case, a key question, which we return to in Section 3, is whether and how easily a human can make sense of this model.

1.1 Machine learning application areas

Machine learning methods have been applied to a huge variety of problems in genomics and genetics (Table 2). Perhaps most significantly, machine learning has been used to annotate a wide variety of genomic sequence elements. In addition to TSSs, algorithms can be trained to identify splice sites [3], promoters [4], enhancers [5], positioned nucleosomes [6], etc. In general, if you can compile a list of sequence elements of a given type, then you can probably train a machine learning method to recognize those elements. Furthermore, models that each recognize an individual type of of genomic elements can be combined, along with (learned) logic about their relative locations, to build machine learning systems capable of annotating genes, including their full UTR/intron/exon structure, along entire eukaryotic chromosomes [7].

Table 2.

Selected applications of machine learning in genetics and genomics.

Input data	Task
DNA sequence	Identify transcription start sites, splice sites, exons, etc.
DNA sequence	Identify TF binding sites
DNA sequence	Identify genes
Gene expression	Predict regulatory relationships
Gene expression data	Identify biomarkers for a disease
Histone and TF ChIP-seq data	Partition and label the genome with chromatin state annotation
DNA sequence + gene expression + …	Predict gene function
DNA sequence + histone mods + …	Predict gene expression
DNA sequence + histone mods + …	Predict variant deleteriousness
Sequence variants + gene expression + …	Predict disease phenotype or prognosis

In addition to learning to recognize patterns in DNA sequences, machine learning can take as input data generated by other genomic assays, such as microarray or RNA-seq expression data, chromatin accessibility assays such as DNase-seq, MNase-seq, and FAIRE, or histone modification, transcription factor (TF) binding ChIP-seq data, etc. Gene expression data can be used to learn to distinguish between different disease phenotypes and, in the process, to identify potentially valuable disease biomarkers (Section 6). Chromatin data can be used, for example, to annotate the genome in an “unsupervised” fashion, thereby potentially allowing for the identification of novel classes of functional elements (Section 2).

Machine learning has also been used extensively to assign functional annotations to genes. Such annotations most frequently take the form of Gene Ontology term assignments [8]. Predictive algorithms can take as input any one or more of a wide variety of data types, including the genomic sequence, gene expression profiles across various experimental conditions or phenotypes, protein-protein interactions, synthetic lethality data, open chromatin data, histone modification or TF binding ChIP-seq data, etc. As an alternative to GO term prediction, some predictors instead identify co-functional relationships; i.e., the machine learning method outputs a network in which genes are nodes and an edge between genes A and B indicates that the two genes share a common function [9].

Finally, a wide variety of machine learning methods have been developed to help understand the mechanisms underlying gene expression. Some techniques aim to predict the expression of a gene based solely on the DNA sequence [10], whereas others take into account ChIP-seq histone modification [11] or TF binding [12] profiles at the gene promoter region. More sophisticated methods attempt to jointly model the expression of all genes in a cell by training a network model [13]. Like a co-functional network, each node in a gene expression network is a gene; however, edges in this case represent, for example, regulatory relationships between TFs and their targets.

Many of the problems listed above can also be solved using techniques drawn from the field of statistics. Indeed, the line between machine learning and statistics is at best blurry, with some preferring the term “statistical learning” over “machine learning” [14]. Historically, the field of machine learning grew out of the artificial intelligence community, where the term “machine learning” became popular in the late 90s. In general, machine learning researchers have tended to focus on a subset of problems within statistics, emphasizing in particular the analysis of large, heterogeneous data sets. Accordingly, many core statistical concepts, such as calibration of likelihood estimates, statistical confidence estimation and power calculations, are essentially absent from the machine learning literature.

1.2 Scope of this review

This review provides an overview of machine learning as it is applied to problems in genomics. We discuss the main categories of machine learning methods and the key considerations that must be made when applying these methods to genomics problems. We do not not attempt to catalogue all machine learning methods or all reported applications of machine learning to genomics, nor do we discuss any particular method in great detail. Instead, the review begins by explaining several key distinctions in machine learning and then outlining some of the major challenges researchers face in applying machine learning methods to practical problems in genomics. We hope that the reader will take away from this review an idea of what problems machine learning approaches might be applicable to and which types of methods are likely to be effective for these problems. For a more detailed treatment of machine learning applied to particular subfields of genetics and genomics, the reader may consult reviews of these specific topics [15, 16, 17, 18].

The review will cover the following topics. Section 1 describes the major classes of machine learning problems: supervised, unsupervised and semisupervised. Section 2 concerns the tradeoff between maximizing a model's performance and interpretability. Sections 3–5 describe strategies a researcher can use to guide a machine learning model, through prior knowledge, means of integrating heterogeneous data sets and feature selection. Sections 6–9 describe several important pitfalls and special cases of machine learning: imbalance between classes in supervised problems, missing data and networks of dependencies between examples. Finally, in Section 10, we describe the outlook for machine learning in genomics in coming years.

2 Supervised versus unsupervised learning

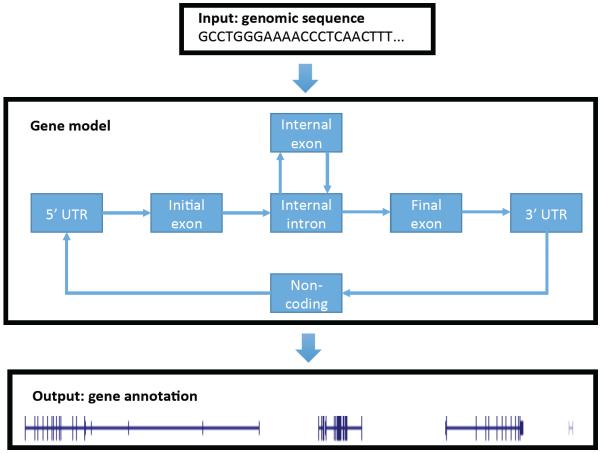
Machine learning methods can usefully be segregated into two primary categories: supervised versus unsupervised methods. To illustrate the difference between the two, consider again the gene finding problem: given the DNA sequence of a chromosome, the goal of a gene finding algorithm is to predict the locations and detailed intron/exon structure of all of the protein-coding genes on the chromosome (Figure 2). The most straightforward solution to this problem leverages what we already know about the genome to help us build a predictive model. In particular, a supervised learning algorithm for gene finding requires as input a training set of labeled DNA sequences, where the labels specify the locations of the start and end of the gene (TSS and TTS) as well as all of the splice sites in between. The model then uses this training data to learn general properties of genes, such as what DNA sequence pattern typically occurs near a donor or acceptor splice site, the fact that in-frame stop codons should not occur within coding exons, the expected length distributions of 5' and 3' untranslated regions (UTRs) and of initial, internal and final introns, etc. The trained model can then use these learned properties to identify novel genes that resemble the genes in the training set.

Figure 2. A gene finding model.

A simplified gene finding model, which captures the basic properties of a protein-coding gene. The model takes as input the DNA sequence of a chromosome or a portion thereof and produces as output detailed gene annotations. Note that this simplified model is incapable of identifying overlapping genes or multiple isoforms of the same gene.

On the other hand, supervised learning only makes sense when a labeled training set is available. Consider, for example, interpreting a heterogeneous collection of epigenomic data sets, such as those generated by the ENCODE and Epigenomics Roadmap consortia. A priori, we expect that the patterns of chromatin accessibility, histone modifications and TF binding along the genome should be able to provide us with a detailed picture of the biochemical and functional activity of the genome. We may also expect that these activities could be accurately summarized using a relatively small set of labels. If we are interested in discovering what types of labels best explain the data rather than imposing a pre-determined set of labels on the data, then we must use unsupervised rather than supervised learning. In this type of approach, the machine learning algorithm takes as input only the unlabeled data and the desired number of different labels to assign [19, 20, 21]. The algorithm then automatically partitions the genome into segments and assigns a label to each segment, with the goal of assigning the same label to segments that have similar data. Because the method is unsupervised, a human must subsequently assign semantics to each label, a step which is not required for a supervised gene finding algorithm. The benefit of the unsupervised approach, however, is the ability to train when labeled examples are unavailable and the ability to identify potentially novel types of genomic elements. The latter is fundamentally impossible with a supervised method, which can only identify more examples of the types of labels it learns from.

2.1 Semi-supervised learning

Intermediate between supervised and unsupervised learning is semi-supervised learning [22]. In supervised learning, the algorithm receives as input a collection of data points, each with an associated label, whereas in unsupervised learning, the algorithm receives the data but no labels. The semi-supervised setting is a mixture of these two: the algorithm receives a collection of data points, but only a subset of those points have associated labels. In practice, gene finding systems are often trained using a semi-supervised approach, where the input is a collection of annotated genes plus a complete (unlabeled) genome sequence. The learning procedure begins by constructing an initial gene finding model based solely on the labeled subset of the training data. Then the model is used to scan the genome, and tentative labels are assigned throughout the genome. These tentative labels can then be used to improve the learned model, and the procedure iterates until no new genes are found. The semi-supervised approach can work much better than a fully supervised approach because the model is able to learn from a much larger set of genes: all genes in the genome, rather than only the subset of genes that have been identified with high confidence.

2.2 Which type of method to use

When faced with a new machine learning task, the first question is often whether to use a supervised, unsupervised or semi-supervised approach. In some cases, the answer to this question is obvious. For example, if no labels are available, then you can only perform unsupervised learning. However, when labels are available, it is not always the case that taking a supervised approach is a good idea. This is because every supervised learning method rests upon the implicit assumption that the distribution responsible for generating the training data set is the same as the distribution responsible for generating the test data set. This assumption will be respected if, for example, you take a single labeled data set and randomly subdivide it into a training set and a testing set. However, it is often the case that you plan to train an algorithm on a training set that is generated differently from the testing data to which the trained model will eventually be applied. A gene finder trained using a training set of human genes will probably not work very well at finding genes in the mouse genome. Often, the train/test divergence is less obvious. For example, a TSS data set generated by cap analysis of gene expression (CAGE) data will not contain non-polyadenylated genes [23]. If such genes also exhibit differences around the TSS, then the resulting TSS predictor will be biased. In general, supervised learning should be employed only when the training set and test set are expected to exhibit similar statistical properties.

What about semi-supervised learning? When supervised learning is feasible, it is often the case that additional, unlabeled data points are easy to obtain. How do you decide whether to use a supervised or semi-supervised approach? In theory, semi-supervised learning requires making certain assumptions about the data set [22]). In practice, however, assessing these assumptions can be very difficult. Therefore, a good rule of thumb is to use semi-supervised learning if two conditions hold: you don't have very much labeled data and you have a very large amount of unlabeled data.

3 Generative versus discriminative modeling

Applications of machine learning methods generally have one of two goals: prediction or interpretation. Consider the problem of predicting, on the basis of a ChIP-seq experiment, the locations at which a given TF will bind genomic DNA. This task is analogous to the TSS prediction task (Figure 1), except that the labels are derived from ChIP-seq peaks. A researcher applying a machine learning method to this problem may either want to understand what properties of a sequence are most important for determining whether or not a TF will bind (interpretation) or simply predict the locations of TF binding as accurately as possible (prediction). There are tradeoffs between accomplishing these two goals—methods that optimize prediction accuracy often do so at the cost of interpretability.

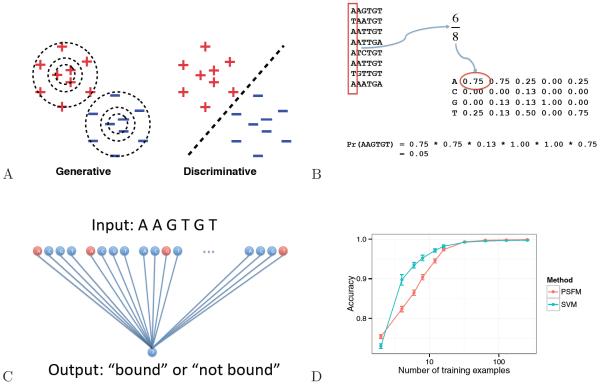
The distinction between generative and discriminative models plays a large role in the tradeoff between interpretability and performance. Generative models build a full model of the distribution of features in each of the two classes and then compares how those two distributions differ from one another. In contrast, the discriminative approach focuses on accurately modeling just the boundary between the two classes. From a probabilistic perspective, the discriminative approach involves modeling just the conditional distribution of the label given the input feature data sets, as opposed to the joint distribution of the labels and features. Schematically, if we imagine that our task is to separate two groups of points in a two-dimensional space (Figure 3A), then the generative approach builds a full model of the distribution of points in each of the two classes and then compares how those two distributions differ from one another, while the discriminative approach focuses only on separating the two classes.

Figure 3. Two models of TF binding.

(A) A position-specific frequency matrix model, in which the entry in row i and column j represents the frequency of the ith base occurring at position j in the training set. (B) A linear support vector machine model of TF binding. Labeled positive and negative training examples are provided as input, and a learning procedure adjusts the weights on the edges to predict the given label. (C) The figure plots the mean accuracy (± 95% confidence intervals), on a set of 500 simulated test sets, of predicting TF binding as a function of the number of training examples. The two series correspond to a PSFM model or an SVM. (D) Schematic of generative versus discriminative modeling. The generative model characterizes both classes completely, whereas the discriminative model focuses on the boundary between the classes.

A researcher adopting a generative approach to the TF binding problem begins by imagining what procedure could be used to generate the observed data. A widely used, generative model of TF binding employs a position-specific frequency matrix (PSFM, Figure 3B), in which a collection of aligned binding sites of width w are summarized in a 4 × w matrix M of frequencies, where the entry at position M_i,j represents the empirical frequency of observing the ith DNA base at position j. We can generate a random bound sequence according to this PSFM model by drawing w random numbers, each in the range [0, 1〉. For the jth random number we select the corresponding DNA base according to the frequencies in the jth column of M. Conversely, scoring a candidate binding site using the model corresponds to computing the product of the corresponding frequencies from the PSFM. This value is called the likelihood. Training a PSFM is simple—you simply compute the empirical frequency of each nucleotide at each position.

A simple example of a discriminative algorithm is the support vector machine (SVM, Figure 3C) [24, 25]. The goal of the SVM is to learn to output a “1” whenever it is given a positive training example and a “−1” whenever it is given a negative training example. In the TF binding prediction problem, the input sequence of length w is encoded as a binary string of length 4w, where each bit corresponds to the presence or absence of a particular nucleotide at a particular position.

This generative modeling approach offers several compelling benefits. First, the generative description of the data implies that the model parameters have well-defined semantics relative to the generative process. Accordingly, as shown in the example above, the model not only makes predictions for where a given TF binds but also provides a story about why the TF binds there. If we compare two different potential binding sites, we can see not only that the model prefers one site over another but also that the preference comes from, e.g., the preference for an A rather than a T at position 7 of the motif. Second, generative models are frequently stated in terms of probabilities, and the probabilistic framework provides a principled way to handle problems like missing data. For example, it is still possible for a PSFM to make a prediction for a binding site where one or more of the bound residues is unknown. This is accomplished by probabilistically averaging over the missing bases. The probabilistic framework is also helpful because the output has well-defined, probabilistic semantics. This can be helpful when making downstream decisions about how much to trust a given prediction.

In many cases, including the TF binding example, the training data set contains a mixture of positive and negative examples. In a generative setting, these two groups of examples are modeled separately, each with its own generative process. For example, for the PSFM model, the negative (or background) model is often a single set B of nucleotide frequencies, representing the overall mean frequency of each nucleotide in the negative training examples. To generate a length-w sequence according to this model, we again generate w random numbers, but now each base is selected according to the frequencies in B. To use the foreground PSFM model together with the background model B, we compute a likelihood ratio, i.e., which is simply the ratio of the likelihoods computed with respect to the PSFM and with respect to B.

The primary benefit of the discriminative approach is that it provably achieves better performance with infinite training data [26, 27]. In practice, analogous generative and discriminative approaches often converge to the same solution, and generative approaches can sometimes perform better with limited training data. However, when the amount of labeled training data is reasonably large, then the discriminative approach will tend to find a better solution, in the sense that it will predict the desired outcome more accurately when tested on previously unseen data (assuming, as usual, that the data are drawn from the same underlying distribution as the training data). To illustrate this phenomenon, we simulated data according to a simple PSFM model and trained a PSFM and SVM, varying the number of training examples. To train a model of width 19 nucleotides to discriminate between bound and non-bound sites with 90% accuracy requires eight training examples for a PSFM model and only four examples for an SVM model (Figure 3D). This improvement in performance is achieved because, by not bothering to accurately characterize the “easy” parts of the 2D space, the discriminative model does a better job at solving the discrimination task at hand. Thus, empirically, the discriminative approach will tend to give more accurate predictions

The flipside of this accuracy, however, is that by solving a single problem well, the discriminative approach fails to solve other problems at all. Specifically, because the internal parameters of a generatively trained model have well-defined semantics, we can use the model to ask a variety of related questions, e.g., not just “Does CTCF bind to this particular sequence?” but “Why does CTCF bind to this sequence more tightly than to some other sequence?” The discriminative model, in contrast, only allows us to answer the single question for which it was designed. Thus, choosing between a generative and discriminative model involves a trade-off between predictive accuracy and interpretability of the model.

While the distinction between generative and discriminative models plays a large role in determining the interpretability of a model, the model's complexity—that is, the number of parameters it has—can be just as imporant. Models of either type with a large number of parameters tend to be difficult to interpret, but can generally achieve higher accuracy than models with few parameters, given enough data. The complexity of a model can be limited either by choosing a simple model or by using a feature selection strategy to restrict the complexity of the learned model.

4 Incorporating prior knowledge

In many applications, the success or failure of a machine learning method depends upon the extent to which the method successfully encodes various types of prior knowledge about the problem at hand. Indeed, much of the “art” of practical machine learning involves understanding the details of a particular problem and then selecting an algorithmic approach that allows those details to be accurately encoded. There is provably no optimal machine learning algorithm that works best for all problems [28], so this selection of approach that matches the researcher's prior knowledge about the problem is crucial to the success of the analysis.

Often, the encoding of prior knowledge is implicit in the framing of the machine learning problem. Consider, for example, the prediction of nucleosome positioning from primary DNA sequence [6]. The “labels” for this prediction task can be derived, for example, from an MNase sequencing assay. In this case, after appropriate processing, each base is assigned an integer count of the number of nucleosome-sized fragments that cover the base. It might seem natural, therefore, to frame the problem as a regression, where the input is, say, a sequence of length 201 bp and the output is the predicted coverage at the center of the sequence. However, in practice we may be particularly interested in identifying nucleosome-free regions. Hence, rather than asking the algorithm to solve the problem of predicting exact coverage at each base, we might instead opt to predict whether each base occurs in a nucleosome-free region or not. Switching from regression to classification makes the problem easier, but more importantly, this switch also encodes the prior knowledge that regions of high MNase accessibility are of particular biological interest.

4.1 Implicit prior knowledge

In other cases, prior knowledge is encoded implicitly in the choice of the data that we provide as input to the machine learning algorithm. For example, Yip et al. [29] trained a collection of machine learning methods to distinguish among various types of genomic elements. Using chromatin data—DNaseI accessibility and ChIP-seq profiles of histone modifications and TF binding—one classifier distinguished between regulatory regions that are close to a gene versus regulatory regions that are far away from any gene. In this context, design of the input space, i.e., the features that are provided as input to the classifier, is of critical importance. In the Yip et al. study, features were computed by averaging over a 100 bp window. The choice of a 100 bp window likely reflects the prior knowledge that, at least for histone modification data, the data are arguably only meaningful at approximately the scale of a single nucleosome (147 bp) or larger. Moreover, replacing a single, averaged feature with 100 separate features may also be problematic (see Section 6). In contrast, for DNase accessibility data, it is plausible that averaging over 100 bp may remove some useful signal. Alternatively, prior knowledge may be implicitly encoded in the learning algorithm itself, where some types of solutions are preferred over others [30]. Therefore, in general, the choice of input data sets, their representations, and any preprocessing must be guided by prior knowledge about data and application.

4.2 Probabilistic priors

In a probabilistic framework, some forms of prior knowledge can be represented explicitly by specifying a prior distribution over the data. A common prior distribution is the uniform, or “uninformative,” prior which, despite the name, can be quite useful in some contexts. Consider, for example, a scenario in which we have gathered a collection of ten validated binding sites for a particular transcription factor (Figure 4), and we observe that the sequences cluster around a clear consensus motif. If we represent these sequences using a pure PSFM, then because our data set is quite small, a significant number of the entries in the PSFM will be zero. Consequently, the model will assign any sequence that contains one of these zero entries an overall probability of zero, even if the sequence otherwise exactly matches the motif. This is counter-intuitive. The solution to this problem is to encode the prior knowledge that every possible DNA sequence has the potential to be bound by a given transcription factor. The result is that even sequences containing nucleotides that we have never observed in a given position can still be assigned a non-zero probability by the model.

Figure 4. Incorporating a prior into a PSFM.

A simple, principled method for putting a probabilistic prior on a PSFM involves augmenting the observed nucleotide counts with “pseudocounts” and then computing frequencies with respect to the sum. The magnitude of the pseudocount corresponds to the weight assigned to the prior.

In many probability models, much more sophisticated priors have been developed to capture more complex prior knowledge. A particularly successful example is the use of Dirichlet mixture priors in protein modeling [31]. Here, the idea is that if we are examining an alignment of protein sequences, and if we see many aligned leucines in a particular column, then because we know that leucine and valine are biochemically similar, we may want to assign a high probability to sequences that contain a valine in that same column, even if we have never seen a valine there in our training data. The name “Dirichlet mixture” refers to the fact that the prior distribution is represented as a Dirichlet distribution, and that the distribution is a mixture in which each component corresponds to a group of biochemically similar amino acids. Such priors lead to significantly improved performance in modeling evolutionarily related families of proteins [31] and in discovering protein motifs [32].

4.3 Prior information in non-probabilistic models

On the other hand, incorporation of prior knowledge into non-probabilistic methods can be more challenging. For example, discriminative classifiers like artificial neural networks (ANNs) or random forests do not provide any explicit mechanism for representing prior knowledge. The topology of a multi-layer ANN can represent information about dependencies between input features in the input space, but more general priors cannot be represented.

One class of discriminative methods does provide a more general mechanism for representing prior knowledge, when that knowledge can be encoded into a generalized notion of similarity. Kernel methods are algorithms that substitute in place of a simple similarity function (specifically, the cosine of the angle between two input vectors) a general class of mathematical functions called kernels [33]. The flagship kernel method is the SVM classifier, which has been widely used in many fields including biological applications ranging from DNA and protein sequence classification to mass spectrometry analysis [25]. Other methods that can employ kernels include support vector regression as well as classical algorithms like k-means clustering, principal components analysis, and hierarchical clustering. Prior knowledge can be provided to a kernel method by selecting or designing an appropriate kernel function. For example, a wide variety of kernels can be defined between pairs of DNA sequences, where the similarity can be based on shared k-mers, irrespective of their positions within the sequences [34], on nucleotides occuring at particular positions [35], or on a mixture of the two [36]. A DNA sequence can even encode a simple model of molecular evolution, using algorithms similar to the Smith-Waterman alignment algorithm [37]. Furthermore, the Fisher kernel provides a general framework for deriving a kernel function from any probability model [38]. In this way, formal probabilistic priors can be used in conjunction with any kernel method. Kernel methods have a rich literature, which is reviewed in more detail in [39].

5 Handling heterogeneous data

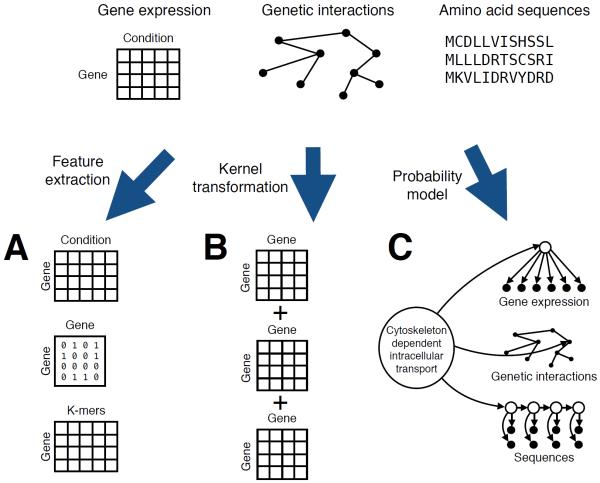
Another common challenge in learning from real biological data is that the data themselves are heterogeneous. For example, consider the problem of learning to assign Gene Ontology terms to genes. For a given term, such as “cytoskeleton dependent intracellular transport,” a wide variety of types of data might be relevant, including the amino acid sequence of the gene's protein product, that protein's inferred evolutionary relationships to other proteins across a variety of species, the microarray or RNAseq expression profile of the gene across a variety of phenotypic or environmental conditions, the number and identity of neighboring proteins identified using yeast two-hybrid or tandem affinity purification tagging experiments, GFP-tagged microscopy images, etc (Figure 5). Such data sets are difficult to analyze jointly because of their heterogeneity: an expression profile is a fixed-length vector of real values; protein-protein interaction information is a binary network, and protein sequences are variable length strings drawn from a discrete alphabet. Many statistical and machine learning methods for classification assume that all of the data can be represented as fixed-length vectors of real numbers. Such methods cannot directly be applied to heterogeneous data.

Figure 5. Three ways to accommodate heterogeneous data in machine learning.

The task of predicting gene function labels requires methods that take as input gene expression data, protein sequences, protein-protein interaction networks, etc. These diverse data types can be encoded into fixed-length features, represented using pairwise similarities (kernels), or directly accommodated by a probability model.

The most straightforward way to solve this problem is to transform each type of data into vector format prior to processing (Figure 5A). This was the approach taken, for example, by Peña-Castillo et al. in a critical assessment of methods for predicting gene function in mice [40]. Participating research groups were provided with separate matrices, each representing a single type of data: gene expression, sequence patterns, protein interactions, phenotypes, conservation profiles, and disease associations. All matrices shared a common set of rows, one per gene, but the number and meanings of the columns differed from one matrix to the next. For example, gene expression data were represented directly, whereas protein sequence data were represented indirectly via annotations from repositories such as Pfam [41] and InterPro [42], and protein-protein interactions were represented as square matrices in which entries were shortest-path lengths between genes.

Alternatively, each type of data can be encoded using a kernel function (Figure 5B), with one kernel for each data type. Mathematically, using kernels is formally equivalent to transforming each data type into a fixed-length vector; however, in the kernel approach the vectors themselves are not always represented explicitly. Instead, the similarity between two data elements—amino acid sequences, nodes in a protein-protein interaction network, etc.—is encoded in the kernel function. The kernel framework allows more complex kernels to be defined from combinations of simple kernels. For example, a simple summation of all the kernels for a given pair of genes is itself a kernel function. Furthermore, the kernels themselves can encode prior knowledge by, e.g., allowing for statistical dependencies within a given data type but not between data types [43]. Kernels also provide a general framework for automatically learning the relative importance of each type of data relative to a given classification task [44].

Finally, probability models provide a very different method for handling heterogeneous data. Rather than forcing all the data into a vector representation or requiring that all data be represented using pairwise similarities, a probability model explicitly represents diverse data types in the model itself (Figure 5C). An early example of this type of approach assigned gene functional labels to yeast genes on the basis of gene expression profiles, physical associations from affinity purification, two-hybrid and direct binding measurements, as well as genetic associations from synthetic lethality experiments [45]. The authors used a Bayesian network, which is a formal graphical language for representing the joint probability distribution over a set of random variables [46]. Querying the network with respect to the variable representing a particular Gene Ontology label yields the probability that a given gene is assigned that label. In principle, the probabilistic framework allows a Bayesian network to represent any arbitrary data type and perform joint inference over heterogeneous data types using a single model.

In practice, such inference can be challenging because a joint probability model over heterogeneous data may contain a very large number of trainable parameters. Therefore, an alternative method for handling heterogeneous data in a probability model is to “chain” the data types together. This approach makes use of the general mechanism for handling prior knowledge by treating one type of data as “prior” to another. For example, as we have discussed, the problem of predicting where along the genome sequence a particular transcription factor will bind can be framed as a classification problem and solved using a PSFM. However, in vivo, the binding of a TF depends not only on the native affinity of the TF for a given DNA sequence, but also upon competitive binding by other molecules. Accordingly, measurements of chromatin accessibility, as provided by assays such as DNase-seq [47], can provide valuable information about the overall accessibility of a given genomic locus to TF binding. A joint probability model can take this accessibility into account [48, 49], but training such a model can be challenging. The alternative approach uses the DNaseI data to create a probabilistic prior and then applies this prior during the scanning of the PSFM [50].

6 Feature selection

In any application of machine learning methods, the researcher must decide which data to provide as input to the algorithm. As noted above, this choice provides a method for incorporating prior knowledge into the procedure, because the researcher can decide which features of the data are likely to be relevant and which are probably irrelevant. On the other hand, choosing relevant features can itself be a scientifically interesting question. Consider, for example, the problem of training a multiclass classifier to distinguish, on the basis of gene expression measurements, among different types of cancers [51]. Such a classifier could be valuable in two ways. First, the classifier itself could help to establish accurate diagnoses in cases of atypical presentation or histopathology. Second, the model produced during the learning phase could perform feature selection, identifying subsets of genes whose expression patterns contribute specifically to different types of cancers. In general, feature selection can be carried out within any supervised learning algorithm, in which the algorithm is given a large set of features (or input variables) and then automatically decides to ignore some or all of the features, focusing on the subset of features most relevant to the task at hand.

In practice, it is important to distinguish among three distinct motivations for performing feature selection with respect to a given task. First, in some cases, we want to identify a very small set of features that yield the best possible classifier. For example, we may want to produce an inexpensive way to identify a disease phenotype on the basis of the measured expression levels of a handful of genes. Such a classifier, if it is accurate enough, might serve as the basis for an inexpensive clinical assay. Second, we may want to use the classifier to understand the underlying biology [52, 53, 54]. In this case, we want the feature selection procedure to identify all and only the genes whose expression is actually relevant to the task at hand, in the hopes that the corresponding functional annotations or biological pathways might provide insight into the etiology of disease. Third, we often simply want to train the most accurate possible classifier [55]. In this case, we hope that the feature selection enables the classifier to identify and eliminate noisy or redundant features. Researchers are often disappointed to find that feature selection cannot optimally perform more than one of these three tasks simultaneously.

Feature selection is especially important in the third case because analysis of high-dimensional data sets, including genomic, epigenomic, proteomic or metabolomic data, suffers from the curse of dimensionality [56]. The “curse” refers to the general observation that many types of analysis become more difficult as the number of input dimensions (i.e., data measurements) grows very large. For example, as the number of data features input to a machine learning classifier grows, it is increasingly likely that, by chance, one feature perfectly separates the training examples into positive and negative classes. This phenomenon leads to good performance on the training data but poor generalization to data not used in training due to the model being overfit to the training data. Feature selection methods and dimensionality reduction techniques, such as principal components analysis or multidimensional scaling, aim to solve this problem by projecting the data from higher to lower dimensions.

7 Imbalanced class sizes

A common stumbling block in many applications of machine learning to genomics is the large imbalance (or skew) in the relative sizes of the groups being classified. For example, suppose you are trying to use a discriminative machine learning method to predict the locations of enhancers in the genome. Starting with a set of 641 known enhancers, you break the genome up into 1000 bp segments and assign each segment a label (“enhancer” or “not enhancer”) based on whether or not it overlaps a known enhancer. This procedure produces 1,711 positive examples and roughly 3,000,000 negative examples—2,000 times as many negative examples as positive. Unfortunately, most software cannot handle 3,000,000 examples.

The most straightforward solution to this problem is to select a random, smaller subset of the data. However, in the case of enhancer prediction, selecting a random 50,000 examples results in 49,971 negative examples and just 28 positive examples. This many positive examples is far too small to train an accurate classifier. To demonstrate this problem, we simulated 93 noisy genomics assays using a Gaussian model for enhancers and background positions based on data produced by the ENCODE Consortium [57]. We trained a logistic regression classifier to distinguish between enhancers and non-enhancers on the basis of these data. The overall accuracy of the predictions, i.e., the percentage of predictions that were correct, was 99.9%. This sounds reasonably good until you consider that a null classifier that simply predicts everything to be non-enhancer achieves nearly the same accuracy.

In this context, it is more appropriate to separately evaluate sensitivity, defined as the fraction of enhancers detected, and the precision, defined as the percentage of predicted enhancers that are truly enhancers. Our balanced classifier has a high precision but a very low sensitivity, detecting only 0.5% of enhancers. The behavior of the classifier can be improved by instead using all the enhancers to train and then picking a random set of 49,000 non-enhancer positions as negative training examples. However, balancing the classes in this way results in the classifier learning to reproduce this artificially balanced ratio. The resulting classifier achieves much higher sensitivity (81%) but very poor precision (40%). This classifier is thus not useful for finding enhancers that can be validated experimentally.

It is possible to trade off sensitivity and precision while retaining the training power of a balanced training set by placing weights on the training examples. In the enhancer prediction case, we use the balanced training set, but during training we weight each negative example 36 times as much as a positive example. Doing so results in an excellent sensitivity of 53% with a precision of 95%.

In general, which performance measure is most appropriate depends on the intended application of the classifier (Table 4). For problems such as identifying which tissue a given cell comes from, where it may be equally important to identify rare and abundant tissues, the overall number of correct predictions may be the most informative measure of performance. In others, such as enhancer detection, predictions in one class may be more important than the other. A wide variety of performance measures are used in practice, including the F1 measure, the receiver operating characteristic (ROC) or precision-recall (PR) curve [58, 59], and others [60]. Machine learning classifiers perform best when they optimize for a realistic performance measure.

Table 4. Measuring performance of a classifier.

Different applications for a machine learning classifier necessitate different performance measures.

Scenario	Example performance measure
All predictions are equally important.	Accuracy (fraction of all predictions that are correct)
Some number of follow-up tests are planned	Precision (fraction of positives that are correct) among a fixed number of predicted enhancers
Positive predictions will be published	Sensitivity (number of enhancers that are identified) among predictions with a pre-determined precision (e.g. 95%).

8 Handling missing data

Machine learning analysis can often be complicated by missing data values. Missing values can come from a variety of sources, such as defective cells in a gene expression microarray, unmappable genome positions in a functional genomics assay, or measurements that are unreliable because they saturate the detection limits of an instrument. Missing data values can be divided into two types: (1) values that are missing at random or for reasons unrelated to the task at hand, such as defective microarray cells, and (2) values whose absences provides information about the task at hand, such as saturated detectors. The presence or absence of values of the second type are usually best incorporated directly into the model.

The simplest way to deal with data that is missing at random is to impute the missing values [61]. This can be done either with a very simple strategy, such as replacing all missing values with zero, or a more sophisticated strategy. For example, Troyanskaya et al. used the correlations between data values to impute missing microarray values [62]. For each target gene expression profile, the authors found the 10 most similar other expression profiles and replaced each missing value in the target profile with an average of the values in the similar profiles. Imputing data points this way can be used as a preprocessing step for any other analysis, but downstream analyses are blind to this information and cannot make use of either the fact that a data point is missing or the added uncertainty resulting from missing data values.

Another method for dealing with missing data is to include in the model informaton about the missingness of each data point. For example, Kircher et al. aim to predict the deleteriousness of mutations based on functional genomics data [63]. The functional genomics data provided a feature vector associated with each mutation, but some of these features were missing. Therefore, for each feature, the authors added a Boolean feature indicating whether the corresponding feature value was present. The missing values themselves were then replaced with zeroes. A sufficiently sophisticated model will be able to learn the pattern that determines the relationship between the feature and presence or absence indicator. An advantage of this approach to handling missing data is that it is applicable whether or not the absence of a data point is significant—if it is not, the model will learn to ignore the absence indicator.

Finally, probability models can explicitly model missing data by considering all the potential missing values. For example, this approach is used by Hoffman et al. to analyze functional genomics data, which contain missing values due to mappability issues from short read sequencing data [21]. The probability model annotates the genome by assigning a label to each position and modeling the probability of observing a certain value given the label. Missing data points are handled by summing over all possibilities for that random variable in the model. This approach, called marginalization, represents the case where a particular variable is unobserved. However, marginalization is only appropriate when data points are missing for reasons unrelated to the task at hand. When the presence or absence of a data point is likely to be correlated with the values themselves, then incorporating presence or absence explicitly into the model is more appropriate.

9 Modeling dependence among examples

So far we have focused on machine learning tasks that involve sets of independent instances of a common pattern. However, in some domains, individual entities, such as genes, are not independent, and the relationships among them are important. By inferring such relationships, it is possible to integrate many examples into a meaningful network. Such a network might represent physical interactions among proteins, regulatory interactions between genes, or symbiosis between microbes. Networks are useful both for understanding the biological relationships between entities and as input into a following analysis that makes use of these relationships.

The most straightforward way to infer the relationships among examples is to consider each pair independently. In this case, the problem of network learning reduces to a normal machine learning problem, defined on pairs of individuals rather than individual examples. Qiu et al. used an SVM classifier to predict whether a given pair of proteins physically interact based on data such as their sequences and cellular localization [64].

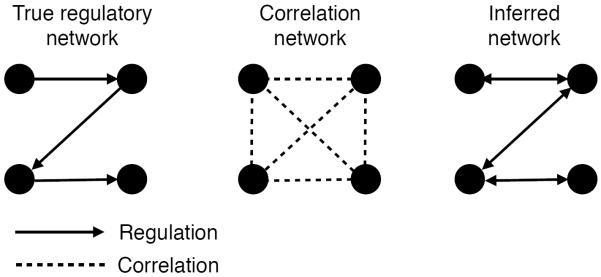
A downside of any approach that considers each relationship independently is that such methods cannot take into account the confounding effects of indirect relationships (Figure 6). For example, in the case of gene regulation, an independent model cannot infer whether a pair of genes directly regulates each other or they are both regulated by a third gene. Such spurious inferred relationships, called transitive relationships, can be removed by methods which infer the graph as a whole. For example, Friedman et al. inferred a Bayesian network on gene expression data that models which genes regulate each other [65]. Such a network includes only direct effects, and models indirect correlations through multiple-hop paths in the network. Methods that infer a network as a whole are therefore more biologically interpretable, because they remove these indirect correlations. A large number of such methods have been described, as reviewed in [66, 67].

Figure 6. Inferring network structure.

Methods that infer each relationship in a network separately, such as computing the correlation between each pair, can be confounded by indirect relationships. Methods that infer the network as a whole can identify only direct relationships. Inferring the direction of causality inherent in networks is generally more challenging than inferring the network structure [68], so many network inference methods, such as Gaussian graphical model learning, infer only the network.

10 Future of machine learning in genomics

Machine learning is most effective in situations where one would like to make sense of large, complex data sets. Accordingly, machine learning methods are likely to become ever more important to genomics as more large sets become available, through projects such as the 1000 Genomes Project or the NIH's 4D Nucleome initiative. On the other hand, even in the presence of massive amounts of data, machine learning techniques cannot generally be applied in a completely arbitrary fashion. In practice, effective application of machine learning methods requires a certain amount of “art.” In particular, theoretical and practical knowledge of both machine learning methodology and the particular application area are often necessary to achieve good performance. As new technologies for generating large genomic and proteomic data sets emerge, pushing beyond DNA sequencing to mass spectrometry, flow cytometry and high-resolution imaging methods, demand will increase not only for new machine learning methods but also for experts capable of applying and adapting them to big data sets. In this sense, both machine learning itself and machine learning researchers are likely to become increasingly important to genetics and genomics.

Table 1.

Glossary of machine learning terminology.

Example	One data instance used in a machine learning task.
Feature	A single measurement or descriptor of an example used in a machine learning task.
Label	The target of a prediction task. In classification, the label is discrete (e.g., “expressed” or “not expressed”); in regression, the label is real-valued (e.g., a gene expression value).
Supervised algorithm	Machine learning algorithm that is trained on labeled examples and used to predict the label of unlabeled examples.
Unsupervised algorithm	Machine learning algorithm that does not require labels, such as a clustering algorithm.
Input space	Set of features chosen as input to a machine learning method.
Kernel methods	A class of machine learning methods (e.g. SVM) that employ a type of similarity measure between feature vectors called a kernel.
Bayesian network	A representation of a probability distribution that specifies the structure of dependencies between variables as a network.
Overfitting	A common pitfall in machine learning analysis where a complex model is trained on too little data and becomes specific to the training data, resulting in poor performance on other data.
Curse of dimensionality	The observation that analysis can sometimes become more difficult as the number of features increases, particularly because overfitting becomes more likely.
Feature selection	The process of choosing a smaller set of features from a larger set, either before applying a machine learning method or as part of training.
Class skew	A case where the two classes in a supervised learning problem are present with differing frequencies. Usually necessitates careful choice of performance measure.

Table 3.

Selected machine learning methods.

Method	Supervised	Unsupervised	Generative	Discriminative
Linear regression	✓		✓
Artificial Neural Network (ANN)	✓	✓		✓
Support Vector Machine (SVM)	✓			✓
k-means clustering		✓	✓
Hierarchical clustering		✓	✓
Hidden Markov Model (HMM)	✓	✓	✓

Online summary.

• The field of machine learning is concerned with the development and application of computer algorithms that improve with experience.

• Machine learning methods can be divided into supervised, semisupervised and unsupervised methods. Supervised methods are trained on examples with labels (e.g. “gene” or “not gene”) and then are used to predict these labels on other examples, whereas unsupervised methods find patterns in data sets without the use of labels, and semisupervised methods leverage patterns in unlabeled data to improve power at predicting labels.

• An application requires different machine learning methods depending on whether one is interested in interpreting the output model or one is simply concerned with predictive power. Generative models, which posit a probabilistic distribution over input data, are generally best for interpretability, whereas discriminative models, which seek only to model labels, are generally best for predictive power.

• Prior information can be added to a model in order to train the model more effectively given limited data, limit the complexity of the model, or incorporate data not used by the model directly. Prior information can be incorporated explicitly in a probabilistic model or implicitly through the choice of features or similarity measures.

• Choosing an appropriate performance measure depends strongly upon the application task. Machine learning methods are most effective when they optimize an appropriate performance measure.

• Network estimation methods are appropriate when the data contains complex dependencies among examples. These methods work best when they take into account the confounding effects of indirect relationships.

Biography

Maxwell Wing Libbrecht graduated from Stanford University in 2011 with a degree in Computer Science, where he was advised by Serafim Batzoglou. He is currently a PhD student in the department of Computer Science and Engineering at the University of Washington, advised by William Noble. Libbrecht works on developing methods that integrate diverse types of data in order to understand gene regulation.

William Stafford Noble received the Ph.D. in computer science and cognitive science from UC San Diego. His research group develops and applies statistical and machine learning techniques for modeling and understanding biological processes at the molecular level. Noble is the recipient of an NSF CAREER award and is a Sloan Research Fellow.