Large-scale mapping of gene regulatory logic reveals context-dependent repression by transcriptional activators

Abstract

Transcription factors (TFs) are key mediators that propagate extracellular and intracellular signals through to changes in gene expression profiles. However, the rules by which promoters decode the amount of active TF into target gene expression are not well understood. To determine the mapping between promoter DNA sequence, TF concentration, and gene expression output, we have conducted in budding yeast a large-scale measurement of the activity of thousands of designed promoters at six different levels of TF. We observe that maximum promoter activity is determined by TF concentration and not by the number of binding sites. Surprisingly, the addition of an activator site often reduces expression. A thermodynamic model that incorporates competition between neighboring binding sites for a local pool of TF molecules explains this behavior and accurately predicts both absolute expression and the amount by which addition of a site increases or reduces expression. Taken together, our findings support a model in which neighboring binding sites interact competitively when TF is limiting but otherwise act additively.

Cells respond to internal and external changes by controlling their gene expression programs. A major mechanism by which this is achieved is by modulating the activity of transcription factors (TFs) that bind to specific sites in gene promoters where they activate or repress transcription (Struhl 1995). For example, in the budding yeast Saccharomyces cerevisiae, almost half of the genome changes expression in response to amino acid starvation. A single transcription factor, Gcn4, is responsible for the activation of over 500 of these genes (Natarajan et al. 2001). While transcriptome and chromatin immunoprecipitation (ChIP) studies are useful for understanding the wiring of these large regulatory networks, they are not informative about how the quantitative relationship between TF and target gene expression is encoded in the DNA. It is still not well understood how promoter architecture determines how each target of a TF will respond to changes in the concentration of active TF ([TF]). Furthermore, many targets of the same transcription factor are expressed at different levels in the absence of that TF, and the fold-induction of the target is largely independent of its expression at low or high [TF] (Carey et al. 2013; Rajkumar et al. 2013). However, the molecular mechanisms that enable this decoupling are largely unknown.

In order to understand how promoters encode the function that maps changes in the amount of active TF to changes in transcriptional output, we measured the dose response curves for 6500 synthetically designed promoters. We have used a synthetic approach (Sharon et al. 2012) in which pairs of promoters differ by a single regulatory element. This is in contrast to native promoters that have many differences between them, preventing systematic investigation of the effect of individual DNA sequence elements on expression response.

Results

Promoter DNA sequence can encode a wide range of transcriptional responses to changes in the amount of active TF

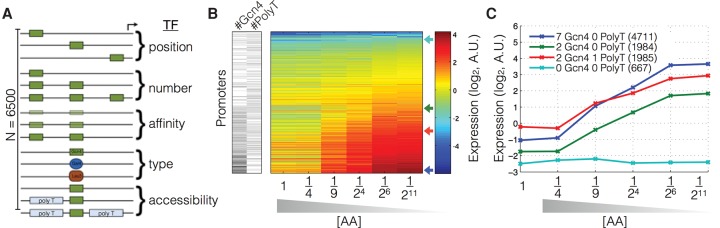
To systematically measure how transcriptional responses are encoded in promoter DNA sequence, we generated a novel data set in which we measured the activity of 6500 designed promoters using a fluorescence reporter (Sharon et al. 2012) in six growth media that each differ in their concentration of amino acids ([AA]) (Supplemental Data 16, 17; see Methods for details). The majority of these promoters contain binding sites for Gcn4, Leu3, Met31, or Bas1—TFs involved in amino acid biosynthesis. At high [AA], the TFs Gcn4, Bas1, Leu3, and Met31 are mostly inactive (Struhl 1992). As [AA] decreases, the concentration of the active form of these TFs increases (their expression and/or ability to activate transcription increases), and their targets increase in expression (Gasch et al. 2000). For these four TFs, the concentration of active TF molecules ([TF]) increases gradually in response to decreasing [AA] (Supplemental Fig. 1; Ljungdahl and Daignan-Fornier 2012). The combinatorial fashion in which TF binding site type, number, affinity, position, and accessibility vary in the designed promoter set enables us to systematically investigate the mapping between promoter DNA sequence, [TF], and the induced expression (Fig. 1A; see Methods for details).

Figure 1.

Measurements of TF concentration-dependent expression for thousands of designed promoters. (A) Schematic depiction of the experimental design. A pooled library of 6500 designed promoters was transformed into yeast, and expression levels of all strains in the pooled library were measured in minimal media at each of six different amino acid concentrations (see Methods). (B) Promoter expression measurements sorted by dynamic range. For each promoter in the library, we obtain an expression measurement at each of the six AA concentrations. For promoters that lack Gcn4, Leu3, Bas1, or Met31 sites, expression does not change with decreasing AA concentration (top of B). For promoters with multiple Gcn4 binding sites, expression increases with decreasing [AA]. The trans-activating transcriptional activity of these transcription factors increases with decreasing [AA]. (C) Shown are four representative induction curves showing the effect of changing the number of Gcn4 binding sites (cyan, green, blue) or adding a polyT nucleosome disfavoring sequence (green, red). IDs show library construct identifiers.

The measurements were carried out using our previously described method that involves FACS sorting and deep sequencing of a barcoded pooled promoter library (Sharon et al. 2012, 2014). Briefly, uniquely barcoded promoters that drive a YFP reporter are FACS sorted into 12 bins of expression that subsequently receive an expression-bin barcode. Deep sequencing thus results in reads that contain both a sequence barcode and an expression barcode. A computational analysis of these reads gives, for each promoter and growth condition, an expression distribution, from which the mean is extracted, resulting in 6500 highly reproducible (Supplemental Fig. 2) dose-response curves (Fig. 1B). Our promoters encode a wide range of responses with a general trend in which more TF binding sites give a greater dynamic range between low and high [AA] (Fig. 1B). We observe that some promoter sequence changes (e.g., addition of a polyT) (Fig. 1C) affect expression independent of [AA], whereas others (e.g., addition of Gcn4 binding sites) (Fig. 1C) affect expression in a manner that depends on [AA]. We refer to the former as (active) [TF]-independent expression change, and the latter as [TF]-dependent expression change.

Decoupled [TF]-dependent and [TF]-independent expression

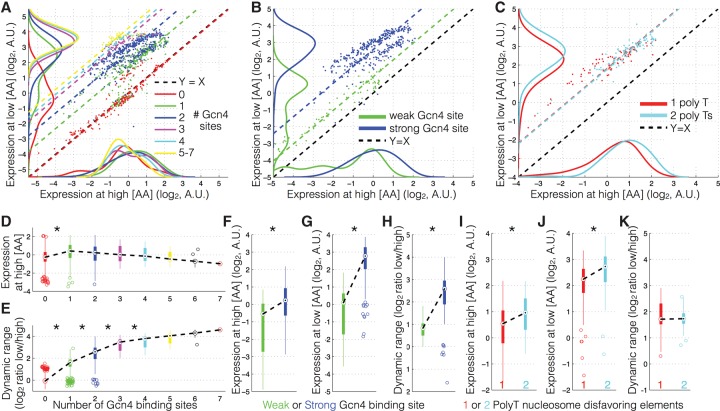
In order to distinguish between promoter sequence features that affect expression in a [TF]-dependent manner and those that affect expression in a [TF]-independent manner, we compare expression at high and low [AA] (see Methods) for promoters grouped by DNA sequence features. We find that the number of Gcn4 binding sites affects expression in a TF-dependent manner: Adding binding sites results, on average, in little increase in expression at high [AA] but a large increase at low [AA] (Fig. 2A,D), and thus an increase in the promoter's dynamic range (Fig. 2E). The same results are observed for increasing the affinity of the Gcn4 binding site: Increasing the affinity results in slightly higher expression at high [AA], much higher expression at low [AA], and an overall increase in the dynamic range of the promoter (Fig. 2B,F–H). Thus, both the affinity and number of Gcn4 sites affect a promoter's expression in a manner that depends on the [TF]. In contrast, adding an additional polyT nucleosome disfavoring sequence results in the same fold-change in expression at low and high [AA] and no change in the dynamic range of the promoter (Fig. 2C,I–K). Adding a binding site for a repressor, changing the position of the binding site, or changing the promoter sequence context to a context with a different predicted nucleosome occupancy also results in no change in the dynamic range (Supplemental Fig. 3). Thus, altering the nucleosome occupancy results in a [TF]-independent change in expression.

Figure 2.

The effect of Gcn4 binding site number and polyT nucleosome disfavoring sequences on [TF]-dependent and -independent expression. (A–C) Expression at high [AA] (x-axis) versus expression at low [AA] (y-axis) for various promoter sequence features. Dashed lines are the diagonal (slope = 1) line that best fit each category of promoters. The black dashed diagonal line (Y = X) represents the regime where expression is constant across conditions. The vertical distance from the Y = X line measures how much any one promoter changes in expression across conditions. Density plots (using ks density estimation) at the x-axis and y-axis show the distributions of expression values for each promoter at high and low [AA], respectively. (D–K) Expression and expression fold-change (y-axis) in box plots as a function of promoter sequence features (x-axis). The dashed black lines connect the medians of each box. Asterisks denote statistically significant (t-test, P < 0.01) changes between subsequent groups. (A) Shown are promoters grouped by the number of Gcn4 binding sites. (B) Shown are promoters with either low- or high-affinity Gcn4 sites. (C) Shown are promoters with either one or two polyT nucleosome disfavoring sequences. (D,E) Box plots of the data in A. Promoters are grouped by the number of binding sites. (D) Shown is expression at high [AA] (y-axis). (E) Shown is expression fold-change—dynamic range, log₂(low [AA]/[high AA]). (F–H) Box plots of the data in B. Shown are expression at high [AA] (F), low [AA] (G), and expression fold-change (dynamic range) (H) for promoters with low- or high-affinity binding sites. All differences are statistically significant (t-test, P < 1 × 10⁻³, P < 1 × 10⁻⁵, P < 1 × 10⁻⁴ for F–H, respectively). (I–K) Box plots of the data in C. Shown are expression at high [AA] (I), low [AA] (J), and expression fold-change (dynamic range) (K) for promoters with either one or two polyT sequences. Expression at high and low [AA] shows significant change as a function of polyT number (t-test, P < 1 × 10⁻⁴, P < 1 × 10⁻⁴, respectively); however dynamic range does not change significantly (t-test, P = 0.77).

Taken together, these results show that sequence-mediated expression changes affect the dynamic range of expression when they change binding site affinity or number but do not measurably change binding site accessibility, and that both the TF-dependent and -independent behavior of promoters can be tuned separately.

Mutations inside binding sites affect expression in a TF-dependent manner

While it is intriguing that addition or removal of entire promoter sequence elements can alter expression either in a [TF]-dependent or -independent manner, we wondered if the same independent control could be achieved by single point mutations that are more readily available in an evolutionary context. To determine this, we examined a set of 21 3-bp scanning mutations made every 3 bp across the native HIS3 promoter. We find that 19 of these affect expression in a TF-independent manner (t-test, P = 0.83) and that mutations that increase the predicted nucleosome occupancy over the TATA box have lower expression (Pearson R = −0.66, P = 9 × 10⁻⁴). Two of the mutations, which fall within the native Gcn4 binding site, appeared to effectively remove response to [AA] change (Supplemental Fig. 14).

In addition, we find that systematically mutating the Gcn4 binding site results in a change in dynamic range that is correlated with PSSM score (Supplemental Figs. 4, 14). We observe a relatively small increase in expression at high [AA] (Pearson R = 0.20, P = 0.09), and a much larger increase in expression at low [AA] (Pearson R = 0.52, P < 3 × 10⁻⁶), resulting in a net increase in dynamic range with increasing PSSM score (Pearson R = 0.63, P < 1.3 × 10⁻⁸ or R = 0.77, P < 3 × 10⁻⁵ when only including values above a previously determined cutoff) (Supplemental Figs. 4, 14; Spivak and Stormo 2012). These results are consistent with models in which low-affinity binding sites are always functional but have a more pronounced effect at high [TF] (Carey et al. 2013).

Maximum expression is set by the amount of active TF and is limited by competition for TF molecules

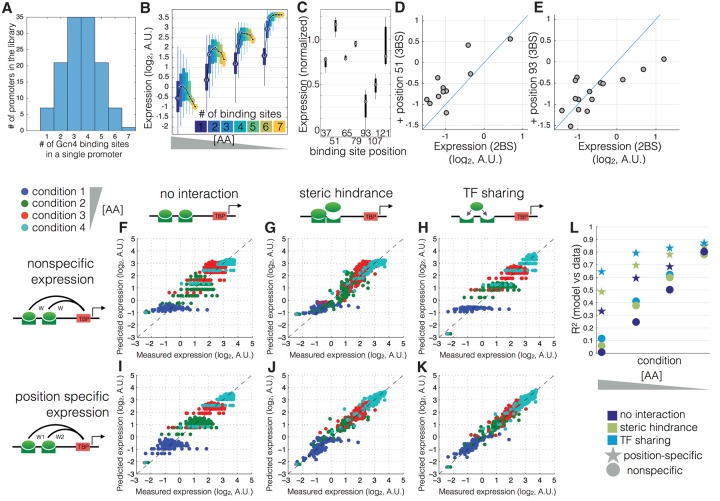
If expression were a simple nondecreasing function of the number of bound TF molecules (Gertz et al. 2009; Raveh-Sadka et al. 2009), we expect expression to increase when either [TF] or the number of binding sites in a promoter increases. Thus, a given expression level might be reachable by changing either one or the other, and any promoter, given enough [TF], would be able to reach a level of maximal expression set by the efficiency of transcription initiation. However, this is not what we observe in homotypic promoters. We find that the maximum reachable expression level is determined by [TF] and not by the number of binding sites (Fig. 3A,B; Supplemental Fig. 5). In all conditions and for all TFs, expression reaches its maximal level at 3–4 sites and then plateaus, decreases, or only slightly increases, depending on the TF, suggesting that this phenomenon is a general consequence of binding site multiplicity and not specific to a particular transcription factor.

Figure 3.

A model that incorporates TF sharing with specific position-expression can best explain expression across all amino acid concentrations. (A) The library consists of promoters with identical Gcn4 binding sites placed at one of seven locations in the promoter. (B) Shown are the measured expression levels (y-axis) as a function of binding site number (different colors) at four AA concentrations (different groups along the x-axis) for Gcn4. Each box contains data for all promoters with that number of binding sites and no other features (e.g., no nucleosome disfavoring sequences or binding sites for other TFs). The black line shows the median expression level for all promoters with that number of binding sites. (C) Shown is the expression for each promoter with a single Gcn4 binding site, normalized so that all conditions have the same mean expression. (D,E) Shown is the effect of adding a third binding site (at position 51 or position 93) to a promoter that already has two binding sites. The expression of the two binding site promoters (x-axis) is graphed against the three binding site promoters (y-axis). (F–L) Each point shows a single promoter measured at one of four conditions (blue, green, red, cyan in decreasing [AA] order) (x-axis) and the predicted expression levels (y-axis) of that promoter, for the six different models, fitted in cross-validation to the data shown in A, which are promoters with one to seven high-affinity Gcn4 binding sites (ATGACTCAT). R² values were computed for absolute predicted expression on the test data. Each model includes either position-specific expression (a unique weight is associated with each unique binding site position) or nonspecific expression (all binding site positions share the same weight), and either no interaction, steric hindrance (a negative weight for multiple bound configurations), or TF sharing (the [TF] weight is divided by the number of sites). We note that the discretization of the y-axis in F–I is due to the fact that, in the absence of interactions and position-specific expression, all binding sites drive equal expression.

We found that, for the set of seven promoters with a single binding site placed at one of seven positions in the promoter, different binding site positions drive different levels of expression (Fig. 3C). Furthermore, we found that when a binding site that drives high expression (e.g., the site at position 51) is added to a promoter with two binding sites (generating a promoter with three sites), expression tends to increase (Fig. 3D). In contrast, when a site that drives low expression (e.g., the site at position 93) is added to a promoter with two sites, expression tends to decrease if the expression of the two binding site promoter is already high (Fig. 3E).

We hypothesized that the observed saturation behavior, which is most pronounced at high [AA] (low [TF]) (Supplemental Fig. 5), is a consequence of competition for limiting TF between binding sites that drive different levels of expression. To compare possible underlying mechanisms, we used thermodynamic modeling of gene expression (see Supplemental Material, “Thermodynamic model” for details). In short, for each promoter, the model enumerates all possible binding configurations of TF and TBP (TATA binding protein that recruits the transcriptional machinery). The weight of each configuration is based on binding site affinities, Gcn4 concentration, and interactions between bound TF molecules and bound TBP molecules, after which the ratio between weighted TBP bound to TBP unbound configurations determines the expression. We fitted a collection of models of increasing level of complexity to the induction curves of a set of promoters that only contain 0–7 high-affinity Gcn4 binding sites. We used a 10-fold cross-validation scheme to assess each model.

A basic model, in which binding to each site is independent and each site has either identical contribution to expression or with position-specific driven expression, is able to explain an increase in expression with increasing [TF] but does not fit the measured data very well (Fig. 3F,I,L).

We reasoned that, in order to reproduce the observed saturation, there must be negative interactions between TF binding sites within the same promoter. We examine two alternative mechanisms of binding site interaction: steric hindrance and TF sharing. The steric hindrance model accounts for a previously suggested mechanism in which a bound TF may sterically hinder the binding of a second TF molecule at a neighboring site (Struhl 1989) by reducing the weight of configurations with multiple bound sites (Gertz et al. 2009; Raveh-Sadka et al. 2009; Giorgetti et al. 2010). The TF sharing model implements competition between neighboring binding sites by dividing the [TF] weight by the total number of binding sites. This mechanism has been observed experimentally, and results from nonspecific binding and subsequent 1D sliding: Two neighboring binding sites will share their TF capture area and as a consequence have the same effective binding rate as one site (Hammar et al. 2012; Mahmutovic et al. 2015).

We find that both interaction models can replicate the observed saturation effect, in which, at all [AA], adding a fourth binding site does not result in a large increase in expression (Fig. 3). However, quantitatively the TF sharing model better fits the experimental data.

Taken together, our results show that activator binding sites do not linearly contribute to expression. Our model suggests that this is due to competition between binding sites, likely due to neighboring binding sites sharing their capture area as a result of most binding events coming from 1D sliding.

Activator binding sites can both increase and decrease expression as predicted by a model of TF molecule sharing

The above observations show that multiple binding sites contribute nonlinearly to expression. In order to understand the effect of adding or removing individual activator sites in more detail, we look at pairs of promoters that differ by only a single binding site. Surprisingly, in 30% of cases, adding an additional Gcn4 site reduces expression, and this effect is significantly stronger at high [AA] (55% versus 5% at low [AA], when [TF] is low (Supplemental Fig. 13). However, expression reduction is never below the minimum expression driven by the individual sites (Supplemental Fig. 6).

This suggests the following: Suppose a promoter has two sites, A and B, with A being a stronger site (having a larger measured ability to drive expression when added to a promoter with zero sites); then at low [TF], adding the new site B will reduce expression. However, if you do the reverse, start with B and add A, expression goes up. So that with two sites, the expression tends to be intermediate between the individual sites, at least at low [TF], a regime in which TF molecules are shared between neighboring sites.

A comparison of thermodynamic models shows that both steric hindrance and TF sharing can produce expression reduction for activator binding site addition when the added site drives lower expression than the existing site. However, only the TF sharing model shows this effect at low [TF]; steric hindrance shows reduction only when [TF] is high. Both steric hindrance and TF sharing models predict that the negative interaction between binding sites is stronger at closer distances. Indeed, this is the case in both expression data and in an independent measurement of the same promoter library in which TF binding to promoters was measured in-vitro (Supplemental Fig. 7). Consistent with the TF sharing model, but not with steric hindrance, this interference is strongest at low TF concentrations, both in vivo and in vitro.

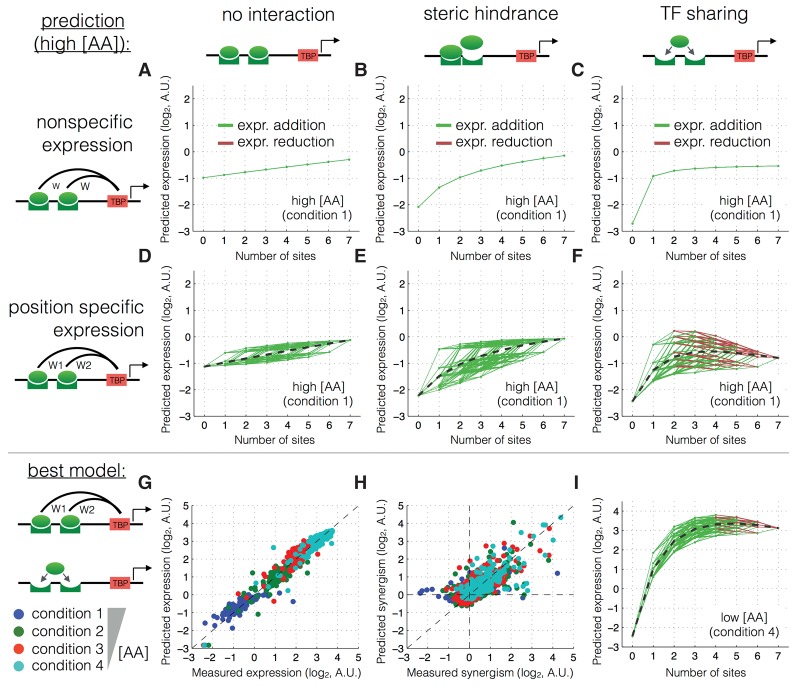
The TF sharing model combined with site-specific expression best predicts absolute expression levels as well as synergism, i.e. the change in expression when adding a site (Fig. 4; Supplemental Figs. 8–11). In fact, the TF sharing model, given site-specific expression, is the only model tested that can explain expression reduction at high [AA] (low [TF]).

Figure 4.

TF sharing but not steric hindrance can explain the decrease in expression due to activator binding site addition. (A–F) Predicted expression as a function of binding site number for six different thermodynamic models, fitted in cross-validation to the Gcn4 measured data. Green lines show a predicted increase in expression upon binding site addition; red lines show a predicted decrease. R² values were computed for absolute predicted expression on the test data. (G–I) Measured versus predicted expression and synergism for the best model at low and high [AA].

Taken together, these results show that site addition can either increase or decrease expression. This synergism is concentration-dependent. Negative synergism mostly occurs at low [TF], likely ruling out steric hindrance. TF sharing in combination with site-specific expression predicts the observed behavior: More often than not, adding an activator-binding site results in a reduction of expression at low [TF].

Discussion

In summary, we presented here a large-scale investigation of the mapping between promoter DNA sequence and dose response curves by measuring the induced gene expression of 6500 designed promoters at six growth conditions in which the regulating TFs are gradually induced.

We observe a wide range of dose-response curves in which the dynamic range is altered by changes in the affinity or number of binding sites, and expression level varies independent of induction (fold-change) through changes in the accessibility of the promoter.

These results are confirmed by systematic mutations in either the whole promoter or only at the binding site, both affecting overall expression, but only the latter affecting the dynamic range. This suggests that random mutations (that occur more frequently outside of binding sites) are more likely to change overall expression and not the promoter's response.

Our current and previous (Sharon et al. 2012) observation that expression saturates with increasing number of activator binding sites suggests that either TF binding or Pol2 recruitment saturates. However, we observe that while expression cannot be increased by adding binding sites, expression can be increased by increasing [TF]. This argues against saturation of Pol2 recruitment being the cause of the observed saturation of expression level as a function of homotypic binding site number in each condition. We find that a model that includes competition between binding sites can quantitatively explain our observations.

We achieved further insight into the nonlinear mapping between promoter configuration and dose-response by comparing pairs of promoters that differ by only a single binding site addition. This analysis revealed that, at low [TF], adding an activator is more likely to reduce expression than it is to increase expression, suggesting that there is interaction between binding sites.

Expression of our synthetic Gcn4 targets maxes out at 3–4 binding sites. Interestingly, the vast majority of native Gcn4 targets have 3–4 binding sites (Schuldiner et al. 1998). The mechanistic models proposed in this paper may explain the reason for the distribution of binding site numbers in native promoters.

Our analysis of the observed dose response curves suggests that they are affected mainly by competition for TF (therefore reducing the effective local TF concentration “seen” by each binding site, referred to as “TF sharing”) rather than steric hindrance between TF molecules. In particular, the two models behave differently with changing [TF]. While steric hindrance will have a stronger effect at high [TF] due to the increased likelihood of bound configurations, “TF sharing” effects are reduced at high [TF], as the TF is no longer limiting, and this is what we observe.

To further investigate the possible mechanism that could explain the measured reduction in expression as a function of activator binding site addition, in addition to the thermodynamic model that was fit to data, we developed a toy mathematical model that describes binding site addition from one to two sites, enabling us to investigate the regimes in which addition will cause a reduction in expression (see Supplemental Material, “Toy model of activator site addition”). This model shows that expression reduction by steric hindrance will increase with increasing [TF], whereas reduction by TF sharing decreases with increasing [TF]. It is the latter behavior that we observe.

We note that alternative models are possible; the TF sharing model fits the data, but modeling can only show that a given model is wrong, not that a given model is correct. Recently, a nonequilibrium promoter-dynamics model was proposed in which TF dissociation is fast and actively driven by transcription (Coulon et al. 2013). Our results from the thermodynamic and toy models are independent of assumptions regarding dissociation. Therefore, our predictions are independent of whether or not TF unbinding is an induced nonequilibrium process. One possible alternative model that will reproduce a decrease in expression at high numbers of binding sites, specifically at low [TF], is a combination of additive activation and cooperative repression in which both the activator and repressor compete for the same binding sites. There is evidence suggesting that the transcriptional repressor Mig1 acts cooperatively (Gertz et al. 2009). While no repressors are predicted to bind with high affinity to the Gcn4 binding site (ATGACTCAT), Yap3 and Yap7 are predicted to bind weakly (de Boer and Hughes 2012). We hypothesized that if the Gcn4 sites have repressive potential, then site addition can cause expression reduction below the level driven by the other sites. We find that, while addition of a binding site often results in expression below the maximum of the expression driven by the individual sites, this expression is always greater than the minimum expression driven by the individual sites. The added site can, at most, reduce expression by an amount that the other sites drive and can never repress beyond that level. In other words, we find that to remove expression, first expression has to be added. This is a strong prediction of the TF sharing model and is not predicted by the cooperative repression model.

A second model that can explain the observation that expression reaches a maximum at around three binding sites is that having more than three bound TF molecules does not increase recruitment of RNA polymerase. It is likely that beyond some number, additional bound transcriptional activators do not contribute to increased expression at a single promoter. However, this model cannot qualitatively explain our observation that, for all four TFs, the expression from three binding sites is lower at higher [AA] (lower [TF]). The “activator saturation” model predicts that the same maximal expression could be reached at all amino acid concentrations, but that it might require more binding sites at lower [AA]. This is not what we observe. Moreover, while, on average, expression saturates at three sites, this is not always the case. Going from three to four sites can both increase (green lines) and decrease (red lines) expression (Fig. 4; Supplemental Figs. 10, 13); expression rarely remains constant, likely ruling out the “activator saturation” model.

Taken together, we have found a strong nonlinear mapping between promoter architecture and dose-response, that, by assuming competition between binding sites, we are able to accurately predict from DNA sequence alone. Specifically, our model points to a reduction in effective local [TF] (per binding site) due to overlapping capture areas. When [TF] is limiting, the effective search time (the time it takes for a TF to find its binding site) is not significantly reduced when another site is added close to an existing one, since search time is dominated by the total capture area. In the regime where [TF] is high, more sites bind more TFs and thus have the ability to drive higher expression.

Our model is also consistent with recent in vitro results performed using the same set of promoters showing that, at low [TF], multiple Gcn4 binding sites increase the likelihood of TF binding but do not increase the number of TF molecules bound to a single molecule of promoter, while at high [TF], adding more binding sites does increase the number of bound molecules (Levo et al. 2015).

Competition for limiting TF, in both one- and three-dimensional space, may also explain some previously unexplainable results regarding titration by large arrays of extraneous TF binding sites. Lee and Maheshri (2012) found that contiguous arrays of tetO binding sites bind less TF than do noncontiguous arrays and that contiguous arrays are less efficient at titrating away TF. Our reanalysis of their data shows that this effect is strongest at low [TF], suggesting that TF sharing may be occurring at these arrays as well, either in 1D space or in 3D space. Splitting the array of decoy binding sites in half results in a larger decrease in expression at low [TF] than at high [TF] (Supplemental Fig. 12), as expected from a model in which large number of binding sites spread throughout the genome (at the promoter of interest and at the decoy sites) are sharing a limiting number of TF molecules.

The yeast genome, which has densely packed genes for a eukaryote, has several promoters (e.g., CLN3) that are longer than 1 kb. Yet, 20 TF binding sites could, in theory, be packed into <200 bp. Intriguingly, the GAL genes, which are highly induced by a large and rapid increase in the active amount of Gal4, tend to have only 1 or 2 nt between the sites. In contrast, genes activated at the G1→S transition (e.g., CLN2) have TF binding sites that are spaced further apart. It was recently shown that Cln3, the protein that activates the TFs bound to the CLN2 promoter, is present in limiting concentrations (Wang et al. 2009); the spacing between binding sites may reduce the effect of sharing. Binding site spacing is known to be influenced by physical interactions between TFs (Kazemian et al. 2013). Here, we suggest that TF sharing between closely spaced binding sites is an additional force acting upon the evolution of promoters. Binding sites for some TFs, especially those with long 1D sliding ranges (Slutsky and Mirny 2004; Gorman and Greene 2008) may need space for maximal TF occupancy at low [TF]. Dense clusters can be used to create a highly responsive behavior (large dynamic range), and less dense clusters might create overall high expression also at low [TF]. Our results suggest that TF sharing can play an important role in determining the response of a promoter to changes in [TF] and therefore influence the evolution of binding site configurations.

Methods

Promoter sequence library

We used a previously described library of 6500 promoters driving YFP expression (Sharon et al. 2012). The pooled library was grown in synthetic media with a 2¹¹-, 2⁶-, 2⁴-, 2³-, 2²-, or 2⁰-fold dilution of amino acids, and gene expression driven by each promoter was measured as previously described (Sharon et al. 2014).

Gcn4 protein measurements

A Gcn4-GFP ura3::TEFpr-mCherry strain was grown overnight in SCD-HL, resuspended in SCD-His-Leu or SCD, and then the SCD was serial-diluted into SCD-HL, resulting in different concentrations of His and Leu. GFP and mCherry were measured using a BD Fortessa flow cytometer using FITC and PE_TexasRed filter sets.

Expression normalization

We observed condition-specific expression differences that did not appear to stem from biological differences. For example, even the promoters that were not induced (such as Gal4 targets) varied, though slightly, across conditions in a nonmonotonic manner (Supplemental Fig. 15). These differences likely stem from day-to-day and experimental variability, as each condition was a separate batch and was sorted on different days. To correct for this effect, we subtracted from all promoters the median expression of all Gal4 targets, thus removing this technical variability. All analysis was carried out on the normalized expression values (Supplemental Data 16, 17).

Growth conditions

Because the two lowest and two highest [AA] conditions induce similar expression, we combined them to get a more robust expression measurement. Thus, for the analyses in which we compare low to high [AA], we use the average of the two lowest and the average of the two highest [AA] conditions. In the analyses in which we compare four conditions, we use the previous two plus the middle two [AA] conditions.

Thermodynamic model of gene expression

We model the transcriptional activity of the promoters using a thermodynamic model that enumerates all binding configurations of the transcriptional activator Gcn4 as well as TBP (TATA binding protein) to the promoter, where we assume that bound Gcn4 recruits (modeled as cooperative binding) TBP to the promoter. The ratio of bound versus unbound TBP configurations then give the transcriptional activity of the promoter. To model several hypothesized regulatory mechanisms, we make different assumptions on the interaction between bound Gcn4 molecules and their interaction with TBP (see Supplemental Material, “Thermodynamic Model” for details).

Data access

The raw and processed sequencing data generated in this study have been submitted to NCBI's BioProject database (https:// www.ncbi.nlm.nih.gov/bioproject/) under accession number PRJNA349780 and Gene Expression Omnibus (GEO; https://www.ncbi.nlm.nih.gov/geo/) under accession number GSE92306. Processed expression values per condition per promoter construct are provided in Supplemental Data 16, 17. Data of model fits and parameter values are provided in Supplemental Data 18–23 and Supplemental Data 24–29, respectively.