BODY SIZE-SPECIFIC EFFECTIVE DOSE CONVERSION COEFFICIENTS FOR CT SCANS

Abstract

Effective dose from computed tomography (CT) examinations is usually estimated using the scanner-provided dose-length product and using conversion factors, also known as k-factors, which correspond to scan regions and differ by age according to five categories: 0, 1, 5, 10 y and adult. However, patients often deviate from the standard body size on which the conversion factor is based. In this study, a method for deriving body size-specific k-factors is presented, which can be determined from a simple regression curve based on patient diameter at the centre of the scan range. Using the International Commission on Radiological Protection reference paediatric and adult computational phantoms paired with Monte Carlo simulation of CT X-ray beams, the authors derived a regression-based k-factor model for the following CT scan types: head–neck, head, neck, chest, abdomen, pelvis, abdomen–pelvis (AP) and chest–abdomen–pelvis (CAP). The resulting regression functions were applied to a total of 105 paediatric and 279 adult CT scans randomly sampled from patients who underwent chest, AP and CAP scans at the National Institutes of Health Clinical Center. The authors have calculated and compared the effective doses derived from the conventional age-specific k-factors with the values computed using their body size-specific k-factor. They found that by using the age-specific k-factor, paediatric patients tend to have underestimates (up to 3-fold) of effective dose, while underweight and overweight adult patients tend to have underestimates (up to 2.6-fold) and overestimates (up to 4.6-fold) of effective dose, respectively, compared with the effective dose determined from their body size-dependent factors. The authors present these size-specific k-factors as an alternative to the existing age-specific factors. The body size-specific k-factor will assess effective dose more precisely and on a more individual level than the conventional age-specific k-factors and, hence, improve awareness of the true exposure, which is important for the clinical community to understand.

INTRODUCTION

Over the last three decades, the number of computed tomography (CT) examinations conducted annually has been exponentially increasing, making CT radiation exposure a large portion of the per capita dose and a public health concern⁽¹⁾. It has become increasingly important to reliably assess radiation exposures, especially patient-specific radiation dose, from CT scans using a method that can be easily implemented in clinical settings.

One metric of exposure that clinicians have gravitated towards is the effective dose^(2–4) because it is a single value and incorporates a measure of cancer risk. Hence, some clinicians find it to be simpler means of expressing both exposure and risk of the exposure. The effective dose concept was originally derived for prospective dose assessment for planning and optimisation in radiological protection as well as demonstration of compliance with dose limits for regulatory purposes^(2–4).

Estimating effective dose for patients undergoing CT imaging typically uses dose-length product (DLP)-to-effective dose conversion factors, also known as k-factors, which are derived from calculations in which computational human phantoms are coupled with the Monte Carlo transport simulation of CT X-ray beams. The k-factor is defined as the proportionality constant between the effective dose and the DLP. In the clinical setting, the DLP is understood to be the product of the CTDI_vol and the scan length:

$$k=\frac{E}{\text{DLP}}=\frac{E}{\text{CTD}{\text{I}}_{\mathrm{vol}}\times l}$$ (1)

where the k is k-factor (mSv mGy⁻¹ cm⁻¹), E is effective dose (mSv), DLP is dose-length product (mGy cm), CTDI_vol is in mGy and l is the scan length (cm) for different scan types.

The k-factors used to date were initially developed by Shrimpton et al.⁽⁵⁾ using stylised (or mathematical) computational phantoms⁽⁶⁾. They developed a set of k-factor for the five general scan regions of adult patients, i.e. head, neck, chest, abdomen and pelvis. Subsequently, the k-factor from Shrimpton et al. was slightly modified in the European Guidelines (EGs)⁽⁷⁾. Following the k-factors for adult patients, k-factors for paediatric patients, including newborn, 1-, 5-, 10-, and 15-y-old, were later introduced for head and trunk CT examinations⁽⁸⁾. The k-factors for extended scan regions were published in the updated EG⁽⁹⁾, which was adopted in the American Association of Physicists in Medicine (AAPM) Report 96⁽¹⁰⁾. Those k-factors were based on the tissue weighting factors published in the International Commission on Radiological Protection (ICRP) Publication 60⁽³⁾ which form the internationally recognised basis of the effective dose. Since the ICRP updated their tissue weighting factors in the ICRP Publication 103⁽⁴⁾, Deak et al.⁽¹¹⁾ derived updated the previous sets of k-factors for paediatric and adult patients using a series of stylised phantoms and Monte Carlo transport calculations based on tissue weighting factors from both ICRP Publications 60 and 103.

The existing k-factors have two limitations. First, the values are based on the conventional stylised phantoms where anatomical structures are described by mathematical equations, which clearly have limitations in terms of realism. Several studies have reported dosimetric errors introduced by the simplified anatomy of the stylised phantoms compared with more realistic and advanced computational human phantoms (e.g. voxel phantoms), particularly for exposure to external photon beams^(12–15). Second, the existing sets of k-factor were only derived from the stylised phantom of the reference body size. When the k-factors are applied to patients who are smaller or larger than the assumed phantom (at a given age), those k-factors may introduce an over- or underestimation of the effective dose compared with a value that can be assumed as more accurate for the actual patient. To account for patient size in CTDI_vol, the AAPM introduced size-specific dose estimates which is the product of the CTDI_vol and body-size dependent weighting factors⁽¹⁰⁾.

In the current work, the authors revised the existing age-specific k-factors based on the stylised phantoms with the goal to provide more realistic anatomy-based data using the ICRP reference paediatric and adult voxel phantoms⁽¹⁶⁾. The authors then derived body size-specific k-factors using their age-specific k-factors and the effective diameter of the phantoms. The authors compared two sets of effective doses calculated from their age- and size-specific k-factors for paediatric and adult patients with various body sizes randomly sampled from patients of the National Institutes of Health (NIH) Clinical Center.

MATERIALS AND METHODS

Calculation of age-specific k-factors from the ICRP phantoms

The authors revised the existing age-specific k-factors^{(9, 10)} that are based on the stylised phantoms⁽⁶⁾ using the National Cancer Institute dosimetry system for CT (NCICT) computer program⁽¹⁷⁾. NCICT is based on organ dose coefficients calculated from the Monte Carlo simulations of CT X-rays coupled with the ICRP reference phantoms^{(16, 18)}. The organ dose coefficients consist of a 5D matrix with entries representing doses for all combinations of age, gender, organ, slice and X-ray spectra. The authors derived the age-specific k-factors for a total of 12 paediatric and adult ICRP phantoms from the ratio of the effective dose (mSv)⁽¹⁹⁾ calculated by NCICT and the DLP (mGy cm) of different scan types listed in the EG⁽⁹⁾: head and neck, head, neck, chest, abdomen and pelvis (AP) and trunk. They added two more scan types: abdomen and pelvis. They adopted the scan range for each scan type being used at NIH Clinical Center, calculated effective dose by weighting the organ doses from male and female phantoms at a given age according to the definition of effective dose⁽⁴⁾ and also calculated the age-specific k-factor with the tissue weighting factors provided by ICRP Publication 60⁽³⁾ for comparison with the existing k-factors, which are also based on the ICRP Publication 60.

Derivation of body size-specific k-factors from age-specific k-factors

To derive body size-specific k-factors from the age-specific k-factors, the authors regressed the ‘effective diameters’ of the ICRP phantoms on the age-specific k-factors where ‘effective diameter’ was determined as the mean of the antero-posterior and lateral dimensions on an axial image of the hybrid phantoms at the centre of the scan coverage. Regression fits to a simple exponential model were derived for all CT scan types except for head and neck, head and neck scans:

$$k_{\mathrm{ss}}=a\times e^{b\times d_{\mathrm{eff}}}$$ (2)

where k_ss is size-specific k-factor, d_eff is effective diameter and a and b are the fitted coefficients of the regression curve. For head and neck, head and neck scan type, the authors did not develop a regression function because the data points did not fit well to any simple model. Instead, size-specific k-factors for a series of consecutive effective diameters were derived by interpolating the existing data and providing the values in a table format. In case of other scan types, regression equations were derived for both head (16 cm) and body (32 cm) CTDI phantoms in chest, abdomen, pelvis, AP and chest–abdomen–pelvis (CAP) scans. The authors also tabulated size-specific k-factors derived using the regression equations and a series of consecutive effective diameters in a table format for users to a body size-specific k-factor using the measurement of effective diameter.

Calculation of body size-specific effective doses for patients

Two sets of effective doses have been selected based on the age- and size-specific k-factors for selected patients and compared with each other to evaluate differences. The authors selected 81 paediatric and 117 adult patients, randomly sampled from patients who underwent chest, AP and CAP scans at the NIH Clinical Center. There were a total of 105 paediatric and 279 adult CT scans (sometimes multiple scans were performed for a single patient): 32 and 100 (for paediatric and adult, respectively) chest CT scans, 36 and 108 AP scans and 37 and 71 CAP scans. The age of each patient, scan type and DLP were manually collected from the CT images and the patient database for effective dose calculations. First, effective doses for those patients were calculated using the age-specific k-factors (E_ASK). Second, effective doses for patients were calculated using the size-specific k-factors (E_SSK) and the effective diameters were measured for each patient. Comparison was conducted separately for paediatric (age <20) and adult patient groups.

RESULTS

Age-specific k-factors from the ICRP phantoms

Age-specific k-factors (mSv mGy⁻¹ cm⁻¹) based on the ICRP reference paediatric and adult phantoms are tabulated in Table 1 for head and neck, head, neck, chest, abdomen, pelvis, AP and CAP scans. The authors found that the age-specific k-factors based on ICRP 103 are not significantly different from the values based on ICRP 60 except for chest and pelvis scans where both ICRP 60- and 103-based k-factors are included in the table. Age-specific k-factors based on ICRP 60 and hybrid phantoms were compared with the values published in the EG⁽⁹⁾ for 0-, 1-, 5-, 10-y-old based on stylised phantoms (see Table 2). Except for the head and neck scan showing insignificant differences from −6.2 to 12.1 %, all scan types show significant discrepancies up to 27.8 % (adult chest scan). Here the authors assumed that the anatomy of the ICRP voxel phantoms is more realistic than that of the stylised phantoms and can be used as a standard for comparison. In that case, the effective doses could be overestimated for chest scans and underestimated for head scans when calculated using the k-factors from the EG. The authors also compared (Table 3) their age-specific k-factors based on ICRP 103 tissue weighting factors with those published by Deak et al.⁽¹¹⁾. Most prominent discrepancy is shown in chest scans (up to 49 % for 5-y-old), which may be caused by the difference in the anatomy and resulting organ doses between the stylised phantoms used by Deak et al. and the ICRP voxel phantoms used in the authors' work. Although identical anatomical landmarks may be used in both phantoms, the organs covered by chest scans and the scan lengths could be different.

Table 1.

Age-specific k-factors (mSv mGy⁻¹ cm⁻¹) for 0-, 1-, 5-, 10- and 15-y-old, and adult ICRP reference phantoms for eight different scan types based on head and body CTDI phantoms. For the chest and pelvis scans where the effective doses based on the ICRP 60 and 103 tissue weighting factors are significantly different, 60 and 103 were added in the parenthesis for the scan types. The k-factors for other scan types are based on ICRP 103.

Scan region	0-y-old		1-y-old		5-y-old		10-y-old		15-y-old		Adult
	Head	Body	Head	Body	Head	Body	Head	Body	Head	Body	Head	Body
Head and neck	0.014		0.009		0.007		0.005		0.004		0.003
Head	0.009		0.006		0.004		0.003		0.002		0.002
Neck	0.023		0.013		0.009		0.007		0.005		0.005
Chest (103)	0.051	0.099	0.033	0.064	0.024	0.047	0.017	0.033	0.012	0.024	0.011	0.021
Chest (60)	0.045	0.087	0.029	0.057	0.021	0.041	0.015	0.028	0.011	0.021	0.009	0.018
AP	0.047	0.092	0.031	0.060	0.022	0.043	0.014	0.028	0.011	0.022	0.009	0.018
CAP	0.044	0.086	0.029	0.056	0.021	0.041	0.014	0.028	0.011	0.021	0.009	0.018
Abdomen	0.045	0.088	0.032	0.063	0.022	0.043	0.017	0.032	0.014	0.027	0.011	0.022
Pelvis (103)	0.028	0.054	0.021	0.041	0.015	0.028	0.009	0.017	0.008	0.015	0.006	0.011
Pelvis (60)	0.036	0.069	0.027	0.053	0.019	0.038	0.012	0.023	0.010	0.020	0.007	0.014

Table 2.

Comparison of the ICRP 60-based age-specific k-factors between the EG based on stylised phantoms and the current study (NCI) based on the ICRP reference phantoms. The k-factors for adult head and neck and paediatric scans assume use of the head CTDI phantom (16 cm). All other k-factors assume use of the body CTDI phantom (32 cm). The percent difference (% diff) was calculated as (NCI − EG)/EG × 100.

Scan type	0-y-old			1-y-old			5-y-old			10-y-old			Adult
	NCI	EG	% diff	NCI	EG	% diff	NCI	EG	% diff	NCI	EG	% diff	NCI	EG	% diff
Head and neck	0.012	0.013	−6.2	0.008	0.009	−5.7	0.006	0.006	12.1	0.005	0.004	9.1	0.003	0.003	−1.9
Head	0.009	0.011	−16.5	0.006	0.007	−10.6	0.004	0.004	6.4	0.003	0.003	−8.7	0.002	0.002	−26.7
Neck	0.021	0.017	23.3	0.012	0.012	0.3	0.009	0.011	−19.3	0.006	0.008	−19.5	0.004	0.006	−26.3
Chest	0.045	0.039	14.5	0.029	0.026	12.0	0.021	0.018	16.7	0.015	0.013	12.3	0.018	0.014	27.8
AP	0.046	0.049	−5.2	0.031	0.030	4.2	0.022	0.020	10.9	0.015	0.015	−0.5	0.018	0.015	22.4
CAP	0.043	0.044	−2.3	0.029	0.028	3.6	0.021	0.019	10.3	0.014	0.014	2.6	0.018	0.015	17.2

Table 3.

Comparison of the ICRP 103-based age-specific k-factors between Deak et al.⁽¹¹⁾ and the current study (NCI). The k-factors for head and neck scans assume use of the head CTDI phantom (16 cm) for paediatric and adult patients and the k-factors for other scans assume use of the body CTDI phantom (32 cm). The percent difference (% diff) was calculated as (NCI − Deak)/Deak × 100.

Scan type	0-y-old			1-y-old			5-y-old			10-y-old			Adult
	NCI	Deak	% diff	NCI	Deak	% diff	NCI	Deak	% diff	NCI	Deak	% diff	NCI	Deak	% diff
Head	0.009	0.009	0.8	0.006	0.005	10.1	0.004	0.004	23.8	0.003	0.003	9.0	0.002	0.002	−12.4
Neck	0.023	0.021	11.3	0.013	0.017	−23.4	0.009	0.012	−23.1	0.007	0.009	−28.1	0.005	0.005	−8.3
Chest	0.099	0.071	39.9	0.064	0.047	37.4	0.047	0.031	48.6	0.033	0.023	39.2	0.021	0.015	45.5
Abdomen	0.088	0.080	9.6	0.063	0.051	22.2	0.043	0.035	21.8	0.032	0.025	31.3	0.022	0.015	41.0
Pelvis	0.054	0.067	−19.8	0.041	0.043	−5.1	0.028	0.029	−3.8	0.017	0.022	−22.8	0.011	0.013	−16.2

Body size-specific k-factors

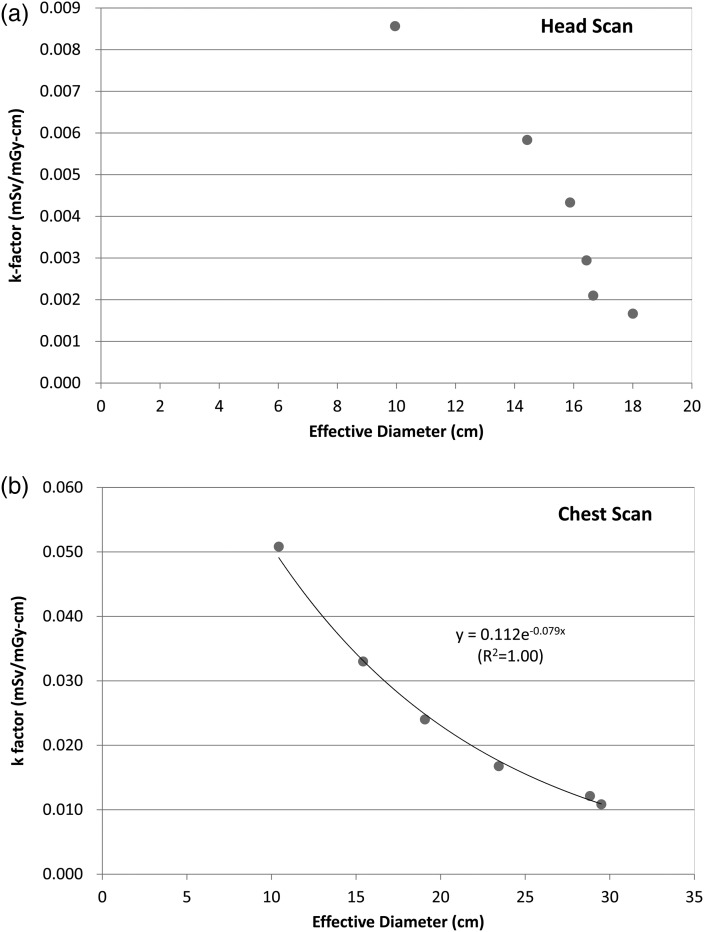
Figure 1 shows the functional relationship of size-specific k-factors (mSv mGy⁻¹ cm⁻¹) as a function of the effective diameter measurements (cm) for (Figure 1a) head and (Figure 1b) chest scans. In case of the head scan (Figure 1a), an exponential function did not fit well so the authors decided to provide the k-factors in a table format. For chest (Figure 1b), for example, and other body scans, exponential functions were the best fit. Based on the fits of regression models, a set of look-up-tables were generated for radiologists to readily pick a size-specific k-factor using the simple measurements of antero-posterior and lateral dimensions. In case of head and neck, interpolation was conducted for consecutive effective diameters ranging from 5 to 20 cm and the results are given in Table 4. Size-specific k-factors for other scan types are given in Table 5 for head and body CTDI phantoms.

Figure 1.

k-Factors (mSv mGy⁻¹ cm⁻¹) as a function of the effective diameter (cm) measured from the hybrid phantom series under (a) head and (b) chest scans.

Table 4.

Size-specific k-factors (mSv mGy⁻¹ cm⁻¹) for head and neck, head and neck CT scans for a series of consecutive effective diameter (cm).

Effective diameter (cm)	Head and neck	Head	Neck
5	0.016		0.033
6	0.015		0.028
7	0.014		0.023
8	0.013	0.010	0.017
9	0.012	0.009	0.012
10	0.011	0.009	0.009
11	0.010	0.008	0.006
12	0.009	0.007	0.005
13	0.008	0.007	0.005
14	0.007	0.006	0.004
15	0.005	0.005	0.004
16	0.004	0.004
17	0.003	0.002
18	0.003	0.002
19	0.003	0.001
20	0.002	0.001

Table 5.

Size-specific k-factors (mSv mGy⁻¹ cm⁻¹) for head and body CTDI phantoms for a series of consecutive effective diameters (cm) for chest, abdomen, pelvis, AP and CAP CT scans from the regression curve coefficients a and b.

Regression coefficients	Head					Body
	Chest	Abdomen	Pelvis	AP	CAP	Chest	Abdomen	Pelvis	AP	CAP
a	0.112	0.128	0.065	0.168	0.137	0.217	0.236	0.134	0.327	0.267
b	−0.079	−0.093	−0.087	−0.116	−0.103	−0.079	−0.091	−0.089	−0.116	−0.103
Effective diameter (cm)
8	0.060	0.061	0.032	0.066	0.060	0.115	0.114	0.066	0.129	0.117
9	0.055	0.055	0.030	0.059	0.054	0.107	0.104	0.060	0.115	0.106
10	0.051	0.051	0.027	0.053	0.049	0.098	0.095	0.055	0.103	0.095
11	0.047	0.046	0.025	0.047	0.044	0.091	0.087	0.050	0.091	0.086
12	0.043	0.042	0.023	0.042	0.040	0.084	0.079	0.046	0.081	0.078
13	0.040	0.038	0.021	0.037	0.036	0.078	0.072	0.042	0.072	0.070
14	0.037	0.035	0.019	0.033	0.032	0.072	0.066	0.039	0.064	0.063
15	0.034	0.032	0.018	0.029	0.029	0.066	0.060	0.035	0.057	0.057
16	0.032	0.029	0.016	0.026	0.026	0.061	0.055	0.032	0.051	0.051
17	0.029	0.026	0.015	0.023	0.024	0.057	0.050	0.030	0.046	0.046
18	0.027	0.024	0.014	0.021	0.021	0.052	0.046	0.027	0.041	0.042
19	0.025	0.022	0.012	0.019	0.019	0.048	0.042	0.025	0.036	0.038
20	0.023	0.020	0.011	0.017	0.017	0.045	0.038	0.023	0.032	0.034
21	0.021	0.018	0.010	0.015	0.016	0.041	0.035	0.021	0.029	0.031
22	0.020	0.017	0.010	0.013	0.014	0.038	0.032	0.019	0.025	0.028
23	0.018	0.015	0.009	0.012	0.013	0.035	0.029	0.017	0.023	0.025
24	0.017	0.014	0.008	0.010	0.012	0.033	0.027	0.016	0.020	0.023
25	0.016	0.013	0.007	0.009	0.010	0.030	0.024	0.014	0.018	0.020
26	0.014	0.011	0.007	0.008	0.009	0.028	0.022	0.013	0.016	0.018
27	0.013	0.010	0.006	0.007	0.008	0.026	0.020	0.012	0.014	0.017
28	0.012	0.009	0.006	0.007	0.008	0.024	0.018	0.011	0.013	0.015
29	0.011	0.009	0.005	0.006	0.007	0.022	0.017	0.010	0.011	0.013
30	0.010	0.008	0.005	0.005	0.006	0.020	0.015	0.009	0.010	0.012
31	0.010	0.007	0.004	0.005	0.006	0.019	0.014	0.008	0.009	0.011
32	0.009	0.007	0.004	0.004	0.005	0.017	0.013	0.008	0.008	0.010
33	0.008	0.006	0.004	0.004	0.005	0.016	0.012	0.007	0.007	0.009
34	0.008	0.005	0.003	0.003	0.004	0.015	0.011	0.007	0.006	0.008
35	0.007	0.005	0.003	0.003	0.004	0.014	0.010	0.006	0.006	0.007
36	0.007	0.004	0.003	0.003	0.003	0.013	0.009	0.005	0.005	0.007
37	0.006	0.004	0.003	0.002	0.003	0.012	0.008	0.005	0.004	0.006
38	0.006	0.004	0.002	0.002	0.003	0.011	0.007	0.005	0.004	0.005
39	0.005	0.003	0.002	0.002	0.002	0.010	0.007	0.004	0.004	0.005
40	0.005	0.003	0.002	0.002	0.002	0.009	0.006	0.004	0.003	0.004

Body size-specific effective doses for patients and comparison with age-specific effective doses

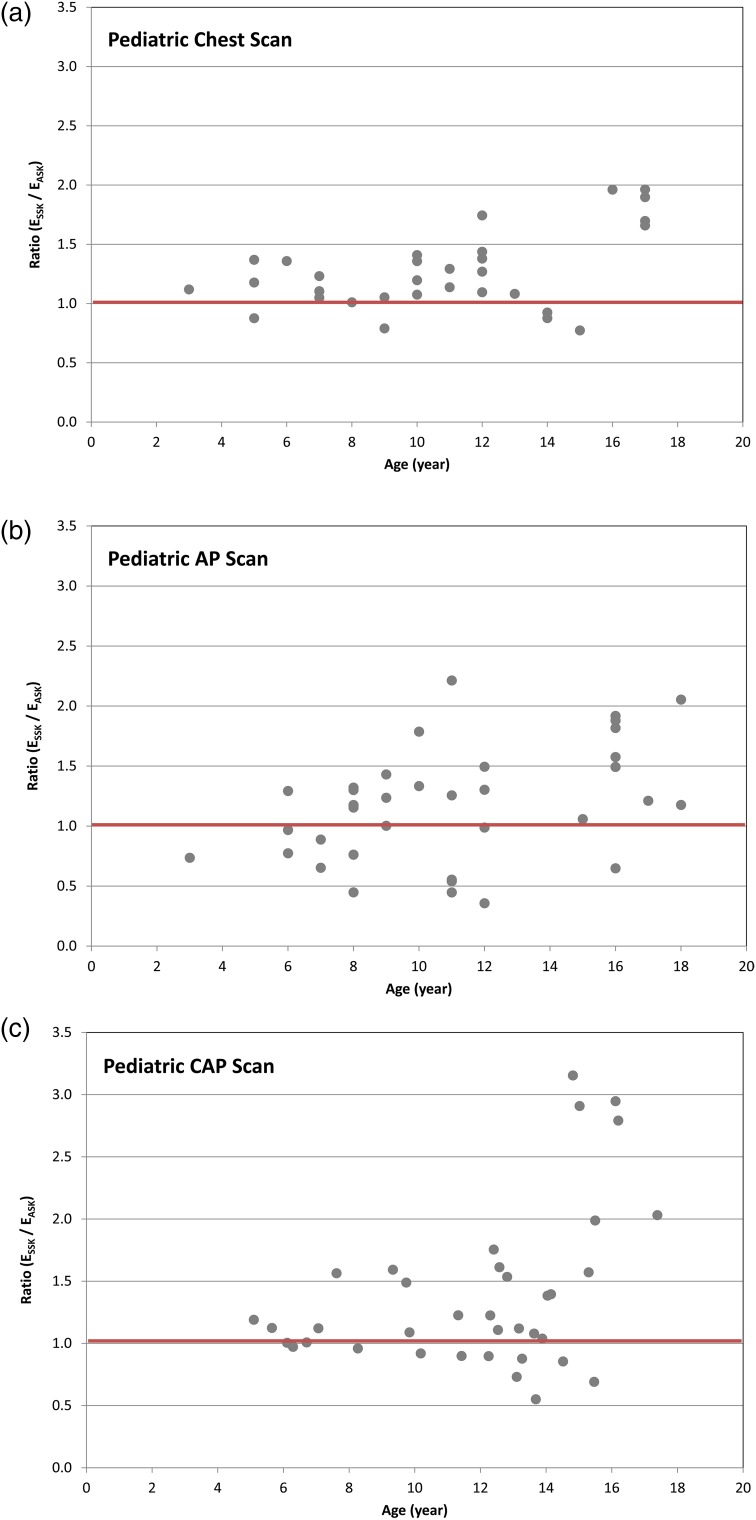
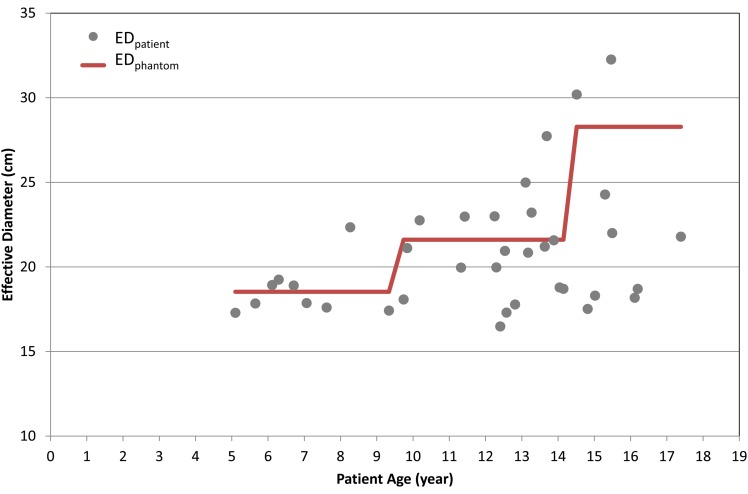
Figure 2 shows the ratio of E_SSK to E_ASK for 105 paediatric scans: (a) 32 chest, (b) 36 AP and (c) 37 CAP scans. The effective diameter ranges from 13.8 to 32.3 cm. E_SSK is greater than E_ASK for 84, 73 and 64 % of the chest, AP and CAP scans, respectively. In 19, 25 and 35 % of the chest, AP and CAP scans, respectively, E_SSK is up to 50 % greater than the value of E_ASK. The E_SSK (10.1 mSv) is up to 3.2-fold greater than E_ASK (3.2 mSv) in one CAP scan, which was conducted for a 15-y-old child whose effective diameter was 17.5 cm. Figure 3 shows the effective diameters of the 37 CAP scans compared with those measured from the Oak Ridge National Laboratory (ORNL) stylised phantoms for different age groups. Sixty-seven per cent of CAP scans were performed for paediatric patients who were thinner than the stylised phantoms that were the basis of the k-factors assigned to each age group. The effective diameter of the 15-y ORNL phantom was 26.0 cm, which could significantly underestimate the actual effective dose received by the underweight patient, the 15-y-old child with the effective diameter of 17.5, for example. With increasing age of patients, the deviation of patient effective diameters from that of the phantoms becomes greater. This is corresponding to a larger difference between E_SSK and E_ASK for older patients as shown in Figure 2.

Figure 2.

Ratio of the effective doses based on size-specific k-factors (E_SSK) to the effective doses based on age-specific k-factors (E_ASK) as a function of patient age for (a) chest, (b) AP, and (c) CAP CT scans for paediatric patients.

Figure 3.

Effective diameter measured from paediatric patients (ED_patient) who underwent CAP scans as a function of patient ages. The effective diameter measured from the ORNL stylised phantoms (5-, 10-y-old and adult) (ED_phantom) is included for comparison (bold line).

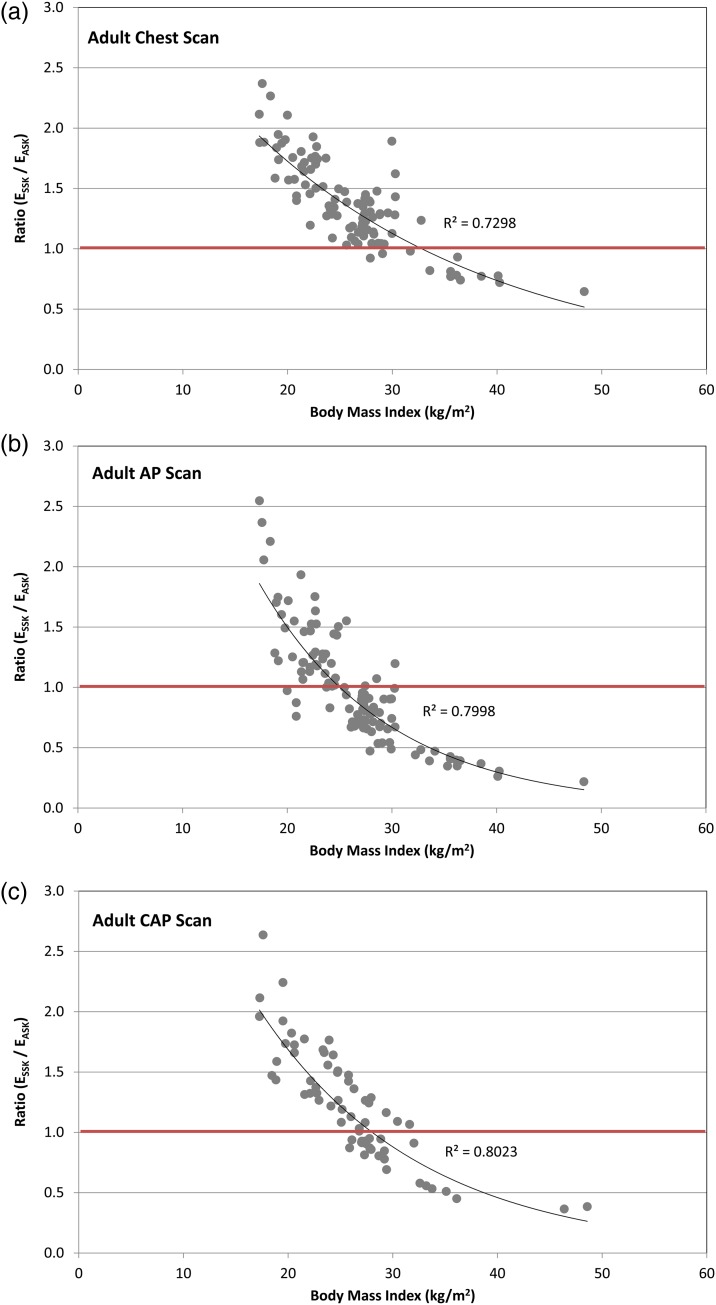
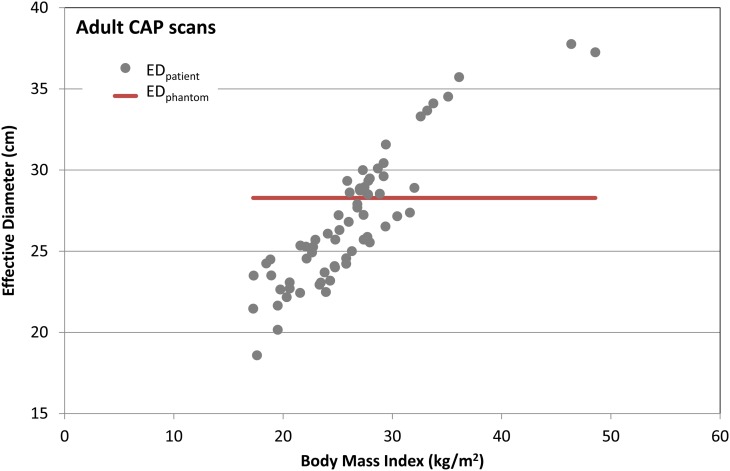
Figure 4 shows the ratio of E_SSK to E_ASK for 279 adult CT scans: (a) 47 chest, (b) 44 AP and (c) 71 CAP scans as a function of body mass index (BMI = weight height⁻²). The ages of patients range from 20 to 80 y, BMI from 16.3 to 48.6 kg m⁻² and effective diameter from 18.6 to 40.7 cm. E_SSK is greater than E_ASK for 87, 44 and 62 % of the chest, AP and CAP scans, respectively. In 33, 15 and 25 % of the chest, AP and CAP scans, respectively, E_SSK is more than 1.5-fold greater than E_ASK. Ninety-six per cent of the total scans were conducted to patients whose BMI is >18.5 kg m⁻², which is the lower threshold of the normal BMI range (18.5–25 kg m⁻²) according to the World Health Organization (http://apps.who.int/bmi/index.jsp?introPage=intro_3.html (accessed September 2015)). Figure 4 shows that age-specific k-factors could underestimate the effective doses for normal to overweight (18.5–30 kg m⁻²) patients by up to 2.6-fold and overestimate the effective dose for the moderately obese (30–35 kg m⁻²) to severely obese (>40 kg m⁻²) patients by up to 4.6-fold. The authors found that the ratio of E_SSK to E_ASK exponentially decreases as the BMI increases (R² > 0.73). Figure 5 shows the effective diameter as a function of BMI in the adult CAP scans compared with the constant effective diameter (red line in Figure 5) measured from the ORNL adult stylised phantom, which forms the basis for the adult age-specific k-factor. Sixty-two per cent of the CAP scans were conducted on patients whose effective diameter were smaller than that of the ORNL stylised phantom (28.3 cm), which explains why E_SSK is greater than E_ASK for the 62 % of CAP scans as shown in Figure 4c.

Figure 4.

Ratio of the effective doses based on size-specific k-factors (E_SSK) to the effective doses based on age-specific k-factors (E_ASK) as a function of patient BMI (kg m⁻²) for (a) chest and (b) AP CT scans for adult patients.

Figure 5.

Effective diameter measured from adult patients (ED_patient) who underwent CAP scans as a function of patient BMI values. The effective diameter measured from the ORNL adult stylised phantom (ED_phantom) is included for comparison (bold line).

DISCUSSION

As noted earlier and elsewhere^{(3, 4)}, effective dose was originally developed for radiation protection purposes, primarily to establish compliance with regulatory limits but also for prospective dose assessment for planning and optimisation in radiological protection. More frequently in past years, effective dose has been used in many contexts for simple risk comparisons. Because of the simplifications that are imposed by the definition of effective dose, the concept has been criticised⁽²⁰⁾ with one of the most significant criticisms that it is not tailored to any specific disease endpoint and that there are marked and differing age (and sometimes ethnic and sex) dependencies for different endpoints which are not taken into account. Nevertheless, in recent years, the use of effective dose has become increasingly popular as metric of exposure in medical applications^(21–24) because it represents, even if overly simplified, a metric of exposure that can be related to cancer risk or provides a means such that the risk of a specific procedure can be compared with another. However, because of the diversity and intensity of opinions on the validity and the flaws of using effective dose in medicine, herein the authors do not comment on or endorse the use of effective dose in medicine. Rather, it is the purpose of this paper to improve the estimation of effective dose for CT imaging such that, regardless of the validity of the concept, clinicians will be able to use it to its greatest advantage by a method, which reduces the dose uncertainty related to body size dependence.

CONCLUSION

To incorporate the effect of patient body size into effective dose calculations, a set of body size-specific k-factors was developed, which can be used to calculate more reliable effective dose for clinical use. The authors found that, in using the conventional age-specific k-factor, paediatric patients tend to have underestimates (up to 3-fold) of effective dose, while adult patients tend to have underestimates (up to 2.6-fold) and overestimates (up to 4.6-fold) for underweight and obese patients, respectively. Based on their application of the size-specific k-factors to actual paediatric and adult patients, the authors found that the use of age-specific k-factors for underweight to normal patients tends to underestimate the effective dose. In contrast, the use of age-specific k-factors tends to overestimate effective dose when compared with size-specific effective dose for overweight patients. For these various reasons, the body size-dependent k-factors the authors have derived, based on the more realistic anatomy of the hybrid phantoms, appear to provide significant advantages to clinicians for providing more reliable estimates of effective dose from CT scans. The authors suggest that effective dose, as derived here, is a more informative indicator of whole-body dose than either CTDI_vol or DLP values. In closing, the authors believe it is worth emphasising that in order to make legitimate and firmly based estimates of individual or population cancer risks, true organ doses to individual patients must be properly assessed, something that effective dose estimation strategies, no matter how sophisticated, cannot provide.

FUNDING

This work was supported by the intramural research program of the National Institutes of Health, National Cancer Institute, Division of Cancer Epidemiology and Genetics. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.