Significance
Limited knowledge about the mechanistic drivers of forest growth and responses to environmental changes creates uncertainties about the future role of circumpolar boreal forests in the global carbon cycle. Here, we use newly acquired tree-ring data from Canada’s National Forest Inventory to determine the growth response of the boreal forest to environmental changes. We find no consistent boreal-wide growth response over the past 60 y across Canada. However, some southwestern and southeastern forests experienced a growth enhancement, and some regions such as the northwestern and maritime areas experienced a growth depression. Growth–climate relationships bring evidence of an intensification of the impacts of hydroclimatic variability on growth late in the 20th century, in parallel with the rapid rise of summer temperature.
Keywords: drought impacts, climate change, dendrochronology, normalized difference vegetation index, ecology
Abstract
Considerable evidence exists that current global temperatures are higher than at any time during the past millennium. However, the long-term impacts of rising temperatures and associated shifts in the hydrological cycle on the productivity of ecosystems remain poorly understood for mid to high northern latitudes. Here, we quantify species-specific spatiotemporal variability in terrestrial aboveground biomass stem growth across Canada’s boreal forests from 1950 to the present. We use 873 newly developed tree-ring chronologies from Canada’s National Forest Inventory, representing an unprecedented degree of sampling standardization for a large-scale dendrochronological study. We find significant regional- and species-related trends in growth, but the positive and negative trends compensate each other to yield no strong overall trend in forest growth when averaged across the Canadian boreal forest. The spatial patterns of growth trends identified in our analysis were to some extent coherent with trends estimated by remote sensing, but there are wide areas where remote-sensing information did not match the forest growth trends. Quantifications of tree growth variability as a function of climate factors and atmospheric CO2 concentration reveal strong negative temperature and positive moisture controls on spatial patterns of tree growth rates, emphasizing the ecological sensitivity to regime shifts in the hydrological cycle. An enhanced dependence of forest growth on soil moisture during the late-20th century coincides with a rapid rise in summer temperatures and occurs despite potential compensating effects from increased atmospheric CO2 concentration.
Circumpolar boreal forests are estimated to store ∼53.9 Pg of carbon or ∼14% of terrestrial vegetation biomass (1). These regions are currently experiencing accelerated changes, including warmer and longer growing seasons, tree line expansion, species migration, increased frequency and severity of drought, and increases in the frequency and severity of disturbances (2–10). These changes create uncertainty about the boreal forests’ future role in the global carbon cycle (11). Adding to this uncertainty is the discrepancy over recent changes in the productivity of boreal and other northern latitude forests. Some empirical evidence suggests increases in the forest productivity (12–14), whereas other studies suggest decreasing productivity over the last decades (7, 8, 15–17). Furthermore, inversion and process-based ecosystem models indicate large carbon sinks (7, 8), whereas field-based bottom-up approaches suggest smaller carbon sinks or small carbon sources (3, 18), or large sinks (19). Quantifying the response of boreal forests to environmental changes and the subsequent effects on the global carbon cycle thus remains a pending, interdisciplinary scientific challenge (11, 18, 20).
Observations of vegetation productivity at northern latitudes may be obtained using either ground- or satellite-based observations, which may represent different components of forest productivity, that is, stem vs. leaf level. Satellite-derived indices of photosynthetic activity, such as the normalized difference vegetation index (NDVI), are now widely used for quantifying responses of forested areas to environmental changes (21, 22). However, a recent comparison of commonly used NDVI datasets showed marked differences in their representation of mean seasonal vegetation productivity and decadal-long trends (21), which stresses the necessity for large-scale, ground-based observations. Ground-based observations of vegetation productivity may originate from permanent sample plots (13, 17) or from tree-ring analyses (12, 14, 16, 23), which differ in the temporal resolution (decadal vs. annual) and spatial scale (stand vs. tree). Both are prone to bias because of unbalanced spatial sampling. Permanent sample plots may be preferentially established in the more productive forests (24). On the other hand, tree-ring data have been typically focused on the dry or cold marginal limits of forest distribution (23, 25). Furthermore, uncertainty in determining the representative vegetation productivity trends for northern latitudes is exacerbated by short observational time series inherent to many of these data sources. The resulting limited quantification of growth, and subsequent uncertainties in mechanistic drivers and predictions of the ecosystem’s fate, emphasize the need for continuous, highly resolved, and spatially extensive datasets that are statistically representative and constitute an unbiased estimate of the forested regions.
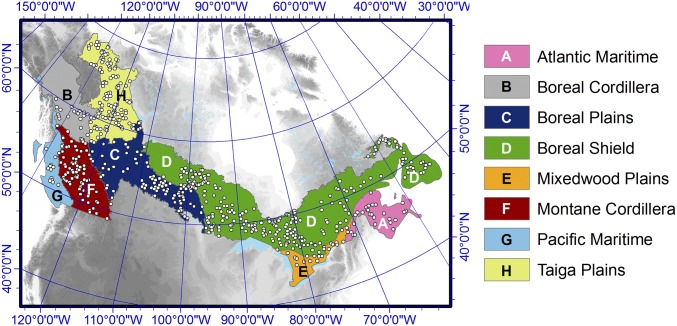
Here, we examine the aboveground growth responses of the Canadian boreal forest to climate change over the past ∼60 y based on a new ground plot network that provides a much more representative sampling of this major North American biome. Information was obtained for a total of 19 boreal tree species from annually resolved and absolutely dated ring width measurements from 2,807 trees at 598 ground plots of Canada’s National Forest Inventory (NFI) (Fig. 1 and SI Appendix, part A). We examine growth trends before and during the satellite era and compare them with trends observed from NDVI datasets. We relate seasonal temperature, soil moisture, and atmospheric carbon dioxide concentration ([CO2]) variation to long-term changes in annual tree growth rates. We also evaluate whether the observed growth trends are consistent with the expected growth rate responses to climate change. Across the vast territory under study, mean annual temperatures increased between 0.5 and 3.0 °C during the 20th century along with global increases in atmospheric CO2 concentrations (9). Given the cold climatic conditions, it could be expected that these changes should have led to increases in forest growth in this subcontinental region.
Fig. 1.
Distribution of Canada’s National Forest Inventory (NFI) sample plots for tree-ring analysis and of the main terrestrial ecozones under study. The nonboreal Pacific Maritime, Mixedwood Plains, and Atlantic Maritime ecozones are included in the study owing to coexisting species with the boreal ecozones.
Results and Discussion
Species and Regions Show Different Long-Term Growth Trends.
The network of NFI plots extends through the Canadian forested area, representing more than 400 Mha, and covers eight of its terrestrial ecozones (Fig. 1). Five species represent a total of 73% of the NFI’s current network of sampled trees: Picea mariana (black spruce: 44%), Picea glauca (white spruce: 10%), Pinus banksiana (jack pine: 7%), Populus tremuloides (trembling aspen: 7%), and Abies balsamea (balsam fir: 6%), with the other 27% of samples distributed among 14 additional species (SI Appendix, part A). Most plots (62%) contained samples of a single species, 31% contained two species, and 7% contained a mixture of three or more species. Separate chronologies were developed for plots containing multiple species, resulting in a total of 873 species-by-plot chronologies available for analysis. Ring width measurement series were scaled to provide annual estimates of tree basal area increments (BAIs) (in square centimeters per year), and were then detrended using species-by-plot generalized additive mixed models (GAMMNFI). We additionally applied a tree-level generalized negative exponential (GNE) procedure, and two uniform species-by-ecozone [GAMMeco and regional curve standardization (RCS)] procedures to generate four different forms of tree growth indices (detailed in Materials and Methods and SI Appendix, part B).
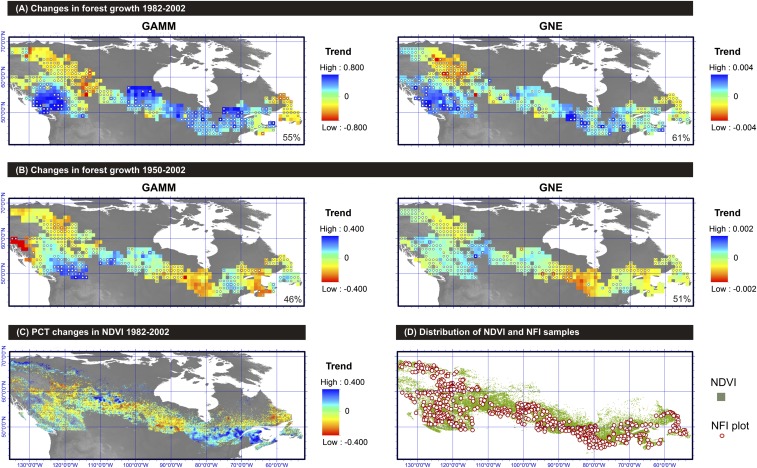
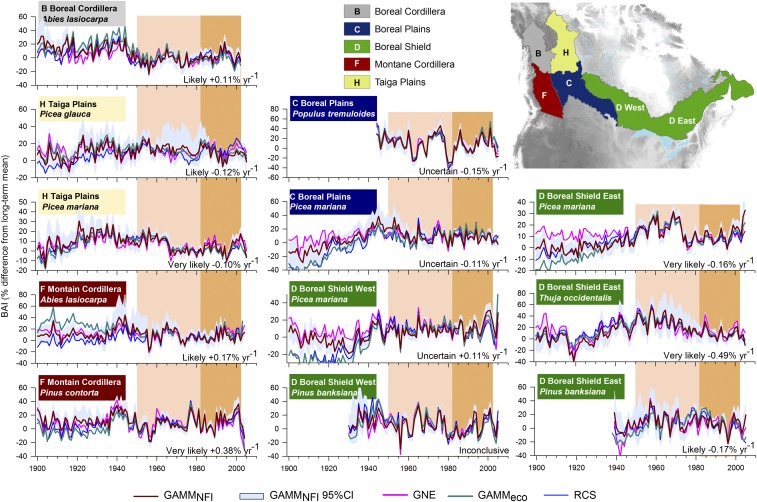
Averaged across Canada’s boreal forest, growth did not change significantly (P > 0.050) from 1950 to 2002 with an overall trend estimated between −0.032%⋅y−1 (GAMMNFI) and 0.054%⋅y−1 (GAMMeco) depending on the growth indices under analysis. This result, however, is a consequence of the compensating positive and negative growth trends prevalent across wide regions and individual species. Declines in forest growth from 1982 to 2002 occurred in northwestern forests east of the Rocky Mountains (up to −0.8%⋅y−1) and also in the Atlantic Maritime area (up to −0.6%⋅y−1; Fig. 2). These declines were observed in the majority of tree-ring standardization methods, with small differences observed, for instance, between species-by-plot GAMMNFI and tree-level GNE procedures (Fig. 2 A and B). Declines in northwestern forests, and to some extent in the eastern Boreal Shield and Atlantic Maritime areas, were not limited to the satellite era and rather seem to be the dominant phenomenon for a period spanning half a century (Fig. 2B). This is particularly evident in the Taiga Plains region, where the growth of needleleaf species Picea glauca, Picea mariana, and Larix laricina stalled and declined during the second half of the 20th century (Fig. 3 and SI Appendix, part C). In the Atlantic Maritime area, the growth decline was largely observed in Picea mariana (−0.1%⋅y−1; SI Appendix, part C), whereas in the eastern Boreal Shield it was found in Picea mariana, Thuja occidentalis and Pinus banksiana (Fig. 3).
Fig. 2.
Spatial distribution of forest growth trends across Canada. (A and B) Trends estimated through the analyses of Canada’s National Forest Inventory (NFI) tree cores for the periods 1982−2002 and 1950−2002, respectively. Tree data were processed through two different standardization methods to increase confidence in results: species-by-plot generalized additive mixed model (GAMMNFI) (trends are expressed in percentage per year) and tree-level generalized negative exponential (GNE) (trends are unitless). (C) Trends estimated through the analyses of normalized difference vegetation index (NDVI) data for the period 1982−2002. The map expresses the percent change in the NDVI per year. (D) Spatial distribution of NDVI and Canada’s NFI plot samples. Dots on maps (A and B) indicate areas for which trends estimated through the analyses of NFI tree cores were of the same sign as trends estimated through the analyses of NDVI data (the percentage of overall agreement is indicated on maps). The Spearman correlation (63) between the 1982−2002 GNE map in B and the NDVI map in C is r = 0.24 (P = 0.102). The correlation between the two maps in A is r = 0.64 (P < 0.001); for maps in B, it is r = 0.63 (P = 0.002). Correlations for other map combinations had probabilities P > 0.200.
Fig. 3.
Examples of species-by-ecozone forest growth variability assessed from tree-ring measurement series. Analyses were performed on data derived from four methods of tree-ring standardization: plot-level and ecozone-level generalized additive mixed models (GAMMNFI and GAMMeco), generalized negative exponential (GNE) procedures, and regional curve standardization (RCS). Confidence intervals for the GAMMNFI estimates are represented by gray bands. Variance in GNE, GAMMeco, and RCS estimates were scaled to that of 1950−2002 GAMMNFI using linear transformation (64). Estimates based on less than 20 trees were excluded from these representations. The slope of the linear trend over 1950−2002 is indicated when exceeding 0.10%⋅y−1, and a level of certainty is given based on the agreement between the four methods (see Materials and Methods and SI Appendix, part C). Shading delineates the two periods on which this study focuses.
Increases in aboveground forest growth from 1982 to 2002 were apparent in the southeastern forests of the Boreal Shield (up to +1.0%⋅y−1) (Fig. 2A). This increased forest growth seemingly reflects a recovery from low growth ∼1970–1990, which was particularly present in the dominant conifer species Abies balsamea, Picea glauca, and Picea mariana (Fig. 3 and SI Appendix, part C). Growth rates have only partially recovered in these forests since observed growth rates therein at the turn of the 21st century were below mid-20th century levels according to trend analyses (Fig. 2B). Accelerated growth rates from 1982 to 2002 were also apparent in some of the westernmost forests of the Montane Cordillera and Pacific Maritime regions (up to +0.98%⋅y−1; Fig. 2A), which is consistent with trend assessments from periodic forest inventory remeasurements of Pseudotsuga menziesii and Tsuga heterophylla stands in these forests (13).
Regional Variation in Growth Trends from Tree Rings Show Moderate Agreement with NDVI Trends.
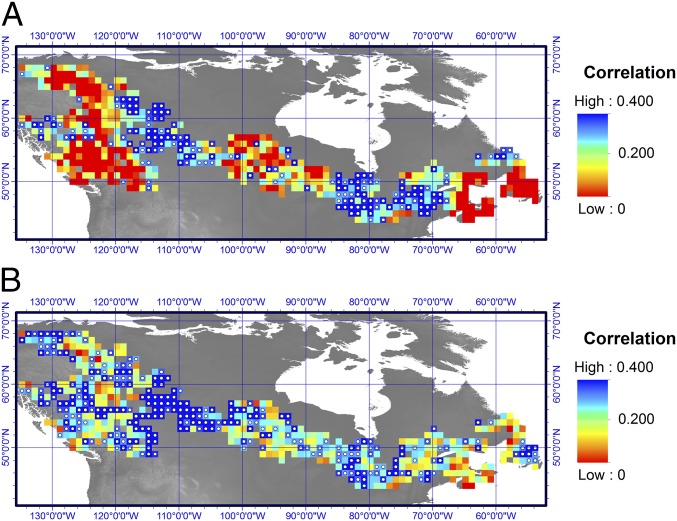
The database of Canada’s NFI tree-ring measurements offers an unprecedented opportunity for comparing remotely sensed estimates of forest productivity with ground-based estimates. Detection of similar trends in both datasets would enhance our confidence that variability is an underlying feature of forest growth. Our analysis showed reasonable agreement between growth trends estimated from tree rings and trends estimated by NDVI across a large portion of Canada’s forested area during the overlapping period of 1982−2002. The ecozones (Fig. 1) showing the best agreement included the Atlantic Maritime, Boreal Cordillera, Boreal Shield east of 90°W, Mixedwood Plains, Pacific Maritime, and Taiga Shield ecozones (overall agreement of 67% for GAMMNFI and 73% for GNE procedures for these combined ecozones). In contrast, our analysis highlighted an absence of relationship with NDVI over large regions that include the Montane Cordillera, Taiga Cordillera, and west Boreal Shield ecozones (31% agreement for GAMMNFI and 37% for GNE procedures). The disagreement was not limited to the trends themselves: pointwise correlations between NDVI and GAMMNFI time series suggest that the two datasets were poorly correlated across the mismatched areas (Fig. 4A and SI Appendix, part D). Interestingly, first-differencing of the NDVI and growth data enhanced correlations across the boreal area (Fig. 4B), which suggests coherence between forest growth and NDVI at high frequencies (interannual) and less so at lower frequencies (multiyear to centennial). The disagreement may point to artifacts in NDVI inherent to the mountainous landscapes dominating the mismatched areas and to the succession of different sensors used over the years (21). On the other hand, ecosystem processes not captured by the tree growth estimates (e.g., large fire disturbances, forest management) and insufficient replication (such as at the edges of the distribution in sampled NFI plots) likely introduce further uncertainties in this comparative analysis.
Fig. 4.
(A) Pointwise correlation computed between gridded GAMMNFI and NDVI across boreal Canada over the 1982–2002 period. Significant correlations (P < 0.10, one-sided test) are indicated by white dots. (B) The pointwise correlation analysis was repeated after applying a first difference transformation to all data. The mean correlation in A is 0.16; in B, it is 0.29. See SI Appendix, part D, for further details.
Annual Growth Variability Is Dominated by Heat and Drought Stress.
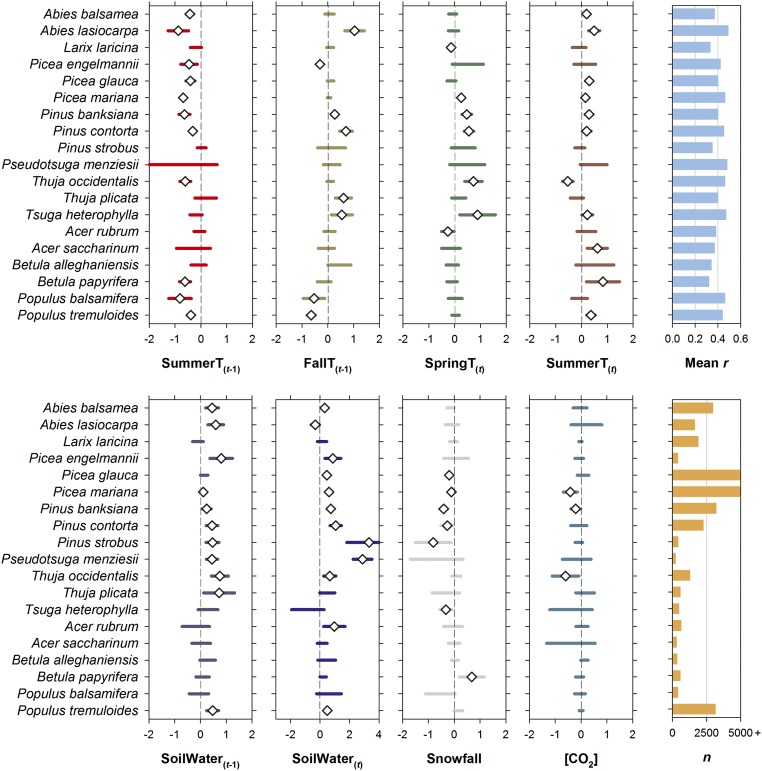
Growth–climate response patterns were computed for each of the 19 boreal tree species to identify the key environmental factors driving the observed changes in Canadian boreal forest growth (Fig. 5). In our analyses, two climatic variables stand out as important growth drivers for many of the species studied: summer temperature and soil moisture. The importance of these two variables is not limited to particular regions but extends across vast boreal areas (Fig. 6 A and B). Specifically, growth of all needleleaf species within the genera Abies, Picea, and Pinus, with the exception of Pinus strobus, was negatively influenced by warm summers in the year before tree growth (Fig. 5). The same relationship was found in broadleaf species Betula papyrifera and Populus spp., and needleleaf Thuja occidentalis. Extreme temperatures are known to be detrimental to plant productivity because of heat-related carbohydrate loss via autotrophic respiration (26, 27). The negative influence of warming on productivity is seemingly taking effect in the summer before tree growth, that is, when nonstructural carbohydrates are being stored.
Fig. 5.
Mean species-specific linear mixed model t statistics for the influence of climatic variables and atmospheric CO2 concentrations on BAI. Mean values exceeding the 95% probability levels are identified by a diamond. Mean r refers to mean values of the plot-level correlation coefficients computed between the fitted estimates from the average model and the response variable. Abbreviations of climatic variables: SummerT, summer temperature; SoilWater, summer soil moisture index; FallT, fall temperature; SpringT, spring temperature; Snowfall, cool season total snowfall; [CO2], atmospheric CO2 concentrations. Terms t − 1 and t describe influences taking place in the year before and of ring formation, respectively; n is total number of sampled years.
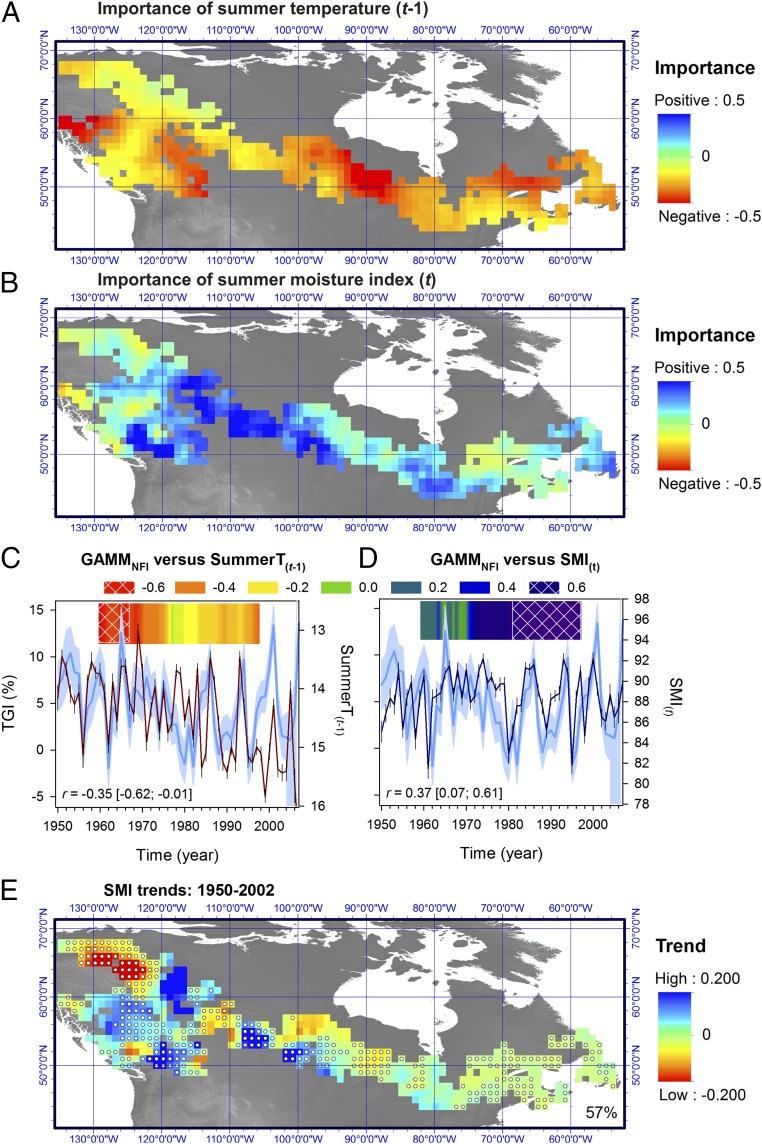
Fig. 6.
Importance of summer temperature and soil moisture on forest growth. Maps in A and B were created by applying a kriging procedure to the plot-level species-specific sums of Akaike weights for these two variables. The sign of the relationship (positive and negative) was given by the averaged model coefficients. (C and D) Averaged Canada-wide species-by-plot chronologies over 1950–2007 (blue curve) plotted against mean summer temperature of the year previous to growth and summer soil moisture index (SMI) of the year of growth. Shaded area delineates the 90% confidence interval for the growth estimates. Note the inverted y scale on the temperature axis. The Spearman correlation r between time series is shown with the 95% confidence intervals computed using a bootstrapping technique accounting for serial persistence in data. The Inset color graphs show 20-y moving window correlation analyses between variables (dark blue and dark red for positive and negative correlation, respectively). Note the shift of the climate relationship from temperature to SMI at the national level starting ∼1970. (E) Spatial distribution of trends in SMI across sampled boreal Canada from 1950 to 2002 (in millimeters per year). Dots on maps indicate areas for which trends in SMI and GAMMNFI (Fig. 2B) were of the same sign (the percent agreement is indicated).
The relationship to temperature was more variable when entering into the fall season before the year of growth, with warm conditions favoring the growth of needleleaf species Abies lasiocarpa, Pinus contorta, Pinus banksiana, Thuja plicata, and Tsuga heterophylla, but remaining detrimental to growth of the broadleaf Populus spp. (warm falls can lead to higher respiration, but no increase in photosynthesis in broadleaf species because the leaves have already fallen). Warm springs in the year of ring formation were also favorable to the growth of needleleaf species Picea mariana, Pinus banksiana, Pinus contorta, Thuya occidentalis, and Tsuga heterophylla. Additionally, the growth of a large majority of species was positively affected by warm summers in the year of ring formation. It is worth noting that for Picea mariana and Pinus banksiana, the negative effect of summer warmth in the year before growth was stronger than its positive effect in the year of ring formation (Fig. 5). This implies that summer warming has a net negative impact on the long-term growth trajectory of these two species.
Our analyses suggest that soil moisture has been an important driver of tree growth in boreal Canada since the mid-20th century: 12 of the 19 species studied clearly show dependence on this variable (Fig. 5), including the most abundant boreal trees such as Picea mariana, Pinus spp., and Populus tremuloides. Decreasing soil moisture leads to reductions in photosynthesis through stomatal closure, whereas extreme drought conditions lead to an increased risk of xylem cavitation (27–30). In such circumstances, structural growth is killed for carbon investment in maintenance respiration and osmoprotection. Thus, the dependence of growth on soil moisture is not a phenomenon solely restricted to semiarid or arid environments (31). Our results suggest that the impact of soil moisture variability on growth is stronger in broadleaf than needleleaf species, although the number of samples analyzed and the geographical coverages between the two leaf traits were highly unbalanced (Fig. 5).
The sensitivity of Canada’s boreal forest to soil moisture during the second half of the 20th century is striking and in agreement with findings from US forests (31). Projections of future climatic drying pose a major concern for Canada’s boreal forest ecosystems (9), especially in the western Prairie Provinces where forest distribution and ecosystem functioning are strongly moisture limited (32). In many Canadian areas, the trends in forest growth were consistent with the directional trend in soil moisture (Figs. 2 and 6E; e.g., Taiga Plains, Taiga Cordillera, Montane Cordillera, Boreal Plains, and Atlantic Maritime). Furthermore, the impacts of hydroclimatic variability on boreal-wide growth intensified late in the 20th century in parallel with the rapid rise of overall summer temperature (Fig. 6 C and D). However, despite significant summer warming in eastern boreal Canada (∼0.02 °C⋅y−1), drying trends were relatively weak (approximately −0.02 mm⋅y−1) (Fig. 6E). Co-occurring factors contributed to offset the impact of temperature on potential evapotranspiration in this region, including increases in relative humidity and decreases in the vapor pressure deficit (SI Appendix, part E). Likewise, hydroclimatic variability was not the main causative factor for the observed forest growth decline in eastern boreal Canada from 1950 to 2002. The high sensitivity to temperature observed during the late 20th century in eastern forests (Fig. 6A), parallel with rapid warming and growth decline, may reflect a temperature-dependent increase in respiration and depletion in carbon reserves, as was recently suggested by process-based modeling of productivity in black spruce stands (16). Such temperature responses are not static, and plants have the capacity to adjust to a warming environment via physiological acclimation (33). However, the extent to which acclimation of respiration to warming can help in maintaining trees’ carbon balance in these boreal regions remains poorly known.
Large-Scale Effects of Elevated Atmospheric CO2 on Tree Growth.
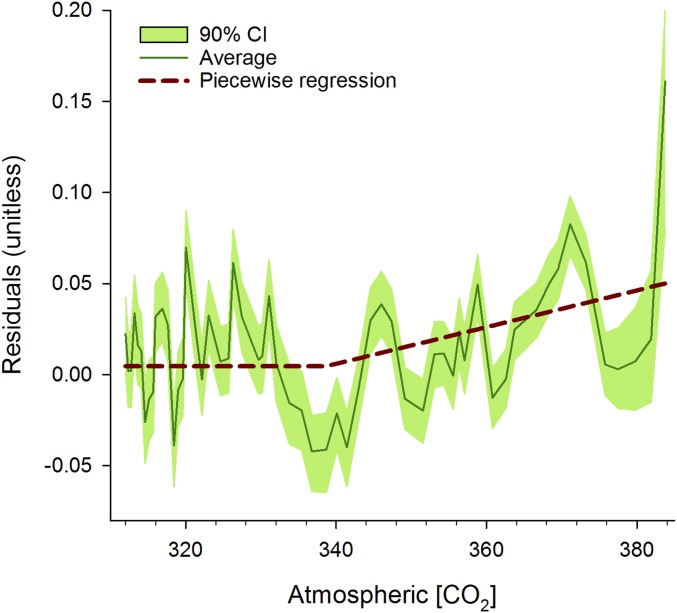
Abrupt exposure to elevated atmospheric [CO2] in controlled experiments has been shown to increase the productivity of various tree species for at least several years (34) (but see refs. 35 and 36). Associated enhancement of water use efficiency has also been observed in natural ecosystems (37, 38). Our analyses of plot-level averaged tree growth did not detect a significant effect of exposure to elevated atmospheric [CO2] over the past 50 y across boreal Canada: none of the species studied exhibited mean positive t values for this variable (Fig. 5), and plot coefficients were significant in less than 5% of the tests (SI Appendix, part F). Analyses performed on the species-by-ecozone GAMMeco chronologies provided support to these plot results (SI Appendix, part F). That being said, the [CO2] effects may be difficult to detect if the increase in plot-level tree growth is below the statistical detection limit. This is likely due to the high interannual variability in growth, and also because the [CO2] increases during the study period were both modest and gradual in comparison with the rapid and high increases in [CO2] typically applied in controlled experiments (14). In support of this thesis, residuals of the mixed models averaged across Canada’s boreal forests (i.e., the BAI variance unexplained by biological and climatic effects) correlate significantly with atmospheric [CO2] (r = 0.42; Fig. 7). Thus, although the correlation with atmospheric [CO2] is not statistically significant at the level of a plot or a region, it becomes a significant factor when sufficient data are aggregated at subcontinental scales (also see ref. 37). Our study suggests that elevated atmospheric CO2 is a large-scale, but subtle phenomenon and the detection of a CO2 effect requires a large spatial covering where local confounding factors and interannual variability in climate and disturbances average each other out and allow the CO2-related effects to be detected. Still, other challenges in attributing the [CO2] factor are worth further exploring and include, among others, the possible alternative pathways for the extra carbon assimilated under increasing [CO2] (36), methodological considerations including collinearity among predictor variables and the standardization of tree-ring data (39), and the impact of sampling design on growth trends (40, 41).
Fig. 7.
Linear-mixed model residuals averaged across Canada and plotted against annual averages of atmospheric concentrations of CO2. The shaded area delineates the 90% confidence interval. The dashed line shows the relationship between residuals and atmospheric concentrations of CO2 modeled using a piecewise regression (r = 0.42) (65). The relationship takes an inflection point at 339 ppmv, suggesting that linear-mixed model predictions are underestimating a potential large-scale growth enhancement in recent years.
Conclusions
Our analyses of a new methodologically standardized tree-ring dataset covering Canada’s boreal forest provide insights into the growth responses of this ecosystem to climate change. Although revealing no overarching “growth enhancement” or “growth decline” in recent years, results do point to significant regional- and species-related trends in growth. The observed link between climate variation and growth variability revealed unique evidence of an intensification of the impacts of hydroclimatic variability on growth late in the 20th century, in parallel with the rapid rise of summer temperature. Such response can be attributed to annual growth variability in these forests being mainly driven by negative sensitivity to summer temperature (warmer summers leading to less growth) and positive sensitivity to summer soil moisture (more moisture leading to more growth), albeit species-specific variations in these responses can be found. We caution that neither mortality nor disturbance impacts are addressed here and that therefore extrapolation of future carbon storage in these forests is neither straightforward nor simple to achieve (3, 6, 8, 42). Furthermore, the complex interplay of different biotic and abiotic drivers of boreal forest productivity, including unpredictable wildfires, insect population outbreaks, and other disturbances, may yield counterbalancing effects on the overall net carbon sequestration (6, 42, 43). Notably, insect-induced collapses in growth in western and eastern Canadian forests played a major role in defining growth trajectories at the turn of the 21st century (3, 44, 45), but their relative effects on growth are only partially, if at all, captured by this current NFI tree-ring analysis. Although remote-sensing products can provide insights into the impacts of these phenomena and of climate change, our results suggested extensive areas of disagreement between forest growth trajectories and remotely sensed NDVI trends: the accelerated growth over large regions was not necessarily correlated with greening and, inversely, with browning where trees experienced a slower growth. Complex effects of climate on growth rates, unpredictable future disturbances, and uncertainties in trends assessed from remotely sensed forest productivity data provide justification for ground-based monitoring of species-specific trends, disturbance impacts, and responses to climate change at local to regional scales.
Materials and Methods
Tree-Ring Data.
The tree-ring width dataset is based on increment cores sampled during the establishment of Canada’s NFI plot survey (24), representing an unprecedented degree of sampling standardization for a large-scale dendrochronological study. The sampled plots (n = 598) were designed to be representative of the distribution of species and growing conditions in the managed forests of Canada (Fig. 1). At each NFI plot, samples were collected from up to 10 living dominant and codominant trees (diameter at breast height, >5 cm; median n per plot was four trees and varied depending on the year of survey, with more recent surveys having larger n; see SI Appendix, part A, for further details). Samples were processed, crossdated, and measured using standard dendrochronological methods (SI Appendix, part A). We only used core samples covering a minimum of 20 y. Over 80% of the samples either contained the innermost ring (pith) or were estimated to lie within a centimeter of it. A high proportion of the samples originated from plots located on moraine (44% of plots) and lacustrine (19% of plots) deposits, followed by bogs (8% of plots; one-half of them north of 60°N), and unspecified organic materials (e.g., sedge, sphagnum; 10% of plots). The remaining 19% of plots represented other types of parent materials (e.g., fluvioglacial, bedrock).
Ring width measurement series were scaled to provide annual estimates of tree BAIs (in square centimeters per year) using the following:
| [1] |
where and are the cumulative stem radial increments (in centimeters) at the end and beginning of a given annual ring increment, respectively. BAI and derived metrics thereof (long-term trends in BAI) are more directly related to tree productivity and stem biomass than to diameter increment (46).
Vegetation Index Data.
Processed NDVI satellite data based on advanced very high-resolution radiometer (AVHRR) raw data were obtained from the latest version (3g) of the Global Inventory for Mapping and Modeling Studies (GIMMS) (47), which covers July 1981 to December 2012 at a temporal resolution of ∼2 wk (24 scenes per y per pixel) and a spatial resolution of 0.083° (∼9 km). For photosynthetically active vegetation, the NDVI ranges from 0 to 1. In this study, we extracted NDVI data for pixels in Canada where the percentage of tree cover was >75% (based on ref. 48), and averaged them by pixel and year to create annual NDVI time series.
Climatic and CO2 Data.
For each plot, daily weather data (maximum and minimum temperature; in degrees Celsius), precipitation (sum; in millimeters), relative humidity (in percentage), and vapor pressure deficits (in kilopascals) were obtained for the period of 1950−2010 using BioSIM, which interpolates site-specific estimates from historical weather observations (49) as described in ref. 50. The quantity of available soil moisture was estimated for each month using the quadratic-plus-linear (QL) formulation procedure described in ref. 51, which accounts for water loss through evapotranspiration (simplified Penman–Monteith potential evapotranspiration) and gain from precipitation. Parameter values for maximum and critical available soil water were set at 300 and 400 mm, respectively; the number of weather stations for interpolation was set to 8. We used annual mean atmospheric concentrations of CO2 recorded at Mauna Loa observatory since 1958 (52); the data were extended to 1950 using estimates from ice cores (53).
Quantification of Past Annual Tree Growth.
Eliminating the intrinsic age- and size-related growth trend in BAI makes it possible to address annual growth variability independently of biological age or tree size, and furthermore permits comparison of long-term growth trends among species and regions. Departures from the detrended growth rates are interpreted as being caused by climate variability, insect disturbances or other external drivers. Here, we used GAMMs (54, 55) to remove internal biological effects for each species-by-plot combination (873 analyses in total). This approach is based on the modeling of BAI as a function of cambial age and tree basal area. Compared with a continental-scale model approach, the species-by-plot-level models were better able to handle the variation in species responses across climate gradients, varying plot disturbance histories, unequal distributions of species-by-plot sample sizes, and regional climate trends. A logarithmic transformation was first applied to deal with the skewed distribution of BAI (LBAI). The fitted GAMM took on the following form:
| [2] |
where i represents the species, j represents the plots, k represents the tree, and t represents the year. Cambial age refers to an estimation of tree age based on the ring counts (age n); we did not adjust age n for missing innermost rings as such error, which concerns a minority of samples, does not cause significant bias in tree-ring chronologies (56). Tree identity () was considered as a random effect. We also included an error term () with an AR1 (p = 1, q = 0) correlation structure, and the residuals of the model (ε). The smooth terms s of the GAMM were represented using cubic regression splines which degree of smoothness was determined through an iterative fitting process (see ref. 54). The growth model was fitted using the mgcv package, version 1.8–4 (57) in R (58). For quantification of past annual growth variability, a back-transformation was applied to estimated LBAI (59):
| [3] |
where is a correction factor of species i computed as follows:
| [4] |
and is the mean-squared error computed as:
| [5] |
where is the number of observations.
Annual growth variability (expressed in percent-difference from the long-term mean) was computed as follows:
| [6] |
The results of these calculations are hereafter referred to as the GAMMNFI growth data.
The ability to detect effects of low-frequency climate variability or rising [CO2] on growth may be limited by the use of detrending techniques that remove long-term growth trends, and by biased sampling of trees that produces spurious trends in growth rates (39, 40). To assess the extent to which the choice of approach for removing age, size, and competition effects might influence our conclusions, we additionally applied a tree level-based statistical procedure, and two uniform ecozone-level procedures to generate three different forms of tree growth indices. Ecozones are areas representative of large and generalized ecological units characterized by interactive and adjusting abiotic and biotic factors (60). The detection of similar trends in all analyses would enhance our confidence that variability is an inherent feature of the tree-ring data. First, a tree-level GNE statistical detrending procedure was used. Here, the ring-width measurement series were rescaled using a power transformation method (61) and detrended using linear (L), negative exponential (NE), or generalized negative exponential (GNE) methods (SI Appendix, part B). The residuals calculated as observed minus fitted estimates are hereafter referred to as the GNE growth data. Note that this GNE approach may remove a greater percentage of low-frequency variance in the LBAI data compared with the GAMM approach. This can limit our ability to track subtle long-term growth trends, particularly when dealing with young trees. Second, for the uniform procedures, we used GAMM models and the RCS technique (56) applied at the scale of ecozones (respectively, GAMMeco and RCS, detailed in SI Appendix, part B). A requirement for the uniform procedures was that at least 20 trees of the same species were available for analysis within an ecozone.
Analysis of Forest Growth Trends.
Species-by-plot GAMMNFI chronologies were computed using robust averaging of the detrended individual tree BAI data, and then spatially averaged to 1° × 1° grids to obtain continuous yearly raster maps of growth covering 1950–2002 (i.e., the period of maximum sample replication). We used ordinary Kriging in ESRI ArcGIS 10.3 with a 5° radius and an exponential model to fit the semivariograms. The Kriging procedure is essentially a weighted average of annual tree growth around the grid to be estimated. Further testing was conducted to confirm that the results of this approach were robust with respect to the inclusion of rare tree species and chronologies with low tree sample replication (SI Appendix, part G). Ordinary least-square regression analyses (using a linear term alone) were conducted for each grid location, and on NDVI data for the periods 1982−2002 (to correspond to the available NDVI time series) and 1950−2002 (for the growth-based maps). Slope estimates from these regressions were then mapped. Furthermore, NDVI data were used for pairwise correlation with gridded growth time series. These procedures were repeated with the GNE, GAMMeco, and RCS data to ensure that our main findings from the GAMMNFI procedure remain valid under alternative treatments of data.
In addition, we examined tree growth variability since the mid-20th century after averaging species-by-plot GAMMNFI chronologies at the level of Canada’s terrestrial ecozones; estimates and their 90% confidence intervals were obtained using bootstrap resampling (61). The procedure was repeated for GNE, GAMMeco, and RCS data. Linear trends for 1950–2002 at the species-by-ecozone level were examined, and direction was interpreted for the level of certainty: “very likely,” if the sign of the trend in GAMMNFI was matched by the three other methods; “likely,” if the sign of the trend in GAMMNFI was matched by two other methods; and “uncertain,” if inconsistency was found between methods; the term “inconclusive” was used when a trend in GAMMNFI was between 0 and ±0.10%⋅y−1.
Analysis of Climate Sensitivity.
Linear mixed models were used to explore the climate effects on species-by-plot averaged residuals of Eq. 2 ()
| [7] |
An error term with an AR1 (P = 1, q = 0) correlation structure was included in the models. Eight explanatory variables (Clim) were tested: mean summer (June to August) soil moisture (in millimeters) and temperature (in degrees Celsius) of the previous year and current year to ring formation, previous fall (September to November) mean temperature, current spring (March to May) mean temperature, cool season (December to May) total snowfall (in millimeters), and mean annual atmospheric CO2 concentrations ([CO2] in parts per million by volume). The period of analysis ranged from 1950 to 2010 depending on the length of the individual records. Multicollinearity among these variables is moderate to low (SI Appendix, part F). Multimodel selection was performed using the MuMIn package (61). In this approach, we ranked all of the potential models that could be generated with the different explanatory variables according to the second-order Akaike information criterion corrected for small sample sizes (AICc). For each model, we considered its Akaike weights (i.e., normalized model likelihoods) for ranking. Among all ranked models, those with cumulative Akaike weights within 95% were considered the best candidate models for multimodel inference. Parameter and error estimates were then computed through averaging of these multiple models (62). We used four different metrics to report the climate sensitivity: the t statistics (i.e., the coefficient divided by its corresponding unconditional SE), the variable relative importance (sum of “Akaike weights” from the selected models), the 95% adjusted confidence intervals for the parameter coefficients of the average model (species-by-plot), and the Pearson correlation between the estimation from the average model and the response variable for each species-by-plot.
Supplementary Material
Acknowledgments
We acknowledge the important contribution of Graham Stinson and the National Forest Inventory program, from which most of the data were obtained. We thank Christine Simard, Julie Fradette, David Gervais, Catherine McNalty, and Thierry Varem-Sanders for valuable contributions to the laboratory work. This work was made possible thanks to the financial and in-kind support provided by the Canadian Forest Service of Natural Resources Canada.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1610156113/-/DCSupplemental.
References
- 1.Pan Y, Birdsey RA, Phillips OL, Jackson RB. The structure, distribution, and biomass of the world’s forests. Annu Rev Ecol Evol Syst. 2013;44:593–622. [Google Scholar]
- 2.Hickling R, Roy D, Hill J, Fox R, Thomas C. The distributions of a wide range of taxonomic groups are expanding polewards. Glob Change Biol. 2006;12:450–455. [Google Scholar]
- 3.Kurz WA, et al. Mountain pine beetle and forest carbon feedback to climate change. Nature. 2008;452(7190):987–990. doi: 10.1038/nature06777. [DOI] [PubMed] [Google Scholar]
- 4.Serreze MC, et al. Observational evidence of recent change in the northern high-latitude environment. Clim Change. 2000;46:159–207. [Google Scholar]
- 5.Esper J, Schweingruber F. Large-scale treeline changes recorded in Siberia. Geophys Res Lett. 2004;31:L06202. [Google Scholar]
- 6.Soja AJ, et al. Climate-induced boreal forest change: Predictions versus current observations. Global Planet Change. 2007;56:274–296. [Google Scholar]
- 7.Wang X, et al. Spring temperature change and its implication in the change of vegetation growth in North America from 1982 to 2006. Proc Natl Acad Sci USA. 2011;108(4):1240–1245. doi: 10.1073/pnas.1014425108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zhang K, et al. Satellite-based model detection of recent climate-driven changes in northern high-latitude vegetation productivity. J Geophys Res. 2008;113:G03033. [Google Scholar]
- 9.Price DT, et al. Anticipating the consequences of climate change for Canada’s boreal forest ecosystems. Environ Rev. 2013;21:322–365. [Google Scholar]
- 10.IPCC . Intergovernmental Panel on Climate Change Fifth Assessment Report: Climate Change (AR5) IPCC; Geneva: 2014. [Google Scholar]
- 11.Kurz W, et al. Carbon in Canada’s boreal forest—a synthesis. Environ Rev. 2013;21:260–292. [Google Scholar]
- 12.Boisvenue C, Running SW. Impacts of climate change on natural forest productivity—evidence since the middle of the 20th century. Glob Change Biol. 2006;12:1–21. [Google Scholar]
- 13.Hember RA, et al. Accelerating regrowth of temperate maritime forests due to environmental change. Glob Change Biol. 2012;18:2026–2040. [Google Scholar]
- 14.Girardin MP, et al. Testing for a CO2 fertilization effect on growth of Canadian boreal forests. J Geophys Res. 2011;116:G01012. [Google Scholar]
- 15.Ma Z, et al. Regional drought-induced reduction in the biomass carbon sink of Canada’s boreal forests. Proc Natl Acad Sci USA. 2012;109(7):2423–2427. doi: 10.1073/pnas.1111576109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Girardin MP, et al. Unusual forest growth decline in boreal North America covaries with the retreat of Arctic sea ice. Glob Change Biol. 2014;20(3):851–866. doi: 10.1111/gcb.12400. [DOI] [PubMed] [Google Scholar]
- 17.Chen HYH, Luo Y. Net aboveground biomass declines of four major forest types with forest ageing and climate change in western Canada’s boreal forests. Glob Change Biol. 2015;21(10):3675–3684. doi: 10.1111/gcb.12994. [DOI] [PubMed] [Google Scholar]
- 18.Hayes D, et al. Is the northern high-latitude land-based CO2 sink weakening? Global Biogeochem Cycles. 2011;25:GB3018. [Google Scholar]
- 19.Pan Y, et al. A large and persistent carbon sink in the world’s forests. Science. 2011;333(6045):988–993. doi: 10.1126/science.1201609. [DOI] [PubMed] [Google Scholar]
- 20.McGuire AD, et al. Sensitivity of the carbon cycle in the arctic to climate change. Ecol Monogr. 2009;79:523–555. [Google Scholar]
- 21.Guay KC, et al. Vegetation productivity patterns at high northern latitudes: A multi-sensor satellite data assessment. Glob Change Biol. 2014;20(10):3147–3158. doi: 10.1111/gcb.12647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Piao S, et al. Evidence for a weakening relationship between interannual temperature variability and northern vegetation activity. Nat Commun. 2014;5:5018. doi: 10.1038/ncomms6018. [DOI] [PubMed] [Google Scholar]
- 23.Beck PSA, et al. Changes in forest productivity across Alaska consistent with biome shift. Ecol Lett. 2011;14(4):373–379. doi: 10.1111/j.1461-0248.2011.01598.x. [DOI] [PubMed] [Google Scholar]
- 24.Gillis MD, Omule AY, Brierley T. Monitoring Canada’s forests: The National Forest Inventory. For Chron. 2005;81:214–221. [Google Scholar]
- 25.Gedalof Z, Berg AA. Tree ring evidence for limited direct CO2 fertilization of forests over the 20th century. Global Biogeochem Cycles. 2010;24:GB3027. [Google Scholar]
- 26.Amthor JS. The McCree–de Wit–Penning de Vries–Thornley respiration paradigms: 30 years later. Ann Bot (Lond) 2000;86:1–20. [Google Scholar]
- 27.McDowell NG, et al. The interdependence of mechanisms underlying climate-driven vegetation mortality. Trends Ecol Evol. 2011;26(10):523–532. doi: 10.1016/j.tree.2011.06.003. [DOI] [PubMed] [Google Scholar]
- 28.Breshears DD, et al. Tree die-off in response to global change-type drought: Mortality insights from a decade of plant water potential measurements. Front Ecol Environ. 2009;7:185–189. [Google Scholar]
- 29.Sevanto S, McDowell NG, Dickman LT, Pangle R, Pockman WT. How do trees die? A test of the hydraulic failure and carbon starvation hypotheses. Plant Cell Environ. 2014;37(1):153–161. doi: 10.1111/pce.12141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Skelton RP, West AG, Dawson TE. Predicting plant vulnerability to drought in biodiverse regions using functional traits. Proc Natl Acad Sci USA. 2015;112(18):5744–5749. doi: 10.1073/pnas.1503376112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Clark JS, et al. The impacts of increasing drought on forest dynamics, structure, and biodiversity in the United States. Glob Change Biol. 2016;22(7):2329–2352. doi: 10.1111/gcb.13160. [DOI] [PubMed] [Google Scholar]
- 32.Hogg EH, Bernier PY. Climate change impacts on drought-prone forests in western Canada. For Chron. 2005;81(5):675–682. [Google Scholar]
- 33.Reich PB, et al. Boreal and temperate trees show strong acclimation of respiration to warming. Nature. 2016;531(7596):633–636. doi: 10.1038/nature17142. [DOI] [PubMed] [Google Scholar]
- 34.Norby RJ, et al. Forest response to elevated CO2 is conserved across a broad range of productivity. Proc Natl Acad Sci USA. 2005;102(50):18052–18056. doi: 10.1073/pnas.0509478102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Norby RJ, Warren JM, Iversen CM, Medlyn BE, McMurtrie RE. CO2 enhancement of forest productivity constrained by limited nitrogen availability. Proc Natl Acad Sci USA. 2010;107(45):19368–19373. doi: 10.1073/pnas.1006463107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bader MFK, et al. Central European hardwood trees in a high‐CO2 future: Synthesis of an 8‐year forest canopy CO2 enrichment project. J Ecol. 2013;101:1509–1519. [Google Scholar]
- 37.Keenan TF, et al. Increase in forest water-use efficiency as atmospheric carbon dioxide concentrations rise. Nature. 2013;499(7458):324–327. doi: 10.1038/nature12291. [DOI] [PubMed] [Google Scholar]
- 38.Frank DC, et al. Water use efficiency and transpiration across European forests during the Anthropocene. Nat Clim Chang. 2015;5:579–583. [Google Scholar]
- 39.Peters RL, Groenendijk P, Vlam M, Zuidema PA. Detecting long-term growth trends using tree rings: A critical evaluation of methods. Glob Change Biol. 2015;21(5):2040–2054. doi: 10.1111/gcb.12826. [DOI] [PubMed] [Google Scholar]
- 40.Brienen RJW, Gloor E, Zuidema PA. Detecting evidence for CO2 fertilization from tree ring studies: The potential role of sampling biases. Global Biogeochem Cycles. 2012;26:GB1025. [Google Scholar]
- 41.Nehrbass-Ahles C, et al. The influence of sampling design on tree-ring-based quantification of forest growth. Glob Change Biol. 2014;20(9):2867–2885. doi: 10.1111/gcb.12599. [DOI] [PubMed] [Google Scholar]
- 42.Bond-Lamberty B, Peckham SD, Ahl DE, Gower ST. Fire as the dominant driver of central Canadian boreal forest carbon balance. Nature. 2007;450(7166):89–92. doi: 10.1038/nature06272. [DOI] [PubMed] [Google Scholar]
- 43.Kurz WA, Stinson G, Rampley G. Could increased boreal forest ecosystem productivity offset carbon losses from increased disturbances? Philos Trans R Soc Lond B Biol Sci. 2008;363(1501):2261–2269. doi: 10.1098/rstb.2007.2198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hogg EH, Brandt JP, Kochtubajda B. Factors affecting interannual variation in growth of western Canadian aspen forests during 1951–2000. Can J Res. 2005;35:610–622. [Google Scholar]
- 45.Pureswaran DS, et al. Climate-induced changes in host tree–insect phenology may drive ecological state-shift in boreal forests. Ecology. 2015;96:1480–1491. [Google Scholar]
- 46.Babst F, Bouriaud O, Alexander R, Trouet V, Frank D. Toward consistent measurements of carbon accumulation: A multi-site assessment of biomass and basal area increment across Europe. Dendrochronologia. 2014;32:153–161. [Google Scholar]
- 47.Pinzon J, Tucker C. A non-stationary 1981–2012 AVHRR NDVI3g time series. Remote Sens. 2014;6:6929–6960. [Google Scholar]
- 48.Beaudoin A, et al. Mapping attributes of Canada’s forests at moderate resolution through kNN imputation and MODIS imagery. Can J Res. 2014;44:521–532. [Google Scholar]
- 49.Environment Canada 2013 National Climate Data and Information Archive. Available at climate.weatheroffice.gc.ca/. Accessed March 15, 2015.
- 50.Régnière J, Bolstad P. Statistical simulation of daily air temperature patterns in eastern North America to forecast seasonal events in insect pest management. Environ Entomol. 1994;23:1368–1380. [Google Scholar]
- 51.Hogg EH, Barr AG, Black TA. A simple soil moisture index for representing multi-year drought impacts on aspen productivity in the western Canadian interior. Agr For Met. 2013;178-179:173–182. [Google Scholar]
- 52.Keeling CD, Bacastow RB, Whorf TP. Measurements of the concentration of carbon dioxide at Mauna Loa Observatory, Hawaii. In: Clarke WC, editor. Carbon Dioxide Review: 1982. Oxford Univ Press; New York: 1982. pp. 377–385. [Google Scholar]
- 53.Etheridge DM, et al. Natural and anthropogenic changes in atmospheric CO2 over the last 1000 years from air in Antarctic ice and fir. J Geophys Res. 1996;101:4115–4128. [Google Scholar]
- 54.Wood SN. Thin plate regression splines. J R Stat Soc B. 2003;65:95–114. [Google Scholar]
- 55.Camarero JJ, Gazol A, Galván JD, Sangüesa-Barreda G, Gutiérrez E. Disparate effects of global-change drivers on mountain conifer forests: Warming-induced growth enhancement in young trees vs. CO2 fertilization in old trees from wet sites. Glob Change Biol. 2015;21(2):738–749. doi: 10.1111/gcb.12787. [DOI] [PubMed] [Google Scholar]
- 56.Esper J, Cook E, Krusic P, Peters K, Schweingruber F. Tests of the RCS method for preserving low-frequency variability in long tree-ring chronologies. Tree-Ring Res. 2003;59:81–98. [Google Scholar]
- 57.Wood SN. Generalized Additive Models: An Introduction with R. Chapman Hall/CRC Press; Boca Raton, FL: 2006. [Google Scholar]
- 58.R Development Core Team . R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna: 2013. [Google Scholar]
- 59.Baskerville GL. Use of logarithmic regression in the estimation of plant biomass. Can J Res. 1972;2:49–53. [Google Scholar]
- 60.Ecological Stratification Working Group . A National Ecological Framework for Canada. Report and National Map at 1:7,500,000 Scale. Ecological Stratification Working Group, Agriculture and Agri-Food Canada and Environment Canada; Ottawa: 1995. [Google Scholar]
- 61.Legendre P, Legendre L. Numerical Ecology. Vol 20 Elsevier; Amsterdam: 2012. [Google Scholar]
- 62.Barton K. 2013 MuMIn: Multi-Model Inference. R Package, Version 1.14.0. Available at https://cran.r-project.org/web/packages/MuMIn/index.html. Accessed January 10, 2015.
- 63.Symonds MRE, Moussalli A. A brief guide to model selection, multimodel inference and model averaging in behavioural ecology using Akaike’s information criterion. Behav Ecol Sociobiol. 2011;65:13–21. [Google Scholar]
- 64.Dutilleul P. Modifying the t test for assessing the correlation between two spatial processes. Biometrics. 1993;49:305–314. [Google Scholar]
- 65.Friedman JH. Multivariate adaptive regression splines. Ann Stat. 1991;19:1–67. doi: 10.1177/096228029500400303. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.