Assembly of long error-prone reads using de Bruijn graphs

Significance

When the long reads generated using single-molecule se-quencing (SMS) technology were made available, most researchers were skeptical about the ability of existing algorithms to generate high-quality assemblies from long error-prone reads. Nevertheless, recent algorithmic breakthroughs resulted in many successful SMS sequencing projects. However, as the recent assemblies of important plant pathogens illustrate, the problem of assembling long error-prone reads is far from being resolved even in the case of relatively short bacterial genomes. We propose an algorithmic approach for assembling long error-prone reads and describe the ABruijn assembler, which results in accurate genome reconstructions.

Abstract

The recent breakthroughs in assembling long error-prone reads were based on the overlap-layout-consensus (OLC) approach and did not utilize the strengths of the alternative de Bruijn graph approach to genome assembly. Moreover, these studies often assume that applications of the de Bruijn graph approach are limited to short and accurate reads and that the OLC approach is the only practical paradigm for assembling long error-prone reads. We show how to generalize de Bruijn graphs for assembling long error-prone reads and describe the ABruijn assembler, which combines the de Bruijn graph and the OLC approaches and results in accurate genome reconstructions.

The key challenge to the success of single-molecule sequencing (SMS) technologies lies in the development of algorithms for assembling genomes from long but inaccurate reads. The pioneer in long reads technologies, Pacific Biosciences, now produces accurate assemblies from long error-prone reads (1, 2). Goodwin et al. (3) and Loman et al. (4) demonstrated that high-quality assemblies can be obtained from even less-accurate Oxford Nanopore reads. Advances in assembly of long error-prone reads recently resulted in the accurate reconstructions of various genomes (5–10). However, as illustrated in Booher et al. (11), the problem of assembling long error-prone reads is far from being resolved even in the case of relatively small bacterial genomes.

Previous studies of SMS assemblies were based on the overlap-layout-consensus (OLC) approach (12) or a similar string graph approach (13), which require an all-against-all comparison of reads (14) and remain computationally challenging (see refs. 15–17 for a discussion of the pros and cons of this approach). Moreover, there is an assumption that the de Bruijn graph approach, which has dominated genome assembly for the last decade, is inapplicable to long reads. This is a misunderstanding, because the de Bruijn graph approach, as well as its variation called the A-Bruijn graph approach, was developed to assemble rather long Sanger reads (18). There is also a misunderstanding that the de Bruijn graph approach can only assemble highly accurate reads and fails when assembling long error-prone reads. Although this is true for the original de Bruijn graph approach to assembly (15, 17), the A-Bruijn graph approach was originally designed to assemble inaccurate reads as long as any similarities between reads can be reliably identified. Moreover, A-Bruijn graphs have proven to be useful even for assembling mass spectra, which represent highly inaccurate fingerprints of amino acid sequences of peptides (19, 20). However, although A-Bruijn graphs have proven to be useful in assembling Sanger reads and mass spectra, the question of how to apply A-Bruijn graphs for assembling long error-prone reads remains open.

de Bruijn graphs are a key algorithmic technique in genome assembly (15, 21–24). In addition, de Bruijn graphs have been used for sequencing by hybridization (25), repeat classification (18), de novo protein sequencing (20), synteny block construction (26), genotyping (27), and Ig classification (28). A-Bruijn graphs are even more general than de Bruijn graphs; for example, they include breakpoint graphs, the workhorse of genome-rearrangement studies (29).

However, as discussed in ref. 30, the original definition of a de Bruijn graph is far from being optimal for the challenges posed by the assembly problem. Below, we describe the concept of an A-Bruijn graph, introduce the ABruijn assembler for long error-prone reads, and demonstrate that it generates accurate genome reconstructions.

The Key Idea of the ABruijn Algorithm

The Challenge of Assembling Long Error-Prone Reads.

Given the high error rates of SMS technologies, accurate assembly of long repeats remains challenging. Also, frequent $k$-mers dramatically increase the number of candidate overlaps, thus, complicating the choice of the correct path in the overlap graph. A common solution is to mask highly repetitive $k$-mers as done in the Celera Assembler (31) and Falcon (32). However, such masking may lead to losing some correct overlaps. Below we illustrate these challenges using the Xanthomonas genomes as an example.

Booher et al. (11) recently sequenced various strains of the plant pathogen Xanthomonas oryzae and revealed the striking plasticity of transcription activator-like (tal) genes, which play a key role in Xanthomonas infections. Each tal gene encodes a TAL protein, which has a large domain formed by nearly identical TAL repeats. Because variations in tal genes and TAL repeats are important for understanding the pathogenicity of various Xanthomonas strains, massive sequencing of these strains is an important task that may enable the development of novel measures for plant disease control (33, 34). However, assembling Xanthomonas genomes using SMS reads (let alone, short reads) remains challenging.

Depending on the strain, Xanthomonas genomes may harbor over 20 tal genes with some tal genes encoding over 30 TAL repeats. Assembling Xanthomonas genomes is further complicated by the aggregation of various types of repeats into complex regions that may extend for over 30 kb in length. These repeats render Xanthomonas genomes nearly impossible to assemble using short reads. Moreover, as Booher et al. (11) described, existing SMS assemblers also fail to assemble Xanthomonas genomes. The challenge of finishing draft genomes assembled from SMS reads extends beyond Xanthomonas genomes (e.g., many genomes sequenced at the Centers for Disease Control are being finished using optical mapping) (35).

Another challenge is using SMS technologies to assemble metagenomics datasets with highly variable coverage across various bacterial genomes. Because the existing assemblers for long error-prone reads generate fragmented assemblies of bacterial communities, there are as yet no publications describing metagenomics applications of SMS technologies. Below we benchmark ABruijn and other state-of-the-art SMS assemblers on Xanthomonas genomes and the Bugula neritina metagenome.

From de Bruijn Graphs to A-Bruijn Graphs.

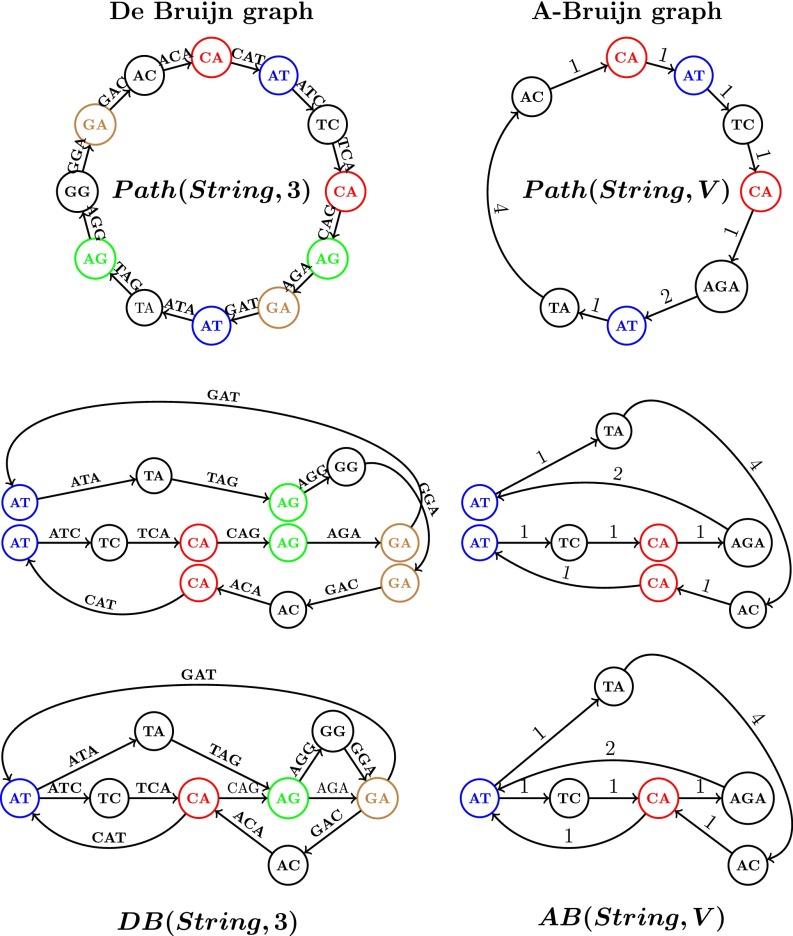
In the A-Bruijn graph framework, the classical de Bruijn graph $DB(String,k)$ of a string $String$ is defined as follows. Let $Path(String,k)$ be a path consisting of $|String|-k+1$ edges, where the $i$-th edge of this path is labeled by the $i$-th $k$-mer in $String$ and the $i$-th vertex of the path is labeled by the $i$-th $(k$-$1)$-mer in $String$. The de Bruijn graph $DB(String,k)$ is formed by gluing together identically labeled vertices in $Path(String,k)$ (Fig. 1). Note that this somewhat unusual definition results in exactly the same de Bruijn graph as the standard definition (see ref. 36 for details).

Fig. 1.

Constructing the de Bruijn graph (Left) and the A-Bruijn graph (Right) for a circular $String$=CATCAGATAGGA. (Left) From $Path(String,3)$ to $DB(String,3)$. (Right) From $Path(String,V)$ to $AB(String,V)$ for $V=\{$CA, AT, TC, AGA, TA, AC$\}$. The figure illustrates the process of bringing the vertices with the same label closer to each other (middle row) to eventually glue them into a single vertex (bottom row). Note that some symbols of $String$ are not covered by strings in $V$. We assign integer $shift(v,w)$ to the edge $(v,w)$ in this path to denote the difference between the positions of $v$ and $w$ in $String$ (i.e., the number of symbols between the start of $v$ and the start of $w$ in $String$).

We now consider an arbitrary substring-free set of strings $V$ (which we refer to as a set of solid strings), where no string in $V$ is a substring of another one in $V$. The set $V$ consists of words (of any length) and the new concept $Path(String,V)$ is defined as a path through all words from $V$ appearing in $String$ (in order) as shown in Fig. 1. Afterward, we glue identically labeled vertices as before to construct the A-Bruijn graph $AB(String,V)$ as shown in Fig. 1. Clearly, $DB(String,k)$ is identical to $AB(String,{\sum }^{k-1})$, where ${\sum }^{k-1}$ stands for the set of all $(k$-$1)$-mers in alphabet $\mathrm{\Sigma }$.

The definition of $AB(String,V)$ generalizes to $AB(Reads,V)$ by constructing a path for each read in the set Reads and further gluing all identically labeled vertices in all paths. Because the draft genome is spelled by a path in $AB(Reads,V)$ (18), it seems that the only thing needed to apply the A-Bruijn graph concept to SMS reads is to select an appropriate set of solid strings $V$, to construct the graph $AB(Reads,V)$, to select an appropriate path in this graph as a draft genome, and to correct errors in the draft genome. Below we show how ABruijn addresses these tasks.

The Challenge of Selecting Solid Strings.

Different approaches to selecting solid strings affect the complexity of the resulting A-Bruijn graph and may either enable further assembly using the A-Bruijn graph or make it impractical. For example, when the set of solid strings $V={\sum }^{k-1}$ consists of all $(k$-$1)$-mers, $AB(Reads,{\sum }^{k-1})$ may be either too tangled (if $k$ is small) or too fragmented (if $k$ is large).

Although this is true for both short accurate reads and long error-prone reads, there is a key difference between these two technologies with respect to their resulting A-Bruijn graphs. In the case of Illumina reads, there exists a range of values $k$ so that one can apply various graph simplification procedures [e.g., bubble and tip removal (18, 23)] to enable further analysis of the resulting graph. However, these graph simplification procedures were developed for the case when the error rate in the reads does not exceed 1% and fail in the case of SMS reads where the error rate exceeds 10%.

An Outline of the ABruijn Algorithm.

We classify a $k$-mer as genomic if it appears in the genome and nongenomic otherwise. Ideally, we would like to select a set of solid strings containing all genomic $k$-mers and no nongenomic $k$-mers.

Although the set of genomic $k$-mers occurring in the set of reads is unknown, we show how to identify a large set of predominantly genomic $k$-mers by selecting sufficiently frequent $k$-mers in reads. However, this is not sufficient for assembly, because some genomic $k$-mers are missing and some nongenomic $k$-mers are present in the constructed set of solid $k$-mers. Moreover, even if we were able to construct a very accurate set of genomic $k$-mers, the de Bruijn graph constructed on this set would be too tangled because typical values of $k$ range from 15 to 25 (otherwise it is difficult to construct a good set of solid $k$-mers). Instead, we construct the A-Bruijn graph on the set of identified solid $k$-mers rather than the de Bruijn graph on all $k$-mers in reads. Although only a small fraction of the $k$-mers in each read are solid (and hence this is a very incomplete representation of reads), overlapping reads typically share many solid $k$-mers (compared with nonoverlapping reads). Therefore, a rough estimate of the overlap between two reads can be obtained by finding the longest common subpath between the two read-paths using a fast dynamic programming algorithm. Hence, the A-Bruijn graph can function as an oracle, from which one can efficiently identify the overlaps of a given read with all other reads by considering all possible overlaps at once. The genome is assembled by repeatedly applying this procedure and borrowing the path extension paradigm from short read assemblers (37–39).

Each assembler should minimize the number of misassemblies and the number of basecalling errors. The described approach minimizes the number of misassemblies but results in an inaccurate draft genome with many basecalling errors. We later describe an error-correction approach, which results in accurate genome reconstructions.

Assembling Long Error-Prone Reads

Selecting Solid Strings for Constructing A-Bruijn Graphs.

We define the frequency of a $k$-mer as the number of times this $k$-mer appears in the reads and argue that frequent $k$-mers (for sufficiently large $k$) are good candidates for the set of solid strings. We define a $(k,t)$-mer as a $k$-mer that appears at least $t$ times in the set of reads.

We classify a $k$-mer as unique (repeated) if it appears once (multiple times) in the genome. Fig. 2 shows the histogram of the number of unique/repeated/nongenomic 15-mers with given frequencies for the ECOLI SMS dataset described in Results, Datasets. As Fig. 2 illustrates, the lion’s share of 15-mers with frequencies above a threshold $t$ are genomic ($t=7$ for the ECOLI dataset). To automatically select the parameter $t$, we compute the number of $k$-mers with frequencies exceeding $t$, and select a maximal $t$ such that this number exceeds the estimated genome length. As Fig. 2 illustrates, this selection results in a small number of nongenomic $k$-mers while capturing most genomic $k$-mers.

Fig. 2.

The histograms of the number of 15-mers with given frequencies for the ECOLI dataset from Escherichia coli. The bars for unique/repeated/nongenomic 15-mers for the E. coli genome are stacked and shown in green/red/blue according to their fractions. ABruijn automatically selects the parameter $t$ and defines solid strings as all 15-mers with frequencies at least $t=7$ for the ECOLI dataset. We found that increasing the automatically selected values of $t$ by 1 results in equally accurate assemblies. There exist 4.1 , 0.1 , and 0.5 million (3.9, 0.1, and 0.3 million) unique, repeated, and nongenomic 15-mers, respectively, for ECOLI at $t=7$ ($t=8$). Although larger values of $k$ (e.g., $k=25$) also produce high-quality SMS assemblies, we found that selecting smaller rather than larger $k$ results in slightly better performance.

Finding the Genomic Path in an A-Bruijn Graph.

After constructing an A-Bruijn graph, one faces the problem of finding a path in this graph that corresponds to traversing the genome and then correcting errors in the sequence spelled by this path (this genomic path does not have to traverse all edges of the graph). Because the long reads are merely paths in the A-Bruijn graph, one can use the path extension paradigm (37–39) to derive the genomic path from these (shorter) read-paths. exSPAnder (38) is a module of the SPAdes assembler (24) that finds a genomic path in the assembly graph constructed from short reads based either on read-pair paths or read-paths, which are derived from SMS reads as in hybridSPAdes (40). Recent studies of bacterial plankton (41), antibiotics resistance (42), and genome rearrangements (43) demonstrated that hybridSPades works well even for coassembly with less-accurate nanopore reads. Below we sketch the hybridSPAdes algorithm (40) and show how to modify the path extension paradigm to arrive at the ABruijn algorithm.

hybridSPAdes.

hybridSPAdes uses SPAdes to construct the de Bruijn graph solely from short accurate reads and transforms it into an assembly graph by removing bubbles and tips (24). It represents long error-prone reads as read-paths in the assembly graph and uses them for repeat resolution.

A set of paths in a directed graph (referred to as $Paths$) is consistent if the set of all edges in $Paths$ forms a single directed path in the graph. We further refer to this path as $ConsensusPath(Paths)$. The intuition for the notion of the consistent (inconsistent) set of paths is that they are sampled from a single segment (multiple segments) of the genomic path in the assembly graph (see ref. 40).

A path $P\prime$ in a weighted graph overlaps with a path $P$ if a sufficiently long suffix of $P$ (of total weight at least $minOverlap$) coincides with a prefix of $P\prime$ and $P$ does not contain the entire path $P\prime$ as a subpath. Given a path $P$ and a set of paths $Paths$, we define $Path{s}_{minOverlap}(P)$ as the set of all paths in $Paths$ that overlap with $P$.

Our sketch of hybridSPAdes omits some details and deviates from the current implementation to make similarities with the A-Bruijn graph approach more apparent (e.g., it assumes that there are no chimeric reads and only shows an algorithm for constructing a single contig).

From hybridSPAdes to longSPAdes.

Using the concept of the A-Bruijn graph, a similar approach can be applied to assembling long reads only. The pseudocode of longSPAdes differs from the pseudocode of hybridSPAdes by only the top three lines shown below:

We note that longSPAdes constructs a path spelling out an error-prone draft genome that requires further error correction. However, error correction of a draft genome is faster than the error correction of individual reads before assembly in the OLC approach (1–4).

Although hybridSPAdes and longSPAdes are similar, longSPAdes is more difficult to implement because bubbles in the A-Bruijn graph of error-prone long reads are more complex than bubbles in the de Bruijn graph of accurate short reads (SI Appendix, section SI1). As a result, the existing graph simplification algorithms fail to work for A-Bruijn graphs made from long error-prone reads. Although it is possible to modify the existing graph simplification procedures for long error-prone reads (to be described elsewhere), this paper focuses on a different approach that does not require graph simplification.

From longSPAdes to ABruijn.

Instead of finding a genomic path in the simplified A-Bruijn graph, ABruijn attempts to find a corresponding genomic path in the original A-Bruijn graph. This approach leads to an algorithmic challenge: Although it is easy to decide whether two reads overlap given an assembly graph, it is not clear how to answer the same question in the context of the A-Bruijn graph. Note that although the ABruijn pseudocode below uses the same terms “overlapping” and “consistent” as longSPAdes, these notions are defined differently in the context of the A-Bruijn graph. The new notions (as well as parameters $jump$ and $maxOverhang$) are described below.

The constructed path in the A-Bruijn graph spells out an error-prone draft genome (or one of the draft contigs). For simplicity, the pseudocode above describes the construction of a single contig and does not cover the error-correction step. In reality, after a contig is constructed, ABruijn maps all reads to this contig and uses the remaining reads to iteratively construct other contigs. Also, ABruijn attempts to extend the path to the “left” if the path extension to the “right” halts.

Common jump-Subpaths.

Given a path $P$ in a weighted directed graph (weights correspond to shifts in the A-Bruijn graph), we refer to the distance $d_P(v,w)$ along path $P$ between vertices $v$ and $w$ in this path (i.e., the sum of the weights of all edges in the path) as the $P$-$distance$. The span of a subpath of a path $P$ is defined as the $P$-distance from the first to the last vertex of this subpath.

Given a parameter $jump$, a $jump$-$subpath$ of $P$ is a subsequence of vertices $v_1\dots v_t$ in $P$ such that $d_P(v_i,v_{i+1})\le jump$ for all $i$ from 1 to $t$−1. We define $Pat{h}_{jump}(P)$ as a $jump$-subpath with the maximum span out of all $jump$-subpaths of a path $P$.

A sequence of vertices in a weighted directed graph is called a common jump-subpath of paths $P_1$ and $P_2$ if it is a $jump$-subpath of both $P_1$ and $P_2$ (Fig. 3). The span of a common $jump$-subpath of $P_1$ and $P_2$ is defined as its span with respect to path $P_1$ (note that this definition is nonsymmetric with respect to $P_1$ and $P_2$). We refer to a common $jump$-subpath of paths $P_1$ and $P_2$ with the maximum span as $Pat{h}_{jump}(P_1,P_2)$ (with ties broken arbitrarily).

Fig. 3.

Two overlapping reads from the ECOLI dataset and their common $jump$-subpath with maximum span that contains 50 vertices and has span 6,714 with respect to the bottom read (for $jump$ =1,000). The left and right overhangs for these reads are 425 and 434. The weights of the edges in the A-Bruijn graph are shown only if they exceed 400 bp.

Below we describe how the ABruijn assembler uses the notion of common $jump$-subpaths with maximum span to detect overlapping reads.

Finding a Common jump-Subpath with Maximum Span.

For the sake of simplicity, below we limit our attention to the case when paths $P_1$ and $P_2$ traverse each of their shared vertices exactly once.

A vertex $w$ is a $jump$-predecessor of a vertex $v$ in a path $P$ if $P$ traverses $w$ before traversing $v$ and $d_P(w,v)\le jump$.

We define $P(v)$ as the subpath of $P$ from its first vertex to $v$. Given a vertex $v$ shared between paths $P_1$ and $P_2$, we define $spa{n}_{jump}(v)$ as the largest span among all common $jump$-subpaths of paths $P_1(v)$ and $P_2(v)$ ending in $v$. The dynamic programming algorithm for finding a common $jump$-subpath with the maximum span is based on the following recurrence:

$$spa{n}_{jump}(v)=\underset{\text{all}\hspace{0.17em}\mathit{jump-}\text{predecessors}\hspace{0.17em}w\hspace{0.17em}\text{of}\hspace{0.17em}v\hspace{0.17em}\text{in}\hspace{0.17em}{P}_1\hspace{0.17em}\text{and}\hspace{0.17em}{P}_2}{\max }\{spa{n}_{jump}(w)+d_{P_1}(w,v)\}$$

Given all paths sharing vertices with a path $P$, common $jump$-subpaths with maximum span with $P$ for all of them can be computed using a single scan of $P$. See SI Appendix, section SI1 for a fast heuristic for finding a common jump-subpath with maximum span.

Overlapping Paths in A-Bruijn Graphs.

We define the right overhang between paths $P_1$ and $P_2$ as the minimum of the distances from the last vertex in $Pat{h}_{jump}(P_1,P_2)$ to the ends of $P_1$ and $P_2$. Similarly, the left overhang between paths $P_1$ and $P_2$ is the minimum of the distances from the starts of $P_1$ and $P_2$ to the first vertex in $Pat{h}_{jump}(P_1,P_2)$.

Given parameters $jump$, $minOverlap$ and $maxOverhang$, we say that paths $P_1$ and $P_2$ overlap if they share a common $jump$-subpath of span at least $minOverlap$ and their right and left overhangs do not exceed $maxOverhang$. To decide whether two reads have arisen from two overlapping regions in the genome, ABruijn checks whether their corresponding read-paths $P_1$ and $P_2$ overlap (with respect to parameters $jump$, $minOverlap$, and $maxOverhang$). Given overlapping paths $P_1$ and $P_2$, we say that $P_1$ is supported by $P_2$ if the $P_1$-distance from the last vertex in $Pat{h}_{jump}(P_1,P_2)$ to the end of $P_1$ is smaller than the $P_2$-distance from the last vertex in $Pat{h}_{jump}(P_1,P_2)$ to the end of $P_2$. SI Appendix, section SI2 describes the range of parameters that work well for genome assembly.

Additional Complications with the Implementation of the Path Extension Paradigm.

Although it seems that the notion of overlapping paths allows us to implement the path extension paradigm for A-Bruijn graphs, there are two complications. First, the path extension algorithm becomes more complex when the growing path ends in a long repeat (39). Second, chimeric reads may end up in the set of overlapping read-paths extending the growing path in the ABruijn algorithm. Also, a set of extension candidates may include a small fraction of spurious reads from other regions of the genome (see SI Appendix, section SI2 for statistics on spurious overlaps). Below we describe how ABruijn addresses these complications.

Most-Consistent Paths.

Given a path $P$ in a set of paths $Paths$, we define $rightSuppor{t}_{Paths}(P)$ as the number of paths in $Paths$ that support $P$. $leftSuppor{t}_{Paths}(P)$ is defined as the number of paths in $Paths$ that are supported by $P$. We also define $Suppor{t}_{Paths}(P)$ as the minimum of $rightSuppor{t}_{Paths}(P)$ and $leftSuppor{t}_{Paths}(P)$. A path $P$ is most-consistent if it maximizes $Suppor{t}_{Paths}(P)$ among all paths in $Paths$ (Fig. 4, Top).

Fig. 4.

(Top) A growing path (shown in green) and a set of five paths $Paths$ above it (extending this path). The gray path with $Suppor{t}_{Paths}(P)=2$ is the most-consistent path in the set $Paths$. (Middle) A growing path (shown in green) ending in a repeat (represented by the internal edge in the graph), and eight read-paths that extend this growing path (five correct extensions shown in blue and three incorrect extensions shown in red. (Bottom) A support graph for the above eight read-paths. Note that the blue read-path 1 is connected by edges with all red read-paths because it is supported by all red paths even though these paths do not contain any short suffix of read-path 1 (the ABruijn graph framework is less sensitive than the de Bruijn graph framework with respect to overlap detection).

Given a set of paths $Paths$ overlapping with $ReadPath$, ABruijn selects a most-consistent path for extending $ReadPath$. Our rationale for selecting a most-consistent path is based on the observation that chimeric and spurious reads usually have either limited support or themselves support few other reads from the set $Paths$. For example, a chimeric read in $Paths$ with a spurious suffix may support many reads in $Paths$ but is unlikely to be supported by any reads in $Paths$. SI Appendix, section SI1 describes how ABruijn detects chimeric reads.

Support Graphs.

When exSPAnder extends the growing path, it takes into account the local repeat structure of the de Bruijn graph, resulting in a rather complex decision rule in the case when the growing path contains a repeat (38, 39). Fig. 4, Middle shows a fragment of the de Bruijn graph with a repeat of multiplicity 2 (internal edge), a growing path ending in this repeat (shown in green), and eight read-paths that extend this growing path. exSPAnder analyzes the subgraph of the de Bruijn graph traversed by the growing path, ignores paths starting in the edges corresponding to repeats, and selects the remaining paths as candidates for an extension (reads 1, 2, and 3 in Fig. 4, Middle). Below we show how to detect that a growing path ends in a repeat in the absence of the de Bruijn graph and how to analyze read-paths ending/starting in a repeat in the A-Bruijn graph framework.

Fig. 4, Bottom shows a support graph with eight vertices (each vertex corresponds to a read-path in Fig. 4, Middle. There is an edge from a vertex $v$ to a vertex $w$ in this graph if read $v$ is supported by read $w$. The vertex of this graph with maximal indegree corresponds to the rightmost blue read-path (read 8) and reveals four other blue read-paths as its predecessors, that is, vertices connected to the vertex 8 (cluster of blue vertices in Fig. 4, Bottom). The remaining three vertices in the graph represent incorrect extensions of the growing path and reveal that this growing path ends in a repeat (cluster of red vertices in Fig. 4, Bottom). This toy example illustrates that decomposing the vertices of the support graph into clusters helps to answer the question of whether the growing path ends in a repeat (multiple clusters) or not (single cluster).

Although exSPAnder and ABruijn face a similar challenge while analyzing repeats, the A-Bruijn graph, in contrast to the de Bruijn graph, does not reveal local repeat structure. However, it allows one to detect reads ending in long repeats using an approach that is similar to the approach illustrated in Fig. 4. Below we show how to detect such reads and how to incorporate their analysis in the decision rule of ABruijn.

Identifying Reads Ending/Starting in a Repeat.

Given a set of reads $Reads$ supporting a given read, we construct a support graph $G(Reads)$ on $|Reads|$ vertices. We further construct the transitive closure of this graph, denoted $G^{\ast }(Reads)$, using the Floyd–Warshall algorithm. Fig. 5 presents the graph $G(Reads)$ for a read that does not end in a long repeat and for another read that ends in a long repeat.

Fig. 5.

(Left) Support graph $G(Reads)$ for a read in the BLS dataset (Results, Datasets) that does not end in a long repeat. Reads in the BLS dataset are numbered in order of their appearance along the genome. The green vertex represents a chimeric read. The blue vertex has maximum degree in $G^{\ast }(Reads)$ and reveals a single cluster consisting of all vertices but the green one. A vertex 281 with large indegree (5) and large outdegree (3) in $G^{\ast }(Reads)$ is a most-consistent read-path, and it is selected for path extension (unless it ends in a repeat). (Right) Support graph $G^{\ast }(Reads)$ for a read in the BLS dataset that ends in a long repeat. The green vertex represents a chimeric read. The blue vertex has maximum degree in $G^{\ast }(Reads)$ and reveals a cluster consisting of nine blue vertices. The vertex 4901 with large indegree (4) and large outdegree (4) in $G^{\ast }(Reads)$ is a most-consistent read-path, and it is selected for path extension if it does not start in a repeat. The red vertex reveals another cluster consisting of five red vertices. Generally, we expect that a read ending in a long repeat of multiplicity $m$ will result in $m$ clusters because reads originating different instances of this repeat are not expected to support each other and, thus, are not connected by edges in $G^{\ast }(Reads)$.

ABruijn partitions the set of vertices in the graph $G^{\ast }(Reads)$ into nonoverlapping clusters as follows. It selects a vertex $v$ with maximum indegree in $G^{\ast }(Reads)$ and, if this indegree exceeds a threshold (the default value is 1), removes this vertex along with all its predecessors from the graph. We refer to the set of removed vertices as a cluster of reads and iteratively repeat this procedure on the remaining subgraph until no vertex in the graph has indegree exceeding the threshold. Fig. 5 illustrates that this decomposition results in a single cluster for a read that does not end in a repeat and in two clusters for a read that ends in a repeat.

We classify a read as a read ending in a repeat if the number of clusters in $G^{\ast }(Reads)$ exceeds 1 (the notion of a read starting from a repeat is defined similarly). A set of reads is called inconsistent if all reads in this set either end or start in a repeat, and consistent otherwise. ABruijn detects all reads ending and starting in a repeat before the start of the path extension algorithm; 3.2 and 6.4% of all reads in ECOLI and BLS datasets, respectively, end in repeats.

The Path Extension Paradigm and Repeats.

ABruijn attempts to exclude reads ending in repeats while selecting a read that extends the growing path. Because this is not always possible, below we describe two cases: The growing path does not end in a repeat and the growing path ends in a repeat.

If the growing path does not end in a repeat, our goal is to exclude chimeric and spurious reads during the path extension process. ABruijn, thus, selects a read from $Reads$ that (i) does not end in a repeat and (ii) supports many reads and is supported by many reads. Condition ii translates into selecting a vertex whose indegree and outdegree are both large (i.e., a most-consistent path). In the case that all reads in $Reads$ end in a repeat, ABruijn selects a read that satisfies the condition ii but ends in a repeat.

If the growing path ends in a repeat, ABruijn uses a strategy similar to exSPAnder to avoid reads that start in a repeat as extension candidates (e.g., all reads in Fig. 4, Middle except for reads 1, 2, and 3). It thus selects a read from $Reads$ that (i) does not start in a repeat and (ii) supports many reads and is supported by many reads. To satisfy condition ii, ABruijn selects a most-consistent read among all reads in $Reads$ that do not start in a repeat. If there are no such reads, ABruijn halts the path extension procedure.

Correcting Errors in the Draft Genome

Matching Reads Against the Draft Genome.

ABruijn uses BLASR (44) to align all reads against the draft genome. It further combines pairwise alignments of all reads into a multiple alignment. Because this alignment against the error-prone draft genome is rather inaccurate, we need to modify it into a different alignment that we will use for error correction.

Our goal now is to partition the multiple alignment of reads to the entire draft genome into thousands of short segments (mini-alignments) and to error-correct each segment into the consensus string of the mini-alignment. The motivation for constructing mini-alignments is to enable accurate error-correction methods that are fast when applied to short segments of reads but become too slow in the case of long segments.

The task of constructing mini-alignments is not as simple as it may appear. For example, breaking the multiple alignment into segments of fixed size will result in inaccurate consensus sequences because a region in a read aligned to a particular segment of the draft genome has not necessarily arisen from this segment [e.g., it may have arisen from a neighboring segment or from a different instance of a repeat (misaligned segments)]. Because many segments in BLASR alignments are misaligned, the accuracy of our error-correction approach (that is designed for well-aligned reads) may deteriorate.

We, thus, search for a good partition of the draft genome that satisfies the following criteria: (i) Most segments in the partition are short, so that the algorithm for their error-correction is fast, and (ii) with high probability, the region of each read aligned to a given segment in the partition represents an error-prone version of this segment. Below we show how to construct a good partition by building an A-Bruijn graph.

Defining Solid Regions in the Draft Genome.

We refer to a position (column) of the alignment with the space symbol “-” in the reference sequence as a nonreference position (column) and to all other positions as a reference position (column). We refer to the column in the multiple alignment containing the $i$-th position in a given region of the reference genome as the $i$-th column. The total number of reads covering a position $i$ in the alignment is referred to as $Cov(i)$.

A nonspace symbol in a reference column of the alignment is classified as a match (or a substitution) if it matches (or does not match, respectively) the reference symbol in this column. A space symbol in a reference column of the alignment is classified as a deletion. We refer to the number of matches, substitutions, and deletions in the $i$-th column of the alignment as $Match(i)$, $Sub(i)$, and $Del(i)$, respectively. We refer to a nonspace symbol in a nonreference column as an insertion and denote $Ins(i)$ as the number of nucleotides in the nonreference columns flanked between the reference columns $i$ and $i+1$ (Fig. 6).

Fig. 6.

(Top Left) The pairwise alignments between a reference region $ref$ in the draft genome and five reads $Reads=\{rea{d}_1,rea{d}_2,rea{d}_3,rea{d}_4,rea{d}_5\}$. All inserted symbols in these reads with respect to the region $ref$ are colored in blue. (Bottom Left) The multiple alignment $Alignment$ constructed from the above pairwise alignments along with the values of $Cov(i)$, $Match(i)$, $Del(i)$, $Sub(i)$ and $Ins(i)$. The last row shows the set $V$ of $(0.8,0.2)$-solid 4-mers. The nonreference columns in the alignment are not numbered. (Right) Constructing $\overline{AB}(Alignment)$, that is, combining all paths $Path(rea{d}_j,V)$ into $\overline{AB}(Alignment)$. Note that the 4-mer ATGA corresponds to two different nodes with labels 1 and 13. The three boundaries of the mini-alignments are between positions 2 and 3, 7 and 8, and 14 and 15. The two resulting necklaces are formed by segments $\{GAATCA,GATTCA,GAAACA,GAAACA,GAGGTA\}$ and $\{GTCAT,GTTCA,TCCTCGAT,GTATTACAT,GTCTTAAT\}$.

For each reference position $i$, $Cov(i)=Match(i)+Sub(i)+Del(i)$. We define the match, substitution, and insertion rates at position $i$ as $Match(i)/Cov(i)$, $Sub(i)/Cov(i)$, $Del(i)/Cov(i)$, and $Ins(i)/Cov(i)$, respectively. Given an $l$-mer in a draft genome, we define its local match rate as the minimum match rate among the positions within this $l$-mer. We further define its local insertion rate as the maximum insertion rate among the positions within this $l$-mer.

An $l$-mer in the draft genome is called $(\alpha ,\beta )$-$solid$ if its local match rate exceeds $\alpha$ and its local insertion rate does not exceed $\beta$. When $\alpha$ is large and $\beta$ is small, $(\alpha ,\beta )$-solid $l$-mers typically represent the correct $l$-mers from the genome. The last row in Fig. 6, Bottom Left shows all of the (0.8, 0.2)-solid 4-mers in the draft genome. SI Appendix, section SI3 describes how to use the draft genome to construct mini-alignments, demonstrates that (0.8, 0.2)-solid $l$-mers in the draft genome are extremely accurate, and describes the choice of parameters $\alpha$ and $\beta$ that work well for assembly.

The contiguous sequence of $(\alpha ,\beta )$-solid $l$-mers forms a solid region. There are 139,585 solid regions in the draft assembly of the ECOLI dataset (for $l$ =10). Our goal now is to select a position within each solid region (referred to as a landmark) and to form mini-alignments from the segments of reads spanning the intervals between two consecutive landmarks.

Breaking the Multiple Alignment into Mini-Alignments.

Because $(\alpha ,\beta )$-$solid$ $l$-mers are very accurate (for appropriate choices of $\alpha$, $\beta$ and $l$), we use them to construct yet another A-Bruijn graph with much simpler bubbles. Because analyzing errors in homonucleotide runs is a difficult problem (2), we select landmarks outside homonucleotide runs as described in SI Appendix, section SI3. ABruijn analyzes each mini-alignment and error-corrects each segment between consecutive landmarks (the average length of these segments is only $\approx$30 nucleotides).

Constructing the A-Bruijn Graph on Solid Regions in the Draft Genome.

We refer to the multiple alignment of all reads against the draft genome as $Alignment$. We label each landmark by its landmark position in $Alignment$ and break each read into a sequence of segments aligned between consecutive landmarks. We further represent each read as a directed path through the vertices corresponding to the landmarks that it spans over. To construct the A-Bruijn graph $\overline{AB}(Alignment)$, we glue all identically labeled vertices in the set of paths resulting from the reads (Fig. 6, Right).

Labeling vertices by their positions in the draft genome (rather than the sequences of landmarks) distinguishes identical landmarks from different regions of the genome and prevents excessive gluing of vertices in the A-Bruijn graph $\overline{AB}(Alignment)$. We note that whereas the A-Bruijn graph constructed from reads is very complex, the A-Bruijn graph $\overline{AB}(Alignment)$ constructed from reads aligned to the draft genome is rather simple. Although there are many bubbles in this graph, each bubble is simple, making the error correction step fast and accurate.

The edges between two consecutive landmarks (two vertices in the A-Bruijn graph) form a necklace consisting of segments from different reads that align to the region flanked by these landmarks (Fig. 6, Right shows two necklaces). Below we describe how ABruijn constructs a consensus for each necklace (called the necklace consensus) and transforms the inaccurate draft genome for the ECOLI dataset into a polished genome to reduce the error rate to 0.0004% for the ECOLI dataset (only 19 putative errors for the entire genome).

A Probabilistic Model for Necklace Polishing.

Each necklace contains read-segments $Segments=\{se{g}_1,se{g}_2,$ $\dots ,se{g}_m\}$ and our goal is to find a consensus sequence $Consensus$ maximizing $Pr(Segments|Consensus)={\prod }_{i=1}^{m}Pr(se{g}_i|Consensus)$, where $Pr(se{g}_i|Consensus)$ is the probability of generating a segment $se{g}_i$ from a consensus sequence $Consensus$. Given an alignment between a segment $se{g}_i$ and a consensus $Consensus$, we define $Pr(se{g}_i|Consensus)$ as the product of all match, mismatch, insertion, and deletion rates for all positions in this alignment.

The match, mismatch, insertion, and deletion rates should be derived using an alignment of any set of reads to any reference genome. SI Appendix, section SI4 illustrates that the statistical parameters for the P6-C4 Pacific Bioscience datasets are nearly identical to the parameters of the older P5-C3 protocol.

ABruijn selects a segment of median length from each necklace and iteratively checks whether the consensus sequence for each necklace can be improved by introducing a single mutation in the selected segment. If there exists a mutation that increases $Pr(Segments|Consensus)$, we select the mutation that results in the maximum increase and iterate until convergence. We further output the final sequence as the error-corrected sequence of the necklace. As described in ref. 2, this greedy strategy can be implemented efficiently because a mutation maximizing $Pr(Segments|Consensus)$ among all possible mutated sequences can be found in a single run of the forward–backward dynamic programming algorithm for each sequence in $Segments$. The error rate after this step drops to 0.003% for the ECOLI dataset.

Error-Correcting Homonucleotide Runs.

The probabilistic approach described above works well for most necklaces but its performance deteriorates when it faces the difficult problem of estimating the lengths of homonucleotide runs, which account for 46% of the E. coli genome (see discussion on pulse merging in ref. 2). We, thus, complement this approach with a homonucleotide likelihood function based on the statistics of homonucleotide runs. In contrast to previous approaches to error-correction of long error-prone reads, this new likelihood function incorporates all corrupted versions of all homonucleotide runs across the training set of reads and reduces the error rate sevenfold (from 0.003 to 0.0004% for the ECOLI dataset) compared with the standard likelihood approach.

To generate the statistics of homonucleotide runs, we need an arbitrary set of reads aligned against a training reference genome. For each homonucleotide run in the genome and each read spanning this run, we represent the aligned segment of this read simply as the set of its nucleotide counts. For example, if a run AAAAAAA in the genome is aligned against AATTACA in a read, we represent this read-segment as 4A3X, where X stands for any nucleotide differing from A. After collecting this information for all runs of AAAAAAA in the reference genome, we obtain the statistics for all read segments covering all instances of the homonucleotide run AAAAAAA (SI Appendix, section SI4). We further use the frequencies in this table for computing the likelihood function as the product of these frequencies for all reads in each necklace (frequencies below a threshold 0.001 are ignored). It turned out that the frequencies in the resulting table hardly change when one changes the dataset of reads, the reference genome, or even the sequencing protocol from P6-C4 to the older P5-C3. To decide on the length of a homonucleotide run, we simply select the length of the run that maximizes the likelihood function. For example, using the frequencies from SI Appendix, Table S2, if $Segments=\{5A,6A,6A,7A,6A1C\}$, $Pr(Segments|6A)$ = $0.156\times {0.439}^2\times 0.115\times 0.074$ $>$ $Pr(Segments|7A)$ = $0.049\times {0.156}^2\times 0.385\times 0.045$ and we select AAAAAA over AAAAAAA as the necklace consensus.

Although the described error-correcting approach results in a very low error rate even after a single iteration, ABruijn realigns all reads and error-corrects the prepolished genome in an iterative fashion (three iterations by default).

Results

Because CANU (1) improved on PBcR (45) with respect to both speed and accuracy, we limited our benchmarking to ABruijn and CANU v1.2 using the following datasets.

Datasets.

The E. coli K12 dataset (46) (referred to as ECOLI) contains 10,277 reads with $\approx$55$\times$ coverage generated using the P6-C4 Pacific Biosciences technology.

The E. coli K12 Oxford Nanopore dataset (4) (referred to as ECOLI_nano) contains 22,270 reads with $\approx$29$\times$ coverage.

The BLS and PXO datasets were derived from X. oryzae strains BLS256 and PXO99A previously assembled using Sanger reads (47, 48) and reassembled using Pacific Biosciences P6-C4 reads in Booher et al. (11). The BLS dataset contains 89,634 reads ($\approx$234$\times$ coverage), and the PXO dataset contains 55,808 reads ($\approx$141$\times$ coverage). The assembly of BLS and PXO datasets is particularly challenging because these genomes have a large number of tal genes.

The B. neritina dataset (referred as BNE) contains 1,127,494 reads (estimated coverage $\approx$25$\times$) generated using the P6-C4 Pacific Biosciences technology. B. neritina is a microscopic marine eukaryote that forms colonies attached to the wetted surfaces and forms symbiotic communities with various bacteria. B. neritina is the source of bryostatin, an anticancer and memory-enhancing compound (49). B. neritina is also a model organism for biofouling, studies of accumulation of various organisms on wetted surfaces that present a risk to underwater construction.

The symbiotic bacteria live inside of B. neritina making it impossible to isolate the B. neritina DNA from the bacterial DNA for genome sequencing. As the result, despite the importance of B. neritina, all attempts to sequence it so far have failed (50). The total genome size of the symbiotic bacteria in B. neritina is significantly larger than the estimated size of the B. neritina genome (135 Mb). Thus, sequencing B. neritina presents a complex metagenomics challenge.

We have also assembled the S. cerevisiae W303 genome (SI Appendix, section SI5).

The Challenge of Benchmarking SMS Assemblies.

High-quality short-read bacterial assemblies typically have error-rates on the order of ${10}^{-5}$, which typically result in 50 to 100 errors per assembled genome (51). Because assemblies of high-coverage SMS datasets are often even more accurate than assemblies of short reads, short-read assemblies do not represent a gold standard for estimating the accuracy of SMS assemblies. Moreover, the E. coli K12 strain used for SMS sequencing of the ECOLI dataset differs from the reference genome. Thus, the standard benchmarking approach based on comparison with the reference genome (52) is not applicable to these assemblies.

We used the following approach to benchmark ABruijn and CANU against the reference E. coli K12 genome. There are 2,892 and 2,887 positions in E. coli K12 genome where the reference sequence differs from ABruijn and CANU+Quiver, respectively. However, ABruijn and CANU+Quiver agree on 2,873 of them, suggesting that most of these positions represent mutations in E. coli K12 compared with the reference genome. Both CANU+Quiver and ABruijn suggest that the ECOLI dataset was derived from a strain that differs from the reference E. coli K12 genome by a 1,798-bp inversion, two insertions (776 and 180 bp), one deletion (112 bp), and seven other single positions. We, thus, revised the E. coli K12 genome to account for these variations and classified a position as an ABruijn error if the CANU+Quiver sequence at this position agreed with the revised reference but not with the ABruijn sequence (CANU errors are defined analogously).

Assembling the ECOLI Dataset.

ABruijn and CANU assembled the ECOLI dataset into a single circular contig structurally concordant with the E. coli genome. We further estimated the accuracy of ABruijn and CANU in projects with lower coverage by down-sampling the reads from ECOLI. For each value of coverage, we made five independent replicas and analyzed errors in all of them.

In contrast to ABruijn, CANU does not explicitly circularize the reconstructed bacterial chromosomes but instead outputs each linear contig with an identical (or nearly identical) prefix and suffix. We used these suffixes and prefixes to circularize bacterial chromosomes and did not count differences between some of them as potential CANU errors. However, for some replicas with coverage 40$\times$, 35$\times$, 30$\times$, and 25$\times$, CANU missed short 2-kb to 7-kb fragments of the genome (possibly due to low coverage in some regions), thus, preventing us from circularization. To enable benchmarking, we did not count these missing regions as CANU errors. Also, at coverage 30$\times$, CANU (i) failed to assemble the ECOLI dataset into a single contig for one out of five replicas and (ii) correctly assembled bacterial chromosome for another replica but also generated a false contig (probably formed by chimeric reads). In contrast, ABruijn correctly assembled all replicas for all values of coverage.

Table 1 illustrates that, in contrast to ABruijn, CANU generates rather inaccurate assemblies without Quiver, a tool that uses raw machine-level HDF5 signals for polishing: 637 errors (160 insertions and 477 deletions) and 19 errors (12 insertions and 7 deletions) for CANU and ABruijn, respectively. However, after applying Quiver, the number of errors reduces to 14 (1 insertion and 13 deletions) and 15 (2 insertions and 13 deletions) for CANU and ABruijn, respectively. SI Appendix, section SI6 describes how to further reduce the error rates by $\approx 20\%$. ABruijn assembled the ECOLI dataset in $\approx$8 min and polished it in $\approx$36 min (the memory footprint was 2 Gb). ABruijn and CANU have similar running times: 2,599 s and 2,488 s, respectively (4,873 s and 4,803 s for ABruijn+Quiver and CANU+Quiver, respectively).

Table 1.

Summary of errors for CANU and ABruijn assemblies of the ECOLI, BLS, and PXO datasets as well as for the downsampled ECOLI datasets with coverage varying from 50$\times$ to 25$\times$

Coverage	CANU	ABruijn	CANU+ Quiver	ABruijn+ Quiver
BLS	73	5	51	31
PXO	1,162	21	130	15
ECOLI	637	19	14	15
ECOLI 50$\times$	703	33	20	18
ECOLI 45$\times$	829	45	29	29
ECOLI 40$\times$	1,158	84	45	45
ECOLI 35$\times$	1,541	153	88	84
ECOLI 30$\times$	2,470	291	175	154
ECOLI 25$\times$	3,053	687	322	329

To offset CANU assembly errors in the case of 30× coverage, we provided the average number of errors for four replicas with best results (out of five).

To enable a fair benchmarking and to offset the artifacts of CANU assemblies at 30$\times$ coverage, we collected statistics of errors for four out of five best assemblies for each value of coverage. Table 1 illustrates that both ABruijn and CANU maintain accuracy even in relatively low coverage projects but CANU assemblies become fragmented and may miss short segments when the coverage is low. SI Appendix, section SI7 illustrates that the lion’s share of ABruijn errors occur in the low-coverage regions.

Assembling the ECOLI_nano Dataset.

Both the Nanocorrect assembler described in Loman et al. (53) and ABruijn assembled the ECOLI_nano dataset into a single circular contig structurally concordant with the E. coli K12 genome with error rates 1.5 and 1.1%, respectively (2,475 substitutions, 9,238 insertions, and 40,399 deletions for ABruijn). We note that, in contrast to the more accurate Pacific Biosciences technology, Oxford Nanopore technology currently has to be complemented by hybrid coassembly with short reads to generate finished genomes (40–43).

Although further reduction in the error rate in Oxford Nanopore assemblies can be achieved by machine-level processing of the signal resulting from DNA translocation (4), it is still two orders of magnitude higher that the error rate for the down-sampled ECOLI dataset with similar 30$\times$ coverage by Pacific Biosciences reads (Table 1) and below the acceptable standards for finished genomes. Because Oxford Nanopore technology is rapidly progressing, we decided not to optimize it further using signal processing of raw translocation signals.

Assembling Xanthomonas Genomes.

Because HGAP 2.0 failed to assemble the BLS dataset, Booher et al. (11) developed a special PBS algorithm for local tal gene assembly to address this deficiency in HGAP. They further proposed a workflow that first launches PBS and uses the resulting local tal gene assemblies as seeds for a further HGAP assembly with custom adjustment of parameters in HGAP/Celera workflows. Although HGAP 3.0 resulted in an improved assembly of the BLS dataset, Booher et al. (11) commented that the PBS algorithm is still required for assembling other Xanthomonas genomes. Because PBS represents a customized assembler for tal genes that is not designed to work with other types of complex repeats, development of a general SMS assembly tool that accurately reconstructs repeats remains an open problem.

We launched ABruijn with the automatically selected parameters $t$ = 28 and $t$ = 18 for the BLS and PXO datasets, respectively (all other parameters were the same default parameters that we used for the ECOLI dataset). ABruijn assembled the BLS dataset into a circular contig structurally concordant with the BLS reference genome. It also assembled the PXO dataset into a circular contig structurally concordant with the PXO reference genome but, similarly to the initial assembly in Booher et al. (11), it collapsed a 212-kb tandem repeat.

CANU assembled the BLS dataset into a circular contig structurally concordant with the BLS reference genome but assembled the PXO dataset into two contigs, a long contig similar to the reference genome (with a collapsed 212-kb tandem repeat and three large indels of total length over 1,500 nucleotides) and a short contig. In summary, ABruijn+Quiver and CANU+Quiver assemblies of the BLS dataset resulted in only 31 and 51 errors, respectively. Surprisingly, ABruijn without Quiver resulted in a better assembly than ABruijn+Quiver with only five errors.

To evaluate errors for the PXO dataset, we decided to ignore the short contig generated by CANU and a collapsed 212-kb repeat (generated by both CANU and ABruijn). ABruijn+Quiver assembly of the PXO dataset resulted in only 15 errors whereas CANU+Quiver assembly resulted in 130 errors, including one insertion of 100 nucleotides.

Assembling the B. neritina Metagenome.

We have assembled the B. neritina metagenome and further analyzed all long contigs at least 50 kb in size (1,319 and 1,108 long contigs for CANU and ABruijn, respectively). We ignored shorter contigs because they are often formed by a few reads or even a single read. The total length of long contigs was 171 Mb for CANU and 202 Mb for ABruijn. SI Appendix, section SI8 shows the histogram of the total length of contigs with a given coverage. Because the spread of the distribution of coverage for B. neritina significantly exceeds the spread we observed in other SMS datasets (typically within 15% of the average coverage), we attribute most bins with coverage below 20$\times$ to contigs from symbiotic bacteria (the tallest peak in the histogram suggests that the average coverage of B. neritina is 25$\times$). Running AntiSmash (54) on the ABruijn assembly revealed nine bacterial biosynthetic gene clusters encoding natural products that, similarly to bryostatin, may represent new bioactive compounds.

We attribute the large difference in the total contig length to fragmentation in CANU assemblies in the case of low-coverage datasets, which we observed in our analysis of the downsampled ECOLI datasets. This fragmentation may have also contributed to differences in the N50 (98 kb vs. 242 kb) between CANU and ABruijn.

However, differences in N50 are poor indicators of assembly quality in the case when the reference genome is unknown. We, thus, conducted an additional analysis using the Core Eukaryotic Genes Mapping Approach (CEGMA) that was used in hundreds of previous studies for evaluating the completeness of eukaryotic assemblies (55). CEGMA evaluates an assembly by checking whether its contigs encode all 248 ultraconserved eukaryotic core protein families. CANU and ABruijn assemblies missed 18 and 11 out of 248 core genes, respectively (7.3% vs. 4.4%). Thus, although both CANU and ABruijn generated better assemblies than typical eukaryotic short read assemblers (that often miss over 20% of core genes), the ABruijn assembly improved on the CANU assembly in this respect.

See SI Appendix, section SI9 for running time and memory footprints of various assemblies.

Discussion

We developed the ABruijn algorithm aimed at assembling bacterial and relatively small eukaryotic genomes from long error-prone reads. Because the number of bacterial genomes that are currently being sequenced exceeds the number of all other genome sequencing projects by an order of magnitude, accurate sequencing of bacterial genomes remains an important goal. Because short-read technologies typically fail to generate long contiguous assemblies (even in the case of bacterial genomes), long reads are often necessary to span repeats and to generate accurate genome reconstructions.

Because traditional assemblers were not designed for working with error-prone reads, the common view is that OLC is the only approach capable of assembling inaccurate reads and that these reads must be error-corrected before performing the assembly (1). We have demonstrated that these assumptions are incorrect and that the A-Bruijn approach can be used for assembling genomes from long error-prone reads. We believe that initial assembly with ABruijn, followed by construction of the de Bruijn graph of the resulting contigs, followed by a de Bruijn graph-aware reassembly with ABruijn may result in even more accurate and contiguous assemblies of SMS reads.