Resting-state hemodynamics are spatiotemporally coupled to synchronized and symmetric neural activity in excitatory neurons

Significance

Resting-state functional connectivity mapping exploits correlations in the functional magnetic resonance imaging (fMRI) blood oxygen level-dependent (BOLD) signal across the brain. However, results are difficult to interpret without an understanding of the neural correlates of these hemodynamic fluctuations. This work uses mice in which neural activity and brain hemodynamics can be mapped simultaneously. We show that resting-state hemodynamics can be predicted from spontaneous neural activity and correspond to a series of driven increases in local blood volume, coupled with spontaneous, bilaterally symmetric fluctuations in excitatory neural activity. This result provides reassurance that resting-state functional connectivity has neural origins. The network-like spontaneous neural activity visualized here represents an underexplored feature of neural activity in the awake brain.

Abstract

Brain hemodynamics serve as a proxy for neural activity in a range of noninvasive neuroimaging techniques including functional magnetic resonance imaging (fMRI). In resting-state fMRI, hemodynamic fluctuations have been found to exhibit patterns of bilateral synchrony, with correlated regions inferred to have functional connectivity. However, the relationship between resting-state hemodynamics and underlying neural activity has not been well established, making the neural underpinnings of functional connectivity networks unclear. In this study, neural activity and hemodynamics were recorded simultaneously over the bilateral cortex of awake and anesthetized Thy1-GCaMP mice using wide-field optical mapping. Neural activity was visualized via selective expression of the calcium-sensitive fluorophore GCaMP in layer 2/3 and 5 excitatory neurons. Characteristic patterns of resting-state hemodynamics were accompanied by more rapidly changing bilateral patterns of resting-state neural activity. Spatiotemporal hemodynamics could be modeled by convolving this neural activity with hemodynamic response functions derived through both deconvolution and gamma-variate fitting. Simultaneous imaging and electrophysiology confirmed that Thy1-GCaMP signals are well-predicted by multiunit activity. Neurovascular coupling between resting-state neural activity and hemodynamics was robust and fast in awake animals, whereas coupling in urethane-anesthetized animals was slower, and in some cases included lower-frequency (<0.04 Hz) hemodynamic fluctuations that were not well-predicted by local Thy1-GCaMP recordings. These results support that resting-state hemodynamics in the awake and anesthetized brain are coupled to underlying patterns of excitatory neural activity. The patterns of bilaterally-symmetric spontaneous neural activity revealed by wide-field Thy1-GCaMP imaging may depict the neural foundation of functional connectivity networks detected in resting-state fMRI.

Functional magnetic resonance imaging (fMRI) measures local changes in deoxyhemoglobin concentration [HbR] as a surrogate for neural activity. In stimulus-evoked studies, the positive fMRI blood oxygen level-dependent (BOLD) signal corresponds to a decrease in [HbR] caused by a local increase in blood flow leading to over-oxygenation of the region. However, a growing number of studies are now using resting-state functional connectivity fMRI (fc-fMRI) in which spontaneous fluctuations in the BOLD signal are recorded in the absence of a task (1). Spatiotemporal correlations in these hemodynamic signals across the brain have been found to be bilaterally symmetric and synchronized in distant brain regions. This synchrony is interpreted as representing the connectivity of intrinsic neural networks (2–6). Many studies have identified changes in these resting-state networks during brain development (7, 8) and in neurological and even psychological disorders (9–11). However, understanding the meaning of both normal and altered functional connectivity networks requires a clearer picture of the neural activity underlying the hemodynamic fluctuations detected by resting-state fMRI.

Prior studies using electrophysiology (12), electrocorticography (13), and magnetoencephalography (14) have observed synchronous patterns of neural activity in distant, often bilateral brain regions, consistent with a neural representation of functional connectivity networks. Studies combining acquisition of electrophysiology and fMRI data in both anesthetized (15, 16) and awake (17) primates have also found correlations between resting-state BOLD signals and local field potentials (LFPs). However, the highest correlations reported to date are around 0.3 for gamma-band powers between 40 and 100 Hz. Questions thus remain regarding the extent to which resting-state hemodynamics correspond to neural activity, the kinds of neural activity represented by resting-state fMRI signals, and whether additional hemodynamic components contribute to and confound fc-MRI analysis.

In this study, simultaneous wide-field optical imaging of hemodynamics and neural activity was performed in awake and anesthetized mice expressing the genetically encoded calcium-sensitive fluorophore GCaMP in layer 2/3 and 5 excitatory neurons. This experimental approach enabled high-speed imaging across the entire dorsal surface of the mouse cortex, depicting both spontaneous neural activity and hemodynamics in parallel (18, 19). Single-site electrophysiology with simultaneous GCaMP imaging was used to confirm that recorded fluorescence, after hemodynamic correction, represents local multiunit activity (MUA). The relationship between spontaneous activity in excitatory neurons and resting-state hemodynamics was then assessed using both deconvolution and a gamma-variate fit-based convolution model. This analysis demonstrates that resting-state hemodynamics in the awake brain can be well predicted by resting-state neural activity over the entire bilateral field of view. This result suggests that resting-state hemodynamics are dominated by the summation of successive increases in blood flow coupled to spontaneous neural events. Urethane anesthesia resulted in slower coupling, and in some cases introduced slow trends in hemodynamics that were not accounted for by Thy1-GCaMP signals. The spontaneous neural activity found to be coupled to resting-state hemodynamics exhibits strong bilateral synchrony in both awake and anesthetized states, with spatial patterns consistent with resting-state functional connectivity networks.

Results

To visualize both neural activity and hemodynamics, awake (Thy1-GCaMP6f) and urethane-anesthetized (Thy1-GCaMP3) mice were imaged using simultaneous fluorescence and multispectral wide-field optical mapping (WFOM) through a thinned-skull cranial window (18, 20). Cyan light (490 nm) provided excitation of GCaMP fluorescence, whereas green (530-nm) and red (630-nm) reflectance signals were converted into images of changes in oxyhemoglobin, deoxyhemoglobin, and total hemoglobin concentrations (Δ[HbO], Δ[HbR], and Δ[HbT] = Δ[HbO] + Δ[HbR]) (Fig. 1B). Hemodynamic signals were also used to correct recorded GCaMP fluorescence for the time-varying effects of hemoglobin absorption. All imaging and analysis methods are described in SI Materials and Methods (18, 20, 21).

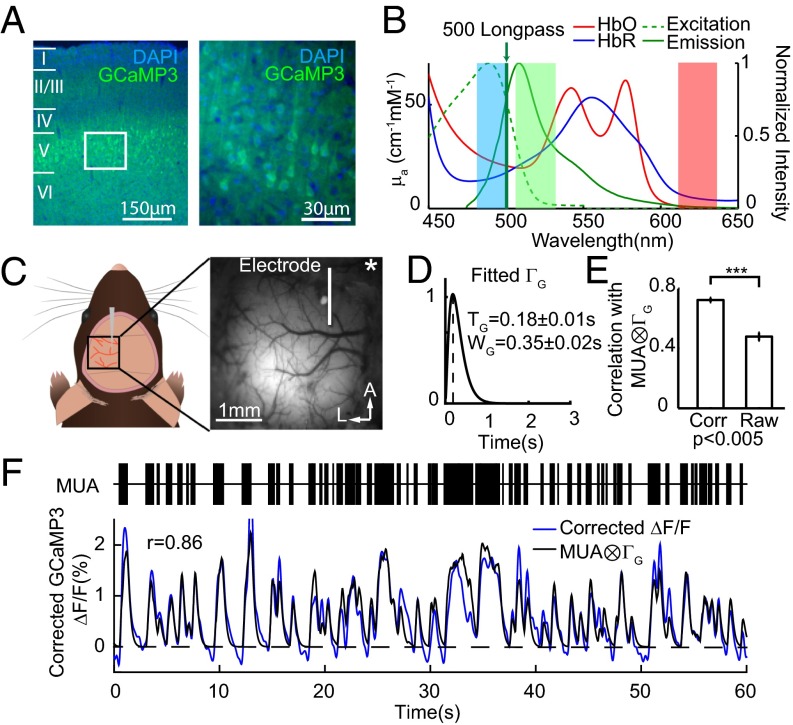
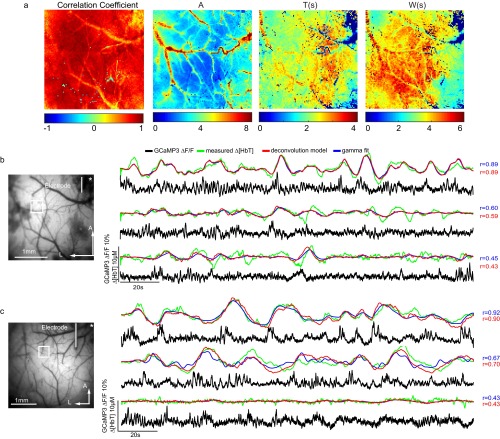
Fig. 1.

Validating wide-field GCaMP fluorescence with point electrophysiology. (A) Thy1-GCaMP3 mouse brain section at 4× (Left) and 20× (Right) shows selective expression of GCaMP in layers 2/3 and 5 pyramidal neurons. (B) Absorption spectra of HbO and HbR (left axis) and the fluorescence excitation and emission spectra of GFP (right axis). Blue, green, and red shading represent the wavelength bands of the LEDs used for imaging. (C) Field of view for simultaneous imaging and microelectrode recording in the somatosensory hindpaw region (urethane anesthetized). Star indicates bregma. (D) Average best-fit gamma-variate function Γ_G fitting convolved MUA to hemodynamics-corrected Thy1-GCaMP3 fluorescence. (E) Hemodynamic correction of GCaMP fluorescence yielded significantly higher correlations with convolved MUA compared with raw fluorescence (r_Corr = 0.72 ± 0.01; error bars show mean ± SEM; n = 9 mice). (F, Top) Example of recorded MUA at the microelectrode. (F, Bottom) Comparison of corrected GCaMP ΔF/F and the best fit of MUA convolved with the gamma function in D (correlation coefficient, 0.86).

Awake mice were imaged head-fixed but positioned on a saucer wheel and were free to run during imaging. The motion of the wheel was monitored throughout imaging using a webcam synchronized with image acquisition. All periods of running were removed, and “resting-state” epochs were defined as periods of at least 30 s of continuous rest.

Validating Wide-Field GCaMP Fluorescence Imaging with Electrophysiology.

Thy1-GCaMP lines were chosen because of their selective expression of calcium-sensitive GCaMP in excitatory pyramidal neurons in cortical layers 2/3 and 5, as shown in Fig. 1A (22). Changes in GCaMP fluorescence reflect changes in intracellular calcium, and have been widely shown to correspond to neural spiking activity in studies using two-photon microscopy (22–24). The kinetics of GCaMP3 and GCaMP6f are similar (25). High-speed wide-field imaging of GCaMP fluorescence provides a depth-integrated, ensemble measurement of neural events over a much larger field of view compared with two-photon microscopy (18, 19, 24, 26). However, an essential consideration when using wide-field GCaMP imaging is the spectral overlap between hemoglobin absorption and GCaMP excitation and emission bands (Fig. 1B) (18). Simultaneous measurement of cortical hemodynamics and GCaMP fluorescence in our experiments enabled a correction for these absorption effects as described in detail in SI Materials and Methods.

To verify that hemodynamics-corrected wide-field Thy1-GCaMP signals represent underlying neural activity, WFOM measurements were acquired simultaneously with MUA in urethane-anesthetized animals (Fig. 1C). GCaMP and MUA, at the same cortical locations, were compared before and after hemodynamic correction, with MUA convolved with a best-fit gamma-variate function mimicking the kinetics of neural calcium and GCaMP’s calcium response (Fig. 1D). Significantly higher correlation coefficients between Thy1-GCaMP fluorescence and convolved MUA were found after hemodynamic correction (Fig. 1E, and Fig. S1 for GCaMP6f). Fig. 1F shows an example of spontaneous MUA with simultaneously recorded hemoglobin-corrected GCaMP3 fluorescence from the same region and the gamma-variate–based convolution fit between the two. Best-fit parameters agree well with two-photon characterization of GCaMP using cell-attached recordings (22) (GCaMP3: time to peak, 0.18 ± 0.01 s; width, 0.35 ± 0.02 s; GCaMP6f time to peak, 0.29 ± 0.09 s; width, 0.36 ± 0.18 s; mean ± SD). We conclude that hemodynamics-corrected wide-field fluorescence signals in Thy1-GCaMP mice provide an accurate representation of the integrated spiking activity of excitatory neurons.

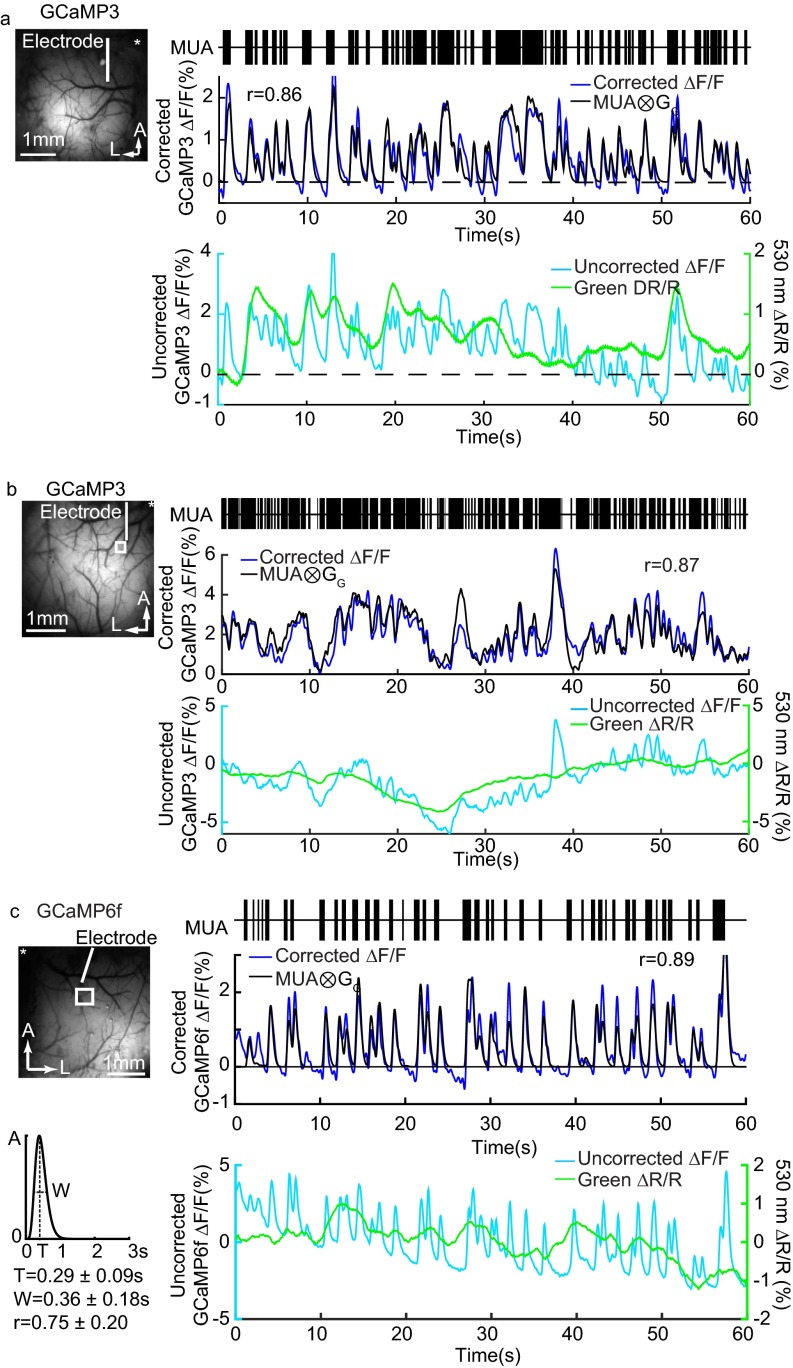
Fig. S1.

Electrophysiology comparison in Thy1-GCaMP3 and Thy1-GCaMP6f mice. (A) Concurrent recordings of MUA and hemodynamics-corrected GCaMP3 fluorescence from Fig. 1F (thinned skull) and (B) recordings from a Thy1-GCaMP3 animal (open-skull craniotomy) accompanied by uncorrected GCaMP fluorescence time courses and simultaneous green (530-nm) reflectance, showing contaminating effects of hemodynamics in the wide-field fluorescence imaging. (C) An example from a Thy1-GCaMP6f animal (unilateral thin skull) showing similar correspondence of electrophysiological recordings and fluorescence changes. The GCaMP6f MUA kernel shows the averaged gamma-variate function used to fit fluorescence with MUA, and the values shown represent mean ± SD. All measurements were made under urethane anesthesia. All fluorescence and hemodynamic data are shown after low-pass filtering at 2 Hz.

Movie S1 shows recorded GCaMP6f data in the awake brain before and after hemodynamic correction, with concurrent Δ[HbT] (also shown as plots in Fig. S1). Fig. S2 shows data acquired on a Thy1-YFP mouse demonstrating expected strong hemodynamic cross talk, but only small variance attributable to intrinsic flavoprotein fluorescence after hemodynamic correction (19).

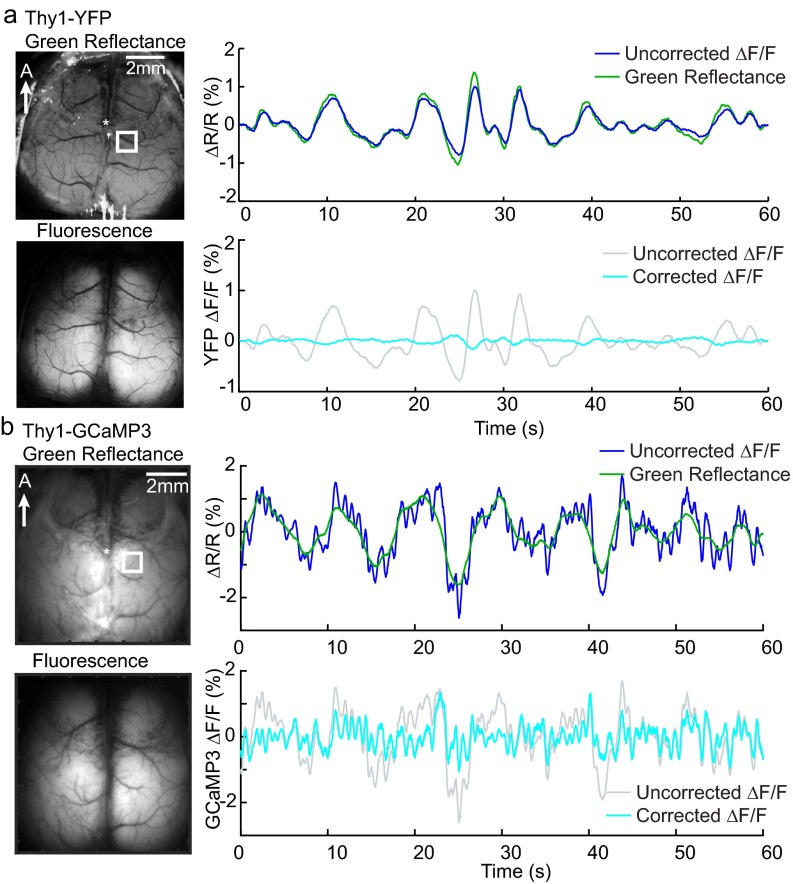
Fig. S2.

Control experiment comparing WFOM measurements in Thy1-YFP and Thy1-GCaMP3 mice. (A) Urethane-anesthetized Thy1-YFP mice were imaged using an EMCCD-based WFOM system. Representative time courses from the somatosensory region (marked by the white box) show that changes in YFP fluorescence closely follow the trend of green reflectance demonstrating the dominant effect of hemodynamic cross talk. B shows equivalent measurements in a urethane-anesthetized Thy1-GCaMP3 mouse. All neural and hemodynamic signals are shown bandpass filtered at 0.02–2 Hz. After correcting for hemodynamic cross talk in the fluorescence signals, residual changes in the Thy1-YFP mouse are around 0.2% compared with >1% spikes of activity remaining following hemodynamic correction of data from the Thy1-GCaMP3 mouse. Residual fluctuations in the YFP signal after hemodynamic correction may be attributable to the dynamics of flavoprotein fluorescence (19), which are expected to follow neural activity (68). The small contribution of flavoprotein fluorescence to GCaMP fluorescence measurements is difficult to discern but would be expected to slightly broaden the apparent GCaMP response kernel.

Spatiotemporal Patterns of Resting-State Neural and Hemodynamic Activity.

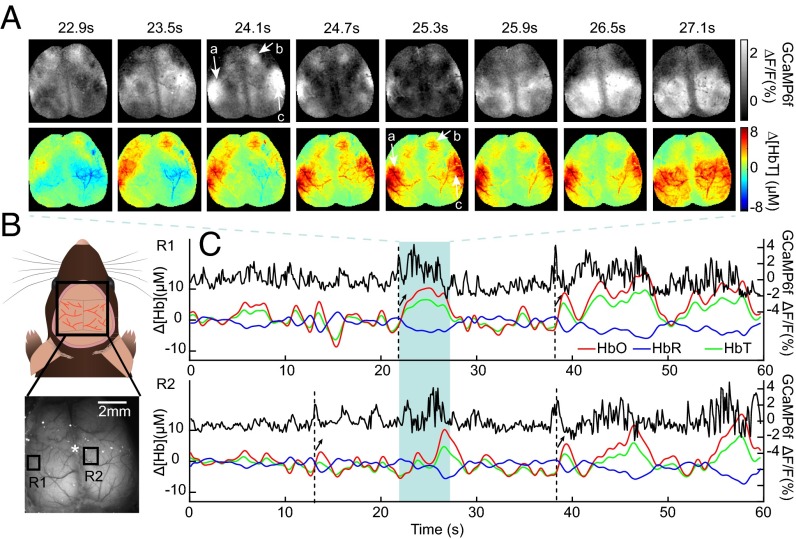
Fig. 2A shows a sequence of the spatial patterns of spontaneous neural activity recorded in the awake mouse brain during a period of rest using wide-field GCaMP6f imaging (after hemodynamic correction), along with concurrent maps of hemodynamics given by Δ[HbT]. The patterns of spontaneous neural activity evolve rapidly, exhibiting synchronization between regions and bilateral symmetry. Changes in [HbT] occur at a much slower pace, yet the [HbT] spatial pattern at t = 25.3 s can be seen to resemble the neural spatial pattern at t = 24.1 s (corresponding patterns marked by a, b, and c). Fig. 2C shows time courses of corrected GCaMP6f fluorescence with concurrent changes in [HbT], [HbO], and [HbR] for the two regions indicated in Fig. 2B during the same awake, resting-state trial. Increased [HbT] and [HbO] and decreased [HbR] can be seen to occur following peaks in the GCaMP signal (black arrows), consistent with stimulus-evoked functional hyperemia (27). Although the need to correct GCaMP fluorescence measurements for hemodynamic contamination is a potential confound, these time sequences underscore that patterns of neural activity are detected many frames before hemodynamic changes, yet are clearly coupled to spatially-correlated hemodynamics.

Fig. 2.

Wide-field imaging of GCaMP fluorescence and hemodynamic activity in the awake mouse brain. (A) (Top) Consecutive maps of corrected GCaMP6f ΔF/F showing spontaneous, symmetric events across the bilaterally exposed cortex of an awake mouse and (Bottom) concurrent maps of hemodynamics (given by Δ[HbT]) showing similar spatial patterns (a–c) but with a time delay. (GCaMP maps show average over each 600-ms window.) (B) Schematic and example of chronic bilateral thinned-skull window imaged in awake animals. Grayscale image shows raw fluorescence; star indicates bregma. (C) Time courses of simultaneously acquired resting-state GCaMP6f ΔF/F (black), Δ[HbO] (red), Δ[HbR] (blue), and Δ[HbT] (green) are shown from the two regions marked in B. Dotted lines indicate neural events with arrows indicating corresponding hyperemias given by increased Δ[HbO], Δ[HbT], and decreased Δ[HbR].

Changes in [HbR] are the primary contributor to the fMRI BOLD signal (28). However, [HbR] can be affected by changes in oxygen consumption, blood flow, and blood volume, making it ambiguous to interpret. Conversely, Δ[HbT] represents a change in the concentration of blood in tissue, independent of local changes in oxygenation, and thus should provide a more pure measure of a physical change in vascular tone. Calculating the average peak amplitude of the cross-correlation between ∆[HbR] and ∆[HbT] across anesthetized resting-state trials and mice (allowing for relative temporal delays), we find a −0.86 ± 0.10 (n = 6 mice) correlation between Δ[HbT] and Δ[HbR]. This result suggests that, as in stimulus-evoked fMRI, the driving component of changes in [HbR] in the resting state are evoked increases in local blood flow causing increased oxygenation [leading to positive BOLD responses (27)] rather than modulations in oxygen consumption. Analysis here thus focuses on [HbT] dynamics rather than [HbR], in order to examine physical coupling of vascular modulations to neural activity.

Analysis of Spatiotemporal Neurovascular Coupling.

Although a qualitative relationship between neural activity and hemodynamics can be appreciated from the data shown in Fig. 2, a more quantitative approach is needed to evaluate the properties of resting-state neurovascular coupling. A commonly used approach is to assume a linear model of neurovascular coupling, such that hemodynamics would correspond to the convolution of neural activity and a gamma-shaped hemodynamic response function (HRF) (29, 30). Here, three different strategies were developed to test this linear relationship: gamma-variate fitting, deconvolution, and spike-triggered averaging.

Gamma-variate fitting analysis has been performed previously to analyze stimulus-evoked neurovascular coupling data (30–32). Here, a three-parameter gamma-variate function was used to approximate an HRF. Parameters were optimized to yield the best-fit (minimized least-squares error) between measured Δ[HbT] and the HRF convolved with corrected GCaMP-based recordings of neural activity (30, 33). The resulting best-fit HRF at each pixel was then convolved with the GCaMP time course of that pixel and compared with measured Δ[HbT] at the same position using Pearson’s correlation coefficient to quantify goodness of fit. Unlike correlation-based analysis of LFP band power (15, 34, 35), this method assumes a clear linear model of neurovascular coupling where excitatory activity is expected to generate a proportional, localized increase in [HbT] (local hyperemia).

Deconvolution is an alternative approach that similarly assumes a linear convolved model of neurovascular coupling but does not impose constraints on the temporal shape of the convolved HRF. A diagonal loading method was used to deconvolve each pixel of Δ[HbT] data from corrected GCaMP data, yielding a similar spatially resolved HRF for each dataset. The resulting HRF at each pixel was then temporally cropped and reconvolved with the pixel’s GCaMP time course, and compared with the pixel’s measured Δ[HbT] using Pearson’s correlation.

Spike-triggered averaging (15, 36) was also used to demonstrate the form of coupling between resting-state neural events and hemodynamic activity independent of GCaMP corrections and model dependencies as described further below.

Model-based analysis of awake, resting-state data.

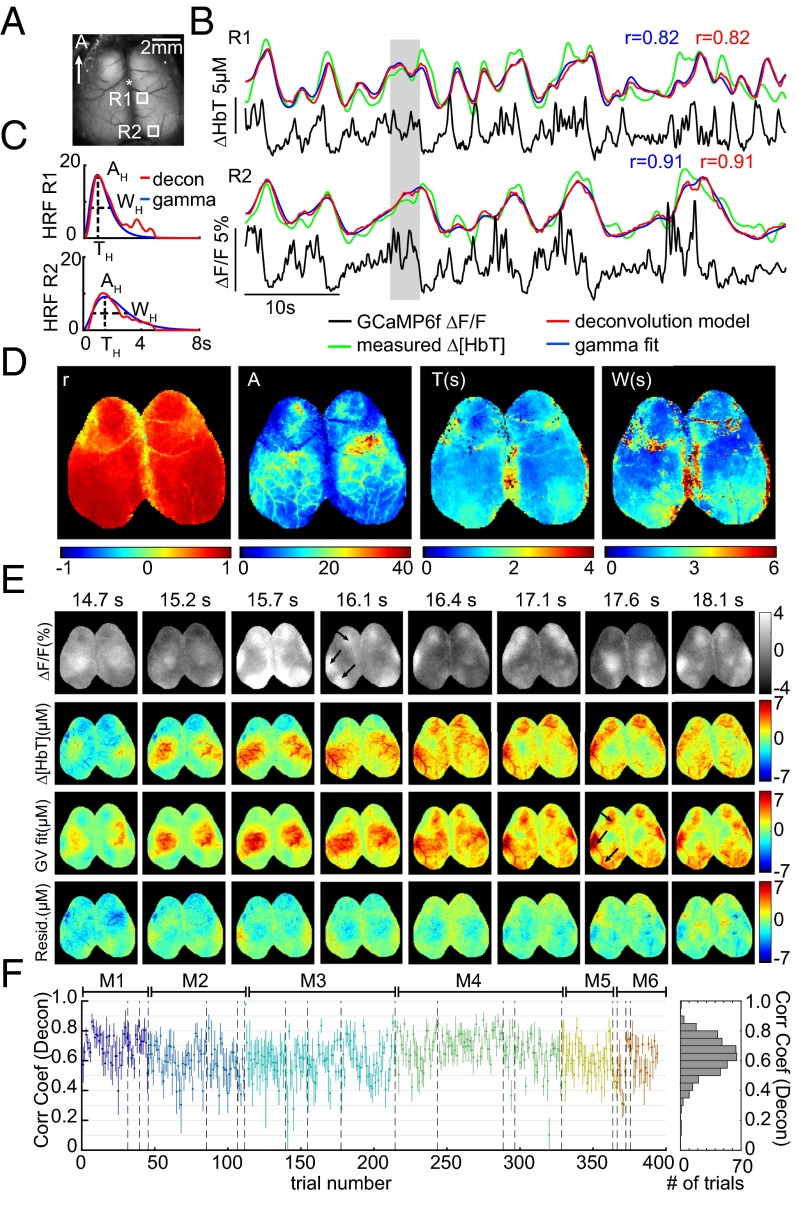
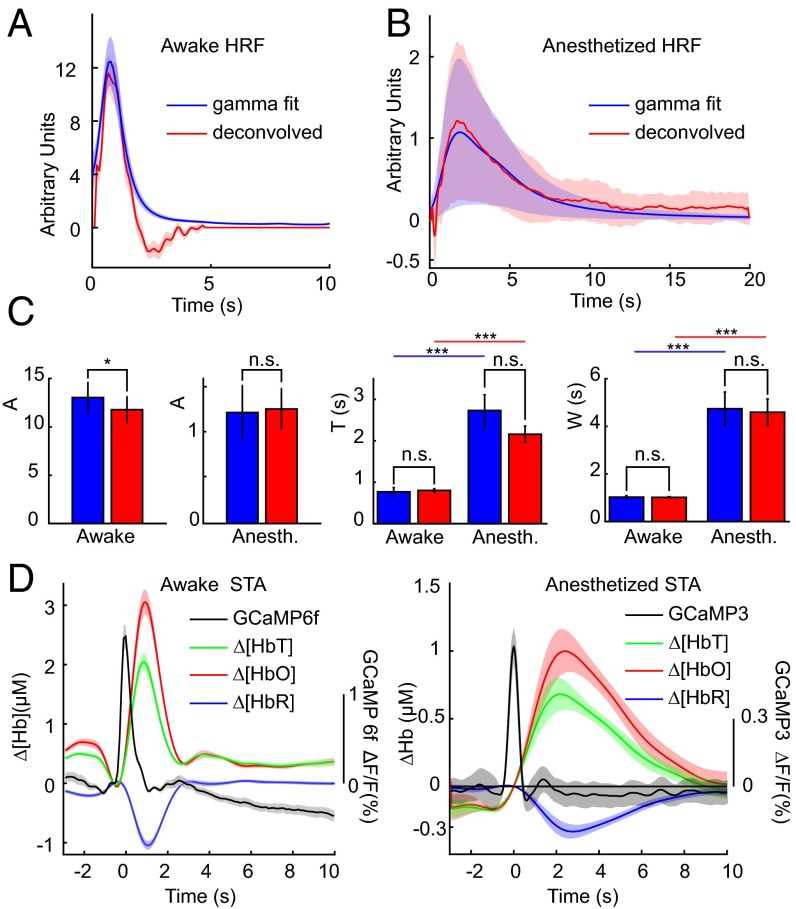
Fig. 3 shows fitting results for awake, resting-state mice. For two cortical locations within the same trial, traces of corrected GCaMP6f are plotted along with measured Δ[HbT], gamma-variate fit Δ[HbT], and deconvolution-predicted Δ[HbT]. Before fitting, both GCaMP6f and Δ[HbT] data were preconditioned using a 0.02-Hz high-pass filter (HPF) to remove slow drifts, as well as a 2-Hz low-pass filter (LPF) to reduce physiological noise (although all corrected GCaMP traces are shown without low-pass filtering). Both fits show good agreement with measured Δ[HbT] and resemble characteristic fluctuations of resting-state hemodynamics. HRFs derived using both methods exhibit similar temporal shapes and correlation coefficients (Fig. 3C).

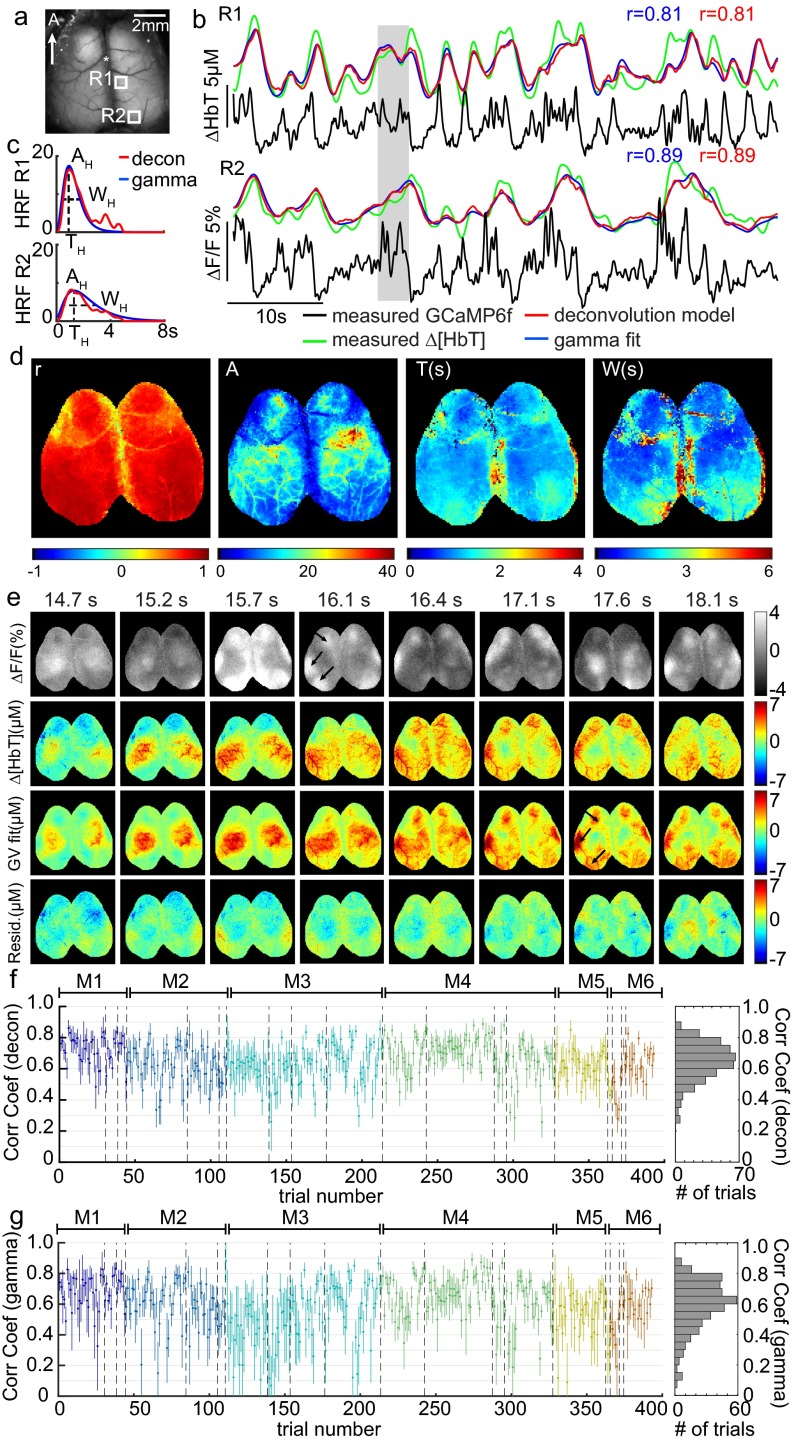
Fig. 3.

Spatiotemporal modeling of hemodynamics from wide-field Thy1-GCaMP6f recordings in the awake, resting brain. (A) Field of view under blue illumination. (B) Sixty-second examples of awake, resting-state GCaMP6f ΔF/F time courses (after hemodynamic correction) with simultaneously recorded Δ[HbT] from the two regions indicated in A (same trial). Red and blue traces show the results of convolving corrected GCaMP fluorescence with hemodynamic response functions (HRFs) derived via deconvolution or gamma-variate fitting, respectively. (C) Deconvolved HRF and best-fit gamma-variate HRF for the time series shown in B illustrating the amplitude A_H, time of peak as T_H, and width at half-maximum as W_H gamma-fit parameters. (D, Left) Map of gamma-variate fit Pearson’s correlation coefficients (r) per pixel. (Right) Gamma-variate HRF best-fit parameters (A_H, T_H, and W_H) for the trial shown in B. (E) Example epoch, top row: corrected Thy1-GCaMP6f ΔF/F; second row: Δ[HbT]; third row: gamma-variate model fit to Δ[HbT] based on the GCaMP signal; bottom row: fit residuals. Arrows highlight specific neural events that are mirrored in later hemodynamics. Movies S2 and S3 show the full time sequence for this trial for gamma-variate and deconvolution fits, respectively. (F) Plot of mean average and SD [over 16 × 16 regions (1 mm²) over S1] Pearson’s correlation coefficients for the deconvolution model for all resting-state epochs in all six mice (histogram at Right shows overall distribution for all trials). Values are chronological with dotted lines indicating different days and colors indicating different mice, M1–M6.

Performing fitting analysis for each pixel individually permits HRFs to vary spatially over the field of view. Fig. 3D shows a map of the Pearson correlation coefficient between measured and gamma-variate modeled Δ[HbT], and maps of optimized fit parameters (gamma function amplitude A_H, peak time T_H, and width W_H) from the same trial shown in Fig. 3B. Fit parameters vary somewhat across the cortex, with A tracing the distinct shapes of the cortical arteries reflecting the higher amplitude contribution of surface vessels to WFOM hemodynamics (18, 37).

Fig. 3E shows a sequence of images from the same trial including corrected GCaMP6f, measured Δ[HbT], the best-fit (gamma-variate) prediction of Δ[HbT], and fit residuals over the full field of view. Even though the spatial patterns of neural activity have a much faster pace compared with the observed hemodynamics, convolution of the GCaMP signal with fitted HRFs yields a predicted Δ[HbT] that is a close match to the measured Δ[HbT] dynamics. Both increases and decreases in Δ[HbT] are accurately modeled from the observed increases and decreases in excitatory neural activity. Movies S2 and S3 show the full 60 s of this trial with gamma-variate and deconvolution models, respectively.

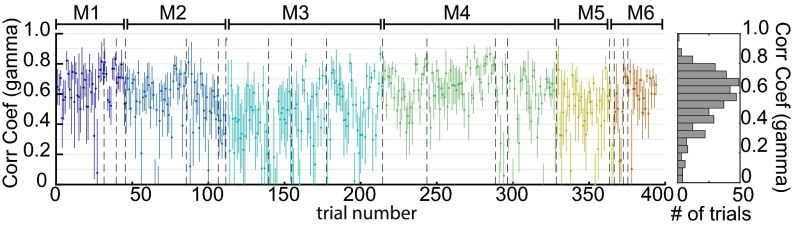
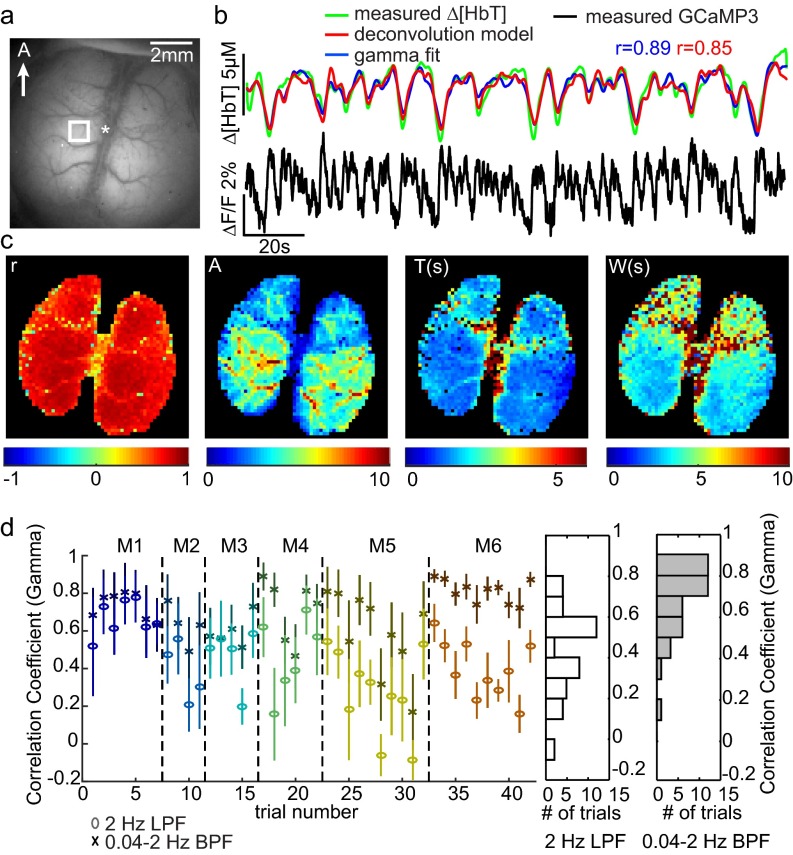
Equivalent analysis was performed for all nonrunning epochs lasting >30 s from six awake mice, each imaged multiple times on different days (two recording days were removed owing to excessive motion artifacts). To summarize fit quality across all trials and all mice, a region over the somatosensory cortex was binned to 16 × 16 pixels (equivalent to a 1-mm² region) and analyzed using both deconvolution and gamma-variate fitting. Fig. 3F shows average Pearson’s correlation coefficients and their standard deviations over these regions for individual trials in chronological order for the deconvolution model (see Fig. S3 for gamma-variate equivalent). The overall distribution of averaged correlation coefficients across trials, days, and animals is also shown. Correlation coefficients ranged from 0.3 to 0.9, with an average across all animals and trials of 0.63 ± 0.02 over six animals (0.53 ± 0.03 for gamma-variate fitting, where the temporal shape of the HRF is more constrained).

Fig. S3.

Mean average and SD Pearson’s correlation for gamma-variate fitting in awake animals. All resting-state trials in all of the awake animals (n = 6) are shown. Values are ordered chronologically with dotted lines indicating recordings on different days and colors indicating different mice. Histogram to Right shows the distribution of average (over S1) Pearson’s correlation coefficient across all resting-state epochs in all trials in all awake mice. Similarly to Fig. 3F, the hemodynamic and corrected neural signals were temporally bandpass filtered between 0.02 and 2 Hz before fitting.

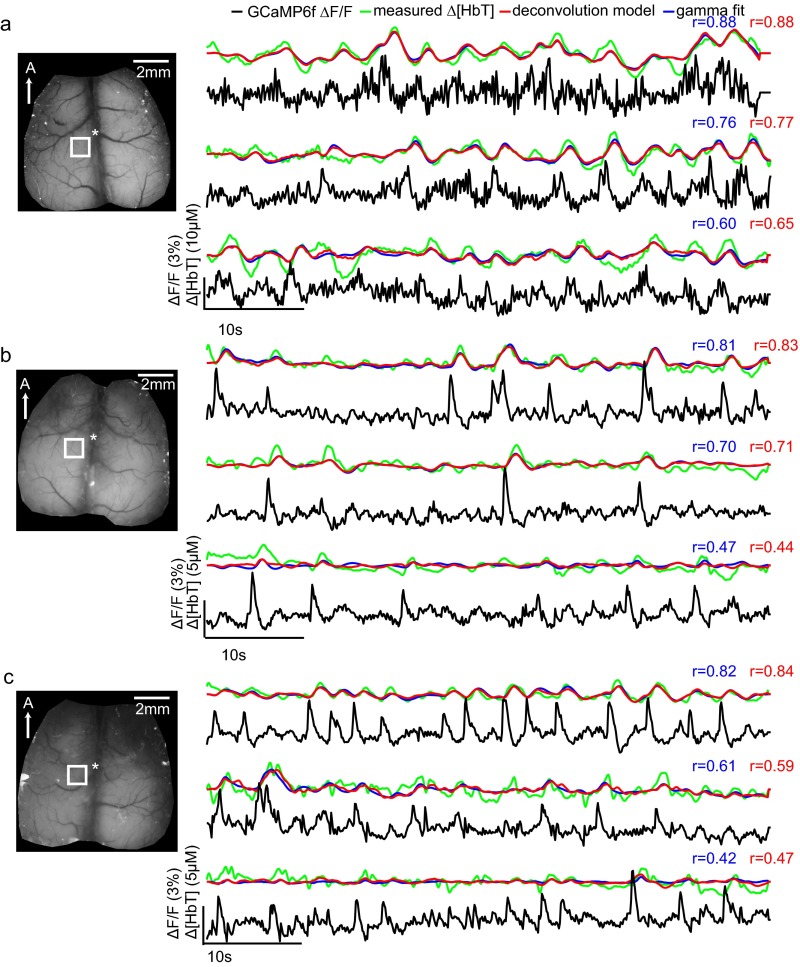
Fig. S4 shows additional examples of time courses and fits from three different awake animals, comparing trials that yielded higher and lower correlation coefficients. In all cases, general trends are well modeled, whereas noise, motion artifacts, and low hemodynamic variance can be seen to degrade fit correlation coefficients. Fig. S5 shows time series fits for different cortical locations within the same trials, demonstrating that hemodynamics are well predicted by local neural activity and evenly correlated across the cortex.

Fig. S4.

Examples of model-based fitting of neural activity to resting-state hemodynamics in awake Thy1-GCaMP6f mice: Same region, different trials. (A–C) Three representative trials in the same imaging session are shown with good, mediocre, and poor fitting results from three different animals. All animals were awake and resting throughout all trials. Time courses shown were all chosen from somatosensory area as marked by white boxes. Thy1-GCaMP6f ΔF/F traces are shown after hemodynamic correction. All time courses were temporally bandpass filtered between 0.02 and 2 Hz before fitting, although GCaMP data are plotted here with only 0.02-Hz high-pass filtering. Red and blue traces show the result of convolving the corrected Thy1-GCaMP6f fluorescence signal with hemodynamic response functions (HRFs) derived via deconvolution or gamma-variate fitting, respectively. Pearson’s correlation coefficients used to evaluate the goodness of fit are color-coded similarly. The performances of the two methods are comparable on the same trials. In all cases, the general trends of [HbT] data are reproduced in the convolved fits. Correlation coefficients are degraded by effects such as slow drifts (visible in the third example in B) and by higher-frequency fluctuations in [HbT], which may be attributable to motion artifacts, especially from breathing (second and third examples in C).

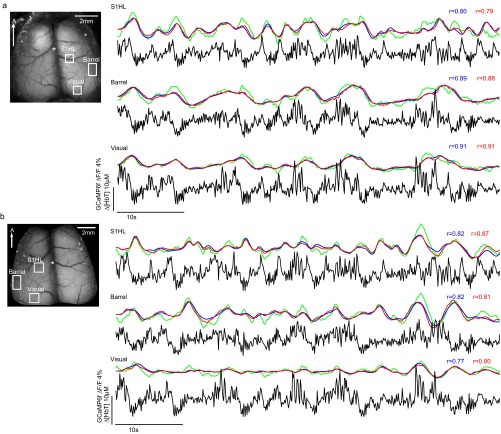
Fig. S5.

Examples of model-based fitting of neural activity to resting-state hemodynamics in awake Thy1-GCaMP6f mice: Same trial, different regions, two imaging sessions. Time courses of corrected GCaMP6f fluorescence, Δ[HbT] and its prediction from gamma-fit and deconvolution models, extracted from approximate hindlimb, barrel cortex, and visual cortex regions within the same imaging trial for two different imaging sessions (A and B). The animals were awake and resting throughout the trials shown. The corrected neural and hemodynamic signals were temporally bandpass filtered between 0.02 and 2 Hz, although GCaMP data are plotted here with only 0.02-Hz high-pass filtering. The gamma-variate fit is shown in blue, whereas the deconvolution model is shown in red. The goodness of fit is consistent across the different functional regions, whereas neural activity differs between each region.

Frequency dependence of neurovascular correlations.

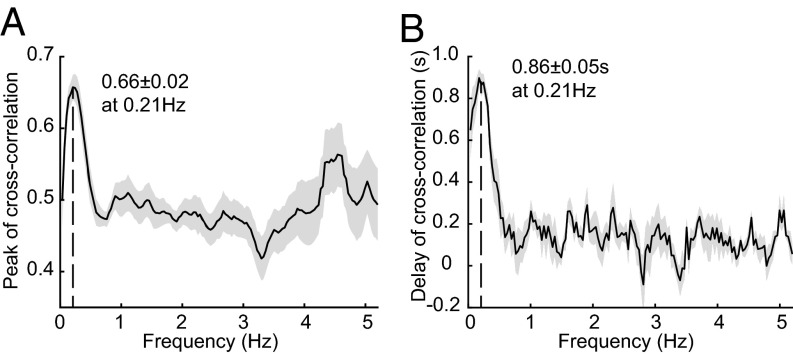
Mathematically, convolution of a broadband signal with a gamma function will act primarily as a low-pass filter, integrating faster activity into a moving average over time. The fits above thus suggest that a low-frequency component of resting-state neural activity accounts for resting-state hemodynamic fluctuations. The frequency dependence of the cross-correlation between corrected GCaMP6f and [HbT] data was assessed by bandpass filtering (BPF) both datasets with a 0.35-Hz sliding frequency-domain window from 0.035 to 5.2 Hz with an increment of 0.035 Hz. The peak amplitude and phase delay of the cross-correlation between neural activity and hemodynamics for each frequency band was calculated for all awake resting-state epochs in all animals. Peak correlations were found at a frequency of around 0.21 Hz, decreasing both toward 0 Hz and above 0.4 Hz (Fig. 4A). The average temporal delay of the cross-correlation at 0.21 Hz was 0.86 ± 0.05 s across all animals representing the phase shift between neural activity and [HbT] (Fig. 4B).

Fig. 4.

Frequency dependence of neurovascular correlations. (A) Plot of the average peak cross-correlation value between Thy1-GCaMP6f and [HbT] signals as a function of temporal bandpass frequency (0.35-Hz window, 0.035-Hz increment up to Nyquist frequency at 5.2 Hz; plotted frequency is the start of each band). (B) Phase delay of the cross-correlation between corrected Thy1-GCaMP6f and [HbT] as a function of frequency. The results show the average and SE for all of the awake animals (n = 6). Time courses and image sequences with <0.4-Hz LPF are compared in Fig. S6 and Movies S4–S6.

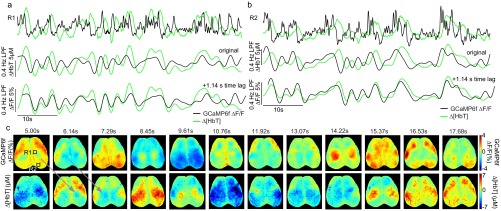
As a simple demonstration of this result, Fig. S6 and Movies S4 and S5 show Thy1-GCaMP6f data low-pass filtered at 0.4 Hz. A clear correlation to [HbT] is seen, with an evident phase delay. Strong correlations within the 0- to 0.4-Hz frequency band imply that hemodynamics act as a temporal integrator of neural spiking activity. The clear time shift further confirms that HRF-based fitting results do not originate from hemodynamic cross talk or the correction of GCaMP fluorescence.

Fig. S6.

The correspondence between neural activity and hemodynamics at <0.4 Hz in awake mouse brain. Time courses from regions R1 (A) and R2 (B) are the same region as shown in Fig. 3A. Changes in corrected Thy1-GCaMP6f fluorescence and Δ[HbT] are plotted as unfiltered (top row), 0.4-Hz low-pass filtered (middle row), and 0.4-Hz low-pass filtered, and temporally shifted by 1.14 s (bottom row). (C) The corresponding time series of images from 5 to 17.5 s of neural activity and hemodynamic after <0.4-Hz filtering (shown in 1.14-s steps, corresponding to the phase lag found between neural and hemodynamics of this trial). Patterns of integrated neural activity closely match subsequent patterns of hemodynamics seen in the following panel. The <0.4-Hz frequency band was chosen based on frequency-dependent cross-correlation analysis shown in Fig. 4. This result demonstrates that, independent of linear model-based fitting, the low-frequency enveloping of neural activity shows strong spatiotemporal correlations with hemodynamics at low frequencies. The clear temporal delay between neural and hemodynamic signals rules out the possibility that this effect results from hemodynamic cross talk. This data are also shown in Movies S4 and S5 with Movie S6 showing the deconvolution-based fit initialized using <0.4-Hz filtered data.

Model-based analysis of anesthetized resting-state data.

In urethane-anesthetized Thy1-GCaMP3 animals (n = 6), data were acquired using both bilateral and unilateral thinned-skull windows (unilateral with simultaneous electrophysiological recordings). Model-fitting analysis was performed using the full 180-s duration of each imaging trial. Because anesthesia caused much higher variability in physiological state, mice were excluded from analysis if poor physiological state led to nontypical patterns of neural activity or hemodynamics, or if physiological monitoring implied poor health.

An example of analysis on a urethane-anesthetized mouse exhibiting a high overall correlation coefficient is shown in Fig. S7. Both gamma-variate and deconvolution models show excellent agreement with measured Δ[HbT] values, with Pearson’s correlation coefficients of 0.89 and 0.85, respectively.

Fig. S7.

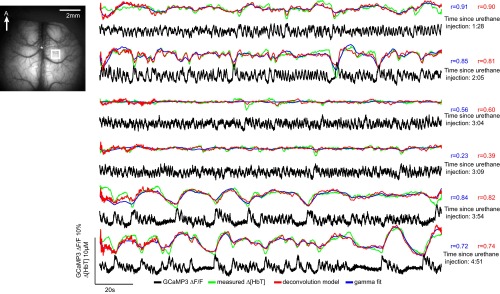
Spatiotemporal modeling of hemodynamics from wide-field GCaMP recordings in the resting-state urethane-anesthetized brain. (A) An example of a urethane-anesthetized Thy1-GCaMP3 mouse imaged with a similar, bilateral window over the cortex to awake mice. (B) ΔF/F time course (after hemodynamic correction) lasting 180 s with simultaneously recorded Δ[HbT] from the region indicated in A. Red and blue traces show the result of convolving the GCaMP fluorescence signal with hemodynamic response functions (HRFs) derived via deconvolution or gamma-variate fitting, respectively. Both the hemodynamic and neural activity time courses were low-pass filtered at 2 Hz. (C) The spatial maps of Pearson’s correlation coefficient of gamma fit, amplitude (A), time to peak (T), and width at half-maximum (W) of gamma-variate function by pixelwise HRF estimation from the trial in B. This example represents the highest correlation value found within urethane-anesthetized mice. Additional anesthetized mice were found to have stronger contributions from low-frequency (<0.04-Hz) hemodynamic trends that were not well predicted by Thy1-GCaMP3 recordings. D shows the gamma-variate equivalent result to Fig. 5F, demonstrating correlation coefficients across anesthetized animals, fitting before and after >0.04-Hz high-pass filtering of [HbT] and corrected Thy1-GCaMP3 fluorescence.

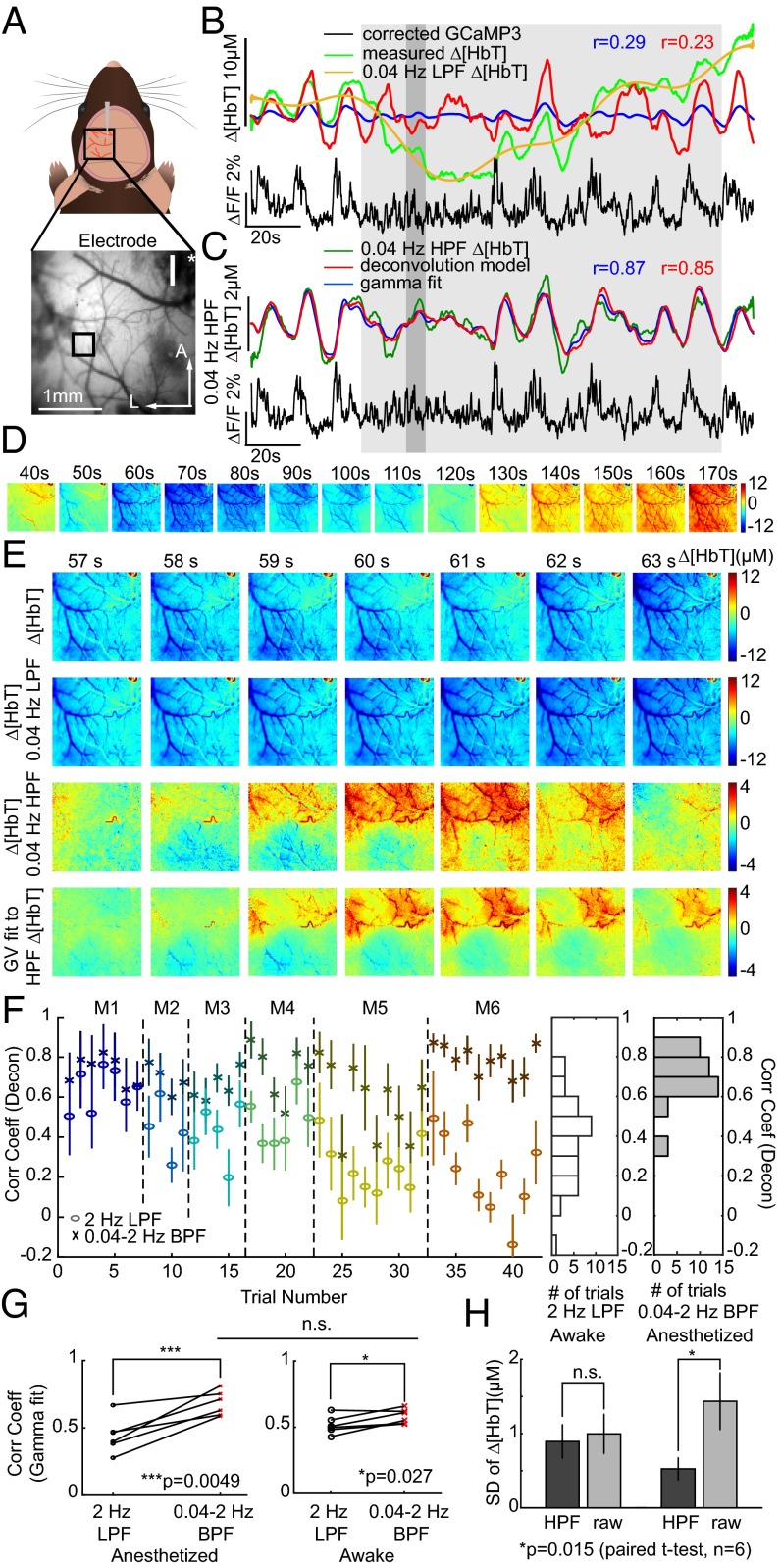
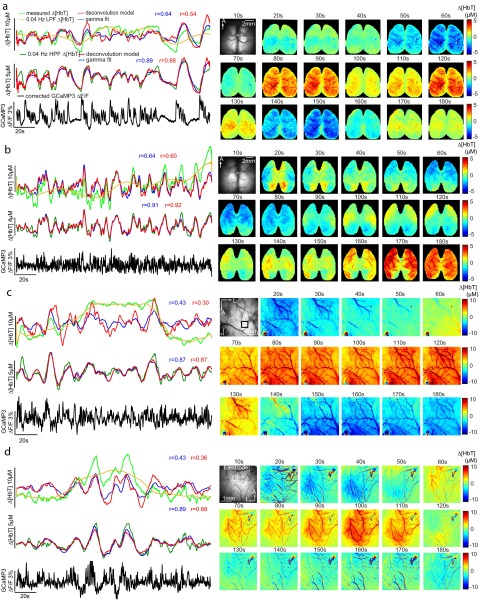
However, other anesthetized trials yielded poorer fits. A trial with a correlation coefficient of 0.19 is shown in Fig. 5B. The measured Δ[HbT] time course in this case exhibits a large decrease in [HbT] in the middle of the trial that is not accounted for in either deconvolution or gamma-variate–based model fitting. High-pass filtering of hemodynamic time courses at 0.04 Hz was found to remove these slow trends, yielding resting-state hemodynamics that more closely resemble those seen in awake data. Performing deconvolution and gamma-variate fitting after 0.04-Hz high-pass filtering of both GCaMP and Δ[HbT] data dramatically improved fit correlation coefficients as shown in Fig. 5C (Movie S7 shows this fit sequence, while spatial patterns of fit parameters for this trial are shown in Fig. S8). Repeated across all anesthetized animals, fitting before and after <0.04-Hz slow-trend removal, the average correlation coefficients across all anesthetized animals and trials improved from 0.44 ± 0.05 to 0.68 ± 0.04 for gamma variate fitting and 0.41 ± 0.06 to 0.70 ± 0.03 for deconvolution (P = 0.005 and P = 0.006, respectively; n = 6; paired t test) (Fig. 5 F and G).

Fig. 5.

Analysis of urethane-anesthetized animals and the presence of slow hemodynamic trends. (A) A smaller, unilateral window over S1. (B) Time courses of original Δ[HbT] and Thy1-GCaMP3 fluorescence (2-Hz LPF only) with “best-fit” deconvolution and gamma-variate fits. Yellow shows <0.04-Hz slow trend in [HbT]. (C) Plots as in B after 0.04- to 2-Hz bandpass filtering (BPF) of both [HbT] and GcaMP3 fluorescence to remove slow trends yielding improved fits. (D) Image sequence showing <0.04-Hz component of Δ[HbT] from 40 to 170 s for the same trial. (E) Image sequence from 57 to 63 s showing from Top to Bottom: original [HbT] (<2-Hz LPF), slow trend [HbT] (<0.04-Hz LPF), [HbT] >0.04- to 2-Hz BPF, gamma-variate fit to 0.04- to 2-Hz BPF Δ[HbT] from 0.04 to 2-Hz BPF-corrected GCaMP3. (F) Mean average Pearson’s correlation coefficients and SD over S1 for deconvolution model for all anesthetized animals (M1–M6) before (circles) and after (crosses) >0.04-Hz HPF of [HbT] and GCaMP3 fluorescence. Histogram to Right shows summary distributions for before (white) and after (gray) >0.04-Hz HPF. Gamma-variate fit results shown in Fig. S7. (G) Pearson’s correlation coefficients for gamma-variate fitting with only a 2-Hz LPF and after 0.04- to 2-Hz BPF of Δ[HbT] for both anesthetized and awake data for each mouse. n.s., P = 0.05. (H) SD of Δ[HbT] (2-Hz LPF) over time before and after >0.04-Hz HPF for awake and anesthetized data.

Fig. S8.

Examples of model-based fitting of neural activity to resting-state hemodynamics in urethane-anesthetized Thy1-GCaMP3 mice: Same region, different trials. (A) Spatial maps of the Pearson’s correlation coefficients, amplitude (A), time to peak (T), and width at half-maximum (W) of gamma-variate pixelwise HRF estimation for a zoomed-in unilateral field of view (same trial as in Fig. 5C, including 0.04- to 2-Hz temporal filtering). (B) Three representative trials for the same animal (lasting 180 s) with good, mediocre, and poor correlation coefficients (equivalent for a second animal are shown in C). Red and blue traces show the results of convolving corrected Thy1-GCaMP3 fluorescence signals from within the white boxes shown with HRFs derived via deconvolution or gamma-variate fitting, respectively (Pearson’s correlation coefficients are similarly color-coded). Slow trends were removed in all cases by temporally bandpass filtering both corrected ΔF/F and hemodynamic signals between 0.04 and 2 Hz before fitting, although ΔF/F time courses are plotted with only 0.04-Hz high-pass filtering to show high-frequency components. As with awake animals, the general trends of [HbT] changes are reproduced in all fits. Correlation coefficients are degraded by higher-frequency fluctuations on [HbT] traces that in some cases can be attributed to motion such as breathing that cannot be reproduced by convolution with a best-fit HRF. Although such artifacts could be removed through low-pass filtering of [HbT], these higher frequencies were retained to enable higher-frequency components of the HRF (such as its fast initial rise) to be maintained in frequency space.

Fig. S8 provides additional examples of urethane-anesthetized Δ[HbT] fits following 0.04-Hz high-pass filtering, comparing trials with different levels of correlation coefficient. Fig. S9 shows successive trials from one animal over a 4-h period, demonstrating that, despite clear changes in the nature of the resting-state neural activity, hemodynamics provide an equivalent representation of this activity, including almost no hemodynamic variability during dense firing (consistent with HRF convolution).

Fig. S9.

Comparison of model-based fitting of neural activity to resting-state hemodynamics during different neural states in a urethane-anesthetized Thy1-GCaMP3 mouse. During a 5-h acute experiment, resting-state trials captured different types of neural activity within the same mouse. Plots show time courses from the same somatosensory region ordered chronologically (time since urethane anesthesia induction is indicated on the Right). Corrected Thy1-GCaMP3 fluorescence and the hemodynamic signals were temporally bandpass filtered from 0.04 to 2 Hz before fitting in all cases, although ΔF/F time courses are plotted with only 0.04-Hz high-pass filtering. Deconvolution and gamma-variate fitting results are shown in red and blue, respectively. Despite clear changes in the type of spontaneous neural activity present in the brain, hemodynamics are well predicted by both linear models. Of note, in the middle time points, neural activity consists of dense firing events, which when convolved with an HRF result in an almost flat [HbT] prediction, which is consistent with the low variance seen in measured [HbT]. It is clear that this fit provides an accurate representation of cortical hemodynamics in this state, although the (amplitude-independent) Pearson correlation coefficient for this fit is degraded by the presence of small fluctuations in measured [HbT], likely caused by motion artifacts.

Spatial properties of <0.04-Hz slow trends.

It is possible to visualize the spatiotemporal properties of <0.04-Hz slow hemodynamic trends. Fig. 5D maps 0.04-Hz low-pass–filtered frames across the duration of the large decrease in [HbT] seen in Fig. 5B, showing a large trend across the field of view with a clear structure of pial arterioles. Fig. 5E shows a shorter epoch, separating frequency components of Δ[HbT] below and above 0.04 Hz, and demonstrates that faster [HbT] components >0.04 Hz are still modeled by gamma-variate fitting to Thy1-GCaMP3 data during slow hemodynamic trends (Movie S8 shows equivalent data), whereas frequencies <0.04 Hz show vascular detail consistent with arterial dilations and constrictions across the field of view. Fig. S10 repeats this analysis for multiple urethane-anesthetized animals. In all cases, slow trends in Δ[HbT] are not well predicted by Thy1-GCaMP data and have vascular structure. In animals with bilateral cortical exposures, slow trends exhibit bilateral symmetry.

Fig. S10.

Demonstration of the spatial representation of slow hemodynamic trends in multiple urethane-anesthetized Thy1-GCaMP3 mice. Examples equivalent to Fig. 5 B–D are shown for four additional mice. In each example, time courses of unfiltered Δ[HbT] (green), its <0.04-Hz slow trend (yellow), and the corresponding fit from deconvolution (red) and gamma-variate (blue) models (Top) are compared with fits after removal of slow trends via 0.04-Hz high-pass filtering (below). All data were low-pass filtered at 2 Hz. Hemodynamics-corrected GCaMP also high-pass filtered at 0.04-Hz ∆F/F is shown in each case. In all cases, Pearson’s correlation coefficients are significantly improved when data are first high-pass filtered at 0.04 Hz to remove slow hemodynamic trends. Image sequences on the Right show the slow hemodynamic trend (temporally low-pass filtered at 0.04 Hz) over the entire duration of the trials on the Left. A and B with bilateral thinned-skull windows show bilateral symmetry of this slow 0.04-Hz slow trend. C and D with the zoomed-in fields of view show that slow trends involve constriction and dilation of pial arteries.

Slow trends in awake vs. anesthetized animals.

To determine whether slow hemodynamic trends are unique to urethane anesthesia, <0.04-Hz slow-trend removal analysis was repeated on all awake data (Fig. S11 shows all analysis in Fig. 3 repeated after >0.04-Hz HPF). With the caveat that awake but nonrunning data epochs were shorter in duration (30–60 s), and thus trends <0.033 Hz may not be fully represented, high-pass filtering awake data at 0.04 Hz before fitting had a much smaller effect on fit correlation coefficients than for anesthetized data (Fig. 5G) (average correlations changed from 0.51 ± 0.02 to 0.58 ± 0.02 for gamma-variate fitting and 0.64 ± 0.01 to 0.63 ± 0.01, n.s. P = 0.63, for deconvolution, all for n = 6, paired t test. Fig. 5H shows that high-pass filtering at 0.04 Hz removes significantly more variance from anesthetized data than data acquired in the awake brain (P = 0.015; n = 6; paired t test).

Fig. S11.

Results of awake resting-state neurovascular coupling analysis including high-pass filtering at 0.04 Hz to reduce slow trends (equivalent to Fig. 3). (A) Awake-mouse field of view under blue illumination. (B) Sixty-second examples of awake, resting-state Thy1-GCaMP6f ΔF/F time courses (after hemodynamic correction) with simultaneously recorded Δ[HbT] from the regions indicated in A. Red and blue traces show the results of convolving the corrected fluorescence signal with HRFs derived via deconvolution or gamma-variate fitting, respectively. (C) Deconvolved HRFs and best-fit gamma-variate HRFs for the two regions shown in A and B, illustrating the amplitude A_H, time of peak as T_H, and width at half-maximum as W_H gamma-fit parameters. (D, Left) Spatially resolved map of the gamma-fit Pearson correlation coefficients (r) per pixel and (Right) gamma-variate HRF parameters (A_H, T_H, and W_H) yielding the best-fitting Δ[HbT] to GCaMP fluorescence at each pixel, for the trial shown in B. (E) Example of fitting for the same trial. Top row shows corrected GCaMP ΔF/F, whereas the second row shows measured Δ[HbT]. The third row shows the gamma-variate model fit to Δ[HbT] based on the GCaMP signal. The bottom row shows fit residuals. Arrows mark specific neural events that are mirrored in later hemodynamics. (F) Plot of mean average and SD (over 16 × 16 pixels over S1) Pearson’s correlation of (F) deconvolution model and (G) gamma-variate fit for every resting-state trial in every animal. Values are ordered chronologically with dotted lines indicating recordings on different days and colors indicating different mice. Histogram to Right shows the distribution of average (over S1) Pearson’s correlation coefficient across all resting-state epochs in all trials in all awake mice. No significant improvement in fitting is seen after 0.04-Hz high-pass filtering compared with Fig. 3, indicating a reduced influence of slow hemodynamic trends in the awake condition.

Comparison of Resting-State Coupling in Awake and Anesthetized States.

HRFs generated in awake and anesthetized conditions across all trials and mice, calculated using both gamma-variate fitting and deconvolution, are compared in Fig. 6. The HRF in awake Thy1-GCaMP6f animals (using 0.02- to 2-Hz BPF) was consistently found to have a shorter time to peak (P < 0.005 for both models) and a narrower peak than anesthetized Thy1-GCaMP3 mice (0.04- to 2-Hz BPF) (Fig. 6C) (P < 0.005 for both models, double-sided Student’s t test; n = 6). These temporal features agree well with stimulus-evoked HRFs measured in awake and urethane-anesthetized rats (31), including the observation of stronger poststimulus undershoots in the awake state (38). Differences cannot be accounted for by the minimal (<0.1-s) difference between the temporal properties of these two GCaMP types, as demonstrated in Fig. 1 and Fig. S1 (25). However, HRF amplitudes between awake (all GCaMP6f) and anesthetized (all GCaMP3) conditions are not compared for this reason. Higher variance of HRF parameters in anesthetized animals may be due to the more widely varying physiological states of the animals during acute experiments compared with robust HRFs in awake animals (Fig. 6B).

Fig. 6.

Summary of HRFs derived from multiple analysis methods. (A and B) Comparisons of HRFs derived from gamma-variate fitting (blue) and deconvolution (red) in awake (A) and anesthetized (B) animals within the somatosensory cortex. Shaded regions show SEM across n = 6 mice in each group. (C) Parametric comparison of values from gamma-variate fits (averaged over S1), A (*P = 0.024, n.s. P = 0.66), T (n.s. awake P = 0.76, anesth P = 0.094, ***P < 0.005), W (n.s. awake P = 0.88, n.s. anesth P = 0.76, ***P < 0.005) (all paired-wise t test, n = 6) group. (D) Spike-triggered averaging for awake and anesthetized animals. Plots show the average among animals; shading shows SEM across animals (n = 6 mice in each group).

Spike-triggered averaging was also performed on data from both awake and anesthetized mice, averaging hemodynamic changes in [HbT], [HbO], and [HbR], corresponding to events identified within resting-state GCaMP recordings (Fig. 6D) (36). This method is not constrained to an expected hemodynamic model and was performed on GCaMP data without hemodynamic correction, and without high or low-pass filtering of hemodynamic data. Results show clear correlated increases in [HbT] and [HbO] with decreases in [HbR], consistent with functional hyperemia, and agree well with the properties of awake and anesthetized HRFs modeled by gamma-variate fitting and deconvolution (Fig. 6D). The anesthetized response agrees well with results reported in resting-state, urethane-anesthetized rats (36). Spike-triggered averaging provides strong, independent evidence that spontaneous neural activity in the resting-state awake or anesthetized brain is coupled to local, correlated functional hyperemia.

SI Materials and Methods

Animal Preparation.

For mice in the anesthetized group, six adult Thy1-GCaMP3 mice [The Jackson Laboratory; B6; CBA-Tg(Thy1-GCaMP3)6Gfng/J] were anesthetized with 1.5 mg/kg urethane administered intraperitoneally, accompanied with 0.5 mg/kg glycopyrrolate. The animal’s core body temperature was monitored and maintained at 36.5 ± 0.5 °C using a homeothermic temperature controller (FHC; 40-90-8D). After the mouse was securely positioned in a stereotaxic frame (Kopf), the scalp was retracted and the skull between the coronal and lambdoid sutures was thinned to translucency. Wide-field optical mapping (WFOM) data were then acquired (18). The animal’s heart rate, breathing rate, and arterial oxygen saturation throughout both surgery and imaging were monitored with a rodent pulse oximeter (Kent Scientific; MouseSTAT). Resting-state trials were acquired for periods of 180 s, and no stimulation was given during these recordings. Electrophysiology methods are described below.

For awake studies, six adult Thy1-GCaMP6f mice [The Jackson Laboratory; C57BL/6J-Tg(Thy1-GCaMP6f)GP5.17Dkim/J] were handled and acclimated to a saucer-wheel treadmill. Animals were then anesthetized with isoflurane; their scalp was retracted and skull thinned over the entire accessible superficial cortex. The thinned skull was then protected with a layer of cyanoacrylate glue, and a custom acrylic headpiece surrounding the craniotomy region was glued onto the skull. Following this preparatory surgery, mice were recovered, receiving buprenorphine analgesic for 72 h postoperatively. A removable layer of Kwik-Sil (WPI) silicone is applied to the cranial window between imaging sessions to provide mechanical protection. One week after window implantation, the animals were imaged in sessions lasting up to 2 h with at least 3 d between each session. For each imaging session, the animal was lightly anesthetized with isoflurane during initial head fixation and was then fully recovered before imaging began.

Mice were allowed to stand, walk, or run freely on a customized transparent saucer-wheel treadmill during imaging. A camera positioned underneath the animal tracked the treadmill’s rotation and hence the animal’s movement in synchrony with imaging of the brain. Up to 40 repeated 60-s resting-state trials were acquired during each imaging session. Trials with at least a continuous 30 s of the animal not moving were identified, and only these nonrunning epochs were included in “resting-state” analysis. Awake animals were trained with acclimatization and handling, and were given treats after imaging. No food or water deprivation was used.

Electrophysiology Acquisition and Analysis.

Simultaneous optical imaging and electrophysiology recordings was performed on urethane-anesthetized Thy1-GCaMP3 animals. In one-half of the animals, a piece of skull (2 × 2 mm) overlaying the somatosensory cortex was carefully removed (e.g., Fig. S1B). In the other half, a unilateral thinned-skull craniotomy was prepared between the coronal and lambdoid sutures, and a small (<200-μm) piece of skull overlying the responding region was removed to allow electrode insertion while imaging was performed through surrounding thinned skull (e.g., Fig. S1 A and C). WFOM imaging during hindlimb stimulation was performed to confirm the location of the somatosensory cortex. A well was then built up around the cranial window with dental acrylic (Henry Schein) and filled with artificial cerebrospinal fluid (ACSF: 124 mM NaCl, 5 mM KCl, 4.1 mM CaCl₂, 10 mM C₆H₁₂O₆, 2.8 mM MgCl, 10 mM C₈H₁₂N₂O₄S). A tungsten single-channel microelectrode (0.5 MΩ; A-M Systems) was then advanced into the somatosensory hindpaw region to a depth of 300∼600 µm by a micromanipulator that was mounted on the stereotaxic frame. The ACSF fluid in the well covering the cortical window served as the ground for the electrophysiological recordings. The animal’s heart rate, breathing rate, and arterial oxygen saturation throughout both surgery and imaging were monitored with a rodent pulse oximeter (Kent Scientific; MouseSTAT).

A differential AC amplifier (model 1700; A-M Systems) was used with 1,000× gain, and the signal was then sampled at 25 kHz (Micro 1401; CED). The high-frequency band (500–3,000 Hz) of the recorded signal was analyzed using spike detection in the Spike2 software (CED). Specifically, the high-frequency signal was thresholded by 2.5 times the SD, and then detected spikes went through template matching to make sure at least 20 repetitions of similar spikes appeared within 60 s. The sorted spikes were then combined together and treated equally as MUA. The time stamps of detected MUAs were then loaded in MATLAB (MathWorks) for further analysis.

Optical Hemodynamic and GCaMP Fluorescence Imaging.

Simultaneous wide-field GCaMP fluorescence and cortical hemodynamics were imaged using WFOM as described in refs. 18 and 20. WFOM can map the dynamics of oxyhemoglobin and deoxyhemoglobin (HbO and HbR) concentrations based on their oxygen-dependent optical absorption spectra. Multispectral reflectance data are acquired interlaced with fluorescence data by using a camera configured to acquire images in synchrony with three strobing light-emitting diodes (LEDs). Reflectance images were acquired during periods of green LED light illumination at 530 nm (M530L2; Thorlabs; with 534/43-nm filter, NT67031; Edmund Optics) or red LED light illumination at 630 nm (M625L2; Thorlabs), whereas a 500-nm long-pass filter (FF01-496/LP-25; Semrock) mounted in front of the camera enabled imaging of GCaMP fluorescence during periods of illumination with blue LED light with a wavelength around 490 nm (M490L2; Thorlabs; with 460/60-nm filter, FB460-60; Thorlabs).

For anesthetized animals, a CCD camera (Dalsa; 1M60) was operated at 45 or 75 frames per s (equivalent three-color frame rate in each channel is 15 or 25 Hz) with 6- to 8-ms exposure and 8 × 8 binning (128 × 128 pixels), mounted with a VZM300 optical zoom lens (Edmund Optics) with operating magnification ranged from 2.5 to 3× (equivalent field of view: 4.1 mm × 4.1 mm). Awake animals were imaged using an EMCCD camera (ANDOR Ixon 897) at 31.22 Hz (equivalent frame rate per spectral channel, 10.41 Hz) with 5-ms exposure and no binning (512 × 512 pixels; equivalent field of view, 8.2 mm × 8.2 mm), mounted with an AF Micro-NIKKOR 60-mm lens (Nikon).

Green and red reflectance data were converted to changes in HbO and HbR concentrations using the modified Beer–Lambert law with Monte Carlo-derived wavelength-dependent pathlength factors (18, 21, 23, 64–66). Interspersed fluorescence images of genetically encoded GCaMP were hemodynamic corrected (as described in more detail below) and converted into ΔF/F, where ΔF is the mean-subtracted raw fluorescence signal and F is the mean of the entire time course.

Imaging Data Preconditioning and Statistics.

For pixelwise HRF fitting, 512 × 512 imaging data from awake animals were downsampled to 128 × 128 to reduce computation time (Fig. 3 D and E). Anesthetized data with a unilateral field of view were analyzed at their native 128 × 128 resolution (Fig. 5 D and E). Anesthetized data with a bilateral field of view were analyzed, downsampled to 64 × 64 resolution (Fig. S7).

Unless otherwise noted, nonrunning awake resting-state epochs ranging from 30 to 60 s in duration were temporally bandpass filtered at 0.02–2 Hz (both fluorescence and hemodynamic signals), with a 2-Hz low pass chosen to reduce physiological noise such as heart rate, and the 0.02-Hz high pass to detrend the baseline. Analysis was repeated with a 0.04-Hz high-pass filtered as noted and shown in Fig. S11.

In most anesthetized results shown, fluorescence and hemodynamic signals were temporally bandpass filtered at 0.04–2 Hz, unless otherwise noted (e.g., Fig. S7). A 0.04-Hz HPF was found to reduce the influence of slow hemodynamic trends as described in the text. All of the filtering was performed using a zero-phase filter (filtfilt) in MATLAB (MathWorks).

GCaMP Fluorescence Correction for Hemodynamic Cross Talk.

As described in the main manuscript, it is important to note that both the excitation and emission wavelengths of GCaMP fluorescence are absorbed by HbO and HbR, whose concentrations are known to be varying substantially over time. If this contamination is not corrected, it could influence analysis of the coupling relationship between neural activity and hemodynamics. However, approximate correction of GCaMP signals can be achieved, especially if simultaneous hemodynamics are acquired via reflectance measurements (18).

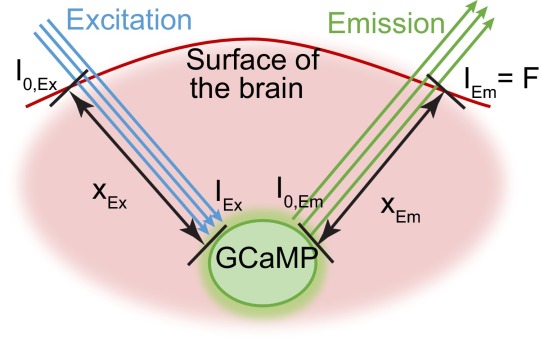
The contamination of GCaMP fluorescence signals from the absorption of excitation and emission light can be described the modified Beer–Lambert law (see diagram below depicting light paths to and from GCaMP-expressing neurons):

$$\frac{I_{Ex}}{I_{0,Ex}}=e^{\left(-{\mu }_{a,Ex}{x}_{Ex}\right)}\hspace{0.17em}\text{and}\hspace{0.17em}\frac{I_{Em}}{I_{0,Em}}=e^{\left(-{\mu }_{a,Em}{x}_{Em}\right)},$$ [S1, S2]

where I₀ is the incident intensity and I is the transmitted intensity. x is the mean path of light traveled, μ_a,λ is the wavelength (λ)-dependent absorption coefficient of the tissue, and the geometry below is assumed.

The amount of excitation light converting to fluorescence emission can be described by the following:

$$I_{0,Em}=I_{Ex}\cdot \sigma \cdot c_{GCaMP}\left(t\right),$$ [S3]

where σ represents fluorescence efficiency of GCaMP, which can be assumed to be a constant for a given intracellular calcium concentration, and c_GCaMP is the concentration of intracellular calcium.

Substituting Eqs. S1 and S2 into Eq. S3, the GCaMP fluorescence emission light emerging from the brain (I_Em) (the readout of our imaging system) can be expressed as follows:

$$F\left(t\right)=I_{Em}=I_{0,Ex}{e}^{-\left({\mu }_{a,Ex}\left(t\right)x_{Ex}+{\mu }_{a,Em}\left(t\right)x_{Em}\right)}.\sigma .c_{GCaMP}\left(t\right).$$ [S4]

The value of F(t) is determined by I_0,Ex and σ, which are difficult to accurately determine, but the change of F(t) relative to baseline cancels these factors, yielding the following:

$$\frac{\mathrm{\Delta }F\left(t\right)}{\overline{F}}=e^{-\left(\mathrm{\Delta }{\mu }_{a,Ex}\left(t\right)x_{Ex}+\mathrm{\Delta }{\mu }_{a,Em}\left(t\right)x_{Em}\right)}.\frac{\mathrm{\Delta }{c}_{GCaMP}\left(t\right)}{\overline{c_{GCaMP}}},$$ [S5]

where the bars represent the average of the trial over time. Thus, the detected fractional change in GCaMP fluorescence is approximately equal to the fractional change in the neural intracellular calcium concentration, scaled by a time-varying multiplicative factor corresponding to time-varying hemoglobin absorption at both the GCaMP excitation and emission bands.

The time-varying absorption coefficient of brain is different at the excitation and emission wavelength bands of GCaMP fluorescence because the primary chromophores in brain at visible wavelengths are HbO and HbR. μ_a,λ can be expressed as a sum of these two chromophores:

$$\mathrm{\Delta }{\mu }_{a,\lambda }\left(t\right)={\xi }_{HbO,\lambda }\mathrm{\Delta }\left[HbO\right]\left(t\right)+{\xi }_{HbR,\lambda }\mathrm{\Delta }\left[HbR\right]\left(t\right),$$ [S6]

where ${\xi }_{\lambda }$ is the wavelength-dependent specific extinction coefficient of HbO or HbR, and [HbO] and [HbR] are their concentrations. Our two reflectance measurements can thus be modeled as follows:

$$\frac{I_{530\mathrm{nm}}\left(t\right)}{{\overline{I}}_{530\mathrm{nm}}}=e^{\left(-\mathrm{\Delta }{\mu }_{a,530\mathrm{nm}}\left(t\right)x_{530\mathrm{nm}}\right)}\hspace{0.17em}\text{and}\hspace{0.17em}\frac{I_{630\mathrm{nm}}\left(t\right)}{{\overline{I}}_{630\mathrm{nm}}}=e^{\left(-\mathrm{\Delta }{\mu }_{a,630\mathrm{nm}}\left(t\right)x_{630\mathrm{nm}}\right)},$$ [S7, S8]

although here it should be noted that the pathlength x_λ represents the average distance of reflectance photons scattering into and out of the tissue, and may not be identical to the excitation or emission pathlengths in the GCaMP case.

Reflectance measurements were used to derive an estimate of μ_aEx(t), where Ex ∼ 490 nm. This was achieved using Eqs. S6–S8, which are already used to convert I(t)/$\overline{I}$ reflectance data into Δ[HbO] and Δ[HbR]. If, for every pixel, values of Δ[HbO] and Δ[HbR] are calculated, these can be used to estimate μ_a490nm(t) using Eq. S6 and the known extinction coefficients of HbO and HbR. An improved estimate of μ_aEm(t) for the emission band of GCaMP can be calculated in the same way. These values can then be used in Eq. S5, with estimates of the pathlength factors x_Ex and x_Em chosen (x_Ex = 0.56 mm⁻¹, x_Em = 0.57 mm⁻¹ in this case; as constants across the image and dataset) that minimize the appearance of vessel artifacts in the hemoglobin-corrected GCaMP images.

Optimizing Gamma-Variate Functions in Fits of GCaMP Response and HRF.

A gamma-variate function was chosen as the kernel to convolve with the time stamp of MUA to predict GCaMP fluorescence (Γ_G) and to convolve with corrected GCaMP fluorescence to predict hemodynamics (Γ_H). The function is defined by three parameters A, T, and W, where

$$\mathrm{\Gamma }\left(t\right)=A\cdot {\left(\frac{t}{T}\right)}^{\alpha }\cdot e^{-\frac{t-T}{\beta }},$$ [S9]

wherein $\alpha ={\left(T/W\right)}^2*8*\log \left(2\right)$, $\beta =\left(W^2/T\right)*8*\log \left(2\right)$. A represents the maximum amplitude, T is the time delay of the peak, and W is full width at half-maximum (Fig. 3C) (30). The total duration of the kernel convolved with the data were set to be 3 s for Γ_G (MUA to GCaMP fluorescence kernel) and 30 s for Γ_H (HRF). To determine these function parameters, optimal values were calculated using the constrained multivariable optimization function in MATLAB (fminsearchbnd, MATLAB File Exchange), minimizing the sum square difference between the predicted and original signal. All of the parameters were constrained to be positive real numbers.

Estimating HRF by Least-Square Deconvolution.

Another method used to estimate the HRF from GCaMP fluorescence and cortical hemodynamics is least-square deconvolution. For a linear system, the convolution can be expressed as follows:

$$\left[\begin{array}{c}\begin{array}{c}{y}_1\\ y_2\end{array}\\ \begin{array}{c}{y}_3\\ ⋮\\ y_t\end{array}\end{array}\right]=\left[\begin{array}{cc}\begin{array}{ccc}{x}_1& 0& 0\\ x_2& x_1& 0\\ x_3& x_2& x_1\end{array}& \begin{array}{cc}\dots & 0\\ \dots & 0\\ \dots & 0\end{array}\\ \begin{array}{ccc}⋮& ⋮& ⋮\\ x_t& x_{t-1}& x_{t-2}\end{array}& \begin{array}{cc}\ddots & ⋮\\ \dots & x_{t-n}\end{array}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{h}_1\\ h_2\\ h_3\end{array}\\ \begin{array}{c}⋮\\ h_n\end{array}\end{array}\right],$$ [S10]

or y = X*h, where X is the system’s input in matrix format, which is changes in fluorescence; y is the system’s output with the length of observations (t), which is the Δ[HbT]; and h is the system’s impulse function, which is the HRF in the context of neurovascular coupling; and its length n is assigned by the user. In our analysis, n was assigned to be one-half of the length of the trial (t/2) or 30 s if the half-length is bigger than that.

Instead of using the direct solution to this linear system:

$$h=X\backslash y,$$ [S11]

a diagonal loading least-square deconvolution method was used to solve for the HRF to avoid the problem of rank deficiency. This least-square method minimizes cost function:

$$J\left(x\right)={\Vert y-Xh\Vert }_2^2+\lambda {\Vert h\Vert }_2^2,$$ [S12]

which is the weighted sum of the energy of the error (${\Vert y-Xh\Vert }_2^2$) and the solution (${\Vert h\Vert }_2^2$). By setting the derivative of the cost function to zero, the solution is given by the following:

$$h={\left(X^{T}X+\lambda I\right)}^{-1}{X}^{T}y.$$ [S13]

The constant weight λ was chosen to be 0.01 throughout our analysis. The first 10 s of the deconvolved function was used as HRF (67). The deconvolution was operated on each pixel individually.

Spike-Triggered Averaging.

As an independent method for analysis of neurovascular coupling, spike-triggered averaging can demonstrate the averaged effect of neural events on a variable without involving estimation of HRFs (36). Spike events were defined as local maxima in the uncorrected ΔF/F time courses from somatosensory cortex and identified using the “findpeaks” function in MATLAB. A local peak was defined as one 0.3% (percentage as the unit for ΔF/F) higher than an adjacent valley and with a full width at half-maximum of at least 0.3 s. The changes in uncorrected GCaMP fluorescence, Δ[HbT], Δ[HbR], and Δ[HbO] 3 s before to 10 s after each identified peak event were averaged across all trials within each animal (for awake and anesthetized conditions separately). Plots show the average spike-triggered averages among animals. Shaded regions represent the SEM between animals.

Frequency-Dependent Cross-Correlation Analysis.

Cross-correlation analysis between Thy1-GCaMP6f and ∆[HbT] measurements was performed as a function of temporal frequency. To ensure consistent sampling in the frequency domain, only the last 30 s in each awake resting-state epoch was used in this analysis. Unfiltered ∆[HbT] and corrected Thy1-GCaMP6f fluorescence data from the somatosensory region of all awake resting-state trials were bandpass filtered with a 0.35-Hz sliding window in the frequency domain from 0.035 to 5.2 Hz with an increment of 0.035 Hz. Bandpass-filtered neural and hemodynamics were then cross-correlated. The peak amplitude of the cross-correlation within a −5- to 5-s window around 0 shift was determined, along with its phase delay for each epoch. Plots of the peak cross-correlation coefficient and phase delay as a function of frequency were then averaged within animals. Plots show the mean ± SEM between animals, with frequencies denoting the start of the frequency window. The peak correlation frequency was determined from the grand average. The phase delay was calculated as the mean and SD of phase delays between animals at the peak correlation frequency.

Statistical Analysis.

Goodness of fit between measured and modeled Δ[HbT] data were evaluated using Pearson’s correlation coefficients. Statistical analyses were performed using a two-tailed Student t test (all pairwise comparisons are specified). All of the results are expressed in the form of mean ± SEM, unless specified. All data analyses were performed using MATLAB (MathWorks).

Discussion

This study used wide-field optical imaging of both neural GCaMP and cortical hemodynamics in awake and anesthetized mice to visualize underlying neural correlates of resting-state hemodynamics. Electrophysiological recordings demonstrated that measured Thy1-GCaMP signals (after hemodynamic correction) could be predicted from MUA, corresponding to spiking of excitatory neurons. Thy1-GCaMP imaging of the bilaterally exposed cortex revealed rapidly changing patterns of symmetric, spontaneous resting-state neural activity in both awake and anesthetized conditions.These patterns of neural activity were shown to predict resting-state hemodynamics across the cortex via a linear HRF-based convolution. Both gamma-variate and deconvolution-based fitting performed well, although slow hemodynamic trends in some anesthetized animals (<0.04 Hz) were not well predicted by Thy1-GCaMP recordings. Together, these results demonstrate that successive hyperemias coupled to distinctive patterns of neural network activity are a major contributor to resting-state hemodynamics.

Comparison with Prior Studies of Resting-State Neurovascular Coupling.

Prior studies exploring resting-state neurovascular coupling have reported relatively low correlations between fMRI BOLD signals and electrophysiological recordings, typically around 0.3 (15–17). We attribute the higher correlation values shown here to a number of factors: (i) high-speed wide-field GCaMP imaging acts as a spatiotemporal integrator, averaging ensemble activity of multiple neurons at a given site and over the time between measurements. The use of Thy1-GCaMP mice enabled selective sensitivity to spiking activity in excitatory neurons, without contributions from other brain cells, other types of electrical activity, or interference from confounds such as simultaneous fMRI acquisition. This integration and selectivity combined might more readily reveal correlations and trends between distant groups of neurons that cannot be appreciated from single-unit recordings, or two-photon microscopy observations of small, unilateral fields of view. (ii) Improvements in GCaMP, illumination sources, and cameras enabled high-speed, large–field-of-view imaging of spontaneous neural activity and concurrent hemodynamics with good signal-to-noise with no averaging. The resulting clear view of patterns of bilaterally synchronous spontaneous neural activity in the awake brain ensure that signals are not contaminated by movement artifacts or other experimental confounds, which can be difficult to distinguish in single-point measures. (iii) The analysis approach used here assumed a neurovascular coupling model in which neural events would (directly or indirectly) evoke a stereotyped Δ[HbT] response, a model with a strong physiological basis (28). HRF parameters were allowed to vary over the cortex to account for expected differences in the dynamics of different vessel types (18, 37, 39, 40). It should be noted that best-fit HRFs were generated for each run and were not assumed to stay constant over time. Our methods therefore test the goodness of fit of an HRF-based linear convolution model but do not cross-validate this model assuming a time-invariant HRF. Finally, analysis focused on modeling Δ[HbT] rather than Δ[HbR], assuming a linear neurogenic hyperemia model and removing the need to account for oxygen consumption as another variable (although Δ[HbT] was shown to be strongly correlated to Δ[HbR], and thus anticipated BOLD signals). (iv) fMRI data are typically acquired at <0.5-Hz volume rates, although longer epochs give access to lower frequencies than examined here. Our HRF analysis revealed that the awake mouse brain has a temporally narrow resting-state hemodynamic response, and frequency-dependent correlation analysis revealed a peak correlation at 0.21 Hz. The temporal resolution of prior fMRI comparisons may thus not have been sufficient to capture hemodynamic coupling at its peak correlated frequency. (v) The removal of hemodynamic cross talk and baseline trends was found to be important in performing fitting analysis. Slow hemodynamics trends seen in some anesthetized animals strongly degraded fitting and correlations. Bilateral imaging enabled the different spatiotemporal patterns of slow trends to be distinguished from higher-speed events predicted by GCaMP imaging.

Together, these factors combined to yield fits across multiple trials and animals exceeding correlations of 0.8 in both awake and anesthetized states.

What Do Observed Patterns of Spontaneous Neural Activity Represent?

Wide-field Thy1-GCaMP imaging revealed bilaterally symmetric, synchronous fluctuations in neural activity across the brain, in both awake and anesthetized states, which were shown to be spatiotemporally coupled to resting-state fluctuations in hemodynamics (Movies S2, S3, and S7). Previous reports using both voltage-sensitive dyes and wide-field GCaMP imaging have noted similar bilaterally symmetric cortical patterns of neural activity, inferring functional connectivity between temporally correlated regions (26, 41). Kozberg et al. (19) demonstrated the transition of spontaneous cortical neural events from unilateral to bilateral in mice between postnatal day 7 (P7) and P14, a period of postnatal development where transcallosal axonal projections are establishing, suggesting a direct link between neural activity patterns and physical networks. Widespread correlations and apparent waves of activity given by correlations between fMRI and discrete LFP recordings have also been noted in the primate brain (16). However, the origin and the physiological meaning of these patterns of neural activity remain controversial (42).

Waves and bursts of neural activity in the cortex are typically reported under conditions of non-rapid eye movement sleep (43), anesthesia (urethane, ketamine), and quiet wakefulness (41, 44). Such events are characterized by alternating subthreshold cortical membrane depolarization and hyperpolarization (UP/DOWN states), slow-wave activity that has been associated with memory consolidation (45), and shaping responses to incoming stimulation (46). Although electrophysiological recordings in both animals (12, 47) and awake human subjects (13) have demonstrated symmetry of spontaneous neural activity, characterization of brain-wide patterns of spontaneous neural activity in the awake brain has been limited (14).

We propose that resting-state neural fluctuations observed here might represent modulations in local excitability within specific functional circuits. A modulation in excitability would increase the likelihood of neuronal firing within a region, but would not necessarily cause the same neuron to fire each time excitability increased. This mechanism could explain why neural network correlations are less evident in cellular-level recordings but are clear in spatiotemporally-integrated wide-field Thy1-GCaMP recordings.

Examining raw Thy1-GCaMP traces and movies (e.g., Movie S4), symmetric neural patterns can be seen to change rapidly from frame to frame. However, a clear enveloping of neural activity can also be seen in most cases, where neural events periodically become more frequent or cluster to form higher amplitude GCaMP signals, preempting subsequent increases in local [HbT]. Fig. S9 shows how this slow enveloping is essential to observe hemodynamic variance. Frequency-resolved cross-correlations (Fig. 4) confirm that hemodynamics and GCaMP share a low frequency component from which neurovascular correlations arise (48) (although we note from Movie S4 that higher frequency coherence between neural activity in functionally-connected regions is also evident).

A relationship between this neural enveloping and rhythmic neocortical UP and DOWN states may relate the detectability of functional connectivity networks to brain state (13). Synchronization of activity in the LFP gamma band during UP states (49) might explain previous findings of correlations between gamma band LFP and fMRI signals (15, 17, 35). However, since Thy1-GCaMP measurements provide sensitivity to spiking activity, with no expected representation of subthreshold membrane potential, our results demonstrate that resting-state hemodynamics result from a pathway of events that includes modulation in the spike rate of excitatory neurons, an effect that may be causally or otherwise coupled to modulations in gamma band LFP (16).

It should also be noted that our results do not exclude the contribution of other cellular activity to resting-state hemodynamics. Interneurons, for example, have been implicated to play a role in neurovascular coupling (38, 50), although there has also been significant debate regarding the BOLD response that should result from interneuron activation (51–54). Our results demonstrate that the activity of excitatory neurons is correlated to resting-state hemodynamics. However, any other form of cellular activity in the brain that is spatiotemporally coupled to neural spiking could thus also be correlated to resting-state hemodynamics. For example, spontaneous interneuron activity could feasibly be correlated to the modulation of excitatory neural activity and could therefore share a correlation with resting-state hemodynamics. This possibility also underscores that correlation does not imply causality. Similarly, synchronous activation of astrocytes, pericytes, or interneurons in the context of neurovascular coupling could contribute to the properties of the HRF, with the delayed undershoot observed in our awake, deconvolved HRFs (Fig. 6A) being particularly interesting in the context of interneuron involvement (38). Thus, although our studies here focused on correlations between excitatory neural activity and resting-state hemodynamics, further work is needed to chart the cellular pathways and dependencies of both neuromodulation, and neurovascular coupling in the resting state.

Effects of Anesthesia and Slow Hemodynamic Trends.

Despite differences in the temporal shape of HRFs between urethane-anesthetized and awake mice, our results demonstrate that resting-state coupling between excitatory neurons and hemodynamics is intact in both conditions. In some cases, anesthetized animals were found to exhibit large, slow (<0.04-Hz) hemodynamic trends that were not well predicted by simultaneous GCaMP recordings. However, despite poor fitting, these periods did not represent complete “uncoupling,” because removal of the slow hemodynamic component using a 0.04-Hz HPF left residual hemodynamics that could still be well predicted by local GCaMP fluctuations.

In considering the origin of these slow hemodynamic trends, it should again be noted that Thy1-GCaMP fluorescence selectively reports spiking activity in excitatory neurons in layers 2/3 and 5. Slower hemodynamic trends could thus be driven by other neuronal or cellular components of the brain whose activity is not spatiotemporally coupled to excitatory neural activity. Many prior studies have reported that activation or inhibition of structures such as the basal forebrain (nucleus basalis of Meynert) and the locus coeruleus (55, 56) can modulate cortical blood flow and might be expected to have lower spatial specificity, consistent with the spatial patterns of slow trends shown in Fig. S10. Pisauro et al. (57) demonstrated “global” hemodynamic fluctuations in awake mice that correlated with pupil diameter, which infers brain arousal or alertness, whereas similar results were also found in awake behaving primates by Cardoso et al. (30). Interneuron subtypes capable of altering blood flow may also play a role here (50), whereas systemic blood pressure changes (23), or even activities such as running (58) and anticipation (59) have been shown to cause blood flow modulations. Hemodynamics caused by these mechanisms may not be driven by the same neural pathways captured through recordings of local cortical spiking in Thy1-GCaMP mice. If the spatial dependencies of these alternative coupling mechanisms are different from local coupling, they could feasibly influence derived functional connectivity networks if present in resting-state fMRI data.

Implications for Resting-State fMRI.

The results presented here demonstrate the clear presence of network-like, bilaterally-symmetric spontaneous neural events in the awake and anesthetized brain that are predictive of spatiotemporal patterns of resting-state hemodynamics. These findings suggest a firm basis for resting-state functional connectivity mapping as resolving the properties of network-based modulations in the spike rate of excitatory neurons. Coupling was most robust in the awake mouse brain, a closer state to awake human studies than conditions under anesthesia. Model-based fitting results imply a linear relationship between neural activity and hemodynamics in the resting state, although best fits were achieved using region-specific HRFs (60–63).

However, our ability to visualize excitatory neural activity also underscored that linearly-coupled resting-state hemodynamics are accompanied by noise, experimental variance, and additional hemodynamic trends that might represent other neural, cellular, or systemic components. Isolation of neurally-coupled signals in resting-state fMRI data is thus a major challenge. Nonspecific preconditioning such as low-pass filtering and global regression could feasibly yield inferred networks with different dependencies on brain state, physiology, epoch duration, or other components of brain activity. The results presented here are the first step towards characterizing both the properties and dependencies of neural network activity and its spatiotemporal coupling to hemodynamics, and could ultimately yield new, more robust approaches to fc-fMRI analysis.

Materials and Methods

Simultaneous WFOM of hemodynamics and GCaMP fluorescence data were acquired on Thy1-GCaMP3 mice (n = 6) under urethane anesthesia, and awake Thy1-GCaMP6f mice (n = 6). All of the data were processed using a zero-phase temporal filter. No spatial smoothing was used. All of the results are expressed as mean ± SEM, unless otherwise stated. For detailed information, see SI Materials and Methods. All experimental procedures were reviewed and approved by the Columbia University Institutional Animal Care and Use Committee.