Features of owl wings that promote silent flight

Abstract

Owls are an order of birds of prey that are known for the development of a silent flight. We review here the morphological adaptations of owls leading to silent flight and discuss also aerodynamic properties of owl wings. We start with early observations (until 2005), and then turn to recent advances. The large wings of these birds, resulting in low wing loading and a low aspect ratio, contribute to noise reduction by allowing slow flight. The serrations on the leading edge of the wing and the velvet-like surface have an effect on noise reduction and also lead to an improvement of aerodynamic performance. The fringes at the inner feather vanes reduce noise by gliding into the grooves at the lower wing surface that are formed by barb shafts. The fringed trailing edge of the wing has been shown to reduce trailing edge noise. These adaptations to silent flight have been an inspiration for biologists and engineers for the development of devices with reduced noise production. Today several biomimetic applications such as a serrated pantograph or a fringed ventilator are available. Finally, we discuss unresolved questions and possible future directions.

1. Introduction

Bird flight has always inspired humans and was especially important for the development of early flight machines like those of Lilienthal. Bird flight continues to inspire biologists and engineers. Attempts to create flapping air vehicles have been successful (e.g. SmartBird: https://www.festo.com/group/de/cms/10238.htm (accessed 9 August 2016)). This issue contains several papers dealing with recent advances in our understanding of bird flight [1,2] and its possible role model for technical applications [3–5]. When trying to use the biological adaptations in biomimetic approaches to problems in the flight of airplanes, it has to be recognized, however, that bird flight differs from the flight of technical aircraft in several respects. First, birds have flexible wings, and use these wings for different modes of flying, among them gliding flight and flapping flight. Second, the aerodynamic characteristics of bird flight differ from those of aircraft. This is especially obvious in the Reynolds number range in which birds operate (less than 10⁶), which is closer to that of model airplanes and small drones than of commercial airplanes. This suggests that bird flight might serve as a role model for airplanes only for the solution of specific problems.

We concentrate here on a specific effect of flight: the noise produced during flight, more precisely, mechanisms that reduce noise production. Reduction of noise is in our view one of the specific problems mentioned in the last section where the biological solutions can serve as a role model. Noise may just be regarded as an unwanted side effect of flying. However, apart from being wasted energy, noise has also detrimental effects. This is especially important for people living close to airports. Noise produced by airplanes has been implicated in health problems such as increased blood pressure. Thus, it is one goal of the aircraft industry to reduce noise produced by airplanes. Likewise, noise generated by fans—be it from computers or from air conditioners—is often disturbing and also needs to be reduced. Noise production cannot, however, be dealt with independently of morphology and aerodynamics. Thus, in this review, we integrate these different directions of research.

Mechanisms of noise reduction have evolved in one order of birds, owls (Strigiformes). Owls occupy many different ecological niches [6]. Some of them like the snowy owl (Bubo scandiacus) are largely diurnal. However, many owl species hunt at night by using auditory information for prey localization [7,8]. To do so effectively, these birds have a highly developed auditory system with a very low hearing threshold [9,10]. Owls also possess a visual system adapted to low light conditions [11,12]. The low hearing threshold would not help the owl, however, if the bird made noise during hunting. This may be the reason why owls developed a silent flight. In the following, we first review early observations on the adaptations of owls to silent flight. Then we discuss recent advances in the field including some technical applications inspired by the silent flight of owls before we finish with a section of open questions.

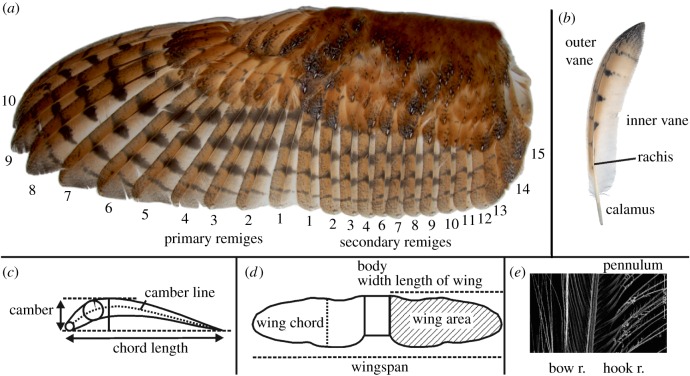
Before we start reviewing the data, we briefly summarize wing and feather morphology (figure 1). We concentrate on the elements that will be important further on. Bird wings are formed by bones of the forelimb and by feathers. Figure 1a shows a barn owl wing. Two major groups of flight feathers (primaries and secondaries) are attached to the skeletal elements of the forelimb and its integument. The 10 primaries are embedded in the soft tissue of the hand wing, while the secondaries are firmly connected to the leading edge of the ulna. A wing may be characterized by its chord length, wing span, wing area, thickness and camber (figure 1c,d). The camber is the quotient of the deviation of the centre line of a wing, the camber line, from the line connecting the leading and trailing edge of the wing, and the chord length. The quotient of wing span and chord length gives the aspect ratio, while the area divided by the weight of the animal gives wing loading. Aspect ratio and wing loading are characteristics for different flight types [13]. The leading edge faces into the air stream that is characterized by the freestream velocity. When the air flows over the surface, the flow field may take a complex shape. Apart from a boundary layer with reduced velocity, vortices may arise and, depending on the angle of attack, separation bubbles may occur. The aerodynamic behaviour may be described by the shear stress and the lift and drag coefficients, among others.

Figure 1.

Owl wing and feather. (a) Topography of a barn owl wing viewed from above. Primary and secondary remiges are numbered. (b) Tenth primary of a barn owl wing. (c,d) Definition of wing parameters. Note that the usage of the term ‘chord’ is as is done in engineering. (e) Close-up view on a feather vane.

A feather consists of a shaft and a vane (figure 1b). The shaft divides into the calamus and the rachis. The vane is subdivided into an outer and inner vane. The vane consists of barbs which again have barbules or radiates. The posterior or proximal barbules are called bow radiates, and the anterior or distal barbules have hooklets and are called hook radiates (figure 1e). In contour feathers, the radiates cross-connect to form a closed vane. Hair-like extensions, called pennula, may be found at the end of the radiates.

2. Early observations

Morphological specializations on owl wings have been noticed by early biologists and engineers alike. In this section, we briefly summarize what we consider to be important contributions in the years before 2005, without the claim of completeness. We start with the work by Mascha [14], who mentioned that the serrations on owl wings are a long-known fact. This author also recognized the elongated pennula as source of the soft surface of the wing of owls. As it feels like velvet, we shall call it velvet-like surface in the following. Graham [15] added the trailing-edge fringes as a third adaptation to silent flight. Graham also stated that ‘It would, therefore, be a mistake to ignore birds as a guide to possible future developments’ (of airplanes (added by the authors)) (p. 837), thus setting the stage for using the adaptations on owl wings as role models for biomimetic applications. Sick [16] provided detailed quantitative information for the aforementioned feather adaptations, which included comparisons of the adaptations from different owl species. Hertel [17] provided a first explanation of how the downy upper surface might prevent noise: he claimed that the velvet-like surface serves as a kind of cushion so that the feathers can slide soundlessly on one another.

To the best of our knowledge, the first quantitative measurements were conducted in the early 1970s. Gruschka et al. [18] studied the noise production of a gliding barred owl (Strix varia). These authors observed sound pressure levels that were inaudible to humans at 3 m distance and further away. These authors also stated that the owl's airframe noise is determined by a mechanism different from that of aircraft, gliders and other birds. The same group also studied the effect of the leading-edge serrations on flight noise [19], but did not observe an effect on noise production when either the serrations were removed or the fringes at the trailing edge were cut. Anderson [20] commented on the results of Kroeger et al. [19] by stating that they ‘tended to indicate that the full aerodynamic capability of the wing was not used at the high glide angle used in the experiment’ (p. 20). Arndt & Nagel [21] examined both the acoustic and aerodynamic characteristics of rotors with and without leading-edge serrations. These authors showed that ‘reduction in noise is possible with specific leading-edge configurations and running conditions’ (p. 1). The authors, however, questioned the practicality of the device as a noise attenuator: ‘The hot-wire data indicate that large eddies shed from the blade are dissipated faster with the serrated edge. This point implies a usefulness not necessarily as a noise attenuator, but possibly as an effective method for reducing aerodynamic disturbances from various types of lifting surfaces’ (p. 6). The purpose of the experimental study by Schwind & Allen [22] was to investigate the surface flow on an aerofoil with and without serrated edges. In measurements carried out at low Reynolds numbers (2.5 × 10⁴), serrations mimicking artificial eyelashes most effectively eliminated the leading-edge bubble by producing turbulence on the aerofoil's upper surface. Likewise, the serrations reduced the peak in RMS pressure for high Reynolds numbers (1.2–6.2 × 10⁶) up to 41%. Neuhaus et al. [23] worked with a tawny owl (Strix aluco). The highest intensities of noise emitted during flight covered a spectral range between 200 and 1500 Hz. In flapping flight, the sound produced by the owl was not affected by the removal of the leading-edge serrations. After the serrations were removed, a clear increase in noise production was, however, seen shortly before landing. Furthermore, wind tunnel analyses conducted by these authors indicated a more pronounced laminar flow character for the wing flow in the owl compared with the flow over wings of other bird species. A variety of serrations were attached at selected locations of the leading edge of a NACA-0012 aerofoil in the experimental study of Hersh et al. [24]. The serrations generated chordwise trailing vortices on the suction surface and tripping of the laminar boundary layer on the pressure surface, thereby changing the character of the wake vortex shedding from periodic or almost periodic to broadband, leading to the reduction or elimination of the tones. At high angles of attack corresponding to stall, the serrations also reduced broadband noise.

Lilley [25] developed a theoretical model of noise production and concluded that far-field noise for both birds and aircraft is dominated by sound scattered by the wing's trailing edge. Lilley [25] further stated that the situation in the owl was more complicated because of the leading-edge serrations, the trailing-edge fringes and the velvet-like surface. Lilley [25] suggested that the leading-edge serrations behaved as a set of closely spaced co-rotating vortex generators that reduce the flight noise emitted by the owl. Likewise, according to Lilley [25], the trailing-edge fringes reduce noise across all frequencies by 18 dB at a flight speed of 6 m s⁻¹. Lilley [25] further suggested that the velvet-like surface causes a cut-off of the radiated noise at 2 kHz.

Liu et al. [26] presented data for the construction of avian wing surfaces. Data were obtained from prepared wings with a three-dimensional laser scanning system. The owl wing was very thin, just a single layer of primary feathers. The camber at 0.4 spanwise position was about 0.05. The maximum thickness was near the leading edge. The normalized circulation distribution had higher values in the owl than in the non-specialized species tested.

3. Recent advances

Much has been learned since 2005 about the specializations of the owls and their functional significance. In the following, we present these new findings in some detail, again without claiming to provide a complete summary. We integrate the new findings on the morphology with those of engineering approaches and applications. We first describe flyover experiments showing a relative decrease in noise production in owl flight, then turn to the mechanisms underlying noise reduction and aerodynamic performance by regarding first the whole wing, and then turn to the three specializations on owl wings, the leading-edge serrations, the trailing-edge fringes and the velvet-like surface.

3.1. Noise production in owls compared with noise production in other birds

It is generally agreed that owls produce less noise during flight than other birds. But it has turned out a very difficult measurement problem to determine how quiet the flight of the owl is in absolute terms. The reason for this is that the flight of owls is so faint that even the most sensitive microphones are at their limit. To circumvent this problem, comparative measurements have been conducted. Sarradj and co-workers [27,28] reported comparative flyover noise measurements of a barn owl, a European kestrel (Falco tinnunculus), and a Harris hawk (Parabuteo unicinctus). For frequencies above the 1.6 kHz third octave band, the noise generated by the barn owl was about 4 dB below that generated by the other species. In the same study, also indoor measurements on prepared wings were performed. It was concluded that the wings from the two owl species tested generated less noise per unit lift force than the wings of non-silent flyers. Geyer et al. [29] further compared the aerodynamic performance of prepared wings at 0.5 spanwise position. It was found that the wings of the two owl species tested produced about 5–10 dB less noise than the other wings at higher Strouhal numbers (1000 in their case (fig. 10 in [29]) when the Strouhal number was based on an arbitrary dimension x₀ = 1 m). Likewise, Chen et al. [30] studied sound production during flight in the eagle-owl (Bubo bubo) in comparison with sound production in the common buzzard (Buteo buteo). The eagle-owl generated about 5–10 dB less noise for frequencies above 400 Hz than the common buzzard during flapping flight.

3.2. New insights in the morphology and function of owl wings

North American barn owls (Tyto furcata pratincola) have a wingspan of approximately 100 cm; the length of a single wing in spanwise direction is 45 cm; the chord has a length of 17 cm; the mean area of a single wing is 706 cm² [31]. The chord of barn owl wings is constant over most of the wing (figure 1a). The fully extended wing appears elongated with a round tip. The aspect ratio is 6.9 (see also data in [32]). As the wings of barn owls are huge in relation to body mass (mean weight: 465 g), a low wing loading of 33 N m⁻² results (see also [32]). Thus, the geometry of the barn owl wing shows an indirect adaptation towards silent flight by being optimized for low flight velocities. Flight speed was estimated to range from 2.5 to 7 m s⁻¹ [33,34]. This also means that these birds operate at Reynolds numbers around 60 000 [34]. Johnson [32] compared wing loading and aspect ratios in 15 species of North American owls. Aspect ratios in the owls studied by Johnson [32] ranged from 4.8 to 8.9, while wing-loading data ranged from 19 to 60 N m⁻², suggesting that very low wing loading is characteristic for flight of owls in general [35]. The low wing loading combined with low aspect ratio on owls suggests an adaptation to hunting allowing high manoeuvrability [13]. The owls grouped well with other birds of prey [36]. A major disadvantage of low flight velocities is the increased influence of induced drag, which negatively affects the flight performance. The general shape of owl wings is suited to reducing this influence, either by an overall elliptical shape, which is especially prominent for barn owls [37,38], or by the expression of slotted wings due to feather emarginations [39,40] that can be found for many species within the Strigidae family.

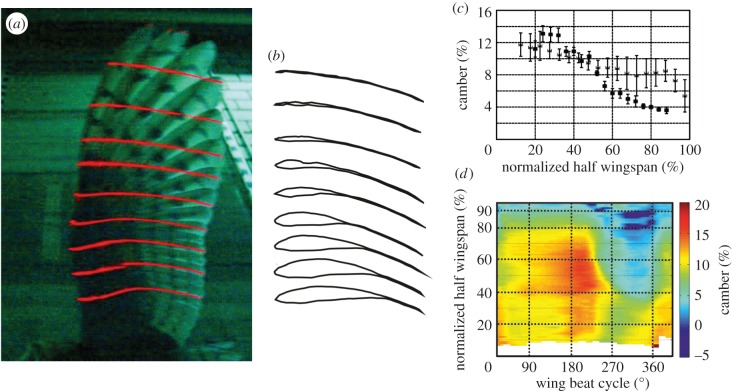
In the following, we discuss one aspect of wing shape in owl (and bird) flight in more detail, camber. Camber is not constant on bird wings (e.g. figure 2). Camber of the proximal wing can be adjusted by a flexible wing membrane called the patagium in combination with a change in elbow joint posture. Camber in the posterior region of the proximal wing may be influenced by a change of the angulations of the rachises of the secondaries to the ulna. In recent years, it became possible to quantitatively measure camber in gliding and flapping flight of barn owls. These new data confirm the high camber observed in fixed wings (figure 2; see also fig. 29 in [34]). More precisely, camber changed during a wing stroke, reaching high values during the downstroke. During the upstroke, camber was smaller and even negative in some positions (figure 2d). Surprisingly, high values of camber were measured in gliding flight (figure 2c). Similar observations have been reported from other bird species [41,42]. Thus, it seems that birds can and do fly stably at a much higher camber than do technical aircraft.

Figure 2.

Camber. (a) Owl wing as photographed during gliding flight. The red lines are laser lines that were used to reconstruct wing form as shown in (b). (c) Dependence of camber on wingspan in gliding flight (triangles) and in fixed wings (squares). (d) Dependence of camber on wing span during a wing-beat period. (d) Adapted from fig. 29 in Wolf & Konrath [34].

Winzen et al. [43,44] used time resolved particle-image velocimetry to investigate the fluid–structure interaction of a barn owl wing. They found no flow separation on the suction side for Reynolds numbers between 40 000 and 120 000 at spanwise positions of 0.3, 0.5, 0.7 and 0.9 and angles of attack, corresponding to the flight envelope of the barn owl, varying between 0° and 6°. By contrast, flow separation occurred on the pressure side. The flow field on the pressure side was characterized by large-scale vortices. These authors also observed trailing-edge deflections which were induced by the flow field on the pressure side due to interactions of the vortices with the flexible wing structure. The absence of a flow separation on the suction side was attributed to the ability of the wing to adapt camber to the surrounding flow field. Thus, the flexibility of the wing and the resulting stabilization of the flow field might be one reason why bird flight is possible with highly cambered wings without stalling. The authors also suggested that ‘implementation of a certain level of flexibility might be beneficial …. and therefore might be applicable to the future design of micro-air vehicles’ [44, p. 21]. From a morphological point of view, the observation of a change of the aerodynamic characteristics of the wing in both the spanwise and chordwise direction would suggest that the shape of the pennula might depend on the position on the wing as does the shape of the serrations [45].

3.3. Recent insights in the morphology and function of owl flight feathers

Bachmann et al. [31] examined a variety of different feathers from the barn owl and compared them with homologous feathers from the pigeon. Owl feathers had fewer radiates and longer pennula than pigeon feathers. Apart from the division into an outer and inner vane, a further division was regarded as important. In barn owl flight feathers, the regions of the feather vane that are covered by the adjacent feather are lighter in colour than the regions of the feather that are not covered (figure 1b). The latter regions appear brownish and are spotted/striped. In other words, while the brownish part is subjected to the air flow along the wing surface, the whitish part typically does not have direct contact to the air stream. However, as birds can actively change wing shape and can also spread the wing, in some occasions also the whitish parts become part of the wing surface that is subject to the air stream.

3.4. Serrations

The serrations at the leading edge of the owl wing continue to generate interest. Serrations are comb-like structures that are formed by detached tips of barbs of the outer vane typically of 10th primaries (P) that are directly hit by the air stream, but in some species also of P7–9 feathers (figure 3a,c). A serrated barb has a base where the bow and hook radiates are long and connected to form a closed vane. In the region of the serration, the length of radiates decreases so that they no longer connect (figure 3a,c). Serrations influence the airflow at the leading edge. The shape of serrations may change from species to species [14,16] (figure 3b) and along the spanwise direction (figure 3b). Mascha [14] stated that serrations are also found in other nocturnal birds like the kakapo (Strigops habroptilus). Weger & Wagner [45] reinvestigated the concept of a serration. These authors defined a serration as a structure that requires not only a detached barb tip but also a bending of the tip away from the feather rachis as well as upward bending and twisting. When these criteria were applied, serrations occurred only on owl feathers. Weger & Wagner [45] further conjectured that if serrations play a role in noise reduction, their shape should be correlated to the lifestyle of owls. Some owl species like the eagle-owl (B. bubo) and the barn owl (Tyto furcata pratincola) are nocturnal while other owls like the snowy owl (B. scandiacus) are more diurnal. Indeed, serrations were more developed in nocturnal species than in diurnal species (figure 3b).

Figure 3.

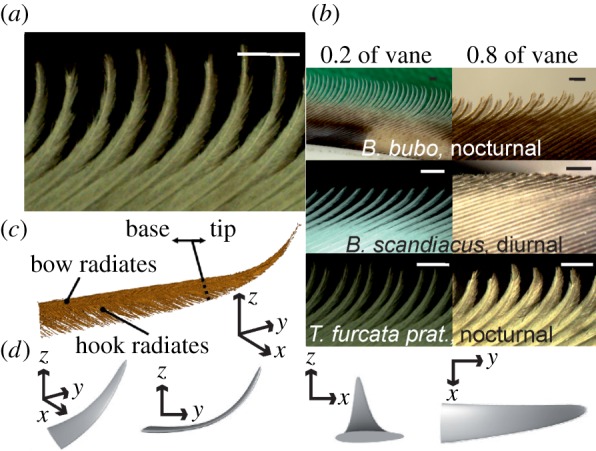
Morphology of serrations. (a) Serrations on a barn owl wing. (b) Serrations at different positions along the feather vane in an eagle-owl (Bubo bubo), a snowy owl (Bubo scandiacus) and a barn owl (Tyto furcata pratincola). (c) A single serration may be divided into a base and tip. Bow and hook radiates are shown as well as the three-dimensional coordinate system used for the description of the serration. (d) View of a first-order serration derived from barn owl data from different perspectives in a Cartesian coordinate system with the origin at the transition between base and tip, the x and y-axes in the plane formed by the bow and hook radiates and the z-axis perpendicular to this plane. Scale bars, 1 mm.

In a separate approach, Bachmann & Wagner [46] quantitatively characterized the shape of serrations found in the barn owl. The three-dimensional structure of the serrations may be characterized by length, width, thickness and three-dimensional position angles (e.g. twisting and curvature angles of individual serrations; figure 3d). These authors proposed a conceptual division into different morphological categories for biomimetic applications of serrations. The crude two-dimensional models of serrations that have typically been used in applications were called the zero-order approximations of serrations. The reconstruction of the three-dimensional shape of a typical natural serration characterized by the mean values of the parameters measured at the different positions was referred to as the first-order approximation of a serration (figure 3d). An even more detailed model, taking into account changes with the position on the wing, was termed a second-order approximation of a natural serration. The first-order approximation of a barn owl serration shows that the serration bends towards the flight path and both tilts upwards and twists so that the serration has an angle of 90° to the free stream. In the future, these values may be implemented by engineers instead of the zero-order approximations used so far. An even further improvement would be to take the orientation of the serrations to the free stream in spanwise positions into account, which change from 74° at 20% spanwise position to 113° at 80% spanwise position.

Klän et al. [47,48] and Winzen et al. [49] have studied the effect of serrations on the aerodynamic behaviour of model and natural owl wings. These authors fitted a wing model with a geometry reflecting the wing shape of a barn owl with different types of serrations, e.g. made of metal or of silicon (figure 4a). Reynolds numbers between 40 000 and 120 000 were tested in a wind tunnel with the wing in static conditions. These authors compared the aerodynamic behaviour of the wing with the modified leading edge with the aerodynamic behaviour of a clean wing. The artificial structures reduced the size of the separation region (figure 4b). The reduction was more pronounced for the model with the silicon serrations than for the model with the metal serrations. The artificial serrations also caused a more uniform size of the vortical structures shed by the separation bubble. The maximum Reynolds shear stress was reduced in the serrated models compared with the clean model (figure 4c). This means that the boundary layer was laminar for most of the chord length. This result indicated an ability for stable gliding flight independent of flight velocity. By contrast, the drag coefficients decreased, while the lift coefficient remained constant. This led to a decreased overall aerodynamic performance because of a reduction of the lift-to-drag ratio (figure 4d). Here the metal and the silicon fitted models behaved similarly. Overall, however, the stabilizing effect of the uniform vortex size caused more advantages, thus overcompensating for the lower aerodynamic performance, especially at low Reynolds numbers. Note, however, that this conclusion holds only for the tested static condition. Results for flapping flight might be different.

Figure 4.

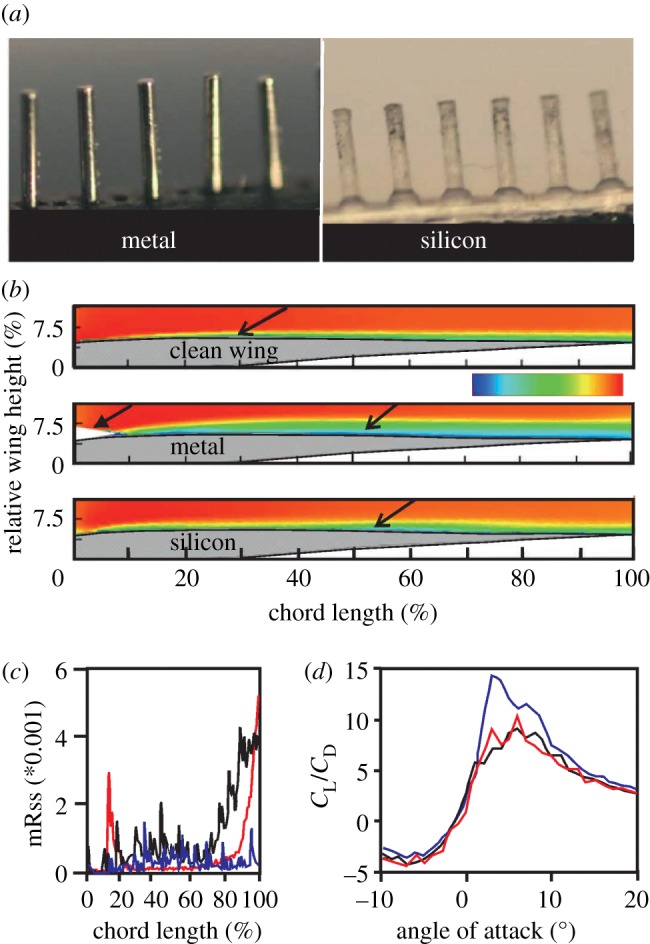
Aerodynamic effect of serrations. (a) The two different types of artificial serrations used. (b) Flow field measured at 0.9 spanwise position, an angle of attack of 3° and a Reynolds number of 60 000. The inset shows the velocity scale (u/u_∞, u_∞ = freestream velocity) ranging from 0 (blue) to 1 (red). The open arrows point to the upper wing surface. The filled arrowhead points to a reflection close to the leading edge that prevented recording of data. (c) Maximum Reynolds shear stress (mRss) as a function of chord length for the different wing configurations. (d) The lift-to-drag ratio as a function of the angle of attack for the different wing configurations. C_L and C_D are the lift and drag coefficients, respectively. Red, metal; black, silicon; blue, clean wing. The relative wing height is the quotient of height z divided by chord length c in per cent. Data in (b), (c) and (d) were redrawn after figs 4, 6a and 11d in Winzen et al. [49], respectively.

In other work, Geyer et al. [50] found that serrations mounted to the leading edge of a NASA/Langley LS(1)-0314 aerofoil led to a noise reduction at low frequencies (less than 1.6 kHz), while the noise at high frequencies increased slightly. In contrast with other results [47–49], no change in aerodynamic performance was observed by these authors. Furthermore, at high angles of attack (24°), Geyer et al. [51] observed a reduction of 5 dB in gliding-flight noise in one of two barn owl wings tested. Cranston et al. [52] found an effect of large zero-order serrations as a decrease in lift and an increase in drag at all angles of attack tested, but still the best stall angle performance. This is again different from the observations in Winzen et al. [49]. The reasons for these differences remain unclear at this moment.

In still other work, Narayanan et al. [53] provided an experimental investigation into the use of leading-edge serrations as a means of reducing the broadband noise generated due to the interaction between the aerofoil's leading edge and turbulences. Noise reductions were found to be insignificant at low frequencies but significant in the mid-frequency range (500 Hz–8 kHz). Noise reductions were significantly higher for a serrated flat plate than for a serrated NACA-65 aerofoil with the same serration profile. The reduction in sound level depended more on the amplitude of the serrations than on their spacing.

In a similar manner, Hansen et al. [54], tested a NACA-0021 aerofoil that had a sinusoidally modulated leading edge. This modification significantly reduced the tonal noise induced by the flow over an aerofoil. For a Reynolds number of 120 000, the authors observed a reduction in the overall broadband noise close to the peak in tonal noise. The authors postulated that tonal-noise elimination is facilitated by the presence of streamwise vortices generated by the modifications and that the spanwise variation in separation location is also an important factor. An additional effect was the confinement of the suction surface separation bubble to the troughs of the undulations, which may reduce the boundary-layer receptivity to external acoustic excitation. Ito [55] imitated serrations by attaching jigsaw blades with different numbers of cutting teeth at the leading edge of a wing. At low Reynolds numbers a serrated wing could produce lift at higher angles of attack than a prototype wing. Gharali et al. [56] studied the effects of serrations on an oscillating SD-7037 aerofoil at a Reynolds number of 40 000 with the reduced frequency of 0.08 while the aerofoil experienced deep dynamic stall phenomena. A significant load difference between the serrated case and the case without serrations was observed at high angles of attack after the first leading-edge vortex formation. The comparison of the leading-edge vortex circulations showed that the serrations did not enrich the leading-edge vortex circulation. This led to the conclusion that lift values were affected by other structures such as the trailing-edge vortices. The lift increase agreed with the leading-edge vortex circulation enrichment in the case of the flat-plate case. The frequency of vortex shedding decreased when the aerofoil was modified by serrations. Vortices also disappeared faster in the wake for the serrated case. Liang et al. [57] studied the effect of saw teeth on noise reduction of fans. Several kinds of sawtooth-shaped leading edges were examined acoustically while the fan was rotating. The experiments showed that the non-smooth shapes prevented the formation of an off-body vortex, which is caused by a turbulent boundary layer on the vane surface.

An application of serrations as a noise-reducing structure is available in the form of a comb-like pantograph designed for the Shinkansen train in Japan (https://issuu.com/eggermont/docs/zq_issue_02final/15?e=15278665/11095381 (Zygote Quarterly Summer 2012 ISSN 1927-8314; accessed 14 August 2016)). The pantograph was shaped like the wing of an owl and includes small serrations. These modifications resulted in less vibrations and thus less noise production.

In summary, serrations have an influence on aerodynamic performance and noise production. The size of this influence is a matter of debate. As suggested by the biological variation and the dependence of serration shape on the lifestyle of a species, the effect of serrations depends on their shape. Thus, zero-order serrations have some effect, but the first-order and even higher order ones may have more effects. Here, specifically the effect of twisting and tilting of a serration has to the best of our knowledge not yet been investigated. Moreover, the relation between serration shape and its effect on aerodynamic performance and noise-reduction properties might be complex, and only have its full impact in the context of the other adaptations found on the owl wing.

3.5. Velvet-like surface

Owls have a velvet-like structure on the wing surface. According to the old literature, such a surface may also occur in other night-active birds such as frogmouths (Podargidae) and night hawks (Caprimulgiformes) [16]. A recent account and adequate quantification across species as for the serrations is to the best of our knowledge not available. The velvet-like surface is formed by pennula, the filamentous distal part of the radiates (figure 1e). Bachmann et al. [31] used several measures for the characterization of the pennula: the mean length of the pennula, the overlap of neighbouring barbs by the pennula, the number of hooklets on the barbs and the density of the pennula. The pennula of the outer vane were always shorter than those of the inner vane. The pennula overlapped up to four neighbouring barb shafts (figure 5b). Likewise, Chen et al. [30] reported that the elongated distal barbules formed a multi-layer grid porous structure in eagle-owl flight. The eagle-owl generated lower noise than the common buzzard during flight. Regarding the outer vane, different characteristics of surface texture were found between covered and uncovered areas. Uncovered areas in comparison with covered areas had a lower density of pennula, the surface had a lower porosity, and the angulations of the pennula were larger (figure 5c), leading to a thinner structure (figure 5c). While these data refer to the outer vane, the differences in pennula shape between the covered, whitish parts on the inner vane and the uncovered, brownish parts on the inner vane have not been studied in detail. Owing to the length and the large numbers of the pennula, the surface of owl wings becomes very fluffy and porous. Two functional aspects were discussed [31]: the velvet-like dorsal surface of the inner vane may serve as a device that reduces friction, or it may affect the aerodynamic behaviour of the wing (or both). We turn to the latter issue in the next section.

Figure 5.

Morphology of velvet-like surface. (a) REM picture of velvet-like surface on a barn owl wing. View from above. (b) Higher resolution REM picture showing the overlap of the radiates of several barbs. View from below. (c) View of velvet-like surface from the side and indication of thickness and angulation parameters. Scale bars are: (a) 1 mm, (b) 200 µm and (c) 100 µm.

Klän et al. [47,58] and Winzen et al. [59,60] conducted experiments with several artificial velvet-like surfaces that mimicked the length and the density of the natural pennula (figure 6a). The softness of the artificial material was also chosen to be similar to that of the natural owl-wing surface. As in the case of the serrations, these authors compared the fluid–structure interaction in a clean wing with wings with a velvet-like surface attached to the suction side. The results showed that the velvet-like surface reduced flow separation and enabled boundary-layer control (figure 6b). The main flow feature of the clean wing was a transitional separation bubble on the suction side (figure 6b, clean wing). The size of the bubble depended on the Reynolds number and the angle of attack, whereas the location was mainly influenced by the angle of attack. Applying a velvet-like surface to the suction side drastically reduced the size of the separation bubble at moderate angles of attack and high Reynolds numbers (figure 6b, velvet 1 and velvet 2). The highest peak value of the maximum Reynolds shear stresses was found for the clean wing (figure 6c). The wing equipped with velvet 2 behaved similarly to the clean wing, although transition occurred earlier in this configuration. This was also the case in the wing equipped with velvet 1. In addition, in this latter case, the shear stress was also considerably lower (figure 6c). The authors further observed a lower lift-to-drag ratio in the wing models with artificial surfaces (figure 6d). In other words, while the reduction of the separation region might have a positive influence on the pressure drag, the aerodynamic performance of the models with the artificial surfaces was significantly reduced owing to an increased skin-friction drag. Furthermore, the models equipped with the velvets possessed a reduced susceptibility to changes in Reynolds number and angle of attack concerning the aerodynamic performance. Thus, the authors concluded that the velvety surfaces stabilize the flow field at low Reynolds numbers, enabling the owl to fly more slowly and thus more silently.

Figure 6.

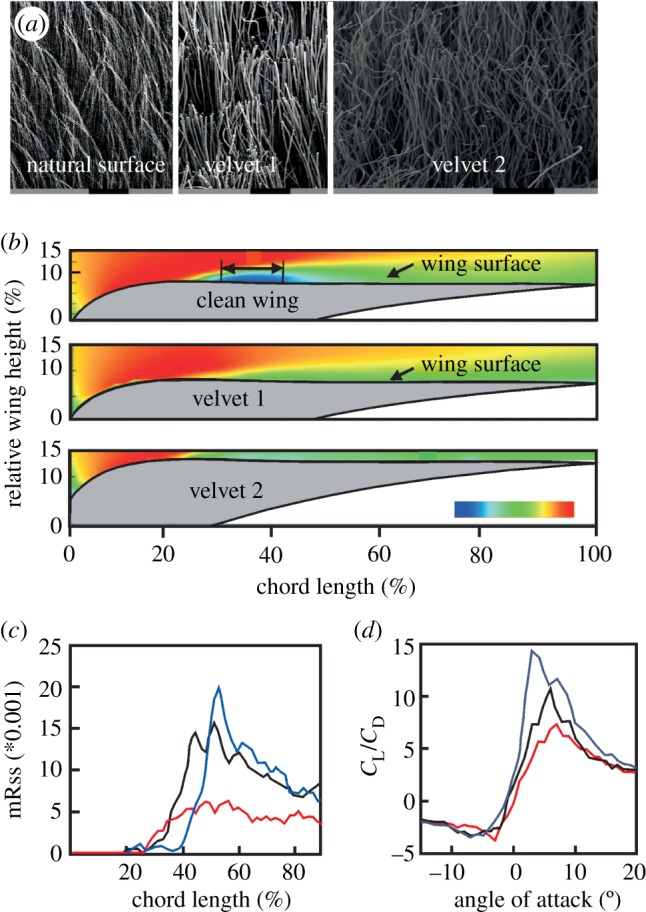
Aerodynamic effects of velvet-like surface. (a) The natural surface, and the artificial structures velvet 1 and velvet 2. The surface of velvet 1 was chosen to mimic the natural surface as much as possible with respect to the softness, length of hairs and density of hairs. Velvet 2 possessed longer hairs. (b) Flow field measured at 0.3 spanwise position, an angle of attack of 6° and a Reynolds number of 60 000 in the different configurations. The inset shows the velocity scale (u/u_∞) ranging from −0.2 (blue) to 1.2 (red). The arrows point to the upper wing surface. (c) Maximum Reynolds shear stress (mRss) as a function of chord length for the different wing configurations. (d) The lift-to-drag ratio as a function of the angle of attack for the different wing configurations. C_L and C_D are the lift and drag coefficients, respectively. Red, velvet 1; black, velvet 2; blue, clean wing. Data in (c) and (d) were redrawn after figs 4a,c,e, 5a and 13d in Winzen et al. [60], respectively.

Following the observations by Geyer et al. [29], Clark et al. [61] performed experiments to examine the noise radiated by vertical filaments that form a canopy above a surface (figure 5c). This structure reduced pressure fluctuations on the underlying surface. The authors concluded that ‘…the reduction in surface pressure fluctuations can reduce the noise scattered from an underlying rough surface at lower frequencies’ (p. 1). Jaworski [62] extended this study by modelling the dynamics and sound generation of a line vortex that moved past a flexible fibre. This author found that the noise signature was affected by the hydro-elastic coupling of the vortex path and fibre motion. The author concluded that such interactions on the upper surface of owl wings might contribute to the silent flight of these birds. However, as mentioned before, Winzen et al. [49] did not find a vortex on the suction side of the real owl wing. Thus, the relevance of the finding of Jaworski [62] for the silent flight of owls remains unclear.

In summary, the velvet-like surface of owl wings influences aerodynamic properties and noise production. Despite this influence no application for this adaption is known to us.

3.6. Fringes

The trailing edge of owl wings and feathers is fringed. It does not exhibit a smooth edge as is found in other bird species (figure 7a,b). Fringes form where the tips of the barbs are separated due to a loss of hooklets on the hook radiates. This leads to unconnected barb ends (figure 7d). The thickness of the feather decreases towards the end of the fringes, partly owing to the end of the velvet-like surface (figure 7c). In addition, the radiates bend towards the barb shafts to support the formation of fringes. The fringes exhibit differences in size and orientation within one feather and between different feathers within one wing. Bachmann et al. [63] quantified fringes by measuring fringe length and fringe density. The length varied between 1 and 4.5 mm. The length of the fringed region typically decreased from the feather base towards the tip. Fringe density again decreased from proximal (5 mm^–1) to distal (2 mm^–1) on the feather vane.

Figure 7.

Morphology of fringes. (a) Fringed end of a 10th primary at the apical end. (b) Fringes in the middle of a 10th primary feather. (c) A view on the fringes from the side. (d) A view on the fringes from above. (e) Two adjacent secondaries are shown on the left with their overlap. The photographs show a selected area as indicated by the inset. The orientation of the fringes was visualized by high-speed recording. The view is from ventral. Under static conditions (photograph on the left), the fringes on the left feather do not align with the barb shafts of the right feather. When flow is turned on, the fringes merge into the grooves formed by the barbs of the adjacent feather (photograph on the right). The white rectangles show the regions presented in larger magnification in (f,g). (f,g) Details of the orientation of single barbules are indicated by the arrows. (e) Adapted from fig. 6 in Bachmann et al. [63].

The trailing edges fringes may have two important functions. First, the fringes positioned within the wing can merge into the grooves between two adjacent barb shafts at neighbouring feathers. Figure 7e–g shows two secondaries (7 and 8) in two flow conditions. While the fringes do not align with the adjacent barb under static conditions (left photograph in figure 7e,f), they merge tightly into the grooves formed by adjacent barb shafts when subject to flow (right photograph in figure 7e,g). This intersection prevents the separation of adjacent feathers and allows the formation of one single trailing edge behind the wing instead of several trailing edges behind the single wing feathers. The reduction of trailing edges subsequently reduces the number of noise sources, as trailing edges are a major noise source in aeroacoustics [64–66].

Herr [65] examined the effect of solid reference trailing edges of varying bluntness on the production of noise. Modified trailing edges were applied to a zero-lift two-dimensional modular generic plate aerofoil and a 2D-NACA-0012-derivative aerofoil. It was observed that the trailing edge might reduce noise up to 10 dB, depending on the configuration. The effects depended on the details of the geometry of the fringes. For example, a minimum chordwise device length (of the order of the turbulent boundary-layer thickness) and a narrow slit width (of about the viscous sublayer thickness) were identified as the major design requirements which need to be fulfilled to maximize the noise-reduction effect. Flexibility of the fringed material was found to be not essential for achieving a noise reduction. Jaworski & Peake [67] modelled the interaction of a turbulent eddy with a semi-infinite poroelastic edge with respect to noise generation. The results demonstrated a modification of radiated acoustic power by edge porosity. In contrast with the well-known fifth-power scaling of rigid edges, a poroelastic edge exhibited a sixth-power velocity dependence for frequencies in the human hearing range. This result suggested, on the one hand, the weakest edge amplification in the frequency range of interest of the owl noise problem and, on the other hand, a possibility to tailor edge properties of wings to reduce noise production in the human hearing range.

An application of these noise-reducing effects on the trailing edges is available in the form of owlet ventilators (http://www.ziehl-abegg.com/ww/index.html).

4. Outlook

The silent flight of owls continues to fascinate researchers and continues to serve as a role model for applications. The results of previous studies have already delivered many insights and applications are available. Still, many problems are not understood in detail, the biological adaptations in many cases need a better description and the applicability of the biological adaptations to technical instruments remains to be tested. In the following, we mention a few cases that seem central to us for future progress.

As the flight of owls is so silent that the available microphones are at their limits, only comparative measurements are available with relative statements. It will be a challenge for the future to develop a set-up in which absolute noise production of owl flight can be measured. In any case, the contribution of the different adaptations should be quantified, as it is now possible not only to cut off the serrations, but also to shave off the velvet-like structure. From a biological point of view, it would also be interesting to do more comparative work like that by Weger & Wagner [45] to find out which evolutionary forces drove the development of these adaptations. From an aerodynamic point of view, the investigation of real owl wings [59,60] has yielded interesting new insights into how the flexibility of the wing may influence the performance of a wing. More studies with real wings should be carried out. While early on the technical implementations were primarily thought to deal with the reduction of aerofoil noise, recently, the focus is more on the development and optimization of micro-aerial-vehicles that operate at lower Reynolds numbers (for a review, see [68]) and on ventilators and fans. While several companies have used the owl's solution to develop ‘owl-like’ devices, there are still many possibilities for the development of new devices. For example, no recent applications with serration-like leading edges are available apart from the pantograph mentioned above, although earlier such rotors existed (W Nachtigall 2012, personal communication), and no application of velvet-like surfaces is known to us.

Authors' contributions

All authors helped with writing the manuscript.

Competing interests

The authors declare no competing interests.

Funding

This research was funded by grants of the German Research Foundation (DFG) to H.W. (WA 606/15) and W.S. (SCHR 309/35).