Wind and water tunnel testing of a morphing aquatic micro air vehicle

Abstract

Aerial robots capable of locomotion in both air and water would enable novel mission profiles in complex environments, such as water sampling after floods or underwater structural inspections. The design of such a vehicle is challenging because it implies significant propulsive and structural design trade-offs for operation in both fluids. In this paper, we present a unique Aquatic Micro Air Vehicle (AquaMAV), which uses a reconfigurable wing to dive into the water from flight, inspired by the plunge diving strategy of water diving birds in the family Sulidae. The vehicle's performance is investigated in wind and water tunnel experiments, from which we develop a planar trajectory model. This model is used to predict the dive behaviour of the AquaMAV, and investigate the efficacy of passive dives initiated by wing folding as a means of water entry. The paper also includes first field tests of the AquaMAV prototype where the folding wings are used to initiate a plunge dive.

1. Introduction

Locomotion in unstructured terrain is a significant challenge to miniature robots operating in an outdoor environment, often requiring operation in water, air and on the ground. The challenges of multimodal locomotion are addressed in many ways in nature, by animals that can adapt their structures and behaviours to address the changing requirements of movement in air and water. Plunge diving birds are a particularly striking example of this, most notably the northern gannet, a predatory seabird able to dive into the water (figure 1a,b) at speeds of up to 60 miles per hour by sweeping its wings fully backward, in order to catch fish beneath the surface [1]. Such plunge diving behaviour is also observed in pelicans and boobies, and even far smaller birds such as the common kingfisher (figure 1c,d). Reproducing the ability to dive directly through the water surface in a miniature flying robot would allow unique operation in a wide variety of environments, such as tidepools, wetlands or canal systems, enabling autonomous monitoring of contaminants and ecosystem health. However, order to dive into the water, a vehicle must be able to accommodate the increased structural loads, fluid inertia and drag encountered underwater, without compromising the weight and lifting area requirements of flight. To achieve this, we are developing a novel robot, called the Aquatic Micro Air Vehicle (AquaMAV) [2] that is capable of aerial and aquatic locomotion, able to dive directly into the water at high speeds to achieve initial depth, subsequently retaking flight using a high powered burst of thrust.

Figure 1.

Plunge diving in nature. (a) Northern gannet (Morus bassanus, 3 kg mass) in flight, and (b) with folded wings about to dive into the water. (c) Common kingfisher (Alcedo atthis, 0.03 kg mass) in a dive with wings partially folded and (d) with wings fully folded. Images reproduced under a creative commons licence, courtesy of: Andreas Trepte (a), Mike Pennington (b), Ryan Cheng (c) and Andy Morffew (d). (Online version in colour.)

Aquatic robots can perform tasks such as monitoring of coral reefs [3], or responding to floods [4], but such environments may contain isolated areas of water and obstacles which impede movement. Amphibious terrestrial robots have been implemented in many forms [5,6], but these robots are not able to cross large, sheer obstacles and generally can only exit the water on gentle inclines, something that would not inhibit an aerial–aquatic robot. By flying, a vehicle can reach areas of interest from a safe location, without the need for manned boats, and do so at higher speeds than can be achieved by man-portable aquatic robots. In an emergency scenario, AquaMAVs could fly quickly to a target, enter the water, collect samples and record data or video, before returning to flight with information for analysis. The utility of water sampling with aerial vehicles has been demonstrated using multirotor platforms which collect samples by lowering a probe from the air [7,8], although this relies on accurate control and sensing of the water surface. By plunge diving into the water and retaking flight, an AquaMAV could avoid these control requirements, and allow robots to be produced more cheaply, and operated in larger numbers. Similar guidance and control considerations apply to producing small floatplane vehicles [2], with the additional limitation that such vehicles are too buoyant for underwater locomotion, as well as requiring large take-off areas and a calm water surface.

Recently, quadrotor platforms able to move underwater have been demonstrated, using aerial propellers to produce thrust in water [9,10]. Both robots use aerial propulsion systems underwater, which means that aquatic propulsion will be highly inefficient, owing to the larger torque loads on the motors when in the water. Generally, quadrotors cannot match the efficiency of a fixed-wing vehicle in forward flight, as they must use significant energy to balance their weight, whereas a vehicle producing aerodynamic lift can use less power while moving forward. Quadrotors will also likely be inhibited by the presence of surface waves during take-off. We instead propose that a robust means of take-off from water is an impulsive leap, thrusting through surface perturbations, as demonstrated in [11] (figure 2). By folding its wings before take-off an AquaMAV can reduce drag and quickly reach flight speed, before deploying wings and transitioning to flight, in a manner analogous to multimodal jumpgliding robots on land [12,13].

Figure 2.

Jet propelled launch by a previous AquaMAV prototype. (a) The AquaMAV uses a pressurized water jet to escape the water. (b) Timelapse of an AquaMAV launch, with wings opened in the final frame. Images adapted from [11]. (Online version in colour.)

Many morphing aircraft have been demonstrated at the less than 1 m wingspan scale [14], most commonly to allow unmanned aerial vehicles (UAVs) to fit into smaller containers for transport or launch [15,16], and also to expand the flight envelope of the vehicle in the air. A miniature flying robot able to dynamically change its wing sweep is able to operate in a broader design envelope, and enhance its agility in complex requirements [17], without compromising efficiency in level flight. Sweeping wings backward has also been shown to allow a vehicle to improve its efficiency at higher speeds by reducing parasitic drag [18]. Wing morphing is also a near ubiquitous feature of flying animals, and has been of interest to many biologically inspired robots, particularly those with multimodal mobility. Reconfigurable wings are used in jumpgliding robots to decrease drag during ascent [19], in aerial terrestrial robots to enhance mobility on the ground [20], or to mitigate hydrodynamic loads in aerial–aquatic robots [21,22].

Plunge diving gannets reconfigure their wings continuously as they dive, sweeping partially back at the start of a dive but, only fully retracting at the point of impact with water. However, this is principally to allow the bird to accurately track prey as they descend towards the surface, and is a level of accuracy not necessarily requisite in a field robot [23]. As an AquaMAV does not necessarily need the aerodynamic control nor the ability to self propel with its wings, the same behaviour can be achieved with less complex, more robust mechanics. The gannet's head and beak are also adapted to mitigate impact loads with the water [24], protecting their neck and face from damage. However, the flexibility of the bird's neck is a consequence of its need to visually track prey, and it again may not be necessary to directly mimic the bird's head structure in order to impact with the water.

In this paper, we introduce a plunge diving AquaMAV, with reconfigurable wings which allow it to dive into the water at speed. The robot uses folding wings to both initiate its dive from flight by changing its aerodynamic behaviour and to protect itself from impact loads as it hits the water, and is the first robot of its kind to do so. We present wind and water tunnel tests of the vehicle, showing the efficacy of the folding design in both delivering high performance with open wings in level flight and in drastically reducing lift and drag when folded. We then use the collected aerodynamic data to predict the behaviour of the vehicle during a dive, using a planar trajectory model, and examine the efficacy of passive dives initiated by wing folding. Finally, we show a preliminary flight test of the vehicle, demonstrating a dive into water from flight.

2. The AquaMAV airframe

The AquaMAV is a small aircraft designed to fly to a target location where it can dive into the water and gather data, before retaking flight and returning to submit samples for analysis. The current prototype is a 201.3 g fixed-wing aircraft (table 1), which builds upon a previous prototype weighing 100 g [11], which demonstrated take-off from beneath the water using a high pressure water jet [25] to escape. Once in the air, this vehicle could deploy wings and transition to gliding flight, but was unpowered (figure 2). The new prototype retains the ability to launch from water, but has propeller propulsion and a more developed folding wing design which is more efficient in flight, and with which the wings can be swept backwards up to 90° (figure 3a–c). This allows the vehicle to dive directly into water without damage, or partially sweep its wings to change its flight behaviour in air.

Table 1.

Component mass breakdown for the AquaMAV.

component	mass (g)	per total (%)
wings	41.0	20
fuselage	27.1	13
propulsion	23.5	12
water jet	37.0	18
empennage	8.5	3
control servos	15.5	8
electronics	22.7	11
batteries	26	13
total	201.3	100

Figure 3.

The AquaMAV airframe. (a–c) Fabricated prototype, shown with wings open (a) and swept 45° (b) and 90° (c) backward. (d) CAD rendering of the wings, showing the lay-up pattern and gear linkage. (e) CAD illustration of fuselage, with internal components labelled. (Online version in colour.)

The current AquaMAV prototype has a conventional fixed-wing layout with a tractor propeller configuration, and a V-tail with dual elevons for control. The V-tail's 45° dihedral angle provides sufficient control in roll pitch and yaw, while minimizing the required control actuator mass, and the positive dihedral also provides some additional roll stability. The robot is provided with sufficient battery for 14 min of flight, which corresponds to approximately 4 km of sample return range at its 10 m s⁻¹ flight speed (table 2). The keel of the robot is formed by a slender aluminium CO₂ tank and hollow carbon tube, which the robot uses to produce a powerful 1 s burst of water jet thrust, allowing it to escape the water and reach sufficient speed for flight in air. The robot's control electronics and actuators are all contained in a waterproof Kevlar fuselage, mounted to the aluminium gas tank (figure 3e).

Table 2.

Summary of key AquaMAV aerodynamic parameters.

open wing span	592 mm
open wing root chord	120 mm
open wing area	0.056 m2
open wing aspect ratio	6.35
tail area	0.010 m2
tail aspect ratio	3.57
flight speed	10 m s−1
flight Reynolds number	796 000
battery capacity	650 mAh
flying time	14 min

The AquaMAV's main wing is separated into three segments, of which two can sweep backward, while the third is fixed directly to the fuselage, but is compliant enough to allow the other wing segments to pass beneath it (figure 3d). The two rotating segments pivot on sealed bearings attached to the wing at the quarter chord line. The wing chord line is fixed at a 5° angle of attack relative to the rest of the aircraft, and so as the wings sweep backward, the two segments pass over the fuselage, deforming and reducing their angle of attack relative to the aircraft. The fully open wing has a Zimmerman planform, which has elliptical leading and trailing edges, joined at the quarter chord line and is a common choice for fixed-wing vehicles at the 10⁻¹ kg scale. While this wing aerodynamically slightly outperforms rectangular platforms of the same aspect ratio at low Reynolds numbers [26], it was primarily chosen for its suitability to the folding design. Most importantly, the tapering of the wing towards the wing tip reduces the deformation needed to fold the wing completely as the trailing edge slides over the fuselage, meaning a stiffer wing can be more easily actuated. Compared with a rectangular wing of equivalent area and aspect ratio, the elliptic wing shape will also produce smaller aerodynamic moment at the wing root hinges.

The wing has a cambered plate section, with a maximum camber of 5%, located at the wing quarter chord line. Such thin cambered plates have been shown to have increased performance when compared with conventional thick aerofoils at low Reynolds numbers [27]. The AquaMAV has a chord Reynolds number of 7.96 × 10⁵ when flying at 10 m s⁻¹ in sea-level air, which is the upper limit at which significant performance benefits are seen, but the use of a cambered section has particular advantages to the folding design: when rotated 90°, a thin cambered wing has a very small frontal area, and so the wing drag when swept fully backward will be greatly reduced compared with a thick wing. Furthermore, a thick wing would have significant buoyancy if watertight, which would inhibit effective locomotion underwater, and if water-permeable the wing would momentarily retain liquid during take-off from water and slow the robot down.

The upper surface of the wing is made from 230 g m⁻² woven prepreg carbon fibre. This is reinforced by a second layer of woven fabric composed of a spanwise strip along the wing quarter chord line, reinforcing the point at which the wings are attached to the hinges and a location with high cross-section curvature, where it adds the most to the wing's bending stiffness. Six perpendicular strips are also cut into this layer to add to the trailing edge stiffness, with additional reinforcement on the inside edge of the wing, to minimize the risk of cracking or fraying of the edges as the wings slide over each other during folding (figure 3d).

The two rotating segments are geared together to ensure symmetry, and are driven by a single 6.5 g servo (MKS DS65 K) with a maximum torque of 0.22 Nm. The rotating wing segments are attached with screws to the acteal gears, via a 3D printed piece which matches the cambered wing surface to the flat gear. A 6 mm diameter aluminium rod runs through each wing into a bearing which is bonded in turn to the fuselage, which is reinforced at the wing attachment point by a 1 mm carbon plate. Two additional bearings are bonded to the centre segment, through which it is bolted to the main wings, allowing the wings to rotate beneath it, while keeping the shafts partially supported at the upper surface.

The internal components of the vehicle can be seen in figure 3e, showing the servos used for wing deployment and tail control surface actuation, the motor for aerial propulsion and the custom aluminium gas tank used to store high pressure CO₂ for underwater take-off (table 2). This is all contained in a streamlined Kevlar fuselage which can be separated by a screw connection to access internal components without compromising the waterproofing (this connection is located just ahead of the wing leading edge, joining the rear, blue coloured section to the forward yellow section). While the vehicle fuselage was designed to be as slender as possible to minimize drag and impact forces, the cross section was primarily determined by the need to accommodate the internal components while allowing easy disassembly. The nose shape is a revolved NACA 0010 aerofoil, chosen to accommodate the propulsion motor, batteries and desired propeller.

3. Wind and water tunnel testing

The AquaMAV was tested at scale in a wind tunnel, in order to evaluate the performance of the wing and the vehicle's longitudinal stability. Aerodynamic coefficients were evaluated and used to predict dive trajectories at various heights and speeds, as well as estimate the vehicle's penetration into the water.

3.1. Wind tunnel experimental set-up

Tests were conducted in a closed circuit wind tunnel, with a 0.95 × 0.95 m working section. Wind speed was measured and controlled using a pitot probe, compensated for changes in ambient conditions. During tests, airspeed was maintained to within 0.5% of demanded velocity.

The vehicle was mounted to a six-axis force balance (ATI Gamma IP68) via a 0.5 m streamlined steel sting, such that the centre of the fuselage was located 0.45 m above the tunnel floor at 0° angle of attack. The force balance was in turn attached to a worm drive, which was used to vary the vehicle angle of attack, α. The 200 step/rev stepper motor used to drive the worm gear gave an accuracy of after the 1 : 150 reduction in the worm drive (figure 4a).

Figure 4.

CAD drawings of wind tunnel test apparatus. (a) Close-up of worm drive system for angle of attack adjustments, with force balance attached. (b) AquaMAV model location in wind tunnel, showing worm drive and force balance attached to the tunnel floor. (c) AquaMAV model location in water tunnel (shown with wings folded). Panels (b,c) are on the same scale. (Online version in colour.)

The force balance had a calibrated range of 100 N in each axis, and 10 Nm in torque, with force and torque resolutions of 25 mN and 1.25 mNm, respectively. Data from this sensor were sampled at 10 kHz, averaging 1000 samples per recorded reading. During testing, zero readings were recorded for 60 s before and after the tunnel was run and averaged together to account for sensor drift. Aerodynamic forces were also recorded for 60 s, once the tunnel had reached the demanded speed.

The wind tunnel, force balance and worm drive were all operated using LabView, which was also used to control the wing servo, allowing the effect of wing sweep angle to be evaluated. The open wing was tested from −6° to 24° angle of attack, in 2° increments at its design flight speed, 10 m s⁻¹, to elucidate the complete stalling behaviour of the wing. The wing was also tested at different sweep angles, sweeping the wings backward in 10° increments from fully open (0°) to fully closed (90°), also at 10 m s⁻¹. The fuselage was also tested with wings, propeller and empennage removed to evaluate the different drag contributions, and to calculate separate aerodynamic coefficients for the wings and fin, so that any pitch damping effects could be accounted for in §5.

It was necessary for the wing to have some compliance in order to fold, as well as being as thin as possible to reduce weight. In order to evaluate the effect of this compliance, a rigid wing with the same planform and camber profile was fabricated from a 2 mm thick aluminium plate, and tested separately, so that a performance comparison could be made.

Once tunnel measurements were collected, the sting was run separately over a large range of angles of attack and tunnel speed. The forces and moments produced by the sting were then subtracted from the model measurements taken at the corresponding speeds and orientations. The maximum wingspan of the vehicle (0.592 m, 73% of tunnel width; figure 4b) meant that some interference from the tunnel with the wing tip vortices was expected. This was corrected for using the method of images, by treating the lifting main wing as a pair of trailing vortices whose strength is determined by geometry and lift of the main wing [28]. This allows the boundary induced upwash to be estimated by taking the upwash induced by the resulting image system of vortices at the tunnel centreline as the average upwash across the section [28]. The resulting corrections were small, for example, the increase in angle of attack due to the boundary effect is 0.09° with the AquaMAV at 0° to the flow at 10 m s⁻¹. The solid blockage of the vehicle and sting was low (1.4% by frontal area at 0° attack angle), and so no speed correction was deemed necessary.

3.2. Water tunnel experimental set-up

Using the same force balance, the AquaMAV was also tested in a water flume, at 0.2–1 m s⁻¹ speed, in 0.2 m s⁻¹ increments. This allowed us to test the AquaMAV at slightly higher Reynolds numbers than those observed during tests in air (13.5 × 10⁴ in water at 1 m s⁻¹ compared with 7.96 × 10⁴ in air at 10 m s⁻¹), and to corroborate wind tunnel measurements. The flume's maximum width is 0.6 m (figure 4c), which meant that the wings could not be tested fully open. Tests were run with wings fully closed, with wings removed and with wings and fins removed, so that the drag contributions of different components underwater could be evaluated. Where the folding propeller was attached to the fuselage it was prevented from rotating, although the propeller blades could fold backward freely. This was deemed reasonable as in practice resistance from the motor and friction where the blades are folded flat against the fuselage will limit autorotation.

4. Results

At its design cruise speed, the AquaMAV performs well, producing sufficient lift to balance its weight (figure 5a), and in level flight is at its maximum lift to drag ratio (figure 5c). The vehicle begins to stall at 8°, but full stall is delayed until 18°. However, at lower speeds, this delayed stall is not observed, and the indication is that this is due to wing compliance. This is investigated further in §4.2.

Figure 5.

Lift and drag of the AquaMAV airframe in air, as measured in a wind tunnel, with the RMS error of the force measurements indictated by the shaded region. Increased error can be seen as the wing nears stall due to the unsteady flow. (a) Lift force in Newtons, (b) drag force in Newtons and (c) lift to drag ratio. (Online version in colour.)

In order to compute dive trajectories, we extract the lift and drag contributions of the fuselage and fins separately, shown in figure 7. For each component, C_L and C_D are calculated from lift, L and drag, D as

4.1

where ρ is the fluid density, V the freestream velocity and A_ref a reference area. The fully open wing planform area is used as the reference area for all calculated coefficients. We also compute the wing centre of pressure from the measured torque on the force sensor, defined as the point of action of the aerodynamic forces about which there is no moment. This point is assumed to lie along the wing chord line, at a preset angle of attack, α₀ to the fuselage (5°). By taking moments around the force transducer, we can equate the location of the centre to the measured torque, M:

4.2

where and are unit vectors defining the sensor coordinate system, S and r are the distances from the intersection of chord line and sting axis to the sensor origin and centre of pressure, respectively (figure 6a). is resultant lift and drag force and R(α) is a rotation matrix about Given the sensor readings and equipment geometry, equation (4.2) can be solved for r at each measurement point.

Figure 7.

Lift and drag of fuselage and fins. (a) Fuselage only, measured with wings and tail removed. (b) Tail fins only, with fuselage lift and drag subtracted from measurements. (c) Open wing only. (d) Fully retracted wing only. Note that (a,b) are plotted on a different scale to (c,d).

Figure 6.

Centre of pressure of the wing and its variation with angle of attack. (a) Centre of pressure definition from measured forces and moments at the sensor. (b) Measured centre of pressure of the open and closed wing, defined here by the distance from the AquaMAV nose, with the AquaMAV shown on the same scale for illustration.

Figure 6b shows the effect of wing retraction on the location of the wing's centre of pressure. The vehicle's centre of gravity (c.g.) is located 205 mm from the vehicle's nose (figure 6b). When open and at 0° angle of attack, the wing's aerodynamic centre is 212 mm from the nose, slightly behind the c.g. and at 32% of the wing chord, but when the wing is folded, this moves significantly rearward to 313 mm from the nose. This movement of the c.g. and the loss in lift means that once the wing is retracted, the AquaMAV will passively enter a stable dive, the trajectory of which is explored further in §4.1.

Figure 7a,b show the forces generated by the fuselage and wing fins. The fins show linear C_L behaviour over the tested range. Fin stall is not observed because of the fins' 45° dihedral angle, which reduces the relative flow normal to each fin and hence the effective angle of attack of fins relative to that of the fuselage. Figure 7c,d show the effect of fully retracting the main wing. We can see that the drag in level flight is reduced by 62%, and lift production is decreased by 92%.

4.1. Partial wing sweep

With the wings fully open, the vehicle will only be able to increase its level flight velocity beyond the design cruise speed by operating at slightly negative trim angles using the tail control surfaces, which is aerodynamically inefficient. Since the wing folding mechanism allows for the wings to be operated at partial sweep angles, the efficacy of sweeping the wings backward to enable the AquaMAV to sprint for short periods was investigated. Figure 8 shows the effect of sweep angle on lift production (figure 8a) and efficiency (figure 8b).

Figure 8.

The effect of partially sweeping the wings on wing aerodynamics. (a) The range of lift coefficients produced at angles of attack between −2° and 20° in 2° increments, plotted for different wing sweep angles. (b) Lift to drag ratio. (c) Wing sweep sequence with the centre segment removed, showing the interference between segments as they fold. Image at 0° sweep is repeated, with the first image showing the centre segment.

As the wings sweep backward, they slide over one another and the fuselage, deforming in order to do so, until they reach a maximum angle of 90°, where a hard stop is reached (figure 8c). In figure 8a, we can observe the effect of the wings deforming as they sweep back, in the rapid drop-off in lift over angles of 60–90°, where the wings are forced upward by the fuselage, decreasing their angle of attack relative to the freestream. However, at 10° the wing shows a slight increase in lift coefficient at α = 0 (C_L0) and aerodynamic efficiency. This is due to the wing trailing edge deflecting downward as it passes under the centre segment, increasing its camber. At 30°, the wing trailing edge reaches the fuselage, is deflected upward and lift production begins to decrease. If the vehicle were to sweep its wings back by 70°, C_L0 would reduce to 0.15 which would allow the vehicle to maintain a level flight speed of 19 m s⁻¹. This would incur a significant drag penalty (figure 8b), and require high thrust, but there is nonetheless the potential for wing sweep to be used in a brief sprint in spite of the inefficiency. Sweeping the wings backward also allows the robot to shift its aerodynamic centre rearward and increase its static margin, altering the handling qualities of the vehicle.

4.2. Wing performance at different speeds

To investigate the impact of the segmented folding mechanism on the wing design, the fully open main wing was tested at different speeds and compared with a single-piece rigid aluminium wing. The lift and drag measured during these tests are shown in figure 9a,b, respectively. From figure 9a, we can see that the rigid wing produces slightly more lift than the folding wing at small angles of attack, which suggests that some warping of the carbon fibre wing occurred after it was demoulded, or a slight manufacturing error in the preset angle of the wing chord relative the the AquaMAV fuselage. We can also see that the carbon wing stalls earlier than the rigid version at low speeds. This could be the result of the protrusions on the wing upper surface which are necessary for the folding mechanism, as well as the discontinuities between the segments, both of which will retard flow over the upper surface, and encourage separation. However, it could also be the result of an interaction between the wing wake and the fuselage, as the rigid wing was not tested attached to the AquaMAV body.

Figure 9.

The effect of the folding design on the open wing's aerodynamic efficiency. (a) Lift curves for the main wing at 6, 8 and 10 m s⁻¹ compared with a rigid aluminium wing at the same speeds. (b) Drag coefficients for the rigid and folding wing. The fuselage drag, measured separately is subtracted from the folding wing measurements, but the rigid wing still exhibits lower drag, suggesting that the flow around the fuselage interferes with the wing detrimentally. (c) Image of the AquaMAV main wing in the wind tunnel and (d) image of the rigid aluminium wing in the wind tunnel.

While the rigid wing exhibits the same lift behaviour at the three tested speeds, the early stall in the compliant wing is only observed at low speeds. At 8 m s⁻¹, the lift curve shows an inflection near the 6 m s⁻¹ stall point, but lift increases beyond. At 10 m s⁻¹, further lift increases are seen beyond 6° attack angle. This disparity at different speeds may too be the result of wake interaction, or the presence of a laminar separation bubble [29]. During the tests, deformation of the wing was observed, both a deflection of the wing trailing edge and a slight increase in dihedral. The wing's compliance, with the wing deforming upward under the increased aerodynamic loads at higher speeds may also contribute to the delayed stall. However, in order to fully determine origin of the disparity it would be necessary to measure either the wing deformation or the flow geometry directly. Nonetheless, the delayed stall will allow the vehicle to be more robust to perturbations in flight.

It was necessary to test the AquaMAV wing attached to the fuselage due to its folding mechanism (figure 9c). However, as it is being compared with the plain aluminium wing (figure 9d), the lift and drag of the fuselage as measured without the wing attached is subtracted from the data shown in figure 9. Examining figure 9b, it can be seen that the rigid wing shows lower drag prior to stall, indicating that the protrusions on the upper surface and gear mechanism on the lower surface, as well as interference with the wing flow from the fuselage, all act to increase folding wing drag relative to the rigid planform.

4.3. Sources of drag

In figure 10, the drag acting on the vehicle at 0° angle of attack is plotted against speed in water. Tests were repeated with the vehicle wings, fins and propeller removed, to show the different contributions (due to the flume's 0.5 m width, the wings were only tested fully folded). For each curve, a quadratic polynomial relating drag, D, to velocity, v (with the form D = Kv², where K is a constant) is fitted by regression, and a drag coefficient of the form in equation (4.1) was extracted. The difference in drag between, for example, the fuselage with propeller attached and fuselage without allowed us to extract the drag contributions of different components (table 3). Reasonable agreement between tests in air and water was found, although the need to disassemble the AquaMAV between tests may have resulted in some inconsistencies. Notably, the measured drag coefficient of the wing underwater is half that which was measured in air. This is most probably due to bending of the wing. Given the folded wing's C_L0 of 0.044 (figure 7d), the wing would produce 0.15 N of force in air at 10 m s⁻¹, but the same lift coefficient in water flowing at 1 m s⁻¹ would produce 1.21 N of force.

Figure 10.

Fuselage drag measurements at 0° angle of attack in a water tunnel, with a quadratic curve fitted to extract C_D.

Table 3.

Comparison between measured drag contributions of AquaMAV components in air and water at 0° angle of attack.

	water		air
component	CD	per total (%)	CD	per total (%)
fuselage	0.0121	39	0.0069	17
fins	0.0047	15	0.0031	7
propeller	0.0002	1	0.0012	3
wings	0.0142	45	0.0299	73
total	0.0312	100	0.0410	100

5. Planar trajectory model

Having measured the longitudinal aerodynamics of the AquaMAV, we use the data gathered to analyse dive trajectories of the vehicle using a planar trajectory model, using an approach similar to a previous study in which planar aerodynamics were show to accurately predict trajectories of a vehicle launching from water [11]. As with [11], the model is quasi-steady state. This assumption has been shown to hold in predicting dynamic trajectories of perching manoeuvres from static force coefficients [30], and the model's validity for predicting motion in this study is evaluated in §7.

In this section, we use subscripts ‘w, f, cg and cb’ to refer to the robot wing, fins, body and centres of gravity and buoyancy, respectively. The trajectory is defined by velocity and acceleration vectors, and in earth-fixed inertial axes with unit vectors We also define position vectors, within a robot-fixed reference frame rotated by an angle θ about from the inertial frame, with its origin at the robot nose and unit vectors The nomenclature for the trajectory model is illustrated in figure 11.

Figure 11.

Nomenclature for the equations of motion used in the planar trajectory model, showing the earth-fixed reference frame the robot-fixed reference frame, with its origin at the vehicle nose and illustrating the definition of body angle of attack, α_cg, pitch angle θ and velocity angle with respect to the earth-fixed frame, β_cg. Also pictured are the wing and tail aerodynamic forces (L_w, D_w and L_f, D_f, respectively), the robot weight and buoyancy B.

5.1. Aerodynamic forces

Coefficients used for the wing, tail and body are taken from the tunnel data shown in figure 7a–d. The measured force coefficients and centres of pressure are used as look-up tables in the trajectory code, with the data interpolated at each time step. For extrapolation outside of the measured range, the post-stall lift coefficient is used, or linear extrapolation for drag coefficient. However, the vehicle was ultimately not simulated reaching an angle of attack outside the measured range, owing to the large tail volume coefficient of the vehicle (36.7%).

The vector forces produced by the wing, and the tail fins, (equations (5.1) and (5.2)), have a lift component perpendicular to the local velocity, , and a drag component opposing it, defined by lift and drag coefficients C_lw and C_dw, respectively, for the main wing, and C_lf and C_df for the fins.

5.1

and

5.2

where A is the component's lifting area, and ρ_a the density of air. The local velocity of the wing is taken as the velocity of the centre of gravity, but the tail velocity, includes the effect of the vehicle's pitch rate, :

5.3

where R is a matrix representing rotation about The angles of attack of the vehicle and its empennage, α_b and α_f, respectively, are calculated from the angle the component's velocity in the inertial frame makes with the horizontal, denoted by β:

5.4

and

5.5

β_f includes pitch damping effects (equation (5.3)), while any pitching damping of the main wing is neglected due to the its proximity to the vehicle centre of mass.

The location of the vehicle's centre of mass, and the moment of inertia about that centre, I_zz, are computed from accurate CAD models of the vehicle, listed in table 3. In the model, wing retraction is treated as instantaneous, represented by a step change in aerodynamic behaviour and inertia at time t = t_d (in practice, the wing takes less than 0.5 s to retract, depending on airspeed, so any transient effect should have little impact on the overall trajectory).

The forces acting on the robot are resolved into inertial axes, and moments are taken about x_cg (equations (5.6) and (5.7)):

5.6

and

5.7

where R is a matrix representing rotation about These equations are numerically integrated in Matlab using a variable step Runge–Kutta solver.

5.2. Underwater motion

While a complete simulation of the vehicle mechanics underwater requires measurement of the forces caused by fluid inertia, it is nonetheless possible to estimate the ability of the AquaMAV to achieve depth by diving by examining the limiting effects of drag underwater. Neglecting any effect from the increase in Reynolds number, we use here the dimensionless aerodynamic coefficients measured during wind tunnel tests to allow us to simulate motion underwater, replacing the density of air in equations (5.2) and (5.1) with that of fresh water. Owing to the presence of buoyancy, we use a CAD model to calculate the total volume displaced by the vehicle, and the centre of displacement which allows us to calculate the torques and moments created by the vehicle's buoyancy,

5.8

where ρ_w is the density of water and D is the volume displaced by the AquaMAV when underwater. The equations of motion then become

5.9

and

6. Dive trajectories

6.1. Aerial phase

When the AquaMAV wings are retracted completely from a level cruise with wings fully open, the vehicle immediately begins to dive, due to the rearward movement of the centre of gravity and decrease in lift production. Initially, we examine a simulated long dive which allows the vehicle to reach steady-state orientation and velocity, initiated at an altitude of 500 m, from level flight at 10 m s⁻¹ (figure 12). Five hundred metres is chosen as a start height as this represents a reasonable maximum operating altitude, given that many countries' civil aviation authorities place a 500 m ceiling on unmanned aircraft operation. Although folding the wings reduces their lift production by 92% (figure 7c,d), the residual lift has a significant effect on the vehicle trajectory. To gain insight into this effect, we compare this dive with another simulation in which the lift coefficient of the folded wing is artificially set to 0, although the wing drag is retained. In both cases, when the wings are folded a short transient pitch oscillation occurs, but is quickly damped out in around 1 s (figure 12c,d), during which time the vehicle has only descended around 3.5 m. We can see from the plots that the residual lift generation of the folded wing has little effect on the vehicle's terminal velocity (36.6 m s⁻¹ with lift compared with 39.9 m s⁻¹ without, figure 12a,b), which is largely determined by its drag, but that it does cause the vehicle to reach an equilibrium pitch of −51° from the horizontal (figure 12c), which means that the vehicle covers significant horizontal distance (figure 12d). This presents a problem in accurately targeting the impact point of the vehicle in the water, as over long distances wind gusts and turbulence are liable to significantly perturb the trajectory.

Figure 12.

The steady state behaviour of the AquaMAV in an unpowered dive simulated in 3 d.f. using tunnel data, showing the effect of the residual lift of the main wing after folding. (a) Velocity profile of the diving AquaMAV. (b) Velocity profile of the vehicle if wing lift coefficient is artificially set to zero, but wing drag is retained. (c) Pitch and angle attack during a dive. (d) Pitch and angle of attack with zero wing lift. (e) Dive trajectories in both cases. The plots show that while the wing lift has little effect on the impact velocity, which is largely determined by drag, it has a strong effect on the impact angle.

Figure 12 illustrates the terminal velocity and attitude of the vehicle, but dives are far more likely to be initiated much nearer the surface in practice. Not least because the vehicle reaches an equilibrium angle at terminal velocity in less than 200 m of vertical descent, so diving from any higher has no effect on the final impact other than to increase the distance travelled. Furthermore, at the 36.6 m s⁻¹ terminal speed will create significant impact loads, liable to damage the robot.

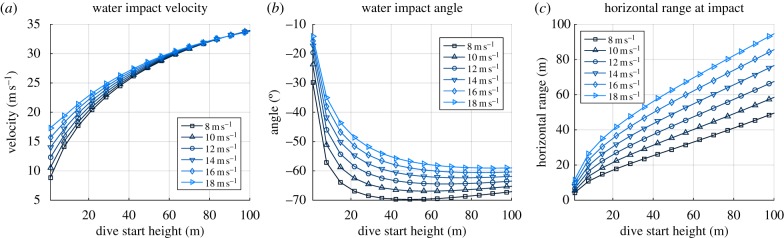
A fully passive dive, initiated only by the vehicle folding its wings is desirable as it reduces reliance on sensing and control, which is useful when performing an aggressive manoeuvre with a miniature robot. We, therefore, examine the effect on water impact of the condition of the vehicle when the dive is initiated. Figure 13 shows the effect of dive height (the point at which wings are folded) on the final impact of the vehicle, plotted for dives starting at several different cruise speeds. Because the vehicle begins to stall at a lift coefficient of 0.9, its minimum stable speed is approximately 8 m s⁻¹, and this is the lowest speed simulated. The vehicle's maximum propelled flight speed is fundamentally limited by its propulsion. The AquaMAV uses a 152 mm diameter folding propeller, which, when used in combination with the vehicle's 55 W motor, has a an approximate maximum velocity of 18 m s⁻¹, above which the propeller cannot rotate sufficiently fast, and produces drag rather than thrust, and this is, therefore, the maximum start speed simulated.

Figure 13.

The effect on speed and height when wings are folded on the water impact conditions. Each marker represents one trajectory simulation. (a) Impact velocity against dive start height at 8–18 m s⁻¹ start speed. (b) Angle from horizontal at impact. (c) Horizontal distance covered between wing fold and impact.

As it dives, the AquaMAV initially pitches more steeply than the equilibrium dive angle observed in figure 12, as it must first gather speed. Increasing the initial speed reduces the speed to be gained, and therefore reduces this overshoot. This means that impact angles will be shallower, although horizontal distance covered will be greater. Changing the initial speed has a smaller effect on the impact velocity, which tends asymptotically to terminal velocity as start height is increased. In all cases, the vehicle covers significant horizontal distance before it hits the water, which can be most effectively decreased by reducing the speed at the dive start.

6.2. Aquatic phase

Using the same trajectory model, we have also undertaken a simple analysis of the vehicle's motion in water, by simulating trajectories underwater over a variety of initial conditions. Our aim in this section is to evaluate the extent to which the vehicle drag limits its penetration into water. As such, we are not considering the significant transient effects the vehicle experiences while impacting the surface, which arise from the rapid accrual of fluid inertia as the vehicle enters the water, and treat the vehicle as starting fully immersed beneath the surface.

The vehicle's tail is hollow which keeps the centre of buoyancy rearward of the wing, and keeps the vehicle stable during a dive. The hollow tail ultimately fills with water through a small check valve, which is then used as propellant to escape the water. The tail filling also shifts the centre of buoyancy forward to make the vehicle float nose up for launch. However, the tail fills through a narrow check valve, and the time taken to fill is much longer than the deceleration time underwater, so the tail is treated as empty throughout. From the dive simulations, we can see that the ability of the AquaMAV to achieve significant depth purely through flight momentum is limited. This is predominantly due to the large drag forces which arrest the vehicle within approximately 1 m of travel through water. Figure 14a shows several example trajectories for impact at 20 m s⁻¹ at a various angles, with numerical integration stopped when the vehicle's vertical velocity reaches zero. We can see that the lifting surfaces keep dive paths fairly straight while the vehicle has some speed, but once the vehicle slows, the nose-down moment from buoyancy in the tail pitches it over. Increasing the impact speed yields no significant increase in dive depth, and the vehicle is brought to a stop within one to two body lengths below the surface (figure 14).

Figure 14.

Trajectory of the AquaMAV underwater under changing initial angle and speed. (a) Example dive trajectories for impact at 20 m s⁻¹; the AquaMAV does not initially pitch over, but as its speed reduces and the aerodynamic surfaces no longer generate significant force, the rearward centre of buoyancy rotates it nose down. (b) Dive depth against impact velocity, plotted for various initial angles. An image of the AquaMAV is included on the same scale as the Y-axis.

7. Discussion

7.1. Model assumptions

The trajectory model outlined in §5 assumes that the behaviour of the vehicle is quasi-steady state, and that the wind tunnel measurements can be used to give an accurate description of the vehicle's dynamic behaviour. Because the manoeuvres simulated involve rapid changes in velocity and attitude, we evaluate the validity of this assumption by examining the reduced frequency of the vehicle in pitch [31],

7.1

where c is the vehicle chord length (0.302 m for the closed wing). Where |k| < 0.03, the quasi-steady assumption can be considered to hold [29]. Plotting this parameter over the course of the trajectories simulated shows that k remains below 0.04 throughout its trajectory in air, only briefly exceeding 0.03 during the transient pitch oscillation as the wings are folded (figure 15a). In water, k is also low, only becoming large as the vehicle velocity reaches zero at the end of a dive (figure 15b), the portion of the trajectory consisting of slow, buoyancy driven movement, which is of least significance to the vehicle design and operation.

Figure 15.

Validity of the quasi-steady assumption for the trajectories shown in §6, evaluated in terms of reduced frequency, k. (a) k against time for trajectories in figure 12, showing that k is below 0.04 for the majority of the simulation. (b) k against absolute velocity for trajectories plotted in figure 14b, showing that the quasi-steady assumption is reasonable for most of the trajectory, until the vehicle's motion is almost arrested, at which point the pitch rate becomes significant relative to the forward velocity.

The model also neglects any changes in behaviour due to changes in Reynolds number from the test conditions. The AquaMAV was tested in the wind tunnel at Reynolds numbers between 47 800 and 79 600, and in the water tunnel between 26 000 and 135 000. In the aerial trajectory simulations, the AquaMAV was predicted to reach speeds of up to 36 m s⁻¹, a Reynolds number of 287 000. This would likely result in extensive turbulent flow, which would increase parasitic drag during the dive, as the AquaMAV is highly slender and travels at a small angle of attack during descent, so parasitic drag is likely to be dominated by skin friction. This was borne out by the water tunnel tests, which showed an increase in drag on the fuselage and fins at zero incidence compared with air (table 4). However, further investigation would be needed to quantify this.

Table 4.

Key parameters for the AquaMAV dynamics computed from a CAD model of the robot. The wings are closed for the majority of the air trajectory simulations and the entirety of the water simulations.

parameter	value
distance from nose to centre of gravity (open wing)	205 mm
distance from nose to centre of gravity (closed wing)	217 mm
distance from nose to centre of buoyancy (closed wing, empty water tank)	252 mm
Izz (open wing)	3.81 kg m−2
Izz (closed wing)	4.06 kg m−2
weight of water displaced, ρwDg (empty water tank)	265 g

Finally, the model neglects the presence of fluid inertia. This plays a significant role in both the impact of the robot with the water, at which point total system inertia rapidly increases, and during the descent, where it may slow the deceleration of the vehicle slightly. In the modelled trajectories, the vehicle angle of attack is small and the robot travels on a near to straight trajectory, so the influence of inertial forces on its trajectory will be less than its effect on the vehicle's linear acceleration. While exploration of these forces was beyond the scope of the current study, future work will investigate the behaviour of the AquaMAV when impacting the water.

7.2. Robot performance

The ability to penetrate the water by diving is strongly a function of scale. As size increases, the significance of fluid resistance (broadly a function of area) in relation to the inertia of a body (broadly a function of volume) declines. The 3 kg northern gannet has been observed reaching depths of up to 10 m in a single dive [1] (figure 1a,b), while the 30 g common kingfisher (figure 1c,d) dives only to around 25 cm [32]. The AquaMAV, weighing 0.2 kg, is predicted to stop under drag within 1 m. As both the AquaMAV and the gannet are near to the density of water, the gannet's 15 times larger mass gives it an advantage. The gannet also is able to fold itself into a more compact shape, owing to the softness of its feather and tissue. However, there are many effects that have not been explored in this study, including the creation of an air cavity during impact [24], or the use of super-hydrophobic surfaces [2] which could potentially increase the range of future AquaMAV prototypes.

For animals, diving is a means of prey capture, and the presence of prey determines the necessity of depth. For the AquaMAV, diving into the water serves two purposes. Firstly, it allows the vehicle to penetrate beneath the water in spite of its buoyancy, and without any additional aquatic propulsion. This will allow it to collect water samples beneath the surface, avoiding any floating contaminants, and make other subsurface observations. Secondly, diving directly into the water is an inherently robust landing strategy, relying on passive hydrodynamic stability. This can be compared with ‘deep-stall’ landings above the surface, or ‘soft’ landings using floatplanes, both of which require accurate knowledge of the water surface's proximity and the vehicle's attitude. But if a vehicle is to impact the water, folding wings become structural necessity, if the vehicle is to be light enough for efficient flight.

The usefulness of diving as a means of water entry is more important in outdoor environments, where the motion of the water surface means that soft landings become more intractable. This is most import for small vehicles, relative to which wave height becomes increasingly large, in an aquatic version of the ‘size-grain hypothesis’. Diving directly through the surface is far more insensitive to surface motion than other means of water entry, and it can be seen from figure 14a that the vehicle initially follows a straight trajectory through the water regardless of the angle at which it impacts (figure 14).

Passive stability in lieu of active control for landing not only ensures robustness, but also means that robots can be operated more cheaply. However, this comes at the expense of accuracy. From the analysis in §6, it is reasonable to suggest that an AquaMAV could autonomously enter a large body of water at a particular point given only a GPS coordinate at which to fold wings, and coarse altimetry. The accuracy with which it hits the water target point will be reduced by the fact that it covers horizontal distance uncontrolled during the dive. If the vehicle is required to dive into more confined spaces, it is important to note that the analysis presented in this paper is limited to the longitudinal dynamics of the AquaMAV, and we have not investigated the behaviour of the vehicle where rolling and yawing are permitted. In order to dive vertically down from the start point of the dive without active control, it may be possible to force the vehicle to take a spiral trajectory, which would reduce the horizontal range covered as the vehicle descends.

In addition to being waterproof, the AquaMAV is adapted specifically for dives into water by its hollow tail, which ensures a stable dive by keeping the centre of buoyancy rearward, but slowly fills with water, orienting the vehicle nose up for take-off after the dive. However, this alone would not ensure penetration beneath the surface, and the ability to fold the wings is essential as it not only protects them from impact but means that the vehicle generates far less lift and drag underwater. A wing large enough to produce lift in flight would produce significantly more force underwater, and force the vehicle off course. The wind tunnel tests of this wing show that the ability to fold does not compromise flight with the wings are open, although the performance of the folding wing is not identical to a rigid equivalent. The folding mechanism has the added advantage of being able to sweep partially backward which expands the vehicle's flight envelope, enhancing the mobility of the prototype.

8. Preliminary flight test

After testing in the wind tunnel, the AquaMAV was flown outdoors and tested diving into the water as a first proof of concept. While these tests were not intended to record precise data, these preliminary tests show the basic functionality of the system. Figure 16a shows a composite image of a dive into water, recorded with a static camera at 120 frames s⁻¹. The AquaMAV was launched from an elevated position and steered to impact in front of a camera placed at the water level, with the wings folded and throttle cut manually by a remote operator. While the flight speed cannot be accurately measured, an estimate of the final impact velocity can be made from the final frames of the sequence in which the vehicle flight path is near vertical, with the AquaMAV itself providing a reference length. The vehicle speed was estimated using a software automatic tracking routine (OpenPhysics Tracker) which yielded an approximate impact velocity of 9.1 m s⁻¹ (figure 16b–d). The vehicle was undamaged by the pictured impact, although it is noteworthy that during a later flight an accidental water impact with open wings resulted in the destruction of one of the wing hinges. For future flights a compact sensing system is under development to allow recording of airspeed and inertial measurements during dives.

Figure 16.

Preliminary flight test of the AquaMAV outdoors. (a) Composite image of a dive into water, with frames 83 ms apart. The impact velocity was estimated from the later video frames. (b) Calibration frame using vehicle length as reference. (c) Final frame showing tracked points. (d) Velocity estimate from tracked points. (e) Image of the AquaMAV at the point of impact with the water. (f) Image of the AquaMAV fully immersed after a dive.

9. Conclusion and future work

In this paper, we have presented a morphing wing aircraft designed to dive into water from flight. Aerodynamic evaluation of the vehicle in at-scale wind tunnel tests show the deployable wing to perform well at cruise condition, in spite of the design constraints created by the folding mechanism. It is able to greatly decrease its lift and drag by morphing its shape, allowing the vehicle to passively dive from flight. Trajectory simulations elucidate the terminal velocity and orientation of the vehicle during and dive, and show the range over which the robot can affect its final impact conditions by changing its cruise speed or altitude. A passively initiated dive is certainly suitable for entering confined bodies of water, and the vehicle's underwater stability means that structural stresses from hydrodynamic loads will be greatly reduced.

While this paper includes preliminary outdoor tests, future work will examine the AquaMAV's plunge dive in the field, using inertial measurements to validate the predictions made in this paper. We will also examine in greater detail the physics of water impact, and the ability of the vehicle to sustain the large impact loads encountered when hitting the water. Currently, the robot has a limited ability to produce thrust underwater using its aerial propeller, but this is very inefficient and draws large currents. An enhanced propulsion system for locomotion underwater is under development which uses a variable transmission to produce thrust efficiently underwater using the aerial propeller. Combining these developments will bring to the field a first of its kind aquatic fixed-wing aircraft, which will allow robotic collection of water data and greatly reduce the resource and manpower costs of monitoring marine environments.

Competing interests

We declare we have no competing interests.

Funding

This project was funded by the UK Engineering and Physical Sciences Research Council, award number EP/N009061/1.