Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2017 Jan 3;7:38244. doi: 10.1038/srep38244

Relaxation oscillations and hierarchy of feedbacks in MAPK signaling

Marek Kochańczyk 1,a, Paweł Kocieniewski 1, Emilia Kozłowska 2,*, Joanna Jaruszewicz-Błońska 1, Breanne Sparta 3, Michael Pargett 3, John G Albeck 3, William S Hlavacek 4, Tomasz Lipniacki 1,b
PMCID: PMC5206726  PMID: 28045041

Abstract

We formulated a computational model for a MAPK signaling cascade downstream of the EGF receptor to investigate how interlinked positive and negative feedback loops process EGF signals into ERK pulses of constant amplitude but dose-dependent duration and frequency. A positive feedback loop involving RAS and SOS, which leads to bistability and allows for switch-like responses to inputs, is nested within a negative feedback loop that encompasses RAS and RAF, MEK, and ERK that inhibits SOS via phosphorylation. This negative feedback, operating on a longer time scale, changes switch-like behavior into oscillations having a period of 1 hour or longer. Two auxiliary negative feedback loops, from ERK to MEK and RAF, placed downstream of the positive feedback, shape the temporal ERK activity profile but are dispensable for oscillations. Thus, the positive feedback introduces a hierarchy among negative feedback loops, such that the effect of a negative feedback depends on its position with respect to the positive feedback loop. Furthermore, a combination of the fast positive feedback involving slow-diffusing membrane components with slower negative feedbacks involving faster diffusing cytoplasmic components leads to local excitation/global inhibition dynamics, which allows the MAPK cascade to transmit paracrine EGF signals into spatially non-uniform ERK activity pulses.

A canonical mitogen-activated protein kinase (MAPK) pathway responsible for transducing signals from growth factors consists of three tiers of sequentially activated protein kinases: RAF, MEK, and ERK1. Activated ERK, considered the output of the cascade, phosphorylates more than 100 substrates including several transcription factors2 and elicits a variety of cellular responses including growth, proliferation, and differentiation3,4. Unsurprisingly, dysregulated MAPK signaling underlies many cancers5. There is growing evidence that the cell fate decisions are regulated by temporal6,7,8 or even spatiotemporal profiles of ERK and RAF9,10,11,12,13,14,15. It is thus important to understand how information about the level and gradient of an extracellular stimulus is encoded and transmitted to intracellular downstream effectors.

In the last two decades, numerous positive and negative feedback loops regulating the MAPK network have been discovered and characterized16,17. A positive feedback from RAS to SOS allows for signal amplification in the vicinity of the receptor and has been proposed to introduce bistability18, which enables the system to respond to inputs in a switch-like (digital) fashion19. Negative feedbacks emanating from ERK have been associated mainly with response attenuation20, but negative feedbacks in general may be harnessed to ensure perfect adaptation21,22 or give rise to oscillations23,24,25,26. System-level mechanisms of controlling information processing in MAPK are still not fully understood, partially due to the fact that systems involving interlocked positive and negative feedback loops may exhibit rich nonlinear dynamical behavior. Dynamics assumed by such complex systems depends on the characteristic time scales involved and network connectivity/topology, i.e., where the feedbacks act and how they relate to each other. For example, sustained oscillations may arise when a negative feedback loop is embedded within a relatively slow positive feedback loop27 or when a positive feedback loop is embedded within a relatively slow negative feedback loop28. In the latter case, the time profiles may be similar to those produced by a relaxation oscillator, i.e., consisting of a fast activation phase and a phase of (usually slow) relaxation to a state in which subsequent activation is possible29. In recent work30, we observed similar pulses using a sensor based on phosphorylation-regulated Förster resonance energy transfer (FRET) to monitor EGF-stimulated ERK activity in single MCF10A cells. These pulses differ from constant-frequency quasisinusoidal oscillations in ERK nuclear translocation observed in other studies26 and are characterized by an EGF dose-independent amplitude and an EGF dose-dependent period.

In this study, we construct a computational model for MAPK/ERK signaling downstream of EGFR with three aims: (i) to verify whether the combination of the positive and negative feedbacks considered in the model leads to observed relaxation oscillations, (ii) to characterize the functional roles of the different feedback loops depending on their position in the network, and (iii) to analyze the consequences of proteins participating in the feedback loops being localized to distinct subcellular compartments (the plasma membrane or the cytosol) for spatiotemporal profiles of the response. We restrict our analysis to four feedbacks: one positive and three negative (shown in Fig. 1 and discussed in Supplementary Text S1). The proposed model is corroborated by experimental analysis of single-cell responses to a broad range of EGF doses using a fast sensor of ERK activity based on phosphorylation-dependent regulation of nucleocytoplasmic shuttling31,32.

Figure 1. Feedback loops in the MAPK/ERK pathway.

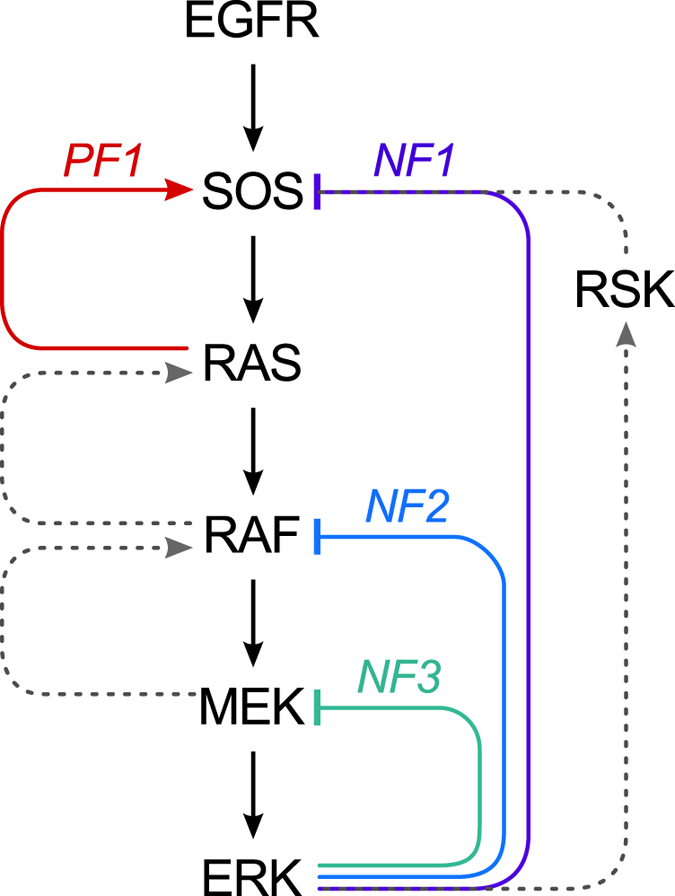
Figure 1

Open in a new tab

Loops captured in the model are shown with solid lines. The arrow labeled PF1 represents positive feedback. This feedback loop has been implicated in mediating bistable switching. The arrows labeled NF1–NF3 represent negative feedbacks. The NF1 feedback loop encompasses the positive feedback loop. The NF2 and NF3 feedback loops are placed out of the positive feedback loop. Dotted lines indicate feedbacks not included in the model.

Results

Model

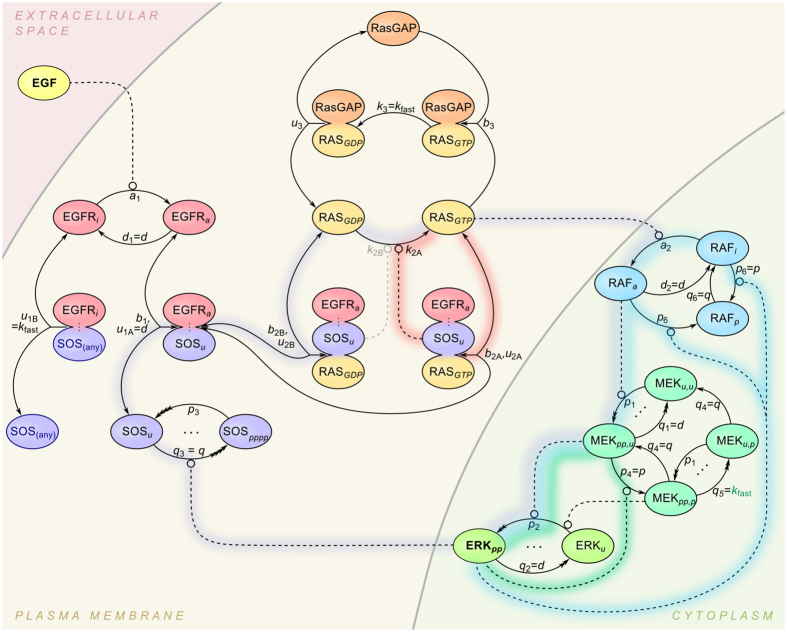
We constructed a model for EGFR-mediated activation of ERK that captures the feedback loops illustrated in Fig. 1. In addition to well-known negative feedbacks from ERK to its upstream signaling partners, MEK, RAF, and SOS, which have been considered in earlier experimental and modeling studies, our model includes a positive feedback loop involving SOS and RAS. This relatively recently discovered feedback loop, labeled PF1 in Fig. 1, is upstream of negative feedback from ERK to RAF (labeled NF2 in Fig. 1), as well as negative feedback from ERK to MEK (labeled NF3 in Fig. 1), and it is encompassed within the negative feedback loop involving ERK and SOS (labeled NF1 in Fig. 1). It is known that interlocked positive and negative feedback loops can give rise to excitatory behavior, which we have observed in a recent study of single-cell ERK dynamics30. Our model was built and analyzed to determine whether positive feedback between plasma membrane-associated signaling proteins could potentially be responsible for the observed behavior, which includes apparent relaxation oscillations in ERK activity.

We formulated the model as a system of coupled ordinary differential equations (ODEs) for the mass-action kinetics of the reaction scheme shown in Fig. 2. Although this scheme provides a simplified representation of the MAPK signaling network downstream of EGFR, it preserves the dynamical structure of the network, meaning that it includes the essential processes responsible for the feedbacks connecting the main signaling proteins of the network (cf. Figs 1 and 2). Importantly, with this model, we can assign values to parameters that determine the relative time scales of activating and inhibiting processes. As we will discuss later, we considered two extensions of the model. One is a Markov chain that includes the same processes as those considered in the ODE model but adds stochastic processes that affect the level of EGFR expression on the surface of a single cell. This model extension is intended to account for extrinsic noise and the heterogeneity of cell populations (see Materials and Methods). The second extended model consists of a set of partial differential equations (PDEs). These equations incorporate the right-hand side terms of the ODE model. Reaction–diffusion processes in the extracellular space, on the plasma membrane, and in the cytosol are coupled through Robin-type boundary conditions. This model extension was formulated to study the subcellular spatial heterogeneity of responses to paracrine signaling, modeled as secretion of EGF at random times and random extracellular locations (see Materials and Methods).

Figure 2. Model for MAPK signaling.

Figure 2

Open in a new tab

Reactions considered in the model are represented by lines with arrowheads. Multiple arrowheads denote reactions with multiple steps (e.g., multi-site phosphorylation of SOS by ERK). Positive influences (e.g., ERK-catalyzed phosphorylation of SOS) are indicated by lines attached to small circles, with the circles identifying the reactions affected. The reactions and influences responsible for various feedback mechanisms are highlighted with shading: RAS-to-SOS positive feedback (red shading), ERK-to-SOS negative feedback (purple shading), ERK-to-MEK negative feedback (green shading), and ERK-to-RAF negative feedback (blue shading). Tripartite arrows, labeled with both binding and unbinding rate constants, are used to represent association and dissociation reactions.

An executable specification of the ODE model and the extended stochastic version of the model are provided in Supplementary Data 1. Default parameter settings for the ODE model are summarized in Supplementary Table S1. Supplementary Text S2 and Supplementary Table S2 contain non-dimensional model equations and parameters, respectively. Code for bifurcation analysis are provided in Supplementary Data 2. The stochastic extension of the ODE model has unique parameters that describe the dynamics of EGFR surface expression (Supplementary Table S3) and is provided in Supplementary Data 3. An executable specification of the PDE model is provided in Supplementary Data 4. This model has unique parameters that describe diffusion processes and paracrine signaling (Supplementary Table S4). Parameters were assigned default values as described in Materials and Methods. Simulations and bifurcation analyses were performed as described in Materials and Methods.

Positive feedback and bistability

According to the model with the default parameter settings of Supplementary Table S1, in the absence of negative feedbacks, the system exhibits bistability, i.e., bistable switching behavior (also known as hysteretic switching). As illustrated in Fig. 3, bistability depends on parameters governing positive feedback between SOS and RAS (Fig. 3A), as well as parameters governing saturation of RasGAP (Fig. 3B).

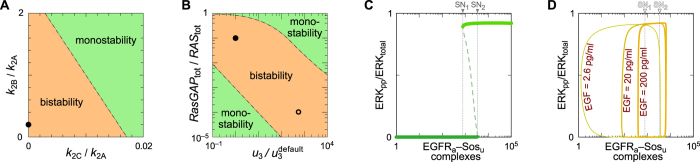
Figure 3. Conditions for bistability and the emergence of relaxation oscillations.

Figure 3

Open in a new tab

With all negative feedbacks removed, the system exhibits either bistable switching or graded responses to EGF stimulation depending on parameter values. (A) Range of parameters governing positive feedback for which the system exhibits bistability (for some EGF concentrations higher than 0.1 pg/ml). The parameters are ratios of rate constants, which characterize the relative nucleotide exchange activity of SOS when the REM domain in SOS is not bound to RAS or bound to RAS-GDP compared to the activity when the REM domain is bound to RAS-GTP (k2C/k2A and k2B/k2A). We vary these ratios with k2A fixed at the value given in Supplementary Table S1. (B) Range of parameters governing saturation of RasGAP for which the system exhibits bistability (for some EGF concentrations higher than 0.1 pg/ml). The parameters considered in this diagram characterize RasGAP activity: the ratio of enzyme (RasGAPtot) to substrate (RAStot) and the rate constant for dissociation of the enzyme-product complex (u3). We vary the ratio RasGAPtot/RAStot by varying RasGAPtot while keeping the value of the product b3 × RasGAPtot constant. This product governs the rate of formation of the enzyme-substrate complex. For more information about parameters, see Supplementary Table S1. In both panels, a solid dot marks the location in parameter space that corresponds to the values of parameters given in Supplementary Table S1. In panel B, an open dot marks the location in parameter space that corresponds to the values of parameters in the model of Stites et al. (Ref. 34). (C) Bifurcation diagram showing the active ERK fraction vs. the level of EGFRa–SOSu complexes in the system without all three negative feedbacks. Solid lines show two stable steady states; dashed line shows unstable steady state. (D) Analysis of the system with the negative feedback from ERK to SOS present and other two negative feedbacks absent. Parametric plot shows a projection of the limit cycle on the (active ERK fraction)—(EGFRa–SOSu complexes) plane.

The results of Fig. 3A are consistent with earlier work, which has implicated positive feedback from SOS to RAS in hysteretic switching33. Positive feedback arises because the product of SOS’s GEF activity, which is RAS-GTP, binds to SOS at SOS’s REM domain, which is non-overlapping with SOS’s GEF domain (also known as the Cdc25 homology domain). The outcome of RAS-GTP binding to SOS is an increase in the GEF activity of SOS. RAS-GDP binding to SOS also increases SOS’s GEF activity, but to a lesser extent. The parameter values of Supplementary Table S1 were selected so that positive feedback from SOS to RAS generates hysteretic switching in the absence of negative feedbacks. The parameter values characterizing SOS GEF activity (k2C, k2B, and k2A) are such that SOS’s GEF activity is zero when its REM domain is not bound to RAS (i.e., k2C = 0), and its GEF activity when SOS’s REM domain is bound to RAS-GDP is an order of magnitude lower than when SOS’s REM domain is bound to RAS-GTP (i.e., k2B = 0.1 × k2A). As shown in Fig. 3A, bistability requires both parameters, k2B and k2C, to be sufficiently small with respect to k2A.

Bistability is enabled by constraints on parameters related to SOS’s GEF activity (mentioned above) or by saturability of RasGAP (Fig. 3B). Saturation of RasGAP may occur during a response to EGF if the abundance of RasGAP is sufficiently lower than that of RAS, or if RasGAP-RAS complexes are sufficiently long lived. We have set parameter values such that RasGAP is saturable (Supplementary Table S1). Different parameter settings used in an independent modeling study34 are also consistent with saturability of RasGAP (Fig. 3B). In the steady state, the outcome of the pathway depends on the level of EGF-activated and SOS-bound receptors. In the bifurcation diagram of Fig. 3C, the level of EGFRa–SOSu complexes serves as a bifurcation parameter. Here, we use the notation “EGFRa–SOSu” to refer to activated EGFR in complex with SOS, which can bind EGFR only when not phosphorylated. Bistability arises for a certain range of EGFRa–SOSu abundance; below this range the system is monostable inactive (i.e., a low fraction of ERK is active), whereas above it, the system is monostable active (i.e., a high fraction of ERK is active).

Negative feedbacks and oscillations

Analysis of the bifurcation diagram in Fig. 3C suggests that the slow negative feedback mediated by ERK, which reduces the number of EGFRa–SOSu complexes (by phosphorylation of SOS to the state in which it cannot bind EGFR), may lead to relaxation oscillations. The mechanism may be explained as follows. In unstimulated cells the level of EGFRa–SOSu complexes is below the level corresponding to the saddle node bifurcation point SN1 in Fig. 3C, and thus ERK is inactive. EGF stimulation activates receptors, with formation of EGFRa–SOSu complexes. When the level of EGFRa–SOSu exceeds the level corresponding to the saddle node bifurcation point SN2, ERK is activated. Subsequently, ERK phosphorylates SOS, reducing the level of EGFRa–SOSu complexes. When this level drops below SN1, ERK activity is terminated. After ERK activity is terminated, SOS is dephosphorylated and the system resets; therefore, with persistent EGF stimulation, ERK activity pulses can be recurrent. The cycle is shown in parametric plot in Fig. 3D.

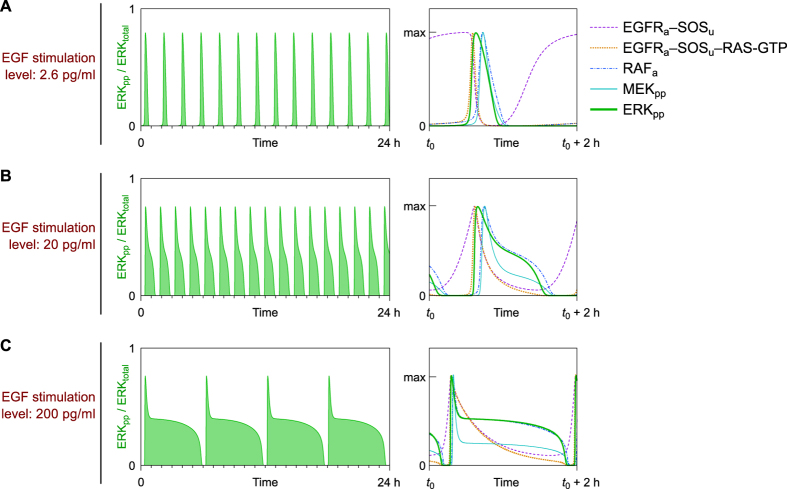
The full system (with all three negative feedbacks illustrated in Fig. 1 and parameterization according to Supplementary Table S1) can exhibit oscillations (Fig. 4). The amplitude of these oscillations very weakly depends on the strength of EGF stimulation, in contrast to the period and pulse width. These properties, indicating that the system switches between on and off states corresponding to the steady states of the system when only the positive feedback is present (Fig. 3C), are characteristic of relaxation oscillations. At a low level of EGF stimulation, ERK activity is pulsatile (Fig. 4A). In contrast, at a high level of EGF stimulation, pulse width is wide and off time is short, such that ERK activity is high most of the time (Fig. 4C). As a consequence, the ERK activity integrated over a population of (unsynchronized) cells would be expected to increase gradually with the EGF dose.

Figure 4. Simulated trajectories for three EGF stimulation doses.

Figure 4

Open in a new tab

The active ERK fraction (left column) together with levels of EGFRa–SOSu complexes, EGFRa–SOSu–RAS-GTP complexes, RAFa and MEKpp normalized to their maxima (right column) are shown as a function of time after stimulation by (A) low, (B) intermediate, and (C) high doses of EGF.

In the analyzed MAPK relaxation oscillator, period of oscillations is controlled by the speed of the inhibition and relaxation processes: inhibition relies on the phosphorylation of SOS by phosphorylated ERK (ERKpp), whereas relaxation relies on the resurgence of dephosphorylated SOS (SOSu) that can form complex with active EGFR (EGFRa) – see Fig. 4, violet dashed line. In the model we assume that SOS phosphorylation and dephosphorylation are possible only when SOS is not bound to EGFR. At a low stimulation dose (Fig. 4a) the resurgence phase is long, because SOSu has to recover to a high level (higher than in the case of a high stimulation dose) in order initiate a next pulse; at a high stimulation dose (Fig. 4c) the inhibition phase is long because SOSu has to drop to a low level (lower than for low stimulation dose) in order to terminate pathway activation.

The prediction of relaxation oscillations (Fig. 4) is consistent with observations of periodic ERK activity made using two different ERK activity reporters, EKAR3 and ERKTR32. The ERKTR reporter indicates bursts of ERK activity separated by distinct periods of essentially no activity. The EKAR3 reporter indicates similar oscillatory dynamics, but the off periods are less pronounced (see Fig. 5B in ref. 32). To determine if these features can be explained by the different kinetics of ERK interaction with the two reporters on the top of the model of Fig. 2 we explicitly included ERK activity reporters (see Materials and Methods). As shown in Supplementary Figure S3, the shape of predicted oscillations in the level of reporter phosphorylation depends on the kinetics of ERK-reporter interaction. With slower interaction kinetics, the off periods become shorter.

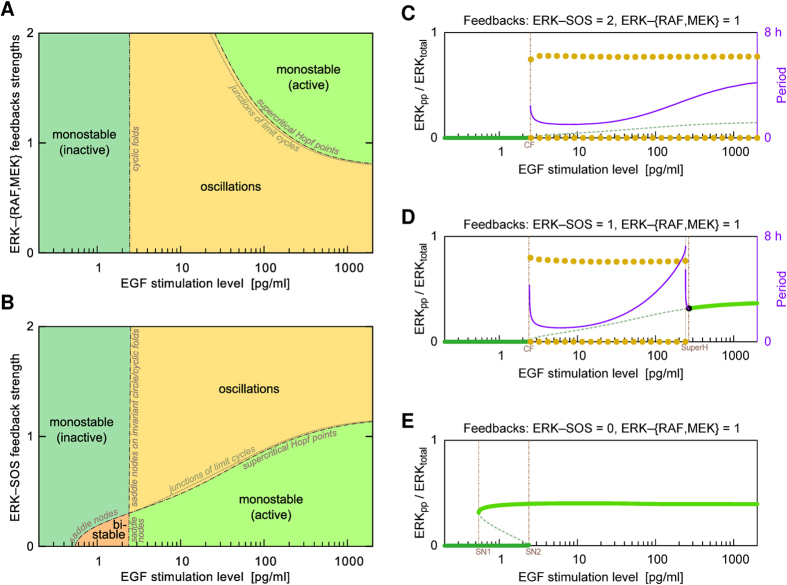
Figure 5. Bifurcation diagrams.

Figure 5

Open in a new tab

Each plot indicates the recurrent solutions for the fraction of activated ERK (ERKpp/ERKtotal) as a function of either one or two bifurcation parameters. EGF dose (or stimulation level) is a bifurcation parameter in each plot. In the two-dimensional bifurcation diagrams, the second bifurcation parameter characterizes the strength of the negative feedbacks from ERK to RAF and MEK (A) and the strength of the negative feedback from ERK to SOS (B). Areas are colored to indicate distinct qualitative behaviors: oscillatory, monostable with low or high ERK activity, and bistable. The boundaries are labeled to indicate the bifurcation types that separate the different regimes of behavior. The one-dimensional bifurcation diagrams correspond to different strengths of the negative feedback from ERK to SOS (i.e., they correspond to different cross-sections of the parameter space of panel B): twice the default strength (C), the default strength (D), and absent (E). Solid green lines indicate stable steady states; dashed green lines indicate unstable steady states. Yellow dots indicate the upper and lower envelopes of stable limit cycles. Purple lines indicate the periods of oscillations. Cyclic fold (CF) bifurcations in panels C and D are accompanied by subcritical Hopf bifurcation points (not marked). In a tiny parameter region between the two bifurcation points there coexist a stable limit cycle, an unstable limit cycle, and a stable steady state. In panel D, supercritical Hopf bifurcation lies close to a series of complex bifurcations (seen as the period discontinuity) which effects in a junction of limit cycles.

To investigate the parameter dependence of oscillatory behavior, we performed a bifurcation analysis (Fig. 5). Two-dimensional bifurcation diagrams (Fig. 5A and B) illustrate how qualitative behavior depends on the strength of EGF stimulation and the strengths of three negative feedbacks. As indicated in Fig. 5B, four regimes of behavior are possible: monostable on and off states, bistability (wherein the steady state occupied depends on history), and oscillations. These regimes are separated by bifurcations of different types, which are indicated by the labeling of boundaries. Figure 5C–E are one-dimensional bifurcation diagrams (with the strength of EGF stimulation chosen as a bifurcation parameter) corresponding to different cross-sections of the parameter space of Fig. 5B. The cross-section in Fig. 5D corresponds to the default parameter values of Supplementary Table S1. This diagram shows that the system is off (on) at low (high) levels of EGF stimulation and exhibits oscillations over a ~100-fold intermediate range of EGF stimulation strength. Over this range, the period of oscillations in ERK activity first decreases and then increases with EGF dose. The default parameters, which were chosen for consistency with observed system behaviors30, allow for a rich repertoire of behaviors. Moreover, the relatively modest modification of these parameters can change the system behavior from bistable to oscillatory, which is in line with the conjecture that complex systems are poised at criticality35.

Oscillatory behavior depends on feedback strengths (Fig. 5A–D), and bistability is only realized when negative feedback from ERK to SOS is weak or absent (Fig. 5B and E). As can be seen by inspecting Fig. 5B and also by comparing Fig. 5C and D, the range of oscillatory behavior increases with the strength of negative feedback from ERK to SOS. Conversely, the range of oscillatory behavior shrinks with stronger feedbacks from ERK to MEK and RAF (Fig. 5A). Generally, for a system with a single negative feedback, increasing the strength of negative feedback tends to switch off the response of the system to a signal. Here, somewhat paradoxically, increasing the strength of the negative feedbacks from ERK to MEK and from ERK to RAF can push the system from oscillatory behavior to a persistent on state if EGF stimulation is sufficiently strong (Fig. 5A). This behavior arises because negative feedbacks from ERK to MEK and from ERK to RAF weaken ERK activity, such that the ERK-to-SOS negative feedback cannot be engaged to induce oscillations.

We note that oscillatory behavior requires not only a sufficiently strong negative feedback from ERK to SOS (Fig. 5) but also multi-site phosphorylation of SOS (Supplementary Figure S2). In the model, the effect of (distributive) multi-site phosphorylation is to introduce a delay in reactivation of SOS after deactivation of ERK. The delay arises from the time required for phosphatases to act and an assumption that phosphorylation of a single site in SOS by ERK is sufficient to suppress SOS activity. The model accounts for four SOS residues that can be phosphorylated by ERK. If the number of such residues is reduced to three, oscillatory behavior is observed over a much narrower range of EGF concentrations and oscillations are not observed for less than three phosphorylatable residues in SOS (Supplementary Figure S2).

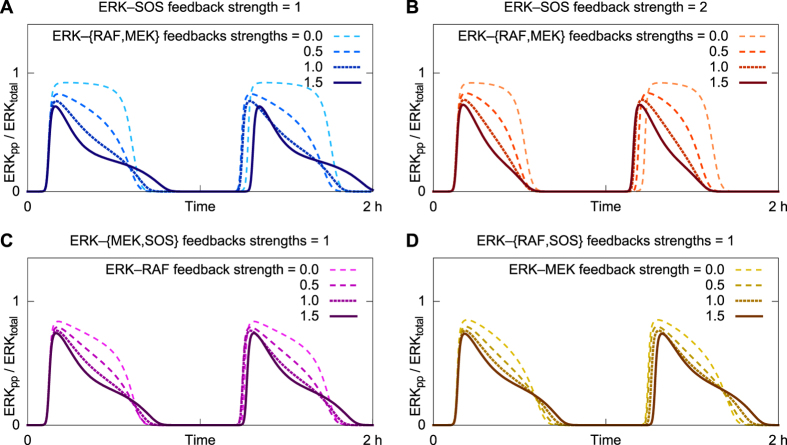
The shape of ERK activity pulses is controlled by the strengths of negative feedbacks from ERK to MEK and from ERK to RAF (Fig. 6). As illustrated in Fig. 6A and B, for a given strength of negative feedback from ERK to SOS, increasing the strengths of negative feedbacks from ERK to MEK and from ERK to RAF changes the waveform of system response from a square wave to a long-tail pulse. Although the ERK-to-MEK and ERK-to-RAF feedbacks are somewhat redundant, both being downstream of positive feedback from RAS to SOS, the ERK-to-RAF feedback is more far ranged and therefore more strongly impacts pulse shape (Fig. 6C and D). Note that we have taken the ERK-to-MEK and ERK-to-RAF feedbacks to be equally strong (Supplementary Table S1). Additional phase space analysis in Supplementary Figure S4 shows in parametric plots that cycle trajectories with two feedback strengths in common group together in tight clusters whereas trajectories with only one feedback strength in common group together in looser clusters.

Figure 6. Negative feedback from ERK to MEK and RAF shape the time profile of response to EGF stimulation at 10 pg/ml.

Figure 6

Open in a new tab

Each time course illustrates an oscillatory response to EGF stimulation. In the top panels, the strength of ERK-to-SOS negative feedback is set at the default level (A) or twice the default level (B). In these panels, different dash patterns correspond to different strengths of feedback from ERK to MEK and RAF, as indicated in the legends. The ERK-to-MEK and ERK-to-RAF feedback strengths are taken to be equal. In the bottom panels, the ERK-to-MEK and ERK-to-RAF feedback strengths are varied separately, as indicated in the legends.

Noisy oscillatory excitation of ERK

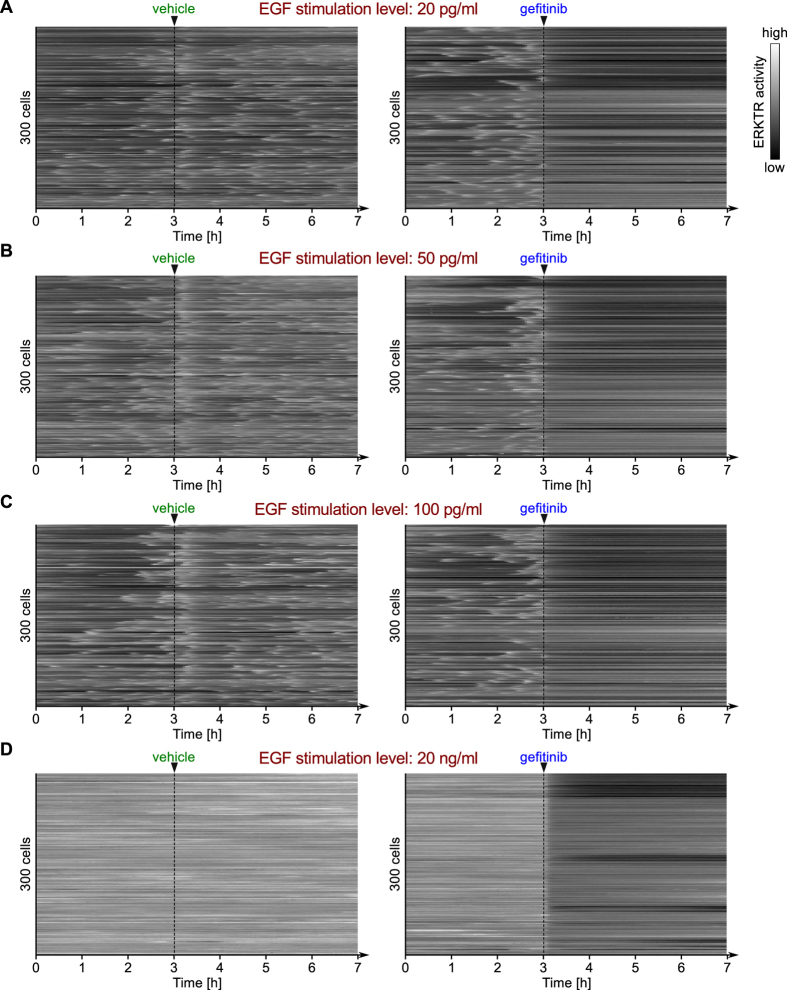
In earlier work30, using the EKAR-EV reporter, we observed bursts of ERK activity at low EGF doses, regular pulses of ERK activity at intermediate EGF doses, and sustained ERK activity with short, intermittent off periods at high EGF doses. These behaviors have been confirmed using the ERKTR reporter (Ref. 32, Fig. 7), which because of its faster kinetics is able to better resolve oscillatory dynamics (Supplementary Figure S3).

Figure 7. Kinetics of ERK activity as reported by ERKTR at four different doses of EGF.

Figure 7

Open in a new tab

EGFR inhibition by gefitinib is sufficient for elimination of ERK pulses. The time points are spaced by 3 minutes. A smaller set of data from the same experiment was published previously32.

As discussed above, the model of Fig. 2 predicts that oscillations, when they appear, will have an EGF dose-dependent frequency and dose-independent amplitude (Fig. 4). These features of predicted oscillatory behavior in single cells are similar to the oscillations in ERK activity that we observe in single cells (Ref. 30 and Fig. 7). However, the experimentally observed oscillations are noisy, with irregularity both within individual cells and across cells in the population monitored in experiments. To investigate how these irregularities could potentially arise (and whether they are consistent with the model), we extended the model of Fig. 2 to account for extrinsic noise. For simplicity, we considered only a single extrinsic noise source, which we took to be stochastic, time-varying cell-specific surface expression of EGFR. This extension is consistent with heterogeneity in protein expression levels across cell populations, which has been extensively studied and linked to bursts of gene expression36,37.

Thus, the extended model was obtained by recasting the original model as a Markov chain and by adding processes for stochastic generation and clearance of EGFR. Parameters introduced with these extensions are summarized in Supplementary Table S3. Parameter values are such that EGFR surface expression changes on a time scale of hours (Fig. 8A). The influence of extrinsic noise characteristics on active ERK dynamics is analyzed in Supplementary Figure S5. Separate influences of the intrinsic and extrinsic noise on ERK dynamics are demonstrated in Supplementary Figure S6 and Supplementary Figure S7.

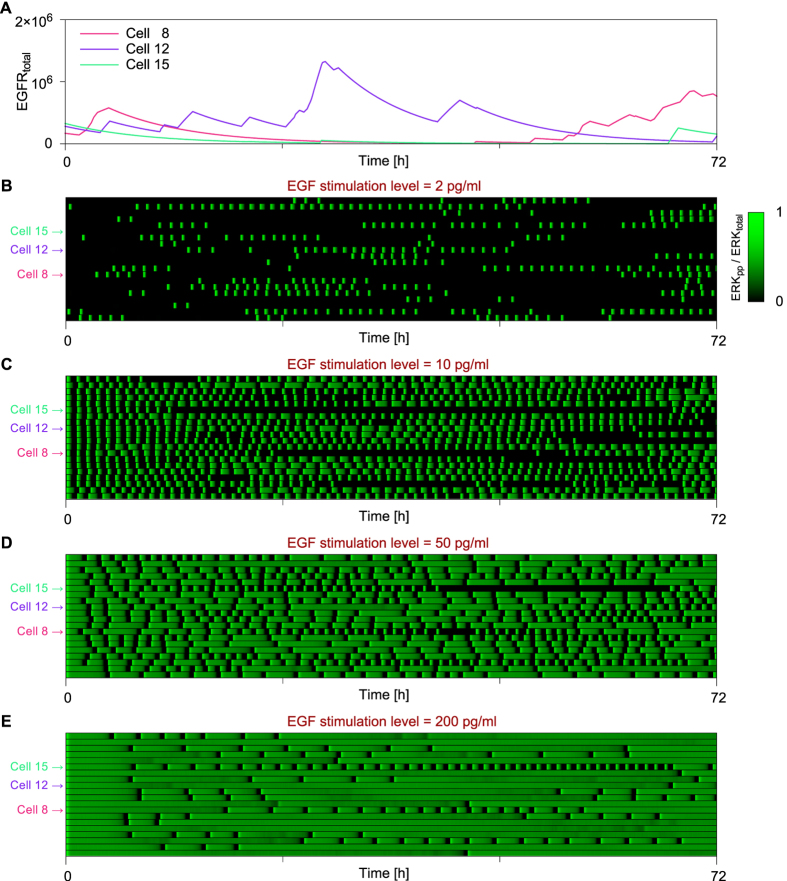
Figure 8. Single-cell temporal EGFR surface expression and ERK activity profiles obtained from stochastic simulations with fluctuating EGFR levels.

Figure 8

Open in a new tab

We considered the effect of extrinsic noise on oscillations in ERK activity. As illustrated in panel (A), which shows representative single-cell simulations, we took EGFR surface expression dynamics to be stochastic and marked by bursts of synthesis/expression of variable size (total amount of EGFR added to the plasma membrane) and duration, with bursts being separated by intervals of variable duration. The bottom four panels show heat maps that indicate single-cell responses (ERK activity as a function of time) to different levels of EGF stimulation: (B) 2 pg/ml, (C) 10 pg/ml, (D) 50 pg/ml, and 200 pg/ml (E). Each row in a heat map corresponds to an individual cell characterized by a unique set of parameters for EGFR surface expression dynamics. The cells considered are otherwise identical. To demonstrate and isolate the effect of EGF dose, we have taken the temporal EGFR expression profile to be the same across panels for each cell (i.e., each row in each heat map corresponds to a common profile). Supplementary Table S3 provides information about the parameters that are unique for the stochastic simulations shown here.

Figure 8 shows time courses obtained from the extended, stochastic model for a collection of 20 individual cells responding to different doses of EGF. As can be seen, the extended model predicts irregular EGF dose-dependent excitations of ERK, suggesting that the similar irregularities observed in experiments (Fig. 7) can be attributed to extrinsic noise, which may arise partly from cell-specific time-varying stochastic EGFR surface expression. For the lowest dose considered, 2 pg/ml, ERK is excited in bursts, which tend to be separated by relatively long periods of inactivity (Fig. 8B). According to the deterministic model, this dose lies outside the oscillatory range (Fig. 5D). Indeed, this dose places the system’s steady state in the monostable, inactive regime. The stochastic model predicts bursts of ERK activity arising due to fluctuations of EGFR that allow the level of activated EGFR to exceed a threshold required for ERK activation. We note that inhibition of EGFR (with the kinase inhibitor gefitinib) immediately eliminates pulsatile ERK activity (Fig. 7), indicating that ERK activity pulses require uninhibited EGFR level being above a threshold. Additional analyses of 10-day-long trajectories is provided in Supplementary Figure S8.

Excitation of ERK by transient EGFR signaling

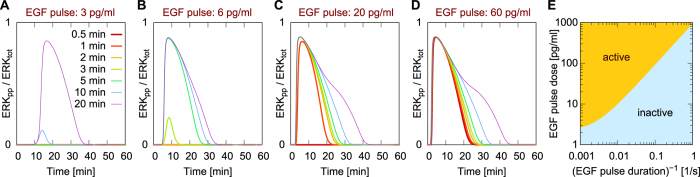
Positive feedback mediated by SOS influences system behavior, such that transient EGF stimulation is expected to produce responses having certain experimentally detectable features. In Fig. 9, we consider predicted responses of the system to different transient doses of EGF. The smallest dose considered, 3 pg/ml, induces a pulse of high ERK activity only for the longest period of EGF stimulation, 20 min (Fig. 9A). In contrast, for a relatively high EGF dose of 60 pg/ml, even the shortest period of EGF stimulation, 30s, induces a pulse of high ERK activity (Fig. 9D). The stimulation time required to induce high ERK activity decreases with increasing EGF dose, which follows from the fact that there exists a threshold level of EGFR that must be activated to trigger downstream signaling. For short EGF stimulation times, active EGFR level increases linearly with time, with a rate proportional to the EGF stimulation dose. Therefore, in this regime, ERK is activated when the product of stimulation time and EGF dose exceeds some threshold. For longer stimulation times, the level of active EGFR saturates; in this limit, the critical dose for long stimulation converges to the critical dose for sustained stimulation, 2.5 pg/ml (cf. Figs 5D and 9E). Figure 9B–D show that for short, transient EGF stimulation periods, ERK activity starts to rise after EGF stimulation stops, which shows that after the level of active EGFR exceeds a threshold, signal propagates independently of further EGF stimulation.

Figure 9. Predicted responses to pulsed EGF stimulations of various doses and durations.

Figure 9

Open in a new tab

Each curve is obtained from a simulation of an experiment wherein EGFR signaling is stimulated by a low (A), intermediate (B,C) or high (D) dose of ligand (EGF) for the duration indicated in the legend. EGF stimulation pulse starts at time = 0. After this pulse of stimulation free ligand is removed. (E) Dependence of critical EGF stimulation dose on stimulation duration.

Recently, we observed a similar effect in which the integral of stimulus (i.e., time × amplitude) determines the fraction of activated cells in a population in the case of LPS stimulation38. As in the case of growth factor signaling, the immunogenic signal is integrated at the membrane and after surpassing a threshold activates a downstream pathway. This property results from ultrasensitivity or positive feedback operating at the membrane level.

ERK responses to localized secretion of EGF

A notable feature of the feedback mechanisms involved in MAPK signaling is their ability to propagate signals through space. Positive feedback requires interactions on the plasma membrane (Fig. 2). In contrast, negative feedback signals are relayed by faster diffusing cytosolic proteins (Fig. 2). Such a combination of feedbacks can potentially give rise to local excitation/global inhibition (LEGI) dynamics. In LEGI-type regulation, the membrane components are activated due to propagation of a heteroclinic traveling wave (enabled by bistability introduced by a positive feedback). Activation of membrane components is followed by more uniform activation of cytoplasmic components and then global inhibition of membrane components via negative feedback. LEGI can generate spatial essential for proper cellular responses to directional cues, such as chemotactic movement of ameboid cells toward a higher concentration of a chemokine39,40,41,42. Detection of directional cues may be an important function of the EGFR signaling network. EGF gradient sensing or ERK heterogeneities have been implicated in mechanotransduction, cell polarization, and motility12,13,14.

To investigate spatial heterogeneities in MAPK signaling, we extended the ODE model of Fig. 2 to obtain a reaction–diffusion PDE-based model. This extended model accounts for both the spatiotemporal kinetics of the signaling network components within the cell and extracellular randomized release of (paracrine) EGF. A more detailed description of this model extension is provided in the Materials and Methods section; parameters introduced with this extension are summarized in Supplementary Table S4. We used the PDE model to predict responses to localized (paracrine) EGF stimulation (Fig. 10). A sequence of simulation snapshots is shown in Fig. 10, which are taken from Supplementary Video 1. This sequence illustrates how non-uniform EGF stimulation, which is visualized in the top row of images, can trigger a traveling wave of activated RAS that spreads over the plasma membrane (Supplementary Video 1) and that produces a transient gradient of ERK activity within the cell, which is visualized in the bottom row of images. This spatiotemporal behavior is in accordance with LEGI dynamics.

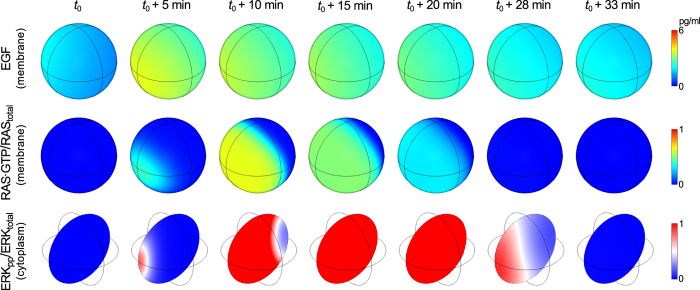
Figure 10. Spatiotemporal dynamics of EGF, RAS activity (RAS-GTP/RAStotal), and ERK activity (ERKpp/ERKtotal) for a cell responding to localized EGF secretion.

Figure 10

Open in a new tab

Shown are sequential snapshots taken from Supplementary Video 1 in the Supporting Information that illustrate the response of a cell to a wave of EGF, which is produced by point sources releasing EGF at random times and locations in a shell surrounding the cell. At each time point, the spatial distribution of EGF at the cell surface is shown in the top row, fraction of activated RAS is shown in the middle row, and the spatial distribution of activated ERK inside the cell is shown in the bottom row (on a cross-section passing through the cell center). Supplementary Table S4 provides information about the parameters that are unique for the spatiotemporal simulations shown here.

Interestingly, ERK may be activated even when the average surface concentration of EGF is below the threshold concentration required for activation in the well-mixed limit (i.e., below the level corresponding to the saddle node bifurcation point SN2 in Fig. 5E). This behavior, which can be seen at approximately 20 hr in Supplementary Video 1, occurs because the local concentration of EGF exceeds the average concentration, as well as SN2, the threshold required to trigger a traveling wave of RAS activation. Once the heteroclinic wave is initiated on the membrane, its propagation requires only that the concentration of EGF remains above the lower limit of the bistability range, i.e., above the level of EGF corresponding to the saddle node bifurcation point SN1 in Fig. 5E.

Discussion

The MAPK signaling cascade transmits signals that control diverse cell functions such as proliferation, differentiation, motility, and apoptosis3. The mechanisms allowing the pathway to achieve specificity are still elusive. There is growing evidence that diverse cellular functions are coordinated through multiple posttranslational modifications of RAF. These modifications allow RAF isoforms to propagate signals into diverse downstream pathways43,44. Another mode of cell fate control is associated with the temporal profiles of RAF, MEK, and ERK activity. Recently, Ryu et al. demonstrated in PC‐12 cells that the choice between proliferation and differentiation depends on the frequency of ERK activity oscillations8. Here, we constructed and analyzed a computational model of MAPK signaling to clarify how such oscillations can be generated in response to persistent stimuli, and how their frequency and time profile (i.e., pulse shape) are controlled.

Within the MAPK/ERK signaling cascade, ERK mediates apparently redundant negative feedback loops that inhibit signal propagation at multiple upstream points. In our modeling study, we focused on the positive feedback loop that involves the small GTPase RAS and its guanine nucleotide exchange factor SOS. In the absence of negative feedbacks, this positive feedback loop leads to bistable switching. However, when this loop is nested within the negative feedback loop from ERK to SOS, the system produces relaxation oscillations, which match experimental time courses. The two other negative feedbacks, from ERK to MEK and RAF, play only auxiliary roles in the generation of oscillations, principally modulating the shape of ERK activity pulses. The presence of these two loops, however, allow for controlling activity of RAF, which has numerous targets in addition to MEK45. The positive feedback introduces a hierarchy between negative feedbacks, such that the ERK to SOS feedback is responsible for generating oscillations and the other two feedbacks considered in our analysis are responsible for shaping the waveform of oscillations.

In addition to the feedbacks discussed above, there are at least two other positive feedbacks that are nested within the ERK–SOS negative feedback loop: the ERK/MEK hidden feedback, in which bistability may arise in the double phosphorylation/dephosphorylation cycle due to distributive phosphorylation and saturability in dephosphorylation reaction46, and the RAS–GAB1–PI3K feedback47. Both feedbacks fit into the discussed topology that can give rise to relaxation oscillations, but, importantly, only the RAS–GAB–PI3K feedback (in addition to the RAS–SOS feedback) can act as an initial signal amplifier, because it is upstream of the RAF/MEK/ERK cascade.

Overall, the feedbacks considered here encode a graded input into constant-amplitude pulses, such that the level of a stimulus is translated to the frequency of oscillation and pulse duration. We speculate that, in comparison with amplitude-to-amplitude coding, amplitude-to-frequency coding may decrease ambiguity in signal interpretation by downstream effectors and increase information channel capacity. The NF-κB signaling system, which is characterized by a constant period of oscillations and thus appears to employ the former scheme48, was found to transmit only ~1 bit of information49,50. Interestingly, in the MAPK pathway, Aoki et al. found that frequency, but not amplitude, of ERK activity pulses is correlated with cell proliferation rates51.

The ERK pathway can modulate cell adhesion and promote cell migration by activation of actin polymerization52 or vimentin filament remodeling53. To respond properly to extracellular, directional cues14,54, the pathway should be organized spatially55. By analyzing the MAPK/ERK network as a reaction–diffusion system we found that when a cell is exposed to localized bursts of EGF, ERK activation exhibits local excitation/global inhibition (LEGI) dynamics56. LEGI dynamics arise because of the existence of a fast positive feedback involving slowly diffusing membrane-bound proteins. Under these conditions, localized EGFR excitation can trigger RAS activation that spreads over the membrane as a traveling wave, which induces a non-uniform surge of RAF, MEK and ERK activity in the cytosol. Ultimately, ERK-mediated phosphorylation of SOS globally inhibits pathway activity because cytosolic proteins diffuse faster than membrane proteins, by at least one order of magnitude. Such a mechanism allows cells to encode information about concentration gradients of extracellular ligand into spatially structured pulses of cytosolic proteins activity. It has been suggested that ERK-controlled EGF shedding can maintain an intrinsic cell spatial polarity15 which may be exploited to induce directed cell migration.

In our spatial model, RAS kinetics is simplified: we consider only a membrane pool of RAS and we neglect the existence of membrane microdomains that can be enriched in RAS. We are however aware that the heterogeneity in RAS distribution combined with the positive feedback between RAS and SOS can substantially influence signaling. In our earlier modelling efforts on B-cell activation57 we demonstrate that clusterization of membrane components can itself lead to a local activation, which can then spread over the membrane by means of a traveling wave. Also, EGFR and RAS trafficking between plasma membrane and subcellular compartments, and trafficking-dependent signaling from inside the cell (in addition to signaling from the plasma membrane) would influence spatiotemporal activity profiles of downstream components, RAF, MEK, and ERK.

In summary, we have shown that the presence of the short positive feedback coupling RAS and SOS introduces bistability into the system and that this bistability, when frustrated by the negative feedback loop from ERK to SOS, introduces relaxation oscillations which can explain pulsatile time courses of active ERK observed in experiments. This regulatory circuitry allows for translation of graded inputs into constant-amplitude oscillations that have a period and pulse duration determined by signal strength. Because the positive feedback operates on a short time scale and involves slow-diffusing membrane components while the negative feedback operates on a longer time scale but involves faster-diffusing cytoplasmic components, in response to localized EGF stimulation, the system exhibits local activation/global inhibition dynamics. This allows for translation of spatially-graded stimuli to spatially oriented pulses of RAF, MEK and ERK activity, which could be used to direct cell migration or induce polarity.

Materials and Methods

Setting parameters

It is challenging to identify parameter values even when abundant experimental data are available to guide parameter estimation58. Here, we selected parameter values so as to obtain certain qualitative system behaviors and to allow for qualitative behavior to change in response to variation in the strength of EGF stimulation. This approach is consistent with the hypothesis that cellular regulatory systems operate close to bifurcation points35,59. First, we considered the system with only the positive feedback loop from RAS to SOS. We set parameter values so that there is a regime of bistability at low EGF stimulation levels. We then adjusted parameter values so that the time required for information to flow from RAS to ERK yields ERK activation kinetics in accord with experimental observations. Then, we considered negative feedback from ERK to SOS. We set parameters influencing this feedback such that SOS inhibition lasts long enough to allow for nearly complete deactivation of RAF, MEK and ERK. Finally, we considered negative feedbacks from ERK to MEK and RAF and set parameter values governing these feedbacks such that the time profiles of ERK activity are sensitive to the feedback strengths.

Active ERK reporters

The ODE-based model was supplemented with two ERK activity reporters, EKAR3 and ERKTR. Their activation and deactivation reaction rate constants (Supplementary Table S1) have been tuned to be reproduce experimentally measured reporter kinetics32.

Numerical integration of ODEs

The deterministic model is based on an assumption of well-mixed reaction compartments. It was written in terms of reaction rules using the BioNetGen language (BNGL)60. The rules, which are provided in Supplementary Data 1, can be processed by BioNetGen60 to obtain a reaction network and a corresponding system of coupled ordinary differential equations (ODEs) for the mass-action kinetics of the reaction network. The ODEs were numerically integrated using CVODE61, which is an integral component of BioNetGen. We used BioNetGen’s default settings for CVODE parameters, which are appropriate for stiff systems.

Construction of bifurcation diagrams

Bifurcation diagrams were obtained using Matlab/Matcont62. Supplementary Data 2 contains scripts which can be used to obtain the bifurcation diagrams shown in Supplementary Figure S1.

Modeling stochastic EGFR surface expression dynamics

To investigate how ERK response dynamics are influenced by stochasticity, we introduced a source of extrinsic noise by allowing the EGFR level to change over time and in this way to modulate cellular sensitivity to EGF stimulation. In the stochastic model, EGFR is expressed in bursts and has a predefined half-life, τEGFR (Supplementary Table S3). Bursts occur at random time points, distributed exponentially with a mean waiting time of λinterburst−1, and have durations that are drawn from an exponential distribution with mean burst duration of λburst−1. The rate of EGFR production in each burst is cell-dependent and is computed as the product of a common intensity factor, Aburst, and a cell-specific factor, αcell, which is drawn from a log-normal distribution having mean of 1. The simulations are performed using an efficient variation of Gillespie’s direct method63 as implemented in BioNetGen60. A BioNetGen input file corresponding to the simulations shown for cell 8 in Fig. 8B is provided in Supplementary Data 3.

PDE simulations

A single cell is considered. It is represented as a sphere of radius Rcell with volume Vcell. Values of these and others parameters specific to this model extension are summarized in Supplementary Table S4. Membrane and cytosolic proteins diffuse with diffusivities Dmem and Dcyt, respectively, with Dcyt = 10 × Dmem. Reaction–diffusion equations on the membrane and in the cytosol are coupled via Robin-type boundary conditions64. We assume that the flux Φ of active RAF at the membrane results from its phosphorylation by membrane-tethered RAS-GTP:

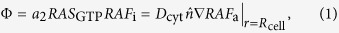graphic file with name srep38244-m1.jpg

where Inline graphic is an outer unit vector normal to the cell surface. The rate of SOS phosphorylation is taken to be proportional to the boundary value of active cytoplasmic ERK. The point sources of EGF appear at random positions in the cell-concentric shell of outer radius REGF_shell_out at random time points throughout the simulation, on average every fEGF_sources−1. EGF releases each have a duration drawn from an exponential distribution with mean duration of λEGF_source−1, and a time-independent intensity AEGF, which is drawn from a log-normal distribution. Released EGF diffuses with diffusivity DEGF in the extracellular 3-D space, which is assumed to be unbounded and devoid of obstacles. EGF undergoes degradation with rate constant γEGF according to the diffusion–degradation equation:

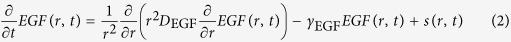graphic file with name srep38244-m3.jpg

where r is the distance from the point source localized at r = 0.

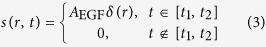graphic file with name srep38244-m4.jpg

EGF(r, t) can be calculated using a Green’s function (specific for the diffusion-degradation problem in 3D):

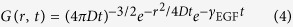graphic file with name srep38244-m5.jpg

as

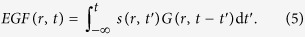graphic file with name srep38244-m6.jpg

Because

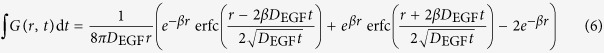graphic file with name srep38244-m7.jpg

where 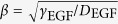Inline graphic and erfc is the complementary error function, the contribution from a single EGF source s(r, t) equals:

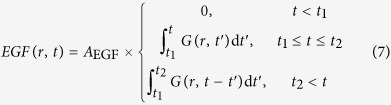graphic file with name srep38244-m9.jpg

PDE-based simulations were performed using Comsol Multiphysics (see Supplementary Data 4). The spatiotemporal evolution of EGF concentration was evaluated as described above, while reaction–diffusion equations for the cell surface and within the cytosol were solved numerically using a finite element method. For simplicity, a nuclear compartment or other intracellular obstacles were not considered.

Materials and experimental protocols

Time-lapse imaging of ERK reporter activity was performed as previously described32. Briefly, MCF-10A cells stably expressing EKAR3-nes (containing a nuclear export sequence to maintain cytosolic localization) and ERKTR-mCherry were plated on #1.5 glass-bottom multi-well plates coated with type I collagen (BD Biosciences). During imaging, cells were cultured in customized low-fluorescence DMEM/F-12 medium in absence of serum and insulin and the presence of the indicated concentrations of recombinant EGF (PeproTech). At the indicated times, 1 μM gefitinib (Selleck) was added to the medium. Images were collected at 6-minute intervals, and custom MATLAB-based algorithms were used to segment images based on the cytosolic localization of EKAR3 in the YFP channel and extract fluorescence intensities; u-track65 was used for cell tracking. ERKTR activity is shown as the ratio of cytosolic to nuclear fluorescence in the mCherry channel.

Additional Information

How to cite this article: Kochańczyk, M. et al. Relaxation oscillations and hierarchy of feedbacks in MAPK signaling. Sci. Rep. 7, 38244; doi: 10.1038/srep38244 (2017).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Material

Supplementary Information
srep38244-s1.pdf (6MB, pdf)
Supplementary Dataset 1
srep38244-s2.zip (13.4KB, zip)
Supplementary Dataset 2
srep38244-s3.zip (25.3KB, zip)
Supplementary Dataset 3
srep38244-s4.zip (7.7KB, zip)
Supplementary Dataset 4
srep38244-s5.zip (222KB, zip)
Supplementary video
Download video file (2.4MB, mov)

Acknowledgments

This study is supported by National Science Center (Poland) grant 2014/13/B/NZ2/03840 (www.ncn.gov.pl) and WWTF grant MA14-049 (www.wwtf.at). MK is supported by National Science Center (Poland) grant 2013/09/N/NZ2/02631 (www.ncn.gov.pl). PK is supported by National Science Center (Poland) grant 2013/11/N/NZ2/02481 (www.ncn.gov.pl). WSH is supported by National Institutes of Health/National Institute of General Medical Sciences grant P50GM085273 (www.nih.gov/www.nigms.nih.gov). MP, BS, and JGA are supported in part by the American Cancer Society (IRG-95-125-16). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Footnotes

Author Contributions Conceived and designed the study: W.S.H., M.K., T.L. Built and analyzed the mathematical models: J.J.-B., M.K., P.K., E.K., T.L. Performed the experiments: J.G.A., B.S. Interpreted the results: J.G.A., W.S.H., M.K., T.L., M.P., B.S., Wrote the manuscript: J.G.A., W.S.H., M.K., T.L.

References

  1. Chang F. et al. Signal transduction mediated by the Ras/Raf/MEK/ERK pathway from cytokine receptors to transcription factors: potential targeting for therapeutic intervention. Leukemia 17, 1263–1293 (2003). [DOI] [PubMed] [Google Scholar]
  2. Roskoski R. Jr. ERK1/2 MAP kinases: Structure, function, and regulation. Pharmacol. Res. 66, 105–143 (2012). [DOI] [PubMed] [Google Scholar]
  3. Schaeffer H. J. & Weber M. J. Mitogen-Activated Protein Kinases: Specific Messages from Ubiquitous Messengers. Mol. Cell. Biol. 19, 2435–2444 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Shaul Y. D. & Seger R. The MEK/ERK cascade: From signaling specificity to diverse functions. Mitogen-Act. Protein Kinases New Insights Regul. Funct. Role Hum. Dis. 1773, 1213–1226 (2007). [DOI] [PubMed] [Google Scholar]
  5. Samatar A. A. & Poulikakos P. I. Targeting RAS-ERK signalling in cancer: promises and challenges. Nat Rev Drug Discov 13, 928–942 (2014). [DOI] [PubMed] [Google Scholar]
  6. Murphy L. O., Smith S., Chen R.-H., Fingar D. C. & Blenis J. Molecular interpretation of ERK signal duration by immediate early gene products. Nat Cell Biol 4, 556–564 (2002). [DOI] [PubMed] [Google Scholar]
  7. Von Kriegsheim A. et al. Cell fate decisions are specified by the dynamic ERK interactome. Nat Cell Biol 11, 1458–1464 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Ryu H. et al. Frequency modulation of ERK activation dynamics rewires cell fate. Mol. Syst. Biol. 11, 838 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Brown G. C. & Kholodenko B. N. Spatial gradients of cellular phospho-proteins. FEBS Lett. 457, 452–454 (1999). [DOI] [PubMed] [Google Scholar]
  10. Kholodenko B. N. Spatially distributed cell signalling. FEBS Lett. 583, 4006–4012 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Zhao Q., Yi M. & Liu Y. Spatial distribution and dose–response relationship for different operation modes in a reaction–diffusion model of the MAPK cascade. Phys. Biol. 8, 55004 (2011). [DOI] [PubMed] [Google Scholar]
  12. Mendoza M. C. et al. ERK-MAPK Drives Lamellipodia Protrusion by Activating the WAVE2 Regulatory Complex. Mol. Cell 41, 661–671 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Mendoza M. C., Vilela M., Juarez J. E., Blenis J. & Danuser G. ERK reinforces actin polymerization to power persistent edge protrusion during motility. Sci. Signal. 8, ra47 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Tschumperlin D. J. et al. Mechanotransduction through growth-factor shedding into the extracellular space. Nature 429, 83–86 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Maly I. V., Steven Wiley H. & Lauffenburger D. A. Self-Organization of Polarized Cell Signaling via Autocrine Circuits: Computational Model Analysis. Biophys. J. 86, 10–22 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Shin S.-Y. et al. Positive- and negative-feedback regulations coordinate the dynamic behavior of the Ras-Raf-MEK-ERK signal transduction pathway. J. Cell Sci. 122, 425–435 (2009). [DOI] [PubMed] [Google Scholar]
  17. Avraham R. & Yarden Y. Feedback regulation of EGFR signalling: decision making by early and delayed loops. Nat Rev Mol Cell Biol 12, 104–117 (2011). [DOI] [PubMed] [Google Scholar]
  18. Das J., Kardar M. & Chakraborty A. K. Positive feedback regulation results in spatial clustering and fast spreading of active signaling molecules on a cell membrane. J. Chem. Phys. 130 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Xiong W. & Ferrell J. E. A positive-feedback-based bistable ‘memory module’ that governs a cell fate decision. Nature 426, 460–465 (2003). [DOI] [PubMed] [Google Scholar]
  20. Cirit M., Wang C.-C. & Haugh J. M. Systematic Quantification of Negative Feedback Mechanisms in the Extracellular Signal-regulated Kinase (ERK) Signaling Network. J. Biol. Chem. 285, 36736–36744 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Barkai N. & Leibler S. Robustness in simple biochemical networks. Nature 387, 913–917 (1997). [DOI] [PubMed] [Google Scholar]
  22. Alon U., Surette M. G., Barkai N. & Leibler S. Robustness in bacterial chemotaxis. Nature 397, 168–171 (1999). [DOI] [PubMed] [Google Scholar]
  23. Nelson D. E. et al. Oscillations in NF-κB Signaling Control the Dynamics of Gene Expression. Science 306, 704–708 (2004). [DOI] [PubMed] [Google Scholar]
  24. Geva-Zatorsky N. et al. Oscillations and variability in the p53 system. Mol. Syst. Biol. 2, 2006.0033 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Kholodenko B. N. Negative feedback and ultrasensitivity can bring about oscillations in the mitogen-activated protein kinase cascades. Eur. J. Biochem. 267, 1583–1588 (2000). [DOI] [PubMed] [Google Scholar]
  26. Shankaran H. et al. Rapid and sustained nuclear–cytoplasmic ERK oscillations induced by epidermal growth factor. Mol. Syst. Biol. 5 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Pękalski J. et al. Spontaneous NF-κB activation by autocrine TNFα signaling: a computational analysis. PLOS One 8, e78887 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Szymańska P., Martin K. R., MacKeigan J. P., Hlavacek W. S. & Lipniacki T. Computational analysis of an autophagy/translation switch based on mutual inhibition of MTORC1 and ULK1. PLOS One 10, e0116550 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Krishna S., Semsey S. & Jensen M. H. Frustrated bistability as a means to engineer oscillations in biological systems. Phys. Biol. 6, 36009 (2009). [DOI] [PubMed] [Google Scholar]
  30. Albeck J. G., Mills G. B. & Brugge J. S. Frequency-Modulated Pulses of ERK Activity Transmit Quantitative Proliferation Signals. Mol. Cell 49, 249–261 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Regot S., Hughey J. J., Bajar B. T., Carrasco S. & Covert M. W. High-Sensitivity Measurements of Multiple Kinase Activities in Live Single Cells. Cell 157, 1724–1734 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Sparta B. et al. Receptor Level Mechanisms Are Required for Epidermal Growth Factor (EGF)-stimulated Extracellular Signal-regulated Kinase (ERK) Activity Pulses. J. Biol. Chem. 290, 24784–24792 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Das J. et al. Digital Signaling and Hysteresis Characterize Ras Activation in Lymphoid Cells. Cell 136, 337–351 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Stites E. C., Trampont P. C., Ma Z. & Ravichandran K. S. Network Analysis of Oncogenic Ras Activation in Cancer. Science 318, 463–467 (2007). [DOI] [PubMed] [Google Scholar]
  35. Mora T. & Bialek W. Are Biological Systems Poised at Criticality? J. Stat. Phys. 144, 268–302 (2011). [Google Scholar]
  36. Raj A., Peskin C. S., Tranchina D., Vargas D. Y. & Tyagi S. Stochastic mRNA Synthesis in Mammalian Cells. PLoS Biol 4, e309 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Dey S. S., Foley J. E., Limsirichai P., Schaffer D. V. & Arkin A. P. Orthogonal control of expression mean and variance by epigenetic features at different genomic loci. Mol. Syst. Biol. 11, 806 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Kellogg R. A., Tian C., Lipniacki T., Quake S. R. & Tay S. Digital signaling decouples activation probability and population heterogeneity. eLife 4, e08931 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Parent C. A. & Devreotes P. N. A Cell’s Sense of Direction. Science 284, 765–770 (1999). [DOI] [PubMed] [Google Scholar]
  40. Xiong Y., Huang C.-H., Iglesias P. A. & Devreotes P. N. Cells navigate with a local-excitation, global-inhibition-biased excitable network. Proc. Natl. Acad. Sci. USA 107, 17079–17086 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Shi C., Huang C.-H., Devreotes P. N. & Iglesias P. A. Interaction of Motility, Directional Sensing, and Polarity Modules Recreates the Behaviors of Chemotaxing Cells. PLoS Comput Biol 9, e1003122 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Bhowmik A., Rappel W.-J. & Levine H. Excitable waves and direction-sensing in Dictyostelium discoideum : steps towards a chemotaxis model. Phys. Biol. 13, 16002 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Romano D. et al. Protein interaction switches coordinate Raf-1 and MST2/Hippo signalling. Nat Cell Biol 16, 673–684 (2014). [DOI] [PubMed] [Google Scholar]
  44. Cseh B., Doma E. & Baccarini M. ‘RAF’ neighborhood: Protein–protein interaction in the Raf/Mek/Erk pathway. FEBS Lett. 588, 2398–2406 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Roskoski R. Jr. RAF protein-serine/threonine kinases: Structure and regulation. Biochem. Biophys. Res. Commun. 399, 313–317 (2010). [DOI] [PubMed] [Google Scholar]
  46. Markevich N. I., Hoek J. B. & Kholodenko B. N. Signaling switches and bistability arising from multisite phosphorylation in protein kinase cascades. J. Cell Biol. 164, 353–359 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Kiyatkin A. et al. Scaffolding Protein Grb2-associated Binder 1 Sustains Epidermal Growth Factor-induced Mitogenic and Survival Signaling by Multiple Positive Feedback Loops. J. Biol. Chem. 281, 19925–19938 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Hat B., Puszynski K. & Lipniacki T. Exploring mechanisms of oscillations in p53 and nuclear factor-κB systems. IET Syst. Biol. 3, 342–355 (2009). [DOI] [PubMed] [Google Scholar]
  49. Cheong R., Rhee A., Wang C. J., Nemenman I. & Levchenko A. Information Transduction Capacity of Noisy Biochemical Signaling Networks. Science 334, 354–358 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Selimkhanov J. et al. Accurate information transmission through dynamic biochemical signaling networks. Science 346, 1370–1373 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Aoki K. et al. Stochastic ERK Activation Induced by Noise and Cell-to-Cell Propagation Regulates Cell Density-Dependent Proliferation. Mol. Cell 52, 529–540 (2013). [DOI] [PubMed] [Google Scholar]
  52. Kempiak S. J., Yip S.-C., Backer J. M. & Segall J. E. Local signaling by the EGF receptor. J. Cell Biol. 162, 781–788 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Ehrenreiter K. et al. Raf-1 regulates Rho signaling and cell migration. J. Cell Biol. 168, 955–964 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Joslin E. J., Opresko L. K., Wells A., Wiley H. S. & Lauffenburger D. A. EGF-receptor-mediated mammary epithelial cell migration is driven by sustained ERK signaling from autocrine stimulation. J. Cell Sci. 120, 3688–3699 (2007). [DOI] [PubMed] [Google Scholar]
  55. Kholodenko B. N., Hancock J. F. & Kolch W. Signalling ballet in space and time. Nat. Rev. Mol. Cell Biol. 11, 414–426 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Mori Y., Jilkine A. & Edelstein-Keshet L. Wave-Pinning and Cell Polarity from a Bistable Reaction-Diffusion System. Biophys. J. 94, 3684–3697 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Hat B., Kazmierczak B. & Lipniacki T. B Cell Activation Triggered by the Formation of the Small Receptor Cluster: A Computational Study. PLoS Comput Biol 7, e1002197 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Nienałtowski K., Włodarczyk M., Lipniacki T. & Komorowski M. Clustering reveals limits of parameter identifiability in multi-parameter models of biochemical dynamics. BMC Syst. Biol. 9, 1–9 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Camalet S., Duke T., Jülicher F. & Prost J. Auditory sensitivity provided by self-tuned critical oscillations of hair cells. Proc. Natl. Acad. Sci. USA 97, 3183–3188 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Faeder J. R., Blinov M. L. & Hlavacek, W. S. In Systems Biology (ed. Maly I. V.) 500, 113–167 (Humana Press, 2009). [DOI] [PubMed] [Google Scholar]
  61. Hindmarsh A. C. et al. SUNDIALS: Suite of Nonlinear and Differential/Algebraic Equation Solvers. ACM Trans Math Softw 31, 363–396 (2005). [Google Scholar]
  62. Dhooge A., Govaerts W. & Kuznetsov Y. A. MATCONT: A MATLAB Package for Numerical Bifurcation Analysis of ODEs. ACM Trans Math Softw 29, 141–164 (2003). [Google Scholar]
  63. Gillespie D. T. Stochastic Simulation of Chemical Kinetics. Annu. Rev. Phys. Chem. 58, 35–55 (2007). [DOI] [PubMed] [Google Scholar]
  64. Kazmierczak B. & Lipniacki T. Regulation of kinase activity by diffusion and feedback. J. Theor. Biol. 259, 291–296 (2009). [DOI] [PubMed] [Google Scholar]
  65. Jaqaman K. et al. Robust single-particle tracking in live-cell time-lapse sequences. Nat Meth 5, 695–702 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep38244-s1.pdf (6MB, pdf)
Supplementary Dataset 1
srep38244-s2.zip (13.4KB, zip)
Supplementary Dataset 2
srep38244-s3.zip (25.3KB, zip)
Supplementary Dataset 3
srep38244-s4.zip (7.7KB, zip)
Supplementary Dataset 4
srep38244-s5.zip (222KB, zip)
Supplementary video
Download video file (2.4MB, mov)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES