Growth in Rapid Automatized Naming from Grades K – 8 in Children with Math or Reading Disabilities

Abstract

Rapid Automatized Naming (RAN) is widely used to identify reading disabilities (RD) and has recently been considered a potential predictor of risk for mathematics disabilities (MLD). Here we longitudinally examine RAN performance from grades K to 8, to view how growth on RAN response time (RT) differs for children with RD vs. MLD. Across all participants, there was significant stability of RAN performance for all three subtests. For all three subtests, there was significant between-child variability in RTs at kindergarten and Grade 8; for select combinations of subtests, there was also between child variability in difference scores over time. Relative to typically achieving peers, children with MLD or RD were slower on all three subtests at kindergarten, but these deficits were most pronounced for children with MLD vs. RD at kindergarten, and more persistent through 8^th grade for children with RD. RAN numbers and letters performance was closely related in the RD group, more so than in the MLD group, despite deficits on both subtests across groups. Our findings prompt us to consider that empirically guided modifications of RAN may be needed for extending its use to evaluating risk for MLD.

The prevalence of co-morbid math and reading difficulties has led to theories that these learning disorders share a deficit in one or more components of phonological processing (Geary, 1993; 2011). Partial support for this notion comes from findings that performance on measures of Rapid Automatized Naming (RAN) predict learning difficulties in reading (Denckla & Rudel, 1976; Wolf, Bowers, & Biddle, 2000) and mathematics (Chard, Clarke, Baker, Otterstedt, Braun, & Katz, 2005; Hecht, Torgesen, Wagner, & Rashotte, 2001; Landerl, Bevan, & Butterworth, 2004), independent of the contributions of additional cognitive skills (Badian, 1993; Hecht et al., 2001). But the mere existence of a common predictor need not indicate a shared pathway (Rubinsten & Henik, 2009). The skills (or deficits) underlying the associations between RAN and LD outcomes may differ for children with a mathematical learning disability (MLD) compared to those with reading disabilities (RD). That is, the skills measured by RAN might not be identical across children with MLD or RD. Indeed, there is growing appreciation for the cognitive complexity underlying the allegedly straightforward skill referred to as RAN (as reviewed by Wolf, O’Rourke, Gidney, Lovett, Cirino, & Morris, et al., 2002). Moreover, skills measured by RAN are likely to vary at different points in development, based on changes in the relative degree of automaticity of task demands at different points in time and other aspects of cognitive maturity. Here we explore whether trajectories of RAN performance over the school age years reveal distinctions between children with math vs. reading disabilities (each relative to typically achieving peers). These longitudinal comparisons may shed light on the reasons for the predictive value of RAN for each of these learning disorders and how (or whether) these reasons differ across these two subgroups.

Our focus on RAN stems from the combination of historical and recent empirical findings concerning the efficacy and specificity of RAN as a clinical and research tool to help identify RD and, more recently, MLD. RAN is a straightforward assessment that can be quickly and easily administered to school age children of any age. It requires timed sequential naming of familiar stimuli presented visually. Individual RAN subtests involve naming letters, numbers (digits), illustrated objects or pictured colored blocks, as quickly and accurately as possible while an examiner records accuracy and monitors speed with a hand-held stopwatch. RAN’s empirically validated association with RD contributes to its long standing status as a widely accepted research and clinical component of screening for or identifying RD (Wagner, Torgesen, Naglieri, & Goldstein, 2009). Yet RAN’s utility for screening or identifying MLD is debatable in view of inconsistent findings of its contributions to describing the MLD profile (e.g., D’Amico & Passolunghi, 2009; Willburger, Fussenegger, Moll, Wood, & Landerl, 2008). In the present study, we administer the RAN to children with RD, MLD, or neither LD, using three of the four original RAN subtests (Denckla & Rudel, 1976) that involve naming letters, numbers, or colors, as these are currently included in most of the standardized tools for clinical assessments of LD (Wagner et al., 2009).

Despite its prominence in the field of RD research and practice, ongoing debates about RAN focus on whether RAN taps skills that are related to or independent of components of phonological processing, whether it underlies a common core deficit of RD, and whether such distinctions in skills being measured exist at the subtest level (e.g., RAN letters vs. colors; as reviewed by Bowers, Ishaik, Swanson, Harris, & Graham, 2003; Wolf et al., 2002). Adding to this debate is the more recent body of evidence for RAN as a predictor of mathematics difficulties, and inconsistent findings regarding whether RAN’s predictive association with MLD is subtest specific (e.g., RAN numbers vs. letters, or more recently developed subtests of Quantity vs. numbers, in which small exact quantities of items are named (e.g., three dots on a die). For instance, van der Sluis reported that 4^th and 5^th graders (roughly 10 years old) with MLD were impaired (slower than controls) when naming quantities or numbers (i.e., digits) but not when naming letters, whereas children with RD were impaired at naming letters or numbers but not quantities (van der Sluis, de Jong, & van der Leij, 2004). Importantly, although both groups (MLD and RD) were impaired at RAN numbers, it is possible that the reasons corresponding to their respective impaired performance differed. Willburger and colleagues (2008) reported a “domain general” RAN deficit for children with RD and numerical-subtest-specific deficits for children with MLD. Like van der Sluis, Willburger found that 8- to 10-year-olds with RD were slower on RAN letters and numbers (and objects) but not quantities, but the MLD group in their study showed impaired performance on RAN quantities only, not digits. Pauly and colleagues (2011) had kindergartners name digits, letters, objects and dice (depicting quantities); those at risk for RD performed most poorly on RAN letters and objects (but not digits), whereas children at risk for MLD had more pronounced difficulty on the dice and digits subtests (but not letters and objects). In contrast, D’Amico & Passolunghi (2009) found that 9 year old children with MLD have slower rapid naming for both letters and numbers, relative to controls. Despite clear discrepancies across these findings, all three of these studies reported additive effects for children with MLD + RD, supporting the notion of independent contributions of RAN related skills underlying each form of LD. Here we ask whether these independent contributions vary across development, from kindergarten through Grade 8.

Findings from studies of RAN performance in children with MLD have theoretical contributions for developing models of cognitive underpinnings of MLD and RD, but also have important practical implications for the common practice of combining scores obtained from RAN letters and numbers in research and clinical settings. This practice may be justified in view of the reported correlations between these two subtests (at least in the general population) and the frequent reports of impaired performance on both subtests among children with dyslexia. Yet if use of the RAN is to be extended as a screen for MLD, there is a need to identify if these correlations are evident across subgroups of children, including children with MLD.

Why might we expect differences in performance across RAN subtests for MLD, but less so for RD? The evidence of subtest specific performance in children with MLD is drawn from recent studies of RAN performance in school age children with MLD, but also from reports of dissociations in neural associations for visual number and letter recognition (Park, Hebrank, Polk, & Park, 2012) and findings that preschool numerical skills selectively predict performance on RAN numbers (but not RAN letters) at 6 years of age (Mazzocco, Feigenson, & Halberda, 2011b). This evidence leads us to question the validity of combining RAN letters and numbers subtests when assessing children at risk for LD, except when evaluating risk for RD. Therefore in this study we examine RAN letters and numbers subtests separately from each other and separately among children with MLD vs. RD.

If we are to examine RAN performance profiles specific to MLD, it is important to consider the reported cognitive heterogeneity of children with MLD included in research studies. Until recently, research participants classified as having MLD have typically included students with a broad range of math achievement levels (e.g., children with math achievement scores < 25^th percentile). We (Murphy, Mazzocco, Hanich, & Early, 2007) and others (Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007) have shown that differentiating those with deficient vs. moderate math difficulties is warranted; these two groups are classified hereafter as having math learning disability (MLD) or low achievement in math (LA_math), respectively. We have also extensively demonstrated that these differences emerge when MLD vs. LA_math classifications are based on a prospective study-based sample (vs. relying normative data only; discussed in the Method section), perhaps because the participant pool in these studies was not an at-risk sample (e.g., Mazzocco & Devlin, 2008; Murphy et al., 2007). When combined into one “MLD” group, these reported differences may be diluted and potential characteristics of children with MLD may fail to emerge. For instance, we recently reported that children with MLD have significant numerical processing deficits (Piazza, Facoetti, Trussardi, Berteletti, Conte, Lucangeli, et al., 2010) that are not observed in children with LA_math (Mazzocco, Feigenson, & Halberda, 2011a), further supporting that these are distinct subgroups of children despite their shared underachievement in mathematics. Herein, we evaluate performance of children with MLD (which we consider synonymous with “dyscalculia”) and children with LA_math, and consider each of these non-overlapping groups as representing a portion of those children with math difficulties not otherwise specified; that is, this broader construct of math difficulties (MD) includes, but is not limited to, children with MLD.

In order to allow for parallel analyses in the present study, we also differentiate subsets of children with RD as having reading learning disability (RD) or low achievement in reading (LA_read). We not only compare each LD (MLD or RD) group with its LA counterpart (LA_math or LA_read), but also examine MLD and RD groups separately. Specifically, we evaluate whether growth trajectories on rapid naming of letters, numbers, and colors reveal developmental differences in the profile of these allegedly automated skills over time across children with math or reading disability, vs. children with no learning disability.

Finally, we include two predictor variables to test hypotheses regarding MLD and RD RAN trajectory profiles. Drawing from the growing body of evidence that early executive function skills predict later academic achievement in reading or math (Best, Miller, Naglieri, 2011; Mazzocco & Kover, 2007), we include a measure of executive function efficiency at Grade 1 as a potential influence on growth in RAN skills. Based on evidence of the predictive value of kindergarten number knowledge on later math achievement (Locuniak & Jordan, 2008; Mazzocco & Thompson, 2005), we include a “number skills” score obtained at kindergarten to test hypotheses concerning the explanations for number-specific RAN deficits in children with MLD. That is, if group differences in RAN trajectories emerge, they may be related to either the executive function or number sense difficulties associated with MLD and LA_math.

Using latent growth models of performance measured longitudinally, we test the hypothesis that disability status (MLD or RD, each vs. no LD) affects both the level and rate of growth in RAN over time, from kindergarten to Grade 8, and that these effects differ for MLD vs. RD. This notion is important because of its implications for the meaningfulness of RAN test performance at kindergarten for predicting later achievement in math or reading, and the differential value of RAN’s predictive value among students at risk for MLD vs. RD. We study a protracted period of time to increase the likelihood of measuring asymptotic level for all participant groups, for all three RAN subtests.

We predicted that the extent to which growth in RAN letter performance precedes growth in RAN number performance will vary for students with MLD vs. LA in math (and vs. RD), with more parallel rates of RAN subtest growth among students with RD (because of the shared lexical retrieval skills measured by these subtests), faster growth in RAN letters (vs. numbers) in students with MLD (because of slowed development in associations between symbolic and non-symbolic aspects of number), and later establishment of performance plateaus for RAN numbers (vs. letters) for the MLD group only. Moreover, the relative similarity between RAN numbers or letters, each relative to RAN colors, may reveal important differences across student groups. These performance and profile differences would support the notion that RAN subtests measure different skills relative to each other and relative to period of development, and that the trajectory of development for some of those skills varies as a function of MLD or RD status.

Method

Participants

Participants were 249 school age children (120 boys) from a longitudinal study of mathematics achievement from kindergarten through Grade 8. These children had enrolled in the study while attending a regular half-day kindergarten program in a large and socio-economically diverse public school district. The seven schools participating in the study were selected on the basis of their relative low rates of student mobility (to reduce attrition) and free and reduced lunch program participation (as a filter for poverty). Accordingly, the sample was representative of public school students from a greater metropolitan urban/suburban area, although most participants were White (86%). One child was excluded based on meeting criteria for intellectual disability. The remaining children completed a standardized IQ test and scored at or above 80. With attrition, 213 children continued through Grade 3, and 161 through Grade 8. The analytic techniques described subsequently allow for partial missing data, thereby allowing us to include the maximum number of participants per year, for each of the nine years of the study.

Materials and Procedure

The assessment measures included in this report were drawn from a more extensive battery of tests administered annually throughout the longitudinal study. During each year of the study, participants were individually evaluated by a female examiner well trained on the comprehensive assessment battery. These assessments were conducted in a small private area away from the child’s classroom, during two or three 45 to 75 minutes sessions, depending on the year of the study. Tests were administered in a fixed order per year, and included core measures administered annually (including standardized and experimenter developed measures) and hypothesis-based instruments developed for specific grade levels.

For this report, our primary outcome variable of interest is children’s performance on the Rapid Automatized Naming Test (RAN; Denckla & Rudel, 1976). Select subtests of the Woodcock Johnson-Revised (WJ-R; Woodcock & Johnson, 1989) test of academic achievement were used to establish children’s achievement level status in reading and mathematics, separately, over the course of the longitudinal study. Additional measures of early executive function efficiency and number knowledge were used as potential cognitive mediators of the relationship between achievement level status and growth parameters on RAN performance, described subsequently.

RAN

RAN is typically used as a measure of lexical access, single word retrieval, or processing speed. It involves naming visually presented letters (p, d, a, o, and s), numbers (2, 6, 9, 4, and 7), or colored squares (red, black, yellow, green, and blue). We used the original version (Denckla & Rudel, 1976) in which only one category of stimuli appears in a given subtest. Each RAN subtest involves an untimed practice trial used to verify that participants have a verbal label for each of five stimuli, which are presented simultaneously in a linear array and named sequentially (left to right). Thereafter, a timed test trial involves rapidly naming each of 50 stimuli, presented in a 5 × 10 array appearing on a single piece of paper also named sequentially. Children are instructed to work as quickly and carefully as possible. The examiner visibly monitors trial response time (RT) with a handheld stopwatch. This RT score is the primary variable of interest, with shorter RT indicating better (faster) performance. In the present study, we examined parameters of growth on RAN RT obtained annually, for RAN letters, numbers, and colors subtests, from kindergarten through Grade 8.

We also included two potential predictors of growth in RAN performance based on findings from our earlier work and that of others, as follows: The Contingency Naming Test was used to measure executive function efficiency at Grade 1, and a Number Skills score was also included as an indicator of basic number knowledge at kindergarten. In each case, the score was obtained from the measure’s first administration during the longitudinal study, in view of our focus on early cognitive influences on growth of RAN skills and based on evidence that early executive functions and number sense skills predict mathematics achievement outcomes.

Contingency Naming Test (CNT)

The CNT is a Stroop-like task that requires naming stimuli according to a one- or two-attribute contingency rule (Anderson, Anderson, Northam, & Taylor, 2000). The stimuli are geometric shapes comprised of a small, inner shape within a larger, outer shape. Sets of nine such stimuli are presented in a single horizontal line for each untimed practice trial, and three rows of nine stimuli appear in each timed test trial. Following a set of warm up trials that involve naming just the color (and later, just the outer shape) of each stimulus, the first experimental trial tests efficiency under moderate working memory demands imposed by a one-attribute switching rule. This rule requires naming the color of a stimulus when the inner and outer shapes match, or naming the outer shape of the stimulus when the inner and outer shapes do not match. Subsequently, stimuli shown for the two-attribute rule are altered slightly, such that select stimuli appear beneath a black arrow pointing leftward. These stimuli are subject to a reversed version of the one-attribute rule (naming the outer shape when the inner and outer shapes do match, and the color if the outer and inner shapes do not match). For each subtest, trial RT is measured explicitly, with a hand held stopwatch, and children’s errors and self-corrections are recorded. A speed-accuracy based efficiency score is calculated based on the ratio of RT and errors (as described by Anderson et al., 2000), with higher scores indicating better (greater) efficiency.

In the present study, we used the efficiency score obtained at Grade 1, from the one-attribute task only, as a predictor variable of interest. In our earlier work, we showed that over 70% of 1st graders are unable to complete the two attribute rule, and that efficiency on the one-attribute task at Grade 1 is positively and significantly correlated with performance on the one- and two-attribute task at Grades 3 and 5 (Rhos ≥ .40, ps ≤ .0007, Mazzocco & Kover, 2007).

Number Skills

From a wide range of composite and item-level scores included in the K-3 portion of this longitudinal study, we previously reported that scores obtained at kindergarten from several items from the Test of Early Mathematics Ability – Second Edition (TEMA-2) were as predictive of later MLD as was a comprehensive psycho-educational assessment that included the entire TEMA-2 (also administered at kindergarten; (Mazzocco & Thompson, 2005), with classification accuracy rates of 83.7% and 79.1%, respectively. These select items involved reading one- and two-digit numbers, adding two values using manipulatives, magnitude judgments (i.e., identifying which of two verbally stated numbers is larger), and number constancy (e.g., recognizing that the quantity of a collection of items remains constant irrespective of the collection’s physical arrangement). In the present study, we included total scores for these items (ranging from 0 to 4) at kindergarten as a potential predictor of growth parameters on RAN numbers (vs. letters and colors).

WJ-R scores used for learning disability classification

Consistent with our earlier work (e.g., Murphy et al., 2007) and that of others (e.g., Geary et al., 2007), we relied on standardized mathematics and reading achievement scores over time to assign participants to a learning disability, low achievement (LA), or typical achievement group (TA). Specifically, we used performance on the Woodcock Johnson-Revised Mathematics Calculations (WJR-Calc) administered at Grades 1 and 3 – 6, and Word Attack (WJR-WA) subtests administered at Grades 1 – 4, to determine math and reading achievement level groupings, respectively. WJR-Calc is an untimed paper and pencil test involving all four arithmetic operations, whole and rational numbers, and algebraic equations presented in order of increasing difficulty. Word attack is a non-word reading test used to evaluate phonological decoding skills, which are known to underlie most instances of RD (Morris, Stuebing, Fletcher, Shaywitz, Lyon, Shankweiler, et al., 1998). Since both subtests are subject to floor effects at Kindergarten, data from Grades 1 onward were targeted for use as LD classification tools in the present study. The 1989 published normative data for the WJ-R were used when the longitudinal study began in 1998, and for consistency we continued to use these norms instead of the versions that were updated twice during the course of our study, in 2001 (WJ-III) and 2007 (WJ-III Normative Update). Thus the resulting standard scores are unreliable for clinical purposes, but were the basis of the sample-based classification criteria described below.

LD status groups were determined as follows: We used WJR-Calc performance to classify children as having MLD or LA in math (LA_math). To meet our criteria for MLD, children needed to have WJR-Calc scores at or below the sample-based 10^th percentile during at least half of the years in which they participated in the study (n=25; mean WJR-Calc score = 85.48, SD = 13.20); children who scored in the 11^th to 25^th percentile during similar time intervals met our criteria for low achievement in mathematics (LA_math; n=46, mean WJR-Calc score = 102.69, SD = 12.13), and the remaining 178 children who scored at or above the 26^th percentile during most of their assessments were classified as having typical achievement in mathematics (TA_math; n=178; mean WJR-Calc score = 118.74, SD = 13.58).

In order to draw meaningful comparisons between analyses of children with reading or mathematics learning difficulties, we used a parallel set of criteria, based on WJR-WA scores. Children were designated as having RD if they scored below the 10^th percentile on the Word Attack at least twice during the first four years of the study (n=19; mean WJR Word Attack score = 94.41, SD = 12.64), low achieving in reading (LA_read;) if their WJR-WA scores were in the 11^th–25^th percentile at least twice (n=41; mean WJR Word Attack score = 101.42, SD =11.16), and TA_read if they had WJR-WA scores at or above the 26^th percentile during this time period (n=189; mean WJR Word Attack score = 111.09, SD =13.53).

Our reliance on sample-based percentiles vs. standard normative percentiles was appropriate for several reasons. First, as aforementioned, we used the same version of the standardized tests over time to maintain consistency within our longitudinal testing batter, and using outdated tests may lead to inflated test scores associated with practice effects and outdated norms. Second, although our cut-off points were somewhat arbitrary in the absence of a gold standard for MLD, we selected them to be aligned with the reported prevalence of dyscalculia and RD (~6–11% for each disorder, e.g., Barbaresi et al.; 2005; Shalev, 2007, and Katusic, Colligan, Barbaresi, Schaid, & Jacobsen, 2001 respectively). Of our 224 children who had at least four assessments during the 9-year study, 25 met criteria for MLD, and 19 met criteria for RD. Finally, our study sample was not subject to large ascertainment bias sometimes present in lab based research nor was it selected as a high-risk sample, and was thus fairly representative of a large public school student body.

The co-occurrence of RD and MLD in our sample was in the low range of what is reported in the MLD literature (e.g., 43% to 65% reported by Barbaresi et al., 2005). Specifically, only 6 children met criteria for both MLD and RD (25% and 32% of the MLD and RD groups, respectively); this small group was not examined separately.

Analytic Techniques

The research questions focus on individual changes in response times for the RAN numbers, letters, and colors. To model within-person changes and between-person differences therein, we fit latent growth models to the repeated RAN response times within the structural equation modeling framework. Specifically, we fit latent basis growth curves (Meredith & Tisak, 1990), which decompose the individual trajectories into two components representing performance in kindergarten and performance in Grade 8. The latent basis growth curve can be expressed as

$$y_{nt}={\beta }_{0n}·A\left[t\right]+{\beta }_{1n}·\left(1-A\left[t\right]\right)+e_{nt}$$ (1)

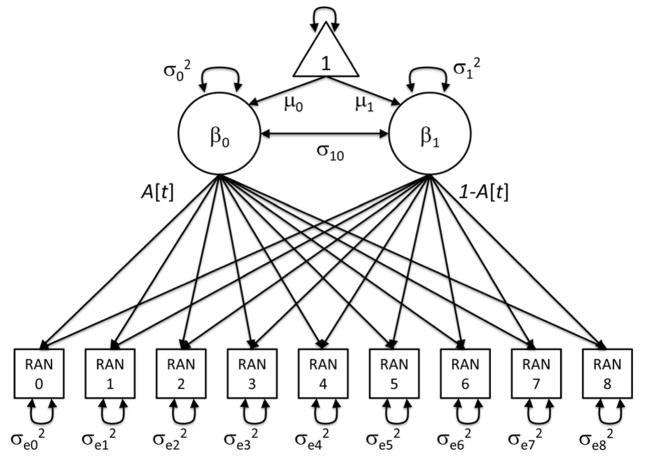
where y_nt are the repeatedly measured response times for the RAN numbers, letters, or colors for individual n at grade t, β_0n is the predicted response time for individual n in kindergarten, β_1n is the response time for individual n in Grade 8, A[t] is the basis coefficient at time t, and e_nt is the time-dependent residual. The basis coefficients describe the pattern of change over the observation period and allow for the nonlinear change trajectories of the RAN. The random coefficients (β_0n and β_1n) are assumed to follow a multivariate normal distribution with means (μ₀ and μ₁), variances ( ${\sigma }_0^2$ and ${\sigma }_1^2$), and a covariance (σ₁₀). The sample-level means represent the predicted sample-level mean response time in kindergarten and Grade 8, respectively. Variances represent true between-person differences in response times at these time points and the covariance represents the linear association between true predicted values in kindergarten and Grade 8. The time-dependent residual (e_nt) is assumed to follow a uniform distribution with a mean of 0 and a time-dependent variance ( ${\sigma }_{et}^2$). A path diagram of the latent basis growth model is contained in Figure 1. In this diagram, squares represent observed variables, circles represent latent variables, and the triangle represents a unit constant. One-headed arrows represent directed relations, such as regression coefficients and factor loadings, and two-headed arrows represent non-directional relations, such as covariances and variances. The RAN scores measured in kindergarten through 8^th grade are the observed variables in the path diagram, the random coefficients of Equation 1 are the latent variables in the path diagram, and their regression coefficients are their factor loadings. The latent variables have means (one-headed arrows from the unit constant), variances (two-headed arrows beginning and ending at the same variable), and a covariance (two-headed arrows beginning and ending at different variables).

Figure 1.

A path diagram of the latent basis growth model for RAN scores (kindergarten through Grade 8). Squares represent observed variables, circles represent latent variables, and the triangle represents a unit constant. One-headed arrows represent directed relations, and two-headed arrows represent non-directional relations, such as covariances and variances.

In subsequent models mathematical and reading learning disability and low achievement classifications, Contingency Naming Test scores, and Number Skills scores were entered into the model as predictors of β_0n and β_1n to understand their impact on the RAN trajectories. The latent basis growth curves were fit in the structural equation modeling framework (Grimm, Ram, & Hamagami, 2011; Ram & Grimm, 2007).

To model changes in the differences between RAN colors and RAN letters as well as the differences between RAN colors and RAN numbers, we fit multiphase growth curves with years since kindergarten as the timing metric. The multiphase growth curve can be written as

$$y_{nt}={\beta }_{0n}+{\beta }_{1n}·A_1\left[t\right]+{\beta }_{2n}·A_2\left[t\right]+e_{nt}$$ (2)

where y_nt are the repeated assessments (difference in RAN performance) for individual n at time t, β_0n is the predicted difference in reaction time for individual n in kindergarten (t = 0), β_1n represents the amount of increases in the differences in response time for individual n that are representative of letter or number recognition becoming automatized, A₁ is a vector of basis coefficients controlling how quickly the increases occur, β_2n represents the amount of decreases in the differences in response time for individual n that are representative of color recognition becoming more automatized, A₂ is a vector of basis coefficients controlling how quickly the decreases occur, and e_nt is the time-dependent residual, which is assumed to follow a normal distribution with a mean of 0 and a time-dependent variance. Individual change parameters (β_0n, β_1n, andβ_2n) are assumed to follow a multivariate normal distribution with estimated variances and covariances.

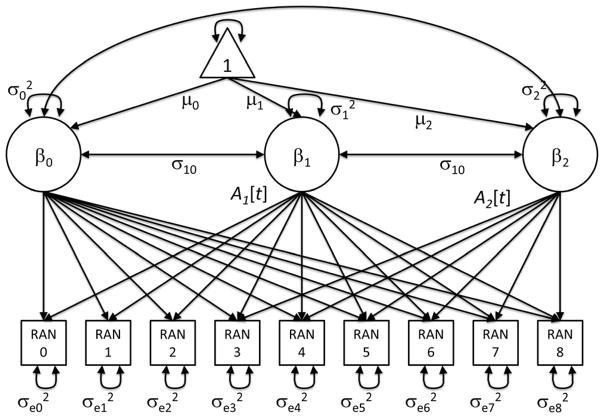
A path diagram of the multiphase latent basis growth model is contained in Figure 2. The three latent variables represent the intercept, the rate of increases, and the rate of decreases (random coefficients of Equation 2). In this path diagram, the increases occur between time 0 and 2 and the decreases occur between time 2 and 8. The timing of the transition varied over outcomes and was determined based upon sample statistics. As in prior models, the latent variables have means, variances, and covariances.

Figure 2.

A path diagram of the multiphase latent basis growth model. The three latent variables represent the intercept, the rate of increases, and the rate of decreases (random coefficients of Equation 2). In this path diagram, the increases occur between time 0 and 2 and the decreases occur between time 2 and 8. The timing of the transition varied over outcomes and was determined based upon sample statistics. The latent variables have means, variances, and covariances.

In presenting the results, our specific hypotheses were based on the premise that between-child variability exists in growth on RAN growth, so the first set of results concerns performance for the entire study sample. All differences reported are for absolute differences in seconds.

Results

Growth on RAN performance across the total study sample

The latent basis growth model fit the data adequately with Comparative Fit Indices (CFI) and Tucker Lewis Indices (TLI) greater than .90 and Root Mean Square Error of Approximations less than .10 for all three RAN subtests (letters: (χ²(33)=98, CFI=.95, TLI=.94, RMSEA=.09), numbers:(χ²(33)=64, CFI=.98, TLI=.98, RMSEA=.06), and colors: (χ²(33)=75, CFI=.97, TLI=.97, RMSEA=.07). The latent basis model showed a steeper initial decline followed by a slower approach to the plateau for RAN letters and numbers compared to RAN colors, where the initial decline was less severe and the approach to the plateau was more gradual.

Growth parameters varied across the three subtests, and significant between-child variability was evident in each parameter of the latent basis growth model for all three subtests. First, the mean predicted response time (RT) in kindergarten was 69.18 seconds for letters, 61.06 seconds for numbers, and 65.89 seconds for colors, suggesting that for most children, labels for all three stimuli are, at kindergarten, retrieved with roughly comparable ease or difficulty (at least when averaged across all children). Syllable length does not affect RAN RT patterns, since the only exceptions to the predominantly one syllable labels were one number (7) and one color (yellow) label and yet the slowest performance occurred on RAN letters. Second, the mean predicted RT in Grade 8 was 13.41, 13.49, and 26.37 suggesting that RAN colors RT was the least automatized at the end of the observation period. Finally, examining the basis coefficients we note that letters showed the quickest relative initial improvement (59% of total improvement occurred between kindergarten and Grade 1), followed by numbers (46% of total improvement occurred between kindergarten and Grade 1), and colors (36% of total improvement occurred between kindergarten and Grade 1). Furthermore, 90% of total improvement in letters and numbers RTs occurred in 5^th grade whereas 80% of total improvement in colors occurred by this time. Thus, near optimal performance was reached more quickly for letters and numbers compared with colors. Not withstanding subtle differences in letters vs. numbers, there was greater similarity in their rates of improvement, both relative to colors. The slower and more gradual rate of improvement for colors reflects a more gradual asymptote, as predicted.

Furthermore, for all three subtests, predicted individual RT in kindergarten was significantly correlated with predicted individual RT in Grade 8, indicating that children who had slower RTs in kindergarten were also slower at the conclusion of the study. This association was strongest for RAN colors (r=.74), followed by RAN numbers (r=.60) and letters (r=.55) subtests.

These analyses verified two important assumptions of our study, which concerned the presence of between-child variability in RAN performance (which we found for both growth parameters), and between-subtest variation in performance trajectories. The following sets of analyses concerned whether some of the between-child variation may be associated with math or reading difficulties, and the extent to which number and executive function skills contribute to that variation.

Growth on RAN performance as a function of LD status

MLD vs. LA_math vs. TA_math

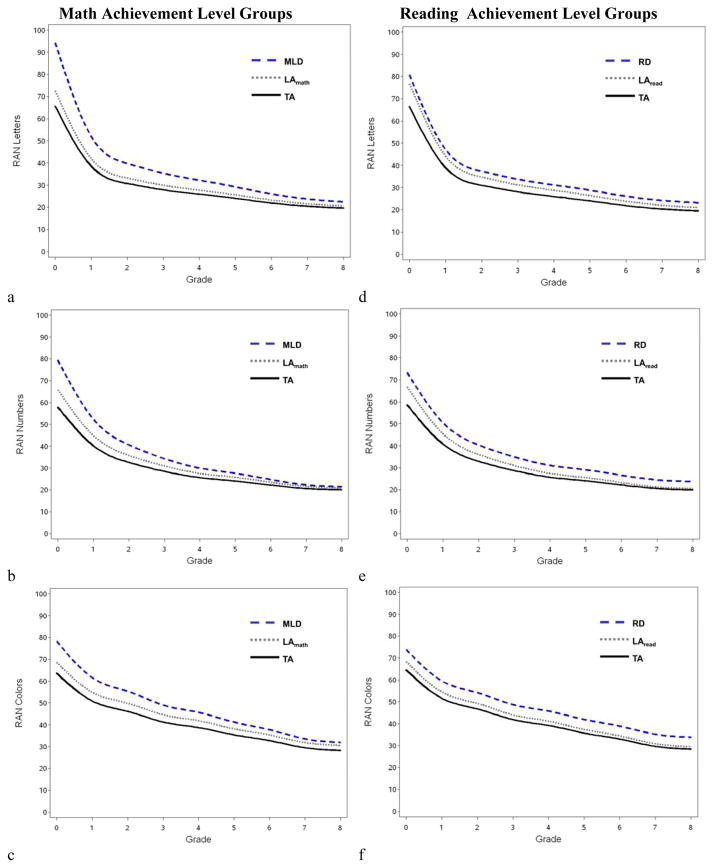
When MLD status variables (MLD or LA_math) were entered as predictors of the two parameters of the latent basis growth model, group differences emerged on all three RAN subtests. Relative to their TA_math peers, children with MLD had significantly slower RT in kindergarten for all three subtests (slower by 28.53, 21.46, and 14.65 seconds for letters, numbers, and colors, respectively). For letters and colors, children with MLD also had longer RT at Grade 8 (by 2.79 seconds for letters and 3.66 for colors), which indicate larger (slower) RTs near their performance plateau. This persistently slower RT performance level was in contrast to the pattern observed for children with LA_math, which reflected somewhat slower RTs than their TA peers, in kindergarten, for all three subtests (by 6.95, 8.05, and 5.05 seconds), but no other significant difference in growth with the exception of a longer (slower) RT at Grade 8 (by 2.28 seconds) on RAN colors (summarized in Table 1). Thus the LA_math group showed a profile of slight delays in RAN performance over time with persistence on RAN colors only, whereas the MLD group showed more global and persistent RT slowing that was not specific to numbers. Slower RTs for RAN numbers were not noted for either group at Grade 8.

Table 1.

LD and LA Subgroup Differences in RAN Growth Parameters Relative to TA Subgroups

	MLD Status		RD Status
	MLD vs. TA	LA vs. TA	RD vs. TA	LA vs. TA
RAN Subtest/growth parameter
Letters
RTpred at kindergarten in seconds	28.53**	6.95*	14.36**	10.50**
RTpred at Grade 8 in seconds	2.79**	0.98	3.70**	1.49*
Numbers
RTpred at kindergarten in seconds	21.46**	8.05**	14.64**	8.19**
RTpred at Grade 8 in seconds	1.38	0.87	3.76**	0.59
Colors
RTpred at kindergarten in seconds	14.65**	5.05*	9.28**	3.93
RTpred at Grade 8 in seconds	3.66**	2.28*	5.53**	1.09

Notes: LA = low achievement; LD = learning disability; MLD = mathematics learning disabilities; pred = prediction; RAN = rapid automatized naming; RD = reading disabilities; RT = response time; TA = typical achievement.

^*p < .05.

^**p < .01.

To address if executive function or early number skills account for some of the variation reported for MLD and LA_math status and across subtests, CNT and number skill scores were entered as predictors of the growth parameters. Outcomes varied across RAN subtests, but CNT contributed more to variation in the overall performance profile than did number skill scores.

On all three RAN subtests, CNT scores were predictive of RT in kindergarten. Children with greater CNT scores (indicating more efficient performance) tended to have faster RTs in kindergarten. Effects were moderate (standardized regression coefficient ranged from −.18 to −.36 with the strongest effect for RAN colors). In contrast, number skill scores were significantly predictive of RT in kindergarten for letters and numbers. These effects were moderate in size (standardized effect sizes were −.19).

When accounting for effects of CNT and Number Skills on RAN letters, the predicted difference in the RT in kindergartners with MLD or TA decreased from 28.53 to 18.50 seconds but remained significant, whereas the predicted difference between LA_math and TA groups decreased from 6.95 to 4.06 seconds and was no longer significant. Likewise, for RAN numbers, the combination of CNT and number skill scores reduced the RT at kindergarten differences between MLD and TA groups from 21.46 to 13.97 seconds (however, the difference in the asymptotic level increased from 2.92 to 3.38, which was now significantly different from zero and thus suggests significantly slower performance in the MLD vs. TA group at Grade 8), and reduced the difference between LA_math and TA_math groups from 8.05 to 5.86.

Only one significant outcome emerged when examining the contribution of CNT and number skills scores on growth parameters for RAN colors performance. Consistent with RAN letters and numbers, CNT scores were predictive of RT in kindergarten, with greater CNT scores linked to faster RTs in kindergarten. This effect was moderate to large (standardized regression coefficient was −.36). Number skill scores were unrelated to each parameter of the exponential growth curve.

RD vs. LA_read vs. TA_read

RD status variables (RD or LA_read) based on WJ-R Word Attack performance were entered as predictors of the two parameters of the latent growth model for RAN Letter, numbers, and colors. Relative to their TA peers, children with RD had significantly slower RTs in kindergarten for the letters, numbers, and colors subtests (by 14.36, 14.64, and 9.28 seconds, respectively). The RD group also had longer RTs in Grade 8 compared with their TA peers on all three subtests (by 3.70, 3.76, and 5.43 seconds, respectively). Children classified as LA_read did not significantly differ from their TA peers on either parameter of the latent basis growth curve for colors subtests; for RAN numbers, this LA_read group differed only in terms of its slower RT in kindergarten (by 8.19 seconds); and for RAN letters, the LA_read group differed in both the predicted RT in kindergarten (by 10.50 seconds) and in Grade 8 (by 1.49 seconds). Thus, the LA_read group consistently scored more poorly than their TA peers on the letters subtest of the RAN (see Figure 3).

Figure 3.

Growth parameters on RAN performance, from kindergarten to Grade 8, for students with math or reading learning disability (MLD/RD), low achievement (LA), or typical achievement (TA).

Number skill and CNT scores were then entered as predictors of the growth parameters. For letters, numbers, and colors subtests, CNT and number skill scores were predictive of RT in kindergarten only, in the expected direction. Children with greater CNT scores (indicating more efficient performance) and larger number skill scores tended to have faster RTs in kindergarten. These effects were moderate in size (standardized regression coefficients ranged from −.20 to −.37). The magnitudes of the effects for number skills were somewhat larger for RAN letters and numbers compared to the effects for CNT. However, the reverse was true for RAN colors with CNT having a larger impact on RTs in kindergarten. Importantly, sizable differences between RD and TA groups remained even when CNT and number skill scores were accounted for.

RAN subtest difference scores

The between-group differences in growth parameters suggest that at least one component of what is measured by RAN is shared across all three subtests, and that this component accounts for some of the continued difficulties seen in the MLD group over time, less so for the LA_math group; and that yet another component of RAN shared by numbers and letters characterizes performance of the RD and LA_read groups. These findings also suggest that measures of RAN letters and numbers bear more similarity to each other (and less with RAN colors) among children with RD (and both TA groups) than we would expect in MLD; whereas numbers and colors may be more similar to each other in MLD vs. RD groups. We therefore examined difference scores between each of the number and letter subtests relative to colors, to test the notion that RAN colors is more closely aligned with numbers than with letters among the MLD group, but not among the RD or LA groups (relative to the respective TA groups).

RAN subtest difference scores among the total study sample

Across all participants, the mean RTs for RAN numbers minus RAN letters was −6.88 seconds in kindergarten, indicating that at this age, children were somewhat quicker naming numbers compared to letters. The mean difference increased to 2.03 and 1.95 in Grades 1 and 2, indicating letter naming becoming automatized more rapidly than numbers. Subsequently, the mean difference declined and fluctuated around 0, indicating comparable RT for numbers and letters over time, consistent with the RAN literature.

The latent basis growth model fit the RAN numbers – letters data fit well (χ²(33)=53, RMSEA=.050, CFI=.868, TLI=.856). In the latent basis model, intercepts were centered at the first (kindergarten) and last (Grade 8) measurement occasions. The kindergarten intercept did not have significant variance, indicating a lack of true individual differences at kindergarten. An examination of the correlation matrix showed that correlations with the kindergarten RAN numbers – letters were near zero until the 7^th and Grade 8 assessments, where the correlations are modest (< .21). For these reasons, we fixed the kindergarten intercept variance to 0 and model fit was unaffected. The Grade 8 intercept had significant variance indicating true individual differences in RAN numbers – letters at the end of the observation period.

Across all participants, the mean difference for RAN colors minus letters was −2.92 in kindergarten, indicating comparable response times for colors and letters. The mean difference then increased to 12.44 and 15.48 in Grades 1 and 2, indicating letter recognition becoming automatized more rapidly than RAN colors. The mean difference then gradually declined to a minimum of 8.86 in Grade 8, and was significantly different from zero at all grade levels except kindergarten.

The multiphase growth model fit the RAN colors – letters data well (χ²(35)=62, RMSEA=.056, CFI=.956, TLI=.954). In the multiphase model, the first phase of changes spanned kindergarten through Grade 2 and the second phase spanned Grades 2 through 8. The first phase of changes showed sharp increases between kindergarten and Grade 1 as 85% of the increases occurred, suggesting that letter recognition mostly became automatized during this year. The second phase represented linear declines suggesting that color recognition was improving at a slightly faster rate than letter recognition during these years.

Across all participants, the mean RT between RAN colors minus numbers was 3.48 in kindergarten, indicating response times for colors and numbers were also comparable. The mean difference increased to 10.42 and 13.51 in Grades 1 and 2 indicating number recognition becoming automatized. The mean difference was more or less constant between Grades 2 and 4 before declining gradually to a minimum of 8.46 in Grade 8.

The multiphase growth model fit the RAN colors – numbers data well (χ²(30)=47, RMSEA=.048, CFI=.972, TLI=.966). In the multiphase model, the first phase of changes spanned kindergarten through Grade 2 and the second phase spanned second through Grade 8. The first phase of changes showed sharp increases between kindergarten and Grade 1 as 68% of the increases occurred suggesting that number recognition was becoming automatized during this year. We note that this relative rate of improvement (68% during the first year) was somewhat slower than the relative rate of improvement for RAN colors – letters (85%). The second phase did not represent linear declines, but had a period of relative stability between Grades 2 and 4 before showing a fairly linear decline from Grades 4 through 8. This was the period where color recognition was improving at a slightly faster rate than number recognition.

RAN subtest differences among MLD and LA_math groups

For each of the three difference score comparisons, as a first step to understanding differences between children with MLD, LA_math, and TA_math, two dummy-coded variables drawing comparisons between MLD and TA groups and between LA and TA groups were entered as predictors of the intercepts at kindergarten and Grade 8. Number skills and CNT scores were then added into the model as predictors of the two intercepts.

For RAN numbers – letters, children with MLD had lower difference scores on the Grade 8 intercept (by 1.34 seconds) indicating that children with MLD were comparatively slower in Letter vs. Number naming compared to children with TA_math. All other effects were not significantly different from 0 despite larger differences in the kindergarten intercept.

Number skills scores were predictive of only the kindergarten intercept with children having greater (positive) number sense scores having higher RAN numbers – letters difference scores. This suggests that children with greater number sense were more automatized for numbers (compared to letters) relative to children with lower number sense scores at kindergarten. All remaining effects were not significant.

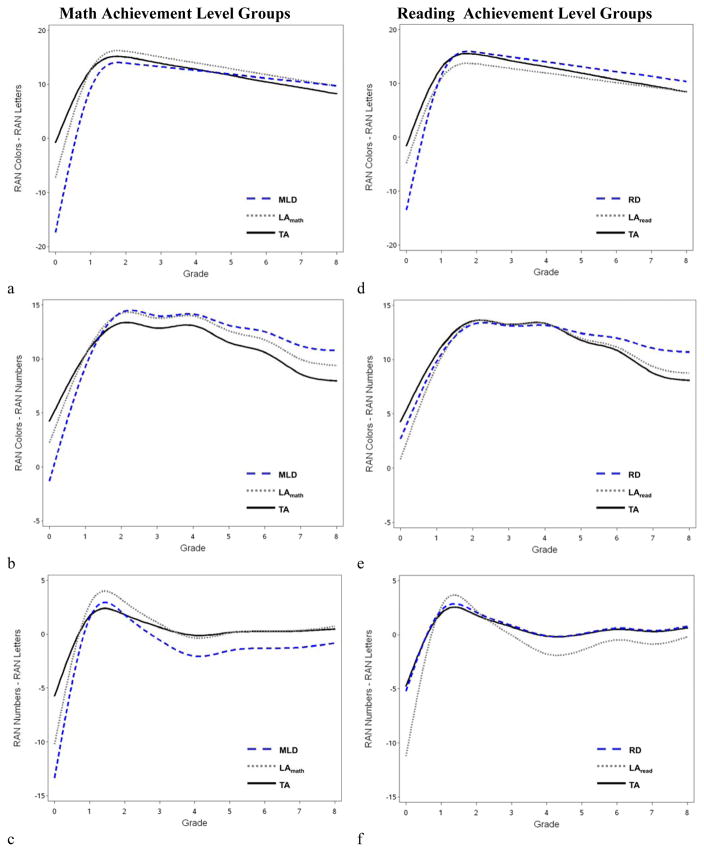
For RAN colors – letters, children with MLD had lower difference scores on the intercept (by 16.64 seconds) indicating MLD children were comparatively slower in recognizing letters compared to colors in kindergarten. Children with MLD also showed a faster rate of increases (by 15.56 second) indicating more rapid relative improvement in letter recognition compared to color name recognition between kindergarten and 2nd. Children with MLD did not significantly differ in the second phase of changes representative of the relative improvements in color recognition over letter recognition. LA_math children did not significantly differ in any of the change parameters of the growth curve compared to typically developing children (Figure 4).

Figure 4.

Growth parameters on RAN difference scores, from kindergarten to Grade 8, for students with learning disability (MLD/RD), low achievement (LA) or typical achievement (TA) in math or reading. A positive difference score indicates slower (longer RT) RAN performance on RAN colors relative to letters or numbers.

CNT scores were predictive of only the changes taking place in the second phase, with individuals having greater CNT scores showing a more consistent advantage to letter vs. color recognition. That is, individuals showed less decline in the differences between RAN colors and letters. Number skill scores were not significantly predictive of any growth parameters.

Children in both the MLD and LA_math groups were found not to differ in any aspect of the multiphase growth curve for RAN colors minus numbers. Differences between MLD and TA groups were in expected directions, but did not reach statistical significance (ps < .13; Figure 4). CNT scores were only related to the second phase of development with individuals having greater CNT scores showing a more consistent advantage to number recognition than color recognition. Number Sense was unrelated to changes in the difference between RAN colors and numbers.

RAN subtest differences among RD and LA_read groups

For all three sets of difference scores, two dummy variables drawing comparisons between RD and TA_read and between LA_read and TA_read were added as predictors of the kindergarten and Grade 8 intercept. Number skills and CNT scores were then added as predictors of the two intercepts.

For RAN numbers – letters difference scores, two significant differences emerged, both involving the LA_read group. Children with LA_read had lower scores in kindergarten (by 6.50 seconds) and Grade 8 (by 0.84 seconds) on RAN numbers – letters, indicating faster number vs. letter naming compared with TA children. Number skills had a positive effect on the kindergarten intercept, indicating that children with greater number skills tended to have quicker recognition for numbers than letters. The difference between the LA_read and TA_read groups on the kindergarten intercept remained; the difference on the Grade 8 intercept became nonsignificant. This supports the notion that, especially for children with RD and LA_read, performance on the Number and Letter subtests of the RAN is highly correlated throughout the school years.

For RAN colors – letters difference scores, there were no significant differences between RD, LA_read, and TA_read groups. However, we note that the difference in the intercept and changes in the first phase of development comparing RD and TA_read groups were similar to those observed for children with MLD (−11.89 and 12.29, respectively) but were not significant (p = .06). CNT scores were predictive of changes during the second phase of development, whereas number skills were predictive of RTs in kindergarten and \ changes during the first phase of development. All of these effects were moderate in size with standardized coefficients ranging from .33 to .40.

For RAN colors – numbers, the only significant difference to emerge was in the trajectories between RD and TA_read groups in the second phase of development. Children with RD did not show the expected decline during this phase and, instead, showed relative stability during this phase. Thus, children with RD maintained the relative advantage of number recognition compared to color recognition. We note that this profile differs from that for children with MLD.

CNT scores were related to the changes during only the second phase of development with individuals having greater CNT scores showing a more consistent advantage to letter versus color recognition. This effect, however, did not account for the difference between RD and TA_read groups in this phase of development. Number skill scores were unrelated to the changes in the difference between RAN colors and numbers.

Discussion

In this study, we based our predictions about differences in RAN performance across LD participant subgroups on the premises that performance on all three RAN subtests is subject to between-child variation from both independent and shared contributions. We predicted differences in cognitive underpinnings of MLD and LA (and RD) would contribute to this variation in RAN performance from kindergarten to Grade 8. Specifically we predicted that the extent to which growth in RAN Letter performance precedes growth in RAN Number performance would vary across groups, and that our findings would support the notion that RAN subtests measure different skills relative to each other and at different points during development. These premises, and some of our predictions, were supported by the findings.

RAN is predictable over time, and variable across individuals

First, there was significant between-child variability in RAN RTs for all three subtests at kindergarten and Grade 8, in the rate of improvement on these subtests between these grades, and in the relative performance across subtests (as seen in the differences score we examined) over time. This between-child variation does not imply within-subject instability; on the contrary, correlations between performance at kindergarten and Grade 8 were significant for all three subtests, especially for RAN colors (r = .74), with comparable correlations among the RAN letters and numbers subtests (.55 and .60, respectively). These findings are consistent with the RAN literature, and extend earlier findings to a 9 year span with a longitudinal sample. Nevertheless, as seen in Figure 3, growth trajectories for the subtests differed from each other, and subtle but important differences emerged as a function of LD group status.

When is RAN automatized?

Across all participants, RAN performance appeared not to be automated by kindergarten, as implicated by slow and comparable RTs for all three subtests (means between 61 and 69 seconds). RAN numbers led to the fastest (shortest) RT of the three subtests at kindergarten, as D’Amico & Passolunghi (2009) also reported for the 9 years olds in their study. In our study, kindergarten RAN letters performance was the slowest of all three subtests, even compared to color naming, by an average of 8 seconds. Still, the number-over-letter naming advantage was not significant at kindergarten, and although it later increased (approached zero) and then fluctuated around 0, there significant between-child variation at Grade 8 remained.

If not at kindergarten, when is RAN performance automatized? Across all participants, the sharpest increases in automaticity (that is, steepest decline in RTs) occurred between kindergarten and Grade 1, and the rate of improvement was quickest for letters, followed by numbers and then colors (in part a reflection of initial intercept but also presumably of the role of literacy instruction during this time period). Performance on numbers and letters reached comparable levels of total improvement by Grade 5, with more gradual improvement for RAN colors. By Grade 8 RTs were twice as long (slower) for colors (group mean = 26.46 seconds) as they were for letters or numbers, which were comparable to each other (means for both were ~ 13.40 seconds). The lack of significant differences between letters and numbers RTs over time supports the practice of averaging these two subtest RTs as one RAN score in research and practice, but the between-child variation at Grade 8 noted above (and seen in Figure 4, panels c and f) implicates that caution may be warranted in some applications of this practice. This caution is further supported by the difference scores comparisons among LD groups, discussed subsequently.

Predictors of RAN performance

What might account for between-child variation in RAN performance? Our measures of executive function (CNT efficiency at Grade 1) and, to a lesser degree, kindergarten “number sense” (number skills at kindergarten) accounted for some of the variation at kindergarten, but not at Grade 8. Children with more efficient CNT performance had faster RTs in kindergarten for all three subtests, but particularly colors. Number skills scores predicted kindergarten RT for numbers and letters only. The lack of an association between these predictors and RAN performance at Grade 8 does not mean that there are no contributions of executive function or number sense to later RAN performance, but rather that our measures of these domains obtained early in the study may not have been sufficiently sensitive to reveal additional influences on between-child variation later in development.

LD and RAN performance

Another potential contribution to between-child variation on RAN is LD status, or the cognitive profiles that underlie MLD or RD status. Several of our findings support this claim. First, children with MLD had slower RAN RTs at kindergarten and at Grade 8. Relative to their TA_math peers, children with MLD were much slower on all three subtests at kindergarten (with more significant slowing on RAN letters, followed by numbers, followed by colors) and were somewhat slower on letters and colors (but not numbers) at Grade 8. In contrast, children with LA_math had only moderately slower RTs on all three subtests at kindergarten and only one small RT difference (on RAN colors) at Grade 8. The lack of specific deficits on RAN numbers in the MLD group may be viewed as inconsistent with evidence of specific number processing deficits in MLD (e.g., Landerl et al., 2004), but it is consistent with similar findings (e.g., Willburger et al., 2008) that suggest that the ability to retrieve a label (e.g., “two”) for a symbol (e.g., “2”) in a non-quantitative context may be an insufficient indicator of MLD. Rousselle and Noël (2007) proposed that MLD results from a deficit in the ability to access numerical meaning from symbols (including digits), a hypothesis that is neither supported nor refuted by our current findings because RAN does not require attending to numerical meaning - solely digit labels. Naming speed, however, could affect performance on a numerical access tasks that involved naming or reporting stimuli, but this contribution of naming speed ability need not be specific to digits. In our study, children with MLD were slower at RAN numbers and letters, although not in the same manner as observed in the RD group.

Relative to their TA_read peers, children with RD were also much slower on all three subtests at kindergarten, although they had comparable rates of slowing for RAN numbers and letters. Despite a smaller effect size than that which emerged for the TA_math – MLD comparison, children with RD were also significantly slower than their TA_read peers on all three subtests at Grade 8, with comparable performance on letters and numbers. Thus, differences in children with MLD vs. TA_math in kindergarten were moderate, but diminished over time; whereas those that differentiated children with RD from their TA_read peers were less pronounced at kindergarten but persisted through Grade 8. Children with LA_read differed from their TA_read peers on only letters and numbers (at kindergarten), on letters only at Grade 8, with no differences on RAN colors at either time point.

Did the predictors (CNT and number skills) contribute to these group differences? When both of these predictors were accounted for, the differences in RAN letters RT at kindergarten between the MLD and TA_math groups diminished but remained significant and moderate in size; whereas the RAN letters RT difference between the LA_math and TA_math groups was no longer significant. These finding are consistent with our earlier work showing differences between MLD and LA_math subgroup cognitive profiles, and with our emphasis on the importance of differentiating these two groups (e.g., Murphy et al., 2007). Likewise, although CNT and number skills also predicted differences in RT between children with RD or TA_read at kindergarten for all three RAN subtests, these differences remained significant when effects of CNT and number skills were accounted for.

The variations across RAN subtests and across participant subgroups implicate both shared and unique contributions to RAN performance, which have theoretical and practical significance regarding interpretation of RAN performance and the role of development in drawing conclusions from RAN performance. For instance, the stronger correlation to emerge for the RAN colors RTs over time suggests that RAN colors performance is less subject to additional influences than is performance on RAN letters and numbers (e.g., it may be less malleable, or less likely to be the target of instruction). The limited variation across letters and numbers suggests shared features. For instance, when we compared growth trajectories for RAN numbers minus letters difference scores, the variances in the growth factors were small, and adding achievement level status to the models showed no significant differences, likely because of the restricted variance in the growth factors. But some of the findings from the MLD group suggest otherwise: If numbers and letters subtests tap identical or near identical skills, we would expect that their respective difference scores relative to RAN colors would also be identical (or near identical) – but Figure 4 reveals otherwise.

When comparing color minus letter RT difference scores, the initially negative difference score revealed slower letter naming at kindergarten, followed by a steep increase in difference scores which in turn reflected the rapid decline in letter RTs by Grade 1, leading to a large positive difference score once letter naming was faster than color naming. This first phase of changes in relative RTs accounted for 85% of the total increase in difference score, followed by a linear decline in difference scores as color naming became more automatized over time (at a slower rate than automatization of letter naming). The only significant group difference in the colors minus letters score was the slower initial RTs for children with MLD; rates of increase and decline in the difference scores over time did not differ across groups.

Relative to the colors – letters difference scores, we note four important differences in the colors – numbers difference scores. First, although the initial negative difference score also rapidly increased from kindergarten to Grade 1, this first phase of changes in relative RTs accounted for only 68% of the total increase in difference score (vs. the 85% increase for colors – letters); second, although this difference score declined as color naming became more automatized over time, the decline was not linear (as it was for color – letter; Figure 4), instead, performance was stable from Grades 2 to 4. Third, while children with TA_math, LA_math, and LA_read showed linear declines in this difference score from Grades 4 to 8, children with RD did not. Of interest is that (as seen in Figure 4, panel d), children with RD were indistinguishable from their LA and TA peers in their relative RT performance for RAN colors and letters during Grades 2 to 4, but this did not mean the three groups were on the same developmental path. Finally, although difference scores for colors – letters clearly showed an initial letter advantage, the initial colors – numbers difference scores were closer to zero, indicating that at kindergarten, number and color naming were more comparable to each other than were number and letter naming, especially for the MLD group.

Whether the patterns observed in this study represent shared or independent obstacles to automaticity of letter vs. number naming, or to differences in typical or atypical development of numerical symbol processing per se (e.g., Holloway, Vogel, Battista, & Ansari, 2012), is not revealed by the current study. Although the current study does support that RAN skills are complex despite the simplicity of the measure itself (Bowers et al., 2003) and that each subset may tap sources of individual differences, future studies are needed to identify potential biological contributions the sources of these behavioral distinctions and what cognitive constructs are represented by the subtest differences. For instance, recent evidence from twin studies demonstrates genetic contributions to distinctions between timed and untimed broad math and reading skills (Petrill, Logan, Hart, Vincent, Thompson, Kovas, & Plomin, 2012). These differences may be associated with the individual differences to emerge on the specific fluency measures evaluated in the present study.

Predicting MLD or RD from RAN

What may account for the findings that both MLD and LA_math groups had performance deficits or slowed growth (of varying types) on RAN, whereas only the RD (and not the LA_read) group did so? One possible explanation stems from the larger empirical knowledge base concerning underpinnings of RD vs. MLD, which affords reliance on focused vs. broad assessment tools to classify the RD vs. MLD groups in this study, respectively. For instance, we used the WJ-R Word Attack subtest, a measure of non-word reading, from Grades 1 to 4 as a basis for RD status, but used a far broader measure of “math” skills (WJ-R Calculation subtest) to assign children to the MLD group. A related explanation concerns the heterogeneity of MLD or LA_math and many cognitive skills associated with underachievement in mathematics. RAN may measure a combination of skills – such as processing speed or lexical access — that are linked both to RAN and to math performance in general (Alloway, Gathercole, Kirkwood, & Elliott, 2009). In this regard, it is not surprising that RAN differentiated the RD vs. TA groups from each other, but not the LA-Reading and TA groups; nor is it surprising that both the MLD and LA_math groups differed from their TA counterparts on various aspects of RAN performance.

Conclusions and future directions

RAN has been widely used in research on reading disability for decades, is commonly included in comprehensive evaluations of reading disability (Wagner et al., 2009), and is gaining momentum as one component of MLD assessments (Chard et al., 2005; Hecht et al., 2001). In this study, MLD status, RD status, CNT efficiency, and number skills were all predictive of at least some aspects of RAN performance, consistent with the literature on the role of number sense (e.g., Locuniak & Jordan, 2008) and executive functions (Best, et al., 2011) in mathematics achievements. Our findings indicated that RAN subtests may tap different skills for different subgroups, and at different developmental periods. Within-group differences reveal different relationships among RAN subtests, and have implications for whether the skills measured by RAN are the same among all children being assessed. These findings do not pose a threat to the construct validity of the RAN so much as they prompt recognition of the sources of individual and developmental differences that should be taken into account during assessment of MLD. Accordingly, it may be prudent to reconsider assumptions about the RAN, such as the notion that RAN letters and numbers (digits) subtests tap the same skills, until the mechanisms underlying these skills are better understood regarding their role in the assessment of risk for MLD. Empirically guided modifications of RAN may be needed for extending its use to evaluating risk for MLD. Several important modifications that have been introduced include the addition of a Quantities subtest (van der Sluis, et al., 2004; Willburger et al., 2008), experimental subtests to measure the contributions of inhibition and cognitive shifting (Willburger et al., 2008), and alternatives to reliance on total RT scores (e.g., Schatschneider, Carlson, Francis, Foorman, & Fletcher, 2002). We add to these the need to further understand how difference scores between subtests may shed light on the skills that RAN evaluates in children with (or at risk for) MLD, and how finer delineation of the underpinnings of MLD will facilitate this pursuit.