Optimization of saturation-recovery dynamic contrast-enhanced MRI acquisition protocol: monte carlo simulation approach demonstrated with gadolinium MR renography

Abstract

Dynamic contrast-enhanced (DCE) MRI is widely used for the measurement of tissue perfusion and to assess organ function. MR renography, which is acquired using a DCE sequence, can measure renal perfusion, filtration and concentrating ability. Optimization of the DCE acquisition protocol is important for the minimization of the error propagation from the acquired signals to the estimated parameters, thus improving the precision of the parameters. Critical to the optimization of contrast-enhanced T₁-weighted protocols is the balance of the T₁-shortening effect across the range of gadolinium (Gd) contrast concentration in the tissue of interest. In this study, we demonstrate a Monte Carlo simulation approach for the optimization of DCE MRI, in which a saturation-recovery T₁-weighted gradient echo sequence is simulated and the impact of injected dose (D) and time delay (TD, for saturation recovery) is tested. The results show that high D and/or high TD cause saturation of the peak arterial signals and lead to an overestimation of renal plasma flow (RPF) and glomerular filtration rate (GFR). However, the use of low TD (e.g. 100 ms) and low D leads to similar errors in RPF and GFR, because of the Rician bias in the pre-contrast arterial signals. Our patient study including 22 human subjects compared TD values of 100 and 300 ms after the injection of 4 mL of Gd contrast for MR renography. At TD = 100 ms, we computed an RPF value of 157.2 ± 51.7 mL/min and a GFR of 33.3 ± 11.6 mL/min. These results were all significantly higher than the parameter estimates at TD = 300 ms: RPF = 143.4 ± 48.8 mL/min (p = 0.0006) and GFR = 30.2 ± 11.5 mL/min (p = 0.0015). In conclusion, appropriate optimization of the DCE MRI protocol using simulation can effectively improve the precision and, potentially, the accuracy of the measured parameters.

INTRODUCTION

Dynamic contrast-enhanced (DCE) MRI is one of the most established imaging techniques for the measurement of tissue function, particularly perfusion, and is widely used in the evaluation of tumors, brain, kidneys and heart, among others (1–5). Dynamic imaging is performed to record the transit of an intravenously injected contrast agent, typically gadolinium (Gd) based, through the tissue of interest. The acquired images are processed and quantified by tracer kinetic modeling to obtain functional parameters, such as perfusion and transit times (4,6). Precise and accurate estimation of the parameters is critical for disease diagnosis and follow-up. For example, comparison of tumor perfusion before and after anti-angiogenesis treatment provides important guidance on tumor management (1). To minimize the measurement error for the parameters, multiple studies have proposed an improvement in post-processing using appropriate tracer kinetics models to analyze the dynamic images (4,6–8). However, it is equally important to optimize the image acquisition, including the dose of injected contrast and the MR pulse sequence parameters, which has been demonstrated by few studies (9,10). For example, using a patient study combined with simulation, Orton et al. (10) showed the advantage of higher temporal resolution in the acquisition of DCE MRI data of the liver, and the importance of the use of accurate vascular input function for quantitative analysis of DCE MRI data. Dale et al. (9) used an error propagation approach to evaluate the sensitivity of tumor perfusion (estimated by K^trans) to measurement errors in pre- and post-contrast vascular and tissue signals, and to background noise. Using a similar approach of error propagation, Zhang and Koh (11) optimized the selection of flip angles in the spoiled gradient echo sequence for the performance of DCE MRI of the breast.

One major application of DCE MRI is MR renography, which measures multiple parameters of renal function, including renal perfusion (renal plasma flow, RPF), glomerular filtration rate (GFR) and mean transit times (MTT_K) with T₁-weighted sequences (12). Critical to the minimization of estimation errors in the parameters is the balance between the contrast concentration and the pulse sequence parameters that account for the T₁-shortening effect of the contrast within the kidney. Specifically, with the saturation-recovery (SR) gradient echo sequence discussed here, the injected dose (D) and time delay (TD), which is the delay between the saturation pulse and the subsequent signal acquisition, can impact the measurement of arterial input and renal parenchymal signals, and thus the estimation precision and accuracy of the resulting parameters.

In this study, we performed a comprehensive Monte Carlo simulation that tested the impact of D and TD in SR MR renography. To simulate MR renography data, we sampled D and TD from their typical ranges, and considered multiple disease scenarios, including low perfusion/filtration and obstructive uropathy. To verify the simulation results, we used two different values of TD to measure arterial signals in MR renography of 22 patients, and compared their estimates of the renal functional parameters.

METHODS AND MATERIALS

Factors to optimize in MR renography – a qualitative consideration

In SR, magnetization along the direction of the magnetic field B₀, or M_Z, increases from zero to equilibrium magnetization (M₀). As the rate of the increase is determined by T₁, this process is often termed T₁ recovery. A short T₁ corresponds to a rapid approach of M_Z towards M₀. Ideally, the MR signal should be acquired when M_Z increases to an intermediate level, i.e. much higher than the noise level but not close to M₀. One major factor to consider in the optimization of the acquisition protocol is the injected dose (D) of Gd-based contrast. Gd-based contrast shortens T₁. With a high value of D, the tissue of interest may accumulate a high concentration of contrast, and the T₁ value can become so short that the acquired signals have already reached their equilibrium level. We term this phenomenon the ‘signal saturation effect’. With this effect, high concentration values produce MR signals of a similar level, which thus cannot be differentiated. For example, to avoid the signal saturation effect for arterial signals, the cardiac perfusion scan is often performed with two injections of Gd contrast, with a low-dose injection for the sampling of the arterial input function (AIF) from the left ventricle (13). High Gd dose also complicates MR signals by adding potential susceptibility effects caused by T₂* shortening (14,15). In our experience with MR renography, a low dose of 4 mL of Gd contrast (concentration, 500 mmol/L) is free of the above-mentioned artifacts, and provides acceptable precision for the estimation of single-kidney GFR (16), but a systematic analysis for dose optimization is warranted.

In addition to the injected dose D, the magnitude of the MR signals can also be influenced by certain MR sequence parameters. For example, in spoiled gradient echo sequences, the flip angle can be optimized so that the error propagation from the MR signals to the estimated contrast concentration is minimized (11,17,18). Similarly, in SR sequences, TD, which is the delay between the saturation pulse and the subsequent signal acquisition, controls the degree of T₁ recovery and thus the magnitude of the acquired signal within a wide range from zero to fully recovered magnetization. The optimal values for the sequence parameters are usually T₁ dependent (19). As T₁ of tissue changes with contrast concentration in the tissue, which is further determined by the injected dose D and the functional status of the tissue, optimization of the injected dose D and of the sequence parameters needs to be performed simultaneously and to consider the tissue function.

For DCE MRI of most organs, a high concentration of contrast agent appears in the arterial input only, but the kidneys are different. The kidneys are highly perfused, and so a high vascular peak is often seen in tracer retention curves of the renal cortex or even the medulla (6). Most Gd-based contrast agent is excreted via the kidneys, and so collecting ducts in the renal medulla may accumulate large amounts of contrast agent. This is particularly the case when obstruction occurs at renal calyces or along the ureter, i.e. obstructive uropathy (20). As described below, we performed a Monte Carlo simulation for a variety of kidney scenarios, and evaluated how the selection of D and TD impacts the estimation of renal functional parameters.

Monte Carlo simulation of MR renography

The simulation was designed for dynamic imaging of the kidneys using a SR sequence. The simulation assumed a bolus input of contrast agent [dose D (mL) at a concentration of 500 mmol/L] and predicted the pattern of transit through the cortex and medulla of the kidney using a convolution-based tracer kinetic modeling technique (12). SR signals from kidney tissue and artery [sampled at TD (ms)] were then generated from tracer concentration data using the Bloch equation. After adding noise of appropriate type and level to the signals, we then applied the inverse procedure, i.e. signal to concentration conversion and tracer kinetic model fitting, to estimate the parameters GFR, RPF and MTT_K from the simulated data. We repeated the entire process for different values of D and TD. Our hypothesis was that, with different D and TD values, the noise in MR signals is propagated into the estimated functional parameters by different degrees (i.e. precision) and possibly with some bias (i.e. inaccuracy).

We first simulated AIF (Gd concentration in a feeding artery) after a bolus injection of 4 mL (500 mmol/L) of Gd contrast. The dose of D₀ = 4 mL was chosen following a previous study (16). Three gamma-variate functions, each with appropriate delay, width and magnitude, were summed to fit typical AIF from our patient data (12,21). To simulate AIF after Gd contrast injection of a dose D of 1–10 mL, we used the following approximation:

$$C_a=(D/D_0)·C_{a0}$$ [1]

where C_a0 is the above simulated AIF for a dose of 4 mL, D ranges from 1 to 10 mL and C_a is the resultant AIF. In a clinical setting, contrast agent is typically injected at a rate of 2–4 mL/s, followed by saline flush at the same rate. Using this injection protocol, the AIF of dose 1–10 mL should result in a comparable shape, but differ only in magnitude (16,22).

Contrast concentration in renal tissue relates to AIF by the following convolution:

$$C_t·V=F{\int }_0^t{C}_a(\tau )·R(t-\tau )d\tau$$ [2]

where C_t is the contrast concentration in renal tissue (mmol/mL), V is the tissue volume (mL), F is the renal blood flow (mL/min), t is the time after contrast injection (min) and R is the impulse retention function (unitless) that characterizes tracer kinetics in the tissue after a unit impulse input (12). The tracer kinetic model assumes a serial three-compartment structure, i.e. renal vascular space, tubules and collecting ducts, for tracer to transit through the kidney; RPF and GFR are the rates of flow delivering tracer into vascular and tubular compartments, respectively, and MTT_K measures the average transit time of filtered tracer through an entire kidney. By specifying different parameter values for GFR, RPF and MTT_K (Table 1), we simulated three types of kidney: healthy, dysfunctional (low GFR and RPF) and obstructive (normal GFR and RPF, but long MTT_K).

Table 1.

Parameter values for different simulated kidney states

	GFR (mL/min)	RPF (mL/min)	MTTK (s)
Healthy	60	210	134
Dysfunctional	15	50	322
Obstructive	60	210	304

GFR, glomerular filtration rate; MTT_K, mean transit time of kidney; RPF, renal plasma flow.

To generate MRI signals from the Gd concentration of arterial blood or renal tissue, we first used the following T₁-shortening equation to derive T₁ values:

$$r_1·C=1/T_1-1/T_1^0$$ [3]

where r₁ is the T₁ relaxivity and $T_1^0$ is the T₁ value of tissue or blood in the absence of Gd contrast. With the SR sequence, the signal S is a function of TD, T₁ and an equilibrium magnetization M₀:

$$S=M_0·(1-e^{-TD/T_1})$$ [4]

We simulated SR signals for blood, renal cortex and renal medulla using the above equations and the following parameter values: D, 1–10 mL with an interval of 1 mL; TD, 100–1000 ms with intervals of 100 ms; acquisition time (relative to contrast injection), 0–300 s with 2-s intervals; volume of renal cortex, 100 mL; volume of medulla, 40 mL; baseline T₁ of blood, 1.6 s (23); baseline T₁ of cortex, 1.5 s; baseline T₁ of medulla, 2.0 s; r₁ = 4.3 mm⁻¹ s⁻¹ for contrast agent gadoteridol (24,25); cortex M₀ = 1380; medulla M₀ = 1436; blood M₀ = 643. These values are typical of our patient data acquired with 3.0-T MRI scanners. We did not repeat the simulation with pre-contrast T₁ of different magnitudes, because, in reality, the accuracy and precision of pre-contrast T₁ can be improved by averaging multiple signal acquisitions.

To simulate noisy MRI signals, we added noise to the above-generated MR signals so that the magnitude of the noisy signal followed a Rician distribution (26). To build such a distribution, we estimated a standard deviation (SD) of 20 from a background region in images of our patient data. We then generated pseudo-random samples, i.e. magnitude of noisy MR signals, by sampling the distribution using conventional inverse transform sampling. To simulate noisy signals from a region of interest (ROI) of a tissue type, we averaged multiple single-voxel signals with independently sampled Rician noise, and assumed a typical ROI for aorta to contain 20 voxels, and renal cortex and medulla from a single slice to contain 100 and 50 voxels, respectively. Signals from renal tissues are often affected by artifacts, such as respiratory motion and mis-segmentation. To accommodate such artifacts, we added Gaussian noise with zero mean and SD of 10 to the ROI-averaged signals for renal cortex and medulla. For each combination of D, TD and renal functional status, one set of noise-free MR signals (blood, cortex and medulla) was generated, from which 1000 sets of noisy MR signals were generated by the above independent noise-addition procedure. In adding noise to the simulated MR signals, we did not use multiple signal-to-noise ratio (SNR) levels, because a previous study has indicated that the impact of background noise is much less than that of the various artifacts.

Each set of noisy signals was first converted to Gd concentrations using Equations [3] and [4], and then fitted by the same tracer kinetic model (12) for generation of the data to estimate GFR, RPF and MTT_K. The entire procedure of the simulation is demonstrated in Figure 1. For each combination of D, TD and renal functional status, we obtained 1000 estimates for each functional parameter. The SD of the 1000 estimates indicates the precision of the parameter, and the mean deviation (MD) from the true parameter value indicates the accuracy.

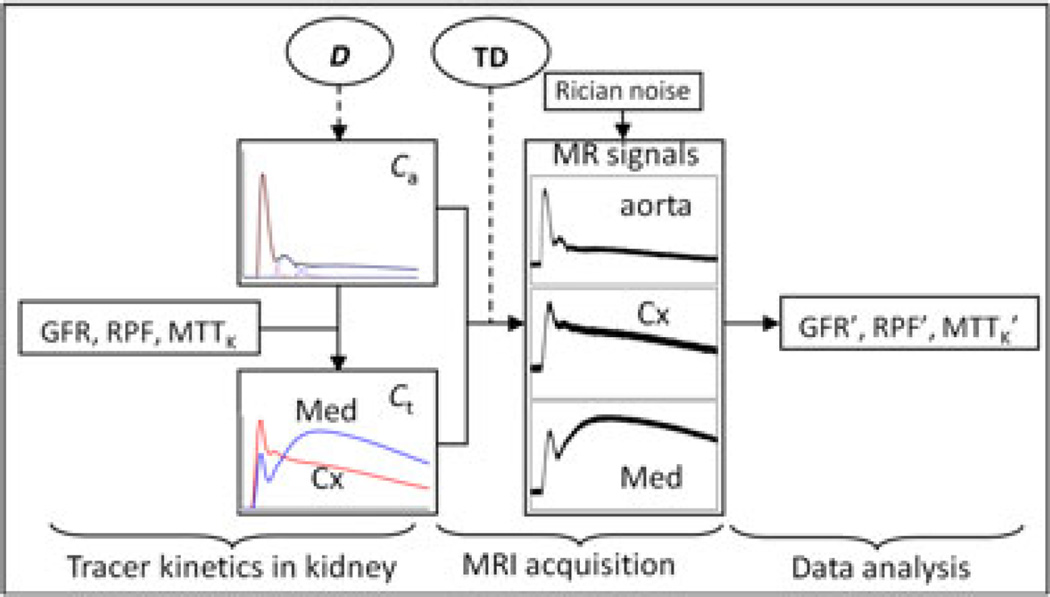
Figure 1.

Diagram of the simulation procedure. The forward simulation includes the simulation of tracer kinetics in the kidney and MR renography acquisition to obtain MR signals. Rician noise was added to the signals, followed by MR renography analysis to estimate the functional parameters (GFR, glomerular filtration rate; MTT_K, mean transit time of kidney; RPF, renal plasma flow). Gadolinium dose (D) determines the magnitude of the arterial input function (C_a), and the scaling effect is further propagated into Gd concentration in kidney tissue (C_t). The time delay (TD) is adjustable to change the MR signal intensity. Cx denotes cortex, and Med denotes medulla.

By comparing SD and MD of the parameters across different combinations of D and TD, we sought to identify the optimal D and TD values, or ranges, for parameter estimation. Specifically, we identified the optimal D and TD values primarily based on the SD data (i.e. precision) as follows. For the measurement of each parameter of a kidney status, there were 100 combinations of D and TD (each with 10 values). Of the 100 combinations, we pre-selected the 25 candidates with the lowest SD values for the parameter. For the other 75 combinations and in the order of increasing SD, we computed the difference between the new combination’s SD value and the average SD of the candidates; if the difference was not significant (<1.96 times the candidates’ SD) or less than 2% of the maximal SD value, we included the new combination into the candidates. At the end of the process, we obtained a subset of combinations (at least 25 combinations) that gave low SD value for a parameter, and this was repeated for all three parameters of the three renal statuses. For a comprehensive evaluation, we counted the number of times for each combination of D and TD being selected as candidates, and used the number as a score (from ‘0’ to ‘9’). A score of ‘9’ for a combination of D and TD means that, by using the combination, all three parameters GFR, RPF and MTT_K for all three kidney statuses were estimated with low SD, or high precision. For the D and TD combinations optimal for SD, we also checked their MD values and excluded a combination if any of the MD values for GFR, RPF and MTT_K were more than 1.96 times the corresponding SD value.

Patient study

Accurate measurement of AIF is critical for DCE MRI (22,27). Our preliminary study indicated that arterial blood experiences a wide range of tracer concentration, and so, for the SR sequence, TD needs to be properly selected to estimate all possible concentration values accurately. Although the above simulation tested the impact of TD in the simulated setting, to verify the simulation findings, we also performed a patient study, in which signals from abdominal aorta were measured with two TD values: 100 and 300 ms.

Twenty-two patients (13 men, nine women; age, 55.5 ± 10.6 years; weight, 88.5 ± 13.1 kg; serum creatinine (SCr), 0.57–1.52 mg/dL) were included in this institutional review board (IRB)-approved study of renal function in patients with liver cirrhosis at the University of Utah. The Child–Pugh scores for these cirrhotic subjects were 6.5 ± 1.5 (range, 5–11). After signing a written consent form, each subject was scanned with a 3-T MRI scanner (TimTrio; Siemens Medical Solutions, Erlangen, Germany), using a two-dimensional T₁-weighted SR turbo fast low-angle shot (FLASH) sequence with the following parameters: slice thickness, 7 mm; TR = 519 ms; TE = 1.15 ms; flip angle, 15°; matrix, 176 × 160; field of view, 500 × 455 mm²; resolution, 2.8 × 2.8 mm². The acquisition at each time point (per 1.5 s) covered three two-dimensional slices: coronal and axial slices through the middle of both kidneys, and a coronal or sagittal slice through the abdominal aorta. The slices used different TDs for the SR preparation: 300 ms for the two kidney slices, and 100 ms for the coronal or sagittal slice through the aorta. After five MR acquisitions, 4 mL of gadoteridol (ProHance; Bracco Diagnostics, Milan, Italy) were administered intravenously at a rate of 2 mL/s, followed by a 20-mL saline flush injected at the same rate. Data acquisition continued for 5 min. To quantify the tracer concentration from the MR signal intensity [Equations [3] and [4]], proton density-weighted images were acquired with the same sequence, but a long TD of 7 s. As part of the clinical protocol for these cirrhotic patients, high-resolution three-dimensional T₁-weighted abdominal VIBEs through the liver and kidneys were acquired during a breath hold (1.4 × 1.4 × 3-mm³ interpolated voxels), from which we estimated the kidney volumes. The data were analyzed with the same techniques as described in the simulation section, with additional details in refs. (28,29).

With the above acquired data, we were able to sample AIF from both the coronal slice through the aorta (with TD = 100 ms) and the axial slice through the middle of the kidneys (with TD = 300 ms). The aortic ROIs drawn in the two slices were of a similar size and were both on the renal artery level, so that the sampled AIFs from the two slices should differ only in their TD values. The patients’ abdomen and chest were covered from the anterior by two four-channel surface coils, so that all blood in the heart and the lungs was saturated to eliminate potential time-of-flight artifact in aortic blood signals. Renal functional parameters were estimated with both AIFs and compared using paired t-tests and Bland–Altman plots.

RESULTS

Monte Carlo simulation

In the following, we first show the SD results, indicating precision, for the parameters estimated with different D and TD combinations, from which optimal combinations of D and TD were determined, and then present the MD results for the combinations that caused significant estimation bias. We then show the impact of artifacts with some D and TD combinations by presenting some intermediate simulation results.

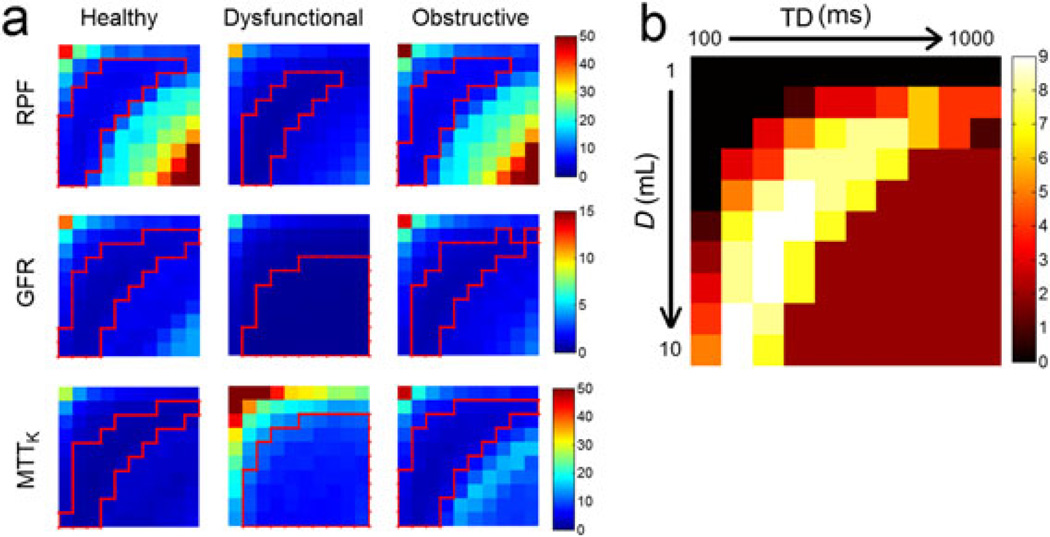
Figure 2a shows the maps of SD for the different parameters, and Fig. 2b shows the overall score map (for the optimal D and TD combinations). Each map in Fig. 2 contains 10 × 10 elements: rows increase from D = 1 mL to D = 10 mL downwards, and columns increase from TD = 100 ms to TD = 1000 ms rightwards, as labeled in (b).

Figure 2.

(a) Standard deviation (SD) for the estimates of renal plasma flow (RPF, mL/min), glomerular filtration rate (GFR, mL/min) and mean transit time of kidney (MTT_K, s) for healthy, dysfunctional and obstructive kidneys. Low SD regions are outlined by red lines. (b) The score map that combines low SD regions in all nine maps. In each map, columns increase from time delay (TD) = 100 ms to TD = 1000 ms and rows increase from dose (D) = 1 mL to D = 10 mL.

In general, the SD and MD maps (not shown) are roughly symmetric along the diagonal line (top left to bottom right). This symmetry indicates that D and TD have a similar impact on error propagation to the parameter estimates. An increase in either D or TD can increase the magnitude of the acquired SR signals, with the same potential benefit of higher SNR and potential risk of signal saturation. For this reason, most estimation error occurs at either low D and low TD (top left corner) or high D and high TD (bottom right corner).

RPF (Fig. 2a, top row) shows relatively large SD values at low D and low TD and at high D and high TD. The healthy and obstructive cases have similar patterns because we used the same RPF value for simulation: SD at D = 1 mL and TD = 100 ms was 45 mL/min, at D = 7 mL and TD = 700 ms was 22 mL/min, and then increased to 59 mL/min at D = 10 mL and TD = 1000 ms. These D/TD combinations also show high positive MD values (Fig. 3a), i.e. high overestimation. These errors are investigated more closely in the next section. The SD values of dysfunctional RPF are low: 22 mL/min at D = 1 mL and TD = 100 ms, and 11 mL/min at D = 10 mL and TD = 1000 ms.

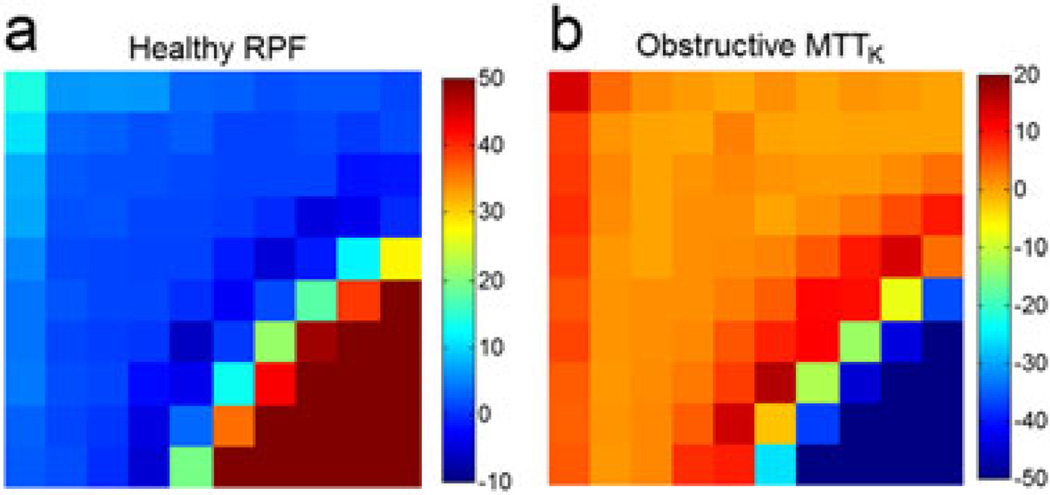
Figure 3.

(a) Mean deviation (MD) for the estimates of healthy renal plasma flow (RPF, mL/min) as a function of dose (D) and time delay (TD). (b) MD for the estimates of obstructive mean transit time of kidney (MTT_K, s). Columns increase from time delay (TD) = 100 ms to TD = 1000 ms and rows increase from dose (D) = 1 mL to D = 10 mL.

SD values for the GFR estimates (Fig. 2a, second row) follow a similar pattern to RPF, with the only difference being that the higher SD values of GFR at high D and high TD are much lower than those for RPF. For example, at D = 7 mL and TD = 700 ms, SD of GFR was less than 2 mL/min. Estimation of GFR is more dependent on the entire AIF and less on just the first-pass segment. Thus, underestimation of the first-pass blood signals with high D and/or TD, which is discussed in the next section, does not impact the estimation of GFR as much as that of RPF. Of note, GFR of the dysfunctional case can be estimated with low SD and low MD (both less than 2 mL/min) with all D and TD combinations, except for very low values, such as D = 1–2 mL and TD = 100–200 ms.

For MTT_K (Fig. 2a, third row), SD values are high at the corner of low D and low TD for all three kidney statuses. This is a result of the low SNR of the signals for such combinations, which is more severe for the dysfunctional case, because its tissue retention curve is even lower. For the obstructive kidney, at D > 6 mL and TD > 600 ms, MTT_K has an intermediate SD level around 7–13 s, but, as shown in Fig. 3b, a highly negative bias of 70–150 s. This underestimation of MTT_K is investigated further in the next section.

In each SD map of Fig. 2a, we show the optimal region with relatively low SD values (outlined in red); the score map that combines the optimal regions in all nine maps is shown in Fig. 2b. For the scenarios considered (three parameters and three kidney statuses), a high dose of D = 7–10 mL, combined with a TD of ~200 ms, gives a score of 8–9 (out of 9); if D is reduced to 3–6 mL, a score of 7–8 can still be achieved as long as TD is 300–600 ms. A low D needs to pair with a high TD, and vice versa.

Investigation of the artifacts

Our simulation shows that the use of very low or high values of D and TD leads to high estimation errors in the functional parameters. To interpret these findings, we show some intermediate simulation results below to illustrate the related artifacts.

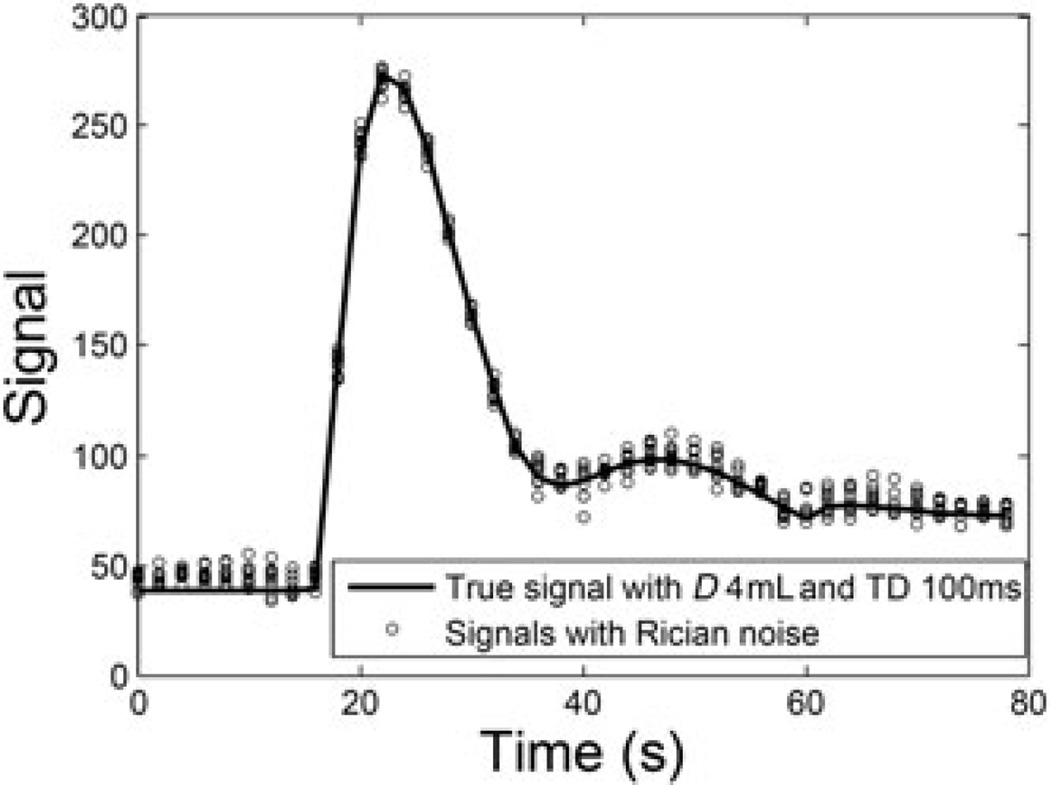
Low values of D and/or TD may lead to a low signal magnitude and thus low SNR. This low SNR may not only be propagated into the parameter estimates as high SD (or low precision), but can also cause a positive bias for low signals because of the Rician distribution of the MR signal magnitude. Figure 4 shows an example of aortic blood signals simulated with D = 4 mL and TD = 100 ms. In this case, with noise following a Rician distribution, the overestimation of the MR signal magnitude is apparent during pre-contrast (0–16 s) and later portions (>40 s) when compared with the true magnitude level. An overestimation of pre-contrast blood signals would lead to an underestimation of the converted tracer concentration in blood, i.e. the magnitude of AIF (30), which would further lead to an overestimation of the flow-related parameters, such as RPF and GFR (12).

Figure 4.

Simulated aortic signals with dose (D) = 4 mL and time delay (TD) = 100 ms. MRI signal noise follows a Rician distribution. At low signal-to-noise ratio (SNR), such as the baseline and the tail segment in this example, noise with a Rician distribution creates a positive bias, compared with the true signals.

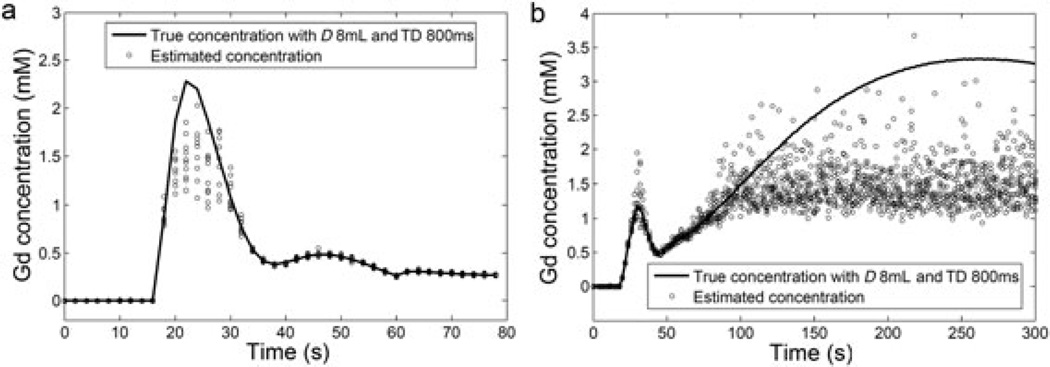
High D and TD values cause a signal-saturation artifact, i.e. sampling of signals at a very late stage of T₁ recovery when the signal has already reached its equilibrium level. Figure 5 (a) shows 10 AIF examples from the simulated data of D = 8 mL and TD = 800 ms, compared with the true noiseless AIF. The first-pass peaks of the estimated AIFs show high SD of 0.5–0.6 mm, and their averaged level is lower than the true values by 0.7–0.8 mm. Both the high uncertainty and the underestimation are caused by the sampling of signals at the equilibrium level. With D = 8 mL, the peak concentration value in the aorta is about 2 mm (Fig. 5a), which shortens T₁ to ~100 ms. With such a relaxation rate, at TD = 800 ms, the signal recovers to more than 99.9% of its equilibrium level. On such a signal level, a tiny noise added to the MR signal could cause a large error in the estimated T₁ and therefore concentration. We also see that such an error in the estimated concentration is mostly negative. This intermediate result explains the large SD and large positive MD in RPF when high D and high TD are used for simulation. In addition to the first pass of aortic blood, a high concentration of Gd can also occur in obstructive kidneys (Fig. 5b). Here, the concentration versus time curve of the renal medulla keeps increasing with time because of downstream obstruction. Similar to aortic concentrations, we see high error and a large underestimation in the estimated tracer concentration in the renal medulla. This underestimation leads to the underestimation of MTT_K. With D = 8 mL and TD = 800 ms, MTT_K is estimated to be 184.2 ± 6.5 s, much lower than the true value of 304 s for the obstructive kidney. It should be noted that the dysfunctional kidney also has a long MTT_K of 322 s, but, with low RPF and GFR, the contrast does not accumulate to a high concentration in the renal medulla.

Figure 5.

MR signals acquired with high dose (D) and high time delay (TD) can cause an inaccurate estimation of the gadolinium concentration, such as the first-pass peak of the arterial input function (AIF) (a) and renal medulla in obstructive kidneys (b). The full lines in the plots are the true noiseless curves for the simulation, and the circles are multiple estimates from the simulated acquisition using D = 8 mL and TD = 800 ms.

In Table 2, we summarize the potential artifacts that may be encountered if TD and D are not properly selected when using the SR sequence for MR renography. We also list the predicted consequences on parameter estimation based on our simulation findings. It should be noted that most of these artifacts and the resulting estimation bias are not dependent on SNR of the MR signals, but the selection of D and TD.

Table 2.

Potential artifacts caused by improper selection of injected dose (D) and time delay (TD) and the consequences

TD and D to avoid	Artifact	Affected signals	Parameter estimation
Low TD and low D	Low SNR	All signals	Low precision for all parameters
	Rician bias	Pre-contrast blood signals	Overestimation of RPF and GFR
High TD and high D	Signal saturation	First-pass blood signals	Overestimation of RPF and GFR
		Medulla signals in obstructive kidneys	Underestimation of MTTK

GFR, glomerular filtration rate; MTT_K, mean transit time of kidney; RPF, renal plasma flow; SNR, signal-to-noise ratio.

Patient study

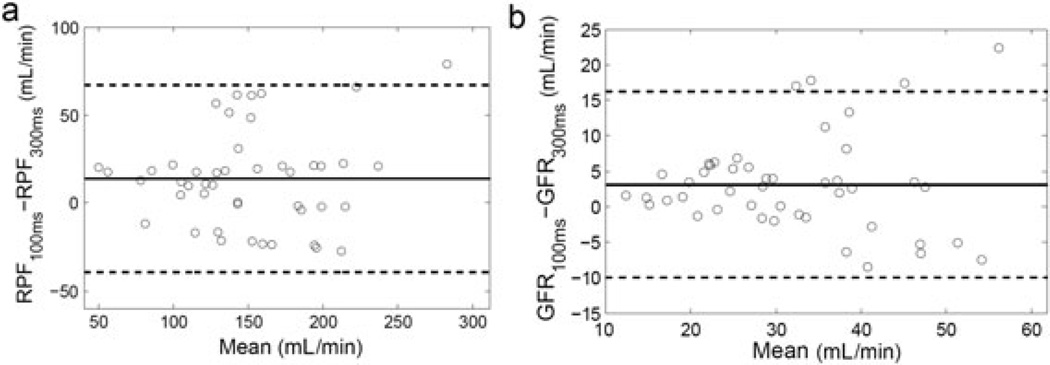
In our patient study with 22 subjects, we used two TD values (100 and 300 ms) to acquire blood signals, and compared the parameter values estimated with the two AIFs. RPF estimated from AIF with TD = 100 ms was 157.2 ± 51.7 mL/min, significantly higher than that with TD = 300 ms, i.e. 143.4 ± 48.8 mL/min (p = 0.0006). The averaged difference between the two was 13.8 ± 27.2 mL/min. GFR estimated from AIF with TD = 100 ms was 33.3 ± 11.6 mL/min, significantly higher than that with TD = 300 ms, i.e. 30.2 ± 11.5 mL/min, with a difference of 3.1 ± 6.7 mL/min (p = 0.0015). These findings agree with our simulation prediction that, when a very low TD value is used, baseline arterial signals suffer from Rician bias and this ultimately causes an overestimation of RPF and GFR. In Bland–Altman plots for both RPF and GFR (Fig. 6), the difference between the two estimates (TD = 100 ms versus TD = 300 ms) becomes more dispersed as the mean parameter value increases. This result indicates that TD-induced variability in RPF and GFR is more severe for higher RPF and GFR than for lower values. This agrees with our simulation results in Fig. 2a.

Figure 6.

Bland–Altman plot to show the difference between parameter values from the arterial input function (AIF) acquired with time delay (TD) = 100 ms and with TD = 300 ms. (a) Renal plasma flow (RPF) difference is 13.8 ± 27.2 mL/min; (b) glomerular filtration rate (GFR) difference is 3.1 ± 6.7 mL/min. The full line denotes the mean difference and the two broken lines are the mean difference ± 1.96 standard deviation of the difference. With very low TD, RPF and GFR tend to be overestimated because of the overestimation of the baseline arterial signals, and the error increases as RPF or GFR increases.

DISCUSSION

In this study, we used Monte Carlo simulation to optimize the key acquisition parameters for MR renography, Gd contrast dose (D) and SR TD for the measurement of renal functional parameters for different functional statuses (healthy, dysfunctional and obstructive). We found that high D and/or high TD resulted in substantial estimation error in RPF, GFR and MTT_K. This was because, with either high D or high TD, MR signals are sampled near the equilibrium level of SR. We also found that, at low TD values, e.g. 100 ms, the arterial signal prior to contrast enhancement is so low that the noise follows a Rician distribution, but not Gaussian distribution, and causes the overestimation of the pre-contrast signal magnitude. This ultimately leads to the overestimation of all functional parameters, particularly RPF and GFR. This overestimation is more severe when low D is used, and thus signal enhancement is lower than the overestimation of the pre-contrast arterial signal. Our patient study, which used a low dose of 4 mL, compared TD values of 100 and 300 ms in the acquisition of aortic signals. The results confirmed that, compared with TD = 300 ms, the use of TD = 100 ms resulted in higher values for GFR and RPF, which agrees with our simulation results.

The optimization of the contrast agent dose has been investigated widely in the field of radiology and low doses are typically desired. High doses are avoided for patient safety, considering that contrast agents, such as Tc^99m-diethylene-triamine-pentaacetate (Tc^99m-DTPA), are radioactive, and iodinated contrast for computed tomography imaging can cause acute kidney injury and allergic reactions. For MRI, despite a few promising non-contrast techniques, including arterial spin labeling (ASL) (31,32) and blood oxygen level-dependent (BOLD) (33,34) methods, DCE MRI using Gd-based contrast is still the most established method for the assessment of renal function. However, recent studies have revealed potential risks of the use of large doses of Gd-based contrast agents. For example, the administration of some Gd-based contrast agents may lead to nephrogenic systemic fibrosis in patients with impaired renal function (35), and also dose-dependent Gd deposition in the brain (36). However, very low dose leads to low contrast enhancement in tissue, and may lower the accuracy or precision of the estimated parameters. Our simulation compared the performance of different doses, from 1 to 10 mL (concentration, 500 mmol/L), and found that a dose of 3–6 mL is optimal for the measurement of renal functional parameters. This optimal range is much lower than the standard dose used in clinical practice (15–25 mL or 0.1 mmol/kg), and can help to avoid the signal-saturation artifact often encountered in blood and medulla signals.

The MRI sequence used was an SR sequence, in which TD is the primary parameter for the adjustment of the signal magnitude. The other popular T₁-weighted sequence used for MR renography is the spoiled gradient echo sequence. In this sequence, the flip angle can be optimized (11,17,18) to maximize the precision of the estimated T₁. In brain imaging, dynamic susceptibility contrast (DSC) MRI utilizes the T₂* shortening effect of Gd contrast medium. With DSC, TE needs to be optimized to give the best estimation accuracy of T₂* for a range of Gd concentrations. These sequences are similar in that their respective signal sampling parameter can be optimized for the measurement of T₁ or T₂* of a targeted range. Because the parameter T₁ or T₂* relies on the injected dose, optimization of the sequence parameters must be performed simultaneously with that of the dose. Ideally, all optimization should be aimed to maximize the precision and accuracy of the functional parameters, instead of intermediate results, such as T₁ or Gd concentration.

One of the limitations of this study was the use of a single MRI sequence for both simulation and patient studies. Although having their advantages and disadvantages, other sequences can result in a different set of optimization parameters. The simulation strategy can be readily applied to other sequences. Another limitation is the comparison of only two TD values (100 versus 300 ms) for the acquisition of aortic signals in the patient study, but no comparison of the injected doses. It is not safe to test the use of a high Gd dose, nor is it beneficial to patients to use an ultra-low dose (such as 1 mL). Testing TD = 100 ms for the acquisition of renal tissue signals was not necessary as the baseline signals for renal tissue were sufficiently high such that the Rician effect was not an issue. Third, the amount of noise added for the simulation may not exactly match the actual noise levels in real data, and so the simulation results should not be used for the prediction of the precision or accuracy of the functional parameters, but rather for a comparison of the relative performance of the different values of TD and D. Fourth, for the simulation, we used a single form of AIF, but did not consider the potential scenario that AIF might take a different shape for patients with impaired cardiac function. Fifth, our simulation focused on the optimization of the adjustable acquisition parameters D and TD, but did not consider other potential error sources, such as motion and ghosting artifacts. Finally, the MRI sequence can be designed to set varying TD values through the imaging time course. This can potentially resolve the artifacts pre- and post-contrast. However, this approach would require a priori information. Nonetheless, the simulation demonstrated these artifacts and can be used for the design of sequences for future studies.

CONCLUSIONS

The optimization of the DCE MRI acquisition protocol using a Monte Carlo simulation can improve the precision and accuracy of the estimated functional parameters. Our simulation suggests that, for T₁-weighted SR MR renography at 3 T, a low dose of 3–6 mL is sufficient for precise parameter estimation and, with such a dose, TD for sampling arterial and renal signals should be around 300–600 ms. The selection of appropriate sequence parameter values needs to consider both the dose and functional status of the tissue. The results shown here and the tools developed may be important for future studies of renal pathophysiology.

Abbreviations used

AIF

arterial input function

ASL

arterial spin labeling

BOLD

blood oxygen level dependent

SCr

serum creatinine

DCE

dynamic contrast enhanced

DSC

dynamic susceptibility contrast

FLASH

fast low-angle shot

Gd

gadolinium

GFR

glomerular filtration rate

IRB

institutional review board

MD

mean deviation

MTT_K

mean transit time of kidney

ROI

region of interest

RPF

renal plasma flow

SD

standard deviation

SNR

signal-to-noise ratio

SR

saturation recovery

Tc^99m-DTPA

Tc^99m-diethylene-triamine-pentaacetate

TD

time delay