Abstract
Protein arginine methyltransferases (PRMTs) are the enzymes responsible for posttranslational methylation of protein arginine residues in eukaryotic cells, particularly within the histone tails. A detailed mechanistic model of PRMT-catalyzed methylation is currently lacking, but it is essential for understanding the functions of PRMTs in various cellular pathways and for efficient design of PRMT inhibitors as potential treatments for a range of human diseases. In this work, we used stopped-flow fluorescence in combination with global kinetic simulation to dissect the transient kinetics of PRMT1, the predominant type I arginine methyltransferase. Several important mechanistic insights were revealed. The cofactor and the peptide substrate bound to PRMT1 in a random manner and then followed a kinetically preferred pathway to generate the catalytic enzyme-cofactor-substrate ternary complex. Product release proceeded in an ordered fashion, with peptide dissociation followed by release of the byproduct S-adenosylhomocysteine. Importantly, the dissociation rate of the monomethylated intermediate from the ternary complex was much faster than the methyl transfer. Such a result provided direct evidence for distributive arginine dimethylation, which means the monomethylated substrate has to be released to solution and rebind with PRMT1 before it undergoes further methylation. In addition, cofactor binding involved a conformational transition, likely an open-to-closed conversion of the active site pocket. Further, the histone H4 peptide bound to the two active sites of the PRMT1 homodimer with differential affinities, suggesting a negative cooperativity mechanism of substrate binding. These findings provide a new mechanistic understanding of how PRMTs interact with their substrates and transfer methyl groups.
Keywords: enzyme catalysis, histone methylation, pre-steady-state kinetics, processivity, protein methylation, PRMT, ordered and random binding mechanism, stopped-flow, transient kinetics
Introduction
Protein arginine methyltransferases (PRMTs)2 mediate the deposition of methyl groups on protein arginine residues by utilizing S-adenosylmethionine (SAM) as a cosubstrate (also frequently called cofactor in the literature) and produce S-adenosylhomocysteine (SAH) as a byproduct (1, 2). According to the degree and regiochemistry of the methylated products, PRMTs are divided into type I (PRMT1, -2, -3, -4, -6, and -8), type II (PRMT5 and -9), and type III (PRMT7) enzymes (3). PRMT1 is the predominant type I methyltransferase that methylates protein substrates to generate monomethylarginine (MMA) and then asymmetric dimethylarginine (ADMA) residues (Fig. 1). PRMT1 plays important roles in various biological processes such as epigenetic regulation, RNA processing, and DNA repair (4). Overexpression of PRMT1 is related to cardiovascular diseases (5, 6), kidney disease (7, 8), and many types of cancers, e.g. prostate cancer (9), breast cancer (10), and leukemia (11, 12). A clear understanding of the cellular function of PRMT1 in regulating biology and disease would be greatly facilitated by illuminating the molecular mechanism of how the enzyme binds with SAM and peptide substrate to form the catalytic ternary complex whereby the chemical turnover is executed. Furthermore, a mechanistic elucidation of PRMT-catalyzed methylation is of pharmacologic significance in the effective design of potent and selective PRMT inhibitors.
FIGURE 1.
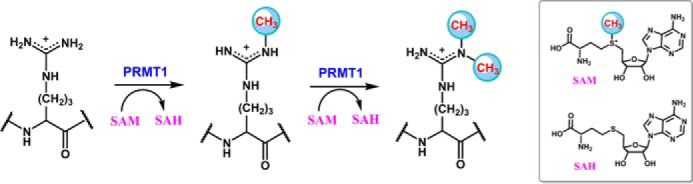
Arginine methylation by PRMT1.
A dozen PRMT X-ray crystal structures have been resolved, which provide detailed structural information about the cofactor binding pocket and key residues involved in arginine methylation (13, 14). All PRMTs show a homodimeric architecture, which is considered the active unit for catalysis. The catalytic core of all type I PRMTs consists of three key structural segments: N-terminal αX and αY helices, a Rossmann fold, and a C-terminal β-barrel domain from which a dimerization arm protrudes (Fig. 2, the αX helix of PRMT1 is invisible in the original crystal structure and was homology-modeled from our previous work (15)) (13, 16). The Rossmann fold forms a deep pocket for the cofactor SAM binding. The N-terminal αX sequence is highly dynamic, as it is invisible in the apo-form of PRMTs, and only in the SAH-bound form does the N-terminal sequence exhibit an ordered helical conformation that folds like a lid onto the cofactor (17–20). Thus it is highly likely that cofactor association and chemical catalysis in PRMTs are accompanied by the structural movement of the N-terminal αX sequence. However, the crystal structure is a static snapshot of an enzyme-ligand complex and does not unveil direct information on the rates of PRMT association with the cofactor and substrate. Rapid kinetic methods are required to investigate real-time cofactor- and substrate-binding dynamics as well as their significance for enzyme catalysis.
FIGURE 2.
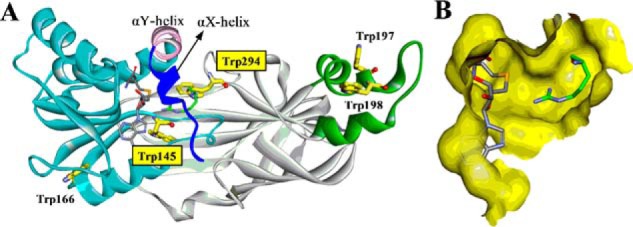
X-ray crystal structure of PRMT1-SAH-Arg complex (Protein Data Bank ID: 1OR8). A, PRMT1 is shown in ribbon mode with the N-terminal αX helix (blue), αY helix (pink), Rossmann fold (cyan), β-barrel (gray), and dimerization arm (green). The αX helix is invisible in the original crystal structure and was homology-modeled from our previous work (15). B, binding pocket for SAH and Arg (without αX helix). Tryptophan residues, SAH, and substrate Arg are shown in stick mode.
Several research groups have reported their studies on the steady-state kinetic properties of PRMT catalysis (21–28). However, there is no unified conclusion on the binding order and processivity in PRMT-catalyzed methylation to date. For instance, based on product and analog inhibition, Thompson and co-workers (21, 22) propose that hPRMT1 and cPRMT5 catalyze H4 methylation with a rapid-equilibrium random binding mechanism involving the formation of dead-end EAP and EBQ complexes. The same mechanism was also recently proposed by Jacques et al. (23) for the catalysis of hCARM1. In contrast, others have reported kinetic results in support of an ordered sequential binding mechanism in which SAM binds first followed by substrate binding; then after PRMT catalysis, the methylated arginine product is the first to dissociate from the enzyme followed by SAH release (26, 28). An ordered mechanism seems to be in better agreement with the X-ray structures, which show that the cofactor is buried underneath the N-terminal αX helix of the PRMTs (19). Moreover, because both type I and type II PRMTs can carry out two rounds of methylation on the same arginine residue in substrates, kinetic studies have been done to understand how the two methylation processes are maneuvered by PRMTs. On the one hand, assessments of the enzymatic activities of PRMT1 (25, 29), PRMT2 (26), PRMT3 (25), PRMT4 (23), PRMT5 (22), and PRMT6 (28) support a distributive mechanism in which the intermediate MMA product is released into the bulk solution and rebinds to the enzyme active site for the second round of methylation reaction. On the other hand, some other reports have proposed a partial processivity for PRMT1 catalysis (21, 24), pointing out that different substrates could influence the degree of processivity (24). The reason for these controversies, to our understanding, could arise from the limits of steady-state methods in elucidating the kinetic mechanisms of substrate binding and catalysis. Technically, the determination of the orders of substrate binding and product release based on competitive versus noncompetitive patterns of product and dead-end inhibitors demands a highly stringent and precise rate determination and quantitation. Most studies in determining PRMT processivity rely on mass spectrometry-based quantitation of the amounts of mono- and dimethylated peptide products over the reaction time, which is only moderately accurate. It is important to point out that steady-state kinetic parameters Km and kcat are complex functions of microscopic rate constants and are of minimal utility in understanding individual elementary steps in enzyme catalysis. Thus, steady-state kinetics does not provide much information about the molecular processes that occur after substrate binding and before product release, such as the formation of possible intermediates and enzyme conformational change. To gain an in-depth understanding of PRMT catalysis, transient kinetic studies would be required to resolve binding and chemical events on the time scale of a single enzyme cycle (30).
One of the key methylation sites for PRMT1 is arginine 3 on histone H4 protein (H4R3), which is a hallmark of epigenetic regulation of gene transcription (31). Therefore, H4R3 methylation has been studied intensively to understand PRMT1-mediated catalysis. The peptide corresponding to the N-terminal 20 amino acid of histone H4 tails (denoted H4(1–20)) exhibits methylation efficiency similar to H4 protein (32) and thus is widely used as a surrogate for H4 protein in many H4R3 methylation studies. Previously we conducted the first transient kinetic measurements of PRMT1 catalysis using fluorescein-labeled H4(1–20) peptide (33). That study shows that the binding of SAM or SAH to PRMT1 affects the association and dissociation of H4 peptides and also demonstrates that the methyl transfer is the rate-limiting step in PRMT1 catalysis (33). However, labeling of the substrate was not able to provide direct information about SAM/SAH binding to PRMT1 and enzyme conformational change. The potential influence of substrate on PRMT-cofactor interaction remains unknown, and a modular understanding of PRMT kinetics is still elusive. In the current study, we interrogated the transient kinetics of PRMT1 by detecting intrinsic tryptophan fluorescence changes of the enzyme during the progress of substrate binding and catalysis, which quantitatively defined all of the major elementary steps pertaining to the kinetic pathway of PRMT1 catalysis. These results provided fresh insights into the mechanism of arginine methylation.
Results
Binding of PRMT1 with SAM or SAH Involves a Conformational Change Step
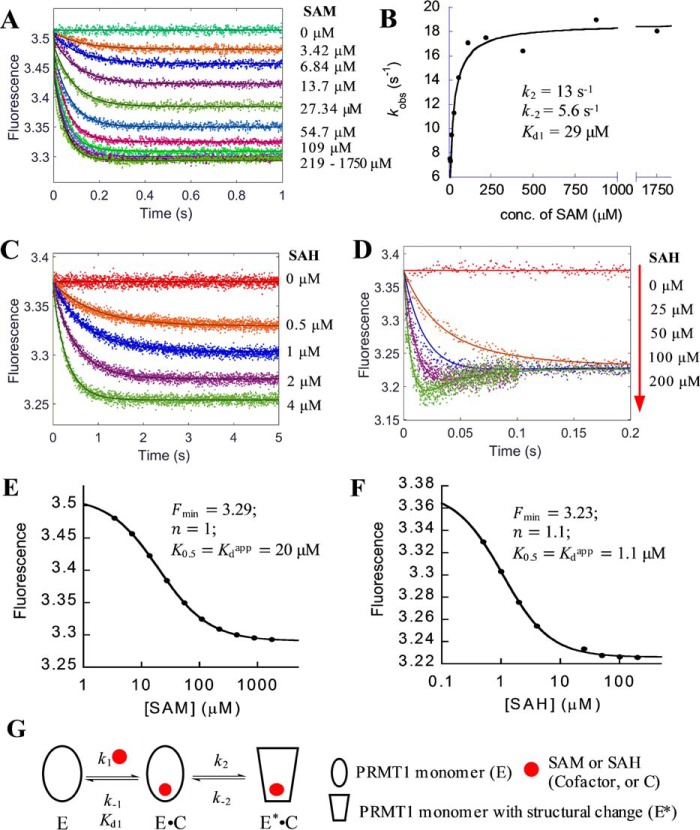
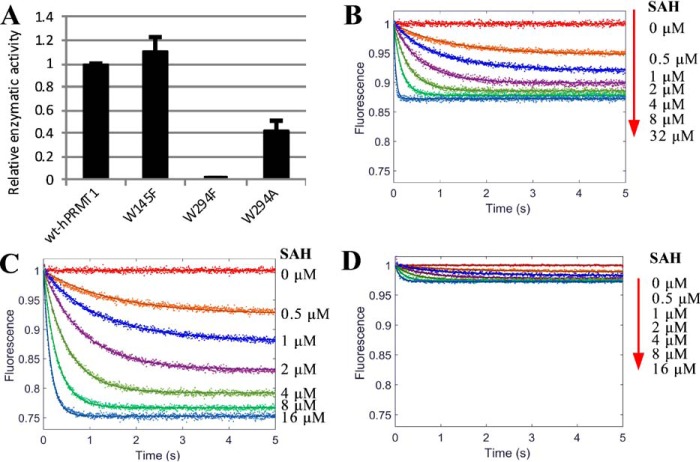
To dissect the kinetics of PRMT1 (symbolized by E (enzyme)) binding with the cofactor, SAM, or its product, SAH (both symbolized by C for brevity), we measured the changes of the intrinsic fluorescence of PRMT1 binding with SAM or SAH by using stopped-flow technology. First, a fixed concentration of PRMT1 (0.4 μm, final) was mixed rapidly with different concentrations of SAM (3.4–1750 μm, final) in an SX20 stopped-flow instrument (Applied Photophysics, Leatherhead, UK). At the point of mixing, the fluorescence detector was switched on to monitor the progress. As seen in Fig. 3A, upon binding with SAM, the fluorescence of PRMT1 decreased and then leveled off within 0.4 s. The end-point fluorescence intensity (at time point of 1 s) showed concentration-dependent fluorescence change against SAM concentration (Fig. 3E). The data points were fitted to the Hill equation (Equation 9), which yielded the apparent dissociation constant Kdapp of 20 μm. Notably, despite of the broad concentration range of SAM (over 500-fold), the Hill coefficient (n) is still equal to 1, which indicates that SAM binding to PRMT1 follows a standard binding isotherm and each monomer in the dimeric unit binds independently with the cofactor. We then analyzed the time course by a conventional mathematical fitting in which the data points were fitted to single or double exponential function (Equation 1 or 2) using the Pro-Data Viewer software. It turned out that single exponential was adequate to fit the kinetic data points well. However, the observed apparent rate constants (kobs) increased linearly with SAM concentration only in the range of 3.4 to 55 μm. The linear line was curved at higher SAM concentrations and reached a plateau when the concentration exceeded 100 μm (Fig. 3B). Such a hyperbolic curve shape clearly illustrates that PRMT1-SAM binding is not a single-step mechanism. Instead, a rapid-equilibrium two-step interaction model (Fig. 3G) would best match this type of bimolecular association process (34). Under such a kinetic scheme, the increasing phase in Fig. 3B reflects the formation of an E·C collision complex, and the later stage plateau represents the maximum apparent rate. Equation 5 was applied to fit the data points from which the dissociation constant (Kd1 in Fig. 3G, 29 μm) of the rapid binding step and the rate constants of the conformational change step (k2 13 s−1 and k−2 5.6 s−1) are calculated (Fig. 3B). To further corroborate the results, we subjected the kinetic data to global simulation with the KinTek Explorer software (35) using the two-step binding model shown in Fig. 3G. The Kd1 (57 μm), k2 (13 s−1), and k−2 (7 s−1) values yielded were in good agreement with the conventional fitting results using Equation 5. We then applied the FitSpace analysis function in the KinTek Explorer software (36) to explore the range wherein a pair of rate constants can co-vary and produce satisfying fits. The yielded confidence contour showed that the Kd1 (48–63 μm), k2 (8–18 s−1), and k−2 (5.6–9.9 s−1) values were constrained within small ranges. The values of k1 and k−1 could not be accurately determined, and only the lower boundaries were given: k1 > 1.14 s−1μm−1 and k−1 > 41 s−1. Together, the kinetic data support the idea that PRMT1 binds SAM rapidly in the first step to form an E·C complex and then undergoes a conformational change to form a slightly tighter E*·C complex (with E* representing the PRMT1 form after the conformational change).
FIGURE 3.
Formation of PRMT1·cofactor complex. A, C, and D, stopped-flow fluorescence data of PRMT1 (0.4 μm) binding with varied concentrations of SAM (A) or SAH (C and D); fitting curves (solid lines) from global simulation are based on the model shown in G. The data in A were fitted with Equation 1 to yield the observed rate constant kobs, which was plotted versus the concentration of SAM (B). The plot was fitted with Equation 5 to determine the dissociation constant Kd1 of the binding step and forward and reverse rate constants (k2, and k−2, respectively) for the conformational change. The steady-state fluorescence intensity of SAM and SAH (in A, C, and D) was plotted with their respective concentrations (E and F, respectively), from which the minimum fluorescence intensity Fmin, the Hill coefficient n, and apparent dissociation constant Kdapp were determined with Equation 9. G, proposed binding model of cofactor.
Using the same method, we measured the stopped-flow fluorescence of PRMT1 binding with different concentrations of the cofactor product, SAH. The kinetic data (Fig. 3, C and D) were subjected to fitting analysis. Similar to SAM binding with PRMT1, the plot of the steady-state fluorescence to SAH concentration is also a typical binding isotherm (Fig. 3F). As to the transient kinetics, although the kinetic data of PRMT1-SAH binding in the lower concentration range could be well fit to a single exponential, which was similar to the case of SAM binding, we clearly observed a two-phase kinetic pattern (i.e. the decrease phase followed by a slight increase phase) when the SAH exceeded 50 μm (Fig. 3D). This observation demonstrates that, like SAM binding, SAH binding is not a single-step mechanism. We thus globally fitted the kinetic data to the same two-step binding model as used for SAM fitting (Fig. 3G) using KinTek Explorer. The calculated k1 and k−1 values (0.78 s−1μm−1 and 5.43 s−1, respectively) for PRMT1-SAH binding were smaller compared with PRMT-SAM binding, whereas the affinity (Kd1 6.9 μm) for SAH was about 8-fold tighter than for SAM. The rate constants of the conformational change were 27.5 s−1 (k2) and 4 s−1 (k−2). We also used FitSpace analysis to examine the accuracy of the calculated rate constants; k1 was well constrained within a small range (0.63–1.16 s−1μm−1), and k−1 varied between 0.6 and 21 s−1. For the conformational change, the lower boundaries for k2 and k−2 were yielded (>0.1 and 1.3 s−1, respectively), and their sum value varied in the range of 30 to 50 s−1. These data are listed in Scheme 1. The global simulation also yielded the relative fluorescence amplitude of E, E·SAH, and E*·SAH to be 1, 0.81, and 0.88, respectively. These numbers show that the fluorescent decrease phase corresponded to the formation of the E·SAH complex because the fluorescence amplitude of E·SAH was lower than that of the E form. The fluorescent increase phases observed later on in the progress curve were due to the conversion of the E·SAH complex to the E*·SAH complex.
SCHEME 1.
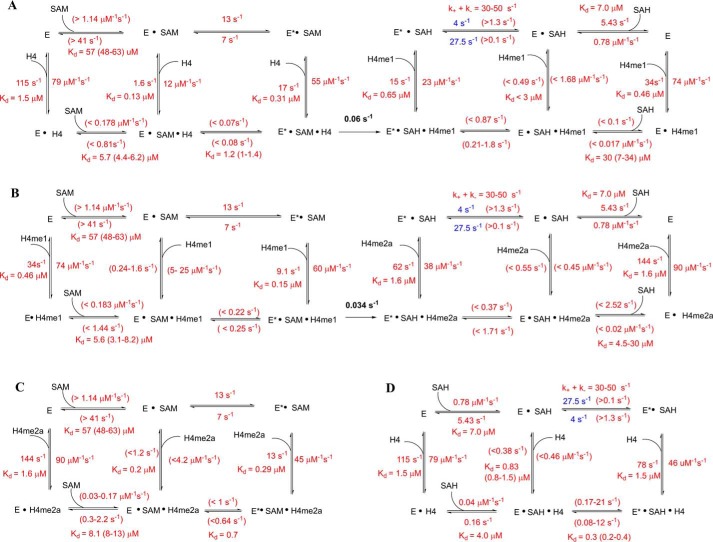
Proposed detailed kinetic model of overall process for the PRMT1-catalyzed H4 peptide methylation. A, first methylation event. B, second methylation event. C and D, formation of dead-end complex. Specific values are given for the rate constants that are well constrained. In the cases where rate constants are not constrained, the boundaries are shown. Blue-colored values are the best fitted results from the global simulation (but not constrained). The rate constants of the chemical reaction were determined in our previous work (33).
Histone Peptides Bind to the Two Binding Sites of the PRMT1 Dimer with Differential Affinities
To investigate the binding between PRMT1 and histone H4 peptides, the fluorescence signal time course was recorded following rapid mixing with different concentrations of un-, mono-, and dimethylated histone H4(1–22) peptides, with H4 standing for acetyl-SGRGKGGKGLGKGGAKRHRKVL, H4me1 for acetyl-SGRme1GKGGKGLGKGGAKRHRKVL, and H4me2a for acetyl-SGRme2aGKGGKGLGKGGAKRHRKVL, where bold letters indicate the methylation site for PRMT1. The histone peptides are symbolized by “H” for brevity in our modeling analysis (Fig. 4C).
FIGURE 4.
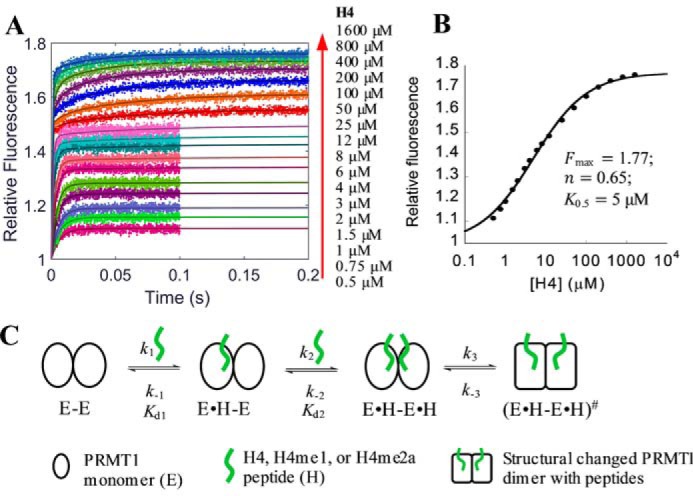
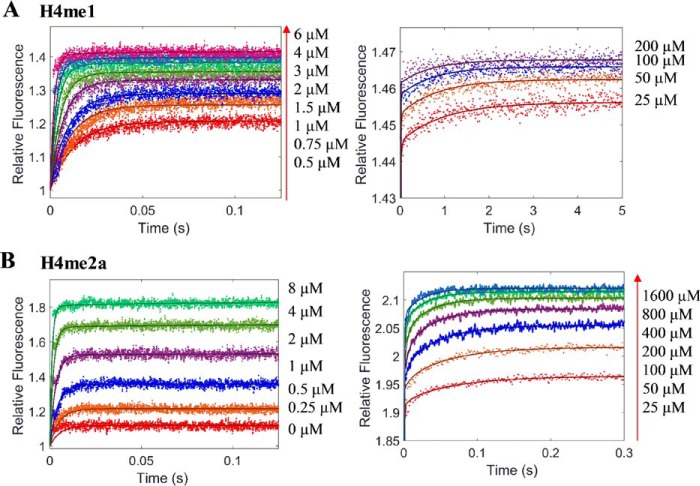
Formation of PRMT1-H4 complex. A, stopped-flow fluorescence data with fitting curves (solid lines) generated from global simulation based on the model shown in C. The fluorescence was acquired for 0.1 s for 0.5–12 μm peptide and 0.2 s for 25–1600 μm peptide. The fluorescence intensity of each signal trace was normalized with that of apo-PRMT1 as 1. B, plot of the steady-state fluorescence intensity in A versus peptide concentration, from which the maximum fluorescence intensity Fmax, the Hill coefficient n, and the concentration producing 50% occupancy of binding sites K0.5 were determined with Equation 10. C, proposed model of peptide binding with PRMT1.
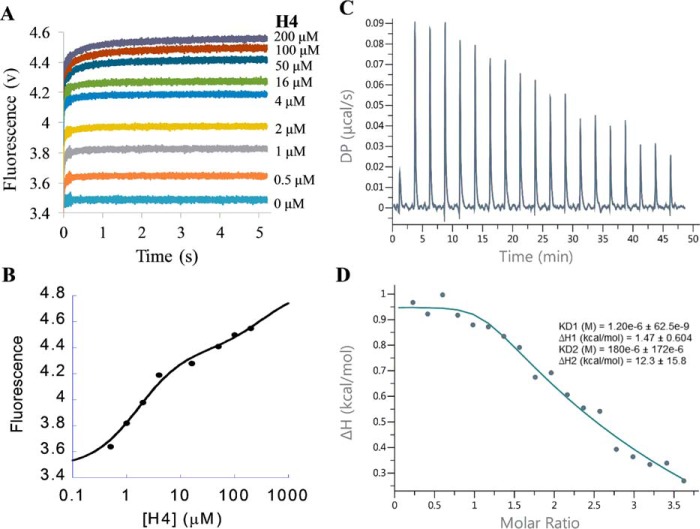
The time-dependent fluorescence change of PRMT1 binding with the unmethylated peptide H4 is shown in Fig. 4A; the tryptophan fluorescence signals increased as a function of time (i.e. transient kinetics) and reached a steady-state plateau at varied time points. Unlike the standard binding isotherms of SAM and SAH (Fig. 3, E and F), however, the steady-state fluorescence from 10 to 90% saturation spans more than 3 orders of magnitude (0.5–1600 μm, Fig. 4B) and the Hill coefficient is smaller than 1 (n = 0.65, calculated with Equation 10), indicating that possible negative cooperativity exists in the peptide binding process (37). In another word, the binding of one peptide on one site of PRMT1 dimer causes lower affinity of the peptide on another binding site. Accordingly, the stopped-flow fluorescence time course displayed distinct phases; the fluorescence data points in the lower concentration range (e.g. 0.5 to 4 μm) reached the plateau in less than 20 ms, whereas the equilibrium in the higher concentration range (e.g. 25 to 1600 μm) was not achieved until 100 ms.
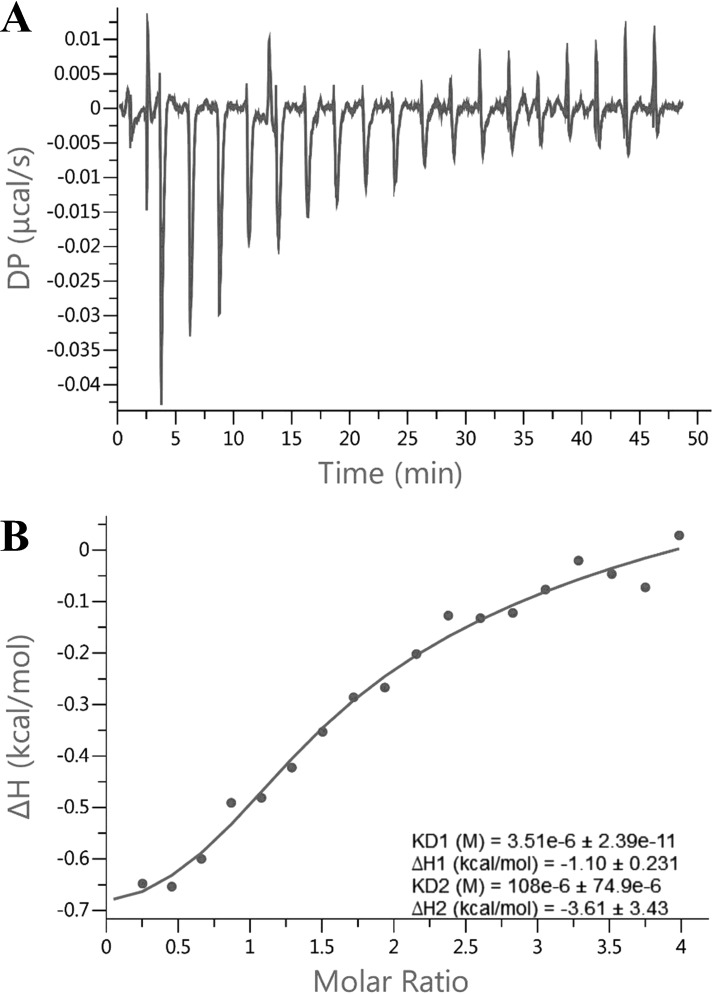
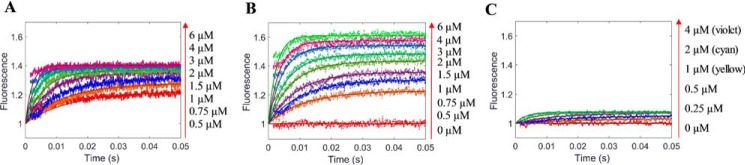
The transient fluorescence data points in the range of 0.5 to 4 μm H4 peptide were well fitted with a single exponential from which the yielded kobs was linear to concentration (Equation 4), indicative of a one-step event for the first binding site (34). On the other hand, the data from 25 to 1600 μm were better fitted with a double exponential rather than a single exponential, suggesting that there might be an additional conformational adjustment following the second peptide binding. Overall, a three-step sequential binding model (Fig. 4C) was appropriate for global simulation analysis of this binding process. The calculation using KinTek Explorer yielded satisfying fitting results (solid lines in Fig. 4A). The k1 and k−1 values (Table 1) were 79 s−1μm−1 and 115 s−1, respectively, yielding a Kd1 around 1.5 μm. Regarding the second peptide binding, k2 (0.51 s−1μm−1) was 2 orders smaller than k1, whereas k−2 (84 s−1) was close to k−1. According to the FitSpace analysis, both k1 and k−1 were constrained within a small range (63 to 110 s−1μm−1 and 92 to 161 s−1, respectively). Although neither k2 nor k−2 was well constrained, the Kd2 varied within a small range (120 to 300 μm), which is about 80–200 times that of Kd1, justifying our proposed negatively cooperative two-site binding model for peptide. As for the putative conformational change following the second peptide binding, both the forward and reverse rate constants (k3 and k−3) of H4 peptide were rather slow (0.25 and 0.5 s−1, respectively). To corroborate the negative cooperativity, we also performed isothermal titration calorimetry (ITC) for the PRMT1-H4 binding (Fig. 5). Fitting the data with the sequential binding model yielded Kd1 = 3.5 μm and Kd2 = 108 μm, values comparable to those from the stopped-flow assay, supporting the hypothesis for negative cooperativity.
TABLE 1.
Kinetic parameters of binary binding between wild type PRMT1 and different H4 peptides
These parameters were yielded from a global simulation of the stopped-flow kinetics based on the model shown in Fig. 4C. NC, not constrained.
| Peptide | k1 (range) | k1 (range) | Kd1 | k2 (range) | k−2 (range) | Kd2 (range) |
|---|---|---|---|---|---|---|
| s−1·μm−1 | s−1 | μm | s−1·μm−1 | s−1 | μm | |
| H4 | 79 (63–110) | 115 (92–161) | 1.46 | 0.51 (0.21–18) | 84 (>18) | 164 (120–300) |
| H4me1 | 74 (65–159) | 34 (18–41) | 0.46 | 0.77 (>0.01) | 25 (NC) | 32 (NC) |
| H4me2a | 90 (78–107) | 144 (125–172) | 1.6 | 0.41 (0.21–1) | 76 (16–377) | 185 (160–230) |
FIGURE 5.
ITC titration curves (A) and binding isotherm (B) of PRMT1 binding with H4 peptide. This sample cell contains a 22 μm PRMT1 dimer. The titration syringe contains 450 μm H4 peptide. The binding isotherm was fitted with the sequential binding model.
The stopped-flow fluorescence kinetics of the other two peptides, H4me1 and H4me2a, binding to PRMT1 were very similar to that of the H4 peptide (Fig. 6). Global simulation was performed using the same three-step binding model to calculate the rate constants of the individual kinetic steps (data summarized in Table 1). It is worth noting that Kd1 of H4me1 (0.46 μm) is moderately smaller than that of the H4 and H4me2a peptides (1.5 and 1.6 μm, respectively), which suggests that the binding of the monomethylated intermediate with PRMT1 is slightly tighter. This agrees well with the previous studies showing that monomethylated peptides are moderately better substrates than unmethylated peptides for PRMT1 (24, 33).
FIGURE 6.
Global simulation for the stopped-flow fluorescence of PRMT1 binding with varied concentrations of peptides. Dots represent stopped-flow fluorescence data of PRMT1 binding with varied concentrations of H4me1 (A) and H4me2a (B). The total concentration of PRMT1 in the final solution is 0.4 μm. The solid line (in A and B) is the fitted curve from a global simulation based on the model shown in Fig. 4C.
The Detected Fluorescence Change in the Stopped-flow Kinetics Reflects the Alteration of the Microenvironment around the Active Site
There are five tryptophan residues in PRMT1 (Fig. 2), three of which are distant from the active site: Trp-166 is located on the surface of the Rossmann fold, and Trp-197 and Trp-198 are located on the dimerization arm. In contrast, Trp-145 and Trp-294 are nearby the active site. Trp-145 is adjacent to the important catalytic residue Glu-144. Trp-294 is located on a conserved THW loop whereby His-293 is considered to form the active site (13). Additionally, the indole group of Trp-294 protrudes toward the guanidino group of the substrate arginine (Fig. 2). These pieces of structural information thus suggest that fluorescence of Trp-145 and/or Trp-294 could be appreciably influenced by cofactor and substrate binding. To test our hypothesis, we mutated these two residues with site-directed mutagenesis to Ala or Phe (W145F, W294F, and W294A). The radiometric assays showed that the enzymatic activity of PRMT1 was barely affected by W145F and only moderately reduced by the W294A mutation (Fig. 7A). In contrast, the W294F mutation completely abolished the enzymatic activity; the underlying reason for this is not yet clear. However, according to the PRMT1 crystal structure (Protein Data Bank ID: 1OR8), one hypothesis could be that, because the nitrogen in the side chain of Trp-294 forms an H-bond with the backbone of substrate arginine, replacing this Trp with Phe will not only break the H-bond but also generate steric hindrance for proper positioning of the substrate arginine. Mutants W145F and W294A were subjected to the stopped-flow fluorescence measurement of PRMT1 binding with SAH or H4me1 peptide. As shown in Table 2, neither of these mutations changed the k1app and k−1app values significantly as compared with wtPRMT1, suggesting that the binding capacity was retained. As shown in Fig. 7 and Table 2, upon binding with SAH, the fluorescence decrease of PRMT1-W145F was 2-fold that of wtPRMT1 (26 versus 13%); most drastically, PRMT1-W294A showed little fluorescence change upon binding with SAH (Fig. 7, B–D). The same trend was observed for binding with the H4me1 peptide; the fluorescence increased by 69, 42, and 8% for W145F, wtPRMT1, and W294A, respectively (Fig. 8 and Table 2). Therefore, these results validated our hypothesis that both Trp-145 (minor) and Trp-294 (major) are responsible for the fluorescence changes upon binding with the cofactor and substrate, supporting that the fluorescent signal is a direct indicator for the microenvironment around the active site.
FIGURE 7.
Study of fluorescence contribution of tryptophan. A, relative enzymatic activity of wt and mutant PRMT1 (W145F, W294F, and W294A). B–D, stopped-flow fluorescence of 0.4 μm wtPRMT1 (B), mutant W145F (C), and W294A (D) binding with varied concentrations of SAH. The relative fluorescence is shown with the unbound enzyme normalized to unity. Solid lines are the fitted curves from a global simulation using the one-step binding model (E + L ↔ EL).
TABLE 2.
Parameters of binary binding between enzyme (E) and ligand (L, including SAH or H4me1 peptide)
k1app, k−1app, Kd1app, and fluorescence change were yielded from a global simulation of each set of signal traces using the one-step model (E + L ↔ EL) with KinTek software.
| E | L | k1app (range) | k−1app (range) | Kd1app | Fluorescence change |
|---|---|---|---|---|---|
| s−1μm−1 | s−1 | μm | % | ||
| wt | SAH | 0.68 (0.64–0.72) | 0.33 (0.29–0.37) | 0.49 | −13 |
| W145F | SAH | 0.39 (0.3–0.39) | 0.38 (0.35–0.38) | 0.97 | −26 |
| W294A | SAH | 0.58 (0.46–0.73) | 0.29 (0.23–0.38) | 0.5 | −3 |
| wt | H4me1 | 79 (63–99) | 19 (16–22) | 0.24 | 42 |
| W145F | H4me1 | 60 (57–62) | 44 (38–50) | 0.73 | 69 |
| W294A | H4me1 | 74 (55–103) | 3.9 (1.0–7.9) | 0.05 | 8 |
FIGURE 8.
Stopped-flow fluorescence of wtPRMT1 (A), W145F mutant (B), and W294A mutant (C) binding with varied concentrations of H4me1. Dots are the fluorescence signal. The total concentration of wt or mutant PRMT1 in the final solution is 0.4 μm. Solid lines are the fitted curves from a global simulation using the one-step binding model (E + L ↔ EL).
The Transient Kinetics of the Formation of the PRMT1-SAH-Peptide Ternary Complex
We next studied the stopped-flow kinetics of the formation of the PRMT1-SAH-peptide ternary complex. To determine the impact of SAH on peptide binding and vice versa the effect of peptide on SAH binding, the kinetic assays were carried out in two separate formats. In the assay format (E+C)+H, PRMT1 was preincubated with SAH before its rapid mixing with the peptide in the stopped-flow instrument. In the other assay format, (E+H)+C, PRMT1 was preincubated with the peptide prior to its subsequent mixing with SAH. In both assay formats, it was the second mixing that triggered the stopped-flow fluorescence detection.
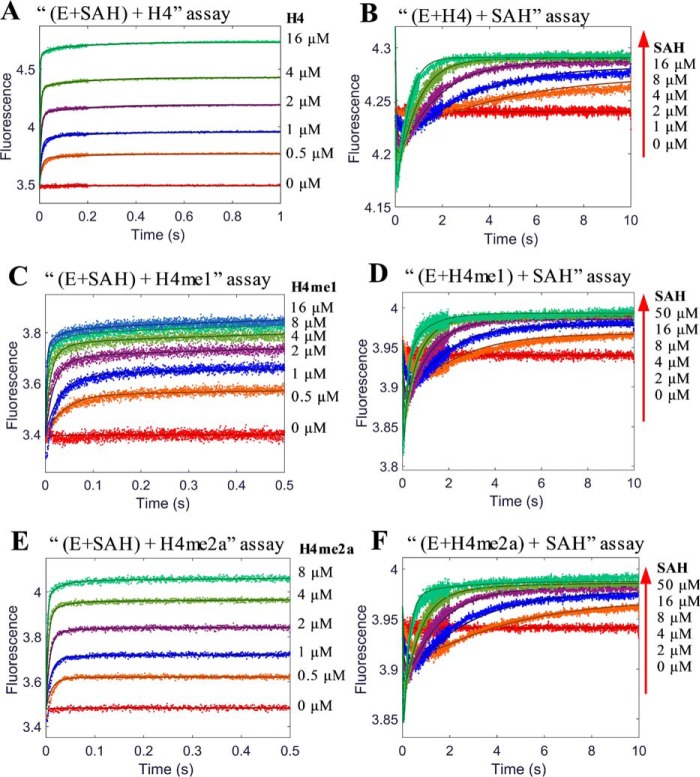
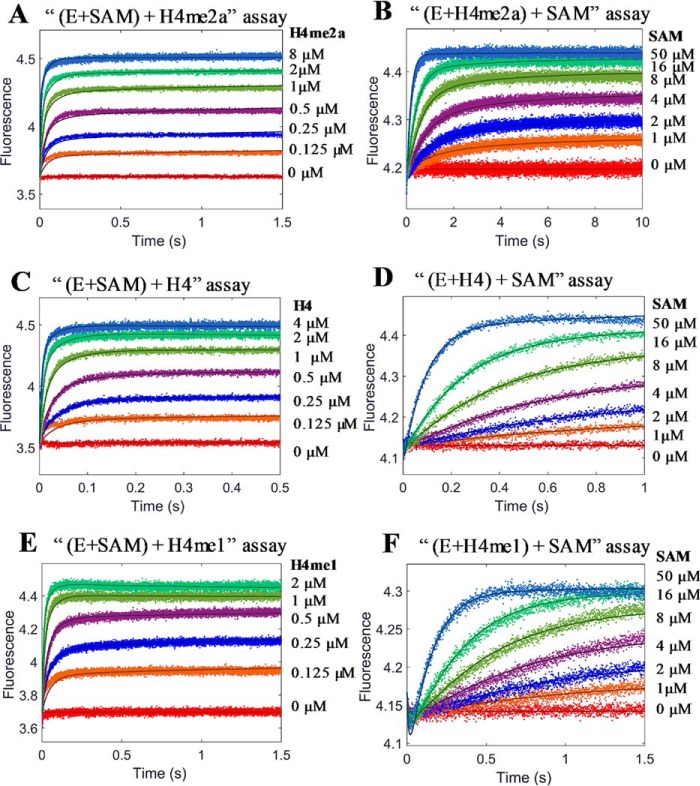
Kinetic experiments were conducted to study the formation of three ternary complexes: PRMT1-SAH-H4, PRMT1-SAH-H4me1, and PRMT1-SAH-H4me2a. As an illustrative example, we describe here the details of the formation of PRMT1-SAH-H4 complex. Similar to the binary PRMT1-H4 binding, both the transient and end-point fluorescence of the (E+C)+H assay showed a biphasic pattern (Fig. 9, A and B). In addition, the ITC data could be well fitted with the sequential binding model (Fig. 9, C and D, Kd1 1.2 μm and Kd2 180 μm). All of these results further supported the hypothesis that PRMT1 dimer has differential affinities sites for the peptide binding. To avoid excessive complexity at high peptide concentrations, we set H4 peptide concentrations in the range of 0.5 to 16 μm in the (E+C)+H assay and 10 μm in the (E+H)+C assay. At this concentration range, at most one peptide molecule binds to the PRMT1 dimeric unit, and the amount of the 2:1 peptide/dimer stoichiometric complex is negligible as calculated from our simulation (data not shown) based on the rate constants yielded from the PRMT1-peptide binary binding. The stopped-flow fluorescence kinetic courses of the formation of the PRMT1-SAH-H4 complex in the two different assay formats are shown in Fig. 11, A and B.
FIGURE 9.
Measurement of the binding of PRMT1-SAH mixture with H4 peptide. A, stopped-flow fluorescence of (E+C)+H assay of the PRMT1-SAH-H4 ternary complex formation. The total concentrations of PRMT1 and SAH in the final solution are 0.4 and 50 μm, respectively. According to the data from 0.5–4 μm H4, the signals increased fast and leveled up at 0.2 s. According to the data from 50–200 μm, there was another slow increase occurring at 0.2–5 s, probably caused by the second peptide binding with the dimer of the PRMT1-SAH complex. B, plot of the steady-state fluorescence intensity in A versus peptide concentration. The data show the biphasic pattern. C and D, ITC titration curve (C) and binding isotherm (D) of the PRMT1-SAH mixture (24.2 μm for PRMT1 dimer and 200 μm for SAH, in cell) binding with the H4-SAH mixture (450 μm for H4 peptide and 200 μm for SAH, in syringe). The data were fitted with the sequential binding model.
FIGURE 11.
Global simulation for the stopped-flow fluorescence for formation of PRMT1-SAH-H4 (A and B), PRMT1-SAH-H4me1 (C and D), and PRMT1-SAH-H4me2a (E and F) ternary complexes. The final concentrations are 0.4 μm for PRMT1, 50 μm for SAH (in A, C, and E), 10 μm for H4 and H4me2a (in B and F), and 1.5 μm for H4me1 (D). Solid lines are the fitted curves from a global simulation based on the model shown in Fig. 10.
In the (E+ SAH)+H4 assay (Fig. 11A), the fluorescence increases after the PRMT1-SAH solution is mixed with H4. Although the data points at 0.5–2 μm could be fitted to a double exponential, the data at 4–16 μm were better fitted to a triple exponential. The kinetics of the (E+H4)+SAH binding (Fig. 11B) exhibited an obvious biphasic pattern (i.e. the fluorescence first decreased and then increased), but the plots of Kobsfast and Kobsslow against SAH concentration could be fitted to any common mathematical model. Therefore, the mechanism involved is too complex to be fitted by the conventional approach. We then applied the global simulation to dissect the transient kinetics of the PRMT1-SAH-H4 complex formation. After several trial rounds, we found that the model shown in Fig. 10 was most appropriate for global fitting because it comprised of all the possible complex species and interconversions involved in this ternary system. Because there is at most one peptide binding to the dimer unit in the experimental condition, we denote E as the monomer subunit involving peptide binding and F as the peptide-free monomer subunit in Fig. 10. In the computer-aided simulation, the rate constants determined previously for binary binding (i.e. in Fig. 10, k1, k−1, k2, k−2, k6, and k−6) were fixed, whereas the others involved in ternary complex formation (i.e. k3, k-3, k4, k−4, k5, k−5, k7, and k−7) were allowed to float and were determined from the global fitting. According to the FitSpace analysis, k3, k−3, k7, and k−7 were well constrained, whereas only the boundaries were given for the other rate constants. The results obtained for the rate constants are listed in Scheme 1D.
FIGURE 10.
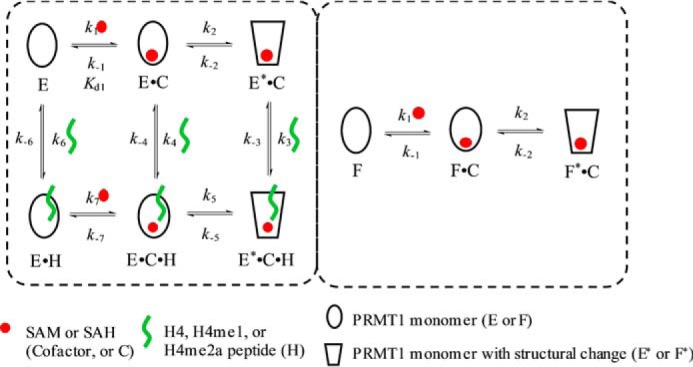
Model used in the simulation for (E+H)+C and (E+C)+H assays. Under the assay conditions, the peptide concentration is low so that only one monomer is able to be bound by peptide, whereas the other is always peptide-free. To differentiate the two monomers, we refer to the one that can bind with peptide as E and the peptide-free one as F. In the (E+H)+C assay, after PRMT1 is preincubated with peptide, the monomer species in solution is E, E·H, and F; that is, the dimer species is E-F and E·H-F. In the (E+C)+H assay, after PRMT1 is presaturated with cofactor, the monomer species in solution is E·C, E*·C, F·C, and F*·C, and the dimer species is four combinations of two monomers: E·C-F·C, E·C-F*·C, E*·C-F·C, and E*·C-F*·C.
An examination of the rate constants showed that the kinetics of SAH binding to the E·H4 complex as determined in the (E+H)+C experiment was remarkably slower, with association and dissociation rate constants of 0.04 s−1μm−1 and 0.16 s−1, respectively, in comparison with the peptide binding to the apo-form E (association and dissociation rate constants of 0.78 s−1μm−1 and 5.43 s−1, respectively) (Scheme 1D). This suggests that a large kinetic hindrance exists for SAH to approach the E·H complex and also for SAH to release from the complex. On the other hand, the results from the (E+C)+H assay showed that, in comparison with the binding with the apo-form E (association and dissociation rate constants 79 s−1μm−1 and 115 s−1, respectively), the association and dissociation rate constants of H4 peptide with the E*·SAH complex were approximately on the same level (46 s−1μm−1 and 78 s−1, respectively).
The kinetics of the formation of the PRMT1-SAH-H4me1 (Fig. 11, C and D) and PRMT1-SAH-H4me2 complexes (Fig. 11, E and F) were very similar to the patterns of the PRMT1-SAH-H4 formation. All of these transient kinetic data were well fitted to the model shown in Fig. 10 in the global simulation, which in turn demonstrated the validity of the proposed model. All of the calculated rate constants are summarized in Scheme 1.
The Transient Kinetics of the Formation of the PRMT1-SAM-Peptide Complex
Transient kinetic assays were also performed for the formation of the PRMT1-SAM-peptide complex. This was particularly important because SAM is the active cosubstrate that supplies methyl groups for substrate methylation. Because the formation of the PRMT1-SAM-H4me2a complex is not followed by methyl transfer, which means that this is a dead-end complex, the progression data were recorded until a plateau (namely, the steady state) was reached (Fig. 12, A and B). For the binding of PRMT1-SAM with the H4 (Fig. 12, C and D) or H4me1 peptide (Fig. 12, E and F), data points were only collected and analyzed in the first 2 s considering the half-time (t½) values for the chemical turnover were 12 and 20 s (calculated based on Equation 8 using kchem of 0.06 and 0.034 s−1, respectively (Scheme 1)). In this time range, the chemical reaction can be neglected. Again, the kinetic model of Fig. 10 was applied for the global data simulation of the kinetic data.
FIGURE 12.
Global simulation for stopped-flow fluorescence for the formation of PRMT1-SAM-H4me2a (A and B), PRMT1-SAM-H4 (C and D), and PRMT1-SAM-H4me1 (E and F) ternary complexes. The final concentrations are 0.4 μm for PRMT1, 400 μm for SAM in (A, C, and E), 10 μm for H4 and H4me2a in (B and D), and 1.5 μm for H4me1 (F). Solid lines are the fitted curves from a global simulation based on the model shown in Fig. 10.
The calculated rate constants are summarized in Scheme 1. Basically, the effect of SAM on peptide binding to PRMT1 and vice versa the effect of peptide on SAM binding to PRMT1 is quite similar to the relationship between SAH and peptide. As determined from the (E+H)+C experiment, the association rate constants of SAM interacting with E·H4 (<0.18 s−1μm−1) were about 10-fold slower than binding to E (>1.14 s−1μm−1). Again, this suggests that prebinding of H4 to PRMT1 likely creates a kinetic hindrance for cofactor binding. On the other hand, the (E+C)+H assay results showed that the binding rate constant of the H4 peptide with E*·SAM (55 s−1μm−1) was quite close to its binding with the apo-E form (79 s−1μm−1). Interestingly, the dissociation rate constant of the H4 peptide from E*·SAM·H4 (17 s−1) was 7-fold slower than from E·H4 (115 s−1). The net effect is that the binding affinity of the H4 peptide with E*·SAM is 5-fold stronger than with E (Kd 0.31 versus 1.5 μm). Therefore, prebinding with SAM produces a positive enhancement for H4 binding.
An interesting observation is that the dissociation rate of E·H4 (i.e. 115 s−1) is particularly fast in comparison with the rate constants of the other elementary steps shown in Scheme 1A. In contrast, the rate constant for the conversion of E·H4 + SAM → E·SAM·H4 is very small (<0.178 s−1μm−1). Therefore, the fate of the E·H4 complex likely follows the pathway of dissociation (namely, E·H4 → E + H4) rather than a direct formation of the ternary complex E·H4 + SAM → E·SAM·H4. Another noticeable observation is that the conformational transition E·SAM·H4 ↔ E*·SAM·H4 was extremely slow (k5 < 0.07 s−1 and k−5 < 0.08 s−1) compared with all the other kinetic equilibrium steps. This suggests that the ground state E·SAM·H4 species is catalytically incompetent and is prone to dissociation with release of H4. The kinetic evidence suggests that the excited state complex E*·SAM·H4 is predominantly formed via the route of E*·SAM + H4 ↔ E*·SAM·H4.
The kinetics of forming the PRMT1-SAM-H4me1 and PRMT1-SAM-H4me2a complexes were very similar to the patterns observed in PRMT1-SAM-H4 formation. The transient kinetic data were well fitted to the model of Fig. 10 using global simulation. The calculated rate constants are summarized in Scheme 1B and Scheme 1C.
Discussion
The Complete Kinetic Model of H4 Peptide Methylation Suggests PRMT1 Catalysis Follows a Random Binary and Ordered Ternary Mechanism
By definition, an ordered binding mechanism requires the compulsory formation of the PRMT1·SAM complex before peptide substrate binds (38). This mechanism has been found to exist in some PRMT inhibitors that occupy the substrate binding site (39, 40). However, the existing data clearly show that peptide substrates bind well to PRMT1 in the absence of cofactor, which is similar to the fact the cofactor binds well to PRMT independently of the presence of substrate (24, 33). This independent binding phenomenon is consistent with the rapid equilibrium random kinetic mechanism that was proposed previously for PRMTs based on product/analog inhibition patterns (21–23, 41). However, although both the cofactor and peptide substrate bind to PRMT1 to form a binary complex in a random and independent manner, our transient kinetic results show that prebinding with either the cofactor or substrate have drastic and different effects on the downstream steps toward ternary complex formation.
The complexity is illustrated below using the formation of E·SAM·H4 as an example (Scheme 1A). The binary binding processes, E + SAM ↔ E·SAM and E + H4 ↔ E·H4, occur randomly and independently. However, for the two paths to form the ternary complex E·SAM + H4 ↔ E·SAM·H4 and E·H4 + SAM ↔ E·SAM·H4, the former is the preferred and the latter is disfavored. This is not only because the E·H4 complex has a slow rate constant of association with SAM to form the ternary complex E·SAM·H4 (0.178 s−1μm−1) but also because E·H4 has a high dissociation rate constant (115 s−1). Therefore, the E·H4 complex is more prone to breaking down into the free enzyme form rather than associating directly with SAM to form the ternary complex. Another important feature in the kinetic scheme of PRMT1 catalysis is that there are two kinds of ternary complexes, E·SAM·H4 and E*·SAM·H4, with the latter being the catalytically active intermediate (presumably this complex has a structure resembling the transition state of arginine methylation). Uniquely, the mutual interconversion between E·SAM·H4 and E*·SAM·H4 are exceedingly slow (forward rate constant < 0.07 s−1 and inverse rate constant < 0.08 s−1). Therefore, E·SAM·H4 is prone to revert to the more efficient pathway, E·SAM·H4 ↔ E·SAM ↔ E*·SAM ↔ E*·SAM·H4, instead of undergoing the direct conversion of E·SAM·H4 ↔ E*·SAM·H4 as long as there is a sufficient amount of E·SAM and E*·SAM in the equilibrium system. This kinetic feature suggests that to form the active ternary complex E*·SAM·H4 primed for methyl transfer, PRMT1 would prefer to bind first with SAM and then with the peptide substrate. Taken together, PRMT1 can bind with the cofactor and peptide substrate randomly, but the catalytic complex E*·SAM·H4 is formed via a kinetically ordered pathway. We term this type of kinetics a “random binary and ordered ternary” mechanism. Nonetheless, because the intracellular context is quite complicated, the predominant pathway could be influenced by many factors, such as the concentrations of enzyme, SAM, and available histone H4 protein, as well as the concentration of other nonhistone PRMT1 substrates under specific physiological condition. Besides, different regulatory proteins might also alter the pathway of PRMT1-mediated methylation.
It is worth noting that when using the steady-state kinetic methods based on product/analog inhibition patterns, it is very difficult, if not impossible, to distinguish this random binary and ordered ternary sequential mechanism from the classic random sequential mechanism. This might explain why some previous steady-state studies report that PRMT catalysis follows the classic random sequential mechanism (21–23).
The breakdown of the E*·SAH·H4me1 complex can undergo either the path of releasing the peptide (E*·SAH·H4me1 → E*·SAH) or the path of undergoing a conformational change (E*·SAH·H4me1 → E·SAH·H4me1). Because the former step is much faster (15 s−1) than the latter (<0.87 s−1), it is quite clear that the breakdown of the E*·SAH·H4me1 complex to free E follows an ordered pathway in which the release of peptide occurs fast and first and is then followed by the dissociation of SAH.
Arginine Methylation Occurs in a Fully Distributive Manner
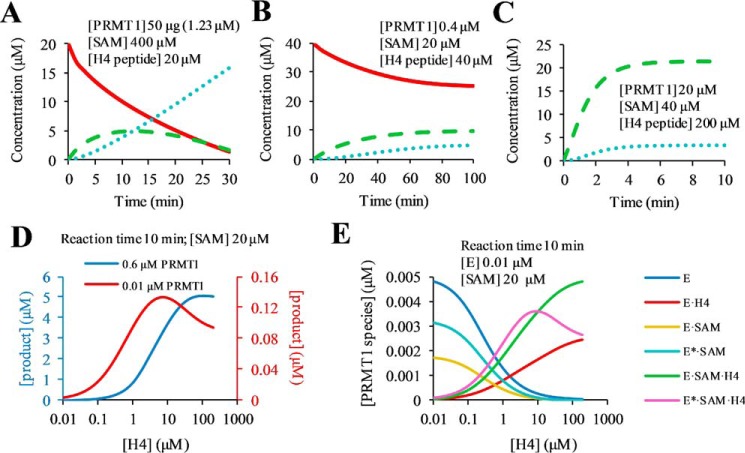
Mechanistically, highly processive methylation (42) would require dissociation of the intermediate product (i.e. the monomethylated substrate) to be much slower than the forward chemistry step, so that the methyltransferase could consecutively carry out two or multiple rounds of turnovers without releasing the substrate into the bulk solution. Processivity can be described quantitatively in terms of processivity probability, which is defined as the value of the methyl transfer rate divided by the substrate dissociation rate (Equation 12) (43). Our kinetic model and the dissected kinetic rate constants allow for a rigorous quantitation of the processivity of PRMT1 catalysis. The dissociation rate constant of H4me1 from the E*·SAM·H4me1 complex is 9.1 s−1, and the forward methyl transfer reaction rate constant is 0.034 s−1 (Scheme 1B), so the calculated processivity probability is 0.4%. This means that only 0.4% of the catalytic complex is destined to methyl transfer, whereas 99.6% undergoes quick dissociation to release the peptide into bulk solution. Thus, the methylation is a fully distributive process. The distributive propensity is ascribed to the fast substrate dissociation rate and relatively slow chemistry rate, such that the active site of PRMT1 is unable to keep the substrate in the active site for two consecutive turnovers. This conclusion is consistent with the findings from many groups showing that different PRMT members follow a distributive methylation mechanism for di- and multi-methylations (25). Although some previous reports have suggested a semiprocessive mechanism for PRMT1-catalyzed methylation of H4 and eIF4A1 peptides (24, 32), those studies were based on the quantitation of the amounts of mono- and dimethylated products over the reaction time using a MALDI-MS quantitation, which lacks strict accuracy. More importantly, it is very difficult to determine precisely whether an enzyme is processive or distributive by simply examining the proportions of un-, mono-, and dimethylated substrates over a given reaction time. In this regard, our kinetic model can be applied to simulate the time course of product formation. We predicted three progress curves of H4 methylation at different concentrations of PRMT1, SAM, and the H4 substrate. In the case of high [SAM] (400 μm) and low [H4] (20 μm), H4me1 formation and decay are steady, which may make the shape of the time course data curve look like a feature of semi-processivity (Fig. 13A; see the definition of “semi-processive” in Ref. 32). In the case of [SAM] (20 μm) lower than [H4] (40 μm), the formation of H4me1 is dominant (Figs. 13B and 8C), which is consistent with the complete distributive manner (25). Of note is that in the case where [H4] is in large excess (200 μm) to [H4me1] (20 μm), there is still a detectable amount of H4me2a generated (Fig. 13C). Overall, the shape of the time course data curve of substrate consumption, intermediate formation and decay, and final product formation can be greatly influenced by the experimental conditions, especially by the concentrations of enzyme, cofactor, and substrate. A rigorous determination of enzyme processivity would have to be based on a specific enzyme mechanism and the magnitude of substrate release rate with respect to chemical turnover rate.
FIGURE 13.
Simulations of the methylation time course and steady-state kinetics. A–C, time-dependent concentration changes of H4 (red solid line), H4me1 (green dashed line), and H4me2a (blue dotted line) peptide are shown. The concentrations of PRMT1, SAM, and H4 peptide are set the same as in Ref. 32 for A, as in Ref. 25 for B, and as in Ref. 24 for C. D, simulation of steady-state product curves under 0.01 (red) and 0.6 (blue) μm PRMT1. E, generation of PRMT1 (E) species under 0.01–200 μm H4 peptide.
The conclusion reached on distributive arginine methylation is in accord with the observed high abundance of MMA level in cells (44, 45). The implication of distributive methylation suggests that MMA generation and ADMA generation are two independent, uncoupled biochemical processes. So far it is unknown whether there is any significant mechanism that regulates the substrate specificity of a particular PRMT enzyme for selecting unmethylated arginine residues versus monomethylated arginine residues. We want to emphasize that the idea that PRMT1 utilizes a distributive mechanism does not contradict the experimental observation that ADMA is more abundant than MMA in certain substrates and in certain cell contexts. First, any enzyme-catalyzed chemical reaction, including arginine methylation, is a time-dependent process. If given sufficient time, substrate arginine residues will ultimately be completely dimethylated regardless of the processive or distributive mechanism. Second, we and others have found that monomethyl arginine is a moderately better substrate than arginine (24, 33). Therefore, at equivalent concentration levels, monomethylated arginines can competently compete against unmethylated arginines for methylation. Third, PRMTs and their substrates may be confined within subcellular locations or organelles. The confinement could lead to a rapid increase in the local concentration of monomethylated PRMT substrates, which speed up the conversion of MMA to ADMA. Fourth, the protein-protein interaction may introduce additional and enhanced binding of monomethylated substrates to PRMT leading to intermediate product enrichment around the active site, a condition that favors efficient transition of MMA to ADMA.
Structural Explanation of the Enzyme Conformational Change and the Negative Cooperativity of Peptide Binding with the PRMT1 Dimer
According to our transient kinetics study, a conformational change E·C ↔ E*·C exists following the initial collision between SAM (or SAH) and PRMT1. Even though the αX helix is missing in the co-crystal structure of the PRMT1-SAH complex (16), the crystal structure of CARM1 has shown that upon the binding of SAH, αX helix undergoes a disordered-to-ordered transition and fully cages SAH in the binding site (18, 19). Such structural information suggests that the conformational change step detected in this study is likely caused by the open-to-closed transition gated by the αX helix (Fig. 14). However, the time scale is at the millisecond level (13 s−1 and 7 s−1 for forward and reverse rate constants, respectively), corresponding to ligand-enzyme molecular recognition (46). Therefore, we could not rule out the possibility of other secondary or overall structural adjustments occurring simultaneously in addition to the N-terminal structural transition observed in structures of CARM1 (18, 19) or PRMT8 (47). In the open state, the protruding α-helix could probably generate steric hindrance, thus making the substrate binding site less accessible to the peptide and also harder to escape from after binding, which might explain why E·C binds the peptide with smaller association and dissociation rate constants than E*·C does. Notably, the conformational change of E·C·H ↔ E*·C·H is extremely slow, indicating that the conversion is hindered by the bound peptide. The reason for this slowed open-to-closed conversion is not clear at this time. It could be caused by the difficult positioning of the αX helix due to the crowded microenvironment around the active site. As to the hampered reverse direction (E*·C·H → E·C·H), a plausible explanation is that the extensive interactions between the substrate peptide and the αX/αY helices as seen in several PRMT-cofactor-peptide complexes (39, 48–50) likely impedes the flip of the αX helix (Fig. 14).
FIGURE 14.
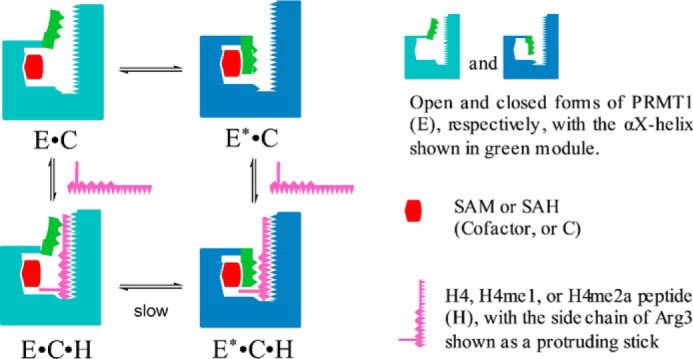
Structural model for the formation of the ternary complex. The conversion between the “closed” and “open” status of PRMT1 might be caused by the movement of the αX helix.
The homodimer is the basic functional architecture for all of the type I PRMTs. In principle, the dimer unit has the capacity to bind two molecules of SAM and two molecules of peptide substrate. In analyzing the transient kinetic data of cofactor and substrate binding with PRMT1, we did not see any hints that two SAM molecules bind to the PRMT1 dimer differentially. Therefore, we concluded that the two active sites of the PRMT1 dimeric unit bind SAM or SAH independently and with identical affinity. On the contrary, a careful analysis of the stopped-flow kinetics of peptide binding revealed a stoichiometry of differential binding; the first peptide molecule binds PRMT1 with a higher affinity and the second one with a much weaker affinity (e.g. Kd1H4 1.5 μm and Kd2H4 164 μm, respectively, Table 1). This indicates that the first peptide creates a negative cooperativity for the second substrate binding. In agreement with this finding, a recent study using native mass spectrometry shows the stoichiometry of PRMT6:SAH:H4(1–21) is 2:2:1 in the ternary complex (20). Also, in one CARM1 crystal structure (Protein Data Bank ID: 5DWQ) (48), only one peptide was found to bind in the dimer, albeit the crystallization was performed under a very high concentration of peptide (0.5–2 mm). The preference of the PRMT1 dimer for one substrate molecule binding rather than equivalent binding of two substrates suggests that it might be possible that only one monomer actively catalyzes arginine methylation at any given time. This half-site active mechanism is also reminiscent of the observation that worm or mouse PRMT7 has a pseudo-dimer structure but that only one catalytic site is active (51, 52).
Explanation for Substrate-induced Inhibition at High Concentrations
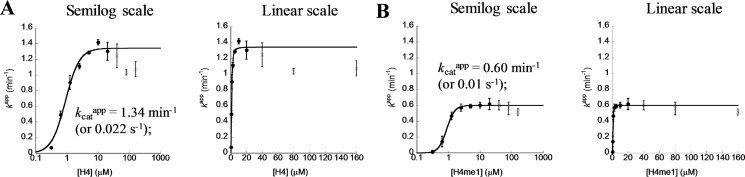
Our determination of the steady-state kinetics of H4 peptide methylation by PRMT1 (Fig. 15) showed that the catalytic rate is inhibited partially at high substrate concentrations. Similarly, Martin and co-workers (53) recently reported partial substrate inhibition PRMT1- and PRMT6-catalyzed arginine methylation. These authors (53) also found that partial substrate inhibition can be overcome by increased enzyme concentration. To understand the mechanism underlying the substrate inhibition in PRMT1 catalysis, we simulated the steady-state kinetics using our kinetic model. As shown in Fig. 13D (red), the amount of methylated product increases as a function of H4 concentration but slowly decreases at higher concentrations (>10 μm). Such a pattern of partial substrate inhibition is consistent with the experimental data (Fig. 15). Also, the simulation shows that a higher PRMT1 concentration (0.6 μm) overcame substrate inhibition (Fig. 13D, blue). A more detailed analysis of the distributions of the enzyme species shows that the rate reduction at high substrate concentrations is paralleled by increased proportions of E·H4 and E·SAM·H4 and a reduced proportion of the active complex, E*·SAM·H4 (Fig. 13E). As mentioned above, E, E·SAM, and E*·SAM are key enzyme species leading to the formation of E*·SAM·H4. A high peptide concentration (>10 μm) shifted the equilibrium toward the formation of E·H4 and E·SAM·H4, thus reducing the amount of E*·SAM·H4. Therefore, the substrate inhibition pattern observed in steady-state kinetics is caused by the intrinsic kinetic properties of the enzyme mechanism, namely the accumulation of large amounts of E·H4 and E·SAM·H4, which themselves are catalytically incompetent. Further, because reversible interconnectivity exists between different enzyme species even at high substrate concentrations, our kinetic model precisely predicts that the rate decrease at high concentrations of H4 is only a partial inhibition behavior instead of a complete inhibition.
FIGURE 15.
Steady-state kinetics under 0.3125–160 μm H4 peptide (A) and H4me1 peptide (B). The initial reaction velocity was averaged from quadruplicate experiments and plotted against peptide concentration. The data from peptide concentration 0.3125–10 μm (filled circles) were fitted by a Hill equation (Equation 11). kcatapp is calculated based on 0.01 μm PRMT1 presuming that only half of the dimer is active.
Taken together, using transient kinetics and global simulation, we brought about a complete kinetic model of PRMT1-catalyzed methylation with the individual elementary steps resolved. The model suggests that PRMT1 catalysis follows a catalytic schematic, what we termed a random binary and ordered ternary kinetic mechanism, in which PRMT1 randomly binds either the cofactor or the peptide to form a binary complex that is subsequently followed by a kinetically ordered pathway to form the catalytically competent E*·SAM·H4 ternary complex. The product release follows a sequential order: peptide is released first and SAH last. In addition, the finding that the dissociation rate constants of peptide are remarkably faster than the rate constants of the methyl transfer step provides strong evidence for a distributive mechanism of di- and multi-methylation events. Our model is also validated by predicting the theoretical progress of product formation and steady-state kinetics, which are consistent with the experimental data. Given the high structural conservation of all type I PRMTs (13, 14, 54, 55), the mechanism of PRMT1 catalysis disclosed herein could be extended to other PRMT members as a whole.
Experimental Procedures
Materials
Fmoc (N-(9-fluorenyl)methoxycarbonyl)-protected amino acids and resins were purchased from Novabiochem or ChemPep, and HCTU (2-(6-chloro-1H-benzotriazole-1-yl)-1,1,3,3-tetramethylaminium hexafluorophosphate) was purchased from ChemPep Inc. [3H]SAM (18 Ci/mmol, catalog No. NET155V001MC), [14C]SAM (56.3 mCi/mmol, catalog No. NEC363050UC), and streptavidin-coated polyvinyltoluene scintillation proximity assay (SPA) beads were purchased from PerkinElmer, Inc. Isopropyl β-d-1-thiogalactopyranoside was obtained from RPI Corp. Other chemical reagents were purchased from Fisher, Sigma, and VWR International.
Synthesis of Modified H4 Peptides
The N-terminal 22-residue peptide of histone H4 protein was termed the H4 peptide. The modified H4 peptide, in which R3 is monomethylated or asymmetrically dimethylated, was abbreviated as H4me1 or H4me2a, respectively. These peptides were synthesized using standard solid phase peptide synthesis protocols, purified on C-18 RP-HPLC, and confirmed with MALDI-MS as described elsewhere (33, 56, 57).
Mutagenesis, Expression, and Purification of PRMT1
His6-tagged human PRMT1 was subcloned into the pET-28b+ vector. Mutations of E153Q, W294F, W145F, and W294A were introduced into the pET28b-hPRMT1 plasmid by using the QuikChange® kit (Stratagene). The expression and purification of recombinant wild type or mutant His6-tagged hPRMT1 has been described in previous work (33, 58). Briefly, the pET28b-hPRMT1 plasmid was transformed into Escherichia coli BL21(DE3) cells (Stratagene). The transformed bacteria were incubated in LB medium at 37 °C for growth (until A595 = 0.6–0.8) and then at 16 °C for protein expression, which was induced by 0.3 mm isopropyl β-d-1-thiogalactopyranoside. Next, the bacteria were precipitated by centrifugation (3200 × g) and harvested with lysis buffer (25 mm Na-HEPES, pH 8.0, 150 mm NaCl, 1 mm PMSF, 1 mm MgSO4, 5% glycerol, and 5% ethylene glycol) followed by cell lysis in a cell disruptor. The supernatant from centrifugation (18,000 × g) containing PRMT1 protein was loaded onto the nickel-charged His6 tag binding resin (Novagen), which was equilibrated with column buffer (25 mm Na-HEPES, pH 7.0, 300 mm NaCl, 1 mm PMSF, and 30 mm imidazole). Beads were washed thoroughly with column buffer (10 column volumes, three times) followed by three washes in 10 column volumes of the washing buffer (25 mm Na-HEPES, pH 7.0, 300 mm NaCl, 1 mm PMSF, and 70 mm imidazole), and the protein was eluted with elution buffer (25 mm Na-HEPES, pH 7.0, 300 mm NaCl, 1 mm PMSF, 100 mm EDTA, and 200 mm imidazole). Different eluent fractions were checked by 12% SDS-PAGE. The fractions containing the target protein were pooled and dialyzed against dialysis buffer (25 mm Na-HEPES, pH 7.0, 500 mm NaCl, 10% glycerol, 1 mm EDTA, and 1 mm DTT). Protein concentration was determined by the Bradford assay.
Radiometric Methyltransferase Assay
Methylation assays of different H4 peptides were performed using 14C isotope-labeled SAM at 30 °C. The reaction buffer contained 50 mm HEPES, pH 8.0, 50 mm NaCl, 1 mm EDTA, and 0.5 mm DTT. Varied concentrations (0.3125 to 160 μm, 2-fold dilution) of H4 peptide substrate and a fixed concentration of [14C]SAM were preincubated in the reaction buffer for 5 min prior to the initiation of the methyl transfer reaction by PRMT1. The final concentrations of SAM and PRMT1 were 20 μm (>5 KmSAM) and 0.02 μm, respectively (The active enzyme concentration was considered to be 0.01 μm presuming that only one monomeric unit in the dimer was active). The reaction time was controlled under initial rate conditions such that typical reaction yields were less than 10%. The reaction was quenched by spotting the reaction mixture on P81 phosphocellulose square disks (catalog No. 20-134, EMD Millipore). The disks were air-died, washed three time with 50 mm NaHCO3 pH 9.0, oven-dried, and immersed in 5 ml of liquid scintillation mixture (Ultima Gold mixture, PerkinElmer). Scintillation counting was then performed to measure the amount of methylated products. Each experiment was repeated in quadruplicate.
A scintillation proximity assay was performed as described previously (59, 60). The final concentration of each ingredient in the reaction mixture was: 0.04 μm enzyme, 0.5 μm [3H]SAM, and 1 μm biotinylated H4(1–20). The reaction was initiated by the addition of enzyme into a mixture containing SAM and peptide and quenched by the addition of 0.5 m guanidinium chloride (final concentration in the reaction mixture). The reaction time was limited to 15 min to make sure the reaction occurred at the linear initial rate. Each experiment was repeated in duplicate.
Stopped-flow Fluorescence Measurements
The transient kinetics were studied through stopped-flow spectrometry (SX20, Applied Photophysics). The widths of the entrance and exit slits of the monochromator were set to 2 mm, corresponding to a 9.3-nm bandpass. An equal volume of samples from two syringes was driven into a 20-μl observation cell to mix at 22–23 °C, and 6–8 shots (drives) were taken for each concentration of the varied species. The buffer used in all of the experiments was the same as the reaction buffer. The time courses of PRMT1 tryptophan fluorescence change was recorded using an excitation wavelength of 295 nm and a wavelength cutoff emission filter ≥ 320 nm. For binary binding, 0.4 μm PRMT1 (final concentration) was mixed with an equal volume of serially concentrated SAM, SAH, or peptide solution (as shown in Figs. 3 and 4) in the observation cell.
In the ternary complex formation, double-mixing assays with different mixing orders were studied. One was denoted as the (E+C)+H assay, in which PRMT1 (E) was presaturated with SAM or SAH (cofactor, C) in the first mixing and then mixed with an equal volume at increasing concentrations of H4, H4me1, or H4me2a peptide (H). The concentrations were 0.4 μm for PRMT1, 50 μm for SAH, and 400 μm for SAM in the final solution. The final peptide concentrations are listed in Table 3. In the other assay, denoted as the (E+H)+C assay, the PRMT1 and peptide were mixed first, and then this solution was mixed with serial concentrations of cofactor. The final concentrations were 0.4 μm for PRMT1, and 10 μm, 1.5 μm, and 10 μm for the H4, H4me1, and H4me2a peptides, respectively. The final concentrations of SAH and SAM are listed in Table 4. In both assays, the time-dependent fluorescence signal changes were recorded for the second mixing.
TABLE 3.
Final concentrations of peptide in stopped-flow (E+C)+H assays
| Peptide | (E+SAH)+H assay | (E+SAM)+H assay |
|---|---|---|
| μm | μm | |
| H4 | 0.5, 1, 2, 4, 16 | 0.125, 0.25, 0.5, 1, 2, 4 |
| H4me1 | 0.5, 1, 2, 4, 8, 16 | 0.125, 0.25, 0.5, 1, 2 |
| H4me2a | 0.5, 1, 2, 4, 8, | 0.125, 0.25, 0.5, 1, 2, 8 |
TABLE 4.
Final concentrations of SAM or SAH in stopped-flow (E+H)+C assays
| SAH/SAM | (E+H4)+C assay | (E+H4me1)+C assay | (E+H4me2a)+C assay |
|---|---|---|---|
| μm | μm | μm | |
| SAH | 1, 2, 4, 8, 16 | 2, 4, 8, 16, 50 | 2, 4, 8, 16, 50 |
| SAM | 1, 2, 4, 8, 16, 50 | 1, 2, 4, 8, 16, 50 | 1, 2, 4, 8, 16, 50 |
Kinetic Data Analysis
In conventional fitting, averaged data of the same concentration from the stopped-flow assay were fitted with a single or double exponential function (Equation 1 or 2, respectively) or “single exponential + slope” function (Equation 3) using the in-built Pro-Data Viewer software of the SX20 stopped-flow apparatus, where F is the fluorescence intensity, A is the amplitude of the signal change, kobs is the observed rate constant, b is the rate for tryptophan fluorescence photobleaching, [L] is the concentration of various ligands (SAH, SAM, or peptide substrate), and ki and k−i are the association and dissociation rate constants, respectively, of step i. If the fluorescent signals were fitted with Equation 1, the kobs value was then plotted versus the concentration of the variable species and data were fitted by using Equation 4 (“one-step binding model”) or Equation 5 (“rapid-equilibrium two-step binding model”). If the signals were fitted with Equation 2, it indicates a general two-step binding, and thus the plots of Kobsfast and Kobsslow versus the concentration were fitted with Equations 6 and 7, respectively. The half-life (t½) of the pseudo first order reaction was calculated by Equation 8. The plot of end-point fluorescence to the concentration of varied ligand (SAH, SAM, or peptide substrate) was fitted with a transformed Hill equation (Equation 9 or 10), where Fmax and Fmin are the maximum and minimum fluorescence values, respectively; n is the Hill coefficient; K0.5 is the substrate concentration that produces 50% efficacy (in this case, 50% occupancy of the binding site), which is equal to the apparent rate constant Kdapp when n = 1; and [L] is the concentration of varied ligand. The data from the steady-state kinetics were fitted with a Hill equation (Equation 11), where K0.5 is the substrate concentration that gives rise to 50% of kcatapp in this case, [L] is the substrate peptide concentration, kapp is the apparent reaction rate constant, kcatapp is the apparent catalytic constant, and n is the Hill coefficient. Processive probability (p) is calculated from Equation 12 according to the literature (43), where kchem is the rate constant of the chemistry step, and koffme1 is the dissociation rate constant for the intermediate peptide H4me1.
| (Eq. 1) |
| (Eq. 2) |
| (Eq. 3) |
| (Eq. 4) |
| (Eq. 5) |
| (Eq. 6) |
| (Eq. 7) |
| (Eq. 8) |
| (Eq. 9) |
| (Eq. 10) |
| (Eq. 11) |
| (Eq. 12) |
Global simulations of the transient kinetics data were performed using KinTek ExplorerTM (version 5.2, KinTek Corp.) (35). For binary binding, the signal traces recorded for different concentrations of the variable species were fitted simultaneously to a predefined binding model. The initial estimates of each parameter (e.g. initial intensity, amplitude, and rate constants) were set according to the results from conventional mathematical fitting.
In the study of the binary binding between SAH (or H4me1 peptide) and wtPRMT1 (or W145F or W294A mutant), because the kobs of SAH is linear to the concentration within 0.5 to 16 μm, the simulation was simplified by fitting the data of 0.5 to 16 μm with the one-step binding model (E + L ↔ EL), which generated the fluorescence intensity difference between ligand-bound enzyme and apo-enzyme ((FIligand-enzyme − FIapo-enzyme) × 100%) as well as the apparent association and dissociation rate constants (k1app and k−1app, respectively). The same simulation method was also performed for the data from the H4me1 assay, in which the peptide concentration is 0.5–6 μm.
Simulations of double-mixing assays (formation of ternary complex) were performed in two steps: (a) in the first mixing, the concentrations of each species at equilibrium state were determined using the rate constants obtained from the simulation of the binary binding; (b) in the second mixing, the simulation was performed by using half of the end-point concentrations (because of the 2-fold dilution in the second mixing step) simulated from step a and the concentration of the new reactant. In this simulation, the rate constants determined from binary binding (Fig. 6, k1, k−1, k2, k−2, k6, and k−6) were fixed, with the other rate constants (k3, k−3, k4, k−4, k5, k−5, k7, and k−7) floating. During the simulation, the rate constants that were allowed to float were set within a reasonably confined range (e.g. the upper limit of association is set at the diffusion limit) to avoid non-sense results. For step i in the kinetic model, the equilibrium dissociation constant (Kdi) was calculated by Kdi = k−i/ki. Because the two sets of signals from the (E+H)+C and (E+C)+H assays are governed by the same sets of parameters, they were simulated together.
In the FitSpace exploration (36), a 10% increase of the minimal Chi2 was set as the basis for the confidence range, such that the boundaries of the parameters reflect fits within 1.1-fold of the minimal Chi2. For step i, in which the slope of k−i/ki (Kdi) was better constrained than either parameter individually, the upper and lower boundaries (confidence range) of Kdi were estimated from the confidence contour of the pair (k−i and ki).
Isothermal Titration Calorimetry
ITC assays were performed on a MicroCal PEAQ-ITC at 25 °C. The concentration of PRMT1 was determined by the Bradford assay. The buffer for PRMT1 and peptide contains 50 mm HEPES, pH 8.0, 50 mm NaCl, 1 mm EDTA, and 0.5 mm TCEP. Data were fitted to the sequential binding model using the ITC data analysis module provided by MicroCal PEAQ-ITC.
Author Contributions
H. H., C. L., and Y. G. Z. designed the research, and H. H. performed the experiments. H. H. and Y. G. Z analyzed the data and wrote the paper.
Acknowledgment
We thank the Proteomics and Mass Spectrometry facility (PAMS) at the University of Georgia for MS support.
This work was supported by American Heart Association Grant 12GRNT12070056 and National Institutes of Health Grant R01 GM086717. The authors declare that they have no conflicts of interest with the contents of this article. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
- PRMT
- protein arginine methyltransferase
- SAM
- S-adenosylmethionine
- SAH
- S-adenosylhomocysteine
- MMA
- monomethylarginine
- ADMA
- asymmetric dimethylarginine
- ITC
- isothermal titration calorimetry.
References
- 1. Zheng Y. G., Wu J., Chen Z., and Goodman M. (2008) Chemical regulation of epigenetic modifications: opportunities for new cancer therapy. Med. Res. Rev. 28, 645–687 [DOI] [PubMed] [Google Scholar]
- 2. Bedford M. T., and Clarke S. G. (2009) Protein arginine methylation in mammals: who, what, and why. Mol. Cell 33, 1–13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Yang Y., and Bedford M. T. (2013) Protein arginine methyltransferases and cancer. Nat. Rev. Cancer 13, 37–50 [DOI] [PubMed] [Google Scholar]
- 4. Nicholson T. B., Chen T., and Richard S. (2009) The physiological and pathophysiological role of PRMT1-mediated protein arginine methylation. Pharmacol. Res. 60, 466–474 [DOI] [PubMed] [Google Scholar]
- 5. Bouras G., Deftereos S., Tousoulis D., Giannopoulos G., Chatzis G., Tsounis D., Cleman M. W., and Stefanadis C. (2013) Asymmetric dimethylarginine (ADMA): a promising biomarker for cardiovascular disease? Curr. Top. Med. Chem. 13, 180–200 [DOI] [PubMed] [Google Scholar]
- 6. Matsuguma K., Ueda S., Yamagishi S., Matsumoto Y., Kaneyuki U., Shibata R., Fujimura T., Matsuoka H., Kimoto M., Kato S., Imaizumi T., and Okuda S. (2006) Molecular mechanism for elevation of asymmetric dimethylarginine and its role for hypertension in chronic kidney disease. J. Am. Soc. Nephrol. 17, 2176–2183 [DOI] [PubMed] [Google Scholar]
- 7. Cvetković T., Pavlović R., [strok]Dorðević V., Stojanović I., Veličković-Radovanović R., Ignjatović A., Stefanović N., Živanović S., and Ðorðević V. (2012) Dimethylarginine: biomarkers in progression of kidney disease. J. Med. Biochem. 31, 301–308 [Google Scholar]
- 8. Raptis V., Kapoulas S., and Grekas D. (2013) Role of asymmetrical dimethylarginine in the progression of renal disease. Nephrology 18, 11–21 [DOI] [PubMed] [Google Scholar]
- 9. Seligson D. B., Horvath S., Shi T., Yu H., Tze S., Grunstein M., and Kurdistani S. K. (2005) Global histone modification patterns predict risk of prostate cancer recurrence. Nature 435, 1262–1266 [DOI] [PubMed] [Google Scholar]
- 10. Le Romancer M., Treilleux I., Bouchekioua-Bouzaghou K., Sentis S., and Corbo L. (2010) Methylation, a key step for nongenomic estrogen signaling in breast tumors. Steroids 75, 560–564 [DOI] [PubMed] [Google Scholar]
- 11. Cheung N., Chan L. C., Thompson A., Cleary M. L., and So C. W. (2007) Protein arginine-methyltransferase-dependent oncogenesis. Nat. Cell Biol. 9, 1208–1215 [DOI] [PubMed] [Google Scholar]
- 12. Shia W. J., Okumura A. J., Yan M., Sarkeshik A., Lo M. C., Matsuura S., Komeno Y., Zhao X., Nimer S. D., Yates J. R. 3rd, and Zhang D. E. (2012) PRMT1 interacts with AML1-ETO to promote its transcriptional activation and progenitor cell proliferative potential. Blood 119, 4953–4962 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Schapira M., and Ferreira de Freitas R. (2014) Structural biology and chemistry of protein arginine methyltransferases. MedChemComm 5, 1779–1788 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Hu H., Qian K., Ho M. C., and Zheng Y. G. (2016) Small molecule inhibitors of protein arginine methyltransferases. Expert Opin. Investig. Drugs 25, 335–358 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Zhou R., Xie Y., Hu H., Hu G., Patel V. S., Zhang J., Yu K., Huang Y., Jiang H., Liang Z., Zheng Y. G., and Luo C. (2015) Molecular mechanism underlying PRMT1 dimerization for SAM binding and methylase activity. J. Chem. Inf. Model. 55, 2623–2632 [DOI] [PubMed] [Google Scholar]
- 16. Zhang X., and Cheng X. (2003) Structure of the predominant protein arginine methyltransferase PRMT1 and analysis of its binding to substrate peptides. Structure 11, 509–520 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Zhang X., Zhou L., and Cheng X. (2000) Crystal structure of the conserved core of protein arginine methyltransferase PRMT3. EMBO J. 19, 3509–3519 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Troffer-Charlier N., Cura V., Hassenboehler P., Moras D., and Cavarelli J. (2007) Functional insights from structures of coactivator-associated arginine methyltransferase 1 domains. EMBO J. 26, 4391–4401 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Yue W. W., Hassler M., Roe S. M., Thompson-Vale V., and Pearl L. H. (2007) Insights into histone code syntax from structural and biochemical studies of CARM1 methyltransferase. EMBO J. 26, 4402–4412 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Bonnefond L., Stojko J., Mailliot J., Troffer-Charlier N., Cura V., Wurtz J. M., Cianférani S., and Cavarelli J. (2015) Functional insights from high resolution structures of mouse protein arginine methyltransferase 6. J. Struct. Biol. 191, 175–183 [DOI] [PubMed] [Google Scholar]
- 21. Obianyo O., Osborne T. C., and Thompson P. R. (2008) Kinetic mechanism of protein arginine methyltransferase 1. Biochemistry 47, 10420–10427 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Wang M., Xu R. M., and Thompson P. R. (2013) Substrate specificity, processivity, and kinetic mechanism of protein arginine methyltransferase 5. Biochemistry 52, 5430–5440 [DOI] [PubMed] [Google Scholar]
- 23. Jacques S. L., Aquino K. P., Gureasko J., Boriack-Sjodin P. A., Porter Scott M., Copeland R. A., and Riera T. V. (2016) Carm1 preferentially methylates h3r17 over h3r26 through a random kinetic mechanism. Biochemistry 55, 1635–1644 [DOI] [PubMed] [Google Scholar]
- 24. Gui S., Wooderchak-Donahue W. L., Zang T., Chen D., Daly M. P., Zhou Z. S., and Hevel J. M. (2013) Substrate-induced control of product formation by protein arginine methyltransferase 1. Biochemistry 52, 199–209 [DOI] [PubMed] [Google Scholar]
- 25. Kölbel K., Ihling C., Bellmann-Sickert K., Neundorf I., Beck-Sickinger A. G., Sinz A., Kühn U., and Wahle E. (2009) Type I arginine methyltransferases PRMT1 and PRMT3 act distributively. J. Biol. Chem. 284, 8274–8282 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Lakowski T. M., and Frankel A. (2009) Kinetic analysis of human protein arginine N-methyltransferase 2: formation of monomethyl-and asymmetric dimethyl-arginine residues on histone H4. Biochem. J. 421, 253–261 [DOI] [PubMed] [Google Scholar]
- 27. Wang M., Fuhrmann J., and Thompson P. R. (2014) Protein arginine methyltransferase 5 catalyzes substrate dimethylation in a distributive fashion. Biochemistry 53, 7884–7892 [DOI] [PubMed] [Google Scholar]
- 28. Lakowski T. M., and Frankel A. (2008) A kinetic study of human protein arginine N-methyltransferase 6 reveals a distributive mechanism. J. Biol. Chem. 283, 10015–10025 [DOI] [PubMed] [Google Scholar]
- 29. Wooderchak W. L., Zang T., Zhou Z. S., Acuña M., Tahara S. M., and Hevel J. M. (2008) Substrate profiling of PRMT1 reveals amino acid sequences that extend beyond the “RGG” paradigm. Biochemistry 47, 9456–9466 [DOI] [PubMed] [Google Scholar]
- 30. Johnson K. A. (2013) A century of enzyme kinetic analysis, 1913 to 2013. FEBS Lett. 587, 2753–2766 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Di Lorenzo A., and Bedford M. T. (2011) Histone arginine methylation. FEBS Lett. 585, 2024–2031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Osborne T. C., Obianyo O., Zhang X., Cheng X., and Thompson P. R. (2007) Protein arginine methyltransferase 1: positively charged residues in substrate peptides distal to the site of methylation are important for substrate binding and catalysis. Biochemistry 46, 13370–13381 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Feng Y., Xie N., Jin M., Stahley M. R., Stivers J. T., and Zheng Y. G. (2011) A transient kinetic analysis of PRMT1 catalysis. Biochemistry 50, 7033–7044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Johnson K. A. (1992) Transient-state kinetic analysis of enzyme reaction pathways, in The Enzymes (David S. S., ed) pp. 1–61, Academic Press, Orlando, FL [Google Scholar]
- 35. Johnson K. A., Simpson Z. B., and Blom T. (2009) Global Kinetic Explorer: A new computer program for dynamic simulation and fitting of kinetic data. Anal. Biochem. 387, 20–29 [DOI] [PubMed] [Google Scholar]
- 36. Johnson K. A., Simpson Z. B., and Blom T. (2009) FitSpace Explorer: An algorithm to evaluate multidimensional parameter space in fitting kinetic data. Anal. Biochem. 387, 30–41 [DOI] [PubMed] [Google Scholar]
- 37. Copeland R. A. (2004) Enzymes: A Practical Introduction to Structure, Mechanism, and Data Analysis, 2nd ed., Wiley-VCH, Hoboken, NJ [Google Scholar]
- 38. Segel I. H. (1993) Enzyme Kinetics: Behavior and Analysis of Rapid Equilibrium and Steady-State Enzyme Systems, Wiley, Hoboken, NJ [Google Scholar]
- 39. Sack J. S., Thieffine S., Bandiera T., Fasolini M., Duke G. J., Jayaraman L., Kish K. F., Klei H. E., Purandare A. V., Rosettani P., Troiani S., Xie D., and Bertrand J. A. (2011) Structural basis for CARM1 inhibition by indole and pyrazole inhibitors. Biochem. J. 436, 331–339 [DOI] [PubMed] [Google Scholar]
- 40. Chan-Penebre E., Kuplast K. G., Majer C. R., Boriack-Sjodin P. A., Wigle T. J., Johnston L. D., Rioux N., Munchhof M. J., Jin L., Jacques S. L., West K. A., Lingaraj T., Stickland K., Ribich S. A., Raimondi A., et al. (2015) A selective inhibitor of PRMT5 with in vivo and in vitro potency in MCL models. Nat. Chem. Biol. 11, 432–437 [DOI] [PubMed] [Google Scholar]
- 41. Obianyo O., and Thompson P. R. (2012) Kinetic mechanism of protein arginine methyltransferase 6 (PRMT6). J. Biol. Chem. 287, 6062–6071 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Tymoczko J. L., Berg J. M., and Stryer L. (2011) Nucleic acid structure and DNA replication, in Biochemistry: A Short Course, p. 606, W. H. Freeman and Co., New York [Google Scholar]
- 43. Svedruzić Z. M, and Reich N. O. (2005) Mechanism of allosteric regulation of Dnmt1's processivity. Biochemistry 44, 14977–14988 [DOI] [PubMed] [Google Scholar]
- 44. Dhar S., Vemulapalli V., Patananan A. N., Huang G. L., Di Lorenzo A., Richard S., Comb M. J., Guo A., Clarke S. G., and Bedford M. T. (2013) Loss of the major Type I arginine methyltransferase PRMT1 causes substrate scavenging by other PRMTs. Sci. Rep. 3, 1311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Larsen S. C., Sylvestersen K. B., Mund A., Lyon D., Mullari M., Madsen M. V., Daniel J. A., Jensen L. J., and Nielsen M. L. (2016) Proteome-wide analysis of arginine monomethylation reveals widespread occurrence in human cells. Sci. Signal. 9, rs9. [DOI] [PubMed] [Google Scholar]
- 46. Da L. T., Sheong F. K., Silva D. A., and Huang X. (2014) Application of Markov State Models to simulate long timescale dynamics of biological macromolecules. Adv. Exp. Med. Biol. 805, 29–66 [DOI] [PubMed] [Google Scholar]
- 47. Lee W. C., Lin W. L., Matsui T., Chen E. S., Wei T. Y., Lin W. H., Hu H., Zheng Y. G., Tsai M. D., and Ho M. C. (2015) Protein arginine methyltransferase 8: tetrameric structure and protein substrate specificity. Biochemistry 54, 7514–7523 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Boriack-Sjodin P. A., Jin L., Jacques S. L., Drew A., Sneeringer C., Scott M. P., Moyer M. P., Ribich S., Moradei O., and Copeland R. A. (2016) Structural insights into ternary complex formation of human CARM1 with various substrates. ACS Chem. Biol. 11, 763–771 [DOI] [PubMed] [Google Scholar]
- 49. Wang C., Zhu Y., Caceres T. B., Liu L., Peng J., Wang J., Chen J., Chen X., Zhang Z., Zuo X., Gong Q., Teng M., Hevel J. M., Wu J., and Shi Y. (2014) Structural determinants for the strict monomethylation activity by Trypanosoma brucei protein arginine methyltransferase 7. Structure 22, 756–768 [DOI] [PubMed] [Google Scholar]
- 50. Antonysamy S., Bonday Z., Campbell R. M., Doyle B., Druzina Z., Gheyi T., Han B., Jungheim L. N., Qian Y., Rauch C., Russell M., Sauder J. M., Wasserman S. R., Weichert K., Willard F. S., Zhang A., and Emtage S. (2012) Crystal structure of the human PRMT5:MEP50 complex. Proc. Natl. Acad. Sci. 109, 17960–17965 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Hasegawa M., Toma-Fukai S., Kim J. D., Fukamizu A., and Shimizu T. (2014) Protein arginine methyltransferase 7 has a novel homodimer-like structure formed by tandem repeats. FEBS Lett. 588, 1942–1948 [DOI] [PubMed] [Google Scholar]
- 52. Cura V., Troffer-Charlier N., Wurtz J. M., Bonnefond L., and Cavarelli J. (2014) Structural insight into arginine methylation by the mouse protein arginine methyltransferase 7: a zinc finger freezes the mimic of the dimeric state into a single active site. Acta Crystallogr. D Biol. Crystallogr. D 70, 2401–2412 [DOI] [PubMed] [Google Scholar]
- 53. t Hart P., Thomas D., van Ommeren R., Lakowski T. M., Frankel A., and Martin N. I. (2012) Analogues of the HIV-Tat peptide containing Nη-modified arginines as potent inhibitors of protein arginine N-methyltransferases. MedChemComm 3, 1235–1244 [Google Scholar]
- 54. Fuhrmann J., Clancy K. W., and Thompson P. R. (2015) Chemical biology of protein arginine modifications in epigenetic regulation. Chem. Rev. 115, 5413–5461 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Morales Y., Cáceres T., May K., and Hevel J. M. (2016) Biochemistry and regulation of the protein arginine methyltransferases (PRMTs). Arch. Biochem. Biophys. 590, 138–152 [DOI] [PubMed] [Google Scholar]
- 56. Xie N., Elangwe E. N., Asher S., and Zheng Y. G. (2009) A dual-mode fluorescence strategy for screening HAT modulators. Bioconjug. Chem. 20, 360–366 [DOI] [PubMed] [Google Scholar]
- 57. Feng Y., Xie N., Wu J., Yang C., and Zheng Y. G. (2009) Inhibitory study of protein arginine methyltransferase 1 using a fluorescent approach. Biochem. Biophys. Res. Commun. 379, 567–572 [DOI] [PubMed] [Google Scholar]
- 58. Sinha S. H., Owens E. A., Feng Y., Yang Y., Xie Y., Tu Y., Henary M., and Zheng Y. G. (2012) Synthesis and evaluation of carbocyanine dyes as PRMT inhibitors and imaging agents. Eur. J. Med. Chem. 54, 647–659 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Hu H., Owens E. A., Su H., Yan L., Levitz A., Zhao X., Henary M., and Zheng Y. G. (2015) Exploration of cyanine compounds as selective inhibitors of protein arginine methyltransferases: synthesis and biological evaluation. J. Med. Chem. 58, 1228–1243 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Wu J., Xie N., Feng Y., and Zheng Y. G. (2012) Scintillation proximity assay of arginine methylation. J. Biomol. Screen. 17, 237–244 [DOI] [PMC free article] [PubMed] [Google Scholar]