Diffusion and Uptake of Tobacco Mosaic Virus as Therapeutic Carrier in Tumor Tissue: Effect of Nanoparticle Aspect Ratio

Abstract

Nanoparticle-based technologies, including platforms derived from plant viruses, hold great promise for targeting and delivering cancer therapeutics to solid tumors by overcoming dose-limiting toxicities associated with chemotherapies. A growing body of data indicates advantageous margination and penetration properties of high aspect-ratio nanoparticles, which enhance payload delivery, resulting in increased efficacy. Our lab has demonstrated that elongated rod-shaped and filamentous macromolecular nucleoprotein assemblies from plant viruses have higher tissue diffusion rates than spherical particles. In this study, we developed a mathematical model to quantify diffusion and uptake of tobacco mosaic virus (TMV) in a spheroid system approximating a capillary-free segment of a solid tumor. Model simulations predict TMV concentration distribution with time in a tumor spheroid for different sizes and cell densities. From simulations of TMV concentration distribution, we can quantify the effect of TMV aspect ratio (e.g., nanorod length-to-width) with and without cellular uptake by modulated surface chemistry. This theoretical analysis can be applied to other viral or nonviral delivery systems to complement the experimental development of the next generation of nanotherapeutics.

Graphical Abstract

INTRODUCTION

Nanoparticle carriers are used for targeting chemotherapies and immunotherapies to tumors to increase tissue specificity and effective payload delivery with reduced systemic adverse effects. Most nanoparticle-encapsulated cancer therapeutics are delivered to the tumor site by exploiting the local tumor environment consisting of the combination of leaky vasculature and deficient lymphatic clearance, i.e., enhanced permeability and retention (EPR). Some strategies also exploit the targeting of disease-specific molecular signatures, as yet no targeted nanoparticle has been translated into clinical treatment. If a target site can be identified, then the carrier diffusion and distribution of the delivered payload are critical to treatment success. Nanoparticles injected in the systemic circulation target either the vasculature or the periphery of the tumor. Limited nanoparticle-carrier diffusion can prevent drug accumulation to a lethal concentration in the tumor tissue and therefore promote cancer cell survival. Surviving cancer cells often become more aggressive and develop a drug resistance phenotype.¹ Here, we develop the basis for quantitative analysis of nanoparticle diffusion and uptake in a solid tumor.

Nanoparticle Shape

Nanoparticle size and shape as well as surface chemistry determine the fate of the carrier and its efficacy. A growing body of data shows increased tumor homing and tissue penetration with elongated, rather than spherical, nanomaterials.^2–4 Elongated, rod-shaped or filamentous nanoparticles have enhanced margination (migration toward blood-vessel walls) and increased transport across tissue membranes. Geng et al.⁵ demonstrated that virus-like filomicelles with higher aspect ratios than spherical particles deliver the chemo-therapeutic drug paclitaxel to human-derived tumor xenografts in mice more effectively and with increased efficacy. Chauhan et al.⁶ compared the intratumoral diffusion of biostable colloidal quantum dots as nanorods and nanospheres with identical charge and surface coating. Nanorods penetrated tumors 4.1 times faster than nanospheres of the same hydrodynamic radius and occupied a tumor volume 1.7 times greater. Correspondingly, we found that filamentous potato virus X (PVX) compared to spherical cowpea mosaic virus (CPMV) has enhanced tumor homing and tissue penetration, particularly in the core of the tumor.⁷ Contradictory results were obtained by Reuter et al.,⁸ who compared sphere-like and rod-shaped nanogels using PRINT technology. They observed that smaller nanospheres had 5-fold greater tumor accumulation compared to higher aspect-ratio nanorods. We hypothesize that this difference may be due to the different tumor model used. It has been previously shown that differences in tumor vasculature (e.g., density and leakiness) affect shape-dependent nanoparticle extravasation.⁹ In addition, other factors may have influenced the results, such as the differences in surface charge (CPMV has a negatively charged surface while the nanogels have a positively charged surface) and aspect ratio (PVX has an aspect ratio of 40 while the rod-shaped nanogel only has an aspect ratio of 4). Therefore, there is a need to investigate the mechanics of diffusion and accumulation of high aspect-ratio nanoparticles within the tumor microenvironment.

Mathematical Modeling

To complement experimental work in nanoparticle therapies, mechanistic mathematical modeling and computer simulation can be used to better understand experimental results and provide quantitative guidance for more efficient design of nanotherapeutics. Optimizing carrier and drug penetration into the tumor tissue is critical to maximize the therapeutic effect. Toward this goal, we developed a mathematical model of nanoparticle diffusion and uptake in a spheroid approximation of a solid tumor segment without capillaries. Our model differs from other models that can be found in the literature^10,11 by taking into account the effect of shape and size on the diffusion constant of nanoparticles. Our model also builds on the previous models by incorporating the rate of endocytosis and how it is affected by size, shape, and surface modification (e.g., shielding vs targeting) of nanoparticles. As the model nanoparticle, we used the nucleoprotein components of the tobacco mosaic virus (TMV). Virus-based plant nanoparticles, such as TMV, provide a unique platform for nanomedical engineering because their dimensions are known and tunable on the molecular level, which cannot readily be accomplished with synthetic nanoparticles.

TMV Nanoparticles

Native TMV particles form a cylindrical structure measuring 300 × 18 nm with a 4 nm-wide hollow interior channel. TMV is composed of single-stranded RNA wrapped inside a hollow nanotube formed by 2130 identical coat proteins. TMV offers a programmable scaffold for both genetic engineering and chemical bioconjugation to impart new functionalities, e.g., therapeutic payloads.^12,13 TMV virion formation can be initiated by self-assembly of coat proteins from an RNA hairpin forming sequence. This origin of assembly site (OAS) is the only sequence required to promote a bidirectional coat protein self-assembly along the template RNA. This principle has been exploited to produce TMV nanotubes with diverse shapes such as kinked nanoboomerangs or branched tetrapods.¹⁴ This RNA-templated self-assembly principle has also been used to produce TMV-like nanotubes with distinct longitudinal domains¹⁵ as well as materials of defined aspect ratio.¹⁶ In previous studies, we have shown that biodistribution and tumor homing is a function of the carrier’s aspect ratio. With higher aspect ratio, particles avoid clearance by the mononuclear phagocyte system, resulting in increased tumor homing.¹⁶ Nevertheless, a balance must be established between immune evasion, tumor homing, and tissue penetration. While higher aspect-ratio materials have enhanced tumor homing, the higher molecular weight particles have slower diffusion rates. The TMV platform technology provides a high precision platform with which to specify aspect ratio and surface chemistries that affect tissue penetration in tumor spheroids.

Diffusion in Tumor Spheroid System

We chose to study TMV diffusion in a spheroidal cell-culture system with different sizes and cell densities. This 3D cellular system mimics a small segment of a solid tumor between capillaries and bridges the gap between 2D tissue culture and in vivo mouse models for screening therapeutics.^{10,11,17–19} In tumor tissue, the combination of leaky vasculature and deficient lymphatic clearance leads to diffusion as the driving mode of nanoparticle transport and penetration into the tumor tissue.²⁰ For this study, we focused on “stealth” TMV formulations with reduced cell uptake rates produced by coating the particle surface with polyethylene glycol (PEG). Targeted TMV formulations with molecular specificity and increased cellular uptake rates were simulated by displaying the integrin specific peptide ligand RGD on their surface. PEG and RGD are surface modifiers frequently used in nanoparticle engineering to promote immune invasion and targeted endocytosis, respectively. These coatings serve as good model systems whose results can be translated to other nanoparticle formulations.

THEORETICAL METHODS

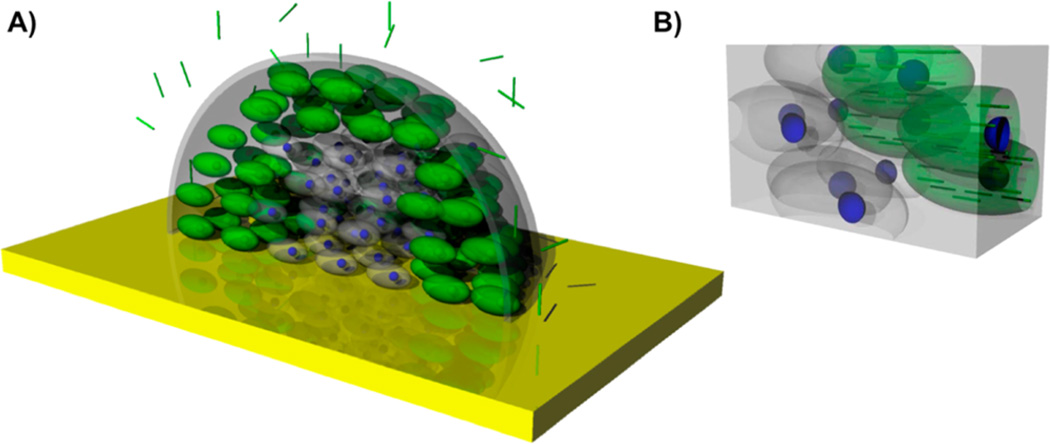
We developed a mathematical model of TMV diffusion and uptake in a spheroid tumor model to evaluate the effect of particle aspect ratio (maximum to minimum principal axis lengths). The input to this model was a bolus injection of a known TMV mass in the medium surrounding the tumor (Figure 1A). TMV diffuses from the surrounding medium into the spheroid interstitial space. The rate of diffusion in the interstitial space is much slower than in the surrounding medium so that the distribution of TMV in the surrounding medium is uniform (Supporting Information S1). In addition, the volume of the surrounding medium is much greater than the volume of the spheroid so that the changes in TMV concentration in the surrounding medium are negligible (Supporting Information S1). The tumor cell density within the spheroid segment is uniform and considered as a continuum. The rates of cell proliferation and death are assumed negligible relative to the other TMV rate processes so that the viable cell volume remains constant. From the interstitial space, we assume that TMV is taken up irreversibly by tumor cells at a constant rate that is dependent on the aspect ratio and surface chemistry of TMV nanorods (Figure 1B). Furthermore, the TMV does not interact with extracellular matrix (ECM) components and cannot bind to them.

Figure 1.

(A) 3D schematic of the diffusion of high aspect-ratio nanoparticles into the tumor half spheroid model. (B) Zoom-in schematic of the interior of the spheroid. Cells in green represent cancer cells that have taken up TMV particles, while cells in gray are cancer cells without TMV inside them.

TMV Dynamics

The dynamic mass concentration distribution of TMV within the interstitial space of a spheroid segment of radius R can be described as

$$\frac{\partial C_{\mathrm{S}}}{\partial t}=D\frac{1}{r^2}\frac{\partial }{\partial r}\lfloor r^2\frac{\partial C_{\mathrm{S}}}{\partial r}\rfloor -k{C}_{\mathrm{S}},0\le r\le R$$ (1)

where C_S is the concentration of TMV in the interstitial space at any location in the spheroid, D is the constant TMV diffusion coefficient, and k is the constant rate at which TMV is irreversibly taken up by cells. At the interface of the surrounding medium with the spheroid, the TMV concentration is continuous with the interstitial fluid of the spheroid:

$$r=R:\hspace{1em}{C}_{\mathrm{S}}=C_{\mathrm{M}}$$ (2)

where C_M is the concentration of TMV in the surrounding medium. After a bolus injection of TMV into the surrounding medium, C_M equals the ratio of the injected mass of TMV (m_TMV) to the volume of the surrounding medium (V_M). At the center of the spheroid, by spherical symmetry there is no net diffusion flux so that the concentration gradient is zero:

$$r=0:\hspace{1em}\frac{\partial C_{\mathrm{S}}}{\partial r}=0$$ (3)

Initially, there is no TMV in the interstitial space of the spheroid:

$$t=0:\hspace{1em}{C}_{\mathrm{S}}=0,\hspace{1em}0\le r\le R$$ (4)

Model Transformation

As described in the Supporting Information (S2), we can transform the governing equation of the spheroid into rectangular coordinates with constant coefficients by defining g(r, t) = rC_S(r, t). Consequently, we obtain

$$\frac{\partial g}{\partial t}=D\frac{{\partial }^{2}g}{\partial r^2}-kg$$ (5)

with the initial condition:

$$t=0:\hspace{1em}g=0,\hspace{1em}0\le r\le R$$ (6)

and the boundary conditions:

$$r=0:\hspace{1em}g=0$$ (7)

$$r=R:\hspace{1em}g=R{C}_{\mathrm{M}}$$ (8)

As described in the Supporting Information (S3), we solve these model equations by the numerical method of lines in which the spatial derivatives are discretized; consequently, the problem is expressed as an initial-value problem involving a set of differential-difference equations. For the numerical solution, we used the MATLAB code “ode15s”.

Model Parameter Values

The model parameter values known from direct measurement are the mass of TMV (m_TMV) injected, the volume of the surrounding medium (V_M), and the radius of the spheroid (R). The parameters that must be estimated indirectly are the cellular uptake rate coefficient (k) and the diffusion coefficient (D). For each experiment, these coefficients are constants. This implies that free receptors are always available at the cell surface so that k is constant in any experiment. For different experiments, however, their values change depending on their surface area, shape (i.e., aspect ratio), and cell density within the spheroid (ϕ). The uptake rate coefficient is directly proportional to the total cell surface area as indicated by the cell density, where k = k₀ϕ. The diffusion coefficient is a complex function of the cell shape and cell density.

Diffusion Coefficients

The diffusion of spherical nanomaterials can be estimated using the Stokes–Einstein equation:

$$D_0=\frac{k_{\mathrm{B}}T}{6\pi \eta R_{\mathrm{H}}}$$ (9)

where k_B is the Boltzmann constant, T is the temperature of the system, η is the solvent viscosity, and R_H is the hydrodynamic radius of the particle. For cylindrical TMV nanoparticles, we consider the diffusion coefficients for axial (ν_t) and transverse (ν_r) motions:²¹

$$D_{\mathrm{t}}=\frac{\left(\text{ln}\right(\frac{L}{d})+{\nu }_{\mathrm{t}})k_{\mathrm{B}}T}{2\pi \eta L};D_{\mathrm{r}}=\frac{\left(\text{ln}\right(\frac{L}{d})+{\nu }_{\mathrm{r}})k_{\mathrm{B}}T}{4\pi \eta L}$$ (10)

where L and d are the length and the diameter of TMV respectively, ν_t is the characteristic axial velocity of TMV, and ν_r is the characteristic transverse velocity of TMV. As presented in the Supporting Information (S4), the values of ν_t and ν_r for TMV were established on the basis of literature.²² For random diffusion (D_rt) of an elongated cylindrical nanoparticle in the surrounding medium:²¹

$$D_{\mathrm{r}\mathrm{t}}=\frac{\left(\text{ln}\right(\frac{L}{d})+\nu )k_{\mathrm{B}}T}{3\pi \eta L};\nu =\frac{|{\nu }_{\mathrm{t}}|+|{\nu }_{\mathrm{r}}|}{2}$$ (11)

Furthermore, to evaluate the diffusion coefficient of TMV within the tumor spheroid space (D_int), we take into account the presence of matrix proteins, mostly collagen:²³

$$D_{\text{int}}=D_{\mathrm{r}\mathrm{t}}{\mathrm{e}}^{-r_{\mathrm{p}}\sqrt{\epsilon }/r_{\mathrm{f}}}$$ (12)

where ε is the volume fraction of the tumor interstitial matrix (0.06 for spheroids),¹¹ r_p is the effective radius of TMV (70 nm),²⁴ and r_f is the effective radius of tumor matrix proteins (20 nm for collagen).²⁵ Finally, the diffusion coefficient of TMV in the porous spheroid containing cells (D) takes into account the presence of immobilized cells:^11,26

$$D=D_{\text{int}}{(1-\varphi )}^2$$ (13)

where ϕ is the cell density. The effects of the aspect ratio on diffusion coefficients in the surrounding medium and in the spheroid are presented in the Supporting Information (S5).

EXPERIMENTAL METHODS

Rate of Cellular Uptake

The rate of cellular uptake of RGD-modified or PEGylated TMV in cancer cells expressing α_vβ₃ integrins was characterized experimentally. First, the rate of cellular uptake of TMV-RGD with a length of 300 nm was quantified in vitro. MDA-MB-231 cells (triple negative breast cancer) were cultured in high glucose Dulbecco’s modified Eagle medium (DMEM) with l-glutamine (Fisher), and supplemented with 10% (v/v) FBS and 1% (v/v) penicillin– streptomycin. Cells were grown to confluency at 37 °C and 5% CO₂. MDA-MB-231 cells were collected using enzyme-free Hank’s-based cell dissociation buffer (Invitrogen). To an untreated 96-well v-bottom plate, 500,000 cells/200 µL media/well were added. Triplicates of sulfo-Cyanine5 azide (Cy5)-labeled TMV-RGD (300 nm long) were added at a concentration of 100,000 particles/cell and incubated for 3, 1.5, and 0.5 h at 37 °C, 5% CO₂. The Cy5-TMV-RGD particles were synthesized and characterized as described by Pitek et al.²⁷ Control experiments were conducted, in triplicate, with no particles present. Post incubation with TMV nanoparticles, cells were spun down at 500g for 4 min. Supernatant was discarded, cells were washed twice in FACS buffer (0.1 mL 0.5MEDTA, 0.5 mL FBS, and 1.25 mL 1MHEPES pH 7.0 in Ca²⁺ and Mg²⁺ free PBS (50 mL total volume)), and fixed in 2% (v/v) paraformaldehyde in FACS buffer at room temperature for 10 min. Cells were washed twice after fixing and resuspended in PBS. Samples were transferred to a 384 flat bottom black polystyrene plate (Corning) for fluorescence analysis. The resulting fluorescence intensity (ex/em 600/665 nm) was quantified using an Infinite 200 plate reader and the software Tecan i-control (version 1.10.4.0). The number of Cy5-TMV-RGD particles internalized per cell was calculated using a standard curve. The rate of cellular uptake of PEGylated or RGD targeted TMV of various aspect ratios (L/d) of constant diameter (d = 18 nm) but distinct length (L = 300 nm, L = 135 nm, and L = 59 nm) was then extrapolated from data published by our lab¹⁶ by comparing the rate of cellular uptake of TMV-RGD (L = 300 nm) calculated above to the relative rate of cellular uptake of PEGylated or RGD targeted TMV.

RESULTS AND DISCUSSION

Our tumor microenvironment system consists of a spheroidal cancer cell-culture whose diameter can vary between a few hundred micrometers to 1 mm, which corresponds to the heterogeneous spacing of capillary distribution within the tumor (Figure 1). Modeling the diffusion of nanoparticles in the tumor tissue and quantifying the time scales as a function of capillary and cell density could inform dosing and administration schedules. The physiological barriers and diffusion rates of nanoparticles also depend on nanoparticle shape, size, and surface chemistry. The simulated effects of spheroid radius, cell density, and aspect ratio on the TMV concentration distributions without cellular uptake are shown in Figures 2, 3 and 4, respectively. The parameters used in each of these figures are summarized in Table 1. These results and their significance are discussed in the following sections.

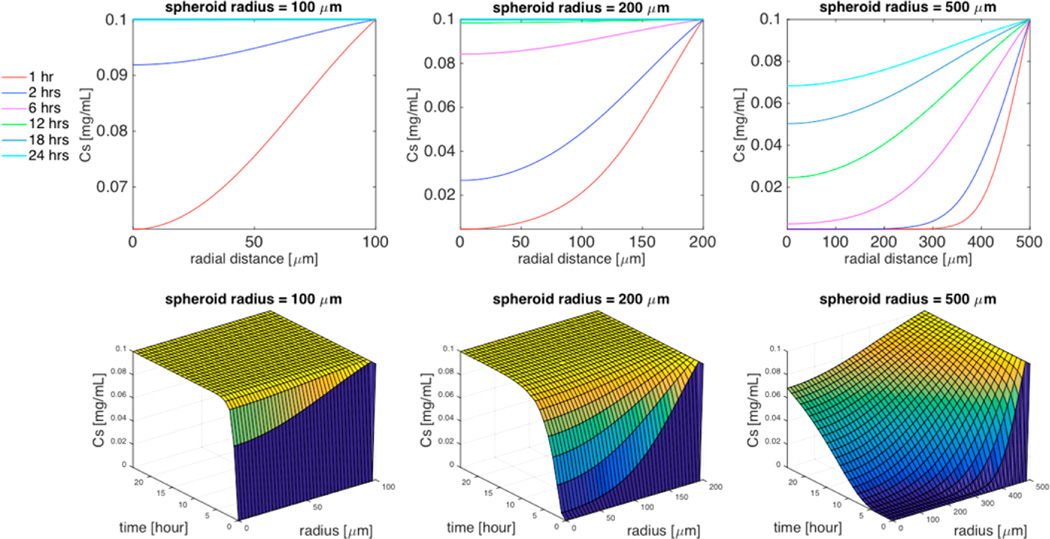
Figure 2.

Simulation of the effect of spheroid radius (R = 100 µm, R= 200 µm, or R = 500 µm) on TMV concentration distribution within the spheroid in the absence of cellular uptake. Top 3 panels are 2D plots of the concentration of TMV as a function of the radial distance within the spheroid for specific time interval (1 h, 2 h, 6 h, 12 h, 18 h, 24 h), and the bottom 3 panels are the corresponding 3D plots of the concentration of TMV as a function of both time and radial distance. Cell density ϕ = 0.5, TMV concentration in the surrounding medium C_M = 0.1 mg/mL, cell uptake k = 0, and TMV aspect ratio L/d = 300/18.

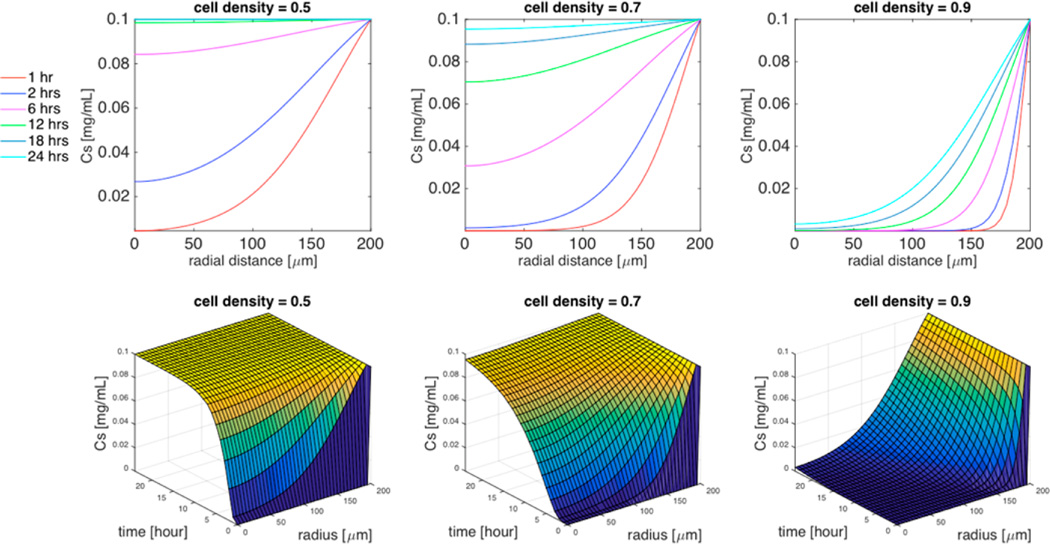
Figure 3.

Simulation of the effect of cell density (ϕ = 0.5, ϕ = 0.7, or ϕ = 0.9) on TMV concentration distribution within the spheroid in the absence of cellular uptake. Top 3 panels are 2D plots of the concentration of TMV as a function of the radial distance within the spheroid for specific time interval (1 h, 2 h, 6 h, 12 h, 18 h, 24 h), and the bottom 3 panels are the corresponding 3D plots of the concentration of TMV as a function of both time and radial distance. Spheroid radius R = 200 µm, TMV concentration in the surrounding medium C_M = 0.1 mg/mL, cell uptake k = 0, TMV aspect ratio L/d = 300/18.

Figure 4.

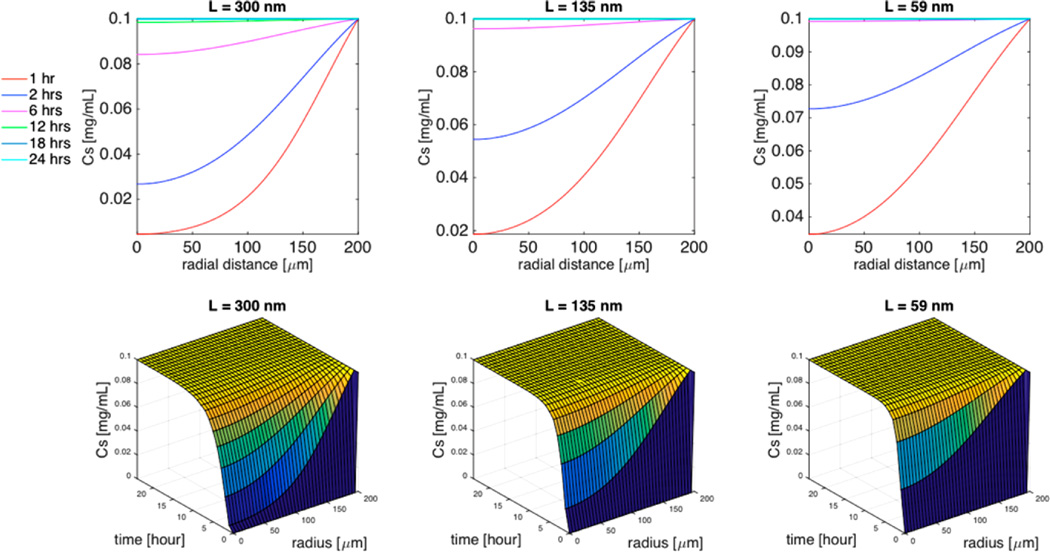
Simulation of the effect of the TMV aspect ratio (L/d = 300/18, L/d = 135/18, or L/d = 59/18) on TMV concentration distribution within the spheroid in the absence of cellular uptake. Top 3 panels are 2D plots of the concentration of TMV as a function of the radial distance within the spheroid for specific time interval (1 h, 2 h, 6 h, 12 h, 18 h, 24 h), and the bottom 3 panels are the corresponding 3D plots of the concentration of TMV as a function of both time and radial distance. Cell density ϕ = 0.5, spheroid radius R = 200 µm, TMV concentration in the surrounding medium C_M = 0.1 mg/mL, cell uptake k = 0.

Table 1.

Summary of the Parameters Used for the Model Simulations in Figures 2, 3, and 4

	spheroid radius (R) [nm]	cell density	aspect ratio (L/d)	diffusion coefficient (D) [mm2/sec]
Figure 2	100
	200	0.5	300/18	5.38×10−7
	500
Figure 3		0.5
	200	0.7	300/18	5.38 × 10−7
		0.9
Figure 4			300/18	5.38 × 10−7
	200	0.5	135/18	8.98 × 10−7
			59/18	1.25 × 10−6

Effect of Tumor Spheroid Radius on TMV Diffusion (without Cellular Uptake)

The spheroid segment radius represents the distance between capillaries. The intercapillary distance is highly regulated by a fine balance between angiogenic factors that promote or inhibit vessel growth, as well as the oxygen and nutrient consumption by the surrounding cells.²⁸ In healthy tissue, particle diffusion from the vessels to the cytoplasmic membrane of surrounding cells does not exceed 100 µm.²⁹ In the tumor microenvironment, however, the oxygen consumption is lowered and the tolerance of cancer cells to hypoxic conditions is increased. Tumors with a high rate of oxygen consumption have a higher microvascular density and, therefore, a smaller intercapillary distance. On the other hand, tumors with a low rate of oxygen consumption have a lower microvascular density and, therefore, a higher intercapillary distance.³⁰ This phenomenon is currently being investigated for nanoparticle-based antiangiogenic tumor therapy.³¹ By reducing the oxygen supply to the tumor site, antiangiogenic tumor therapies aim to prevent the growth and aggressiveness of the tumor.

To quantify the effect of different intercapillary distances within the tumor microenvironment, we simulated the diffusion of TMV in a spheroid system without cellular uptake for a range of radii in the absence of cellular uptake (Figure 2). Within the tumor cell spheroid, the simulated concentration distributions at various times of TMV with different spheroid radii are shown in two and three dimensions. The TMV concentration is highest at the interface with the surrounding medium (r = R) and decreases as TMV diffused to the center of the tumor spheroid (r = 0). A spheroid of radius R = 100 µm corresponds to relatively low intercapillary distance as in healthy tissue, whereas R = 500 µm corresponds to higher intercapillary distance as with tumors. For R = 100 µm, the steady-state concentration, which is equal to the concentration of TMV in the surrounding medium (0.1 mg/mL), is reached at the spheroid center in less than 6 h, whereas for R = 200 µmit takes 18 h (Figure 2). For R = 500 µmonly 68% of the initial TMV concentration reaches the spheroid center within 24 h. This poor tumor penetration correlates with increasing risks of survival of cancer cells and promotes drug resistance.¹

Effect of Cell Density on TMV Diffusion (without Cellular Uptake)

When the tumor cell density increases, the cytotoxicity of chemotherapeutic drugs such as vincristine, bleomycin, and doxorubicin is impaired.³² Increasing the cancer cell density within the spheroid decreases the void volume through which nanoparticles can diffuse as represented by a smaller diffusion coefficient. With high cell density, the limitation of TMV nanoparticle penetration is a major barrier to chemotherapeutic drug delivery in the deep tissue, which also correlates with increasing risks of survival of cancer cells and promotes drug resistance.¹

The effect of cell density ϕ on the diffusion coefficient of TMV nanorods (as expressed by eq 13) is computed in Supporting Information (S5). For a spheroid radius of 200 µmin the absence of cell uptake, the simulations shown in Figure 3 quantify the effect of cell density ϕ on the time required for the TMV to reach the spheroid center. When ϕ = 0.9, the concentration at the center of the spheroid reaches 3.3% of the initial TMV concentration within 24 h. For ϕ = 0.7, there is a 30-fold increase of TMV concentration at the center within the same time interval. A further decrease to ϕ = 0.5 allows TMV to reach the steady-state concentration at the center of the spheroid within 18 h.

Effect of TMV Aspect Ratio on Diffusion (without Cellular Uptake)

In the spheroid cell system, we investigated diffusion of TMV with different nanorod aspect ratios indicated by L/d: TL-long (300/18–16.5), TM-medium (135/18–7.5), and TS-short (59/18–3.5). The model parameters were set as follows: cell density ϕ = 0.5, spheroid radius R = 200 µm, and cell uptake k = 0. As observed from Figure 4, the time necessary for TMV to reach the spheroid center was reduced when the aspect ratio was decreased: TL, TM, and TS require 18, 10, and 7 h, respectively, to reach steady-state concentration.

While smaller aspect-ratio rod-shaped nanoparticles have higher diffusion and accumulate more easily in the deep tumor tissue, the higher aspect-ratio nanoparticles have enhanced margination toward blood-vessel walls, increased transport across tissue membranes, and reduced clearance by phagocytosis.^2–4,16,33 In other words, a “one-size-fits-all” nanoparticle does not exist and a compromise must be made to optimize the diffusion and accumulation of nanoparticles within the tumor without impairing their ability to extravasate (i.e., move from blood to extravascular space), cross tissue membranes, and evade the immune system. With complementary data, this model can provide a basis for predicting the aspect ratio that promotes optimal accumulation of nanoparticles injected intravenously.^5–7 Perhaps, a better approach would be to intravenously inject a cocktail of TMV nanoparticles with various aspect ratios. In this scenario, the lowest aspect-ratio TMV are less likely to reach the tumor site, but the fraction that do penetrate the tumor can diffuse more readily than the higher aspect-ratio TMV in the deep tumor tissue. In the meantime, the higher aspect-ratio nanoparticles can reach the tumor site more readily, but only accumulate in the peripheral tissue of the tumor. The net result would be to improve overall drug distribution and maximize efficacy.

Effects of TMV Characteristics on the Rate of Cell Uptake

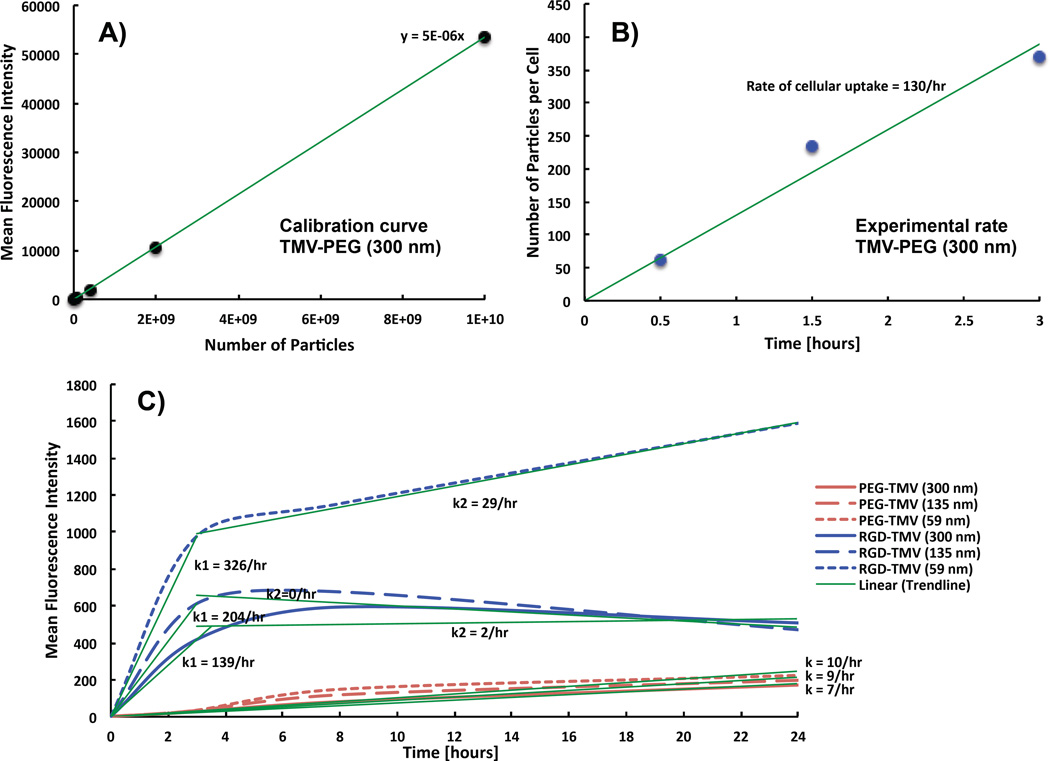
The simulations presented above do not include TMV uptake by cells so that the effects on diffusion are not obfuscated. While targeted nanoparticle formulations can increase delivery, endocytotic clearance of targeted nanoparticle can reduce drug distribution and tumor cell access.³⁴ To assess the effect of cell uptake on TMV distribution throughout the spheroid, we evaluated the cell uptake rates of TMV in cancer cells experimentally: fluorescently labeled, RGD-targeted TMV formulations were obtained as described by Pitek et al.²⁷ A fluorescence assay was developed to quantify TMV particle uptake cancer cells over time (Figures 5A,B). We chose triple negative breast cancer cells (MDA-MB-231) as our model cell line for their relatively high expression of α_vβ₃ integrins.³⁵ We determined that the targeted TMV formulation exhibits a cell uptake rate of 130 particles/hour/cell. With this experimental value, we can extrapolate cell uptake rates of PEGylated and RGD-targeted TL, TM, and TS particles (Figure 5C).¹⁶ These data and resulting cell uptake rates are summarized in Table 2.

Figure 5.

Experimental rate of cellular uptake. (A) Plate reader quantification of fluorescence intensity of Cy5-TMV-PEG (L/d = 300/18 nm) suspended in PBS solution to establish a calibration curve. (B) Resulting number of Cy5-TMV-PEG (L/d = 300/18 nm) internalized in MDA-MB-231 cells after 30 min, 1.5 h, and 3 h incubation. The slope of the curve corresponds to the rate of cellular uptake. (C) Flow cytometry quantification data from a previous study of the mean fluorescence intensity of TMV-PEG and TMV-RGD formulations, with distinct aspect ratio, which were internalized in HT-29 cells.¹⁶

Table 2.

Quantification of the Rate of Cellular Uptake of Three Aspect Ratios of TMV-PEG and TMV-RGD

	[TMV/hour/cell] (L = 300 nm)	[TMV/hour/cell] (L = 135 nm)	[TMV/hour/cell] (L = 59 nm)
TMV-RGD	130	139	178
TMV-PEG	7	5	4

While RGD-targeted formulations are readily taken up by the cells, PEGylated formulations show negligible cell interactions. The PEGylated formulations with TS and TM aspect ratios have comparable effects on uptake. The targeted formulations with TL and TM have comparable effects on uptake, but the uptake with TS increases significantly (Table 2). The experimental data (Figure 5C)¹⁶ shows that TMV-PEG formulations exhibit low uptake with time. The TMV-RGD formulations, however, display a biphasic behavior: rapid cell uptake within the first 3 h followed by a plateau region with little to no cellular uptake, most likely indicating saturation. This behavior is typical of particle internalization mediated by cell surface receptors.³⁶

The rate of cellular uptake of TMV reported in this study is much smaller than the rates reported for synthetic nanoparticles. Doiron et al.³⁷ reported that spherical polystyrene nanoparticles with diameters ranging from 20 to 500 nm had uptake rates ranging from 6.6 × 10⁷ particles/hour/cell to 12 000 particles/hour/cell respectively within the first 3 h of incubation. In addition Huang et al.³⁴ reported rod-shaped gold nanocrystals (aspect ratio = 3) displaying RGD peptides on their surface had a rate of internalization in A549 lung carcinoma cells equivalent to 4500 particles/cell/hour within the first 2 h of incubation at 37°C. However, the same nanoparticles coated with single-chain variable fragment peptide to target the epidermal growth factor receptor were internalized at a slower rate of 1250 particles/cell/hour. This demonstrates that the rate of cellular uptake is dependent on nanoparticle shape, surface chemistry, and the nature of the molecular receptor targeted.

Model Simulated Uptake of TMV

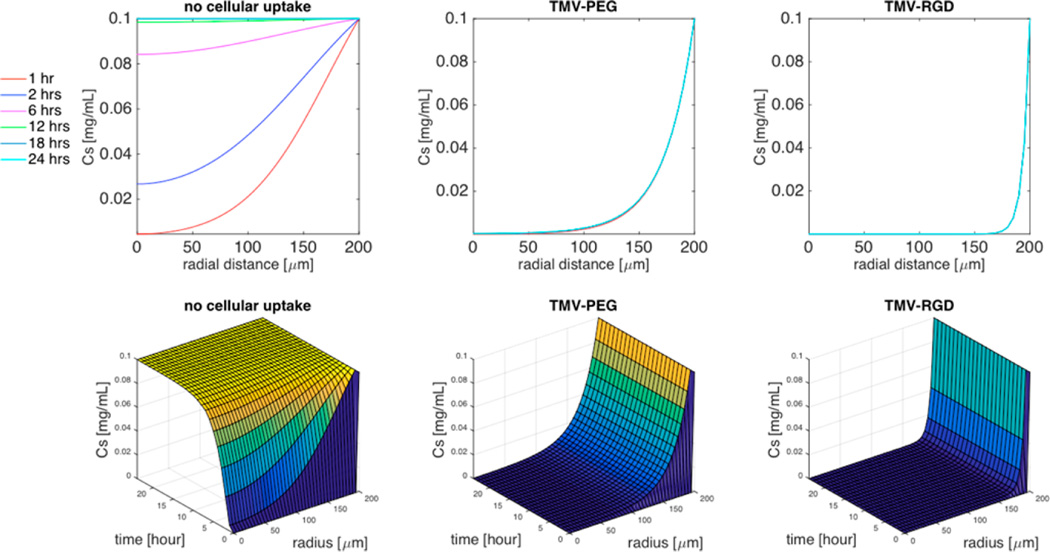
Using the evaluated cellular uptake (k) of TMV formulations (Table 2), we simulated TMV diffusion in a spheroid cell system with different rate coefficients of cell uptake (Figure 6) and aspect ratios (Figure 7). Figure 6 shows the 2D and 3D responses with no uptake (k = 0), low uptake as observed for TMV-PEG, and enhanced uptake as achieved for the TMV-RGD formulation. For these simulations, we set L/d = 300/18, R = 200 µm, and ϕ = 0.5. The TMV concentration decreases significantly with distance into the spheroid even at low cell uptake rate (k = 7) associated with PEGylated particles. As characterized by the dimensionless parameter group (D/kR₂), the cellular uptake of TMV-PEG was 1000-fold greater than its rate of diffusion (Supporting Information S1). This prevents deep tissue penetration because cell uptake occurs at a rate much higher than diffusion. Coating TMV with RGD peptides to target integrin receptors further decreases the TMV concentration within the spheroid. Active targeting of receptors overexpressed on cancer cells (e.g., TMV-RGD targets α_vβ₃ integrin receptors overexpressed on cancer cells) is commonly used to promote tissue specificity and accumulation. However, it is counterproductive for tissue penetration.^38,39

Figure 6.

Simulation of the effect of cellular uptake on the concentration distribution of high aspect ratio (L/d = 300/18) TMV within the spheroid. Top 3 panels are 2D plots of the concentration of TMV formulations as a function of the radial distance within the spheroid for specific time interval (1 h, 2 h, 6 h, 12 h, 18 h, 24 h), and the bottom 3 panels are the corresponding 3D plots of the concentration of TMV as a function of both time and radial distance. Cell density ϕ = 0.5, spheroid radius R = 200 µm, TMV concentration in the surrounding medium C_M = 0.1 mg/mL.

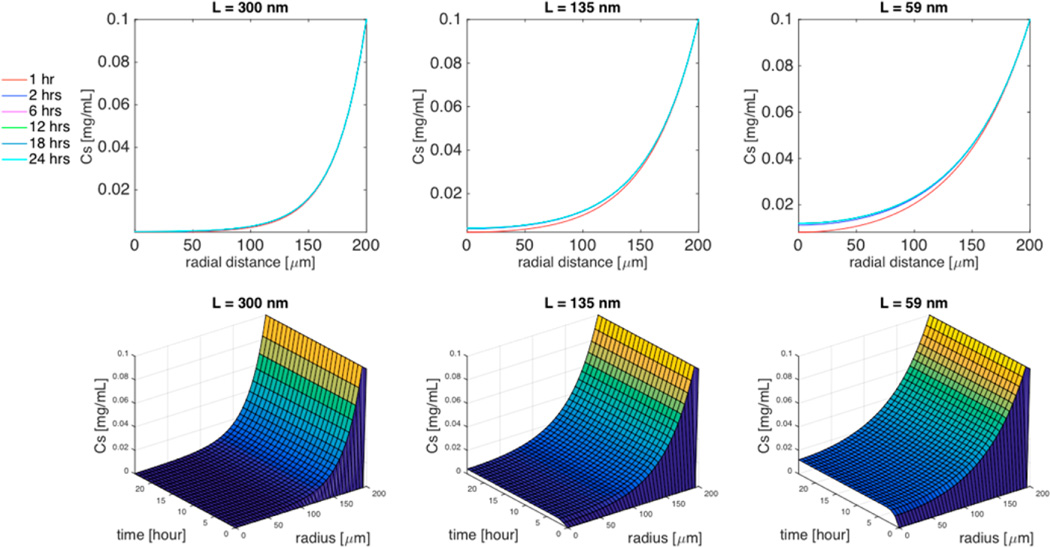
Figure 7.

Simulation of the effect of aspect ratio (L/d = 300/18, L/d = 135/18, or L/d = 59/18) on TMV-PEG concentration distribution within the spheroid. Top 3 panels are 2D plots of the concentration of TMV formulations as a function of the radial distance within the spheroid for specific time interval (1 h, 2 h, 6 h, 12 h, 18 h, 24 h), and the bottom 3 panels are the corresponding 3D plots of the concentration of TMV as a function of both time and radial distance. Cell density ϕ = 0.5, spheroid radius R = 200 µm, TMV concentration in the surrounding medium C_M = 0.1 mg/mL.

The effect of TMV aspect ratio on its concentration distribution in the spheroid with cellular uptake is shown in Figure 7. Here, we assume a TMV-PEG formulation with R = 200 µm, and ϕ = 0.5. In 24 h, the concentration of TMV with the highest aspect ratio (L/d = 300/18) penetrated only 140 µm within the spheroid. For TM (L/d = 135/18), the TMV concentration reached the center of the tumor within 3 h. At steady state, its concentration at the center was 4% of the concentration in the surrounding medium. For TS (L/d = 59/ 18), the TMV concentration reached the center of the tumor within 3 h, but its steady-state concentration at the center was 12% of the concentration in the surrounding medium.

CONCLUSIONS

We developed a mechanistic, mathematical model to describe the intratumoral diffusion properties and cellular interactions of PEGylated and RGD-targeted TMV nanoparticles with distinct aspect ratios. Simulations of our model quantify the effects of spheroid size, cell density aspect ratio, and cellular uptake on TMV diffusion in a spheroid tumor system. Specifically, an increase in cell density decreased the constant rate of diffusion of nanoparticles, while increasing the cellular uptake rate of TMV that prevented deep penetration. Simulations show that PEGylated TMV formulations with the lower aspect ratio accumulate further within the spheroid tumor system because they can diffuse faster than those with a higher aspect ratio. In contrast, TMV nanorods with the targeting ligand RGD of any aspect ratio were rapidly taken up and therefore could not diffuse deeply in the spheroid tumor system. Nonetheless, higher aspect-ratio nanoparticles have enhanced margination toward blood-vessel walls, increased transport across tissue membranes, and reduced clearance by phagocytosis. In that regard, a balance must be established between immune evasion, tumor homing, and tissue penetration. Although our model takes into account only some factors of tumor pathophysiology and nanoparticles design, it can be enhanced to incorporate other important factors. Together with corresponding experimental data, this model can provide an important advance in nanomedical science and engineering.