Circular Photogalvanic Effect in Organometal Halide Perovskite CH₃NH₃PbI₃

Abstract

We study the circular photogalvanic effect in the organometal halide perovskite solar cell absorber CH₃NH₃PbI₃. The calculated photocurrent density for a system with broken inversion symmetry is about 10⁻⁹ A/W, comparable to the previously studied quantum well and bulk Rashba systems. The circular photogalvanic effect relies on inversion symmetry breaking, so that by tuning the optical penetration depth, the degree of inversion symmetry breaking can be probed at different depths from the sample surface. We propose that measurements of this effect may clarify the presence or absence of inversion symmetry, which remains a controversial issue and has been argued to play an important role in the high conversion efficiency of this material.

Organometal halide perovskites are emerging thin-film photovoltaic materials which can be fabricated with solution methods and exhibit remarkable power conversion efficiency. Both ABX₃ (A: CH₃NH₃, HC(NH₂)₂; B: Pb, Sn; X: Cl, Br, I) and their hybrids have exceptional photovoltaic performance and also show promise as LEDs, lasers and X-ray detectors.^1–3 In spite of the rapid progress in the power conversion efficiency, reaching more than 20 % since its first application in 2009, a basic question about the crystal structure persists regarding the presence or absence of inversion symmetry. This question is especially important in light of theoretical works which propose that inversion asymmetry inhibits recombination and therefore plays an important role in the high efficiency of these materials.^4–6 Stoumpos et al. proposed that the crystal belongs to the noncentrosymmetric I4cm space group with a ferroelectric distortion and octahedra rotation.⁷ First-principles calculations suggest that a ferroelectric distortion could be stable.^4,8,9 In addition, Rashba spin-splitting of the electronic band structure due to inversion symmetry breaking was observed in angle resolved photoemission (ARPES) measurements.¹⁰ However, there is also a significant body of work which indicates that the material is centrosymmetric. The hysteretic current-voltage behavior has been ascribed to charge trapping at the surface and ionic migration under applied bias.^11–15 The crystal structure has been assigned to the centrosymmetric I4/mcm space group^16–18 and centrosymmetry was assumed to explain the observed temperature-dependent spin dynamics.¹⁹

The magnitude of inversion symmetry breaking generically differs between the surface and bulk regions; indeed, inversion symmetry is always strongly broken at surfaces. The distinction between bulk and surface inversion symmetry properties has important consequences for the interpretation of surface sensitive experimental techniques, such as ARPES. Signatures of inversion symmetry breaking, such as Rashba splitting of the energy bands observed in ARPES, may be specific to the surface and may not be present in the bulk¹⁰.

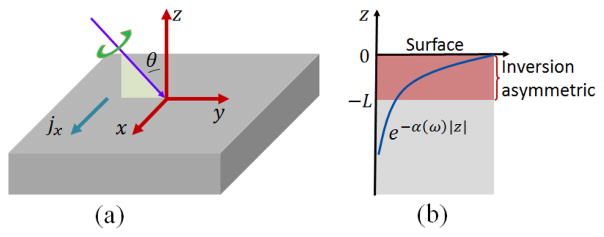
In this paper, we propose that the circular photogalvanic effect offers a route to determining the degree of inversion symmetry breaking at the surface and in the bulk separately. The magnitude of the circular photogalvanic effect is parameterized by the response function χ, which relates the induced charge current density to the electric field intensity of the incoming circularly polarized light. χ is nonzero only in materials which lack inversion symmetry. Fig. 1 (a) shows the cartoon of the circular photogalvanic effect measurement setup in which circularly polarized light induces a photocurrent J.

FIG. 1.

(a) Schematic of the circular photogalvanic measurement. The incident light with right circular polarization is propagating within the ŷ-ẑ plane (indicated by the light green triangle) with incidence angle θ. Inversion symmetry breaking is assumed along ẑ direction. Photocurrent is flowing perpendicular to the plane of incidence. In our model system, the photocurrent is along the x̂ direction. (b) Schematic of a situation that the inversion asymmetry is only present over a distance L from the sample surface indicated by the pink rectangle. The light intensity follows an exponential decay e^−α(ω)|z| with α(ω) being the absorption coefficient and |z| being the distance away from the surface.

Circularly polarized light with different energies ħωand absorption coefficients α(ω) probes different depths away from the surface. One can therefore distinguish between the circular photogalvanic response (or, the degree of inversion symmetry) at the surface versus the bulk by evaluating the energy dependence of the photocurrent J(ω). Fig. 1 (b) shows a schematic in which inversion symmetry is broken only over a distance L from the sample surface. In this case, the circular photogalvanic current is only generated over the thickness L from the surface and the photocurrent J(ω) is proportional to χ(ω) (1 − e^−α(ω)L). The energy-dependence of J(ω) is determined by the energy dependence of α(ω) convoluted with the intrinsic energy dependence of the circular photogalvanic response function χ(ω). A measurement of J(ω) can therefore determine the spatial dependence of centrosymmetry only given a priori knowledge of the energy dependence of the absorption α(ω) and the response function χ(ω).

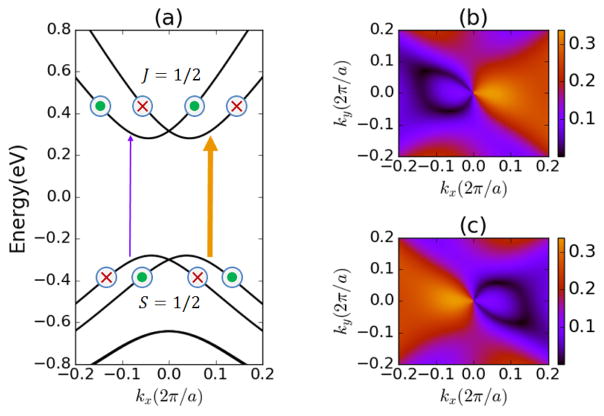
Motivated by these considerations, we report a first-principles density functional theory study on the energy dependent circular photogalvanic effect, focusing on noncentrosymmetric tetragonal CH₃NH₃PbI₃. The absence of inversion symmetry, together with the strong spin-orbit coupling in the heavy element Pb, leads to the Rashba-type band splitting as depicted in Fig. 2 (a). The conduction band states near the Fermi level are derived from the p orbital of Pb (with orbital angular momentum L = 1). Due to the spin-orbit coupling, the bands are labeled by total angular momentum J = L + S, and the conduction band consists of the split-off J = 1/2 states.^20,21 For the valence bands, the states are composed of the anti-bonding Pb s orbital and I p orbital, forming a singlet s-orbital symmetry. This leads to a Rashba-type splitting in S = 1/2 space with spin-orbit coupling.

FIG. 2.

(a) depicts the Rashba-type band structure of CH₃NH₃PbI₃ along k_x(k_y = 0, k_z = 0). For S = 1/2 valence bands, circles with cross (red) and dot (green) indicate the spin orientations pointing into and out of the paper, respectively. For J = 1/2 conduction bands, the labeled orientations correspond to the total angular momenta. The arrows with different thickness represent the asymmetric transition rates at k and −k for right circularly polarized light. (b) and (c) show matrix elements $\frac{1}{2}\mid \langle {\psi }_{\mathrm{c}}(\mathbf{k})\mid {\widehat{p}}_x\pm i{\widehat{p}}_z{\mid {\psi }_{\mathrm{v}}(\mathbf{k})\rangle \mid }^2$ for transitions between highest valence band and lowest conduction band. + and − correspond to right and left circularly polarized light, respectively.

In these Rashba-type bands, the valence band S and conduction band J have a preferred orientation perpendicular to both the momentum and the inversion symmetry breaking direction.²² Because of angular momentum selection rules, optical transitions between conduction and valence energy states respond differently to light with different circular polarization direction. The asymmetric distribution of excited charge carriers leads to a photocurrent in the absence of an external bias. For a Rashba model, the photocurrent direction is normal to the plane formed by the light angular momentum and the bulk symmetry breaking direction.²³ A characteristic feature of circular photogalvanic effect is that incident light with right and left circular polarization will lead to photocurrents flowing along opposite directions.

Figs. 2 (b) and (c) show the optical transition amplitudes versus wave vector for right and left circularly polarized light. The transitions exhibit strong k dependence and energy states with k_x > 0 (< 0) make more contribution to the photocurrent for right (left) circularly polarized light. Moreover, the transition at k for right circular polarization is equal to that at −k for left circular polarization, indicating the characteristic dependence of photocurrent on circular polarization. This effect has been observed in bulk Te, GaAs and InAs quantum wells as well as bulk GaAs subjected to an external magnetic field.^23–26 It was also used to demonstrate the Rashba spin splitting in GaN-based heterostructures and to detect the lattice polarity of InN.^27,28 Recently this effect was observed in bulk Rashba system BiTeBr and theoretical studies have been reported on an ultrathin film of topological insulators and on graphene deposited on heavy-element substrates.^29–31

Because the spin-orbit coupling effect is dominated by the heavy element Pb, the molecular orientation and the ensuing distortion of PbI₆ octahedron plays an important role in determining the symmetry breaking.³² We study a system with all molecules initially arranged along ẑ direction to obtain a larger inversion symmetry breaking. The density functional theory calculations are carried out using local density approximation in the form of norm-conserving pseudopotentials as implemented in Quantum-ESPRESSO³³. Technical details of the DFT calculations are found in Ref. 34. To remedy the underestimation of the energy gap in local density approximation, the calculated curve has been rigidly shifted to match an experimental energy gap of 1.5 eV. The tetragonal lattice structure we consider is noncentrosymmetric and exhibits ferroelectricity. The polarization is calculated to be 10.7 μC/cm² using Berry phase approach.

By considering the response of the system to a monochromatic electric field of frequency ω

$$\mathbf{E}(t)=\mathbf{E}(\omega )e^{-i\omega t}+{\mathbf{E}}^{\ast }(\omega )e^{i\omega t},$$ (1)

we solve semiconductor optical Bloch equations perturbatively to first order in the field intensity³⁵ and derive the photocurrent generation rate J̇ given by

$$j^i={\chi }^{\mathit{ilm}}(\omega )E^{l\ast }(\omega )E^m(\omega ),$$ (2)

where

$${\chi }^{\mathit{ilm}}(\omega )=\frac{2\pi e^2}{{\hslash }^2{\omega }^2}\frac{1}{V}\sum _{\mathbf{k}}\sum _{\mathrm{c},\mathrm{v}}(J_{\mathrm{c}}^i-J_{\mathrm{v}}^i)\times v_{\text{cv}}^{l\ast }(\mathbf{k})v_{\text{cv}}^m(\mathbf{k})\delta [{\omega }_{\text{cv}}(\mathbf{k})-\omega ].$$ (3)

In Eq. 3, $v_{\text{cv}}^m(\mathbf{k})=\langle {\psi }_{\mathrm{c}}(\mathbf{k})\mid {\widehat{v}}^m\mid {\psi }_{\mathrm{v}}(\mathbf{k})\rangle$ is the velocity operator matrix element between conduction and valence band states, $J_{\mathrm{c}(\mathrm{v})}^i=\langle {\psi }_{\mathrm{c}(\mathrm{v})}(\mathbf{k})\mid e{\widehat{v}}^i\mid {\psi }_{\mathrm{c}(\mathrm{v})}(\mathbf{k})\rangle$, and ω_cv(k) = (E_ck − E_vk)/ħ. ψ_c(v) (k) represents the wave function of conduction (valence) band with energy E_c(v)k. The superscripts i, l and m indicate Cartesian components and summation over repeated indices is implied. We first calculate the energies and momentum matrix elements on a coarse grid in momentum space and employ Wannier interpolation technique^36–38 to evaluate the photocurrent response (Eq. 3) on a fine grid of 100 × 100 × 75 k-points. This method has been applied in the study of optically injected spin current.³⁴

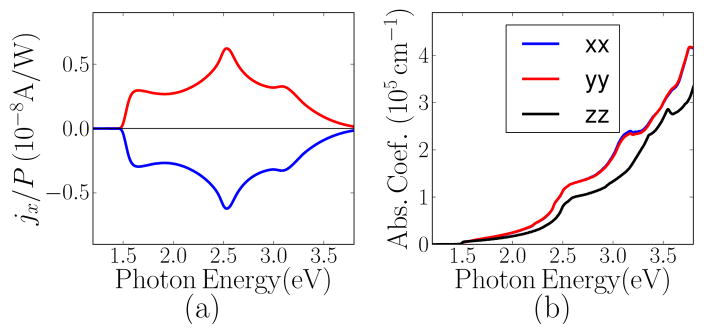
Since the system under study assumes inversion symmetry breaking along ẑ direction, the spin orientation is confined in the x̂–ŷ plane as expected from the Rashba model. Neglecting reflection from the surface, we find the largest response corresponds to the circularly polarized light incident along the ŷ direction (incidence angle θ = 90°, see Fig. 1) with electric field $\mathbf{E}(\omega )=\frac{1}{\sqrt{2}}{E}^0(\widehat{x}\pm i\widehat{z})$ where + and − correspond to right and left circular polarization, respectively. In the momentum relaxation time approximation under direct optical transitions we have j_x = J̇^xτ.²³ We assume the momentum relaxation time τ = 1 fs for both electrons and holes. Fig. 3 (a) depicts the calculated ratio of photocurrent density j_x to radiation power P as a function of photon energy ħω and clearly shows the switching of photocurrent direction upon the circular polarization reversal, a characteristic feature of the circular photogalvanic effect. The peak value is about 0.6 × 10⁻⁸ A/W, which is comparable with the previously reported photocurrents in n-InAs and p-GaAs quantum wells²³ and bulk Rashba semiconductor BiTeBr³⁹.

FIG. 3.

(a) Photocurrent density j_x normalized to the radiation power P as a function of the incident photon energy ħω with respect to the energy gap for an incidence angle θ = 90°. Positive (Negative) photocurrent direction corresponds to right (left) circularly polarized light. (b) Absorption coefficients for different polarizations as a function of incident photon energy. The close similarity between absorption coefficients for xx and yy polarizations corresponds to the symmetry of the system under study.

We next calculate the absorption coefficient as a function of the incident photon energy ħω as depicted in Fig. 3 (b). The calculated absorption coefficient is comparable to the experimental value,⁴⁰ and to the value obtained in other density functional theory studies.^41,42 Fig. 3 (b) indicates that the absorption depth goes from 1000 nm for photon energies near the band gap, to 50 nm at 3 eV. The surface and bulk dominate the photocurrent for large and small photon energies, respectively. As discussed in the introduction, this enables a systematic study of the inversion asymmetry at different depths away from the surface.

For the depth-dependent circular photogalvanic response, the current versus optical frequency varies as:

$$J(\omega )\propto {\int }_0^{\infty }{e}^{-\alpha (\omega )z}\chi (\omega ,z)dz.$$ (4)

In the above, the z-dependence of χ is derived from the spatial variation of the inversion symmetry breaking. We consider a model in which inversion symmetry is assumed to be uniformly broken over a length L from the surface (see Fig. 1 (b)): χ (ω, z) = χ (ω) θ (z + L) for z < 0, where θ (x) is the Heaviside step function. In this case a photocurrent is generated if the absorption occurs within a length scale of L. For metals, L is only a few atomic layers⁴³, but in semiconductors, L can be as large as the depletion width.

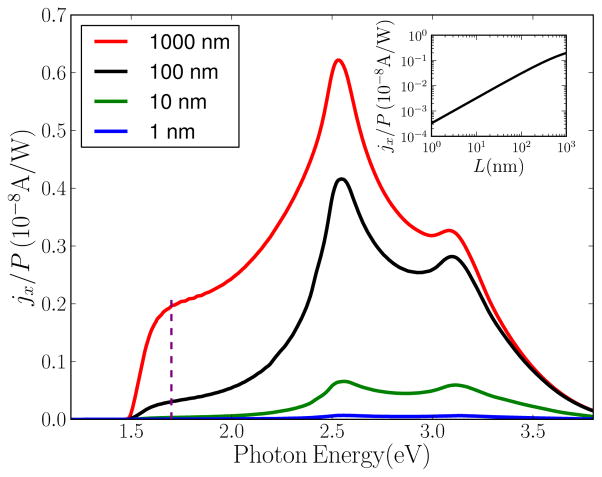
To illustrate how the photocurrent response varies with the symmetry breaking length L, in Fig. 4 we show the normalized photocurrent density j_x/P (see Fig. 3 (a)) scaled by the factor 1 − e^−α(ω)L for L varying from 1 nm to 1 μm. As expected, a smaller inversion asymmetric region L suppresses the photogalvanic current, especially at lower photon energies which probe further from the surface. As shown in the inset, the photocurrent density for photon energy of 1.7 eV varies monotonically with L, and measurements which vary the angle and energy of the incident beam can be used to estimate L experimentally. The growth of mm-sized single crystals of CH₃NH₃PbI₃ makes it possible to observe the intrinsic bulk and surface inversion symmetry.^44,45 In polycrystalline samples, grain boundaries may break inversion symmetry locally, and could therefore contribute to the circular photogalvanic effect. However, if the optical spot size is much greater than the grain size, there should be substantial cancellation between the circular photogalvanic effect arising from grain boundaries with different orientations, so that on average their contribution would be negligible. On the other hand, for grain sizes similar to (or larger than) the spot size, the circular pho-togalvanic effect arising from individual grain boundaries may be present and could serve as a useful probe of the symmetry properties of the material near grain boundaries.

FIG. 4.

The normalized photocurrent density j_x/P scaled by the factor 1 − e^−α(ω)L for L = 1000, 100, 10 and 1 nm. The log-scale photocurrent density at 1.7 eV indicated by the vertical dashed line is plotted in the inset as a function of log-scale symmetry breaking length L.

In order to observe photocurrent response when the inversion symmetry breaking is due to the sample surface (as shown in Fig. 1), oblique incidence (θ ≠ 0) is required. If the x̂–ŷ plane is isotropic and inversion symmetric, then normally incident light (θ = 0) leads to the cancellation for the photocurrent contributions at k and −k and therefore, zero net photocurrent. We estimate the photocurrent response reaches its maximum at θ ≈ 45°.²³ However, lattice distortion transverse to the surface normal may be present. McLeod et al. found that perovskite thin films made by the one-step deposition method exhibit angle-dependent features in X-ray absorption spectroscopy measurements, indicating long-range alignment of the dipolar CH₃NH₃ molecules parallel to the surface.⁴⁶ In this case, the photocurrent response can be detected with a nonzero photocurrent response for θ = 0.

As referenced in the introduction, inversion symmetry breaking could play an important role in the properties of photovoltaic materials. In the case where the bulk is inversion symmetric, the presence of inversion asymmetry at the surface may nevertheless be useful. In Ref. 34, we showed that the Rashba splitting associated with broken inversion symmetry leads to spin accumulation in illuminated samples due to the Edelstein effect. The spin direction is oriented perpendicular to the symmetry breaking direction and carrier velocity. Measuring the spin density could therefore indicate the velocity direction of carriers, which could in turn help elucidate the role of grain boundaries and other defects on charge transport.

In summary, we report on first-principles density functional study on the optical generation of photocurrent with circularly polarized light in the organometal halide perovskite CH₃NH₃PbI₃. We found that the photocurrent response is comparable with that of previously studied quantum well and bulk Rashba systems. We propose that the circular pho-togalvanic effect would be useful in determining the degree of inversion symmetry breaking near the sample surface and in the bulk.