Measuring transport of water across the peritoneal membrane

Abstract

Introduction

Mechanisms of water flow across the peritoneal membrane include diffusion, convection, and reabsorption.

Objectves

To understand these processes more clearly we have developed a method to measure transport of water across the peritoneal membrane.

Methods

An artificial gradient of deuterated water (HDO) between blood and dialysate compartments was created in five subjects who took 0.3g per kg of body weight of D₂O, which was allowed to equilibrate with total body water. During a test dwell (2 L, bicarbonate:lactate buffer, 1.36% glucose to minimize convection), frequent dialysate samples were drawn to determine the abundance of deuterium and other solutes and to calculate their time constants. Dialysate deuterium abundance was measured using flowing afterglow mass spectrometry (FA-MS). The method was combined with ^l25iodine-labeled albumin (RISA) to enable simultaneous estimates of intraperitoneal volume and thus calculation of the mass transfer area coefficient (MTAC) for small solutes using the Garred equation.

Results

The appearance of HDO in dialysate in four subjects is described by a single exponential fit with residuals of <1%, similar to method precision. In a fifth subject, the resolution of this method demonstrated that the best fit was a double exponential. When compared to other solutes, the time constant for water was as predicted by its molecular weight, with a MTAC of 38.7 ± 4.4 mL/min. Total body water could also be estimated from the equilibrated dialysate deuterium abundance, with repeat estimates within 0.5%.

Conclusion

Transport of water across the peritoneum can be measured with remarkable accuracy and when combined with an intraperitoneal volume estimation can be used to determine mass transfer. In conditions of low convection, the relative rate of deuterium appearance and mass transfer compared to other solutes suggests that water diffuses predominantly through the intercellular small pores.

Variability in membrane function is the only intrinsic aspect of peritoneal dialysis treatment that has been shown to influence clinical outcome, with poor ultrafiltration an important cause of technique failure [1]. Diffusion, convection, and reabsorption (part convective, part lymphatic) are all mechanisms involved in the movement of water across the peritoneal membrane. The “three-pore” and “distributed” models have been developed to describe the net movement of water by convection and reabsorption and the diffusive and convective components of solute transport [2-5]. However, water also diffuses across the membrane, and an understanding of all these processes is required to extend our knowledge of the anatomic structure and physiology of the peritoneum. We have developed a method for measuring the rate of deuterium appearance, and thus transport of water across the peritoneal membrane following the creation of an artificial gradient of deuterated water (HDO) between blood and dialysate compartments. Comparison of transport rate, expressed as the time constant, was made with other molecular species of varying sizes. The method was also combined with the intraperitoneal volume marker, ¹²⁵RISA, to determine convection and reabsorption, and thus calculate the mass transfer area coefficient (MTAC) for water using the Garred equation.

STUDY DESIGN

In order to measure the transport of any species across a semipermeable membrane, it is necessary to establish a concentration gradient. This presents a problem when the species concerned is water, which we resolved by creating an artificial deuterated water (HDO) gradient, achieved by loading the total body water space with a standard dose of D₂O and then performing a test dialysate exchange to measure the rate of appearance of HDO in the peritoneal cavity. This was then compared with the rates of appearance of a number of other solutes, selected for their molecular weights, ranging between 60 and 68,000 D. Intraperitoneal volumes were determined from the dilution of ¹²⁵I labeled albumin (90 kBq) after correction for incomplete recovery due to reabsorption as described [6].

STUDY PROTOCOL

Detailed studies were carried out in five stable peritoneal dialysis patients. The overnight peritoneal fluid was drained out and deuterium oxide (D₂O, 99.9% pure, dose 0.3g per kg of body weight) was administered orally, mixed up to a volume of 100 mL with water, followed by 100 mL of tap water. Fresh dialysate fluid was instilled into the peritoneal cavity and 3 hours were allowed for equilibration between HDO and the total body water. Previous studies have demonstrated this occurs between 2 and 3 hours [7]. Following equilibration, a test exchange, consisting of 2 L normal pH, bicarbonate/lactate solution (Physioneal, Baxter, Thetford, UK) was infused. In each case a three- to fourfold deuterium abundance gradient between fresh dialysate (∼156 ppm) and the total body water (∼500 ppm) was achieved. A low, 1.36%, glucose concentration was specifically selected to minimize the effects of convection. Normal pH, bicarbonate solution was selected to avoid interference by acetaldehyde in the flowing afterglow mass spectrometry (FA-MS) assay.

ANALYTICAL METHODS

Dialysate deuterium abundance was measured using FA-MS. This recently described method [8, 9] exploits mass spectrometry allied to fast flow tube technology to measure changes in the fraction of the deuterated ${\mathrm{H}}_8{\mathrm{DO}}_4^{+}$ ions compared to nondeuterated ions ${\mathrm{H}}_9{\mathrm{O}}_4^{+}$ in an ion swarm as a direct measure of the deuterium content of the headspace water vapor above dialysate. Samples are aliquoted into sealed flasks, which are brought to body temperature (37°C) in a water bath. Sampling of the headspace is achieved by passing a needle through a rubber septum, enabling the water vapor to enter the flow tube via a calibrated capillary leak. The accuracy and precision of the method in evaluating deuterium abundance are within 1% [10]. Plasma and dialysate concentrations of urea, creatinine, urate, and glucose were determined on an automated discrete random access analyzer (DAX 72, Bayer Instruments, Basingstoke, UK). Solutes were assayed by indirect ion electrode or enzymatic assay in the case of urate and albumin by the bromocresyl purple method.

DATA ANALYSIS

Time constants, τ, for the appearance of each solute in dialysate were calculated using the formula:

$$D\left(t\right)=P-(P-D\left(0\right))\exp \left(-\frac{t}{\tau }\right)$$

where D = dialysate and P = plasma concentration of solutes. The unweighted least squares method was used to find, where possible, the best fit single exponential function to describe the data, from which the time constant (in minutes) was derived. Examining the residuals assessed the quality of the fit. The derived time constants for each solute were then averaged and plotted against their molecular weight.

Estimates of the intraperitoneal volume were combined with the dialysate and plasma solute/HDO concentrations to calculate the mass transfer coefficients using the Garred equation:

$$\mathit{MTAC}=\frac{V\left(t_d\right)}{t_d}\ln \left(\frac{V\left(0\right)(P-D\left(0\right))}{V\left(t_d\right)(P-D\left(t_d\right))}\right)$$

where V = intraperitoneal volume and t_d is the dwell time, (selected at 120 minutes) [11]. Total body water was calculated from the known administered dose of deuterium oxide and the incremental increase in dialysate deuterium abundance from baseline to asymptotic value using the dilution principle [7].

RATE CONSTANTS FOR HDO TRANSPORT

Demographic and routine clinical characteristics of the patients are described in Table 1. The increase in the deuterium abundance in dialysate was best described by a single exponential fit in four subjects and a double exponential in the fifth subject (Figs. 1 and 2). The quality of fit was excellent with the residuals being less than 1% in each case (Table 2). The time constant for water transport in the individuals exhibiting a single exponential ranged between 46 and 53 minutes. In the fifth subject, two time constants could be resolved, a short time constant of 33 minutes and a longer time constant of 156 minutes. This individual had the highest transport rate for all solutes of all the subjects studied, suggesting that the diffusion of HDO across the peritoneal membrane outstrips the equilibration between the total body water intracellular and extracellular compartments with the blood compartment (Table 1). We thus took the shorter time constant as indicative of transport across the peritoneum in this individual, giving an average rate constant of water diffusion for these five subjects of 44 ± 7 minutes (mean ± SD).

Table 1.

Demography, peritoneal solute transport characteristics and derived time constants for water

Subject	Age	Body surface area	Months on peritoneal dialysis	Solute transport (D/Pcreatinine at 4 hours)	HDO time constant minutes	MTAC for HDO mL/min	Total body water kg	Body water (as % body weight)
1. (Male) BW	35	2.09	24	0.72	43	36.6	49.18	57.9
2. (Male) AW	53	2.08	13	0.61	47	40.2	51.14	56.7
3. (Male) JK	53	1.59	31	0.71	46	45.2	33.9	63.3
4. (Male) PJ	63	1.77	19	0.73	53	38.7	40.9	52.8
5. (Male) AB	61	1.71	35	0.81	33	33.1	35.8	61.8

Abbreviations are: HDO, deuterated water; MTAC, mass transfer area coefficient.

Fig. 1. Dialysate deuterium appearance in one subject described by a single exponential function.

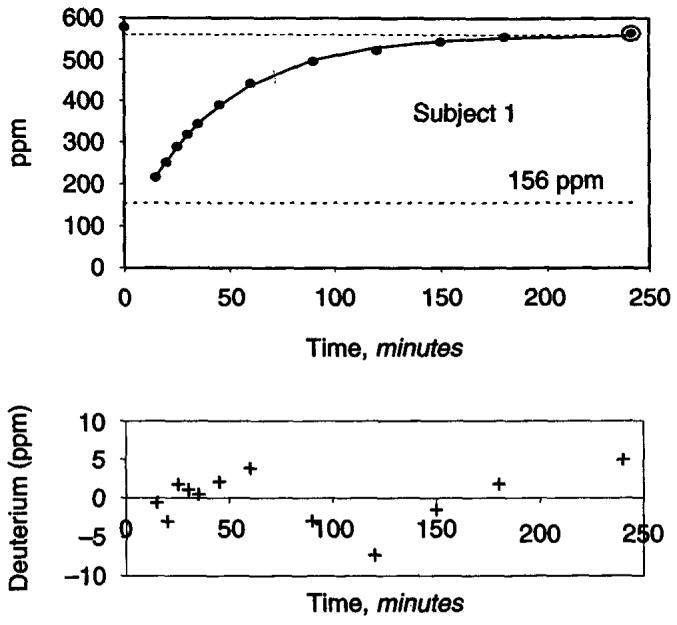
Lower panel shows the plot of residuals (difference between actual and predicted deuterium abundance).

Fig. 2. Dialysate deuterium appearance in one subject described by a double exponential function.

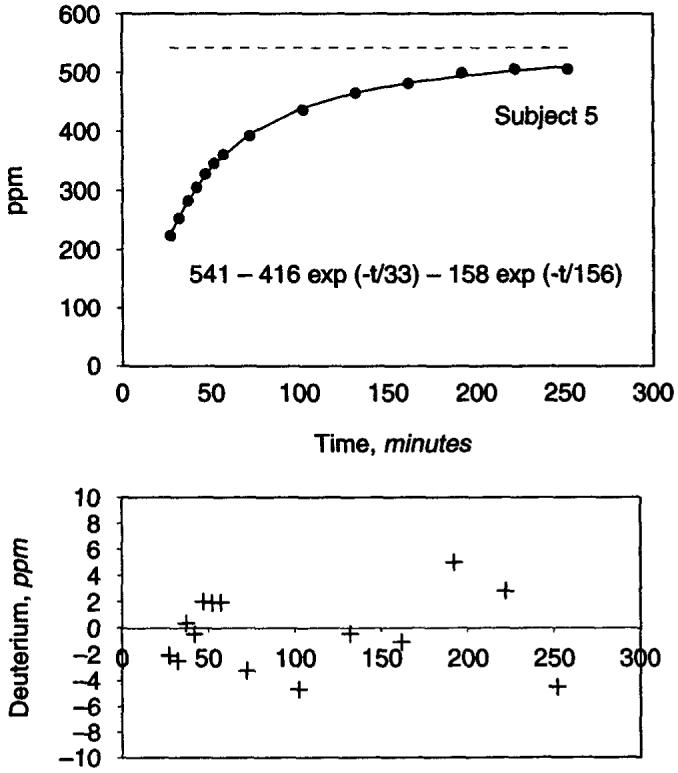
Lower panel shows the plot of residuals.

Table 2.

Actual measurements of dialysate deuterium abundance during each peritoneal exchange and the difference (residual) between these and values obtained from curve-fitting used to obtain rate constants

	Deuterium abundance ppm
Time minutes	Subject 1		Subject 2		Subject 3		Subject 4		Subject 5
	Actual	R	Actual	R	Actual	R	Actual	R	Actual	R
Previous equilibrated exchange	578		588		517		582		512
15	216	−1	219	−5	260		272		224	−2
20	258	−3	266	7	284	1	293	1	254	−3
25	289	2	289	−2	303	−2	317	0	283	0
30	318	1	318	−1	324	−1	340	0	305	0
35	344	1	348	3	345	2	359	−1	327	2
45	390	2	389	0	371	−2	391	−5	361	2
60	442	4	434	−5	409	1	443	4	392	−3
90	496	−3	505	4	452	1	501	5	436	−5
120	522	−7	534	0	471	−3	526	−2	466	0
150	543	−2	550	−1	488	3	542	−5	481	−1
180	554	2	556	−4	490	−1	560	3	499	5
240	563	5	572	4	496	0	567	0	505	−5

R is residual.

COMPARISON WITH OTHER SOLUTES

With the exception of urate, increase in molecular size was associated with a progressive increase in time constants reflecting slower transport across the peritoneum (Fig. 3A). The calculated time constants for urea, molecular weight of 60 Daltons (D), creatinine (molecular weight, 113 D), and glucose (molecular weight, 180 D) were 115 ± 21 minutes, 178 ± 54 minutes, and 235 ± 45 minutes, respectively. Albumin, with a significantly larger molecular weight of 68000 D, exhibited much slower progression across the peritoneum with time constants of 27332 ± 7600 minutes. Despite its size, movement of urate (molecular weight, 168 D) was faster than anticipated at 154 ± 54 minutes (Fig. 3A). The MTAC for water was 38.7 ± 4.4 mL/min (individual values shown in Table 1), urea 18.2 ± 2.3 mL/min, creatinine 10.5 ± 2.04 mL/min, urate 8.9 ± 3.4 mL/min, and glucose 8.7 ± 1.7 mL/min (for log-linear plot against molecular size, see Fig. 3B).

Fig. 3.

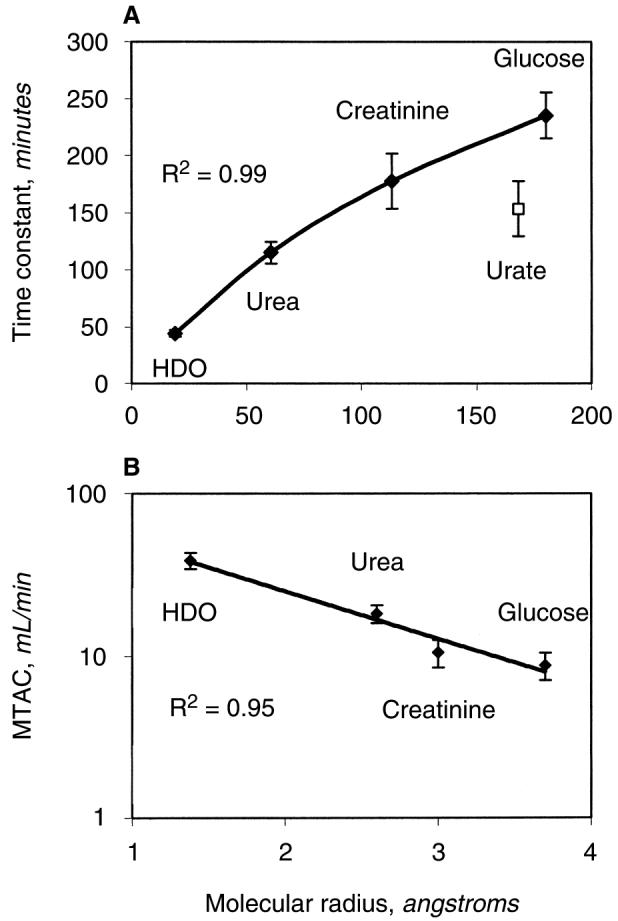
Relationship between (A) the time constants and (B) the mass transfer area coefficients (MTAC) for small solutes and their molecular weight.

TOTAL BODY WATER

The values for volume of distribution are shown in Table 1 along with body water expressed as a percentage of body weight. These values are typical for adult males. It was possible to estimate body water twice during these experiments, first from the equilibrated value prior to the test exchange and then again from the test exchange itself. The average difference between these two estimates was 1.84 ± 0.26 kg, very close to the actual volume of dialysate instilled (2 L), indicating that the average error of this estimate is 160 mL or 0.4%.

We have, for the first time, measured transport of water transport across the dialyzed peritoneal membrane in humans. When combined with estimates of intraperitoneal volume, this enabled determination of the mass transfer, and thus an estimate of the diffusive component of water flow. It is based on the assumption that the diffusion characteristics of HDO closely resemble those of H₂O. The molecular weight (18 vs. 19 D) and radius of these molecules are similar and well within the pore size that has been proposed for diffusion of small solutes [2-5]. In contrast to convection, which for water occurs through two distinct pore systems (inter- and transcellular routes), ∼95% of the diffusion of water will occur through the intercellular pores, estimated at 43 Å [2]. It is, therefore, unlikely that the diffusion characteristics of H₂0 and HDO are significantly different. The method also enables determination of total body water in these patients with remarkable precision (<1%).

For any solute diffusing passively down a gradient that is diminishing with time, changes in concentration will be best described by a single exponential function, as was seen here for deuterated water in the majority of our subjects. The precision of the sampling and analysis of deuterium were exceptional using this procedure, as demonstrated by the very low residuals obtained when fitting the exponential functions. In all cases, they were within 1% of the measured deuterium abundance, or within just 5 ppm of those predicted. This is typical of the exceptional accuracy and precision that can be achieved using the new FA-MS method developed in our laboratory [10]. This observation also suggests that mixing of water once it had entered the peritoneal cavity was rather uniform. It is largely because of this degree of accuracy that we were able to resolve a double exponential fit to the data for one of the subjects. The distinguishing characteristics of this individual were the relatively high transport rate across the peritoneum for all solutes and previous aortic aneurysm surgery. This mismatch between the effective peritoneal surface area for small solutes and the appearance of water has led us to hypothesize that in this case the transport between blood and dialysate either outstrips the diffusion between the rest of the body water space and blood or that peritoneal blood flow is the limiting factor [5]. Normally the diffusion of solutes across the peritoneal membrane is envisaged using a two-compartment model, whereas this observation would suggest that for very small solutes, when the peritoneum has high solute transport rates, that a three-compartment model should be used. This case also illustrates that if total body water is to be determined from this method, sufficient samples during the dwell must be taken to enable calculation of the asymptotic value.

When the rate constant and mass transfer for HDO are compared with other solutes, it is apparent that water transport across the peritoneal membrane is at a rate commensurate with its molecular weight and size. This would imply that water passes predominantly through the same intercellular pore system as the other solutes examined and that under these conditions of low convection, (the mean intraperitoneal volume at 2 hours was 1957 ± 151 mL, with a peak ultrafiltration rate of ∼lmL/min), additional transport through aquaporins is minimal. This is in keeping with observations comparing tritiated water transport in normal and aquaporin knockout mice, in which no difference in the rate of disappearance from dialysate was seen, again under conditions of minimum convection [12]. This preliminary conclusion will need to be confirmed from paired experiments to remove confounding factors such as the influence of dialysate sump volume within the pelvis, using different osmotic agents to explore the various pore pathways.

The exception to the rest of the solutes measured in this study was urate, which exhibited a shorter time constant than predicted for its molecular weight, possibly because it is an ion, although this usually results in longer time constants. This has not been reported previously, although there are data that suggest that unrestricted diffusion is not the only mechanism of urate transport across the peritoneal membrane [13].