Tight Graph Framelets for Sparse Diffusion MRI q-Space Representation

Abstract

In diffusion MRI, the outcome of estimation problems can often be improved by taking into account the correlation of diffusion-weighted images scanned with neighboring wavevectors in q-space. For this purpose, we propose in this paper to employ tight wavelet frames constructed on non-flat domains for multi-scale sparse representation of diffusion signals. This representation is well suited for signals sampled regularly or irregularly, such as on a grid or on multiple shells, in q-space. Using spectral graph theory, the frames are constructed based on quasi-affine systems (i.e., generalized dilations and shifts of a finite collection of wavelet functions) defined on graphs, which can be seen as a discrete representation of manifolds. The associated wavelet analysis and synthesis transforms can be computed efficiently and accurately without the need for explicit eigen-decomposition of the graph Laplacian, allowing scalability to very large problems. We demonstrate the effectiveness of this representation, generated using what we call tight graph framelets, in two specific applications: denoising and super-resolution in q-space using ℓ₀ regularization. The associated optimization problem involves only thresholding and solving a trivial inverse problem in an iterative manner. The effectiveness of graph framelets is confirmed via evaluation using synthetic data with noncentral chi noise and real data with repeated scans.

1 Introduction

Diffusion-weighted MR signals, in addition to the diffusion time, are controlled by a quantity called wavevector. The wavevector is dependent on the length, strength, and orientation of the gradient pulses during the measurement sequence. It is often denoted as vector q, which can be separated into a scalar wavenumber |q| and a diffusion encoding direction q̂ = q/|q|. The effects of both diffusion time, t, and wavenumber are summarized using a quantity called b-value, which is defined as b = t|q|². A diffusion MRI protocol normally acquires multiple diffusion-weighted images, each corresponding to a wavevector q in q-space. For example, in shell acquisition schemes, b is fixed by fixing both t and |q| and only the gradient direction varies among measurements. This can be extended to multi-shell acquisition, where the measurements are collected at shells of different b-values. These images afford microstructural information that can be harnessed for tissue characterization and axonal tracing.

Due to the noisy nature of diffusion MRI, it is often beneficial to leverage the correlation between diffusion-weighted images acquired with neighboring wavevectors in q-space for improving estimation robustness in applications such as denoising and compressed-sensing reconstruction. To achieve this, a common practice is by fitting a diffusion model to the data, concurrently taking into account all q-space measurements at each voxel. Such approach, however, is dependent on specific assumptions the model makes regarding the data. For example, the diffusion tensor model assumes that the signals at each voxel reflect only axon bundles that are aligned in one coherent direction, hence falling short in capturing the complexity of the water diffusion patterns in the human brain.

In this paper, we take a wavelet-based approach, which is less dependent on specific biophysical assumptions, to constructing sparse representations for diffusion signals. To cater to the fact that q-space sampling schemes can differ significantly, ranging from Cartesian sampling in diffusion spectrum imaging (DSI) to multi-shell sampling with multiple distinct b-values, we propose to represent the q-space signals using tight wavelet frames defined on graphs [1, 2], which can be flexibly adapted to different sampling domains. The power of tight wavelet frames lies in their ability to sparsely approximate piecewise smooth functions and the existence of fast decomposition and reconstruction algorithms associated with them. A wide range of tight wavelet frames can be generated conveniently using the unitary extension principle (UEP) [3]. We use the term tight graph framelets to denote basic functions that, when dilated and shifted, form tight wavelet frames on graphs. Tight graph framelets have compact support, are not restricted to signals of a certain shape (e.g., the “donut” [4]), and provide a natural bridge between continuous and discrete representations [1].

We demonstrate the utility and effectiveness of tight graph framelets in two specific applications: denoising and super-resolution reconstruction in q-space. To take advantage of the high redundancy of graph framelets, we regularize the associated problems using a sparse-inducing norm. Instead of the more conventional ℓ₁ regularization, which has been shown in the theory of compressed sensing to produce sparse solutions, we opted to use ℓ₀ regularization. In [5], both iterative soft and hard thresholding algorithms were adopted and the latter was found to achieve better image quality. In [6], wavelet frame based ℓ₀ regularization also shows better edge-preserving quality compared with the conventional ℓ₁ regularization. Evaluation performed using synthetic data with noncentral chi signal distribution as well as real data with repeated scans indicates that the proposed method is superior to denoising and interpolation using spherical radial basis functions (sRBF) [7].

2 Approach

2.1 Graph Framelets

In q-space, sampling points and their relationships can be encoded, respectively, using vertices and edges of a graph. We denote a graph by 𝒢 ≔ {ℰ, 𝒱, w}, where 𝒱 ≔ {υ_k ∈ ℳ : k = 1, …, K} is a set of vertices representing points on a manifold ℳ, ℰ ⊂ 𝒱 × 𝒱 is a set of edges relating the vertices, and w : ℰ ↦ ℝ⁺ is a weight function. The associated adjacency matrix 𝒜 ≔ (w_k,k′) is symmetric with w_k,k′ > 0 if υ_k and υ_k′ are connected by an edge in ℰ; otherwise w_k,k′ = 0. Given the degree matrix D ≔ diag{d[1], d[2], …, d[K]}, where d[k] ≔ ∑_k′ w_k,k′, the graph Laplacian, defined as ℒ ≔ D − W, is consistent with the Laplace-Beltrami operator of the manifold [8]. Denote by ${\{{\lambda }_k,u_k\}}_{k=0}^{K-1}$ the pairs of eigenvalues and eigenvectors of ℒ with 0 = λ₀ ≤ λ₁ ≤ λ₂ ≤ … ≤ λ_K−1 = λ_max. The eigenvectors form an orthonormal basis for all functions on the graph: $\langle u_k,u_{k\prime }\rangle ≔{\sum }_{n=1}^K{u}_k[n]u_{k\prime }[n]={\delta }_{k,k\prime }$. The Fourier transform of a function f_𝒢 : 𝒱 ↦ ℝ on the graph 𝒢 is given by $\widehat{f_{𝒢}}[k]≔{\sum }_{n=0}^{K-1}{f}_{𝒢}[n]u_k[n]$.

The key idea involved in constructing wavelet frames on a graph is to view eigenvectors of the graph Laplacian as Fourier basis on graphs and the associated eigenvalues as frequency components [1,2]. One then slices the frequency spectrum in a multi-scale fashion by using a set of masks {â_r(·) : r = 0, …, R}, where â₀(·) acts as a low-pass filter and â_r(·) with 0 < r ≤ R as band-pass or high-pass filters. More specifically, the graph framelet analysis transform is defined as W f_𝒢 ≔ {W_l,r f_𝒢 : (l, r) ∈ ℬ_L}, with ℬ_L ≔ {(1, 1), (1, 2), …, (1, R), (2, 1), …, (L, R)} ∪ {(L, 0)} and

$$\widehat{W_{l,r}{f}_{𝒢}}[k]≔\{\begin{array}{cc}{â}_r({\gamma }^{-L+1}{\tilde{\lambda }}_k)\widehat{f_{𝒢}}[k]\hfill & l=1,\hfill \\ {â}_r({\gamma }^{-L+l}{\tilde{\lambda }}_k){â}_0({\gamma }^{-L+l-1}{\tilde{\lambda }}_k)\cdots {â}_0({\gamma }^{-L+1}{\tilde{\lambda }}_k)\widehat{f_{𝒢}}[k]\hfill & 2\le l\le L,\hfill \end{array}$$ (1)

where λ̃_k = (λ_k/λ_max)π and γ > 1 is the dilation factor. Noting the eigen-decomposition ℒ = UΛU^⊤, where Λ = diag{λ₀, λ₁, …, λ_K−1}, we have

$$W_{l,r}≔\{\begin{array}{cc}U{\hat{\mathrm{\Omega }}}_r({\gamma }^{-L+1}\tilde{\mathrm{\Lambda }})U^{\top }\hfill & l=1,\hfill \\ U{\hat{\mathrm{\Omega }}}_r({\gamma }^{-L+1}\tilde{\mathrm{\Lambda }}){\hat{\mathrm{\Omega }}}_0({\gamma }^{-L+l-1}\tilde{\mathrm{\Lambda }})\cdots {\hat{\mathrm{\Omega }}}_0({\gamma }^{-L+1}\tilde{\mathrm{\Lambda }})U^{\top }\hfill & 2\le l\le L,\hfill \end{array}$$ (2)

where Λ̃ = diag{λ̃₀, λ̃₁, …, λ̃_K−1} and

$${\hat{\mathrm{\Omega }}}_r(\beta \tilde{\mathrm{\Lambda }})=\text{diag}\{{â}_r(\beta {\tilde{\lambda }}_0),{â}_r(\beta {\tilde{\lambda }}_1),\dots ,{â}_r(\beta {\tilde{\lambda }}_{K-1})\}.$$ (3)

Letting α ≔ W f_𝒢 ≔ {α_r,l ≔ W_l,r f_𝒢 : (l, r) ∈ ℬ_L} and if the masks satisfy ${\sum }_{r=0}^R{|{â}_r(\xi )|}^2=1$, which is one of the requirements of the unitary extension principle (UEP) [1, 3]), it is easy to show that the synthesis transform W^⊤α gives W^⊤α = W^⊤W f_𝒢 = I f_𝒢 = f_𝒢. To avoid explicit decomposition of a potentially large Laplacian matrix, we approximate the masks using Chebyshev polynomials, i.e., ${â}_r(\xi )={𝒯}_r^n(\xi )$, where ${𝒯}_r^n(\xi )=\frac{1}{2}{c}_{r,0}+{\sum }_{k=1}^{n-1}{c}_{r,k}{T}_k(\xi )$ with T_k(ξ) being the k-th order Chebyshev polynomial and

$$c_{r,k}=\frac{2}{\pi }{\int }_0^{\pi }\text{cos}(k\theta ){â}_r(\frac{\pi }{2}(\text{cos }\theta +1))d\theta .$$ (4)

Equation (2) can be shown to be equivalent to

$$W_{r,l}≔\{\begin{array}{cc}{𝒯}_r^n({\gamma }^{-L+1}ℒ)\hfill & l=1,\hfill \\ {𝒯}_r^n({\gamma }^{-L+l}ℒ){𝒯}_r^n({\gamma }^{-L+l-1}ℒ)\cdots {𝒯}_r^n({\gamma }^{-L+1}ℒ)\hfill & 2\le l\le L.\hfill \end{array}$$ (5)

Note the interchange between scalar-valued and matrix-valued polynomials. See [1, 2] for more details. Some examples of framelet masks are shown in Table 1.

Table 1.

Framelet masks.

Haar	Linear	Quadratic
â0(ξ) = cos(ξ/2)	â0(ξ) = cos2(ξ/2)	â0(ξ) = cos3(ξ/2)
â1(ξ) = sin(ξ/2)	${â}_1(\xi )=\frac{1}{\sqrt{2}}\text{sin}(\xi )$	${â}_1(\xi )=\sqrt{3}\text{ sin}(\xi /2){\text{ cos}}^2(\xi /2)$
	â2(ξ) = sin2(ξ/2)	${â}_2(\xi )=\sqrt{3}{\text{ sin}}^2(\xi /2)\text{ cos}(\xi /2)$
		â3(ξ) = sin3(ξ/2)

2.2 Sparse Recovery

Given the observation vector f ∈ ℝ^K′, we are interested in recovering u ∈ ℝ^K by solving the following problem:

$$\underset{u}{\text{min }}\{\varphi (u)={\Vert Au-f\Vert }_{2,𝒢}^2+\sum _{(l,r)\in {ℬ}_L}{\lambda }_{l,r}{\Vert W_{l,r}u\Vert }_{0,𝒢}\},$$ (6)

where ${\Vert •\Vert }_{2,𝒢}^2≔{\sum }_i^{K\prime }{(•[i])}^{2}d[k_i]$ and ${\Vert •\Vert }_{0,𝒢}≔{\sum }_{k=1}^Kℐ(•[k])d[k]$ with ℐ(z) being an indicator function that returns 1 when z ≠ 0 or 0 otherwise. Here, u is defined on 𝒢 with degree matrix D ≔ diag{d[1], d[2], …, d[K]}. The observation vector f is defined in relation to a subset of vertices of 𝒢, indexed by {k_i : i = 1, …, K′}. We let D′ ≔ diag{d[k₁], d[k₂], …, d[k_K′]}. K′ and K are in general not necessarily equal. We require K′ ≤ K.

The problem (6) can be solved effectively using penalty decomposition (PD) [6, 9]. Defining auxiliary variables υ ≔ (υ_l,r) ≔ (W_l,ru), this amounts to minimizing the following objective function with respect to u and υ:

$$L_{\mu }(u,\upsilon )={\Vert Au-f\Vert }_{2,𝒢}^2+\sum _{(l,r)\in {ℬ}_L}{\lambda }_{l,r}{\Vert {\upsilon }_{l,r}\Vert }_{0,𝒢}+\frac{\mu }{2}\sum _{(l,r)\in {ℬ}_L}{\Vert W_{l,r}u-{\upsilon }_{l,r}\Vert }_2^2.$$ (7)

In PD, we (i) alternate between solving for u and υ using block coordinate descent (BCD). Once this converges, we (ii) increase μ > 0 by a multiplicative factor that is greater than 1 and repeat step (i). This is repeated until increasing μ does not result in further changes to the solution [6, 9].

First Subproblem

We solve for υ in the first problem, i.e., min_υ L_μ(u, υ):

$$\underset{\upsilon }{\text{min}}\sum _{(l,r)\in {ℬ}_L}\{\frac{{\lambda }_{l,r}}{\mu }{\Vert {\upsilon }_{l,r}\Vert }_{0,𝒢}+\frac{1}{2}{\Vert W_{l,r}u-{\upsilon }_{l,r}\Vert }_2^2\}.$$ (8)

The solution can be obtained via hard thresholding [10, 11]:

$${\upsilon }_{l,r}[k]=\{\begin{array}{cc}(W_{l,r}u)[k]\hfill & {((W_{l,r}u)[k])}^2\ge \frac{2{\lambda }_{l,r}d[k]}{\mu },\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$ (9)

Second Subproblem

By taking the partial derivative of L_μ(u, υ) with respect to u, the solution to the second subproblem, i.e., min_u L_μ(u, υ), is

$$(A^{\top }D\prime A+\frac{\mu }{2}\sum _{(l,r)\in {ℬ}_L}{W}_{l,r}^{\top }{W}_{l,r})u=A^{\top }D\prime f+\frac{\mu }{2}\sum _{(l,r)\in {ℬ}_L}{W}_{l,r}^{\top }{\upsilon }_{l,r}.$$ (10)

Since ${\sum }_{(l,r)\in {ℬ}_L}{W}_{l,r}^{\top }{W}_{l,r}={\mathbf{W}}^{\top }\mathbf{W}=I$, the problem can be simplified to become

$$(A^{\top }D\prime A+\frac{\mu }{2}I)u=A^{\top }D\prime f+\frac{\mu }{2}\sum _{(l,r)\in {ℬ}_L}{W}_{l,r}^{\top }{\upsilon }_{l,r},$$ (11)

which is a set of linear equations that can be solved, for example, using the conjugate gradient method.

2.3 Denoising and Super-Resolution

We are interested in the super-resolution problem of recovering signals when given only a subset of noisy measurements. We partition u as u = [u₁; u₂] ∈ ℝ^K, where u₁ ∈ ℝ^K′ is defined on vertices whose observed values are given by f ∈ ℝ^K′. No observed values are available for u₂. To recover u, we set in (6) A = [I_{K′ × K′} 0] ∈ ℝ^{K′ × K}, where I_{K′ × K′} is an identity matrix of size K′ × K′. When K′ = K, i.e., u = u₁ and A = I_{K′ × K′}, the problem reduces to a denoising problem, where we are interested in recovering the noiseless version of f. Since

$$A^{\top }D\prime A={[I_{K\prime \times K\prime }0]}^{\top }D\prime [I_{K\prime \times K\prime }0]=\left[\begin{array}{cc}\hfill D\prime \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right],$$ (12)

the resulting matrix on the left of (11) is diagonal and the solution can hence be obtained easily without matrix inversion.

3 Experiments

3.1 Parameter Settings

For all experiments, we used the quadratic masks, set the decomposition level to L = 5, and set the maximum order of Chebyshev polynomials to n = 8. No significant gain in improvement was obtained beyond these values. The dilation factor was set to a standard value γ = 2. The tuning parameters for the sparse recovery problem were set as

$${\lambda }_{l,r}=\{\begin{array}{cc}{\eta }^{-l+1}\lambda \hfill & 1\le l\le L,r\ne 0,\hfill \\ 0\hfill & l=L,r=0,\hfill \end{array}$$ (13)

with η = 0.75 and $\lambda ={\sigma }_{\text{noise}}^2\text{log}(K|{ℬ}_L|)$ (i.e., the universal penalty level [12]). We define the adjacency matrix 𝒜 ≔ (w_k,k′) of the q-space samples by letting

$$w_{k,k\prime }=\text{exp }\{-\frac{3(1-{\hat{\mathbf{q}}}_k^{\top }{\hat{\mathbf{q}}}_{k\prime })}{(1-{\text{cos}}^2(\theta ))}\}\text{exp }\{-\frac{{(b_{k\prime }-b_k)}^2}{2{\sigma }_b^2}\},$$ (14)

where σ_b = 10 and θ is set to the maximum of the angles between neighboring gradient directions.

3.2 Results

Synthetic Data

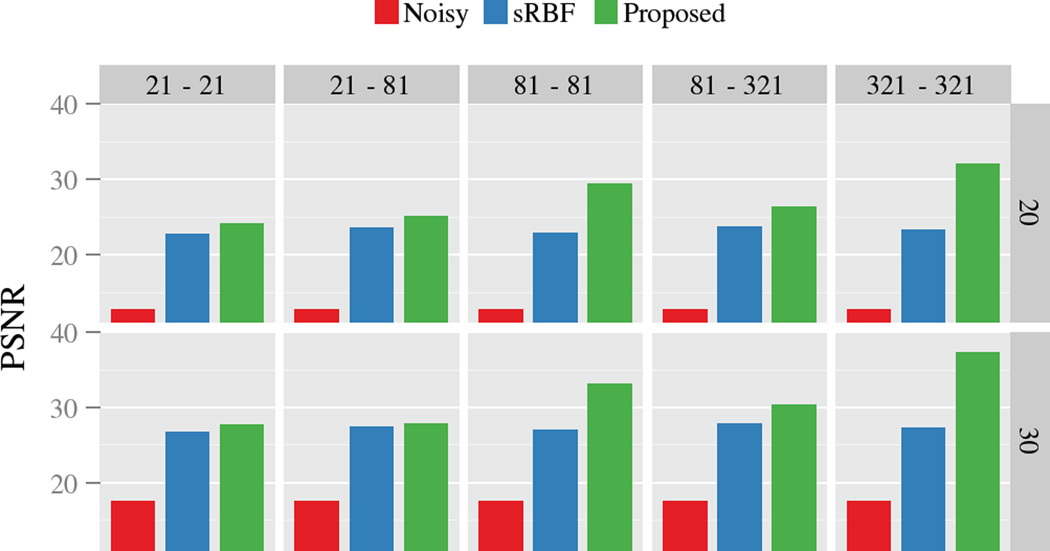
We generated a synthetic dataset consisting of a set of voxels with white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF) signal profiles. Combinations of these signal profiles were also included to simulate partial volume effects. To generate the WM signal profiles, mixtures of up to two tensor models were used. The diffusivities for WM, GM, and CSF are respectively [1.7, 0.3, 0.3] × 10⁻³ mm²/s, 0.9 × 10⁻³ mm²/s, and 2.5 × 10⁻³ mm²/s. The number of non-collinear gradient directions were 21, 81, and 321, each generated by subdividing the faces of an icosahedron a number of times. Three shells were generated, i.e., b = 1000, 2000, 3000 s/mm². For evaluation, two levels of 32-channel noncentral chi noise [13] was added, corresponding to SNR = 20 and 30 with respect to the non-diffusion-weighted signal of WM.

Results for denoising (21 − 21, 81 − 81, 321 − 321) and super-resolution (21 − 81, 81 − 321), averaged over 10 realizations of noise, are shown in Fig. 1. The comparison baseline is the spherical radial basis function (sRBF) method described in [7]. This basically amounts to weighted averaging of signals on the shells using the weights given by (14). The results confirm that our method yields consistent PSNR improvements. Note that, for both synthetic and real data, noncentral chi bias was removed from the solution of (6) using the method described in [13].

Fig. 1.

Performance evaluation in terms of PSNR for two levels of noise, i.e., SNR=20 and 30. We have used here the notation K′ − K, where K′ and K are the numbers of input and output gradient directions, respectively. The standard errors are negligible and are hence not shown here.

Real Data

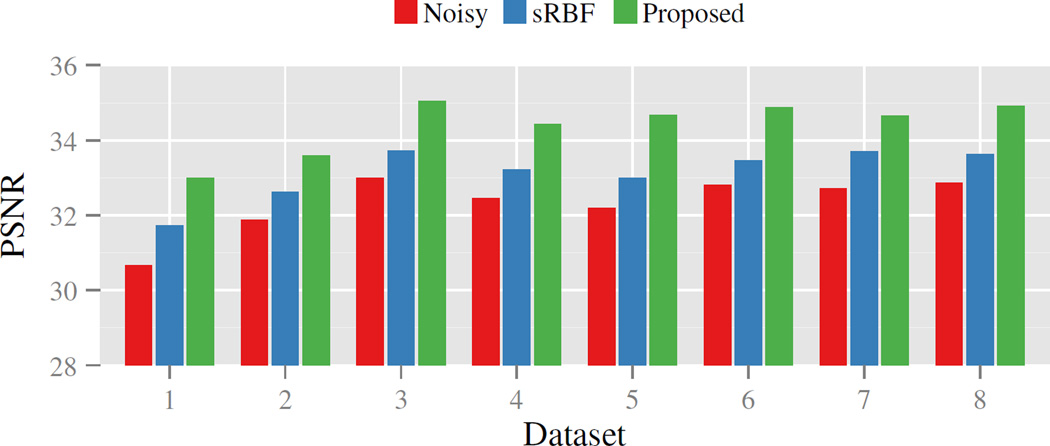
The real datasets were acquired using Siemens 3T TRIO MR scanner with b = 2000 s/mm² and 48 non-collinear gradient directions. The imaging protocol is as follows: 128 × 96 imaging matrix, voxel size of 2 × 2 × 2 mm³, TE = 97 ms, TR = 11,300 ms. Imaging acquisition was repeatedly performed on the same subject for 8 times. We averaged the 8 sets of diffusion-weighted images and removed the bias caused by the noncentral chi noise to obtain the ground truth for evaluation.

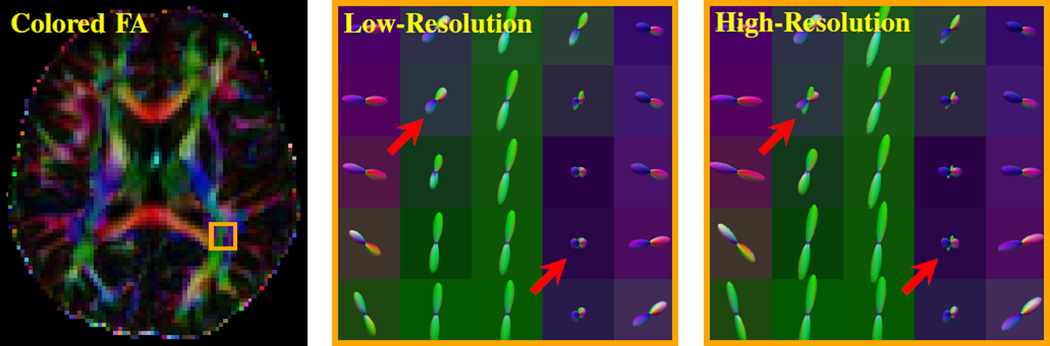
The performance statistics for the denoising of the 8 sets of diffusion-weighted images are shown in Fig. 2, again confirming that our method yields results that are in close agreement with the ground truth with higher PSNRs. We also show in Fig. 3 the white matter fiber orientation distribution functions (ODFs) to demonstrate the benefit of q-space super-resolution. We used the measurements from the original 48 gradient directions to generate the data for 81 directions. It can be observed from the figure that increasing the angular resolution helps resolve some fiber crossings.

Fig. 2.

Performance statistics of the denoising of the real data consisting of 8 repeated sets of diffusion-weighted images.

Fig. 3.

Fiber ODFs of the low-angular-resolution data with 48 gradient directions and high-angular resolution data with 81 gradient directions. Visible improvements in resolving fiber crossings are marked with red arrows.

4 Conclusion

In this paper, we present preliminary results confirming that tight graph framelets can be employed for sparse representation of diffusion signals in q-space. The effectiveness of this representation is demonstrated with applications involving denoising and super-resolution. Future work will be directed to incorporating this representation with spatial framelet representation to obtain a joint representation for both spatial and wavevector dimensions.