Probing the Interaction of Quantum Dots with Chiral Capping Molecules Using Circular Dichroism Spectroscopy

Abstract

Circular dichroism (CD) induced at exciton transitions by chiral ligands attached to single component and core/shell colloidal quantum dots (QDs) was used to study the interactions between QDs and their capping ligands. Analysis of the CD line shapes of CdSe and CdS QDs capped with l-cysteine reveals that all of the features in the complex spectra can be assigned to the different excitonic transitions. It is shown that each transition is accompanied by a derivative line shape in the CD response, indicating that the chiral ligand can split the exciton level into two new sublevels, with opposite angular momentum, even in the absence of an external magnetic field. The role of electrons and holes in this effect could be separated by experiments on various types of core/shell QDs, and it was concluded that the induced CD is likely related to interactions of the highest occupied molecular orbitals of the ligands with the holes. Hence, CD was useful for the analysis of hole level–ligand interactions in quantum semiconductor heterostructures, with promising outlook toward better general understanding the properties of the surface of such systems.

Induction of chirality and/or optical activity in inorganic nanocrystals is a promising way to introduce a new dimension of intriguing and useful complexity to their properties. Unique chiroptical effects associated with chirality, such as circular dichroism (CD), which is the differential absorption of left and right circularly polarized light, have been studied in nanocrystals that interact with chiral molecules.^1,2 Specifically, in semiconductor QDs, induced CD accompanies the quantum confinement based effects leading to size-tunable chiroptical properties. Gun’ko and co-workers were the first to report on observation of a CD response induced in the excitonic transitions of CdS QDs capped with chiral molecules.³ Four possible mechanisms were considered in reports on induced chiroptical effects in QDs. First, the whole inorganic core may become chiral due to the binding of chiral molecules. This mechanism has generally been excluded for achiral materials such as Cd and Zn chalcogenides and is only possible for materials that crystallize in chiral space groups.^4,5 Second, surface atoms can be slightly distorted to a chiral geometry and/or the ligands pack in a chiral configuration on the surface, creating a chiral shell layer.^3,6,7 Third, chiral defects such as screw dislocations can occur in QDs, and chiral molecules can be used to enantiomerically enrich samples.⁸ Last, the inorganic core and surface remain achiral, and the molecules induce a chiroptical response in the quantum dots’ exciton transitions as a result of an electronic interaction between molecular and core levels.^9,10 This electronic interaction can be a simple dipolar interaction between the inorganic core’s excitations and molecular excitations, as suggested by Tang and co-workers.⁹ This type of interaction was earlier described by Govorov and co-workers as the leading mechanism for chiroptical activity induction in plasmonic metal nanosystems.¹¹ However, since the magnitude of the induced CD scales with the dielectric constant of the material in the framework of this model, it is expected to be much weaker for semiconductor nanostructures relative to plasmonic particles. In another report, it was suggested, alternatively, that this interaction can be an actual hybridization of quantum dot and molecular orbitals.¹⁰ This hypothesis is based on the fact that this kind of hybridization is known to occur between the hole levels of quantum dots and molecular electronic levels of their ligands.¹² In fact, the influence that this effect has on the regular absorption of QDs can become relatively strong, when molecules are properly chosen to exhibit an efficient hybridization between their highest occupied molecular orbitals (HOMO) and quantum dots’ valence band (VB) hole levels. These ideas were described recently in several reports by Weiss and co-workers.^13,14 Early reports on induced chiroptical activity in QDs were based on samples prepared in water in the presence of chiral ligands, which had relatively broad size distributions and poor optical properties.^3,7,10 More recently, Balaz and co-workers demonstrated induction of chiroptical activity in higher quality QD samples, prepared using conventional hot injection methods in organic solvents.¹⁵ Chiroptical properties were induced by postsynthetic ligand exchange and phase transfer, from achiral hydrophobic ligands in an organic solvent to chiral hydrophilic ligands in water. This process gives much better samples in terms of size distribution, resulting in much sharper and more detailed induced CD spectra. DFT calculations were also used to support the claim that the QD’s (hole) levels hybridize with molecular levels, to induce the chiroptical activity.¹⁶ In a more recent report by that group, it was argued that both individual ligand’s absolute configurations, as well as multiple ligands packing arrangement and hybridization of molecular electronic and QD hole states, all lead concurrently to induction of chiroptical activity at QD absorption bands.¹⁷ While past reports try to account for the mechanism of induction of chiroptical activity, there was no attempt to analyze the complex CD line shape and fully assign features in the spectra to different excitonic levels. In addition, even though the calculations indicated that the CD induction mechanism acts on hole rather than electron levels, there has not been an experiment designed to verify which charge carrier is indeed more dominant in this effect.

Here we report on several experiments and data analysis designed to explain the complex induced CD line shape in terms of the excitonic states of the QD. In addition, it is demonstrated how this effect can be used to probe charge carrier–ligand interactions. This topic becomes even more relevant due to the recent growing interest in the role of surfaces of quantum dots in determining their properties.¹⁸⁻²⁰ By probing a size series of CdS and CdSe QDs, it is shown that the whole induced CD spectrum can be decomposed to a sum of contributions from the different excitonic states and that it is possible to unambiguously assign exciton levels in the CD spectrum, making it an informative technique to probe excitonic band structure in quantum dots. Each exciton absorption line is accompanied by a derivative linsehape in the CD spectrum. This generally indicates a split of the original exciton level into two sublevels, preferentially excited by opposite circular polarizations. Following this, it is shown in experiments on core/shell QDs that it is possible to separate the role of electrons and holes in the process and that CD can actually be used to probe charge carrier (hole)–ligand interactions at semiconductor heterostructure surfaces. Overall, ligand induced CD is proven to be a useful technique to analyze the full excitonic level structure, facilitating the discrimination of the contribution of the various transitions as compared with conventional absorption measurements. Even more importantly, this technique is especially sensitive to the confinement of holes and their interactions with the ligand shell, in contrast to more common spectroscopy methods such as absorption and fluorescence measurements which can only reveal how the whole exciton wave function is affected by various surface effects. Last, some experimental observations in the current work suggest that CD spectroscopy goes beyond the exciton level assignment and hole energetics, into retrieving information on the angular momentum dependent fine structure, which is usually only observed in experiments conducted under the influence of magnetic fields.

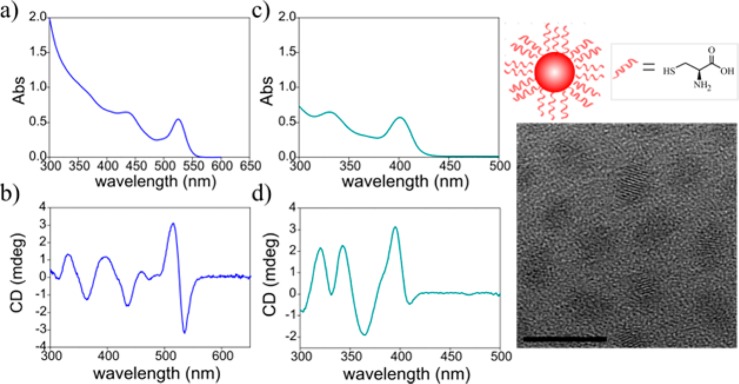
Samples of CdSe, CdS, and core–shell CdSe/CdS and CdS/CdSe QDs were prepared using conventional hot injection methods in organic solvents (see Supporting Information). These were then transferred to water, while exchanging the surface ligands from relatively weakly bound achiral molecules (such as oleic acid and different hydrophobic alkyl-phosphonic acids) to more strongly bound chiral cysteine molecules. This phase transfer approach followed the reports of Balaz and co-workers¹⁵⁻¹⁷ with slight modifications (see Supporting Information). Typical absorption and CD spectra of samples of CdSe and CdS dots, after the phase transfer are presented in Figure 1. The complex line shape of the induced CD spectrum exhibits multiple features with alternating polarities of the signal.

Figure 1.

(a,b) Absorption and CD spectra of CdSe QDs sample 1. (c,d) Absorption and CD spectra of CdS QDs. On the right-hand side a TEM image of the CdSe QDs. The scale bar is 10 nm. The prolate achiral shape is typical for all samples addressed in this work. The CD only originates from interactions with chiral cysteine molecules as depicted in the drawing above the TEM image.

Analysis of Induced CD Spectra

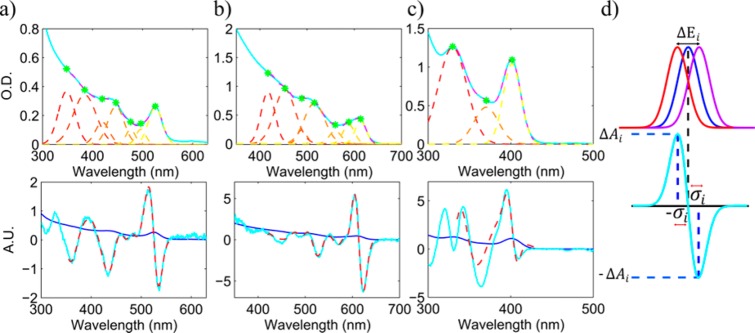
In Figure 2 absorption and CD spectra of a size series of CdSe QDs are presented (similar spectra for CdS can be found in the Supporting Information). The average size is evaluated based on the wavelength of the first absorption peak.²¹ The CD line shape follows the expected red shift that accompanies a size increase. It is important to notice that the line shape is very well preserved for different sizes. This indicates that the CD is directly related to the excitonic band structure of the QDs. With this realization in mind, it should be possible to further analyze the CD line shape and assign all of the features to different transitions in the absorption spectra. Many reports dealt with the extraction of different transitions that convolute to form the absorption line shape of QDs and the assignment of the exciton level structure. In an early key report, Norris and Bawendi measured and assigned the size-dependent optical spectrum of CdSe QDs using photoluminescence excitation (PLE) experiments combined with theoretical predictions.²² In the current report a protocol to analyze and similarly assign the induced CD spectrum is suggested. First, each absorption spectrum is fitted with a sum of Gaussians that correspond to different exciton levels. Their centers are extracted from the second derivative of the absorption spectrum. Following that, in order to reconstruct the CD spectrum, the derivative of each Gaussian is taken, and the whole CD line is constructed from a linear sum of the derivative functions while maintaining the same center wavelengths. (Details of the analysis are described in the Supporting Information.) The results of this analysis are depicted in Figure 3a–c for several representative samples that cover the whole size regime as well as different materials (CdSe and CdS). Specifically panels a and c are the samples presented in Figure 1. In the Supporting Information section this analysis is presented for other samples.

Figure 2.

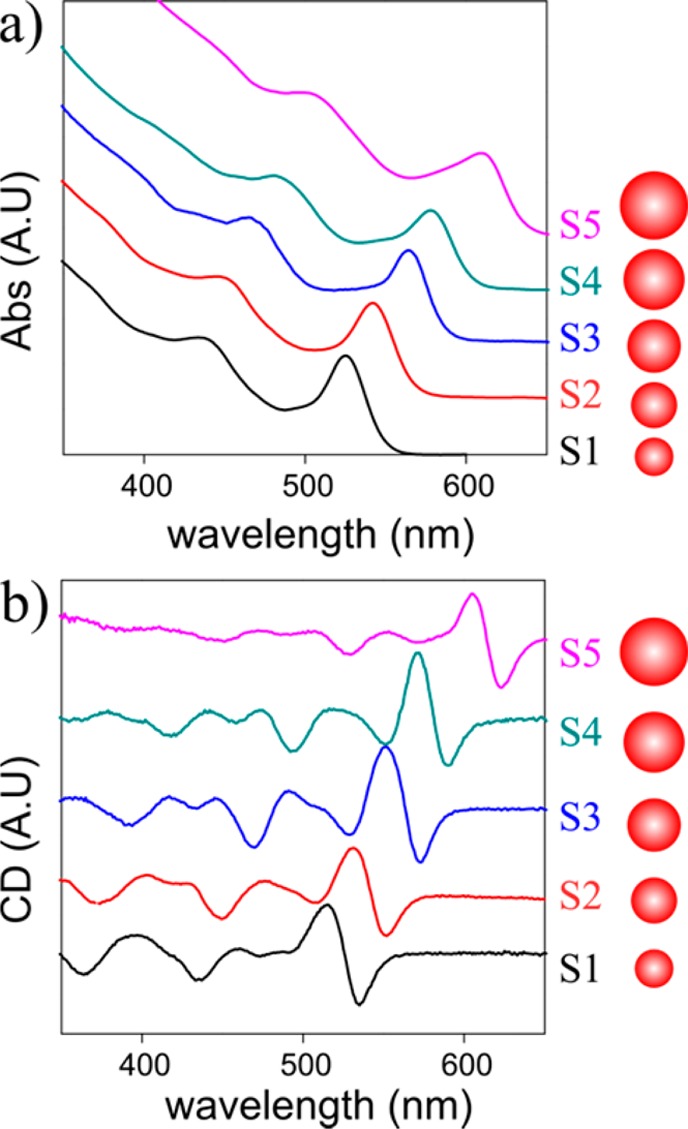
(a) Absorption and (b) CD spectra of a size series of CdSe QDs. The diameters of samples S1–S5 are 2.6, 2.9, 3.4, 3.8, and 5.3 nm correspondingly. The CD and absorption red shift with growing size. The complex line shape of the CD is qualitatively preserved.

Figure 3.

Analysis of absorption and CD spectra. Top (a–c): Absorption spectra of (a) CdSe sample S1, (b) CdSe sample S2, and (c) CdS QDs. The measured spectra appear in cyan. The Gaussians that reconstruct the spectra in dashed colored lines, where the green dots mark their maxima. These peaks can be assigned to the different excitonic transitions²² (from low to high energy): 1S_3/21S_e, 2S_3/21S_e, 1S_1/21S_e, 1P_3/21P_e, 2S_1/21S_e, 1P_5/21P_e or 1P^l_1/21P_e (light hole subband), and 3S_1/21S_e. The dashed pink lines mark the reconstructed absorption spectra. Bottom (a–c): Reconstructed CD spectra for the same samples as in the top images, using the derivatives of the Gaussians at the same center wavelengths. The blue line marks again the measured absorption spectrum. The cyan lines mark the measured CD and the dashed pink lines the CD spectrum that was reconstructed using the sum of derivatives. (d) A scheme depicting the relevant quantities to determine energy splitting (ΔE_i) from the CD and absorption measurements. The energy splitting is proportional to .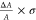

There is an excellent fit between the reconstructed CD line shape and the measured one, indicating that each exciton transition is accompanied by a derivative line shape in the CD spectrum. The overlap of many of these derivative shaped signals gives rise to the complex spectrum observed. This point has to be elaborated upon, as it is not a trivial result when compared with CD spectra of chiral organic molecules. In the vicinity of an isolated electronic transition of a molecule with a single chiral center, the CD spectrum is normally characterized by a single peak (not a bisignated, derivative shaped), with the CD peak intensity overlapping the absorption maximum. The sign of the CD band reflects which circular polarization is preferably absorbed. The associated optical rotatory dispersion spectrum is characterized by a derivative line shape crossing zero and changing sign at the wavelength of the peak CD and absorption response. This characteristic behavior is known as the “Cotton effect” in chiroptical activity.²³ A bisignated line shape in the CD, which is not a dispersive phenomenon, is normally associated with a splitting of the fundamental transition to two bands that are preferentially excited by alternating circular polarizations. This is the situation observed throughout this work and described in Figure 3.

A common, well-understood case, relates to coupling of two chiral chromophores, or “exciton coupled circular dichroism”.^23,24 The Coulomb interaction might couple two excited molecular chromophores that are close enough and form a chiral configuration. This coupling splits the original electronic state of each chromophore into two hybrid levels, preferentially excited by opposite circular polarizations, giving rise to the derivative line shape. Such a line shape is also found in several cases of chiral molecule–plasmon dipolar interactions, as shown in model calculations of Govorov and co-workers.¹¹ There, the coupling can be viewed as the interaction of molecular and plasmonic dipoles or coupling of plasmonic dipoles of chirally arranged metal nanoparticles.²⁵

In semiconductor QDs, wave function hybridization type coupling between the HOMO of a ligand and VB states (hole level) may also be expected to split the original hole level to two subbands. For the case of efficient hybridization, this coupling can become large, and one of the two subbands would be pushed significantly higher than the original VB edge, changing the optical properties of the core by narrowing the bandgap.¹⁴

A third, and completely different case of a derivative line shape, appears in magnetic circular dichroism (MCD). This effect, which has been studied also in QDs,²⁶ is related to Zeeman splitting of spin-degenerate states by an external magnetic field and is not related to chirality. It can become very large for the case of dilute magnetic semiconductor QDs, as reported by Gamelin and co-workers.²⁷

In all of these cases, the original level is split in energy into two subbands, each preferentially excited by one circular polarization. The current results suggest, effectively, that a splitting can also be induced by interaction of electronic states with chiral molecules, but without a detailed theory, we are unable to pinpoint the mechanism underlying this effect. However, one interesting outcome for electronic properties of QDs can be understood. Based on angular momentum conservation one can relate the circular polarization of an exciting photon to the angular momentum of the excited electron and hole in a QD. Since a split in energy is observed in the CD line shape between opposite circular polarizations, the energy level of the exciton can be viewed as split according to angular momentum of states of the electron and hole (exciton). While recent reports on electron transmission through chiral molecules suggest a relation between spin and chirality,²⁸ it cannot be concluded for the present work, in the absence of a theoretical model, whether a similar mechanism applies for excitations in QDs. Yet, any theoretical description of energy splitting of QDs’ levels, induced by chiral molecules, will have to make use of the CD line shape analysis protocol presented in this paper.

The relevant quantity related to this splitting is not the magnitude of the measured CD (ΔA) but rather the normalized quantity called “dissymmetry factor”, ΔA/A. The use of this quantity cancels the dependence of CD on oscillator strength and concentration. Both the total absorption and total CD at the peak position of an exciton transition are affected by overlapping transitions in the optical spectrum, which is why dissymmetry assigned to each exciton state can only be measured once the spectra are deconvoluted to different transitions. It can be shown that the fitting procedure used to reconstruct the CD spectra as sum of derivatives of Gaussians in the absorption spectra directly relates the energy splitting to the linear coefficients in the derivative summation that builds the CD line shape and that it is proportional to the dissymmetry: 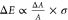(see Supporting Information). The relevant quantities are schematically depicted in Figure 3d. In Table 1, energy splitting values for the two first band edge transitions in CdSe QDs samples S1–S5 are presented. Values for higher energy transitions are presented in the Supporting Information for all samples and are typically of the order of 10–100 μeV. A typical value for MCD of CdSe QDs, with a diameter of 3.2 nm for example, is around 300 μeV, in a five Tesla magnetic field.²⁹

Table 1. Energy Splitting Values for CdSe QDs Samples S1–S5.

	ΔEi (μeV)
sample	first band edge transition	second band edge transition
S1	27	–19
S2	36	–26
S3	38	–37
S4	45	–38
S5	51	8

Several trends can be observed in these results. First, values of energy splitting for the first band edge transition increase with size. Second, a clear sign reversal is observed between the first and the second band edge transitions. This stems experimentally from the fact that one circular polarization that was absorbed at higher energy in the first transition is now absorbed at lower energy in the second transition and vice versa. When considering a hybridization effect between the hole level and the ligand’s HOMO, the increase of splitting magnitude with size for the first band edge transition may indicate the importance of an energetic resonance between the ligand and hole levels. In this picture, it is assumed that the HOMO level of the thiol lies just above the VB of CdSe, and as the size of QDs increases, their VB is pushed closer to resonance with the ligand’s HOMO.³⁰ When considering such a mechanism, wave functions’ spatial overlap is also important, and that should generally decrease when the size of the dots increases. It can be concluded, for the samples studied here, that resonance effects are more prominent than wave functions’ overlap (for the first band edge transition). The latter, however, can become more important for different samples, where the VB of QDs is far from resonance with the ligand’s HOMO. In that case, it can be expected that the spatial overlap between the ligand’s wave function and that of the hole will be more important than energetic resonance considerations, and induced CD will decay with size, as observed in our past work for very small CdS QDs.¹⁰

In addition to these considerations, several reports by Kambhampati and co-workers call for evaluation of the contribution of several additional surface-mediated mechanisms that affect the hole level energetics and dynamics. In one report, they showed the importance of surface trap states in determining the energetics of excited states in quantum dots.³¹ In another report, they showed the importance of vibrational coupling to ligands in carrier cooling (specifically holes).³² The topic of exciton to ligand vibrational coupling was also discussed recently by Lifshitz.³³ However, in the current results we cannot evaluate the role of these mechanisms in the observed effect.

The current report, combined with the additional information in the above-mentioned work, should, however, stimulate interest in future experiments on chiral ligand induced circularly polarized luminescence (CPL) and Raman optical activity, which are more suitable chiroptical spectroscopies for evaluation of excited state dynamics and coupling to vibrational modes.

The observation of a sign reversal for the energy splitting between the first and second band edge transitions is another point of experimental resemblance to MCD. In ref (26), the sign reversal in MCD is attributed to deviation from spherical symmetry in quantum dots, as well as consideration of the fine structure of the first and second band edge excitons.

Experiments with Core/Shell QDs

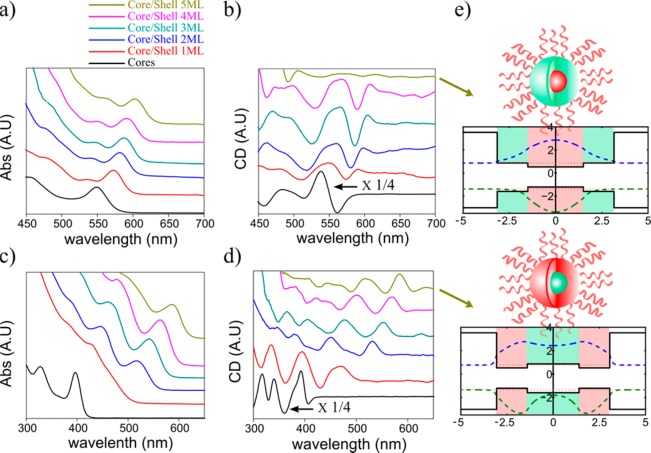
Nanoscale heterostructures of several materials, such as core–shell quantum dots^34,35 and seeded rods or tetrapods,^36,37 are commonly studied in the past few years, as a class of materials which enable better control of the properties of these semiconductor nanosystems relative to single component systems. In semiconductor core–shell nanocrystals the hole and electron wave functions can be located in the core or shell, or delocalized over the whole structure, based on the relative band alignment of the two materials. Here, a core/shell design was used to verify that the hole plays the dominant role in coupling to the chiral molecule. This is done by monitoring the change in CD magnitude as a function of growing shell thickness in core/shell CdSe/CdS and CdS/CdSe. In comparison between the two systems, due to the localization of the hole at different parts (core in CdSe/CdS and shell in CdS/CdSe), the trend is different. These results are depicted in Figure 4.

Figure 4.

Absorption and CD spectra of core/shell QDs. The evolution of absorption and CD as a function of growing shell for (a,b) CdSe/CdS core/shell series and (c,d) CdS/CdSe core/shell series. The cores CD spectra for both series are divided by 4 for clarity. The colors of different lines in all of the spectra are black—cores, red—core/shell 1 monolayer (ML) of shell, blue—2 ML, cyan—3 ML, pink—4 ML, and dark yellow—5 ML. (e) Diagrams showing effective mass calculations of the electron and hole wave functions for the final samples of each series with the thickest shell. In the top diagram of CdSe/CdS, it is clear that the hole is completely localized in the core. For the bottom diagram of CdS/CdSe, it is localized in the shell.

The absorption and induced CD response of a series of CdSe core and CdSe/CdS core/shell QDs as a function of the growing shell thickness are presented in Figure 4a,b. (Sample characterizations using TEM appear in the Supporting Information.) The samples were measured at similar optical densities (at the first band edge peak position) to make sure the CD strength does not depend on the relative absorption. In the limit of a very thick shell, the hole is confined to the core, since the valence band of CdSe is higher than that of CdS. This is depicted in Figure 4e in the top image, showing an effective mass calculation of the wave functions of the hole and the electron for the last sample of CdSe/CdS with the thickest shell. The strong CD signal observed for the CdSe cores is completely suppressed in this sample, as expected of an effect mediated by the interaction of the hole with the surface. The behavior for samples in the middle between bare cores and the thickest shell is more complex and nonmonotonic. The interaction of the hole with the surface, and as a result the CD intensity, is affected by two considerations. It decays exponentially with the thickness of the CdS shell, which serves as an energy barrier for the hole. On the other hand, the addition of shell layers reduces the confinement energy of the hole, shifting the VB edge higher. As a result, the hole level is pushed closer to resonance with the molecular level. Effective mass calculations for all of these samples are presented in the Supporting Information to help understanding the trend. This experiment proves that an induced CD can be used to monitor the extent to which a ligand can affect the hole wave function through an energetic barrier like the CdS shell. In CdTe/CdSe samples, where the separation of charges is even more effective, with the hole localized in the core and the electron in the shell,³⁸ the induced CD decays even faster with growing shell, further validating the role of holes in this process (see the Supporting Information).

In the opposite core/shell system, where the larger band gap material CdS is in the core, and CdSe is in the shell with a higher valence band, it is expected that the interaction between holes and the surface will not be suppressed and that the CD will not decay with growing shell. This is indeed the result, as presented for a series of CdS and CdS/CdSe samples in Figure 4c,d. The CD does decay after the growth of the first monolayer of CdSe shell. This initial decay is not surprising, keeping in mind that the CD induction effect is very sensitive to the specific adsorption conformation and nature of chemical bonding of the ligand to the surface, which probably significantly changes between CdS and CdSe. More informative is the observation that the induced CD does not further decay upon addition of CdSe layers, indicating that the interaction of the hole with the surface is not suppressed. For the last sample, with the thickest CdSe shell, an effective mass calculation of the wave functions is presented in the bottom image of Figure 4e. It is very clear, that contrary to the case of CdSe/CdS the hole is now localized in the shell.

The fact that the CD intensity does not change with growing shell can be qualitatively understood in a manner similar to the considerations invoked for bare CdSe QDs. The magnitude of the effect is dependent on two competing effects. Energetic resonance between the hole level and the HOMO of the ligand is improved with growing shell, however, the spatial overlap between wave functions of the hole and the ligand is diminished.

One important clarification has to be made. The experiment on core/shell QDs cannot differentiate between a geometric distortion mechanism and an electronic hybridization mechanism. Both effects are expected to decay when the surface with the ligands on it is separated from the hole.

In conclusion, the ligand induced CD response of single component and core/shell QDs has been studied. It was shown that the CD is directly assigned to the exciton band structure. Each transition is accompanied by a CD derivative line shape that indicates a small split of the original level to two levels with opposite angular momentum. This effect would be interesting for future studies of spin-polarized transport with potential applications in QD spintronics. The exciton splitting might become larger with proper choice of different ligands. In addition, it was shown that the induced CD response can be used to probe the interaction of the hole with ligands in core/shell QDs (a purely electronic interaction, and/or the effect ligands have on the hole level through surface structural distortion). Alongside these results, two reasons why induced CD can become an important tool for studies of quantum dots can be stressed. First, it is background free, in the sense that the response comes solely from the interaction with the ligand, unlike the regular absorption that is only slightly modified by the ligands. Second, this method can become a powerful tool to probe the magnetic transition dipole moment of the excitonic transition. This is since, by definition, CD is proportional to the scalar product of electric and magnetic transition dipole moments²¹ and is sensitive to both contributions (unlike regular absorption, where the magnetic part is commonly negligible). All of the results presented here will become even more significant with future progress toward a better theoretical description of induced chirality and chiroptical activity in QDs.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.6b03143.

• Details of experimental methods, TEM images, analysis of absorption and CD spectra, and results of effective mass calculations of the core/shell QDs (PDF)

Author Contributions

A.B.-M. and A.T. contributed equally.

The authors declare no competing financial interest.