mSieve: Differential Behavioral Privacy in Time Series of Mobile Sensor Data

Abstract

Differential privacy concepts have been successfully used to protect anonymity of individuals in population-scale analysis. Sharing of mobile sensor data, especially physiological data, raise different privacy challenges, that of protecting private behaviors that can be revealed from time series of sensor data. Existing privacy mechanisms rely on noise addition and data perturbation. But the accuracy requirement on inferences drawn from physiological data, together with well-established limits within which these data values occur, render traditional privacy mechanisms inapplicable. In this work, we define a new behavioral privacy metric based on differential privacy and propose a novel data substitution mechanism to protect behavioral privacy. We evaluate the efficacy of our scheme using 660 hours of ECG, respiration, and activity data collected from 43 participants and demonstrate that it is possible to retain meaningful utility, in terms of inference accuracy (90%), while simultaneously preserving the privacy of sensitive behaviors.

INTRODUCTION

Smart phones with their onboard sensors and their ability to interface with a wide variety of external body worn sensors, provide an appealing mobile health (mHealth) platform that can be leveraged for continuous and unobtrusive monitoring of an individual in their daily life. The collected data can be shared with health care providers who can use the data to better understand the influence of the environment on an individual and be proactive with their prognosis. On one hand, mHealth platforms have the potential to usher in affordable healthcare, but, on the other hand, their ability to continuously collect data about an individual raises serious privacy concerns and limits their adoption – concerns that are largely absent during traditional episodic treatments.

Motivating example

Consider a scientific study being conducted to assess the daily activities (e.g., sedentary versus active life styles) and behaviors of a user. To this end, the user participating in the study shares data from several body-worn sensors (e.g., respiration (RIP), electrocardiogram (ECG) and accelerometer sensors) with the study investigators. The data collected can be used to infer physical activities such as walking, running, stationary (from accelerometers), but also correlate these activities with behaviors such as conversation episodes, stress episodes, detect when the user is eating or drinking water/coffee, and if the user smokes or takes cocaine. Note, activity can be detected from accelerometer data [5], conversation episodes [35] from respiration data, onset of stress [34, 26] can be inferred from ECG data, eating from wrist-worn sensors [40], smoking from respiration and wrist-worn sensors [32, 3, 38] and cocaine use from ECG data [25].

On one hand, some of the above inferences such as walking, conversation, eating are extremely useful in investigation of behavioral risk factors on health and wellness. But, on the other hand, inferences such as smoking, cocaine use and stress may be sensitive to the user and needs to be kept private. Thus, we have a conundrum, where the same time series data can be used for making both utility providing inferences (that are desirable) and also sensitive inferences (that need to be protected).

Challenges unique to physiological data

While there exists a large body of prior work on data privacy, there are several challenges that are unique to maintaining privacy of inferences drawn from time series of physiological data. First, the inferences themselves (e.g., detecting variation in heart rate, respiratory disorders) are extremely critical to proper diagnosis and incorrect inferences can severely affect and even threaten human life. Second, there are well-defined limits for various physiological signals (e.g., the interbeat interval in ECG is typically between 300ms and 2, 000ms [13], and so on) and non-conformance to those thresholds can render the data unusable. Third, there is high degree of correlation between an observed human behavior and the data recorded by these physiological sensors. For example, physical activities such as walking or running are associated with higher heart and respiration rates. Finally, physiological signals are high-dimensional, are extremely rich in information, and when continuously collected embed minute elements of an individual’s lifestyle patterns. These patterns or inferences are often correlated making it difficult to protect the privacy of one inference in isolation of the others.

These above challenges place constraints on the mechanisms that can be used to protect privacy of physiological data. The constraints are in terms of the magnitude of noise that can be added while retaining the utility of the inferences and in handling of the correlation between the data streams from the various sensors. Anonymization techniques such as k-anonymity [39], l-diversity [30], and t-closeness [27] propose data obfuscation aimed towards protecting the identity of a user within a subpopulation. However, we consider a setting where a single-user shares data with (possibly) many recipients (primary/secondary researchers), and the identity of the user is already known to the data recipients.

A principled mechanism for preserving privacy during analysis is differential privacy [17]. While several variants of differential privacy have been proposed [23, 37, 21], the central idea there is to adequately obfuscate a query response computed on a multi-user statistical database (by adding noise typically drawn from a Laplace distribution) such that the presence or absence of any user in the database is protected. However, this notion of differential privacy cannot be directly applied to our single user setting to protect behavioral privacy. Recent model-based approaches for location privacy such as [24, 22] focus on effective data suppression to protect sensitive inferences, but these can’t be applied directly to protect behavioral privacy from mobile sensor data either due to unique challenges listed above.

Our approach

In this paper, we propose mSieve, a model-based data substitution approach to address the privacy challenges arising from sharing of personal physiological data. We group the inferences that can be drawn from shared data into two sets – a whitelist and a blacklist [11, 10]. Inferences that are desirable for the user, such as tracking activity, conversation episodes, frequency of eating, are all utility providing to the user and are part of a whitelist. Other inferences such as smoking and onset of stress are sensitive to the user and need to be kept private. These inferences form part of the blacklist. Our goal is to prevent an adversary from making any of the inferences in the user-specified blacklist while being able to accurately compute the whitelisted inferences.

Figure 1 illustrates the flow of data and the various components of mSieve. In summary, given various streams of sensor data from a user, mSieve identifies sensitive data segments and substitutes them with the most-plausible non-sensitive data segments. To do so, it computes a Dynamic Bayesian Network (DBN) model over the user’s data. The model maintains a distribution over the various behavioral states (e.g., smoking, running, conversation etc.) of the user. Note, these states are computed using the data collected from the body-worn sensors. To perform substitution, segments of data that reveal sensitive behavior are detected and removed. The DBN model is then used to identify candidate replacement segments from the same user’s data that can be used in place of the deleted segments. We use several techniques (such as dynamic programming approach, and a greedy approach based best fit algorithm) to select the best segments that preserve privacy and simultaneously retain the overall statistics of the physiological signal (providing utility). To assess the privacy guarantees of our scheme, inspired by the privacy definition of differential privacy, we define the notion of differential behavioral privacy to protect sensitive inferences. The metric ensures that the information leaked about a sensitive inference from a substituted segment is always bounded.

Figure 1.

Illustration of the mSieve process.

We evaluate the efficacy of our substitution scheme using 660 hours of ECG, respiration, location and accelerometer data collected over multiple user studies with over 43 participants. We demonstrate that sensitive behavioral inferences, contributing to privacy loss, such as onset of stress, smoking, and cocaine use can be protected while still retaining meaningful utility (≥ 85% accuracy when privacy sensitivity is high and ≥ 90% on average) of the shared physiological signals in terms of its use for tracking heart rate, breathing irregularities, and detecting conversation episodes.

DEFINITIONS AND PROBLEM STATEMENT

We first introduce notations and define terms we use throughout the paper and also formalize the problem statement.

Sensor Data

Let r_i(t) denote the sensor data from the i^th sensor at time t, where i = 1, …, n_s. We define $\overrightarrow{r_i}=\{r_i(t)|t_s\le t\le t_e\}$ as the time-series of measurements from the i^th sensor, from starting time t_s to ending time t_e. Finally, r(t) denotes the collection of time-series data from all the different sensors, i.e., r(t) = {r₁(t), r₂(t), …, r_ns(t)}.

Inferences

An inference is a function computed (e.g., using a machine learning model) over a window of data values. Time-series data from different sensors (such as ECG, respiration, accelerometer) are used for computing inferences using data buffered over a chosen time interval. Let x_i(t) be inference value of the i^th inference at time t. We assume that all our inferences are binary classifiers, which output true when the inference occurs within the time interval and false otherwise¹, i.e., x_i(t) ∈ {0, 1}. We define $\overrightarrow{x_i}=\{x_i(t)|t_s\le t\le t_e\}$ to be the time-series for the i^th inference within the time interval (t_s, t_e). Again, x(t) = {x₁(t), x₂(t), …, x_n(t)} represents the collection of all possible inference time-series.

Whitelist and Blacklist of inferences

As mentioned earlier, a key component of our privacy mechanism is the separation of the possible inferences into a Whitelist (denoted by W) and a Blacklist (denoted by B). In mSieve, a whitelist is a set of inferences that are essential for obtaining utility from the shared data, and the goal of the recipient is to accurately compute the distribution p(x_i), where x_i ∈ W. Similarly, the blacklist B, is a list of inferences x_i, whose release the user would like to protect from the recipient.

State

A bit vector of length n is used to represent a user state x = (x₁, x₂, …, x_n) ∈ {0, 1}ⁿ. The i^th element of the bit vector represents the value of the i^th inference. Without loss of generality, we assign the first n_w bit values of state x to the whitelist, i.e., x_i for 1 ≤ i ≤ n_w and the remaining n_b bit values to the blacklist. We assume that whitelist and blacklist forms a disjoint partition of the inference set, i.e., n = (n_w + n_b). A state is sensitive, if one or more bits corresponding to inferences in set B, are set to one. All sensitive states are included in set 𝕊_B and the non-sensitive states are in set 𝕊_W.

State Interval

We define a state interval, s = (x, t_s, t_e) as a state x at which the user dwells during an interval (t_s, t_e). Successive state intervals are indexed by s^j, where j = 1, …, τ. The value of each inference stays the same during an interval. Interval changes to the next one when any of the inference values change. Unless otherwise specified, we use the shorthand notation $s_i^j$ for s^j.x_i.

State Sequence

We define a state sequence, s = (s¹, s², …, s^τ), where s^j.x ≠ s^j+1.x and s^j.t_e == s^j+1.t_s for all j = 1, …, τ − 1.

User Model

Transition among different user states can be modeled using graphical models such as Markov Chain (MC), Hidden Markov Models (HMM), and Dynamic Bayesian Network (DBN). The Markov models, while suitable for modeling the temporal correlation among the states across time intervals, do not capture their conditional independence within a particular time interval. Therefore, we model the transition between states as a DBN, D_u. In each time slice of the DBN, we maintain a uniform Bayesian Network described below:

• Nodes: Each node of the DBN is a random variable S^j representing a user state at time interval j. Denoting the i^th inference within the state as $S_i^j$, we can write $S^j=\{S_1^j,S_2^j\dots ,S_n^j\}$.

In addition to nodes, a DBN also contains two types of edges:

• Intra-slice links: For any time slice j, conditional independence between individual inferences X₁ to X_n is maintained as a Bayesian Network (BN). Denoting the parents of node S^j by Pa(S^j) we have:

  $$P(S_i^j|Pa(S_i^j));\text{where }Pa(S_i^j)=\{S_k^j:P(S_i^j|S_k^j)\}$$
• Inter-slice links: A DBN not only models conditional independence among states within a time slice but also captures their temporal correlations across time slices. These transition probabilities among nodes in different BNs are represented by the inter slice links. We use a first order model, so these links are only between adjacent time slices.

  $$P(S_i^j|S_i^1,\dots ,S_i^{j-1})=P(S_i^j|S_i^{j-1});$$

These conditional probabilities are stored in a Conditional Probability table (CPT), which is associated with each node S^j. An illustration of a DBN representing temporal behavior among states is presented in Figure 2.

Figure 2.

DBN showing user states over different time slices.

Adversary Model

We use a DBN to capture adversarial knowledge. A DBN is a powerful graphical model that can effectively encode both the temporal and spatial correlation among inferences. It is also a generalization of Markov models (including the HMM) that are typically used to encode these information. We consider two types of adversarial attacks.

• Data-based attack: In this setting, the attacker has access to the raw sensor data.

• Model-based attack: The attacker has access to released inferences computed over raw data but not the raw data.

In addition, we assume that in both settings the attacker is aware of the blacklist inferences B, and the mSieve algorithm is publicly known.

The algorithms in mSieve, are designed under an assumption that an adversary uses a DBN or a less powerful model for capturing the correlation among the user states. However, if an adversary uses a model that is more expressive in terms of modeling state correlations, or has access to side channel information that is not contained in the user model then additional leakage may occur from the released data.

Privacy

The privacy guarantee we seek is such that an adversary with access to data released by mSieve should not be able to suspect a sensitive behavior in a released data with significantly higher likelihood than when suspecting the same behavior in a corresponding reference data.

Corresponding Reference Data

For a given sensor time series r⃗, a corresponding reference data $\overrightarrow{\overline{\mathbf{r}}}$ is such that it releases no more information about the blacklisted inferences than a null time-series, but is otherwise maximally close to r⃗.

Differential Behavioral Privacy

A system Λ preserves ε-privacy, if for any input sensor time series r⃗ with start time t_s and end time t_e, it produces an output $\overrightarrow{\hat{\mathbf{r}}}$ with same t_s and t_e such that for any query q(․; ․) on $\overrightarrow{\hat{\mathbf{r}}}$ about any sensitive state b ∈ 𝕊_B and for all K ∈ Range(q), and the same query q(․; ․) on any $\overrightarrow{\overline{\mathbf{r}}}$ with the same t_s and t_e, the output is bounded by e^ε.

$$D(\overrightarrow{\hat{\mathbf{r}}}\Vert \overrightarrow{\overline{\mathbf{r}}})=\frac{P(q(\overrightarrow{\hat{\mathbf{r}}};b)\in K)}{P(q(\overrightarrow{\overline{\mathbf{r}}};b)\in K)}\le e^{\epsilon }$$ (1)

The parameter ε denotes privacy sensitivity. A low value of ε implies a high privacy level and vice-versa.

Utility

We define utility over an entire released episode. Released data should preserve the same white list of inferences as the original data. Utility metric minimizes distribution difference between the original and released data.

Let p_i be the probability of inference x_i occurring in the actual signal. For simplicity, suppose Inference x_i occurs for $t_i={\sum }_{j=1}^{\tau }{I}_{x_j^i=1}*(s^j.t_e-s^j.t_s)$ duration out of a total of $T={\sum }_{j=1}^{\tau }(s^j.t_e-s^j.t_s)$ time units in the original data, where I is the identity function. Then $p_i=\frac{t_i}{T}$.

Utility Loss

Let P = (p₁, p₂, …, p_nw) be the probability vector of the white listed inferences in the actual data and $\hat{P}=(\widehat{p_1},\widehat{p_2},\dots ,p{\hat{n}}_w)$ be the probability vector of the white listed inferences in the released data, where ${\hat{p}}_i=\frac{{\hat{t}}_i}{T}$ and t̂_i is the duration of inference x_i in the released data. Then, we define our utility loss metric as,

$$U_{\mathit{\text{loss}}}=\Vert P-\hat{P}\Vert =\sum _{i=1}^{n_w}|p_i-{\hat{p}}_i|=\frac{1}{T}\sum _{i=1}^{n_w}|t_i-{\hat{t}}_i|$$ (2)

Problem Definition

The goal of mSieve is to obfuscate time series data r⃗ ∈ DB and generate $\overrightarrow{\hat{\mathbf{r}}}$ with the same start and end time such that it satisfies the privacy constrains in Equation (1) and minimizes the utility loss in Equation (2).

Problem 1

For any given tolerable privacy loss ε > 0, the utility-plausibility tradeoff can be formulated as the following optimization problem:

$$\mathit{\text{minimize}}\hspace{1em}\hspace{1em}\hspace{1em}{U}_{\mathit{\text{loss}}}$$

$$s.t.\hspace{1em}\hspace{1em}D(\overrightarrow{\hat{\mathit{r}}}\Vert \overrightarrow{\overline{\mathit{r}}})\le e^{\epsilon }$$

SYSTEM OVERVIEW

We now present an overview of the components, as shown in Figure 3, that are required to implement the end-to-end system from sensor data, to user states, to privacy preserving safe states, and finally to the release of sensor data.

Figure 3.

An overview of the mSieve framework.

Context Engine

The Context Engine (CE) generates inferences from raw sensor data. Inferred signals are more suitable for data modeling than unprocessed, raw sensor signals as it simplifies the modeling task. CE transforms the raw sensor signals to task-specific feature signals. For example, RR-interval is more suitable to infer heart rate than raw ECG signal. CE takes raw signals as input and produces time series of inference values as output. All the white list and black list inferences are inferred by the CE.

Substitution Mechanism

We begin by segmenting the time series of inferences. Let τ be the total number of segments, where each segment is represented by state interval s^j where 1 ≤ j ≤ τ. As mentioned earlier, we assume that inferences are represented by a single bit and thus at a particular time interval the CE provides as output a bit vector of size n, which also constitutes the user state s^j.x ∈ {0, 1}ⁿ. Finally, the segmentation generates a sequence of such state intervals, s⃗ =< s¹, s², …, s^τ >.

Some of the states in s⃗ can be sensitive to the user. The first step in our substitution algorithm is to remove the sensitive states and also all other states that might lead to the sensitive states. This introduces discontinuity in that state sequence; we call these gaps as holes. The next step is to perform a DBN lookup to identify plausible candidates to fill all the holes. This lookup operation on user DBN, D_u, provides a set of candidate states for filling holes in any time interval j. We note that the plausible states are checked for continuation with the previous state. To select the best state from among the candidate states, we consider utility loss as our metric. We substitute a hole with a state or sequence of states that minimizes utility loss.

Context to Sensor Data

Another important consideration in the substitution process is to maintain signal continuity. The Context-to-Sensor-Data module accepts possible substitution candidates generated by the substitution mechanism and produces safe, privacy-preserving sensor data as output. This module communicates with the database to ensure that the released sensor data is safe, i.e., meets the privacy and utility criteria.

SOLUTION DETAILS

In this section, we discuss our proposed solution to mitigate privacy risks. Algorithm 1 takes raw sensor data r⃗, sensitive states 𝕊_B, and user DBN D_u, and outputs raw data $\overrightarrow{\hat{r}}$ that does not contain any signature about sensitive inferences.

Algorithm 1.

mSieve: Plausible Substitution Mechanism

Require: r⃗, 𝕊B, Du, ε
1:	s⃗ = getStateSequence(r⃗)
2:	k ← 1
3:	ŝ⃗ ← s⃗
4:	for each interval j ∈ {1, 2, …, τ} do
5:	if isHole(sj, Du, 𝕊B, ε) is true then
6:	$\overrightarrow{s^j}=h_k=(\varnothing ,s^j.t_s,s^j.t_e)$
7:	ℂk = getPlausibleCandidateSet(Du, s⃗, hk, ε)
8:	k ← k + 1
9:	end if
10:	end for
11:	Selected candidate {c1, …, ck} = FillHole({hk}, {ℂk})
12:	$\overrightarrow{\hat{r}}\leftarrow \overrightarrow{r}$
13:	for each hole hk = (․, ts, te), selected candidate ck do
14:	r̂(ts, te) = getSensorDataFromDB(ck, te − ts)
15:	end for
16:	return $\overrightarrow{\hat{r}}$

Step 1: Sensor Data to State Sequence

We first convert the time-series of raw data samples from various sensors, r⃗, to time-series of inferences using (classifier) models. The classifier models are specific to an inference and detects the time interval over which the inference occurs. Let e_i = {(t_s, t_e)} denote the set of time intervals over which the i^th inference is detected by a model where 1 ≤ i ≤ n = (n_w + n_b) (recall n_w and n_b are the number of whitelisted and blacklisted inferences respectively). We create the inference time series x_i(t) for the i^th inference as

$$x_i(t)=\{\begin{array}{cc}1\hfill & \text{if }{t}_s\le t\le t_e\text{ for any }(t_s,t_e)\in e_i\hfill \\ 0\hfill & \text{Otherwise}.\hfill \end{array}$$

Collectively, we define, x(t) = (x₁(t), x₂(t), …, x_n(t)) as the n-dimensional state at time t.

Let $\mathbf{t}={\cup }_{i=1}^n{\cup }_{(t_s,t_e)\in e_i}\{t_s,t_e\}$ be the set of all time points (whether start or end) corresponding to the inference occurrences, arranged in ascending order and τ = |t| − 1. Note, a user stays in same state between time interval (t_i, t_i+1) for i = 1, 2, …, τ and t_i ∈ t. We denote by sⁱ = (x(t), t_i, t_i+1), where t_i < t < t_i+1, the i^th state interval. It is clear that two consecutive states are different. It forms a state sequence s⃗ = < s¹, s², …, s^τ >.

Step 2: Locate and Delete Sensitive and Unsafe States

We consider three types of states. a) Sensitive state, b) Unsafe state, and c) Safe state. We define a state s^j as sensitive state if any of the last n_b bits are set to one, i.e., if ${\bigvee }_{i=n_w+1}^n{s}_i^j=1$, where ∨ is logical or operation (recall 𝕊_B is the set of sensitive states).

We define a state s^j as unsafe state if it is not directly sensitive but may contain some information about blacklist, e.g., act of walking outside of a building to smoke and returning back after smoking. We use the following local privacy check, which is similar as [22, 9], to mark a state as unsafe

$$\frac{P(S^{j+1}\in {𝕊}_B|S^j=s^j)}{P(S^{j+1}\in {𝕊}_B)}\le {\epsilon }^{\delta }.$$ (3)

This condition provides us with a mechanism to stem privacy leakage from unsafe states. Here, δ is our local privacy sensitivity. Lemma 1 below describes how to select δ.

Lemma 1

For any given ε > 0 there exist a δ < ε/2τ such that if

$$\frac{P(S^i\in {𝕊}_B|S^{i-1}=s^{i-1})}{P(S^i\in {𝕊}_B)}<e^{\delta }$$

then $D(\overrightarrow{\hat{r}}\Vert \overrightarrow{\overline{r}})\le e^{\epsilon }$

A proof appears in the Appendix.

Deletion of sensitive and unsafe states in s⃗ results into $\overrightarrow{\overline{s}}$ that is punctuated with holes. Each hole consists of a starting time t_s, and an end time t_e. Thus, the k^th hole is defined as h_k = (t_s, t_e). We denote the state occurring immediately before a hole h_k as pre(h_k), and the state after h_k as next(h_k).

Step 3: Candidate Generation

A candidate (i.e., a state sequence) is a sequence of states that can be substituted in place of a hole. A candidate should be such that it does not contain any sensitive or unsafe state and it maintains continuity, i.e., transitions among the states in the filled up time series should be plausible using similar criteria as in (3). If there does not exist a candidate long enough to fill the hole by itself, multiple state segments can be composed together to obtain the desired length. We use a recursive function, described in Algorithm 2, to generate candidates for each hole h_k in time interval given by (t_s, t_e). For k^th hole, the GenerateCandidate function generates all the possible candidates cand for the duration given by the interval length of the hole, i.e., dur = h_k.t_e − h_k.t_s, and stores the candidates in the set ℂ_k. Prior to invoking the GenerateCandidate function, we initialize set ℂ_k = ∅ and current candidate cand =< ․ > to an empty vector. Note, isConnect(s^j, s^j+1) returns true iff Equation (3) returns true.

If GenerateCandidate does not generate any candidate state sequence, i.e., ℂ_k = ∅, then we delete either the previous state pre(h_k) or the next state next(h_k) (whichever provides a lower utility loss), to enlarge the size of the existing hole. We then invoke GenerateCandidate again for this newly created hole. This iterative process of increasing the size of the hole increases the chances of finding a candidate and in our experiments we did not encounter any instance when the algorithm failed to find a suitable candidate. But, theoretically speaking, it is possible that the algorithm may not find any candidates due to the continuity constraint. Further improving this algorithm and proving its convergence is still an open question that we leave for future work.

Algorithm 2.

GenerateCandidate

Require: cand =< c1, …, cl >, ℂk, hk, remDur
1:	if dur == 0 and isConnect(cl, next(hk)) then
2:	ℂk = ℂk ∪ cand
3:	else if dur > 0 then
4:	for each sj ∈ 𝕊 do
5:	if isConnect(cl, sj) then
6:	remDur′ = remDur − (sj.te − sj.ts)
7:	cand′ =< c1, …, cl, sj >
8:	GenerateCandidate(cand′, ℂk, hk, remDur′)
9:	end if
10:	end for
11:	end if

Complexity analysis

Since length of the holes and the states are dynamic we will use expected values to analyze complexity of this step. Let l_h be the expected length of the hole, l_s be expected length of a state and y be the expected number of states reachable from any state. Here, y is the branching factor and ℓ = ⌈(l_h/l_s)⌉ is the expected depth of the search tree. Then, the expected time complexity is O(ℓ^y).

Step 4: Select Candidate and Fill Holes

After the hole creation and candidate generation steps, we obtain a series of holes h₁, …, h_nh and a set of candidates ℂ_i for the i^th hole. Let c⃗ =< c₁, c₂, …, c_m >, where 1 ≤ j ≤ m is the index assigned to the candidate c_j, it is the j^th candidate to be encountered as we enumerate through candidates in sets ℂ₁, ℂ₂, …, ℂ_nh in that order. We define an allocator matrix A[i][k], where A[i][k] = 1 implies that candidate state sequence c_k ∈ ℂ is a candidate for the i^th hole, i.e. c_k ∈ ℂ_i. Let, after hole creation, $\overline{t_j}$ be the duration of the j^th whitelist in $\overrightarrow{\overline{s}}$. Thus, the initial duration difference is $\overline{d_j}=\overline{t_j}-t_j$ and the initial utility loss, $U_{\mathit{\text{Loss}}}^0={\sum }_{j=1}^{n_w}|{\overline{d}}_j|$. The next step is to select a candidate for each hole that minimizes the objective function specified in Equation 1. We formulate the above as a Hole Filing Problem stated below.

Problem 2

Hole filling Problem: As stated earlier, for the j^th whitelisted inference, t_j denotes its total duration in r⃗ and $\widehat{t_j}$ its duration in $\overrightarrow{\hat{\mathbf{r}}}$. Let $d_j=\widehat{t_j}-t_j$. The goal is to fill all the holes with candidate state sequences such that

$$\mathit{\text{objective function}}\mathit{:}\mathit{\text{ min}}\sum _{i=j}^{n_w}|\widehat{t_j}-t_j|=\mathit{\text{min}}\sum _{j=1}^{n_w}|d_j|$$

It can be shown that the above problem minimizes utility loss U_loss (in Equation 2). By reducing the bin packing problem to the unconstrained version of the hole filling problem, i.e., by setting A[i][k] = 1 for all i and k and the privacy sensitivity parameter ε, to a large number, it can be shown that the hole filling problem is NP-hard. Therefore, we first provide a dynamic programming based solution that gives optimal result but requires exponential memory. We then provide a greedy based solution that is not optimal but runs in polynomial time.

Dynamic Programming Solution

The main idea here is to compute the solutions to smaller sub-problems and store the solutions in a table, so that they can be reused repeatedly later to solve the overall problem. To do so, we need to decompose the hole filling problem in terms of smaller sub-problems and find a relation between the structure of the optimal solution for the original problem, and solution of the smaller sub-problems. We begin by defining the problem recursively as follows:

Recurrence Relation

Let L be similar to A, except that the entry L[i][j] stores the minimum utility loss achieved if the k^th candidate is used to fill the i^th hole, where 1 ≤ i ≤ n_h and 1 ≤ k ≤ m.

To solve the problem, we use a bottom-up approach. At first, we compute the optimal result for the first hole. Then, using this result we compute the optimal result for the second hole and so on. We begin with the following initialization

$$L[i][k]=\{\begin{array}{cc}\hfill U_{\mathit{\text{Loss}}}^0\hfill & \text{if }i=0\hfill \\ \hfill \infty \hfill & \text{Otherwise}.\hfill \end{array}$$

Let ${\overrightarrow{d}}_{i,k}=<d_1^{i,k},\dots ,d_{n_w}^{i,k}>$ be the duration difference vector after assigning candidate c_k to i^th hole. Initialize $d_j^{0,k}=\overline{d_j}$ for all 1 ≤ k ≤ m and 1 ≤ j ≤ n_w. To understand the working of the algorithm, suppose that holes h₁ through h_i−1 have all been assigned, and we are now ready to make an assignment for h_i, i.e., we are now in stage i. Let dur_j(c_k) be the duration of the j^th whitelist in candidate c_k. Then, we update L[i][k] with

$$\underset{1\le l\le m}{\text{min}}\{L[i-1][l]+\sum _{j=1}^{n_w}-|d_j^{i-1,l}|+|d_j^{i-1,l}+{\mathit{\text{dur}}}_j(c_k)|\}\text{for }1\le i\le n_h\text{ and }1\le k\le m$$ (4)

For the l, that results into a minimum, we update $d_j^{i,k}=d_j^{i-1,l}+{\mathit{\text{dur}}}_j(c_k)$ for 1 ≤ j ≤ n_w. We also maintain an additional data structure pre(i, k) that stores index of previous candidate from where we update L[i][k], i.e. pre(i, k) = l. We continue this process till i = n_h and k = m. Finally, we select c_k for last hole h_nh such that L[n_h][k] is minimum. Using the pre data structure, we determine complete assignment of the holes by invoking AssignCandidate(n_h, k) (Algorithm 3).

Complexity analysis

Maximum number of candidates for each hole is O(ℓ^y) (since any combination of whitelisted inferences can be a candidate sequence) and the maximum number of holes is O(τ). Thus, the upper bound on space required for a dynamic program based solution is O(τℓ^y) and the upper bound on time is O(τℓ^yℓ^y).

Algorithm 3.

AssignCandidate

Require: pre(․, ․), i, k
1:	if i > 0 then
2:	Assign ck in ith hole
3:	call AssignCandidate(pre, i − 1, pre(i, k))
4:	end if

Greedy Solution

We now provide a greedy strategy for the hole filling problem. For each hole, we choose an item that minimizes the utility loss, U_loss, among all the candidates. We repeat this process until all the holes are filled. This process is described in Algorithm 4.

Algorithm 4.

GreedySolution

Require: ${\{{ℂ}_i\}}_{i=1}^{n_h},{\{h_i\}}_{i=1}^{n_h},\overrightarrow{\overline{d}}$
1:	$\overrightarrow{d}=\overrightarrow{\overline{d}}$
2:	for each i = 1, 2, …, nh do
3:	select $\underset{c_k\in {ℂ}_i}{\text{min}}{\sum }_{j=1}^{n_w}-|d_j|+|d_j+du{r}_j(c_k)|$
4:	dj = dj + durj(ck); for all 1 ≤ j ≤ nw
5:	end for

Since, in every iteration, we select an item that locally minimizes U_loss for that hole, this method does not always provide an optimal result. However, the space complexity reduces to O(τ) and time complexity reduces to O(τℓ^y) which is ℓ^y times smaller than the previous solution using dynamic programming.

Step 5: Sensor Data Substitution

Now, for each hole h_k, we have to select a segment of sensor data that corresponds to the selected candidate state c_k ∈ ℂ_k. For this, we maintain a mapping database, M, that stores sensor segment of different length for each possible state. However, for substituting the sensor data for a state within an interval, we have to maintain consistency at both boundaries of the hole. We use the case of ECG signals to illustrate feature value consistency. One can also consider morphological consistency or others relevant characteristics.

Feature value consistency

Let rr_i be the i^th RR interval in an ECG data, $\overrightarrow{\hat{\mathbf{r}}}$. The RR interval is used to calculate other features of the signal defined as below.

1. Point of time error: Limit check on the current value

   $$e(r{r}_i)=\{\begin{array}{cc}0\hfill & \text{if }300<r{r}_i<2000\hfill \\ 1\hfill & \text{Otherwise}.\hfill \end{array}$$
2. Continuity error: Limit check on the first order difference

   $$e(r{r}_i|r{r}_{i-1})=\{\begin{array}{cc}0\hfill & \text{if }|r{r}_i-r{r}_{i-1}|<200\hfill \\ 1\hfill & \text{Otherwise}.\hfill \end{array}$$

Let {rr₁, …, rr_k} be sequence of RR intervals calculated in an ECG data, $\overrightarrow{\hat{\mathbf{r}}}$. We define feature value error by,

$$e_f(\overrightarrow{\hat{\mathbf{r}}})=\frac{e(r{r}_1)+{\sum }_{i=2}^{k}e(r{r}_i)\vee e(r{r}_i|r{r}_{i-1})}{n}$$

mSieve maintains a database of sensor data corresponding to each candidate state, and while substituting, it selects sensor data corresponding to a released state that minimizes the boundary errors on both boundaries.

Limits of the mSieve Algorithm

We discuss three limits of mSieve. First, if all the inferences are part of the blacklist, then the released data will correspond to the null state x = ∅, i.e. x_i = 0 for i = 1, …, n. No data release is possible in this case because every inference is sensitive.

Second, if either the number of data sources or the number of inferences are increased, then the size of the DBN will grow. This will increase the complexity of learning the adversary model. It will also increase the amount of space and time required to obtain a solution (see the complexity analysis of the dynamic program approach).

Finally, since there are imperfections in any computational model that can be used by mSieve to detect data segments corresponding to a blacklisted inference, there are some lower bounds on the privacy level that can be achieved with mSieve. We formalize it with the following lemma.

Lemma 2

Suppose false negative rate of the computational model used in mSieve for detecting black list b ∈ B is F_b. Define $\eta =\underset{b\in {𝕊}_B}{\text{max}}\{F_b\}$. Then lower bound of ε is ln(η).

A proof appears in the Appendix. We note that the above limit can be improved by using better inference models.

EVALUATION

Study Design and Data Collection

We use data collected in two different studies to evaluate mSieve. We first summarize the data collection process and provide statistics of data from both studies which were approved by the IRB. In the first study (D₁), physiological data was collected from 37 participants. The goal of this study was to evaluate the value of wearable sensors in monitoring and reflecting upon daily stress, activity, and conversation. Each participant wore mobile-sensors for one full day. In total, 37 days of data was collected (one participant per day).

In the second study (D₂), data was collect from 6 daily smokers. Each participant wore mobile-sensors for three days, for a total of 18 days of data. The goal of this study was to develop and validate a computational model to detect smoking. In both studies, each participant wore a physiological chest band, inertial wristband, and GPS-enabled smartphone for a day. Each sensor transmitted data continuously to a mobile phone during the study period. At the end of each day, the data collected on the phone was transferred to a server.

In both studies, participants wore the sensors for 12.04±2.16 hours per day during their awake period. Using the accelerometer sensor, we found that participants were physically active for 22.19% of the time, on average. Physiological data in the natural environment can be of poor quality for several reasons, such as physical activity, loose attachment, wireless disconnection, etc. [36]. We note that stress assessment model is applied to the data to obtain stress at each minute only when data collected was of good quality and not affected by these confounders [26]. Table 2 summarizes the number of data-points collected from participants in each study.

Table 2.

Data statistics from both studies (M = million).

Sensor	Avg. # sample per participant		Total # sample
	D1 (1 day)	D2 (3 days)	D1 (37×1 days)	D2 (6×3 days)
Respiration	0.78M	1.66M	28.80M	9.98M
ECG	2.15M	5.95M	79.76M	35.74M
Accelerometer	2.04M	4.58M	75.81M	27.47M
Gyroscope	2.07M	4.58M	76.60M	27.48M

Inferences from Sensor Data

We implemented the cStress model [26] to infer stress inference. It uses a set of features from both ECG and respiratory waveforms. If the stress probability of a particular minute is above 0.33, it is labeled as a stressed minute. We detected physical activity from wearable accelerometers using the model in [4]. We used the puff-Marker model [38] to detect smoking episodes from wrist sensor data and respiration data. Finally, we used the mConverse model [35] to infer conversation episodes.

Model Learning

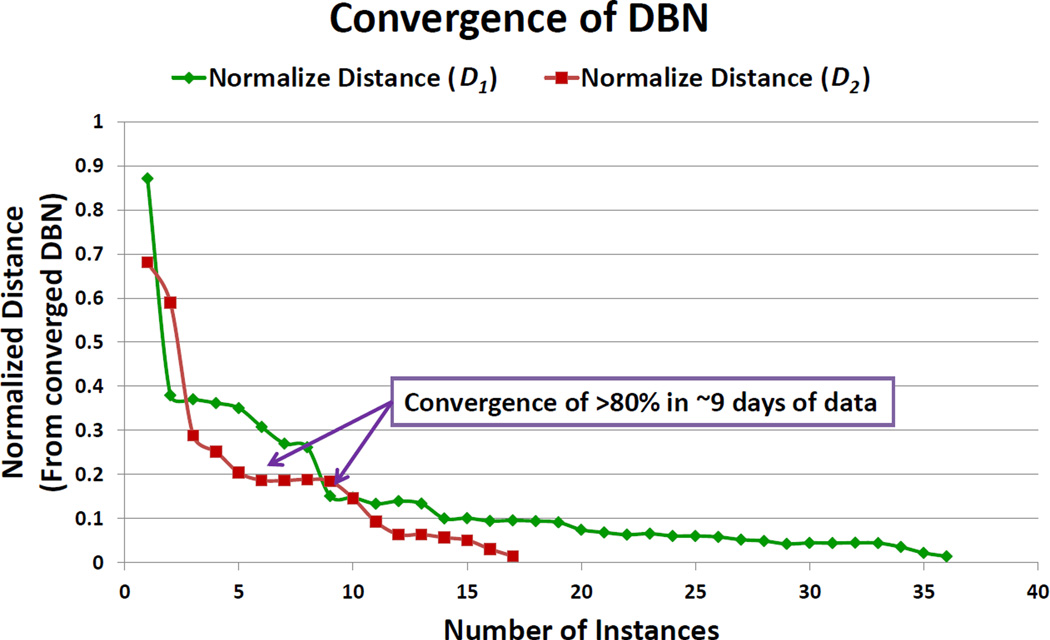
A key element of our scheme is the DBN model that we use for identifying the substitution segments. For model learning, we divided the day into state intervals. We then used the data from all the users (not a specific user) to study the convergence of the model learning, i.e., find the time interval over which the transition probabilities converged to a stable value. Let D_con be the converged transition matrix, and D_d be the conditional dependency probability matrix on day d. We define our normalized distance as $\frac{\sum (D_{\mathit{\text{con}}}-D_d)}{\sum D_{\mathit{\text{con}}}}$ where the sum is over all elements of the matrix. Figure 4 shows the convergence of DBN for multiple users. For both cases, more than 80% convergence occurs within first 9 days and 90% convergence occurs within 14 days.

Figure 4.

Convergence rate for DBN training. The model is trained using aggregate data from all the users.

Privacy-Utility Tradeoff

To understand the privacy-utility tradeoff of both the dynamic program and greedy approaches, we vary the privacy parameter ε and observe the utility loss U_loss in each case. We conducted four experiments, two on each dataset, by changing the configuration of the blacklist. In the first experiment, we set the Blacklist = {Stress}, and in the second experiment we set the Blacklist = {Conversation}, and performed our evaluation on dataset D₁. In third and fourth experiments, we set the Blacklist = {Smoking} and Blacklist = {Stress} respectively and conducted the evaluation on dataset D₂. In all the experiments, we vary ε from zero to one in steps of size 0.05. Figure 5 shows the results obtained for each of the four experiments. Note, in each plot we show the utility loss for both the dynamic program and greedy approaches. Note also init utility loss is the utility loss after creating holes. When ε = 0 we get e^ε = 1, which means that the posterior belief about blacklist should not be more than the prior expectation. At that point, U_loss is maximum and we get an average of 11% utility loss for the greedy algorithm and 7% utility loss for the DP algorithm. As we increase the value of ε, U_loss reduces. On average, we get less than 10% utility loss for both algorithm.

Figure 5.

Privacy-Utility tradeoff for different blacklist configurations and varying privacy sensitivity ε. Results are shown for both the datasets.

Dynamic Program vs. Greedy Algorithm

Utility Loss

We computed the U_loss value for both the dynamic programming algorithm and the greedy algorithm. In Figure 8, we also show U_loss after substitution. DP always produces better result than the greedy algorithm and both produce better results than the initial U_loss. For some users, initial U_loss is less than our solution. This is because, using our approach, we always fill each hole resulting in occasional overfilling of the whitelist inferences.

Figure 8.

Comparison of utility loss for the DP and Greedy algorithms. The user IDs are sorted according to the utility loss using the DP algorithm.

Distribution of Safe, Unsafe, and Sensitive States

We investigate the distribution of the three states in the data released by each algorithm. To do so, we vary the value of the privacy sensitivity ε and observe the percentage of nodes that are safe, unsafe, and sensitive. Figure 6 shows the results. Recall that because of plausible substitution, in addition to safe and sensitive states, we also have unsafe states that are not-sensitive, yet unsuitable for release as they are highly correlated with sensitive states. As we increase the value of ε, the number of safe states also increases. For a given privacy sensitivity to ε = 0.5, the average distribution of the various state types in a user trajectory is shown in Figure 7.

Figure 6.

Variation in the percentage of node types with privacy sensitivity ε. Recall, lower value of ε means higher privacy.

Figure 7.

Percentage of node types for the different users. Users IDs are sorted in ascending order of safe node percentage. Privacy sensitivity ε = 0.5.

RELATED WORK

Various transformation techniques have been proposed to protect data privacy. Below, we summarize some of the techniques relevant to our problem setting.

Anonymization metrics

A vast majority of the literature on privacy preserving data publishing consider anonymization metrics, such as k-anonymity [39], l-diversity [30], and t-closeness [27]. These approaches operate under the threat model in which an adversary is aware of quasi-identifiers in a multi-user dataset and wants to perform linkage attack using other auxiliary data sources to infer the sensitive attributes of individuals within the same dataset. We consider a different setting where data from a single user (no multi-user database is present) is being protected against sensitive inferences. We further assume that the identity of the user is known and hence the anonymization mechanisms are not useful. In addition, instead of static (time-independent) relational databases, we consider time-series of physiological sensor data.

Data Randomization

Randomization techniques add noise to the data in order to protect the sensitive attributes of records [2, 1]. Evfimievski et al. [20] proposed a series of randomization operators to limit the confidence of inferring an item’s presence in a dataset using association rule mining. Differential privacy offers a formal foundation for privacy-preserving data publishing [15, 18]. It can be classified as a data distortion mechanism that uses random noise (typically from a Laplace distribution) to ensure that an attacker, with access to the noisy query response, fails to guess the presence or absence of a particular record in the dataset. Compared to the general-purpose data publication offered by k-anonymity, differential privacy is a strictly verifiable method [28]. A survey of results on differential privacy can be found in [17]. While most of the research on differential privacy has focussed on interactive settings [23, 37, 21], non-interactive settings as an alternate to partition-based privacy models have also been considered in recent works [6, 19, 42]. Since we focus on physiological data, the randomization approaches are often unsuitable as they distort the data making it unusable for critical inferences, especially for physiological data.

Distributed privacy preservation

Results are aggregated from datasets that are partitioned across entries [33]. Partitioning could be horizontal [12, 14, 16, 29], i.e., records distributed across multiple entries, or vertical [12, 14, 41], i.e., attributes distributed across multiple entries. It is possible that individual entities may not allow sharing their entire dataset. However, they consent to limited information sharing with the use of a variety of protocols. The overall goal of such techniques is to maintain privacy for each individual entity, while obtaining aggregated results. We consider a single user setting for which the above techniques do not work.

Data Synthesis

Synthetic data generators exists for location data [8] that are used to protect the privacy of sensitive places. To obtain these synthetic traces, data from different users are pooled together into a population-scale model, which is then used to generate the data. Physiological data of each person is unique and used for obtaining bio-metrics [7, 31]. Thus, population-scale models often results in significant degradation in utility of the data. The well-defined temporal correlation between data segments in a physiological time series (i.e., continuity between presiding and succeeding contexts) makes it even harder to generate synthetic data.

In summary, protecting behavioral privacy when sharing time series of mobile sensor data (especially physiological data), pose new challenges and unique research opportunities that have usually not been considered in prior works.

LIMITATIONS AND DISCUSSION

We presented mSieve, as a first step towards building systems that can use substitution as an effective mechanism to protect privacy of behavior while sharing personal physiological data. Instead of random substitution of sensitive segments, which can degrade the utility of the overall dataset, mSieve performs model-based substitution. Our approach opens up new directions in privacy and differential privacy research, namely to define suitable metrics and mechanisms that can be used to protect private behaviors in a time series of mobile sensor data. Specific challenges are as follows:

• Algorithmic Scalability: There are several aspects that constitute the scalability of the system. Although, we have applied our model to several data sources, its applicability to other newer sources of mobile sensor data is yet to be established. Furthermore, an increase in the number of sensors, would imply a significant increase in the number of possible inferences (obtained using different combinations of the sensors), and a corresponding increase in the whitelist and blacklist set sizes. Improving the efficiency of our algorithms in computing candidate segments in such scenarios, which effectively would depend on the size of the DBN model, is an interesting open question.

• Offline vs. Online: Our model is an offline model that assumes availability of all data. In practice, data may need to be shared in real-time as they are produced. Significant adaptations may be needed to develop an online version of mSieve that can run in real-time on mobile phones.

• Adversarial Setting: Stronger adversarial models, where the adversary may possess more information regarding the user than the behavioral model captures, may lead to new challenges in ensuring privacy guarantees and represents interesting privacy research. In fact, this also represents a significant bottleneck for model-based privacy approaches, where a model is essential for maintaining the utility of the shared data, but the very use of a specific model leads to assumptions on adversarial capabilities. While in principle such approaches can be modified to protect against a worst-case adversary, it is difficult to provide meaningful utility in such cases.

• Plausibility: The current formulation of mSieve only provided local plausibility by adjusting the boundaries of substituted segments. Incorporating plausibility as part of the privacy formulation itself will be an interesting extension of the current work.

• Privacy leakage due to Graylist: We consider inferences that are associated with whitelist or blacklist, but other behaviors could be inferred from raw sensor data. We call those additional inferences as graylist. Information leakage due to graylist need to be investigated further.

• New and emerging inferences: Finally, rapid advances are being made in being able to infer human behaviors from seemingly innocuous sensor data, which may challenge the notion of white list and black list, especially when raw sensor data is being shared.

CONCLUSION

We presented mSieve, a system that uses substitution as a mechanism to protect privacy of behaviors to facilitate sharing of personal physiological data collected continuously in the natural environment. Instead of random substitution of sensitive segments, which can degrade the utility of the overall dataset, we perform model-based substitution. We employ a Dynamic Bayesian Network model that allows us to search for plausible user-specific candidate segments that satisfy the statistics of the sensitive segment and thus preserve the overall consistency of the shared data. Through experimentation on real-life physiological datasets, we demonstrated that our substitution strategies can indeed be used for preserving the utility of inferences while achieving differential behavioral privacy. This work opens the doors for follow up research and real-life deployment as adoption of physiological sensors in daily wearables such as smartwatches grow.

Table 1.

Summary of notations used.

User model, DBN	Du
Raw sensor data	$\overrightarrow{r_i}=\{r_i(t)|t_{\mathit{\text{start}}}\le t\le t_{\mathit{\text{end}}}\}$
Actual sensor data	$\overrightarrow{\mathbf{r}}=\{\overrightarrow{r_1},\overrightarrow{r_2},\dots ,{\overrightarrow{r}}_{n_s}\}$
Released sensor data	$\overrightarrow{\hat{\mathbf{r}}}(t)=\{{\overrightarrow{\hat{r}}}_1,{\overrightarrow{\hat{r}}}_2,\dots ,{\overrightarrow{\hat{r}}}_{n_s}\}$
Duration difference	di = ti − t̂i ∀1 ≤ i ≤ n
State	x = (x1, …, xn) ∈ {0, 1}n
State interval	s = (x, ts, te)
Actual state sequence	s⃗ =< s1, s2, …, sτ >
Obfuscated state sequence	ŝ⃗ =< ŝ1, ŝ2, …, ŝτ >
Set of sensitive states	𝕊B
Set of safe states	𝕊W
Set of all states	𝕊 = 𝕊W ∪ 𝕊B
Hole	hk
Candidate states for kth hole	ℂk

APPENDIX

PROOF OF LEMMAS 1 AND 2

Proof. (Lemma 1)

If we take a sample from expected output $\overrightarrow{\overline{s}}$ then $\frac{P(S^i\in {𝕊}_B|S^{i-1}=s^{i-1})}{P({\overline{S}}^i\in {𝕊}_B|{\overline{S}}^{i-1}={\overline{s}}^{i-1})}<e^{\delta }$ and ${\prod }_{i=1}^{\tau }\frac{P(S^i\in {𝕊}_B|S^{i-1}=s^{i-1})}{P({\overline{S}}^i\in {𝕊}_B|{\overline{S}}^{i-1}={\overline{s}}^{i-1})}<e^{{\tau }^{\delta }}$. Recall, inferences are computed over time intervals. We assume that inferences calculation are independent between time intervals, i.e., P(rⁱ → Sⁱ ∈ 𝕊_B|rⁱ⁻¹) = P(rⁱ → Sⁱ ∈ 𝕊_B) (rⁱ is independent of rⁱ⁻¹). Thus, $\frac{P(r^i\to S^i\in {𝕊}_B)}{P(r^i\to {\overline{S}}^i\in {𝕊}_B)}<e^{\delta }$ and correspondingly, ${\prod }_{i=1}^{\tau }\frac{P(r^i\to S^i\in {𝕊}_B)}{P(r^i\to {\overline{S}}^i\in {𝕊}_B)}<e^{{\tau }^{\delta }}$.

Combining the above equations together and denoting P(Sⁱ ∈ 𝕊_B|rⁱ) by P(rⁱ → Sⁱ ∈ 𝕊_B) we get, $\frac{P(S^1\in {𝕊}_B|r^1)}{P({\overline{S}}^1\in {𝕊}_B|{\overline{r}}^1)}{\prod }_{i=2}^{\tau }\frac{P(S^i\in {𝕊}_B|s^i)P(S^i\in {𝕊}_B|S^{i-1})}{P({\overline{S}}^i\in {𝕊}_B|{\overline{r}}^i)P({\overline{S}}^i\in {𝕊}_B|{\overline{S}}^{i-1})}<e^{2\tau \delta }$. This is same as $\frac{P(S^1\in {𝕊}_B|r^1,\dots ,S^{\tau }\in {𝕊}_B|r^{\tau })}{P({\overline{S}}^1\in {𝕊}_B|{\overline{r}}^1,\dots ,{\overline{S}}^{\tau }\in {𝕊}_B|{\overline{r}}^{\tau })}\le e^{2\tau \delta }$. Finally, if the ratio of the joint probabilities of states is bounded then a blacklist query corresponding to the states will also be bounded by the same value. Thus, $\frac{P(q(\widehat{r^1},\dots ,\widehat{r^{\tau }};b\in {𝕊}_B)\in K)}{P(q(\overline{r^1},\dots ,\overline{r^{\tau }};b\in {𝕊}_B)\in K)}\le e^{2\tau \delta }$ Since, $\delta <\epsilon /2\tau \frac{P(q(\hat{r};b)\in K)}{P(q(\overline{r}\in DB;b)\in K)}\le e^{\epsilon }$ Thus, $D(\overrightarrow{\hat{r}}\Vert \overrightarrow{\overline{r}})\le e^{\epsilon }$

Proof. (Lemma 2)

The probability of detecting a blacklist inference from released data is equal to the false negative of the computational model, i.e. P(r̂ → X ∈ B) = F_b. Let r̄ be the data segment drawn from the reference database. Thus, probability of detecting blacklist from r̄ is close to zero, i.e. P(r̄ → X ∈ B) → 0 thus ln(P(r̄ → X ∈ B)) → 0. Using our privacy definition, |ln(P(r̂ → X ∈ B)) − ln((P(r̄ → X ∈ B))| ≤ ln(η) − 0 = ln(η). Thus, we pick ε such that ln(η) ≤ ε.