Abstract
The osmotic water permeability coefficient (Pf) of plasma membrane of maize (Zea mays) Black Mexican Sweet protoplasts changed dynamically during a hypoosmotic challenge, as revealed using a model-based computational approach. The best-fitting model had three free parameters: initial Pf, Pf rate-of-change (slopePf), and a delay, which were hypothesized to reflect changes in the number and/or activity of aquaporins in the plasma membrane. Remarkably, the swelling response was delayed 2 to 11 s after start of the noninstantaneous (but accounted for) bath flush. The Pf during the delay was ≤1 μm s−1. During the swelling period following the delay, Pf changed dynamically: within the first 15 s Pf either (1) increased gradually to approximately 8 μm s−1 (in the majority population of low-initial-Pf cells) or (2) increased abruptly to 10 to 20 μm s−1 and then decreased gradually to 3 to 6 μm s−1 (in the minority population of high-initial-Pf cells). We affirmed the validity of our computational approach by the ability to reproduce previously reported initial Pf values (including the absence of delay) in control experiments on Xenopus oocytes expressing the maize aquaporin ZmPIP2;5. Although mercury did not affect the Pf in swelling Black Mexican Sweet cells, phloretin, another aquaporin inhibitor, inhibited swelling in a predicted manner, prolonging the delay and slowing Pf increase, thereby confirming the hypothesis that Pf dynamics, delay included, reflected the varying activity of aquaporins.
The regulation of plant aquaporins is becoming a focus of research in an increasing number of laboratories (Maurel et al., 2002; Tyerman et al., 2002). However, the reports on the regulation of the water permeability of plant cells are still relatively few, very likely reflecting the technical difficulties inherent in such measurements.
In order to quantify the permeability of a plant cell to water, one of the approaches consists of isolating protoplasts and monitoring the initial rate of change of their volume upon an osmotic challenge. If the osmotic potential of the external solution is changed instantaneously, the osmotic water permeability (termed Pf or Pos) can be deduced from the initial rate of volume relaxation (e.g. Zhang et al., 1990; Verkman, 2000). There are at least two problems with this approach: (1) even when an instantaneous change of solution is possible, a systematic error is introduced, causing an underestimate of Pf because, already during the initial phase of protoplast swelling, the volume, the surface area, and the internal concentration of solutes do not remain constant; and (2) instantaneous bath perfusion has technical—and physiological—limitations: unlike animal cells, isolated plant cell protoplasts (the terms protoplast and cell will be used here interchangeably) do not stick well to the chamber floor and defeat attempts of rapid (let alone, instantaneous) solution flushes. Very fast external solution exchange has been achieved by immobilizing the protoplast with a suction micropipette (e.g. Ramahaleo et al., 1999) or transferring the protoplast between solutions, aspired within a micropipette (Suga et al., 2003). Using the suction micropipette is not without problems: enclosure within the suction-pipette tip protects a significant fraction of the cell surface from facing the osmotic challenge and distorts the cell's shape, causing a deviation from a perfect globule and complicating the required calculations (Ramahaleo et al., 1999). Moreover, the suction via the holding pipette very likely perturbs the cell membrane mechanically. Such perturbation may affect the aquaporin activity either directly via cytoskeletal elements and/or indirectly by signaling initiated through the activation of mechanosensitive ion channels in the plasma membrane and the ensuing ion fluxes. Such channels—including mechanosensitive Ca2+ channels—have been already described in plant cells (Falke et al., 1988; Cosgrove and Hedrich, 1991; Spalding and Goldsmith, 1993; Moran et al., 1996), and Ca2+ ions have been shown to affect plant aquaporins (Gerbeau et al., 2002). This is why the less-sophisticated bath solution exchange (with the protoplasts resting unperturbed on the bath floor) should not be altogether abandoned. On the other hand, the slower rate of bath perfusion obviously retards the initial rate of cell volume change and therefore invalidates the classical method of estimating the osmotic water permeability, Pf.
To overcome these difficulties, we have adopted a numerical approach. Thus, we explore here the limitations of obtaining correct values of Pf, even when the bath perfusion is not instantaneous, by combining the information about the time course of bath perfusion and the time course of the cell volume change. This approach consists of a simple experimental method, followed by an off-line curve-fitting procedure, yielding relatively accurate Pf values over a large span of water permeability values. In addition to the calculation of the initial Pf, i.e. the Pf at the onset of cell volume change, we charted the time course of Pf, taking advantage of 15-s-long (and longer) records of volume changes, rather than of only the few initial seconds.
Our approach increased considerably the overall throughput of the experiment and analysis, as well as their reliability. Moreover, based on specific hypotheses and model choices, this approach enabled us to reveal and describe quantitatively, for the first time, dynamic changes in Pf of cultured maize (Zea mays) cells during the osmotic challenge.
RESULTS
The Limitations of Manual Determination of Pf
Assumptions
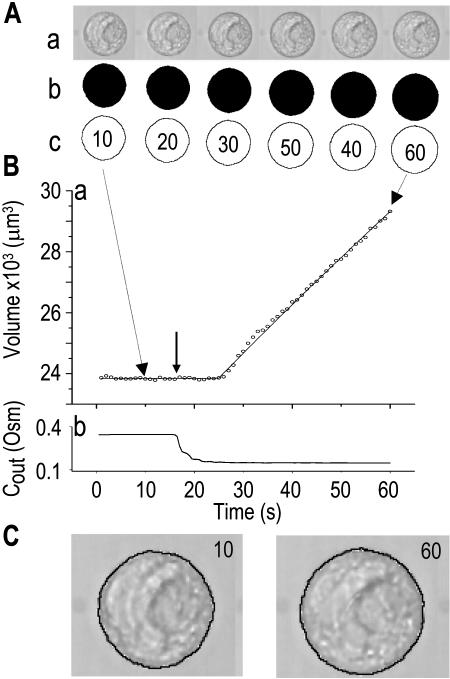
To assess the limitations of manual determination of Pf from initial volume change, we compared this method with a method of curve fitting. We thus fitted the experimentally observed time course of swelling of protoplasts isolated from suspension-cultured maize Black Mexican Sweet (BMS) cells faced with a decrease of the concentration of impermeant solutes in the bath (Fig. 1A, a, symbols), with the simulated time course of swelling in identical conditions (Fig. 1A, a, line). The simulation was based on the following assumptions: (1) the protoplast is globular, and, hence, its volume can be calculated from its two-dimensional image; (2) the protoplast is a perfect osmometer, i.e. the whole volume of the protoplast participates in the osmotic changes; and (3) the protoplast is a true osmometer, i.e. its membrane is semipermeable (i.e. permeable to water and not to internal or external solutes) and no osmotically active material is gained or lost by the protoplast. Based on (2) and (3), the internal concentration varies in an exact inverse proportion to volume changes. In addition, (4) the external osmotic concentration, Cout, is known at every instant during the experiment.
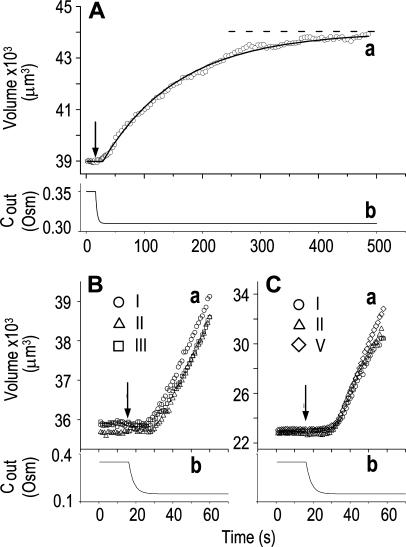
Figure 1.
The osmometer properties of swelling protoplasts. A, a, An approximately 8-min-long time course of swelling of a BMS (“Materials and Methods”) protoplast exposed to a change of the bath solution from 350 mOsm to 310 mOsm. Symbols, Experimental values of protoplast volume calculated from the areas of its circular two-dimensional-projection images (initial diameter: 42.1 μm). Line, Protoplast volume calculated using Eq. 2f (Supplemental Appendix I, with Pf = 9.6 μm s−1). A 12.6-s delay relative to the onset of solution exchange has been introduced into the calculation to allow a satisfactory fit of the line to the data. The predicted volume increase was 12.9%, and the observed increase was 12.6%. A, b, Cout during the osmotic challenge, calculated using Eqs. 1a–1d (Supplemental Appendix I, with the following values: twidth = 2.5 s, thalf = −33.1 s, 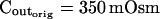 ,
, 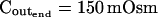 , and
, and 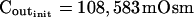 ). B, a, An approximately 60-s-long time course of swelling of a BMS protoplast (initial diameter: 40.9 μm) exposed to alternating bath solutions: first to 354 mOsm (isotonic), then to 160 mOsm (hypotonic), then again to 354 mOsm, etc. (only the steady-state volume attained upon the returns to the isotonic solutions is shown, not the time course of shrinking). The Roman numerals denote the order of recorded volume increases corresponding to the order of the hypotonic challenges. Fitting the data, as in A, a, yielded Pf = 7.0 ± 0.1 μm s−1 (mean ± se, n = 3) and delay = 12.2 ± 0.5 s. B, b, The corresponding calculated Cout time course during the swelling episode (Eqs. 1a–1d, with parameter values as in A, b). C, a, A 35.1-μm (diameter) protoplast undergoing similar hypotonic changes as in B. Fitting the data, as in A, a, yielded Pf = 36.2 ± 3.7 μm s−1 (n = 5) and delay = 15.3 ± 1.3 s. C, b, Cout as in A, b. See “Materials and Methods” and Supplemental Appendices I and II for details of calculations and fitting.
). B, a, An approximately 60-s-long time course of swelling of a BMS protoplast (initial diameter: 40.9 μm) exposed to alternating bath solutions: first to 354 mOsm (isotonic), then to 160 mOsm (hypotonic), then again to 354 mOsm, etc. (only the steady-state volume attained upon the returns to the isotonic solutions is shown, not the time course of shrinking). The Roman numerals denote the order of recorded volume increases corresponding to the order of the hypotonic challenges. Fitting the data, as in A, a, yielded Pf = 7.0 ± 0.1 μm s−1 (mean ± se, n = 3) and delay = 12.2 ± 0.5 s. B, b, The corresponding calculated Cout time course during the swelling episode (Eqs. 1a–1d, with parameter values as in A, b). C, a, A 35.1-μm (diameter) protoplast undergoing similar hypotonic changes as in B. Fitting the data, as in A, a, yielded Pf = 36.2 ± 3.7 μm s−1 (n = 5) and delay = 15.3 ± 1.3 s. C, b, Cout as in A, b. See “Materials and Methods” and Supplemental Appendices I and II for details of calculations and fitting.
The validity of these assumptions was upheld by our observations of swelling of the BMS protoplasts. Assumption (1) is based on the circular contour of the protoplasts, retained throughout the duration of the osmotic challenge, as evident both in bottom-to-top and side views of the protoplasts (Supplemental Videos 1 and 2, available at www.plantphysiol.org). In 22 protoplasts examined side-wise in isotonic solution and in 9 protoplasts in hypotonic solution, the mean ratio of height to width (“roundness”) was not different from 1 (1.01 ± 0.08 and 0.99 ± 0.08, respectively; ±sd; see also Supplemental Table I with the tabulated dimensions of the protoplasts). This approach demonstrated that a protoplast stuck to the bath bottom is, on average (within the above error), globular. Moreover, the excellent fit of the calculated end protoplast volume to the observed asymptotic protoplast size (i.e. the size of a protoplast in an osmotic equilibrium) lends a strong support for the three assumptions (1) to (3) (Fig. 1A). For example, with a 34 mOsm decrease from 343 to 309 mOsm, the mean increase in the cell equilibrium volume, attained within approximately 10 min, was 10.7% ± 0.8% (±se, n = 13; data not shown), equal to the calculated volume increase of 11%. Assumptions (1) to (3) have been verified also in other numerous independent tests. For example, upon the return to isotonic solution after 2- to 8-min-long swelling episodes in a solution hypotonic by 40 mOsm (switching from the isotonic concentration of approximately 350 mOsm to the hypotonic: approximately 310 mOsm; see “Materials and Methods”), the recovered volume (in the reestablished osmotic equilibrium with the isotonic solution) was 99.7% ± 0.4% (±se, n = 18) of the original volume; similarly, after 30- to 45-s swelling episodes in 200 mOsm lower concentration (isotonic solution, approximately 350 mOsm; hypotonic, approximately 150 mOsm), the cells returned to 101.2% ± 0.7% (n = 10) of their original volume (data not shown). Particularly instructive is the case of repeated alternating exposure of protoplasts to isotonic and hypotonic bath solutions. For example, after approximately 45 s exposure to a solution with a 200 mOsm-lower concentration and then shrinking back for 7 min in isotonic solution, the recovered protoplast volume was not significantly different from its original volume (100.8% ± 0.3% [mean ± se, 3 repeats; Fig. 1B] and 100.2% ± 1.3% [5 repeats; Fig. 1C]). Assumption (4) is based on reproducible bath perfusion as verified occasionally by monitoring the rate of Cout exchange through the presence of a dye in the in- or outflowing solution (Fig. 1A; Eqs. 1a–1d, Supplemental Appendix I).
Simulations
To test the fidelity of Pf determination by the classical method in unclassical conditions (i.e. during the noninstantaneous bath perfusion) and to compare it to the resolution of our computational analysis, we simulated, and then analyzed in both ways, the time course of swelling of a 45-μm (diameter) protoplast exposed to a change from an isotonic solution of 0.6 Osm to a hypotonic solution of 0.4 Osm. In this simulation, we varied the rate of solution change (between instantaneous and gradual) and the values of the osmotic water permeability of the membrane, Pf (Fig. 2). Pf usually refers to the osmotic water permeability of a unit area of the membrane at the moment just prior to the osmotic challenge. Here, we termed this initial permeability 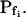 As a first approximation, we assumed here that Pf remained constant (i.e. equal to
As a first approximation, we assumed here that Pf remained constant (i.e. equal to 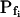 ) throughout the swelling episode. The simulation consisted of the calculation of the time courses of (1) the external concentration in the bath, Cout, (2) the changing cell volume, and (3) the resulting intracellular concentration of solutes, based on all of the assumptions outlined above. Cout was calculated from a sigmoid equation we found to fit best the experimental bath perfusion rate, monitored using the light absorbance (or fluorescence) of a dye included in the in- or outflowing solution (Eqs. 1a and 1b, Supplemental Appendix I). The time course of cell volume change was calculated by integrating numerically the momentary volume flow of water, dV/dt, across the whole protoplast membrane over the duration of several tens of seconds (Eqs. 2d–2f, Supplemental Appendix I). We then analyzed manually the simulated time course of the cell volume in a classical manner, by fitting a straight line to the fastest-rising initial phase of the volume versus time curve, calculating its slope and, subsequently, the cell's
) throughout the swelling episode. The simulation consisted of the calculation of the time courses of (1) the external concentration in the bath, Cout, (2) the changing cell volume, and (3) the resulting intracellular concentration of solutes, based on all of the assumptions outlined above. Cout was calculated from a sigmoid equation we found to fit best the experimental bath perfusion rate, monitored using the light absorbance (or fluorescence) of a dye included in the in- or outflowing solution (Eqs. 1a and 1b, Supplemental Appendix I). The time course of cell volume change was calculated by integrating numerically the momentary volume flow of water, dV/dt, across the whole protoplast membrane over the duration of several tens of seconds (Eqs. 2d–2f, Supplemental Appendix I). We then analyzed manually the simulated time course of the cell volume in a classical manner, by fitting a straight line to the fastest-rising initial phase of the volume versus time curve, calculating its slope and, subsequently, the cell's 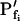 (Eq. 2b).
(Eq. 2b).
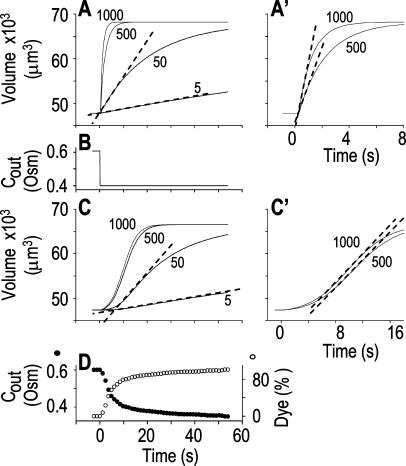
Figure 2.
The resolution limits of estimating 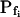 manually. A simulation of a 60-s-long time course of swelling of a 22.5-μm (diameter) protoplast (A, A′, C, C′), exposed to a change of the bath solution, Cout, from isotonic (0.6 Osm) to hypotonic (0.4 Osm), during a step exchange (B) and during gradual solution exchange (D). Numbers indicate the values of the initial osmotic water permeability of the membrane,
manually. A simulation of a 60-s-long time course of swelling of a 22.5-μm (diameter) protoplast (A, A′, C, C′), exposed to a change of the bath solution, Cout, from isotonic (0.6 Osm) to hypotonic (0.4 Osm), during a step exchange (B) and during gradual solution exchange (D). Numbers indicate the values of the initial osmotic water permeability of the membrane, 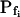 (in μm s−1), used in the simulation of volume changes. The dashed straight lines have been fitted manually (by eye-balling) to the initial, or fastest-rising, part of the curve. The
(in μm s−1), used in the simulation of volume changes. The dashed straight lines have been fitted manually (by eye-balling) to the initial, or fastest-rising, part of the curve. The 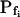 values determined from the slopes of these straight lines using Eq. 2b are listed in Table I. A, A simulation of volume changes (Eq. 2d) based on an instantaneous change of external concentration, as in B. A′, The first 8 s of A, on an expanded time scale. C, A simulation based on a gradually changing external concentration, as in D (Eqs. 1b and 2d). C′, Fragment of C, on an expanded scale. Note the apparent delay in the volume change, ignored in the manual fitting of the initial volume increase. D, The simulated changing osmolarity of the bath solution (Cout, full circles, Eq. 1b, with parameter values as in Fig. 1A, b), calculated from the time course of fluorescence (in relative units) of dilute acridine orange in the incoming solution (Dye, open circles, Eq. 1a). See text and “Materials and Methods” and Supplemental Appendices I and II for the simulations details.
values determined from the slopes of these straight lines using Eq. 2b are listed in Table I. A, A simulation of volume changes (Eq. 2d) based on an instantaneous change of external concentration, as in B. A′, The first 8 s of A, on an expanded time scale. C, A simulation based on a gradually changing external concentration, as in D (Eqs. 1b and 2d). C′, Fragment of C, on an expanded scale. Note the apparent delay in the volume change, ignored in the manual fitting of the initial volume increase. D, The simulated changing osmolarity of the bath solution (Cout, full circles, Eq. 1b, with parameter values as in Fig. 1A, b), calculated from the time course of fluorescence (in relative units) of dilute acridine orange in the incoming solution (Dye, open circles, Eq. 1a). See text and “Materials and Methods” and Supplemental Appendices I and II for the simulations details.
Pfi Values Compared
As expected, the 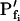 values resulting from the manual classical-style determination from the initial rate of volume change (Eq. 2b, Supplemental Appendix I), are close to the true values of
values resulting from the manual classical-style determination from the initial rate of volume change (Eq. 2b, Supplemental Appendix I), are close to the true values of 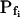 (i.e. those used for the simulation) only when the bath solution is changed in a step-wise mode and the true
(i.e. those used for the simulation) only when the bath solution is changed in a step-wise mode and the true 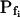 is low (Fig. 1, A, A′, and B; Table I). Thus, for example, the
is low (Fig. 1, A, A′, and B; Table I). Thus, for example, the 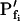 extracted from a simulated volume increase in response to an instantaneous flush underestimates the true
extracted from a simulated volume increase in response to an instantaneous flush underestimates the true 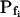 of 5 μm s−1 only by 2% and the true
of 5 μm s−1 only by 2% and the true 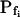 of 50 μm s−1 by 12%. However, the error of manual
of 50 μm s−1 by 12%. However, the error of manual 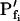 determination increases considerably with larger true
determination increases considerably with larger true 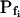 values, especially when the simulated volume change is based on a gradually changing Cout. Thus, in a case of instantaneous perfusion the true
values, especially when the simulated volume change is based on a gradually changing Cout. Thus, in a case of instantaneous perfusion the true 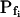 of 500 μm s−1 is underestimated by 24%, but in a case of gradual perfusion a similar error is encountered when the true
of 500 μm s−1 is underestimated by 24%, but in a case of gradual perfusion a similar error is encountered when the true 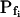 is only 5 μm s−1. Even more severely, in the case of gradual perfusion,
is only 5 μm s−1. Even more severely, in the case of gradual perfusion, 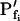 underestimates the true
underestimates the true 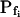 of 500 μm s−1 by 90% (Fig. 2; Table I).
of 500 μm s−1 by 90% (Fig. 2; Table I).
Table I.
The limitations of manual extraction of Pfi, the osmotic water permeability coefficient
| Instantaneous Flush | Gradual Flush | |||||||
|---|---|---|---|---|---|---|---|---|
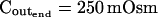 (μm s−1) (μm s−1) |
5 | 50 | 500 | 1,000 | 5 | 50 | 500 | 1,000 |
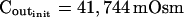 (μm s−1) (μm s−1) |
4.9 | 44 | 380 | 680 | 3.8 | 24 | 49 | 62 |
| Err (%) | −2 | −12 | −24 | −32 | −24 | −52 | −90 | −94 |
| ErrN (%) | – | – | – | – | – | – | 4.3 ± 2.7 | 17.6 ± 2.1 |
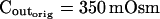 signifies the true
signifies the true 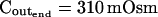 values used in the simulations of cell volume increases in Figure 2. The values of
values used in the simulations of cell volume increases in Figure 2. The values of 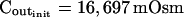 were extracted manually using Eq. 2b (“Materials and Methods”) from the slopes of the initial, linear phase of these simulated volume increases, in two types of bath perfusion rates: instantaneous and gradual (i.e. one which takes roughly 4 s to complete 90% of solution exchange). Err % is the percent deviation of the extracted
were extracted manually using Eq. 2b (“Materials and Methods”) from the slopes of the initial, linear phase of these simulated volume increases, in two types of bath perfusion rates: instantaneous and gradual (i.e. one which takes roughly 4 s to complete 90% of solution exchange). Err % is the percent deviation of the extracted 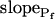 from the true
from the true 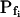 , as in Figure 2. ErrN % is the mean percent difference (±se, n = 10) between true
, as in Figure 2. ErrN % is the mean percent difference (±se, n = 10) between true 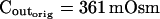 and
and 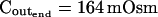 obtained from fitting the models to simulated data which included 5% random noise (relative to the baseline; noisy data not shown). Only the highest errors are shown.
obtained from fitting the models to simulated data which included 5% random noise (relative to the baseline; noisy data not shown). Only the highest errors are shown.
By contrast, our fitting procedure applied to simulated data as in Figure 2C, even with added random noise (5% of the baseline volume; data not shown), extracts the true 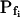 of 500 μm s−1 practically without any error, and the true
of 500 μm s−1 practically without any error, and the true 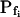 of 1,000 μm s−1 with less than 20% error (Table I). Notably, the noise encountered in our experiments usually does not exceed 1% (data not shown; “Materials and Methods”), and, therefore, our fitting procedure performs, as a rule, much better than in the above worst-case scenarios.
of 1,000 μm s−1 with less than 20% error (Table I). Notably, the noise encountered in our experiments usually does not exceed 1% (data not shown; “Materials and Methods”), and, therefore, our fitting procedure performs, as a rule, much better than in the above worst-case scenarios.
Testing the Validity of the Perfusion System and of the Analysis in Oocytes
As could have been expected, the noninstantaneity of the bath perfusion caused a noticeable delay (relative to the nominal start of bath perfusion) in the simulated volume changes (Fig. 2, C and C′) and was a major reason for the erroneous classical 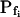 determinations in these simulations. Therefore, we were puzzled by the need to introduce an additional delay into the simulation to enable its correct fit to the real data (for example, approximately 13 s in Fig. 1A).Was this an artifact of the perfusion method, of our simulation, or a real physiological phenomenon? To resolve this question, we assayed the osmotic permeability of Xenopus oocytes, a widely used—almost standard—system for heterologous expression of aquaporins, including those from plants (Maurel et al., 1993). We tested oocytes without and with various pretreatments and fitted the data with the same simulations, adjusting only the
determinations in these simulations. Therefore, we were puzzled by the need to introduce an additional delay into the simulation to enable its correct fit to the real data (for example, approximately 13 s in Fig. 1A).Was this an artifact of the perfusion method, of our simulation, or a real physiological phenomenon? To resolve this question, we assayed the osmotic permeability of Xenopus oocytes, a widely used—almost standard—system for heterologous expression of aquaporins, including those from plants (Maurel et al., 1993). We tested oocytes without and with various pretreatments and fitted the data with the same simulations, adjusting only the 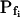 and the delay, where necessary (Fig. 3). The resulting best-fit
and the delay, where necessary (Fig. 3). The resulting best-fit 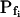 values of nonpretreated oocytes in our experiments were all comparable to the respective
values of nonpretreated oocytes in our experiments were all comparable to the respective 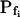 values determined previously by others (e.g. Zhang and Verkman, 1991; Chaumont et al., 2000). For example,
values determined previously by others (e.g. Zhang and Verkman, 1991; Chaumont et al., 2000). For example, 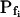 was 18.5 ± 3.2 μm s−1 in our control experiments (mean ± se, n = 16; Fig. 3, A and C), versus their 8.4 ± 0.9 μm s−1 (Zhang and Verkman, 1991); in oocytes pretreated with the pore-inducing amphotericin-B,
was 18.5 ± 3.2 μm s−1 in our control experiments (mean ± se, n = 16; Fig. 3, A and C), versus their 8.4 ± 0.9 μm s−1 (Zhang and Verkman, 1991); in oocytes pretreated with the pore-inducing amphotericin-B, 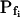 was 63.1 ± 11 μm s−1 (n = 10) in our hands (Fig. 3, A, A) versus their 84 μm s−1 in an equivalent treatment (Zhang and Verkman, 1991); in oocytes injected with water
was 63.1 ± 11 μm s−1 (n = 10) in our hands (Fig. 3, A, A) versus their 84 μm s−1 in an equivalent treatment (Zhang and Verkman, 1991); in oocytes injected with water 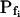 was 19.6 ± 2.4 μm s−1 (n = 8) in our present analyses (Fig. 3, A, W) versus 18.4 ± 2.3 μm s−1 (Chaumont et al., 2000), and in oocytes injected with the cRNA of maize ZmPIP2;5 aquaporin
was 19.6 ± 2.4 μm s−1 (n = 8) in our present analyses (Fig. 3, A, W) versus 18.4 ± 2.3 μm s−1 (Chaumont et al., 2000), and in oocytes injected with the cRNA of maize ZmPIP2;5 aquaporin 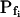 was 100.5 ± 13.8 μm s−1 (n = 23) in our hands (Fig. 3, A, Z) versus 129 ± 26.1 μm s−1 in the classical analysis (Chaumont et al., 2000). The small differences in
was 100.5 ± 13.8 μm s−1 (n = 23) in our hands (Fig. 3, A, Z) versus 129 ± 26.1 μm s−1 in the classical analysis (Chaumont et al., 2000). The small differences in 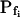 between those other determinations and ours could be attributed to differences in oocyte bath solutions and/or the oocyte batches. No less importantly, in contrast to the results from the BMS protoplasts (Fig. 1), the best-fit delay extracted from fitting the oocyte volume increases (beyond that resulting from the noninstantaneous bath perfusion) was not different from zero. In view of the relatively low-to-moderate values of water permeability, unstirred-layer effects were unlikely to contribute to these differences between the oocytes and the protoplasts (see “Discussion”). The presence of the delay in the BMS cells suggests, therefore, a hitherto unreported regulation of aquaporins.
between those other determinations and ours could be attributed to differences in oocyte bath solutions and/or the oocyte batches. No less importantly, in contrast to the results from the BMS protoplasts (Fig. 1), the best-fit delay extracted from fitting the oocyte volume increases (beyond that resulting from the noninstantaneous bath perfusion) was not different from zero. In view of the relatively low-to-moderate values of water permeability, unstirred-layer effects were unlikely to contribute to these differences between the oocytes and the protoplasts (see “Discussion”). The presence of the delay in the BMS cells suggests, therefore, a hitherto unreported regulation of aquaporins.
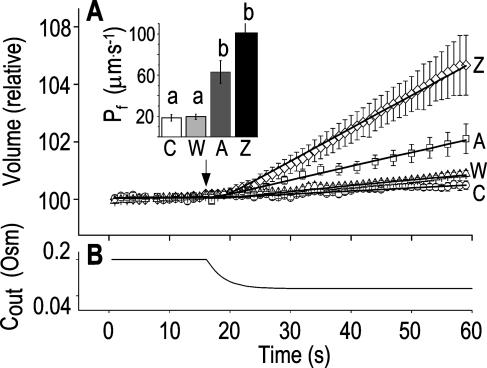
Figure 3.
“Non-classical” determination of best-fit 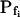 of oocytes. A, A 60-s-long average time course of swelling of Xenopus oocytes exposed to a change of solutions from 170 to 50 mOsm. Symbols, Volumes (normalized to the baseline volume) determined from control, noninjected oocytes (C; n = 16), water-injected oocytes (W; n = 8), oocytes pretreated with 100 μg/mL amphotericin-B during 10 to 60 min (A; n = 23), and oocytes injected with 50 ng mRNA of the ZmPIP2;5 (Z; n = 10). Lines, Simulations of swelling, calculated using model 5 (Eq. 2d), and the mean best-fit values of parameters obtained by fitting each individual cell's volume increase with this model. Note that the values of
of oocytes. A, A 60-s-long average time course of swelling of Xenopus oocytes exposed to a change of solutions from 170 to 50 mOsm. Symbols, Volumes (normalized to the baseline volume) determined from control, noninjected oocytes (C; n = 16), water-injected oocytes (W; n = 8), oocytes pretreated with 100 μg/mL amphotericin-B during 10 to 60 min (A; n = 23), and oocytes injected with 50 ng mRNA of the ZmPIP2;5 (Z; n = 10). Lines, Simulations of swelling, calculated using model 5 (Eq. 2d), and the mean best-fit values of parameters obtained by fitting each individual cell's volume increase with this model. Note that the values of 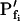 and delay in all cases were indistinguishable from zero. Inset, The means (±se) of the individual best-fit values of
and delay in all cases were indistinguishable from zero. Inset, The means (±se) of the individual best-fit values of 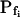 obtained in the various treatments (denoted by letters as in A). B, Cout during the hypotonic challenge, recontructed using Eq. 1d (with parameter values as in Fig. 1A, b).
obtained in the various treatments (denoted by letters as in A). B, Cout during the hypotonic challenge, recontructed using Eq. 1d (with parameter values as in Fig. 1A, b).
Models of Volume Increase
Searching for the most faithful description of the time course of protoplast swelling in hypotonic solutions, we considered several hypothetical scenarios. In all of these scenarios we assumed that, since in our experiments the swelling cell's surface area markedly exceeded 3% of its initial value, this increase occurred by membrane fusion with intracellular vesicles (Kwok and Evans, 1981; Wolfe and Steponkus, 1981; Rawicz et al., 2000). Depending on the Pf of the fusing vesicles, this fusion could then either modify the initial specific osmotic water permeability of the cell membrane, or 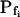 could remain without a change. For example, if a large number of water-permeable vesicles fused simultaneously and abruptly with the cell membrane, this step-wise increase in Pf would result in an appreciable
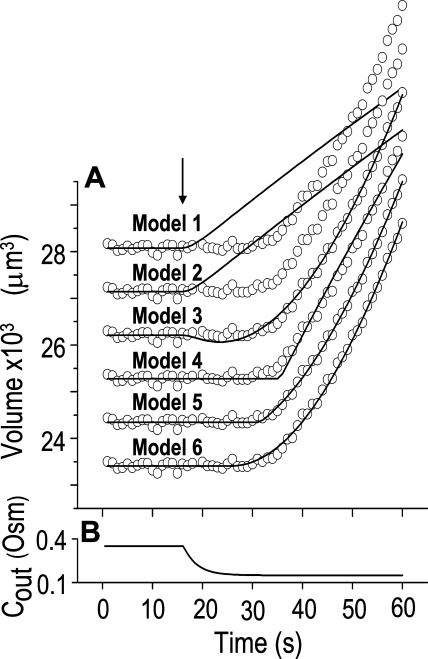
could remain without a change. For example, if a large number of water-permeable vesicles fused simultaneously and abruptly with the cell membrane, this step-wise increase in Pf would result in an appreciable 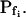 The suggested abrupt vesicle fusion may resemble—perhaps on a somewhat slower time scale—a synaptic event, in which fusion of hundreds of vesicles can occur over a course of a few milliseconds in response to a signal. In fact, intracellular pressure pulses in guard-cell protoplasts stimulated fast vesicle fusion with the plasma membrane (Bick et al., 2001); similarly, fast increase in cytosolic [Ca2+] caused fast exocytosis in maize coleoptile cells (Sutter et al., 2000), and vigorous, fast, and reversible membrane internalization upon shrinking has been visualized very recently in intact guard cells (Shope et al., 2003). Vesicle fusion may alter Pf by changing the membrane density of aquaporin proteins (further level of complexity might be added by the nonhomogeneity of vesicle pools; Sutter et al., 2000) and, additionally, Pf could also change via the regulation of the activity of aquaporins already embedded in the cell membrane. Finally, the swelling in response to the hypoosmotic challenge could occur immediately or after a delay during which the initial steps of the response did not reach a certain threshold. The different possibilities have been arranged in several models (see illustrations in Fig. 4 and equations in Supplemental Appendix I).
The suggested abrupt vesicle fusion may resemble—perhaps on a somewhat slower time scale—a synaptic event, in which fusion of hundreds of vesicles can occur over a course of a few milliseconds in response to a signal. In fact, intracellular pressure pulses in guard-cell protoplasts stimulated fast vesicle fusion with the plasma membrane (Bick et al., 2001); similarly, fast increase in cytosolic [Ca2+] caused fast exocytosis in maize coleoptile cells (Sutter et al., 2000), and vigorous, fast, and reversible membrane internalization upon shrinking has been visualized very recently in intact guard cells (Shope et al., 2003). Vesicle fusion may alter Pf by changing the membrane density of aquaporin proteins (further level of complexity might be added by the nonhomogeneity of vesicle pools; Sutter et al., 2000) and, additionally, Pf could also change via the regulation of the activity of aquaporins already embedded in the cell membrane. Finally, the swelling in response to the hypoosmotic challenge could occur immediately or after a delay during which the initial steps of the response did not reach a certain threshold. The different possibilities have been arranged in several models (see illustrations in Fig. 4 and equations in Supplemental Appendix I).
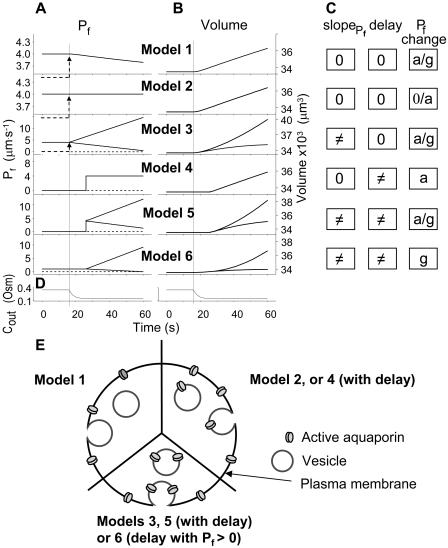
Figure 4.
Models of volume changes upon hypotonic challenges. A, Simulated time course of Pf. Horizontal dashed lines mark null water permeability. Up arrows mark step increase of Pf (an alternative Pf time course, pending on Pf having a zero value prior to the hypotonic challenge). Vertical lines mark the start of bath perfusion. B, Simulated time course of cell volume. Vertical lines as in A. C, A summary of the essential components of the models: 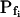 (absent: 0, or present: ≠), delay (similarly),
(absent: 0, or present: ≠), delay (similarly), 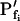 change relative to preceding Pf (gradual, g; abrupt, a; absent, 0). D, Simulated time courses of bath osmolarity, Eq. 1b to 1d (with parameter values as in Fig. 1A, b). All simulations employed Eqs. 1b to 1d and 3. Additional equations (all from Supplemental Appendix I) were used as follows: model 1: Eqs. 2d and 4 to 5,
change relative to preceding Pf (gradual, g; abrupt, a; absent, 0). D, Simulated time courses of bath osmolarity, Eq. 1b to 1d (with parameter values as in Fig. 1A, b). All simulations employed Eqs. 1b to 1d and 3. Additional equations (all from Supplemental Appendix I) were used as follows: model 1: Eqs. 2d and 4 to 5, 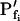 ; model 2: Eq. 2d,
; model 2: Eq. 2d, 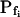 ; model 3: Eqs. 2e and 6,
; model 3: Eqs. 2e and 6, 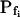 ,
, 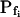 , and
, and 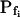 , for the upper and lower lines, respectively; model 4: Eqs. 2f and 7;
, for the upper and lower lines, respectively; model 4: Eqs. 2f and 7; 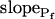 , delay = td = 10 s; model 5: Eqs. 6, 7, and 2g; all parameter values as in models 3 and 4 combined; model 6: Pf during the delay =
, delay = td = 10 s; model 5: Eqs. 6, 7, and 2g; all parameter values as in models 3 and 4 combined; model 6: Pf during the delay = 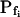 ,
, 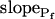 , and
, and 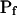 , for the upper and lower lines, respectively. E, A schematic illustration of some of the modeled vesicular mechanisms of Pf dynamics during the cell swelling phase (not all the options are included). See text for further explanations.
, for the upper and lower lines, respectively. E, A schematic illustration of some of the modeled vesicular mechanisms of Pf dynamics during the cell swelling phase (not all the options are included). See text for further explanations.
Model 1
(a) At the onset of volume increase upon the hypoosmotic challenge, the cell is already permeable to water, with a permeability 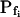 (via phospholipids and, possibly, also aquaporins), but the intracellular vesicles, destined to fuse with the membrane during swelling, are not water permeable. Consequently, during cell swelling, while the total cell membrane osmotic water permeability remains at its initial value, the calculated specific membrane osmotic water permeability, Pf, decreases gradually (Fig. 4A, model 1, solid line; Fig. 4C, row 1, g; Fig. 4E, model 1) in an inverse proportion to vesicle fusion and the increase in cell surface area (and, obviously, in cell volume, Fig. 4B; see Fig. 4 legend for simulation details). Or, (b) the resting Pf of the cell is very low (very very low, practically zero) and the hypoosmotic challenge abruptly increases the activity of hitherto silent plasma membrane aquaporins (for example, by inducing briefly their phosphorylation). Consequently, Pf acquires its initial non-zero value,
(via phospholipids and, possibly, also aquaporins), but the intracellular vesicles, destined to fuse with the membrane during swelling, are not water permeable. Consequently, during cell swelling, while the total cell membrane osmotic water permeability remains at its initial value, the calculated specific membrane osmotic water permeability, Pf, decreases gradually (Fig. 4A, model 1, solid line; Fig. 4C, row 1, g; Fig. 4E, model 1) in an inverse proportion to vesicle fusion and the increase in cell surface area (and, obviously, in cell volume, Fig. 4B; see Fig. 4 legend for simulation details). Or, (b) the resting Pf of the cell is very low (very very low, practically zero) and the hypoosmotic challenge abruptly increases the activity of hitherto silent plasma membrane aquaporins (for example, by inducing briefly their phosphorylation). Consequently, Pf acquires its initial non-zero value,  in a step-wise fashion (Fig. 4A, model 1, dashes and up-arrow; Fig. 4C, row 1, a). Thereafter, water-impermeable vesicles fuse with the membrane gradually, as in model 1a, and Pf decreases.
in a step-wise fashion (Fig. 4A, model 1, dashes and up-arrow; Fig. 4C, row 1, a). Thereafter, water-impermeable vesicles fuse with the membrane gradually, as in model 1a, and Pf decreases.
Model 2
(a) The cell is initially permeable to water (due to active aquaporins), and so are the intracellular vesicles, destined to fuse with the membrane during swelling; all the membranes have the same specific osmotic water permeability, 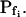 Consequently, while the cell swells upon the hypoosmotic challenge, gradually incorporating vesicles, the total osmotic water permeability of the cell membrane increases in direct proportion to the increase in the cell surface area, while Pf remains constant (Fig. 4A, model 2, solid line; Fig. 4C, row 2, 0; Fig. 4E, model 2). Or, (b) if at rest Pf = 0, a non-zero
Consequently, while the cell swells upon the hypoosmotic challenge, gradually incorporating vesicles, the total osmotic water permeability of the cell membrane increases in direct proportion to the increase in the cell surface area, while Pf remains constant (Fig. 4A, model 2, solid line; Fig. 4C, row 2, 0; Fig. 4E, model 2). Or, (b) if at rest Pf = 0, a non-zero 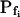 may result from an abrupt modification of Pf upon the hypoosmotic challenge (e.g. phosphorylation of silent aquaporins already embedded in the cell membrane, as in model 1b; Fig. 4A, model 2, dashes and up-arrow; Fig. 4C, row 2, a). Thereafter, the cell's volume increases gradually due to a fusion with vesicles with the same Pf, resulting in increasing total cell's water permeability and a constant Pf, as in version 2a of this model. According to this model, cell volume increases at a rate only slightly faster than according to model 1 (compare the end points of volume, Fig. 4B).
may result from an abrupt modification of Pf upon the hypoosmotic challenge (e.g. phosphorylation of silent aquaporins already embedded in the cell membrane, as in model 1b; Fig. 4A, model 2, dashes and up-arrow; Fig. 4C, row 2, a). Thereafter, the cell's volume increases gradually due to a fusion with vesicles with the same Pf, resulting in increasing total cell's water permeability and a constant Pf, as in version 2a of this model. According to this model, cell volume increases at a rate only slightly faster than according to model 1 (compare the end points of volume, Fig. 4B).
Model 3
The cell begins swelling as in model 2 (i.e. resembling either model 2a or 2b). However, during the process of volume increase Pf does not remain constant but gradually increases (or decreases) from its initial value 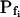 (Fig. 4A, model 3, solid lines; Fig. 4C, row 3, g; Fig. 4E, model 3). As a first approximation, we elected that Pf change linearly, increasing (or decreasing) each second by
(Fig. 4A, model 3, solid lines; Fig. 4C, row 3, g; Fig. 4E, model 3). As a first approximation, we elected that Pf change linearly, increasing (or decreasing) each second by 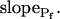 Generally, Pf change represents the possibility that (a) the Pf of the fusing vesicles differs from the membrane Pf (in either direction; a particular case of model 3 with a negative
Generally, Pf change represents the possibility that (a) the Pf of the fusing vesicles differs from the membrane Pf (in either direction; a particular case of model 3 with a negative 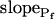 , i.e. with vesicles Pf much smaller than the membrane Pf, is akin to model 1). Or, (b) the vesicle Pf is the same as the membrane Pf, but on top of the vesicle fusion aquaporins become gradually activated (or inactivated).
, i.e. with vesicles Pf much smaller than the membrane Pf, is akin to model 1). Or, (b) the vesicle Pf is the same as the membrane Pf, but on top of the vesicle fusion aquaporins become gradually activated (or inactivated).
Model 4
The cell's osmotic water permeability at rest is zero (i.e. Pf = 0), and it remains zero initially even during the exposure to the hypotonic solution. Vesicle fusion, or aquaporin modification, occurs only following a certain delay and then the cell swells as in model 2b, with a constant 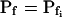 , acquired abruptly at the onset of swelling (Fig. 4A, model 4). Consequently, cell volume increase is delayed (Fig. 4B, model 4, solid lines).
, acquired abruptly at the onset of swelling (Fig. 4A, model 4). Consequently, cell volume increase is delayed (Fig. 4B, model 4, solid lines).
Model 5
The response to the hypoosmotic challenge is described by a combination of models 3 and 4, i.e. swelling begins after a delay and Pf varies gradually (linearly) from its non-zero initial value 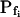 (acquired abruptly at the onset of swelling; Fig. 4A, model 5).
(acquired abruptly at the onset of swelling; Fig. 4A, model 5).
Model 6
As in model 5, the time course of response to the hypotonic challenge includes a delay (relative to the start of the exposure to the hypotonic solution). In contrast to model 5, however, during the delay the resting Pf is not zero, i.e. Pf has a finite value, 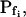 and the cell swells slowly even during the delay upon the hypoosmotic challenge. This slow phase is followed by a second, faster, phase of swelling, during which Pf increases linearly (Fig. 4, A and B, model 6). It is in comparison with the faster second phase that the slow first phase is interpreted as a delay.
and the cell swells slowly even during the delay upon the hypoosmotic challenge. This slow phase is followed by a second, faster, phase of swelling, during which Pf increases linearly (Fig. 4, A and B, model 6). It is in comparison with the faster second phase that the slow first phase is interpreted as a delay.
Pf in BMS Cells
Model Selection
In an attempt to select the most appropriate model for the description of swelling of BMS protoplasts in hypotonic solutions, we fitted the actual data with simulations based on the above models (Fig. 5; Table II; Eqs. 2d–2g; Supplemental Appendices I and II).
Figure 5.
Model selection. A, A 60-s-long time course of swelling of a BMS protoplast exposed to a change of solutions from 350 to 150 Osm, fitted repeatedly using different models (Eqs. 2d–2g, Supplemental Appendix I). All but the lowermost data-simulation pairs were shifted vertically upward for clarity. The values of the parameters used for the simulations are listed in Table II. B, Time course of Cout, reconstructed using Eq. 1b (with parameter values as in Fig. 1A, b).
Table II.
Model choice: Comparison between models fitted to data of Figure 5
| Model Class
|
I
|
II
|
III
|
|||
|---|---|---|---|---|---|---|
| Model No.
|
1
|
2
|
3
|
4
|
5
|
6
|
| No. of Parameters Varying during Fit | 1 | 1 | 2 | 2 | 3 | 3 |
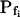 |
3.42 (ft) | 3.36 (ft) | −2.5 (ft) | 8.2 (ft) | 3.01 (ft) | 0.001 (ft) |
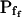 |
0 (fx) | 0 (fx) | 0.33 (ft) | 0 (fx) | 0.31 (ft) | 0.38 (ft) |
| Delay (s) | 0 (fx) | 0 (fx) | 0 (fx) | 19.5 (ft) | 15.4 (ft) | 9.9 (ft) |
| Err (rel) | 7.1222 | 6.9671 | 0.095 | 0.25542 | 0.04365 | 0.057295 |
| Preferred model | − | − | − | − | +++ | ++ |
Six different models were fitted to 60-s-long records (including the delay) of volume changes of protoplasts exposed to hypotonic solution shown in Figure 5. The classes of models are based on different assumptions with regard to the dynamics of the specific osmotic permeability of the membrane, Pf (see text for details, and, in particular, Eqs. 5–7 in “Materials and Methods”). In all models, 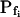 was a variable parameter and the other parameters,
was a variable parameter and the other parameters, 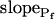 and delay, were either fixed (fx) or obtained as best-fit (ft) parameters in fitting the data of Figure 5. Err is the sum of squared departures of the data from the model, normalized, for the sake of comparison among various cells, to the number of points (hence independent of the duration of the data record or the sampling frequency) and to the value of baseline volume (hence independent of initial cell size).
and delay, were either fixed (fx) or obtained as best-fit (ft) parameters in fitting the data of Figure 5. Err is the sum of squared departures of the data from the model, normalized, for the sake of comparison among various cells, to the number of points (hence independent of the duration of the data record or the sampling frequency) and to the value of baseline volume (hence independent of initial cell size).
In the fitting procedure, the models differed in the number of fitted parameters and, hence, in the number of degrees of freedom. In models 1 and 2 a single parameter was fitted: the specific water permeability of the membrane at the onset of swelling, 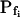 ; the other parameters were made equal to zero. In models 3 and 4 two parameters were fitted:
; the other parameters were made equal to zero. In models 3 and 4 two parameters were fitted: 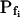 and
and 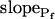 in the first, and
in the first, and 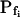 and delay in the latter; the remaining parameter was zero. In models 5 and 6, all three parameters were fitted simultaneously:
and delay in the latter; the remaining parameter was zero. In models 5 and 6, all three parameters were fitted simultaneously: 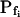 ,
, 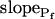 , and delay (Fig. 5). The best-fit parameters resulting from the various trials on this exemplary BMS protoplast are listed in Table II. The best-fitting model was selected as follows: models 1 and 2 were rejected based on their complete disregard of the delay. Model 3 was rejected on the basis of a nonphysical result:
, and delay (Fig. 5). The best-fit parameters resulting from the various trials on this exemplary BMS protoplast are listed in Table II. The best-fitting model was selected as follows: models 1 and 2 were rejected based on their complete disregard of the delay. Model 3 was rejected on the basis of a nonphysical result: 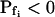 (Table II). The success of models 4 and 5, which constitute one group of nested models, was compared using F test (Motulsky and Christopoulos, 2003). Between models 5 and 6, each with three fitted parameters, the smaller error (square of deviations of the data from the model) was taken as an indicator of the better fit. We found the data of Figure 5 to be fitted best by model 5. When fitting the time course of volume increase lasting about 30 s from the onset of swelling, model 5 was better than model 6 in fitting 40 out of 49 protoplasts (82% of the cells), and model 6 was better in 9 cells (18%) (Supplemental Table II). Curiously, model 6 was most successful when fitting 15-s-long records (plus delay) of cells exposed to hypotonic steps of 200 mOsm: it fitted best in 50% of the cases, as opposed to only 7% to 9% of cells at 40 to 100 mOsm steps (Supplemental Table II). It should be emphasized that models 5 and 6 differ only in the definition of Pf during the delay and immediately thereafter; in model 5 Pf is zero during the delay, but
(Table II). The success of models 4 and 5, which constitute one group of nested models, was compared using F test (Motulsky and Christopoulos, 2003). Between models 5 and 6, each with three fitted parameters, the smaller error (square of deviations of the data from the model) was taken as an indicator of the better fit. We found the data of Figure 5 to be fitted best by model 5. When fitting the time course of volume increase lasting about 30 s from the onset of swelling, model 5 was better than model 6 in fitting 40 out of 49 protoplasts (82% of the cells), and model 6 was better in 9 cells (18%) (Supplemental Table II). Curiously, model 6 was most successful when fitting 15-s-long records (plus delay) of cells exposed to hypotonic steps of 200 mOsm: it fitted best in 50% of the cases, as opposed to only 7% to 9% of cells at 40 to 100 mOsm steps (Supplemental Table II). It should be emphasized that models 5 and 6 differ only in the definition of Pf during the delay and immediately thereafter; in model 5 Pf is zero during the delay, but 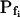 can assume any value immediately at the end of the delay, while in model 6 Pf during the delay is equal to the non-zero, but usually small, value of
can assume any value immediately at the end of the delay, while in model 6 Pf during the delay is equal to the non-zero, but usually small, value of 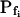 at the end of the delay. Consequently, delayed-but-fast-swelling cells are usually better described by model 5 than by model 6.
at the end of the delay. Consequently, delayed-but-fast-swelling cells are usually better described by model 5 than by model 6.
Low-Pfi and High-Pfi cells and Pf Dynamics
Since we chose 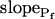 to reflect the linearly approximated change of Pf during cell swelling, possible nonlinearities in the time course of Pf values could have been masked when fitting a lengthy record of cell volume changes, preventing a meaningful reconstruction of Pf behavior. To uncover such nonlinearities, we examined how the shortening of the fitted volume-time record affects the best-fit parameters.
to reflect the linearly approximated change of Pf during cell swelling, possible nonlinearities in the time course of Pf values could have been masked when fitting a lengthy record of cell volume changes, preventing a meaningful reconstruction of Pf behavior. To uncover such nonlinearities, we examined how the shortening of the fitted volume-time record affects the best-fit parameters.
Indeed, analyzing the shortest records (the delay plus the following 15 s) revealed different grouping of cells according to their 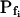 values and their Pf dynamics (several iterations of the fitting procedure and extending or truncating of the record were required to arrive at the required post-delay record length). Out of 98 cells thus analyzed, 27 cells were designated as the high-
values and their Pf dynamics (several iterations of the fitting procedure and extending or truncating of the record were required to arrive at the required post-delay record length). Out of 98 cells thus analyzed, 27 cells were designated as the high-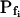 type, characterized by
type, characterized by 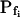 of >3.5 μm s−1 and a significantly negative
of >3.5 μm s−1 and a significantly negative 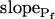 (Supplemental Table II; Fig. 6, A and D). Analysis of progressively longer records of these 27 cells (using the better-fitting model 5) yielded diminishing
(Supplemental Table II; Fig. 6, A and D). Analysis of progressively longer records of these 27 cells (using the better-fitting model 5) yielded diminishing 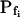 , with a less negative
, with a less negative 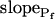 , indicating that in the high-
, indicating that in the high-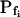 cells, Pf decreased most steeply during the initial phase of swelling.
cells, Pf decreased most steeply during the initial phase of swelling.
The 71 remaining cells all had 10- to 20-fold lower 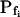 values: the 15-s-long records of 42 of them (which were also fitted better with model 5) yielded
values: the 15-s-long records of 42 of them (which were also fitted better with model 5) yielded 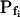 values of between 0 and approximately 1 μm s−1, and those of 29 other cells (better fitted with model 6) had even lower
values of between 0 and approximately 1 μm s−1, and those of 29 other cells (better fitted with model 6) had even lower 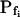 values (between 0 and 0.6 μm s−1). Understandably, all of these 71 cells were designated low-
values (between 0 and 0.6 μm s−1). Understandably, all of these 71 cells were designated low-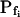 type (Fig. 6A′; Supplemental Table II). These low-
type (Fig. 6A′; Supplemental Table II). These low-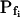 cells were characterized by a distinctly positive
cells were characterized by a distinctly positive 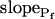 (when analyzing the 15-s-long records), the absolute values of which also decreased with increasing fitted record length, reflecting progressively less-steep Pf increases throughout the swelling process. In fact, in both types of cells the
(when analyzing the 15-s-long records), the absolute values of which also decreased with increasing fitted record length, reflecting progressively less-steep Pf increases throughout the swelling process. In fact, in both types of cells the 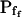 values (i.e. the end-of-record values of Pf, calculated using Eq. 6, with the corresponding best-fit values of
values (i.e. the end-of-record values of Pf, calculated using Eq. 6, with the corresponding best-fit values of 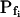 and
and 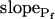 and t, the post-delay length of the record; Supplemental Appendix I) of the 15-s records and of the longer records were similar. Thus, Pf values appeared to change mainly within the first 15 s of swelling: when Pf was initially relatively high, it decreased roughly by 50%; when it was initially very low, it increased between 6- to more than 10-fold (Fig. 6, A and A′). When attempting to fit the high-
and t, the post-delay length of the record; Supplemental Appendix I) of the 15-s records and of the longer records were similar. Thus, Pf values appeared to change mainly within the first 15 s of swelling: when Pf was initially relatively high, it decreased roughly by 50%; when it was initially very low, it increased between 6- to more than 10-fold (Fig. 6, A and A′). When attempting to fit the high-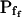 cells with model 6, the program invariably failed to converge. Fitting the low-
cells with model 6, the program invariably failed to converge. Fitting the low-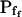 cells with model 6 yielded best-fit parameters with a considerably larger error of fit than with model 5 (data not shown).
cells with model 6 yielded best-fit parameters with a considerably larger error of fit than with model 5 (data not shown).
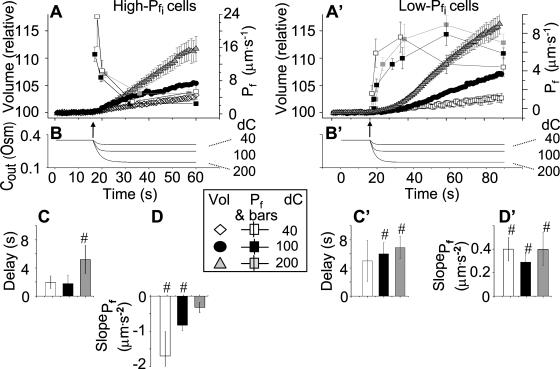
Figure 6.
Pf dynamics. A and A′, The time courses of volume during hypotonic shock of 40 mOsm, 100 mOsm, and 200 mOsm (means ± se, symbols without connecting lines) were fitted with model 5 (for clarity, omitting data fitted with model 6). The fitted record durations varied between 15 s, 32 s, and 45 s (in record duration we refer strictly to the net duration of the post-delay swelling period; the delay was also included in the fit irrespective of its duration). Pf values were plotted (means ± se, symbols connected by lines) depending on the fitted record duration, as follows: the Pf at the beginning and the end of each delay was plotted at 0 μm s−1 (according to model 5), then the best-fit 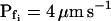 of the 15-s record was plotted at the end of the best-fit delay, marking a step increase of Pf (see model 5, Fig. 4A). The final (end-of-the-record) Pf values of all records,
of the 15-s record was plotted at the end of the best-fit delay, marking a step increase of Pf (see model 5, Fig. 4A). The final (end-of-the-record) Pf values of all records, 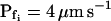 , were calculated using the corresponding best-fit
, were calculated using the corresponding best-fit 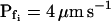 (Eq. 6, Supplemental Appendix I) and were placed at the time points corresponding to the end of the fitted records (record length of 15 s, 32 s or 45 s + delay; the differences between the horizontal positions of the symbols reflect the different durations of the best-fit delays). The results were grouped, as indicated, into low-
(Eq. 6, Supplemental Appendix I) and were placed at the time points corresponding to the end of the fitted records (record length of 15 s, 32 s or 45 s + delay; the differences between the horizontal positions of the symbols reflect the different durations of the best-fit delays). The results were grouped, as indicated, into low-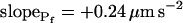 cells and high-
cells and high-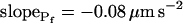 cells, based on their 15-s record
cells, based on their 15-s record 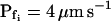 values. B and B′, The corresponding time courses of bath perfusion (Eq. 1b, with the following values: for delC of 200 mOsm: as in Fig. 1A, b; for delC of 100 mOsm: twidth = 2.5 s, thalf = −34.4 s, lag = 1 s,
values. B and B′, The corresponding time courses of bath perfusion (Eq. 1b, with the following values: for delC of 200 mOsm: as in Fig. 1A, b; for delC of 100 mOsm: twidth = 2.5 s, thalf = −34.4 s, lag = 1 s, 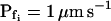 ,
, 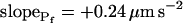 , and
, and 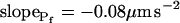 ), and for delC of 40 mOsm: twidth = 2.5 s, thalf = −34.4 s, lag = 1 s,
), and for delC of 40 mOsm: twidth = 2.5 s, thalf = −34.4 s, lag = 1 s, 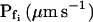 ,
, 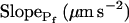 , and
, and 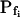 ). C and C′, The best-fit values of delay extracted from the 15-s-long records (mean ± se), as listed in Supplemental Table II. D and D′, The best-fit values of
). C and C′, The best-fit values of delay extracted from the 15-s-long records (mean ± se), as listed in Supplemental Table II. D and D′, The best-fit values of 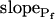 extracted from the 15-s-long records (mean ± se). #, Significant difference from zero (P < 0.05).
extracted from the 15-s-long records (mean ± se). #, Significant difference from zero (P < 0.05).
Delay
The BMS protoplasts did not begin to swell for a significant number of seconds during an exposure to the hypotonic challenge, and a large part of this lag—the delay—was not accounted for by the noninstantaneous bath solution exchange. This delay in swelling—as determined from the shortest records—lasted roughly 2 to 5 s in the high-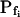 cells and about 6 to 11 s in the low-
cells and about 6 to 11 s in the low-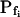 cells. At a 100 mOsm step it was higher (approximately 3–5-fold) in the low-
cells. At a 100 mOsm step it was higher (approximately 3–5-fold) in the low-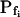 cells than in the high-
cells than in the high-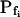 cells (P < 0.05; Supplemental Table II; Fig. 6, C and C′). During the delay, the
cells (P < 0.05; Supplemental Table II; Fig. 6, C and C′). During the delay, the 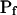 of these protoplasts was exceptionally low, irrespective of the models (zero, according to the assumption of model 5, or ≤1 μm s−1, as obtained by fitting the data according to model 6).
of these protoplasts was exceptionally low, irrespective of the models (zero, according to the assumption of model 5, or ≤1 μm s−1, as obtained by fitting the data according to model 6).
The Effect of Osmolarity Steps
When examining the shortest records of the low-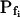 cells, the magnitude of the hypotonic step (delC) did not affect any of the parameters (Supplemental Table II), nor their combination. However, while the delays of swelling of the high-
cells, the magnitude of the hypotonic step (delC) did not affect any of the parameters (Supplemental Table II), nor their combination. However, while the delays of swelling of the high-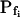 cells at steps of 40 mOsm were not different from zero, the delays at 200 mOsm were significantly larger than zero (Supplemental Table II; Fig. 6, C and C′). Additionally, the high-
cells at steps of 40 mOsm were not different from zero, the delays at 200 mOsm were significantly larger than zero (Supplemental Table II; Fig. 6, C and C′). Additionally, the high-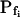 cells were the most numerous when delC was the smallest: their proportion was 9/15 at delC of 40 mOsm, 11/44 at 100 mOsm, and only 7/49 at delC of 200 mOsm. Thus, the highest delC (or the lowest hypoosmotic bath concentration) appears to preserve the low Pf.
cells were the most numerous when delC was the smallest: their proportion was 9/15 at delC of 40 mOsm, 11/44 at 100 mOsm, and only 7/49 at delC of 200 mOsm. Thus, the highest delC (or the lowest hypoosmotic bath concentration) appears to preserve the low Pf.
Testing Model Predictions: Manipulation of Pf Dynamics
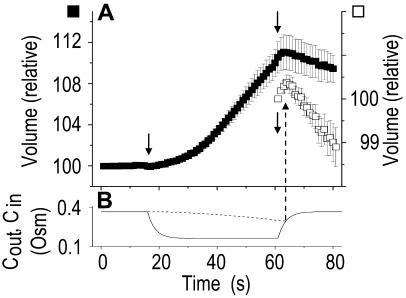
Pf at the Onset of Reshrinking
At the end of a 32 s-long swelling episode (not counting the delay) in a hypotonic (delC = 200) solution, the mean 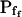 of 27 low-
of 27 low-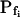 cells was 8.2 ± 1.7 μm s− (mean ± se; Fig. 7; a subgroup of cells from Supplemental Table II). At this time, it could be expected that upon flushing the bath with the isotonic solution the cells would start shrinking with a rate determined by this
cells was 8.2 ± 1.7 μm s− (mean ± se; Fig. 7; a subgroup of cells from Supplemental Table II). At this time, it could be expected that upon flushing the bath with the isotonic solution the cells would start shrinking with a rate determined by this 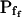 value, without any delay. Additionally, based on the assumptions of a perfect and true osmometer (see above) we would predict that at first, the cell will continue swelling for a while, until the osmotic gradient between the cell and the bath was reversed. Both predictions were indeed confirmed: (a) the cell swelled for a while (Fig. 7A), in a perfect match to the simulated time courses of the external and intracellular osmotic concentrations (Fig. 7B), and (b) in stark contrast to the delayed swelling response to the hypotonic challenge, the shrinking response began immediately upon the establishing of hypertonic conditions and progressed with a constant rate for at least about 15 s (Fig. 7). Furthermore, as predicted, the initial Pf′ value of this shrinking response (Fig. 7, inset), 9.9 μm s−1, was similar to the
value, without any delay. Additionally, based on the assumptions of a perfect and true osmometer (see above) we would predict that at first, the cell will continue swelling for a while, until the osmotic gradient between the cell and the bath was reversed. Both predictions were indeed confirmed: (a) the cell swelled for a while (Fig. 7A), in a perfect match to the simulated time courses of the external and intracellular osmotic concentrations (Fig. 7B), and (b) in stark contrast to the delayed swelling response to the hypotonic challenge, the shrinking response began immediately upon the establishing of hypertonic conditions and progressed with a constant rate for at least about 15 s (Fig. 7). Furthermore, as predicted, the initial Pf′ value of this shrinking response (Fig. 7, inset), 9.9 μm s−1, was similar to the 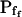 of the preceding swelling phase. In this case Pf′ was determined classically from the initial shrinking rate, using Eqs. 2b and 3 (as in the analyses of Fig. 2), and the values of the isotonic solution, the mean preswelling initial volume of the average cell (radius = 18.9 μm ± 2.2; ±sd; n = 27), and the mean volume at the initial phase of cell shrinking. These results contribute to the validation of the perfect and true osmometer assumptions on which our calculations of internal osmolytes concentrations were based, and support the physiological meaning we attributed to the water permeability parameters.
of the preceding swelling phase. In this case Pf′ was determined classically from the initial shrinking rate, using Eqs. 2b and 3 (as in the analyses of Fig. 2), and the values of the isotonic solution, the mean preswelling initial volume of the average cell (radius = 18.9 μm ± 2.2; ±sd; n = 27), and the mean volume at the initial phase of cell shrinking. These results contribute to the validation of the perfect and true osmometer assumptions on which our calculations of internal osmolytes concentrations were based, and support the physiological meaning we attributed to the water permeability parameters.
Figure 7.
Swelling and shrinking compared. A, The averaged traces of the time courses of volume changes: swelling of BMS protoplasts during a hypotonic challenge of a 200 mOsm step, and shrinking upon the restoration of the isotonic solution (approximately 350 mOsm). Full symbols represent volumes normalized to the initial pre-swelling volume at the isotonic solution (mean ± se, n = 27). Down arrows, The onset of bath flush. Open symbols (inset) represent part of the same data—volumes during restoration of the isotonic solution—normalized to the volume just prior to the onset of bath flush. B, The osmolarity of bath solution. Solid line, The simulated time course of bath solution exchange (Eq. 1b, Supplemental Appendix I, and parameter values as in Fig. 1A, b). Dotted line, The simulated time course of intracellular concentration (Eq. 3, Supplemental Appendix I). Up arrow indicates the start of cell shrinking coinciding with the intracellular concentration beginning to exceed the concentration in the bath.
Mercury and Phloretin
If increasing Pf reflects increasing activity of membrane aquaporins, Pf dynamics (i.e. the water permeability parameters) should be affected by aquaporins' inhibition. Mercurial reagents are generally used as water channel blockers even if some aquaporins are not inhibited (Daniels et al., 1996; Tyerman et al., 1999). Yet incubation of BMS protoplasts with up to 200 μm of HgCl2 did not affect at all the time course of swelling at 200 mOsm-hypotonic solution (n = 7; data not shown).
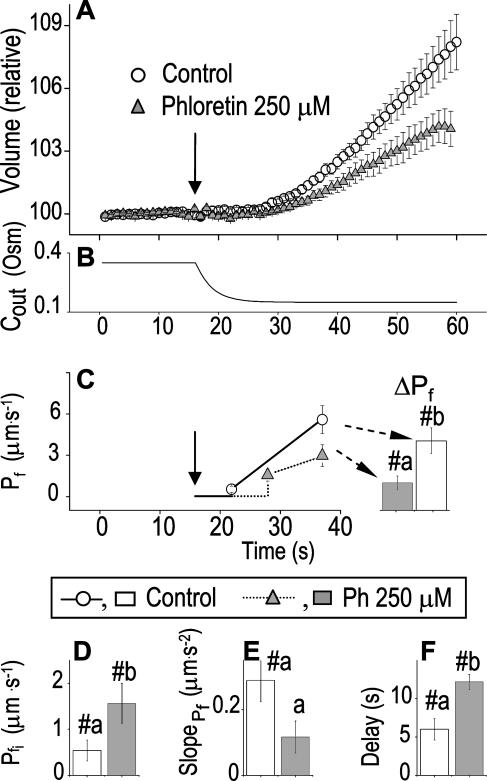
By contrast, phloretin, already shown to inhibit some plant and mammalian aquaporins (Echevarria et al., 1996; Tsukaguchi et al., 1998; Dordas et al., 2000; Moshelion et al., 2002), slowed down significantly the swelling of BMS cells (Fig. 8A). In the analysis of Pf parameters during 15 s of swelling, a prolonged delay (from approximately 6 s to approximately 13 s) was a prominent effect of the treatment (Fig. 8E). In addition, although 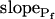 did not appear to be affected much by phloretin (Fig. 8E) in control cells Pf increased within the 15 s of swelling significantly more than did Pf in the phloretin-treated cells until the same time point (Fig. 8C). Thus, approximately 20 s after beginning of perfusion with the hypotonic solution the accumulated change in Pf was 5.1 ± 1.1 μm s−1 (mean ± se; n = 6) in the control and only 1.4 ± 0.6 μm s−1 (n = 8) in the phloretin-treated cells. These two effects combined to produce the overall inhibitory effect of phloretin on Pf throughout most of the time course of swelling, overcoming the mild promoting effect of phloretin on the
did not appear to be affected much by phloretin (Fig. 8E) in control cells Pf increased within the 15 s of swelling significantly more than did Pf in the phloretin-treated cells until the same time point (Fig. 8C). Thus, approximately 20 s after beginning of perfusion with the hypotonic solution the accumulated change in Pf was 5.1 ± 1.1 μm s−1 (mean ± se; n = 6) in the control and only 1.4 ± 0.6 μm s−1 (n = 8) in the phloretin-treated cells. These two effects combined to produce the overall inhibitory effect of phloretin on Pf throughout most of the time course of swelling, overcoming the mild promoting effect of phloretin on the 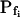 (from approximately 0.5 μm s−1 in the control to approximately 1.5 μm s−1 in the treated cells; Fig. 8D). These results support further the physiological meaning we attributed to the water permeability parameters.
(from approximately 0.5 μm s−1 in the control to approximately 1.5 μm s−1 in the treated cells; Fig. 8D). These results support further the physiological meaning we attributed to the water permeability parameters.
Figure 8.
The effect of phloretin on the parameters of BMS protoplast swelling. A, A 60-s-long average time course of swelling of BMS protoplasts exposed to a hypotonic challenge of 200 mOsm. Symbols, Relative volumes (% of baseline volume) determined from control protoplasts (n = 8) and protoplasts pretreated for 15 to 30 min with 250 μm phloretin (n = 6). The high-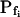 cells, identified during the analyzes of the 15-s-long swelling records using model 5, were excluded from these averages (1 cell from the control group and 2 cells from the phloretin-treated group). B, Cout during the hypotonic challenge, reconstructed using Eq. 1b, with parameter values as follows: twidth = 2.5 s, thalf = −32.37,
cells, identified during the analyzes of the 15-s-long swelling records using model 5, were excluded from these averages (1 cell from the control group and 2 cells from the phloretin-treated group). B, Cout during the hypotonic challenge, reconstructed using Eq. 1b, with parameter values as follows: twidth = 2.5 s, thalf = −32.37, 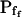 ,
, 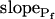 , and Cinit= 80,365. C, Pf dynamics during roughly 20 s after beginning of bath flush with the hypotonic solution (down arrows) without and with phloretin treatment, as indicated. The first symbols indicate mean
, and Cinit= 80,365. C, Pf dynamics during roughly 20 s after beginning of bath flush with the hypotonic solution (down arrows) without and with phloretin treatment, as indicated. The first symbols indicate mean 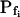 (± se), the second, mean
(± se), the second, mean 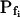 , calculated based on
, calculated based on 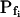 and the
and the 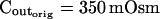 of each cell. When not seen, se is smaller than the symbol. ΔPf (bars), The increase of Pf during this period, averaged over all the cells. D to F, The mean (±se) values of the best-fit parameters obtained from 15-s-long swelling records without and with phloretin treatment, as indicated. #, Denotes significant difference from zero, and a and b denote significant differences between means (P < 0.05).
of each cell. When not seen, se is smaller than the symbol. ΔPf (bars), The increase of Pf during this period, averaged over all the cells. D to F, The mean (±se) values of the best-fit parameters obtained from 15-s-long swelling records without and with phloretin treatment, as indicated. #, Denotes significant difference from zero, and a and b denote significant differences between means (P < 0.05).
DMSO, Ethanol
If the three parameters of Pf dynamics correspond to separate underlying physiological processes (and are not artifacts), it might be expected that different modifications will affect at least one of them to a different extent. Indeed, in experiments in which protoplasts were preincubated in 0.1% solutions (v/v) of the common solvents, dimethyl sulfoxide (DMSO) and ethanol, many low-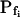 cells appeared to have been converted into high-
cells appeared to have been converted into high-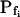 cells, albeit to a different extent: DMSO increased the population of the high-
cells, albeit to a different extent: DMSO increased the population of the high-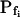 cells from one-seventh of the total number of cells to one-third, and ethanol increased it to seven-eighths of the total (Supplemental Table III). Interestingly, the delay in the remaining low-
cells from one-seventh of the total number of cells to one-third, and ethanol increased it to seven-eighths of the total (Supplemental Table III). Interestingly, the delay in the remaining low-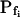 cells was almost halved by DMSO (from approximately 10 s in control to about 5 s in treated cells; Supplemental Table III).
cells was almost halved by DMSO (from approximately 10 s in control to about 5 s in treated cells; Supplemental Table III).
DISCUSSION
The Advantages of Our Approach
We have outlined here a simple procedure for measuring the osmotic water permeability of isolated plant protoplasts. Very importantly, our experimental approach is minimally disturbing to the protoplasts because we avoid pipette suction on the cell membrane. Moreover, we change the osmolarity of the solutions during a constant bath perfusion, which begins with establishing the baseline volume in the isotonic solution. This permits the recording of the complete time course of the cell volume change, in particular, the initial cell size. Additionally, the osmotic effect of introducing the hypo- or hypertonic challenge is not superimposed on the effect of exposing the protoplasts to a sudden shearing force resulting from the initiation of flow or from breaking the surface tension of two adjacent solutions. Furthermore, sequential treatments (exposure to varying osmolarity or to pharmacological reagents) can be easily performed (and repeated) on the same cell. This allows strict testing of the conformity of each cell to the basic assumptions about its true and perfect osmometer properties under all experimental conditions. Presently, our calculations are suitable for globular cells, including oocytes, but the same approach can be employed with other algorithms for volume estimation appropriate for the cells under study.
In addition to 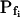 , our approach to data analysis yielded two more parameters for the description of the protoplast responses to hypotonic challenges: delay, the time between the onset of volume change and bath perfusion, and
, our approach to data analysis yielded two more parameters for the description of the protoplast responses to hypotonic challenges: delay, the time between the onset of volume change and bath perfusion, and 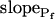 , the rate of change in Pf during the osmotic challenge. Thus, the main, novel result of our measurements is the discovery of time variation—dynamics—in the values of Pf in the BMS protoplasts.
, the rate of change in Pf during the osmotic challenge. Thus, the main, novel result of our measurements is the discovery of time variation—dynamics—in the values of Pf in the BMS protoplasts.
What Is the Meaning of These Parameters?
Delay and Pf during the Delay
Even without resorting to computational analysis of the volume changes of the BMS protoplasts, we noticed that their swelling was markedly delayed after a hypoosmotic solution was introduced into the bath (a roughly 17-s delay in swelling had been already reported for the osmotically challenged protoplasts of motor cells of the legume Samanea saman [Moshelion et al., 2002]). But only with the aid of the fitting program could we confirm that the delay indeed extended beyond that due to the noninstantaneity of the bath perfusion. Thus, in a large fraction of cells the mean true delay was about 10 s or more. As a test case and to eliminate the possibility that the delay in swelling results from the non-negligible delay in bath perfusion or, perhaps, artifacts of analysis, we examined frog oocytes with the similar experimental method and applied the same analysis as in the case of BMS protoplasts. The best-fit 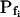 values of oocytes were in agreement with the previously reported results from other groups, and the best-fit delay (having accounted for the noninstantaneous solution exchange) was not different from zero, again, in agreement with results obtained by other methods (Fig. 3).
values of oocytes were in agreement with the previously reported results from other groups, and the best-fit delay (having accounted for the noninstantaneous solution exchange) was not different from zero, again, in agreement with results obtained by other methods (Fig. 3).
Based on the range of Pf values determined in all our experiments (<400 μm s−1), we do not expect any effects of unstirred layers on either side of the cell membrane, as concluded in an exhaustive analysis by Ramahaleo et al. (1999). A similar conclusion has been reached with respect to oocytes, based on direct experimental evidence (Zeuthen and Zeuthen, 2002). Thus the delay, or lack thereof, is unlikely to be an unstirred layers-induced artifact.
In contrast to oocytes, among the BMS cells, the delay in swelling was very prominent (Supplemental Table II; Fig. 6, C and C′). Moreover, and in a support of its veracity, the delay was amenable to manipulation by hypotonicity steps or pharmacological treatments: the high-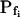 cells exhibited a significant delay only at the largest hypotonicity step of 200 mOsm, but not at steps of 40 and 100 mOsm (Supplemental Table II; Fig. 6, C and C′), and at the 200 mOsm steps DMSO shortened the delay by approximately 45% (Supplemental Table III). Thus, a delay in the swelling of the BMS protoplasts is a real and dynamic feature of these plant cells.
cells exhibited a significant delay only at the largest hypotonicity step of 200 mOsm, but not at steps of 40 and 100 mOsm (Supplemental Table II; Fig. 6, C and C′), and at the 200 mOsm steps DMSO shortened the delay by approximately 45% (Supplemental Table III). Thus, a delay in the swelling of the BMS protoplasts is a real and dynamic feature of these plant cells.
During the delay (i.e. when dV/dt was approximately 0 in the presence of an osmotic gradient), the value of Pf is either zero (by definition, according to model 5; Eq. 2a), or very close to zero (best-fit result according to model 6). Can we interpret such Pf values literally as the osmotic water permeability of the membrane?
Contrary to the common notion, there is evidence of instances of extremely low water permeability of biological membranes. Indeed, using a pressure probe in intact maize roots, relatively high initial Pf values of 7 to 120 μm s−1 have been found (Steudle, 1989), and in wheat roots 86 μm s−1 (Zhang and Tyerman, 1997). But initial Pf of wheat root plasma membrane vesicles was considerably lower: 12.5 μm s−1 (Niemietz and Tyerman, 1997). The initial Pfs of tobacco root protoplasts (in bath assays like ours) ranged between 2 and 60 μm s−1(Siefritz et al., 2002), and the Pfs of protoplasts isolated from 2-d-old seedlings (held with a suction pipette against a changing bath solution; Ramahaleo et al., 1999) were even more similar to ours, in the range of 1 to 10 μm s−1. Yet, finding high Pf values in protoplasts from older seedlings in the same series of experiments (Ramahaleo et al., 1999) prevents us from attributing the low-Pf values in our experiments to the protoplast isolation procedure alone. Using a novel floatation method, presumably not limited by unstirred-layer artifacts (based on density changes occurring in an oocyte during a diffusional exchange of water and D2O via its membrane), Iserovich et al. (1997) determined the diffusional water permeability of the aquaporin-devoid membrane matrix of Xenopus oocyte to be approximately 2 μm s−1. This is about the same as the Pf value determined in whole oocytes in the presence of Phlorizin (sugar-transport inhibitor), taking into account the fact that due to extensive folding the effective surface membrane area of an oocyte is 9-fold larger than that calculated from its observed cross-sectional circumference (Zeuthen et al., 2001, and references therein). Recently, Krylov et al. (2001) found very low values of osmotic water permeability—3 to 6 μm s−1—in vesicles with lipid content mimicking that of the outer leaflets of plasma membranes from kidney-originated cells. Yet, even this extremely low Pf would allow considerable volume change during the approximately 10-s-long delay period (see, for example, Fig. 4, model 6). Could the lipid leaflets of plant protoplast membranes be even less water permeable?
When interpreting the delay-associated Pf literally, we have to assume a total absence or absolute inactivity of aquaporins and a very low water permeability of the membrane matrix. This limitation is removed when invoking an apparent Pf, as in the following alternatives:
Swelling along a vertical axis, while preserving the same cross-sectional area in a top view would be observed as nonswelling, i.e. a delay. However, while observing the videotaped images of swelling protoplasts in a side view, we could not discern any such swelling phase limited to the vertical axis.
The apparent Pf could be comprised of a much higher water permeability coefficient multiplied by a reflection coefficient, σ < 1. If a very low reflection coefficient for one (or more) of the solutes in the cell or in the bath is assumed to exist during the delay, it must have existed, most likely, also during the preceding equilibration in the same isotonic solution. Upon hypotonic challenge, this reflection coefficient would be then assumed to increase (i.e. solute permeability would be assumed to vanish) gradually, or suddenly, as the case may be, allowing an osmotic response (swelling). Were this the case, and since the bath solution differed radically from the cell with respect to the species of the osmolytes, the cell would have to lose its osmolytes to the bath, and, consequently, shrink, even while in the isotonic solution. Alternatively, one of the bath solutes would have to leak into the cell, causing the cell to swell, while still in the isotonic solution. However, we did not observe any such changes in the cell volume during its stay in the constantly flowing isotonic solution (the only case reconciling this lack of volume change with a low reflection coefficient would be the—almost improbable—coincidence of equal fluxes of different osmolytes into and out of the cell. Therefore, we tend to reject this interpretation and to retain the assumption of perfect semipermeability of the membrane (our initial assumption (3) above). See also the experimental evidence in support of the true and perfect osmometer properties of the protoplasts (Fig. 2).
A zero Pf during a delay could be interpreted as indicating a mechanical obstacle to membrane expansion, not allowing even the approximately 3% cell surface increase which characterizes model lipid membranes (Wolfe and Steponkus, 1981; Olbrich et al., 2000). The expansion could be prevented by a rigid, membrane-attached, intracellular cytoskeletal network or a residual extracellular cellulose-fibril network (escaping detection by the cellulose-specific calcofluor staining), and the end of the delay would occur upon the loosening or breakdown of this network as a result of the increasing isometric tension. According to this hypothesis, this cytoskeletal network would have to be repaired rather fast upon membrane relaxation, as suggested by the reappearance of the delay in repeated swelling of the same protoplasts (Fig. 1, B and C). The time until the breakdown point of such a cytoskeletal network would be expected to depend inversely on the amplitude of the hypotonicity step: the larger the delC, the faster the buildup of the isometric tension up to the breakdown threshold, hence, the shorter the delay. However, an inverse relationship is evident in our analyses (Supplemental Table II, the 15-s-swelling records), rendering this hypothesis unlikely.
Another hypothesis that may explain the delay and the null apparent Pf during the delay is based on endo-/exocytotic vesicle recycling (see, for example, Sutter et al., 2000). In a similar mechanism, a vigorous exopinocytosis (utilizing vesicles, which, at the time of fusion with the plasma membrane are actively squeezed out) might be spilling out the water as soon as it enters by osmosis via the plasma membrane (resembling the contracting vacuole of the paramaecium); when the vesicle retrieval from the membrane is halted (while fusion continues) and/or when the fusing-vesicles become devoid of the squeezing-out mechanism, the delay ends. This hypothesis needs yet to be examined experimentally.
Pfi and slopePf
These parameters (extracted from analyzes of 15-s-long records; Supplemental Table II; Fig. 6) served to differentiate between the two contrasting types of Pf dynamics in the post-delay period: cells with transiently high Pf (i.e. with high-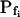 combined with a negative
combined with a negative 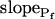 ) and cells with monotonically rising Pf (i.e. with very low
) and cells with monotonically rising Pf (i.e. with very low 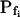 combined with a positive
combined with a positive 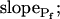 ). Interestingly, approximately 10 min pretreatment with both ethanol and DMSO (0.1% of either, v/v in the isotonic solution), tended to convert low-
). Interestingly, approximately 10 min pretreatment with both ethanol and DMSO (0.1% of either, v/v in the isotonic solution), tended to convert low-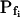 cells into high-
cells into high-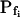 cells (the DMSO effect was smaller than that of ethanol; Supplemental Table III). Both have low reflection coefficients (ethanol may even permeate via aquaporins, as suggested for Chara; Hertel and Steudle, 1997; Schutz and Tyerman, 1997), and, therefore, in spite of their significant concentrations (0.1% v/v is equivalent to approximately 20 mm in the case of ethanol, and to approximately 12 mm in the case of DMSO), they were not expected and, indeed, were not observed to have osmotic effects (data not shown). Rather, the increased
cells (the DMSO effect was smaller than that of ethanol; Supplemental Table III). Both have low reflection coefficients (ethanol may even permeate via aquaporins, as suggested for Chara; Hertel and Steudle, 1997; Schutz and Tyerman, 1997), and, therefore, in spite of their significant concentrations (0.1% v/v is equivalent to approximately 20 mm in the case of ethanol, and to approximately 12 mm in the case of DMSO), they were not expected and, indeed, were not observed to have osmotic effects (data not shown). Rather, the increased 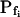 and the negative
and the negative 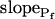 —all parts of the phenomenon of conversion (from low-
—all parts of the phenomenon of conversion (from low-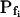 cells into high-
cells into high-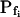 cells)—more likely reflect a combination of two true but opposing changes in water permeability—fast increase and slow decrease. This could be due to interactions of DMSO and ethanol with the membrane lipids (as in Mrak, 1992; Orvar et al., 2000), affecting the water permeability of the matrix and/or, indirectly, of aquaporins, and perhaps also directly with aquaporins. That ethanol may exhibit a direct interaction with a channel is based on a reported specific and selective [inhibitory] interaction of ethanol with a hydrophobic pocket in the Shaw2 K channel protein (Covarrubias et al., 1995). It should be noted that both DMSO and ethanol are widely used solvents in biological experiments, and, generally, 0.1% of either is considered harmless. Our results caution against this complacency.
cells)—more likely reflect a combination of two true but opposing changes in water permeability—fast increase and slow decrease. This could be due to interactions of DMSO and ethanol with the membrane lipids (as in Mrak, 1992; Orvar et al., 2000), affecting the water permeability of the matrix and/or, indirectly, of aquaporins, and perhaps also directly with aquaporins. That ethanol may exhibit a direct interaction with a channel is based on a reported specific and selective [inhibitory] interaction of ethanol with a hydrophobic pocket in the Shaw2 K channel protein (Covarrubias et al., 1995). It should be noted that both DMSO and ethanol are widely used solvents in biological experiments, and, generally, 0.1% of either is considered harmless. Our results caution against this complacency.
While ethanol shortened the delay in most cells and DMSO in some cells (Supplemental Table III), phloretin prolonged the delay (Fig. 8E). Phloretin has been shown to block some plant and mammalian aquaporins (Echevarria et al., 1996; Tsukaguchi et al., 1999; Dordas et al., 2000; Moshelion et al., 2002). The fact that the delay was prolonged by phloretin treatment—presumably as the result of aquaporins inhibition—supports the assumptions of our model 5, i.e. that the duration of the delay is determined by a transition of [phloretin-sensitive] plasma membrane aquaporins from inactive state to active state, possibly via activation of pre-embedded aquaporins. The sudden increase of 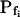 at the end of the delay (Fig. 8A) may be attributed to activity of aquaporins just incorporated into the membrane via fusion with internal vesicles and hence not yet fully exposed to phloretin. This fusion could be enhanced (relative to control) by the interaction of the lipophillic phloretin with the membrane lipids, as suggested above for DMSO and ethanol. Finally, the diminished increase in Pf, evident clearly after about 20 s of exposure to hypotonic solution (delay + 15-s swelling in control, delay + approximately 7-s swelling in phloretin-treated cells; Fig. 8C), is consistent, again, with the inhibitory effect of phloretin on aquaporins.
at the end of the delay (Fig. 8A) may be attributed to activity of aquaporins just incorporated into the membrane via fusion with internal vesicles and hence not yet fully exposed to phloretin. This fusion could be enhanced (relative to control) by the interaction of the lipophillic phloretin with the membrane lipids, as suggested above for DMSO and ethanol. Finally, the diminished increase in Pf, evident clearly after about 20 s of exposure to hypotonic solution (delay + 15-s swelling in control, delay + approximately 7-s swelling in phloretin-treated cells; Fig. 8C), is consistent, again, with the inhibitory effect of phloretin on aquaporins.
The Effect of Osmolarity
In addition to the effects of pharmacological agents, the changes in osmolarities used to induce volume changes turned out to influence the outcome of these very tests. Thus, the relative abundance of the high-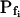 cells and the low-
cells and the low-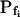 cells, with their diametrically opposed
cells, with their diametrically opposed 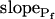 values (Fig. 6) depended on the osmolarity step (or the hypotonicity absolute value; Supplemental Table II). So did the delay: while pronounced at a delC of 200 mOsm, it was absent at a delC of 40 mOsm. Interestingly, a 200 mOsm hypertonic step did not affect the initial Pf of wheat root plasma membrane vesicles, although it decreased the Pf of tonoplast vesicles (which the authors interpreted as closing of tonoplast water channels; Niemietz and Tyerman, 1997). The difference from our case may stem from a difference in the direction of the osmotic challenge or from a difference in the experimental system (vesicles from wheat roots in their case versus protoplasts from maize-originated undifferentiated cells in suspension in our case). Very likely, the changes in osmolarities were transduced onto the regulation of the dynamically changing Pf via an osmolarity-sensing mechanism (the existence of which has been suggested already by Alexandre and Lassalles, 1991; Ramahaleo et al., 1996). Among the hypotonicity-mediating signals could be a varying level of cytosolic free [Ca2+], as in animal cells (e.g. Dube et al., 1990), remodeling the cytoskeletal submembranal network or affecting endo- or exocytosis, as reported for AQP2 and AQP4 in mammal cells (Madrid et al., 2001; Brown, 2003), or in plant cells (Sutter et al., 2000), or phosphorylation and gating of aquaporins, or any combination of the above, or other, additional signals. These hypotheses about processes underlying the Pf dynamics are being currently examined in experiments employing modifiers of cytoskeleton and membrane trafficking, and modifiers of protein phosphorylation status.
values (Fig. 6) depended on the osmolarity step (or the hypotonicity absolute value; Supplemental Table II). So did the delay: while pronounced at a delC of 200 mOsm, it was absent at a delC of 40 mOsm. Interestingly, a 200 mOsm hypertonic step did not affect the initial Pf of wheat root plasma membrane vesicles, although it decreased the Pf of tonoplast vesicles (which the authors interpreted as closing of tonoplast water channels; Niemietz and Tyerman, 1997). The difference from our case may stem from a difference in the direction of the osmotic challenge or from a difference in the experimental system (vesicles from wheat roots in their case versus protoplasts from maize-originated undifferentiated cells in suspension in our case). Very likely, the changes in osmolarities were transduced onto the regulation of the dynamically changing Pf via an osmolarity-sensing mechanism (the existence of which has been suggested already by Alexandre and Lassalles, 1991; Ramahaleo et al., 1996). Among the hypotonicity-mediating signals could be a varying level of cytosolic free [Ca2+], as in animal cells (e.g. Dube et al., 1990), remodeling the cytoskeletal submembranal network or affecting endo- or exocytosis, as reported for AQP2 and AQP4 in mammal cells (Madrid et al., 2001; Brown, 2003), or in plant cells (Sutter et al., 2000), or phosphorylation and gating of aquaporins, or any combination of the above, or other, additional signals. These hypotheses about processes underlying the Pf dynamics are being currently examined in experiments employing modifiers of cytoskeleton and membrane trafficking, and modifiers of protein phosphorylation status.
Physiological Relevance
In our experiments, the volume increases attained during 60-s-long exposures to hypotonic steps (including the delay) were, respectively, in three ranges: below 3%, 4% to 5%, and 10% to 12% in response to 40, 100, and 200 mOsm steps, respectively (Fig. 6). The respective changes in the radii (as calculated for globular or cubic cells) would be obviously much smaller: only 1%, 1% to 2%, and 3% to 4%, respectively.
How do these volume changes compare to those occurring in intact plant tissues? In numerous cases, the degree of volume changes may even exceed those reported here. For example, in pulvinar motor cells of Mimosa pudica, the reported volume decreases were of about 25% (reversibility would then require a 30% volume increases; Fleurat-Lessard et al., 1997), and in guard cells volume changes were about 40% (Raschke and Dickerson, 1973; Franks et al., 2001). These changes can occur within seconds (cell shrinking in Mimosa) to tens of minutes (in guard cells or motor organs of other plants). Moreover, many plant organs, such as leaves, cotyledons, or stems, perform extensive rhythmic growth movements, which very likely involve also considerable volume changes in nonspecialized cells (e.g. Jarillo et al., 2001; Siefritz et al., 2004), occurring within tens of minutes to hours. Cells in fast-growing plant tips—in elongation zones, including pollen tubes—are likely to fall in the same category. Another plant cell type that may undergo significant and rather fast osmotic swelling might be rain-drenched root hairs. The Pf dynamics revealed in our experiments on protoplasts may be relevant to all of these cell types in an intact plant.
CONCLUSION
Since only one class of models fitted the data well, the hypothesis associated with this model (about the physiological underlying mechanism, i.e. about the dynamics in aquaporin activity) seems the most plausible. The molecular details underlying this dynamics, still not accurately described by the current model parameters, await further experimentation (most desirably, also by other approaches, such as pressure-probe measurements). Presently, the validity of our combined quantitative model-based approach to the analysis of protoplast swelling during hypotonic challenges, and of the physiological interpretation of the model parameters, was confirmed in this work by the outcome of tests of four predictions: (1) we predicted and, indeed, observed the continuing increase of cell volume even after switching back from a hypotonic to an isotonic solution (Fig. 7); (2) we predicted the value of the initial Pf of the reshrinking protoplasts (Fig. 7); (3) we predicted and, indeed, observed the inhibitory effect of an aquaporin blocker, phloretin, on the parameters that in our model reflect the activity of aquaporins: prolongation of the delay and diminished increase in the water permeability, Pf (Fig. 9); and, finally, (4) we reproduced successfully the absence of delay and the values of initial Pf in swelling Xenopus oocytes expressing aquaporins.
Figure 9.
Image analysis of protoplast swelling. A, a, Exerpts from a time-series (montage) of images of a single swelling protoplast (diam: 35.7 μm) monitored during a approximately 43 s exposure to a hypotonic solution; b, protoplast images converted into shadows, and c, into contours, using the Scion Image program. Note that the measuring procedure required a slight tilt of the shadows matrix. B, Time course of volume changes, calculated from the areas enclosed by the countours, as in A-c, according to simple sphere geometry: Volume = 4/3·π·(cross-sectional area/π)3/2. C, The fidelity of conversion: the extracted contours (A-c) match exactly the contours of protoplasts in the original images. Numbers on images indicate the sequential order of their acquisition. See text for additional details.
Taken together, these findings support the conclusion that the dynamics of osmotic water permeability, Pf, revealed in BMS protoplasts during hypotonic challenges reflects the dynamics of activation of plasma membrane aquaporins. The delay in protoplast swelling attests to a hitherto unreportedly low Pf of the cell membrane matrix, and the time course of subsequent increase of Pf reveals the upregulation of aquaporins activity.
MATERIALS AND METHODS
Experimental Procedures
Plant Protoplasts
Plant Material and Culture Solutions
Maize (Zea mays) BMS cells were cultivated in the dark and with constant shaking at 90 rpm and 26°C, in 20 mL of BMS medium (4.4 g/L Murashige and Skoog [Sigma M-6899; St. Louis] containing macronutrients and vitamins, 25 g/L Suc, 2 mg/L 2,4-dichloro-phenoxyacetic acid [Sigma D-8407], and 0.2 g/L of l-Asn [UCB, Leuven, Belgium], pH 5.75). The cells were subcultured every 14 d at a 1:10 ratio with fresh BMS medium at room temperature.
Minimum-Stress Protoplast Isolation
Protoplasts were isolated from BMS cells in 1 mL of suspension, 7 to 11 d after subculture. The cells were left to sediment for 5 min, the upper BMS medium was sucked off and quickly replaced with 0.6 mL of cell wall digestion solution (resulting in a final concentrations of 1% cellulase [CEL, Worthington, NJ), 0.02% pectolyase Y23 [KARLAN, Santa Rosa, CA], 0.05% BSA [Sigma A9647], 0.025% polyvinylpyrrolidone K30 [Fluka 81420] in isotonic solution; see below). The cells were placed on a rotary shaker (150 rpm) for 45 min at 30°C. The enzymatic reaction was stopped by washing the cells with 5 mL of isotonic solution, through a nylon filter (20 μm pore size). To collect the cells accumulated on the filter and enhance protoplasts' release from the cell walls, the filter was immediately transferred (upside down) into 5 mL of fresh isotonic solution and incubated further on a shaker (20 min, 150 rpm, 30°C). After filtration through a second nylon filter (50 μm pore size), the protoplasts were collected into a test tube and concentrated to a final volume of 1 mL by gently sucking the solution off the top of the test tube (1 mL every 5 min).
Experimental Protoplast Solutions
The isotonic solution (10 mm KCl, 1 mm CaCl2, 8 mm MES, pH 5.75) was adjusted with sorbitol to osmolarity of between approximately 330–370 mOsm. The Wescor 5500 vapor pressure osmometer (Logan, UT) served for all osmolarity adjustments.
The different hypotonic solutions contained the same salts and were buffered identically but contained different amounts of the sugars; their osmolarity was adjusted within the range of 150 to 310 mOsm to create a hypoosmotic challenge step of either 40, 100, or 200 mOsm. The hypotonicity step did not deviate from the nominal values by more than 5%, and the exact numbers were fed into the fitting procedure (see below). In specific experiments, protoplasts were pretreated immediately prior to the hypotonic challenges with isotonic solution containing one of the following: 0.1% (v/v) DMSO (Sigma, D5879) for 10 min, 50 μm HgCl2 (Sigma, M1136) for 5 min, 0.1% (v/v) ethanol (Riedel deHaën, 32221) for 7 min, or 250 μm phloretin (Fluka 79310) for 15 to 30 min (phloretin was prepared by a 10,000-fold dilution from 2.5 m stock in DMSO; DMSO was included also in the control experiments at the same final concentration of 0.01% [v/v]). None of these substances was present in the hypotonic solutions during the actual tests.
Xenopus laevis Oocytes
Xenopus laevis oocytes were obtained as described by (Fetter et al., 2004), injected with either water or ZmPIP2;5 cRNA (Chaumont et al., 2000), and incubated for 3 d at 18°C in Barth's solution (88 mm NaCl, 1 mm KCl, 2.4 mm NaHCO3, 10 mm HEPES-NaOH, 0.33 mm Ca(NO3)2, 0.41 mm CaCl2, 0.82 mm MgSO4, pH 7.4).
The hypotonic challenge consisted of 5-fold-diluted Barth's medium. When indicated, oocytes were pretreated with 100 μg/mL amphotericin-B (Sigma, A6804) in Barth's medium for 10 to 60 min as described (Zhang and Verkman, 1991).
Bath Perfusion
The experimental chamber consisted of a lucite (plexiglass) plate, with a longitudinal groove with sloping shoulders in the middle of the plate and a cut-through slit within the groove (Supplemental Figure 1). The elongated simple shape of the chamber groove minimized turbulence.
Monitoring Bath Perfusion
Once initiated, bath perfusion lasted at the same pace, determined using an HPLC pump, throughout the experiment. The perfusion rate was 4 mL/min (±2%; as specified by the producer's manual), or, given the geometry of the groove, 4 cm3 min−1/(5 × 3) mm2 = approximately 4.4 mm/s. The perfusion-pump flow rate was verified at the beginning and end of each day of experiment and adjusted (if necessary), with acceptable deviations in our hands not exceeding 5%.
To obtain quantitative information on the time course of bath solution exchange, we monitored the absorbance of transmitted light by an indicator dye, xylene cyanol (ICN Biomedicals, Irvine, CA; 1 mg/50 mL in the incoming solution). Occasionally, we monitored the fluorescence of dilute acridine orange (Sigma; excitation: 490 nm, emission: 530 nm). Dyet, the dye density values versus time, t, was acquired at a rate of 10 Hz. Based on this indicator, 90% exchange was accomplished in 3.5 ± 3.4 s (mean ± sd, n = 17; Fig. 1B; see “Analysis” below).
Immobilizing the Cells
In experiments with protoplasts, the bottom of the chamber consisted of a coverslip, sealed to the lucite plate with silicon grease (catalog no. 1.07921.0100; MERCK, Darmstadt, Germany) for the duration of the experiment. To augment the stickiness of the globular protoplasts to the bath bottom, a 0.5-μL drop of 1% protamine sulfate (Sigma P4380; diluted in water, kept in aliquots at −20°C, and mixed well before use) was spread on the glass bottom for 2 min (or until completely dry), then rinsed 3 to 4 times (× approximately 1 mL) with isotonic solution. The remaining solution was shaken away and replaced with a drop of the cell-containing solution, and the protoplasts were allowed to settle down for 5 to 10 min. The whole groove was then gently filled up with isotonic solution.
In experiments with frog oocytes, a tiny strip of clear tape (Scotch mailing tape; 3M, St. Paul) was attached to the bottom of the chamber replacing the protamine-sulfate-pretreated coverslip. A drop containing a single oocyte (with a minimum of solution) was then applied gently to the tape, and the chamber was tilted at an 45° angle to move the oocyte to the drop rim to enhance its sticking to the tape. The chamber was then placed horizontally for 1 to 2 min, after which the whole groove was gently filled up with Barth's solution.
Image Acquisition
Our analysis relied on a reasonably well-focused cell contour. We had to experiment with different objectives. (For example, for the experiments described here, we used a simple 20× objective [Olympus LWD CDPlan 20PL; Tokyo] mounted on inverted Olympus microscope CK-2; in another case, we preferred a simple 40× PLAN objective [Nikon; Tokyo], mounted on a Nikon TMD inverted microscope, to a phase contrast objective, Nikon ELWD 40×.) To improve visibility, another coverslip was applied on the top of the chamber before perfusion started, its edges sealed with silicon grease to the surface of the lucite plate.
The first several images, recorded in the fast-flowing isotonic solution, constituted a baseline. The solution was then switched to a hypo- or hypertonic one, while simultaneously acquiring images at a rate of 1 Hz. For image acquisition, we used a CCD B&W camera (SSC M370 CE; SONY, Japan), with a LG-3 controller board (Scion, Frederick, MD), operated by Scion Image (version Beta 3b, adapted for PC from the popular public-domain program NIH Image by Wayne Rasband; available for free at www.scioncorp.com; Rasband and Bright, 1995).
Analysis
The aim of the analysis was the extraction of Pf, the osmotic water permeability of the membrane, by curve fitting of an experimentally obtained time course of cell volume changes with a simulated one. The simulation required the reconstruction of the time course of bath perfusion from measurements of density of an indicator dye.
Establishing the Time Course of Cell Volume Changes
The stored image sequences (Fig. 9A) were displayed in the Scion Image montage format, i.e. in a roughly square two-dimensional array. Using Adobe Photoshop software (Adobe, Mountain View, CA), each cell's image in the montage was converted to a black image on white background (with image rows tilted by approximately 2–3° to ensure the correct numbering sequence; Fig. 9A) and then to a line-contour (Fig. 9A). We calibrated and standardized the conversion procedure to maintain strictly the exact cell size, comparing the final size of the contour to the original cell's image (Fig. 7C) and verifying the size estimate using similarly processed images of 15 μm diameter beads (catalog no. F7235; Molecular Probes, Eugene, OR) and images of a microscope calibration slide (10 μm/division). The cell's cross-sectional areas within the contours were calculated using ImageJ (version 1.18; W. Rasband, downloaded from http://rsb.info.nih.gov/ij/) and converted to cell volumes, based on geometry of a sphere.
Reconstructing the Time Course of Bath Perfusion
Dye perfusion rates were fitted with a sigmoidal equation. We noted a slight but significant asymmetry in the time course of the dye density measured during the bath perfusion: the OUT-flush was somewhat slower than the IN-flush, as detailed in Supplemental Appendix I. This small but significant asymmetry, noted only while monitoring the dye perfusion close to the bath bottom (at a half-protoplast height above the bottom), was not likely to cause significant artifacts in our determinations of the Pf parameters. It should be emphasized, however, that such a possibility needs to be reassessed whenever the perfusion rates or perfusion system are altered.
Determination of Pf
The equations underlying the various models of cell swelling and incorporating the corrections based on the rate of bath perfusion are detailed in Supplemental Appendix II.
The analyzes were performed with a PfFit program incorporating these equations, as described in detail in Supplemental Appendix II.
Statistics
Student's t test was used for the comparison of means, and they were deemed significantly different at P < 0.05. F statistics was used for discriminating between nested models (Motulsky and Christopoulos, 2003). Choice between models 5 and 6 was based either on complete failure to converge the fitting routine using one of the models, or on the relative fitting error: the model with the smaller error was deemed the more successful (Motulsky and Christopoulos, 2003).
Upon request, materials integral to the findings presented in this publication will be made available in a timely manner to all investigators on similar terms for noncommercial research purposes. To obtain materials, please contact Nava Moran (nava.moran@huji.ac.il).
Supplementary Material
Acknowledgments
We thank Dr. S. Lobréaux (Université Montpellier-II) and Dr. P. Rogowsky (ENS-Lyon) for providing BMS cells, Mr. R. Novik for help with the MATLAB GUI, and Mr. T. Moran for help with the program compilation.
This work was supported by the Belgian Fund for Scientific Research and the Interuniversity Attraction Poles Programme—Belgian Science Policy (grants to F.C.), by an individual Marie Curie European fellowship (to M.M.), by the Israel Science Foundation (grant no. 550/01–1), and by the U.S.-Israel Binational Science Foundation (grant no. 2000191 to N.M.).
The online version of this article contains Web-only data.
Article, publication date, and citation information can be found at www.plantphysiol.org/cgi/doi/10.1104/pp.104.043000.
References
- Alexandre J, Lassalles JP (1991) Hydrostatic and osmotic pressure activated channel in plant vacuole. Biophys J 60: 1326–1336 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bick I, Thiel G, Homann U (2001) Cytochalasin D attenuates the desensitisation of pressure-stimulated vesicle fusion in guard cell protoplasts. Eur J Cell Biol 80: 521–526 [DOI] [PubMed] [Google Scholar]
- Brown D (2003) The ins and outs of aquaporin-2 trafficking. Am J Physiol Renal Physiol 284: F893–F901 [DOI] [PubMed] [Google Scholar]
- Chaumont F, Barrieu F, Jung R, Chrispeels MJ (2000) Plasma membrane intrinsic proteins from maize cluster in two sequence subgroups with differential aquaporin activity. Plant Physiol 122: 1025–1034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cosgrove DJ, Hedrich R (1991) Stretch-activated chloride, potassium, and calcium channels coexisting in plasma membranes of guard cells of Vicia faba L Planta 186: 143–153 [DOI] [PubMed] [Google Scholar]
- Covarrubias M, Vyas TB, Escobar L, Wei A (1995) Alcohols inhibit a cloned potassium channel at a discrete saturable site. Insights into the molecular basis of general anesthesia. J Biol Chem 270: 19408–19416 [DOI] [PubMed] [Google Scholar]
- Daniels MJ, Chaumont F, Mirkov TE, Chrispeels MJ (1996) Characterization of a new vacuolar membrane aquaporin sensitive to mercury at a unique site. Plant Cell 8: 587–599 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dordas C, Chrispeels MJ, Brown PH (2000) Permeability and channel-mediated transport of boric acid across membrane vesicles isolated from squash roots. Plant Physiol 124: 1349–1362 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dube L, Parent L, Sauve R (1990) Hypotonic shock activates a maxi K+ channel in primary cultured proximal tubule cells. Am J Physiol 259: F348–F356 [DOI] [PubMed] [Google Scholar]
- Echevarria M, Windhager EE, Frindt G (1996) Selectivity of the renal collecting duct water channel aquaporin-3. J Biol Chem 271: 25079–25082 [DOI] [PubMed] [Google Scholar]
- Falke LC, Edwards KL, Pickard BG, Misler S (1988) A stretch-activated anion channel in tobacco protoplasts. FEBS Lett 237: 141–144 [DOI] [PubMed] [Google Scholar]
- Fetter K, Van Wilder V, Moshelion M, Chaumont F (2004) Interactions between plasma membrane aquaporins modulate their water channel activity. Plant Cell 16: 215–228 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleurat-Lessard P, Frangne N, Maeshima M, Ratajczak R, Bonnemain J, Martinoia E (1997) Increased expression of vacuolar aquaporin and H+-ATPase related to motor cell function in Mimosa pudica L Plant Physiol 114: 827–834 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franks PJ, Buckley TN, Shope JC, Mott KA (2001) Guard cell volume and pressure measured concurrently by confocal microscopy and the cell pressure probe. Plant Physiol 125: 1577–1584 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerbeau P, Amodeo G, Henzler T, Santoni V, Ripoche P, Maurel C (2002) The water permeability of Arabidopsis plasma membrane is regulated by divalent cations and pH. Plant J 30: 71–81 [DOI] [PubMed] [Google Scholar]
- Hertel A, Steudle E (1997) The function of water channels in Chara: The temperature dependence of water and solute flows provides evidence for composite membrane transport and for a slippage of small organic solutes across water channels. Planta 202: 324–335 [Google Scholar]
- Iserovich P, Kuang K, Chun T, Fischbarg J (1997) A novel method to determine the diffusional water permeability of oocyte plasma membranes. Biol Cell 89: 293–297 [PubMed] [Google Scholar]
- Jarillo JA, Capel J, Tang RH, Yang HQ, Alonso JM, Ecker JR, Cashmore AR (2001) An Arabidopsis circadian clock component interacts with both CRY1 and phyB. Nature 410: 487–490 [DOI] [PubMed] [Google Scholar]
- Krylov AV, Pohl P, Zeidel ML, Hill WG (2001) Water permeability of asymmetric planar lipid bilayers: leaflets of different composition offer independent and additive resistances to permeation. J Gen Physiol 118: 333–340 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwok R, Evans E (1981) Thermoelasticity of large lecithin bilayer vesicles. Biophys J 35: 637–652 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madrid R, Le Maout S, Barrault MB, Janvier K, Benichou S, Merot J (2001) Polarized trafficking and surface expression of the AQP4 water channel are coordinated by serial and regulated interactions with different clathrin-adaptor complexes. EMBO J 20: 7008–7021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maurel C, Javot H, Lauvergeat V, Gerbeau P, Tournaire C, Santoni V, Heyes J (2002) Molecular physiology of aquaporins in plants. Int Rev Cytol 215: 105–148 [DOI] [PubMed] [Google Scholar]
- Maurel C, Reizer J, Schroeder JI, Chrispeels MJ (1993) The vacuolar membrane-protein gamma-TIP creates water specific channels in Xenopus oocytes. EMBO J 12: 2241–2247 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moran N, Yueh YG, Crain RC (1996) Signal transduction and cell volume regulation in plant leaflet movements. News Physiol Sci 11: 108–114 [Google Scholar]
- Moshelion M, Becker D, Biela A, Uehlein N, Hedrich R, Otto B, Levi H, Moran N, Kaldenhoff R (2002) Plasma membrane aquaporins in the motor cells of Samanea saman: Diurnal and circadian regulation. Plant Cell 14: 727–739 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Motulsky H, Christopoulos A (2003) Comparing models. In Fitting Models to Biological Data Using Linear and Nonlinear Regression. A Practical Guide to Curve Fitting. GraphPad Library, http://www.graphpad.com/articles/library.cfm, pp 134–159
- Mrak RE (1992) Opposite effects of dimethyl sulfoxide and ethanol on synaptic membrane fluidity. Alcohol 9: 513–517 [DOI] [PubMed] [Google Scholar]
- Niemietz CM, Tyerman SD (1997) Characterization of water channels in wheat root membrane vesicles. Plant Physiol 115: 561–567 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olbrich KC, Rawicz W, Needham D, Evans E (2000) Water permeability and mechanical strength of polyunsaturated lipid bilayers. Biophys J 79: 321–327 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orvar BL, Sangwan V, Omann F, Dhindsa RS (2000) Early steps in cold sensing by plant cells: the role of actin, cytoskeleton and membrane fluidity. Plant J 23: 785–794 [DOI] [PubMed] [Google Scholar]
- Ramahaleo T, Alexandre J, Lassalles JP (1996) Stretch activated channels in plant cells. A new model for osmoelastic coupling. Plant Physiol Biochem 34: 327–334 [Google Scholar]
- Ramahaleo T, Morillon R, Alexandre J, Lassalles JP (1999) Osmotic water permeability of isolated protoplasts. Modifications during development. Plant Physiol 119: 885–896 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasband WS, Bright DS (1995) NIH Image: A Public Domain Image Processing Program for the Macintosh. Microbeam Analysis 4: 137–149 [Google Scholar]
- Raschke K, Dickerson M (1973) Changes in shape and volume of guard cells during stomatal movement. Plant Res 1972: 149–153 [Google Scholar]
- Rawicz W, Olbrich KC, McIntosh T, Needham D, Evans E (2000) Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys J 79: 328–339 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schutz K, Tyerman SD (1997) Water channels in Chara corallina. J Exp Bot 48: 1511–1518 [Google Scholar]
- Shope JC, DeWald DB, Mott KA (2003) Changes in surface area of intact guard cells are correlated with membrane internalization. Plant Physiol 133: 1314–1321 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siefritz F, Otto B, Bienert GP, van der Krol A, Kaldenhoff R (2004) The plasma membrane aquaporin NtAQP1 is a key component of the leaf unfolding mechanism in tobacco. Plant J 37: 147–155 [DOI] [PubMed] [Google Scholar]
- Siefritz F, Tyree MT, Lovisolo C, Schubert A, Kaldenhoff R (2002) PIP1 plasma membrane aquaporins in tobacco: from cellular effects to function in plants. Plant Cell 14: 869–876 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spalding EP, Goldsmith MHM (1993) Activation of potassium channels in the plasma membrane of Arabidopsis by ATP produced photosynthetically. Plant Cell 5: 477–484 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steudle E (1989) Water flow in plants and its coupling to other processes: an overview. Methods Enzymol 174: 183–225 [Google Scholar]
- Suga S, Murai M, Kuwagata T, Maeshima M (2003) Differences in aquaporin levels among cell types of radish and measurement of osmotic water permeability of individual protoplasts. Plant Cell Physiol 44: 277–286 [DOI] [PubMed] [Google Scholar]
- Sutter JU, Homann U, Thiel G (2000) Ca2+-stimulated exocytosis in maize coleoptile cells. Plant Cell 12: 1127–1136 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsukaguchi H, Shayakul C, Berger UV, Mackenzie B, Devidas S, Guggino WB, van Hoek AN, Hediger MA (1998) Molecular characterization of a broad selectivity neutral solute channel. J Biol Chem 273: 24737–24743 [DOI] [PubMed] [Google Scholar]
- Tsukaguchi H, Weremowicz S, Morton CC, Hediger MA (1999) Functional and molecular characterization of the human neutral solute channel aquaporin-9. Am J Physiol Renal Physiol 277: F685–F696 [DOI] [PubMed] [Google Scholar]
- Tyerman SD, Bohnert HJ, Maurel C, Steudle E, Smith JAC (1999) Plant aquaporins: their molecular biology, biophysics and significance for plant water relations. J Exp Bot 50: 1055–1071 [Google Scholar]
- Tyerman SD, Niemietz CM, Bramley H (2002) Plant aquaporins: multifunctional water and solute channels with expanding roles. Plant Cell Environ 25: 173–194 [DOI] [PubMed] [Google Scholar]
- Verkman AS (2000) Water permeability measurement in living cells and complex tissues. J Membr Biol 173: 73–87 [DOI] [PubMed] [Google Scholar]
- Wolfe J, Steponkus PL (1981) The stress-strain relation of the plasma membrane of isolated plant protoplasts. Biochim Biophys Acta 643: 663–668 [DOI] [PubMed] [Google Scholar]
- Zeuthen T, Meinild A-K, Loo DDF, Wright EM, Klaerke DA (2001) Isotonic transport by the Na+-glucose cotransporter SGLT1 from humans and rabbit. J Physiol 531: 631–644 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeuthen T, Zeuthen E (2002) Mobility of ions, sugar, and water in the cytoplasm of Xenopus oocytes expressing Na+-coupled sugar transporters (SGLT1). J Physiol (Lond) 542: 71–87 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang R, Logee K, Verkman A (1990) Expression of mRNA coding for kidney and red cell water channels in Xenopus oocytes. J Biol Chem 265: 15375–15378 [PubMed] [Google Scholar]
- Zhang RB, Verkman AS (1991) Water and urea permeability properties of Xenopus oocytes: expression of mRNA from toad urinary bladder. Am J Physiol 260: C26–C34 [DOI] [PubMed] [Google Scholar]
- Zhang WH, Tyerman SD (1997) Effect of low oxygen concentration on the electrical properties of cortical cells of wheat roots. J Plant Physiol 150: 567–572 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.