Experimental and Theoretical Bases of Specific Affinity, a Cytoarchitecture-Based Formulation of Nutrient Collection Proposed To Supercede the Michaelis-Menten Paradigm of Microbial Kinetics

Abstract

A theory for solute uptake by whole cells was derived with a focus on the ability of oligobacteria to sequester nutrients. It provided a general relationship that was used to obtain the kinetic constants for in situ marine populations in the presence of naturally occurring substrates. In situ affinities of 0.9 to 400 liters g of cells⁻¹ h⁻¹ found were up to 10³ times smaller than those from a “Marinobacter arcticus ” isolate, but springtime values were greatly increased by warming. Affinities of the isolate for usual polar substrates but not for hydrocarbons were diminished by ionophores. A kinetic curve or Monod plot was constructed from the best available data for cytoarchitectural components of the isolate by using the theory together with concepts and calculations from first principles. The order of effect of these components on specific affinity was membrane potential > cytoplasmic enzyme concentration > cytoplasmic enzyme affinity > permease concentration > area of the permease site > translation coefficient > porin concentration. Component balance was influential as well; a small increase in cytoplasmic enzyme concentration gave a large increase in the effect of permease concentration. The effect of permease concentration on specific affinity was large, while the effect on K_m was small. These results are in contrast to the Michaelis-Menten theory as applied by Monod that has uptake kinetics dependent on the quality of the permease molecules, with K_m as an independent measure of affinity. Calculations demonstrated that most oligobacteria in the environment must use multiple substrates simultaneously to attain sufficient energy and material for growth, a requirement consistent with communities largely comprising few species.

The rate of nutrient transport into microorganisms is typically described by using the equations of Monod (30), formulations that are based on measurements of in vitro enzyme solutions and the theory described by Michaelis and Menten (29). Affinity for solute is usually taken as the Michaelis constant (K_m), the concentration of substrate at half the maximal rate of uptake, and taken as an inherent property of both the population (42) and its permeases (36). However, the variation of 10¹⁰ in K_m values was too great to be attributed to differences in proteins of common function and appears simply to reflect the concentration of proteins involved in substrate acquisition, metabolism, and biosynthesis. This concept was reinforced by equations that reflected the uptake rates from the number of permease molecules, the time required for each permease to translocate a molecule of substrate (6), and internal pool concentrations generated at the resulting dynamic steady-state equilibrium (5). Specific affinity for substrate S (a_S), a second-order rate constant for substrate sequestering that scales with nutrient acquisition power independently of the maximal rate (37), could thus be related to cytoarchitectural composition, including permease abundance and properties. The purpose of this communication is to develop a relationship between the concentration-limited rate of nutrient transport and organism cytoarchitecture based on available theory, in situ and laboratory kinetic data, and derived concepts. These tools are used to describe the concentration-dependent nutrient flux into an isolate of “Marinobacter arcticus” from the content of various proteins and pools specified, in an attempt to understand the metabolic strategies of organisms that substantially maintain the nutrient chemistry of aquatic environments.

MATERIALS AND METHODS

In situ measurements.

Seawater samples were collected from either near the mouth of Resurrection Bay, Alaska, during an incoming tide or 10 km out into the Gulf of Alaska, all at a 10-m depth. Processing took place aboard the R/V Alpha Helix. Samples were sieved through 2.5-μm-pore-size filters to remove phytoplankton when it was abundant, amended with radiolabeled substrate, and incubated at ambient temperatures. Uptake rates were calculated from four or five measurements of particle radioactivity retained on 0.08-μm-pore-size filters from six 100-ml subsamples containing radiolabeled substrate at known concentrations over 2 to 12 h in random order to minimize systematic error. Activity was measured on shipboard, and incubation times were adjusted to achieve the incorporation of about 100 dpm in the low-activity samples. Pyrolyzed prerinsed glassware was used throughout. Uptake was calculated from the ratio of filtered radioactivity to total radioactivity. Specific activities of radiolabeled substrates were calculated from known dilutions with unlabeled substrate and included a mixture of nine major amino acids (all at the highest specific activity available; ICN Pharmaceuticals, Inc.). Specific affinities (a_S) were calculated from the incorporation rate of the labeled substrate as given by the radioactivity and specific activity of cell material retained on filters (v_R) and cell yield (Y) by using the equation

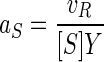(1)

where [S] is the concentration of substrate S. (The derivation appears as equations 1 to 4 at the URL http://www.ims.uaf.edu/fcm-kinetics/kinetics-derivations.pdf) For abbreviations and symbol definitions, see Table 1, and for dimensional analyses see reference 6. Bacterial biomass (X) was calculated from light scatter data by flow cytometry and the conversion factor of 5.5 g (wet weight)/g (dry weight) (10). Uptake rates per unit biomass (v) were obtained from apparent rates (v_a) by correcting added substrate concentrations ([S_a]) for in situ or naturally occurring amino acid concentrations ([S_n]) using high performance liquid chromatography (21) data and a material balance according to the equation

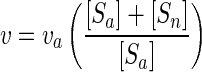(2)

Rates were typically linear over time, with r² values of 0.95 to 0.99. However, numerous replicates in parallel gave values that varied by as much as 20%, and variation was greatest when activity was low. Thus, while the measurements are taken as a best available reflection of absolute rates, r² values overstate precision, and values here are insufficient to address the precise shape of kinetic curves. A similar large disparity was previously noted for phosphate kinetics and was minimized by reducing culture disturbance during sampling (26). This topic will be further addressed in combination with freshwater kinetics.

TABLE 1.

Nomenclature

Term	Definition	Examples of value(s) used
Å	Avogadro's number	6.02 × 1023 molecules/mol
a	ac, affinity of metabolic enzyme for cytoplasmic substrate; aS, affinity of organism for substrate (v/[S] at ambient [S] and associated saturation); a°S, base or maximal specific affinity assuming hyperbolic kinetics; aSmax, maximal value of the affinity for nonhyperbolic kinetics	ac = 5 liters g of cells−1 h−1 from Vm/Km, where Km = 10−3 M and Vm = 5 mg of S g of cells−1 h−1
D	Molecular diffusion constant for [S]	9 × 10−6 cm2/s for alanine
[E]	Concentration of cytoplasmic enzymes	Defined by Vm and kcat for the conversion of cytoplasmic alanine to cell material
ɛ	Effectiveness factor	Change in kinetic parameter/change in cytoarchitectural parameter
i	A particular S among n total	Near 1 μg/liter for many aquatic substrates
k	Rate constant for reaction steps (odd, forward; even, back); kcat, catalytic constant; kind, induction constant for increased metabolic capacity with the concentration of ambient substrate	kcat = 86 mol of substrate transformed mol of protein−1 s−1 (20); kind = 60 liters g of cells−1 h−1 gives a threshold concentration of 2 μg liter−1
K	Ka (affinity constant), [S] at a°S/2; Keq, equilibrium constant; Kind, induction or stimulation constant of added substrate; Km, (Michaelis constant), [S] at Vm/2; KΔΨ, membrane potential constant; KΣS, multisubstrate stimulation constant, concentration for half maximal increase; KHS, proton-substrate cooperativity constant	Ka, = 4 μg of S liter−1 for alanine; Km, = 890 mg of [Sc]/liter for alanine; KΔΨ (value of ΔΨ at [S]) = 5 μg liter−1 in Hill equation with n = 2
L	Translation coefficient from flux to concentration of cytoplasmic substrate	2.5 g of cells • h/liter to give [Sc] in mg/liter
M	Molecular weight	89 Da for alanine
μ	Specific rate of growth	8.5 × 10−4 h−1 for in situ limitation by leucine
N	Number of molecules of a particular permease; Na, number of Δψ-activated molecules	Molecules cell−1, 480 from a 60,000-molecular-weight protein (43) when 1% of the membrane protein mass is the permease in question and cell membrane comprises 1% of the dry cell mass
n	Hill constant for positive cooperativity	Dimensionless; n = 2 from cooperativity between protons and S
Δψ	Chemical potential of ions that can be involved in permease activity for solute transport	Maximal value, 150 mV (22)
ρ	Organism density	1.03 g of cell material cm−3 (39)
Q10	Factor change in rate with a change in temperature of 10°C	Dimensionless; 2.8
Rm	Resistence of outer membrane to molecular diffusion of substrate as ameliorated by porins	2 × 10−3 times the expected rate in the absence of resistance to porins (28)
r	Radius; rx, radius of a spherical cell; rs, effective radius of an active site	rx, 0.4 × 10−4 cm; rs, 3 × 10−8 cm
[S]	Concn of a particular substrate such as alanine; [Sa], concn of added substrate; [Sc], concn of cytoplasmic substrate; [Sn], concn of natural or background substrate; [SP], concn of periplasmic substrate	[S] = 0 to 1 × 10−5 g of alanine liter−1 in kinetic curves for whole cells
v	Rate of S uptake by a cell population with biomass X; vR, rate of uptake of labeled Sa retained in the presence of Sn at the prevailing yield (Y); va, apparent rate of labeled substrate uptake in the presence of Sn	g of substrate g of cells−1 h−1
V	Maximal rate for a reaction step (odd, forward; even, back); Vm, maximal net rate	Vm = 5 mg of S g of cells−1 (wet weight) h−1 from initial uptake experiments
X	Biomass	g of cells (wet weight) liter−1
Y	Cell yield	g of cells produced/g of substrate consumed

Laboratory measurements.

“Marinobacter arcticus,” a 0.3-μm³ 3.8-Mb gram-negative marine isolate (12) was cultivated as previously described (38). Briefly, the isolate, was grown in artificial seawater amended with a 5-g/liter amino acid mixture and incubated on a shaker table at 22°C. For short-term uptake rates, populations of 400 to 900 mg/liter were harvested by centrifugation at 14,000 × g, resuspended by vortex mixer, washed twice with basal medium, diluted to a Coulter Counter wet biomass of 0.6 to 0.9 mg/liter computed from cell volume and a density of 1.04 g/cm³, incubated for 1 h to deplete substrate reserves, and amended with radiolabeled substrate in 6 ml of amino acid-free basal medium. Uptake was measured by collecting cells on 0.2-μm-pore-size Nuclepore filters arranged in a manifold over 4 to 6 min. Uptake rates over 50 min were measured using populations of 1 to 5 mg/liter collected on filters. Respired ¹⁴CO₂ was collected by a trap of phenethylamine scintillation cocktail following purification by a train of H₂SO₄ and Tenax traps at −70°C (14).

Metabolic inhibitors included 10 μM carbonyl m-chlorophenylhydrazone (CCCP), 10 μM dicyclohexylcarbodiimide, and 20 μM monensin.

Kinetics for whole cells.

Heterotrophic bacterial activity in aquatic systems depends on the rate at which organisms are able to accumulate organic solutes. This rate is the product of specific affinity and substrate concentration. Where several substrates are commonly used simultaneously, the total rate of uptake (v) is given by the sum of the n individual rates according to the concentration and associated rate constant or specific affinity of each substrate, i.e.,

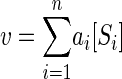(3)

where i is a particular substrate and specific affinity is the ratio of rate to concentration (v/[S]) at any specified [S]. Where each of the n substrates (S_i) is accumulated at a rate (v_i) according to hyperbolic or saturation kinetics, the contribution of the rate of one substrate to v is given by the equation (9)

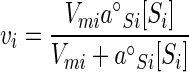(4)

This is the relationship described by Monod written in terms of the specific affinity (a°_Si), initial slope or maximal value of the slope of the rate versus concentration curve, and maximal velocity (V_mi), the apparent upper limit of the transport rate. So written, this formulation separates processes of substrate collection and enzyme saturation to provide for the independent assignment of each. It also specifies the half-saturating concentrations for substrate collection (K_a) according to the equation K_a = V_m/a°_S. Since V_m often increases with [S], K_a is related to the maximal value of this rate constant (a°_S) to focus on nutrient collection. For hyperbolic kinetics, K_a equals K_m. Since both K_a and K_m depend on transport capacity, neither term, unlike a°_S, adequately compares organismal kinetics in the absence of biomass-specific V_m data (7).

Background substrate.

Values for a°_Si and K_ai are of interest in the environment because they help anticipate the ambient concentrations of nutrients at which kinetic control is achieved, reflect the cytoarchitectural composition of the microflora, and suggest a cytoarchitecture that is distinct from that of most laboratory cultures (11, 39). However, values remain elusive because most aquatic dissolved organics remain unquantified. To address this difficulty, water samples are often amended with radiolabeled substrates as tracers of nutrient flux (44). Still, rates can remain indeterminate because added substrate increasingly dilutes the naturally occurring substrate as the small ambient concentrations are approached or exceeded. This result gives the appearance of hyperbolic saturation kinetics, but the background substrate decreases the apparent values of both the specific affinity and the associated saturation constant, K_a (8). Absent isotope effect, when both added and incorporated radiolabeled substrates are equally diluted by the S_n, the specific affinity is given by the ratio v_a/[S_a] (equations 6 to 11 at http://www.ims.uaf.edu/fcm-kinetics/kinetics-derivations.pdf). Then, assuming hyperbolic kinetics, where a_S equals V_m/K_a, equation 4 linearized to affinity plot form becomes

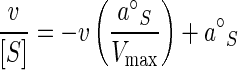(5)

where a°_S, the base value of the specific affinity, is given by the v/[S] intercept (hence the term affinity plot), the v intercept gives the maximal rate, and the slope is −1/K_a (equations 22 to 24 at http://www.ims.uaf.edu/fcm-kinetics/kinetics-derivations.pdf). Additional substrates that may be cotransported again add equally to both v and [S], so that the a°_S intercept obtained was taken as the correct specific affinity, assuming that the kinetics were hyperbolic and that saturation and artifactual insults to the sample were insignificant.

Cytoarchitectural model.

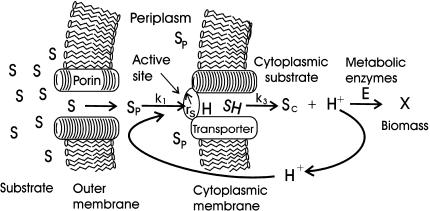
The diagram used for nutrient flow into a transthreptic (surface-feeding) cell is shown in Fig. 1. . Periplasmic concentrations are reduced to a value that depends on the porin concentration in the outer membrane, the rate of diffusion through the membrane, and the rate of removal to the cytoplasm. These periplasmic concentrations specify the molecular collision rate with transporters having a specified density distribution within the inner cell membrane. The transport rate is controlled by collision success and affected by the transporter occupancy with substrate, availability of energizing protons, and effective radius of the active site. Resulting substrate concentrations in the cytoplasmic pool concentration [S_c] reflect this transport rate together with metabolism and other losses. Metabolism is done by the enzyme sequence surrogate (E) having a net specific affinity, catalytic constant, and molecular abundance that specify flow from the cytoplasmic pool to cell material (with a biomass of X).

FIG. 1.

Cytoarchitectural model of nutrient kinetics. Ambient nutrient S diffuses through a porin to periplasmic concentration ([S_P]), where it combines with a proton-empowered permease having an active-site radius of r_s. Transport produces a [S_c] that generates both a proton potential and a concentration-driving force that facilitates substrate flow through an enzyme sequence (E) to produce cell material (X).

Computational techniques.

Formulations describing nutrient flow through the nutrient sequestering process were solved in sequence. The substrate concentration for each step was calculated from the kinetics and concentrations associated with the preceding step as described below. The metabolic sequence was taken as at a unique set of steady states for each external [S]. Kinetic curves shown give only the final flux, i.e., the rate of formation of cell material, for each value of external [S].

RESULTS

In situ kinetics.

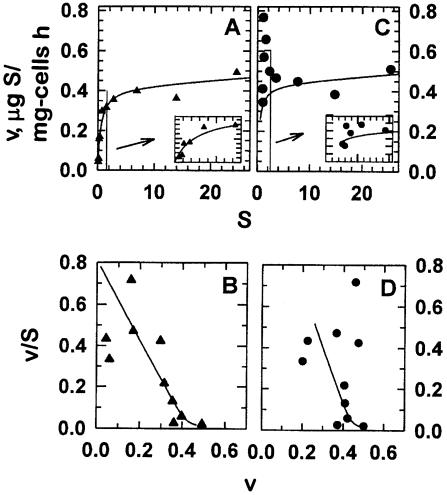
Since in situ kinetic constants are difficult to evaluate but essential to the description of oligobacterial activity, we explored their values. Figure 2. shows Monod (Fig. 2A and C) and Scatchard or affinity plots (Fig. 2B and D) of amino acid uptake rates in the Gulf of Alaska. Plots using specific activities corrected for analytically determined leucine are shown in Fig. 2C and D. The hyperbolic nature of the Monod plot in Fig. 2A was ascribed to systematic dilution of added leucine by naturally occurring leucine because the apparent first-order region (when [S] was near 0) was eliminated by the correction of specific activities with analytical leucine. This artifact was confirmed with computer simulations (8). However, as formulated above, both incorporated and added substrate were equally diluted by S_n, so that the ratio of v_a to [S_a] remained unaffected. This result was supported by the similar data patterns in Fig. 2B and D, where values for v/[S] were similar whether corrected for background substrate or not. The agreement, allowing for usual variation in uptake rate measurements among separate samples from a common source of low-activity populations, established that the specific affinity was near maximal, i.e., near the base value (a°_S), at 0.4 liters mg of cells⁻¹ h⁻¹ in the small S_a aliquots of this in situ sample and without imposing an unjustified extrapolation. Specific affinities shown were therefore taken to be reflective of the best available method for determining amino acid accumulation rates and therefore reflective of the ability of low-substrate-adapted bacteria to sequester substrate during steady-state growth at the chosen site.

FIG. 2.

Monod (A and C) and affinity (B and D) plots of leucine uptake from Resurrection Bay, Alaska, seawater at a 10-m depth in Thumb Cove during June. Panels A and B show apparent rates from the specific activity of the [³H]leucine added; panels C and D show rates corrected for an ambient leucine concentration ([S_n]) of 0.85 μg/liter. Insets expand data near the origin. Both rates were corrected for an incorporation-to-uptake ratio of cell yields (Y) using a value of 0.45 from ¹⁴CO₂ liberation and ³H incorporation rate data. When fit to the equation v = V_m[S]/(K_a + [S]) + k_ind[S], the parameters for observed (A and B) and S_n-corrected (C and D) rates (V_m) were 0.42 and 0.50 μg of leucine mg of cells⁻¹ h⁻¹, and k_ind was 0.002 and 0.003 liters g of cells⁻¹ h⁻¹. The affinity constants (K_a) obtained from [S] at the half-maximal value of v/[S] and the rate v (the affinity plot abscissa) were 1.5 and 1.9 μg/liter from panels B and D, respectively.

Additional kinetic data (Table 2) show that mean values for specific affinity were small throughout the year, compared to those of laboratory cultures, but much larger during summer than winter. Looking for the active water necessary for autoradiographic determinations of substrate preferences, we sampled during a heavy spring bloom in the Gulf of Alaska associated with unusually warm 6°C El Niño waters in May 1998, but the smallness of the specific affinities was unexpected. Values for a_S were, however, increased within an hour by warming with an Arrhenius activation energy of 230 kJ/mol, consistent with recent reports (45). The large activation energy demonstrated ready capacity to achieve at least moderate values for specific affinity, capacity not yet realized by these springtime populations. According to the largest specific affinity from Table 2 and 2 cell yield of 2.5 g (wet weight) of cells/g of amino acids used from radioactive substrate incorporated versus that liberated as carbon dioxide (data not shown) by organisms that are 18% dry weight (39), the growth rate with a single substrate was small by the equation μ = a_S[S]Y = (400 liters/g of cells⁻¹ h⁻¹) (8.5 × 10⁻⁷ g of leucine liter⁻¹) (2.5 g of cells/g of substrate used) = 8.5 × 10⁻⁴/h, for a very long doubling time of 34 days.

TABLE 2.

Specific affinities for bacterioplankton in Gulf of Alaska coastal water

Date (1998)	Substratea	Biomass (μg/liter)	Affinity (liters g of cells−1 h−1)
3 May	Leucine	400	6.0 (110b)
22 July	Leucine	340	400
10 August	Leucine	270	50-140c
27 August	Amino acid mix	74	48
19 October	Leucine	140	30
13 December	Amino acid mix	27	4.3
13 December	Glucose	27	0.9
14 December	Glutamate	25	4.4
14 December	Leucine	25	7.4

^aUntil 19 October, substrates were at trace levels. On 13 December and thereafter, levels were at 1 μg/liter and below. All substrates were radiolabeled.

^bAffinity after the temperature was raised from 6 to 15°C over 2 h.

^cRange over 24 h.

Uptake kinetics by oligobacterial isolates.

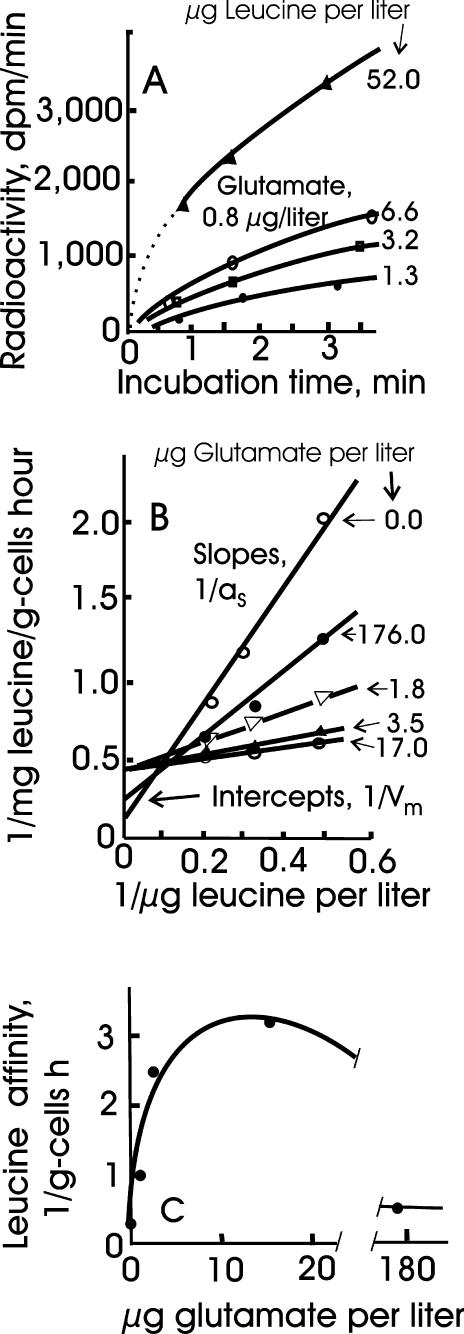
A membrane potential (Δψ) provides the energy used in concentrative symport of many substrates (34). That specific affinities for the uptake of amino acids by bacterioplankton ranged from small in summer to nearly negligible in winter (Table 2) brought into question the ability of the organisms to effect sufficient nutrient flux for a sustained membrane potential during periods of low productivity, given the costs of ion leakage (41), substrate leakage (37), molecule repair, and other endogenous processes (32). Glutamate collection at low temperature by “M. arcticus,” when it is washed and starved, was stimulated threefold by the addition of a mixture of amino acids (Table 3), as reflected by the larger specific affinity. This result was consistent with a loss of membrane potential during the starvation step that was sufficiently replenished to enable scavenging of small concentrations of glutamate due to increased permease activity. Transport capacity, according to V_m values, was greatly stimulated as well. Further, glutamate addition stimulated the transport of leucine (Fig. 3) according to the kinetic parameters shown in Table 3. Rates were about the same as those from active waters (Fig. 2) but unsustainable, as demonstrated by the concave-down curvature of the graphed values (Fig. 3A). Substrate use was insufficient to remove a significant portion of the leucine which would otherwise cause such curvature as well. The incubation time was too short and the curvature was in the opposite direction for the effect to be one of protein induction. The immediate stimulation of leucine uptake by glutamate, with a multisubstrate stimulation constant (K_ΣS) of 3 μg/liter (Fig. 3B), agreed with a general finding of stimulation by auxiliary substrates in very-low-carbon and low-energy systems (25, 27). Larger additions of glutamate inhibited leucine transport, suggesting an indirect effect on the steady-state flux. Such uncompetitive inhibition is consistent with small maximal velocities that result from rate restriction at a point different from that of the initial reaction (35). This result was found for in situ rates as well; increasing substrate concentrations from 1 to 8 μg/liter caused no increase in the December Gulf of Alaska rates shown in Table 2 (data not shown), and the saturation constant for alanine in “M. arcticus” (Table 3) was only 0.011 mg of alanine/liter (calculated by the equation K_m = V_m/a°_S = 3.4 mg of alanine/g of cells • h [288 liters g of cells⁻¹ h⁻¹]⁻¹).

TABLE 3.

Effect of cosubstrates and inhibitors on amino acid uptake by Marinobacter arcticus

Substrate	Unamended culture		Amended culture
	Specific affinity (liters g of cells−1 h−1)	Vm (mg of S g of cells−1 h−1)	Unique addition	Specific affinity (liters g of cells−1 h− 1)	Vm (mg of S g of cells−1 h−1)
Glutamate	373	0.58	Acid mixa	1,150	17
Leucine	270	7	Glutamateb	3,100	2.2
Leucine	5,900	NDe	CCCP	27	ND
Toluene	290	0.52	CCCPc	260	ND
Alanined	288	3.4	CCCP	0.0	ND

^aKinetic constants were calculated from the sum of nine added amino acids.

^bK_a = 3.0 μg/liter; K_ΣS = 3 μg of glutamate/liter for glutamate stimulation of leucine uptake by glutamate with maximal increase in leucine specific affinity at 17 μg of glutamate/liter (Fig. 3).

^cForty-five percent of the toluene uptake into cell material and CO₂ was diverted to acid-nonvolatile products.

^dAffinity was measured at 3.9 μg of alanine/liter; the sodium motive force affecting ionophore monensin had no effect.

^eND, not determined.

FIG. 3.

Uptake of [¹⁴C]leucine by “M. arcticus” in the presence of glutamate. (A) Time course showing effect of leucine concentration on incorporated radioactivity. (B) Lineweaver-Burk plot based on the equation 1/v = a°_S(1/[S]) + 1/V_m, with leucine as the variable substrate and glutamate as the auxiliary substrate. Rates were taken from the best line through the data points independent of the origin. (C) Dependence of the specific affinity for leucine on the concentration of glutamate.

Leucine transport may be particularly facile among amino acids owing to both difficulty in biosynthesis (40) and lipophilicity; the highest specific affinity measured is for uptake of the nonpolar substrate toluene (6). Transport of more-polar amino acids by “M. arcticus ” was inhibited by protonophores, such as CCCP (Table 3), but not by the sodium ionophore monensin. The absence of inhibition by monensin, and a low 10% inhibition by the proton ejecting F₁F₀ ATPase-specific dicyclohexylcarbodiimide (data not shown), was consistent with organism dependence on the chemical potential of a proton gradient. Toluene transport was little inhibited by CCCP, and there was only minor inhibition of toluene metabolism as measured by carbon dioxide production. This hydrophilic substrate is thought to be accumulated by vectorial partitioning (4), which eliminates the energy requirement for a transmembrane concentration gradient of substrate (38). These data indicated that polar substrate transport rather than metabolism was inhibited by the protonophores. While the data supported the absence of a chemical potential requirement for the accumulation of nonpolar substrates, they were also consistent with a need for a proton potential to transport polar substrates in the observed system, whether directly by symport or indirectly through ATP or other energy-transducing reserves (33).

To further test whether membrane potential is a significant variable in polar solute transport by oligobacteria, alanine transport by washed but not starved cultures of “M. arcticus” was examined in the presence of protonophores (Table 3). The specific affinity was low compared to that of usual enrichment culture isolates, and maximal rates of growth were still small compared with those expected. However, values were adequate for large mixtures of substrates due to the increased value of [S] in the calculation a_S = v/[S]. The addition of CCCP completely abolished transport, again consistent with a membrane potential requirement for transport.

Cytoarchitecture and nutrient flux.

Available data were integrated into a formulation of concentration-dependent nutrient flux based on the cellular composition and catalytic activity of specified components beginning with membrane potential.

Proton gradient.

Growth in low-nutrient systems requires concentrative transport, as described above, so that the many metabolic enzymes can operate efficiently. This “uphill” transport involves osmotic work. The increase in specific affinity with auxiliary substrate addition, the inhibition of the transport of polar substrates but not the transport of lipophilic substrates by protonophores, and the absence of sensitivity to sodium-specific ionophores indicated that the energy for transport was from substrate metabolism as mediated by protons with a membrane potential (Δψ). Membrane potential was formulated to increase in proportion to [S] at substrate concentrations near the affinity constant K_a by setting the membrane potential constant (K_Δψ) at 5 μg of alanine liter⁻¹. Values were from sodium-ion-dependent transport of threonine (16), with a maximal potential (Δψ_max) of 150 mV, as often observed in microbial systems (22). Binding of substrate to the permease complex must precede the active transport step. Completion of this step is also required to generate the energy necessary for solute accumulation so that the process is autocatalytic until permease-saturating potential is achieved. Transport was therefore formulated with positive cooperativity (23) between protons produced from the metabolism of transported substrate and available substrate that can be metabolized. The two substrates, H⁺ and S, were accommodated with an n of 2 in the sigmoidal relationship for proton gradient by the equation

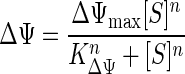(6)

Permease concentration.

The dependence of substrate-permease collision success on membrane potential was formulated from positive cooperativity theory because permeases both require and produce the membrane potential needed to activate the transporters (equation 7).

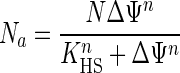(7)

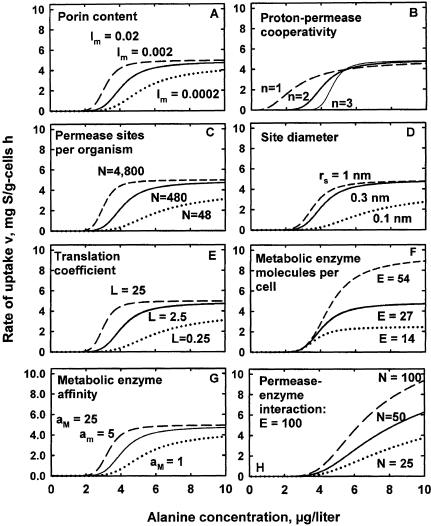
N_a is the number of active transporters among N total permeases. It is specified by the proton-substrate interaction constant K_HSⁿ, where n is the number of interacting species (H⁺ + N = 2), and by N at large values of Δψ, where all permeases are activated. N was set at 2,400 molecules/cell from “Cycloclasticus oligotrophus” dimensions, kinetics, collision frequency calculations, and the dioxygenase concentration associated with toluene uptake (13) by assuming transport by vectorial partitioning (4). K_HS was set at 20 to specify that half the permease molecules were active at the observed affinity constant for alanine transport of 1.4 μg/liter in substrate-deficient “M. arcticus.” n was set at 2 to reflect the interactive effect of electrical gradient and transporter concentration. The linear increase in N_a with [S] is then preceded by a region without energized permeases at low values of [S] and truncated at a maximal value of N_a (equal to N) when the value of [S] is large (Fig. 4B).

FIG. 4.

Kinetics of alanine uptake by “M. arcticus” to 10 μg/liter. The solid line in each panel shows the base calculation. The effects of changing each parameter by the amounts indicated are shown by the broken lines.

Transport.

A theoretical value for a°_S can be obtained from the per-site rate constant for bimolecular collisions (k, equal to 4Dr_s/1,000, where D is a molecular diffusion constant and r_s is the effective radius of an active site) according to the number of permeases, the diffusion constant, the areas of the permease sites, and substrate mass (2). Dividing by cell mass and using a spherical cell of density ρ (1.03 g of cell material cm⁻³) gives an equation for determining a°_S of

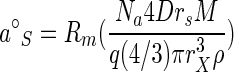(8)

so that the rate of transport from the exterior at values of [S] large enough to maintain membrane potential but too small to saturate the permeases remains calculable by the equation v = a°_S[S]. The resistance of the outer cell membrane to substrate diffusion into the periplasmic space (R_m) depends on the concentration and properties of porins in the outer membrane. It is taken as the ratio of observed rate in the presence of an outer membrane to the expected rate in the absence of an outer membrane, as discussed below.

Some of the permeases will be occupied and unable to collect substrate. Where saturation is hyperbolic, the rate decreases with [S] according to equation 4, and the specific affinity is equal to v/[S] at any [S]. For membrane potential-sufficient cells, the maximal rate of transport (V_m) is given by the rate or velocity (v) asymptote of the v-versus-[S] Monod plot. Neglecting interactive enhancement, the value of V_m depends on the number of molecules of the S_i-compatible transporters per gram of cell material and the associated catalytic constant (k_cat). Again converting from cell volume to mass, the maximal rate of transport is given by the equation

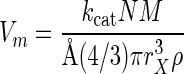(9)

Calculations included a small additional term (k_ind[S]) to describe the effects of large substrate concentrations that induce additional proteins usually observed in systems over a range of steady states (37). This induction results in additional capacity that increases the value of V_m. Substituting equations 8 and 9 for affinity and maximal velocity in equation 4 gives the concentration-dependent rate of transport in a way that depends on the number of transporters together with their catalytic properties and bioenergetic requirements but neglects the downstream constraints considered below.

Cytoplasmic substrate.

Unregulated cytoplasmic concentrations of substrate ([S_c]) depend on the rates of import and use of the substrates. When use is proportional to concentration, i.e., saturation is insignificant, [S_c] becomes a function of active transport rate alone. Since transport through a porous medium depends on the pressure gradient across the medium (Darcy's law) (31), and pressure at constant volume is proportional to concentration (Boyle's law), [S_c] is a linear function of transport rate over the relevant values of [S], as documented below. The value of [S_c] is then equal to Lv, where L is the translation coefficient (equations 5 and 33 to 37 at http://www.ims.uaf.edu/fcm-kinetics/kinetics-derivations.pdf) and v is the rate of transport. Support for the relationship together with the value of L was taken from measurements of external [S] in phosphate-limited continuously cultivated Rhodotorula rubra samples. There, the concentrations of phosphate in the metabolic pools were proportional to the rates at which phosphate was transported (37). Absolute concentrations were taken from glutamic acid in the pools of arginine-limited continuous cultures of marine isolate 198, which ranged from 5 to 16 mg/liter with growth rate (24). The present calculations assumed that transport capacity and restriction to substrate flow by the outer membrane in “M. arcticus” were similar to those in the two pelagic isolates.

Rate of metabolism.

The use of accumulated substrate in the metabolic pools depends on the concentration and catalytic properties of the associated catabolic and anabolic enzymes operating in their intracellular environment beginning with S_c. For Michaelian or hyperbolic kinetics, the rate is given by the maximal velocity and specific affinity associated with the cytoplasmic enzyme assemblage according to the equation

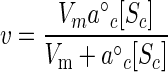(10)

where a°_c is the affinity of metabolic enzyme for cytoplasmic substrate. Maximal velocity was taken from observed rates and converted to numbers of enzyme molecules per cell by using the value for cell mass used above and typical k_cat values for metabolic enzymes in the cytoplasm (1). The specific affinity for this enzyme assemblage was calculated from typical values for K_m and the relationship a°_c = V_m/K_m for hyperbolic kinetics (9, 15).

Solutions of the rate equation.

The kinetics specified by equations 6 through 10 together with the cytoarchitectural and kinetic properties specified in Table 1 are shown as the Monod plot given by the central curve in Fig. 4A. The size of the threshold in substrate concentration was affected by the extent of cooperativity in the absence of an auxiliary energy source in this experimental single-substrate environment as specified by n in equation 6. The change in curve shape and properties effected by a 10-fold increase or reduction in porin concentration is shown as well. Shown in Fig. 4B through G are changes in this concentration-velocity relationship at steady state by the following additional cytoarchitectural parameters: permease cooperativity, permease concentration, size of the active site, value for the translation coefficient, concentration of metabolic enzymes in the cytoplasm, and mean kinetic properties of cytoplasmic enzymes.

Quantitative effects.

The effect of changing cytoarchitectural parameters by specific amounts can be seen by comparing the broken lines in Fig. 4 with the central curves. These were used to obtain the change in kinetic parameters with respect to the change in cytoarchitecture (Table 4).

TABLE 4.

Proportional change in kinetic parameters for whole cells by quantitative change in isolated cytoarchitectural properties calculated as an effectiveness factor^a

Structural property	Specific affinity	Maximal velocity	Michaelis constant	Substrate threshold
Porin concentration	2	0	−3	−2
Hill constant	−100	0	17	66
Permease concentrationb	2	0	−3	−3
Permease concentrationc	25	7	−3	−3
Site diameter	11	0	−33	−19
Translation coefficient	2	2	−2	−3
Enzyme concentration	31	100	−20	−3
Enzyme affinity	15	0	−10	−2.6

^aAll table values are percent changes in effectiveness factor, ɛ.

^bVariation in permease-dependent transport rates, where rates are further constrained by a limited concentration of cytoplasmic enzymes (Fig. 4C).

^cRates with additional cytoplasmic enzymes (Fig. 4H).

The porin concentration influences nutrient flux into the periplasm and depends on the species examined. A change from a ratio of 0.002 between measured flux and that calculated for an organism without outer membrane resistance (28) had only a moderate effect on the specific affinity (v/[S]) at particular concentrations of substrate (Fig. 4A and Table 4). The maximal affinity was little affected by porin concentration because rates were metabolism-limited, as discussed below.

Changes in substrate-proton cooperativity with departure from the theoretical Hill constant value of 2 had a major effect on both specific affinity and the size of the substrate threshold, i.e., the substrate concentration necessary for endergonic transport (Fig. 4B; Table 4). Maximal velocity remained constant (Fig. 4C) as rates became dependent on substrate processing time (1/k_cat for cytoplasmic enzyme concentration, [E]) at the larger concentrations of substrate.

Permease concentration affected the specific affinity only marginally (Fig. 4B) because flux was again largely controlled by enzyme concentration. Specific affinity increased with the active-site area below a diameter of 6 Å (r_s = 0.3 nm). Larger permease sites shifted limitation to enzyme concentration, and there was no effect on the value of V_m (Fig. 4D) due to flux control by the limited amounts of E.

An increase in the translation coefficient effected an increase in specific affinity, particularly with an L of <2.5 g of cells • h liter⁻¹ (Fig. 4E), due to the increase in the internal substrate concentration-driving force with increases in the intercellular concentration of substrate. At higher concentrations, rates again were truncated due to limitation by the metabolic enzyme concentration of the cell.

Additional metabolic enzymes had a moderate effect on specific affinity because of an improved balance between permease and enzyme concentrations over the base calculation when [S] was large, but there was a greater effect on maximal rate as the constraint to substrate flow was reduced (Fig. 4F). When the affinity of the enzymes changed, so did that of the organisms, while V_m, set by the number of enzyme molecules and their catalytic constants, was unaffected (Fig. 4G). In Fig. 4H, the effect of permease concentration on specific affinity is shown together with a 3.7-fold increase in enzyme concentration over that in Fig. 4F. This effect alleviated much of the constraint of enzyme concentration on specific affinity, so that changes in permease concentration became 12-fold more effective in generating nutrient flux.

DISCUSSION

Specific affinity measurements.

The comparison of specific affinities obtained from affinity plots of in situ data showed that these data (calculated by v/[S]) remained only lightly affected by background substrate, as predicted by the theory. Thus, improved values for the specific affinities of both natural and defined populations can be obtained from rates of radiolabeled substrate uptake where nutrient concentrations are too low for accurate measurement. In the absence of a substrate threshold, the effect of background substrate on the specific affinity becomes significant only when the total concentration is near or above the affinity constant (K_a). For example, if [S_n] is 1 μg/liter and K_a is only 2 μg/liter, the computed underestimate in the base specific affinity (a°_S) is 45%. However, if K_m is taken as a measure of organism affinity, the error may be many powers of 10 because the variation in V_m is so large (6). When other energy-yielding substrates are present and used by the population but do not compete with S_a, the effect will be to decrease the size of the substrate threshold. The shape of the kinetic curve cannot be determined when the concentration of background substrate approaches that of S_a, because S_n is particularly effective in reducing apparent flux at small values of [S] (cf. Fig. 2A and C). Because the hyperbolic nature of the curve (Fig. 2A) is due to isotope dilution rather than saturation, scatter in the data due to a systematical change in apparent [S] is also minimized, which could lead to false confidence in the kinetics. In situ specific affinities (Table 2) were similar to those of the isolate measured under conditions of starvation. The absolute flux of a particular nutrient, as calculated from specific affinity, can be determined only to the accuracy that the concentration of substrate and population size or mass are known. Ambient concentrations for many substrates have been measured, such as the amino acids here, and flow cytometry reduces error in biomass measurements (39). In situ microbial activities toward a particular substrate can therefore now be accurately compared from apparent specific affinity data. Also, reasonable estimates of nutrient fluxes can be obtained for substrates that can be chemically measured from the specific affinity of the population.

Interpretations of kinetic data.

The calculated doubling time for “M. arcticus” of 34 days with a single substrate at 1 μg/liter together with stimulation by auxiliary substrate, and inhibition of transport at only 17 μg/liter, was consistent with low-capacity systems that necessarily saturate at very small concentrations. Thus, the number of substrates (n) in equation 3 must be large; 34 substrates at 1 μg/liter are needed for a doubling time of 1 day. This large number of necessary substrates is consistent with the appearance of more than 100 transport-associated genes in many species of aquatic bacteria (http://www.tigr.org/∼ipaulsen/). Upper estimates of in situ growth rates exceed 1 per day (33), while many substrate concentrations are likely to be smaller than 1 μg/liter. This fact suggests that even more different utilizable substrates are present and used by most bacteria. That the affinity constant (K_a) is small can be due either to the ability to collect, transport, and process substrate so that V_m is approached at low [S] or to low downstream enzyme capacity so that product inhibition limits the effective catalytic constants (cf. Fig. 4C and F). The increase in both specific affinity and maximal velocity by auxiliary substrates in the laboratory system (Fig. 3) was attributed to an increase in the membrane potential produced by the multiple substrate-adapted species. That natural populations were not stimulated by cosubstrate addition is consistent with a strong barrier to active transport from both the low temperature and the low membrane potential associated with small concentrations of substrate. Saturating concentrations for both the oligobacterial isolate and in situ activity were exceedingly small compared to most determinations (6), with K_a values in the microgram per liter range. Specific affinities were very small as well. In contrast to kinetic data from common laboratory cultures (4, 6), these data show limited ability to transport substrate at growth-sustaining rates, particularly when a single substrate is supplied as the sole carbon and energy source. Further, a membrane potential is needed, and the need may remain unsatisfied when there are few substrates at small concentrations unless an energy reserve has been stored and sustained. Preferences for tested substrates, according to a°_S, were rather similar. This similarity was also evident for the mixture, interpreted as use through separate pathways, with the overall value remaining constant due to division by the sum of the concentrations of the number of substrates supplied. The net flux should increase in accord with equation 3, consistent with a necessity for most environmental bacteria to use numerous substrates simultaneously. This need for multiple substrates decreases the number of available metabolic niches, leading to the single-digit number of dominant species in common samples according to terminal restriction fragment length polymorphism (unpublished data).

Flux calculations.

Use of a sequential solution for calculating flux through a multistep process was rationalized by the apparent unidirectional nature of several steps in the metabolic sequence, such as intermediate and macromolecule biosynthesis, steps that are either strongly exergonic or mechanistically irreversible due to physical partitioning. Effects of such irreversible steps on the associated rate constants may be anticipated from the Haldane relationship (19) that relates the equilibrium constant of a reaction (K_eq) to its kinetic constants. Simplifying, the active transport step to a bimolecular reaction between periplasmic substrate and permease molecules with instantaneous movement to the cytoplasm gives the following equation (Fig. 1): K_eq = V₁K_c/V₂K_m, where V₁ and V₂ are the maximal forward and reverse rates and K_m and K_c are the associated Michaelis constants. Converting the kinetic constants to rate constants (35) and setting the collection rate of cytoplasmic protons by permease in the alkaline electronegative environment at 0 to render the rate irreversible give the following equation (equations 49 to 51 at http://www.ims.uaf.edu/fcm-kinetics/kinetics-derivations.pdf): K_eq ≈ k₁^2k₃, where k₁ and k₃ are rate constants for reaction steps. This equation formalizes the situation where, for irreversible sequences, flow depends on the concentrations and catalytic constants of the enzymes together with the concentrations of the reactants. Resistances of downstream concentrations to forward rates were taken as integral components of the associated kinetic constants because hyperbolic kinetics remain hyperbolic even in the presence of product inhibition (35). The magnitude of the back reaction rate constant k₂ is essential to the calculation of K_m from the Michaelis-Menten equation, but it does not necessarily mean that there is formation of substrates and uncombined permease from the ternary complex. Hyperbolic kinetics may also be derived from the residence time needed to move substrate through the permease, time during which an additional substrate molecule may not be accepted (6; equations 12 to 30 at http://www.ims.uaf.edu/fcm-kinetics/kinetics-derivations.pdf). Thus, the absence of a back reaction does not preclude saturation kinetics.

Cytoarchitectural effects.

Among the major calculated influences was the effect of the Hill constant on the substrate threshold and thus the specific affinity at small concentrations of substrate. Because of the interactive effects of transporter concentration and membrane potential, this effect should be diminished by auxiliary chemical potential-generating substrates. In low-activity systems, such as winter seawater or starved cultures, the magnitude of the Hill constant should be important, since small values can increase the concentrations of substrate necessary for transport.

A unique kinetic theory for microbial growth, as opposed to one borrowed from enzyme kinetics, was further supported by temperature studies. Large in situ activation energies for transport of 211 kJ/mol during the onset of the spring bloom in the Gulf of Alaska and 70 to 90 kJ/mol during various seasons in Harding Lake, Alaska, were observed (unpublished data). These activation energies were well above the 40 kJ/mol usually observed for either isolated enzymes (19) or nutrient-sufficient microbial growth (18). Acceleration of each step due to warming increases pool concentrations for the succeeding enzymatic reaction, which is temperature accelerated, and increases the temperature effect according to the number of steps in the sequence. And all steps in a metabolic sequence, according to the flux control theorem (3), participate in rate control so that control is spread among fast as well as slow steps (17). During nutrient limitation, the temperature effect can be large because several steps can influence the rate, while the change of the flux associated with a single component, such as porin concentration, is small; a doubling of the porin concentration resulted in only a 1.6% change in the organism's specific affinity (Table 4).

The concentration of transporters in bacteria and other cells remains unmeasured; however, estimates from electrophoretically separated inducible membrane proteins gave specific affinities near values reported here, assuming specified resistance from the outer membrane and more from steps downstream. This result supports the formulations of molecular collision frequency incorporated into equation 8. The formulations describe far faster movement of dissolved substrates to active sites than does traditional Fickian diffusion. This effect had been observed much earlier from the weight loss of leaves due to the diffusion of water through stomata (A. Koch, personal communication) and is also expressed as the cage effect that enhances calculated rates of enzymatic reaction (1). The calculation of maximal velocity from equation 9 also depends on the effective residence time of the substrate in the permease (the reciprocal of k_cat) together with permease concentration. Catalytic constants for permeases are unknown, so values for complex enzymatic reactions were used. That different cellular components are required to specify specific affinity and maximal velocity (equations 8 and 9) demonstrates that effectors of flux control in a multistep pathway need not be the same step at different concentrations. This is an advantage of equation 4 for describing nutrient flux. For example, the effect of variable permease concentration among species on specific affinity or the effect of additional substrate on maximal velocity through induction of additional enzyme is easily accommodated, as demonstrated in Fig. 4.

The diameter of the active site was estimated from the diameter of the substrate molecule; however, the effective value remains unknown. The diameter had a major effect on specific affinity, but its effectiveness was truncated here on the large side by the limitation of flux due to a small downstream [E] (Fig. 4D).

Transport involves the collision of protons as well as substrate with the active site, increasing the order of reaction from second to third, depending on the residence time of protons in the permease following collision. While low (10⁻⁸ M) external concentrations of H⁺ might be expected to reduce the specific affinity, a fourfold increase in a_S was observed with an increase in pH (data not shown). Neglecting pH effects on the permease, proton limitation alone should have produced the opposite effect.

The [S_c] at steady state depends on saturable input from transport (equation 4), product inhibition of transport that was taken as an inherent component of the kinetic constants in the forward direction, and losses due to S_c metabolism and leakage. Given the likely limited permease concentration for any specific substrate ([S_i]) together with the environmentally small values of [S_i], the resulting transport rate will be low. Therefore, translation to pool concentration is likely to result in much smaller concentrations than are measured in commonly cultivated organisms. When the resulting pool concentrations are less than K_m for the enzymes, L should strongly affect the whole-cell affinity, as the calculations showed (Fig. 4E). The use of cytoplasmic substrate was formulated with Michaelis-Menten kinetics and recast to specify the unsaturated and saturated rates with independent parameters (equation 10). The cytoplasmic enzymes were assumed to be a solution of enzymes whose catalytic rates could be approximated by hyperbolic kinetics, i.e., without threshold.

Component balance.

The relative effectiveness (ε) of model components on the specific affinity in this metabolic enzyme-restricted system (Table 4) in decreasing order was as follows: membrane potential > cytoplasmic enzyme concentration > metabolic enzyme affinity > permease concentration > effective permease site diameter > translation coefficient > porin concentration. Decreasing the permease concentration 10-fold to 50 molecules per cell allowed permease content to become dominant in affinity control (cf. Fig. 4H and C). Oligobacteria have special need for biochemical conservation, due to limited resources. Increasing the permease concentration is of greater advantage than increasing the enzyme concentration because the sequences of unique enzymes are longer in the catabolic and anabolic pathways than in the transport process, and their dilute cytoarchitecture (39) is thus explained. The permease concentration was particularly effective in reducing the substrate threshold when metabolic enzymes were restricted because of the additional membrane potential generated for transport. The substrate threshold became far less significant in the absence of a requirement for cooperativity with a cosubstrate, such as hydrogen ions, and the kinetic curve became more nearly hyperbolic. This large threshold resulted from model conditions of limitation by a single substrate. It will decrease in proportion to additional utilizable substrates at microgram per liter concentrations. But the thresholds may be significant even in multisubstrate systems, such as those of dormant cold-seawater organisms during warming (Table 1). There, the large activation energies associated with small specific affinities observed were consistent with sufficient transport being generated by warming both to form a membrane potential and to load pools that contain temperature-affected enzymes. The membrane potential necessary to prime active transport may also be generated in mixotrophic organisms by the proteorhodopsin system, as indicated by a wide distribution of the related genes (16a).

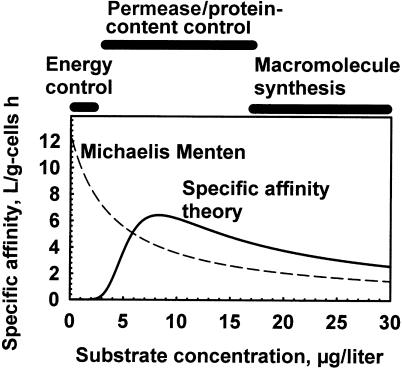
The specific affinity for the model organism over a range of concentrations (Fig. 5) was calculated from the central distribution of cytoarchitectural components of Fig. 4 as a function of nutrient concentration to suggest changes in factors controlling the rates. Energy levels dominate at low substrate concentrations because nutrient accumulation is thermodynamically impossible without energy. This result suggests that the delay in bacterial activity during springtime could be due to the need of a membrane potential for substrate transport together with the need for transported substrate to generate a membrane potential. At intermediate concentrations of substrate, both the permease concentration and the enzyme concentration of the cell help to control organism affinity. At high nutrient concentrations, unspecified and uninvestigated macromolecular processes, such as cell wall formation, may limit net rates of growth at values characteristic of the species. Alternatively, the dominant small-genome forms may lack efflux pumps that prevent inhibition by common substrates such as amino acids at high concentrations (I. Paulsen, personal communication). Specific affinities calculated from Monod kinetics are also shown to demonstrate limitations imposed by linking the kinetics of a heterogeneous system to a single step. Thus, one might use the Michaelis constant to suggest concentrations where substrates become limiting but not to indicate the ability of a culture, population, or permease to transport and collect that substrate, as indicated by the disparity between specific affinity and K_m values in Table 4. Instead, the data argue that the ability to sequester substrates can be reported with the least ambiguity by a specific affinity. Transport capacity is then independently expressed by maximal velocity, since the two kinetic constants can be controlled at different points in the transport-metabolism sequence.

FIG. 5.

Effect of substrate concentration on specific affinity (solid line) calculated from equations 6 through 1010 showing processes postulated to effect major control. Affinities as v/[S] from the Michaelis-Menten hyperbola are shown as a broken line.

A result of the kinetics calculated for Fig. 4 was that, with the assumptions and data specified, they matched measurements from whole cells reasonably well (cf. Table 2 and 3 and Fig. 4) without adjustments. This agreement was by chance due to the large uncertainty in kinetic and cytoarchitectural parameters, such as those of equation 8. However, the effect of any enzyme-catalyzed step on the flux through a metabolic sequence decreases inversely with the number of steps in that sequence (3), so error in formulating any single step in minimized. This may be seen here, where the change in specific affinity was only 1.6% of the change in porin concentration (Table 4). Yet the data demonstrated satisfactory model function, considering the good agreement between theoretical and measured rates.

These data and calculations demonstrate that bacterial proteomes are mosaics whose cross-species differences affect nutrient utilization through variation in protein concentration as well as identity. Minimal size increases the optimal surface-to-mass ratio and decreases susceptibility to predation, but small size limits both the abundance of each protein and the number of different biochemical components as set in turn by space requirements for the encoding DNA. The result is a distribution of major cytoarchitectural components that is hypothesized to approach those specified.